Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.
Practice Set 5.1 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals
Question 1.
Diagonals of a parallelogram WXYZ intersect each other at point O. If ∠XYZ∠ = 135°, then measure of ∠XWZ and ∠YZW? If l(OY) = 5 cm, then l(WY) = ?
Solution:
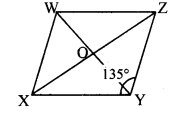
i. ∠XYZ = 135°
□WXYZ is a parallelogram.
∠XWZ = ∠XYZ
∴ ∠XWZ = 135° …..(i)
ii. ∠YZW + ∠XYZ = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠YZW + 135°= 180° [From (i)]
∴ ∠YZW = 180°- 135°
∴ ∠YZW = 45°
iii. l(OY) = 5 cm [Given]
l(OY) = \(\frac { 1 }{ 2 }\) l(WY) [Diagonals of a parallelogram bisect each other]
∴ l(WY) = 2 x l(OY)
= 2 x 5
∴ l(WY) = 10 cm
∴∠XWZ = 135°, ∠YZW = 45°, l(WY) = 10 cm
Question 2.
In a parallelogram ABCD, if ∠A = (3x + 12)°, ∠B = (2x – 32)°, then liptl the value of x and the measures of ∠C and ∠D.
Solution:
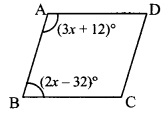
□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary],
∴ (3x + 12)° + (2x-32)° = 180°
∴ 3x + 12 + 2x – 32 = 180
∴ 5x – 20 = 180
∴ 5x= 180 + 20
∴ 5x = 200
∴ x = \(\frac { 200 }{ 5 }\)
∴ x = 40
ii. ∠A = (3x + 12)°
= [3(40) + 12]°
=(120 +12)°= 132°
∠B = (2x – 32)°
= [2(40) – 32]°
= (80 – 32)° = 48°
∴ ∠C = ∠A = 132°
∠D = ∠B = 48° [Opposite angles of a parallelogram]
∴ The value of x is 40, and the measures of ∠C and ∠D are 132° and 48° respectively.
Question 3.
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
Solution:
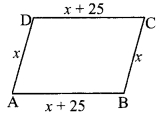
i. Let □ABCD be the parallelogram and the length of AD be x cm.
One side is greater than the other by 25 cm.
∴ AB = x + 25 cm
AD = BC = x cm
AB = DC = (x + 25) cm [Opposite angles of a parallelogram]
ii. Perimeter of □ABCD = 150 cm [Given]
∴ AB + BC + DC + AD = 150
∴ (x + 25) +x + (x + 25) + x – 150
∴ 4x + 50 = 150
∴ 4x = 150 – 50
∴ 4x = 100
∴ x = \(\frac { 100 }{ 4 }\)
∴ x = 25
iii. AD = BC = x = 25 cm
AB = DC = x + 25 = 25 + 25 = 50 cm
∴ The lengths of the sides of the parallelogram are 25 cm, 50 cm, 25 cm and 50 cm.
Question 4.
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
Solution:
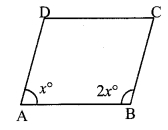
i. Let □ABCD be the parallelogram.
The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.
Let the common multiple be x.
∴ ∠A = x° and ∠B = 2x°
∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ x + 2x = 180
∴ 3x = 180
∴ x = \(\frac { 180 }{ 3 }\)
∴ x = 60
ii. ∠A = x° = 60°
∠B = 2x° = 2 x 60° = 120°
∠A = ∠C = 60°
∠B = ∠D= 120° [Opposite angles of a parallelogram]
∴ The measures of the angles of the parallelogram are 60°, 120°, 60° and 120°.
Question 5.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO show that □ABCD is a rhombus.
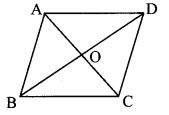
Given: AO = 5, BO = 12 and AB = 13.
To prove: □ABCD is a rhombus.
Solition:
Proof:
AO = 5, BO = 12, AB = 13 [Given]
AO2 + BO2 = 52 + 122
= 25 + 144
∴ AO2 + BO2 = 169 …..(i)
AB2 = 132 = 169 ….(ii)
∴ AB2 = AO2 + BO2 [From (i) and (ii)]
∴ ∆AOB is a right-angled triangle. [Converse of Pythagoras theorem]
∴ ∠AOB = 90°
∴ seg AC ⊥ seg BD …..(iii) [A-O-C]
∴ In parallelogram ABCD,
∴ seg AC ⊥ seg BD [From (iii)]
∴ □ABCD is a rhombus. [A parallelogram is a rhombus perpendicular to each other]
Question 6.
In the adjoining figure, □PQRS and □ABCR are two parallelograms. If ∠P = 110°, then find the measures of all the angles of □ABCR.
Solution:
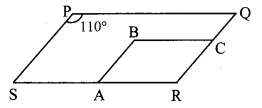
□PQRS is a parallelogram. [Given]
∴ ∠R = ∠P [Opposite angles of a parallelogram]
∴ ∠R = 110° …..(iii)
□ABCR is a parallelogram. [Given]
∴ ∠A + ∠R= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠A+ 110°= 180° [From (i)]
∴ ∠A= 180°- 110°
∴ ∠A = 70°
∴ ∠C = ∠A = 70°
∴ ∠B = ∠R= 110° [Opposite angles of a parallelogram]
∴ ∠A = 70°, ∠B = 110°,
∴ ∠C = 70°, ∠R = 110°
Question 7.
In the adjoining figure, □ABCD is a parallelogram. Point E is on the ray AB such that BE = AB, then prove that line ED bisects seg BC at point F.
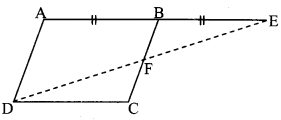
Given: □ABCD is a parallelogram.
BE = AB
To prove: Line ED bisects seg BC at point F i.e. FC = FB
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ seg AB ≅ seg DC …….(i) [Opposite angles of a parallelogram]
seg AB ≅ seg BE ……..(ii) [Given]
seg DC ≅ seg BE ……..(iii) [From (i) and (ii)]
side DC || side AB [Opposite sides of a parallelogram]
i.e. side DC || seg AE and seg DE is their transversal. [A-B-E]
∴ ∠CDE ≅ ∠AED
∴ ∠CDF ≅ ∠BEF …..(iv) [D-F-E, A-B-E]
In ∆DFC and ∆EFB,
seg DC = seg EB [From (iii)]
∠CDF ≅ ∠BEF [From (iv)]
∠DFC ≅ ∠EFB [Vertically opposite angles]
∴ ∆DFC ≅ ∆EFB [SAA test]
∴ FC ≅ FB [c.s.c.t]
∴ Line ED bisects seg BC at point F.
Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Practice Set 5.1 Intext Questions and Activities
Question 1.
Write the following pairs considering □ABCD. (Textbook pg. no 57)
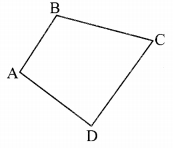
Pairs of adjacent sides:
i. AB, AD
ii. AD, DC
iii. DC, BC
iv. BC, AB
Pairs of adjacent angles:
i. ∠A, ∠B
ii. ∠C, ∠D
iii. ∠B, ∠C
iv. ∠D, ∠A
Pairs of opposite sides:
i. AB, DC
ii. AD, BC
Pairs of opposite angles:
i. ∠A, ∠C
ii. ∠B, ∠D
Question 2.
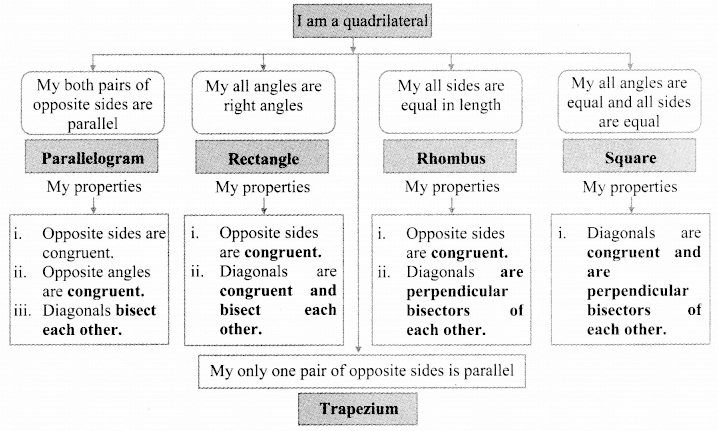
Complete the following tree diagram. (Textbook pg. no 57)
Question 3.
In the above theorem, to prove ∠DAB ≅ ∠BCD, is any change in the construction needed? If so, how will you write the proof making the change? (Textbook pg. no. 60)
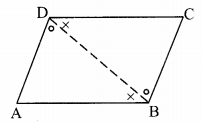
Solution:
Yes
Construction: Draw diagonal BD.
Proof:
side AB || side CD and diagonal BD is their transversal. [Given]
∴ ∠ABD ≅ ∠CDB ……..(i) [Alternate angles]
side BC || side AD and diagonal BD is their transversal. [Given]
∴ ∠ADB ≅ ∠CBD ……..(ii) [Alternate angles]
In ∆DAB and ∆BCD,
∠ABD ≅ ∠CDB [From (i)]
seg BD ≅ seg DB [Common side]
∴ ∠ADB ≅ ∠CBD [From (ii)]
∴ ∆DAB ≅ ∆BCD [ASA test]
∴ ∠DAB ≅ ∠BCD [c.a.c.t.]
Note: ∠DAB s ∠BCD can be proved using the same construction as in the above theorem.
∠BAC ≅ ∠DCA …..(i)
∠DAC ≅ ∠BCA ……(ii)
∴ ∠BAC + ∠DAC ≅ ∠DCA + ∠BCA [Adding (i) and (ii)]
∴ ∠DAB ≅ ∠BCD [Angle addition property]