Prasanna

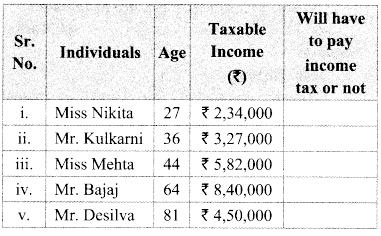
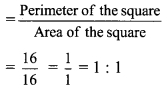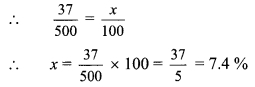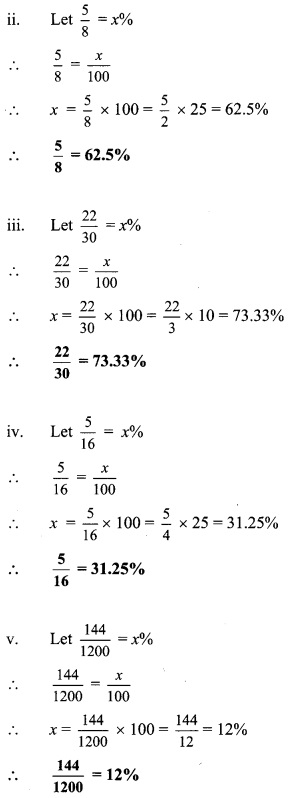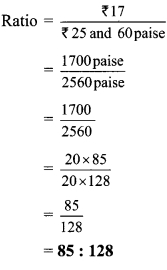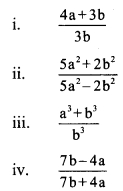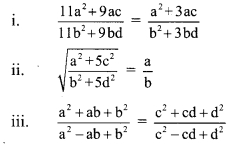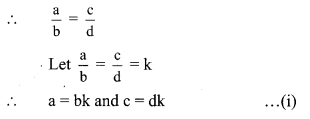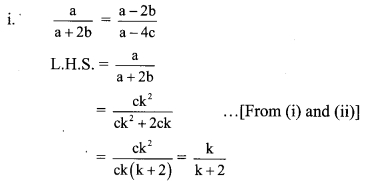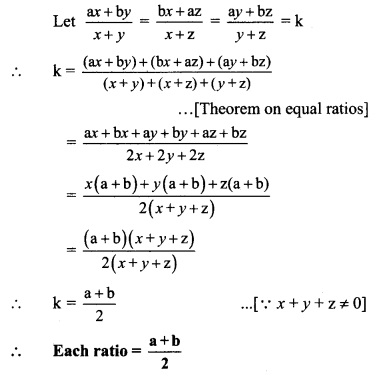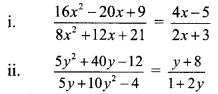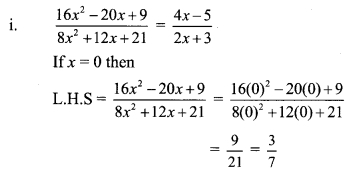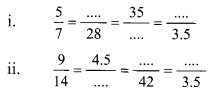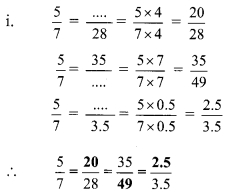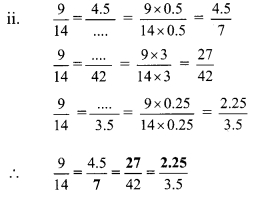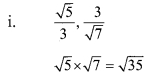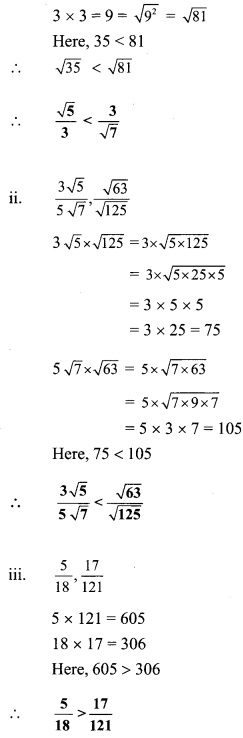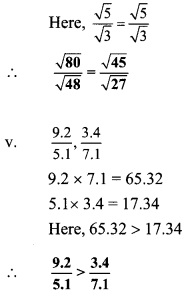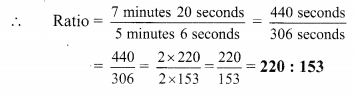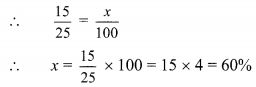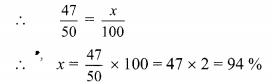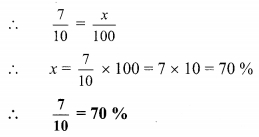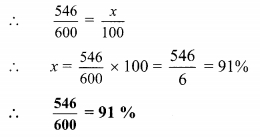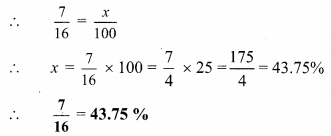Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

Practice Set 5.2 Algebra 9th Std Maths Part 1 Answers Chapter 5 Linear Equations in Two Variables

Question 1.
In an envelope there are some ₹5 notes and some ₹10 notes. Total amount of these notes together is ₹350. Number of ₹5 notes are less by 10 than twice the number of ₹10 notes. Then find the number of ₹5 and ₹10 notes.
Solution:
Let the number of ₹5 notes be ‘x’ and the number of ₹10 notes be ‘y’
Total amount of x notes of ₹ 5 = ₹ 5x
Total amount ofy notes of ₹ 10 = ₹ 10y
∴ Total amount = 5x + 10y
According to the first condition,
total amount of the notes together is ₹350.
∴ 5x + 10y = 350 …(i)
According to the second condition,
Number of ₹ 5 notes are less by 10 than twice the number of ₹ 10 notes.
∴ x = 2y – 10
∴ x – 2y = -10 …..(ii)
Multiplying equation (ii) by 5,
5x – 10y = -50 …(iii)
Adding equations (i) and (iii),
5x + 10y =350
+ 5x – 10y = -50
10x =300
∴ x = \(\frac { 300 }{ 10 }\)
∴ x = 30
Substituting x = 30 in equation (ii),
x – 2y = -10
30 – 2y = -10
∴ 30 + 10 = 2y
∴ 40 = 2y
∴ y = \(\frac { 40 }{ 2 }\)
∴ y = 20
There are 30 notes of ₹ 5 and 20 notes of ₹ 10 in the envelope.

Question 2.
The denominator of a fraction is 1 less than twice its numerator. If 1 is added to numerator and denominator respectively, the ratio of numerator to denominator is 3 : 5. Find the fraction.
Solution:
Let the numerator of the fraction be ‘x’ and its denominator be ‘y’.
Then, the required fraction is \(\frac { x }{ y }\) .
According to the first condition,
the denominator is 1 less than twice its numerator.
∴ y = 2x – 1
∴ 2x – y = 1 …(i)
According to the second condition,
if 1 is added to the numerator and the denominator, the ratio of numerator to denominator is 3 : 5.
∴ \(\frac { x+1 }{ y+1 }\) = \(\frac { 3 }{ 5 }\)
∴ y + 1 = 5
∴ 5(x + 1) = 3(y + 1)
∴ 5x + 5 = 3y + 3
∴ 5x – 3y = 3 – 5
∴ 5x – 3y = -2 ……(ii)
Multiplying equation (i) by 3,
6x – 3y = 3 …(iii)
Subtracting equation (ii) from (iii),

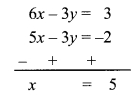
Substituting x = 5 in equation (i),
∴ 2x – y = 1
∴ 2(5) – y = 1
∴ 10 – y = 1
∴ y= 10 – 1 =9
∴ The required fraction is \(\frac { 5 }{ 9 }\).

Question 3.
The sum of ages of Priyanka and Deepika is 34 years. Priyanka is elder to Deepika by 6 years. Then find their present ages.
Solution:
Let the present age of Priyanka be ‘x’ years and that of Deepika be ‘y’ years.
According to the first condition,
Priyanka’s age + Deepika’s age = 34 years
∴ x + y = 34 …(i)
According to the second condition,
Priyanka is elder to Deepika by 6 years.
∴ x =y + 6
∴ x – y = 6 …..(ii)
Adding equations (i) and (ii),

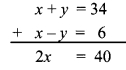
∴ x = 20
Substituting x = 20 in equation (i),
x + y = 34
∴ 20 + y = 34
∴ y = 34 -20= 14
∴ The present age of Priyanka is 20 years and that of Deepika is 14 years.

Question 4.
The total number of lions and peacocks in a certain zoo is 50. The total number of their legs is 140. Then find the number of lions and peacocks in the zoo.
Solution:
Let the number of lions in the zoo be ‘x’ and the number of peacocks be ‘y’.
According to the first condition,
the total number of lions and peacocks is 50.
∴ x + y = 50 …(i)
Lion has 4 legs and Peacock has 2 legs.
According to the second condition,
the total number of their legs is 140.
∴ 4x + 2y = 140
Dividing both sides by 2,
2x + y = 70 …(ii)
Subtracting equation (i) from (ii),

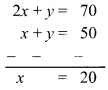
Substituting x = 20 in equation (i),
x + y = 50
∴ 20 + y = 50
∴ y = 50 – 20 = 30
∴ The number of lions and peacocks in the zoo are 20 and 30 respectively.

Question 5.
Sanjay gets fixed monthly income. Every year there is a certain increment in his salary. After 4 years, his monthly salary was ₹ 4500 and after 10 years his monthly salary became ₹ 5400, then find his original salary and yearly increment.
Solution:
Let the original salary of Sanjay be ₹ ‘x’ and his yearly increment be ₹ ‘y’.
According to the first condition, after 4 years his monthly salary was ₹ 4500
∴ x + 4y = 4500 …..(i)
According to the second condition,
after 10 years his monthly salary became ₹ 5400
∴ x + 10y = 5400 …(ii)
Subtracting equation (i) from (ii),

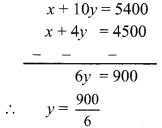
∴ y = 150
Substituting y = 150 in equation (i),
x + 4y = 4500
∴ x +4(150) = 4500
∴ x + 600 = 4500
∴ x = 4500 – 600 = 3900
∴ The original salary of Sanjay is ₹ 3900 and his yearly increment is ₹ 150.

Question 6.
The price of 3 chairs and 2 tables is ₹ 4500 and price of 5 chairs and 3 tables is ₹ 7000, then find the price of 2 chairs and 2 tables.
Solution:
Let the price of one chair be ₹ ‘x’ and that of one table be ₹ ‘y’.
According to the first condition,
the price of 3 chairs and 2 tables is ₹ 4500
∴ 3x + 2y = 4500 ,..(i)
According to the second condition, the price of 5 chairs and 3 tables is ? 7000
∴ 5x + 3y = 7000 …(ii)
Multiplying equation (i) by 3,
9x + 6y = 13500 ….(iii)
Multiplying equation (ii) by 2,
10x + 6y= 14000 …(iv)
Subtracting equation (iii) from (iv),

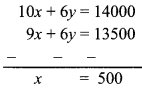
Substituting x = 500 in equation (i),
3x + 2y = 4500
∴ 3(500)+ 2y = 4500
∴ 1500 + 2y = 4500
∴ 2y = 4500- 1500
∴ 2y = 3000
∴ y = \(\frac { 3000 }{ 2 }\)
∴ y = 1500
∴ Price of 2 chairs and 2 tables = 2x + 2y
= 2(500)+ 2(1500)
= 1000 + 3000 = ₹ 4000
∴ The price of 2 chairs and 2 tables is ₹ 4000.

Question 7.
The sum of the digits in a two-digit number is 9. The number obtained by interchanging the digits exceeds the original number by 27. Find the two-digit number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the first condition.
the sum of the digits in a two-digit number is 9
x + y = 9 …(i)
According to the second condition,
the number obtained by interchanging the digits exceeds the original number by 27
∴ 10x + y = 10y + x + 27
∴ 10x – x + y – 10y = 27
∴ 9x – 9y = 27
Dividing both sides by 9,
x – y = 3 …….(ii)
Adding equations (i) and (ii),

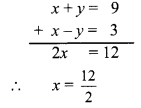
∴ x = 6
Substituting x = 6 in equation (i),
x + y = 9
∴ 6 + y = 9
∴ y = 9 – 6 = 3
∴ Original number = 10y + x = 10(3)+ 6
= 30 + 6 = 36
∴ The two digit number is 36.

Question 8.
In ∆ABC, the measure of ∠A is equal to the sum of the measures of ∠B and ∠C. Also the ratio of measures of ∠B and ∠C is 4 : 5. Then find the measures of angles of the triangle.
Solution:
Let the measure of ∠B be ‘x°’ and that of ∠C be ‘y°’.
According to the first condition,
m∠A = m∠B + m∠C
∴ m∠A = x° + y°
In AABC,
m∠A + m∠B + m∠C = 180° …[Sum of the measures of the angles of a triangle is 180°]
∴ x + y + x + y = 180 ,
∴ 2x + 2y = 180
Dividing both sides by 2,
x + y = 90 …(i)
According to the second condition,
the ratio of the measures of ∠B and ∠C is 4 : 5.
∴ \(\frac { x }{ y }\) = \(\frac { 4 }{ 5 }\)
∴ 5x = 4y
∴ 5x – 4y = 0 …….(ii)
Multiplying equation (i) by 4,
4x + 4y = 360 …(iii)
Adding equations (ii) and (iii),

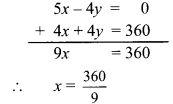
∴ x = 40
Substituting x = 40 in equation (i),
x + y = 90
∴ 40 + y = 90
∴ y = 90 – 40
∴ y = 50
∴ m∠A = x° + y° = 40° + 50° = 90°
∴ The measures of ∠A, ∠B and ∠C are 90°, 40°, and 50° respectively.

Question 9.
Divide a rope of length 560 cm into 2 parts such that twice the length of the smaller part is equal to \(\frac { 1 }{ 3 }\) of the larger part. Then find the length of the larger part.
Solution:
Let the length of the smaller part of the rope be ‘x’ cm and that of the larger part be ‘y’ cm.
According to the first condition,
total length of the rope is 560 cm.
∴ x + y = 560 …(i)
Twice the length of the smaller part = 2x
\(\frac { 1 }{ 3 }\)rd length of the larger part = \(\frac { 1 }{ 3 }\)y
According to the second condition,
2x = \(\frac { 1 }{ 3 }\) 3
∴ 6x = y
∴ 6x – y = 0 ……(ii)
Adding equations (i) and (ii),

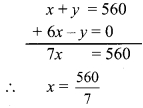
∴ x = 80
Substituting x = 80 in equation (ii),
6x – y = 0
∴ 6(80) – y = 0
∴ 480 – y = 0
∴ y = 480
∴ The length of the larger part of the rope is 480 cm.

Question 10.
In a competitive examination, there were 60 questions. The correct answer would carry 2 marks, and for incorrect answer 1 mark would be subtracted. Yashwant had attempted all the questions and he got total 90 marks. Then how many questions he got wrong?
Solution:
Let us suppose that Yashwant got ‘x’ questions right and ‘y’ questions wrong.
According to the first condition, total number of questions in the examination are 60.
∴ x + y = 60 …(i)
Yashwant got 2 marks for each correct answer and 1 mark was deducted for each wrong answer.
∴ He got 2x – y marks.
According to the second condition,
he got 90 marks.
2x – y = 90 … (ii)
Adding equations (i) and (ii),

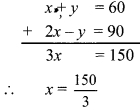
∴ x = 50
Substituting x = 50 in equation (i),
50 + y = 60
∴ y = 60 – 50 = 10
∴ Yashwant got 10 questions wrong.

Maharashtra Board Class 9 Maths Chapter 5 Linear Equations in Two Variables Practice Set 5.2 Intext Questions and Activities

Question 1.
The population of a certain town was 50,000. In a year, male population was increased by 5% and female population was increased by 3%. Now the population became 52020. Then what was the number of males and females in the previous year? (Textbook pg. no. 89)
Solution:
Step 1: Read the given word problem carefully and try to understand it.

Step 2: Make assumptions using two variables x and y.
Let the number of males in previous year be
‘x’ and the number of females be ‘y’.

Step 3: From the given information, form mathematical statements using the above variables.
According to the first condition,
the total population of town was 50,000.
∴ x + y = 50000 …(i)
Male population increased by 5%.
∴ Number of males = x + 5% of x , 5

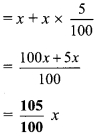
Female population increased by 3%.
∴ Number of females = y + 3% of y

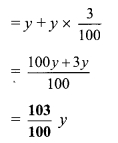
According to the second condition,
in a year population became 52020
∴ \(\frac{105}{100} x+\frac{103}{100} y=52020\)
∴ 105 x + 103 y = 5202000 …(ii)
Multiplying equation (i) by 103,
103 x + 103 y = 5150000 …(iii)

Step 4: Here, we use elimination method.
Subtracting equation (iii) from (ii),

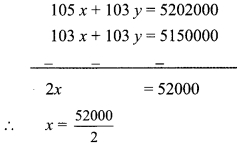
∴ x = 26000
Substituting x = 26000 in equation (i),
∴ 26000 + y = 50000
∴ y = 50000 – 26000
∴ y = 24000
∴ Number of males = x = 26000
∴ Number of females = y = 24000

Step 5: Write the answer.
The number of males and females in the previous year were 26,000 and 24,000 respectively.

Step 6: Verify your result using smart check.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.

Practice Set 6.2 Algebra 9th Std Maths Part 1 Answers Chapter 6 Financial Planning

Question 1.
Observe the table given below. Check and decide, whether the individuals have to pay income tax.

Solution:
i. Miss Nikita’s age = 27 years < 60 years
Miss Nikita’s income = ₹ 2,34,000
Miss Nikita’s income is below the basic
exemption limit of ₹ 2,50,000.
∴ Miss Nikita will not have to pay income tax.

ii. Mr. Kulkarni’s age 36 years < 60 years
Mr. Kulkarni’s income = ₹3,27,000
Mr. Kulkarni’s income is above the basic exemption Limit of ₹2,50,000.
∴ Mr. Kulkarni will have to pay income tax.

iii. Miss Mehta’s age = 44 years < 60 years Miss Mehta’s income = ₹5.82,000
Miss Mehta’s income is above the basic exemption limit of ₹2,50,000.
∴ Miss Mehta will have to pay income tax.

iv. Mr. Bajaj’s age = 64 years (Age 60 to 80 years)
Mr. Bajaj’s income = ₹8,40,000
Mr. Bajaj’s income is above the basic exemption Limit of ₹3,00,000.
∴ Mr. Bajaj will have to pay income tax.

v. Mr. Desilva’s age = 81 years > 80 years
Mr. Desilva’s income = ₹4,50,000
Mr. Desilva’s income is below the basic exemption limit of ₹ 5,00.000.
∴ Mr. Desilva will not have to pay income tax.

Question 2.
Mr. Kartarsingh (age 48 years) works in a private company. His monthly income after deduction of allowances is ₹ 42,000 and every month he contributes ₹ 3000 to GPF. He has also bought ₹ 15,000 worth of NSC (National Savings Certificate) and donated ₹ 12,000 to the PM’s Relief Fund. Compute his income tax.
Solution:
Mr. Kartarsingh’s monthly income = ₹ 42,000
Mr. Kartarsingh’s yearly income = 42,000 x 12 = ₹ 5,04,000

Mr. Kartarsingh’s investment
= GPF + NSC
= (3000 x 12)+ 15,000
= 36,000 + 15,000
= ₹ 51,000

Donation to PM’s relief fund = ₹ 12, 000
∴ Taxable income
= yearly income – (investment + donation)
= 5,04,000 – (51,000 + 12,000)
= 5,04,000 – 63,000 = ₹ 4,41,000
Mr. Kartarsingh income falls in the slab 2,50,001 to 5,00,000.
∴ Income tax = 5% of (Taxable income – 250000) = 5% of (4,41,000 – 2,50,000)
= \(\frac { 5 }{ 100 }\) x 1,91,000 100
= ₹ 9550
Education cess = 2% of income tax
= \(\frac { 2 }{ 100 }\) x 9550
= 191
Secondary and Higher Education cess = 1% of income tax
= \(\frac { 1 }{ 100 }\) x 9550 100
= 95.50
Total income tax = Income tax + Education cess + Secondary and higher education cess
= 9550 + 191 + 95.50
= ₹ 9836.50
∴ Mr. Kartarsingh’s income tax is ₹ 9836.50

Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Practice Set 6.2 Intext Questions and Activities

Question 1.
Use Table I given above and write the appropriate amount/figure in the boxes for the example given below. (Textbook pg. no. 102)
Mr. Mehta’s annual income is ₹4,50,000
i. If he does not have any savings by which he can claim deductions from his income, to which slab does his taxable income belong ? ______
ii, What is the amount on which he will have to pay income tax and at what percent rate? on ₹ _______
percentage _______
iii. On what amount will the cess be levied? _______
Answer:
1. ₹2,50,001 to ₹5,00,000
ii. 5% of (4,50,000 – 2,50,000)
i.e. 5% of ₹2,00,000
iii. income tax = 5% of 2,00,000
= \(\frac { 5 }{ 100 }\) x 2,00,000
= ₹10,000
∴ Education cess and Secondary and higher education cess will be levied on the income tax i.e., on ₹10,000.

Question 2.
Use table lito carry out the following activity.
Mr. Pandit is 75 years old. Last year his annual income was ₹ 13,25,000. How much is his taxable income? How much tax does he have to pay? (Textbook pg. no. 103)
Solution:
Mr. Pandit’s age = 75 years (Age 60 to 80 years)
Mr. Pandit’s income is more than 10,00,000.
According to the table,
Income tax = ₹ 1,10,000 + 30 % of (taxable income – 10,00,000)
Taxable income – 10,00,000 = 13,25,000 – 10,00,000 = 3,25,000
In addition, on ₹ 3,25,000 rupees he has to pay 30% income tax.
3,25,000 x \(\frac { 30 }{ 100 }\) = ₹ 97500
Therefore, his total income tax amounts to 1,10,000 + 97,500 ₹ 207500
Besides this, education cess willi be 2% of income tax 207500 x \(\frac { 2 }{ 100 }\) = ₹ 4150.
A secondary and higher education cess at 1% of income tax = 207500 x \(\frac { 1 }{ 100 }\) = ₹ 2075.
∴ Total income tax = Income tax + education cess + secondary and higher education cess
= 207500 + 4150 + 2075
= ₹2,13,725

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

Practice Set 5.1 Algebra 9th Std Maths Part 1 Answers Chapter 5 Linear Equations in Two Variables

Question 1.
By using variables x and y form any five linear equations in two variables.
Answer:
The general form of a linear equation in two variables x and y is ax + by + c = 0,
where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Five linear equations in two variables are as follows:
i. 3x + 4y – 12 = 0
ii. 3x – 4y + 12 = 0
iii. 5x + 5y – 6 = 0
iv. 7x + 12y – 11 = 0
v. x – y + 5 = 0

Question 2.
Write five solutions of the equation x + y = 1.
Answer:
i. x = 1, y = 6
ii. x = -1, y = 8
iii. x = 5, y = 2
iv. x = 0, y = 7
v. x = 10, y = -3

Question 3.
Solve the following sets of simultaneous equations.
i. x + y = 4 ; 2x – 5y = 1
ii. 2x + y = 5 ; 3x – y = 5
iii. 3x – 5y = 16; x – 3y= 8
iv. 2y – x = 0; 10x + 15y = 105
v. 2x + 3y + 4 = 0; x – 5y = 11
vi. 2x – 7y = 7; 3x + y = 22
Solution:
i. Substitution Method:
x + y = 4
∴ x = 4 – y …(i)
2x – 5y = 1 ……(ii)
Substituting x = 4 – y in equation (ii),
2(4 – y) – 5y = 1
∴ 8 – 2y – 5y = 1
∴ 8 – 7y = 1
∴ 8 – 1 = 7y
∴ 7 = 7y
∴ y = \(\frac { 7 }{ 7 }\)
∴ y = 1
Substituting y = 1 in equation (i),
x = 4 – 1 = 3
∴ (3,1) is the solution of the given equations.

Alternate method:
Elimination Method:
x + y = 4 …(i)
2x – 5y = 1 ……(ii)
Multiplying equation (i) by 5,
5x + 5y = 20 … (iii)
Adding equations (ii) and (iii),
2x – 5y = 1
+ 5x + 5y = 20
7 = 21
∴ x = \(\frac { 21 }{ 7 }\)
∴ x = 3
Substituting x = 3 in equation (i),
3 + y = 4
∴ y = 4 – 3 = 1
(3,1) is the solution of the given equations.

ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = \(\frac { 10 }{ 5 }\)
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.

iii. 3x – 5y = 16 …(i)
x – 3y = 8
∴x = 8 + 3y …..(ii)
Substituting x = 8 + 3y in equation (i),
3(8 + 3y) – 5y = 16
24 + 9y- 5y = 16
∴4y= 16 – 24
∴ 4y = -8
∴ y = \(\frac { -8 }{ 4 }\)
y = -2
Substituting y = -2 in equation (ii),
x = 8 + 3 (-2)
∴ x = 8 – 6 = 2
∴ (2, -2) is the solution of the given equations.

iv. 2y – x = 0
∴ x = 2y …(i)
10x + 15y = 105 …(ii)
Substituting x = 2y in equation (ii),
10(2y) + 15y = 105
∴ 20y + 15y = 105
∴ 35y = 105
∴ y = \(\frac { 105 }{ 35 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y
∴ x = 2(3) = 6
∴ (6, 3) is the solution of the given equations.

v. 2x + 3y + 4 = 0 …(i)
x – 5y = 11
∴x = 11 + 5y …(ii)
Substituting x = 11 + 5y in equation (i),
2(11 +5y) + 3y + 4 = 0
∴ 22 + 10y + 3y + 4 = 0
∴ 13y + 26 = 0
∴ 13y = -26
∴y = \(\frac { -26 }{ 13 }\)
∴ y = -2
Substituting y = -2 in equation (ii),
x = 11 + 5y
∴ x = 11 + 5(-2)
∴ x = 11 – 10 = 1
∴ (1, -2) is the solution of the given equations.

vi. 2x – 7y = 7 …(i)
3x + y = 22
∴ y = 22 – 3x ……(ii)
Substituting y = 22 – 3x in equation (i),
2x – 7(22 – 3x) = 7
∴ 2x – 154 + 21x = 7
∴ 23x = 7 + 154
∴ 23x = 161
∴ x = \(\frac { 161 }{ 23 }\)
∴ x = 7
Substituting x = 7 in equation (ii),
y = 22 – 3x
∴ y = 22 – 3(7)
∴ 7 = 22 -21= 1
∴ (7, 1) is the solution of the given equations.

Question 1.
Solve the following equations. (Textbook pg. no. 80)
i. m + 3 = 5
ii. 3y + 8 = 22
iii. \(\frac { x }{ 3 }\) = 2
iv. 2p = p + \(\frac { 4 }{ 9 }\)
Solution:
i. m + 3 = 5
m = 5 – 3
∴m = 2

ii. 3y + 8 = 22
∴ 3y = 22 – 8
∴ 3y = 14
∴ y = \(\frac { 14 }{ 9 }\)

iii. \(\frac { x }{ 3 }\) = 2
∴ x = 2 × 3
∴ x = 6

iv. 2p = p + \(\frac { 4 }{ 9 }\)
∴ 2p – p = \(\frac { 4 }{ 9 }\)
∴ p = \(\frac { 4 }{ 9 }\)

Question 2.
Which number should be added to 5 to obtain 14? (Textbook pg. no. 80)
Solution:
x + 5 = 14
∴ x = 14 – 5
x = 9
∴ 9 + 5 = 14

Question 3.
Which number should be subtracted from 8 to obtain 2? (Textbook pg. no. 80)
Solution:
8 – y = 2
∴ y = 8 – 2
∴ y = 6
∴ 8 – 6 = 2

Question 4.
x + y = 5 and 2x + 2y= 10 are two equations in two variables. Find live different solutions of x + y = 5, verify whether same solutions satisfy the equation 2x + 2y = 10 also. Observe both equations. Find the condition where two equations in two variables have all solutions in common. (Textbook pg. no. 82)
Solution:
Five solutions of x + y = 5 are given below:
(1,4), (2, 3), (3, 2), (4,1), (0, 5)
The above solutions also satisfy the equation 2x + 2y = 10.
∴ x + y = 5 …[Dividing both sides by 2]
∴ If the two equations are the same, then the two equations in two variables have all solutions common.

Question 5.
3x – 4y – 15 = 0 and y + x + 2 = 0. Can these equations be solved by eliminating x ? Is the solution same? (Textbook pg. no. 84)
Solution:
3x – 4y – 15 = 0
∴ 3x – 4y = 15 …(i)
y + x + 2 = 0
∴ x + y = -2 ……(ii)
Multiplying equation (ii) by 3,
3x + 3y = -6 …(iii)
Subtracting equation (iii) from (i),

∴ y = -3
Substituting y = -3 in equation (ii),
∴ x – 3 = -2
∴ x = – 2 + 3
∴ x = 1
∴ (x, y) = ( 1, -3)
Yes, the given equations can be solved by eliminating x. Also, the solution will remain the same.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.3 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Ratio and Proportion Practice Set 4.3 Question 1.
If \(\frac { a }{ b }\) = \(\frac { 7 }{ 3 }\), then find the aIues of the following ratios.

Solution:

Ratio and Proportion Class 9 Practice Set 4.3 Question 2.
If \(\frac{15 a^{2}+4 b^{2}}{15 a^{2}-4 b^{2}}=\frac{47}{7}\), then find the value of the following ratios.

Solution:

Practice Set 4.3 Algebra 9th Question 3.
If \(\frac{3 a+7 b}{3 a-7 b}=\frac{4}{3}\)then find the value of the ratio \(\frac{3 a^{2}-7 b^{2}}{3 a^{2}+7 b^{2}}\).
Solution:

Class 9 Maths Chapter 4 Ratio And Proportion Practice Set 4.3 Question 4.
Solve the following equations.

Solution:

This equation is true for x = 0
∴ x = 0 is one of the solutions.
If x ≠ 0, then x² ≠ 0
∴ \(\frac { 1 }{ 12x – 20 }\) = \(\frac { 1 }{ 8x + 12 }\) … [Dividing both sides by x²]
∴ 8x + 12 = 12x – 20
∴ 12 + 20 = 12x – 8x
∴ 32 = 4x
∴ x = 8
∴ x = 0 or x = 8 are the solutions of the given equation.

∴ 21(x – 5) = 4(2x + 3)
∴ 21x – 105 = 8x + 12
∴ 21x – 8x = 12 + 105
∴ 13x = 117
∴ x = 9
∴ x = 9 ¡s the solution of the given equation.

∴ 9(4x + 1) = 25(x + 3)
∴36x + 925x + 75
∴ 36x – 25 = 75 – 9
∴11x = 66
∴ x = 6
∴ x = 6 is the solution of the given equation.


∴ 4(3x – 4) = 5(x + 1)
∴ 12x – 16 = 5x + 5
∴ 12x – 5x = 5 + 16
∴ 7x = 21
∴ x = 3
∴ x = 3 ¡s the solution of the given equation.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Problem Set 4 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Select the appropriate alternative answer for the following questions.

i . If 6 : 5 = y : 20, then what will be the value of y?
(A) 15
(B) 24
(C) 18
(D) 22.5
Answer:
(B) 24

ii. What is the ratio of 1 mm to 1 cm ?
(A) 1 : 100
(B) 10: 1
(C) 1 : 10
(D) 100: 1
Answer:
(C) 1 : 10

iii. The ages of Jatin, Nitin and Mohasin are 16, 24 and 36 years respectively. What is the ratio of Nitin’s age to Mohasin’s age ?
(A) 3 : 2
(B) 2 : 3
(C) 4 : 3
(D) 3 : 4
Answer:
(B) 2 : 3

iv. 24 bananas were distributed between Shubham and Anil in the ratio 3 : 5, then how many bananas did Shubham get?
(A) 8
(B) 15
(C) 12
(D) 9
Answer:
(D) 9

v. What is the mean proportional of 4 and 25?
(A) 6
(B) 8
(C) 10
(D) 12
Answer:
(C) 10

Hints:
i . \(\frac{6}{5}=\frac{y}{20}\)
∴ \(\quad y=\frac{6 \times 20}{5}=24\)

ii. \(\frac{1 \mathrm{mm}}{1 \mathrm{cm}}=\frac{1 \mathrm{mm}}{10 \mathrm{mm}}=\frac{1}{10}=1 : 10\)

iii. \(\frac{\text { Age of Nitin }}{\text { Age of Mohasin }}=\frac{24}{36}=\frac{12 \times 2}{12 \times 3}\)
\(\frac { 2 }{ 3 }\) = 2 : 3

iv. 3x + 5x = 24
∴ 8x = 24
∴ x = 3
∴ Number of bananas with Shubham = 3x = 9

v. x² = 4 x 25
∴ x² = 100
∴ x = 10

Question 2.
For the following numbers write the ratio of first number to second number in the reduced form. [1 Mark each]
i. 21,48
ii. 36,90
iii. 65,117
iv. 138,161
v. 114,133
Solution:
i. 21,48
\(\text { Ratio }=\frac{21}{48}=\frac{3 \times 7}{3 \times 16}=\frac{7}{16}=7 : 16\)
ii. 36,90
\(\text { Ratio }=\frac{36}{90}=\frac{18 \times 2}{18 \times 5}=\frac{2}{5}=2 : 5\)
iii. 65,117
\(\text { Ratio }=\frac{65}{117}=\frac{13 \times 5}{13 \times 9}=\frac{5}{9}=5 : 9\)
iv. 138,161
\(\text { Ratio }=\frac{138}{161}=\frac{23 \times 6}{23 \times 7}=\frac{6}{7}=6 : 7\)
v. 114,133
\(\text { Ratio }=\frac{114}{113}=\frac{19 \times 6}{19 \times 7}=\frac{6}{7}=6 : 7\)

Question 3.
Write the following ratios in the reduced form.
i. Radius to the diameter of a circle.
ii. The ratio of diagonal to the length of a rectangle, having length 4 cm and breadth 3 cm.
iii. The ratio of numbers denoting perimeter to area of a square, having side 4 cm.
Solution:
i. Radius to the diameter of a circle.
Let radius of the circle be r
then, diameter = 2 x radius = 2r
Ratio of radius to diameter of circle

∴ Ratio of radius to diameter of circle is 1 : 2.

ii. The ratio of diagonal to the length of a rectangle, having length 4 cm and breadth 3 cm.

Let □ ABCD be a rectangle.
In ∆ABC, ∠B = 90°
AC² = AB² + BC² … [Pythagoras theorem]
= 4² + 3² = 16 + 9
∴ AC² = 25
AC = 5 … [Taking square root on both side]
The ratio of diagonal to the length of a rectangle = \(\frac { AC }{ AB }\)
= \(\frac { 5 }{ 4 }\)
= 5 : 4
∴ The ratio of diagonal to the length of a rectangle is 5 : 4

iii. The ratio of numbers denoting perimeter to area of a square, having side 4 cm. side of square = 4cm
Perimeter of square = 4 x side = 4 x 4 = 16 cm
Area of square = (side)² = (4)² = 16 cm²
Ratio of numbers denoting perimeter to area of square

∴ The ratio of numbers denoting perimeter to area of a square is 1 : 1.

Question 4.
Check whether the following numbers are in continued proportion.
i. 2, 4, 8
ii. 1, 2, 3
iii. 9, 12, 16
iv. 3, 5, 8
Solution:
If a, b, c are in continued proportion then b² = ac.
i. 2, 4, 8
Let, a = 2, b = 4 and c = 8
Here, b² = 4² = 16
ac = 2 x 8 = 16
∴ b² = ac
∴ 2, 4,8 are in continued proportion.

ii. 1, 2, 3
Let, a = 1, b = 2 and c = 3
Here, b² = 2² = 4
ac = 1 x 3 = 3
∴ b² ≠ ac
∴ 1, 2,3 are not in continued proportion.

iii. 9, 12, 16
Let, a = 9, b = 12 and c = 16
Here, b² = 12² = 144
ac = 9 x 16 = 144
∴ b² = ac
∴ 9, 12, 16 are in continued proportion.

iv. 3, 5, 8
Let, a = 3, b = 5 and c = 8
Here, b² = 5² = 25
ac = 3 x 8 = 24
∴ b² ≠ ac
∴ 3, 5, 8 are not in continued proportion.

Question 5.
a, b, c are in continued proportion. If a = 3 and c = 27, then find b.
Solution:
a, b, c are in continued proportion. …[Given]
∴ b² = ac
∴ b² = 3 x 27 …[∵ a = 3 and c = 27]
∴ b² = 81
∴ b = 9 …[Taking square root of both sides]

Question 6.
Convert the following ratios into percentages.

Solution:
i. Let 37 : 500 = x%

∴ 37 : 500 = 7.4%

Question 7.
Write the ratio of first quantity to second quantity in the reduced form.
i. 1024 MB, 1.2 GB [(1024 MB = 1GB)]
ii. ₹ 17, ₹ 25 and 60 paise
iii. 5 dozen, 120 units
iv. 4 sq.m, 800 sq.cm
v. 1.5 kg, 2500 gm
Solution:
i. 1024 MB, 1.2 GB
1024 MB = 1 GB

ii. ₹ 17, ₹ 25 and 60 paise
₹ 17 = 17 x 100 paise = 1700 paise
₹ 25 and 60 paise = (25x 100) paise + 60 paise
= (2500 + 60) paise
= 2560 paise

iii. 5 dozen, 120 units
5 dozen = 5 x 12 units = 60 units

iv. 4 sq.m, 800 sq.cm
4 sq.m = 4 x 10000 sq.cm = 40000 sq.cm

v. 1.5 kg, 2500 gm
1.5 kg = 1.5 x 1000 gm = 1500gm

Question 8.
If \(\frac { a }{ b }\) = \(\frac { 2 }{ 3 }\), then find the values of the following expressions.

Solution:

Question 9.
If a, b, c, d are in proportion, then prove that

Solution:
a, b, c are in continued proportion. …[Given]

Question 10.
If a, b, c are ¡n continued proportion, then prove that

Solution:
a, b, c are in continued proportion. … [Given]
∴ \(\frac { a }{ b }\) = \(\frac { b }{ c }\)
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk
= (ck)k . .. [From (j)]
a = ck² …(ii)

Question 11.
Solve:
\( \frac{12 x^{2}+18 x+42}{18 x^{2}+12 x+58}=\frac{2 x+3}{3 x+2}\)
Solution:


∴ 29(2x + 3) = 21 (3x + 2)
∴ 5 + 87= 63x + 42
∴ 87 – 42 = 63x – 58x
∴ 45 = 5x
∴ x = 9
∴ x = 9 is the solution of the given equation.

Question 12.
If \( \frac{2 x-3 y}{3 z+y}=\frac{z-y}{z-x}=\frac{x+3 z}{2 y-3 x}\) ,then prove that every ratio = \(\frac { x }{ y }\).
Solution:

Question 13.
If \(\frac{b y+c z}{b^{2}+c^{2}}=\frac{c z+a x}{c^{2}+a^{2}}=\frac{a x+b y}{a^{2}+b^{2}}\), then prove \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\)
Solution:

Question 1.
Take 5 pieces of card paper. Write the following statements, one on each paper.

a, b, c, d are positive numbers and \(\frac{a}{b}=\frac{c}{d}\) is given. Which of the above statements are true or false, write at the back of each card, if false explain why. (Textbook pg. no. 70)
Answer:
i. True
ii. True
iii. False
Here, numerator and denominator are multiplied by two different numbers a and b.
iv. False
Here, different numbers a and b are subtracted from numerator and denominator.
v. True

Question 2.
In the following activity, the values of a and b can be changed. That is by changing a : b we can create many examples. Teachers should give lot of practice to the students and encourage them to construct their own examples. (Textbook pg. no. 70)

Question 3.
Observe the political map of India from a Geography text book. Study the scale of this map.
From the given scale find the straight line distances between various cities like
i. New Delhi to Bengaluru
ii. Mumbai to Kolkata
iii. Jaipur to Bhuvaneshvar. (Textbook pg. no. 77)
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.2 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Practice Set 8.2 8th Std Maths Answers Chapter 8 Quadrilateral: Constructions and Types

Question 1.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l(BC) = 4.5 cm.
Solution:

Question 2.
Draw a square WXYZ with side 5.2 cm.
Solution:

Question 3.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
Solution:

Question 4.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Solution:

Let ₹ABCD be the rectangle.
l(BC) = 24cm, l(AC) = 26cm
In ∆ABC,
m∠ABC = 90° …[Angle of a rectangle]
∴[l(AC)]² = [l(AB)]2 + [l(BC)]²
…[Pythagoras theorem]
∴ (26 )² = [l(AB)]² + (24)²
∴(26)² – (24)² = [l(AB)]²
∴(26 + 24) (26 – 24) = [l(AB)]²
…[∵ a² – b² = (a + b)(a – b)]
∴50 x 2 = [l(AB)]²
∴100 = [l(AB)]²
i.e. [l(AB)]² = 100
∴l(AB) = √100
…[Taking square root of both sides]
∴l(AB) =10 cm
∴The length of the other side is 10 cm.

Question 5.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
Solution:
In rhombus ABCD,

l(AC) = 16 cm and l(BD) = 12 cm.
Let the diagonals of rhombus ABCD intersect at point O.
l(AO) = \(\frac { 1 }{ 2 }\) l(AC)
…[Diagonals of a rhombus bisect each other]
∴l(AO) = \(\frac { 1 }{ 2 }\) × 16
∴l(AO) = 8 cm
Also, l(DO) = \(\frac { 1 }{ 2 }\) l(BD)
…[Diagonals of a rhombus bisect each other]
∴l(DO) = \(\frac { 1 }{ 2 }\) × 12
∴l(DO) = 6 cm
In ∆DOA,
m∠DOA = 90°
..[Diagonals of a rhombus are perpendicular to each other]
[l(AD)]² = [l(AO)]² + [l(DO)]²
…[Pythagoras theorem]

= (8)² + (6)²
= 64 + 36
∴[l(AD)]² = 100
∴l(AD) = √100
… [Taking square root of both sides]
∴l(AD) = 10 cm
∴l(AB) = l(BC) = l(CD) = l(AD) = 10 cm
…[Sides of a rhombus are congruent]
Perimeter of rhombus ABCD
= l(AB) + l(BC) + l(CD) + l(AD)
= 10+10+10+10
= 40 cm
∴The side and perimeter of the rhombus are 10 cm and 40 cm respectively.

Question 6.
Find the length of diagonal of a square with side 8 cm.
Solution:
Let ₹XYWZ be the square of side 8cm.

seg XW is a diagonal.
In ∆ XYW,
m∠XYW = 90°
… [Angle of a square]
∴ [l(XW)]² = [l(XY)]² + [l(YW)]²
…[Pythagoras theorem]
= (8)² + (8)²
= 64 + 64
∴ [l(XW)]² = 128
∴ l(XW) = √128
…[Taking square root of both sides]
= √64 × 2
= 8 √2 cm
∴ The length of the diagonal of the square is 8 √2 cm.

Question 7.
Measure of one angle of a rhombus is 50°, find the measures of remaining three angles.
Solution:
Let ₹ABCD be the rhombus.

m∠A = 50°
m∠C = m∠A
….[Opposite angles of a rhombus are congruent]
∴ m∠C = 50°
Also, m∠D = m∠B …(i)
….[Opposite angles of a rhombus are congruent]
In ₹ABCD,
m∠A + m∠B + m∠C + m∠D = 360°
….[Sum of the measures of the angles of a quadrilateral is 360°]
∴ 50° + m∠B + 50° + m∠D = 360°
∴ m∠B + m∠D + 100° = 360°
∴ m∠B + m∠D = 360° – 100°
∴ m∠B + m∠B = 260° …[From (i)]
∴ 2m∠B = 260°
∴ m∠B = \(\frac { 260 }{ 2 }\)
∴ m∠B = 130°
∴ m∠D = m∠B = 130° …[From (i)]
∴ The measures of the remaining angles of the rhombus are 130°, 50° and 130°.

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.2 Intext Questions and Activities

Question 1.
Construct a rectangle PQRS by taking two convenient adjacent sides. Name the point of intersection of diagonals as T. Using divider and ruler, measure the following lengths.
i. lengths of opposite sides, seg QR and seg PS.
ii. lengths of seg PQ and seg SR.
iii. lengths of diagonals PR and QS.
iv. lengths of seg PT and seg TR, which are parts of the diagonal PR.
v. lengths of seg QT and seg TS, which are parts of the diagonal QS.
Observe the measures. Discuss about the measures obtained by your classmates. (Textbook pg. no. 44)
Solution:
Draw a rectangle PQRS such that, l(PQ) = 3 cm and l(QR) = 4 cm.

Steps of construction:
i. As shown in the rough figure, draw seg QR of length 4 cm.
ii. Placing the centre of the protractor at point Q, draw ray QW making an angle of 90° with seg QR.
iii. By taking a distance of 3 cm on the compass and placing it at point Q, draw an arc on ray QW. Name the point as P.
iv. Draw ray PV and ray RU making an angle of 90° with seg PQ and seg QR respectively.
v. Name the point of intersection of ray PV and ray RU as S.
₹PQRS is the required rectangle.

From the figure,
i. l(QR) = l(PS) = 4 cm
ii. l(PQ) = l(SR) = 3 cm
iii. l(PR) = l(QS) = 5 cm
iv. l(PT) = l(TR) = 2.5 cm
v. l(QT) = l(TS) = 2.5 cm

From the above measures, we can say that for any rectangle,
i. Opposite sides are congruent.
ii. Diagonals are congruent.
iii. Diagonals bisect each other.

Question 2.
Draw a square by taking convenient length of side. Name the point of intersection of its diagonals as E. Using the apparatus in a compass box, measure the following lengths.
i. lengths of diagonal AC and diagonal BD.
ii. lengths of two parts of each diagonal made by point E.
iii. all the angles made at the point E.
iv. parts of each angle of the square made by each diagonal, (e.g. ∠ADB and ∠CDB).
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 44)
Solution:
Draw a square ABCD such that its side is 5cm

Steps of construction:
i. As shown in the rough figure, draw seg BC of length 5 cm.
ii. Placing the centre of the protractor at point B, draw ray BP making an angle of 90° with seg BC.
iii. By taking a distance of 5 cm on the compass and placing it at point B, draw an arc on ray BP. Name the point as A.
iv. Placing the centre of the protractor at point C, draw ray CQ making an angle of 90° with seg BC.
v. By taking a distance of 5 cm on the compass and placing it at point C, draw an arc on ray CQ. Name the point as D.
vi. Draw seg AD.
₹ABCD is the required square.

From the figure,
i. l(AC) = l(BD) ≅ 7cm
ii. l(AE) = l(EC) ≅ 3.5cm,
l(BE) = l(ED) ≅ 3.5cm
iii. m∠AED = m∠BEC = m∠CED = m∠BEA = 90°
iv. Angles made by diagonal AC:
m∠BAC = m∠DAC = 45°
m∠BCA = m∠DCA = 45°
Angles made by diagonal BD:
m∠ABD = m∠CBD = 45°
m∠ADB = m∠CDB = 45°

From the above measures, we can say that for any square,
i. Diagonals are congruent.
ii. Diagonals bisect each other.
iii. Diagonals are perpendicular to each other.
iv. Diagonals bisect the opposite angles.

Question 3.
Draw a rhombus EFGH by taking convenient length of side and convenient measure of an angle.
Draw its diagonals and name their point of Intersection as M.
i. Measure the opposite angles of the quadrilateral and angles at the point M.
ii. Measure the two parts of every angle made by the diagonal.
iii. Measure the lengths of both diagonals. Measure the two parts of diagonals made by point M.
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 45)
Solution:
Draw a rhombus EFGH such that its side is 5 cm and m∠F = 60°.

Steps of construction:
i. As shown in the rough figure, draw seg FG of length 5 cm.
ii. Placing the centre of the protractor at point F, draw ray FX making an angle 60° with seg FG.
iii. By taking a distance of 5 cm on the compass and placing it at point F, draw an arc on ray FX. Name the point as E.
iv. By taking a distance of 5 cm on the compass and placing it at point E and point G, draw arcs. Name the point of intersection of arcs as H. ₹EFGH is the required rhombus.

From the figure,
i. Opposite angles:
m∠EFG = m∠GHE = 60°,
m∠FEH = m∠HGF = 120°
Angles at the point M:
m∠EMF = m∠FMG = m∠GMH = m∠HME = 90°

ii. Angles made by diagonal FH:
m∠EFH = m∠GFH = 30° m∠EHF = m∠GHF = 30°
Angles made by diagonal EG:
m∠FEG = m∠HEG = 60° m∠FGE = m∠HGE = 60°

iii. l(FH) ≈ 8.6 cm
l(EG) = 5 cm
l(FM) = l(HM) ≈ 4.3 cm
l(EM) = l(GM) ≈ 2.5 cm

From the above measures, we can say that for any rhombus,
i. Opposite angles are congruent.
ii. Diagonals bisect the opposite angles.
iii. Diagonals bisect each other and they are perpendicular to each other.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.4 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Fill in the blanks of the following.

Solution:

Question 2.
5m – n = 3m + 4n, then find the values of the following expressions.

Solution:
5m – n = 3m + 4n … [Given]
∴ 5m – 3m = 4n + n
∴ 2m = 5n

Question 3.
Solve:
i. If a(y + z) = b(z + x) = c(x + y) and out of a, b, c no two of them are equal, then show that, \( \frac{y-z}{a(b-c)}=\frac{z-x}{b(c-a)}=\frac{x-y}{c(a-b)}\).
Solution:
Here, no two of a, b and c are equal.
∴ values of (b – c), (c – a) and (a – b) are not zero.
a(y + z) = b(z + x) = c(x + y) … [Given]

ii. If \(\frac{x}{3 x-y-z}=\frac{y}{3 y-z-x}=\frac{z}{3 z-x-y}\) and x + y + z ≠ 0, then show that the value of each ratio is equal to 1.
Solution:

iii. \(\frac{x}{3 x-y-z}=\frac{y}{3 y-z-x}=\frac{z}{3 z-x-y}\) and x + y + z ≠ 0,then show that \(\frac { a+b }{ 2 }\).
Solution:

iv. If \(\frac{y+z}{a}=\frac{z+x}{b}=\frac{x+y}{c}\) , then show that \(\frac{x}{b+c-a}=\frac{y}{c+a-b}=\frac{z}{a+b-c}\).
Solution:

v. If \(\frac{3 x-5 y}{5 z+3 y}=\frac{x+5 z}{y-5 x}=\frac{y-z}{x-z}\) , then show that every ratio = \(\frac { x }{ y }\).
Solution:

Ratio And Proportion Class 9 Practice Set 4.4 Question 4.
Solve:

Solution:


∴ 7(4x – 5)3(2x + 3)
∴ 28x – 35 = 6x + 9
∴ 28x – 6x = 9 + 35
∴ 22x = 44
∴ x = 2
∴ x = 2 is the solution of the given equation.

ii. \(\frac{5 y^{2}+40 y-12}{5 y+10 y^{2}-4}=\frac{y+8}{1+2 y}\)


∴ y + 8 = 3(1 + 2y)
∴ y + 8 = 3 + 6y
∴ 8 – 3 = 6y – y
∴ 5 = 5y
∴ y = 1
∴ y = 1 is the solution of the given equation.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.2 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Using the property \(\frac { a }{ b }\) = \(\frac { ak }{ bk }\), fill in the blanks by substituting proper numbers in the following.

Solution:

Question 2.
Find the following ratios.
i. The ratio of radius to circumference of the circle.
ii. The ratio of circumference of circle with radius r to its area.
iii. The ratio of diagonal of a square to its side, if the length of side is 7 cm.
iv. The lengths of sides of a rectangle are 5 cm and 3.5 cm. Find the ratio of numbers denoting its perimeter to area.
Solution:
i. Let the radius of circle be r.
then, its circumference = 2πr
Ratio of radius to circumference of the circle

The ratio of radius to circumference of the circle is 1 : 2π.

ii. Let the radius of the circle is r.
∴ circumference = 2πr and area = πr²
Ratio of circumference to the area of circle

∴ The ratio of circumference of circle with radius r to its area is 2 : r.

iii. Length of side of square = 7 cm
∴ Diagonal of square = √2 x side
= √2 x 7
= 7 √2 cm
Ratio of diagonal of a square to its side

∴ The ratio of diagonal of a square to its side is √2 : 1.

iv. Length of rectangle = (l) = 5 cm,
Breadth of rectangle = (b) = 3.5 cm
Perimeter of the rectangle = 2(l + b)
= 2(5 + 3.5)
= 2 x 8.5
= 17 cm
Area of the rectangle = l x b
= 5 x 3.5
= 17.5 cm²
Ratio of numbers denoting perimeter to the area of rectangle

∴ Ratio of numbers denoting perimeter to the area of rectangle is 34 : 35.

Question 3.
Compare the following

Solution:

Question 4.
Solve.
ABCD is a parallelogram. The ratio of ∠A and ∠B of this parallelogram is 5 : 4. FInd the measure of ∠B. [2 Marksl
Solution:
Ratio of ∠A and ∠B for given parallelogram is 5 : 4
Let the common multiple be x.

m∠A = 5x°and m∠B=4x°
Now, m∠A + m∠B = 180° …[Adjacent angles of a parallelogram arc supplementary]
∴ 5x° + 4x°= 180°
∴ 9x° = 180°
∴ x° = 20°
∴ m∠B=4x°= 4 x 20° = 80°
∴ The measure of ∠B is 800.

ii. The ratio of present ages of Albert and Salim is 5 : 9. Five years hence ratio of their ages will be 3 : 5. Find their present ages.
Solution:
The ratio of present ages of Albert and Salim is 5 : 9
Let the common multiple be x.
∴ Present age of Albert = 5x years and
Present age of Salim = 9x years
After 5 years,
Albert’s age = (5x + 5) years and
Salim’s age = (9x + 5) years
According to the given condition,
Five years hence ratio of their ages will be 3 : 5
\(\frac{5 x+5}{9 x+5}=\frac{3}{5}\)
∴ 5(5x + 5) = 3(9x + 5)
∴ 25x + 25 = 27x + 15
∴ 25 – 15 = 27 x – 25 x
∴ 10 = 2x
∴ x = 5
∴ Present age of Albert = 5x = 5 x 5 = 25 years
Present age of Salim = 9x = 9 x 5 = 45 years
∴ The present ages of Albert and Salim are 25 years and 45 years respectively.

iii. The ratio of length and breadth of a rectangle is 3 : 1, and its perimeter is 36 cm. Find the length and breadth of the rectangle.
Solution:
The ratio of length and breadth of a rectangle is 3 : 1
Let the common multiple be x.
Length of the rectangle (l) = 3x cm
and Breadth of the rectangle (b) = x cm
Given, perimeter of the rectangle = 36 cm
Since, Perimeter of the rectangle = 2(l + b)
∴ 36 = 2(3x + x)
∴ 36 = 2(4x)
∴ 36 = 8x
∴ \(x=\frac{36}{8}=\frac{9}{2}=4.5\)
Length of the rectangle = 3x = 3 x 4.5 = 13.5 cm
∴ The length of the rectangle is 13.5 cm and its breadth is 4.5 cm.

iv. The ratio of two numbers is 31 : 23 and their sum is 216. Find these numbers.
Solution:
The ratio of two numbers is 31 : 23
Let the common multiple be x.
∴ First number = 31x and
Second number = 23x
According to the given condition,
Sum of the numbers is 216
∴ 31x + 23x = 216
∴ 54x = 216
∴ x = 4
∴ First number = 31x = 31 x 4 = 124
Second number = 23x = 23 x 4 = 92
∴ The two numbers are 124 and 92.

v. If the product of two numbers is 360 and their ratio is 10 : 9, then find the numbers.
Solution:
Ratio of two numbers is 10 : 9
Let the common multiple be x.
∴ First number = 10x and
Second number = 9x
According to the given condition,
Product of two numbers is 360
∴ (10x) (9x) = 360
∴ 90x² = 360
∴ x² = 4
∴ x = 2 …. [Taking positive square root on both sides]
∴ First number = 10x = 10x² = 20
Second number = 9x = 9x² = 18
∴ The two numbers are 20 and 18.

Question 5.
If a : b = 3 : 1 and b : c = 5 : 1, then find the value of [3 Marks each]

Solution:
Given, a : b = 3 : 1
∴ \(\frac { a }{ b }\) = \(\frac { 3 }{ 1 }\)
∴ a = 3b ….(i)
and b : c = 5 : 1
∴ \(\frac { b }{ c }\) = \(\frac { 5 }{ 1 }\)
b = 5c …..(ii)
Substituting (ii) in (i),
we get a = 3(5c)
∴ a = 15c …(iii)

Ratio and Proportion 9th Class Practice Set 4.1 Question 6. If \(\sqrt{0.04 \times 0.4 \times a}=0.4 \times 0.04 \times \sqrt{b}\) , then find the ratio \(\frac { a }{ b }\).
Solution:
\(\sqrt{0.04 \times 0.4 \times a}=0.4 \times 0.04 \times \sqrt{b}\) … [Given]
∴ 0.04 x 0.4 x a = (0.4)² x (0.04)² x b … [Squaring both sides]

9th Algebra Practice Set 4.2 Question 7. (x + 3) : (x + 11) = (x – 2) : (x + 1), then find the value of x.
Solution:
(x + 3) : (x + 11) = (x- 2) : (x+ 1)
\(\quad \frac{x+3}{x+11}=\frac{x-2}{x+1}\)
∴ (x + 3)(x +1) = (x – 2)(x + 11)
∴ x(x +1) + 3(x + 1) = x(x + 11) – 2(x + 11)
∴ x² + x + 3x + 3 = x² + 1 lx – 2x – 22
∴ x² + 4x + 3 = x² + 9x – 22
∴ 4x + 3 = 9x – 22
∴ 3 + 22 = 9x – 4x
∴ 25 = 5x
∴ x = 5

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.1 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
From the following pairs of numbers, find the reduced form of ratio of first number to second number.
i. 72,60
ii. 38,57
iii. 52,78
Solution:
i. 72, 60
\(\text { Ratio }=\frac{72}{60}=\frac{12 \times 6}{12 \times 5}=\frac{6}{5}=6 : 5\)

ii. 38, 57
\(\text { Ratio }=\frac{38}{57}=\frac{19 \times 2}{19 \times 3}=\frac{2}{3}=2 : 3\)

iii. 52, 78
\(\text { Ratio }=\frac{52}{78}=\frac{26 \times 2}{26 \times 3}=\frac{2}{3}=2 : 3\)

Question 2.
Find the reduced form of the ratio of the first quantity to second quantity.
i. ₹ 700, ₹ 308
ii. ₹ 14, ₹ 12 and 40 paise
iii. 5 litres, 2500 ml
iv. 3 years 4 months, 5 years 8 months
v. 3.8 kg, 1900 gm
vi. 7 minutes 20 seconds, 5 minutes 6 seconds
Solution:
i. ₹ 700, ₹ 308
\( \text { Ratio }=\frac{700}{308}=\frac{28 \times 25}{28 \times 11}=\frac{25}{11}=25 : 11\)

ii. ₹ 14, ₹12 and 40 paise
₹ 14 = 14 x 100 paise = 1400 paise
₹ 12 and 40 paise = 12 x 100 paise + 40 paise
= (1200 + 40) paise
= 1240 paise

iii. 5 litres, 2500 ml
5 litres = 5 x 1000 ml = 5000ml

iv. 3 years 4 months, 5 years 8 months
3 years 4 months = 3×12 months + 4 months
= (36 + 4) months
= 40 months
5 years 8 months = 5 x 12 months + 8 months
= (60 + 8) months
= 68 months

v. 3.8 kg, 1900 gm
3.8 kg = 3.8 x 1000 gm = 3800 gm

vi. 7 minutes 20 seconds, 5 minutes 6 seconds
7 minutes 20 seconds = 7 x 60 seconds + 20 seconds
= (420 + 20) seconds
= 440 seconds
5 minutes 6 seconds = 5 x 60 seconds + 6 seconds
= (300 + 6) seconds
= 306 seconds

Question 3.
Express the following percentages as ratios
i. 75 : 100
ii. 44 : 100
iii. 6.25%
iv. 52: 100
v. 0.64%
Solution:

Question 4.
Three persons can build a small house in 8 days. To build the same house in 6 days, how many persons are required?
Solution:
Let the persons required to build a house in 6 days be x.
Days required to build a house and number of persons are in inverse proportion.
∴ 6 × x = 8 × 3
∴ 6 x = 24
∴ x = 4
∴ 4 persons are required to build the house in 6 days.

Question 5.
Convert the following ratios into percentages.
i. 15 : 25
ii. 47 : 50
iii. \(\frac { 7 }{ 10 }\)
iv. \(\frac { 546 }{ 600 }\)
v. \(\frac { 7 }{ 16 }\)
Solution:
Let 15 : 25 = x %

∴ 15 : 25 = 60 %

ii. Let 47 : 50 = x%

∴ 47 : 50 = 94 %

iii. Let \(\frac { 7 }{ 10 }\) = x %

iv. Let \(\frac { 546 }{ 600 }\) = x %

v. Let \(\frac { 7 }{ 16 }\) = x %

Question 6.
The ratio of ages of Abha and her mother is 2 : 5. At the time of Abha’s birth her mothers age was 27 years. Find the present ages of Abha and her mother.
Solution:
The ratio of ages of Abha and her mother is 2 : 5.
Let the common multiple be x.
∴ Present age of Abha = 2x years and
Present age of Abha’s mother = 5x years
According to the given condition, the age of Abha’s mother at the time of Abha’s birth = 27 years
∴ 5x – 2x = 27
∴ 3x = 27
∴ x = 9
∴ Present age of Abha = 2x = 2 x 9 = 18 years
∴ Present age of Abha’s mother = 5x =5 x 9 = 45 years
The present ages of Abha and her mother are 18 years and 45 years respectively.

Question 7.
Present ages of Vatsala and Sara are 14 years and 10 years respectively. After how many years the ratio of their ages will become 5 : 4?
Solution:
Present age of Vatsala = 14 years
Present age of Sara = 10 years
After x years,
Vatsala’s age = (14 + x) years
Sara’s age = (10 + x) years
According to the given condition,
After x years the ratio of their ages will become 5 : 4
∴ \(\frac { 14 + x }{ 10 + x }\) = \(\frac { 5 }{ 4 }\)
∴ 4(14 + x) = 5(10 + x)
∴ 56 + 4x = 50 + 5x
∴ 56 – 50 = 5x – 4x
∴ 6 = x
∴ x = 6
∴ After 6 years, the ratio of their ages will become 5 : 4.

Question 8.
The ratio of present ages of Rehana and her mother is 2 : 7. After 2 years, the ratio of their ages will be 1 : 3. What is Rehana’s present age ?
Solution:
The ratio of present ages of Rehana and her mother is 2 : 7
Let the common multiple be x.
∴ Present age of Rehana = 2x years and Present age of Rehana’s mother = 7x years
After 2 years,
Rehana’s age = (2x + 2) years
Age of Rehana’s mother = (7x + 2) years
According to the given condition,
After 2 years, the ratio of their ages will be 1 : 3
∴ \(\frac { 2x + 2 }{ 7x + 2 }\) = \(\frac { 1 }{ 3 }\)
∴ 3(2x + 2) = 1(7x + 2)
∴ 6x + 6 = 7x + 2
∴ 6 – 2 = 7x – 6x
∴ 4 = x
∴ x = 4
∴ Rehana’s present age = 2x = 2 x 4 = 8 years
∴ Rehana’s present age is 8 years.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

Problem Set 3 Algebra 9th Std Maths Part 1 Answers Chapter 3 Polynomials

Question 1.
Write the correct alternative answer for each of the following questions.

i. Which of the following is a polynomial?

Answer:
(D) √2x² + \(\frac { 1 }{ 2 }\)

ii. What is the degree of the polynomial √7 ?
(A) \(\frac { 1 }{ 2 }\)
(B) 5
(C) 2
(D) 0
Answer:
(D) 0

iii. What is the degree of the polynomial ?
(A) 0
(B) 1
(C) undefined
(D) any real number
Answer:
(C) undefined

iv. What is the degree of the polynomial 2x² + 5xsup>3 + 7?
(A) 3
(B) 2
(C) 5
(D) 7
Answer:
(A) 3

v. What is the coefficient form of x³ – 1 ?
(A) (1, -1)
(B) (3, -1)
(C) (1, 0, 0, -1)
(D) (1, 3, -1)
Answer:
(C) (1, 0, 0, -1)

vi. p(x) = x² – x + 3, then p (7√7) = ?
(A) 3
(B) 7√7
(C) 42√7+3
(D) 49√7
Answer:
(D) 49√7

vii. When x = – 1, what is the value of the polynomial 2x³ + 2x ?
(A) 4
(B) 2
(C) -2
(D) -4
Answer:
(A) 4

viii. If x – 1 is a factor of the polynomial 3x² + mx, then find the value of m.
(A) 2
(B) -2
(C) -3
(D) 3
Answer:
(C) -3

ix. Multiply (x² – 3) (2x – 7x³ + 4) and write the degree of the product.
(A) 5
(B) 3
(C) 2
(D) 0
Answer:
(A) 5

x. Which is the following is a linear polynomials?
(A)  x + 5
(B)  x² + 5
(C) x³ + 5
(D) x⁴ + 5
Answer:
(A)  x + 5

Hints:
v. x³ – 1 = x³ + 0x² + 0x – 1

vi. p(7√ 7) = (7√ 7)² (7√ 7) (7√ 7) + 3
= 3

vii. p(-1) = 2(-1)³ + 2(-1)
= -2 – 2 = -4

vii. p(1) = 0
∴ 3(1)² + m(1) = 0
∴ 3 + m =0
∴ m = -3

ix. Here, degree of first polynomial = 2 and
degree of second polynomial 3
∴ Degree of polynomial obtained by multiplication = 2 + 3 = 5

Question 2.
Write the degree of the polynomial for each of the following.
i. 5 + 3x⁴
ii. 7
iii. ax⁷ + bx⁹ (a, b are constants)
Answer:
i. 5 + 3x⁴
Here, the highest power of x is 4.
∴Degree of the polynomial = 4

ii. 7 = 7x°
∴ Degree of the polynomial = 0

iii. ax⁷ + bx⁹
Here, the highest power ofx is 9.
∴Degree of the polynomial = 9

Question 3.
Write the following polynomials in standard form. [1 Mark each]
i. 4x² + 7x⁴ – x³ – x + 9
ii. p + 2p³ + 10p² + 5p⁴ – 8
Answer:
i. 7x⁴ – x³ + 4x² – x + 9
ii. 5p⁴ + 2p³ + 10p² + p – 8

Question 4.
Write the following polynomial in coefficient form.
i. x⁴ + 16
ii. m⁵ + 2m² + 3m+15
Answer:
i. x⁴ + 16
Index form = x⁴ + 0x³ + 0x² + 0x + 16
∴ Coefficient form of the polynomial = (1,0,0,0,16)

ii. m⁵ + 2m² + 3m + 15
Index form = m⁵ + 0m⁴ + 0m³ + 2m² + 3m + 15
∴ Coefficient form of the polynomial = (1, 0, 0, 2, 3, 15)

Question 5.
Write the index form of the polynomial using variable x from its coefficient form.
i. (3, -2, 0, 7, 18)
ii. (6, 1, 0, 7)
iii. (4, 5, -3, 0)
Answer:
i. Number of coefficients = 5
∴ Degree = 5 – 1 = 4
∴Index form = 3x⁴ – 2x³ + 0x² + 7x + 18

ii. Number of coefficients = 4
∴Degree = 4 – 1 = 3
∴ Index form = 6x³ + x² + 0x + 7

iii. Number of coefficients = 4
∴ Degree = 4 – 1 = 3
∴ Index form = 4x³ + 5x² – 3x + 0

Question 6.
Add the following polynomials.
i. 7x⁴ – 2x³ + x + 10;
3x⁴ + 15x³ + 9x² – 8x + 2
ii. 3p³q + 2p²q + 7;
2p²q + 4pq – 2p³q
Solution:
i. (7x⁴ – 2x³ + x + 10) + (3x⁴ + 15x³ + 9x² – 8x + 2)
= 7x⁴ – 2x³ + x + 10 + 3x⁴ + 15x³ + 9x² – 8x + 2
= 7x⁴ + 3x⁴ – 2x³ + 1 5x³ + 9x² + x – 8x + 10 + 2
= 10x⁴ + 13x³ + 9x² – 7x + 12

ii. (3p³q + 2p²q + 7) + (2p²q + 4pq – 2p³q)
= 3p³q + 2p²q + 7 + 2p²q + 4pq – 2p³q
= 3p³q – 2p³q + 2p²q + 2p²q + 4pq + 7
= p³q + 4p²q + 4pq + 7

Question 7.
Subtract the second polynomial from the first.
i. 5x² – 2y + 9 ; 3x² + 5y – 7
ii. 2x² + 3x + 5 ; x² – 2x + 3
Solution:
i. (5x² – 2y + 9) – (3x² + 5y – 7)
= 5x² – 2y+ 9 – 3x² – 5y + 1
= 5x² – 3x² – 2y – 5y + 9 + 7
= 2x² – 1y + 16

ii. (2x²+ 3x + 5) – (x² – 2x + 3)
= 2x² + 3x + 5 – x² + 2x – 3
= 2x² – x² + 3x + 2x + 5 – 3
= x² + 5x + 2

Question 8.
Multiply the following polynomials.
i. (m³ – 2m + 3) (m⁴ – 2m² + 3m + 2)
ii. (5m³ – 2) (m² – m + 3)
Solution:
i. (m³ – 2m + 3) (m⁴ – 2m² + 3m + 2)
= m³(m⁴ – 2m² + 3m + 2) – 2m(m⁴ – 2m² + 3m + 2) + 3(m⁴ – 2m² + 3m + 2)
= m⁷ – 2m⁵ + 3m⁴ + 2m³ – 2m⁵ + 4m³ – 6m² – 4m + 3m⁴ – 6m² + 9m + 6
= m⁷ – 2m⁵ – 2m⁵ + 3m⁴ + 3m⁴ + 2m³ + 4m³ – 6m² – 6m² – 4m + 9m + 6
= m⁷ – 4m⁵ + 6m⁴ + 6m³ – 12m² + 5m + 6

ii. (5m³ – 2) (m² – m + 3)
= 5m³(m² – m + 3) – 2(m² – m + 3)
= 5m⁵ – 5m⁴ + 15m³ – 2m² + 2m – 6

Question 9.
Divide polynomial 3x³ – 8x² + x + 7 by x – 3 using synthetic method and write the quotient and remainder.
Solution:
Dividend = 3x³ – 8x² + x + 7
∴ Coefficient form of dividend = (3, – 8, 1,7)
Divisor = x – 3
∴ Opposite of – 3 is 3

Coefficient form of quotient = (3, 1,4)
∴ Quotient = 3x² + x + 4 and
Remainder =19

Question 10.
For which value of m, x + 3 is the factor of the polynomial x³ – 2mx + 21?
Solution:
Here, p(x) = x³ – 2mx + 21
(x + 3) is a factor of x³ – 2mx + 21.
∴ By factor theorem,
Remainder = 0
∴ P(- 3) = 0
p(x) = x³ – 2mx + 21
∴ p(-3) = (-3)³ – 2(m)(-3) + 21
∴ 0 = – 27 + 6m + 21
∴ 6 + 6m = 0
∴ 6m = 6
∴ m = 1
∴ x + 3 is the factor of x³ – 2mx + 21 for m = 1.

Question 11.
At the end of the year 2016, the population of villages Kovad, Varud, Chikhali is 5x² – 3y², 7y² + 2xy and 9x² + 4xy respectively. At the beginning of the year 2017, x² + xy – y², 5xy and 3x² + xy persons from each of the three villages respectively went to another village for education, then what is the remaining total population of these three villages ?
Solution:
Total population of villages at the end of 2016 = (5x² – 3y²) + (7y² + 2xy) + (9x² + 4xy)
= 5x² + 9x² – 3y² + 7y² + 2xy + 4xy
= 14x² + 4y² + 6xy …….(i)
Total number of persons who went to other village at the beginning of 2017 = (x² + xy – y²) + (5xy) + (3x² + xy)
= x² + 3x² – y² + xy + 5xy + xy
= 4x² – y² + 7xy … (ii)
Remaining total population of villages = Total population at the end of 2016 – total number of persons who went to other village at the beginning of 2017
= 14x² + 4y² + 6xy – (4x² – y² + 7xy) … [From (i) and (ii)]
= 14x² + 4y² + 6xy – 4x² + y² – 7xy
= 14x² – 4x² + 4y² + y² + 6xy – 7xy = 1
= 10x² + 5y² – xy
∴ The remaining total population of the three villages is 10x² + 5y² – xy.

Question 12.
Polynomials bx² + x + 5 and bx³ – 2x + 5 are divided by polynomial x – 3 and the remainders are m and n respectively. If m – n = 0, then find the value of b.
Solution:
When polynomial bx² + x + 5 is divided by (x – 3), the remainder is m.
∴ By remainder theorem,
Remainder = p(3) = m
p(x) = bx² + x + 5
∴ p(3) = b(3)² + 3 + 5
∴m = b(9) + 8
m = 9b + 8 …(i)
When polynomial bx³ – 2x + 5 is divided by x – 3 the remainder is n
∴ remainder = p(3) = n
p(x) = bx³ – 2x + 5
∴ P(3)= b(3)³ – 2(3) + 5
∴ n = b(27) – 6 + 5
∴ n = 27b – 1 …(ii)
Now, m – n = 0 …[Given]
∴ m = n
∴ 9b + 8 = 27b – 1 …[From (i) and (ii)]
∴ 8 + 1 = 27b – 9b
∴ 9 = 18b
∴ b = \(\frac { 1 }{ 2 }\)

Question 13.
Simplify.
(8m² + 3m – 6) – (9m – 7) + (3m² – 2m + 4)
Solution:
(8m² + 3m – 6) – (9m – 7) + (3m² – 2m + 4)
= 8m² + 3m – 6 – 9m + 7 + 3m² – 2m + 4
= 8m² + 3m² + 3m – 9m – 2m – 6 + 7 + 4
= 11m² – 8m + 5

Question 14.
Which polynomial is to be subtracted from x² + 13x + 7 to get the polynomial 3x² + 5x – 4?
Solution:
Let the required polynomial be A.
∴ (x² + 13x + 7) – A = 3x² + 5x – 4
∴ A = (x² + 13x + 7) – (3x² + 5x – 4)
= x² + 13x + 7 – 3x² – 5x + 4
= x² – 3x² + 13x – 5x + 7+4
= -2x² + 8x + 11
∴ – 2x² + 8x + 11 must be subtracted from x² + 13x + 7 to get 3x² + 5x – 4.

Question 15.
Which polynomial is to be added to 4m + 2n + 3 to get the polynomial 6m + 3n + 10?
Solution:
Let the required polynomial be A.
∴ (4m + 2n + 3) + A = 6m + 3n + 10
∴ A = 6m + 3n + 10 – (4m + 2n + 3)
= 6m + 3n + 10 – 4m – 2n – 3
= 6m – 4m + 3n – 2n + 10 – 3
= 2m + n + 7
∴ 2m + n + 7 must be added to 4m + 2n + 3 to get 6m + 3n + 10.

Question 1.
Read the following passage, write the appropriate amount in the boxes and discuss.
Govind, who is a dry land farmer from Shiralas has a 5 acre field. His family includes his wife, two children and his old mother. He borrowed one lakh twenty five thousand rupees from the bank for one year as agricultural loan at 10 p.c.p.a. He cultivated soyabean in x acres and cotton and tur in y acres. The expenditure he incurred was as follows :
He spent ₹10,000 on seeds. The expenses for fertilizers and pesticides for the soyabean crop was ₹ 2000x and ₹ 4000x² were spent on wages and cultivation of land. He spent ₹ 8000y on fertilizers and pesticides and ₹ 9000y2 for wages and cultivation of land for the cotton and tur crops.

Let us write the total expenditure on all the crops by using variables x and y.
₹ 10000 + 2000x + 4000×2 + 8000y + 9000y²
He harvested 5x² quintals soyabean and sold it at ₹ 2800 per quintal. The cotton crop yield was \(\frac { 5 }{ 3 }\) y² quintals which fetched ₹ 5000 per quintal.
The tur crop yield was 4y quintals and was sold at ₹ 4000 per quintal. Write the total income in rupees that was obtained by selling the entire farm produce, with the help of an expression using variables x and y. (Textbook pg. no. 44)
Answer:
Total income = income on soyabean crop + income on cotton crop + income on tur crop
= ₹ (5x² x 2800) + ₹(\(\frac { 5 }{ 3 }\) y² x 5000) + ₹ (4y x 4000)
= ₹ ( 14000x² + \(\frac { 25000 }{ 3 }\)y² + 16000y)

Question 2.
We have seen the example of expenditure and income (in terms of polynomials) of Govind who is a dry land farmer. He has borrowed rupees one lakh twenty-five thousand from the bank as an agriculture loan and repaid the said loan at 10 p.c.p.a. He had spent ₹ 10,000 on seeds. The expenses on soyabean crop was ₹ 2000x for fertilizers and pesticides and ₹ 4000x² was spent on wages and cultivation. He spent ₹ 8000y on fertilizers and pesticides and ₹9000y² on cultivation and wages for cotton and tur crop.
His total income was
₹ (14000x² + \(\frac { 25000 }{ 3 }\)y² + 16000y)
By taking x = 2, y = 3 write the income expenditure account of Govind’s farming. (Textbook pg. no. 52)
Solution:
–           Credit (Income)
₹ 1,25,000   Bank loan
₹ 56000      Income from soyabean
₹ 75000      Income from cotton
₹ 48000      Income from tur
₹ 304000     Total income

–                     Debit (Expenses)
₹ 1,37,000       loan paid with interest for seeds
₹ 10000          For seeds
₹ 4000            Fertilizers and pesticides for soyabean
₹ 16000         Wages and cultivation charges for soyabean
₹ 24000          Fertilizers and pesticides for cotton & tur
₹ 81000         Wages and cultivation charges for cotton & tur
₹ 272000       Total expenditure