Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.
Practice Set 4.1 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion
Question 1.
From the following pairs of numbers, find the reduced form of ratio of first number to second number.
i. 72,60
ii. 38,57
iii. 52,78
Solution:
i. 72, 60
\(\text { Ratio }=\frac{72}{60}=\frac{12 \times 6}{12 \times 5}=\frac{6}{5}=6 : 5\)
ii. 38, 57
\(\text { Ratio }=\frac{38}{57}=\frac{19 \times 2}{19 \times 3}=\frac{2}{3}=2 : 3\)
iii. 52, 78
\(\text { Ratio }=\frac{52}{78}=\frac{26 \times 2}{26 \times 3}=\frac{2}{3}=2 : 3\)
Question 2.
Find the reduced form of the ratio of the first quantity to second quantity.
i. ₹ 700, ₹ 308
ii. ₹ 14, ₹ 12 and 40 paise
iii. 5 litres, 2500 ml
iv. 3 years 4 months, 5 years 8 months
v. 3.8 kg, 1900 gm
vi. 7 minutes 20 seconds, 5 minutes 6 seconds
Solution:
i. ₹ 700, ₹ 308
\( \text { Ratio }=\frac{700}{308}=\frac{28 \times 25}{28 \times 11}=\frac{25}{11}=25 : 11\)
ii. ₹ 14, ₹12 and 40 paise
₹ 14 = 14 x 100 paise = 1400 paise
₹ 12 and 40 paise = 12 x 100 paise + 40 paise
= (1200 + 40) paise
= 1240 paise

iii. 5 litres, 2500 ml
5 litres = 5 x 1000 ml = 5000ml
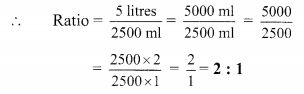
iv. 3 years 4 months, 5 years 8 months
3 years 4 months = 3×12 months + 4 months
= (36 + 4) months
= 40 months
5 years 8 months = 5 x 12 months + 8 months
= (60 + 8) months
= 68 months
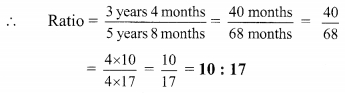
v. 3.8 kg, 1900 gm
3.8 kg = 3.8 x 1000 gm = 3800 gm
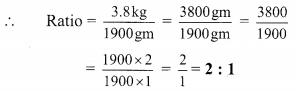
vi. 7 minutes 20 seconds, 5 minutes 6 seconds
7 minutes 20 seconds = 7 x 60 seconds + 20 seconds
= (420 + 20) seconds
= 440 seconds
5 minutes 6 seconds = 5 x 60 seconds + 6 seconds
= (300 + 6) seconds
= 306 seconds
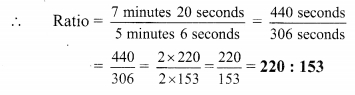
Question 3.
Express the following percentages as ratios
i. 75 : 100
ii. 44 : 100
iii. 6.25%
iv. 52: 100
v. 0.64%
Solution:

Question 4.
Three persons can build a small house in 8 days. To build the same house in 6 days, how many persons are required?
Solution:
Let the persons required to build a house in 6 days be x.
Days required to build a house and number of persons are in inverse proportion.
∴ 6 × x = 8 × 3
∴ 6 x = 24
∴ x = 4
∴ 4 persons are required to build the house in 6 days.
Question 5.
Convert the following ratios into percentages.
i. 15 : 25
ii. 47 : 50
iii. \(\frac { 7 }{ 10 }\)
iv. \(\frac { 546 }{ 600 }\)
v. \(\frac { 7 }{ 16 }\)
Solution:
Let 15 : 25 = x %
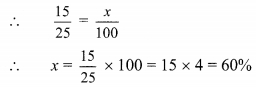
∴ 15 : 25 = 60 %
ii. Let 47 : 50 = x%
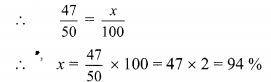
∴ 47 : 50 = 94 %
iii. Let \(\frac { 7 }{ 10 }\) = x %
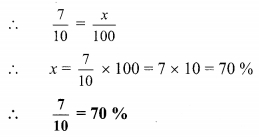
iv. Let \(\frac { 546 }{ 600 }\) = x %
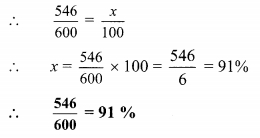
v. Let \(\frac { 7 }{ 16 }\) = x %
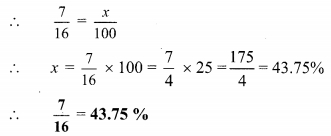
Question 6.
The ratio of ages of Abha and her mother is 2 : 5. At the time of Abha’s birth her mothers age was 27 years. Find the present ages of Abha and her mother.
Solution:
The ratio of ages of Abha and her mother is 2 : 5.
Let the common multiple be x.
∴ Present age of Abha = 2x years and
Present age of Abha’s mother = 5x years
According to the given condition, the age of Abha’s mother at the time of Abha’s birth = 27 years
∴ 5x – 2x = 27
∴ 3x = 27
∴ x = 9
∴ Present age of Abha = 2x = 2 x 9 = 18 years
∴ Present age of Abha’s mother = 5x =5 x 9 = 45 years
The present ages of Abha and her mother are 18 years and 45 years respectively.
Question 7.
Present ages of Vatsala and Sara are 14 years and 10 years respectively. After how many years the ratio of their ages will become 5 : 4?
Solution:
Present age of Vatsala = 14 years
Present age of Sara = 10 years
After x years,
Vatsala’s age = (14 + x) years
Sara’s age = (10 + x) years
According to the given condition,
After x years the ratio of their ages will become 5 : 4
∴ \(\frac { 14 + x }{ 10 + x }\) = \(\frac { 5 }{ 4 }\)
∴ 4(14 + x) = 5(10 + x)
∴ 56 + 4x = 50 + 5x
∴ 56 – 50 = 5x – 4x
∴ 6 = x
∴ x = 6
∴ After 6 years, the ratio of their ages will become 5 : 4.
Question 8.
The ratio of present ages of Rehana and her mother is 2 : 7. After 2 years, the ratio of their ages will be 1 : 3. What is Rehana’s present age ?
Solution:
The ratio of present ages of Rehana and her mother is 2 : 7
Let the common multiple be x.
∴ Present age of Rehana = 2x years and Present age of Rehana’s mother = 7x years
After 2 years,
Rehana’s age = (2x + 2) years
Age of Rehana’s mother = (7x + 2) years
According to the given condition,
After 2 years, the ratio of their ages will be 1 : 3
∴ \(\frac { 2x + 2 }{ 7x + 2 }\) = \(\frac { 1 }{ 3 }\)
∴ 3(2x + 2) = 1(7x + 2)
∴ 6x + 6 = 7x + 2
∴ 6 – 2 = 7x – 6x
∴ 4 = x
∴ x = 4
∴ Rehana’s present age = 2x = 2 x 4 = 8 years
∴ Rehana’s present age is 8 years.