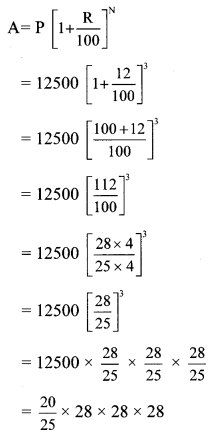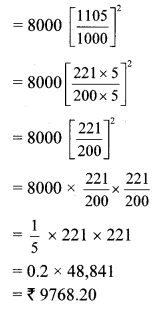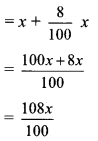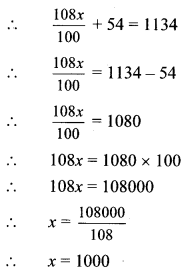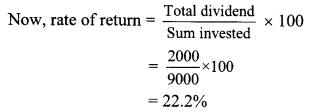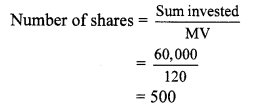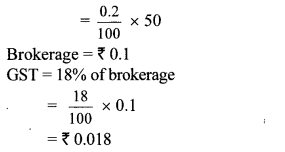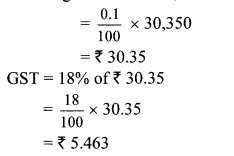Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.4 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.4 8th Std Maths Answers Chapter 15 Area

Question 1.
Sides of a triangle are 45 cm, 39 cm and 42 cm, find its area.
Solution:
Sides of a triangle are 45 cm, 39 cm and 42 cm.
Here, a = 45cm, b = 39cm, c = 42cm
Semi perimeter of triangle = s = \(\frac { 1 }{ 2 }(a+b+c)\)
= \(\frac { 1 }{ 2 }(45+39+42)\)
= \(\frac { 126 }{ 2 }\)
= 63
Area of a triangle

∴ The area of the triangle is 756 sq.cm.

Question 2.
Look at the measures shown in the given figure and find the area of ☐PQRS.

Solution:
A (☐PQRS) = A(∆PSR) + A(∆PQR)
In ∆PSR, l(PS) = 36 m, l(SR) = 15 m
A(∆PSR)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(SR) x l(PS)
= \(\frac { 1 }{ 2 }\) x 15 x 36
= 270 sq.m
In ∆PSR, m∠PSR = 90°
[l(PR)]² = [l(PS)]² + [l(SR)]²
…[Pythagoras theorem]
= (36)² + (15)²
= 1296 + 225
∴ l(PR)² = 1521
∴ l(PR) = 39m
…[Taking square root of both sides]
In ∆PQR, a = 56m, b = 25m, c = 39m

A(☐PQRS) = A(∆PSR) + A(∆PQR)
= 270 + 420
= 690 sq. m
∴ The area of ☐PQRS is 690 sq.m

Question 3.
Some measures are given in the figure, find the area of ☐ABCD.

Solution:
A(☐ABCD) = A(∆BAD) + A(∆BDC)
In ∆BAD, m∠BAD = 90°, l(AB) = 40m, l(AD) = 9m
A(∆BAD) = \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AB) x l(AD)
= \(\frac { 1 }{ 2 }\) x 40 x 9
= 180 sq. m
In ∆BDC, l(BT) = 13m, l(CD) = 60m
A(∆BDC) = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x l(CD) x l(BT)
= \(\frac { 1 }{ 2 }\) x 60 x 13
= 390 sq. m
A (☐ABCD) = A(∆BAD) + A(∆BDC)
= 180 + 390
= 570 sq. m
∴ The area of ☐ABCD is 570 sq.m.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.3 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.3 8th Std Maths Answers Chapter 15 Area

Question 1.
In the given figure, ☐ABCD is a trapezium, side AB || side DC, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area ☐ABCD.

Solution:
☐ABCD is a trapezium, side AB || side DC,
l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm,
Area of a trapezium = \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A (☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC)] x l(AD)
= \(\frac { 1 }{ 2 }\) x (13 + 9) x 8
= \(\frac { 1 }{ 2 }\) x 22 x 8
= 11 x 8
= 88 sq.cm
∴ The area of ☐ABCD is 88 sq. cm.
[Note: The question is modified.]

Question 2.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Solution:
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x (8.5 + 11.5) x 4.2
= \(\frac { 1 }{ 2 }\) x 20 x 4.2
= 10 x 4.2
= 42 sq. cm
∴ The area of the trapezium is 42 sq. cm.

Question 3.
☐PQRS is an isosceles trapezium. l(PQ) = 7 cm, seg PM ⊥ seg SR, l(SM) = 3 cm. Distance between two parallel sides is 4 cm, find the area of ☐PQRS.

Solution:
☐PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In ☐PMNQ,
seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ ☐PMNQ is a rectangle.

Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]² = [l(PM)]² + [l(SM)]² … [Pythagoras theorem]
∴ [l(PS)]² = (4)² + (3)²
∴ [l(PS)]² = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm
…[Taking square root of both sides]
☐PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]² = [l(QN)]² + [l(NR)]²
… [Pythagoras theorem]
∴ (5)² = (4)² + [l(NR)]²
∴ 25 = 16 + [l(NR)]²
∴ [l(NR)]² = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm
…[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3
= 13 cm
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐PQRS) = \(\frac { 1 }{ 2 }\) x [l(PQ) + l(SR)] x l(PM)
= \(\frac { 1 }{ 2 }\) x (7+ 13) x 4
= \(\frac { 1 }{ 2 }\) x 20 x 4
= 40 sq.cm
∴ The area of ☐PQRS is 40 sq. cm.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.2 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.2 8th Std Maths Answers Chapter 15 Area

Question 1.
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 15 cm and 24 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 15 × 24
= 15 × 12
= 180 sq.cm
∴ The area of the rhombus is 180 sq. cm.

Question 2.
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 16.5 × 14.2
= 16.5 × 7.1
= 117.15 sq cm
∴ The area of the rhombus is 117.15 sq. cm.

Question 3.
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution:
Let ₹ABCD be the rhombus. Diagonals AC and BD intersect at point E.

l(AC) = 48 cm …(i)
l(AE) = \(\frac { 1 }{ 2 }l(AC)\) …[Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) × 48 …[From (i)]
= 24 cm …(ii)
Perimeter of rhombus = 100 cm …[Given]
Perimeter of rhombus = 4 × side
∴ 100 = 4 × l(AD)
∴ l(AD) = \(\frac { 100 }{ 4 }\) = 25 cm …(iii)
In ∆ADE,
m∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
∴ [l(AD)]² = [l(AE)]² + [l(DE)]² … [Pythagoras theorem]
∴ (25)² = (24)² + l(DE)² … [From (ii) and (iii)]
∴ 625 = 576 + l(DE)²
∴ l(DE)² = 625 – 576
∴ l(DE)² = 49
∴ l(DE) = √49
… [Taking square root of both sides]
l(DE) = 7 cm …(iv)
l(DE) = \(\frac { 1 }{ 2 } l(BD)\) ….[Diagonals of a rhombus bisect each other]
∴ 7 = \(\frac { 1 }{ 2 } l(BD)\) …[From (iv)]
∴ l(BD) = 7 × 2
= 14 cm …(v)
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × l(AC) × l(BD)
= \(\frac { 1 }{ 2 }\) × 48 × 14 … [From (i) and (v)]
= 48 × 7
= 336 sq.cm
∴ The area of the quadrilateral is 336 sq.cm.

Question 4.
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq.cm, find its perimeter.
Solution:
Let ₹ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and A(₹ABCD) = 240 sq. cm .. .(ii)

Area of the rhombus = \(\frac { 1 }{ 2 }\) × product of lengths of diagonal
∴ 240 = \(\frac { 1 }{ 2 }\) × l(AC) x l(BD) …[From (ii)]
∴ 240 = \(\frac { 1 }{ 2 }\) × 30 × l(BD) …[From (i)]
∴ l(BD) = \(\frac { 240\times 2 }{ 30 }\)
∴ l(BD) = 8 × 2 = 16 cm …(iii)
Diagonals of a rhombus bisect each other.
∴ l(AE) = \(\frac { 1 }{ 2 }l(AC)\)
= \(\frac { 1 }{ 2 }\) × 30 … [From (i)]
= 15 cm …(iv)
and l(DE) = \(\frac { 1 }{ 2 }l(BD)\)
= \(\frac { 1 }{ 2 }\) × 16
= 8 cm
In ∆ADE,
m∠AED = 90°
…[Diagonals of a rhombus are perpendicular to each other]
∴[l(AD)]² = [l(AE)]² + [l(DE)]²
…[Pythagoras theorem]
∴l(AD)² = (15)² + (8)² … [From (iv) and (v)]
= 225 + 64
∴l(AD)² = 289
∴l(AD) = √289
…[Taking square root of both sides]
∴l(AD) = 17 cm
Perimeter of rhombus = 4 × side
= 4 × l(AD)
= 4 × 17
= 68 cm
∴The perimeter of the rhombus is 68 cm.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.1 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.1 8th Std Maths Answers Chapter 15 Area

Question 1.
If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
Solution:
Given, base = 18 cm, height = 11 cm
Area of a parallelogram = base × height
= 18 × 11
= 198 sq.cm
∴ Area of the parallelogram is 198 sq.cm.

Question 2.
If area of a parallelogram is 29.6 sq. cm and its base is 8 cm, find its height.
Solution:
Given, area of a parallelogram = 29.6 sq.cm,
base = 8 cm
Area of a parallelogram = base × height
∴ 29.6 = 8 × height
∴ height = \(\frac { 29.6 }{ 8 }\) = 3.7 cm
∴ Height of the parallelogram is 3.7 cm.

Question 3.
Area of a parallelogram is 83.2 sq.cm. If its height is 6.4 cm, find the length of its base.
Solution:
Given, area of a parallelogram = 83.2 sq.cm, height = 6.4 cm
Area of a parallelogram = base × height
∴ 83.2 = base × 6.4
∴ base = \(\frac { 83.2 }{ 6.4 }\) = 13 cm
∴ The length of the base of the parallelogram is 13 cm.

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.1 Intext Questions and Activities

Question 1.
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = base × height (Textbook pg. no.94)

Solution:
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = Area of a rectangle = length × breadth = base × height

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 14.1 8th Std Maths Answers Solutions Chapter 14 Compound Interest.

Practice Set 14.1 8th Std Maths Answers Chapter 14 Compound Interest

Practice Set 14.1 Class 8 Question 1.
Find the amount and the compound interest.

No	Principal (Rs)	Rate (p.c.p.a.)	Duration (years)
i.	2000	5	2
ii.	5000	8	3
iii.	4000	7.5	2

Solution:
i. Here P = Rs 2000, R = 5 p.c.p.a. and N = 2 years

= 5 × 441
∴ A = Rs 2205
I = Amount (A) – Principal (P)
= 2205 – 2000
= Rs 205
∴ The amount is Rs 2205 and the compound interest is Rs 205.

ii. Here, P = Rs 5000, R = 8 p.c.p.a. and N = 3 years

∴ A = Rs 6298.56
I = Amount (A) – Principal (P)
= 6298.56 – 5000
= Rs 1298.56
∴ The amount is Rs 6298.56 and the compound interest is Rs 1298.56.

iii. Here, P = Rs 4000, R = 7.5 p.c.p.a. and N = 2 years

∴A = Rs 4622.50
I = Amount (A) – Principal (P)
= 4622.50 – 4000
= Rs 622.50
∴The amount is Rs 4622.50 and the compound interest is Rs 622.50.

Compound Interest Practice Set 14.1 Question 2.
Sameerrao has taken a loan of Rs 12500 at the rate of 12 p.c.p.a. for 3 years. If the interest is compounded annually then how many rupees should he pay to clear his loan?
Solution:
Here, P = Rs 12,500, R = 12 p.c.p.a. and
N = 3 years

= 0.8 × 28 × 28 × 28
= Rs 17,561.60
Sameerrao should pay Rs 17,561.60 to clear his loan.

8th Standard Maths Practice Set 14.1 Question 3.
To start a business Shalaka has taken a loan of Rs 8000 at a rate of \(10\frac { 1 }{ 2 }\) p.c.p.a. After two years how much compound interest will she have to pay?
Solution:
Here, P = Rs 8000, N = 2 years and


I = Amount (A) – Principal (P)
= 9768.20 – 8000
= Rs 1768.20
∴ After two years Shalaka will have to pay Rs 1768.20 as compound interest.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.2 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Practice Set 12.2 8th Std Maths Answers Chapter 12 Equations in One Variable

Equation In One Variable Practice Set 12.2 Question 1.
Mother is 25 years older than her son. Find son’s age, if after 8 years ratio of son’s age to mother’s age will be \(\frac { 4 }{ 9 }\).
Solution:
Let the son’s present age be x years.
∴ Mother’s present age = (x + 25) years
After 8 years,
Son’s age = (x + 8) years
Mother’s age = (x + 25 + 8) = (x + 33) years
Since, the ratio of the son’s age to mother’s age after 8 years is \(\frac { 4 }{ 9 }\).
∴ \(\frac{x+8}{x+33}=\frac{4}{9}\)
∴ 9 (x + 8) = 4 (x + 33)
∴ 9x + 72 = 4x + 132
∴ 9x – 4x = 132 – 72
∴ 5x = 60
∴ x = \(\frac { 60 }{ 5 }\)
∴ x = 12
∴ Son’s present age is 12 years.

8th Std Maths Practice Set 12.2 Question 2.
The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent to \(\frac { 1 }{ 2 }\) . Find the fraction.
Solution:
Let the numerator of the fraction be x.
The denominator of a fraction is greater than its numerator by 12.
∴ Denominator of the fraction = (x + 12)
∴ The required fraction = \(\frac { x }{ x+12 }\)
For the new fraction,
numerator is decreased by 2.
∴ The new numerator = (x – 2)
Also, denominator is increased by 7.
∴ The new denominator = (x + 12) + 7
= (x + 19)
Since, the new fraction is equivalent to \(\frac { 1 }{ 2 }\).
∴ \(\frac{x-2}{x+19}=\frac{1}{2}\)
∴ 2(x – 2) = 1(x + 19)
∴ 2x – 4 = x + 19
∴ 2x – x = 19 + 4
∴ x = 23
∴ The required fraction = \(\frac{x}{x+12}=\frac{23}{23+12}=\frac{23}{35}\)
∴ The required fraction is \(\frac { 23 }{ 35 }\)

Practice Set 12.2 Class 8 Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.

∴ Weight of copper in the brass utensil = \(\left(\frac{13}{7} x\right)\) gm
The weight of the brass utensil = 700 gm
∴ \(\frac { 13 }{ 7 }x+x=700\)
∴ \(\frac { 13 }{ 7 }x\) x × 7 + x × 7 = 700 × 7
∴ 13x + 7x = 4900
∴ 20x = 4900
∴ \(x=\frac { 4900 }{ 20 }\)
∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Practice Set 12.2 8th Class Question 4.
Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let the three consecutive whole numbers be (x – 1), x and (x + 1).
∴ Sum of the three numbers
= (x – 1) + x + (x + 1)
= 3x
Given that, the sum of the three numbers is greater than 45 and less than 54.
When the sum of the three numbers is 45,
3x = 45
∴ x = \(\frac { 45 }{ 3 }\)
∴ x = 15
When the sum of the three numbers is 54,
∴ 3x = 54
∴ x = \(\frac { 54 }{ 3 }\)
∴ x = 18
∴ the value of x is greater than 15 and less than 18.
∴ the value of x is either 16 or 17

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17

Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.

Practice Set 12.2 8th Standard Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x

	Digit in units place	Digit in tens place	Number
Original Number	x	2x	(2x × 10) + x = 20x + x = 21x
New Number	2x	x	(x × 10) + 2x = 10x + 2x = 12x

Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = \(\frac { 66 }{ 33 }\)
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.

8th Standard Maths Practice Set 12.2 Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ \(x=\frac { 33000 }{ 300 }\)
∴ x = 110
∴ 110 tickets of Rs 100 were sold.

8th Maths Practice Set 12.2 Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.

Raju Sold A Bicycle to Amit at 8 Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x

Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134

∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Class 8 Maths Practice Set 12.2 Question 9.
A cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Let the number of runs required by the cricket player to score in the third match be x.
Number of runs scored by the player in first match = 180
Number of runs scored in second match = 257
∴ Total runs scored by the player = 180 + 257 + x = 437 + x
Average of runs in the three matches = \(\frac { 437+x }{ 3 }\)
Since, the average of runs should be 230.
\(\frac { 437+x }{ 3 }=230\)
∴ 437 + x = 230 × 3
∴ 437 + x = 690
∴ x = 690 – 437
∴ x = 253
∴ The cricket player should score 253 runs in the third match.

8th Class Math Practice Set 12.2 Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
∴ Anil’s present age = \(\left(\frac{3 x+5}{2}\right)\) years
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.

∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = \(\frac { 15 }{ 3 }\)
∴ x = 5
∴ Viru’s present age is 5 years.

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.2 Intext Questions and Activities

8th Math Practice Set 12.2 Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.1 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Practice Set 12.1 8th Std Maths Answers Chapter 12 Equations in One Variable

Equation in One Variable Practice Set 12.1 Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.

Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.

Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.

ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.

Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.

Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.

iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.

Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.

Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.

iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.

Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.

Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.

Practice Set 12.1 Question 2.
Solve the following equations:
i. 17p – 2 = 49
ii. 2m + 7 = 9
iii. 3x + 12 = 2x – 4
iv. 5 (x – 3) = 3 (x + 2)
v. \(\frac { 9x }{ 8 }+1=10\)
vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)
vii. 13x – 5 = \(\frac { 3 }{ 2 }\)
viii. 3 (y + 8) = 10 (y – 4) + 8
ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
x. \(\frac{y-4}{3}+3 y=4\)
xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51
∴ \(\frac{17 p}{17}=\frac{51}{17}\) …[Dividing both the sides by 17]
p = 3

ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2
∴ \(\frac{2 m}{2}=\frac{2}{2}\) [Dividing both the sides by 2]
∴ m = 1

iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16

iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21
∴ \(\frac{2 x}{2}=\frac{21}{2}\) …[Dividing both the sides by 2]
∴ \(x=\frac{21}{2}\)

v. \(\frac { 9x }{ 8 }+1=10\)

vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)

vii. 13x – 5 = \(\frac { 3 }{ 2 }\)

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56
∴ \(\frac{-7 y}{-7}=\frac{-56}{-7}\)…[Dividing both the sides by – 7]
∴ y = 8

ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
∴\(\frac{x-9}{x-5} \times 7(x-5)=\frac{5}{7} \times 7(x-5)\)
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38
∴\(\frac{2 x}{2}=\frac{38}{2}\) …[Dividing both the sides by 2]
∴x = 19

x. \(\frac{y-4}{3}+3 y=4\)
∴\(\frac{y-4}{3} \times 3+3 y \times 3=4 \times 3\)
…[Multiplying both the sides by 3]
∴y – 4 + 9y = 12
∴10y – 4 = 12
∴10y – 4 + 4=12 + 4
…[Adding 4 on both the sides]
∴10y = 16
∴\(\frac{10 y}{10}=\frac{16}{10}\)…[Dividing both the sides by 10]
∴y = \(\frac { 8 }{ 5 }\)

xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
∴\(\frac{b+(b+1)+(b+2)}{4} \times 4=21 \times 4\)
…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.1 Intext Questions and Activities

Std 8 Maths Practice Set 12.1 Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __

ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __

iii. [latex]\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × __ = 4 ×__
∴x = __

iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5

ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9

iii. \(\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12

iv. 4x = 24
∴ \(\frac{4 x}{[4]}=\frac{24}{[4]}\)
… [Dividing both the sides by 4]
∴x = 6

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.3 8th Std Maths Answers Solutions Chapter 11 Statistics.

Practice Set 11.3 8th Std Maths Answers Chapter 11 Statistics

Exercise 11.3 Class 8 Question 1.
Show the following information by a percentage bar graph.

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75

Solution:

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75
Percentage of students securing grade A	75%	60%	25%	20%
Percentage of students not securing grade A	25%	40%	75%	80%

Statistics for Class 8 Question 2.
Observe the following graph and answer the questions.

1. State the type of the bar graph.
2. How much percent is the Tur production to total production in Ajita’s farm?
3. Compare the production of Gram in the farms of Yash and Ravi and state whose percentage of production is more and by how much?
4. Whose percentage production of Tur is the least?
5. State production percentages of Tur and Gram in Sudha’s farm.

Solution:

1. The given graph is a percentage bar graph.
2. Percent of tur production to the total production in Ajita’s farm is 60%.
3. Production of Gram in the farm of Yash = 50%
   Production of Gram in the farm of Ravi = 30%
   ∴ Difference in the production = 50% – 30% =20%
   ∴ Yash’s production of Gram is more and by 20%.
4. Sudha’s percentage production of Tur is the least.
5. Production percentages of Tur and Gram in Sudha’s farm are 40% and 60% respectively.

8th Standard Statistics Question 3.
The following data is collected in a survey of some students of 10th standard from some schools. Draw the percentage bar graph of the data.

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24

Solution:

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24
Total number of students	150	80	50	40
Percentage of students having inclination towards science stream	60%	75%	50%	40%
Percentage of students having inclination towards commerce stream	40%	25%	50%	60%

Maharashtra Board Class 8 Maths Chapter 11 Statistics Practice Set 11.3 Intext Questions and Activities

Statistics 8th Class Question 1.
Compare and discuss a percentage bar diagram and a subdivided bar diagram. Use it to learn the graphs in the subjects like Science, Geography. (Textbook pg, no. 74)
Solution:
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.1 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.1 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
Show the following numbers on a number line. Draw a separate number line for each example.
i. \(\frac{3}{2}, \frac{5}{2},-\frac{3}{2}\)
ii. \(\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}\)
iii. \(\frac{-5}{8}, \frac{11}{8}\)
iv. \(\frac{13}{10}, \frac{-17}{10}\)
Solution:
i. \(\frac{3}{2}, \frac{5}{2},-\frac{3}{2}\)

Here, the denominator of each fraction is 2.
∴ Each unit will be divided into 2 equal parts.

ii. \(\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}\)

Here, the denominator of each fraction is 5.
∴ Each unit will be divided into 5 equal parts.

iii. \(\frac{-5}{8}, \frac{11}{8}\)

Here, the denominator of each fraction is 8.
∴ Each unit will be divided into 8 equal parts.

iv. \(\frac{13}{10}, \frac{-17}{10}\)

Here, the denominator of each fraction is 10.
∴ Each unit will be divided into 10 equal parts.

Question 2.
Observe the number line and answer the questions.

i. Which number is indicated by point B?
ii. Which point indicates the number \(1\frac { 3 }{ 4 }\) ?
iii. State whether the statement, ‘the point D denotes the number \(\frac { 5 }{ 2 }\) is true or false.
Solution:
Here, each emit is divided into 4 equal parts.
i. Point B is marked on the 10th equal part on the left side of O.
∴ The number indicated by point B is \(\frac { -10 }{ 4 }\).

ii.

Point C is marked on the 7th equal part on the right side of O.
∴ The number \(1\frac { 3 }{ 4 }\) is indicated by point C.

iii. True
Point D is marked on the 10th equal part on the right side of O.
∴ D denotes the number \(\frac{10}{4}=\frac{5 \times 2}{2 \times 2}=\frac{5}{2}\)

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 4B Algebra 10th Class Maths Part 1 Answers Solutions Chapter 4 Financial Planning.

Problem Set 4B Algebra 10th Std Maths Part 1 Answers Chapter 4 Financial Planning

Financial Planning Class 10 Problem Set 4b
Question 1.
Write the correct alternative for the following questions.

i. If the Face Value of a share is ₹ 100 and Market value is ₹ 75, then which of the following statement is correct?
(A) The share is at premium of ₹ 175
(B) The share is at discount of ₹ 25
(C) The share is at premium of ₹ 25
(D) The share is at discount of ₹ 75
Answer:
(B)

ii. What is the amount of dividend received per share of face value ₹ 10 if dividend declared is 50%.
(A) ₹ 50
(B) ₹ 5
(C) ₹ 500
(D) ₹ 100
Answer:
Dividend = 10 × \(\frac { 50 }{ 100 } \) = ₹ 5
(B)

iii. The NAV of a unit in mutual fund scheme is ₹ 10.65, then find the amount required to buy 500 such units.
(A) 5325
(B) 5235
(C) 532500
(D) 53250
Answer:
(A)

iv. Rate of GST on brokerage is _______
(A) 5%
(B) 12%
(C) 18%
(D) 28%
Answer:
(C)

v. To find the cost of one share at the time of buying the amount of Brokerage and GST is to be ______ MV of share.
(A) added to
(B) subtracted from
(C) Multiplied with
(D) divided by
Answer:
(A)

Problem Set 4b Algebra Class 10 Question 2. Find the purchase price of a share of FV ₹ 100 if it is at premium of ₹ 30. The brokerage rate is 0.3%.
Solution:
Here, Face Value of share = ₹ 100,
premium = ₹ 30, brokerage = 0.3%
MV = FV + Premium
= 100 + 30
= ₹ 130
Brokerage = 0.3% of MV
= \(\frac { 0.3 }{ 100 } \) × 130 = ₹ 0.39
Purchase price of a share = MV + Brokerage
= 130 + 0.39
= ₹ 130.39
Purchase price of a share is ₹ 130.39.

Question 3.
Prashant bought 50 shares of FV ₹ 100, having MV ₹ 180. Company gave 40% dividend on the shares. Find the rate of return on investment.
Solution:
Here, Number of shares = 50, FV = ₹ 100,
MV = ₹ 180, rate of dividend = 40%
∴ Sum invested = Number of shares × MV
= 50 × 180
= ₹ 9000
Dividend per share = 40% of FV
= \(\frac { 40 }{ 100 } \) × 100
Dividend = ₹ 40
∴ Total dividend on 50 shares = 50 × 40
= ₹ 2000

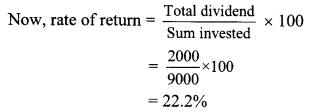
∴ Rate of return on investment is 22.2%.

Question 4.
Find the amount received when 300 shares of FV ₹ 100, were sold at a discount of ₹ 30.
Solution:
Here, FV = ₹ 100, number of shares = 300,
discount = ₹ 30
MV of 1 share = FV – Discount
= 100 – 30 = ₹ 70
∴ MV of 300 shares = 300 × 70
= ₹ 21,000
∴ Amount received is ₹ 21,000.

Question 5.
Find the number of shares received when ₹ 60,000 was invested in the shares of FV ₹ 100 and MV ₹ 120.
Solution:
Here, FV = ₹ 100, MV = ₹ 120,
Sum invested = ₹ 60,000

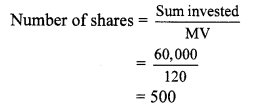
∴ Number of shares received were 500.

Question 6.
Smt. Mita Agrawal invested ₹ 10,200 when MV of the share is ₹ 100. She sold 60 shares when the MV was ₹ 125 and sold remaining shares when the MV was ₹ 90. She paid 0.1% brokerage for each trading. Find whether she made profit or loss? and how much?
Solution:
For purchasing shares:
Here, sum invested = ₹ 10,200, MV = ₹ 100

For selling shares:
60 shares sold at MV of ₹ 125.
∴ MV of 60 shares = 125 × 60
= ₹ 7500
Brokerage = \(\frac { 0.1 }{ 100 } \) × 7500 = ₹ 7.5
∴ Sale value of 60 shares = 7500 – 7.5 = ₹ 7492.5
Now, remaining shares = 102 – 60 = 42
But 42 shares sold at MV of ₹ 90.
∴ MV of 42 shares = 42 × 90 = ₹ 3780
∴ Brokerage = \(\frac { 0.1 }{ 100 } \) × 3780 = ₹ 3.78
∴ Sale value of 42 shares = 3780 – 3.78 = ₹ 3776.22
Total sale value = 7492.5 + 3776.22 = ₹ 11268.72
Since, Purchase value < Sale value
∴ Profit is gained.
∴ Profit = Sale value – Purchase value
= 11268.72 – 10210.2
= ₹ 1058.52
∴ Smt. Mita Agrawal gained a profit of ₹ 1058.52.

Question 7. Market value of shares and dividend declared by the two companies is given below.
Face value is same and it is 7 100 for both the shares. Investment in which company is more profitable?
i. Company A – ₹ 132,12%
ii Company B – ₹ 144,16%
Solution:
For company A:
FV = ₹ 100, MV = ₹ 132,
Rate of dividend = 12%
Dividend = 12% of FV

∴ Rate of return of company B is more.
∴ Investment in company B is more profitable.

Question 8. Shri. Aditya Sanghavi invested ₹ 50,118 in shares of FV ₹ 100, when the market value is ₹ 50. Rate of brokerage is 0.2% and Rate of GST on brokerage is 18%, then How many shares were purchased for ₹ 50,118?
Solution:
Here, FV = ₹ 100, MV = ₹ 50
Purchase value of shares = ₹ 50118,
Rate of brokerage = 0.2%, Rate of GST = 18%
Brokerage = 0.2% of MV


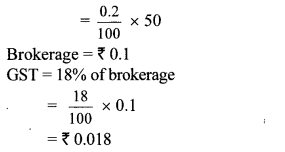
∴ 1000 shares were purchased for ₹ 50,118.

Question 9. Shri. Batliwala sold shares of ₹ 30,350 and purchased shares of ₹ 69,650 in a day. He paid brokerage at the rate of 0.1% on sale and purchase. 18% GST was charged on brokerage. Find his total expenditure on brokerage and tax.
Solution:
Total amount = sale value + Purchase value
= 30350 + 69650
= ₹ 1,00,000
Rate of Brokerage = 0.1 %
Brokerage = 0.1 % of 1,00,000
= \(\frac { 0.1 }{ 100 } \) × 1,00,000
= ₹ 100
Rate of GST = 18%
∴ GST = 18 % of brokerage
= \(\frac { 18 }{ 100 } \) × 100
∴ GST = ₹ 18
Total expenditure on brokerage and tax
= 100 + 18 = ₹ 118
∴ Total expenditure on brokerage and tax is ₹ 118.

Alternate Method:
Brokerage = 0.1 %, GST = 18%
At the time of selling shares:
Total sale amount of shares = ₹ 30,350
Brokerage = 0.1% of 30,350

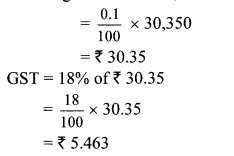
For purchasing shares:
Total purchase amount of shares = ₹ 69,650
Brokerage = 0.1% of 69,650
= \(\frac { 0.1 }{ 100 } \) × 69650
= ₹ 69.65
GST = 18% of 69.65
= \(\frac { 18 }{ 100 } \) × 69.65
= ₹ 12.537
∴ Total expenditure on brokerage and tax = Brokerage and tax on selling + Brokerage and tax on purchasing
= (30.35 + 5.463) + (69.65 + 12.537)
= ₹ 118
∴ Total expenditure on brokerage and tax is ₹ 118.

Question 10. Sint. Aruna Thakkar purchased 100 shares of FV 100 when the MV is ₹ 1200. She paid brokerage at the rate of 0.3% and 18% GST on brokerage. Find the following –
i. Net amount paid for 100 shares.
ii. Brokerage paid on sum invested.
iii. GST paid on brokerage.
iv. Total amount paid for 100 shares.
Solution:
Here, FV = ₹ 100,
Number of shares = 100, MV = ₹ 1200
Brokerage = 0.3%, GST = 18%
i. Sum invested = Number of shares × MV
= 100 × 1200 = ₹ 1,20,000
∴ Net amount paid for 100 shares is ₹ 1,20,000.

ii. Brokerage = 0.3% of sum invested
= \(\frac { 0.3 }{ 100 } \) × 1,20,000 = ₹ 360
∴ Brokerage paid on sum invested is ₹ 360.

iii. GST = 18% of brokerage
= \(\frac { 18 }{ 100 } \) × 360 = ₹ 64.80
∴ GST paid on brokerage is ₹ 64.80.

iv. Total amount paid for 100 shares
= Sum invested + Brokerage + GST
= 1,20,000 + 360 + 64.80
= ₹ 1,20,424.80
∴ Total amount paid for 100 shares is ₹ 1,20,424.80.

Question 11. Smt. Anagha Doshi purchased 22 shares of FV ₹ 100 for Market Value of ₹ 660. Find the sum invested. After taking 20% dividend, she sold all the shares when market value was ₹ 650. She paid 0.1% brokerage for each trading done. Find the percent of profit or loss in the share trading. (Write your answer to the nearest integer)
Solution:
For purchasing shares:
Here, FV = ₹ 100, MV = ₹ 660, Number of shares = 22, rate of brokerage = 0.1%
Sum invested = MV × Number of shares
= 660 × 22
= ₹ 14,520
Brokerage = 0.1 % of sum invested
= \(\frac { 0.1 }{ 100 } \) × 14520 = ₹ 14.52
∴ Amount invested for 22 shares
= Sum invested + Brokerage
= 14520 + 14.52
= ₹ 14534.52
For dividend:
Rate of dividend = 20%
∴ Dividend per share = 20 % of FV

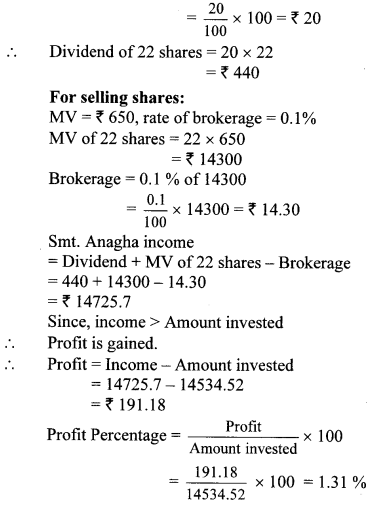
∴ Percentage of profit in the share trading is 1 % (nearest integer).

Alternate Method:
For purchasing share:
Here, FV = ₹ 100, MV = ₹ 660, Number of shares = 22, rate of brokerage = 0.1%
Sum invested = MV × Number of shares
= 660 × 22
= ₹ 14,520
Brokerage = 0.1 % of MV
= \(\frac { 0.1 }{ 100 } \) × 660 = ₹ 0.66
Amount invested for 1 share = 660 + 0.66
= ₹ 660.66
For dividend:
Rate of dividend = 20%
Dividend = 20% of FV = \(\frac { 20 }{ 100 } \) × 100 = ₹ 20
For selling share:
MV = ₹ 650, rate of brokerage = 0.1%
Brokerage = 0.1 % of MV
= \(\frac { 0.1 }{ 100 } \) × 650 = ₹ 0.65 100
Amount received after selling 1 share
= 650 – 0.65 = 649.35
∴ Amount received including divided
= selling price of 1 share + dividend per share
= 649.35 + 20
= ₹ 669.35
Since, income > Amount invested
∴ Profit is gained.
∴ profit = 669.35 – 660.66 = ₹ 8.69
Profit Percentage = \(\frac { 8.69 }{ 660.66 } \) × 100= 1.31%
∴ Percentage of profit in the share trading is 1 % (nearest integer).