Prasanna

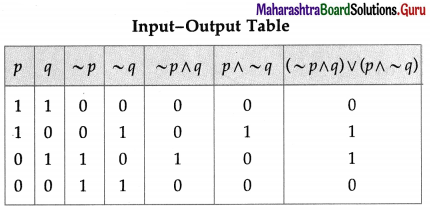
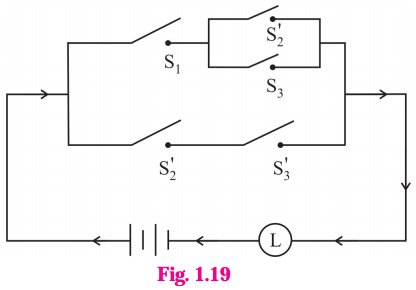
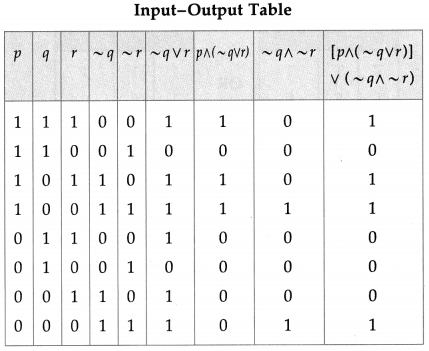
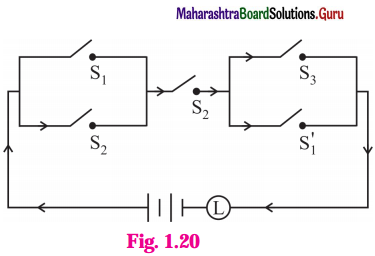
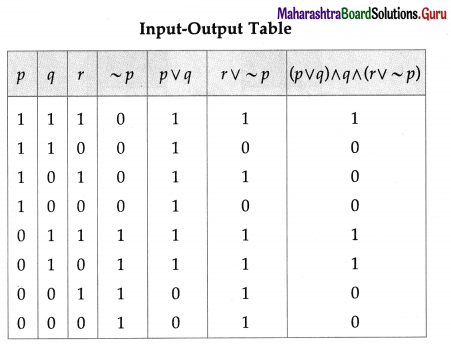
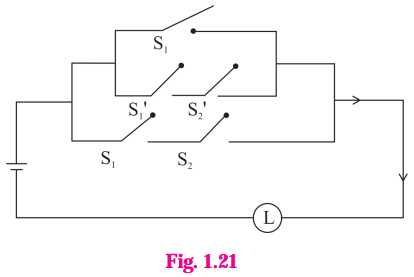
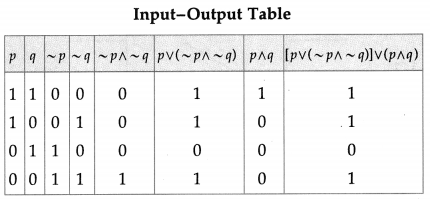
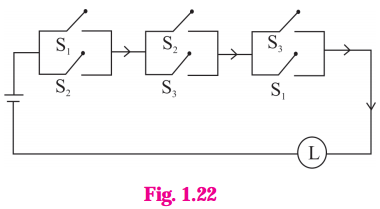
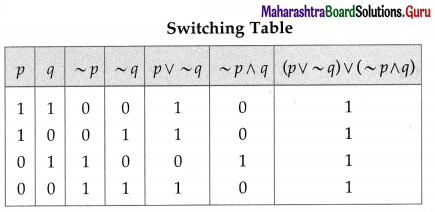
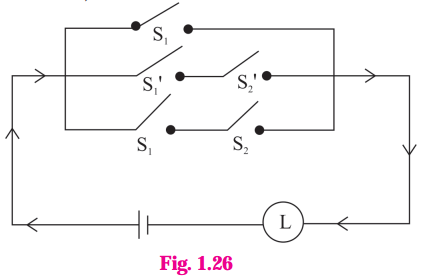
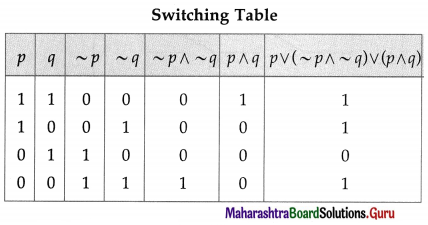
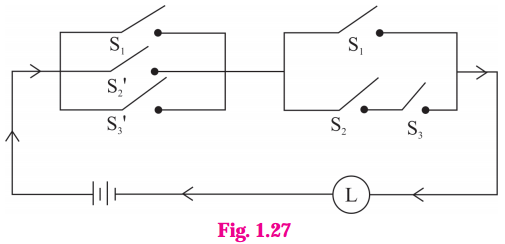
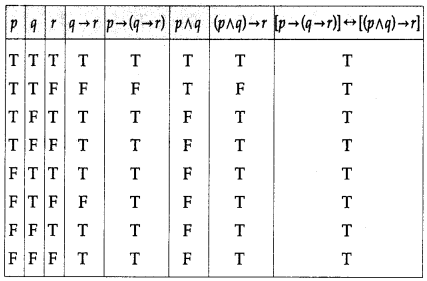
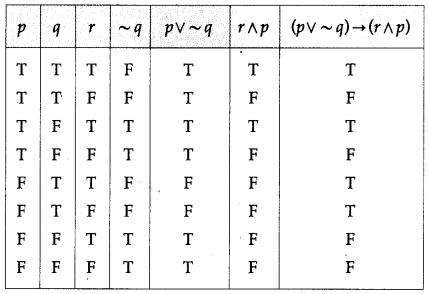
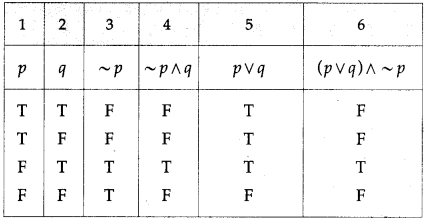
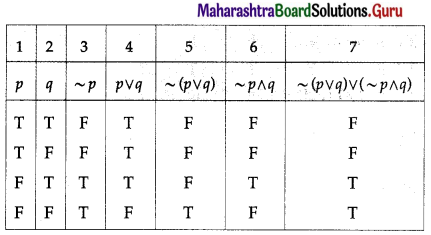
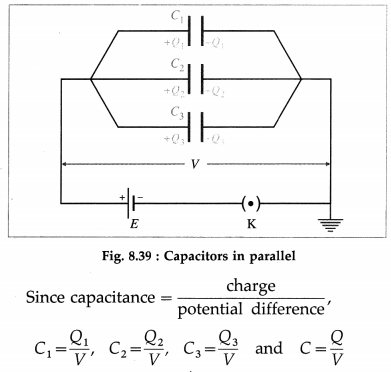
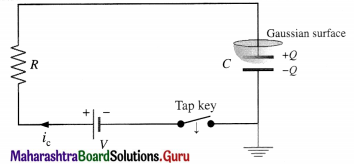
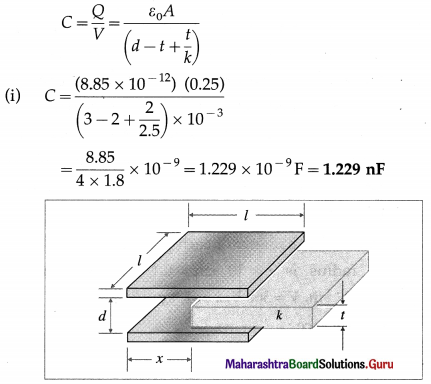
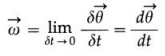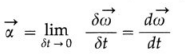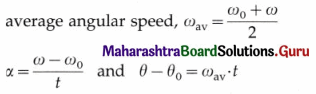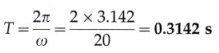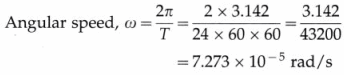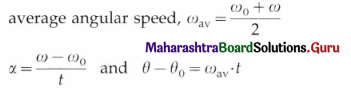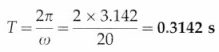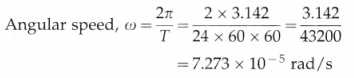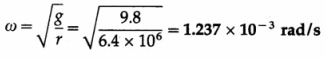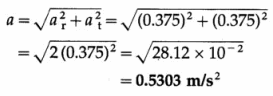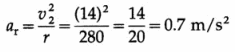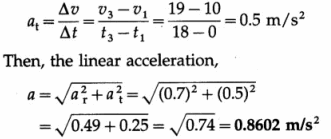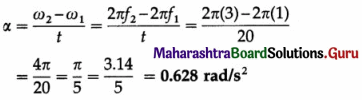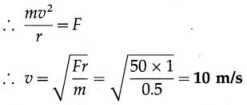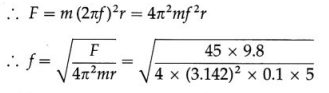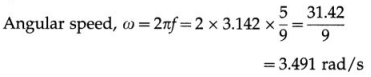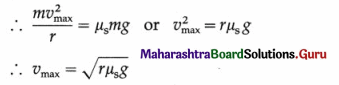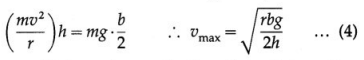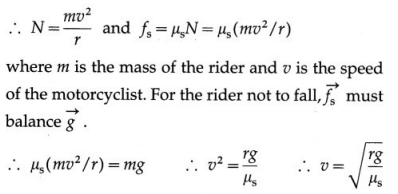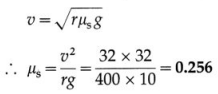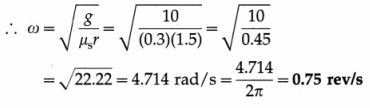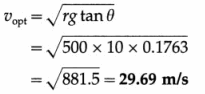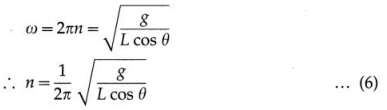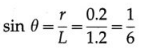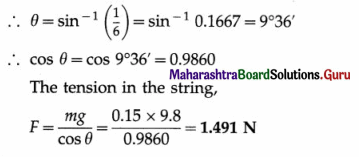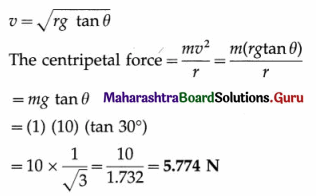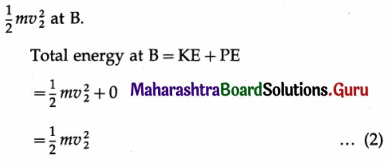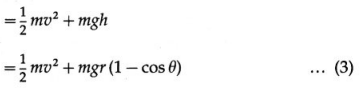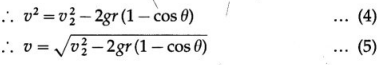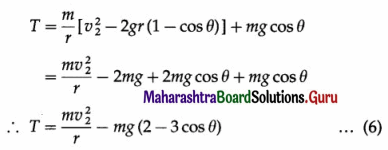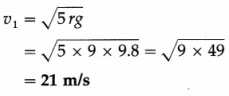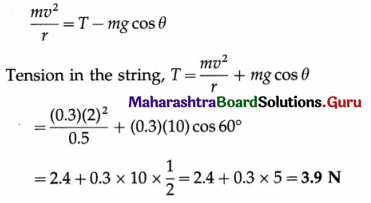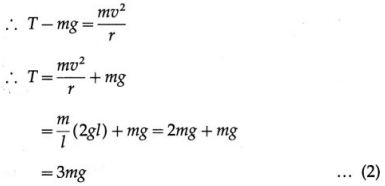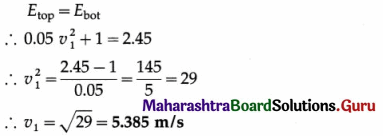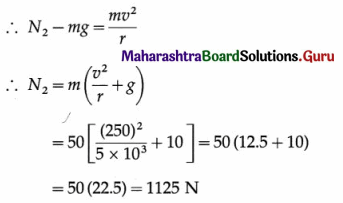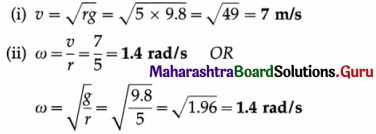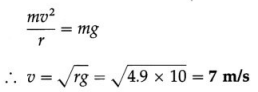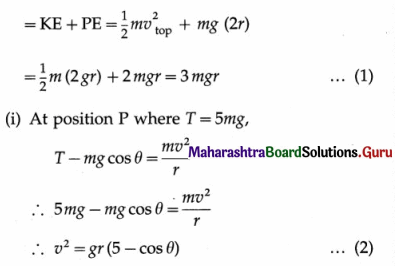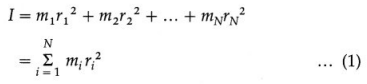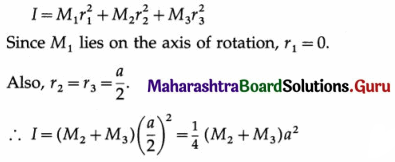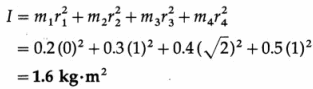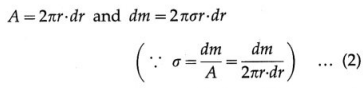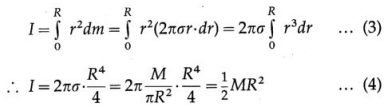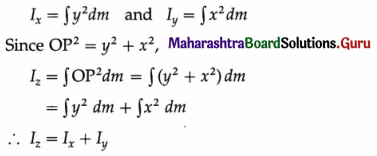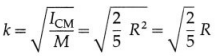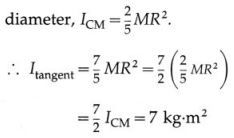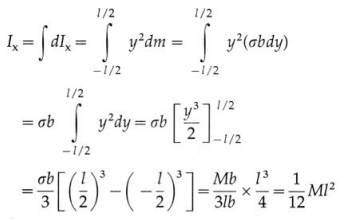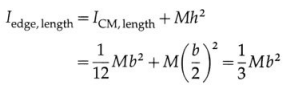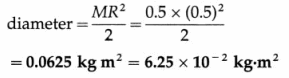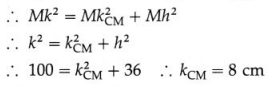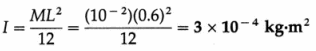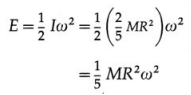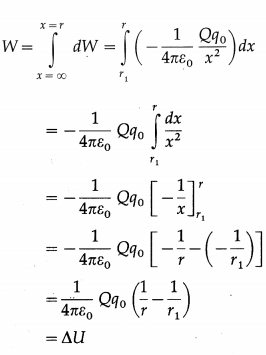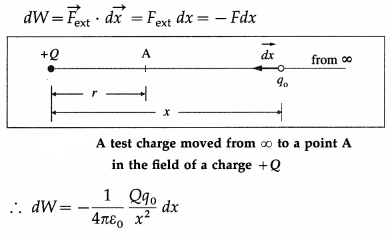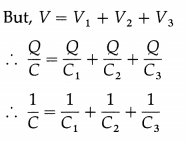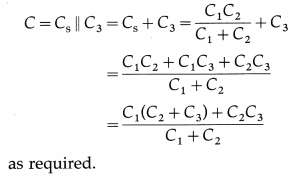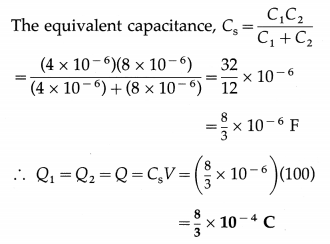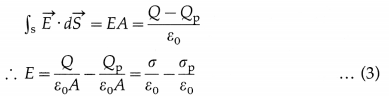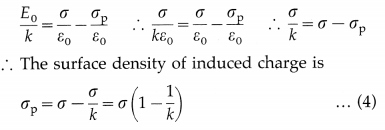Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 1 Rotational Dynamics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 1 Rotational Dynamics

Question 1.
What is circular motion?
Answer:
The motion of a particle along a complete circle or a part of it is called circular motion.

Question 2.
What is a radius vector in circular motion?
Answer:
For a particle performing circular motion, its position vector with respect to the centre of the circle is called the radius vector.
[Note : The radius vector has a constant magnitude, equal to the radius of the circle. However, its direction changes as the position of the particle changes along the circumference.]

Question 3.
What is the difference between rotation and revolution?
Answer:
There is no physical difference between them. It is just a question of usage. Circular motion of a body about an axis passing through the body is called rotation. Circular motion of a body around an axis outside the body is called revolution.

Question 4.
State the characteristics of circular motion.
Answer:

1. It is an accelerated motion : As the direction of velocity changes at every instant, it is an accelerated motion.
2. It is a periodic motion : During the motion, the particle repeats its path along the same trajectory. Thus, the motion is periodic.

Question 5.
Explain angular displacement in circular motion.
Answer:
The change in the angular position of a particle performing circular motion with respect to a reference line in the plane of motion of the particle and passing through the centre of the circle is called the angular displacement.

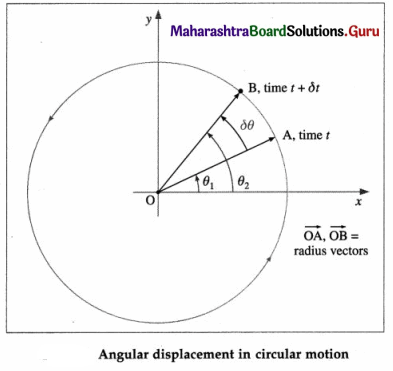
As the particle moves in its circular path, its angular position changes, say from θ₁ at time t to θ₂ at a short time δt later. In the interval δt, the position vector \(\vec{r}\) sweeps out an angle δθ = θ₂ – θ₁. δθ is the magnitude of the change in the angular position of the particle.

Infinitesimal angular displacement \(\overrightarrow{\delta \theta}\) in an infinitesimal time interval δt → 0, is given a direction perpendicular to the plane of revolution by the right hand thumb rule.

Question 6.
Explain angular velocity. State the right hand thumb rule for the direction of angular velocity.
Answer:
Angular velocity : The time rate of angular displacement of a particle performing circular motion is called the angular velocity.

1. If the particle has an angular displacement \(\delta \vec{\theta}\) in a short time interval δt, its angular velocity
   
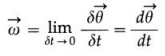
2. \(\vec{\omega}\) is a vector along the axis of rotation, in the direction of \(d \vec{\theta}\), given by the right hand thumb rule.

Right hand thumb rule : If the fingers of the right hand are curled in the sense of revolution of the particle, then the outstretched thumb gives the direction of the angular displacement.

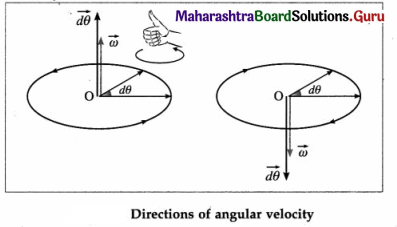
[Note : Angular speed, ω = |\(\vec{\omega}\)| = \(\frac{d \theta}{d t}\) is also called angular frequency. ]

Question 7.
Explain the linear velocity of a particle performing circular motion.
OR
Derive the relation between the linear velocity and the angular velocity of a particle performing circular motion.
Answer:
Consider a particle performing circular motion in an anticlockwise sense, along a circle of radius r. In a very small time interval δt, the particle moves from point A to point B through a distance δs and its angular position changes by δθ.

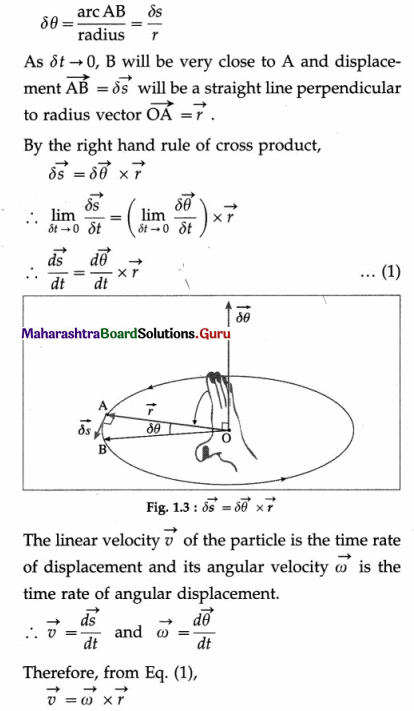
Since is tangential, the instantaneous linear velocity \(\vec{v}\) of a particle performing circular motion is along the tangent to the path, in the sense of motion of the particle.

\(\vec{v}\), \(\vec{\omega}\) and \(\vec{r}\) are mutually perpendicular, so that in magnitude, v = ωr.

Question 8.
State the relation between the linear velocity and the angular velocity of a particle in circular motion.
Answer:
Linear velocity, \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\) where ω is the angular velocity and r is the radius vector.

At every instant, \(\vec{v}\), \(\vec{\omega}\) and \(\vec{r}\) are mutually perpendicular, so that in magnitude v = ωr.

Question 9.
Define uniform circular motion (UCM).
Answer:
A particle is said to perform uniform circular motion if it moves in a circle or a circular arc at constant linear speed or constant angular velocity.

Question 10.
A stone tied to a string is rotated in a horizontal circle (nearly). If the string suddenly breaks, in which direction will the stone fly off ?
Answer:
In a circular motion, the instantaneous velocity \(\vec{v}\) is always tangential, in the sense of the motion. Hence, an inertial observer will see the stone fly off tangentially, in the direction of \(\vec{v}\) at the instant the string breaks.

Question 11.
What is the angular speed of a particle moving in a circle of radius r centimetres with a constant speed of v cm/s ?
Answer:
Angular speed, ω = \(\frac{v \mathrm{~cm} / \mathrm{s}}{r \mathrm{~cm}}\) = \(\frac{v}{r}\) rad/s.

Question 12.
Define the period and frequency of revolution of a particle performing uniform circular motion (UCM) and state expressions for them. Also state their SI units.
Answer:
(1) Period of revolution : The time taken by a particle performing UCM to complete one revolution is called the period of revolution or the period (T) of UCM.
T = \(\frac{2 \pi r}{v}\) = \(\frac{2 \pi}{\omega}\)
where v and ω are the linear and angular speeds, respectively.
SI unit: the second (s)
Dimensions : [M°L°T¹].

(2) Frequency of revolution : The number of revolutions per unit time made by a particle in UCM is called the frequency of revolution (f).

The particle completes 1 revolution in periodic time T. Therefore, it completes 1/T revolutions per unit time.
∴ Frequency f = \(\frac{1}{T}\) = \(\frac{v}{2 \pi r}\) = \(\frac{\omega}{2 \pi}\)
SI unit : the hertz (Hz), 1 Hz = 1 s^-1
Dimensions : [M°L°T^-1]

Question 13.
If the angular speed of a particle in UCM is 20π rad/s, what is the period of UCM of the particle?
Answer:
The period of UCM of the particle,
T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{20 \pi}\) = 0.1 s

Question 14.
Why is UCM called a periodic motion?
Answer:
In a uniform motion, a particle covers equal distances in equal intervals of time. Any motion which repeats itself in equal intervals of time is called a periodic motion. In a uniform circular motion (UCM), the particle takes the same time to complete each revolution, a distance equal to the circumference of the circle. Therefore, it is a periodic motion.

Question 15.
Give one example of uniform circular motion.
Answer:

1. Circular motion of every particle of the blades of a fan or the dryer drum of a washing machine when the fan or the drum is rotating with a constant angular speed.
2. Motion of the hands of a clock.
3. Motion of an Earth-satellite in a circular orbit.

Question 16.
What can you say about the angular speed of an hour hand as compared to that of the Earth’s rotation about its axis ?
Answer:
The periods of rotation of an hour hand and the Earth are T_h = 12 h and T_E = 24 h, respectively, so that their angular speeds are ω_h = \(\frac{2 \pi}{12}\) rad/h and ω_E = \(\frac{2 \pi}{24}\) rad/h.
∴ ω_h = 2ω_E

Question 17.
Explain the acceleration of a particle in UCM. State an expression for the acceleration.
Answer:
A particle in uniform circular motion (UCM) moves in a circle or circular arc at constant linear speed v. The instantaneous linear velocity \(\vec{v}\) of the particle is along the tangent to the path in the sense of motion of the particle. Since \(\vec{v}\) changes in direction, without change in its magnitude, there must be an acceleration that must be

1. perpendicular to \(\vec{v}\)
2. constant in magnitude
3. at every instant directed radially inward, i.e., towards the centre of the circular path.

Such a radially inward acceleration is called a centripetal acceleration.
∴ \(\vec{a}\) = \(\frac{d \vec{v}}{d t}\) = \(\overrightarrow{a_{\mathrm{r}}}\)

If \(\vec{\omega}\) is the constant angular velocity of the particle and r is the radius of the circle,
\(\overrightarrow{a_{\mathrm{r}}}\) = –\(\omega^{2} \vec{r}\)
where ω = |\(\vec{\omega}\)| and the minus sign shows that the direction of \(\vec{a}_{\mathrm{r}}\) is at every instant opposite to that of the radius vector \(\vec{r}\). In magnitude,
a_r = ω²r = \(\frac{v^{2}}{r}\) = ωv

[Note : The word centripetal comes from Latin for ‘centre-seeking’.]

Question 18.
Draw a diagram showing the linear velocity, angular velocity and radial acceleration of a particle performing circular motion with radius r.
Answer:

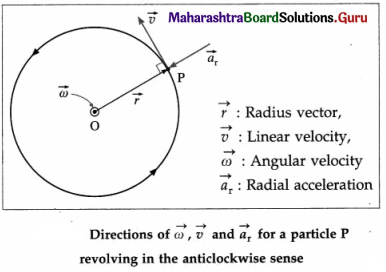
Question 19.
If a particle in UCM has linear speed 2 m/s and angular speed 5 rad/s, what is the magnitude of the centripetal acceleration of the particle ?
Answer:
The magnitude of the centripetal acceleration of the particle is a_r = ωv = (5)(2) = 10 m/s²

Question 20.
State any two quantities that are uniform in UCM.
Answer:
Linear speed and angular speed. (Also, kinetic energy, angular speed and angular momentum.)

Question 21.
State any two quantities that are nonuniform in UCM.
Answer:
Velocity and acceleration are nonuniform in UCM.
(Also, centripetal force.)

Question 22.
What is a nonuniform circular motion?
Answer:
Consider a particle moving in a plane along a circular path of constant radius. If the particle is speeding up or slowing down, its angular speed ω and linear speed v both change with time. Then, the particle is said to be in a non uniform circular motion.

Question 23.
Explain angular acceleration.
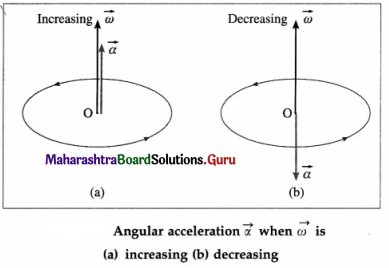
Answer:
Angular acceleration : The time rate of change of angular velocity of a particle performing circular motion is called the angular acceleration.

(i) If \(\delta \vec{\omega}\) is the change in angular Velocity in a short time interval St, the angular acceleration

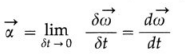
(ii) The direction of \(\vec{\alpha}\) is the same as that of \(d \vec{\omega}\). We consider the case where a change in \(\vec{\omega}\) arises due to a change in its magnitude only. If the particle is speeding up, i.e., ω is increasing with time, then \(\vec{\alpha}\) is in the direction of \(\vec{\omega}\). If the particle is slowing down, i.e., ω is decreasing with time, then \(\vec{\alpha}\) is directed opposite to \(\vec{\omega}\).

(iii) If the angular speed changes from ω₁ to ω₂ in time f, the magnitude (α) of the average angular acceleration is
α = \(\frac{\omega_{2}-\omega_{1}}{t}\)

Question 24.
Explain the tangential acceleration of a particle in non uniform circular motion.
Answer:
Tangential acceleration : For a particle performing circular motion, the linear acceleration tangential to the path that produces a change in the linear speed of the particle is called the tangential acceleration.
Explanation :
(i) If a particle performing circular motion is speeding up or slowing down, its angular speed co and linear speed v both change with time.

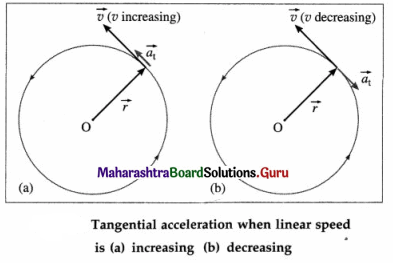
The linear acceleration that produces a change only in the linear speed must be along \(\vec{v}\). Hence, it is called the tangential acceleration, \(\overrightarrow{a_{\mathrm{t}}}\). In magnitude, a_t = dv/dt

(ii) If the linear speed v of the particle is increasing, \(\overrightarrow{a_{\mathrm{t}}}\) is in the direction of \(\vec{v}\). If v is decreasing, \(\overrightarrow{a_{\mathrm{t}}}\) is directed opposite to \(\vec{v}\).

Question 25.
Obtain the relation between the magnitudes of the linear (tangential) acceleration and angular acceleration in non uniform circular motion.
Answer:
Consider a particle moving along a circular path of constant radius r. If the particle is speeding up or slowing down, its motion is nonuniform, and its angular speed ω and linear speed v both change with time. At any instant, v, ω and r are related by v = ωr
The angular acceleration of the particle is
α = \(\frac{d \omega}{d t}\)

The tangential acceleration \(\overrightarrow{a_{\mathrm{t}}}\) is the linear acceleration that produces a change in the linear speed of the particle and is tangent to the circle. In magnitude,

This is the required relation.

Question 26.
Obtain an expression for the acceleration of a particle performing circular motion. Explain its two components.
OR
For a particle performing uniform circular motion, \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\). Obtain an expression for the linear acceleration of a particle performing non-uniform circular motion.
OR
In circular motion, assuming \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\), obtain an expression for the resultant acceleration of a particle in terms of tangential and radial components.
Answer:
Consider a particle moving along a circular path of constant radius r. If its motion is nonuniform, then its angular speed ω and linear speed v both change with time.

acceleration is called the radial or centripetal acceleration \(\overrightarrow{a_{\mathrm{r}}}\).
\(\overrightarrow{a_{\mathrm{r}}}\) = \(\vec{\omega}\) × \(\vec{v}\) … (5)
In magnitude, a_r = ωv
since \(\vec{\omega}\) is perpendicular to \(\vec{v}\).
∴ \(\vec{a}\) = \(\overrightarrow{a_{\mathrm{t}}}\) + \(\overrightarrow{a_{\mathrm{r}}}\) …. (6)
This is the required expression.

Question 27.
What is the angle between linear acceleration and angular acceleration of a particle in nonuniform circular motion ?
Answer:
In a nonu niform circular motion, the angular acceleration is an axial vector, perpendicular to the plane of the motion. The linear acceleration is in the plane of the motion. Hence, the angle between them is 90°.

Question 28.
What are the differences between a nonuniform circular motion and a uniform circular motion? (Two points of distinction) Give examples.
Answer:
(i) Nonuniform circular motion :

1. The angular and tangential accelerations are non-zero, so that linear and angular speeds both change with time.
   
2. The net linear acceleration, being the resultant of the radial and tangential accelerations, is not radial, \(\vec{a}\) = \(\overrightarrow{a_{\mathrm{c}}}\) + \(\overrightarrow{a_{t}}\),
3. The magnitudes of the centripetal acceleration and the centripetal force are not constant.
4. Example : Motion of the tip of a fan blade when the fan is speeding up or slowing down.

(ii) Uniform circular motion :

1. The angular and tangential accelerations are zero, so that linear speed and angular velocity are constant.
2. The net linear acceleration is radially inward, i.e., centripetal.
3. The magnitudes of the centripetal acceleration and the centripetal force are also constant.
4. Example : Motion of the tips of the hands of a mechanical clock.

Question 29.
Write the kinematical equations for circular motion in analogy with linear motion.
Answer:
For circular motion of a particle with constant angular acceleration α,

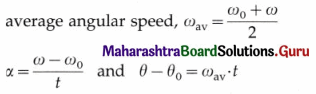
where ω₀ and ω are the initial and final angular speeds, t is the time, ω_av the average angular speed and θ_o and θ the initial and final angular positions of the particle.

Then, the angular kinematical equations for the circular motion are (in analogy with linear kinematical equations for constant linear acceleration)
ω = ω₀ + αt
θ – θ₀ = ω₀t + \(\frac{1}{2} \alpha t^{2}\)
ω² = \(\omega_{0}^{2}\) + 2α (θ – θ₀)

Question 30.
Solve the following :

Question 1.
Certain stars are believed to be rotating at about 1 rot/s. If such a star has a diameter of 40 km, what is the linear speed of a point on the equator of the star?
Solution :
Data : d = 40 km, /= 1 rot/s
∴ r = \(\frac{d}{2}\) = \(\frac{40 \mathrm{~km}}{2}\) = 20 km = 2 × 10⁴ m
Linear speed, v = ωr = (2πf)r
= (2 × 3.142 × 1)(2 × 10⁴)
= 6.284 × 2 × 10⁴
= 1.257 × 10⁵ m/s (or 125.6 km/s)

Question 2.
A body of mass 100 grams is tied to one end of a string and revolved along a circular path in the horizontal plane. The radius of the circle is 50 cm. If the body revolves with a constant angular speed of 20 rad/s, find the

1. period of revolution
2. linear speed
3. centripetal acceleration of the body.

Solution :
Data : m = 100 g = 0.1 kg, r = 50 cm = 0.5 m, ω = 20 rad/s

1. The period of revolution of the body,
   
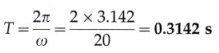
2. Linear speed, v = ωr = 20 × 0.5 = 10 m/s
3. Centripetal acceleration,
   a_c = w²r = (20)² × 0.5 = 200 m/s²

Question 3.
Calculate the angular speed of the Earth due to its spin (rotational motion).
Solution :
Data : T = 24 hours = 24 × 60 × 60 s

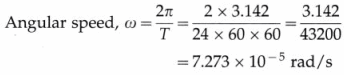
The angular speed of the Earth due to its spin (rotational motion) is 7.273 × 10^-5 rad/s.

Question 4.
Find the angular speed of rotation of the Earth so that bodies on the equator would feel no weight. [Radius of the Earth = 6400 km, g = 9.8 m/s²]
Solution :
Data : Radius of the Earth = r = 6400 km = 6.4 × 10⁶ m, g = 9.8 m/s²

As the Earth rotates, the bodies on the equator revolve in circles of radius r.

Question 31.
Write the kinematical equations for circular motion in analogy with linear motion.
Answer:
For circular motion of a particle with constant angular acceleration α,

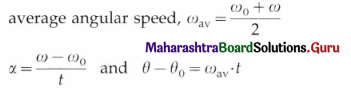
where ω₀ and ω are the initial and final angular speeds, t is the time, ω_av the average angular speed and 0o and 0 the initial and final angular positions of the particle.

Then, the angular kinematical equations for the circular motion are (in analogy with linear kinematical equations for constant linear acceleration)
ω = ω₀ + αt
θ – θ_o = ω₀t + \(\frac{1}{2} \alpha t^{2}\)
ω² = \(\omega_{0}^{2}\) + 2α (θ – θ_o)

Question 32.
Solve the following :

Question 1.
Certain stars are believed to be rotating at about 1 rot/s. If such a star has a diameter of 40 km, what is the linear speed of a point on the equator of the star?
Solution :
Data : d = 40 km, f= 1 rot/s
∴ r = \(\frac{d}{2}\) = \(\frac{40 \mathrm{~km}}{2}\) = 20 km = 2 × 10⁴ m
Linear speed, v = ωr = (2πf)r
= (2 × 3.142 × 1)(2 × 10⁴)
= 6.284 × 2 × 10⁴
= 1.257 × 10⁵ m/s (or 125.6 km/s)

Question 2.
A body of mass 100 grams is tied to one end of a string and revolved along a circular path in the horizontal plane. The radius of the circle is 50 cm. If the body revolves with a constant angular speed of 20 rad/s, find the

1. period of revolution
2. linear speed
3. centripetal acceleration of the body.

Solution :
Data : m = 100 g = 0.1 kg, r = 50 cm = 0.5 m, ω = 20 rad/s

1. The period of revolution of the body,
   
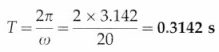
2. Linear speed, v = ωr = 20 × 0.5 = 10 m/s
3. Centripetal acceleration,
   a_c = ω² = (20)² × 0.5 = 200 m/s²

Question 3.
Calculate the angular speed of the Earth due to its spin (rotational motion).
Solution :
Data : T = 24 hours = 24 × 60 × 60 s

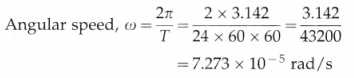
The angular speed of the Earth due to its spin (rotational motion) is 7.273 × 10^-5 rad/s.

Question 4.
Find the angular speed of rotation of the Earth so that bodies on the equator would feel no weight. (Radius of the Earth = 6400 km, g = 9.8 m/s²]
Solution :
Data : Radius of the Earth = r = 6400 km
= 6.4 × 10⁶ m, g = 9.8 m/s²
As the Earth rotates, the bodies on the equator revolve in circles of radius r.
These bodies would not feel any weight if their centripetal acceleration (ωr) is equal to the acceleration due to gravity (g).
∴ ω²r = g
The angular speed of the Earth’s rotation,

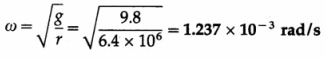
Question 5.
To simulate the acceleration of large rockets, astronauts are seated in a chamber and revolved in a circle of radius 9.8 m. What angular speed is required to generate a centripetal acceleration 8 times the acceleration due to gravity? [g = 9.8 m/s²]
Solution :
Data : r = 9.8 m, g = 9.8 m/s², a = 8g
Centripetal acceleration = ω²r
∴ ω²r = 8g
∴ 9.8 ω² = 8(9.8)
∴ ω² = 8
The required angular speed, ω = \(\sqrt{8}\) = 2\(\sqrt{2}\) = 2.828 rad/s

Question 6.
The angular position of a rotating object is given by θ(t) = (1.55t² – 7.75 t + 2.87) rad, where t is measured in second.
(i) When is the object momentarily at rest ?
(ii) What is the magnitude of its angular acceleration at that time ?
Solution :

Question 7.
A motor part at a distance of 1.5 m from the motor’s axis of rotation has a constant angular acceleration of 0.25 rad/s². Find the magnitude of its linear acceleration at the instant when its angular speed is 0.5 rad/s.
Solution :
Data : r = 1.5 m, α = 0.25 rad/s², ω = 0.5 rad/s² a_r = ω²r = (0.5)²(1.5) = 0.25 × 1.5 = 0.375 m/s² a_t = αr = 0.25 × 1.5 = 0.375 m/s²
The linear acceleration,

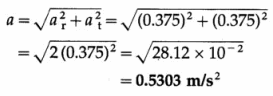
Question 8.
A coin is placed on a stationary disc at a distance of 1 m from the disc’s centre. At time t = 0 s, the disc begins to rotate with a constant angular acceleration of 2 rad/s² around a fixed vertical axis through its centre and perpendicular to its plane.
Find the magnitude of the linear acceleration of the coin at t = 1.5 s. Assume the coin does not slip.
Solution :

Question 9.
A railway locomotive enters a stretch of track, which is in the form of a circular arc of radius 280 m, at 10 m/s and with its speed increasing uniformly. Ten seconds into the stretch its speed is 14m/s and at 18s its speed is 19 m/s. Find
(i) the magnitude of the locomotive’s linear acceleration when its speed is 14 m/s
(ii) the direction of this acceleration at that point with respect to the locomotive’s radial acceleration
(iii) the angular acceleration of the locomotive.
Answer:
Data : r = 280 m, v₁ = 10 m/s at t₁ = 0, v₂ = 14 m/s at t₂ = 10 s, v₃ = 19 m/s at t₃ = 18 s
(i) At t = t₂, the radial acceleration is

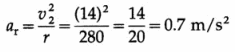
Since the tangential acceleration is constant, it may be found from the data for any two times.

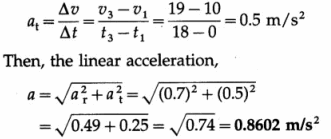
(ii) If θ is the angle between the resultant linear acceleration and the radial acceleration,
tan θ = \(\frac{a_{\mathrm{t}}}{a_{\mathrm{r}}}\) = \(\frac{0.5}{0.7}\) = 0.7142
∴ θ = tan^-1 0.7142 = 35°32′

(iii) a_t = αr
The angular acceleration,
α = \(\frac{a_{\mathrm{t}}}{r}\) = \(\frac{0.5}{280}\)
= 1.785 × 10^-3 rad/s²
= 1.785 mrad/s²

Question 10.
The frequency of revolution of a particle performing circular motion changes from 60 rpm to 180 rpm in 20 seconds. Calculate the angular acceleration of the particle.
Solution :
Data : f₁ =60 rpm = \(\frac{60}{60}\) rev/s = 1 rev/s, f₂ = 180 rpm = \(\frac{180}{60}\) rev/s = 3 rev/s, t = 20 s
The angular acceleration in SI units,

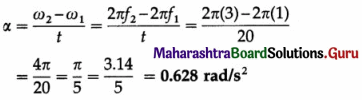
OR
Using non SI units, the angular frequencies are ω₁ = 60 rpm = 1 rps and ω₂ = 180 rpm = 3 rps.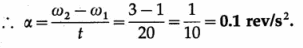

Question 11.
The frequency of rotation of a spinning top is 10 Hz. If it is brought to rest in 6.28 s, find the angular acceleration of a particle on its surface.
Solution:
Data: f₁ = 10Hz, f₂ = 0 Hz, t = 6.28s
The angular acceleration,

Question 12.
A wheel of diameter 40 cm starts from rest and attains a speed of 240 rpm in 4 minutes. Calculate its angular displacement in this time interval.
Solution:

Question 13.
A flywheel slows down uniformly from 1200 rpm to 600 rpm in 5 s. Find the number of revolutions made by the wheel in 5 s.
Solution :
Data : ω₀ = 1200 rpm, ω = 600 rpm, f = 5 s
Since the flywheel slows down uniformly, its angular acceleration is constant. Then, its average angular speed,

Its angular displacement in time t,
θ = ω_av.t = 15 × 5 = 75 revolutions

Question 33.
Define and explain centripetal force.
Answer:
Definition : In the uniform circular motion of a particle, the centripetal force is the force on the particle which at every instant points radially towards the centre of the circle and produces the centripetal acceleration to move the particle in its circular path.

Explanation : A uniform circular motion is an accelerated motion, with a radially inward (i.e., centripetal) acceleration –\(\frac{v^{2}}{r} \hat{\mathrm{r}}\) or \(-\frac{v^{2}}{r} \hat{\mathrm{r}}\), where \(\vec{r}\) is the radius vector and \(\hat{\mathbf{r}}\) is a unit vector in the direction of \(\vec{r}\). Hence, a net real force must act on the particle to produce this acceleration. This force, which at every instant must point radially towards the centre of the circle, is called the centripetal force. If m is the mass of the particle, the centripetal force is

Notes :

1. As viewed from an inertial frame of reference, the centripetal force is necessary and sufficient for the particle to perform UCM. At any instant, if the centripetal force suddenly vanishes, the particle would fly off in the direction of its linear velocity at that instant.
2. In case the angular or linear speed changes with time, as in nonuniform circular motion, the force is not purely centripetal but has a tangential component which accounts for the tangential acceleration.

Question 34.
Give any two examples of centripetal force.
Answer:
Examples of centripetal force :

1. For an Earth-satellite in a circular orbit, the centripetal force is the gravitational force exerted by the Earth on the satellite.
2. In the Bohr atom, the centripetal force on an electron in circular orbit around the nucleus is the attractive Coulomb force of the nucleus.
3. When an object tied at the end of a string is revolved in a horizontal circle, the centripetal force is the tension in the string.
4. When a car takes a turn in a circular arc on a horizontal road with constant speed, the force of static friction between the car tyres and road surfaces is the centripetal force.

Note : The tension in a string or the force of friction is electromagnetic in origin.

Question 35.
Define and explain centrifugal force.
Answer:
Definition : In the reference frame of a particle performing circular motion, centrifugal force is defined as a fictitious, radially outward force on the particle and is equal in magnitude to the particle’s mass times the centripetal acceleration of the reference frame, as measured from an inertial frame of reference.

Explanation : A uniform circular motion is an accelerated motion, with a centripetal acceleration of magnitude v²/r or ω²r. A frame of reference attached to the particle also has this acceleration and, therefore, is an accelerated or noninertial reference frame. The changing direction of the linear velocity appears in this reference frame as a tendency to move radially outward. This is explained by assuming a fictitious centrifugal, i.e., radially outward, force acting on the particle. Since the particle is stationary in its reference frame, the magnitude of the centrifugal force is mv²/r or mω²r, the same as that of the centripetal force on the particle.

Note : The word ‘centrifugal’ comes from the Latin for ‘fleeing from the centre’. The word has the same root fuge from the Latin ‘to flee’ as does refugee.

Question 36.
Give any two examples of centrifugal force.
Answer:
Examples of centrifugal force :

1. A person in a merry-go-round experiences a radially outward force.
2. Passengers of a car taking a turn on a level road experience a force radially away from the centre of the circular road.
3. A coin on a rotating turntable flies off for some high enough angular speed of the turntable.
4. As the Earth rotates about its axis, the centrifugal force on its particles is directed away from the axis. The force increases as one goes from the poles towards the equator. This leads to the bulging of the Earth at the equator.

Question 37.
Explain why centrifugal force is called a pseudo force.
Answer:
A force which arises from gravitational, electromagnetic or nuclear interaction between matter is called a real force. The centrifugal force does not arise due to any of these interactions. Therefore, it is not a real force.

The centrifugal force in the noninertial frame of reference of a particle in circular motion is the effect of the acceleration of the frame of reference. Therefore, it is called a pseudo or fictitious force.

Question 38.
Distinguish between centripetal force and centrifugal force. State any two points of distinction.
Answer:

Centripetal force	Centrifugal force
1. Centripetal force is the force required to provide centri­petal acceleration to a par­ticle to move it in a circular path.	1. The centrifugal tendency of the particle, in its acceler­ated, i.e., non-inertial, frame of reference, is explained by assuming a centrifugal force acting on it.
2. At every instant, it is directed radially towards the centre of the circular path.	2. At every instant, it is directed radially away from the centre of the circular path.
3. It is a real force arising from gravitational or electromag­netic interaction between matter.	3. It is a pseudo force since it is the effect of the acceleration of the reference frame of the revolving particle.

Question 39.
Solve the following :

Question 1.
An object of mass 0.5 kg is tied to a string and revolved in a horizontal circle of radius 1 m. If the breaking tension of the string is 50 N, what is the maximum speed the object can have?
Solution :
Data : m = 0.5 kg, r = 1 m, F = 50 N
The maximum centripetal force that can be applied is equal to the breaking tension.

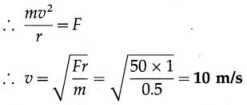
This is the maximum speed the object can have.

Question 2.
A certain string 500 cm long breaks under a tension of 45 kg wt. An object of mass 100 g is attached to this string and whirled in a horizontal circle. Find the maximum number of revolutions that the object can make per second without breaking the string, [g = 9.8 m/s²]
Solution :
Data : m = 100 g = 0.1 kg, r = 500 cm = 5 m, g = 9.8 m/s², F = 45 kg wt = 45 × 9.8 N
The breaking tension is equal to the maximum centripetal force that can be applied.
∴ F = mω²r ,
But ω = 2πf, where/is the corresponding frequency of revolution.

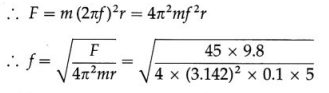
The maximum number of revolutions per second, f = 4.726 Hz

Question 3.
A disc of radius 15 cm rotates with a speed of 33\(\frac{1}{3}\) rpm. Two coins are placed on it at 4 cm and 14 cm from its centre. If the coefficient of friction between the coins and the disc is 0.15, which of the two coins will revolve with the disc ?
Solution :
Data : r = 15 cm = 0.15 m,
f = 33\(\frac{1}{3}\) rpm = \(\frac{100}{3 \times 60}\)rev/s = \(\frac{5}{9}\) Hz, µ_s = 0.15, r₁ = 4 cm = 0.04 m, r₂ = 14 cm = 0.14 m

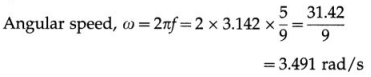
To revolve with the disc without slipping, the necessary centripetal force must be less than or equal to the limiting force of static friction.

Limiting force of static friction, f_s = µ_s N = µ_s (mg) where m is the mass of the coin and N = mg is the normal force on the coin.
∴ mω²r ≤ µ_s(mg) or ω²r ≤ µ_sg
µ_sg = 0.15 × 9.8 = 1.47 m/s²
For the first coin, r₁ = 0.04 m.
∴ ω²r₁ = (3.491)² × 0.04 = 12.19 × 0.04 = 0.4876 m/s²
Since, ω²r₁ < µ_sg, this coin will revolve with the disc. For the second coin, r₂ = 0.14 m.
∴ ω²r₂ = (3.491)² × 0.14 = 12.19 × 0.14 = 1.707 m/s²
Since, ω²r₂ > µ_sg, this coin will not revolve with the disc.
Thus, only the coin placed at 4 cm from the centre will revolve with the disc.

Question 40.
Derive an expression for the maximum safe speed for a vehicle on a horizontal circular road without skidding off. State its significance.
Answer:
Consider a car of mass m taking a turn of radius r along a level road. If µ_s is the coefficient of static friction between the car tyres and the road surface, the limiting force of friction is f_s = µ_sN = µ_smg where N = mg is the normal reaction. The forces on the car, as seen from an inertial frame of reference are shown in below figure.

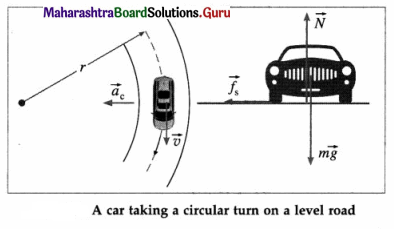
Then, the maximum safe speed v_max with which the car can take the turn without skidding off is set by maximum centripetal force = limiting force of static friction

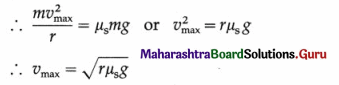
This is the required expression.
Significance : The above expression shows that the maximum safe speed depends critically upon friction which changes with circumstances, e.g., the nature of the surfaces and presence of oil or water on the road. If the friction is not sufficient to provide the necessary centripetal force, the vehicle is likely to skid off the road.

[Note : At a circular bend on a level railway track, the centrifugal tendency of the railway carriages causes the flange of the outer wheels to brush against the outer rail and exert an outward thrust on the rail. Then, the reaction of the outer rail on the wheel flange provides the necessary centripetal force.]

Question 41.
Derive an expression for the maximum safe speed for a vehicle on a circular horizontal road without toppling/overturning/rollover.
Answer:
Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are :

1. the lateral limiting force of static friction \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels-acting along the axis of the wheels and towards the centre of the circular path which provides the necessary centripetal force.
2. the weight \(m \vec{g}\) acting vertically downwards at the centre of gravity (C.G.)
3. the normal reaction \(\vec{N}\) of the road on the wheels, acting vertically upwards effectively at the C.G. Since maximum centripetal force = limiting force of static friction,
   

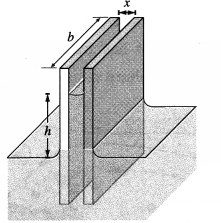
In a simplified rigid-body vehicle model, we consider only two parameters-the height h of the C.G. above the ground and the average distance b between the left and right wheels called the track width.

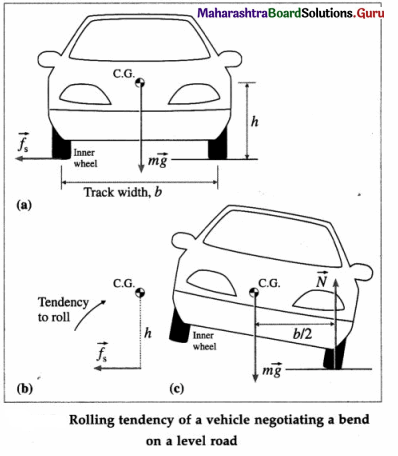
The friction force \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels produces a torque T, that tends to overturn/rollover the car about the outer wheel. Rotation about the front-to-back axis is called roll

When the inner wheel just gets lifted above the ground, the normal reaction \(\vec{N}\) of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque \(\tau_{\mathrm{r}}\) which tends to restore the car back on all four wheels
\(\tau_{\mathrm{r}}\) = mg.\(\frac{b}{2}\) … (3)

The car does not topple as long as the restoring torque \(\tau_{\mathrm{r}}\) counterbalances the toppling torque \(\tau_{\mathrm{t}}\). Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by

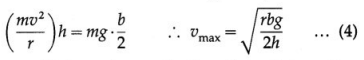
Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force \(m \vec{g}\) passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower centre of gravity.

Question 42.
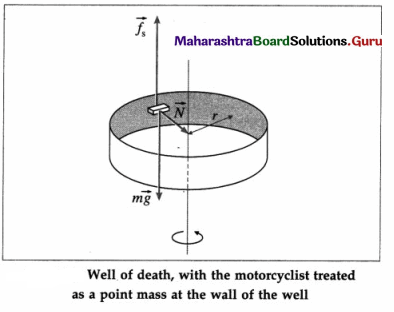
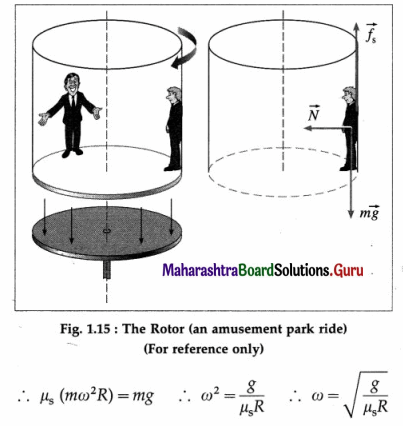
A carnival event known as a “well of death” consists of a large vertical cylinder inside which usually a stunt motorcyclist rides in horizontal circles. Show that the minimum speed necessary to keep the rider from falling is given by v = \(\sqrt{r g / \mu_{s}}\), in usual notations.
Answer:
The forces exerted on the rider are

1. the normal force \(\vec{N}\) exerted by the wall, directed radially inward, is the centripetal force,
2. the upward frictional force \(\overrightarrow{f_{\mathrm{s}}}\) exerted by the wall, since the motorcycle has a tendency to slide down,
3. the downward gravitational force \(m \vec{g}\).

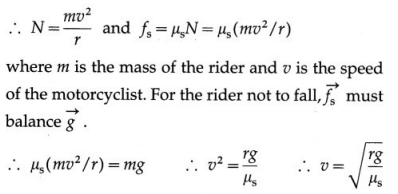
which is the required expression.

Question 43.
A road at a bend should be banked for an optimum or most safe speed v₀. Derive an expression for the required angle of banking.
OR
Obtain an expression for the optimum or most safe speed with which a vehicle can be driven along a curved banked road. Hence show that the angle of banking is independent of the mass of a vehicle.
Answer:
Consider a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum or most safe speed v₀. Let m be the mass of the car. In general, the forces acting on the car are
(a) its weight \(m \vec{g}\), acting vertically down
(b) the normal reaction of the road \(\vec{N}\), perpendicular to the road surface
(c) the frictional force \(\overrightarrow{f_{s}}\) along the inclined surface of the road.

At the optimum speed, frictional force is not relied upon to contribute to the necessary lateral centripetal force. Thus, ignoring \(\overrightarrow{f_{\mathrm{s}}}\), resolve \(\vec{N}\) into two perpendicular components : N cos θ vertically up and N sin θ horizontally towards the centre of the circular path. Since there is no acceleration in the vertical direction, N cos θ balances mg and N sin θ provides the necessary centripetal force.

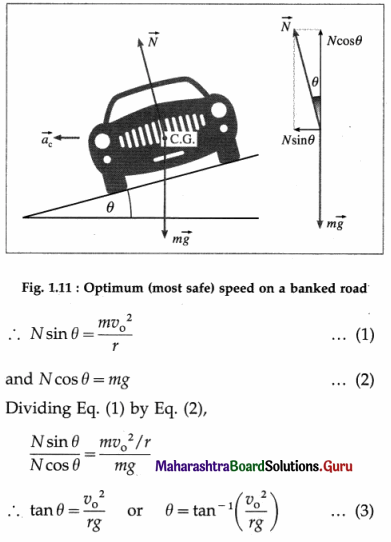
Equation (3) gives the expression for the required angle of banking. From EQ. (3), we can see that θ depends upon v₀, r and g. The angle of banking is independent of the mass of a vehicle negotiating the curve. Also, for a given r and θ, the recommended optimum speed is
v₀ = \(\sqrt{r g \tan \theta}\) … (4)

Question 44.
State any two factors on which the most safe speed of a car in motion along a banked road depends.
Answer:
The angle of banking of the road and the radius of the curved path.

Question 45.
A curved horizontal road must be banked at an angle θ’ for an optimum speed v. What will happen to a vehicle moving with a speed v along this road if the road is banked at an angle θ such that
(i) θ < θ’
(ii) θ > θ’?
Answer:
(i) For θ < θ’, the horizontal component of the normal reaction would be less than the optimum value and will not be able to provide the necessary centripetal force. Then, the vehicle will tend to skid outward, up the inclined road surface.

(ii) For θ > θ’, the horizontal component of the normal reaction would be more than the necessary centripetal force. Then, the vehicle will tend to skid down the banked road.

Question 46.
A banked circular road is designed for traffic moving at an optimum or most safe speed v₀. Obtain an expression for
(a) the minimum safe speed
(b) the maximum safe speed with which a vehicle can negotiate the curve without skidding.
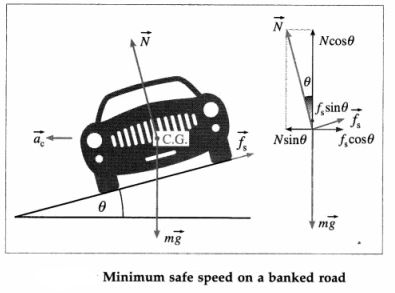
Answer:
Consider a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum speed v. Let m be the mass of the car. In general, the forces acting on the car are
(a) its weight \(m \vec{g}\), acting vertically down
(b) the normal reaction of the road \(\vec{N}\), perpendicular to the road surface
(c) the frictional force \(\overrightarrow{f_{\mathrm{s}}}\) along the inclined surface of the road.
If µ_s is the coefficient of static friction between the tyres and road, f_s = µ_sN.

(a) For minimum safe speed : If the car is driven at a speed less than the optimum speed v₀, it may tend to slide down the inclined surface of the road so that \(\overrightarrow{f_{\mathrm{s}}}\) is up the incline.

Resolve \(\vec{N}\) and \(\overrightarrow{f_{\mathrm{s}}}\) into two perpendicular components : Ncos θ and f_s sin θ vertically up; N sin θ horizontally towards centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components N sin θ and f_s cos θ together provide the necessary centripetal force, and N cos θ balances the sum mg + f_s sin θ. If v_max is the maximum safe speed without skidding,

(b) For maximum safe speed : If the car is driven fast enough, at a speed greater than the optimum speed v, it may skid off up the incline so that \(\overrightarrow{f_{\mathrm{s}}}\) is down the incline.

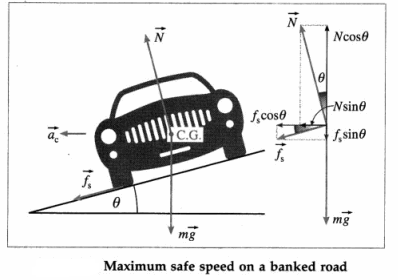
Resolve \(\vec{N}\) and \(\overrightarrow{f_{\mathrm{s}}}\) into two perpendicular components : N cos θ vertically up and f_s sin θ vertically down; N sin θ and f_s cos θ horizontally towards the centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components N sin θ and f cos θ together provide the necessary centripetal force, and N cos θ balances the sum mg + f sin θ. If v is the maximum safe
speed without skidding,

Ignoring few special cases, the maximum value of µ_s = 1. Thus, for θ ≥ 45°, v_max = ∞, i.e., on a heavily banked road a car is unlikely to skid up the incline and the minimun limit is more important.

Question 47.
Solve the following :

Question 1.
Find the maximum speed with which a car can be safely driven along a curve of radius 100 m, if the coefficient of friction between its tyres and the road is 0.2 [g = 9.8 m/s²].
Solution :
Data : r = 100 m, µ_s = 0.2, g = 9.8 m/s²
The maximum speed, v = \(\sqrt{r \mu_{s} g}\)
= \(\sqrt{100 \times 0.2 \times 9.8}\) = 14 m/s

Question 2.
A flat curve on a highway has a radius of curvature 400 m. A car goes around the curve at a speed of 32 m/s. What is the minimum value of the coefficient of friction that will prevent the car from sliding?
Solution:
Data : r = 400 m, v = 32 m/s, g = 10 m/s²

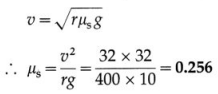
Question 3.
A car can be driven on a flat circular road of radius r at a maximum speed v without skidding. The same car is now driven on another flat circular road of radius 2r on which the coefficient of friction between its tyres and the road is the same as on the first road. What is the maximum speed of the car on the second road such that it does not skid?
Solution:
Data: v₁ = v, r₁ = r, r₂ = 2r
On a flat circular road, the maximum safe speed is

Question 4.
On a dry day, the maximum safe speed at which a car can be driven on a curved horizontal road without skidding is 7 m/s. When the road is wet, the frictional force between the tyres and road reduces by 25%. How fast can the car safely take the turn on the wet road ?
Solution:
Let subscripts 1 and 2 denote the values of a quantity under dry and wet conditions, respectively.
Data : v₁ = 7 m/s, f₂ = f₁, – 0.25f₁ = 0.75f₁

On a dry horizontal curved road, the frictional force between the tyres and road is f₁ = µ₁mg, where m is the mass of the car and g is the gravitational acceleration.

The maximum safe speed for taking a turn of radius r on a dry horizontal curved road is

Question 5.
A coin kept at a distance of 5 cm from the centre of a turntable of radius 1.5 m just begins to slip when the turntable rotates at a speed of 90 rpm. Calculate the coefficient of static friction between the coin and the turntable. [g = π² m/s²]
Solution:
Data: r = 5 cm = 0.05 m, f = 90 rpm = \(\frac{90}{60}\) rps = 1.5 rps, g = π² m/s²

The centripetal force for the circular motion of the coin is provided by the friction between the coin and the turntable. The coin is just about to slip off the turntable when the limiting force of friction is equal to the centripetal force.

Question 6.
A thin cylindrical shell of inner radius 1.5 m rotates horizontally, about a vertical axis, at an angular speed ω. A wooden block rests against the inner surface and rotates with it. If the coefficient of static friction between block and surface is 0.3, how fast must the shell be rotating if the block is not to slip and fall ?

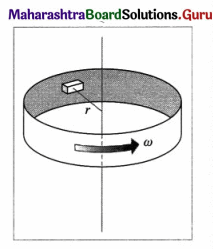
Solution :
Data : r = 1.5 m, µ_s = 0.3
The normal force \(\vec{N}\) of the shell on the block is the centripetal force which holds the block in place. \(\vec{N}\) determines the friction on the block, which in turn keeps it from sliding downward. If the block is not to slip, the friction force \(\overrightarrow{f_{\mathrm{s}}}\) must balance the weight \(m \vec{g}\) of the block.
∴ N = mω²r and f_s = μ_sN = mg
∴ μ_s(ω²r) = mg

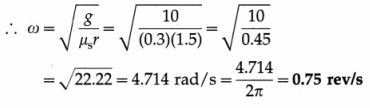
This gives the required angular speed.

Question 7.
A motorcyclist rounds a curve of radius 25 m at 36 km/h. The combined mass of the motorcycle and the man is 150 kg.

1. What is the centripetal force exerted on the motorcyclist ?
2. What is the upward force exerted on the motorcyclist?

Solution :
Data : r = 25m, v = 36 km/h = 36 × \(\frac{5}{18}\)m/s = 10 m/s, m = 150 kg, g = 10 m/s²

1. Centripetal force, F = \(\frac{m v^{2}}{r}\) = \(\frac{150 \times(10)^{2}}{25}\) = 600 N
2. Upward force = normal reaction of the road surface = mg = 150 × 10 = 1500 N

Question 8.
A motorcyclist is describing a circle of radius 25 m at a speed of 5 m/s. Find his inclination with the vertical. What is the value of the coefficient of friction between the tyres and ground ?
Solution :
Data : v = 5 m/s, r = 25 m, g = 10 m/s²

Question 9.
A motor van weighing 4400 kg (i.e., a motor van of mass 4400 kg) rounds a level curve of radius 200 m on an unbanked road at 60 km/h. What should be the minimum value of the coefficient of friction to prevent skidding ? At what angle should the road be banked for this velocity?
Solution :
Data : m = 4400 kg, r = 200 m,
v = 60 km/h = 60 × \(\frac{5}{18}\)m/s = \(\frac{50}{3}\) m/s, g = 10 m/s²

[Note : In part (ii), v is to be taken as the optimum speed.]

Question 10.
An amusement park ride (known variously as the Rotor, the Turkish Twist and the Gravitron) consists of a large vertical cylinder that is spun about it axis fast enough such that the riders remain pinned against its inner wall. The floor drops away once the cylinder has attained its full rotational speed. The radius of the cylinder is R and the coefficient of static friction between a rider and the wall is μ_s.
(i) Show that the minimum angular speed necessary to keep a rider from falling is given by ω = \(\sqrt{g / \mu_{s} R} \text {. }\).
(ii) Obtain a numerical value for the frequency of rotation of the cylinder in rotations per minute if R =4 m and
µ_s = 0.4.
Solution:
Data: R = 4 m, µ_s = 0.4, g = 10 m/s²
The forces exerted on the rider, when the floor
drops away, are

1. the normal force \(\vec{N}\) exerted by the wall, directed radially inward, is the centripetal force
2. the upward frictional force \(\overrightarrow{f_{\mathrm{s}}}\) exerted by the wall
3. the downward gravitational force mg .

∴ N = mω²R and f_s = µ_sN = µ_s (mω²R) where m is the mass of the rider and ω is the angular speed of the Rotor cylinder. For the rider not to fall, \(\overrightarrow{f_{\mathrm{s}}}\) must balances \(m \vec{g}\).

This is the minimum angular speed necessary. Since ω = 2πf, the corresponding frequency of rotation of the cylinder is

Question 11.
The two rails of a broad-gauge railway track are 1.68 m apart. At a circular curve of radius 1.6 km, the outer rail is raised relative to the inner rail by 8.4 cm. Find the angle of banking of the track and the optimum speed of a train rounding the curve.
Solution :
Data : l = 1.68 m = 168 cm, r = 1.6 km = 1600 m, h = 8.4 cm, g = 10 m/s²

Question 12.
A metre gauge train is moving at 72 kmph along a curved railway track of radius of curvature 500 m. Find the elevation of the outer rail above the inner rail so that there is no side thrust on the outer rail.
Solution :
Data : r = 500 m, v = 72 kmph = 72 × \(\frac{5}{18}\) m/s = 20 m/s, g = 10 m/s², l = 1 m
tan θ = \(\frac{v^{2}}{r g}\)
= \(\frac{(20)^{2}}{500 \times 10}\) = 0.08
The required angle of banking,
θ = tan^-1 (0.08) = 4°4′
The elevation of the outer rail relative to the inner rail,
h = l sin θ
= (1)(sin 4°4′) = 0.0709 m = 7.09 cm

Question 13.
A circular race course track has a radius of 500 m and is banked at 10°. The coefficient of static friction between the tyres of a vehicle and the road surface is 0.25. Compute
(i) the maximum speed to avoid slipping
(ii) the optimum speed to avoid wear and tear of the tyres.
Solution :
Data : r = 500 m, θ = 10°, µ_s = 0.25, g = 9.8 m/s², tan 10° = 0.1763

(i) On the banked track, the maximum speed of the vehicle without slipping (skidding) is

(ii) The optimum speed of the vehicle on the track is

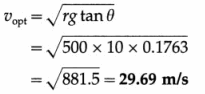
Question 48.
Define a conical pendulum.
Answer:
A conical pendulum is a small bob suspended from a string and set in UCM in a horizontal plane with the centre of its circular path below the point of suspension such that the string makes a constant angle θ with the vertical.
OR
A conical pendulum is a simple pendulum whose bob revolves in a horizontal circle with constant speed such that the string describes the surface of an imaginary right circular cone.

Question 49.
Derive an expression for the angular speed of the bob of a conical pendulum.
OR
Derive an expression for the frequency of revolution of the bob of a corical pendulum.
Answer:
Consider a conical pendulum of string length L with its bob of mass m performing UCM along a circular path of radius r.
At every instant of its motion, the bob is acted upon by its weight \(m \vec{g}\) and the tension \(\vec{F}\) in the string. If the constant angular speed of the bob is ω, the necessary horizontal centripetal force is F_c = mω²r

F_c is the resultant of the tension in the string and the weight. Resolve \(\vec{F}\) into components F cos θ vertically opposite to the weight of the bob and F sin θ horizontal. F cos θ balances the weight. F sin θ is the necessary centripetal force.
∴ F sin θ = mω²r … (1)
and F cos θ = mg … (2)

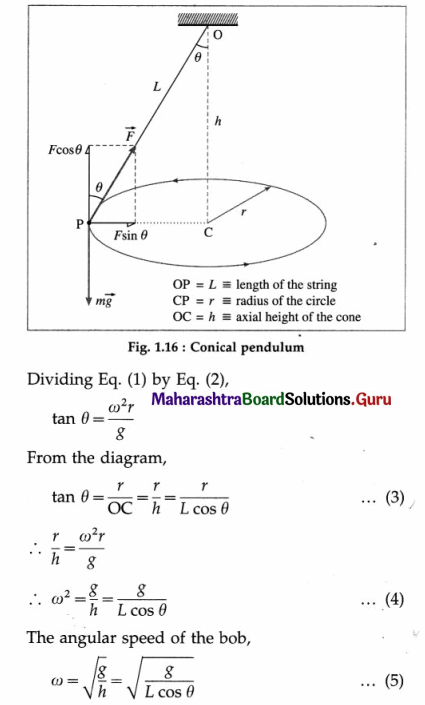
is the required expression for ω.
[Note : From Eq. (4), cos θ = g/ω²L. Therefore, as ω increases, cos θ decreases and θ increases.
If n is the frequency of revolution of the bob,

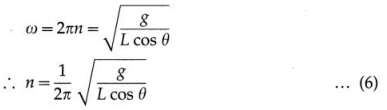
is the required expression for the frequency.

Question 50.
What will happen to the angular speed of a conical pendulum if its length is increased from 0.5 m to 2 m, keeping other conditions the same?
Answer:
The angular speed of the conical pendulum will become half the original angular speed.

Question 51.
Write an expression for the time period of a conical pendulum. State how the period depends on the various factors.
Answer:
If T is the time period of a conical pendulum of string length L which makes a constant angle θ with the vertical,
T = 2π\(\sqrt{\frac{L \cos \theta}{g}}\)
is the required expression
(Note: L cos θ = OC = h, where h is the axial height of the cone.
∴ T = 2π\(\sqrt{\frac{h}{g}}\)

where g is the acceleration due to gravity at the place.

From the above expression, we can see that

1. T ∝ \(\sqrt{L}\)
2. T ∝ \(\sqrt{\cos \theta}\) if θ increases, cos θ and T decrease
3. T ∝ \(\frac{1}{\sqrt{g}}/latex]
4. The period is independent of the mass of the bob.

Question 52.
Solve the following :

Question 1.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of a 1.5 m long string. If the string makes an angle of 30° with the vertical, compute its period.
Solution :
Data : L = 1.5 m, θ = 30°, g = 10 m/s²
The period of the conical pendulum,

Question 2.
A string of length 0.5 m carries a bob of mass 0. 1 kg at its end. If this is to be used as a conical pendulum of period 0.4πs, calculate the angle of inclination of the string with the vertical and the tension in the string.
Solution :
Data : L = 0.5m, m = 0.1 kg, T = 0.4πs, g = 10 m/s²

Question 3.
In a conical pendulum, a string of length 120 cm is fixed at a rigid support and carries a bob of mass 150 g at its free end. If the bob is revolved in a horizontal circle of radius 0.2m around a vertical axis, calculate the tension in the string. [g = 9.8 m/s²]
Solution:
Data : L = 120 cm = 1.2 m, m = 150 g = 0.15 kg,
r = 0.2 m, g = 9.8 m/s²

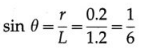
Question 4.
A stone of mass 1 kg, attached at the end of a 1 m long string, is whirled in a horizontal circle. If the string makes an angle of 30° with the vertical, calculate the centripetal force acting on the stone.
Solution :
Data : m = 1 kg, L = 1 m, θ = 30°, g = 10 m/s²

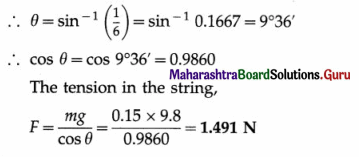
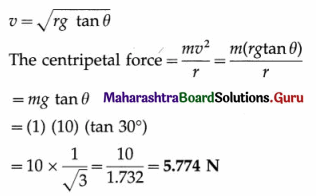
Question 53.
What is vertical circular motion? Comment on its two types.
Answer:
A body revolving in a vertical circle in the gravitational field of the Earth is said to perform vertical circular motion.

A vertical circular motion controlled only by gravity is a nonuniform circular motion because the linear speed of the body does not remain constant although the motion can be periodic.

In a controlled vertical circular motion, such as that a body attached to a rod, the linear speed of the body can be constant (including zero) so that such a motion can be uniform and periodic.

Question 54.
A body, tied to a string, performs circular motion in a vertical plane such that the tension in the string is zero at the highest point. What is the linear speed of the body at the

1. lowest position
2. highest position ?

Answer:

1. [latex]\sqrt{5 r g}\)
2. \(\sqrt{r g}\) in the usual notation.

Question 55.
A body, tied to a string, performs circular motion in a vertical plane such that the tension in the string is zero at the highest point. What is the angular speed of the body at the

1. highest position
2. lowest position ?

Answer:

1. \(\sqrt{g / r}\)
2. \(\sqrt{5 g / r}\) in the usual notation.

Question 56.
In a vertical circular motion controlled by gravity, derive an expression for the speed at an arbitrary position. Hence, show that the speed decreases while going up and increases while coming down.
OR
In a nonuniform vertical circular motion, derive expressions for the speed and tension/normal force at an arbitrary position.
OR
Show that a vertical circular motion controlled by gravity is a non uniform circular motion.
Answer:
Consider a small body of mass m tied to a string and revolved in a vertical circle of radius r. At every instant of its motion, the body is acted upon by its weight \(m \vec{g}\) and the tension \(\vec{T}\) in the string. At any instant, when the body is at the position P, let the string make an angle θ with the vertical, \(m \vec{g}\) is resolved into components, mg cos θ (radial) and mg sin θ (tangential).

At point P shown, the net force on the body towards the centre, T-mg cos θ, is the necessary centripetal force on the body. If v is its speed at P,


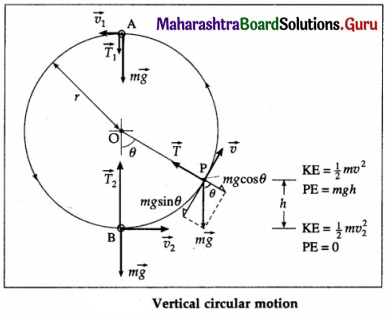
Let v₂ be the speed of the body at the lowest point B, which is the reference level for zero potential energy. Then, the body has only kinetic energy

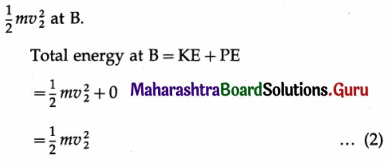
As the body goes from B to P, it rises through a height h = r – r cos θ = r(1 – cos θ).
Total energy at P = KE + PE

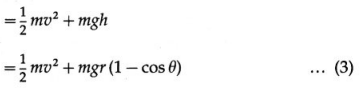
Assuming that the total energy of the body is conserved, total energy at any point = total energy at the bottom.
Then, from Eqs. (2) and (3),

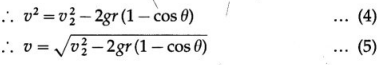
From the above expression, it can be seen that the linear speed v changes with θ. Thus, as θ increases, (while going up) cos θ decreases, 1 – cos θ increases, and v decreases. While coming down, θ decreases and v increases. Hence, a vertical circular motion controlled by gravity is a nonuniform circular motion.

Substituting for v² from Eq. (4) in Eq. (1),

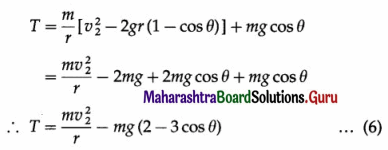
Equation (6) is the expression for the tension in the string at any instant in terms of the speed at the lowest point.

Question 57.
A body at the end of a rod is revolved in a non-uniform vertical circular motion. Show that
(i) it must have a minimum speed 2\(\sqrt{g r}\) at the bottom
(ii) the difference in tensions in the rod at the highest and lowest positions is 6 mg.
Answer:
Consider a body of mass m attached to a rod and revolved in a vertical circle of radius r at a place where the acceleration due to gravity is g. We shall assume that the rod is not rigid so that the tension in the rod changes. As the rod is rotated in a nonuniform circular motion, the tension in the rod changes from a minimum value T₁ when the body is at the highest point to a maximum value T₂ when the body is at the bottom of the circle. At every instant, the body is acted upon by two forces, namely/its weight \(m \vec{g}\) and the tension \(\vec{T}\) in the string.

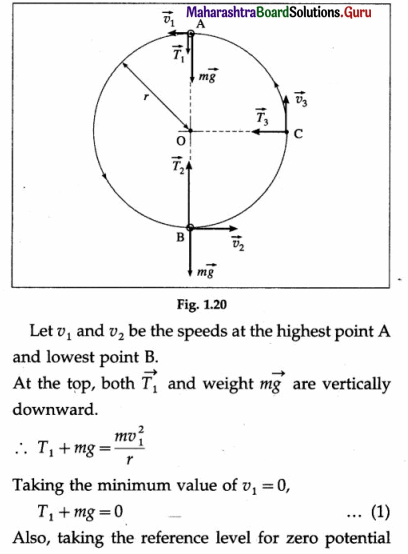
Question 58.
You may have seen in a circus a motorcyclist driving in vertical loops inside a hollow globe (sphere of death). Explain clearly why the motor-cyclist does not fall down when at the highest point of the chamber.
Answer:
A motorcyclist driving in vertical loops inside a hollow globe performs vertical circular motion. Suppose the mass of the motorcycle and motorcyclist is m and the radius of the chamber is r. At every instant of the motion, the motorcyclist is acted upon by the weight \(m \vec{g}\) and the normal reaction \(\vec{N}\).

At the highest point, let v₁ be the speed and \(\vec{N}_{1}\) the normal reaction. Here, both \(\vec{N}_{1}\) and \(m \vec{g}\) are parallel, vertically downward. Hence, the net force on the motorcyclist towards the centre O is N₁ + mg. If this force is able to provide the necessary centripetal force at the highest point, the motorcycle does not lose contact with the globe and fall down.

The minimum value of this force is found from the limiting case when N, just becomes zero and the weight alone provides the necessary centripetal force :
\(\frac{m v_{1}^{2}}{r}\) = mg
This requires that the motorcycle has a minimum speed at the highest point given by \(v_{1}^{2}\) = gr or v₁ = \(\sqrt{g r}\)

[Note : The ‘globe of death’ is a circus stunt in which stunt drivers ride motorcycles inside a mesh globe. Starting from small horizontal circles, they eventually perform revolutions along vertical circles. The linear speed is more for larger circles but angular speed is more for smaller circles as in conical pendulum.]

Question 59.
A car crosses over a bridge which is in the form of a convex arc with a uniform speed,
(i) State the expression for the normal reaction on the car.
OR
How does the normal reaction on the car vary with speed?
(ii) Hence show that the maximum speed with which the car can cross the bridge without losing contact with the road is equal to \(\sqrt{r g}\).
Answer:
Suppose a car of mass m, travelling with a uniform speed v, crosses over a bridge which is in the form of a convex arc of radius r.
(i) The forces acting on it at the highest point are as shown in below figure. Their resultant mg-N provides the centripetal force.

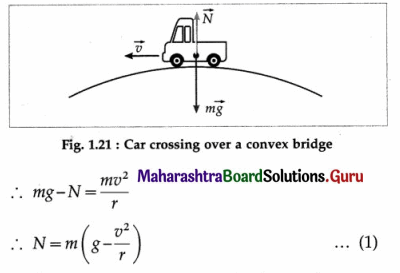
is the required expression. It shows that as v increases, N decreases.

(ii) Equation (1) shows that for g – \(\frac{v^{2}}{r}\) = 0, i.e., for centripetal acceleration equalling the gravitational acceleration, N = 0. That is, for \(\frac{v^{2}}{r}\) = g or v = \(\sqrt{r g}\), the
car just loses contact with the road. Therefore, this is the maximum speed with which a car can cross the bridge, irrespective of its mass.

[Data : Take g = 10 m/s² unless specified otherwise]

Question 60.
Solve the following :

Question 1.
An object of mass 1 kg tied to one end of a string of length 9 m is whirled in a vertical circle. What is the minimum speed required at the lowest position to complete the circle ? [g = 9.8 m/s²]
Solution :
Data : m = 1 kg, r = 9 m, g = 9.8 m/s²
The minimum speed of the object at the lowest position is

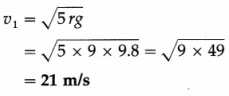
Question 2.
A stone of mass 5 kg, tied at one end of a rope of length 0.8 m, is whirled in a vertical circle. Find the minimum velocity at the highest point and at the midway point, [g = 9.8 m/s²]
Solution:
Data : m = 5 kg, r = l = 0.8 m, g = 9.8 m/s²

1. The minimum velocity of the stone at the highest point in its path,
   v = \(\sqrt{r g}\) = \(\sqrt{0.8 \times 9.8}\) = 2.8 m/s
2. The minimum velocity of the stone at the midway point in its path,
   v = \(\sqrt{3 r g}\) = \(\sqrt{3 \times 0.8 \times 9.8}\) = 4.85 m/s

Question 3.
A small body of mass 0.3 kg oscillates in a vertical plane with the help of a string 0.5 m long with a constant speed of 2 m/s. It makes an angle of 60° with the vertical. Calculate the tension in the string.
Solution :
Data : m = 0.3 kg, r = 0.5 m, v = 2 m/s, θ = 60°, g = 10 m/s²

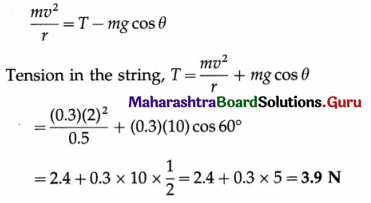
Question 4.
A bucket of water is whirled in a vertical circle at an arm’s length. Find the minimum speed at the top so that no water spills out. Also find the corresponding angular speed. [Assume r = 0.75 m]
Solution :
Data : r = 0.75 m, g = 10 m/s²
At the highest point the minimum speed required is v = \(\sqrt{r g}\) = \(\sqrt{0.75 \times 10}\) = 2.738 m/s
The corresponding angular speed is 2.738
ω = \(\frac{v}{r}\) = \(\frac{2.738}{0.75}\) = 3.651 rad/s

Question 5.
A pendulum, with a bob of mass m and string length l, is held in the horizontal position and then released into a vertical circle. Show that at the lowest position the velocity of the bob is \(\sqrt{2 g l}\) and the tension in the string is 3 mg.
Solution :
Taking the reference level for zero potential energy to be the bottom of the vertical circle, the initial potential energy of the bob at the horizontal position = mgh = mgl.

Hence, at the bottom where the speed of the bob is v, it has only kinetic energy = \(\frac{1}{2}\)mv².

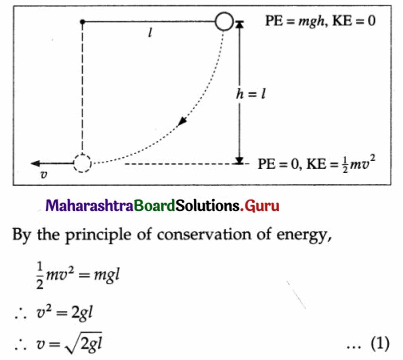
This gives the required velocity at the lowest position.
Also, at the bottom, the tension (T) and the centripetal acceleration are upward while the force of gravity is downward.

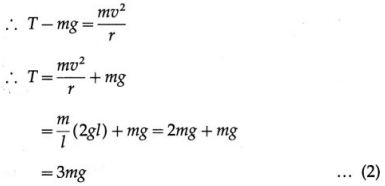
Equations (1) and (2) give the required expressions for the velocity and tension at the lowest position.

Question 6.
A stone of mass 100 g attached to a string of length 50 cm is whirled in a vertical circle by giving it a velocity of 7 m/s at the lowest point. Find the velocity at the highest point.
Solution :
Data : m = 0.1 kg, r = l = 0.5 m, v₂ = 7 m/s, g = 10 m/s²
The total energy at the bottom, E_bot
= KE + PE = \(\frac{1}{2} m v_{2}^{2}\) + 0 = \(\frac{1}{2}\)(0.1) (7)² = 2.45 J
The total energy at the top, E_top = KE + PE = \(\frac{1}{2} m v_{1}^{2}\) + mg (2r)
= \(\frac{1}{2}\)(0.1)\(v_{1}^{2}\) + (0.1) (10) (2 × 0.5)
= 0.05\(v_{1}^{2}\) + 1
By the principle of conservation of energy,

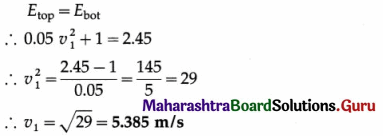
Question 7.
A pilot of mass 50 kg in a jet aircraft executes a “loop-the-loop” manoeuvre at a constant speed of 250 m/s. If the radius of the vertical circle is 5 km, compute the force exerted by the seat on the pilot at
(i) the top of the loop
(ii) the bottom of the loop.
Solution :
Data: m = 50 kg, v = 250m/s, r = 5 km = 5 × 10³ m, g = 10 m/s²

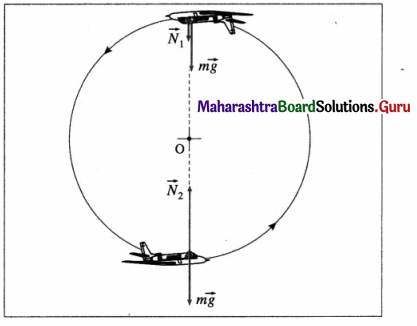
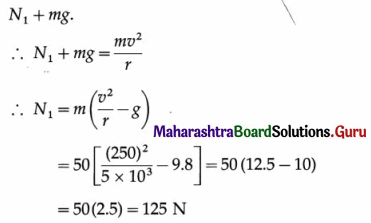
(i) At the top of the loop : The forces on the pilot are the gravitational force \(m \vec{g}\) and the normal force \(\vec{N}_{1}\), exerted by the seat, both acting downward. So the net force downward that causes the centripetal acceleration has a magnitude

(ii) At the bottom of the loop : The forces on the pilot are the downward gravitational force \(m \vec{g}\) and the upward normal force \(\vec{N}_{2}\) exerted by the seat. So the net upward force that causes the centripetal acceleration has a magnitude N₂ – mg.

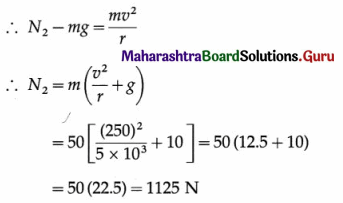
The forces exerted by the seat on the pilot at the top and bottom of the loop are 125 N and 1125 N, respectively.

Question 8.
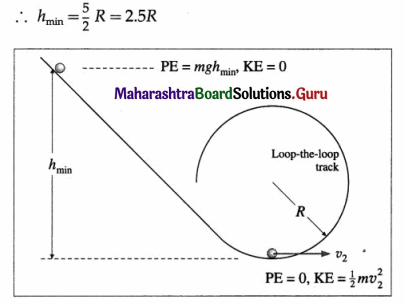
A ball released from a height h along an incline, slides along a circular track of radius R (at the end of the incline) without falling vertically downwards. Show that h_min = \(\frac{5}{2}\) R.
Solution:
To just loop-the-loop, the ball must have a speed v₂ = \(\sqrt{5 R g}\) at the bottom of the circular track.

If h_min is the minimum height above the bottom of the circular track from which the ball must be released, by the principle of conservation of energy, we have,
mgh_min = \(\frac{1}{2} m v_{2}^{2}\) = \(\frac{1}{2} m(5 R g)\)

Note : 1f the ball rolls all along the track without slipping, its total energy at the top of the circular track should take into account the rotational kinetic energy of the ball.

Question 9.
A block of mass 1 kg is released from P on a frictionless track which ends with a vertical quarter circular turn.

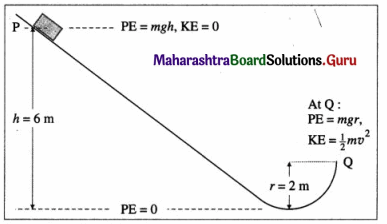
What are the magnitudes of the radial acceleration and total acceleration of the block when it arrives at Q ?
Solution :
Data : m = 1 kg, h = 6 m, r = 2 m, g = 10 m/s²
Let v be the speed of the block at Question Then, the total energy of the block at Q is
E = KE + PE = \(\frac{1}{2} m v^{2}\) + mgr
By the principle of conservation of energy,

The radial acceleration has a magnitude 40 m/s². The total acceleration has a magnitude 41.23 m/s² and makes an angle of 14°2′ with the radial acceleration.

Question 10.
A loop-the-loop cart runs down an incline into a vertical circular track of radius 3 m and then describes a complete circle. Find the minimum height above the top of the circular track from which the cart must be released.
Solution :

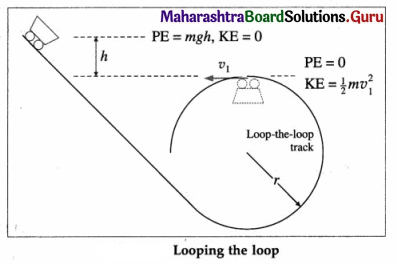
Data : r = 3 m
To just loop-the-loop, the cart must have a speed V₁ = \(\sqrt{r g}\) at the top of the loop.

If h is the minimum height above the top of the loop from which the cart must be released, by the principle of conservation of energy, we have, mgh = \(\frac{1}{2} m v_{1}^{2}\) = \(\frac{1}{2} m g r\)
∴ h = \(\frac{r}{2}\) = \(\frac{3}{2}\) = 1.5 m

Question 11.
A motorcyclist rides in vertical circles in a hollow sphere of radius 5 m. Find the required minimum speed and minimum angular speed, so that he does not lose contact with the sphere at the highest point. [g = 9.8 m/s²]
Solution :
Data : r = 5 m, g = 9.8 m/s²
Let v and ω be respectively the required minimum speed and angular speed at the highest point.

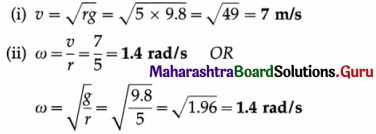
Question 12.
The vertical section of a road over a bridge in the direction of its length is in the form of an arc of a circle of radius 4.4 m. Find the maximum speed with which a vehicle can cross the bridge without losing contact with the road at the highest point, if the centre of gravity of the vehicle is 0.5 m from the ground.
Solution :
Data: While travelling along the bridge, the vehicle moves along a vertical circle of radius r = 4.4 + 0.5 = 4.9 m, g = 10 m/s².
If m is the mass and v is the maximum speed of the vehicle, then at the highest point,

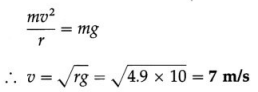
Question 13.
A small body tied to a string is revolved in a vertical circle of radius r such that its speed at the top of the circle is \(\sqrt{2 g r}\). Find
(i) the angular position of the string when the tension in the string is numerically equal to 5 times the weight of the body.
(ii) the KE of the body at this position
(iii) the minimum and maximum KEs of the body.
[Take m = 0.1 kg, r = 1.2 m, g = 10 m/s²]
Solution :
Data : v_top = \(\sqrt{2 g r}\), T = 5 mg, m = 0.1 kg, r = 1.2 m, g = 10 m/s²

Let the angular position of the string, θ = 0° when the body is at the bottom of the circle.

We assume total energy to be conserved and take the reference level for zero potential energy to be the bottom of the circle.

Total energy at the top, E

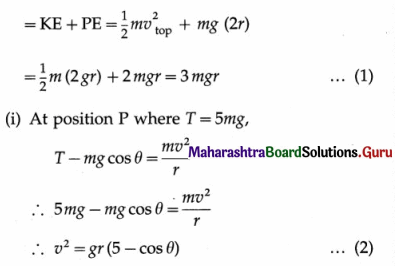
At P, the vertical displacement of the body from the bottom is r(1 – cos θ). Its total energy there is also E.

Question 14.
An object of mass 0.5 kg attached to a rod of length 0.5 m is whirled in a vertical circle at a constant angular speed. If the maximum tension in the rod is 5 kg wt, calculate the linear speed of the object and the maximum number of revolutions it can complete in a minute.
Solution :
Data : m = 0.5 kg, r = l = 0.5 m, g = 10 m/s²,
T₂ = 5 kg wt = 5 × 10 N

As the rod is rotated in a vertical circle at a constant angular speed, the linear speed of the object at the end of the rod is constant, say v. However, the tension in the rod changes from a minimum value T₁ when the object is at the highest point to a maximum value T₂ when the object is at the bottom of the circle.

At the bottom of the circle, the tension and acceleration are upward while the force of gravity is downward.

∴ The maximum number of revolutions the object can complete in a minute is 127.98.

Question 15.
A small body of mass m = 0.1 kg at the end of a cord 1 m long swings in a vertical circle. Its speed is 2 mIs when the cord makes an angle θ = 30° with the vertical. Find the tension in the cord.
Solution:
Data: m = 0.1 kg, r = 1 m, y = 2 m/s, θ = 30°,
g = 9.8 m/s²
When the cord makes an angle θ with the vertical, the centripetal force on the body is

Question 16.
A bucket of water is tied to one end of a rope 8 m long and rotated about the other end in a vertical circle. Find the number of revolutions per minute such that water does not spill.
Solution:
[Important note : The circular motion of the bucket in a vertical plane under gravity is not a uniform circular motion. Assuming the critical case of the motion such that the bucket has the minimum speed at the highest point required for the water to stay put in the bucket, we can find the minimum frequency of revolution. ]
Data :r = 8m, g = 9.8 m/s², π = 3.142
Assuming the bucket has a minimum speed v = \(\sqrt{r g}\) at the highest point, the corresponding angular speed is

Question 61.
Derive an expression for the kinetic energy of a body rotating with constant angular velocity.
Answer:
Consider a rigid body rotating with a constant angular velocity \(\vec{\omega}\) about an axis passing through the point O and perpendicular to the plane of the figure. Suppose that the body is made up of N particles of masses m₁, m₂, …, m_N situated at perpendicular distances r₁, r₂, , r_N, respectively, from the axis of rotation as shown in below figure.

As the body rotates, all the particles perform uniform circular motion with the same angular velocity \(\vec{\omega}\). However, they have different linear speeds depending upon their distances from the axis of rotation.

The linear speed of the particle with mass ml is v₁ = r₁ω. Therefore, its kinetic energy is

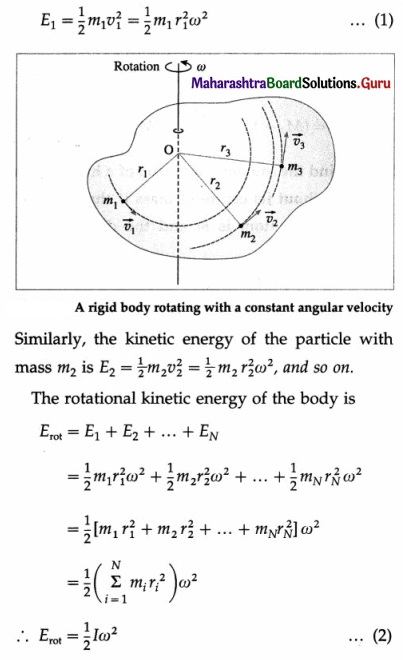
where I = \(\sum_{i=1}^{N} m_{i} r_{i}^{2}\) is the moment of inertia of the body about the axis of rotation.
Equation (2) gives the required expression.

Question 62.
Define moment of inertia. State the factors which it depends on. Obtain its dimensions and state its SI unit.
OR
Define moment of inertia. State its dimensions and SI units.
Answer:
(1) Moment of inertia : The moment of inertia of a body about a given axis of rotation is defined as the sum of the products of the masses of the particles of the body and the squares of their respective distances from the axis of rotation.

If the body is made up of N discrete particles of masses m₁, m₂, …,m_N situated at respective distances r₁, r₂, …, r_N from the axis of rotation, the moment of inertia of the body is

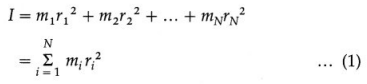
For a rigid body, having a continuous and uniform distribution of mass, the moment of inertia is
I = \(\int r^{2} d m\) …(2)
where dm is the mass of an infinitesimal element, situated at distance r from the axis of rotation.

(2) The moment of inertia of a rigid body depends on

1. the mass and shape of the body
2. orientation and position of the rotation axis
3. distribution of the mass about the rotation axis.

(3) Dimensions :
[Moment of inertia] = [mass] [distance]²
= [M] [L²] = [M¹L²T⁰]

(4) SI unit : The kilogram-metre² (kg.m²).

Question 63.
Explain the physical significance of moment of inertia.
Answer:
(1) The physical significance of moment of inertia can be understood by comparing the formulae in the following table.

Linear motion	Rotational motion
1. Momentum = mass × velocity	1. Angular momentum = moment of inertia × angular velocity
2. Force = mass × acceleration	2. Torque = moment of inertia × angular acceleration
3. Kinetic energy = \(\frac{1}{2} M v^{2}\)	3. Kinetic energy = \(\frac{1}{2} I \omega^{2}\)

(2) Force produces acceleration, while torque produces angular acceleration. Force and torque are analogous quantities. Also, momentum and angular momentum are analogous quantities.
(3) By comparing the above formulae, we find that moment of inertia plays the same role in rotational motion as that played by mass in linear motion. The moment of inertia of a body is its rotational inertia, that which opposes any tendency to change its angular velocity. In the absence of a net torque, the body continues to rotate with a uniform angular velocity.

Question 64.
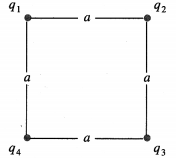
Three point masses M₁, M₂ and M₃ are located at the vertices of an equilateral triangle of side a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through M₁ ?
Answer:

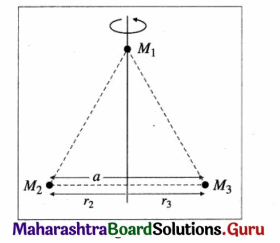
The moment of inertia of the system about the altitude passing through M₁ is

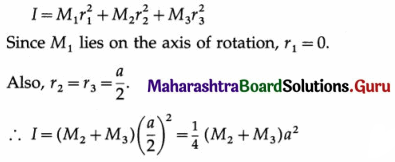
Question 65.
Find the moment of inertia of a hydrogen molecule about its centre of mass if the mass of each hydrogen atom is m and the distance between them is R.
Answer:
We assume the rotation axis to be a transverse axis through the centre of mass of the linear molecule H₂. Then, each of the hydrogen atom is a distance \(\frac{1}{2}\)R from the CM. Therefore, the MI of the molecule about this axis,

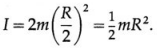
Notes :

1. For a H₂ molecule, mH = 1.674 × 10^-27 kg and bond length = 7.774 × 10^-11 m, so that I = 5.065 × 10^-48 kg.m².
2. As atoms are treated as particles, we do not consider rotation about the line passing through the atoms.

Question 66.
Solve the following :

Question 1.
Four particles of masses 0.2 kg, 0.3 kg, 0.4 kg and 0.5 kg respectively are kept at comers A, B, C and D of a square ABCD of side 1 m. Find the moment of inertia of the system about an axis passing through point A and perpendicular to the plane of the square.
Solution :
Data : m₁ = 0.2 kg, m₂ = 0.3 kg, m₃ = 0.4 kg, m₄ = 0.5 kg

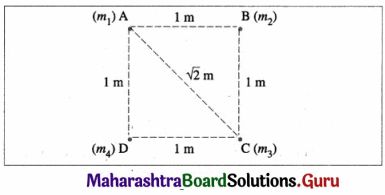
The axis of rotation passes through point A and is perpendicular to the plane of the square. Hence the distance (r₁) of mass ml from the axis is r₁ =0, that of mass m₂ is r₂ = AB = 1 m, that of mass m₃ is r₃ = \(\sqrt{2}\)AC m and that of mass m₄ is r₄ = AD = 1 m.
The moment of inertia,

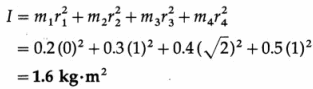
Question 2.
The moment of inertia of the Earth about its axis of rotation is 9.83 × 10 kg.m² and its angular speed is 7.27 × 10^-5 rad/s. Calculate its
(i) kinetic energy of rotation
(ii) radius of gyration. [ Mass of the Earth = 6 × 10²⁴ kg]
Solution :
Data : I = 9.83 × 10³⁷ kg.m², ω = 7.27 × 10^-5 rad/s, M = 6 × 10²⁴ kg

(i) The kinetic energy of rotation of the Earth,

Question 67.
State an expression for the moment of inertia of a thin ring about its transverse symmetry axis.
Answer:
A thin uniform ring (or hoop) has all its mass uniformly distributed along the circumference of a circle. It is taken to be a two-dimensional body. It is also assumed that the radial thickness of the ring is so small as to be completely negligible in comparison to its radius.

Consider a thin ring (or hoop) of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM).

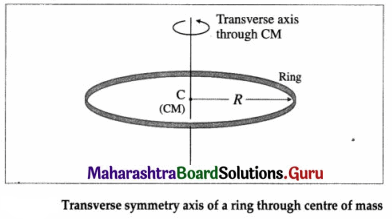
The MI of the ring about the transverse symmetry axis is
I_CM = MR²

Question 68.
Derive an expression for the moment of inertia of a thin uniform disc about its transverse symmetry axis.
Answer:
A thin uniform disc has all its mass homogeneously distributed over its circular surface area. It is taken to be a two-dimensional body, i.e., its axial thickness is small as to be completely negligible in comparison to its radius. Consider a thin disc of radius R and mass M. Its mass per unit area is

The axis of rotation is the transverse symmetry axis, through its centre of mass (CM) and perpendicular to its plane. For rotation about this axis, we consider the disc to consist of a large number of thin concentric rings, having the same rotation axis as the transverse symmetry axis of the disc. One such elemental ring at a distance r from the rotation axis shown in below figure, has mass dm and radial width dr.

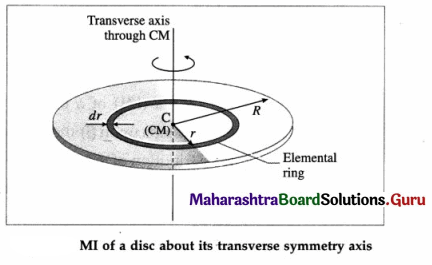
Since the disc is uniform, the area and mass of this elemental ring are

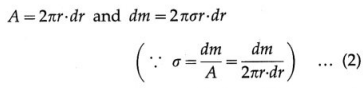
and its moment of inertia (MI) about the given axis is dm.r².
Therefore, the MI of the disc is

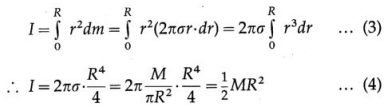
This gives the required expression.

Question 69.
Is radius of gyration of a rigid body a constant quantity?
Answer:
Radius of gyration of a rigid body depends on the distribution of mass of the body about a rotation axis and, therefore, changes with the choice of the rotation axis. Hence, unlike the mass of the body which is constant, radius of gyration and moment of inertia of the body are not constant.

Question 70.
State an expression for the radius of gyration of
(i) a thin ring
(ii) a thin disc, about respective transverse symmetry axis.
OR
Show that for rotation about respective transverse symmetry axis, the radius of gyration of a thin disc is less than that of a thin ring.
Answer:
(i) The MI of the ring about the transverse symmetry axis is
I_CM = MR² … (1)
Radius of gyration : The radius of gyration of the ring about the transverse symmetry axis is
K = \(\sqrt{I_{\mathrm{CM}} / M}\) = \(\sqrt{R^{2}}\) = R …… (2)

(ii) The MI of the disc about the transverse symmetry axis is
I_CM = \(\frac{1}{2}\)MR<² … (3)
Radius of gyration : The radius of gyration of the disc for the given rotation axis is

Question 71.
State and prove the theorem of parallel axis.
Answer:
Theorem of parallel axis : The moment of inertia of a body about an axis is equal to the sum of

1. its moment of inertia about a parallel axis through its centre of mass and
2. the product of the mass of the body and the square of the distance between the two axes.

Proof : Let I_CM be the moment of inertia (MI) of a body of mass M about an axis through its centre of mass C, and I be its MI about a parallel axis through any point O. Let h be the distance between the two axes.

Consider an infinitesimal mass element dm of the body at a point P. It is at a perpendicular distance CP from the rotation axis through C and a perpendicular distance OP from the parallel axis through O. The MI of the element about the axis through C is CP²dm. Therefore, the MI of the body about the axis through the CM is I_CM = \(\int \mathrm{CP}^{2} d m\). Similarly, the MI of the body about the parallel axis through O is I = \(\int \mathrm{OP}^{2} d m\).

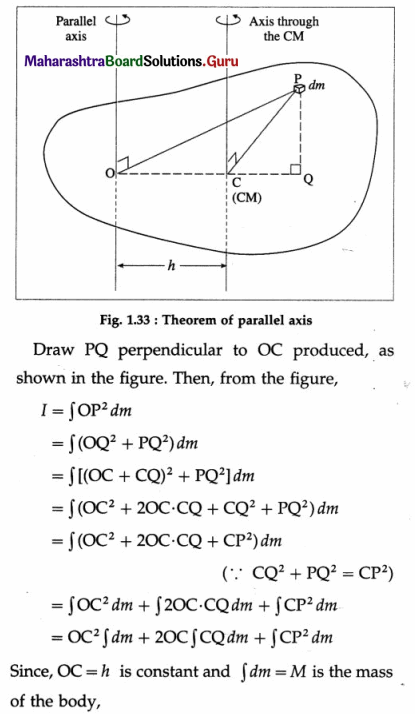
∴ I = I_CM + Mh²
This proves the theorem of parallel axis.

Question 72.
State and prove the theorem of perpendicular axes about moment of inertia.
Answer:
Theorem of perpendicular axes : The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two mutually perpendicular axes in its plane and through the point of intersection of the perpendicular axis and the lamina.

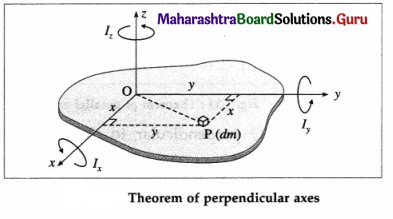
Proof : Let Ox and Oy be two perpendicular axes in the plane of the lamina and Oz, an axis perpendicular to its plane. Consider an infinitesimal mass element dm of the lamina at the point P(Y, y). MI of the lamina about the z-axis, I_z = \(\int \mathrm{OP}^{2} d m\)

The element is at perpendicular distance y and x from the x- and y- axes respectively. Hence, the moments of inertia of the lamina about the x- and y-axes are, respectively,

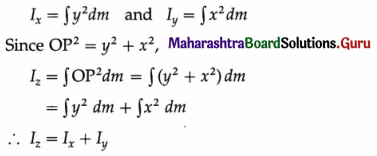
This proves the theorem of perpendicular axes.

Question 73.
About which axis of rotation is the radius of gyration of a body the least ?
Answer:
The radius of gyration of a body is the least about an axis through the centre of mass (CM) of the body.

From the parallel axis theorem, we know that a given body has the smallest possible moment of inertia about an axis through its CM. The radius of gyration of a body about a given axis is directly proportional to the square root of its moment of inertia about that axis. Hence, the conclusion.
{OR I = I_CM + Mh². ∴ Mk² = \([/latexM k_{\mathrm{CM}}^{2}] + Mh².
∴ k² = [latex]k_{\mathrm{CM}}^{2}\) + h², which shows that k is minimum, equal to k_CM when h = 0.}

Question 74.
State an expression for the moment of inertia of a thin uniform rod about an axis through its centre and perpendicular to its length. Hence deduce the expression for its moment of inertia about an axis through its one end and perpendicular to its length.
OR
State an expression for the moment of inertia of a thin uniform rod about its transverse symmetry axis. Hence, deduce the expression for its moment of inertia about a parallel axis through one end. Also deduce the expressions for the corresponding radii of gyration.
Answer:
(1) MI about a transverse axis through centre : Consider a thin uniform rod AB of mass M and length L, rotating about a transverse axis through its centre C. C is also its centre of mass (CM).

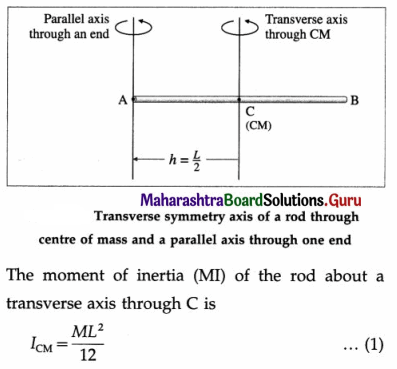
(2) MI about a transverse axis through one end : Let I be its MI about a transverse axis through its end A. By the theorem of parallel axis,
I = I_CM + Mh² … (2)
In this case,

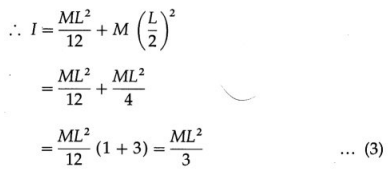
(3) Radii of gyration : The radius of gyration of the rod about its transverse symmetry axis is

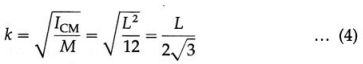
The radius of gyration of the rod about the transverse axis through an end is

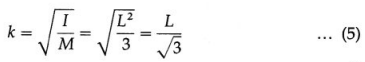
Question 75.
State the expression for the MI of a thin spherical shell (i.e., a thin-walled hollow sphere) about its diameter. Hence obtain the expression for its MI about a tangent.
Answer:
Consider a uniform, thin-walled hollow sphere radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass. The MI of the thin spherical shell about its diameter is
I_CM = \(\frac{2}{3}\)MR²

Let I be its MI about a tangent parallel to the diameter. Here, h = R = distance between the two axes. Then, according to the theorem of parallel axis,

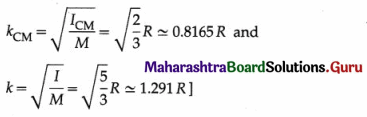
Question 76.
Calculate the moment of inertia by direct integration of a thin uniform rod of mass M and length L about an axis perpendicular to the rod and passing through the ród at L/3, as shown below.
Check your answer with the parallel-axis theorem.

Answer:
Method of direct integration : Consider a thin uniform rod of mass M and length L. The axis of rotation is perpendicular to the rod and passing through the rod at L/3. We consider the origin of coordinates to be at this point and the x-axis to be along the rod,

Since the mass density is constant, the linear mass density is
λ = M/L
An element of the rod has mass dm and length dl = dx.

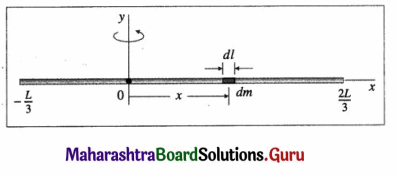
If the distance of each mass element from the axis is given by the variable x, the moment of inertia of an element about the axis of rotation is dI = x²dm
Since the rod extends from x= – L/3 to x = 2L/3, the MI of the rod about the axis is

Method of parallel-axis : The MI of the thin rod about a transverse axis through its CM is
I_CM = \(\frac{1}{12} M L^{2}\)
The given axis of rotation is at a distance h = \(\frac{L}{2}\) – \(\frac{L}{3}\) = \(\frac{L}{6}\) from the transverse symmetry axis.
Therefore, the MI of the rod about the given axis is

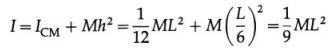
the same as arrived at by direct integration method.

Question 77.
State an expression for the moment of inertia of a thin ring about its transverse symmetry axis. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane. Also deduce the expressions for the corresponding radius of gyration.
Answer:
(1) MI about the transverse symmetry axis : Consider a thin ring (or hoop) of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM). It is assumed that the radial thickness of the ring is so small as to be completely negligible in comparison to radius R.

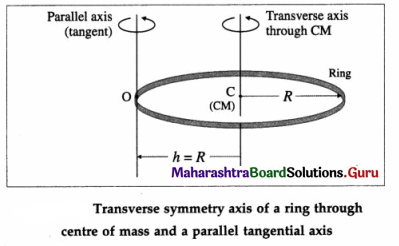
The MI of the ring about the transverse symmetry axis is
I_CM = MR² …(1)
Radius of gyration : The radius of gyration of the ring about the transverse symmetry axis is
k = \(\sqrt{I_{\mathrm{CM}} / M}\) = \(\sqrt{R^{2}}\) = R …(2)

(2) MI about a tangent perpendicular to its plane : Let I be its MI about a parallel axis, tangent to the ring. Here, h = R = distance between the two axes.
By the theorem of parallel axis,
I = I_CM + Mh² … (3)
= MR² + MR² = 2MR² …(4)
Radius of gyration : The radius of gyration of the ring about a transverse tangent is
k = \(\sqrt{I / M}\) = \(\sqrt{2 R^{2}}\) = \(\sqrt{2} R\) …(5)

Question 78.
Assuming the expression for the moment of inertia of a ring about its transverse symmetry axis, obtain the expression for its moment of inertia about
(1) a diameter
(2) a tangential axis in its plane. Also deduce the expressions for the corresponding radii of gyration.
Answer:
Let M be the mass of a thin ring of radius R. Let /CM be the moment of inertia (MI) of the ring about its transverse symmetry axis. Then,
I_CM = MR … (1)

(1) MI about a diameter : Let x- and y-axes be along two perpendicular diameters of the ring as shown in below figure. Let I_x, I_y and I_z be the moments of inertia of the ring about the x, y and z axes, respectively.

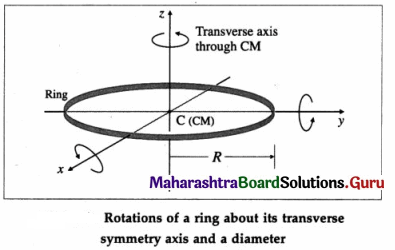
Both I_x and I_y represent the moment of inertia of the ring about its diameter and, by symmetry, the MI of the ring about any diameter is the same.
∴ I_x = I_y ….. (2)
Also, I_z being the MI of the ring about its transverse symmetry axis,

(2) MI about a tangent in its plane: Let I be its MI about an axis in plane of the ring, i.e., parallel to a diameter, and tangent to it. Here, h = R and
I_CM = I_x = \(\frac{1}{2}\)MR².
By the theorem of parallel axis,
= \(\frac{1}{2} M R^{2}\) + MR² = \(\frac{3}{2} M R^{2}\) … (7)

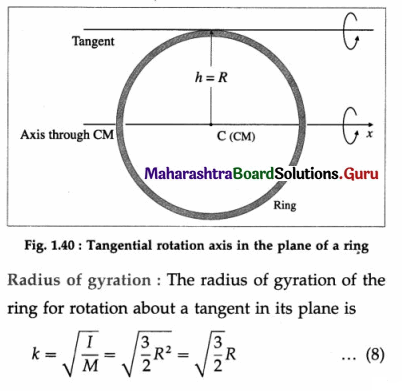
Question 79.
State an expression for the MI of a thin uniform disc about a transverse axis through its centre. Hence, derive an expression for the MI of the disc about its tangent perpendicular to the plane. Deduce the expressions for the corresponding radii of gyration.
Answer:
(1) MI about the transverse symmetry axis : Consider a thin uniform disc of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM).

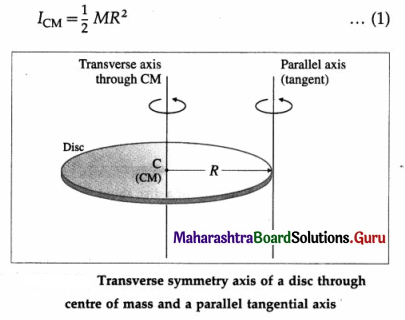
Radius of gyration : The radius of gyration of the disc for the given rotation axis is

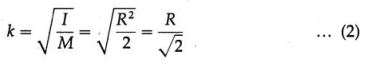
(2) MI about a tangent perpendicular to its plane : Let I be the MI of the disc about a tangent perpendicular to its plane.

According to the theorem of parallel axis,

Question 80.
Assuming the expression for the moment of inertia of a thin uniform disc about a transverse axis through its centre, obtain an expression for its moment of inertia about any diameter. Hence, write the expression for the corresponding radius of gyration.
Answer:
Consider a thin uniform disc of mass M and radius R in the xy plane, as shown in below figure. Let I_x, I_y and I_z be the moments of inertia of the disc about the x, y and z axes respectively. But, I_x = I_y, since each

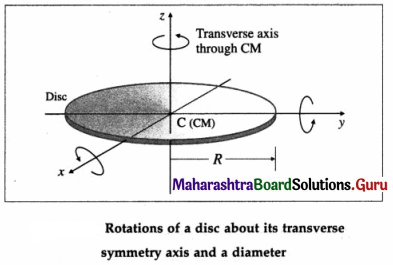
represents the moment of inertia (MI) of the disc about its diameter and, by symmetry, the MI of the disc about any diameter is the same.
As I_z is the MI of the disc about the z-axis through its centre and perpendicular to its plane,
I_z = \(\frac{1}{2}\)MR² … (1)

According to the theorem of perpendicular axes,

Question 81.
Given the moment of inertia of a thin uniform disc about its diameter to be \(\frac{1}{4}\)MR², where M and R are respectively the mass and radius of the disc, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Answer:
Consider a thin uniform disc of mass M and radius R in the xy plane. Let Ix, ly and Iz be the moments of inertia of the disc about the x, y and z axes respectively.
Now, I_x = I_y
since each represents the moment of inertia (MI) of the disc about its diameter and, by symmetry, the MI of the disc about any diameter is the same.
∴ I_x = I_y = \(\frac{1}{4}\)MR² (Given)
According to the theorem of perpendicular axes,
I_z = I_x + I_y = 2(\(\frac{1}{4}\)MR²) = \(\frac{1}{2}\)MR²
Let I be the MI of the disc about a tangent normal to the disc and passing through a point on its edge (i.e., a tangent perpendicular to its plane). According to the theorem of parallel axis,
I = I_CM + Mh²
Here, I_CM = I_z = \(\frac{1}{2}\)MR² and h = R.
∴ I = \(\frac{1}{2}\)MR² + MR² = \(\frac{3}{2}\)MR²
which is the required expression.

Question 82.
Assuming the expression for the moment of inertia of a thin uniform disc about its diameter, show that the moment of inertia of the disc about a tangent in its plane is \(\frac{5}{4}\)MR². Write the expression for the corresponding radius of gyration.
Answer:
Let M be the mass and R be the radius of a thin uniform disc. Let I_CM be the moment of inertia (MI) of the disc about a diameter. Then,

Question 83.
State the expressions for the moment of inertia of a solid cylinder of uniform cross section about
(1) an axis through its centre and perpendicular to its length
(2) its own axis of symmetry.
OR
State the expressions for the MI of a solid cylinder about
(1) a transverse symmetry axis
(2) its cylindrical symmetry axis. Also deduce the expressions for the corresponding radii of gyration.
Answer:
Consider a solid cylinder of uniform density, length L, radius R and total mass M.

Notes :

1. For R « L, a solid cylinder can be approximated as a thin rod, and the expression for the MI about its transverse symmetry axis reduces to the corresponding expression for a thin rod, viz., ML²/12.
2. The MI of a solid cylinder about its cylindrical symmetry axis is the same as that of a disc about its transverse symmetry axis and having the same mass and radius.

Question 84.
Assuming the expression for the moment of inertia of a uniform solid cylinder about a transverse symmetry axis, obtain the expression for its moment of inertia about a transverse axis through its one end.
Answer:
Let M be the mass, L the length and R the radius of a uniform solid cylinder. Let I_CM be the moment of inertia (MI) of the cylinder about a transverse symmetry axis. Then,

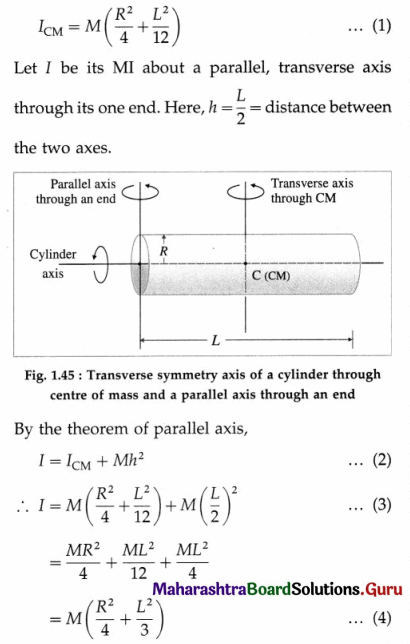
Question 85.
State an expression for the moment of inertia of a solid sphere about its diameter. Write the expression for the corresponding radius of gyration.
Answer:
Consider a solid sphere of uniform density, radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass.

The MI of the solid sphere about its diameter is
I_CM = \(\frac{2}{5}\)MR²
The corresponding radius of gyration is

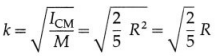
Question 86.
A uniform solid sphere of mass 15 kg has radius 0.1 m. What is its moment of inertia about a diameter?
Answer:
Moment of inertia of the sphere about a diameter
= \(\frac{2}{5}\)MR² = \(\frac{2}{5}\) × 15 × (0.1)² = 6 × 10^-2 kg.m²

Question 87.
Assuming the expression for the MI of a uniform solid sphere about its diameter, obtain the expression for its moment of inertia about a tangent.
Answer:
Let M be the mass of a uniform solid sphere of radius R. Let I_CM be its MI about any diameter.

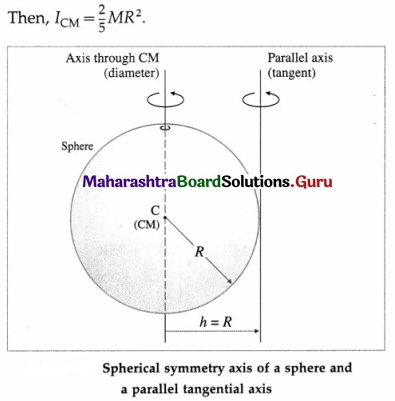
Let I be its MI about a parallel axis, tangent to the sphere. Here, h = R = distance between the two axis.
By the theorem of parallel axis, I = I_CM + Mh²
= \(\frac{2}{5}\)MR² + MR² = \(\frac{7}{5}\)MR²

Question 88.
The moment of inertia of a uniform solid sphere about a diameter is 2 kg m². What is its moment of inertia about a tangent ?
Answer:
Moment of inertia of a solid sphere about its 2
diameter, I_CM = \(\frac{2}{5}\)MR².

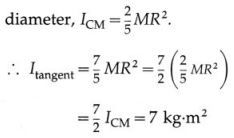
Question 89.
The radius of gyration of a uniform solid sphere of radius R is \(\sqrt{\frac{2}{5}}\)R for rotation about its diameter. Show that its radius of gyration for rotation about a tangential axis of rotation is \(\sqrt{\frac{7}{5}}\)R.
Answer:
Let the mass of the uniform solid sphere of radius R be M. Let I_CM and k_d be its MI about any diameter and the corresponding radius of gyration, respectively. Then,

Let I and k_t be its MI about a parallel tangential axis and the corresponding radius of gyration, respectively. Here, h = R = distance between the two axis.
∴ I = \(M k_{\mathrm{t}}^{2}\)
By the theorem of parallel axis,
I = I_CM + Mh²

Question 90.
State the expression for the MI of a thin spherical shell (i.e., a thin-walled hollow sphere) about its diameter. Hence obtain the expression for its MI about a tangent.
Answer:
Consider a uniform, thin-walled hollow sphere radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass. The MI of the thin spherical shell about its diameter is
I_CM = \(\frac{2}{3} M R^{2}\)

Let I be its MI about a tangent parallel to the diameter. Here, h = R = distance between the two axes. Then, according to the theorem of parallel axis,

Question 91.
Find the ratio of the radius of gyration of a solid sphere about its diameter to the radius of gyration of a hollow sphere about its tangent, given that both the spheres have the same radius.
Answer:
The radius of gyration of a body about a given axis, k = \(\sqrt{I / M}\), where M and I are respectively the mass of the body and its moment of inertia (MI) about the axis.

For a solid sphere rotating about its diameter,

Question 92.
Calculate the moment of inertia by direct integration of a thin uniform rectangular plate of mass M, length l and breadth b about an axis passing through its centre and parallel to its breadth.
Answer:
Consider a thin uniform rectangular plate of mass M, length l and breadth b. The axis of rotation passes through its centre and is parallel to its breadth. We consider the origin of coordinates to be at the centre of the plate and orient the axes as shown in below figure. Since the plate is thin, we can take the mass as distributed entirely in the xy-plane. Then, the surface mass density is constant and equal to

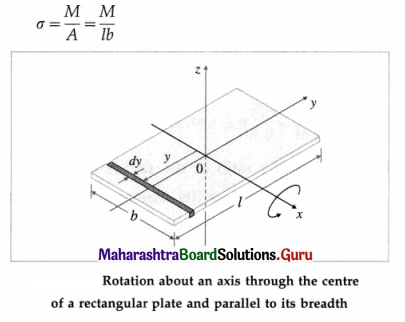
A rectangular element of the plate, shown shaded, has mass dm, length b and breadth dy.
∴ dm = σdA = σ(b dy)

If the distance of each element from the rotation axis is given by the variable y, the moment of inertia of :
an element about the axis of rotation is
dI_x = y²dm
Since the rod extends from y = -1/2 to y = 1/2, the MI of the thin plate about the axis is

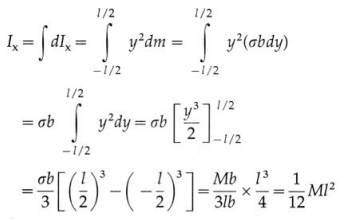
Notes:

(1) The MI of a thin rectangular plate about an axis passing through its centre and parallel to its length (i.e., about the y-axis) is I_y = \(\frac{1}{12}\)Mb². Then, by the theorem of perpendicular axes, the MI of a thin plate about its transverse symmetry axis (i.e., about the z-axis) is I_z = I_x + I_y = \(\frac{1}{12} M\left(l^{2}+b^{2}\right)\)

(2) Suppose, for a rectangular bar of sides l, b and w, we take the origin of coordinates at the centre of mass of the bar and the x, y and z axes parallel to the respective sides. Then, I_x = \(\frac{1}{12}\)M(b² + w²), I_y = \(\frac{1}{12}\)M(w² + l²) and I_z = \(\frac{1}{2} M\left(l^{2}+b^{2}\right)\)

Question 93.
State the MI of a thin rectangular plate-of mass M, length l and breadth b- about an axis passing through its centre and parallel to its length. Hence find its MI about a parallel axis along one edge.
Answer:
Consider a thin rectangular plate of mass M, length l and breadth b. The MI of the plate about an axis passing through its centre and parallel to its edge of length l is

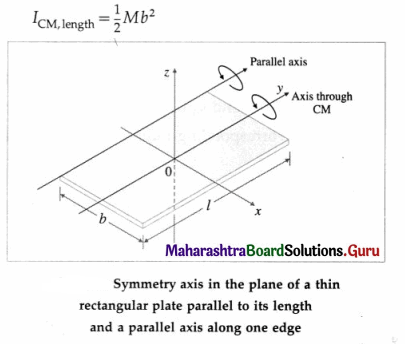
For a parallel axis along its one edge, h = \(\frac{1}{2} b\).
Therefore, by the theorem of parallel axis, the MI about this axis is

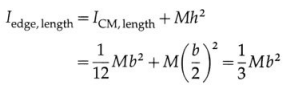
Question 94.
State the MI of a thin rectangular plate-of mass M, length l and breadth b about its transverse axis passing through its centre. Hence find its MI about a parallel axis through the midpoint of edge of length b.
Answer:
Consider a thin rectangular plate of mass M, length l and breadth b. The MI of the plate about its transverse axis passing through its centre is
I_CM = M(l² + b²)
For a parallel axis through the midpoint of its breadth, h = \(\frac{1}{2} l\). Therefore, by the theorem of parallel axis, the MI about this axis is

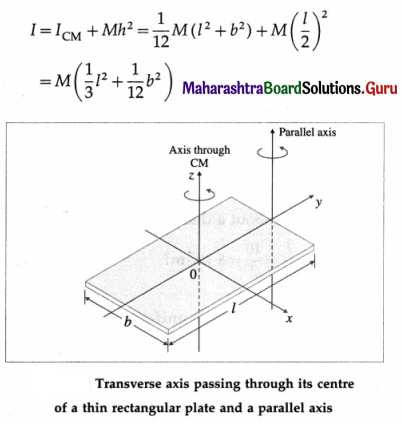
Question 95.
A uniform solid right circular cone of base radius R has mass M. Prove that the moment of inertia of the cone about its central symmetry axis is \(\frac{3}{10} M R^{2}\).
Answer:
Consider a uniform solid right circular cone of mass M, base radius R and height h. The axis of rotation passes through its centre and the vertex, Its constant mass density is

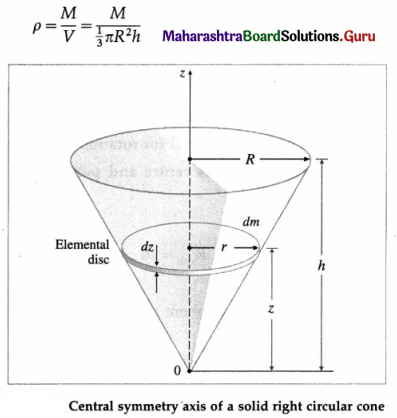
We consider an elemental disc of mass dm, radius r and thickness dz. If the distance of each mass element from the axis is given by the variable z,

Question 96.
Solve the following :

Question 1.
Calculate the moment of inertia of a ring of mass 500 g and radius 0.5 m about an axis of rotation passing through
(i) its diameter
(ii) a tangent perpendicular to its plane.
Solution :
Data : M = 500 g 0.5 kg, R = 0.5 m

(i) The moment of inertia of the ring about its

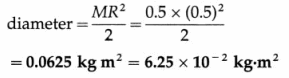
(ii) The moment of inertia of the ring about a tangent perpendicular to its plane
= 2MR² = 2 × 0.5 × (0.5)² = 0.25 kg.m²

Question 2.
A thin uniform rod 1 m long has mass 1 kg. Find its moment of inertia and radius of gyration for rotation about a transverse axis through a point midway between its centre and one end.
Solution :
Data : M = 1 kg, L = 1 m
Let I_CM and I be the moments of inertia of the rod about a transverse axis through its centre, and a parallel axis midway between its centre and one end.

Question 3.
The moment of inertia of a disc about an axis through its centre and perpendicular to its plane is 10 kg.m². Find its MI about a diameter.
Solution :
Data : I_z = 10 kg.m²
If the disc lies in the xy plane with its centre at the origin then, according to the theorem of perpendicular axes,
I_x + I_y = I_z
Since, I_x = I_y, 2I_x = I_z
∴ Its MI about a diameter,
I_x = \(\frac{I_{z}}{2}\) = \(\frac{10}{2}\) = 5 kg.m²

Question 4.
A solid cylinder of uniform density and radius 2 cm has a mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
Solution :
Data : M = 50 g, R = 2 cm, L = 12 cm

Question 5.
A compound object is formed of a thin rod and a disc attached at the end of the rod. The rod is 0.5 m long and has mass 2 kg. The disc has mass of 1 kg and its radius is 20 cm. Find the moment of inertia of the compound object about an axis passing through the free end of the rod and perpendicular to its length.
Solution :
Data : L = 0.5 m, R = 0.2 m, M_rod = 2 kg, M_disk = 1 kg About a transverse axis through CM,

Question 6.
The radius of gyration of a body about an axis at 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
Solution :
Let O be a point at 6 cm from the centre of mass of the body.
Let I = MI about an axis through O,
k = radius of gyration about the axis through O,
I_CM = MI about a parallel axis through the centre of mass of the body,
k_CM = radius of gyration about a parallel axis through the centre of mass,
M = mass of the body,
h = distance between the two axes.
Data : h = 6 cm, k = 10 cm
By the theorem of parallel axis,
I = I_CM + Mh²
Also, I = Mk² and I_CM = \(M k_{\mathrm{CM}}^{2}\)

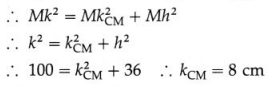
The radius of gyration about a parallel axis through its centre of mass is 8 cm.

Question 7.
The radius of gyration of a disc about its transverse symmetry axis is 2 cm. Determine its radius of gyration about a diameter.
Solution :
Data : k_CM = 2 cm
Let M and R be the mass and radius of the disc. Let I_CM and k_CM be the MI and radius of gyration of the disc about its transverse symmetry axis. Let I and k be the MI and radius of gyration of the disc about its diameter. Then

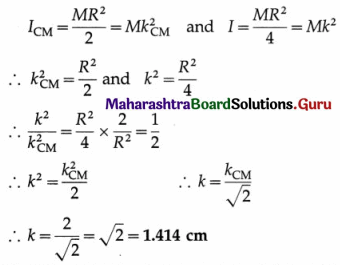
Question 8.
Calculate the MI and rotational kinetic energy of a thin uniform rod of mass 10 g and length 60 cm when it rotates about a transverse axis through its centre at 90 rpm.
Solution :
Data : M = 10 g = 10^-2 kg, L = 60 cm = 0.6 m,
f = 90 rpm = 90/60 Hz = 1.5 Hz
The MI of the rod about a transverse axis through its centre is

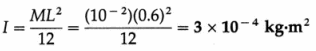
Angular speed, ω = 2πf = 2 × 3.142 × 1.5 = 9.426 rad/s
Rotational KE = \(\frac{1}{2}\)Iω² = \(\frac{1}{2}\left(3 \times 10^{-4}\right)(9.426)^{2}\)
= 0.01333 J

Question 9.
A thin rod of uniform cross section is made up of two sections made of wood and steel. The wooden section has length 50 cm and mass 0.6 kg. The steel section has length 30 cm and mass 3 kg. Find the moment of inertia of the rod about a transverse axis passing through the junction of the two sections.
Solution:
Data : L₁ =0.5m, M₁ =0.6 kg, L₂ = 0.3m,
The moment of inertia of a thin rod about a transverse axis through its end is \(\frac{M L^{2}}{3}\).

Question 10.
The mass and the radius of the Moon are, respectively, about \(\frac{1}{81}\) time and about \(\frac{1}{3.7}\) time those of the Earth. Given that the rotational period of the Moon is 27.3 days, compare the rotational kinetic energy of the Earth with that of the Moon.
Solution :
Data : M_M = \(\frac{1}{81}\)M_E, R_M = \(\frac{1}{3.7}\)R_E, T_M = 27.3 days, T_E = 1 day

Let I_E and I_M be the moments of inertia of the Earth and the Moon about their respective axes of rotation, and ω_E and ω_M be their respective rotational angular speeds. Assuming the Earth and the Moon to be solid spheres of uniform densities,

Question 11.
A solid sphere of radius R, rotating with an angular velocity ω about its diameter, suddenly stops rotating and 75% of its KE is converted into heat. If c is the specific heat capacity of the material in SI units, show that the temperature of 3R²CO²
the sphere rises by \(\frac{3 R^{2} \omega^{2}}{20 c}\).
Answer:
The MI of a solid sphere about its diameters, I = \(\frac{2}{5}\)MR²
where M is its mass.
The rotational KE of the sphere,

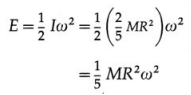
If ∆θ is the rise in temperature,

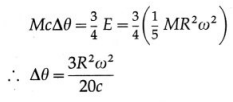
Question 97.
Define the angular momentum of a particle.
Answer:
Definition : The angular momentum of a particle is defined as the moment of the linear momentum of the particle. If a particle of mass m has linear momentum \(\vec{p}(=m \vec{v})\)), then the angular momentum of this particle with respect to a point O is a vector quantity defined as \(\vec{l}=\vec{r} \times \vec{p}=m(\vec{r} \times \vec{v})\)), where \(\vec{r}\) is the position vector of the particle with respect to O.

It is the angular analogue of linear momentum.

[Note : As the particle moves relative to O in the direction of its momentum \(\vec{p}(=m \vec{v})\), position vector \(\vec{r}\) rotates around O. However, to have angular momentum about O, the particle does not itself have to rotate around O.]

Question 98.
State the dimensions and SI unit of angular momentum.
Answer:

1. Dimensions : [Angular momentum] = [M¹L²T^-1]
2. SI unit: The kilogram.metre²/second (kg.m²/s).

Question 99.
Express the kinetic energy of a rotating body in terms of its angular momentum.
Answer:
The kinetic energy of a body of moment of inertia I and rotating with a constant angular velocity ω is
E = \(\frac{1}{2} I \omega^{2}\)
The angular momentum of the body, L = Iω.
∴E = \(\frac{1}{2}(I \omega) \omega=\frac{1}{2} L \omega\)
This is the required relation.

Question 100.
Why do grinding wheels have large mass and moderate diameter?
Answer:
A grinding wheel, used for abrasive machining operations (e.g., sharpening), is typically in the form of a heavy disc of moderate diameter. A grinding machine needs to have a high frequency of revolution but the machining operations exert braking torques on its wheel.

Angular momentum is directly proportional to mass. Hence, heavier the wheel, the greater is its angular momentum and lesser is the decelerating effect of the braking torques. Also, angular acceleration is inversely proportional to the moment of inertia. Since the wheel is made heavy, its diameter is kept moderate so that a large angular acceleration and high angular velocity can be achieved with a motor of given power.

Question 101.
Solve the following :

Question 1.
The angular momentum of a body changes by 80 kg.m²/s when its angular velocity changes from 20 rad/s to 40 rad/s. Find the change in its kinetic energy of rotation.
Solution :
Data : ω₁ = 20 rad/s, ω₂ = 40 rad/s
If I is the MI of the body, its initial angular momentum is Iω₁, and final angular momentum is Iω₂.
Change in angular momentum
= Iω₂ – Iω₁(ω₂ – ω₁)
∴ 80 = I(40 – 20)
∴ I = 4 kg.m²

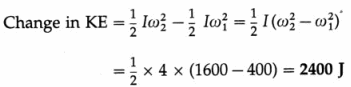
Question 2.
A wheel of moment of inertia 1 kg.m² is rotating at a speed of 40 rad/s. Due to the friction on the axis, the wheel comes to rest in 10 minutes. Calculate the angular momentum of the wheel, two minutes before it comes to rest.
Solution :
Data : I = 1 kg.m², ω₁ = 40 rad/s, ω₂ = 0 at
t = 10 minutes = 60 × 10 s = 600 s,
t’ = 8 minutes = 60 × 8 s = 480 s

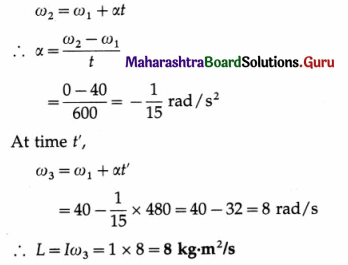
This is the required angular momentum of the wheel.

Question 3.
A flywheel rotating about an axis through its centre and perpendicular to its plane loses 100 J of energy on slowing down from 60 rpm to 30 rpm. Find its moment of inertia about the given axis and the change in its angular momentum.
Solution :
Data : f₁ = 60 rpm = 60/60 rot/s = 1 rot/s, f₂ = 30 rpm = 30/60 rot/s = \(\frac{1}{2}\) rot/s, ∆E = – 100 J

This gives the MI of the flywheel about the given axis.

(ii) Angular momentum, L = Iω = I(2πf) 2πIf
The change in angular momentum, ∆L
= L₂ – L₁ = 2πI(f₂ – f₁)
= 2 × 3.142 × 6.753\(\left(\frac{1}{2}-1\right)\)
= -3.142 × 6.753= -21.22 kg.m²/s

Question 102.
A torque of 4 N-m acting on a body of mass 1 kg produces an angular acceleration of 2 rad/s². What is the moment of inertia of the body?
Answer:
The moment of inertia of the body.

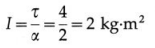
Question 103.
Two identical rings are to be rotated about different axes of rotation as shown by applying torques so as to produce the same angular acceleration in both. How is it possible ?

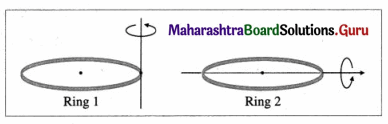
Answer:
The MI of ring 1 about a transverse tangent is I₁ = 2MR²
The MI of ring 2 about its diameter is
I₂ = \(\frac{1}{2}\)MR²
Since, torque T = \(\tau=I \alpha\), to produce the same angular acceleration in both,

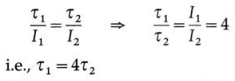
∴ It will be possible to produce the same angular acceleration in both the rings only if \(\tau_{1}=4 \tau_{2}\).

Question 104.
Two wheels have the same mass. First wheel is in the form of a solid disc of radius R while the second is a disc with inner radius r and outer radius R. Both are rotating with same angular velocity ω₀ about transverse axes through their centres. If the first wheel comes to rest in time t₁ while the second comes to rest in time t₂, are t₁ and t₂ different? Why?
Answer:
The moments of inertia of the two wheels about transverse axes through their centres are

Question 105.
Solve the following :

Question 1.
A torque of magnitude 400 N-m, acting on a body of mass 40 kg, produces an angular acceleration of 20 rad/s². Calculate the moment of inertia and radius of gyration of the body.
Solution :
Data : T = 400 N.m, M = 40 kg, α = 20 rad/s²

Question 2.
A body starts rotating from rest. Due to a couple of 20 N.m, it completes 60 revolutions in one minute. Find the moment of inertia of the body.
Solution :

Question 3.
A wheel of moment of inertia 2 kg-m2 rotates at 50 rpm about its transverse axis. Find the torque that can stop the wheel in one minute.
Solution :
Data : I = 2 kg.m², f₀ = 50 rpm = \(\frac{50}{60}\) = \(\frac{5}{6}\) rev/s, t = 60 s

Question 4.
A circular disc of moment of inertia 10 kg.m² is rotated about its transverse symmetry axis at a constant frequency of 60 rpm by an electric motor of power 31.42 watts. When the motor is switched off, how many rotations does it complete before coming to rest?
Solution :
Data : I = 10 kg.m², P = 31.42 watts,
f = 60 rpm = 60/60 Hz = 1 Hz
In rotational motion,
power = torque × angular velocity

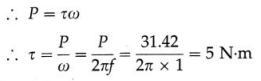
This torque provided by the motor overcomes the torque of the frictional forces and maintains a constant frequency of rotation.

When the motor is switched off, the disc slows down due to the retarding torque of the frictional forces.

Question 5.
A flywheel of mass 4 kg and radius 10 cm, rotating with a uniform angular velocity of 5 rad/s, is subjected to a torque of 0.01 N.m for 10 seconds.
If the torque increases the speed of rotation, find
(i) the final angular velocity of the flywheel
(ii) the change in its angular velocity
(iii) the change in its angular momentum
(iv) the change in its kinetic energy.
Solution :
Data : M = 4 kg, R = 10 cm = 0.1 m, ω₁ = 5 rad/s, \(\tau\) = 0.01 N.m, t = 10 s

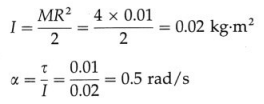
(i) The final angular velocity of the flywheel,
ω₂ = ω₁ + αt
= 5 + 0.5 × 10 = 10 rad/s

(ii) The change in its angular velocity
= ω₂ – ω₁ = 5 rad/s

(iii) The change in its angular momentum
= Iω₂ – Iω₁ = I (ω₂ – ω₁)
= 0.02 × 5 = 0.1 kg.m²/s

(iv) The change in its kinetic energy

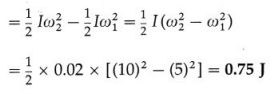
Question 6.
A torque of 20 N.m sets a stationary circular disc into rotation about a transverse axis through its centre and acts for 2π seconds. If the disc has a mass 10 kg and radius 0.2 m, what is its frequency of rotation after 2π seconds ?
Solution :
Data : \(\tau\) = 20 N.m, t = 2π s, M = 10 kg, R = 0.1 m Let f₁ and f₂ be the initial and final frequencies of rotation of the disc, and ω₁ and ω₂ be its initial and final angular speeds. Since the disc was initially stationary, f₁ = ω₁, = 0 and ω₂ = 2πf₂.
The MI of the disc about the given axis is

Now, ω₂ = ω₁ + αt = 0 + α t
∴ 2πf₂ = αt
∴ f₂ = \(\frac{\alpha t}{2 \pi}\) = \(\frac{100(2 \pi)}{2 \pi}\) = 100 Hz

Question 7.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. If the rope is pulled downwards with a force of 30 N, find
(i) the angular acceleration of the cylinder
(ii) the linear acceleration of the rope.
Solution :
Data : M = 3 kg, R = 0.4 m, F = 30 N
(i) The MI of a hollow cylinder about its cylinder axis, I = MR²

(ii) The linear acceleration of the rope = the tangential acceleration at = αR = 25 × 0.4 = 10 m/s²

Question 106.
State and prove the principle (or law) of conservation of angular momentum.
Answer:
Principle (or law) of conservation of angular momentum : The angular momentum of a body is conserved if the resultant external torque on the body is zero.
Proof : Consider a moving particle of mass m whose position vector with respect to the origin at any instant is \(\vec{r}\).
Then, at this instant, the linear velocity of this particle is \(\vec{v}=\frac{\overrightarrow{d r}}{d t}\), its linear momentum is \(\vec{p}=m \vec{v}\) and its angular momentum about an axis through the origin is \(\vec{l}=\vec{r} \times \vec{p}\).

Suppose its angular momentum \(\vec{l}\) changes with time due to a torque \(\vec{\tau}\) exerted on the particle.

∴ \(\vec{l}\) = constant, i.e., \(\vec{l}\) is conserved. This proves the principle (or law) of conservation of angular momentum.

Alternate Proof : Consider a rigid body rotating with angular acceleration \(\vec{\alpha}\) about the axis of rotation. If I is the moment of inertia of the body about the axis of rotation, \(\vec{\omega}\) the angular velocity of the body at time t and \(\vec{L}\) the corresponding angular momentum of the body, then

∴ \(\vec{L}\) = constant, i.e., \(\vec{L}\) is conserved. This proves the principle (or law) of conservation of angular momentum.

Question 107.
What happens when a ballet dancer stretches her arms while taking turns?
Answer:
When a ballet dancer stretches her arms while pirouetting, her moment of inertia increases, and consequently her angular speed decreases to conserve angular momentum.

Question 108.
If the Earth suddenly shrinks so as to reduce its volume, mass remaining unchanged, what will be the effect on the duration of the day?
Answer:
If the Earth suddenly shrinks, mass remaining constant, the moment of inertia of the Earth will decrease, and consequently the angular velocity of rotation ω about its axis will increase. Since period \(T \propto \frac{1}{\omega}\), the duration of the day T will decrease.

Question 109.
Two discs of moments of inertia I₁ and I₂ about their transverse symmetry axes, respectively rotating with angular velocities to ω₁ and ω₂, are brought into contact with their rotation axes coincident. Find the angular velocity of the composite disc.
Answer:
We assume that the initial angular momenta (\(\vec{L}_{1}\) and \(\vec{L}_{2}\)) of the discs are either in the same direction or in opposite directions. Then,
the total initial angular momentum = \(\vec{L}_{1}+\vec{L}_{2}=I_{1} \overrightarrow{\omega_{1}}+I_{2} \overrightarrow{\omega_{2}}\)

After they are coupled, the total moment of inertia, i.e., the moment of inertia of the composite disc is I = I₁ + I₂ and the common angular velocity is \(\vec{\omega}\). Assuming conservation of angular momentum,

Question 110.
A boy standing at the centre of a turntable with his arms outstretched is set into rotation with angular speed ω rev/min. When the boy folds his arms back, his moment of inertia reduces to \(\frac{2}{5}\)th its initial value. Find the ratio of his final kinetic energy of rotation to his initial kinetic energy.
Answer:
Data : I₂ = \(\frac{2}{5}\)I₁
L = Iω
Assuming the angular momentum \(\vec{L}\) is conserved, in magnitude,

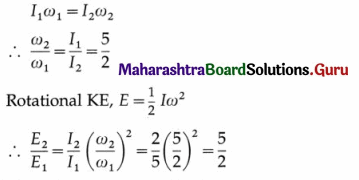
This gives the required ratio.

Question 111.
Name the quantity that is conserved when

1. \(\vec{F}_{\text {external }}\) is zero
2. \(\vec{\tau}_{\text {external }}\) is zero.

Answer:

1. Total linear momentum is conserved when \(\vec{F}_{\text {external }}\) is Zer0
2. Angular momentum is conserved when \(\vec{\tau}_{\text {external }}\) is zero.

Question 112.
What is the rotational analogue of the equation \(\vec{F}_{\text {external }}\) = \(\frac{d \vec{p}}{d t}\)?
Answer:
\(\vec{F}_{\text {external }}\) = \(\frac{d \vec{L}}{d t}\)

Question 113.
Fly wheels used in automobiles and steam engines producing rotational motion have discs with a large moment of inertia. Explain why?
Answer:
A flywheel is used as

(i) a mechanical energy storage, the energy being stored in the form of rotational kinetic energy

(ii) a direction and speed stabilizer. A flywheel rotor is typically in the form
of a disc. Rotational kinetic energy, \(E_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}\), where I is the moment of inertia and ω is the angular speed. That is, E_rot ∝ I. Therefore, higher the moment of inertia, the higher is the rotational kinetic energy that can be stored or recovered.

Also, angular momentum, \(\vec{L}=I \vec{\omega}\), i.e., \(|\vec{L}| \propto I\). A torque aligned with the symmetry axis of a flywheel can change its angular velocity and thereby its angular momentum. A flywheel with a large angular momentum will require a greater torque to change its angular velocity. Thus, a flywheel can be used to stabilize direction and magnitude of its angular velocity by undesired torques.

Question 114.
Solve the following :

Question 1.
A uniform horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of 180 rpm. A blob of wax of mass 1.9 g falls on it and sticks to it at 25 cm from the axis. If the frequency of rotation is reduced by 60 rpm, calculate the moment of inertia of the disc.
Solution :
Data : f₁ = 180 rpm = 180/60 rot/s = 3 rot/s, f₂ = (180 – 60) rpm = 120/60 rot/s = 2 rot/s, m = 1.9 g = 1.9 × 10^-3 kg, r = 25 cm = 0.25 m
Let I₁ be the MI of the disc. Let I₂ be the MI of the disc and the blob.

Question 2.
A horizontal disc is rotating about a transverse axis through its centre at 100 rpm. A 20 gram blob of wax falls on the disc and sticks to it at 5 cm from its axis. The moment of inertia of the disc about its axis passing through its centre is 2 × 10^-4 kg.m². Calculate the new frequency of rotation of the disc.
Solution :
Data : f₁ = 100 rpm, m = 20 g = 20 × 10^-3 kg, r = 5 cm = 5 × 10^-2 m, I₁ = I_disc = 2 × 10^-4 kg.m²
The MI of the disc and blob of wax is
I₂ = I₁ + mr²

This is the new frequency of rotation.

Question 3.
A ballet dancer spins about a vertical axis at 2.5 π rad/s with his arms outstretched. With the arms folded, the MI about the same axis of rotation changes by 25%. Calculate the new speed of rotation in rpm.
Solution:
Let I₁, ω₁, and f₁, be the moment of inertia, angular velocity and frequency of rotation of the ballet dancer with arms outstretched, and I₂, ω₂ and f₂ be the corresponding quantities with arms folded.
Data : ω₁ = 2.5 π rad /s
Since moment of inertia with arms folded is less than that with arms outstretched,

Question 4.
Two wheels, each of moment of inertia 4 kg.m², rotate side by side at the rate of 120 rpm and 240 rpm in opposite directions. If both the wheels are coupled by a weightless shaft so that they now rotate with a common angular speed, find this new rate of rotation.
Solution :
Data : I = 4 kg.m², f₁ = 120 rpm, f₂ 240 rpm
Initially, the angular velocities of the two wheels \(\overrightarrow{\omega_{1}}\), and \(\overrightarrow{\omega_{2}}\)) and, therefore, their angular momenta (\(\vec{L}_{1}\) and \(\vec{L}_{2}\)) are in opposite directions.

The magnitude of the total initial angular momentum
= – L₁ + L₂ = -Iω₁ + Iω₂ (∵ I₁ = I₂ = I)
= 2πl(f₂ – f₁) … (1)

After coupling onto the same shaft, the total moment of inertia is 21. Let ω = 2πf be the common angular speed.

The magnitude of the total final angular momentum = 2I.ω = 4πl.f … (2)

From Eqs. (1) and (2), by the principle of conservation of angular momentum,
4πf = 2πl(f₂ – f₁)
∴ f = \(\frac{f_{2}-f_{1}}{2}\) = \(\frac{240-120}{2}\) = 60 rpm
This gives their new rate of rotation.

Question 5.
A homogeneous (uniform) rod XY of length L and mass M is pivoted at the centre C such that it can rotate freely in a vertical plane. Initially, the rod is horizontal. A blob of wax of the same mass M as that of the rod falls vertically with speed V and sticks to the rod midway between points C and Y. As a result, the rod rotates with angular speed ω. What will be the angular speed in terms of V and L?
Solution :
The initial angular momentum of the rod is zero.
The initial angular momentum of the falling blob of wax about the point C is (in magnitude)
= mass × speed × perpendicular distance between its direction of motion and point C
= MV.\(\frac{L}{4}\)
The total initial angular momentum of the rod and blob of wax = \(\frac{M V L}{4}\) … (1)

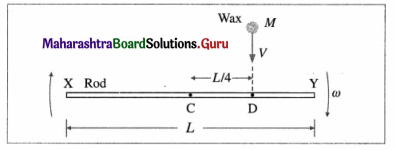
After the blob of wax sticks to the rod, and the system rotates with an angular speed ω about the horizontal axis through point C perpendicular to the plane of the figure, the total final angular momentum of the system about this axis

This gives the required angular speed.

Question 6.
A satellite moves around the Earth in an elliptical orbit such that at perigee (closest approach) it is two Earth radii above the Earth’s surface. At apogee (farthest position), it travels with one-fourth the speed it has at perigee. In terms of the Earth’s radius R, what is the maximum distance of the satellite from the Earth’s surface ?
Solution:
Let r_p and r_a be the distances of the satellite from the centre of the Earth at perigee and apogee, respectively. Let v_p and v_a be its linear (tangential) velocities at perigee and apogee.
Data : r_p = 2R + R = 3R, v_a = \(\frac{1}{4}\)v_p

Let L_p and L_a be the angular momenta of the satellite about the Earth’s centre. Because the gravitational force (\(\vec{F}\)) on the satellite due to the Earth is always radially towards the centre of the Earth, its direction is opposite to that of the position vector (\(\vec{r}\)) of the satellite relative to the centre of the Earth, so that the torque \(\vec{\tau}=\vec{r} \times \vec{F}=0\). Hence, the angular momentum of the satellite about the Earth’s centre is constant in time.

At apogee, the distance of the satellite from the Earth’s surface is 12R – R = 11R.

Question 7.
A torque of 100 N.m is applied to a body capable of rotating about a given axis. If the body starts from rest and acquires kinetic energy of 10000 J in 10 seconds, find
(i) its moment of inertia about the given axis
(ii) its angular momentum at the end of 10 seconds.
Solution :
Data : \(\tau\) = 100 N.m, ω_i = 0, E_i = 0, E_f = 10⁴J, t = 10 s

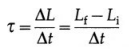
Since the body starts from rest, its initial angular momentum, L_i = 0.
The final angular momentum,
L_f = τ∆t = (100)(10) = 10³ kg.m²/s
The final rotational kinetic energy, E_f = \(\frac{1}{2} L_{\mathrm{f}} \omega_{\mathrm{f}}\)

Question 8.
Two identical metal beads, each of mass M but negligible width, can slide along a thin smooth uniform horizontal rod of mass M and length L. The rod is capable of rotating about a vertical axis passing through its centre. Initially, the beads are almost touching the axis of rotation and the rod is rotating at speed of 14 rad/s. Find the angular speed of the system when the beads have moved up to the ends of the rod. (Assume that no external torque acts on the system.)
Solution :
Data : ω₁ = 14 rad/s
The MI of the rod about a transverse axis through its CM,
I_rod = \(\frac{M L^{2}}{12}\)
Since the beads are almost particle-like, and initially touching the rotation axis, their MI about the vertical axis is taken to be zero.
When the beads move upto the ends of the rod, r = L/2, their MI about the vertical axis is

Question 115.
Discuss how pure rolling (i.e., rolling without slipping) on a plane surface is a combined translational and rotational motion.
Answer:
Rolling motion (without slipping) is an important case of combined translation and rotation. Consider a circularly symmetric rigid body, like a wheel or a disc, rolling on a plane surface with friction along a straight path.

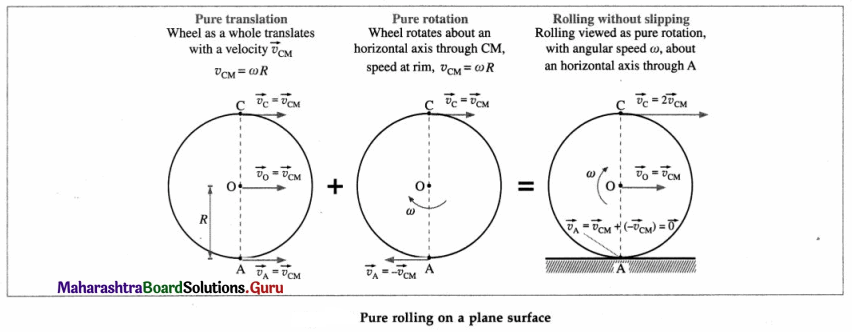
The centre of mass of the wheel is at its geometric centre O. For purely translational motion (the wheel sliding smoothly along the surface without rotating at all), every point on the wheel has the same linear velocity \(\vec{v}_{\mathrm{CM}}\) = \(\vec{v}_{\mathrm{O}}\) as the centre O. For purely rotational motion (as if the horizontal rotation axis through O were stationary), every point on the wheel rotates about the axis with angular velocity \(\vec{\omega}\); in this case, every point on the rim has the same linear speed ωR.

We view the combined motion in the inertial frame of reference in which the surface is at rest. In this frame, since there is no slipping, the point of contact of the wheel with the surface is instantaneously stationary, v_A = 0, so that the wheel is turning about an instantaneous axis through the point of contact A. The instantaneous linear speed of point C (at the top) is V_C = ω(2R) – faster than any other point of the wheel.

Question 116.
Deduce an expression for the kinetic energy of a body rolling on a plane surface without slipping.
OR
Obtain an expression for the total kinetic energy of a rolling body in the form \(\frac{1}{2} M v^{2}\left[1+\frac{k^{2}}{R^{2}}\right]\)
OR
Derive an expression for the kinetic energy when a rigid body is rolling on a horizontal surface without slipping. Hence, find the kinetic energy of a solid sphere.
Answer:
Consider a symmetric rigid body, like a sphere or a wheel or a disc, rolling on a plane surface with friction along a straight path. Its centre of mass (CM) moves in a straight line and, if the frictional force on the body is large enough, the body rolls without slipping. Thus, the rolling motion of the body can be treated as translation of the CM and rotation about an axis through the CM. Hence, the kinetic energy of a rolling body is
E = E_tran + E_rot ….. (1)
where E_tran and E_rot are the kinetic energies associated with translation of the CM and rotation about an axis through the CM, respectively.

Let M and R be the mass and radius of the body. Let ω, k and I be the angular speed, radius of gyration and moment of inertia for rotation about an axis through its centre, and v be the translational speed of the centre of mass.

Equation (4) or (5) or (6) gives the required expression.

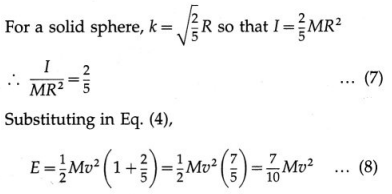
Question 117.
A uniform solid sphere of mass 10 kg rolls on a horizontal surface. If its linear speed is 2 m/s, what is its total kinetic energy?
Answer:
Total kinetic energy of the sphere
= \(\frac{7}{10}\)Mv² = \(\frac{7}{10}\) × 10 × (2)² = 28 J

Question 118.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/s, what is its total kinetic energy?
Answer:
Total kinetic energy of the disc
= \(\frac{3}{4}\)Mv² = \(\frac{3}{4}\) × 4 × (3)² = 27 J

Question 119.
Assuming the expression for the kinetic energy of a body rolling on a plane surface without slipping, deduce the expression for the total kinetic energy of rolling motion for
(i) a ring
(ii) a disk
(iii) a hollow sphere. Also, find the ratio of rotational kinetic energy to total kinetic energy for each body.
Answer:
For a body of mass M and radius of gyration k, rolling on a plane surface without slipping with speed v, its total KE and rotational KE are respectively

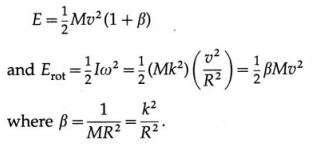
[Note : The moment of inertia of all the round bodies above can be expressed as I = βMR², where β is a pure number less than or equal to 1. β is equal to 1 for a ring or a thin-walled hollow cylinder, \(\frac{1}{2}\) for a disc or solid cylinder, \(\frac{2}{3}\) for a hollow sphere and \(\frac{2}{5}\) for a solid sphere.
All uniform rings or hollow cylinders of the same mass and moving with the same speed have the same total kinetic energy, even if their radii are different. All discs or solid cylinders of the same mass and moving with the same speed have the same total kinetic energy; all solid spheres of the same mass and moving with the same speed have the same total kinetic energy. Also, for the same mass and speed, bodies with small c have less total kinetic energy.

Question 120.
State the expression for the speed of a circularly symmetric body rolling without slipping down an inclined plane. Hence deduce the expressions for the speed of
(i) a ring
(ii) a solid cylinder
(iii) a hollow sphere
(iv) a solid sphere, having the same radii.
Answer:
Consider a circularly symmetric body, of mass M and radius of gyration k, starting from rest on an inclined plane and rolling down without slipping. Its speed after rolling down through a height h is

[Note : If the inclined plane is ‘smooth’, i.e., there is no friction, the bodies will slide along the plane without any rotation. They will then have only translational kinetic energy, undergo equal acceleration and all three would arrive at the bottom at the same time with the same speed.]

Question 121.
State with reason if the statement is true or false : A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
Answer:
The statement is true.
Explanation : Rolling on a surface (horizontal or inclined) without slipping may be viewed as pure rotation about an horizontal axis through the point of contact, when viewed in the inertial frame of reference in which the surface is at rest. The point of contact of the wheel with the surface will be instantaneously at rest, resulting in a rolling motion, provided the wheel is able to ‘grip’ the surface, i.e., friction is necessary. With little or no friction, the wheel will slip at the point of contact. On an inclined plane, this will result in pure translation along the plane. On a horizontal surface, the wheel will simply rotate about its axis through the centre without translation.

Question 122.
A ring and a disc roll down an inclined plane through the same height. Compare their speeds at the bottom of the plane.
Answer:

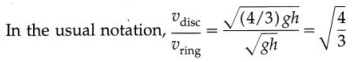
Question 123.
State the expression for the acceleration of a circularly symmetric rigid body rolling without slipping down an inclined plane. Hence, deduce the acceleration of
(i) a ring
(ii) a solid cylinder
(iii) a hollow cylinder
(iv) a solid sphere, rolling without slipping down an inclined plane.
Answer:
A circularly symmetric rigid body, of radius R and radius of gyration k, on rolling down an inclined plane of inclination θ has an acceleration

Question 124.
A spherical shell rolls down a plane inclined at 30° to the horizontal. What is its acceleration ?
Answer:
The acceleration of the spherical shell,
a = \(\frac{3}{5} g \sin \theta\) = 0.6g sin 30° = 0.6g × \(\frac{1}{2}\) = 0.3g m

Question 125.
A spherical shell and a uniform solid sphere roll down the same inclined plane. Compare their accelerations.
Answer:
The ratio of the accelerations, in the usual notation,

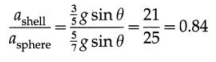
Question 126.
A solid sphere, starting from rest, rolls down two different inclined planes from the same height but with different angles of inclination θ₁ > θ₂. On which plane will the sphere take longer time to roll down?
Answer:
Let L₁ and L₂ be the distances rolled down by the sphere along the corresponding inclines from the same height h.
∴ L₁ sin θ₁ = L₂ sin θ₂ = h

The sphere will take longer time to roll down from the same height on the plane with smaller inclination.

Question 127.
Two circular discs A and B, having the same mass, have four identical small circular discs placed on them, as shown in the diagram. They are simultaneously released from rest at the top of an inclined plane. If the discs roll down without slipping, which disc will reach the bottom first?

Answer:
The disc A has the smaller discs closer to the centre than disc B. Hence, the moment of inertia of disc A (I_A) is less than that of disc B (I_B).

[Suppose the larger discs have radius R, the smaller discs have mass m and radius r, and the centre of each smaller disc on disc A is at a distance x from the centre. Then, x = \(\sqrt{2} r\)r and, it can be shown that, I_B – I_A = 4m[R² – (x – r)²] > 0.]

Each composite disc is equivalent to a disc of the same radius R and mass M’ = M + 4m, where m is the mass of each smaller disc, but of different thicknesses.

Suppose, starting from rest, the composite discs roll down the same distance L along a plane inclined at an angle θ, their respective accelerations will be

i.e., the disc A will reach the bottom first.

Question 128.
Solve the following :

Question 1.
A lawn roller of mass 80 kg, radius 0.3 m and moment of inertia 3.6 kg.m², is drawn along a level surface at a constant speed of 1.8 m/s. Find
(i) the translational kinetic energy
(ii) the rotational kinetic energy
(iii) the total kinetic energy of the roller.
Answer:
Data : M = 80 kg, R = 0.3 m, I = 3.6 kg.m², v = 1.8 m/s
(i) The translational kinetic energy of the centre of mass of the roller,

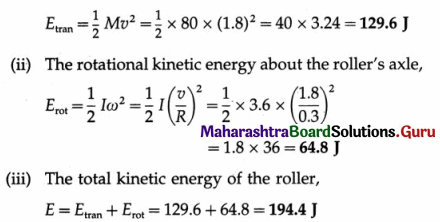
Question 2.
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
Solution :
Data : M = 1 kg, v = 2 m/s
The total kinetic energy of a rolling body,

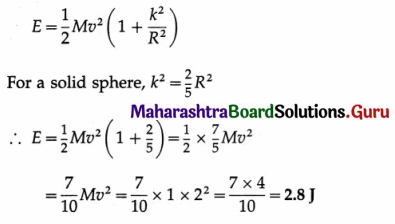
Question 3.
A ring and a disc having the same mass roll on a horizontal surface without slipping with the same linear velocity. If the total KE of the ring is 8 J, what is the total KE of the disc?
Solution :
Data : M_ring = M_disc = M, v_ring = v_disc = v, E_ring = 8J
The total kinetic energies of rolling without slipping on a horizontal surface,
E_ring = Mv² and E_disc = \(\frac{3}{4} M v^{2}\)
since they have the same mass and linear velocity.
∴ E_disc = \(\frac{3}{4}\)E_ring = \(\frac{3}{4}\) × 8 = 6J

Question 4.
A solid cylinder, of mass 2 kg and radius 0.1 m, rolls down an inclined plane of height 3 m. Calculate its rotational energy when it reaches the foot of the plane.
Solution :
Data : M = 2 kg, R = 0.1 m, h = 3 m, g = 10 m/s²

Question 5.
A solid sphere rolls up a plane inclined at 45° to the horizontal. If the speed of its centre of mass at the bottom of the plane is 5 m/s, find how far the sphere travels up the plane.
Solution :
Data : v = 5 m/s, θ = 45°, g = 9.8 m/s²
The total energy of the sphere at the bottom of the plane is
E = \(\frac{7}{10} M v^{2}\)
where M is the mass of the sphere.
In rolling up the incline through a vertical height h, it travels a distance L along the plane. Then,

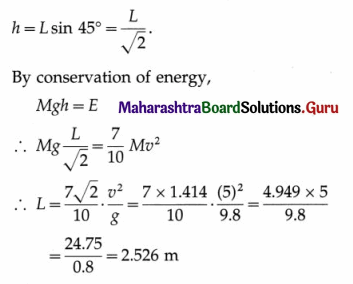
The sphere travels 2.526 m up the plane.

Question 129.
Choose the correct option:

Question 1.
The bulging of the Earth at the equator and flattening at the poles is due to
(A) centripetal force
(B) centrifugal force
(C) gravitational force
(D) electrostatic force.
Answer:
(B) centrifugal force

Question 2.
A body of mass 0.4 kg is revolved in a horizontal circle of radius 5 m. If it performs 120 rpm, the centripetal force acting on it is
(A) 4π² N
(B) 8π² N
(C) 16π² N
(D) 32π² N.
Answer:
(D) 32π² N.

Question 3.
Two particles with their masses in the ratio 2 : 3 perform uniform circular motion with orbital radii in the ratio 3 : 2. If the centripetal force acting on them is the same, the ratio of their speeds is
(A) 4 : 9
(B) 1 : 1
(C) 3 : 2
(D) 9 : 4.
Answer:
(C) 3 : 2

Question 4.
When a motorcyclist takes a circular turn on a level race track, the centripetal force is
(A) the resultant of the normal reaction and frictional force
(B) the horizontal component of the normal reaction
(C) the frictional force between the tyres and road
(D) the vertical component of the normal reaction.
Answer:
(C) the frictional force between the tyres and road

Question 5.
The maximum speed with which a car can be driven safely along a curved road of radius 17.32 m and banked at 30° with the horizontal is [g = 10 m/s²]
(A) 5 m/s
(B) 10 m/s
(C) 15 m/s
(D) 20 m/s.
Answer:
(B) 10 m/s

Question 6.
A track for a certain motor sport event is in the form of a circle and banked at an angle 6. For a car driven in a circle of radius r along the track at the optimum speed, the periodic time is

Answer:
(C) \(2 \pi \sqrt{\frac{r}{g \tan \theta}}\)

Question 7.
The period of a conical pendulum in terms of its length (l), semivertical angle (θ) and acceleration due to gravity (g), is

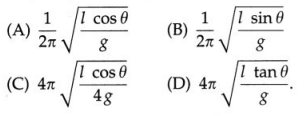
Answer:
(C) \(4 \pi \sqrt{\frac{l \cos \theta}{4 g}}\)

Question 8.
A conical pendulum of string length L and bob of mass m performs UCM along a circular path of radius r. The tension in the string is

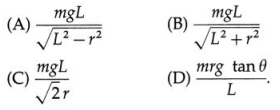
Answer:
(A) \(\frac{m g L}{\sqrt{L^{2}-r^{2}}}\)

Question 9.
The centripetal acceleration of the bob of a conical pendulum is

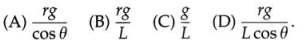
Answer:
(D) \(\frac{r g}{L \cos \theta}\)

Question 10.
A small object tied at the end of a string is to be whirled in a vertical circle of radius r. If its speed at the lowest point is \(2 \sqrt{g r}\), then
(A) the string will be slack at the lowest point
(B) it will not reach the midway point
(C) its speed at the highest point will be \(\sqrt{g r}\)
(D) it will just reach the highest point with zero speed.
Answer:
(D) it will just reach the highest point with zero speed.

Question 11.
A small bob of mass m is tied to a string and revolved in a vertical circle of radius r. If its speed at the highest point is \(\sqrt{3 r g}\), the tension in the string at the lowest point is
(A) 5 mg
(B) 6 mg
(C) 7 mg
(D) 8 mg.
Answer:
(D) 8 mg.

Question 12.
A small object, tied at the end of a string of length r, is launched into a vertical circle with a speed \(2 \sqrt{g r}\) at the lowest point. Its speed when the string is horizontal is
(A) > \(3 \sqrt{g r}\)
(B) = \(3 \sqrt{g r}\)
(C) = \(2 \sqrt{g r}\)
(D) 0.
Answer:
(C) = \(2 \sqrt{g r}\)

Question 13.
Two bodies with moments of inertia I₁ and I₂ (I₁ > I₂) rotate with the same angular momentum. If E₁ and E₂ are their rotational kinetic energies, then
(A) E₂ > E₁
(B) E₂ = E₁
(C) E₂ < E₁
(D) E₂ ≤ E₁
Answer:
(A) E₂ > E₁

Question 14.
The radius of gyration k for a rigid body about a given rotation axis is given by

Answer:
(B) \(k^{2}=\frac{1}{M} \int r^{2} d m\)

Question 15.
Three point masses m, 2m and 3m are located at the three vertices of an equilateral triangle of side l. The moment of inertia of the system of particles about an axis perpendicular to their plane and equidistant from the vertices is
(A) 2ml²
(B) 3ml²
(C) \(2 \sqrt{3}\) ml²
(D) 6ml²
Answer:
(A) 2ml²

Question 16.
The moment of inertia of a thin uniform rod of mass M and length L, about an axis passing through a point midway between the centre and one end, and perpendicular to its length, is
(A) \(\frac{48}{7}\)ML²
(B) \(\frac{7}{48}\)ML²
(C) \(\frac{1}{48}\)ML²
(D) \(\frac{1}{16}\)ML²
Answer:
(B) \(\frac{7}{48}\)ML²

Question 17.
A thin uniform rod of mass M and length L has a small block of mass M attached at one end. The moment of inertia of the system about an axis through its CM and perpendicular to the length of the rod is
(A) \(\frac{13}{12}\) ML²
(B) \(\frac{1}{3}\) ML²
(C) \(\frac{5}{24}\) ML²
(D) \(\frac{7}{48}\) ML²
Answer:
(C) \(\frac{5}{24}\) ML²

Question 18.
A thin wire of length L and uniform linear mass density λ is bent into a circular ring. The MI of the ring about a tangential axis in its plane is

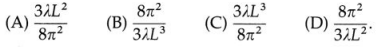
Answer:
(C) \(\frac{3 \lambda L^{3}}{8 \pi^{2}}\)

Question 19.
When a planet in its orbit changes its distance from the Sun, which of the following remains constant ?
(A) The moment of inertia of the planet about the Sun
(B) The gravitational force exerted by the Sun on the planet
(C) The planet’s speed
(D) The planet’s angular momentum about the Sun
Answer:
(D) The planet’s angular momentum about the Sun

Question 20.
If L is the angular momentum and I is the moment of inertia of a rotating body, then \(\frac{L^{2}}{2 I}\) represents its
(A) rotational PE
(B) total energy
(C) rotational KE
(D) translational KE.
Answer:
(C) rotational KE

Question 21.
A thin uniform rod of mass 3 kg and length 2 m rotates about an axis through its CM and perpendicular to its length. An external torque changes its frequency by 15 Hz in 10 s. The magnitude of the torque is
(A) 3.14 N.m
(B) 6.28 N.m
(C) 9.42 N.m
(D) 12.56 N.m.
Answer:
(C) 9.42 N.m

Question 22.
The flywheel of a motor has mass 300 kg and radius of gyration 1.5 m. The motor develops a constant torque of 2000 N.m and the flywheel starts from rest. The work done by the motor during the first 4 revolutions is
(A) 2 kJ
(B) 8 kJ
(C) 8n kJ
(D) 16π kJ.
Answer:
(D) 16π kJ.

Question 23.
Two uniform solid spheres, of the same mass but radii in the ratio R₁ : R₂ = 1 : 2, roll without slipping on a plane surface with the same total kinetic energy. The ratio ω₁ : ω₂ of their angular speed is
(A) 2 : 1
(B) \(\sqrt{2}\) : 1
(C) 1 : 1
(D) 1 : 2.
Answer:
(A) 2 : 1

Question 24.
A circularly symmetric body of radius R and radius of gyration k rolls without slipping along a flat surface. Then, the fraction of its total energy associated with rotation is [c = k²/R²]
(A) c
(B) \(\frac{c}{1+c}\)
(C) \(\frac{1}{c}\)
(D) \(\frac{1}{1+c}\)
Answer:
(B) \(\frac{c}{1+c}\)

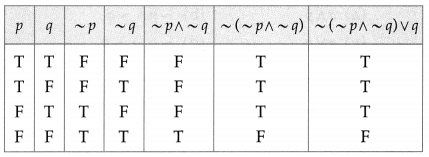
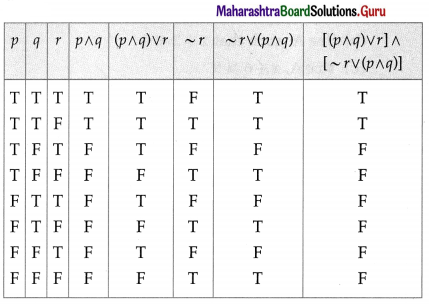
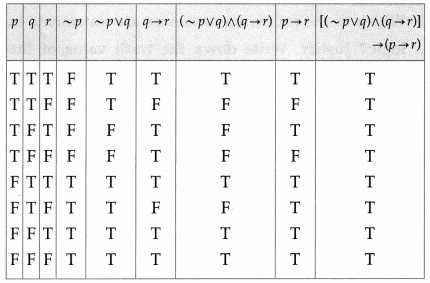
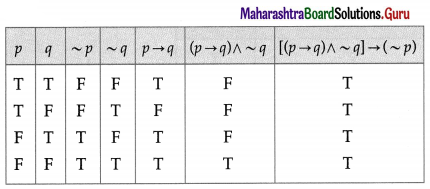
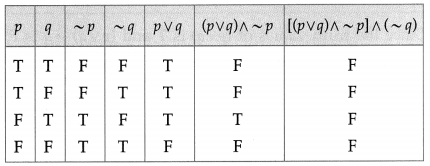
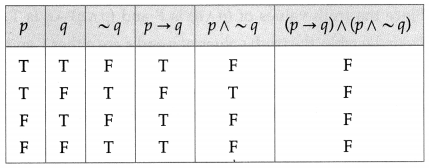
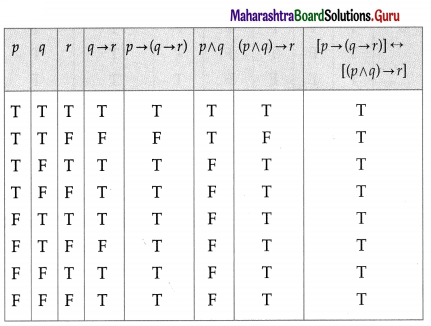
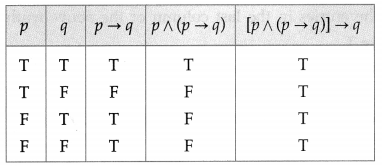
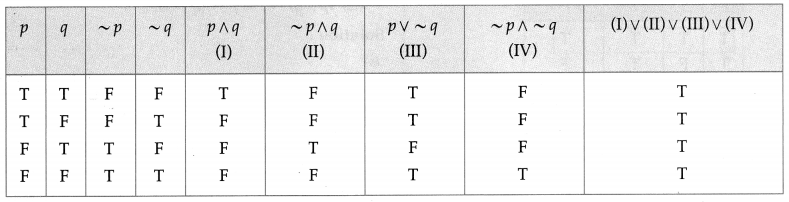
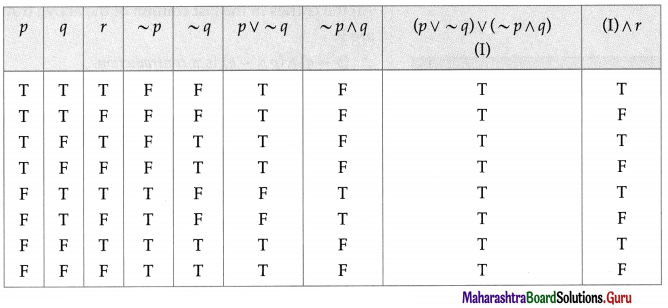
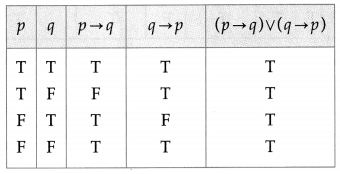
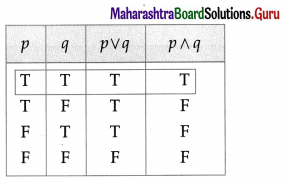
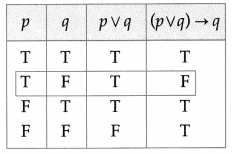
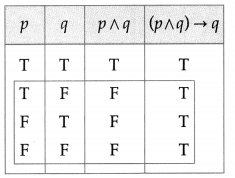
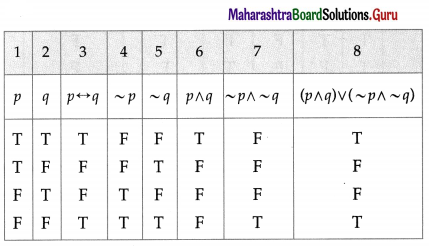
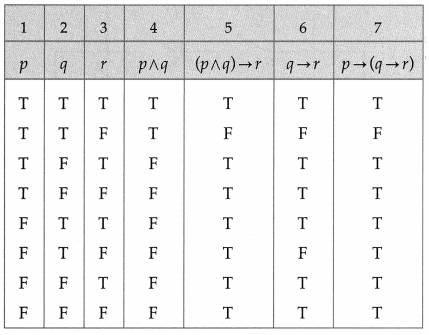
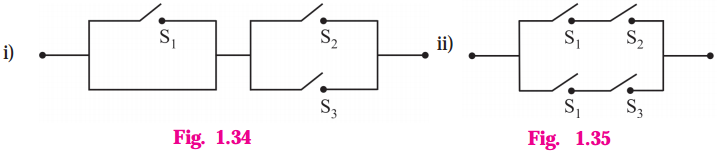
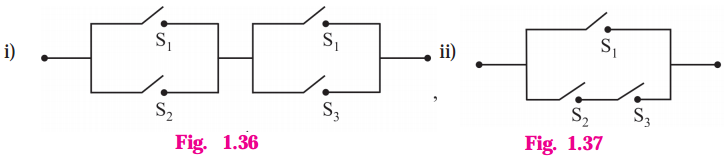
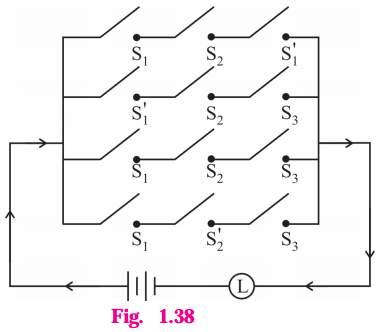
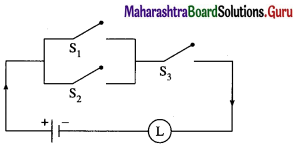
Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 2 Mechanical Properties of Fluids Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 2 Mechanical Properties of Fluids

Question 1.
What is a fluid? Give two examples.
Answer:
A fluid is a substance that can flow. A fluid has shear modulus O and yield to shear. Under a shear stress and a pressure gradient, a fluid begins to flow. Liquids, gases and plasmas are collectively called fluids.

Examples : All gases, all liquids, molten glass and lava, honey, etc.

Question 2.
What is an ideal fluid?
OR
State the characteristics of an ideal fluid.
Answer:
An ideal fluid is one that has the following properties:

1. It is incompressible, i.e., its density has a constant value throughout the fluid.
2. Its flow is irrotational, i.e., the flow is steady or laminar. In an irrotational flow, the fluid doesn’t rotate like in a whirlpool arid the velocity of the moving fluid at a specific point doesn’t change over time. (Many fluids change from laminar to turbulent flow as the speed of the fluid increases above some specific value. This can dramatically change the properties of the fluid.)
3. Its flow is nonviscous or inviscid, i.e., internal friction or viscosity is zero so that no energy lost due the motion of the fluid.

Question 3.
How does a fluid differ from a solid ?
Answer:
In response to a shear as well as normal force, a solid deforms and develops a restoring force. Within the elastic limit, both types of deformation is reversible. A solid changes its shape under a shear. A normal force causes a change in its length or volume. If the elastic limit is exceeded, the solid gets an irreversible deformation called a permanent set.

A fluid, on the other hand, can only be subjected to normal compressive stress, called pressure. A fluid does not have a definite shape, so that under a shear it begins to flow, Real fluids, with non-zero viscosity, display a weak resistance to shear.

Question 4.
State the properties of a fluid.
Answer:
Properties of a fluid :

1. They do not resist deformation and get permanently deformed.
2. They are capable of flowing.
3. They take the shape of the container.

Question 5.
Define pressure. State its SI and CGS units and dimensions.
Answer:
Definition : The pressure at a point in a fluid in hydrostatic equilibrium is defined as the normal force per unit area exerted by the fluid on a surface of infinitesimal area containing the point.
Thus, the pressure, p = \(\lim _{\Delta A \rightarrow 0} \frac{F}{\Delta A}\)
where F is the magnitude of the normal force on a surface of area ∆A. The pressure is defined to be a scalar quantity.

SI unit: the pascal (Pa), 1 Pa = 1 N∙m^-2
CGS unit: the dyne per square centimetre (dyn/cm²)
Dimensions : [p] = [F][A^-1] = [MLT^-2, L^-2]
= [ML^-1 T^-2]

Question 6.
State two non-SI units of pressure.
Answer:
Two non-SI units, which are either of historical interest, or are still used in specific fields are the bar and the torr.
1 bar = 0.1 MPa = 100 kPa = 1000 hPa = 10⁵Pa
1 torr = (101325/760) Pa = 133.32 Pa
[Note : Their use in modern scientific and technical work is strongly discouraged.]

Question 7.
If a force of 200 N is applied perpendicular to a surface of area 10 cm², what is the corresponding pressure ?
Answer:
Pressure, p = \(\frac{F}{A}=\frac{200 \mathrm{~N}}{10 \times 10^{-6} \mathrm{~m}^{2}}\) = 2 × 10⁷ N/m²

Question 8.
Explain why the forces acting on any surface within a fluid in hydrostatic equilibrium must be normal to the surface.
Answer:
In a fluid, the molecules are in a state of random motion and the intermolecular cohesive forces are weak. If a fluid is subjected to a tangential force (shear) anywhere within it, the layers of the fluid slide over one another, i.e., the fluid begins to flow. Thus, a fluid cannot sustain a tangential force. So, in

turn, a fluid at rest cannot exert a tangential force on any surface with which it is in contact. It can exert only a force normal to the surface. Hence, if a fluid is in hydrostatic equilibrium (i.e., at rest), the force acting on any surface within the fluid must be normal to the surface.

Question 9.
Would you rather have someone wearing studs step on your foot or have someone wearing tennis shoes step on your foot ?
Answer:
A person would exert the same downward force regardless of whether he or she was wearing studs or tennis shoes. However, if the person were wearing studs, the force would be applied over a much smaller area, so the pressure would be greater (and so would be more painful).

Question 10.
Would you rather have an elephant stand on your foot directly or have an elephant balance on a thumbtack on top of your foot?
Answer:
The downward force of the elephant’s weight would be applied over a much smaller area if it were balancing on a thumbtack, so the pressure would be greater.

Question 11.
Derive an expression for pressure exerted by a liquid column.
Answer:
At a point at depth h below the surface of a liquid of uniform density ρ, the pressure due to the liquid is due to the weight per unit area of a liquid column of height h above that point.

In above figure to find the pressure due to the liquid at point P, consider the cylindrical liquid column, of cross section A and height h, above that point.

The weight of this liquid column = volume × density × acceleration due to gravity
= (Ah)(ρ)(g)
∴ Pressure due to the liquid at depth h
= \(\frac{\text { weight of the liquid column }}{\text { cross sectional area }}\)
= \(\frac{A h \rho g}{A}\) = hpg
If the free surface of the liquid is open to the atmosphere, the pressure on the surface is the atmosphere pressure p₀. Then, the absolute pressure within the liquid at a depth h is p = p₀ + hρg

Question 12.
State the characteristics of pressure due to a liquid at rest at a point within it.
Answer:
Characteristics of pressure due to a liquid at rest at a point within it:

1. Within a liquid of constant density, the pressure is directly proportional to the depth.
2. At the same depth within liquids of different densities, the pressure is directly proportional to the density of the liquid.
3. Within a liquid of constant density, the pressure at a given depth is directly proportional to the acceleration due to gravity.
4. The pressure at a point within a given liquid is the same in all directions.
5. The pressure at all points at the same horizontal level within a given liquid is the same.

Question 13.
How much force is exerted on one side of an 8.50 cm by 11.0 cm sheet of paper by the atmosphere? How can the paper withstand such a force ?
Answer:
Pressure p = F/A. Therefore, the force on one side is F = ρ ∙ A = (1.013 × 10⁵ Pa) (8.50 × 11.0 × 10^-4 m²) = 947.2 N.

The pressure at a point within a fluid being the same in all directions, the same force acts on the other side of the paper. Thus, the net force on the paper is zero.

Question 14.
What is the pressure exerted by a water column of height 1 m?[ρ = 10³ kg/m³, g = 9.8 m/s²]
Answer:
Pressure exerted by the water column = hρg
= 1 m(10³ kg/m³) × (9.8 m/s²)
= 9.8 × 10³Pa

Question 15.
Would you rather breathe through a 2 m long tube to the surface in 1.5 m of water in the ocean or breathe at the beach near the ocean?
Answer:
The pressure on one’s lungs would be much greater under water than standing on the beach because the force exerted by the water on the lungs ‘ is greater than the force exerted by the air. Because the pressure of the water on the lungs is so much greater than the outward pressure of the air inside, it would be difficult to take a breath under 1.5 m of water than on the beach.

Question 16.
What is atmospheric pressure ? Define standard atmospheric pressure.
Answer:
The Earth’s surface is covered with a layer of atmosphere, with more than 99% of the atmosphere lying within 31 km of the surface. The weight of the atmosphere exerts a downward thrust on any surface lying within it. This gives rise to atmospheric pressure. The atmospheric pressure at any height above the Earth’s surface is the weight of a column of air of unit cross section from that altitude to the top of the atmosphere.

Definition : Standard atmospheric pressure, or one atmosphere of pressure, is defined as the pressure equivalent of a column of mercury that is exactly 0.7600 m in height at 0 °C.

We can calculate this equivalent pressure in SI unit by using the density of mercury
ρ = 13.6 × 10³ kg/m³ and g = 9.80 m/s².
1 atm = (0.76 m) . (13.6 × 10³ kg/m³) . (9.80 m/s²)
= 1.013 × 10⁵ Pa = 101.3 kPa
[Note : 1000 mbar = 100 kPa. Therefore, 1 atm = 1013 mbar.]

Question 17.
Explain gauge pressure and absolute pressure within a liquid open to the atmosphere.
OR
Explain the effect of gravity on fluid pressure.
Answer:
Consider a cylindrical fluid column of uniform density ρ, area of cross section A and height h,

The mass of the fluid within the column is
m = density × volume
= ρAh

If p₁ and p₂ are the pressures at the top and bottom faces of the column, the forces on the top and bottom faces are respectively.
F₁ = p₁A + mg (downward)
and F₂ = p₂A (upward)
If the column is in equilibrium,
F₂ = F₁
∴ p₂A = p₁A + mg = p₁A + ρAhg
∴ P₂ ~ P₁ = ρhg
If p₁ = p₀ = atmospheric pressure, the gauge pressure
P₂ – P₀ = ρhg

In the absence of gravity, p₂ = p₀ But since atmospheric pressure is equal to the weight per unit area of the entire air column above, even p0 will be zero in the absence of gravity.

Question 18.
Define gauge pressure.
When is gauge pressure (i) positive (ii) negative ?
Give two examples where gauge pressure is more relevant.
Answer:
Definition : Gauge pressure is the pressure exerted by a fluid relative to the local atmospheric pressure.

Gauge pressure, p_g = p – p₀

where p is the absolute pressure and p₀ is the local atmospheric pressure.

When the pressure inside a closed container or tank is greater than atmospheric pressure, the pressure reading on a pressure gauge is positive. The pressure inside a ‘vacuum chamber’-a rigid chamber from which some of the air is pumped out-is less than the atmospheric pressure, so a pressure gauge on the chamber designed to measure negative pressure reads a negative value.

At a depth within a liquid of density ρ, the gauge pressure is p_g = p – p₀ = hpg

Examples : Tyre pressure gauge, blood pressure gauge, pressure gauge on an oxygen or scuba tank.

Question 19.
Define absolute pressure.
Answer:
Definition : The absolute pressure, or total press-ure, is measured relative to absolute zero on the pressure scale-which is a perfect vacuum-and is the sum of gauge pressure and atmospheric press-ure. It is the same as the thermodynamic pressure.

Absolute pressure accounts for the atmospheric pressure, which in effect adds to the pressure in any fluid which is not enclosed in a rigid container i.e., the fluid is open to the atmosphere.
p = p₀ + P_g
where p₀ and p_g are respectively atmospheric pressure and the gauge pressure.

Absolute pressure can be never negative.

Question 20.
If your tyre gauge reads 2.31 atm (234.4 kPa), what is the absolute pressure ?
Answer:
The absolute pressure, p = p₀ + p_g = 1 atm + 2.31 atm = 3.31 atm (≅ 335 kPa).

Question 21.
State and explain the hydrostatic paradox. OR Explain hydrostatic paradox.
Answer:
Hydrostatic paradox : The normal force exerted by a liquid at rest on the bottom of the containing vessel is independent of the amount of liquid or the shape of the container, but depends only on the area of the base and its depth from the liquid surface.

Consider several vessels of the same base area as shown in figure (a). A liquid is poured into them to the same level, so that the pressure is the same at the bottom of each vessel. Then it must follow that the normal force on the base of each vessel is also the same. However, when placed on a scale balance they are found to have different weights. Herein lies the paradox.

Explanation : Since a liquid always exerts a normal force on a wall of the container, in turn, the wall exerts an equal and opposite reaction on the liquid. In the case of tube A, this reaction is everywhere horizontal; so that the normal force at the base of A is only due to the weight of the liquid column above.

The reaction of the slanted wall of vessel C has a – vertical component, as shown in figure (b), which supports the weight of the liquid above the slanted side. Hence, the normal force at the base of C is only due to the weight of the vertical liquid column above the base, shown by dashed lines. Since the vessels A and C are filled to the same height and have the same base area, the pressures at the bases of the two vessels are also same. However, the volume of the liquid being clearly different, they have different weights.

In the case of vessel B, the downward vertical component of the reaction of the wall provides an extra normal force at the base, as shown in figure (c).

Question 22.
Can pressure in a fluid be increased by pushing directly on the fluid ? Give an example.
Answer:
Yes, but it is much easier if the fluid is enclosed.

Examples : (1) The heart increases the blood pressure by pushing on the blood in an enclosed ventricle.
(2) Hydraulic brakes, lifts and cranes operate by pushing on oil in an enclosed system.

Question 23.
State Pascal’s law.
Answer:
Pascal’s law : A change in the pressure applied to an enclosed fluid at rest is transmitted un-diminished to every point of the fluid and to the walls of the container, provided the effect of gravity can be ignored.

[Note : The law does not say that ‘the pressure is the same at all points of a fluid’ – rightly so, since the pressure in a fluid near Earth varies with height. Rather, the law applies to the change in pressure. According to Pascal’s law, if the pressure on an enclosed static fluid is changed by a certain amount, the pressure at all points within the fluid changes by the same amount.

The above law is due to Blaise Pascal (1623 – 62), French mathematician and physicist.]

Question 24.
Describe an experimental proof of Pascal’s law.
Answer:
Consider a spherical vessel having four cylindrical tubes A, B, C and D each fitted with air-tight

frictionless pistons of areas of cross section A, A/2, 2A and 3A, respectively, as shown in above figure. The vessel is filled with an incompressible liquid such that there is no air between the liquid and the pistons.

If the piston A is pushed with a force F, the pressure on the piston and the liquid in the vessel is p_A = F/A. It is seen that the other three pistons are pushed outwards. To keep these pistons at their respective original positions, forces of F/2, IF and 3F, respectively are required to be applied on pistons B, C and D respectively to hold them. Then, the pressures on the respective pistons are
p_B = \(\frac{F / 2}{A / 2}\) = F/A, p_C = 2F/2A = F/A, and
p_D = 3F/3A = F/A
∴ p_A = p_B = p_C = p_D = F/A

This indicates that the pressure applied is trans-mitted equally to all parts of liquid. This proves Pascal law.

Question 25.
Explain the principle of multiplication of thrust.
Answer:
Principle of multiplication of thrust by transmission of fluid pressure : The normal force exerted by a fluid on any surface in contact with it is called the thrust. Consider two hydraulically connected cylinders, one of cross section a and the other A, as in figure. If a force F_a is exerted on the smaller piston, pressure p = \(\frac{F_{\mathrm{a}}}{a}\) is produced and transmitted undiminished throughout the liquid. Then, the thrust F_A on the larger piston is
F_A = pA = \(\frac{A}{a}\) F_a
If A = na, F_A = nF_a, i.e., the thrust on the larger piston is multiplied n times. This is known as the principle of multiplication of thrust by transmission of fluid pressure.

Question 26.
State any two applications of Pascal’s law.
Briefly explain their working.
Ans.
Applications of Pascal’s law :

1. Hydraulic car lift and hydraulic press
2. Hydraulic brakes.

All the above applications work on the principle of multiplication of thrust by transmission of fluid pressure.

(1) Working of a hydraulic lift : Two hydraulically connected cylinders, one of cross section a and the other A, are such that A is many times larger than a : A = na. If a force F_a is exerted on the smaller piston, a pressure p = \(\frac{F_{\mathrm{a}}}{a}\) is produced and transmitted undiminished throughout the liquid. Then, the thrust F_A on the larger piston
F_A = pA = \(\frac{A}{a}\) F_a = nF_a
is n times greater than that on the smaller piston. A platform attached to the larger piston can lift a car (as in a hydraulic car lift), or press bales of cotton or paper against a fixed rigid frame (as in Brahma’s.)

(2) Working of hydraulic brakes in a car: Brakes which are operated by means of hydraulic pressure are called hydraulic brakes. An automobile hydraulic brake system, shown schematically in below figure, has fluid-filled master and slave cylinders connected by pipes. When the brake pedal is pushed, it depresses the piston of the pedal or master cylinder through a lever. The change in pressure in the master cylinder is transmitted to the four wheel or slave cylinders. Since the brake fluid is incompressible, the pistons of the slave cylinders are pushed out, pressing braking pads onto the braking discs on the wheels. Note that we can add as many wheel cylinders as we wish.

The master cylinder has a much smaller area of cross section A_m compared to the combined area A_s

of the slave cylinders. Hence, with a small force F_m on the master cylinder, a force F_s = \(\frac{A_{\mathrm{s}}}{A_{\mathrm{m}}}\) F_m which is greater than F_m is applied on each slave cylinder. Consequently, the master piston has to travel sev-eral inches to move the slave pistons the fraction of an inch it takes to apply the brakes. But the arrangement allows great force to be exerted at the brake pads.

[Note : (1) Pascal’s law laid the foundation for hydraulics, the use of a liquid under pressure to transfer force or motion, or to increase an applied force. It is one of the most important branches in modern engineering. (2) A hydraulic system, as an example of a simple machine, can increase force but cannot do more work than is done on it. Work being force times the distance moved, the piston in a wheel cylinder moves through a smaller distance than that in the pedal cylinder. Power brakes in modern automobiles have a motorized pump that does most of the work in the system.]

Question 27.
Why are liquids used in hydraulic systems but not gases?
Answer:
Liquids are used in a hydraulic system because liquids are incompressible and transmit a change in pressure undiminished to all parts of the system. On the other hand, on increasing the pressure, a gas will be compressed into a smaller volume due to which there will be no transmission of force or motion.

Question 28.
State one advantage of hydraulic brakes in an automobile.
Answer:
Advantages of

1. By Pascal’s law, equal braking effort is applied to all the wheels.
2. It is easily possible to increase or decrease the applied force-during the design stage-by changing the size of piston and cylinder relative to other.

Question 29.
What is a barometer? Explain the use of a simple mercury barometer to measure atmospheric pressure.
Answer:
A barometer is an instrument to measure atmospheric pressure. The mercury barometer was in-vented by Evangelista Torricelli (1609-47). Italian physicist and mathematician.

A strong glass tube, about one metre long and closed at one end, is filled with mercury. With a finger over the open end, the tube is inverted and the open end is immersed into a bowl of mercury. When the finger is removed, the mercury level in the tube drops. The mercury column in the tube stands at a height h for which the pressure at point A inside the tube due to the weight of the mercury column is equal to the atmospheric pressure p0 outside (at point B).

The space at the closed end of the tube, after the mercury level drops, is nearly a vacuum, known as the Torricellian vacuum, so the pressure there can be taken as zero. It, therefore, follows that p₀ = pgh Where p is the density of mercury and h is the height of the mercury column.

Question 30.
What is an open tube manometer? Briefly describe its function with a neat diagram.
Answer:
An open tube manometer is a device to measure the pressure of a gas in a vessel. It consists of a U-shaped tube containing a liquid (say, mercury) of density p, as shown in below figure.

One end of the tube is connected to the vessel while the other end is open to the atmosphere. The pressure p at point A is the (unknown) pressure of the gas in the vessel. The pressure on the mercury column in the open tube is the atmospheric pressure p₀.

A point B, at the same horizontal level as A, is at a depth h from the surface of mercury in the open tube. Therefore, the pressure at B is p₀ + ρgh.

The pressures at points A and B at the same liquid level being the same, equating the unknown pressure p (at A) to the pressure at B.
p = p₀ + ρgh
The pressure p is called the absolute pressure, and the difference in pressure p – p₀ is called the gauge pressure.

Question 31.
An open tube manometer is connected to (i) a vacuum-packed candy jar, with the atmospheric pressure in the open tube supporting a column of fluid of height h (ii) a gas tank, with the absolute pressure in the tank supporting a column of fluid of height h. Is the absolute pressure in the jar and the gas tank greater than or less than the atmospheric pressure ? By how much ?
Answer:
In the first case, p_abs is less than the atmospheric pressure, whereas in the second case, p_abs is greater than the atmospheric pressure. In both cases, p_abs differs from the atmospheric pressure by the gauge pressure hρg, where ρ is the density of the fluid in the manometer.

32. Solve the following

Question 1.
For diver’s safety, a 10 m platform diving pool should be 5 m deep. However, with an excellent dive, a diver usually reaches a maximum depth of 2.5 m.
(i) Calculate the pressure due to the weight of the water at the depth of 2.5 m.
(ii) Calculate the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm. [Density of water = 10³ kg/m³, 1 atm = 101.3 kPa]
Solution:
Data : h = 250 m, ρ = 1000 kg/m³, g = 9.8 m/s², 1 atm = 101.3 kPa
(i) ρ = hpg = (250)(1000)(9.8) = 2.45 mPa
= \(\frac{2.45 \times 10^{6}}{1.013 \times 10^{5}}\) = 24.18 atm
This gives the pressure at a depth of 250 m.

(ii) h = \(\frac{p}{\rho g}=\frac{1.013 \times 10^{5}}{10^{3} \times 9.8}\) = 10.34 m
This gives the required depth.

Question 2.
Suppose a dam is 250 m wide and the water is 40 m deep at the dam. What is
(i) the average pressure on the dam
(ii) the force exerted against the dam due to the water?
Solution :
Data : Width, L = 250 m, depth H = 40 m, ρ = 1000 kg/m³, g = 9.8 m/s²
Since pressure increases linearly with depth, the average pressure p_av due to the weight of the water is the pressure at the average depth h of 20 m. The force exerted on the dam by the water is the average pressure times the area of contact, F = p_av A = p_av LH.
(i) p _av = hρg = (20)(1000)(9.8) = 1.96 × 10⁵Pa
(ii) F = p_avA = p_avLH = (1.96 × 10⁵)(250)(40)
= 1.96 × 10⁵ N

Question 3.
A car lift at a service station has a piston of diameter 30 cm. The lift and piston weigh 800 kg wt. What pressure (in excess of the atmospheric pressure) must be exerted on the piston to raise a car weighing 1700 kg wt at a constant speed? [g = 9.8 m/s²]
Solution:
Data : Piston diameter, D = 30 cm = 0.3 m. mass of lift and piston, m = 800 kg, mass of car, M = 1700 kg
Cross-sectional area of the piston.
A = \(\frac{\pi D^{2}}{4}=\frac{3.142(0.3 \mathrm{~m})^{2}}{4}\) = 7.07 × 10^-2 m ²
Total weight of the car and lift,
W = (m + M)g
= (800 kg + 1700 kg) (9.8 m/s²)
= 2.45 × 10⁴ N
Therefore, the pressure on the piston
p = \(\frac{F}{A}=\frac{W}{A}=\frac{2.45 \times 10^{4} \mathrm{~N}}{7.07 \times 10^{-2} \mathrm{~m}^{2}}\)
= 3.465 × 10⁵ Pa
A pressure of 3.465 × 10⁵ Pa must be exerted on the piston.

Question 4.
The diameters of two pistons in a hydraulic press are 5 cm and 25 cm respectively. A force of 20 N is applied to the smaller piston. Find the force exerted on the larger piston.
Solution:
Data : D₁ = 5 cm, D₂ = 25 cm, F₁ = 20 N
By Pascal’s law,

Question 5.
In a hydraulic lift, the input piston has surface area 20 cm². The output piston has surface area 1000 cm². If a force of 50 N is applied to the input piston, it raises the output piston by 2 m. Calculate the weight of the support on the output piston and the work done by it.
Solution:
Data : A₁ = 20 cm² = 2 × 10^-3 m²,
A₂ = 1000 cm² = 10^-1 m², F₁ = 50 N, s₂ = 2m
(i) By Pascal’s law,

This gives the weight of the support on the output piston.

(ii) The work done by the force transmitted to the output piston is
F₂S₂ = (2500 N) (2 m)
= 5000 J

Question 6.
A driver pushes the brake pedal of a car exerting a force of 100 N that is increased by the simple lever to a force of 500 N on the pedal (master) cylinder. The hydraulic system transmits this force to the four wheel (slave) cylinders. If the pedal cylinder has a diameter of 0.5 cm and each wheel cylinder has a diameter of 2.5 cm, calculate the magnitude of the force F_s on each of the wheel cylinder.
Solution:
Data : F_m = 500 N, D_m = 1 cm, D_s = 2.5 cm
\(\frac{F_{\mathrm{s}}}{A_{\mathrm{s}}}=\frac{F_{\mathrm{m}}}{A_{\mathrm{m}}}\)
∴ The magnitude of the force on each of the wheel cylinders,
F_s = \(\frac{A_{\mathrm{s}}}{A_{\mathrm{m}}}\) F_m = (\(\frac{D_{\mathrm{s}}}{D_{\mathrm{m}}}\))² F_m = (\(\frac{2.5}{0.5}\))² (500)
= 25 × 500 = 12.5 kN

Question 7.
Mercury manometers are often used to measure arterial blood pressure. The typical blood pressure of a young adult raises the mercury to a height of 120 mm at systolic and 80 mm at diastolic. Express these values in pascal and bar. [Density of mercury = 13600 kg/m³, 1 mbar = 100 Pa]
Solution:
Data : p_max = p_syst = 120 mm of Hg, p_min = p_dias = 80 mm of Hg, ρ = 13600 kg/m³, g = 9.8 m/s², 1 mbar = 100 Pa
p = hρg
∴ p_syst = (0.120)(1.36 × 10⁴)(9.8)
= 1.6 × 10⁴ Pa = 16 kPa
= 1600 mbar = 1.5 bar

and P_dias = (0.08)(1.36 × 10⁴)(9.8)
= 1.066 × 10⁴ Pa = 10.66 kPa
= 1066 mbar = 1.066 bar

Question 33.
Describe the phenomenon of surface tension, giving four examples.
Answer:
Surface tension is a unique property of liquids that arises because the net intermolecular force of attraction on the liquid molecules at or near a liquid surface differs from that on molecules deep in the interior of the liquid. This results in the tendency of the free surface of a liquid to minimize its surface area and behave somewhat like a stressed elastic membrane.

Surface tension is important in understanding the peculiar behaviour of the free surface of a liquid in many cases as illustrated below :

1. Small quantities of liquids assume the form of spherical droplets, as in mist, or a mercury droplet on a flat surface. This is because the stressed surface ‘skin’ tends to contract and mould the liquid into a shape that has minimum surface area for its volume, i.e., into a sphere.
2. Surface tension is responsible for the spherical shape of freely-falling raindrops and the behaviour of bubbles and soap films.
3. The bristles of a paint brush cling together when it is drawn out of water or paint.
4. A steel needle or a razor blade can, with care, be supported on a still surface of water which is much less dense than the metal from which these objects are made of.
5. Many insects like ants, mosquitoes, water striders, etc., can walk on the surface of water.

Question 34.
Define (1) cohesive force (2) adhesive force.
Give one example in each case.
Answer:
(1) Cohesive force : The intermolecular force of attraction between two molecules of the same material is called the cohesive force.
Example : The force of attraction between two water molecules.

(2) Adhesive force : The intermolecular force of attraction between two molecules of different materials is called the adhesive force.
Example : The force of attraction between a water molecule and a molecule of the solid surface which is in contact with water.

Question 35.
Define (1) range of molecular attraction or molecular range (2) sphere of influence.
Answer:
1) Range of molecular attraction or molecular range : Range of molecular aftraction or molecular range is defined as the maximum distance between two molecules up to which the intermolecular force of attraction is appreciable.

[Note : The intermolecular force is a short range force, LeV, it is effective over a very short range-about 10^-9 m. Beyond this distance, the force is negligible. The inter molecular force does not obey inverse square law.]

2) Sphere of influence : The sphere of influence of a molecule is defined as an imaginary sphere with the molecule as the centre and radius equal to the range of molecular attraction.

[Note : All molecules lying within the sphere of influence of a molecule are attracted by (as well as attract) the molecule at the centre. For molecules which lie outside this sphere, the intermolecular force due to the molecule at the centre is negligible.]

Question 36.
What is meant by a surface film?
Answer:
The layer of the liquid surface of thickness equal to the range of molecular attraction is called a surface film.

Question 37.
What is meant by free surface of a liquid ?
Answer:
The surface of a liquid open to the atmosphere is called the free surface of the liquid.

Question 38.
Explain the phenomenon of surface tension on the basis of molecular theory.
Answer:
The phenomenon of surface tension arises due to the cohesive forces between the molecules of a liquid. The net cohesive force on the liquid molecules within the surface film differs from that on molecules deep in the interior of the liquid.

Consider three molecules of a liquid : A molecule A well inside the liquid, and molecules B and C lying within the surface film, shown in figure. The figure also shows their spheres of influence of radius R.

(1) The sphere of influence of molecule A is entirely inside the liquid and the molecule is surrounded by its nearest neighbours on all sides. Hence, molecule A is equally attracted from all sides, so that the resultant cohesive force acting on it is zero. Hence, it is free to move anywhere within the liquid.

(2) For molecule B, a part of its sphere of influence is outside the liquid surface. This part contains air molecules whose number is negligible compared to the number of molecules in an equal volume of the liquid. Therefore, molecule B experiences a net cohesive force downward.

(3) For molecule C, the upper half of its sphere of influence is outside the liquid surface. Therefore, the resultant cohesive force on molecule C in the
downward direction is maximum.

(4) Thus, all molecules lying within a surface film of thickness equal to R experience a net cohesive force directed into the liquid.

(5) The surface area is proportional to the number of molecules on the surface. To increase the surface area, molecules must be brought to the surface from within the liquid. For this, work must be done against the cohesive forces. This work is stored in the liquid surface in the form of potential energy. With a tendency to have minimum potential energy, the liquid tries to reduce the number of molecules on the surface so as to have minimum surface area. This is why the surface of a liquid behaves like a stressed elastic membrane.

Question 39.
Define surface tension.
State its formula and CGS and SI units.
Answer:
The surface tension of a liquid is defined as the tangential force per unit length, acting at right angles on either side of an imaginary line on the free surface of the liquid.

If F is the force on one side of a line of length Z, drawn on the free surface of a liquid, the surface tension (T) of the liquid is

The CGS unit of surface tension : The dyne per centimetre (dyn/cm) or, equivalently, the erg per square centimetre (erg/cm²).

The SI unit of surface tension : The newton per metre (N/m) or, equivalently, the joule per square metre (J/m²).

Question 40.
Obtain the dimensions of surface tension.
Answer:
Surface tension is a force per unit length.

Question 41.
Define and explain surface energy of a liquid.
OR
Define surface energy.
OR
State its dimensions and SI unit.
OR
Why do molecules of a liquid in the surface film possess extra energy?
Answer:
Surface energy : The surface energy is defined as the extra (or increased) potential energy possessed by the molecules in a liquid surface with an isothermal increase in the surface area of the liquid.

A liquid exerts a resultant cohesive force on every molecule of its surface, trying to pull it into the liquid. To increase the surface area, it is necessary to bring more molecules from inside the liquid to the liquid surface. For this, external work must be done against the net cohesive forces on the molecules. This work is stored in the liquid surface in the form of potential energy.

This extra potential energy that the molecules in the liquid surface have is called the surface energy. Thus, the molecules of a liquid in the surface film possess extra energy.
Dimensions : [surface energy] = [ML²T^-2]
SI unit: the joule (J).

Question 42.
Why is the surface tension of paints and lubricating oils kept low?
Answer:
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oils must be low.

Question 43.
Derive the relation between the surface tension and surface energy of a liquid.
OR
Derive the relation between surface tension and surface energy per unit area.
OR
Show that the surface tension of a liquid is numerically equal to the surface energy per unit area.
Answer:
Suppose a soap film is isothermally stretched over the area enclosed by a U-shaped frame ABCD and a w cross-piece PQ that can slide smoothly along the frame, as shown in the figure. Let T be the surface tension of the soap solution and l, the length of wire PQ in contact with the soap film.

The film has two surfaces, both of which are in contact with the wire. The film tends to contract by exerting a force on wire PQ. As each surface exerts a force Tl, the net force on the wire is 2Tl.

Suppose that wire PQ is pulled outward very slowly through a distance dx to the position P’Q’ by an external force of magnitude 2T l. The work done by the external force against the force due to the film is
W = applied force × displacement
∴ W = Fdx = ITldx (∵ F = 2Tl)
This work is stored in the unit surface area in the form of potential energy. This potential energy is called the surface energy.

Due to the displacement dx, the surface area of the film increases. As the film has two surfaces, the increase in its surface area is
A = 2ldx
Thus, the work done per unit surface area is
\(\frac{W}{A}=\frac{2 T l d x}{2 l d x}\) = T
Thus, the surface energy per unit area of a liquid is equal to its surface tension.

Question 44.
Two soap bubbles of the same soap solution have diameters in the ratio 1 : 2. What is the ratio of work done to blow these bubbles ?
Answer:
Work done oc surface area.
∴ W₁/W₂ = (r₁/r₂)² = (\(\frac{1}{2}\))² = \(\frac{1}{4}\)
∴ W₁ : W₁ = 1 : 4.

Question 45.
If the surface tension of a liquid is 70 dyn/cm, what is the total energy of the free surface of the liquid drop of radius 0.1 cm ?
Answer:
E = 4πr²T = 4 × \(\frac{22}{7}\) × (0.1)² × 70
= 88 × 10^-2 × 10 = 8.8 ergs

Question 46.
The total energy of the free surface of a liquid drop of radius 1 mm is 10 ergs. What is the total energy of a liquid drop (of the same liquid) of radius 2 mm ?
Answer:
E = 4πr²T ∴ \(\frac{E_{2}}{E_{1}}=\left(\frac{r_{2}}{r_{1}}\right)^{2}=\left(\frac{2}{1}\right)^{2}\) = 4
∴ E₂ = 4E₁ = 4 × 10 = 40 ergs is the required

47. Solve the following

Question 1.
Calculate the work done in blowing a soap bubble of radius 4 cm. The surface tension of the soap solution is 25 × 10^-3 N/m.
Solution:
Data : r = 4 cm = 4 × 10^-2 m, T = 25 × 10^-3 N/m
Initial surface area of soap bubble = 0
Final surface area of soap bubble = 2 × 4πr²
Increase in surface area = 2 × 4πr² The work done
= surface tension x increase in surface area
= T × 2 × 4πr²
= 25 × 10^-3 × 2 × 4 × 3.142 × (4 × 10^-2)2
= 1.005 × 10^-3 J

Question 2.
Two soap bubbles have radii in the ratio 4 : 3. What is the ratio of work done to blow these bubbles?
Solution:
Data : \(\frac{r_{1}}{r_{2}}=\frac{4}{3}\)
Work done, W = 2TdA
∴ W₁ = 2T(4πr₁²), W₂ = 2T(4πr₂²)
∴\(\frac{W_{1}}{W_{2}}=\frac{2 T\left(4 \pi r_{1}^{2}\right)}{2 T\left(4 \pi r_{2}^{2}\right)}=\left(\frac{r_{1}}{r_{2}}\right)^{2}\)
= (\(\frac{4}{3}\))² = \(\frac{16}{9}\)

Question 3.
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of the soap solution is 30 dyn/cm.
Solution:
Data : r₁ = 1 cm, r₂ = 2 cm, T = 30 dyn/cm
Initial surface area = 2 × 4πr₁²
Final surface area = 2 × 4πr₂²
∴ Increase in surface area
= 2 × 4πr₂² – 2 × 4πr₁² = 8π(r₂² – r₁²)
∴ The work done
= surface tension × increase in surface area
= T × 8π(r₂² – r₁²)
= 30 × 8 × 3.142 × [(2)² – (1)²]
= 2262 ergs

Question 4.
A mercury drop of radius 0.5 cm falls from a height on a glass plate and breaks into one million droplets, all of the same size. Find the height from which the drop fell. [Density of mercury = 13600 kg/m3, surface tension of mercury = 0.465 N/m]
Solution:
Data : R = 0.5 cm = 0.5 × 10^-2 m, n = 10⁶, ρ = 13600 kg m³, T = 0.465 N/m, g = 9.8 m/s²
\(\frac{4}{3}\) πR³ = n × \(\frac{4}{3}\) πr³
as the volume of the mercury remains the same.
∴ r = \(\frac{R}{\sqrt[3]{n}}=\frac{0.5 \times 10^{-2}}{\sqrt[3]{10^{6}}}\) = 0.5 × 10^-4 m
This gives the radius of a droplet.
By energy conservation, if h is the height from which the drop of mass m falls,

This gives the required height.

Question 5.
Eight droplets of mercury, each of radius 1 mm, coalesce to form a single drop. Find the change in the surface energy. [Surface tension of mercury = 0.472 J/m²]
Solution:
Data : r = 1 mm = 1 × 10^-3 m, T = 0.472 J/m²
Let R be the radius of the single drop formed due to the coalescence of 8 droplets of mercury.
Volume of 8 droplets = volume of the single drop as the volume of the liquid remains constant.
∴ 8 × \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) πR³
∴ 8r³ = R³
∴ 2r = R
Surface area of 8 droplets = 8 × 4πr²
Surface area of single drop = 4πR²
∴ Decrease in surface area = 8 × 4πr² – 4πR²
= 4π(8r² – R²)
= 4π[8r² – (2r)²]
= 4π × 4r²
∴ The energy released
= surface tension × decrease in surface area
= T × 4π × 4r²
= 0.472 × 4 × 3.142 × 4 × (1 × 10^-3)²
= 2.373 × 10^-5 J

Question 6.
The total energy of the free surface of a liquid drop is 2 × 10^-4 π times the surface tension of the liquid. What is the diameter of the drop ? (Assume all terms in SI unit.)
Solution:
Data : 4πr²T = 2 × 10^-4 πT (numerically)
∴ 2r² = 10^-4
∴ r = \(\frac{10^{-2}}{\sqrt{2}}=\frac{10^{-2}}{1 \cdot 414}\)
= 0.7072 × 10^-2 m
∴ d = 2r = 2 × 0.7072 × 10^-2
= 1.4144 × 10^-2 m
This gives the diameter of the liquid drop.

Question 48.
Define angle of contact.
Answer:
The angle of contact for a liquid-solid pair (a liquid in contact with a solid) is defined as the angle between the surface of the solid and the tangent drawn to the free surface of the liquid at the extreme edge of the liquid, as measured through the liquid.

Question 49.
Draw neat diagrams to show the angle of contact in the case of a liquid which
(i) completely wets
(ii) partially wets
(iii) does not wet the solid. State the characteristics of the angle of contact in each case, giving one example of each.
Answer:
Characteristics :
(1) For a liquid, which completely wets the solid, the angle of contact is zero.
For example, pure water completely wets clean glass. Therefore, the angle of contact at the water glass interface is zero [from figure (a)].

(2) For a liquid which partially wets the solid, the angle of contact is an acute angle. For example, kerosine partially wets glass, so that the angle of contact is an acute angle at the kerosine glass interface [from figure (b)].
(3) For a liquid which does not wet the solid, the angle of contact is an obtuse angle. For example, mercury does not wet glass at all, so that the angle of contact is an obtuse angle at the mercury-glass interface [from figure (c)].
(4) The angle of contact for a given liquid solid pair is constant at a given temperature, provided the liquid is pure and the surface of the solid is clean.

Question 50.
State any two characteristics of angle of contact.
Answer:
Characteristics of angle of contact:

1. It depends upon the nature of the liquid and solid in contact, and is constant for a given liquid-solid pair, other factors remaining unchanged.
2. It depends upon the medium (gas) above the free surface of the liquid.
3. It is independent of the inclination of the solid to the liquid surface.
4. It changes with surface tension and, hence, with the temperature and purity of the liquid.

Question 51.
Explain why the free surface of some liquids in contact with a solid is not horizontal.
OR
Explain the formation of concave and covex surface of a liquid on the basis of molecular theory.
Answer:
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely the solid-liquid adhesive force \(\vec{F}_{\mathrm{A}}=\overrightarrow{P A}\) and the liquid- liquid cohesive force \(\vec{F}_{\mathrm{C}}=\overrightarrow{P C} \vec{F}_{A}\) is normal to the solid surface and \(\vec{F}_{\mathrm{C}}\) is at 45° with the horizontal, from figure (a). The free surface of a liquid at rest is always perpendicular to the resultant \(\vec{F}_{\mathrm{R}}=\overrightarrow{P R}\) of these forces.

If F_C = \(\sqrt{2} F_{\mathrm{A}}, \vec{F}_{\mathrm{R}}\) is along the solid surface, the contact angle is 90° and the liquid surface is horizontal at the edge where it meets the solid, as in figure (a). In general this is not so, and the liquid surface is not horizontal at the edge.

For a liquid which completely wets the solid (e.g., pure water in contact with clean glass), F_C << F_A. For a liquid which partially wets the solid (e.g., kerosine . or impure water in contact with glass), F_C < \(\sqrt{2} F_{\mathrm{A}}\). If F_C << F_A or if F_C < \(\sqrt{2} F_{\mathrm{A}}\), the contact angle is correspondingly zero or acute and the liquid surface curves up and acquires a concave shape until the tangent PT is tangent to \(\vec{F}_{\mathrm{R}}\) fron figure (b).

If F_C > \(\sqrt{2} F_{\mathrm{A}}\), the contact angle is obtuse and the liquid surface curves down and acquires a convex shape until the tangent PT is tangent to \(\vec{F}_{\mathrm{R}}\), from figure (c).

Question 52.
State the conditions for concavity and convexity of a liquid surface where it is in contact with a solid.
Answer:
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely
(i) the solid-liquid adhesive force \(\vec{F}_{\mathrm{A}}\) normal and into the solid surface and
(ii) the liquid-liquid cohesive force \(\vec{F}_{\mathrm{C}}\) at nearly 45° with the horizontal.

If F_C << F_A or if F_C < \(\sqrt {2}\)F_A , the contact angle is correspondingly zero or acute and the liquid sur-face is concave with the solid.

If F_C > \(\sqrt {2}\)F_A, the contact angle is obtuse and the liquid surface curves down, i.e., convex, with the Solid.

Question 53.
Draw neat labelled diagrams to show angle of contact between (a) pure water and clean glass . (b) mercury and clean glass.
Answer:

Question 54.
Explain the shape of a liquid drop on a solid surface in terms of interfacial tensions.
OR
Account for the angle of contact in terms of interfacial tensions.
OR
Draw diagram showing force due to surface tension at the liquid-solid, air-solid, air-liquid interface, in case of (i) a drop of mercury on a plane solid surface and (ii) a drop of water on a plane solid surface. Discuss the variation of angle of contact.
Answer:
A liquid surface, in general, is curved where it meets a solid. The angle between the solid surface and the tangent to the liquid surface at the extreme edge of the liquid, as measured through the liquid, is called the angle of contact.

Above figure shows the interfacial tensions that act in equilibrium at the common point of the liquid, solid and gas (air + vapour).
T₁ = the liquid-solid interfacial tension
T₂ = the solid-gas interfacial tension
T₃ = the liquid-gas interfacial tension
θ = the angle of contact for the liquid-solid pair is the angle between T₁ and T₃
The equilibrium force equation (along the solid surface) is
T₃ Cos θ + T₁ – T₂ = 0
∴ cos θ = \(\frac{T_{2}-T_{1}}{T_{3}}\) …………… (1)

Case (1) : If T₂ > T₁, cos θ is positive and contact angle θ < 900, so that the liquid wets the surface.
Case (2) : If T₂ < T₁, cos θ is negative and θ is obtuse, so that the liquid is non-wetting.
Case (3): If T₂ – T₁ T₃, cos θ = 1 and θ ≅ 0°.
Case (4) : If T₂ – T₁ ≅ T₃, cos θ will be greater than 1 which is impossible, so that there will be no equilibrium and the liquid will spread over the solid surface.

Question 55.
State the expression for the angle of contact in terms of interfacial tensions?
Answer:
cos θ = \(\frac{T_{2}-T_{1}}{T_{3}}\), where θ is the angle of contact for a liquid-solid pair, T₁ is the liquid-solid interfacial tension, T₂ is the solid-gas (air + vapour) inter-facial tension and T₃ is the liquid-gas interfacial tension.

Question 56.
In terms of interfacial tension, when is the angle of contact acute ?
Answer:
The angle of contact is acute when the solid-gas (air + vapour) interfacial tension is greater than the liquid-solid interfacial tension.

Question 57.
In terms of interfacial tensions, when is the angle of contact obtuse ?
Answer:
The angle of contact is obtuse when the solid-gas (air + vapour) interfacial tension is less than the liquid-solid interfacial tension.

Question 58.
State the factors affecting a liquid-solid angle of contact.
Answer:
Factors affecting a liquid-solid angle of contact:

1. the nature of the liquid and the solid in contact,
2. impurities in the liquid,
3. temperature of the liquid.

Question 59.
Explain the effect of impurity on the angle of contact (or surface tension of a liquid).
Answer:
Effect of impurity :
(i) The angle of contact or the surface tension of a liquid increases with dissolved impurities like common salt. For dissolved impurities, the angle of contact (or surface tension) increases linearly with the concentration of the dissolved materials.

(ii) It decreases with sparingly soluble substances like phenol or alcohol. A detergent is a surfactant whose molecules have hydrophobic and hydrophilic ends; the hydrophobic ends decrease the surface tension of water. With reduced surface tension, the water can penetrate deep into the fibres of a cloth and remove stubborn stains.

(iii) It decreases with insoluble surface impurities like oil, grease or dust. For example, mercury surface contaminated with dust does not form perfect spherical droplets till the dust is removed.

Question 60.
Explain the effect of temperature on the angle of contact (or surface tension of a liquid).
Answer:
Effect of temperature : The surface tension of a liquid decreases with increasing temperature of the liquid. For small temperature differences, the decrease in surface tension is nearly directly proportional to the temperature rise.

If T and T₀ are the surface tensions of a liquid at temperatures θ and 0 °C, respectively, then T = T₀(1 – αθ) where α is a constant for a given liquid. The surface tension of a liquid becomes zero at its critical temperature. The surface tension increases with increasing temperature only in case of molten copper and molten cadmium.

Question 61.
Why cold wash is recommended for new cotton fabrics while hot wash for removing stains?
Answer:
Cold wash is recommended for new/coloured cotton fabrics. Cold water, due to its higher surface tension, does not penetrate deep into the fibres and thus does not fade the colours. Hot water, because of its lower surface tension, can penetrate deep into fabric fibres and remove tough stains.

Question 62.
Explain in brief the pressure difference across a curved liquid surface.
Answer:
Every molecule lying within the surface film of a static liquid is pulled tangentially by forces due to surface tension. The direction of their resultant, \(\vec{F}_{\mathrm{T}}\), on a molecule depends upon the shape of that liquid surface and decides the cohesion pressure at a point just below the liquid surface.

Consider two molecules, A and B, respectively just above and below the free surface of a liquid. So, the level difference between them is negligibly small and the atmospheric pressure on both is the same, p₀, Let \(\vec{F}_{\mathrm{atm}}\) be the downward force on A and B due to the atmospheric pressure.

If the free surface of a liquid is horizontal, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B is zero, from figure (a). Then, the cohesion pressure is negligible and the net force on A and B is \(\vec{F}_{\mathrm{atm}}\). The pressure difference on the two sides of the liquid surface is zero.

If the free surface of a liquid is concave, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B is outwards (away from the liquid), from figure (b), opposite to \(\vec{F}_{\mathrm{atm}}\). Then, the net force on B is less than \(\vec{F}_{\mathrm{atm}}\) and the cohesion pressure is decreased. The pressure above the concave liquid surface is greater than that just below the liquid surface.

If the free surface of a liquid is convex, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B acts inwards (into the liquid), from figure (c), in the direction of \(\vec{F}_{\mathrm{atm}}\). Then, the net force on B is greater than \(\vec{F}_{\mathrm{atm}}\) and the cohesion pressure is increased. The pressure below the convex liquid surface is greater than that just above the liquid surface.

Question 63.
Derive an expression for the excess pressure inside a soap bubble.
OR
Derive Laplace’s law for spherical membrane of a bubble due to surface tension.
Answer:
Consider a small, spherical, thin-filmed soap bubble with a radius R. Let the pressure outside the drop be Po and that inside be p. A soap bubble in air is like a spherical shell and has two gas-liquid interfaces. Hence, the surface area of the bubble is
A = 8πR² ………. (1)
Hence, with a hypothetical increase in radius by an infinitesimal amount dR, the differential increase in surface area and surface energy would be
dA = 16πR ∙ dR and
dW = T ∙ dA = 16πTRdR ………….. (2)
We assume that dR is so small that the pressure inside remains the same, equal to p. All parts of the surface of the bubble experiences an outward force per unit area equal to p – p_o. Therefore, the work done by this outward pressure-developed force against the surface tension force during the increase in radius dR is
dW = (excess pressure × surface area) ∙ dR
= (p – p_o) × 4πR² ∙ dR ………. (3)
From Eqs. (2) and (3),
(p – p_o) × 4πR² ∙ dR = 16πTRdR
∴ p – p_o = \(\frac{4 T}{R}\) …………… (4)
which is the required expression.

[Note : The excess pressure inside a drop or bubble is inversely proportional to its radius : the smaller the bubble radius, the greater the pressure difference across its wall.]

Question 64.
What is the excess of pressure inside a soap bubble of radius 3 cm if the surface tension of the soap solution is 30 dyn/cm ?
Answer:
Excess of pressure, p – p_o = \(\frac{4 T}{R}=\frac{4 \times 30}{3}\)
= 40 dyn/cm²

Question 65.
Two soap bubbles of the same soap solution have radii 3 cm and 1.5 cm. If the excess pressure inside the bigger bubble is 40 dyn/cm², what is the excess pressure inside the smaller bubble ?
Answer:
Excess pressure ∝ T/R. In this case, the surface tension is the same in the two cases. Hence, the excess pressure inside the smaller bubble will be 80 dyn/cm².

Question 66.
Explain : In the absence of gravity or other external forces, a liquid drop assumes a spherical shape.
Answer:
A spherical shape has the minimum surface area-to-volume ratio of all geometric forms. If any . external force distorts the sphere, molecules must be brought from the interior to the surface in order to provide for the increased surface area. This process requires work to be done in order to raise the potential energy of a molecule. The change in free surface energy is equal to the net work done to alter the surface area of the liquid.

However, spontaneous processes are associated with a decrease in free energy. Hence, in the absence of external forces, a liquid drop will spontaneously assume a spherical shape in order to minimize its exposed surface area and thereby its free surface energy.

[ Note : The spontaneous coalescence of two similar liquid droplets into one large drop when brought into contact is a dramatic demonstration of the decrease in free surface energy brought about by the decrease in total surface area by the formation of a single larger drop.]

Question 67.
A small air bubble of radius r in water is at a depth h below the water surface. If p₀ is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
Answer:
The absolute pressure within the liquid at a depth h is p = p₀ + ρgh.
Since the excess pressure inside a bubble is \(\frac{2 T}{R}\), the pressure inside the bubble is
P_in = p + \(\frac{2 T}{R}\) = p₀ + ρgh + \(\frac{2 T}{R}\)

68. Solve the following

Question 1.
What is the excess pressure (in atm) inside a soap bubble with a radius of 1.5 cm and surface tension of 3 × 10^-2 N/m? [1 atm = 101.3 kPa]
Solution:
Data : R = 1.5 × 10^-2 m, T = 3 × 10^-2 N/m,
1 atm = 1.013 × 10⁵ Pa
The excess pressure inside a soap bubble is
p – p₀ = \(\frac{4 T}{R}\)
= \(\frac{4 \times 3 \times 10^{-2}}{1.5 \times 10^{-2}}\) = 8Pa
= \(\frac{8}{1.013 \times 10^{5}}\) atm = 7.897 × 10^-5 atm

Question 2.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the rain drop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 × 10⁵ N/m²)
Solution:
Data : D = 4 × 10^-3 m, T = 0.072N/m,
p₀ = 1013 × 10⁵ N/m²
R = \(\frac{D}{2}\) = 2 × 10^-3 m
The excess pressure inside the raindrop is
p – p₀ = \(\frac{2 I}{R}=\frac{2(0.072)}{2 \times 10^{-3}}\) = 72 N/m²
∴ p = 101300 + 72 = 101372 N/m²

Question 3.
What should be the diameter of a soap bubble such that the excess pressure inside it is 51.2 Pa? [Surface tension of soap solution = 3.2 × 10^-2 N/m]
Solution:
Data : p – p₀ = 51.2 Pa, T = 3.2 × 10^-2 N/m
Forasoapbubb1e, p – p₀ = \(\frac{4T}{R}\)
∴ The radius of the soap bubble should be
R = \(\frac{4 T}{p-p_{0}}=\frac{4 \times 3.2 \times 10^{-2}}{51.2}\) = 2.5 × 10^-3 m = 2.5 mm
∴ the diameter of the soap bubble should be 2 × 2.5 = 5 mm.

Question 4.
The lower end of a capillary tube of diameter 1 mm is dipped 10 cm below the water surface in a beaker. What pressure is required to blow a hemispherical air bubble at the lower end of the tube? Present your answer rounded off to 4 significant figures. [Surface tension = 0.072 N/m, density = 10³ kg/m³, atmospheric pressure = 101.3 kPa, g = 9.8 m/s²]
Solution:
Data : r = 0.5 mm = 5 × 10^-4 m, d = 10 cm = 0.1 m,
T = 0.072 N/m, p = 10³ kg/m³, g = 9.8 m/s²,
P = 1 atm = 1.013 × 10⁵ Pa
The pressure outside the bubble at the depth d is
p₀ = P + dρg
= 1.013 × 10⁵ +0.1 × 10³ × 9.8
= (1.013 + 0.0098) × 10⁵ = 1.0228 × 10⁵ Pa
Since a bubble within water has only one, gas-liquid interface, the excess pressure inside the bubble is
p – p₀ = \(\frac{2 T}{r}=\frac{2 \times 0.072}{5 \times 10^{-4}}\) = 0.0288 × 10⁴ Pa
= 0.00288 × 10⁵ Pa
∴ P = (1.0228 + 0.00288) × 10⁵ = 1.02568 × 10⁵ Pa
The pressure inside the air bubble is 1.026 × 10⁵ Pa (or 102.6 kPa), rounded off to four significant figures.

Question 5.
There is an air bubble of radius 1.0 mm in a liquid of surface tension 0.072 N/m and density 10³ kg/m³. The bubble is at a depth of 10 cm below the free surface of the liquid. By what amount is the pressure inside the bubble greater than the’ atmospheric pressure?
Solution:
Data : R = 10^-3 m, T = 0.072 N/m, ρ = 10³ kg/m³, h = 0.1 m
Let the atmospheric pressure be p0. Then, the absolute pressure within the liquid at a depth h is
p = p₀ + ρgh
Hence, the pressure inside the bubble is
p_in = p₀ + \(\frac{2 T}{R}\) = p₀ + ρgh + \(\frac{2 T}{R}\)
The excess pressure inside the bubble over the atmospheric pressure is
p_in – p₀ = ρgh + \(\frac{2 T}{R}\)
= (10³) (9.8) (0.1) + \(\frac{2(0.072)}{10^{-3}}\)
= 980 + 144 = 1124 Pa

Question 6.
Two soap bubbles A and B, of radii 2 cm and 4 cm, respectively, are in a closed chamber where air pressure is maintained at 8 N/m ². If n_A and n_B are the number of moles of air in bubbles A and B, respectively, then find the ratio n_B : n_A. [Surface tension of soap solution = 0.04 N/m. Ignore the effect of gravity.]
Solution:
Data : R_A = 0.02 m, R_B = 0.04 m, p₀ = 8 N/m², T = 0.04 N/m

This is the required ratio.

Question 69.
What is capillary? What is capillarity or capillary action?
Answer:
(1) A tube of narrow bore (i.e. very small diameter) is called a capillary tube. The word capillary is derived from the Latin capillus meaning hair, capillaris in Latin means ‘like a hair’.

(2) If a capillary tube is just partially immersed in a wetting liquid the liquid rises in the capillary tube. This is called capillary rise.

If a capillary tube is just partially immersed in a non-wetting liquid, the liquid falls in the capillary tube. This is called capillary depression.

The rise of a wetting liquid and fall of a non-wetting liquid in a capillary tube is called capillarity.

Question 70.
State any four applications of capillarity.
Answer:
Applications of capillarity:

1. A blotting paper or a cotton cloth absorbs water; ink by capillary action.
2. Oil rises up the wick of an oil lamp and sap rises up xylem tissues of a tree by capillarity.
3. Ground water rises to the open surface through the capillaries formed in the soil. In summer, the farmers plough their fields to break these capillaries and prevent excessive evaporation.
4. Water rises up the crevices in rocks by capillary action. Expansion and contraction of this water due to daily and seasonal temperature variations cause the rocks to crumble.

[Note: The rise of sap is due to the combined action of capilarity and transpiration. The transpiration pull, is considered to be the major driving force for water transport throughout a plant.]

Question 71.
Two capillary tubes have radii in the ratio 1: 2. If they are dipped in the same liquid, what will be the ratio of capillary rise in the two tubes ?
Answer:
T = \(\frac{h r \rho g}{2 \cos \theta}\)
In this case, hr = constant
∴ h₁ : h₂ = r₂ : r₁ = 2 : 1.

Question 72.
The radii of two columns of a U-tube are r₁ and r₂. When a liquid of density ρ and angle of contact θ = 0° is filled in it, the level difference of the liquid in the two columns is h. Find the surface tension of the liquid.
Answer:
Capillary rise, h = \(\frac{2 T \cos \theta}{r \rho g}\), where θ is the angle of contact.
Assuming the two columns of the U-tube to be sufficiently thin,

73. Solve the following

Question 1.
A liquid of density 900 kg/m³ rises to a height of 9 mm in a capillary tube of 2.4 mm diameter. If the angle of contact is 25°, find the surface tension of the liquid.
Solution:
Data : ρ = 900 kg/m³, h = 9 mm = 9 × 10^-3 m,
θ = 25°, g = 9.8 m/s²
r = \(\frac{1}{2}\) × diameter = \(\frac{2.4}{2}\) = 1.2 mm = 1.2 × 10^-3 m
cos θ = cos 25° = 0.9063
The surface tension of the liquid,
T = \(\frac{r h \rho g}{2 \cos \theta}\)
= \(\frac{1.2 \times 10^{-3} \times 9 \times 10^{-3} \times 900 \times 9.8}{2 \times 0.9063}\)
= 5.257 × 10^-2 N/m

Question 2.
A capilary tube of uniform bore is dipped vertically in water which rises by 7 cm in the tube. Find the radius of the capillary tube if the surface tension of water is 70 dyn/cm. [g = 980 cm/s²]
Solution:
Data : h = 7 cm, T = 70 dyn/cm, g = 980 cm/s², ρ = 1 g/cm³ and θ = 0° (for water)
∴ cos θ = 1 .
Surface tension, T = \(\frac{r h \rho g}{2 \cos \theta}\)
∴ The radius of the capillary tube,
r = \(\frac{2 T \cos \theta}{h \rho g}\)
= \(\frac{2 \times 70 \times 1}{7 \times 1 \times 980}\) = 0.02041 cm

Question 3.
A liquid rises to a height of 9 cm in a glass capillary tube of radius 0.02 cm. What will be the height of the liquid column in a glass capillary tube of radius 0.03 cm ?
Solution:
Data : h₁ = 9 cm, r₁ = 0.02 cm, r₂ = 0.03 cm
For the first capillary, T = \(\frac{r_{1} h_{1} \rho g}{2 \cos \theta}\)
For the second capillary, T = \(\frac{r_{2} h_{2} \rho g}{2 \cos \theta}\)
∴ \(\frac{r_{1} h_{1} \rho g}{2 \cos \theta}=\frac{r_{2} h_{2} \rho g}{2 \cos \theta}\)
∴ r₁h₁ = r₂h₂
The height of the liquid column in the second capillary,
h₂ = \(\frac{r_{1} h_{1}}{r_{2}}=\frac{0.02 \times 9}{0.03}\) = 6 cm

Question 4.
Water rises to a height of 5 cm in a certain capillary tube. In the same capillary tube, mercury is depressed by 2.02 cm. Compare the surface tensions of water and mercury.
[Density of water = 1000 kg/m³, density of mercury = 13600 kg/m³, angle of contact for water = 0°, angle of contact for mercury = 148°]
Solution:
Let T_w, θ_w, h_w and ρ_w be the surface
tension, angle of contact, capillary rise and density of water respectively. Let T_m, θ_m, h_m and ρ_m be the corresponding quantities for mercury. The radius (r) of the capillary is the same in both cases.

Data : h_w = 5 cm = 5 × 10^-2 m, θ_w = 0°, ρ_w = 1000 kg/m³, h_m = -2.02 cm
= -2.02 × 10^-2 m,
ρ_m = 13600 kg/m³, θ_m= 148°
[Note : h_m is taken to be negative because for mercury there is capillary depression.]
cos θ_w = cos 0° = 1
cos θ_m = cos 148° = – cos 32° = -0.8480

Question 5.
When a glass capillary tube of radius 0.4 mm is dipped into mercury, the level of mercury inside the capillary stands 1.50 cm lower than that outside. Calculate the surface tension of mercury. [Angle of contact of mercury with glass = 148 °, density of mercury = 13600 kg/m³]
Solution:
Data : r = 0.4 mm = 4 × 10^-4 m, h = -1.50 cm = – 1.50 × 10^-2 m,
ρ = 13.6 × 10³ kg/m³, g = 9.8 m/s², θ = 148°
cos θ = cos 148° = – cos 32 ° = – 0.8480
The surface tension of mercury is
T = \(\frac{r h \rho g}{2 \cos \theta}\)
= \(\frac{\left(4 \times 10^{-4}\right)\left(-1.50 \times 10^{-2}\right)\left(13.6 \times 10^{3}\right)(9.8)}{2(-0.8480)}\)
= 0.4715 N/m

Question 6.
The tube of a mercury barometer is 1 cm in diameter. What correction due to capillarity is to be applied to the barometric reading if the surface tension of mercury is 435.5 dyn/cm and the angle of contact of mercury with glass is 140° ? [Density of mercury = 13600 kg/m³]
Solution:
Data : d = 1 cm, T = 435.5 dyn/cm, θ = 140°, ρ = 13660 kg/m³ = 13.66 g/cm³,
g = 9.8 m/s² = 980 cm/s²

∴ The correction due to capillarity = -0.1001 cm

Question 7.
Calculate the density of paraffin oil, if within a glass capillary of diameter 0.25 mm dipped in paraffin oil of surface tension 0.0245 N/m, the oil rises to a height of 4 cm. [Angle of contact of paraffin oil with glass = 28°, acceleration due to gravity = 9.8 m/s²]
Solution :
Data : d = 0.25 mm, T = 0.0245 N/m, h = 4 cm = 4 × 10^-2 m, θ = 28°, g = 9.8 m/s²

This gives the density of paraffan oil.

Question 8.
A capillary tube of radius r can support a liquid column of weight 6.284 × 10^-4 N. Calculate the radius of the capillary if the surface tension of the liquid is 4 × 10^-2 N/m.
Solution:
Data : mg = 6.284 × 10^-4 N, T = 4 × 10^-2 N/m
Net upward force = weight of liquid column
∴ 2πrT cos θ = mg
Assuming the angle of contact, θ = 0° (∵ data not given), the radius of the capillary is
r = \(\frac{m g}{2 \pi T}=\frac{6.284 \times 10^{-4}}{2(3.142)\left(4 \times 10^{-2}\right)}\) = 2.5 × 10^-3 m

Question 9.
Two vertical glass plates are held parallel 0.5 mm apart, dipped in water. If the surface tension of water is 70 dyn/cm , calculate the height to which water rises between the two plates.
Solution:
Data : x = 0.5 mm = 5 × 10^-4 m, T = 0.07 N/m, ρ(water) = 10³ kg/m³

Let the width of each glass plate be b and the height to which the water rises between the plates be h.

Then, the upward force on the water between the plates due to surface tension = 2Tb cos θ

where θ is the angle of contact of water with glass. The weight of the water between the plates = mg = (bxhρ) = g

where x is the separation between the plates and p is the density of water.
Equating, (bxhρ)g = 2Tb cosθ
∴ The height to which water rises between the two plates,
h = \(\frac{2 T \cos \theta}{x \rho g}=\frac{2\left(7 \times 10^{-2}\right)(1)}{\left(5 \times 10^{-4}\right)\left(10^{3}\right)(9.8)}=\frac{0.2}{7}\)
= 0.02857 m = 2.857 cm

Question 10.
A glass capillary of radius 0.4 mm is inclined at 60° with the vertical in water. Find the length of water column in the capillary tube. [Surface tension of water = 7 × 10^-2 N/m]
Solution:
Data : r = 4 × 10^-4 m, Φ = 60°, T = 7 × 10^-2 N/m
Let h be the capillary rise when the capillary tube is immersed vertically in water. Let l be the length of the water column in the capillary tube above that of the outside level.

Question 74.
What is hydrodynamics?
Answer:
Hydrodynamics is the branch of physics that deals with fluid dynamics, i.e., the study of fluids in motion. Since the most basic fluid motion is highly complex, we consider only ideal fluids-non-viscous and incompressible, i.e., fluids whose internal friction is negligible and density is constant throughout.

Question 75
What is meant by a steady flow ?
Answer:
When a liquid flows slowly over a surface or through a pipe such that its velocity or pressure at any point within the fluid is constant, it is said to be in steady flow.

Question 76.
Explain a streamline and streamline flow.
Answer:
Streamline : Consider point A, from figure, within a fluid. The velocity \(\vec{v}\) at A does not change with time. Hence, every particle passes point A with the same speed and in the same direction. The same is true about the other points such as B and C. A curve which is tangent or parallel to the velocity of the fluid particles at every point will be the path of every particle arriving at A. It is called a streamline. A fluid particle cannot cross a streamline but only flow along it.

Streamline flow : When a liquid flows slowly over a surface or through a pipe with a velocity less than a certain critical velocity, the motion of its molecules is orderly. All molecules passing a given point proceed with the same velocity. This kind of fluid motion is called streamline or steady flow.

Question 77.
Explain a flow tube.
Answer:
A bundle of adjacent streamlines form a tube of flow or flow tube through which the fluid is flowing. In a flow tube, where the streamlines are close together the velocity is high, and where they are widely separated, the fluid is moving slowly. No fluid can cross the boundary of a tube of flow.

Question 78.
Explain turbulent flow.
Answer:
Turbulent flow or turbulence is a non-steady fluid flow in which streamlines and flowtubes change continuously. It has two main causes. First, any obstruction or sharp edge, such as in a tap, creates

turbulence by imparting velocities perpendicular to the flow. Second, if the speed with which a fluid moves relative to a solid body is increased beyond a certain critical velocity the flow becomes unstable or one of extreme disorder. In both cases, the fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause them to cross and recross the main direction continuously. The orderly streamlines break up into eddies or vertices and the result is turbulence. In a turbulent flow, regions of fluid move in irregular, colliding paths, resulting in mixing and swirling.

Question 79.
Distinguish between streamline flow and turbulent flow.
Answer:

Streamline flow	Turbulent flow
1. The steady flow of a fluid, with velocity less than certain critical velocity is called streamline or laminar flow.	1. A non-steady irregular fluid flow in which stream­lines and flowtubes change continuously with a veloc­ity greater than certain critical velocity.
2. In a streamline flow, the velocity of a fluid at a given point is always constant.	2. In a turbulent flow, the vel­ocity of a fluid at any point does not remain constant.
3. Streamlines do not change and never intersect.	3. Streamlines and flowtubes change continuously.
4. over a surface, and is in the form of coaxial cylinders through a pipe.	4. Fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause eddies or vortices.

Question 80.
Explain the Reynolds number.
OR
What is Reynolds number?
Answer:
Osborne Reynolds found that if the free-stream velocity of a fluid increases when it moves relative to a solid body, a point is reached where the steady flow becomes turbulent. From experiments, he found that the transition from steady to turbulent flow depends on the value of the quantity \(\frac{v_{0} d}{\eta / \rho}\), where v₀ is the free-stream velocity, d is some characteristic dimension of the system, ρ the density of the fluid and η its coefficient of viscosity. For a sphere in a fluid stream, d is its diameter; for water in a pipe, d is the pipe diameter.

This dimensionless number, defined as
Re = \(\frac{v_{0} d \rho}{\eta}\) is called the Reynolds number.
In a system of particular geometry, transition from a steady to turbulent flow is given by a certain value of the Reynolds number called the critical Reynolds number. The free-stream velocity for this critical Reynolds number is called the critical velocity, v_critical = \(\frac{n R_{\mathrm{e}}}{\rho d}\). For a given system geometry, the free stream velocity beyond which a streamline flow becomes turbulent is called critical velocity.

Steady flow takes place for Re up to about 1000. For 1000 < Re < 2000, there is a transition region in which the flow is extremely sensitive to all sorts of small disturbances. For Re > 2000, the flow is completely turbulent.

[Notes : (1) See Q. 95 for “free-stream velocity”. (2) The dimensionless number is named after Osborne Reynolds (1842-1912), British physicist.]

Question 81.
Explain the term viscosity.
Answer:
Suppose a constant tangential force is applied to the surface of a liquid. Under this shearing force, the liquid begins to flow. The motion of a thin layer of the liquid at the surface, relative to a layer below, is opposed by fluid friction. Because of this internal fluid friction, horizontal layers of the liquid flow with varying velocities.

This also happens in a gas. When a solid surface is moved through a gas, a thin layer of the gas moves with the surface. But its motion relative to a layer away is opposed by fluid friction.

The resistance to relative motion between the adjacent layers of a fluid is known as viscosity.

It is a property of the fluid. The resistive force in fluid motion is called the viscous drag.

Question 82.
When a-liquid contained in a bucket is stirred and left alone, it comes to rest after some time. Why?
Answer:
This happens due to the internal friction (viscosity) and friction with the walls and bottom of the bucket.

Question 83.
What do you mean by viscous drag?
Answer:
When a fluid flows past a solid surface, or when a solid body moves through a fluid, there is always a force of fluid friction opposing the motion. This force of fluid friction is called the drag force or viscous drag.

Question 84.
What causes viscous drag in fluids?
Answer:
In liquids, the viscous drag is due to short range molecular cohesive forces while in gases it is due to collisions between fast moving molecules. For laminar flow in both liquids and gases, the viscous drag is proportional to the relative velocity between the layers, provided the relative velocity is small. For turbulent flow, the viscous drag increases rapidly and is proportional to some higher power of the relative velocity.

Question 85.
Define and explain velocity gradient in a steady flow.
Answer:
Definition : In a steady flow of a fluid past a solid surface, the rate at which the velocity changes with distance within a limiting distance from the surface is called the velocity gradient.

When a fluid flows past a surface with a low velocity, within a limiting distance from the surface, its velocity varies with the distance from the surface, from below figure. The layer in contact with the surface is at rest relative to the surface. Starting outwards from the surface, the next layer has an extremely small velocity; each successive layer has a slightly higher velocity than its inner neighbour, as shown. Finally, a layer is reached which has approximately the full, or free-stream, velocity v₀ of the fluid. The situation is reversed if a body is moving in a stationary fluid : the fluid velocity reduces as the distance of a layer from the body increases. Thus, the velocity in each layer increases with its distance from the surface.

Consider the layer of thickness dy at y from the solid surface. Let v and v + dv be the velocities of the fluid at the base and upper edge of this layer. The change in velocity across the layer is dv. Therefore, the rate at which the velocity changes dv between the layers is \(\frac{d v}{d y}\). This is called the velocity gradient.

Question 86.
State and explain Newton’s law of viscosity.
Answer:
Newton’s law of viscosity: In a steady flow of a fluid past a solid surface, a velocity profile is set up such that the viscous drag per unit area on a layer is directly proportional to the velocity gradient.

When a fluid flows past a solid surface in a streamline flow or when a solid body moves through a fluid, the force of fluid friction opposing the motion is called the viscous drag. The magnitude of the viscous drag of a fluid is given by Newton’s law of viscosity.

If \(\frac{d v}{d y} \) is the velocity gradient, the viscous drag per unit area on a layer,
\(\frac{F}{A} \propto \frac{d v}{d y}\)
∴ \(\frac{F}{A}=\eta \frac{d v}{d y}\)
where the constant of proportionality, y, is called the coefficient of viscosity of the fluid.

Question 87.
Define coefficient of viscosity.
Answer:
Coefficient of viscosity : The coefficient of viscosity of a fluid is defined as the viscous drag per unit area acting on a fluid layer per unit velocity gradient established in a steady flow.

Question 88.
Find the dimensions of the coefficient of viscosity. State its SI and CGS units.
Answer:
By Newton’s law of viscosity,
\(\frac{F}{A}=\eta \frac{d v}{d y}\)
where \(\frac{F}{A}\) is the viscous drag per unit area, \(\frac{d v}{d y}\) is the velocity gradient and y is the coefficient of viscosity of the fluid. Rewriting the above equation as
η = \(\frac{(F / A)}{(d v / d y)}\)
[η] = \(\frac{\left[F A^{-1}\right]}{[d v / d y]}\) = [ML^-1T^-2][T¹] = [ML^-1T^-1]
SI unit: the pascal ∙ second (abbreviated Pa ∙ s), 1 Pa ∙ s = 1 N ∙ m^-2 ∙ s

CGS unit: dyne ∙ cm^-2 ∙ s, called the poise [symbol P, named after Jean Louis Marie Poiseuille (1799-1869), French physician].

[Note : The most commonly used submultiples are the millipascal-second (mPa ∙ s) and the centipoise (cP). 1 mPa ∙ s = 1 cP.]

Question 89.
Define the SI and CGS units of coefficient of viscosity.
Answer:
The SI unit of coefficient of viscosity is the pascal- second.

Definition : If a tangential force per unit area of one newton per square metre is required to maintain a difference in velocity of one metre per second between two parallel layers of a fluid in streamline flow separated by one metre, the coefficient of viscosity of the fluid is one pascal-second.

The CGS unit of coefficient of viscosity is the poise.

Definition : If a tangential force per unit area of one dyne per square centimetre is required to maintain a difference in velocity of one centimetre per second between two parallel layers of a fluid in streamline flow separated by one centimetre, the coefficient of viscosity of the fluid is one poise.

Question 90.
Find the conversion factor between the SI and CGS units of coefficient of viscosity using dimensional analysis.
Answer:
The dimensions of the coefficient of viscosity η are
[η] = [ML^-1T^-1]
The SI and CGS units of coefficient of viscosity are the pascal-second and poise, respectively.
1 Pa ∙ s = 1 N ∙ m^-2 ∙ s = 1 kg-m^-1 ∙ s^-1
1 P = 1 dyn ∙ cm^-2 ∙ s = l g-cm^-1 ∙ s^-1
Let 1 Pa ∙ s = xP
∴ 1[M₁L₁^-1T₁^-1] = x[M₂L₂^-1T₂^-1]
where subscripts 1 and 2 pertain to SI and CGS units.

Question 91.
State Stokes’ law. Derive Stokes’ law using dimensional analysis.
Answer:
Stokes’ law : If a fluid flows past a sphere or a sphere moves through a fluid, for small enough
∴ Viscous force = gravitational force-buoyant force
= mg – m_Lg
where m = mass of the sphere = \(\frac{4}{3} \pi r^{3} \rho\) and m_{L</sub. = mass of the liquid displaced = \(\frac{4}{3} \pi r^{3} \rho_{\mathrm{L}}\).}

At its terminal speed v_t, the magnitude of the viscous force by Stokes’ law is

[Note : Theoretically, v → v_t as time t → ∞. In practice, if η is appreciable, then v tends to v_t in a very small time interval.]

[Data: g = 9.8 m/s²]

92. Solve the following

Question 1.
The relative velocity between two layers of a fluid, separately by 0.1 mm, is 2 cm/s. Calculate the velocity gradient.
Solution :
Data : dy = 0.1 mm = 10^-2 cm, dv = 2 cm/s
The velocity gradient, \(\frac{d v}{d y}=\frac{2 \mathrm{~cm} / \mathrm{s}}{10^{-2} \mathrm{~cm}}\) = 200 s^-1

Question 2.
Calculate the force required to move a flat glass plate of area of 10 cm² with a uniform velocity of 1 cm/s over the surface of a liquid 2 mm thick, if the coefficient of viscosity of the liquid is 2 Pa.s.
Solution :
Data : η = 2 Pa.s; A = 10 cm² = 10^-3 m²;
dv = 1 cm/s = 0.01 m/s; dy = 2 mm = 2 × 10^-3 m
According to Newton’s formula,
viscous force f = \(\eta A \frac{d v}{d y}\)
= \(\frac{(2 \mathrm{~Pa} \cdot \mathrm{s})\left(10^{-3} \mathrm{~m}^{2}\right)(0.01 \mathrm{~m} / \mathrm{s})}{2 \times 10^{-3} \mathrm{~m}}\)
= 0.01 N

This force retards the motion of the glass plate. Therefore, in order to keep the plate moving with a uniform velocity, an equal force must be exerted on the plate in the forward direction.

The required force to move the glass plate is 0.01 N

Question 3.
A metal plate of length 10 cm and breadth 5 cm is in contact with a layer of oil 1 mm thick. The horizontal force required to move it with a velocity of 4 cm/s along the surface of the oil is 0.32 N. Find the coefficient of viscosity of the oil. Also express it in poise.
Solution:

Question 4.
A spherical liquid drop of diameter 2 × 10^-4 m is falling with a constant velocity through air, under gravity. If the density of the liquid is 500 kg/m3 and the coefficient of viscosity of air is 2 × 10^-5 Pa.s, determine the terminal velocity of the drop and the viscous force acting on it. Ignore the density of air.
Solution :
Data : r = 1 × 10^-4 m, ρ = 500 kg/m³, ρ_air \(\ll \rho\) η = 2 × 10^-5 Pa.s

(i) The terminal velocity,

Question 5.
If the speed at which water flows through a long cylindrical pipe of radius 8 mm is 10 cm/s, find the Reynolds number. [Density of water = 1 g/cm³, coefficient of viscosity of water = 0.01 poise]
Solution :
Data : v₀ = 10 cm/s, ρ = 1 g/cm³, r = 8 mm
∴ d = 2r = 16 mm = 1.6 cm, η = 0.01 poise

Question 93.
Define volume flow rate or volume flux. Explain how it is related to the velocity of fluid.
OR
What is the difference between flow rate and fluid velocity ? How are they related ?
Answer:
Definition : The volume of fluid passing by a given location per unit time through an area is called the volume flow rate, or simply flow rate, Q.Q = dV/dt

Consider an ideal fluid flowing with velocity v through a uniform flow tube of cross section A. If, as shown in Fig. 2.34, the shaded cylinder of fluid of length x and volume V flows past point P in time t,

which is the required relation.

Question 94.
State the SI unit for volume flow rate.
Answer:
The SI unit for volume flow rate is the cubic metre per second (m³/s).

[Note : Another common unit accepted in SI is the litre per minute (L/min). 1 L = 10^-3 m³ = 10³ cm³. An old non-SI unit from FPS system still used is the cubic feet per second (symbol, cusec).]

Question 95.
Define mass flow rate or mass flux. Explain how it is related to the velocity of fluid.
Answer:
Definition : The mass of fluid passing by a given point per unit time through an area is called the mass flow rate, dmldt.

Consider an ideal fluid of density ρ flowing with velocity v through a uniform flow tube of cross section A. If, as shown in Fig. 2.34, the shaded cylinder of fluid of length x and volume V flows past point P in time t,

which is the required relation.

Question 96.
Explain the continuity condition for a flow tube. Show that the flow speed is inversely proportional to the cross-sectional area of a flow tube.
Answer:
Consider a fluid in steady or streamline flow. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude. Suppose the velocity is \(\overrightarrow{v_{1}}\) at point P and \(\overrightarrow{v_{2}}\) at point Q. If A₁ and A₂ are the cross-sectional areas of the tube and ρ₁ and ρ₂ are the densities of the fluid at these two points, the mass of the fluid passing per unit time across A₁ is A₁ρ₁v₁ and that passing across A₂ is A₂ρ₂v₂. Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires
A₁ρ₁v₁ = A₂ρ₂v₂ …………. (1)

Equation (1) is called the equation of continuity of flow. It holds true for a compressible fluid, (like all gases) for which the density of the fluid may differ from point to point in a tube of flow. For an incompressible fluid (like all liquids), ρ₁ = ρ₂ and Eq. (1) takes the simpler form
A₁v₁ = A₂v₂ ………… (2)
∴ \(\frac{v_{1}}{v_{2}}=\frac{A_{2}}{A_{1}}\) …………… (3)
that is, the flow speed is inversely proportional to the cross-sectional area of a flow tube. Where the area is large, the speed of flow is small, and vice versa.

Equations (2) is the equation of continuity for an incompressible fluid for which density is constant throughout.

Question 97.
Explain why flow speed is greatest where streamlines are closest together.
Answer:
By the equation of continuity, the flow speed is inversely proportional to the area of cross section of a flow tube. Where the area of cross section is small, i. e., streamlines are close, the flow speed is large and vice versa.

Question 98.
You can squirt water a considerably greater distance by placing your thumb over the end of a garden hose. Explain.
Answer:
Placing one’s thumb over the end of a garden hose constricts the open end. By the continuity condition, the speed of water increases as it passes through the constriction. Hence, water squirts out and reaches a longer distance.

99. Solve the following

Question 1.
A liquid is flowing through a horizontal pipe of varying cross section. At a certain point, where the diameter of the pipe is 5 cm, the flow velocity is 0.25 m/s. What is the flow velocity where the diameter is 1 cm ?
Solution:
Data : d₁ = 5 cm, v₁ = 0.25 m/s, d₂ = 1 cm According to the equation of continuity of flow,
A₁ρ₁v₁ = A₂ρ₂v₂
where A₁ and ρ₁ are the cross-sectional area and density of the liquid where the flow velocity is v₁; A₂ and ρ₂ are the corresponding quantities where the flow velocity is v₂.
Assuming the liquid is incompressible,

Question 100.
State Bernoulli’s principle.
Answer:
Where the velocity of an ideal fluid in streamline flow is high, the pressure is low, and where the velocity of a fluid is low, the pressure is high. OR At every point in the streamline flow of an ideal (i.e., nonviscous and incompressible) fluid, the sum of the pressure energy, kinetic energy and potential energy of a given mass of the fluid is constant at every point.

[Note : The above principle is equivalent to a statement of the law of conservation of mechanical energy as applied to fluid mechanics. It was published in 1738 by Daniel Bernoulli (1700 – 82), Swiss mathematician.]

Question 101.
Explain Bernoulli’s equation of fluid flow.
Answer:
Consider an ideal fluid incompressible and nonviscous of density ρ flowing along a flow tube of varying cross section. The system under consideration is the flow tube between points 1 and 2, and the Earth (below figure). From the continuity equation it follows that pressure and speed must be different in regions of different cross section. If the height also changes, there is an additional pressure difference.

The fluid enters the system at point 1 through a. surface of cross section A₁ at speed v₁. The point 1 lies at a height h₁, with respect to an arbitrary reference level y = 0, and the local pressure there is p₁. The fluid leaves the system at point 2 where the corresponding quantities are A₂, v₂, h₂ and p₂.

Consider a small fluid element, of volume ∆V and mass ∆m = ρ∆V, that enters at point 1 and leaves at point 2 during small time interval ∆t. In the absence of internal fluid friction, it can be shown that the work done on the fluid element by the surrounding fluid is
∆W= (p₁ – p₂)∆V
This is sometimes called the pressure energy. During At, the changes in the kinetic energy and potential energy are
∆KE = \(\frac{1}{2}\) ∆m (V₂² – V₁²) = \(\frac{1}{2}\) ρ∆V(v₂² – v₁²)
∆PE = ∆mg(h₂ – h₁) = ρ∆Vg(h₂ – h₁)
Since ∆W is the work done by a non-conservative force,
∆W = ∆KE + ∆PE
∴ (p₁ – p₂)∆V = \(\frac{1}{2}\) ρ∆V(v₂2² – v₁²) + ρ∆Vg(h₂ – h₁) ……….. (1)
∴ p₁ – p₂ = \(\frac{1}{2}\) ρ(v₂² – v₁²) + ρg(h₂ – h₁)
∴ p₁ + \(\frac{1}{2}\) ρv₁² + ρgh₁ = p₂ + \(\frac{1}{2}\) ρv₂² + ρgh₂
or p + \(\frac{1}{2}\) ρv² + ρgh = constant …………. (2)
This is known as Bernoulli’s equation.

[Notes : Equation (1) can be rewitten as
p₁∆V + \(\frac{1}{2}\)ρ∆Vv₁² + ρ∆Vgh₁
p₂∆V + \(\frac{1}{2}\) ρ∆v₂² + ρ∆Vgh₂
or p∆V + \(\frac{1}{2}\)ρ∆v² + ρ∆Vgy = constant ………. (3)
i.e., pressure energy + KE + PE = constant
Dividing Eq. (3) by ∆m = ρ∆V,
\(\frac{p}{\rho}\) + \(\frac{1}{2}\) v² + gy constant

i.e., pressure energy per unit mass + KE per unit mass + PE per unit mass = constant, which is Bernoulli’s principle. Note that in writing

∆W = ∆KE + ∆PE, we have assumed principle of conservation of energy.

Dimensionally, pressure is energy per unit volume. Both terms on the right side of Eq. (2) also have the same dimensions. Hence, the term (p₁ – p₂) is often referred to as pressure energy per unit volume or pressure head. The first term on the right, \(\frac{1}{2}\) p (v₂² – v₁²) head and the second term, pg(h₂ – h₁), is called the potential head.]

Question 102.
State the limitations of Bernoulli’s principle.
Answer:
Limitations: Bernoulli’s principle and his equation for fluid flow is valid only for
(1) an ideal fluid, i.e., one that is incompressible and nonviscous, so that the density remains constant throughout a flow tube and there is no viscous drag which results in energy dissipation or loss,
(2) streamline flow.

Question 103.
State the applications of Bernoulli’s principle.
Answer:
Applications :

1. Venturi meter : It is a horizontal constricted tube that is used to measure flow speed in a gas.
2. Atomizer : It is a hydraulic device used for spraying insecticide, paint, air perfume, etc.
3. Aerofoil : The aerofoil shape of the wings of an aircraft produces aerodynamic lift.
4. Bunsen’s burner : Bernoulli effect is used to admit air into the burner to produce an oxidising flame.

Question 104.
State the law of efflux. Derive an expression for the speed of efflux for a tank discharging through an opening at a depth h below the liquid surface. Hence or otherwise show that the speed of efflux for an open tank is \(\sqrt{2 g h}\).
Answer:
Law of efflux (Torricelli’s theorem) : The speed of efflux for an open tank through an orifice at a depth h below the liquid surface is equal to the speed acquired by a body falling freely through a vertical distance h.

Consider a tank with cross-sectional area A₁ holding a static liquid of density ρ. The tank discharges through an opening (of cross-sectional area A₂) in the side wall at a depth h below the surface of the liquid. The flow speed at which the liquid leaves the tank is called the speed of efflux.

The pressure at point 2 it is the atmospheric pressure p₀. Let the pressure of the air above the liquid at point 1 be ρ. We assume that the tank is large in cross section compared to the opening (A₁ >> A₂), so that the upper surface of the liquid will drop very slowly. That is, we may regard the liquid surface to be approximately at rest v₁ ≈ 0). Bernoulli’s equation, in usual notation, states
p₁ + \(\frac{1}{2}\) ρv₁² + ρgy₁ = p₂ + \(\frac{1}{2}\) ρv₂² + ρgy₂
Substituting p₁ = p, p₂ = p₀, v₁ ≈ 0 and (y₁ – y₂) = h,
v₂² = 2 \(\frac{p-p_{0}}{\rho}\) + 2gh
If the tank is open to the atmosphere, then p = p₀,
v₂ = \(\sqrt{2 g h}\).
which is the law of efflux.

[Note : For an open tank, the speed of the liquid, v₂, leaving a hole a distance h below the surface is equal to that acquired by an object falling freely through a vertical distance h.]

Question 105.
What is a Venturi tube? Explain the working of a Venturi tube.
OR
What is a Venturi meter? Briefly explain its use to determine the flow rate in a pipe.
Answer:
A Venturi meter is a horizontal constricted tube that is used to measure the flow speed through a pipeline. The constricted part of the tube is called the throat. Although a Venturi meter can be used for a gas, they are most commonly used for liquids. As the fluid passes through the throat, the higher speed results in lower pressure at point 2 than at point 1. This pressure difference is measured from the difference in height h of the liquid levels in the U-tube manometer containing a liquid of density ρ_m (from below figure). The following treatment is limited to an incompressible fluid.

Let A₁ and A₂ be the cross-sectional areas at points 1 and 2, respectively. Let v₁ and v₂ be the corresponding flow speeds, p is the density of the fluid in the pipeline. By the equation of continuity,
v₁A₁ = v₂A₂ …………. (1)
Since the meter is assumed to be horizontal, from Bernoulli’s equation we get,
p₁ = \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\) ρv₂²
∴ p₁ = \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\) ρv₁² \(\left(\frac{A_{1}}{A_{2}}\right)^{2}\) [from Eq. (1)]
∴ p₁ – p₁ = \(\frac{1}{2}\) ρv₁² [\(\left(\frac{A_{1}}{A_{2}}\right)^{2}\) – 1] …………. (2)
The pressure difference is equal to pm gh, where h is the differences in liquid levels in the manometer. Then,

Equation (3) gives the flow speed of an incom-pressible fluid in the pipeline. The flow rates of practical interest are the mass and volume flow ‘ rates through the meter.
Volume flow rate = A₁v₁
and mass flow rate = density x volume flow rate = ρA₁v₁
[Note ; When a Venturi meter is used in a liquid pipeline, the pressure difference is measured from the difference in height h of the levels of the same liquid in the two vertical tubes, as shown in below figure. Then, the pressure difference is equal to ρgh.

The flow meter is named after Giovanni Battista Venturi (1746-1822), Italian physicist.]

Question 106.
Explain aerodynamic lift on the wings of an aeroplane.
OR
Explain why the upper surface of the wings of an aeroplane is made convex and the lower surface concave.
Answer:
An aeroplane wing has a special characteristic aerodynamic shape called an aerofoil. An aerofoil is convex on the top and slightly concave on the bottom. Its leading edge is well rounded while the trailing edge is sharp. As an aeroplane moves through air, the aerofoil shape makes the air moving over the top and along the bottom of a wing in a certain way.

If the air over the top surface travels faster than the air below the wing, this decreases the air pressure above the wing. The air flowing below the wing moves almost in a straight line, so its speed and air pressure remain the same. The air under the wings therefore pushes upward more than the air on top of the wings pushes downward, thus producing an upward force \(\vec{F}\). It is the pressure difference that generates this force. The component of \(\vec{F}\) perpendicular to the direction of motion is called the aerodynamic lift or, simply, the lift. The component parallel to the direction of flight is the drag. The lift is the force that allows an aeroplane to get off the ground and stay in the air. For an aeroplane to stay in level flight, the lift is equal in magnitude and opposite in direction to the force of gravity.

[Note: For an airborne aeroplane to get to the ground, the direction of \(\vec{F}\) must be reversed. Then, the upper surface should be more concave than the lower surface such that air above the wing travels slower than the air below it, decreasing the air pressure below the wing. This is achieved by small flaps, called ailerons, attached at the trailing end of each wing.]

Question 107.
Explain the working of an atomizer.
OR
A perfume bottle or atomizer sprays a fluid that is in the bottle. How does the fluid rise up in the vertical tube in the bottle?
Answer:
An atomizer is a device which entraps or entrains liquid droplets in a flowing gas. Its working is based on Bernoulli’s principle. A squeeze bulb or a pump is used to create a jet of air over an open tube dipped into a liquid. By Bernoulli’s principle, the high-velocity air stream creates low pressure at the open end of the tube. This causes the liquid to rise in the tube. The liquid is then dispersed into a fine spray of droplets. This type of system is used in a perfume bottle, a paint sprayer, insect and perfume sprays and an automobile carburetor.

[Notes : A Bunsen burner uses an adjustable gas nozzle to entrain air into the gas stream for proper combustion. Aspirators, used as suction pumps, in dental and surgical situations (for draining body fluids) or for draining a flooded basement, is another similar applica-tion. Some chimney pipes have a T-shape, with a cross-piece on top that helps draw up gases whenever there is even a slight breeze.]

Question 108.
Roofs are sometimes blown off vertically during a tropical cyclone, and houses sometimes explode outward when hit by a tornado. Use Bernoulli’s principle to explain these phenomena.
Answer:
A cyclonic high wind blowing over a roof creates a low pressure above it, in accordance with Bernoulli’s principle. The pressure below the roof is equal to the atmospheric pressure which is now greater than the pressure above the roof. This pressure difference causes an aerodynamic lift that lifts the roof up. Once the roof is lifted up, it blows off in the direction of the wind.

Wind speeds in a tornado may be much higher and thus create much greater pressure differences. Sometimes, wooden houses hit by a tornado explode.

Question 109.
Describe what happens : (1) Hold the short edge of a paper strip (2″ × 6″) up to your lips-the strip slanting downward over your finger-and blow over the top of the strip. (2) Hold two strips of paper up to your lips, separated by your fingers and blow between the strips.
Answer:
(1) The air stream over the top surface travels faster than the air stream below the paper strip. This decreases the air pressure above the strip relative o that below. This produces an aerodynamic lift in accordance with Bernoulli’s principle and the paper strip will lift up.

(2) Air passing between the paper strips flows in a narrower channel and, in accordance with Be rnoulli’s principle, must increase its speed, causing the pressure between them to drop. This will pinch the two strips together.

110. Solve the following

Question 1.
Water is flowing through a horizontal pipe of varying cross section. At a certain point where the velocity is 0.12 m/s, the pressure of water is 0.010 m of mercury. What is the pressure at a point where the velocity is 0.24 m/s?
Solution:
Data : v₁ = 0.12 m/s, p₁ = 0.010 m of Hg, v₂ = 0.24 m/s, y₁ = y₂ (horizontal pipe), ρ_Hg = 13600 kg/m², ρ_w = 1000 kg/m³, g = 9.8 m/s²
p₁ = 0.010 m of Hg .
= (0.010 m) ρ_Hgg
= (0.010 m) (13600 kg/m³) (9.8 m/s²)
= 1332.8 Pa ≅ 1333 Pa
According to Bernoulli’s principle,

This gives the pressure of the water in the pipe where the flow velocity is 0.24 m / s.

Question 2.
A building receives its water supply through an undergound pipe 2 cm in diameter at an absolute pressure of 4 × 10⁵ Pa and flow velocity 4 m/s. The pipe leading to higher floors is 1.5 cm in diameter. Find the flow velocity and pressure at the floor inlet 10 m above.
Solution:
Data : d₁ = 3 cm, p₁ = 4 × 10⁵ Pa, v₁ = 4 m/s,
d₂ = 2 cm, h₂ – h₁ = 10 m
By continuity equation, the flow velocity at the higher floor inlet

Question 3.
Calculate the total energy per unit mass possessed by water at a point where the pressure is 0.1 × 10⁵ N/m², the velocity is 0.02 m/s and the height of the water level from the ground is 10 cm. Density of water = 1000 kg/m³.
Solution:
Data : p = 0.1 × 10⁵ N/m² = 10⁴ Pa, v = 0.02 m/s, y = 10 cm = 0.1 m, ρ = 1000 kg/m³, g = 9.8 m/s²
The total energy per unit mass of water
= \(\frac{p}{\rho}\) + \(\frac{1}{2}\)v² + gy
= \(\frac{10^{4} \mathrm{~Pa}}{10^{3} \mathrm{~kg} / \mathrm{m}^{3}}\) + \(\frac{1}{2}\) (2 × 10^-2 m/s)² + (9.8 m/ s²) (0.1 m)
= 10 + 0.0002 + 0.98 = 10.9802 J/kg

Question 4.
A horizontal wind with a speed of 11 m/s blows past a tall building which has large windowpanes of plate glass of dimensions 4 m × 1.5 m. The air inside the building is at atmospheric pressure. What is the total force exerted by the wind on a window pane ? [Density of air = 1.3 kg/m³]
Solution:
Data : v₁ (inside) = 0 m/s, v₂ (outside) = 11 m/s, ρ = 1.3 kg/m³, p₁ = p₀ = atmospheric pressure,
A = 4m × 1.5 m = 6m
Let p₂ be the air pressure outside a window. At the same height, Bernoulli’s equation gives
∴ p₁ + \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\)ρv₂²
∴ p₀ + 0 = p₂ + \(\frac{1}{2}\) ρv₂²
∴ The difference in pressure across a windowpane is
p₀ – p₂ = \(\frac{1}{2}\) ρv₂²
Since the right hand side is positive,
p₀ > p₂ and p₀ – p₂ is directed outward.
∴ The total force on a window pane is
F = (p₀ – p₂)A = \(\frac{1}{2}\) ρv₂² A
= \(\frac{1}{2}\) (1.3 kg/m³) (11 m/s)² (6 m²)
= 3.9 × 121 = 471.9 N (outward)

Question 5.
A water tank has a hole at a distance x from the free surface of water in the tank. If the radius of the hole is 2 mm and the velocity of efflux is 11 m/s, find x.
Solution:
Data: r = 2 mm, v = 11 m/s, g = 9.8 m/s²
By Torricelli’s law of efflux, the velocity of efflux,
v = \(\sqrt{2 g x}\)
∴ x = \(\frac{v^{2}}{2 g}=\frac{(11 \mathrm{~m} / \mathrm{s})^{2}}{2\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)}\)
= \(\frac{121}{19.6}\) = 6.173 m

Multiple Choice Questions

Question 1.
Consider the following statements:
I. A fluid in hydrostatic equilibrium exerts only normal force on any surface within the fluid.
II. A fluid can resist a tangential force. Of these,
(A) only (I) is correct
(B) only (II) is correct
(C) both are correct
(D) both are false.
Answer:
(A) only (I) is correct

Question 2.
Which of the following is correct ?
(A) The free surface of a liquid at rest is horizontal.
(B) The pressure at a point within a liquid at rest is the same in all directions.
(C) The pressure at all points within a liquid at rest is the same.
(D) Both (A) and (B).
Answer:
(D) Both (A) and (B).

Question 3.
The surface of a liquid (of uniform density p) in a container is open to the atmosphere. The atmospheric pressure is ρ₀. The pressure ρgh, at a depth h below the surface of the liquid, is called the
(A) absolute pressure
(B) normal pressure
(C) gauge pressure
(D) none of these.
Answer:
(C) gauge pressure

Question 4.
Three vessels having the same base area are filled with water to the same height, as shown. The force exerted by water on the base is

(A) largest for vessel P
(B) largest for vessel Q
(C) largest for vessel R
(D) the same in all three.
Answer:
(D) the same in all three.

Question 5.
Rain drops or liquid drops are spherical in shape, especially when small, because
(A) cohesive force between the molecules of water have spheres of influence
(B) for a given volume, a spherical drop has the least surface energy
(C) for a given volume, a spherical drop has the maximum surface energy
(D) the pressure inside a drop is many times the atmospheric pressure outside.
Answer:
(B) for a given volume, a spherical drop has the least surface energy

Question 6.
The surface tension acts
(A) perpendicular to the surface and vertically up-wards
(B) perpendicular to the surface and vertically into the liquid
(C) tangential to the surface
(D) only at the liquid-solid interface.
Answer:
(C) tangential to the surface

Question 7.
A thin ring of diameter 8 cm is pulled out of water (surface tension 0.07 N/m). The force required to break free the ring from water is
(A) 0.0088 N
(B) 0.0176 N
(C) 0.0352 N
(D) 3.52 N.
Answer:
(C) 0.0352 N

Question 8.
A matchstick 5 cm long floats on water. The water film has a surface tension of 70 dyn/cm. A little comphor put on one side of stick reduces the surface tension there to 50 dyn/cm. The net force on the matchstick is
(A) 4 dynes
(B) 20 dynes
(C) 100 dynes
(D) 600 dynes.
Answer:
(C) 100 dynes

Question 9.
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be
(A) 10 R
(B) \(\frac{R}{10}\)
(C) \(\frac{R}{100}\)
(D) \(\frac{R}{1000}\)
Answer:
(B) \(\frac{R}{10}\)

Question 10.
The work done in breaking a spherical drop of a liquid (surface tension T) of radius R into 8 equal drops is
(A) πR²T
(B) 2πR²T
(C) 3πR²T
(D) 4πR²T.
Answer:
(D) 4πR²T.

Question 11.
If for a liquid in a vessel, the force of cohesion is more than the force of adhesion,
(A) the liquid does not wet the solid
(B) the liquid wets the solid
(C) the surface of the liquid is plane
(D) the angle of contact is zero.
Answer:
(A) the liquid does not wet the solid

Question 12.
If a liquid does not wet a solid surface, its angle of contact with the solid surface is
(A) zero
(B) acute
(C) 90°
(D) obtuse.
Answer:
(D) obtuse.

Question 13.
The pressure within a bubble is higher than that outside by an amount proportional
(A) directly to both the surface tension and the bubble size
(B) directly to the surface tension and inversely to the bubble size
(C) directly to the bubble size and inversely to the surface tension
(D) inversely to both the surface tension and the bubble size.
Answer:
(B) directly to the surface tension and inversely to the bubble size

Question 14.
The pressure difference across the surface of a spherical water drop of radius 1 mm and surface tension 0.07 N/m is
(A) 28 Pa
(B) 35 Pa
(C) 140 Pa
(D) 280 Pa.
Answer:
(C) 140 Pa

Question 15.
An air bubble just inside a soap solution and a soap bubble blown using the same solution have their radii in the ratio 3 : 2. The ratio of the excess pressure inside them is
(A) 1 : 12
(B) 1 : 6
(C) 1 : 3
(D) 1 : 2.
Answer:
(C) 1 : 3

Question 16.
A liquid rises to a height of 5 cm in a glass capillary tube of radius 0.02 cm. The height to which the liquid would rise in a glass capillary tube of radius 0.04 cm is
(A) 2.5 cm
(B) 5 cm
(C) 7.5 cm
(D) 10 cm.
Answer:
(A) 2.5 cm

Question 17.
In a gravity free space, the liquid in a capillary tube will rise to
(A) the same height as that on the Earth
(B) a lesser height than on the Earth
(C) slightly more height than that on the Earth
(D) the top and overflow.
Answer:
(D) the top and overflow.

Question 18.
In which of the following substances, does the surface tension increase with an increase in tempera¬ture?
(A) Copper
(B) Molten copper
(C) Iron
(D) Molten iron
Answer:
(B) Molten copper

Question 19.
A fluid flows in steady flow through a pipe. The pipe has a circular cross section, but its radius varies along its length. The mass of the fluid passing per second at the entrance point (radius R) of the pipe is Q₁ while that at the exit point (radius R/2) is Q₂. Then, Q₂ is equal to
(A) \(\frac{1}{4}\) Q₁
(B) Q₁
(C) 2Q₁
(D) 4Q₁.
Answer:
(B) Q₁

Question 20.
The dimensions of coefficient of viscosity are
(A) [ML^-1T^-2]
(B) [M^-1LT^-2]
(C) [MLT^-2]
(D) [ML^-1T^-1].
Answer:
(D) [ML^-1T^-1].

Question 21.
The unit of coefficient of viscosity is
(A) the pascal-second
(B) the pascal
(C) the poise-second
(D) both (A) and (C).
Answer:
(A) the pascal-second

Question 22.
A fluid flows past a sphere in streamline flow. The viscous force on the sphere is directly proportional to
(A) the radius of the sphere
(B) the speed of the flow
(C) the coefficient of viscosity of the fluid
(D) all of these.
Answer:
(D) all of these.

Question 23.
Water flows in a streamlined flow through the pipe shown in the following figure. The pressure

(A) is greater at A than at B
(B) at A equals that at B
(C) is less at A than at B
(D) at A is unrelated to that at B.
Answer:
(A) is greater at A than at B

Question 24.
Two steel marbles (of radii R and \(\frac{R}{3}\)) are released in a highly viscous liquid. The ratio of the terminal velocity of the larger marble to that of the smaller is
(A) 9
(B) 3
(C) 1
(D) \(\frac{1}{9}\)
Answer:
(A) 9

Question 25.
A large tank, filled with a liquid, is open to the atmosphere. If the tank discharges through a small hole at its bottom, the speed of efflux does NOT depend on
(A) cross-sectional area of the hole
(B) depth of the hole from the liquid surface
(C) acceleration due to gravity
(D) all of these.
Answer:
(A) cross-sectional area of the hole

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 8 Electrostatics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 8 Electrostatics

Question 1.
State Gauss’s law in electrostatics.
Answer:
Gauss’s law : The net flux through a closed surface in free space is related to the net charge qenci that is enclosed by that surface and is given by
Φ = \(\oint \vec{E} \cdot \overrightarrow{d \mathrm{~s}}=\frac{q_{\mathrm{encl}}}{\varepsilon_{0}}\)
where e0 is the permittivity of free space and the electric flux \(\vec{E} \cdot \overrightarrow{d \mathrm{~s}}\) is integrated over the entire area of the surface.

[Note: The SI unit of electric flux is the newton metre squared per coulomb (N∙m²/C) or, equivalently, the voltmetre (V\vec{E} \cdot \overrightarrow{d \mathrm{~s}}m).]

Question 2.
A Gaussian surface in the form of a cube is centred on a point charge Q. What is the flux through one face of the cube?
Answer:
Since the point charge is at the centre of the cube, the electric flux through each face is the same. Therefore, the electric flux through one face is \(\frac{1}{6}\)th of the electric flux originating from or terminating at the point charge.

If ε is the permittivity of the medium, the electric flux through one face = \(\frac{Q}{6 \varepsilon}\).

Question 3.
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
Answer:
Since the net charge enclosed by the surface is zero, the net electric flux through the surface is also zero. . v

Question 4.
Obtain an expression for the electric field intensity at a point outside a charged conducting spherical shell.
Hence, obtain an expression for the electric intensity (i) on the surface of (i.e., just outside) the spherical conductor (ii) inside the spherical conductor.
Answer:
Consider an isolated charged hollow spherical conductor A, of radius R and surface charge density σ, placed in a medium of permittivity ε. Consider a . point P outside the conductor at a distance r from its centre. To find the electric field intensity at P, we choose a spherical Gaussian surface S of radius r through P and concentric with conductor A. A small element of this surface containing P has an area dS.

The charge Q is uniformly distributed over the outer surface of the spherical conductor. Then, by symmetry, the electric field intensity at every point on surface S is normal to the surface and has the same magnitude E. If charge Q is positive, \(\vec{E}\) at every point on S is radially outward.
The angle θ between \(\vec{E}\) and \(d \vec{S}\) being zero for every surface element, the electric flux through every element is
dΦ = \(\vec{E} \cdot d \vec{S}\) = E dS
Therefore, the flux through the Gaussian surface S is

where ε₀ is the permittivity of free space and k = \(\frac{\varepsilon}{\varepsilon_{0}}\) is the relative permittivity (dielectric constant) of the surrounding medium.
∴ E = \(\frac{\sigma\left(4 \pi R^{2}\right)}{4 \pi \varepsilon r^{2}}=\frac{\sigma R^{2}}{\varepsilon r^{2}}\) …………… (6)
Equations (5) and (6) give the magnitude of the electric field intensity at a point P outside a hollow spherical conductor. If the net charge Q enclosed by the Gaussian surface is positive, \(\vec{E}\) is radially outward; if Q is negative, \(\vec{E}\) is radially inward. Equation (5) shows that for a point outside a hollow spherical conductor carrying a charge Q, the conductor behaves like a point charge Q at its centre.

Case (1) : At a point just outside the sphere, r ≅ R.
∴ E = \(\frac{\sigma}{\varepsilon}=\frac{\sigma}{k \varepsilon_{0}}\)

Case (2) : Since electric charge resides on the outer surface of a hollow conductor, the charge inside the hollow spherical conductor is zero. Then, E_inside = 0.

[Notes : (1) The surface of a charged conductor is an equipotential surface so that the electric field just outside it must be normal to the surface of the conductor. For a spherical charged conductor, it follows that the field is radial, and because the net charge is, by symmetry, uniformly distributed over its outer surface, the field is spherically symmetric, the same as for a point charge.
(2) The electric field intensity is zero at all points inside a hollow charged conductor of arbitrary shape because under electrostatic condition the net charge of the charged conductor resides on its surface. This is also true for a hollow charged spherical conductor, if there is no charge in the cavity (e.g., on a conductor inside the cavity but insulated from the outer shell).]

Question 5.
Does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
Answer:
No. Electric flux, or the number of electric field lines, passing through the Gaussian surface is independent of the size of the Gaussian surface and depends on the number of field lines originating from or terminating at the point charge, which in turn depends on the magnitude of the point charge and the permittivity of the medium.

Question 6.
Obtain an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
Answer:
Consider an isolated cylindrical conductor A, of radius R and carrying a charge per unit length λ. We assume the conductor to be infinitely long. Consider a point P outside the conductor at a distance r from its axis. To find the electric field intensity at P, we choose a cylindrical Gaussian surface S of radius r through P and coaxial with the conductor A. As λ is the charge per unit length of conductor A, the net charge enclosed by the Gaussian cylinder of length l is
Q = λl ………….. (1)
A small element on the curved part of the Gaussian surface and containing P has an area dS.

Charge is uniformly distributed over the outer surface of the cylindrical conductor. Then, by symmetry, the electric field intensity at any point outside the conductor is perpendicular to the cylinder axis. Hence, the component of the electric field intensity perpendicular to the plane circular faces of the Gaussian surface is zero. Therefore, the electric flux through these flat faces is zero.

By symmetry, the electric field intensity \(\vec{E}\) at every point on the curved face of surface S is normal to the surface and has the same magnitude \(\vec{E}\). If the charge on conductor A is positive, E is directed along the outward drawn normal \(d \vec{S}\).

The angle θ between \(\vec{E}\) and \(d \vec{S}\) being zero for every surface element, the electric flux through every element is
dΦ = \(\vec{E} \cdot d \vec{S}\) = E dS
Therefore, the flux through the curved face of the Gaussian surface S is
Φ = \(\oint\) E dS = E \(\oint\) dS ……….. (2)
\(\oint\) dS = area of the curved surface = 2πrl, where l is the length of the cylinder as shown in the figure.
∴ Φ = E × 2πrl ………….. (3)
Then, by Gauss’s theorem,
Φ = \(\frac{Q}{\varepsilon}\) = E × 2πrl ……………. (4)
∴ E = \(\frac{\lambda l}{\varepsilon(2 \pi r l)}=\frac{\lambda}{2 \pi \varepsilon r}=\frac{\lambda}{2 \pi k \varepsilon_{0} r}\) ……………… (5)
where ε₀ is the permittivity of free space and k = \(\frac{\varepsilon}{\varepsilon_{0}}\) is the relative permittivity (dielectric constant) of the surrounding medium.

This gives the magnitude of the electric field intensity in terms of the linear charge density λ. For positive λ, \(\vec{E}\) is outward, while for negative λ, \(\vec{E}\) is inward.

[Notes : (1) If σ is the surface charge density (charge per unit area), σ = \(\frac{\lambda l}{2 \pi R l}=\frac{\lambda}{2 \pi R}\) ∴ λ = 2πRσ
∴ E = \(\frac{2 \pi R \sigma}{2 \pi \varepsilon_{0} k r}=\frac{R \sigma}{\varepsilon_{0} k r}\) (2) If the charge on the conductor is negative, \(\vec{E}\) is inward.]

Question 7.
An infinitely long positively charged straight wire has a linear charge density λ. An electron is revolving around the wire as its centre with a constant speed in a circular plane perpendicular to the wire. Deduce the expression for its kinetic energy.
Answer:
Let r be the radius of the uniform circular motion of the electron. The electric field intensity \(\vec{E}\) at every point on the circular path is radially outward and has the same magnitude E = \(\frac{\lambda}{2 \pi \varepsilon r}\) .

∴ The centripetal force on the electron,
F_c = \(\frac{m_{\mathrm{e}} v^{2}}{r}\) = eE = \(\frac{e \lambda}{2 \pi \varepsilon r}\)
where m_e and v are the mass and linear speed of the electron.
∴ m_ev² = \(\frac{e \lambda}{2 \pi \varepsilon}\)
∴ The kinetic energy of the electron,
\(\frac{1}{2}\) m_ev² = \(\frac{e \lambda}{4 \pi \varepsilon}\)

Question 8.
Obtain an expression for the electric field intensity at a point outside a uniformly charged thin infinite plane sheet.
Answer:
Consider a thin, flat, infinite, positively charged conducting sheet, with a uniform surface charge density σ. let the permittivity of the surrounding medium be ε. The charge density has a planar symmetry, i.e., it appears the same from all points on a plane parallel to the sheet. Then, by symmetry, the electric field intensity \(\vec{E}\) (1) is perpendicular to the sheet (in this case, outwards) at all points outside the sheet, and (2) has the same magnitude E at any given distance on either side of the sheet.

To find E at a point P outside the sheet, imagine a Gaussian surface in the form of a small closed cylinder. Its axis is perpendicular to the sheet, with the point P on one end face, shown in below figure. The cylinder encloses a small area dS of the sheet. So, the charge enclosed by the cylinder = σdS …………. (1)
The flux through one end = EdS
∴ The flux through the Gaussian surface,
Φ = 2EdS …………… (2)
By Gauss’s theorem,
εΦ = net charge enclosed
∴ ε(2EdS) = σdS …………. (3)
∴ E = \(\frac{\sigma}{2 \varepsilon}=\frac{\sigma}{2 k \varepsilon_{0}}\) …………. (4)
where ε₀ is the permittivity of free space and k = \(\frac{\varepsilon}{\varepsilon_{0}}\) is the relative permittivity (dielectric constant) of the surrounding medium.

Equation (4) shows that the magnitude of the electric field intensity outside the charged sheet is uniform and independent of the distance from the sheet.

[Notes : (1) The electric field lines are straight, parallel to each other, and perpendicular to the sheet. (2) If the sheet is negatively charged, \(\vec{E}\) on either side of the sheet is directed towards the sheet.]

9. Solve the following

Question 1.
Two metal spheres, of radii 2 cm and 1 cm with respective charge densities 5 mC/m² and -2 mC/m², are inside a hypothetical closed surface in vacuum. What is the net electric flux through the surface ?
Solution:
Data : σ₁ = 5 × 10^-6 C / m²,
σ₂ = -2 × 10^-6 C/m², r₁ = 2 × 10^-2 m, r₂ = 2 × 10^-2 m
ε₀ = 8.85 × 10^-12 F/m
Surface charge density, σ = \(\frac{Q}{A}=\frac{Q}{4 \pi r^{2}}\)
∴ The charges on the metal spheres are
Q₁ = σ₁ (4πr₁²) and Q₂ = σ₂(4πr₂²)
∴ Net charge enclosed, Q = Q₁ + Q₂ = 4π(σ₁r₁² + σ₂r₂²) = Q₁ + Q₂
= 4π[(5 × 10^-6)(2 × 10^-2)² +(- 2 × 10^-6)(10^-2)²]
= 4π[(5 × 10^-6)(4 × 10^-4) + (- 2 × 10^-6)(10^-4)]
= 4π(10^-10)(20 – 2) = 72π × 10^-10 C
∴ By Gauss’s theorem, the net flux through the surface
= \(\frac{Q}{\varepsilon_{0}}=\frac{72 \times 3.142 \times 10^{-10}}{8.85 \times 10^{-12}}\) = 2.556 × 10³ V∙m or N∙m²/C

Question 2.
A hollow metal ball 10 cm in diameter is given a charge of 1 × 10^-2 C. What is the magnitude of the electric field intensity at a point 20 cm from the centre of the ball ?
Solution:
Data : D = 10 cm, R = \(\frac{D}{2}\) = 5 cm, q = 1 × 10^-2 C,
r = 20cm = 0.2 m, ε₀ = 8.85 × 10^-12
Electric field intensity,

Question 3.
The electric field intensity at a point 1 m from the centre of a charged sphere of radius 25 cm in air is 10⁴ N/C. Find the surface charge density of the sphere.
Solution:
Data : r = 1 m,R = 0.25 m, E = 10⁴ N/C, ε₀ = 8.85 × 10^-12 F/m
E = \(\frac{\sigma R^{2}}{\varepsilon r^{2}}\)
As the sphere is situated in air, ε ≅ ε₀.
∴ The surface charge density,
σ = ε₀E(\(\frac{r}{R}\))²
= (8.85 × 10^-12)(10⁴)(\(\frac{1}{0.25}\))²
= 1.416 × 10^-10 C/m²

Question 4.
A long cylindrical conductor of radius 2 cm carries a charge of 5 μC/m and is kept in a medium of dielectric constant 10. Find the electric field intensity at a point 1 m from the axis of the cylinder.
[\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ \(\frac{\mathbf{N} \cdot \mathbf{m}^{2}}{\mathrm{C}^{2}}\)]
Solution :
Data : R = 2 cm, λ = 5 × 10^-6 C/m, k = 10,
r = 1 m, \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ N∙m²/C²
Electric field intensity,

Question 5.
The electric field intensity at a point on the surface of a long, charged cylinder in air is 100 V/m. Find the surface charge density on the cylinder.
Solution:
Data: E = 100 V/m, ε₀ = 8.85 × 10^-12 C²/N∙m²,
k = 1 (for air)
Let σ be the surface charge density on the cylinder.
E = \(\frac{\sigma}{\varepsilon_{0} k}\) :. σ = Eε₀k
= 100 × 8.85 × 10^-2 × 1
= 8.85 × 10^-10 C/m²

Question 10.
Obtain an expression for the electric potential energy of a system of two isolated point charges.
Answer:
Consider a test charge q0 in the electric field \(\vec{E}\) of a source charge + Q. The electric force acting on the test charge, q₀\(\vec{E}\), is a conservative force. When the test charge is moved in the field at constant velocity by some external agent, the work done by the field on the charge is equal to the negative of the work done by the external agent causing the displacement. Suppose an external agent moves the test charge without acceleration from a point B, at a distance r₁ from + Q, up to a point A, at a distance r, shown in below figure.

Since the electric field surrounding a point charge is not uniform, the electrostatic force on q0 increases as it approaches Q. Consequently, the external agent has to exert on q₀ a force of increasing magnitude and, for equal displacements, do increasing amount of work. Because the force exerted varies along the path, we imagine the total displacement to be made up of a large number of infinitesimal displacements \(d \vec{x}\). The distance dx is so small that, at an average distance x from Q, the electrostatic force \(\vec{F}\) on q₀ has a constant magnitude
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q_{0}}{x^{2}}\)
over the distance dx. The force \(\vec{F}_{\mathrm{ext}}\) by the external agent is equal and opposite to \(\vec{F}\) at every instant : \(\vec{F}_{\text {ext }}=-\vec{F}\)
Therefore, the infinitesimal work dW done by the external agent for the displacement \(\overrightarrow{d x}\) is

The total work done by the external agent in moving the test charge from A up to B is the line intergral of dW between the limits x = r₁ and x = r.

where ∆U = U_A – U_B is the change in the potential energy of the test charge in moving it from the point B to the point A. Choosing the potential energy of q0 to be zero when it is infinitely far away from Q, i.e., r₁ = ∞, its potential energy at a distance r from Q is
U(r) = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q_{0}}{r}\)
Thus, the potential energy of a system of two point charges q₁ and q₂, a distance r apart is
U(r) = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r}\)
[Note Taking U(∞) = 0 is often a convenient reference level in electrostatics, but in circuit analysis other reference levels are often more convenient.]

Question 11.
Explain the concept of electric potential difference and electric potential.
Answer:
A charge in an electric field possesses electric potential energy just as a particle in a gravitational field possesses gravitational potential energy. Consider a test charge q₀ in an electric field, moved very slowly by an external agent from point B where its electric potential energy is U_B to a point A where its electric potential energy is U_A.

The change in the potential energy, U_A – U_B is defined as the work W_{B → A} that must be done by an external agent to move the test charge from B to A against the electric force, keeping the charge always in equilibrium, i.-e., without accelerating the charge so as not to give it any kinetic energy.

W_{B → A} = ∆U = U_A – U_B
The potential difference ∆V = V_AB = V_A – V_B between two points A and B in electric field is
∆V = \(\frac{W_{\mathrm{B} \rightarrow \mathrm{A}}}{q_{0}}=\frac{\Delta U}{q_{0}}\)

Definition : The electric potential difference between two points in an electric field is defined as the work done per unit charge by an external agent against the electric force in moving an infinitesimal positive charge from one point to the other without acceleration.

We choose the potential energy U_B and potential V_B to be zero when the initial point B is infinitely far from the source charges which produce the field. Then, the work done per unit test charge by an external agent in bringing a test charge from infinity to a point is the electric potential at that point.
The electric potential at a distance r from a source charge,
V(r) = \(\frac{W_{\infty \rightarrow r}}{q_{0}}=\frac{U(r)}{q_{0}}\)
Definition : The electric potential V at a point in an electric field is defined as the work per unit charge that must be done by an external agent against the electric force to move without acceleration a sufficiently small positive test charge from infinity to the point of interest.

[Note : It is more correct to speak about potential difference ∆V between two points than just the potential V at a given point because the latter implies a choice of .zero reference potential. The choice is one of convenience and we may choose the zero reference potential for a point at infinity or at some other location convenient for the problem as is done for gravitational potential.]

Question 12.
State the SI unit and one non-SI unit of potential energy.
Answer:
SI unit of energy : the joule (J)
Non-SI unit of energy : the electronvolt (eV).

In electrostatics, one joule is the change in electric potential energy when a charge of one coulomb is moved through a potential difference of 1 volt. Therefore, 1J = 1C × 1V, so that 1V = 1J/C.

Question 13.
State the dimensions and SI unit of electric potential difference.
Answer:
Dimensions : [V] = \(\frac{[W]}{\left[q_{0}\right]}=\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{TI}]}\)
= [ML²T^-3I^-1]
SI unit : the volt (V) = the joule per coulomb (J/C).

Question 14.
If the work done in bringing a charge of 10^-18 C from infinity to point P is 2 × 10^-17 J, what is the electric potential at P?
Answer:
V = \(\frac{W}{q_{0}}=\frac{2 \times 10^{-17} \mathrm{~J}}{10^{-18} \mathrm{C}}\)
= 20 volts is the electric potential at P.

Question 15.
Explain and define the electronvolt.
OR
What is electronvolt?
Answer:
When an electric charge moves under the influence of an electric field, the work done by the field on the charge increases the kinetic energy of the charge as the electric force is a conservative force. Since the elementary charge e is widely encountered in atomic and nuclear physics, a convenient non-SI unit of energy used is the electronvolt.

Definition ; An electronvolt (symbol, eV) is the increase in the kinetic energy of a particle with a charge equal in magnitude to the elementary charge e when the particle is accelerated through a potential difference of one volt.
∆(KE) = qAV
where q is the charge and ∆V is the potential difference.
∴ 1 eV = e(1V)
= (1.602 × 10^-19 C) (1 J/C)
= 1.602 × 10^-19 J

[Notes : (1) SI prefixes are commonly used with the unit. Therefore, 1 keV = 10³ eV = 1.602 × 10^-16 J, 1 MeV = 10⁶ eV = 1.602 × 10^-13 J, etc. (2) In practice, it is not unusual to use the electronvolt as an energy unit in nonelectrical situations. For example, an air molecule at room temperature has a kinetic energy of about \(\frac{1}{40}\) eV, the electron mass is 511 keV / c₀², and the proton mass is 938 MeV/c₀², where c₀ is the speed of light in free space.]

Question 16.
Obtain the relation between the magnitude of electric field intensity and electric potential.
Answer:
Consider a test charge q₀ as it moves from point A to point B in an electric field. The electric force on q₀ at any point along the path is
\(\vec{F}=q_{0} \vec{E}\)
where \(\vec{E}\) is the field at that point.

The incremental work dW done by the field as q₀ undergoes a displacement \(\overrightarrow{d l}\) along the path is
dW = \(\vec{F} \cdot \overrightarrow{d l}\)
= q₀ \(\vec{E} \cdot \overrightarrow{d l}\) = q₀ E dl
In the process, the charge q₀ is moved from a higher potential to a lower potential, thereby losing potential energy. Therefore, the change in potential energy
dU = -dW = -q₀ Edl
By definition, the change in electric potential is dv

The quantity \(\frac{d V}{d l}\) is the rate at which the electric potential changes with distance and is called the electric potential gradient. The above equation thus shows that the magnitude of the electric field intensity at a point is equal to the negative of the potential gradient at that point.

[Note : (1) The negative sign shows that if we move in the direction of the electric field, the potential decreases. In the opposite direction, it increases. (2) If we draw equipotentials [see Unit 8.5] so that adjacent surfaces have equal potential differences, then in regions where the magnitude of \(\vec{E}\) is large, the equipotential surfaces are close together because the field does a relatively large amount of work on a test charge in a relatively small displacement. Conversely, in regions where the field s weaker, the equipotential surfaces are farther apart. (3) Potential gradient is an another name for electric field. (4) From the relation E = – dV/dx, we get another very common SI unit of electric field intensity, namely, the volt per metre (V/m).]

Question 17.
Define electric potential gradient.
Ans
Definition The rate of change of electric potential with distance in a specified direction is called the electric potential gradient in that direction.

Question 18.
Obtain an expression for the electric potential at a point due to an isolated point charge.
Answer:
Consider a point A at a distance r from a static point charge ± Q, as shown in below figure. To determine the electric potential at the point A (due to Q), imagine a test charge q₀ being moved from infinity
up to the point A without acceleration. Because the electric field of a point charge is not uniform, the force exerted by Q on q₀ increases as it approaches Q. We imagine the total displacement to be made up of a large number of infinitesimal displacements. \(\overrightarrow{d x}\). The distance dx is so small that, at an average distance x from Q, the electrostatic force \(\vec{F}\) on q₀ has a constant magnitude
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q_{0}}{x^{2}}\)
over the distance dx. The force F_ext by the external agent is equal and opposite to \(\vec{F}\) at every instant : \(\vec{F}_{\mathrm{ext}}=-\vec{F}\)

Therefore, the infinitesimal work dW done by the external agent for the displacement \(\overrightarrow{d x}\) is

The total work done by the external agent in moving the test charge from infinity up to the point P (from x = ∞ to x = r) is the integral of dW between the limits x = ∞ and x = r.
W = \(\int_{x=\infty}^{x=r} d W=\int_{\infty}^{r}\left(-\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q_{0}}{x^{2}}\right) d x\)

where ∆U = U_A – U_B is the change in the potential energy of the test charge in moving it from to the point A. Choosing the potential energy of q0 to be zero when it is infinitely far away from Q, its potential energy at a distance r from Q is
U_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q_{0}}{r}\)
Therefore, the electric potential at a distance r from Q is
V = \(\frac{U_{\mathrm{A}}}{q_{0}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r}\)
The above equation also gives the electric potential either outside or on the external surface of a spherically symmetric charge distribution,

[Notes: (I) A positive charge produces a positive electric potential. A negative charge produces a negative electric potential. (2) A negative electric potential means a positive charge would be attracted from a larger distance, since the potential is lower (more negative) than at larger distances. Conversely, a negative charge would be repelled, as expected. (3) Only differences between potentials at two points are physically significant. Potential at a point is ambiguous unless we specify which is the reference point. (4) Electric potential, like electric field intensity, is independent of the magnitude of the test charge that we use to define it.]

Question 19.
What is the electric potential at 10 Å from a point charge 10^-18 C in vacuum?
[\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ N∙m²/C²]
Answer:
V = \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{r}\)
= \(\frac{9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2} \times 10^{-18} \mathrm{C}}{10 \times 10^{-10} \mathrm{~m}}\)
= 9 volts is the required electric potential.

Question 20.
Obtain an expression for the electric potential at a point due to several point charges.
Answer:
Consider a point P at distances r₁, r₂, r₃, …, r_N from point charges q₁, q₂, q₃, ………, q_N, respectively. The electric potentials of P due to the individual charges are
V₁ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{r_{1}}\) , V₂ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}}{r_{2}}\) …………. , V_N = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{N}}{r_{N}}\)
Since potential is a scalar quantity, the potential of P due to all the charges is the algebraic sum of the potentials due to the individual charges.
∴ V = V₁ + V₁ + ………. + V_N
= \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{q_{1}}{r_{1}}+\frac{q_{2}}{r_{2}}+\ldots+\frac{q_{N}}{r_{N}}\right)\)
= \(\frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{N} \frac{q_{i}}{r_{i}}\)
[Note : Electric potential is a scalar quantity. To calculate the resultant potential due to two or more point charges, the potentials due to individual charges are added as simple scalars along with its sign, determined by the sign of the q that produces V.]

Question 21.
Derive an expression for the electric potential at a point due to a short electric dipole. Hence, write the expression for the electric potential at a point
(i) on the dipole axis (ii) on the dipole equator.
OR
Derive an expression for the electric potential at a point due to an electric dipole.
Answer:
Consider an electric dipole AB of dipole length 21 and point charges + q and – q. Its electric dipole moment \(\vec{p}\) has magnitude p = 2ql. Let P be a point at a distance r from O, the centre of the dipole, in a direction θ with the dipole axis, as shown in below figure. Let AP = r₁ and BP = r₂.

The electric potential at P due to the charge +q is
V₁ = +\(+\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{1}}\) …………….. (1)
and that due to the charge -q is
V₂ = \(-\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{2}}\) …………….. (2)
Method 1

In the figure, PA₁ = PA = r₁ and PB₁ = PB = r₂.
For short dipole (2l << r), ∠OA₁A ≅ ∠OB₁B ≅ 90°.
Hence, in the right angled ∆s OA₁A and OB₁B,
OA₁ = OB₁ = l cos θ
∴ r₂ – r₁ = PA₁ – PB₁ = A₁B₁ = 2l cos θ
Also, r₁r₂ = PA₁ × PB₂ = (PO + OA₁)(PO – OB₁)
= (r + l cos θ)(r – l cos θ)
= l² – l² cos² θ
= r² (∵ l << r) …………… (4)

Method 2:
From △PAA₁, by cosine rule,


This is the required expression.

Particular cases :
(i) At a point on the dipole axis, θ = 0° (nearer to the charge + q) or 180° (nearer to the charge – q).
∴ cos θ = ±1
∴ V_axis = \(\pm \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p}{r^{2}}\)

(ii) At a point on the dipole equator, θ = 90° or 270°.
∴ Cos θ = 0 ∴ V_equator = 0

[Note : Since V_equator = 0, the equatorial plane of a dipole is an equipotential plane of electric potential equal to zero. No work is required to move a charge anywhere in the equatorial plane.]

Question 22.
What is the electric potential at a point on the axis of a short electric dipole of moment 27 Cm if the point is at 0.5 m from the centre of the dipole and is located in vacuum? [\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ N∙m²/C²]
Answer:
V = \(\pm \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p}{r^{2}}\)
= \(\pm \frac{\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)\left(10^{-27} \mathrm{C} \cdot \mathrm{m}\right)}{(0.5 \mathrm{~m})^{2}}\)
= ±3.6 × 10^-17 V
is the required electric potential.

Question 23.
Distinguish between electric field intensity and electric potential.
Answer:

Electric field intensity	Electric potential
1. Electric field intensity is a vector quantity associated with an electric field.	1. Electric potential is a scalar quantity associated with an electric field.
2. It is the electric force per unit positive charge placed at a point in an electric field.	2. It is the work per unit charge which must be done by an external agent against the electric force to bring an infinitesimal posi­tive charge from infinity to a given point in an electric field, without acceleration.
3. Its SI unit is the newton per coulomb or the volt per metre.	3. Its SI unit is the volt.

Question 24.
Distinguish between the volt and the electron volt.
Answer:

Volt	Electronvolt
1. The volt is the SI unit of electric potential (or poten-tial difference).	1. The electronvolt is a non- SI unit of energy.
2. If one joule per coulomb of work is done by an external agent against the electric force in moving an infini-tesimal charge from one point to another keeping the charge in equilibrium, the potential difference between the two points is called one volt.	2. It is the increase in the kinetic energy of a particle carrying a charge equal to the elementary charge e when it is accelerated through a potential differ¬ence of one volt.
3. 1 V = 1 J/C.	3. 1 eV = 1.602 × 10-19 J.

25. Solve the following

[Data : [\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ N∙m²/C²]
Question 1.
A helium nucleus carries a charge of + 2e, where e is the elementary charge. Find the electric potential at 10^-10 m from the helium nucleus.
[e = 1.6 × 10^-19 C]
Solution:
Data : If q is the charge on helium nucleus,
q = +2e = 2 × 1.6 × 10^-19 C,r = 10^-10m,
1/4πε₀ = 9 × 10⁹ N∙m²/C²
The electric potential,
V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\)
= \(\frac{2\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)}{10^{-10} \mathrm{~m}}\)
= 28.8V

Question 2.
Determine the electric potential at the midpoint of the line joining two charges 2 × 10^-6 C and -1 × 10^-6 C placed in vacuum 10cm apart.
Solution:
Data: q₁ = 2 × 10^-6 C, q₂ = -1 × 10^-6 C,
r = \(\frac{10 \mathrm{~cm}}{2}\) = 5cm = 0.05m,
1/4πε₀ = 9 × 10⁹ N∙m²/C²
The electric potential at a distance r from a charge q is
V = \(\frac{q}{4 \pi \varepsilon_{0} r}\)
Since potential is a scalar quantity, the total electric potential at the midpoint is
V = V₁ + V₂ = \(\frac{1}{4 \pi \varepsilon_{0}}\) (q₁ + q₂)
= \(\frac{\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)}{0.05 \mathrm{~m}}\) (2 – 1) × 10^-6 C
= 1.8 × 10⁵ V

Question 3.
The electric field and electric potential at a certain point due to a point charge in vacuum are 9000 V/m and 18000 V, respectively. Find the distance of the point from the charge and the magnitude of the charge.
Solution:
Data: E = 9000 V/m, V = 18000 V,
1/4πε₀ = 9 × 10⁹ N∙m²/C²
E = \(\frac{q}{4 \pi \varepsilon_{0} r^{2}}\), V = \(\frac{q}{4 \pi \varepsilon_{0} r}\)
\(\frac{V}{E}\) = r
∴ The distance, r = \(\frac{18000 \mathrm{~V}}{9000 \mathrm{~V} / \mathrm{m}}\) = 2 m
∴ The magnitude of the charge is

Question 4.
What is the electric potential at the centre of a square of side 1 m if point charges 1 × 10^-8 C, -2 × 10^-8 C, 3 × 10^-8 C and 2 × 10^-8 C are placed at the corners of the square?
Solution:
Data: q₁ = 1 × 10^-8 C, q₂ = -2 × 10^-8 C, q₃ = 3 × 10^-8 C, q₄ = 2 × 10^-8 C,
1/4πε₀ = 9 × 10⁹ N∙m²/C²
The distance of the point of intersection O of the diagonals, from each charge is \(\sqrt {2}\) / 2 = 1/\(\sqrt {2}\) m.
∴ r = 1/\(\sqrt {2}\) m

The potential at a distance r from a charge q is
V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\)
As potential is a scalar quantity, the total electric potential at O is
V = V₁ + V₂ + V₃ + V₄
= \(\frac{1}{4 \pi \varepsilon_{0} r}\) (q₁ + Vq₂ + q₃ + q₄)
= \(\frac{\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)}{(1 / \sqrt{2} \mathrm{~m})}\) [(1 – 2 + 3 + 2) × 10^-8 C]
= 360\(\sqrt {2}\) = 509.2 V

Question 5.
The electric potential due to a dipolar molecule of electric dipole moment 6 × 10^-30 A∙m² at a point along the axis of the dipole is 1 V. Find the distance of the point from the centre of the dipole.
Solution:
Data : p = 6 × 10^-30 A∙m², V = 1 V,
θ = 0° (axial point), 1/4πε₀ = 9 × 10⁹ N∙m²/C²
Electric potential,

Question 6.
Two charged particles, carrying – 2 pC each, are held in place 10 cm apart. A point B is at distance of 18 cm from both.
(a) Calculate the electric potential at point B.
(b) A third charged particle, of mass 10^-15 kg and carrying charge – 1 pC, is released from rest at point B. What is its speed when it is far from the two fixed charged particles?
Solution:
Data : q₁ = q₂ = q = – 2 × 10^-12 C,
r₁ = r₂ = r = 18 cm = 0.18m,. q₃ = – 1 × 10^-12 C,
m₃ = 10^-15 kg
The electric potential at B,
V_B = V₁ + V₂ = 2(\(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\))
= 2(9 × 10⁹)(\(\frac{-2 \times 10^{-12}}{0.18}\)) = – 0.2 V

(b) By definition, the potential energy of an electric charge at infinity, i.e., far away from other charges, is U_∞ = 0. To find the speed of the third charged particle at infinity, we use the principle of conservation of energy.
K_B + U_B = K_∞ + U_∞
where the KE of the particle at B, K_B = 0, since it is released from rest. The PE,
U_B = q₃V_B = (-1 × 10^-12)(- 0.2) = 2 × 10^-13 J

∴ The KE of the particle at infinity,
k_∞ = \(\frac{1}{2}\) mv² = U_B = 2 × 10^-13 J
∴ v = \(\sqrt{\frac{2 K_{\infty}}{m}}=\sqrt{\frac{2\left(2 \times 10^{-13}\right)}{10^{-15}}}\) = 20 m/s
This gives the required speed.

[Note: The PE of the third charge at Bis +2 × 10^-13 J, while at inifinity it is zero. All of the initial electrical PE is converted to KE because of the positive work done on it by the repulsive field due to the other two charges. The negatively charged third particle gains kinetic energy when it moves from a lower-potential point to a higher- potential point, in this case from V_B = – 0.2 V to V_∞ = 0. Also note that the net force on the third negatively charged particle decreases as it moves away from point B. Its acceleration is not constant, so kinematical equations cannot be used to find its final speed. Hence, we have used the principle of conservation of energy.]

Question 7.
A proton is released from rest in vacuum in a uniform electric field of intensity 100 V/m. What is its speed after it has travelled a distance of 1 m ? [m_p = 1.67 × 10^-27 kg, 1 eV = 1.6 × 10^-19J]
Solution :
Data : u = 0 m/s, E = 100 V/m, l = 1 m, m_p = 1.67 × 10^-27 kg, 1 eV = 1.6 × 10^-19 C
In a uniform electric field \(\vec{E}\), the potential difference between two points a distance l apart (along \(\vec{E}\)) is
∆V = El = (100 V/m) (1 m) = 100 V
The change in the kinetic energy of the proton is
∆KE = eA V = e (100 V) = 100 eV
= 100 × 1.6 × 10^-19
= 1.6 × 10^-17 J
Since the proton starts from rest, the initial kinetic, energy is zero. Therefore, the change in kinetic energy equals the final kinetic energy \(\frac{1}{2}\) m_pv².
∴ \(\frac{1}{2}\) m_pv² = 1.6 × 10^-17 J
∴ v² = \(\frac{2\left(1.6 \times 10^{-17} \mathrm{~J}\right)}{1.67 \times 10^{-27} \mathrm{~kg}}\)
= 1.916 × 10¹⁰ (m/s)²
∴ v = 1.384 × 10⁵ m/s
The speed of the proton after it has travelled a distance of 1 m is 1.384 × 10⁵ m/s.

Question 8.
A particle carrying 5 electrons starts from rest and is accelerated through a potential difference of 8900 V. Calculate the KE acquired by it in MeV. [Charge on electron = 1.6 × 10^-19 C]
Solution :
Data : q = 5e, u = 0, V = 8900 V, e = 1.6 × 10^-19 C
q = 5(1.6 × 10^-19 C) = 8 × 10^-19 C
Initial KE = KE_i = \(\frac{1}{2}\) mu² = 0
∴ ∆KE = KE_f – KE_i = KE_f
∆KE = qV
∴ The final KE, KE_f = qV
= (8 × 10^-19 C) (8900 V)
= 7.12 × 10^-15 J
= \(\frac{7.12 \times 10^{-15}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 4.45 × 10⁴ eV
= (4.45 × 10^-2) × 10⁶ eV
= 4.45 × 10^-2 MeV

Question 9.
A proton is accelerated from rest through a potential difference of 500 volts. Find its final momentum. [m_p = 1.67 × 10^-27 kg, e = 1.6 × 10^-19 C]
Solution:
Data : m_p = 1.67 × 10^-27 kg, e = 1.6 × 10^-19 C, u = 0, V = 500 V
Initial KE, KE; = \(\frac{1}{2}\) m_pu² = 0
∴ ∆KE = KE_f – KE_i = KE_f
∆KE = qV
∴ KE_f = qV KE_f = \(\frac{1}{2}\) m_pv² = \(\frac{p_{\mathrm{f}}^{2}}{2 m_{\mathrm{p}}}\)
where p_f = m_pv ≡ the magnitude of the final momentum of the proton.
∴ P_f² = 2 m_pqV
∴ P_f = \(\sqrt{2 m_{\mathrm{p}} q V}\)
= \(\sqrt{2\left(1.67 \times 10^{-27} \mathrm{~kg}\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)(500 \mathrm{~V})}\)
= 5.169 × 10^-22 kg∙m/s
The momentum is directed along the applied electric field.

Question 10.
A proton and an α-particle are accelerated from rest through the same potential difference. Compare their final speeds. Charge on an α-particle = 2 × charge on a proton, mass of an α-particle = 4 × mass of a proton.
Solution:
Lution: Let q₁ = charge on an α-partic1e, q₂ = charge on a proton, m₁ = mass of an α-particle, m₂ = mass of a proton, v₁ = final speed of the α-particle, v₂ = final speed of the proton

Question 26.
What do you mean by an equipotential surface? What is the shape of equipotential surfaces for the special case of (i) a uniform field (ii) a single point charge?
Answer:
An equipotential surface, in a region where an electric field is present, is a three-dimensional surface on which the electric potential is the same at every point.

Electric field lines and equipotential surfaces are always mutually perpendicular. In a diagram, only a few representative equipotentials are shown, usually with equal potential differences between adjacent surfaces. Also, equipotential surfaces for different potentials do not touch or intersect since a point cannot be at two electric potentials simultaneously.

For the special case of a uniform field, in which the field lines are equally-spaced parallel lines, the equipotentials are parallel planes perpendicular to the field lines, from figure (a).

For equal potential differences between adjacent planes, these equipotentials are equally spaced. For the special case of a single point charge, for which the field lines are radial, the equipotentials are concentric spheres centred on the point charge, from figure (b).

For a given point charge q.
V = \(\frac{C}{r}\)
where C = \(\frac{q}{4 \pi \varepsilon_{0}}\) is a constant. Since \(\frac{1}{r}\) is not a linear function of r, equipotentials with equal potential differences between adjacent surfaces are not evenly spaced in radius.

Question 27.
Electric field lines and equipotential surfaces are always mutually perpendicular. Explain.
Answer:
If a test charge q₀ is moved on an equipotential surface of potential V, the electric potential energy U = q₀V remains constant. Because U does not change as q₀ is moved, the work done by the electric field on q₀ must be zero. If \(\vec{E}\) is the electric field on the surface,

Hence, the electric force q₀\(\vec{E}\) is always perpendicular to the displacement of a charge moving on an equilateral surface. Thus, electric field lines and equipotential surfaces are always mutually perpendicular.

Note that if \(\vec{E}\) is not perpendicular to a equipotential surface everywhere, it would have a component E_|| along the surface, so that for a displacement dx between two points on the surface, the work done dW = E_||dx ≠ 0. This would imply a potential difference between the two points which contradicts the definition of a equipotential surface.

Question 28.
Draw a diagram showing the equipotential surfaces and electric field lines in the plane of (i) an electric dipole (ii) a system of two equal positive charges.
Answer:


[Note: At each crossing of an equipotential and a field line, the two are perpendicular.]

Question 29.
What can you say about the direction of the electric field on the surface (just outside) of a charged conductor in an electrostatic situation?
Answer:
When all charges on a conductor are at rest, the tangential component of the electric field \(\vec{E}\) is zero at every point on the surface (just outside) of a conductor; otherwise, charges would move around on the surface. If follows that, in an electrostatic situation, the electric field just outside a conductor must be perpendicular to the surface at every point and a conducting surface is always an equipotential surface.

Question 30.
What are the electric potentials outside and inside a charged spherical conductor in electro static equilibrium?
Answer:
Consider a spherical conductor of radius R and static charge q. By Gauss’s law, the electric field due to the charged conducting sphere is
\(\vec{E}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}} \hat{r}\) (r ≥ R)
= 0 (r < R)
because for r < R, charge enclosed by a Gaussian surface inside the sphere is zero but in the region r ≥ R, outside, the charged sphere is identical to a point charge at the centre of the sphere.

Consequently, since V(r) = \(-\int \vec{E} \cdot \overrightarrow{d r}\), the electric potential outside the sphere must be the same as that of an isolated point charge q located a r = 0.
∴ V(r) = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\) (r ≥ R)

Thus, a conducting sphere in electrostatic equilibrium is a spherical equipotential surface at potential V(R) and in the region r ≥ R, the equipotentials are concentric spheres.

Inside the sphere, r < R, E = 0, so V(r) is constant in this region. Since V(R) = q/4πε₀R,

Question 31.
Draw diagrams showing the equipotential sur faces and electric field lines (a) within a charged parallel-plate capacitor (a pair of parallel metal plates with charges of equal magnitude and opposite sign)
OR
(b) if one of the plates of the capacitor is replaced by a charged spherical conductor.
Answer:
(a) A pair of charged parallel metal plates sets up a uniform electric field between the plates, away from its edges, as shown by their even spacing. The field is perpendicular to the plates, in the direction from the positive plate toward the negative plate. Conductors are equipotential surfaces, so the negative plate is an equipotential surface with potential taken as zero and the positive plate is an equipotential surface with potential = V. The equipotential surfaces between the plates are parallel to the plates. Electric field lines and equipotential surfaces are perpendicular to each other. Also, because the electric field is uniform between the plates, equipotential surfaces representing equal potential differences are equally spaced.

Question 32.
What are the advantages of using electrostatic potential?
Answer:
The electrostatic potential at each point in space in the vicinity of the source charges represents a scalar field.

The advantages of electrostatic potential field associated with a given distribution of charges are as follows:

• If we know the potential difference between any two points, we can easily obtain the change in potential energy and the work done when a charge placed in the field moves between these two points.
• Electric field is a vector field. Electrostatic potential being a scalar field, the potential at any point due to several charges is simply the algebraic sum of the potentials due to the individual charges.
• The construction of equipotential surfaces helps to visualize the electric field pattern.
• It is possible to calculate the electric field \(\vec{E}\) from the scalar potential field function V (by differentiating V with respect to the space coordinates.)

Question 33.
Derive an expression for the potential energy of a system of two point charges.
Answer:
The electric potential energy of a system of point charges at rest in free space is defined as the work done by an external agent against the electric force in assembling the charges by bringing them from infinity to their locations in the configuration, always keeping the charges in equilibrium.

Consider assembling a system of two point charges q₁ and q₂ at points A and B, respectively, in a region free of external electric field. Let \(\vec{r}_{1}\) and \(\vec{r}_{2}\) be the position vectors of A and B, respectively,, with respect to an arbitrary reference frame.

In the absence of charge q₂, since there is no external electric field in the region, no work is done in bringing the first charge q₁ from infinity to A, so W₁ = 0. Subsequently, due to q₁ the potential at B is
V_B = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{r_{21}}\)
where r₂₁ = \(\left|\vec{r}_{21}\right|, \vec{r}_{21}=\vec{r}_{2}-\vec{r}_{1}\) being the position vector of B with respect to A. Consequently, the work done by an external agent in bringing q₂ from infinity to B in the electric field of q₁ is
W₂ = V_B ∙ q₂ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Hence, the total work done is
W = W₁ + W₂ = 0 + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
= \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Since the charges were always kept in equilibrium, the change in the potential energy U_f – U_i equals W.

Since the charges were brought from infinity where their potential energy is assumed to be zero, U_i = 0. Therefore, the potential energy of the system of two point charges is
U = U_f = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)

Question 34.
A system consisting of a charged spherical shell and an electron has negative electric potential energy U = -15 × 10^-20 J, with U(∞) = 0.
(a) What is the sign of the charge on the shell?
(b) If the electron is replaced by a proton, what would be the electric potential energy of the new system?
Answer:
A charged spherical conductor is equivalent to a point charge at its centre. For U(∞) = 0, the potential energy of two point charges q₁ and q₂ a distance r₂₁ apart is
U = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Since the FE of the charged shell and electron system is negative, the shell must be positively charged, electron being negatively charged.

If the electron is replaced by a proton, the PE of the new system would be positive equal to U’ = ±15 × 10^-20 J.

Question 35.
Obtain an expression for the potential energy of a configuration of N point charges.
Answer:
Consider assembling a configuration of N point charges q₁, q₂, q₃, …………., q at points A, B, C, D, …, respectively, in a region free of external electric field. Let \(\overrightarrow{r_{1}}, \overrightarrow{r_{2}}, \overrightarrow{r_{3}}, \ldots, \overrightarrow{r_{N}}\) be the position vectors of the points A, B, C, D, … etc., respectively, with respect to an arbitrary reference frame.

No work is done in bringing the first charge q₁ from infinity to point A, so W₁ = 0. Subsequently, the potential at B is
V_B = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{r_{21}}\)
where r₂₁ = \(\left|\vec{r}_{21}\right|, \vec{r}_{21}=\vec{r}_{2}-\vec{r}_{1}\) being the position vector of B with respect to A. Consequently, the work done by an external agent in bringing q₂ from infinity, to B in the electric field of q₁ is
W₂ = V_B . q₂
= \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Subsequently, the potential at C is
V_C = V₁ + V₂
where V₁ and V₂ are the potentials due to q₁ and q₂.

Consequently, the work done by the external agent in bringing the third charge q₃ from infinity to C in the electric fields of q₁ and q₂ is
W₃ = V_C . q₃
= \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{q_{1} q_{3}}{r_{31}}+\frac{q_{2} q_{3}}{r_{32}}\right)\)
Now, the potential at D is
V_D = V₁ + V₂ + V₃
= \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{q_{1}}{r_{41}}+\frac{q_{2}}{r_{42}}+\frac{q_{3}}{r_{43}}\right)\)

Since the charges were brought from infinity where the potential energy is assumed to be zero, U_i = 0. Therefore, the potential energy of the con figuration of N point charges is

Question 36.
What is the potential energy of a point charge in an external electric field?
Answer:
Consider a charge q placed in an external electric field at a point whose position vector with respect to an arbitrary reference frame is \(\vec{r}\). If V(\(\vec{r}\)) is the potential of the point, with respect to an arbitrary reference zero at infinity, then the potential energy of the charge q at the point is
U(\(\vec{r}\)) = qV(\(\vec{r}\))
where it is assumed that q is sufficiently small and does not significantly distort the electric field and the potential at the point.

Question 37.
Derive an expression for the potential energy of a system of two point charges in an external field.
Answer:
Consider assembling a system of two point charges q₁ and q₂ at points A and B, respectively, in a region of external electric field. Let \(\vec{r}_{1}\) and \(\vec{r}_{2}\) be the position vectors of A and B, respectively, with respect to an arbitrary reference frame. \(\vec{r}_{21}=\overrightarrow{r_{2}}-\overrightarrow{r_{1}}\) is the position vector of B with respect to A. Let V₁ and V₂ be the electric potentials of A and B due to the external field.

The work done in bringing the charge q_1,from infinity to A against the electric force of the external field is
W₁ = q₁ V₁
Subsequently, the electric potential at B is
V_B = V₂ + V’_{due t0 q1}
= V₂ + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{r_{21}}\)

Consequently, the work done in bringing the second charge q₂ from infinity to B is
W₂ = q₂V_B
= q₂V₂ + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Hence, the total work done by an external agent in assembling the two point charges in a region of external electric field is
W = W₁ + W₂
= q₁V₁ + q₂V₂ + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
Since the charges were always kept in equilibrium, the change in the potential energy of the system U_f – U_i = W. Also, since the charges were brought from infinity where their potential energy is assumed to be zero, U_i = 0. Therefore, the potential energy of the system of two charges in an external field is
U = U_f = q₁V₁ + q₂V₂ + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)

Question 38
Derive an expression for the electric potential energy of an electric dipole in a uniform electric field.
OR
Derive an expression for the total work done in rotating an electric dipole through an angle θ in a uniform electric field.
Answer:
Consider an electric dipole of dipole moment \(\vec{p}\) placed in a uniform electric field \(\vec{E}\) making an
angle Φ with \(\vec{E}\). The torque \(\vec{\tau}=\vec{p} \times \vec{E}\) tends to rotate the dipole and align it with \(\vec{E}\).

Suppose an external torque \(\vec{\tau}_{\text {ext }}\), equal in magnitude and opposite in direction to \(\vec{\tau}\), is applied to rotate the dipole through an infinitesimal angular displacement dΦ, always keeping the dipole in equilibrium.

The work done by this torque is
dW = τ_ext dΦ
= p E sin Φ dΦ
In a finite angular displacement from θ₀ to θ, the total work done on the dipole by the external agent is

If the dipole was initially parallel to \(\vec{E}\), θ₀ = 0 and cos θ₀ = 1.
∴ W = pE (1 – cos θ) …………. (2)
If the dipole was initially parallel to \(\vec{E}\), its potential energy U₀ = – pE is minimum (more negative). If we arbitrarily assign U₀ = 0 to the minimum of potential energy, the potential energy for the system for an inclination θ is
U_θ = – pEcos θ = – \(\vec{p} \cdot \vec{E}\)
This is the required expression.

39. Solve the following

Question 1.
Consider a point charge q = 1.5 × 10^-8 C. What is the radius of an equipotential surface having a potential of 30V?
Solution:
Data: q = 1.5 × 10^-8 C,
1/4πε₀ = 9 × 10⁹ N∙m²/C², V = 30 V
An equipotential surface surrounding an isolated point charge is a sphere centred on the charge. Let r be the radius of such an equipotential for which V = 30 V.

Question 2.
Two charged spherical conductors, of radii R₁ and R₂ and surface charge densities σ₁ and σ₂, are connected by a thin conducting wire. Except for this connecting wire, the spheres are sufficiently separated to be considered as isolated. Show that σ₁R₁ = σ₂R₂.
Solution:
The electrical potential at the surface of an isolated, charged conducting sphere of radius R is

Since the spherical conductors are connected by a conducting wire, the system must be equipotential, i.e.,
V₁ = V₂.
∴ \(\frac{\sigma_{1} R_{1}}{\varepsilon_{0}}=\frac{\sigma_{2} R_{2}}{\varepsilon_{0}}\)
∴ σ₁R₁ = σ₂R₂ as required

[Note : Although the above connected system is different from a typical conductor with a variable radius of curvature, the above relation qualitatively indicates how charge density varies over the surface of a conductor of arbitrary shape. The equation indicates that σ and E are small where the radius of curvature is large. Conversely, σ and E are higher at locations with a small radius of curvature. A practical application of this phenomenon is the lightning rod.]

Question 3.
Two equipotential surfaces A and B in a uniform electric field, with V_A = 50 V and V_B = 30 V, are 10 cm apart. Two point charges, q₁ = 3 nC and q₂ = 5 nC, are placed on A and B, respectively.
(i) What is the magnitude of the electric field?
(ii) 1f the line joining the two charges is parallel to the field, what is the total work done in assembling the two charges?
Solution:
Data: V_A = 50 V, V_B = 30 V, l = 10 cm = 0.1 m,
q₁ = 3 nC = 3 × 10^-9 C, q₂ = 5 nC = 5 × 10^-9 C,
1/4πε₀ = 9 × 10⁹ N∙m²/C²

Since the line joining the two charges is parallel to the fle1d,\(\overrightarrow{r_{21}}\) = l = 0.1 m.

The work done by an external agent in assembling the two charges by bringing them from infinity is
W = q₁V_A + q₂V_B + \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}}\)
=(3 × 10^-9 C)(50 V) + (5 × 10^-9 C)(30 V) + (9 × 10⁹ N∙m²/C²) \(\frac{\left(3 \times 10^{-9} \mathrm{C}\right)\left(5 \times 10^{-9} \mathrm{C}\right)}{0.1 \mathrm{~m}}\)
= 1.5 × 10^-7 + 1.5 × 10^-7 + 13.5 × 10^-7
= 16.5 × 10^-7 = 1.65 × 10^-6 J (= 1.65 μJ)

Question 4.
An electron is circulating around the nucleus of an H-atom in a circular orbit of radius 5.3 × 10^-11 m Calculate the electric potential energy of the atom in eV.
Solution:
Data: e = 1.6 × 10^-19 C, r = 5.3 × 10^-11 m,
1/4πε₀ = 9 × 10⁹ N∙m²/C²
The charge of the single proton in the nucleus of a hydrogen atom, q₁ = + e = 1.6 × 10^-19 C
The charge on the electron,
q₂ = -e = -1.6 × 10^-19 C
The potential energy of an H-atom,

Question 5.
A proton is to be suspended in vacuum between two parallel plates separated by 1 mm. Find (i) the electric field required (ii) the potential difference between the plates corresponding to the desired field. [m_p = 1.67 × 10^-27 kg]
Solution:
The gravitational force on the proton should be balanced by the force due to the electric field. So, the electric field must be directed up; the upper plate should be at negative potential and the lower plate at positive potential, as shown in below figure.

For uniform field,
E = \(\frac{V}{d}\), where V = potential difference between the plates and d = distance between the plates.
The potential difference,
V = Ed = (1.023 × 10^-7 V/m)(10^-3 m)
= 1.023 × 10^-10 V

Question 6.
Two point charges, q₁ = – 1 μC and q₂ = +1 μC, are located in vacuum on the x-axis at x = 0 and x = a, respectively. (i) Find the potential energy of the system. (ii) If a third point charge q₃ = + 1 μC is brought from infinity to x = 2a, find the total potential energy of the system of the three charges. (iii) What work has been done by an external agent to bring in the third charge? Take a = 10 cm.
Solution:
Data:q1 = – 1 μC = – 1 × 10^-6 C, q₂ = q₃ = 1 μC
= 1 × 10^-6 C, r₂₁ = a = 0.1 m, r₃₁ = 2a = 0.2 m,
r₃₂ = a = 0.1 m, 1/4πε₀ = 9 × 10⁹ N∙m²/C²

(ii) The total potential energy of the system of three charges,

(iii) Additional work done in bringing the third charge
= U₃ – U₂
= (- 4.5 + 9) × 10^-2 J
= 4.5 × 10^-2 J

Question 7.
What is the electric potential energy of the following charge configuration?Take q₁ = +1 × 10^-8 C, q₂ = – 2 × 10^-8 C, q₃ = +3 × 10^-8 C, q₄ = 2 × 10^-8 C and a = 1 m. Assume the charges to be in vacuum.

Solution:
Data : q₁ = +1 × 10^-8 C, q₂ = – 2 × 10^-8 C, q₃ = +3 × 10^-8 C, q₄ = 2 × 10^-8 C
a = 1 m, 1/4πε₀ = 9 × 10⁹ N∙m²/C²
r₂₁ = r₄₁ = r₃₂ = r₄₃ = 1 m, r₃₁ = r₄₂ = \(\sqrt {2}\) m
The electric potential energy of the given configuration of our charges is

Question 8.
An electric dipole has two point charges of 1.6 × 10^-19 C and -1.6 × 10^-19 C separated by 2 A. ¡f the dipole is placed in a uniform electric field of 10 N/C, making an angle of 300 with the dipole moment, find (i) the magnitude of the torque acting on the dipole due to the field (ii) the potential energy of the dipole.
Solution:
Data: q = 1.6 × 10^-19 C, 2l = 2Å = 2 × 10^-10 m,
E = 10 N/C, θ = 30°
Electric dipole moment,
p = 2ql = q (2l) = (1.6 × 10^-19 C)(2 × 10^-10 m)
= 3.2 × 10^-29 A∙m²
(j) The magnitude of the torque,
τ = pE sin θ
= (3.2 × 10^-29 Am²)(10 N/C) sin 30°
= 3.2 × 10^-28 × 0.5
= 1.6 × 10^-28 N∙m

(ii) The potential energy,
U = -pE cosθ
= -(3.2 × 10^-29 A∙m²)(10 N/C) cos30°
= -3.2 × 10^-28 × 0.866
= -2.771 × 10^-28 J

Question 9.
A water molecule is made up of two hydrogen atoms and one oxygen atom, with a total of 10 electrons and 10 protons. The molecule is modelled as a dipole with an effective separation d = 3.9 × 10^-12 m between its positive and negative particles. What is the electric potential energy stored in the dipole? What does the sign of your answer mean?
Solution :

The minus sign means that in bringing the particles together horn infinity, energy is transferred from the system to the surrounding and it would take positive work by an external agent to separate the charged particles of the dipole.

Question 10.
An electric dipole consists of two unlike charges of magnitude 2 × 10^-6 C separated by 4 cm. The dipole is placed in an external field of 10⁵ N/C. Find the work done by an external agent to turn the dipole through 180°.
Solution:
Data: q = 2 × 10^-6, 2l = 4cm = 4 × 10^-2 m.
E = 10⁵ N/C, θ = 180° + θ₀
Let us assume the dipole is initially aligned parallel to the field, i.e., θ₀ = 0.
Then, θ = 180°.
The work done by an external agent,
W = pE(1 – cos θ)
= q (2l) E(1 – cos 180°)
= (2 × 10^-6 C)(4 × 10^-2 m)(10⁵ N/C) [1 – (-1)]
= 16 × 10^-3 J

Question 11.
An electric dipole has opposite charges of magnitude 2 × 10^-15 C separated by 0.2 mm. It is placed in a uniform electric field of 10³ N/C. (i) Find the magnitude of the dipole moment. (ii) What is the torque on the dipole when the dipole moment is at 60° with respect to the field?
Solution:
Data : q = 2 × 10^-15 C, 2l = 0.2 mm = 2 × 10^-4 m,
E = 10³ N/C, θ = 60°
(i) The magnitude of the dipole moment is
V = q (2l)
= (2 × 10^-15 C) (2 × 10^-4 m)
= 4 × 10^-19 C∙m

(ii) The torque on the dipole is
τ = pE sin θ
= (4 × 10^-19 C∙m) (10³ N/C) sin 60°
= 4 × 10^-16 × 0.866 = 3.46 × 10^-16 N∙m

Question 40.
What constitutes an electric shock?
Answer:
Living organisms are electrical conductors. Electric shock is the result of the passage of electric current through our body. During electric shock we experience an extreme stimulation of nerves and muscles. It needs a minimum of 1 mA of electric current to pass through our body for us to experience a shock.

Question 41.
Birds perched on electrical transmission wires do not suffer electric shock, but if a person touches both the wires at once receives a tremendous shock. Why?
Answer:
The danger of electric shock arises not from mere contact with a live wire but rather from simultaneous contact with a live wire and another body or wire at a different potential so that our body provides a conducting path between the two and a current passes through our body.

Touching a single wire by the birds does not result in a current through their bodies because then the electric circuit is not complete. But if a person touches two wires at different potentials at once, or if a bare-footed person touches the live wire only, the electric circuit is complete and the person receives an electric shock. In the latter case, the current from the wire passes to the Earth through the body.

[Notes : (1) We must not touch any electric appliance. when bare-footed or with wet hands. When a bare-footed person touches a short-circuited electric appliance, the current from such an appliance goes to the Earth through his body, thus completing the circuit. When our skin is dry, the electrical resistance of our body is about 50 kΩ, a wet skin lowers the resistance to 10 kΩ. It needs a minimum of 1 mA of electric current to pass through our body for us to experience a shock. Thus, when dry, it needs at least 50 V potential difference to get a shock, but only 10 V is enough when wet. (2) The Earth often serves as a charge reservoir known as a ground. A ground can accept or provide electrons freely, and it is so large that the addition or subtraction of electrons has a negligible effect on it. So, the ground remains essentially neutral at all times. When something is connected to the ground by a conductor, we say that it is earthed or grounded.]

Question 42.
State the properties of conductors in electrostatic conditions.
Answer:
Properties of a charged conductor in electrostatic conditions :

1. Net electric field inside the conductor is zero.
2. Net electric field just outside the conductor is normal to its surface at every point.
3. Electric potential inside the conductor is constant and equal to that on its surface.
4. Excess charges reside only on the surface of the conductor but, for a conductor of arbitrary shape, the surface charge density at a point is inversely proportional to the local curvature of the surface.

Question 43.
Explain electrostatic shielding. What is a Faraday cage ?
Answer:
When an isolated conductor, uncharged or charged, is placed in an external electric field, as in figure, all points of the conductor come to the same potential. The free conduction electrons in the conductor distribute themselves on the surface, leaving a net positive charge on some regions of the surface and a net negative charge on other regions.

This charge distribution causes an additional electric field at interior points such that the total field at every point inside is zero.

The charge distribution on the conductor is such that the net electric field at all points on the surface to be perpendicular to the surface, thereby altering the shapes of the field lines near the conductor.

The use of a conducting box to protect sensitive instruments from stray electric fields, or the use of a conducting wire cage to protect a person near a high-voltage installation or from lightning strike, is called electrostatic shielding. The hollow conductor or the conducting wire cage that shields its interior from external electric fields is called a Faraday cage or Faraday shield. A Faraday cage, made from a contiguous metal sheet or from a fine metal mesh, is used to shield its content or occupant from static and nonstatic electric fields.

Question 44.
Aran and Careena were driving in the countryside in a car when they get caught in a thunderstorm. Arun is worried that if lightning hits the car, the petrol tank may explode. Careena thinks they should wait out the storm in the car. Is Careena right ?
Answer:
In circumstances where there is danger of lightning strikes, it is wise to enclose oneself in a cavity inside a conducting shell, where the electric field is guaranteed to be zero. A car with a metal body is an almost ideal Faraday cage. When a car is struck by lightning, the charge flows on the outside surface of the car to the ground but the electric field inside remains zero. This leaves the passengers inside unharmed. Also, the petrol is in a metal tank which also acts like a Faraday cage. So, Careena is right.

Question 45.
Explain the electrical behaviour of conductors and insulators on the basis of free and bound charges inside the materials.
Answer:
In a material, the inner shell electrons are tightly bound to their respective nuclei and together they have fixed lattice positions. They are called bound charges.

In metals, the outermost valence electrons are loosely bound to their respective nucleus and, due to the regular atomic arrangement in a lattice, are set free to move inside the metal. They are called free charges or free electrons. Under an applied electric field, the free electrons drift in a direction opposite to the electric field and constitute an electric current in the metal. In electrolytes, electrical dissociation of ionic molecules results in both positive and negative free charges, and electric conduction is due to both types of free charges. Under electrostatic conditions, excess charges reside only on the surface of a conductor.

In insulators, all inner shell and outer shell electrons are tightly bound to their respective nuclei so that even at room temperature the number of free charges is several orders lower than that in a metallic conductor. Hence, they are poor conductors of electricity and heat. In the absence of free conduction electrons, excess charges transferred to an insulator remain localized. An insulator can have non-zero surface charge density as well as volume charge density.

Question 46.
You can charge a glass or rubber rod by holding one end of the rod and rubbing the other end with a silk cloth. But you cannot charge a copper rod in the same way. Explain.
Answer:
Glass and rubber are insulators. An excess charge (positive or negative) building up on some part of an insulator remains localized. So, a glass or rubber rod can be held at one end while the far end is being rubbed with silk. The far end of the rod acquires a surplus of electrons but those electrons never flow into the ground through the hand.

A copper rod is an example of a conductor which has free conduction electrons. On holding one end of the copper rod and rubbing the other end with silk, electrons are transferred from the silk to the copper rod, and those excess electrons are free to flow. Because like charges repel, the electrons move away from one another, travel through the rod to the ground through the hand. As a result, the copper rod remains neutral despite the rod being rubbed with silk.

Question 47.
What do you mean by a polar molecule and a nonpolar molecule ? Give two examples of each.
Answer:
A polar molecule is an asymmetric molecule with a permanent electric dipole moment that arises from the finite separation of the centres of the net positive charge and the net negative charge in the molecule, even in the absence of an external electric field.
Dipole moments of polar molecules are of the order of 10^-30 C∙m.

Examples : Gaseous hydrogen halides (HF, HCl, etc.); NH₃, NO₂, N₂O, water molecules; all hetero- nuclear diatomic molecules (with any covalent bond between two different atoms).

A nonpolar molecule is one which does not have a permanent electric dipole moment because in the absence of an external electric field, the centres of the net positive charge and the net negative charge in the molecule coincide. Thus, it is a symmetric molecule.

Examples : H₂, CO₂, N₂, O₂, methane, polyethylene, polystyrene.

[Note : The asymmetric charge distribution in a polar molecule arises from differences in electronegativity and other features of bonding. A heteronuclear polyatomic molecule may be nonpolar if the vector sum of the bond dipole moments is zero, as in CO₂, CH₄, CCl₄, etc. The absence or presence of a dipole moment in a polyatomic molecule can be a revealing clue to the structure of the molecule. For example, BF₃ with a planar trigonal sym-metric structure is nonpolar, while PF₃ with a trigonal pyramidal structure is polar. Of the two isomers of dichloroethylene, cis is polar while trans is nonpolar.]

Question 48.
What is the bond angle and bond dipole moment of a water molecule?
Answer:
In a water molecule, the bond angle between the two O-H bonds is 104.5° and the dipole moment (known as the bond dipole moment) is about 6.17 × 10^-30 C∙m

[Note: The SI unit of dipole moment, the coulomb-metre is too large at molecular level. Hence, bond dipole moments are commonly expressed in the CGS unit, the debye (D); 1 D = 3.335 × 10^-30 C m. So, the bond dipole moment of a water molecule is 1.85 D while that of HF, NH₃ and HCl are 1.82 D, 1.47 D and 1.08 D, respectively.]

Question 49.
What is a dielectric? State its two types. Give two examples in each case.
Answer:
A dielectric is an electrical insulator i.e., a nonconducting material, that can be polarised by an applied electric field which slightly displaces the positive and negative charges of each molecule. A dielectric can sustain a high electric field up to a certain limit. An ideal dielectric has no free charges.

Important commercial dielectrics are of two types, polar and nonpolar.

Examples :
Polar dielectrics : Silicones, halogenated hydrocarbons.

Nonpolar dielectrics : (1) Solid : Ceramics, glasses, plastics (polyethylene, polystyrene, etc.) mica, paper. (2) Liquid : Mineral oils.

Question 50.
With the help of neat diagrams, explain how a nonpolar dielectric material is polarised in an external electric field.
OR
Explain the behaviour of nonpolar dielectric material in an external electric field.
Answer:
In the absence of an external electric field, the molecules of a nonpolar dielectric have no inherent electric dipole moments. An applied electric field slightly separates the centres of negative and positive charges. Then, a nonpolar molecule acquires an induced dipole moment in the direction of the applied field, as shown in figure. The induced dipole moments of all the molecules add up giving the dielectric a net induced electric dipole moment • in the presence of the applied field.

Question 51.
With the help of neat diagrams, explain how a polar dielectric material acquires a dipole moment in an external electric field.
OR
Explain the behaviour of polar dielectric material in an external electric field.
Answer:
In the absence of an external electric field, the permanent electric dipole moments of the molecules of a polar dielectric orient in random directions due to thermal agitation such that their vector sum is zero, from figure (a).

An applied electric field does slightly increase the separation between the centres of negative and positive charges. But, a much larger effect is the tendency of the dipole moments to align with the field, although thermal agitation prevents complete alignment, as shown in from figure (b). Due to the partial alignment of the dipole moments, a polar dielectric also acquires a net induced electric dipole moment in the direction of the applied field. The extent of polarisation depends on the relative values of the two opposing tendencies : (1) the tendency of the applied field to align the dipoles
(2) thermal agitation that tends to randomize.

Question 52.
What is a linear isotropic dielectric? Give one example.
Answer:
A linear isotropic dielectric is one which when placed in a uniform electric field acquires an induced electric dipole moment in the direction of the field and proportional to the applied electric field intensity.
Examples : Mica, glass.

Question 53.
Define electric polarization in dielectrics.
Answer:
Definition The electric polarization at every point within a dielectric is defined as the electric dipole moment per unit volume. It has the direction of the external electric field.

Question 54.
What is electric susceptibility ?
Ans. In a linearly isotropic dielectric placed in a uniform electric field, the electric polarization \(\vec{P}\) is directly proportional to the electric field intensity \(\vec{E}\) inside the dielectric.
∴ \(\vec{P}\) = χ_eε₀\(\vec{E}\)
where the proportionality constant χ_e, a positive quantity, is called the electric susceptibility of the dielectric.
[Note : χ_e is dimensionless. SI units of P and E are C/m² and N/C.]

Question 55.
Explain the reduction of electric field inside a polarized dielectric.
OR
Explain the behaviour of a dielectric slab which is subjected to an external electric field.
Answer:
Consider a rectangular slab of a linear isotropic dielectric placed in a uniform external electric field.

In case of a nonpolar dielectric, the applied field slightly separates the centres of negative and positive charge in a molecule inducing an electric dipole moment in the direction of the field. In most cases, this separation is a very small fraction of a molecular diameter. In case of a polar dielectric, the permanent dipole moments of its molecules are partially aligned with the field. In either case, the dielectric is said to become polarized.

In a uniformly polarized dielectric, the charges of adjacent interior dipoles add to zero. But due to the unbalanced positive ends of dipoles at one face of the slab, bound positive charge appears on that exterior surface. Similarly, bound negative charge appears on the opposite exterior surface of the slab. These bound surface charges are called polarization charges. There is, however, no excess charge in any volume element within the slab and the slab as a whole remains electrically neutral.

The external electric field \(\overrightarrow{E_{0}}\) polarizes the dielectric, with a net polarization \(\vec{P}\) parallel to \(\overrightarrow{E_{0}}\). Within the dielectric, the induced field \(\vec{E}_{\mathrm{p}}=-\vec{P} / \varepsilon_{0}\) due to the polarization charges is opposite to the applied field, from figure.
\(\vec{E}=\vec{E}_{0}+\vec{E}_{\mathrm{p}}=\vec{E}_{0}-\vec{P} / \varepsilon_{0}\)
i.e., E = E₀ – E_p in magnitude.
Assuming the dielectric to be isotropic and linear,
\(\vec{P}\) = χ_eε₀ \(\vec{E}\)
where χ_e is the electric susceptibility of the dielectric.
∴ \(\overrightarrow{E_{0}}\) = (1 + χ_e)\(\vec{E}\) = k\(\vec{E}\)
where k = 1 + χ_e is the dielectric constant. This implies E = E₀/k, thus less than E₀. Thus, the effect of a dielectric material is always to decrease the electric field below the applied electric field.

[Note : The charges + Q and – Q on the plates of a capacitor are said to be free charges because they can move when the potential difference between the plates is changed.]

Question 56.
How does the electric field inside a dielectric decrease when it is placed in an external electric field?
Answer:
Suppose a rectangular slab of dielectric is placed in an electric field \(\overrightarrow{E_{0}}\), with two of its parallel sides perpendicular to the field. The dielectric becomes polarized. Polarization charges appear on the external surfaces of these two parallel sides such that within the dielectric the field due to the polarization charges is opposite to \(\overrightarrow{E_{0}}\). Thus, the magnitude of the net electric field \(\vec{E}\) within the dielectric is less than \(\left|\overrightarrow{E_{0}}\right| \cdot E=\frac{E_{0}}{k}\), where k is the relative permittivity (dielectric constant) of the dielectric.

Question 57.
Is vacuum the best dielectric, meaning is its dielectric strength infinite ?
Answer:
In principle, an absence of particles mean no breakdown. However, practical vacuum still has large number of particles of residual gases. In practice, only pressures lower than 10^-2 mbar can be considered to provide a real dielectric insulation. In such vacuum, free electrical charges under a sufficiently high force can produce ionization and breakdown of its insulation properties. Thus, the dielectric strength of vacuum is only about 20 kV/mm, better than air but lower than most solid dielectrics.

Question 58.
What is a capacitor ?
Explain capacitance of a capacitor.
Answer:
A capacitor is a device used to store electrical charge and electrical energy. It consists of at least two electrical conductors, called as capacitor plates, separated by a distance. The space between the plates may simply be air or, usually, filled with a dielectric.

Consider a capacitor having two conducting plates close to, but not touching, one another shown in figure. Imagine that each plate is neutral, so the potential difference between the plates is zero. If a small positive charge q is transferred from one plate

to the other, the second plate acquires a charge + q while that on the first plate is — q and a small potential difference appears between the plates. As the amount of charge on each plate increases, so does the potential difference between the plates. The potential difference AV between the plates is directly proportional to the magnitude of charge Q on each plate : Q ∝ ∆V.
∴ Q = C∆V
The constant of proportionality C is called the capacitance. The capacitance depends only on the geometry of the plates and the type of dielectric between the plates.

When the terminals of a battery are connected to the plates of an initially uncharged capacitor, the battery potential V moves a small amount of charge of magnitude Q from the plate at the higher potential to the other plate. The capacitor remains neutral overall, but with charges + Q and – Q on opposite plates. The capacitance C is then the ratio of the maximum charge Q that can be stored in the capacitor to the applied voltage V across its plates or, in other words, capacitance is the largest amount of charge per unit potential difference that can be stored on the device.

[Note : A capacitor is represented in circuit diagrams by the symbol, ]

Question 59.
The graph shows the potential difference ∆V between the plates of a capacitor versus the charge Q on its plates. Use the graph to find (1) the capacitance of the capacitor (2) the magnitude of the excess charge on its plates.

Solution:
C = \(\frac{Q}{\Delta V}=\frac{1}{\text { slope }}=\frac{1.5 \mathrm{nC}}{30 \mathrm{~V}}\) = 0.05 nF = 50 pF
From the graph, for Q = 0.5 nC, ∆V = 10 V.

Question 60.
Define the capacitance of a capacitor. State and define the SI unit of capacitance.
Answer:
(1) Definition : The capacitance (capacity) of a capacitor is defined as the ratio of the charge on either conductor to the potential difference between the two conductors forming the capacitor.

(2) The SI unit of capacitance is the farad.
Definition : The capacitance of a capacitor is said to be one farad if a charge of one coulomb is required to increase the potential difference between the two conductors forming the capacitor by one volt.
1 farad = 1 coulomb/volt; 1 F = 1 C/V
[Note : Capacitors in common electronic circuits are in microfarad (10^-6 F), nanofarad (10^-9 F) or picofarad (10^-12 F).]

Question 61.
State and explain the principle of a capacitor.
Answer:
Principle of a capacitor : Any conductor can be used to store charges, however, its capacity can be increased by keeping a grounded conductor near it.

Consider a metal plate A whose potential is raised to V by depositing a charge + Q on it, so that its capacity is C = Q/V. Now, if an uncharged metal plate B is brought close to plate A, then negative bound charge – Q will be induced on the surface of B near A and positive free charge + Q on the other side of B, from figure (a).

If plate B is grounded, i.e., connected to the Earth, the free charge on it will escape to the Earth, from figure (b). The bound charge (- Q) thus remaining on B will lower the potential of A, as if superimposing a potential – V₁ on the potential V of plate A. The resultant potential of A will become V – V₁ and its capacity will be Q/(V – V₁).

C’ = \(\frac{Q}{V-V_{1}}\)
Keeping plate B very close to A, V – V₁ can be made very small, so that the capacity of the combination can become very much greater than the capacity of conductor A alone. C’ >> C

Question 62.
What are the different types of capacitors? Describe in brief.
Answer:
The three main types of capacitors depending on their shape are (1) parallel-plate capacitor (2) spherical capacitor (3) cylindrical capacitor.
(1) Parallel-plate capacitor: It consists of two parallel metal plates, separated by a small gap [from figure (a)] of air or filled with a dielectric. The charge to be stored is given to one plate (A) while the other plate (B) is earthed.

(2) Spherical capacitor: It consists of two concentric spherical conductors, separated by a small gap of air or filled with a dielectric [from figure (b)]. The charge to be stored is given to the inner sphere (A), while the outer sphere (B) is earthed.

(3) Cylindrical capacitor : It consists of two coaxial, cylindrical conductors separated by a small gap of air or filled with a dielectric [from figure (c)]. The charge to be stored is given to the inner cylinder (A), while the outer cylinder (B) is earthed.

Depending on the dielectric used, the capacitors of different types are (1) mica capacitor (2) air capacitor (3) paper capacitor (4) electrolytic capacitor, etc.

Question 63.
Derive an expression for the effective or equivalent capacitance (capacity) of a combination of a number of capacitors connected in series.
OR
Derive an expression for the effective capacitance of three capacitors connected in series.
Answer:
In the series arrangement of capacitors, the capacitors are connected end to end and a cell is connected across the combination of the capacitors as shown in figure.

Let C₁, C₂, C₃ be the capacitances of the three capacitors connected in series and Q, the charge on each capacitor. Let V₁, V₂, V₃ be the potential differences across the capacitors.

Now, charge = capacitance x potential difference
∴ Q = C₁V₁ = C₂V₂ = C₃V₃
∴ V₁ = \(\frac{Q}{C_{1}}\), V₂ = \(\frac{Q}{C_{2}}\) and V₃ = \(\frac{Q}{C_{3}}\)
If Vis the potential difference across the combination and C is the equivalent or effective capacitance of the combination, we have,
C = \(\frac{Q}{V}\) ∴ V = \(\frac{Q}{V}\)

In general, if n capacitors of capacitances C₁, C₂, C₃, …, C, are connected in series, the equivalent capacitance (C) of the combination is given by
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\ldots+\frac{1}{C_{n}}\)

Question 64.
Derive an expression for the effective or equivalent capacitance (capacity) of a combination of a
number of capacitors connected in parallel.
OR
Derive an expression for the effective or equivalent capacitance of three capacitors connected in parallel.
Answer:
In the parallel arrangement of capacitors, the capacitors are connected between two common points and a cell is connected across the combination of the capacitors as shown in below figure. Thus, the potential difference (V ) across each capacitor is the same, Let C₁, C₂, C₃ be the capacitances of the three capacitors connected in parallel and C, the equivalent or effective capacitance of the combination. The charge Q supplied by the cell is distributed as Q₁, Q₂ and Q₃ on the capacitors.

∴ Q₁ = C₁V, Q₂ = C₂V, Q₃ = C₃V and Q = CV
Since, Q = Q₁ + Q₂ + Q₃
CV = C₁V + C₂V + C₃V
∴ C = C₁ + C₂ + C₃
In general, if n capacitors are connected in parallel,
C = C₁ + C₂ + ……. + C_n .

65. Solve the following

Question 1.
Three capacitors have capacities 2 µF, 4 µF and 8 µF. Find the equivalent capacity when they are connected in (a) series (b) parallel.
Solution:
Data : C₁ = 2 µF, C₂ = 4 µF, C₃ = 8 µF
(a) Series arrangement:
\(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{7}{8}\)
The equivalent capacity,
∴ C_s = \(\frac{8}{7}\) = 1.143 µF

(b) Parallel arrangement:
The equivalent capacity is
C_p = C₁ + C₂ + C₃ = 2 + 4 + 8 = 14 µF

Question 2.
The equivalent capacitance of two capacitors is 6 µF when they are connected in series and 25 µF when they are connected in parallel. Find the capacitance of each capacitor.
Solution:
Data : C_s = 6 µF, C_p = 25 µF
Let C₁ and C₂ be the capacitances of the two capacitors respectively.
In parallel combination,
C_p = C₁ + C₂ = 25
In series combination,
\(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}=\frac{C_{1}+C_{2}}{C_{1} C_{2}}\)
∴ C_s = \(\frac{C_{1} C_{2}}{C_{1}+C_{2}}\)
∴ 6 = \(\frac{C_{1} C_{2}}{25}\)
∴ C₁C₂ = 150
∴ C₁(25 – C₁) = 150
∴ 25C₁ – C₁² = 150
∴ C₁² – 25C₁ + 150 = 0
∴ (C₁ – 15) (C₁ – 10) = 0
∴ C₁ = 15 µF or 10 µF
∴ C₂ = 25 – C₁ = 10 µF or 15 µF
∴ The capacitances of the capacitors are 15 µF and 10 µF.

Question 3.
With four capacitors of the same capacity, when three of them are connected in parallel and the remaining one in connected in series with this combination, the resultant capacity is 3.75 µF. Find the capacity of each capacitor.
Solution:
Data : C_eff = 3.75 µF
Let the capacity of each of the four capacitors be C. The equivalent capacity of three of them in parallel is
C_p = C + C + C = 3C
The equivalent capacity of the series combination of C_p and the fourth capacitor is
C_eff = \(\frac{C_{\mathrm{p}} C}{C_{\mathrm{P}}+C}=\frac{(3 C) C}{3 C+C}=\frac{3}{4} C\)
∴ By the data, \(\frac{3}{4}\) C = 3.75 µF
∴ C = \(\frac{4}{3}\) × 3.75 = 5 µF
∴ The capacity of each capacitor = 5 µF.

Question 4.
Two capacitors of capacities C₁ and C₂ are joined in series and this combination is joined in parallel with a capacitor of capacity C₃. Show that the capacity of the system is C = \(\frac{C_{1}\left(C_{2}+C_{3}\right)+C_{2}
Solution:
The equivalent capacitance of the series combination of C₁ and C₂ is
C_s = [latex]\frac{C_{1} C_{2}}{C_{1}+C_{2}}\)
The equivalent capacitance of the parallel combination of C_s and C₃ is

Question 5.
Capacitors of capacities 5 µF and 10 µF are connected in parallel in a circuit with a cell of emf 2 V. What should be the capacity of the capacitor to be connected in series with the parallel combination of the capacitors to get 1 µC charge on the combination?
Solution:
Data : C₁ = 5 µF, C₂ = 10 µF, V = 2 V, Q = 1 µC
The effective capacity of the parallel combination of C₁ and C₂ is
C_p = C₁ + C₂ = 5 + 10 = 15 µF

Let C be the capacity of the capacitor to be connected in series with C_p to get the charge of 1 coulomb on the combination. The equivalent capacity (C_s) of the series combination is given by

Question 6.
Three capacitors of capacities 8 µF, 8 µF and 4 µF are connected in series and a potential difference of 120 V is maintained across the combination. Calculate the charge on the capacitor of capacity 4 µF. Also calculate the potential difference across it.
Solution:
Data : C₁ = 8 µF, C₂ = 8 µF, C₃ = 4 µF, V = 120 V
Let C_s = equivalent capacity of the series combination of the capacitors
∴ \(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{8}+\frac{1}{8}+\frac{1}{4}\)
= \(\frac{1+1+2}{8}=\frac{4}{8}=\frac{1}{2}\)
∴ C_s = 2 µF = 2 × 10^-6 F
In series combination, the charge on each capacitor is the same. It is given by Q = C_sV
∴ Q = 2 × 10^-6 × 120
= 2.4 × 10^-4 coulomb
V₃ = \(\frac{Q}{C_{3}}=\frac{2.4 \times 10^{-4}}{4 \times 10^{-6}}=\frac{240}{4}\) = 60 V (∵ C₃ = 4 µF = 4 × 10^-6 F)
The charge on the 4 µF capacitor is 2.4 × 10^-4 C and the potential difference across it is 60 V.

Question 7.
A 100 V battery is connected across the combination of capacitors of capacities 4 µF and 8 µF in parallel and then in series. Calculate the charge on each capacitor in parallel and in series combination.
Solution:
Data : V = 100 V, C₁ = 4 × 10^-6 F, C₂ = 8 × 10^-6 F
(i) Parallel combination :
Q₁ = C₁V = (4 × 10^-6)(100) = 4 × 10^-4 C
Q₂ = C₂V = (8 × 10^-6)(100) = 8 × 10^-4 C

(ii) Series combination :

Question 8.
Three capacitors are connected as shown in the figure below.

Calculate the effective capacitance between A and B.
Solution:
Data : C₁ = 2 µF, C₂ = 3 µF, C₃ = 4 µF
The resultant capacitance C_s of C₁ and C₂ in series is given by
\(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}=\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\)
∴ C_s = \(\frac{6}{5}\) = 1.2 µF
The effective capacitance between A and B is due to the parallel combination of C_s and C₃.
C_p = C_s + C₃ = 1.2 + 4 = 5.2 µF

Question 9.
Four capacitors are of the same capacitance.
(a) If three of them are connected in parallel and the remaining one is connected in series with this combination, the resultant capacitance is 3.75 µF. Find the capacitance of each capacitor.
(b) When three of them are connected in series and the remaining one is connected in parallel with this combination, find the resultant capacitance of the combination.
Solution:
(a) Let C be the capacitance of each capacitor.

Between points A and B, three capacitors, each of capacitance C, are connected in parallel from figure. Their effective capacitance (C_p) is given by
C_p = C + C + C = 3C
When a capacitor of capacitance C is connected in series with C_p, their resultant capacitance (C_s) is given by
\(\frac{1}{C_{s}}=\frac{1}{C_{p}}+\frac{1}{C}=\frac{1}{3 C}+\frac{1}{C}=\frac{4}{3 C}\)
∴ C_s = \(\frac{3 C}{4}\)
Given : C_s = 3.75 µF
∴ \(\frac{3 C}{4}\) = 3.75
∴ C = \(\frac{4 \times 3.75}{3}=\frac{15}{3}\) = 5 µF

(b) The arrangement is shown in below figure.

The effective capacitance (C_s) of the series combination of three capacitors, each of capacitance C, is given by
\(\frac{1}{C_{s}}=\frac{1}{C}+\frac{1}{C}+\frac{1}{C}=\frac{3}{C}\)
∴ C_s = \(\frac{C}{3}\)
When another capacitor of capacitance C is connected in parallel with the combination, the result ant capacitance is
C_p = C_s + C = \(\frac{C}{3}\) + c
= \(\frac{4 C}{3}=\frac{4 \times 5}{3}=\frac{20}{3}\)
= 6.667 µF

Question 10.
In below figure, C₁ = 10 µF, C₂ = 30 µF, C₃ = 20 µF, C₄ = 40 µF. Find the capacitance between the points A and B when (i) the key K is closed (ii) the key K is open.

Solution:
(i) Key K closed :
The parallel combination of C₁, and C₃ is in series with the parallel combination of C₂ and C₄. Let
C₅ = C₁ || C₃ and C₆ = C₂ || C₄.
∴ C₅ = C₁ + C₃ = 10 + 20 = 30 µF
and C₆ = C₂ + C₄ = 30 + 40 = 70 µF
The capacitance between A and B is the equivalent capacitance of C₅ and C₆ in series, i.e.,
C_AB = \(\frac{C_{5} C_{6}}{C_{5}+C_{6}}=\frac{30 \times 70}{30+70}=\frac{2100}{100}\) = 21 µF

(ii) Key K open :
The series combination of C₁ and C₂ is in parallel with the series combination of C₃ and C₄. Let C₇ and C₈ be the equivalent capacitances of the respective series combinations.

The capacitance between A and B is the equivalent capacitance of C₇ and C₈ in parallel, i.e.,
C_AB = C₇ + C₈ = \(\frac{15}{2}+\frac{40}{3}=\frac{45+80}{6}\)
= \(\frac{125}{6}\) = 20.83 µF

Question 11.
A network of four capacitors, 5 µF each, are connected to a 240 V supply. Determine the equivalent capacitance of the network and the charge on each capacitor.

Solution:
Data : C₁ = C₂ = C₃ = C₄ = 5 µF, V = 240 V

The equivalent capacitance C₅ of the series combination is given by
\(\frac{1}{\mathrm{C}_{5}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}=\frac{3}{5}\)
∴ C₅ = \(\frac{5}{3}\) µF
The equivalent capacitance of the parallel combination of C₅ with C₄ is
C = C₅ + C₄ = \(\frac{5}{3}\) + 5 = \(\frac{20}{3}\) µF = 6.667 µF
The potential difference across each of the three capacitors in series = \(\frac{V}{3}=\frac{240}{3}\) = 80 V
and the charge on each of them is the same.
∴ Q₁ = Q₂ = Q₃ = C₁ × \(\frac{V}{3}\) = (5 × 10^-6)(80)
= 4 × 10^-4 C
The charge on the capacitor C₄ is
Q₄ = C₄V = (5 × 10^-6)(240) = 1.2 × 10^-3 C

Question 12.
Six capacitors of capacities 5 µF, 5 µF, 5 µF, 5 µF, 10 µF, and X µF are connected as shown in the network given below :

Find (a) the value of X if the network is balanced (b) the resultant capacitance between A and C.
Solution:
(a) The effective capacitance of the series combination in the arm DC is \(\frac{10 X}{10+X}\) µF
Using the balancing condition for the network,

(b) As the network is balanced, no charge flows through the arm BD.
Effective capacitance 5×5 25
C_ABC = \(\frac{5 \times 5}{5+5}=\frac{25}{10}\)= 2.5 µF (series combination)
Similarly,
C_ADC =\(\frac{5 \times 5}{5+5}=\frac{25}{10}\) = 2.5 µF (series combination)
Effective (resultant) capacitance between A and C .
= C_ABC + C_ADC (parallel combination)
= 2.5 + 2.5 = 5 µF

Question 66.
Derive an expression for the capacitance of a parallel-plate air/vacuum capacitor.
Answer:
Consider a parallel-plate capacitor, consisting of two parallel plates A and B separated by a distance d as shown in below figure. Let A be the area of each plate. Plate B is connected to the Earth. Suppose that the capacitor is connected to the terminals of a battery of potential difference V. The battery transfers a charge + Q to the insulated plate A. A charge – Q is induced on the near surface of the grounded plate B while the + Q charge on the far side of B flows to the ground.

1f the area A is very large and the distance between the plates is very small, the electric field in the region between the plates is almost uniform, except near the edges. The magnitude of the electric field E at a point between the plates and the potential difference V between the plates are related by E = V/d. Outside the capacitors, the electric fields due to the two charged plates cancel out:
\(\frac{\sigma}{2 \varepsilon_{0}}-\frac{\sigma}{2 \varepsilon_{0}}\) = 0.
But, E = \(\frac{\sigma}{\varepsilon_{0}}\), where σ is the surface charge density on the plates.
∴ \(\frac{\sigma}{\varepsilon_{0}}=\frac{V}{d}\) …………. (1)
Now, = \(\frac{Q}{A}\) ∴ E = \(\frac{Q}{\varepsilon_{0} A}=\frac{V}{d}\) …………… (2)
The capacity (capacitance) of a capacitor is, by definition, C = \(\frac{Q}{V}\)
∴ C = \(\frac{\varepsilon_{0} A}{d}\) …………… (3)
This gives the capacitance of a parallel-plate capacitor without a dielectric, i.e., an air or vacuum capacitor.

Question 67.
What is the electric field intensity in the region between the plates of a parallel-plate capacitor if the separation between the plates is 1 mm and the potential difference across the plates is 2V?
Answer:
E = \(\frac{V}{d}=\frac{2}{1 \times 10^{-3}}\) = 2000 N/C is the required electric field intensity.

Question 68.
The capacitance of a parallel-plate air capacitor is 12 µF. If the separation between its plates is doubled, what will be the new capacitance?
Answer:
\(\frac{C_{2}}{C_{1}}=\frac{d_{1}}{d_{2}}\)
∴ C₂ = \(\frac{d_{1}}{d_{2}}\) × C₁ = \(\frac{1}{2}\) × 12 = 6pF
is the new capacitance.

Question 69.
Explain the effect of a dielectric on the capacitance of a isolated charged parallel-plate capacitor.
Hence, show that if a dielectric of relative permit-tivity (dielectric constant) k completely fills the space between the plates, the capacitance increases by a factor k.
Answer:
Consider a parallel-plate capacitor without a dielectric, of plate area A, plate separation d and capacitance C₀, charged to a potential difference V₀ and then isolated.
Suppose the charges on its conducting plates are + Q and – Q, from figure (a). The surface density of free charge is

If A is very large and d is very small, the electric field in the region between the plates is almost uniform, except near the edges. The magnitude of the electric field intensity is
E₀ = \(\frac{V_{0}}{d}=\frac{\sigma}{\varepsilon_{0}}=\frac{Q}{\varepsilon_{0} A}\)
Without the dielectric, the capacitance of the parallel plate capacitor is, by definition, C₀ = \(\frac{Q}{V_{0}}=\frac{\varepsilon_{0} A}{d}\) ……………. (3)

Now, suppose a dielectric slab of permittivity e and thickness t (t < d) is introduced in the space between, and parallel to, the charged plates, from figure (b). A polarisation charge – Q_p appears on the exterior surface of the dielectric nearer to the positive plate while a polarisation charge + Q_p appears on its opposite face. Since the capacitor was isolated after charging, the free charge Q on the plates is the same as earlier. Within the dielectric, the induced field \(\vec{E}_{\mathrm{p}}\) due to the polarisation charges is opposite to the applied field. The net electric field within the dielectric \(\vec{E}\) is less than the applied field. In magnitude,
E = E₀ – E_p …………. (4)
By definition, the relative permittivity (dielectric constant) of the dielectric, k = \(\frac{\varepsilon}{\varepsilon_{0}}=\frac{E_{0}}{E}\) ………. (5)

Between the plates, the field within the dielectric of thickness t is E = E₀/k, and that in the region (d – t) is E₀. Therefore, the new potential difference between the plates is

Equations (7) and (8) give the capacitance of a capacitor with a dielectric.

Special case: If the dielectric completely fills the space between the plates, t = d. Therefore, from Eq. (7),
C = C₀ \(\frac{d}{\left(d-d+\frac{d}{k}\right)}\) = C₀ \(\frac{d}{d / k}\) = kC₀
Thus, the capacitance increases by the factor of k.

[Notes : (1) It‘is useful to check the other limits :
(i) As the thickness of the dielectric approaches zero, i.e., t → 0, we have C → ε₀A/ d = C₀, as expected for no dielectric.
(ii) If k = 1, we again have C = ε₀A/d = C₀, as expected for air or vacuum, capacitor where the dielectric is absent.
(2) The equation, V = \(\frac{V_{0}}{d}\) ( d – t + \(\frac{t}{k}\)), shows that V too is less than V0 for the same charge Q.
(3) Note that the configuration is equivalent to two capacitors of plate separations (d -1) and t connected in series, as shown in below figure. For capacitors connected in series, the equivalent capacitance is given by

Thus, if the dielectric slab is replaced by a conducting slab of the same thickness f, the right-hand plates in above figure will be shorted and the equivalent capacitance C = C₁ = \(\frac{\varepsilon_{0} A}{d-t}=\frac{d}{d-t}\) C₀. Therefore, C > C₀.

(4) If a battery supplying a potential difference V0 remains connected as a dielectric is inserted filling the space, the charge on the plates is increased by a factor k, the p.d. across the capacitor remaining constant Q = kQ₀/ where Q₀ is the charge on the plates without the dielectric. The capacitance becomes
C = \(\frac{Q}{V_{0}}=\frac{k Q_{0}}{V_{0}}\) = kC₀
which is the same as in Eq. (9) where the charge remained constant, but now the charge has increased.]

Question 70.
State the expression for the capacitance of a parallel-plate capacitor filled with a dielectric. Explain how its capacitance can be increased.
Answer:
The capacitance of a parallel-plate capacitor filled with a dielectric is C = \(\frac{A k \varepsilon_{0}}{d}\)

where A is the area of each plate, k is the relative permittivity (dielectric constant) of the medium between the plates, ε₀ is the permittivity of free space and d is the uniform plate separation.

The capacitance of a parallel-plate capacitor can be increased by

1. increasing the area of each plate
2. decreasing the distance between the two plates
3. filling the space between the two plates by a medium of greater relative permittivity.

Question 71.
What are the functions of a dielectric in a capacitor?
Answer:
A dielectric material between the plates of a capacitor

1. increases the capacitance of the capacitor
2. provides mechanical support to the plates
3. increases the maximum operating voltage, i.e., the maximum voltage to which the capacitor may be charged without breakdown of the insulating property of the medium between the plates.

Question 72.
A parallel-plate capacitor consists of n dielectric slabs of end-face areas A₁, A₂, ………, A_n and respective relative permittivities (dielectric constants) k₁, k₂, ….., k_n, in the space between the plates as shown in below figure. Find the equivalent capacitance of this arrangement. Hence, show that if the areas are equal, the capacitance is C = \(\frac{\varepsilon_{0} A}{n d} \sum_{j} k_{j}\).

Answer:
Consider a parallel-plate capacitor without a dielectric, of plate area A, plate separation d and capacitance C₀, charged to a potential difference V₀ and then isolated. Without a dielectric, the capacitance of the parallel-plate capacitor is, by definition
C₀ = \(\frac{Q}{V_{0}}=\frac{\varepsilon_{0} A}{d}\) …………… (1)
Now, suppose n dielectric slabs of end-face areas
A₁, A₁, …, A₃ and respective relative permittivities
(dielectric constants) k₁, k₂, ………, k_n fills the space between the plates as shown in above figure. The charge on the plates remaining the same, the reduced potential difference (V) between the plates is the same across each dielectric slab. Therefore, the capacitor is equivalent to a parallel combination of n capacitors of the same plate separation d but different plate areas and dielectric constants, as shown in below figure.

Then, C₁ = k₁0A₁/d, C₂ = k₂e0A₂/d, … and so on.
Therefore, their equivalent capacitance is
C = C₁ + C₂ + ………… + C_n
= \(\frac{\varepsilon_{0}}{d}\)(k₁A₁ + k₂A₂ + …….. + k_nA_n) ………… (2)
If the dielectric slabs have equal thickness such that their end-face areas are equal, i.e., A₁ = A₂ = …….. = A_n = A/n.
C = \(\frac{\varepsilon_{0} A}{n d}\)(k₁ + k₂ + ………… + k_n) = \(\frac{\varepsilon_{0} A}{n d}\) Σ_j K\(\frac{\varepsilon_{0} A}{n d}\)

Question 73.
A dielectric of relative permittivity (dielectric constant) k completely fills the space between the plates of a parallel-plate capacitor with a surface charge density σ. Show that the induced density of surface charge on the dielectric is σ_p = σ (1 – \(\frac{1}{k}\))
Answer:
Consider a parallel-plate capacitor without a dielectric, of plate area A, plate separation d and capacitance C₀, charged to a potential difference V and then isolated.

Suppose the charges on its conducting plates are +Q and -Q, from figure (a). The surface density of free charge is
σ = \(\frac{Q}{A}\) …………. (1)

When no dielectric is present, the electric field \(\overrightarrow{E_{0}}\) in the region between the plates can be found by applying Gauss’s law to the Gaussian surface :

When a dielectric is inserted as in figure (b), there is an induced charge – Q, on the surface, and . the net charge enclosed by the Gaussian surface is Q – Q_p. Then, by Gauss’s law,

The effect of the dielectric is to weaken the original field E₀ by a factor k.
Writing E = \(\frac{E_{0}}{k}\),

Question 74.
The capacitance of a parallel-plate air capacitor is 2 pF. If the air is replaced by a medium of dielectric constant 10. What will be its capacitance?
Answer:
\(\frac{C_{2}}{C_{1}}=\frac{k_{2}}{k_{1}}\)
C₂ = \(\frac{k_{2}}{k_{1}}\) × C₁ = \(\frac{10}{1}\) × 2 = 20 pF
is the required capacitance.

Question 75.
Explain the concept of displacement current.
Answer:
Consider an uncharged parallel-plate capacitor with capacitance C connected to a resistor R and a battery of voltage V, below figure. For a parallel-plate capacitor, of plate area A, separation d and filled with a dielectric of permittivity ¡, its capacitance is C = εA/d.

When the key is closed, charge begins to flow into the capacitor via the resistor. The initial voltage across the capacitor is zero and the current in the circuit now is called the charging current. As the capacitor charges up, the potential difference across its plates slowly increases. During the charging, the charge on the capacitor grows as Q(t) = Q(1 – e ^-t/T).

While a capacitor is being charged, there is no current through the capacitor but the electric field between the plates, and the electric flux through a Gaussian surface enclosing one of the plates, increases as the charge on its plates increases. The instantaneous charge on the capacitor is
Q(t) = (εA)E(f) [ε = kε₀]
∴ \(\frac{d}{d t}\) Q(t) = (εA)\(\frac{d}{d t}\)E(t) = ε\(\frac{d}{d t}\)Φ_e(t)
where Φ_e(t) = AE(t) is the electric flux through the surface. The rate of change of charge, \(\frac{d}{d t}\) Q(t), has the
dimension of current and is the conduction current i_c. The fictitious current arising from the changing electric flux is called the displacement current:
i_d = ε\(\frac{d}{d t}\)Φ_e(t)
That is, we imagine the changing flux through the dielectric is somehow equivalent to the conduction current in the circuit. This lets us generalize Kirchhoff’s junction rule : considering the top plate of the capacitor in the figure, when we include the displacement current, we see that the conduction current coming in from top and an equal displacement current coming out of the bottom. With this generalized meaning of the term “current”, we speak of current going through the capacitor.

Maxwell introduced the concept of displacement current to generalize Ampere’s law in his formulation of electromagnetic theory that led to the discovery of electromagnetic waves.

[Notes : (1) The lowercase i is used to denote instantaneous value of current. (2) The actual time taken for the charge on the capacitor to reach 63% of its maximum possible voltage is known as one time constant (T = RC). For all practical purposes, a capacitor is considered to be fully charged to Q after a time t = 5T. (3) In the pheno-menon of electromagnetic induction (Chapter 12), we see that a changing magnetic field gives rise to an induced electric field. Remarkably, it turns out that a changing electric field gives rise to a magnetic field – an example of the symmetry in nature. These two effects together explain the existence of all types of electromagnetic waves.]

Question 76.
Show that the energy of a charged capacitor is \(\frac{1}{2}\) CV². Also, express this in other forms.
OR
Derive an expression for the energy stored in a charged capacitor. Express it in different forms.
Answer:
To charge a capacitor, an external agent has to do work against the electrostatic forces due to the charges already present on the plates of the capacitor.

Let C be the capacitance of the capacitor. Let Q and V be the final charge and the potential difference respectively when the capacitor is charged. Let q be the charge on the capacitor at some stage during the charging and v, the corresponding potential difference between the plates. The work done by an external agent in bringing additional small charge dq from infinity and depositing it on the capacitor is
dW = potential difference × charge = v dq
But C = \(\frac{q}{v}\) ∴ v = \(\frac{q}{C}\)
∴ dW = \(\frac{q}{C}\) dq
The total work done in charging the capacitor is
W = \(\int d W=\int_{0}^{Q} \frac{q d q}{C}=\frac{1}{C}\left[\frac{q^{2}}{2}\right]_{0}^{Q}=\frac{1}{2} \frac{Q^{2}}{C}\)
Now, Q = CV
W = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\)(CV)V = \(\frac{1}{2}\) QV
This work is stored in the form of potential energy, in the electric field in the medium between the plates of the capacitor.
∴ Energy of a charged capacitor
= \(\frac{1}{2} \frac{Q^{2}}{C}=\frac{1}{2} C V^{2}=\frac{1}{2} Q V\)

Question 77.
How does the energy stored in a charged capacitor change if the plates of the capacitor are moved farther apart
(i) after the battery is disconnected
(ii) the battery remaining connected?
Answer:
(i) If the plates of a charged capacitor are moved farther apart after the battery is disconnected, the energy stored increases by the amount of work done by the external agent in pulling the plates apart against the force of attraction between the opposite charges on the plates.

(ii) With the battery still connected, increasing the separation between the plates decreases the energy stored in the charged capacitor.

[Notes : (1) The charge on the capacitor does not change after the battery is disconnected. Because the electric field of a large plate is independent of the distance from the plate, the electric field \(\vec{E}\) between the plates also remains the same. Therefore, since E = V/d, the p.d. between the plates (V) changes in the same proportion as d. Since the energy stored,
U = \(\frac{1}{2} C V^{2}=\frac{1}{2}\left(\frac{A \varepsilon}{d}\right)(E d)^{2}=\frac{1}{2}(A \varepsilon D) E^{2}\)
U also changes in the same proportion as d. The addi-tional energy is transferred to the system from the work done by the external agent.

(2) With the battery still connected, the p.d. between the plates remains the same. Since the energy stored,
U = \(\frac{1}{2} C V^{2}=\frac{1}{2}\left(\frac{A \varepsilon}{d}\right) V^{2}\), U is inversely proportional to d. With decrease in capacitance, the charge on the plates decreases.]

Question 78.
When a capacitor is charged by a battery, is the energy stored in the capacitor the same as the energy supplied by the battery? Why?
Answer:
Yes. To charge a capacitor, an external agent (the battery) has to do work against the electrostatic force due to the charges already present on the plates of the capacitor. This work done is stored in the form of potential energy in the electric field in the medium between the plates of the capacitor.

Question 79.
If the charge on a capacitor is 2 µC and the potential difference across the conductors forming the capacitor is 100 V, what is the electrostatic energy stored in the capacitor?
Answer:
U = \(\frac{1}{2}\)QV = \(\frac{1}{2}\) × 2 × 10^-6 C × 100V = 10^-4 J
is the required energy.

Question 80.
The capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of the charge on the capacitor ?
Answer:
Let Q be the charge on the capacitor. Then, the energy stored in it is
U = \(\frac{1}{2} \frac{Q^{2}}{C}\)
∴ Q = \(\sqrt{2 U C}\)

Question 81.
Which combination of four identical capacitors has the maximum capacitance? Which combination of these capacitors will store minimum energy when a constant p.d. is applied across it ?
Answer:
The maximum capacitance of four identical capacitors, each of capacitance C, is obtained for their parallel combination : C_p = 4C.

Their series combination has the minimum capacitance. The charge stored in their parallel combination is four times that in their series combination. For the same constant p.d. V, the energy stored in the parallel combination is \(\frac{1}{2}\) (4Q)V and that in the series combination is \(\frac{1}{2}\) QV. Thus, the series combination will store minimum energy.

82. Solve the following

Data : ε₀ = 8.85 × 10^-12 F/m]
Question 1.
A 3 mm gap between the square metal plates of area 0.25 m2 that form a parallel plate capacitor is partly filled, as in figure (b), by a dielectric slab of the same shape and area, of thickness 2 mm and relative permittivity 2.5. Ignoring edge effects, calculate : .
(i) the capacitance when the dielectric slab covers the full area of the plates
(ii) the capacitance when the dielectric slab is partly withdrawn a distance x(x = 0.2 m) in a direction parallel to an edge of the plates.
Solution:
Data : d = 3mm = 3 × 10^-3 m, A = l² = 0.25m², t = 2mm = 2 × 10^-3 m, k = 2.5, x = 0.3m, ε₀ = 8.85 × 10^-12 F/m

(ii) From below figure, the system is equivalent to a parallel combination of two capacitors : C, is air-filled with plate area A₁ = lx and C₂ has dielectric with plate area A₂ = l (l – x).

since l² = 0.25 m², Z = 0.5 m

Question 2.
A parallel-plate air capacitor has an area 2 × 10^-4 m² and the separation between the two plates is 1 mm. Find its capacitance.
Solution:
Data : A = 2 × 10^-4 m², d = 1 mm = 10^-3 m,
ε₀ = 8.85 × 10^-12 C²/N.m², k = 1 (for air)
The capacitance,
C = \(\frac{A k \varepsilon_{0}}{d}=\frac{\left(2 \times 10^{-4}\right)(1)\left(8.85 \times 10^{-12}\right)}{10^{-3}}\)
= 1.77 × 10^-12 F = 1.77 pF

Question 3.
A parallel-plate air capacitor has circular plates, each of diameter 20 cm, separated by a distance of 2 mm. The potential difference between the plates is maintained at 360 volts. Calculate its capacitance and charge. What is the intensity of the electric field between the plates of the capacitor? [k = 1]
Solution:
Data : The diameter of each plate is 20 cm. Hence, its radius is r = 10 cm = 0.1 m, d = 2 mm = 2 × 10^-3 m, V = 360 V, k = 1, ε₀ = 8.85 × 10^-12 F/m
(i) Capacitance :

Question 4.
A parallel-plate air capacitor has rectangular plates, each of area 20 cm² separated by a distance of 2 mm. The potential difference between the plates is 500 volts. Calculate (i) its capacitance (ii) the charge on each plate (iii) the electric field intensity between the two plates.
Solution:
Data : A = 20 cm² = 20 × 10^-4 m² = 2 × 10^-3 m², k = 1, V = 500V, d = 2 mm = 2 × 10^-3 m, ε₀ = 8.85 × 10^-12 F/m
(i) Capacitance :
C = \(\frac{A \varepsilon_{0} k}{d}=\frac{\left(2 \times 10^{-3}\right)\left(8.85 \times 10^{-12}\right)(1)}{2 \times 10^{-3}}\)
= 8.85 × 10^-12 F ( = 8.85 pF)

(ii) Charge :
Q = CV = (8.85 × 10^-12)(500)
= 4.425 × 10^-9 C (= 4.425 nC)

(iii) Intensity of the electric field :
E = \(\frac{V}{d}=\frac{500}{2 \times 10^{-3}}\) = 2.5 × 10⁵ V/m

Question 5.
A parallel-plate air capacitor has rectangular plates each of length 20 cm and breadth 10 cm. The separation between the plates is 1 mm.
(a) Calculate the potential difference between the plates if 1 µC charge is given to the capacitor.
(b) With the same charge of 1 µC, if the separation between the plates is doubled, what is the new potential difference?
(c) Calculate the electric field between the plates.
Solution:
Data : Q = 1 nC = 10^-9 C, l = 20 cm, b = 10 cm, d = 1 mm = 10^-3 m, ε₀ = 8.85 × 10^-12 F/m, k = 1 (air)
Area of the plates, A = lb = 20 × 10 = 200 cm² = 0.02 m²
(a) The capacitance of the capacitor,

V₂ = V₁ × \(\frac{d_{2}}{d_{1}}\) = 5.65 × 2 = 11.3 V (∵\(\frac{d_{2}}{d_{1}}\) = 2, by the data )

(c) The electric field between the plates,
E = \(\frac{V}{d}=\frac{5.65}{10^{-3}}\) = 5650 N/C

Question 6.
A parallel-plate air capacitor has a capacity (capacitance) of 20 µF. What will be its new capacity if
(i) the distance between the plates is doubled
(ii) a marble slab of dielectric constant 8 is introduced filling the entire space between the two plates?
Solution:
Data : C₁ = 20 µF, d₂ = 2d₁, k₁ = 1 (air), k₂ = 8 (marble)
C = \(\frac{A k \varepsilon_{0}}{d}\)
(i) With air as the dielectric,

This gives the new capacity (capacitance) on doubling the plate separation.

(ii) With the plate separation d = d₁,

This gives the new capacity (capacitance) with marble as the dielectric.

Question 7.
A parallel-plate air capacitor of plate separation 2 mm and capacitance 1 µF is charged to 200 V. A dielectric of relative permittivity 50 is now inserted so as to fill the space between the plates.
(i) Find the new value of capacitance.
(ii) Find the polarisation charge on one of the boundaries of the dielectric.
(iii) Find the magnitude of the polarisation of the dielectric.
(iv) What is the magnitude of the electric field inside the dielectric?
Solution:
Data : C₀ = 10^-6 F, d = 2 × 10^-3 m, k = 50, V = 200 V, ε₀ = 8.85 × 10^-12 F/m
(i) The new value of the capacitance is
C = kC₀ = 50 × 10^-6 F (or 50µF)

Question 8.
A parallel-plate capacitor consists of two identical metal plates. Two dielectric slabs having dielectric constants (relative permittivities) k₁ and k₂ are introduced in the space between the plates as shown in figures. Show that the capacity (capacitance) of the capacitor in figure (a) is given by C’ = \(\frac{A \varepsilon_{0}\left(k_{1}+k_{2}\right)}{2 d}\) and that in figure (a) is given by C” = \(\frac{2 A \varepsilon_{0}}{d} \cdot \frac{k_{1} k_{2}}{k_{1}+k_{2}}\)
Solution:
(i) The capacitor in figure(a) is equivalent to a parallel combination of two capacitors of plate separation d and plate area A/2, with C₁ filled with dielectric of relative permittivity k₁ and C₂ filled with dielectric of relative permittivity k₂, as shown in figure (b).

The equivalent capacitance of their parallel combination is
C’ = C₁ + C₂ = \(\frac{A \varepsilon_{0} k_{1}}{2 d}+\frac{A \varepsilon_{0} k_{2}}{2 d}=\frac{A \varepsilon_{0}\left(k_{1}+k_{2}\right)}{2 d}\) ……………. (1)

(ii) Suppose the capacitor in figure (a) is charged by connecting it to a battery. Let the potential of the positive plate a be V_a, the potential of the negative plate c be V_c, and the potential midway between the plates at the interface b of the dielectrics be V_b.

The electric field in the absence of any dielectric is
E₀ = \(\frac{Q}{\varepsilon_{0} A}\)
The electric field in the first dielectric, E₁ = \(\frac{E_{0}}{k_{1}}\)

Equations (1) and (2) give the required expressions.

INote : The capacitor in figure (a) is equivalent to a series combination of two capacitors of plate separation d/2 and plate area A, with C₃ filled with dielectric of relative permittivity k₁ and C₄ filled with dielectric of relative permittivity k₂, as shown in below figure.]

Question 9.
The energy stored in a charged capacitor of capa city 25 µF is 4J. Find the charge on its plate.
Solution:
Data: C = 25 pF = 25 × 10^-12 F, U = 4 J
U = \(\frac{1}{2} \frac{Q^{2}}{C}\)
∴ The charge, Q = \(\sqrt{2 U C}\)
= \(\sqrt{2 \times 4 \times 25 \times 10^{-12}}\)
= 1.414 × 10^-5 C (= 14.14 µC)

Question 10.
The electrostatic energy of 3.5 × 10^-4 J is stored in a capacitor at 700 V. What is the charge on the capacitor?
Solution:
Data: U = 3.5 × 10^-4 J, V = 700V
U = \(\frac{1}{2}\) QV
∴ Q = \(\frac{2 U}{V}=\frac{2 \times 3.5 \times 10^{-4}}{700}\) = 10^-6 C
This is the charge on the capacitor.

Question 11.
Two capacitors, each of capacity 5 µF, and a battery of emf 180 V are given to you. Which combination gives the maximum energy? What is its value? Also find the charge on each capacitor of that combination.
Solution:
Data : C₁ = C₂ = 5 µF = 5 × 10^-6 F, V = 180 V
(i) The effective capacity (C_p) of their parallel combination is
C_p = C₁ + C₁
= 5 × 10^-6 F + 5 × 10^-6 F
= 10 × 10^-6F

Series combination :

(ii) The energy of a charged capacitor is U = \(\frac{1}{2}\) CV²
For a given value of V, the combination of maximum capacity will give maximum energy.
As C_p > C_s, the parallel combination gives maximum energy.

(iii) The value of maximum energy is
U_max = \(\frac{1}{2}\) C_pV² = \(\frac{1}{2}\) × 10 × 10^-6 × (180)²
= 0.162 J

(iv) If Q₁ and Q₂ are the charges on C₁ and C₂,
Q₁ = C₁V= 5 × 10^-6 × 180 = 9 × 10^-4 C
Q₂ = C₂V = 5 × 10^-6 × 180 = 9 × 10^-4C

Question 83.
What is the Van de Graaff generator?
Answer:
The Van de Graaff generator is a high-voltage electrostatic generator that is used to produce very high potential differences of several million volts. It was constructed by US physicist Robert Van de Graaff in 1931. The high potential difference produced by the Van de Graaff generator is used to produce high-energy ion beams in a linear accelerator inside.

Question 84.
State the principle of working of the Van de Graaff generator. Describe its construction with a neat labelled diagram.
Answer:
Principle of working : The Van de Graaff generator works on the principles of corona or point discharge, that the charge on hollow conductor resides entirely on its outer surface and that the charge supplied to an insulated conductor increases its potential.

Construction : A hollow spherical conductor C is supported and insulated from the ground by a tower of ceramic insulators. A long, vertical, endless belt made of special insulating paper or fabric (rubberised silk) is continuously

driven by an electric motor from the ground up to the inside of the conductor. Near the ground, the belt passes close to a spraycomb A which is connected to a high-voltage source. The spraycomb consists of a set of sharp needle points. Another spraycomb collector B is connected inside conductor C at the top. The entire apparatus is usually enclosed in a pressurized vessel containing a gas such as nitrogen or Freon.

Housed inside the assembly is an evacuated tube through which positively charged particles may be accelerated from a source at the same potential as the conductor C to a target at the ground potential.

Question 85.
Describe the working and uses of the Van de Graaff generator with a neat labelled diagram.
Answer:
Working : A high-voltage source, consisting of a high-voltage transformer rectifier circuit, is used to apply a potential difference of several thousand volts (about 50 kV to 100 kV) between spraycomb A and the ground. As a result of the high potential to spraycomb A, a continuous electric discharge takes place between comb A and the nonconducting belt that sprays electric charges onto the belt by corona or point discharge.

The moving belt carries this charge upward and transfers it to the hollow conductor. Collector comb B y inside the hollow conductor removes the charge from the belt by point discharge. Then, the charge flows to the outer surface of the hollow conductor where it accumulates as the process continues. The potential difference between the conductor and the Earth cumulatively increases until the energy density of the electric field builds up to such a high value that the insulating property of the surrounding gas breaks down and a corona discharge takes place through the surrounding gas between the conductor and the ground. If C is the capacitance of – the system and |Q| is the magnitude of the charge transferred from the ground to the conductor, the potential difference V between them is given by V = |Q|/C.

If the hollow conductor is well insulated from the Earth, the accumulated charge |Q| can be large enough and V can build up to several million volts. Since V is limited by the breakdown voltage of the surrounding medium, the entire apparatus is usually enclosed in a pressurized vessel containing a gas such as nitrogen or Freon. This raises the breakdown voltage considerably.

Positively charged particles may be accelerated in the evacuated tube from a source at the same potential as the dome conductor toward a target at the ground potential.

Uses : Machines equipped with positive ion sources and arranged for positive ion acceleration are widely used for research in nuclear structure and nuclear reactions, and for production of radioisotopes. Machines equipped with electron sources are used for X-ray therapy, industrial radiography, food and drug sterilization as well as research.

[Note : in a Van de Graaff single-stage accelerator, an ion source is located inside the high-voltage terminal (the dome conductor). Since the electric field inside a charged conductor is zero, the source must be at the same potential as the terminal. The ions are accelerated to the target (at the ground potential) by repulsion. Early quan-titative data on nuclear properties and processes came from Van de Graaff positive ion accelerators, which had a positive ion (proton, deuteron, alpha particle) source and the high voltage terminal raised to a high positive potential.

Van de Graaff electron accelerators had also been very successful as sources for X-rays for radiotherapy and industrial radiography. For an electrostatic electron accel-erator, the terminal is charged to a high negative potential and a thermionic cathode replaces the ion source. Accel-erated electrons impinging on watercooled gold targets provided for the first time high energy X-rays (~2 MeV) for cancer therapy. A number of such X-ray generators were developed by Prof. J. G. Trump and R.J. Van de Graaff which were installed in hospitals and industries. These instruments were about 3 ft in diameter and 6 ft long, and could be swung into any position to direct the X-ray beam.]

Multiple Choice Questions

Question 1.
Electric Intensity due to a charged sphere at a point outside the sphere dectea.ses with
(A) an increase in the charge on the sphere
(B) an increase in the dielectric constant
(C) a decrease m the distance from the centre of the sphere
(D) a decrease in the square of the distance from the centre of the sphere.
Answer:
(B) an increase in the dielectric constant

Question 2.
A charged spherical conductor in a medium of permittivity e basa surface charge density σ. At an outside point, a distance r from the centre of the conductor, the electric field intensity is

Answer:
(A) \(\frac{\sigma}{\varepsilon}\)

Question 3.
The electric field intensity in free space at a distance r outside a charged conducting sphere of radius R, in terms of its surface charge density e is

Answer:
(A) \(\frac{\sigma}{\varepsilon_{0}}\left(\frac{R}{r}\right)^{2}\)

Question 4.
If the radius of a sphere is doubled without chianging the charge on it then the electric flux originating from the sphere is
(A) double
(B) half
(C) the same
(D) zero.
Answer:
(C) the same

Question 5.
The intensity of electric field at a point clone but outside a charged conducting cylinder is proportional to
[r is the distance of the point from the axis of the cylinder]
(A) \(\frac{1}{r}\)
(B) \(\frac{1}{r^{2}}\)
(C) \(\frac{1}{r^{3}}\)
(D) r.
Answer:
(A) \(\frac{1}{r}\)

Question 6.
In the diagram, \(\vec{E}\) is a uniform electric field. Point B is to the west of point A while point C is to the east and point D is to the south. Which of the following is correct?

(A)V_B > V_A > V_C
(B) V_B < V_A < V_C
(C) V_B = V_C
(D) V_D = V_A
Answer:
(C) V_B = V_C

Question 7.
The figure shows three capacitors C₁, C₂ and C₃. The dashed lines are equipotential surfaces within each capacitor. In which of the capacitors is the pd. between the two equipotentials ∆V = 50V?

(A) Only in C₁
(B) Only in C₁ and C₂
(C) Only in C₃
(D) In all three capacitors
Answer:
(D) In all three capacitors

Question 8.
The potential energy of a dipole iii a uniform electric held \(\vec{E}\) is minimum when the dipole moment is
(A) transverse to \(\vec{E}\)
(B) parallel to \(\vec{E}\)
(C) antiparallel to \(\vec{E}\)
(D) either parallel or antiparallel to \(\vec{E}\).
Answer:
(B) parallel to \(\vec{E}\)

Question 9.
Which of the following molecules is nonpoLar?
(A) N₂O
(B) H₂O
(C) HCl
(D) CO₂
Answer:
(D) CO₂

Question 10.
A paralel-plate capacitor is charged by connecting it to a battery. The battery is then disconnected and the distance between the plates is doubled. This doubles
(A) the electric field at each point
(B) the charge density on each conductor
(C) the potential difference between the conductors
(D) the stored energy.
Answer:
(D) the stored energy.

Question 11.
A dielectric of relative permittivity k completely fills the space between the plates of a parallel.plate capacitor. When the surface charge density on the plates is σ, the polarization of the dielectric is
(A) σ (k – \(\frac{1}{k}\))
(B) \(\frac{\sigma}{k}\)
(C) σ (1 – \(\frac{1}{k}\))
(D) σ (k – 1)
Answer:
(C) σ (1 – \(\frac{1}{k}\))

Question 12.
If at a certain stage during the charging of a capacitor of capacitance C. the charge and potential difference are q and e, the work dW required to transfer an additional amount of charge dq is
(A) vdq
(B) \(\frac{d q}{v}\)
(C) \(\frac{v d q}{C}\)
(D) \(\frac{q^{2}}{2 C}\)
Answer:
(A) vdq

Question 13.
The energy density in the region between the plates of a charged parallel-plate air capacitor is given by the expression
(A) \(\frac{1}{2}\)ε₀E²
(B) \(\frac{1}{2}\)ε₀E
(C) \(\frac{E^{2}}{2 \varepsilon_{0}}\)
(D) \(\frac{\sigma^{2}}{\varepsilon_{0}}\)
Answer:
(A) \(\frac{1}{2}\)ε₀E²

Question 14.
A 5 μF capacitor is charged to a p.d. of 10 V. If it is further charged, so that its p.d. increases to 20 V, the electric energy stored in it increases by
(A) 450 μJ
(B) 500 μJ
(C) 750 μJ
(D) 900 μJ
Answer:
(C) 750 μJ

Question 15.
A 5 pF capacitor is connected in series with a 10 μF capacitor and the combination is connected across a 9 V battery. The potential differences across the capacitors are in the ratio
(A) 4 : 1
(B) 3 : 1
(C) 2 : 1
(D) 1 : 1
Answer:
(C) 2 : 1

Question 16.
A 2 μF capacitor, charged to a p.d. of 200 V, is connected across an uncharged capacitor. If the common p.d. is 20 V, the capacitance of the second capacitor is
(A) 18 μF
(B) 20 μF
(C) 36 μF
(D) 40 μF
Answer:
(A) 18 μF

Question 17.
Three capacitors of capacitances 2 μF, 3 μF and 6 μF are connected in series. The equivalent capacitance of the combination is
(A) 0.5 μF
(B) 1 μF
(C) 1.1 μF
(D) 11 μF
Answer:
(B) 1 μF

Question 18.
Two capacitors each of capacitance 4 μF are connected in series, and a third capacitor of capacitance 4 μF is connected in parallel with the combination. Then, the equivalent capacitance of the arrangement is
(A) 12 μF
(B) 8 μF
(C) 6 μF
(D) 2.65 μF
Answer:
(C) 6 μF

Question 19.
A parallel-plate air capacitor of a plate area A and plate separation d has capacitance C₀. A dielectric of thickness d, width A/2 and relative permittivity k, is inserted between the plates as shown. The capacitance of the capacitor is

(A) 2(k + 1) C₀
(B) (k + 1 )C₀
(C) kC₀
(D) \(\frac{k+1}{2}\) C₀
Answer:
(D) \(\frac{k+1}{2}\) C₀

Question 20.
The resultant capacitance between the points A and B in the figure below is

(A) 1 μF
(B) 1.5 μF
(C) 2 μF
(D) 3 μF.
Answer:
(A) 1 μF

Question 21.
Two parallel plates, separated by a distance d, are kept at potential difference V volt. A charge q of mass m enters between the parallel plates with some velocity. The acceleration of the charged particle will be
(A) \(\frac{q V}{d m}\)
(B) \(\frac{d m}{q V}\)
(C) \(\frac{q m}{d V}\)
(D)\(\frac{d V}{q m}\)
Answer:
(A) \(\frac{q V}{d m}\)

Question 22.
The capacitance of an isolated spherical conductor of radius R in vacuum is
(A) not defined
(B) zero
(C) 4πε₀R
(D) infinite.
Answer:
(C) 4πε₀R

Question 23.
Three parallel plates, each of area A, form a capacitor. The separation between the first and second plates is d1 and that between the second and third is d₂. The gaps are completely filled with dielectrics of dielectric constant k₁ and k₂, respectively. The capacitance of this capacitor is

Answer:
(D) \(\frac{\varepsilon_{0} A k_{1} k_{2}}{k_{2} d_{1}+k_{1} d_{2}}\)

Question 24.
A parallel-plate capacitor, of plate area A and plate separation d, is filled with dielectrics of dielectric constants k₁, k₂ and k₃, as shown

Answer:
(C) \(\frac{\varepsilon_{0} A}{d}\left(\frac{k_{1}}{2}+\frac{k_{2} k_{3}}{k_{2}+k_{3}}\right)\)

Question 25.
With three 6 μF capacitors, which of the capacitance values are available to you ?
(A) 2 μF and 18 μF
(B) 2 μF, 9 μF, 12 μF and 18 μF
(C) 2 μF, 9 μF and 18 μF
(D) 2 μF, 6 μF, 9 μF, 12 μF and 18 μF
Answer:
(D) 2 μF, 6 μF, 9 μF, 12 μF and 18 μF

Question 26.
A capacitor of plate separation 0.02 mm is completely filled with a dielectric material of strength 20 kV/mm. The maximum voltage rating of the capacitor is
(A) 100 V
(B) 200 V
(C) 400 V
(D) 800 V
Answer:
(C) 400 V

Question 27.
Three capacitors C₁, C₂ and C₃ are connected to a battery of p.d. V as shown. Which of the following are the correct relations for the charges on the capacitors and the p.d.s across them ?

(A) Q₁ = Q₁ = Q₃ andV₁ = V₂ = V₃ = V
(B) Q₁ = Q₂ + Q₃ and V = V₁ + V₂ + V₃
(C) Q₁ = Q₂ + Q₃ and V= V₁ + V₂
(D) Q₂ – Q₃ and V₂ = V₃
Answer:
(C) Q₁ = Q₂ + Q₃ and V= V₁ + V₂

Question 28.
A copper plate of thickness b is inserted between the plates of a parallel-plate capacitor of plate separation d. If b = d/3, the capacitances before and after the insertion of the plate are in the ratio

(A) 2 : 3
(B) 3 : 2
(C) 1 : \(\sqrt {3}\)
(D) \(\sqrt {3}\) : 1.
Answer:
(A) 2 : 3

Question 29.
The energy stored in a charged capacitor is U. The capacitor is isolated and connected across the terminals of an identical uncharged capacitor. The energy stored in each capacitor is
(A) U
(B) 3U/4
(C) U/2
(D) U/4
Answer:
(D) U/4

Question 30.
An uncharged parallel-plate capacitor filled with a material of dielectric constant k is connected to a parallel-plate air capacitor of identical geometry charged to a potential V. At equilibrium, common potential difference across them is V’. The dielectric constant k is equal to V’-V

Answer:

Question 31.
Two parallel capacitors of capacitances C and 2C are connected in parallel and charged to a potential V. The battery is then disconnected and the space between the plates of the first capacitor is filled with a material of dielectric constant k. The potential difference across the capacitors is
(A) \(\frac{3 V}{k}\)
(B) \(\frac{3 V}{k+2}\)
(C) \(\frac{3 V}{3k+2}\)
(D) \(\frac{4 V}{2k+3}\)
Answer: