Maharashtra Board Class 12 Physics Important Questions Chapter 2 Mechanical Properties of Fluids

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 2 Mechanical Properties of Fluids Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 2 Mechanical Properties of Fluids

Question 1.
What is a fluid? Give two examples.
Answer:
A fluid is a substance that can flow. A fluid has shear modulus O and yield to shear. Under a shear stress and a pressure gradient, a fluid begins to flow. Liquids, gases and plasmas are collectively called fluids.

Examples : All gases, all liquids, molten glass and lava, honey, etc.

Question 2.
What is an ideal fluid?
OR
State the characteristics of an ideal fluid.
Answer:
An ideal fluid is one that has the following properties:

1. It is incompressible, i.e., its density has a constant value throughout the fluid.
2. Its flow is irrotational, i.e., the flow is steady or laminar. In an irrotational flow, the fluid doesn’t rotate like in a whirlpool arid the velocity of the moving fluid at a specific point doesn’t change over time. (Many fluids change from laminar to turbulent flow as the speed of the fluid increases above some specific value. This can dramatically change the properties of the fluid.)
3. Its flow is nonviscous or inviscid, i.e., internal friction or viscosity is zero so that no energy lost due the motion of the fluid.

Question 3.
How does a fluid differ from a solid ?
Answer:
In response to a shear as well as normal force, a solid deforms and develops a restoring force. Within the elastic limit, both types of deformation is reversible. A solid changes its shape under a shear. A normal force causes a change in its length or volume. If the elastic limit is exceeded, the solid gets an irreversible deformation called a permanent set.

A fluid, on the other hand, can only be subjected to normal compressive stress, called pressure. A fluid does not have a definite shape, so that under a shear it begins to flow, Real fluids, with non-zero viscosity, display a weak resistance to shear.

Question 4.
State the properties of a fluid.
Answer:
Properties of a fluid :

1. They do not resist deformation and get permanently deformed.
2. They are capable of flowing.
3. They take the shape of the container.

Question 5.
Define pressure. State its SI and CGS units and dimensions.
Answer:
Definition : The pressure at a point in a fluid in hydrostatic equilibrium is defined as the normal force per unit area exerted by the fluid on a surface of infinitesimal area containing the point.
Thus, the pressure, p = \(\lim _{\Delta A \rightarrow 0} \frac{F}{\Delta A}\)
where F is the magnitude of the normal force on a surface of area ∆A. The pressure is defined to be a scalar quantity.

SI unit: the pascal (Pa), 1 Pa = 1 N∙m^-2
CGS unit: the dyne per square centimetre (dyn/cm²)
Dimensions : [p] = [F][A^-1] = [MLT^-2, L^-2]
= [ML^-1 T^-2]

Question 6.
State two non-SI units of pressure.
Answer:
Two non-SI units, which are either of historical interest, or are still used in specific fields are the bar and the torr.
1 bar = 0.1 MPa = 100 kPa = 1000 hPa = 10⁵Pa
1 torr = (101325/760) Pa = 133.32 Pa
[Note : Their use in modern scientific and technical work is strongly discouraged.]

Question 7.
If a force of 200 N is applied perpendicular to a surface of area 10 cm², what is the corresponding pressure ?
Answer:
Pressure, p = \(\frac{F}{A}=\frac{200 \mathrm{~N}}{10 \times 10^{-6} \mathrm{~m}^{2}}\) = 2 × 10⁷ N/m²

Question 8.
Explain why the forces acting on any surface within a fluid in hydrostatic equilibrium must be normal to the surface.
Answer:
In a fluid, the molecules are in a state of random motion and the intermolecular cohesive forces are weak. If a fluid is subjected to a tangential force (shear) anywhere within it, the layers of the fluid slide over one another, i.e., the fluid begins to flow. Thus, a fluid cannot sustain a tangential force. So, in

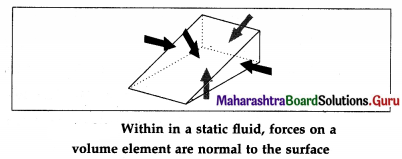
turn, a fluid at rest cannot exert a tangential force on any surface with which it is in contact. It can exert only a force normal to the surface. Hence, if a fluid is in hydrostatic equilibrium (i.e., at rest), the force acting on any surface within the fluid must be normal to the surface.

Question 9.
Would you rather have someone wearing studs step on your foot or have someone wearing tennis shoes step on your foot ?
Answer:
A person would exert the same downward force regardless of whether he or she was wearing studs or tennis shoes. However, if the person were wearing studs, the force would be applied over a much smaller area, so the pressure would be greater (and so would be more painful).

Question 10.
Would you rather have an elephant stand on your foot directly or have an elephant balance on a thumbtack on top of your foot?
Answer:
The downward force of the elephant’s weight would be applied over a much smaller area if it were balancing on a thumbtack, so the pressure would be greater.

Question 11.
Derive an expression for pressure exerted by a liquid column.
Answer:
At a point at depth h below the surface of a liquid of uniform density ρ, the pressure due to the liquid is due to the weight per unit area of a liquid column of height h above that point.

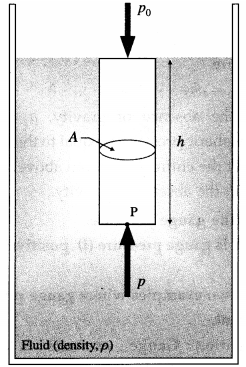
In above figure to find the pressure due to the liquid at point P, consider the cylindrical liquid column, of cross section A and height h, above that point.

The weight of this liquid column = volume × density × acceleration due to gravity
= (Ah)(ρ)(g)
∴ Pressure due to the liquid at depth h
= \(\frac{\text { weight of the liquid column }}{\text { cross sectional area }}\)
= \(\frac{A h \rho g}{A}\) = hpg
If the free surface of the liquid is open to the atmosphere, the pressure on the surface is the atmosphere pressure p₀. Then, the absolute pressure within the liquid at a depth h is p = p₀ + hρg

Question 12.
State the characteristics of pressure due to a liquid at rest at a point within it.
Answer:
Characteristics of pressure due to a liquid at rest at a point within it:

1. Within a liquid of constant density, the pressure is directly proportional to the depth.
2. At the same depth within liquids of different densities, the pressure is directly proportional to the density of the liquid.
3. Within a liquid of constant density, the pressure at a given depth is directly proportional to the acceleration due to gravity.
4. The pressure at a point within a given liquid is the same in all directions.
5. The pressure at all points at the same horizontal level within a given liquid is the same.

Question 13.
How much force is exerted on one side of an 8.50 cm by 11.0 cm sheet of paper by the atmosphere? How can the paper withstand such a force ?
Answer:
Pressure p = F/A. Therefore, the force on one side is F = ρ ∙ A = (1.013 × 10⁵ Pa) (8.50 × 11.0 × 10^-4 m²) = 947.2 N.

The pressure at a point within a fluid being the same in all directions, the same force acts on the other side of the paper. Thus, the net force on the paper is zero.

Question 14.
What is the pressure exerted by a water column of height 1 m?[ρ = 10³ kg/m³, g = 9.8 m/s²]
Answer:
Pressure exerted by the water column = hρg
= 1 m(10³ kg/m³) × (9.8 m/s²)
= 9.8 × 10³Pa

Question 15.
Would you rather breathe through a 2 m long tube to the surface in 1.5 m of water in the ocean or breathe at the beach near the ocean?
Answer:
The pressure on one’s lungs would be much greater under water than standing on the beach because the force exerted by the water on the lungs ‘ is greater than the force exerted by the air. Because the pressure of the water on the lungs is so much greater than the outward pressure of the air inside, it would be difficult to take a breath under 1.5 m of water than on the beach.

Question 16.
What is atmospheric pressure ? Define standard atmospheric pressure.
Answer:
The Earth’s surface is covered with a layer of atmosphere, with more than 99% of the atmosphere lying within 31 km of the surface. The weight of the atmosphere exerts a downward thrust on any surface lying within it. This gives rise to atmospheric pressure. The atmospheric pressure at any height above the Earth’s surface is the weight of a column of air of unit cross section from that altitude to the top of the atmosphere.

Definition : Standard atmospheric pressure, or one atmosphere of pressure, is defined as the pressure equivalent of a column of mercury that is exactly 0.7600 m in height at 0 °C.

We can calculate this equivalent pressure in SI unit by using the density of mercury
ρ = 13.6 × 10³ kg/m³ and g = 9.80 m/s².
1 atm = (0.76 m) . (13.6 × 10³ kg/m³) . (9.80 m/s²)
= 1.013 × 10⁵ Pa = 101.3 kPa
[Note : 1000 mbar = 100 kPa. Therefore, 1 atm = 1013 mbar.]

Question 17.
Explain gauge pressure and absolute pressure within a liquid open to the atmosphere.
OR
Explain the effect of gravity on fluid pressure.
Answer:
Consider a cylindrical fluid column of uniform density ρ, area of cross section A and height h,

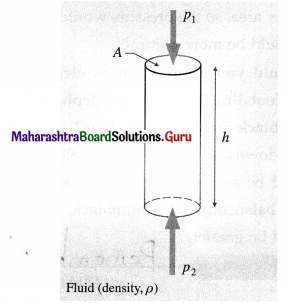
The mass of the fluid within the column is
m = density × volume
= ρAh

If p₁ and p₂ are the pressures at the top and bottom faces of the column, the forces on the top and bottom faces are respectively.
F₁ = p₁A + mg (downward)
and F₂ = p₂A (upward)
If the column is in equilibrium,
F₂ = F₁
∴ p₂A = p₁A + mg = p₁A + ρAhg
∴ P₂ ~ P₁ = ρhg
If p₁ = p₀ = atmospheric pressure, the gauge pressure
P₂ – P₀ = ρhg

In the absence of gravity, p₂ = p₀ But since atmospheric pressure is equal to the weight per unit area of the entire air column above, even p0 will be zero in the absence of gravity.

Question 18.
Define gauge pressure.
When is gauge pressure (i) positive (ii) negative ?
Give two examples where gauge pressure is more relevant.
Answer:
Definition : Gauge pressure is the pressure exerted by a fluid relative to the local atmospheric pressure.

Gauge pressure, p_g = p – p₀

where p is the absolute pressure and p₀ is the local atmospheric pressure.

When the pressure inside a closed container or tank is greater than atmospheric pressure, the pressure reading on a pressure gauge is positive. The pressure inside a ‘vacuum chamber’-a rigid chamber from which some of the air is pumped out-is less than the atmospheric pressure, so a pressure gauge on the chamber designed to measure negative pressure reads a negative value.

At a depth within a liquid of density ρ, the gauge pressure is p_g = p – p₀ = hpg

Examples : Tyre pressure gauge, blood pressure gauge, pressure gauge on an oxygen or scuba tank.

Question 19.
Define absolute pressure.
Answer:
Definition : The absolute pressure, or total press-ure, is measured relative to absolute zero on the pressure scale-which is a perfect vacuum-and is the sum of gauge pressure and atmospheric press-ure. It is the same as the thermodynamic pressure.

Absolute pressure accounts for the atmospheric pressure, which in effect adds to the pressure in any fluid which is not enclosed in a rigid container i.e., the fluid is open to the atmosphere.
p = p₀ + P_g
where p₀ and p_g are respectively atmospheric pressure and the gauge pressure.

Absolute pressure can be never negative.

Question 20.
If your tyre gauge reads 2.31 atm (234.4 kPa), what is the absolute pressure ?
Answer:
The absolute pressure, p = p₀ + p_g = 1 atm + 2.31 atm = 3.31 atm (≅ 335 kPa).

Question 21.
State and explain the hydrostatic paradox. OR Explain hydrostatic paradox.
Answer:
Hydrostatic paradox : The normal force exerted by a liquid at rest on the bottom of the containing vessel is independent of the amount of liquid or the shape of the container, but depends only on the area of the base and its depth from the liquid surface.

Consider several vessels of the same base area as shown in figure (a). A liquid is poured into them to the same level, so that the pressure is the same at the bottom of each vessel. Then it must follow that the normal force on the base of each vessel is also the same. However, when placed on a scale balance they are found to have different weights. Herein lies the paradox.

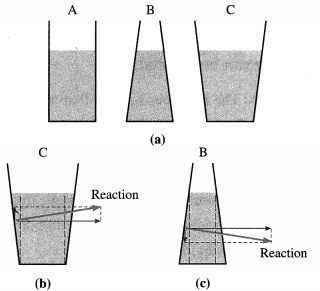
Explanation : Since a liquid always exerts a normal force on a wall of the container, in turn, the wall exerts an equal and opposite reaction on the liquid. In the case of tube A, this reaction is everywhere horizontal; so that the normal force at the base of A is only due to the weight of the liquid column above.

The reaction of the slanted wall of vessel C has a – vertical component, as shown in figure (b), which supports the weight of the liquid above the slanted side. Hence, the normal force at the base of C is only due to the weight of the vertical liquid column above the base, shown by dashed lines. Since the vessels A and C are filled to the same height and have the same base area, the pressures at the bases of the two vessels are also same. However, the volume of the liquid being clearly different, they have different weights.

In the case of vessel B, the downward vertical component of the reaction of the wall provides an extra normal force at the base, as shown in figure (c).

Question 22.
Can pressure in a fluid be increased by pushing directly on the fluid ? Give an example.
Answer:
Yes, but it is much easier if the fluid is enclosed.

Examples : (1) The heart increases the blood pressure by pushing on the blood in an enclosed ventricle.
(2) Hydraulic brakes, lifts and cranes operate by pushing on oil in an enclosed system.

Question 23.
State Pascal’s law.
Answer:
Pascal’s law : A change in the pressure applied to an enclosed fluid at rest is transmitted un-diminished to every point of the fluid and to the walls of the container, provided the effect of gravity can be ignored.

[Note : The law does not say that ‘the pressure is the same at all points of a fluid’ – rightly so, since the pressure in a fluid near Earth varies with height. Rather, the law applies to the change in pressure. According to Pascal’s law, if the pressure on an enclosed static fluid is changed by a certain amount, the pressure at all points within the fluid changes by the same amount.

The above law is due to Blaise Pascal (1623 – 62), French mathematician and physicist.]

Question 24.
Describe an experimental proof of Pascal’s law.
Answer:
Consider a spherical vessel having four cylindrical tubes A, B, C and D each fitted with air-tight

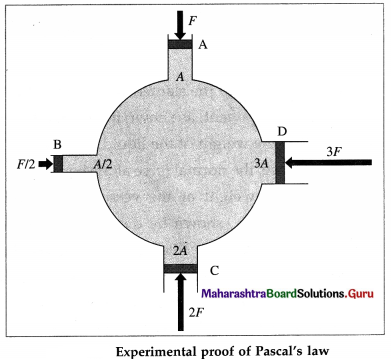
frictionless pistons of areas of cross section A, A/2, 2A and 3A, respectively, as shown in above figure. The vessel is filled with an incompressible liquid such that there is no air between the liquid and the pistons.

If the piston A is pushed with a force F, the pressure on the piston and the liquid in the vessel is p_A = F/A. It is seen that the other three pistons are pushed outwards. To keep these pistons at their respective original positions, forces of F/2, IF and 3F, respectively are required to be applied on pistons B, C and D respectively to hold them. Then, the pressures on the respective pistons are
p_B = \(\frac{F / 2}{A / 2}\) = F/A, p_C = 2F/2A = F/A, and
p_D = 3F/3A = F/A
∴ p_A = p_B = p_C = p_D = F/A

This indicates that the pressure applied is trans-mitted equally to all parts of liquid. This proves Pascal law.

Question 25.
Explain the principle of multiplication of thrust.
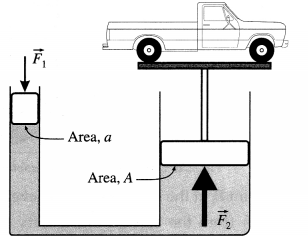
Answer:
Principle of multiplication of thrust by transmission of fluid pressure : The normal force exerted by a fluid on any surface in contact with it is called the thrust. Consider two hydraulically connected cylinders, one of cross section a and the other A, as in figure. If a force F_a is exerted on the smaller piston, pressure p = \(\frac{F_{\mathrm{a}}}{a}\) is produced and transmitted undiminished throughout the liquid. Then, the thrust F_A on the larger piston is
F_A = pA = \(\frac{A}{a}\) F_a
If A = na, F_A = nF_a, i.e., the thrust on the larger piston is multiplied n times. This is known as the principle of multiplication of thrust by transmission of fluid pressure.

Question 26.
State any two applications of Pascal’s law.
Briefly explain their working.
Ans.
Applications of Pascal’s law :

1. Hydraulic car lift and hydraulic press
2. Hydraulic brakes.

All the above applications work on the principle of multiplication of thrust by transmission of fluid pressure.

(1) Working of a hydraulic lift : Two hydraulically connected cylinders, one of cross section a and the other A, are such that A is many times larger than a : A = na. If a force F_a is exerted on the smaller piston, a pressure p = \(\frac{F_{\mathrm{a}}}{a}\) is produced and transmitted undiminished throughout the liquid. Then, the thrust F_A on the larger piston
F_A = pA = \(\frac{A}{a}\) F_a = nF_a
is n times greater than that on the smaller piston. A platform attached to the larger piston can lift a car (as in a hydraulic car lift), or press bales of cotton or paper against a fixed rigid frame (as in Brahma’s.)

(2) Working of hydraulic brakes in a car: Brakes which are operated by means of hydraulic pressure are called hydraulic brakes. An automobile hydraulic brake system, shown schematically in below figure, has fluid-filled master and slave cylinders connected by pipes. When the brake pedal is pushed, it depresses the piston of the pedal or master cylinder through a lever. The change in pressure in the master cylinder is transmitted to the four wheel or slave cylinders. Since the brake fluid is incompressible, the pistons of the slave cylinders are pushed out, pressing braking pads onto the braking discs on the wheels. Note that we can add as many wheel cylinders as we wish.

The master cylinder has a much smaller area of cross section A_m compared to the combined area A_s

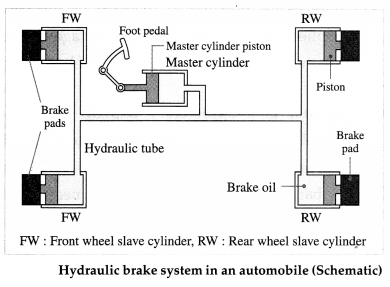
of the slave cylinders. Hence, with a small force F_m on the master cylinder, a force F_s = \(\frac{A_{\mathrm{s}}}{A_{\mathrm{m}}}\) F_m which is greater than F_m is applied on each slave cylinder. Consequently, the master piston has to travel sev-eral inches to move the slave pistons the fraction of an inch it takes to apply the brakes. But the arrangement allows great force to be exerted at the brake pads.

[Note : (1) Pascal’s law laid the foundation for hydraulics, the use of a liquid under pressure to transfer force or motion, or to increase an applied force. It is one of the most important branches in modern engineering. (2) A hydraulic system, as an example of a simple machine, can increase force but cannot do more work than is done on it. Work being force times the distance moved, the piston in a wheel cylinder moves through a smaller distance than that in the pedal cylinder. Power brakes in modern automobiles have a motorized pump that does most of the work in the system.]

Question 27.
Why are liquids used in hydraulic systems but not gases?
Answer:
Liquids are used in a hydraulic system because liquids are incompressible and transmit a change in pressure undiminished to all parts of the system. On the other hand, on increasing the pressure, a gas will be compressed into a smaller volume due to which there will be no transmission of force or motion.

Question 28.
State one advantage of hydraulic brakes in an automobile.
Answer:
Advantages of

1. By Pascal’s law, equal braking effort is applied to all the wheels.
2. It is easily possible to increase or decrease the applied force-during the design stage-by changing the size of piston and cylinder relative to other.

Question 29.
What is a barometer? Explain the use of a simple mercury barometer to measure atmospheric pressure.
Answer:
A barometer is an instrument to measure atmospheric pressure. The mercury barometer was in-vented by Evangelista Torricelli (1609-47). Italian physicist and mathematician.

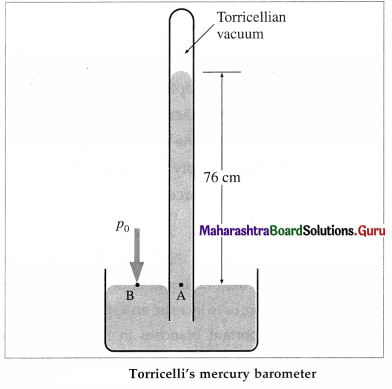
A strong glass tube, about one metre long and closed at one end, is filled with mercury. With a finger over the open end, the tube is inverted and the open end is immersed into a bowl of mercury. When the finger is removed, the mercury level in the tube drops. The mercury column in the tube stands at a height h for which the pressure at point A inside the tube due to the weight of the mercury column is equal to the atmospheric pressure p0 outside (at point B).

The space at the closed end of the tube, after the mercury level drops, is nearly a vacuum, known as the Torricellian vacuum, so the pressure there can be taken as zero. It, therefore, follows that p₀ = pgh Where p is the density of mercury and h is the height of the mercury column.

Question 30.
What is an open tube manometer? Briefly describe its function with a neat diagram.
Answer:
An open tube manometer is a device to measure the pressure of a gas in a vessel. It consists of a U-shaped tube containing a liquid (say, mercury) of density p, as shown in below figure.

One end of the tube is connected to the vessel while the other end is open to the atmosphere. The pressure p at point A is the (unknown) pressure of the gas in the vessel. The pressure on the mercury column in the open tube is the atmospheric pressure p₀.

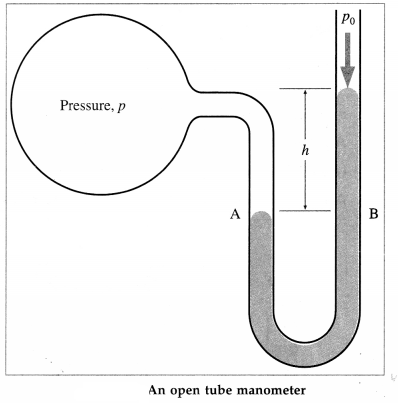
A point B, at the same horizontal level as A, is at a depth h from the surface of mercury in the open tube. Therefore, the pressure at B is p₀ + ρgh.

The pressures at points A and B at the same liquid level being the same, equating the unknown pressure p (at A) to the pressure at B.
p = p₀ + ρgh
The pressure p is called the absolute pressure, and the difference in pressure p – p₀ is called the gauge pressure.

Question 31.
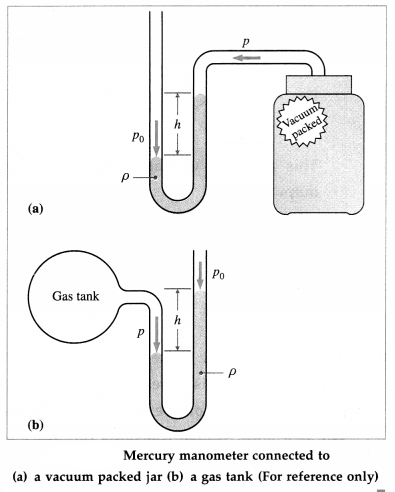
An open tube manometer is connected to (i) a vacuum-packed candy jar, with the atmospheric pressure in the open tube supporting a column of fluid of height h (ii) a gas tank, with the absolute pressure in the tank supporting a column of fluid of height h. Is the absolute pressure in the jar and the gas tank greater than or less than the atmospheric pressure ? By how much ?
Answer:
In the first case, p_abs is less than the atmospheric pressure, whereas in the second case, p_abs is greater than the atmospheric pressure. In both cases, p_abs differs from the atmospheric pressure by the gauge pressure hρg, where ρ is the density of the fluid in the manometer.

32. Solve the following

Question 1.
For diver’s safety, a 10 m platform diving pool should be 5 m deep. However, with an excellent dive, a diver usually reaches a maximum depth of 2.5 m.
(i) Calculate the pressure due to the weight of the water at the depth of 2.5 m.
(ii) Calculate the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm. [Density of water = 10³ kg/m³, 1 atm = 101.3 kPa]
Solution:
Data : h = 250 m, ρ = 1000 kg/m³, g = 9.8 m/s², 1 atm = 101.3 kPa
(i) ρ = hpg = (250)(1000)(9.8) = 2.45 mPa
= \(\frac{2.45 \times 10^{6}}{1.013 \times 10^{5}}\) = 24.18 atm
This gives the pressure at a depth of 250 m.

(ii) h = \(\frac{p}{\rho g}=\frac{1.013 \times 10^{5}}{10^{3} \times 9.8}\) = 10.34 m
This gives the required depth.

Question 2.
Suppose a dam is 250 m wide and the water is 40 m deep at the dam. What is
(i) the average pressure on the dam
(ii) the force exerted against the dam due to the water?
Solution :
Data : Width, L = 250 m, depth H = 40 m, ρ = 1000 kg/m³, g = 9.8 m/s²
Since pressure increases linearly with depth, the average pressure p_av due to the weight of the water is the pressure at the average depth h of 20 m. The force exerted on the dam by the water is the average pressure times the area of contact, F = p_av A = p_av LH.
(i) p _av = hρg = (20)(1000)(9.8) = 1.96 × 10⁵Pa
(ii) F = p_avA = p_avLH = (1.96 × 10⁵)(250)(40)
= 1.96 × 10⁵ N

Question 3.
A car lift at a service station has a piston of diameter 30 cm. The lift and piston weigh 800 kg wt. What pressure (in excess of the atmospheric pressure) must be exerted on the piston to raise a car weighing 1700 kg wt at a constant speed? [g = 9.8 m/s²]
Solution:
Data : Piston diameter, D = 30 cm = 0.3 m. mass of lift and piston, m = 800 kg, mass of car, M = 1700 kg
Cross-sectional area of the piston.
A = \(\frac{\pi D^{2}}{4}=\frac{3.142(0.3 \mathrm{~m})^{2}}{4}\) = 7.07 × 10^-2 m ²
Total weight of the car and lift,
W = (m + M)g
= (800 kg + 1700 kg) (9.8 m/s²)
= 2.45 × 10⁴ N
Therefore, the pressure on the piston
p = \(\frac{F}{A}=\frac{W}{A}=\frac{2.45 \times 10^{4} \mathrm{~N}}{7.07 \times 10^{-2} \mathrm{~m}^{2}}\)
= 3.465 × 10⁵ Pa
A pressure of 3.465 × 10⁵ Pa must be exerted on the piston.

Question 4.
The diameters of two pistons in a hydraulic press are 5 cm and 25 cm respectively. A force of 20 N is applied to the smaller piston. Find the force exerted on the larger piston.
Solution:
Data : D₁ = 5 cm, D₂ = 25 cm, F₁ = 20 N
By Pascal’s law,

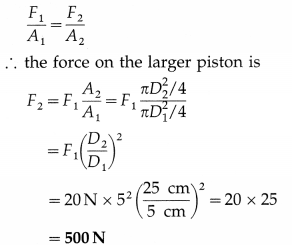
Question 5.
In a hydraulic lift, the input piston has surface area 20 cm². The output piston has surface area 1000 cm². If a force of 50 N is applied to the input piston, it raises the output piston by 2 m. Calculate the weight of the support on the output piston and the work done by it.
Solution:
Data : A₁ = 20 cm² = 2 × 10^-3 m²,
A₂ = 1000 cm² = 10^-1 m², F₁ = 50 N, s₂ = 2m
(i) By Pascal’s law,

This gives the weight of the support on the output piston.

(ii) The work done by the force transmitted to the output piston is
F₂S₂ = (2500 N) (2 m)
= 5000 J

Question 6.
A driver pushes the brake pedal of a car exerting a force of 100 N that is increased by the simple lever to a force of 500 N on the pedal (master) cylinder. The hydraulic system transmits this force to the four wheel (slave) cylinders. If the pedal cylinder has a diameter of 0.5 cm and each wheel cylinder has a diameter of 2.5 cm, calculate the magnitude of the force F_s on each of the wheel cylinder.
Solution:
Data : F_m = 500 N, D_m = 1 cm, D_s = 2.5 cm
\(\frac{F_{\mathrm{s}}}{A_{\mathrm{s}}}=\frac{F_{\mathrm{m}}}{A_{\mathrm{m}}}\)
∴ The magnitude of the force on each of the wheel cylinders,
F_s = \(\frac{A_{\mathrm{s}}}{A_{\mathrm{m}}}\) F_m = (\(\frac{D_{\mathrm{s}}}{D_{\mathrm{m}}}\))² F_m = (\(\frac{2.5}{0.5}\))² (500)
= 25 × 500 = 12.5 kN

Question 7.
Mercury manometers are often used to measure arterial blood pressure. The typical blood pressure of a young adult raises the mercury to a height of 120 mm at systolic and 80 mm at diastolic. Express these values in pascal and bar. [Density of mercury = 13600 kg/m³, 1 mbar = 100 Pa]
Solution:
Data : p_max = p_syst = 120 mm of Hg, p_min = p_dias = 80 mm of Hg, ρ = 13600 kg/m³, g = 9.8 m/s², 1 mbar = 100 Pa
p = hρg
∴ p_syst = (0.120)(1.36 × 10⁴)(9.8)
= 1.6 × 10⁴ Pa = 16 kPa
= 1600 mbar = 1.5 bar

and P_dias = (0.08)(1.36 × 10⁴)(9.8)
= 1.066 × 10⁴ Pa = 10.66 kPa
= 1066 mbar = 1.066 bar

Question 33.
Describe the phenomenon of surface tension, giving four examples.
Answer:
Surface tension is a unique property of liquids that arises because the net intermolecular force of attraction on the liquid molecules at or near a liquid surface differs from that on molecules deep in the interior of the liquid. This results in the tendency of the free surface of a liquid to minimize its surface area and behave somewhat like a stressed elastic membrane.

Surface tension is important in understanding the peculiar behaviour of the free surface of a liquid in many cases as illustrated below :

1. Small quantities of liquids assume the form of spherical droplets, as in mist, or a mercury droplet on a flat surface. This is because the stressed surface ‘skin’ tends to contract and mould the liquid into a shape that has minimum surface area for its volume, i.e., into a sphere.
2. Surface tension is responsible for the spherical shape of freely-falling raindrops and the behaviour of bubbles and soap films.
3. The bristles of a paint brush cling together when it is drawn out of water or paint.
4. A steel needle or a razor blade can, with care, be supported on a still surface of water which is much less dense than the metal from which these objects are made of.
5. Many insects like ants, mosquitoes, water striders, etc., can walk on the surface of water.

Question 34.
Define (1) cohesive force (2) adhesive force.
Give one example in each case.
Answer:
(1) Cohesive force : The intermolecular force of attraction between two molecules of the same material is called the cohesive force.
Example : The force of attraction between two water molecules.

(2) Adhesive force : The intermolecular force of attraction between two molecules of different materials is called the adhesive force.
Example : The force of attraction between a water molecule and a molecule of the solid surface which is in contact with water.

Question 35.
Define (1) range of molecular attraction or molecular range (2) sphere of influence.
Answer:
1) Range of molecular attraction or molecular range : Range of molecular aftraction or molecular range is defined as the maximum distance between two molecules up to which the intermolecular force of attraction is appreciable.

[Note : The intermolecular force is a short range force, LeV, it is effective over a very short range-about 10^-9 m. Beyond this distance, the force is negligible. The inter molecular force does not obey inverse square law.]

2) Sphere of influence : The sphere of influence of a molecule is defined as an imaginary sphere with the molecule as the centre and radius equal to the range of molecular attraction.

[Note : All molecules lying within the sphere of influence of a molecule are attracted by (as well as attract) the molecule at the centre. For molecules which lie outside this sphere, the intermolecular force due to the molecule at the centre is negligible.]

Question 36.
What is meant by a surface film?
Answer:
The layer of the liquid surface of thickness equal to the range of molecular attraction is called a surface film.

Question 37.
What is meant by free surface of a liquid ?
Answer:
The surface of a liquid open to the atmosphere is called the free surface of the liquid.

Question 38.
Explain the phenomenon of surface tension on the basis of molecular theory.
Answer:
The phenomenon of surface tension arises due to the cohesive forces between the molecules of a liquid. The net cohesive force on the liquid molecules within the surface film differs from that on molecules deep in the interior of the liquid.

Consider three molecules of a liquid : A molecule A well inside the liquid, and molecules B and C lying within the surface film, shown in figure. The figure also shows their spheres of influence of radius R.

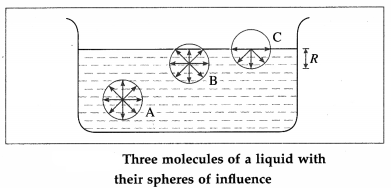
(1) The sphere of influence of molecule A is entirely inside the liquid and the molecule is surrounded by its nearest neighbours on all sides. Hence, molecule A is equally attracted from all sides, so that the resultant cohesive force acting on it is zero. Hence, it is free to move anywhere within the liquid.

(2) For molecule B, a part of its sphere of influence is outside the liquid surface. This part contains air molecules whose number is negligible compared to the number of molecules in an equal volume of the liquid. Therefore, molecule B experiences a net cohesive force downward.

(3) For molecule C, the upper half of its sphere of influence is outside the liquid surface. Therefore, the resultant cohesive force on molecule C in the
downward direction is maximum.

(4) Thus, all molecules lying within a surface film of thickness equal to R experience a net cohesive force directed into the liquid.

(5) The surface area is proportional to the number of molecules on the surface. To increase the surface area, molecules must be brought to the surface from within the liquid. For this, work must be done against the cohesive forces. This work is stored in the liquid surface in the form of potential energy. With a tendency to have minimum potential energy, the liquid tries to reduce the number of molecules on the surface so as to have minimum surface area. This is why the surface of a liquid behaves like a stressed elastic membrane.

Question 39.
Define surface tension.
State its formula and CGS and SI units.
Answer:
The surface tension of a liquid is defined as the tangential force per unit length, acting at right angles on either side of an imaginary line on the free surface of the liquid.

If F is the force on one side of a line of length Z, drawn on the free surface of a liquid, the surface tension (T) of the liquid is

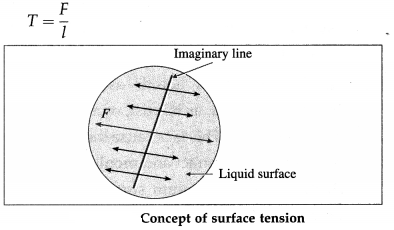
The CGS unit of surface tension : The dyne per centimetre (dyn/cm) or, equivalently, the erg per square centimetre (erg/cm²).

The SI unit of surface tension : The newton per metre (N/m) or, equivalently, the joule per square metre (J/m²).

Question 40.
Obtain the dimensions of surface tension.
Answer:
Surface tension is a force per unit length.

Question 41.
Define and explain surface energy of a liquid.
OR
Define surface energy.
OR
State its dimensions and SI unit.
OR
Why do molecules of a liquid in the surface film possess extra energy?
Answer:
Surface energy : The surface energy is defined as the extra (or increased) potential energy possessed by the molecules in a liquid surface with an isothermal increase in the surface area of the liquid.

A liquid exerts a resultant cohesive force on every molecule of its surface, trying to pull it into the liquid. To increase the surface area, it is necessary to bring more molecules from inside the liquid to the liquid surface. For this, external work must be done against the net cohesive forces on the molecules. This work is stored in the liquid surface in the form of potential energy.

This extra potential energy that the molecules in the liquid surface have is called the surface energy. Thus, the molecules of a liquid in the surface film possess extra energy.
Dimensions : [surface energy] = [ML²T^-2]
SI unit: the joule (J).

Question 42.
Why is the surface tension of paints and lubricating oils kept low?
Answer:
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oils must be low.

Question 43.
Derive the relation between the surface tension and surface energy of a liquid.
OR
Derive the relation between surface tension and surface energy per unit area.
OR
Show that the surface tension of a liquid is numerically equal to the surface energy per unit area.
Answer:
Suppose a soap film is isothermally stretched over the area enclosed by a U-shaped frame ABCD and a w cross-piece PQ that can slide smoothly along the frame, as shown in the figure. Let T be the surface tension of the soap solution and l, the length of wire PQ in contact with the soap film.

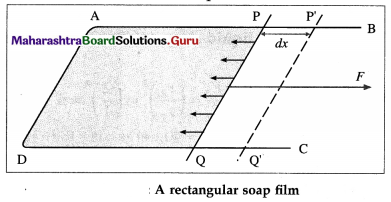
The film has two surfaces, both of which are in contact with the wire. The film tends to contract by exerting a force on wire PQ. As each surface exerts a force Tl, the net force on the wire is 2Tl.

Suppose that wire PQ is pulled outward very slowly through a distance dx to the position P’Q’ by an external force of magnitude 2T l. The work done by the external force against the force due to the film is
W = applied force × displacement
∴ W = Fdx = ITldx (∵ F = 2Tl)
This work is stored in the unit surface area in the form of potential energy. This potential energy is called the surface energy.

Due to the displacement dx, the surface area of the film increases. As the film has two surfaces, the increase in its surface area is
A = 2ldx
Thus, the work done per unit surface area is
\(\frac{W}{A}=\frac{2 T l d x}{2 l d x}\) = T
Thus, the surface energy per unit area of a liquid is equal to its surface tension.

Question 44.
Two soap bubbles of the same soap solution have diameters in the ratio 1 : 2. What is the ratio of work done to blow these bubbles ?
Answer:
Work done oc surface area.
∴ W₁/W₂ = (r₁/r₂)² = (\(\frac{1}{2}\))² = \(\frac{1}{4}\)
∴ W₁ : W₁ = 1 : 4.

Question 45.
If the surface tension of a liquid is 70 dyn/cm, what is the total energy of the free surface of the liquid drop of radius 0.1 cm ?
Answer:
E = 4πr²T = 4 × \(\frac{22}{7}\) × (0.1)² × 70
= 88 × 10^-2 × 10 = 8.8 ergs

Question 46.
The total energy of the free surface of a liquid drop of radius 1 mm is 10 ergs. What is the total energy of a liquid drop (of the same liquid) of radius 2 mm ?
Answer:
E = 4πr²T ∴ \(\frac{E_{2}}{E_{1}}=\left(\frac{r_{2}}{r_{1}}\right)^{2}=\left(\frac{2}{1}\right)^{2}\) = 4
∴ E₂ = 4E₁ = 4 × 10 = 40 ergs is the required

47. Solve the following

Question 1.
Calculate the work done in blowing a soap bubble of radius 4 cm. The surface tension of the soap solution is 25 × 10^-3 N/m.
Solution:
Data : r = 4 cm = 4 × 10^-2 m, T = 25 × 10^-3 N/m
Initial surface area of soap bubble = 0
Final surface area of soap bubble = 2 × 4πr²
Increase in surface area = 2 × 4πr² The work done
= surface tension x increase in surface area
= T × 2 × 4πr²
= 25 × 10^-3 × 2 × 4 × 3.142 × (4 × 10^-2)2
= 1.005 × 10^-3 J

Question 2.
Two soap bubbles have radii in the ratio 4 : 3. What is the ratio of work done to blow these bubbles?
Solution:
Data : \(\frac{r_{1}}{r_{2}}=\frac{4}{3}\)
Work done, W = 2TdA
∴ W₁ = 2T(4πr₁²), W₂ = 2T(4πr₂²)
∴\(\frac{W_{1}}{W_{2}}=\frac{2 T\left(4 \pi r_{1}^{2}\right)}{2 T\left(4 \pi r_{2}^{2}\right)}=\left(\frac{r_{1}}{r_{2}}\right)^{2}\)
= (\(\frac{4}{3}\))² = \(\frac{16}{9}\)

Question 3.
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of the soap solution is 30 dyn/cm.
Solution:
Data : r₁ = 1 cm, r₂ = 2 cm, T = 30 dyn/cm
Initial surface area = 2 × 4πr₁²
Final surface area = 2 × 4πr₂²
∴ Increase in surface area
= 2 × 4πr₂² – 2 × 4πr₁² = 8π(r₂² – r₁²)
∴ The work done
= surface tension × increase in surface area
= T × 8π(r₂² – r₁²)
= 30 × 8 × 3.142 × [(2)² – (1)²]
= 2262 ergs

Question 4.
A mercury drop of radius 0.5 cm falls from a height on a glass plate and breaks into one million droplets, all of the same size. Find the height from which the drop fell. [Density of mercury = 13600 kg/m3, surface tension of mercury = 0.465 N/m]
Solution:
Data : R = 0.5 cm = 0.5 × 10^-2 m, n = 10⁶, ρ = 13600 kg m³, T = 0.465 N/m, g = 9.8 m/s²
\(\frac{4}{3}\) πR³ = n × \(\frac{4}{3}\) πr³
as the volume of the mercury remains the same.
∴ r = \(\frac{R}{\sqrt[3]{n}}=\frac{0.5 \times 10^{-2}}{\sqrt[3]{10^{6}}}\) = 0.5 × 10^-4 m
This gives the radius of a droplet.
By energy conservation, if h is the height from which the drop of mass m falls,

This gives the required height.

Question 5.
Eight droplets of mercury, each of radius 1 mm, coalesce to form a single drop. Find the change in the surface energy. [Surface tension of mercury = 0.472 J/m²]
Solution:
Data : r = 1 mm = 1 × 10^-3 m, T = 0.472 J/m²
Let R be the radius of the single drop formed due to the coalescence of 8 droplets of mercury.
Volume of 8 droplets = volume of the single drop as the volume of the liquid remains constant.
∴ 8 × \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) πR³
∴ 8r³ = R³
∴ 2r = R
Surface area of 8 droplets = 8 × 4πr²
Surface area of single drop = 4πR²
∴ Decrease in surface area = 8 × 4πr² – 4πR²
= 4π(8r² – R²)
= 4π[8r² – (2r)²]
= 4π × 4r²
∴ The energy released
= surface tension × decrease in surface area
= T × 4π × 4r²
= 0.472 × 4 × 3.142 × 4 × (1 × 10^-3)²
= 2.373 × 10^-5 J

Question 6.
The total energy of the free surface of a liquid drop is 2 × 10^-4 π times the surface tension of the liquid. What is the diameter of the drop ? (Assume all terms in SI unit.)
Solution:
Data : 4πr²T = 2 × 10^-4 πT (numerically)
∴ 2r² = 10^-4
∴ r = \(\frac{10^{-2}}{\sqrt{2}}=\frac{10^{-2}}{1 \cdot 414}\)
= 0.7072 × 10^-2 m
∴ d = 2r = 2 × 0.7072 × 10^-2
= 1.4144 × 10^-2 m
This gives the diameter of the liquid drop.

Question 48.
Define angle of contact.
Answer:
The angle of contact for a liquid-solid pair (a liquid in contact with a solid) is defined as the angle between the surface of the solid and the tangent drawn to the free surface of the liquid at the extreme edge of the liquid, as measured through the liquid.

Question 49.
Draw neat diagrams to show the angle of contact in the case of a liquid which
(i) completely wets
(ii) partially wets
(iii) does not wet the solid. State the characteristics of the angle of contact in each case, giving one example of each.
Answer:
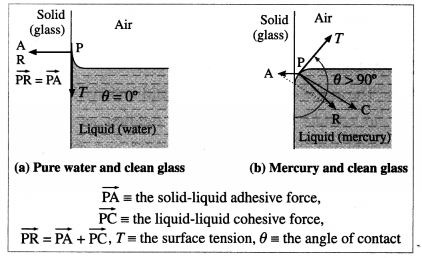
Characteristics :
(1) For a liquid, which completely wets the solid, the angle of contact is zero.
For example, pure water completely wets clean glass. Therefore, the angle of contact at the water glass interface is zero [from figure (a)].

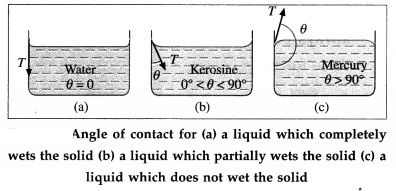
(2) For a liquid which partially wets the solid, the angle of contact is an acute angle. For example, kerosine partially wets glass, so that the angle of contact is an acute angle at the kerosine glass interface [from figure (b)].
(3) For a liquid which does not wet the solid, the angle of contact is an obtuse angle. For example, mercury does not wet glass at all, so that the angle of contact is an obtuse angle at the mercury-glass interface [from figure (c)].
(4) The angle of contact for a given liquid solid pair is constant at a given temperature, provided the liquid is pure and the surface of the solid is clean.

Question 50.
State any two characteristics of angle of contact.
Answer:
Characteristics of angle of contact:

1. It depends upon the nature of the liquid and solid in contact, and is constant for a given liquid-solid pair, other factors remaining unchanged.
2. It depends upon the medium (gas) above the free surface of the liquid.
3. It is independent of the inclination of the solid to the liquid surface.
4. It changes with surface tension and, hence, with the temperature and purity of the liquid.

Question 51.
Explain why the free surface of some liquids in contact with a solid is not horizontal.
OR
Explain the formation of concave and covex surface of a liquid on the basis of molecular theory.
Answer:
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely the solid-liquid adhesive force \(\vec{F}_{\mathrm{A}}=\overrightarrow{P A}\) and the liquid- liquid cohesive force \(\vec{F}_{\mathrm{C}}=\overrightarrow{P C} \vec{F}_{A}\) is normal to the solid surface and \(\vec{F}_{\mathrm{C}}\) is at 45° with the horizontal, from figure (a). The free surface of a liquid at rest is always perpendicular to the resultant \(\vec{F}_{\mathrm{R}}=\overrightarrow{P R}\) of these forces.

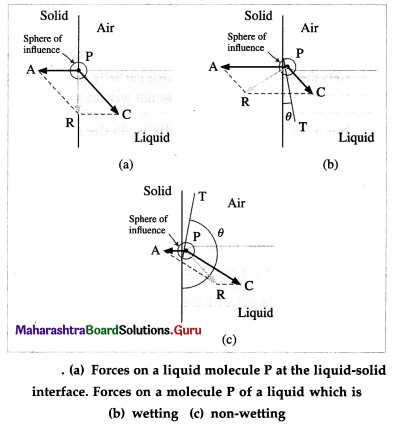
If F_C = \(\sqrt{2} F_{\mathrm{A}}, \vec{F}_{\mathrm{R}}\) is along the solid surface, the contact angle is 90° and the liquid surface is horizontal at the edge where it meets the solid, as in figure (a). In general this is not so, and the liquid surface is not horizontal at the edge.

For a liquid which completely wets the solid (e.g., pure water in contact with clean glass), F_C << F_A. For a liquid which partially wets the solid (e.g., kerosine . or impure water in contact with glass), F_C < \(\sqrt{2} F_{\mathrm{A}}\). If F_C << F_A or if F_C < \(\sqrt{2} F_{\mathrm{A}}\), the contact angle is correspondingly zero or acute and the liquid surface curves up and acquires a concave shape until the tangent PT is tangent to \(\vec{F}_{\mathrm{R}}\) fron figure (b).

If F_C > \(\sqrt{2} F_{\mathrm{A}}\), the contact angle is obtuse and the liquid surface curves down and acquires a convex shape until the tangent PT is tangent to \(\vec{F}_{\mathrm{R}}\), from figure (c).

Question 52.
State the conditions for concavity and convexity of a liquid surface where it is in contact with a solid.
Answer:
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely
(i) the solid-liquid adhesive force \(\vec{F}_{\mathrm{A}}\) normal and into the solid surface and
(ii) the liquid-liquid cohesive force \(\vec{F}_{\mathrm{C}}\) at nearly 45° with the horizontal.

If F_C << F_A or if F_C < \(\sqrt {2}\)F_A , the contact angle is correspondingly zero or acute and the liquid sur-face is concave with the solid.

If F_C > \(\sqrt {2}\)F_A, the contact angle is obtuse and the liquid surface curves down, i.e., convex, with the Solid.

Question 53.
Draw neat labelled diagrams to show angle of contact between (a) pure water and clean glass . (b) mercury and clean glass.
Answer:

Question 54.
Explain the shape of a liquid drop on a solid surface in terms of interfacial tensions.
OR
Account for the angle of contact in terms of interfacial tensions.
OR
Draw diagram showing force due to surface tension at the liquid-solid, air-solid, air-liquid interface, in case of (i) a drop of mercury on a plane solid surface and (ii) a drop of water on a plane solid surface. Discuss the variation of angle of contact.
Answer:
A liquid surface, in general, is curved where it meets a solid. The angle between the solid surface and the tangent to the liquid surface at the extreme edge of the liquid, as measured through the liquid, is called the angle of contact.

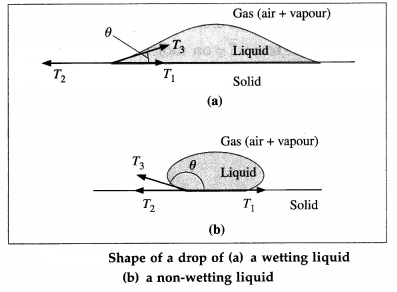
Above figure shows the interfacial tensions that act in equilibrium at the common point of the liquid, solid and gas (air + vapour).
T₁ = the liquid-solid interfacial tension
T₂ = the solid-gas interfacial tension
T₃ = the liquid-gas interfacial tension
θ = the angle of contact for the liquid-solid pair is the angle between T₁ and T₃
The equilibrium force equation (along the solid surface) is
T₃ Cos θ + T₁ – T₂ = 0
∴ cos θ = \(\frac{T_{2}-T_{1}}{T_{3}}\) …………… (1)

Case (1) : If T₂ > T₁, cos θ is positive and contact angle θ < 900, so that the liquid wets the surface.
Case (2) : If T₂ < T₁, cos θ is negative and θ is obtuse, so that the liquid is non-wetting.
Case (3): If T₂ – T₁ T₃, cos θ = 1 and θ ≅ 0°.
Case (4) : If T₂ – T₁ ≅ T₃, cos θ will be greater than 1 which is impossible, so that there will be no equilibrium and the liquid will spread over the solid surface.

Question 55.
State the expression for the angle of contact in terms of interfacial tensions?
Answer:
cos θ = \(\frac{T_{2}-T_{1}}{T_{3}}\), where θ is the angle of contact for a liquid-solid pair, T₁ is the liquid-solid interfacial tension, T₂ is the solid-gas (air + vapour) inter-facial tension and T₃ is the liquid-gas interfacial tension.

Question 56.
In terms of interfacial tension, when is the angle of contact acute ?
Answer:
The angle of contact is acute when the solid-gas (air + vapour) interfacial tension is greater than the liquid-solid interfacial tension.

Question 57.
In terms of interfacial tensions, when is the angle of contact obtuse ?
Answer:
The angle of contact is obtuse when the solid-gas (air + vapour) interfacial tension is less than the liquid-solid interfacial tension.

Question 58.
State the factors affecting a liquid-solid angle of contact.
Answer:
Factors affecting a liquid-solid angle of contact:

1. the nature of the liquid and the solid in contact,
2. impurities in the liquid,
3. temperature of the liquid.

Question 59.
Explain the effect of impurity on the angle of contact (or surface tension of a liquid).
Answer:
Effect of impurity :
(i) The angle of contact or the surface tension of a liquid increases with dissolved impurities like common salt. For dissolved impurities, the angle of contact (or surface tension) increases linearly with the concentration of the dissolved materials.

(ii) It decreases with sparingly soluble substances like phenol or alcohol. A detergent is a surfactant whose molecules have hydrophobic and hydrophilic ends; the hydrophobic ends decrease the surface tension of water. With reduced surface tension, the water can penetrate deep into the fibres of a cloth and remove stubborn stains.

(iii) It decreases with insoluble surface impurities like oil, grease or dust. For example, mercury surface contaminated with dust does not form perfect spherical droplets till the dust is removed.

Question 60.
Explain the effect of temperature on the angle of contact (or surface tension of a liquid).
Answer:
Effect of temperature : The surface tension of a liquid decreases with increasing temperature of the liquid. For small temperature differences, the decrease in surface tension is nearly directly proportional to the temperature rise.

If T and T₀ are the surface tensions of a liquid at temperatures θ and 0 °C, respectively, then T = T₀(1 – αθ) where α is a constant for a given liquid. The surface tension of a liquid becomes zero at its critical temperature. The surface tension increases with increasing temperature only in case of molten copper and molten cadmium.

Question 61.
Why cold wash is recommended for new cotton fabrics while hot wash for removing stains?
Answer:
Cold wash is recommended for new/coloured cotton fabrics. Cold water, due to its higher surface tension, does not penetrate deep into the fibres and thus does not fade the colours. Hot water, because of its lower surface tension, can penetrate deep into fabric fibres and remove tough stains.

Question 62.
Explain in brief the pressure difference across a curved liquid surface.
Answer:
Every molecule lying within the surface film of a static liquid is pulled tangentially by forces due to surface tension. The direction of their resultant, \(\vec{F}_{\mathrm{T}}\), on a molecule depends upon the shape of that liquid surface and decides the cohesion pressure at a point just below the liquid surface.

Consider two molecules, A and B, respectively just above and below the free surface of a liquid. So, the level difference between them is negligibly small and the atmospheric pressure on both is the same, p₀, Let \(\vec{F}_{\mathrm{atm}}\) be the downward force on A and B due to the atmospheric pressure.

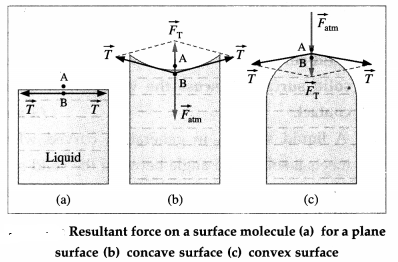
If the free surface of a liquid is horizontal, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B is zero, from figure (a). Then, the cohesion pressure is negligible and the net force on A and B is \(\vec{F}_{\mathrm{atm}}\). The pressure difference on the two sides of the liquid surface is zero.

If the free surface of a liquid is concave, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B is outwards (away from the liquid), from figure (b), opposite to \(\vec{F}_{\mathrm{atm}}\). Then, the net force on B is less than \(\vec{F}_{\mathrm{atm}}\) and the cohesion pressure is decreased. The pressure above the concave liquid surface is greater than that just below the liquid surface.

If the free surface of a liquid is convex, the resultant force \(\vec{F}_{\mathrm{T}}\) on molecule B acts inwards (into the liquid), from figure (c), in the direction of \(\vec{F}_{\mathrm{atm}}\). Then, the net force on B is greater than \(\vec{F}_{\mathrm{atm}}\) and the cohesion pressure is increased. The pressure below the convex liquid surface is greater than that just above the liquid surface.

Question 63.
Derive an expression for the excess pressure inside a soap bubble.
OR
Derive Laplace’s law for spherical membrane of a bubble due to surface tension.
Answer:
Consider a small, spherical, thin-filmed soap bubble with a radius R. Let the pressure outside the drop be Po and that inside be p. A soap bubble in air is like a spherical shell and has two gas-liquid interfaces. Hence, the surface area of the bubble is
A = 8πR² ………. (1)
Hence, with a hypothetical increase in radius by an infinitesimal amount dR, the differential increase in surface area and surface energy would be
dA = 16πR ∙ dR and
dW = T ∙ dA = 16πTRdR ………….. (2)
We assume that dR is so small that the pressure inside remains the same, equal to p. All parts of the surface of the bubble experiences an outward force per unit area equal to p – p_o. Therefore, the work done by this outward pressure-developed force against the surface tension force during the increase in radius dR is
dW = (excess pressure × surface area) ∙ dR
= (p – p_o) × 4πR² ∙ dR ………. (3)
From Eqs. (2) and (3),
(p – p_o) × 4πR² ∙ dR = 16πTRdR
∴ p – p_o = \(\frac{4 T}{R}\) …………… (4)
which is the required expression.

[Note : The excess pressure inside a drop or bubble is inversely proportional to its radius : the smaller the bubble radius, the greater the pressure difference across its wall.]

Question 64.
What is the excess of pressure inside a soap bubble of radius 3 cm if the surface tension of the soap solution is 30 dyn/cm ?
Answer:
Excess of pressure, p – p_o = \(\frac{4 T}{R}=\frac{4 \times 30}{3}\)
= 40 dyn/cm²

Question 65.
Two soap bubbles of the same soap solution have radii 3 cm and 1.5 cm. If the excess pressure inside the bigger bubble is 40 dyn/cm², what is the excess pressure inside the smaller bubble ?
Answer:
Excess pressure ∝ T/R. In this case, the surface tension is the same in the two cases. Hence, the excess pressure inside the smaller bubble will be 80 dyn/cm².

Question 66.
Explain : In the absence of gravity or other external forces, a liquid drop assumes a spherical shape.
Answer:
A spherical shape has the minimum surface area-to-volume ratio of all geometric forms. If any . external force distorts the sphere, molecules must be brought from the interior to the surface in order to provide for the increased surface area. This process requires work to be done in order to raise the potential energy of a molecule. The change in free surface energy is equal to the net work done to alter the surface area of the liquid.

However, spontaneous processes are associated with a decrease in free energy. Hence, in the absence of external forces, a liquid drop will spontaneously assume a spherical shape in order to minimize its exposed surface area and thereby its free surface energy.

[ Note : The spontaneous coalescence of two similar liquid droplets into one large drop when brought into contact is a dramatic demonstration of the decrease in free surface energy brought about by the decrease in total surface area by the formation of a single larger drop.]

Question 67.
A small air bubble of radius r in water is at a depth h below the water surface. If p₀ is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
Answer:
The absolute pressure within the liquid at a depth h is p = p₀ + ρgh.
Since the excess pressure inside a bubble is \(\frac{2 T}{R}\), the pressure inside the bubble is
P_in = p + \(\frac{2 T}{R}\) = p₀ + ρgh + \(\frac{2 T}{R}\)

68. Solve the following

Question 1.
What is the excess pressure (in atm) inside a soap bubble with a radius of 1.5 cm and surface tension of 3 × 10^-2 N/m? [1 atm = 101.3 kPa]
Solution:
Data : R = 1.5 × 10^-2 m, T = 3 × 10^-2 N/m,
1 atm = 1.013 × 10⁵ Pa
The excess pressure inside a soap bubble is
p – p₀ = \(\frac{4 T}{R}\)
= \(\frac{4 \times 3 \times 10^{-2}}{1.5 \times 10^{-2}}\) = 8Pa
= \(\frac{8}{1.013 \times 10^{5}}\) atm = 7.897 × 10^-5 atm

Question 2.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the rain drop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 × 10⁵ N/m²)
Solution:
Data : D = 4 × 10^-3 m, T = 0.072N/m,
p₀ = 1013 × 10⁵ N/m²
R = \(\frac{D}{2}\) = 2 × 10^-3 m
The excess pressure inside the raindrop is
p – p₀ = \(\frac{2 I}{R}=\frac{2(0.072)}{2 \times 10^{-3}}\) = 72 N/m²
∴ p = 101300 + 72 = 101372 N/m²

Question 3.
What should be the diameter of a soap bubble such that the excess pressure inside it is 51.2 Pa? [Surface tension of soap solution = 3.2 × 10^-2 N/m]
Solution:
Data : p – p₀ = 51.2 Pa, T = 3.2 × 10^-2 N/m
Forasoapbubb1e, p – p₀ = \(\frac{4T}{R}\)
∴ The radius of the soap bubble should be
R = \(\frac{4 T}{p-p_{0}}=\frac{4 \times 3.2 \times 10^{-2}}{51.2}\) = 2.5 × 10^-3 m = 2.5 mm
∴ the diameter of the soap bubble should be 2 × 2.5 = 5 mm.

Question 4.
The lower end of a capillary tube of diameter 1 mm is dipped 10 cm below the water surface in a beaker. What pressure is required to blow a hemispherical air bubble at the lower end of the tube? Present your answer rounded off to 4 significant figures. [Surface tension = 0.072 N/m, density = 10³ kg/m³, atmospheric pressure = 101.3 kPa, g = 9.8 m/s²]
Solution:
Data : r = 0.5 mm = 5 × 10^-4 m, d = 10 cm = 0.1 m,
T = 0.072 N/m, p = 10³ kg/m³, g = 9.8 m/s²,
P = 1 atm = 1.013 × 10⁵ Pa
The pressure outside the bubble at the depth d is
p₀ = P + dρg
= 1.013 × 10⁵ +0.1 × 10³ × 9.8
= (1.013 + 0.0098) × 10⁵ = 1.0228 × 10⁵ Pa
Since a bubble within water has only one, gas-liquid interface, the excess pressure inside the bubble is
p – p₀ = \(\frac{2 T}{r}=\frac{2 \times 0.072}{5 \times 10^{-4}}\) = 0.0288 × 10⁴ Pa
= 0.00288 × 10⁵ Pa
∴ P = (1.0228 + 0.00288) × 10⁵ = 1.02568 × 10⁵ Pa
The pressure inside the air bubble is 1.026 × 10⁵ Pa (or 102.6 kPa), rounded off to four significant figures.

Question 5.
There is an air bubble of radius 1.0 mm in a liquid of surface tension 0.072 N/m and density 10³ kg/m³. The bubble is at a depth of 10 cm below the free surface of the liquid. By what amount is the pressure inside the bubble greater than the’ atmospheric pressure?
Solution:
Data : R = 10^-3 m, T = 0.072 N/m, ρ = 10³ kg/m³, h = 0.1 m
Let the atmospheric pressure be p0. Then, the absolute pressure within the liquid at a depth h is
p = p₀ + ρgh
Hence, the pressure inside the bubble is
p_in = p₀ + \(\frac{2 T}{R}\) = p₀ + ρgh + \(\frac{2 T}{R}\)
The excess pressure inside the bubble over the atmospheric pressure is
p_in – p₀ = ρgh + \(\frac{2 T}{R}\)
= (10³) (9.8) (0.1) + \(\frac{2(0.072)}{10^{-3}}\)
= 980 + 144 = 1124 Pa

Question 6.
Two soap bubbles A and B, of radii 2 cm and 4 cm, respectively, are in a closed chamber where air pressure is maintained at 8 N/m ². If n_A and n_B are the number of moles of air in bubbles A and B, respectively, then find the ratio n_B : n_A. [Surface tension of soap solution = 0.04 N/m. Ignore the effect of gravity.]
Solution:
Data : R_A = 0.02 m, R_B = 0.04 m, p₀ = 8 N/m², T = 0.04 N/m

This is the required ratio.

Question 69.
What is capillary? What is capillarity or capillary action?
Answer:
(1) A tube of narrow bore (i.e. very small diameter) is called a capillary tube. The word capillary is derived from the Latin capillus meaning hair, capillaris in Latin means ‘like a hair’.

(2) If a capillary tube is just partially immersed in a wetting liquid the liquid rises in the capillary tube. This is called capillary rise.

If a capillary tube is just partially immersed in a non-wetting liquid, the liquid falls in the capillary tube. This is called capillary depression.

The rise of a wetting liquid and fall of a non-wetting liquid in a capillary tube is called capillarity.

Question 70.
State any four applications of capillarity.
Answer:
Applications of capillarity:

1. A blotting paper or a cotton cloth absorbs water; ink by capillary action.
2. Oil rises up the wick of an oil lamp and sap rises up xylem tissues of a tree by capillarity.
3. Ground water rises to the open surface through the capillaries formed in the soil. In summer, the farmers plough their fields to break these capillaries and prevent excessive evaporation.
4. Water rises up the crevices in rocks by capillary action. Expansion and contraction of this water due to daily and seasonal temperature variations cause the rocks to crumble.

[Note: The rise of sap is due to the combined action of capilarity and transpiration. The transpiration pull, is considered to be the major driving force for water transport throughout a plant.]

Question 71.
Two capillary tubes have radii in the ratio 1: 2. If they are dipped in the same liquid, what will be the ratio of capillary rise in the two tubes ?
Answer:
T = \(\frac{h r \rho g}{2 \cos \theta}\)
In this case, hr = constant
∴ h₁ : h₂ = r₂ : r₁ = 2 : 1.

Question 72.
The radii of two columns of a U-tube are r₁ and r₂. When a liquid of density ρ and angle of contact θ = 0° is filled in it, the level difference of the liquid in the two columns is h. Find the surface tension of the liquid.
Answer:
Capillary rise, h = \(\frac{2 T \cos \theta}{r \rho g}\), where θ is the angle of contact.
Assuming the two columns of the U-tube to be sufficiently thin,

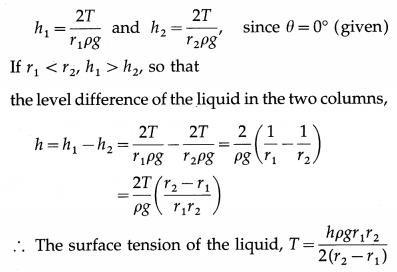
73. Solve the following

Question 1.
A liquid of density 900 kg/m³ rises to a height of 9 mm in a capillary tube of 2.4 mm diameter. If the angle of contact is 25°, find the surface tension of the liquid.
Solution:
Data : ρ = 900 kg/m³, h = 9 mm = 9 × 10^-3 m,
θ = 25°, g = 9.8 m/s²
r = \(\frac{1}{2}\) × diameter = \(\frac{2.4}{2}\) = 1.2 mm = 1.2 × 10^-3 m
cos θ = cos 25° = 0.9063
The surface tension of the liquid,
T = \(\frac{r h \rho g}{2 \cos \theta}\)
= \(\frac{1.2 \times 10^{-3} \times 9 \times 10^{-3} \times 900 \times 9.8}{2 \times 0.9063}\)
= 5.257 × 10^-2 N/m

Question 2.
A capilary tube of uniform bore is dipped vertically in water which rises by 7 cm in the tube. Find the radius of the capillary tube if the surface tension of water is 70 dyn/cm. [g = 980 cm/s²]
Solution:
Data : h = 7 cm, T = 70 dyn/cm, g = 980 cm/s², ρ = 1 g/cm³ and θ = 0° (for water)
∴ cos θ = 1 .
Surface tension, T = \(\frac{r h \rho g}{2 \cos \theta}\)
∴ The radius of the capillary tube,
r = \(\frac{2 T \cos \theta}{h \rho g}\)
= \(\frac{2 \times 70 \times 1}{7 \times 1 \times 980}\) = 0.02041 cm

Question 3.
A liquid rises to a height of 9 cm in a glass capillary tube of radius 0.02 cm. What will be the height of the liquid column in a glass capillary tube of radius 0.03 cm ?
Solution:
Data : h₁ = 9 cm, r₁ = 0.02 cm, r₂ = 0.03 cm
For the first capillary, T = \(\frac{r_{1} h_{1} \rho g}{2 \cos \theta}\)
For the second capillary, T = \(\frac{r_{2} h_{2} \rho g}{2 \cos \theta}\)
∴ \(\frac{r_{1} h_{1} \rho g}{2 \cos \theta}=\frac{r_{2} h_{2} \rho g}{2 \cos \theta}\)
∴ r₁h₁ = r₂h₂
The height of the liquid column in the second capillary,
h₂ = \(\frac{r_{1} h_{1}}{r_{2}}=\frac{0.02 \times 9}{0.03}\) = 6 cm

Question 4.
Water rises to a height of 5 cm in a certain capillary tube. In the same capillary tube, mercury is depressed by 2.02 cm. Compare the surface tensions of water and mercury.
[Density of water = 1000 kg/m³, density of mercury = 13600 kg/m³, angle of contact for water = 0°, angle of contact for mercury = 148°]
Solution:
Let T_w, θ_w, h_w and ρ_w be the surface
tension, angle of contact, capillary rise and density of water respectively. Let T_m, θ_m, h_m and ρ_m be the corresponding quantities for mercury. The radius (r) of the capillary is the same in both cases.

Data : h_w = 5 cm = 5 × 10^-2 m, θ_w = 0°, ρ_w = 1000 kg/m³, h_m = -2.02 cm
= -2.02 × 10^-2 m,
ρ_m = 13600 kg/m³, θ_m= 148°
[Note : h_m is taken to be negative because for mercury there is capillary depression.]
cos θ_w = cos 0° = 1
cos θ_m = cos 148° = – cos 32° = -0.8480

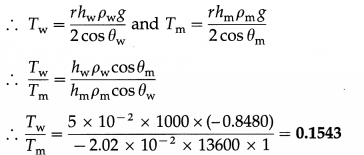
Question 5.
When a glass capillary tube of radius 0.4 mm is dipped into mercury, the level of mercury inside the capillary stands 1.50 cm lower than that outside. Calculate the surface tension of mercury. [Angle of contact of mercury with glass = 148 °, density of mercury = 13600 kg/m³]
Solution:
Data : r = 0.4 mm = 4 × 10^-4 m, h = -1.50 cm = – 1.50 × 10^-2 m,
ρ = 13.6 × 10³ kg/m³, g = 9.8 m/s², θ = 148°
cos θ = cos 148° = – cos 32 ° = – 0.8480
The surface tension of mercury is
T = \(\frac{r h \rho g}{2 \cos \theta}\)
= \(\frac{\left(4 \times 10^{-4}\right)\left(-1.50 \times 10^{-2}\right)\left(13.6 \times 10^{3}\right)(9.8)}{2(-0.8480)}\)
= 0.4715 N/m

Question 6.
The tube of a mercury barometer is 1 cm in diameter. What correction due to capillarity is to be applied to the barometric reading if the surface tension of mercury is 435.5 dyn/cm and the angle of contact of mercury with glass is 140° ? [Density of mercury = 13600 kg/m³]
Solution:
Data : d = 1 cm, T = 435.5 dyn/cm, θ = 140°, ρ = 13660 kg/m³ = 13.66 g/cm³,
g = 9.8 m/s² = 980 cm/s²

∴ The correction due to capillarity = -0.1001 cm

Question 7.
Calculate the density of paraffin oil, if within a glass capillary of diameter 0.25 mm dipped in paraffin oil of surface tension 0.0245 N/m, the oil rises to a height of 4 cm. [Angle of contact of paraffin oil with glass = 28°, acceleration due to gravity = 9.8 m/s²]
Solution :
Data : d = 0.25 mm, T = 0.0245 N/m, h = 4 cm = 4 × 10^-2 m, θ = 28°, g = 9.8 m/s²

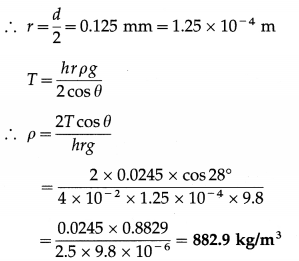
This gives the density of paraffan oil.

Question 8.
A capillary tube of radius r can support a liquid column of weight 6.284 × 10^-4 N. Calculate the radius of the capillary if the surface tension of the liquid is 4 × 10^-2 N/m.
Solution:
Data : mg = 6.284 × 10^-4 N, T = 4 × 10^-2 N/m
Net upward force = weight of liquid column
∴ 2πrT cos θ = mg
Assuming the angle of contact, θ = 0° (∵ data not given), the radius of the capillary is
r = \(\frac{m g}{2 \pi T}=\frac{6.284 \times 10^{-4}}{2(3.142)\left(4 \times 10^{-2}\right)}\) = 2.5 × 10^-3 m

Question 9.
Two vertical glass plates are held parallel 0.5 mm apart, dipped in water. If the surface tension of water is 70 dyn/cm , calculate the height to which water rises between the two plates.
Solution:
Data : x = 0.5 mm = 5 × 10^-4 m, T = 0.07 N/m, ρ(water) = 10³ kg/m³

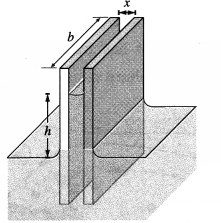
Let the width of each glass plate be b and the height to which the water rises between the plates be h.

Then, the upward force on the water between the plates due to surface tension = 2Tb cos θ

where θ is the angle of contact of water with glass. The weight of the water between the plates = mg = (bxhρ) = g

where x is the separation between the plates and p is the density of water.
Equating, (bxhρ)g = 2Tb cosθ
∴ The height to which water rises between the two plates,
h = \(\frac{2 T \cos \theta}{x \rho g}=\frac{2\left(7 \times 10^{-2}\right)(1)}{\left(5 \times 10^{-4}\right)\left(10^{3}\right)(9.8)}=\frac{0.2}{7}\)
= 0.02857 m = 2.857 cm

Question 10.
A glass capillary of radius 0.4 mm is inclined at 60° with the vertical in water. Find the length of water column in the capillary tube. [Surface tension of water = 7 × 10^-2 N/m]
Solution:
Data : r = 4 × 10^-4 m, Φ = 60°, T = 7 × 10^-2 N/m
Let h be the capillary rise when the capillary tube is immersed vertically in water. Let l be the length of the water column in the capillary tube above that of the outside level.

Question 74.
What is hydrodynamics?
Answer:
Hydrodynamics is the branch of physics that deals with fluid dynamics, i.e., the study of fluids in motion. Since the most basic fluid motion is highly complex, we consider only ideal fluids-non-viscous and incompressible, i.e., fluids whose internal friction is negligible and density is constant throughout.

Question 75
What is meant by a steady flow ?
Answer:
When a liquid flows slowly over a surface or through a pipe such that its velocity or pressure at any point within the fluid is constant, it is said to be in steady flow.

Question 76.
Explain a streamline and streamline flow.
Answer:
Streamline : Consider point A, from figure, within a fluid. The velocity \(\vec{v}\) at A does not change with time. Hence, every particle passes point A with the same speed and in the same direction. The same is true about the other points such as B and C. A curve which is tangent or parallel to the velocity of the fluid particles at every point will be the path of every particle arriving at A. It is called a streamline. A fluid particle cannot cross a streamline but only flow along it.

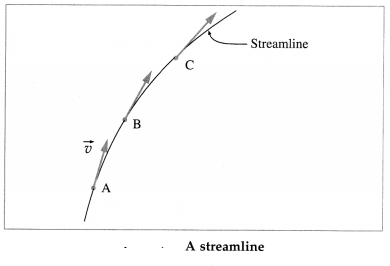
Streamline flow : When a liquid flows slowly over a surface or through a pipe with a velocity less than a certain critical velocity, the motion of its molecules is orderly. All molecules passing a given point proceed with the same velocity. This kind of fluid motion is called streamline or steady flow.

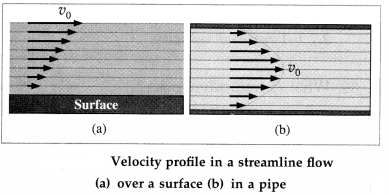
Question 77.
Explain a flow tube.
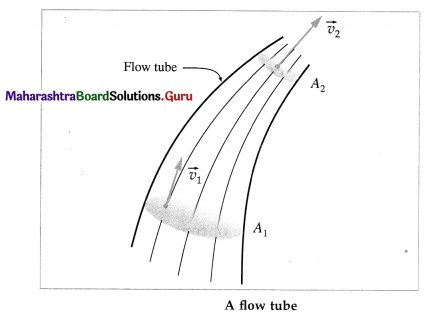
Answer:
A bundle of adjacent streamlines form a tube of flow or flow tube through which the fluid is flowing. In a flow tube, where the streamlines are close together the velocity is high, and where they are widely separated, the fluid is moving slowly. No fluid can cross the boundary of a tube of flow.

Question 78.
Explain turbulent flow.
Answer:
Turbulent flow or turbulence is a non-steady fluid flow in which streamlines and flowtubes change continuously. It has two main causes. First, any obstruction or sharp edge, such as in a tap, creates

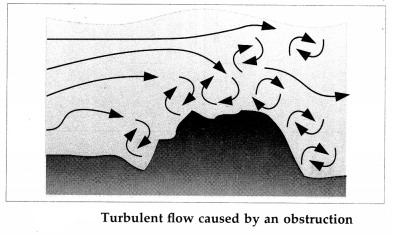
turbulence by imparting velocities perpendicular to the flow. Second, if the speed with which a fluid moves relative to a solid body is increased beyond a certain critical velocity the flow becomes unstable or one of extreme disorder. In both cases, the fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause them to cross and recross the main direction continuously. The orderly streamlines break up into eddies or vertices and the result is turbulence. In a turbulent flow, regions of fluid move in irregular, colliding paths, resulting in mixing and swirling.

Question 79.
Distinguish between streamline flow and turbulent flow.
Answer:

Streamline flow	Turbulent flow
1. The steady flow of a fluid, with velocity less than certain critical velocity is called streamline or laminar flow.	1. A non-steady irregular fluid flow in which stream­lines and flowtubes change continuously with a veloc­ity greater than certain critical velocity.
2. In a streamline flow, the velocity of a fluid at a given point is always constant.	2. In a turbulent flow, the vel­ocity of a fluid at any point does not remain constant.
3. Streamlines do not change and never intersect.	3. Streamlines and flowtubes change continuously.
4. over a surface, and is in the form of coaxial cylinders through a pipe.	4. Fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause eddies or vortices.

Question 80.
Explain the Reynolds number.
OR
What is Reynolds number?
Answer:
Osborne Reynolds found that if the free-stream velocity of a fluid increases when it moves relative to a solid body, a point is reached where the steady flow becomes turbulent. From experiments, he found that the transition from steady to turbulent flow depends on the value of the quantity \(\frac{v_{0} d}{\eta / \rho}\), where v₀ is the free-stream velocity, d is some characteristic dimension of the system, ρ the density of the fluid and η its coefficient of viscosity. For a sphere in a fluid stream, d is its diameter; for water in a pipe, d is the pipe diameter.

This dimensionless number, defined as
Re = \(\frac{v_{0} d \rho}{\eta}\) is called the Reynolds number.
In a system of particular geometry, transition from a steady to turbulent flow is given by a certain value of the Reynolds number called the critical Reynolds number. The free-stream velocity for this critical Reynolds number is called the critical velocity, v_critical = \(\frac{n R_{\mathrm{e}}}{\rho d}\). For a given system geometry, the free stream velocity beyond which a streamline flow becomes turbulent is called critical velocity.

Steady flow takes place for Re up to about 1000. For 1000 < Re < 2000, there is a transition region in which the flow is extremely sensitive to all sorts of small disturbances. For Re > 2000, the flow is completely turbulent.

[Notes : (1) See Q. 95 for “free-stream velocity”. (2) The dimensionless number is named after Osborne Reynolds (1842-1912), British physicist.]

Question 81.
Explain the term viscosity.
Answer:
Suppose a constant tangential force is applied to the surface of a liquid. Under this shearing force, the liquid begins to flow. The motion of a thin layer of the liquid at the surface, relative to a layer below, is opposed by fluid friction. Because of this internal fluid friction, horizontal layers of the liquid flow with varying velocities.

This also happens in a gas. When a solid surface is moved through a gas, a thin layer of the gas moves with the surface. But its motion relative to a layer away is opposed by fluid friction.

The resistance to relative motion between the adjacent layers of a fluid is known as viscosity.

It is a property of the fluid. The resistive force in fluid motion is called the viscous drag.

Question 82.
When a-liquid contained in a bucket is stirred and left alone, it comes to rest after some time. Why?
Answer:
This happens due to the internal friction (viscosity) and friction with the walls and bottom of the bucket.

Question 83.
What do you mean by viscous drag?
Answer:
When a fluid flows past a solid surface, or when a solid body moves through a fluid, there is always a force of fluid friction opposing the motion. This force of fluid friction is called the drag force or viscous drag.

Question 84.
What causes viscous drag in fluids?
Answer:
In liquids, the viscous drag is due to short range molecular cohesive forces while in gases it is due to collisions between fast moving molecules. For laminar flow in both liquids and gases, the viscous drag is proportional to the relative velocity between the layers, provided the relative velocity is small. For turbulent flow, the viscous drag increases rapidly and is proportional to some higher power of the relative velocity.

Question 85.
Define and explain velocity gradient in a steady flow.
Answer:
Definition : In a steady flow of a fluid past a solid surface, the rate at which the velocity changes with distance within a limiting distance from the surface is called the velocity gradient.

When a fluid flows past a surface with a low velocity, within a limiting distance from the surface, its velocity varies with the distance from the surface, from below figure. The layer in contact with the surface is at rest relative to the surface. Starting outwards from the surface, the next layer has an extremely small velocity; each successive layer has a slightly higher velocity than its inner neighbour, as shown. Finally, a layer is reached which has approximately the full, or free-stream, velocity v₀ of the fluid. The situation is reversed if a body is moving in a stationary fluid : the fluid velocity reduces as the distance of a layer from the body increases. Thus, the velocity in each layer increases with its distance from the surface.

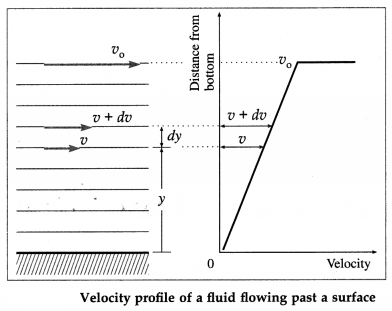
Consider the layer of thickness dy at y from the solid surface. Let v and v + dv be the velocities of the fluid at the base and upper edge of this layer. The change in velocity across the layer is dv. Therefore, the rate at which the velocity changes dv between the layers is \(\frac{d v}{d y}\). This is called the velocity gradient.

Question 86.
State and explain Newton’s law of viscosity.
Answer:
Newton’s law of viscosity: In a steady flow of a fluid past a solid surface, a velocity profile is set up such that the viscous drag per unit area on a layer is directly proportional to the velocity gradient.

When a fluid flows past a solid surface in a streamline flow or when a solid body moves through a fluid, the force of fluid friction opposing the motion is called the viscous drag. The magnitude of the viscous drag of a fluid is given by Newton’s law of viscosity.

If \(\frac{d v}{d y} \) is the velocity gradient, the viscous drag per unit area on a layer,
\(\frac{F}{A} \propto \frac{d v}{d y}\)
∴ \(\frac{F}{A}=\eta \frac{d v}{d y}\)
where the constant of proportionality, y, is called the coefficient of viscosity of the fluid.

Question 87.
Define coefficient of viscosity.
Answer:
Coefficient of viscosity : The coefficient of viscosity of a fluid is defined as the viscous drag per unit area acting on a fluid layer per unit velocity gradient established in a steady flow.

Question 88.
Find the dimensions of the coefficient of viscosity. State its SI and CGS units.
Answer:
By Newton’s law of viscosity,
\(\frac{F}{A}=\eta \frac{d v}{d y}\)
where \(\frac{F}{A}\) is the viscous drag per unit area, \(\frac{d v}{d y}\) is the velocity gradient and y is the coefficient of viscosity of the fluid. Rewriting the above equation as
η = \(\frac{(F / A)}{(d v / d y)}\)
[η] = \(\frac{\left[F A^{-1}\right]}{[d v / d y]}\) = [ML^-1T^-2][T¹] = [ML^-1T^-1]
SI unit: the pascal ∙ second (abbreviated Pa ∙ s), 1 Pa ∙ s = 1 N ∙ m^-2 ∙ s

CGS unit: dyne ∙ cm^-2 ∙ s, called the poise [symbol P, named after Jean Louis Marie Poiseuille (1799-1869), French physician].

[Note : The most commonly used submultiples are the millipascal-second (mPa ∙ s) and the centipoise (cP). 1 mPa ∙ s = 1 cP.]

Question 89.
Define the SI and CGS units of coefficient of viscosity.
Answer:
The SI unit of coefficient of viscosity is the pascal- second.

Definition : If a tangential force per unit area of one newton per square metre is required to maintain a difference in velocity of one metre per second between two parallel layers of a fluid in streamline flow separated by one metre, the coefficient of viscosity of the fluid is one pascal-second.

The CGS unit of coefficient of viscosity is the poise.

Definition : If a tangential force per unit area of one dyne per square centimetre is required to maintain a difference in velocity of one centimetre per second between two parallel layers of a fluid in streamline flow separated by one centimetre, the coefficient of viscosity of the fluid is one poise.

Question 90.
Find the conversion factor between the SI and CGS units of coefficient of viscosity using dimensional analysis.
Answer:
The dimensions of the coefficient of viscosity η are
[η] = [ML^-1T^-1]
The SI and CGS units of coefficient of viscosity are the pascal-second and poise, respectively.
1 Pa ∙ s = 1 N ∙ m^-2 ∙ s = 1 kg-m^-1 ∙ s^-1
1 P = 1 dyn ∙ cm^-2 ∙ s = l g-cm^-1 ∙ s^-1
Let 1 Pa ∙ s = xP
∴ 1[M₁L₁^-1T₁^-1] = x[M₂L₂^-1T₂^-1]
where subscripts 1 and 2 pertain to SI and CGS units.

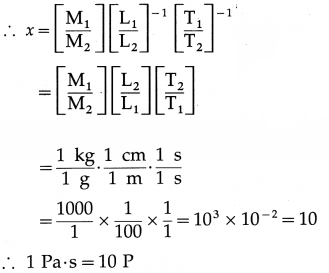
Question 91.
State Stokes’ law. Derive Stokes’ law using dimensional analysis.
Answer:
Stokes’ law : If a fluid flows past a sphere or a sphere moves through a fluid, for small enough
∴ Viscous force = gravitational force-buoyant force
= mg – m_Lg
where m = mass of the sphere = \(\frac{4}{3} \pi r^{3} \rho\) and m_{L</sub. = mass of the liquid displaced = \(\frac{4}{3} \pi r^{3} \rho_{\mathrm{L}}\).}

At its terminal speed v_t, the magnitude of the viscous force by Stokes’ law is

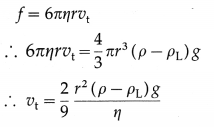
[Note : Theoretically, v → v_t as time t → ∞. In practice, if η is appreciable, then v tends to v_t in a very small time interval.]

[Data: g = 9.8 m/s²]

92. Solve the following

Question 1.
The relative velocity between two layers of a fluid, separately by 0.1 mm, is 2 cm/s. Calculate the velocity gradient.
Solution :
Data : dy = 0.1 mm = 10^-2 cm, dv = 2 cm/s
The velocity gradient, \(\frac{d v}{d y}=\frac{2 \mathrm{~cm} / \mathrm{s}}{10^{-2} \mathrm{~cm}}\) = 200 s^-1

Question 2.
Calculate the force required to move a flat glass plate of area of 10 cm² with a uniform velocity of 1 cm/s over the surface of a liquid 2 mm thick, if the coefficient of viscosity of the liquid is 2 Pa.s.
Solution :
Data : η = 2 Pa.s; A = 10 cm² = 10^-3 m²;
dv = 1 cm/s = 0.01 m/s; dy = 2 mm = 2 × 10^-3 m
According to Newton’s formula,
viscous force f = \(\eta A \frac{d v}{d y}\)
= \(\frac{(2 \mathrm{~Pa} \cdot \mathrm{s})\left(10^{-3} \mathrm{~m}^{2}\right)(0.01 \mathrm{~m} / \mathrm{s})}{2 \times 10^{-3} \mathrm{~m}}\)
= 0.01 N

This force retards the motion of the glass plate. Therefore, in order to keep the plate moving with a uniform velocity, an equal force must be exerted on the plate in the forward direction.

The required force to move the glass plate is 0.01 N

Question 3.
A metal plate of length 10 cm and breadth 5 cm is in contact with a layer of oil 1 mm thick. The horizontal force required to move it with a velocity of 4 cm/s along the surface of the oil is 0.32 N. Find the coefficient of viscosity of the oil. Also express it in poise.
Solution:

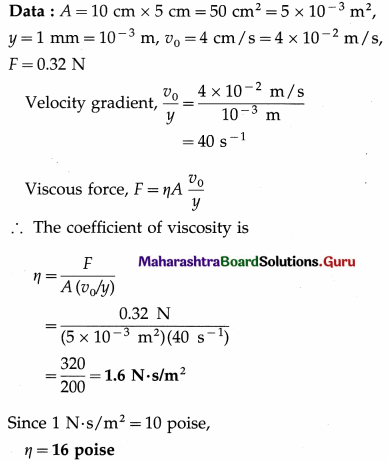
Question 4.
A spherical liquid drop of diameter 2 × 10^-4 m is falling with a constant velocity through air, under gravity. If the density of the liquid is 500 kg/m3 and the coefficient of viscosity of air is 2 × 10^-5 Pa.s, determine the terminal velocity of the drop and the viscous force acting on it. Ignore the density of air.
Solution :
Data : r = 1 × 10^-4 m, ρ = 500 kg/m³, ρ_air \(\ll \rho\) η = 2 × 10^-5 Pa.s

(i) The terminal velocity,

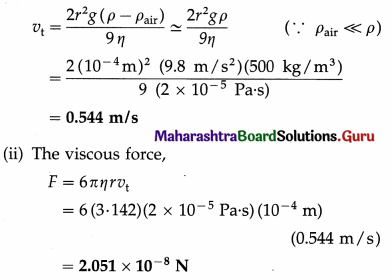
Question 5.
If the speed at which water flows through a long cylindrical pipe of radius 8 mm is 10 cm/s, find the Reynolds number. [Density of water = 1 g/cm³, coefficient of viscosity of water = 0.01 poise]
Solution :
Data : v₀ = 10 cm/s, ρ = 1 g/cm³, r = 8 mm
∴ d = 2r = 16 mm = 1.6 cm, η = 0.01 poise

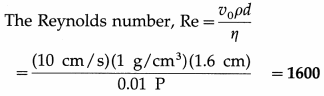
Question 93.
Define volume flow rate or volume flux. Explain how it is related to the velocity of fluid.
OR
What is the difference between flow rate and fluid velocity ? How are they related ?
Answer:
Definition : The volume of fluid passing by a given location per unit time through an area is called the volume flow rate, or simply flow rate, Q.Q = dV/dt

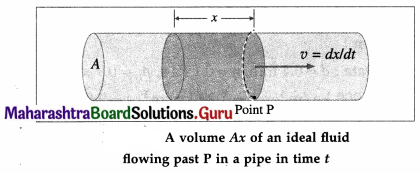
Consider an ideal fluid flowing with velocity v through a uniform flow tube of cross section A. If, as shown in Fig. 2.34, the shaded cylinder of fluid of length x and volume V flows past point P in time t,

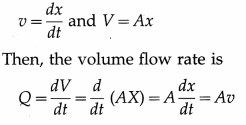
which is the required relation.

Question 94.
State the SI unit for volume flow rate.
Answer:
The SI unit for volume flow rate is the cubic metre per second (m³/s).

[Note : Another common unit accepted in SI is the litre per minute (L/min). 1 L = 10^-3 m³ = 10³ cm³. An old non-SI unit from FPS system still used is the cubic feet per second (symbol, cusec).]

Question 95.
Define mass flow rate or mass flux. Explain how it is related to the velocity of fluid.
Answer:
Definition : The mass of fluid passing by a given point per unit time through an area is called the mass flow rate, dmldt.

Consider an ideal fluid of density ρ flowing with velocity v through a uniform flow tube of cross section A. If, as shown in Fig. 2.34, the shaded cylinder of fluid of length x and volume V flows past point P in time t,

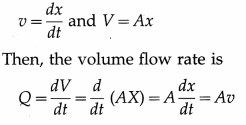
which is the required relation.

Question 96.
Explain the continuity condition for a flow tube. Show that the flow speed is inversely proportional to the cross-sectional area of a flow tube.
Answer:
Consider a fluid in steady or streamline flow. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude. Suppose the velocity is \(\overrightarrow{v_{1}}\) at point P and \(\overrightarrow{v_{2}}\) at point Q. If A₁ and A₂ are the cross-sectional areas of the tube and ρ₁ and ρ₂ are the densities of the fluid at these two points, the mass of the fluid passing per unit time across A₁ is A₁ρ₁v₁ and that passing across A₂ is A₂ρ₂v₂. Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires
A₁ρ₁v₁ = A₂ρ₂v₂ …………. (1)

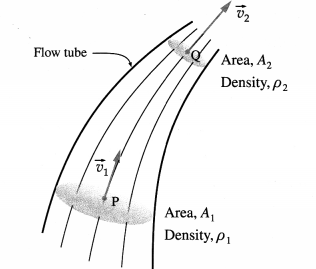
Equation (1) is called the equation of continuity of flow. It holds true for a compressible fluid, (like all gases) for which the density of the fluid may differ from point to point in a tube of flow. For an incompressible fluid (like all liquids), ρ₁ = ρ₂ and Eq. (1) takes the simpler form
A₁v₁ = A₂v₂ ………… (2)
∴ \(\frac{v_{1}}{v_{2}}=\frac{A_{2}}{A_{1}}\) …………… (3)
that is, the flow speed is inversely proportional to the cross-sectional area of a flow tube. Where the area is large, the speed of flow is small, and vice versa.

Equations (2) is the equation of continuity for an incompressible fluid for which density is constant throughout.

Question 97.
Explain why flow speed is greatest where streamlines are closest together.
Answer:
By the equation of continuity, the flow speed is inversely proportional to the area of cross section of a flow tube. Where the area of cross section is small, i. e., streamlines are close, the flow speed is large and vice versa.

Question 98.
You can squirt water a considerably greater distance by placing your thumb over the end of a garden hose. Explain.
Answer:
Placing one’s thumb over the end of a garden hose constricts the open end. By the continuity condition, the speed of water increases as it passes through the constriction. Hence, water squirts out and reaches a longer distance.

99. Solve the following

Question 1.
A liquid is flowing through a horizontal pipe of varying cross section. At a certain point, where the diameter of the pipe is 5 cm, the flow velocity is 0.25 m/s. What is the flow velocity where the diameter is 1 cm ?
Solution:
Data : d₁ = 5 cm, v₁ = 0.25 m/s, d₂ = 1 cm According to the equation of continuity of flow,
A₁ρ₁v₁ = A₂ρ₂v₂
where A₁ and ρ₁ are the cross-sectional area and density of the liquid where the flow velocity is v₁; A₂ and ρ₂ are the corresponding quantities where the flow velocity is v₂.
Assuming the liquid is incompressible,

Question 100.
State Bernoulli’s principle.
Answer:
Where the velocity of an ideal fluid in streamline flow is high, the pressure is low, and where the velocity of a fluid is low, the pressure is high. OR At every point in the streamline flow of an ideal (i.e., nonviscous and incompressible) fluid, the sum of the pressure energy, kinetic energy and potential energy of a given mass of the fluid is constant at every point.

[Note : The above principle is equivalent to a statement of the law of conservation of mechanical energy as applied to fluid mechanics. It was published in 1738 by Daniel Bernoulli (1700 – 82), Swiss mathematician.]

Question 101.
Explain Bernoulli’s equation of fluid flow.
Answer:
Consider an ideal fluid incompressible and nonviscous of density ρ flowing along a flow tube of varying cross section. The system under consideration is the flow tube between points 1 and 2, and the Earth (below figure). From the continuity equation it follows that pressure and speed must be different in regions of different cross section. If the height also changes, there is an additional pressure difference.

The fluid enters the system at point 1 through a. surface of cross section A₁ at speed v₁. The point 1 lies at a height h₁, with respect to an arbitrary reference level y = 0, and the local pressure there is p₁. The fluid leaves the system at point 2 where the corresponding quantities are A₂, v₂, h₂ and p₂.

Consider a small fluid element, of volume ∆V and mass ∆m = ρ∆V, that enters at point 1 and leaves at point 2 during small time interval ∆t. In the absence of internal fluid friction, it can be shown that the work done on the fluid element by the surrounding fluid is
∆W= (p₁ – p₂)∆V
This is sometimes called the pressure energy. During At, the changes in the kinetic energy and potential energy are
∆KE = \(\frac{1}{2}\) ∆m (V₂² – V₁²) = \(\frac{1}{2}\) ρ∆V(v₂² – v₁²)
∆PE = ∆mg(h₂ – h₁) = ρ∆Vg(h₂ – h₁)
Since ∆W is the work done by a non-conservative force,
∆W = ∆KE + ∆PE
∴ (p₁ – p₂)∆V = \(\frac{1}{2}\) ρ∆V(v₂2² – v₁²) + ρ∆Vg(h₂ – h₁) ……….. (1)
∴ p₁ – p₂ = \(\frac{1}{2}\) ρ(v₂² – v₁²) + ρg(h₂ – h₁)
∴ p₁ + \(\frac{1}{2}\) ρv₁² + ρgh₁ = p₂ + \(\frac{1}{2}\) ρv₂² + ρgh₂
or p + \(\frac{1}{2}\) ρv² + ρgh = constant …………. (2)
This is known as Bernoulli’s equation.

[Notes : Equation (1) can be rewitten as
p₁∆V + \(\frac{1}{2}\)ρ∆Vv₁² + ρ∆Vgh₁
p₂∆V + \(\frac{1}{2}\) ρ∆v₂² + ρ∆Vgh₂
or p∆V + \(\frac{1}{2}\)ρ∆v² + ρ∆Vgy = constant ………. (3)
i.e., pressure energy + KE + PE = constant
Dividing Eq. (3) by ∆m = ρ∆V,
\(\frac{p}{\rho}\) + \(\frac{1}{2}\) v² + gy constant

i.e., pressure energy per unit mass + KE per unit mass + PE per unit mass = constant, which is Bernoulli’s principle. Note that in writing

∆W = ∆KE + ∆PE, we have assumed principle of conservation of energy.

Dimensionally, pressure is energy per unit volume. Both terms on the right side of Eq. (2) also have the same dimensions. Hence, the term (p₁ – p₂) is often referred to as pressure energy per unit volume or pressure head. The first term on the right, \(\frac{1}{2}\) p (v₂² – v₁²) head and the second term, pg(h₂ – h₁), is called the potential head.]

Question 102.
State the limitations of Bernoulli’s principle.
Answer:
Limitations: Bernoulli’s principle and his equation for fluid flow is valid only for
(1) an ideal fluid, i.e., one that is incompressible and nonviscous, so that the density remains constant throughout a flow tube and there is no viscous drag which results in energy dissipation or loss,
(2) streamline flow.

Question 103.
State the applications of Bernoulli’s principle.
Answer:
Applications :

1. Venturi meter : It is a horizontal constricted tube that is used to measure flow speed in a gas.
2. Atomizer : It is a hydraulic device used for spraying insecticide, paint, air perfume, etc.
3. Aerofoil : The aerofoil shape of the wings of an aircraft produces aerodynamic lift.
4. Bunsen’s burner : Bernoulli effect is used to admit air into the burner to produce an oxidising flame.

Question 104.
State the law of efflux. Derive an expression for the speed of efflux for a tank discharging through an opening at a depth h below the liquid surface. Hence or otherwise show that the speed of efflux for an open tank is \(\sqrt{2 g h}\).
Answer:
Law of efflux (Torricelli’s theorem) : The speed of efflux for an open tank through an orifice at a depth h below the liquid surface is equal to the speed acquired by a body falling freely through a vertical distance h.

Consider a tank with cross-sectional area A₁ holding a static liquid of density ρ. The tank discharges through an opening (of cross-sectional area A₂) in the side wall at a depth h below the surface of the liquid. The flow speed at which the liquid leaves the tank is called the speed of efflux.

The pressure at point 2 it is the atmospheric pressure p₀. Let the pressure of the air above the liquid at point 1 be ρ. We assume that the tank is large in cross section compared to the opening (A₁ >> A₂), so that the upper surface of the liquid will drop very slowly. That is, we may regard the liquid surface to be approximately at rest v₁ ≈ 0). Bernoulli’s equation, in usual notation, states
p₁ + \(\frac{1}{2}\) ρv₁² + ρgy₁ = p₂ + \(\frac{1}{2}\) ρv₂² + ρgy₂
Substituting p₁ = p, p₂ = p₀, v₁ ≈ 0 and (y₁ – y₂) = h,
v₂² = 2 \(\frac{p-p_{0}}{\rho}\) + 2gh
If the tank is open to the atmosphere, then p = p₀,
v₂ = \(\sqrt{2 g h}\).
which is the law of efflux.

[Note : For an open tank, the speed of the liquid, v₂, leaving a hole a distance h below the surface is equal to that acquired by an object falling freely through a vertical distance h.]

Question 105.
What is a Venturi tube? Explain the working of a Venturi tube.
OR
What is a Venturi meter? Briefly explain its use to determine the flow rate in a pipe.
Answer:
A Venturi meter is a horizontal constricted tube that is used to measure the flow speed through a pipeline. The constricted part of the tube is called the throat. Although a Venturi meter can be used for a gas, they are most commonly used for liquids. As the fluid passes through the throat, the higher speed results in lower pressure at point 2 than at point 1. This pressure difference is measured from the difference in height h of the liquid levels in the U-tube manometer containing a liquid of density ρ_m (from below figure). The following treatment is limited to an incompressible fluid.

Let A₁ and A₂ be the cross-sectional areas at points 1 and 2, respectively. Let v₁ and v₂ be the corresponding flow speeds, p is the density of the fluid in the pipeline. By the equation of continuity,
v₁A₁ = v₂A₂ …………. (1)
Since the meter is assumed to be horizontal, from Bernoulli’s equation we get,
p₁ = \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\) ρv₂²
∴ p₁ = \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\) ρv₁² \(\left(\frac{A_{1}}{A_{2}}\right)^{2}\) [from Eq. (1)]
∴ p₁ – p₁ = \(\frac{1}{2}\) ρv₁² [\(\left(\frac{A_{1}}{A_{2}}\right)^{2}\) – 1] …………. (2)
The pressure difference is equal to pm gh, where h is the differences in liquid levels in the manometer. Then,

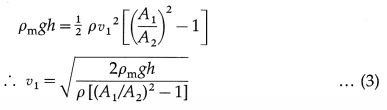
Equation (3) gives the flow speed of an incom-pressible fluid in the pipeline. The flow rates of practical interest are the mass and volume flow ‘ rates through the meter.
Volume flow rate = A₁v₁
and mass flow rate = density x volume flow rate = ρA₁v₁
[Note ; When a Venturi meter is used in a liquid pipeline, the pressure difference is measured from the difference in height h of the levels of the same liquid in the two vertical tubes, as shown in below figure. Then, the pressure difference is equal to ρgh.

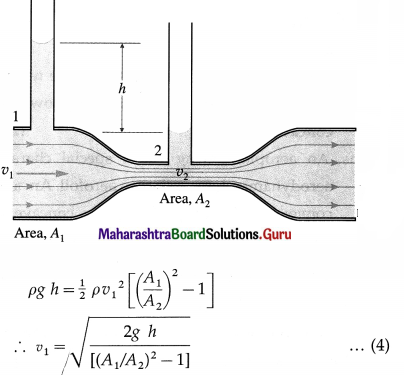
The flow meter is named after Giovanni Battista Venturi (1746-1822), Italian physicist.]

Question 106.
Explain aerodynamic lift on the wings of an aeroplane.
OR
Explain why the upper surface of the wings of an aeroplane is made convex and the lower surface concave.
Answer:
An aeroplane wing has a special characteristic aerodynamic shape called an aerofoil. An aerofoil is convex on the top and slightly concave on the bottom. Its leading edge is well rounded while the trailing edge is sharp. As an aeroplane moves through air, the aerofoil shape makes the air moving over the top and along the bottom of a wing in a certain way.

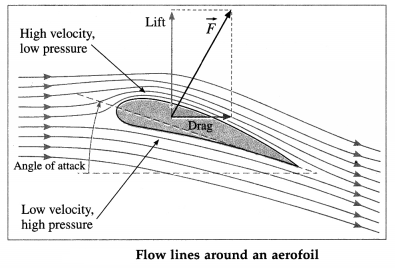
If the air over the top surface travels faster than the air below the wing, this decreases the air pressure above the wing. The air flowing below the wing moves almost in a straight line, so its speed and air pressure remain the same. The air under the wings therefore pushes upward more than the air on top of the wings pushes downward, thus producing an upward force \(\vec{F}\). It is the pressure difference that generates this force. The component of \(\vec{F}\) perpendicular to the direction of motion is called the aerodynamic lift or, simply, the lift. The component parallel to the direction of flight is the drag. The lift is the force that allows an aeroplane to get off the ground and stay in the air. For an aeroplane to stay in level flight, the lift is equal in magnitude and opposite in direction to the force of gravity.

[Note: For an airborne aeroplane to get to the ground, the direction of \(\vec{F}\) must be reversed. Then, the upper surface should be more concave than the lower surface such that air above the wing travels slower than the air below it, decreasing the air pressure below the wing. This is achieved by small flaps, called ailerons, attached at the trailing end of each wing.]

Question 107.
Explain the working of an atomizer.
OR
A perfume bottle or atomizer sprays a fluid that is in the bottle. How does the fluid rise up in the vertical tube in the bottle?
Answer:
An atomizer is a device which entraps or entrains liquid droplets in a flowing gas. Its working is based on Bernoulli’s principle. A squeeze bulb or a pump is used to create a jet of air over an open tube dipped into a liquid. By Bernoulli’s principle, the high-velocity air stream creates low pressure at the open end of the tube. This causes the liquid to rise in the tube. The liquid is then dispersed into a fine spray of droplets. This type of system is used in a perfume bottle, a paint sprayer, insect and perfume sprays and an automobile carburetor.

[Notes : A Bunsen burner uses an adjustable gas nozzle to entrain air into the gas stream for proper combustion. Aspirators, used as suction pumps, in dental and surgical situations (for draining body fluids) or for draining a flooded basement, is another similar applica-tion. Some chimney pipes have a T-shape, with a cross-piece on top that helps draw up gases whenever there is even a slight breeze.]

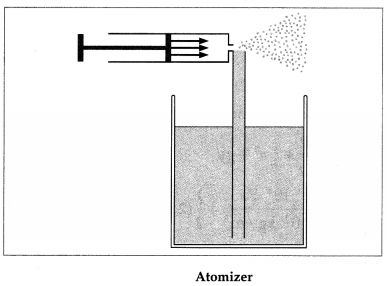
Question 108.
Roofs are sometimes blown off vertically during a tropical cyclone, and houses sometimes explode outward when hit by a tornado. Use Bernoulli’s principle to explain these phenomena.
Answer:
A cyclonic high wind blowing over a roof creates a low pressure above it, in accordance with Bernoulli’s principle. The pressure below the roof is equal to the atmospheric pressure which is now greater than the pressure above the roof. This pressure difference causes an aerodynamic lift that lifts the roof up. Once the roof is lifted up, it blows off in the direction of the wind.

Wind speeds in a tornado may be much higher and thus create much greater pressure differences. Sometimes, wooden houses hit by a tornado explode.

Question 109.
Describe what happens : (1) Hold the short edge of a paper strip (2″ × 6″) up to your lips-the strip slanting downward over your finger-and blow over the top of the strip. (2) Hold two strips of paper up to your lips, separated by your fingers and blow between the strips.
Answer:
(1) The air stream over the top surface travels faster than the air stream below the paper strip. This decreases the air pressure above the strip relative o that below. This produces an aerodynamic lift in accordance with Bernoulli’s principle and the paper strip will lift up.

(2) Air passing between the paper strips flows in a narrower channel and, in accordance with Be rnoulli’s principle, must increase its speed, causing the pressure between them to drop. This will pinch the two strips together.

110. Solve the following

Question 1.
Water is flowing through a horizontal pipe of varying cross section. At a certain point where the velocity is 0.12 m/s, the pressure of water is 0.010 m of mercury. What is the pressure at a point where the velocity is 0.24 m/s?
Solution:
Data : v₁ = 0.12 m/s, p₁ = 0.010 m of Hg, v₂ = 0.24 m/s, y₁ = y₂ (horizontal pipe), ρ_Hg = 13600 kg/m², ρ_w = 1000 kg/m³, g = 9.8 m/s²
p₁ = 0.010 m of Hg .
= (0.010 m) ρ_Hgg
= (0.010 m) (13600 kg/m³) (9.8 m/s²)
= 1332.8 Pa ≅ 1333 Pa
According to Bernoulli’s principle,

This gives the pressure of the water in the pipe where the flow velocity is 0.24 m / s.

Question 2.
A building receives its water supply through an undergound pipe 2 cm in diameter at an absolute pressure of 4 × 10⁵ Pa and flow velocity 4 m/s. The pipe leading to higher floors is 1.5 cm in diameter. Find the flow velocity and pressure at the floor inlet 10 m above.
Solution:
Data : d₁ = 3 cm, p₁ = 4 × 10⁵ Pa, v₁ = 4 m/s,
d₂ = 2 cm, h₂ – h₁ = 10 m
By continuity equation, the flow velocity at the higher floor inlet

Question 3.
Calculate the total energy per unit mass possessed by water at a point where the pressure is 0.1 × 10⁵ N/m², the velocity is 0.02 m/s and the height of the water level from the ground is 10 cm. Density of water = 1000 kg/m³.
Solution:
Data : p = 0.1 × 10⁵ N/m² = 10⁴ Pa, v = 0.02 m/s, y = 10 cm = 0.1 m, ρ = 1000 kg/m³, g = 9.8 m/s²
The total energy per unit mass of water
= \(\frac{p}{\rho}\) + \(\frac{1}{2}\)v² + gy
= \(\frac{10^{4} \mathrm{~Pa}}{10^{3} \mathrm{~kg} / \mathrm{m}^{3}}\) + \(\frac{1}{2}\) (2 × 10^-2 m/s)² + (9.8 m/ s²) (0.1 m)
= 10 + 0.0002 + 0.98 = 10.9802 J/kg

Question 4.
A horizontal wind with a speed of 11 m/s blows past a tall building which has large windowpanes of plate glass of dimensions 4 m × 1.5 m. The air inside the building is at atmospheric pressure. What is the total force exerted by the wind on a window pane ? [Density of air = 1.3 kg/m³]
Solution:
Data : v₁ (inside) = 0 m/s, v₂ (outside) = 11 m/s, ρ = 1.3 kg/m³, p₁ = p₀ = atmospheric pressure,
A = 4m × 1.5 m = 6m
Let p₂ be the air pressure outside a window. At the same height, Bernoulli’s equation gives
∴ p₁ + \(\frac{1}{2}\) ρv₁² = p₂ + \(\frac{1}{2}\)ρv₂²
∴ p₀ + 0 = p₂ + \(\frac{1}{2}\) ρv₂²
∴ The difference in pressure across a windowpane is
p₀ – p₂ = \(\frac{1}{2}\) ρv₂²
Since the right hand side is positive,
p₀ > p₂ and p₀ – p₂ is directed outward.
∴ The total force on a window pane is
F = (p₀ – p₂)A = \(\frac{1}{2}\) ρv₂² A
= \(\frac{1}{2}\) (1.3 kg/m³) (11 m/s)² (6 m²)
= 3.9 × 121 = 471.9 N (outward)

Question 5.
A water tank has a hole at a distance x from the free surface of water in the tank. If the radius of the hole is 2 mm and the velocity of efflux is 11 m/s, find x.
Solution:
Data: r = 2 mm, v = 11 m/s, g = 9.8 m/s²
By Torricelli’s law of efflux, the velocity of efflux,
v = \(\sqrt{2 g x}\)
∴ x = \(\frac{v^{2}}{2 g}=\frac{(11 \mathrm{~m} / \mathrm{s})^{2}}{2\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)}\)
= \(\frac{121}{19.6}\) = 6.173 m

Multiple Choice Questions

Question 1.
Consider the following statements:
I. A fluid in hydrostatic equilibrium exerts only normal force on any surface within the fluid.
II. A fluid can resist a tangential force. Of these,
(A) only (I) is correct
(B) only (II) is correct
(C) both are correct
(D) both are false.
Answer:
(A) only (I) is correct

Question 2.
Which of the following is correct ?
(A) The free surface of a liquid at rest is horizontal.
(B) The pressure at a point within a liquid at rest is the same in all directions.
(C) The pressure at all points within a liquid at rest is the same.
(D) Both (A) and (B).
Answer:
(D) Both (A) and (B).

Question 3.
The surface of a liquid (of uniform density p) in a container is open to the atmosphere. The atmospheric pressure is ρ₀. The pressure ρgh, at a depth h below the surface of the liquid, is called the
(A) absolute pressure
(B) normal pressure
(C) gauge pressure
(D) none of these.
Answer:
(C) gauge pressure

Question 4.
Three vessels having the same base area are filled with water to the same height, as shown. The force exerted by water on the base is

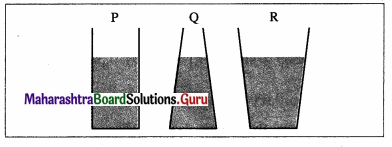
(A) largest for vessel P
(B) largest for vessel Q
(C) largest for vessel R
(D) the same in all three.
Answer:
(D) the same in all three.

Question 5.
Rain drops or liquid drops are spherical in shape, especially when small, because
(A) cohesive force between the molecules of water have spheres of influence
(B) for a given volume, a spherical drop has the least surface energy
(C) for a given volume, a spherical drop has the maximum surface energy
(D) the pressure inside a drop is many times the atmospheric pressure outside.
Answer:
(B) for a given volume, a spherical drop has the least surface energy

Question 6.
The surface tension acts
(A) perpendicular to the surface and vertically up-wards
(B) perpendicular to the surface and vertically into the liquid
(C) tangential to the surface
(D) only at the liquid-solid interface.
Answer:
(C) tangential to the surface

Question 7.
A thin ring of diameter 8 cm is pulled out of water (surface tension 0.07 N/m). The force required to break free the ring from water is
(A) 0.0088 N
(B) 0.0176 N
(C) 0.0352 N
(D) 3.52 N.
Answer:
(C) 0.0352 N

Question 8.
A matchstick 5 cm long floats on water. The water film has a surface tension of 70 dyn/cm. A little comphor put on one side of stick reduces the surface tension there to 50 dyn/cm. The net force on the matchstick is
(A) 4 dynes
(B) 20 dynes
(C) 100 dynes
(D) 600 dynes.
Answer:
(C) 100 dynes

Question 9.
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be
(A) 10 R
(B) \(\frac{R}{10}\)
(C) \(\frac{R}{100}\)
(D) \(\frac{R}{1000}\)
Answer:
(B) \(\frac{R}{10}\)

Question 10.
The work done in breaking a spherical drop of a liquid (surface tension T) of radius R into 8 equal drops is
(A) πR²T
(B) 2πR²T
(C) 3πR²T
(D) 4πR²T.
Answer:
(D) 4πR²T.

Question 11.
If for a liquid in a vessel, the force of cohesion is more than the force of adhesion,
(A) the liquid does not wet the solid
(B) the liquid wets the solid
(C) the surface of the liquid is plane
(D) the angle of contact is zero.
Answer:
(A) the liquid does not wet the solid

Question 12.
If a liquid does not wet a solid surface, its angle of contact with the solid surface is
(A) zero
(B) acute
(C) 90°
(D) obtuse.
Answer:
(D) obtuse.

Question 13.
The pressure within a bubble is higher than that outside by an amount proportional
(A) directly to both the surface tension and the bubble size
(B) directly to the surface tension and inversely to the bubble size
(C) directly to the bubble size and inversely to the surface tension
(D) inversely to both the surface tension and the bubble size.
Answer:
(B) directly to the surface tension and inversely to the bubble size

Question 14.
The pressure difference across the surface of a spherical water drop of radius 1 mm and surface tension 0.07 N/m is
(A) 28 Pa
(B) 35 Pa
(C) 140 Pa
(D) 280 Pa.
Answer:
(C) 140 Pa

Question 15.
An air bubble just inside a soap solution and a soap bubble blown using the same solution have their radii in the ratio 3 : 2. The ratio of the excess pressure inside them is
(A) 1 : 12
(B) 1 : 6
(C) 1 : 3
(D) 1 : 2.
Answer:
(C) 1 : 3

Question 16.
A liquid rises to a height of 5 cm in a glass capillary tube of radius 0.02 cm. The height to which the liquid would rise in a glass capillary tube of radius 0.04 cm is
(A) 2.5 cm
(B) 5 cm
(C) 7.5 cm
(D) 10 cm.
Answer:
(A) 2.5 cm

Question 17.
In a gravity free space, the liquid in a capillary tube will rise to
(A) the same height as that on the Earth
(B) a lesser height than on the Earth
(C) slightly more height than that on the Earth
(D) the top and overflow.
Answer:
(D) the top and overflow.

Question 18.
In which of the following substances, does the surface tension increase with an increase in tempera¬ture?
(A) Copper
(B) Molten copper
(C) Iron
(D) Molten iron
Answer:
(B) Molten copper

Question 19.
A fluid flows in steady flow through a pipe. The pipe has a circular cross section, but its radius varies along its length. The mass of the fluid passing per second at the entrance point (radius R) of the pipe is Q₁ while that at the exit point (radius R/2) is Q₂. Then, Q₂ is equal to
(A) \(\frac{1}{4}\) Q₁
(B) Q₁
(C) 2Q₁
(D) 4Q₁.
Answer:
(B) Q₁

Question 20.
The dimensions of coefficient of viscosity are
(A) [ML^-1T^-2]
(B) [M^-1LT^-2]
(C) [MLT^-2]
(D) [ML^-1T^-1].
Answer:
(D) [ML^-1T^-1].

Question 21.
The unit of coefficient of viscosity is
(A) the pascal-second
(B) the pascal
(C) the poise-second
(D) both (A) and (C).
Answer:
(A) the pascal-second

Question 22.
A fluid flows past a sphere in streamline flow. The viscous force on the sphere is directly proportional to
(A) the radius of the sphere
(B) the speed of the flow
(C) the coefficient of viscosity of the fluid
(D) all of these.
Answer:
(D) all of these.

Question 23.
Water flows in a streamlined flow through the pipe shown in the following figure. The pressure

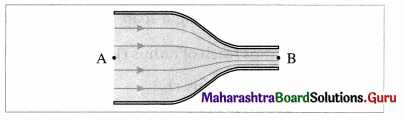
(A) is greater at A than at B
(B) at A equals that at B
(C) is less at A than at B
(D) at A is unrelated to that at B.
Answer:
(A) is greater at A than at B

Question 24.
Two steel marbles (of radii R and \(\frac{R}{3}\)) are released in a highly viscous liquid. The ratio of the terminal velocity of the larger marble to that of the smaller is
(A) 9
(B) 3
(C) 1
(D) \(\frac{1}{9}\)
Answer:
(A) 9

Question 25.
A large tank, filled with a liquid, is open to the atmosphere. If the tank discharges through a small hole at its bottom, the speed of efflux does NOT depend on
(A) cross-sectional area of the hole
(B) depth of the hole from the liquid surface
(C) acceleration due to gravity
(D) all of these.
Answer:
(A) cross-sectional area of the hole