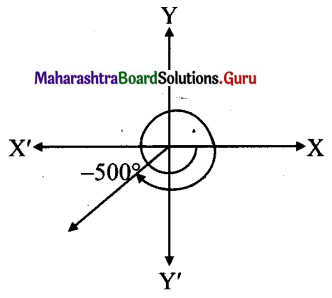
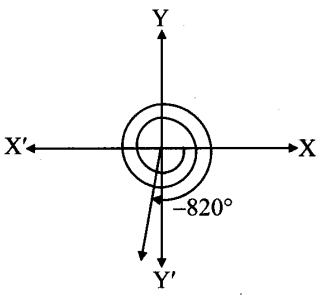
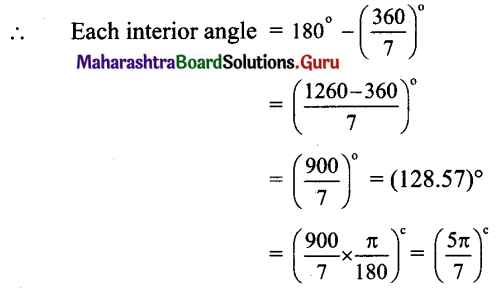
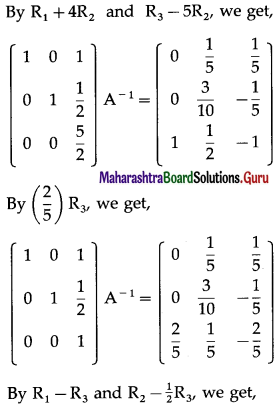
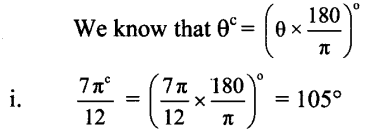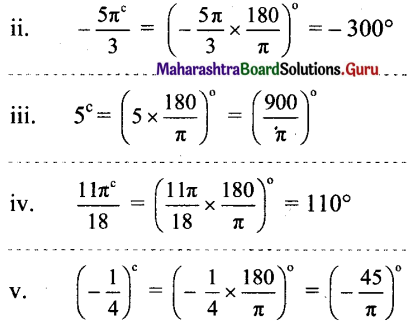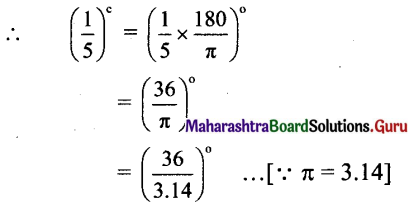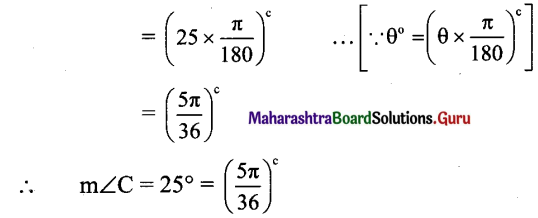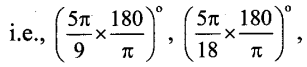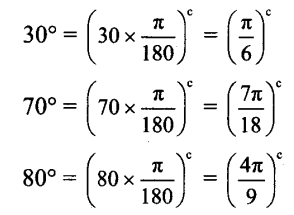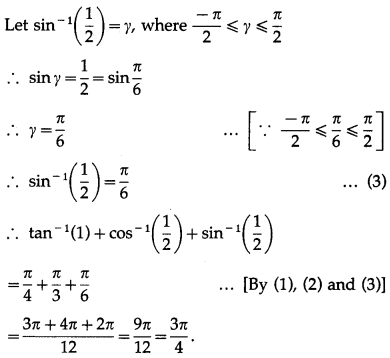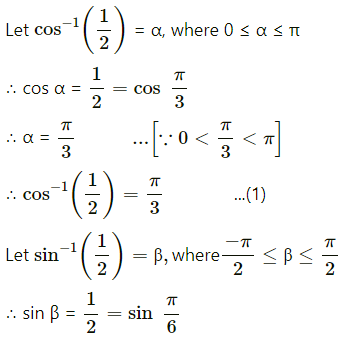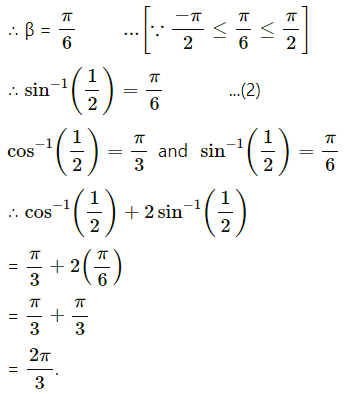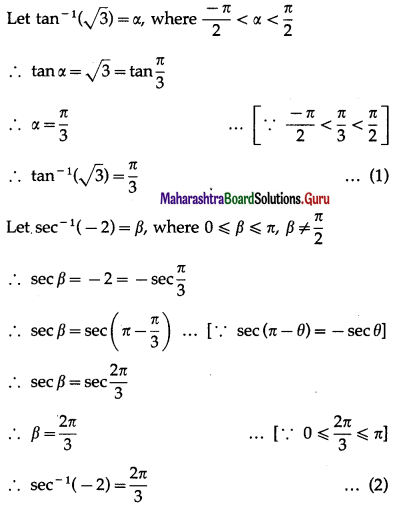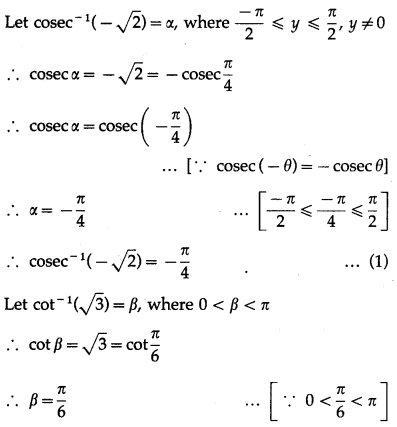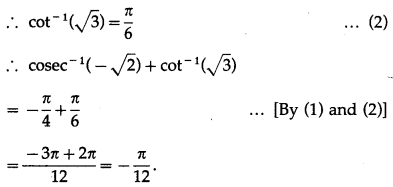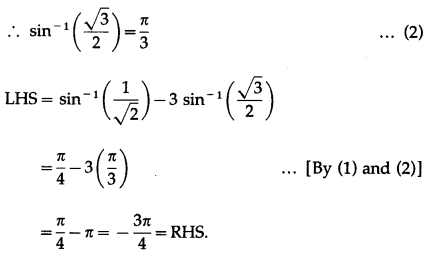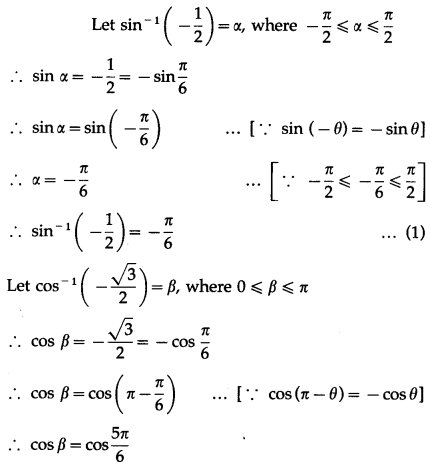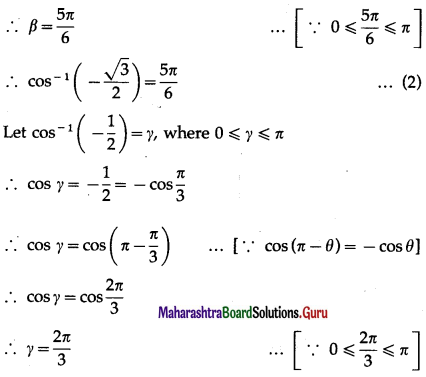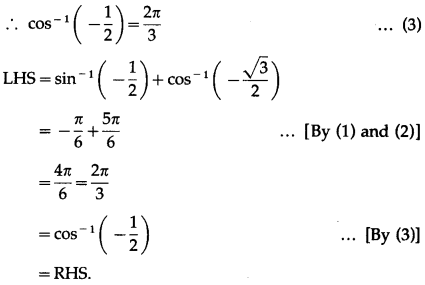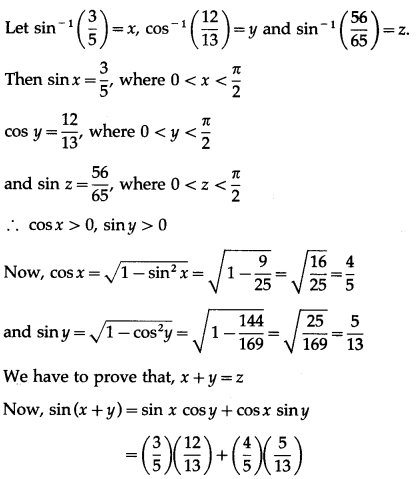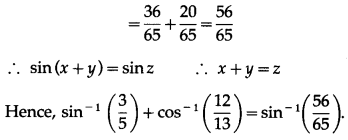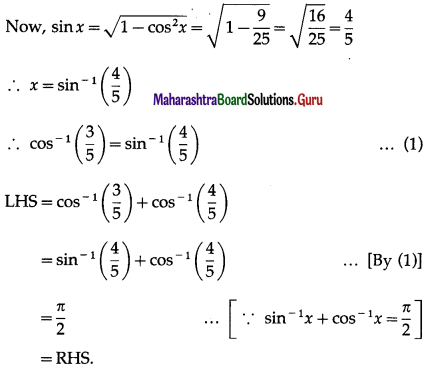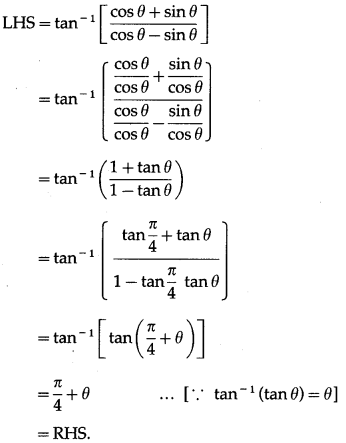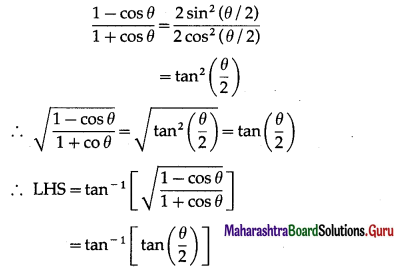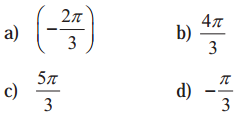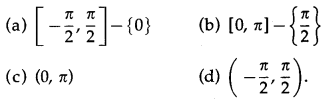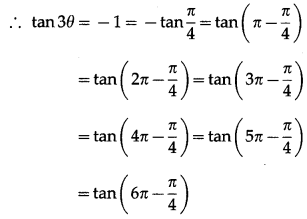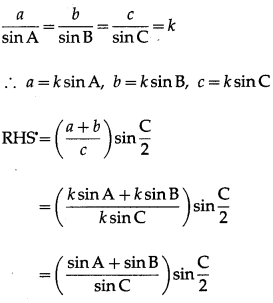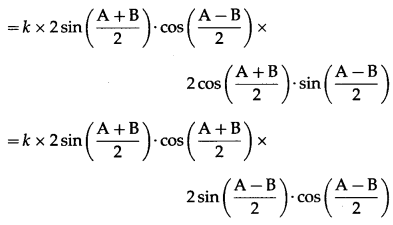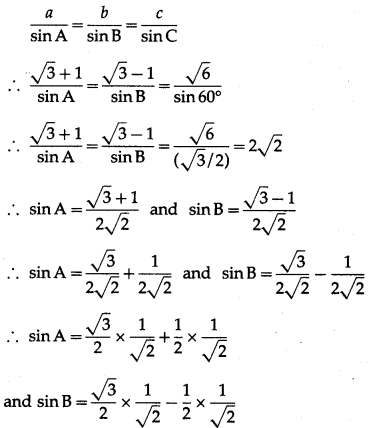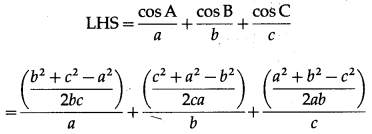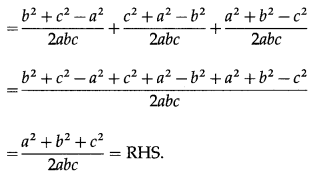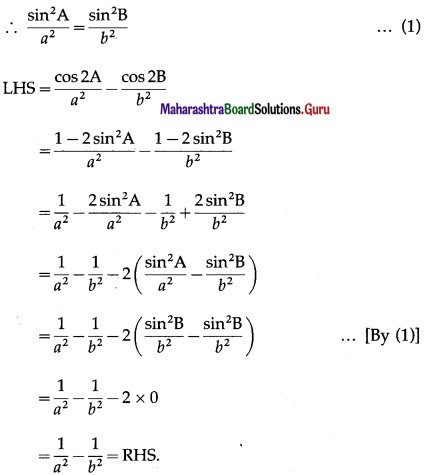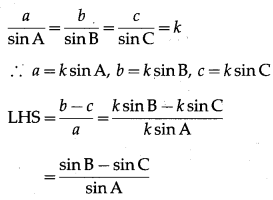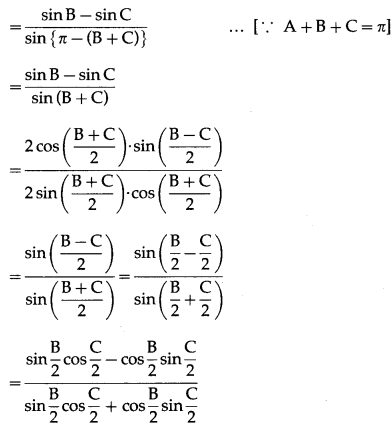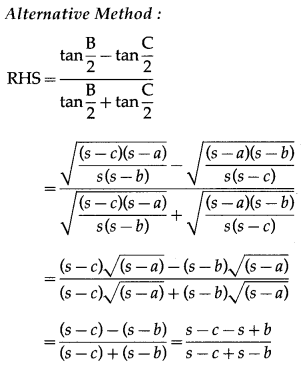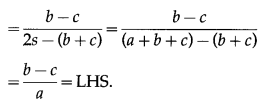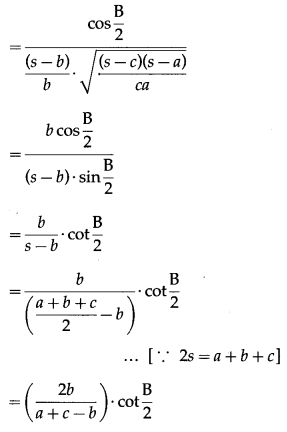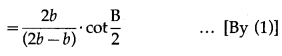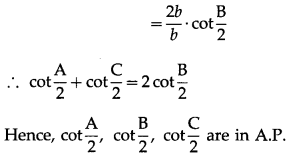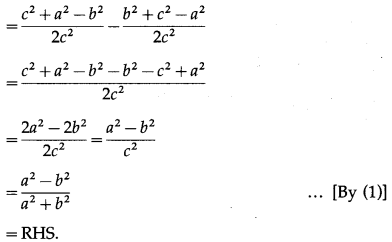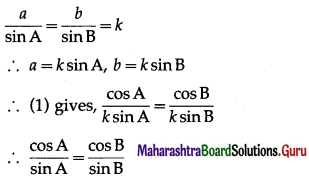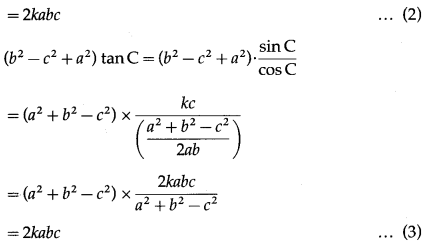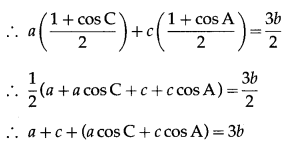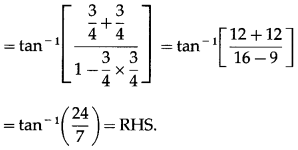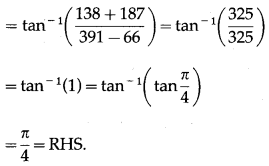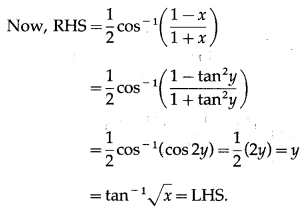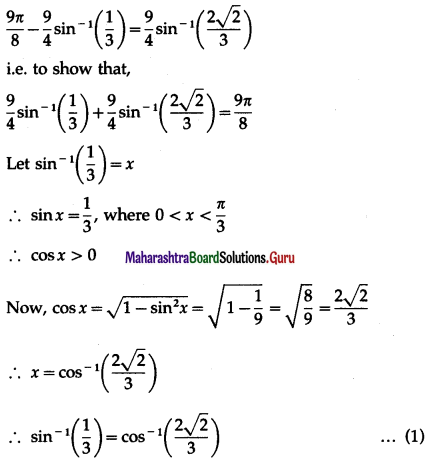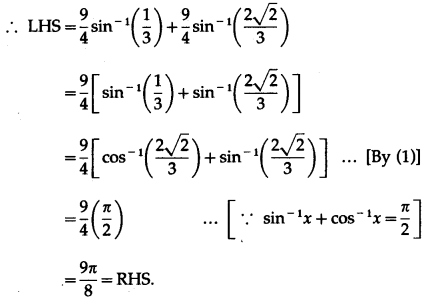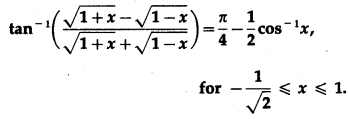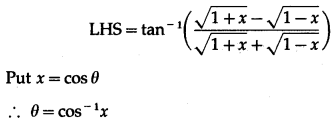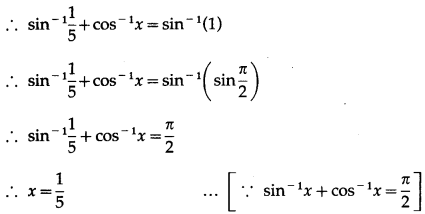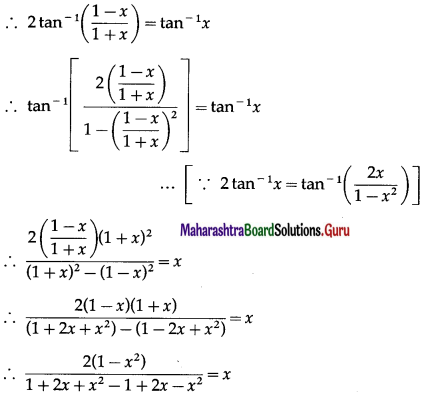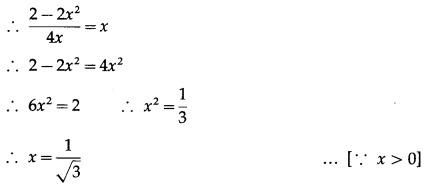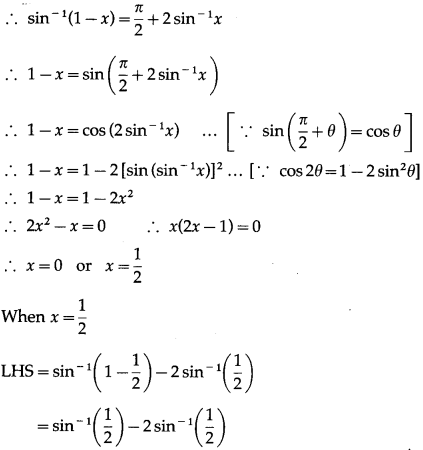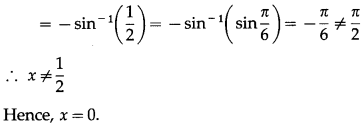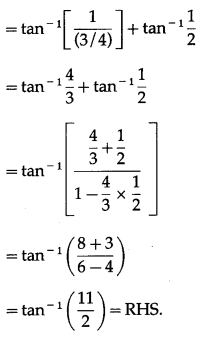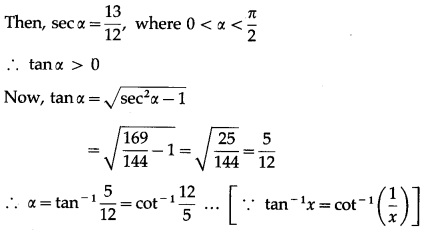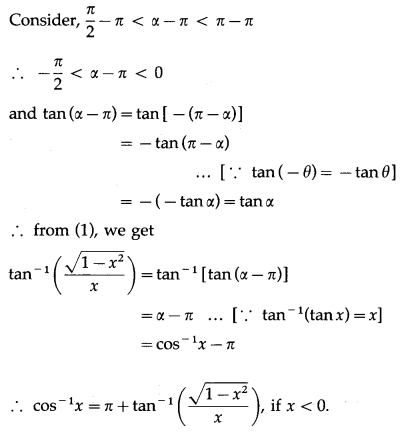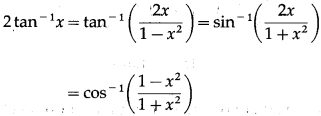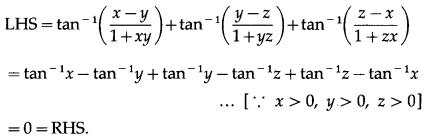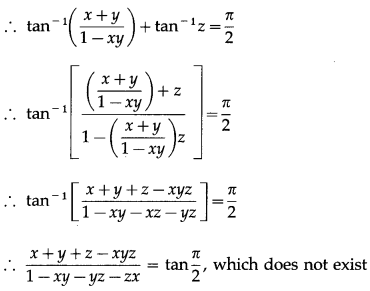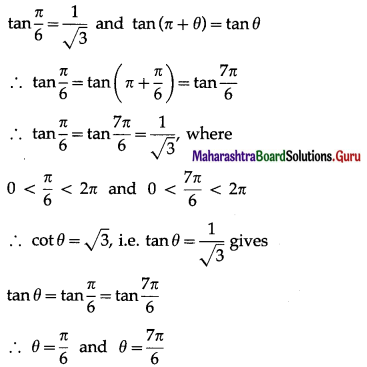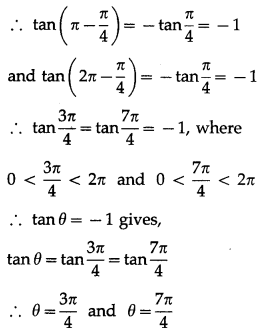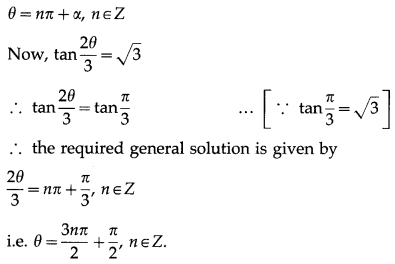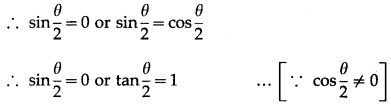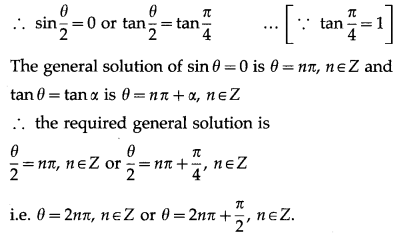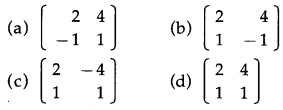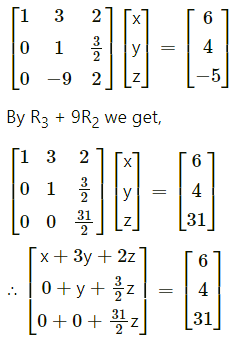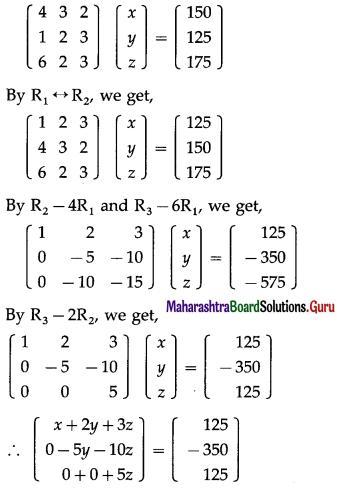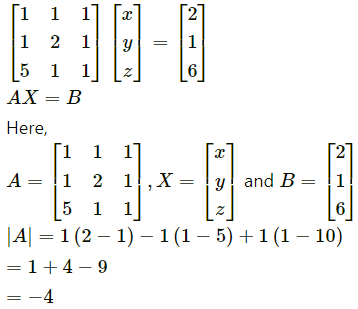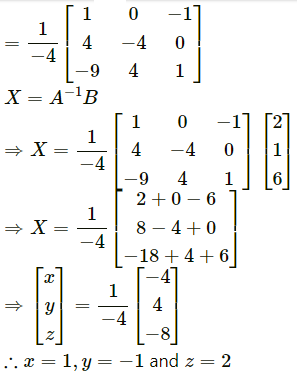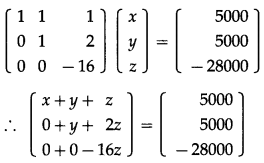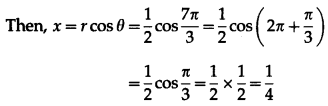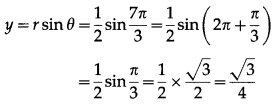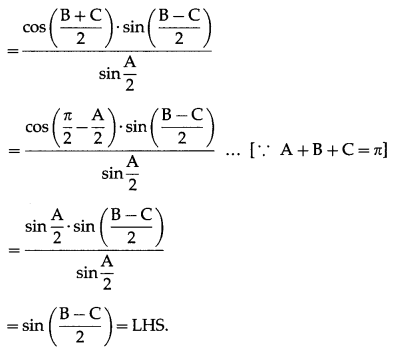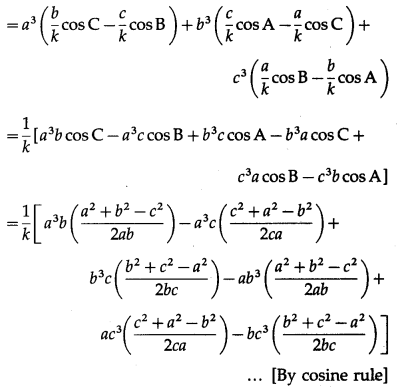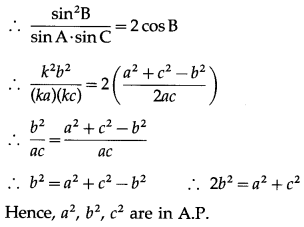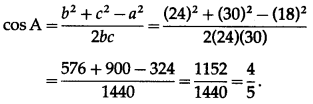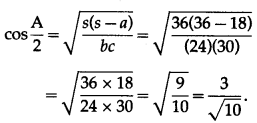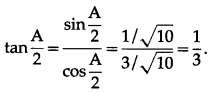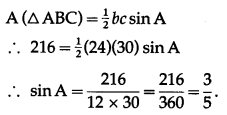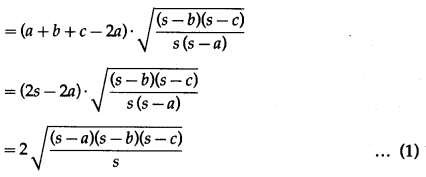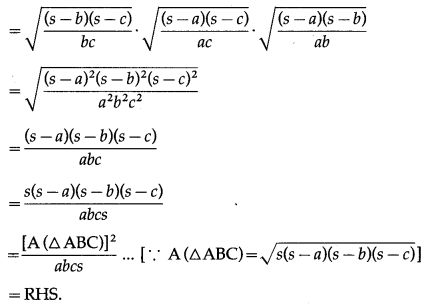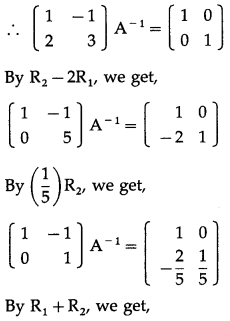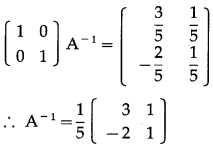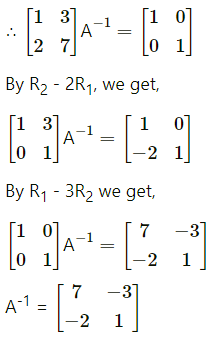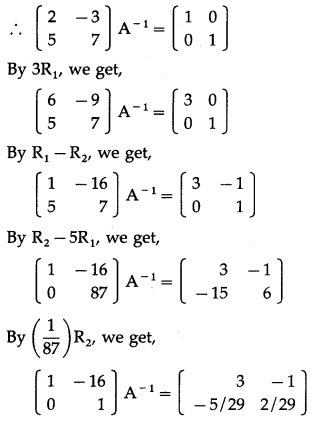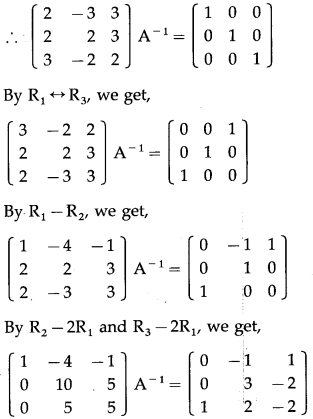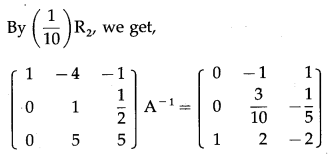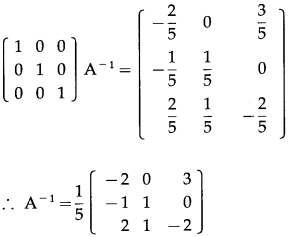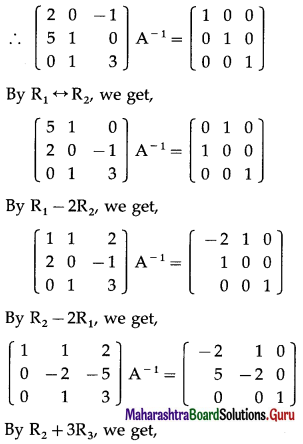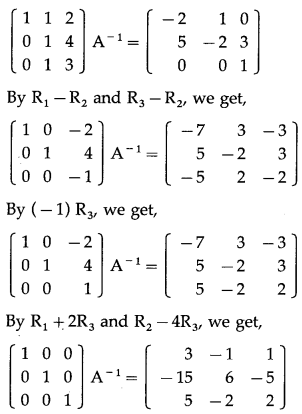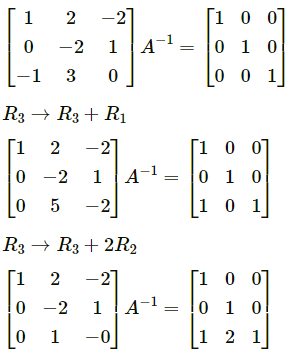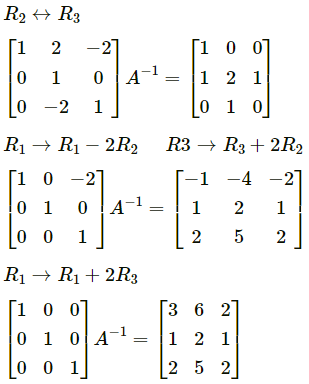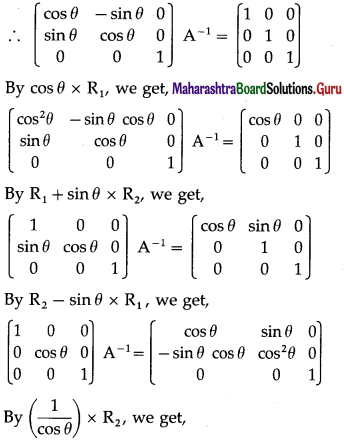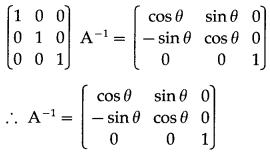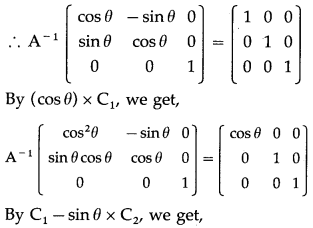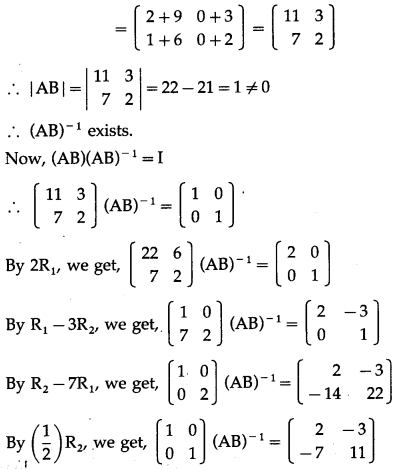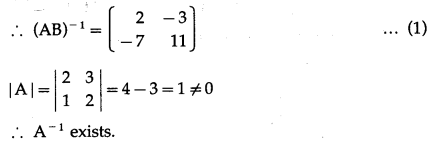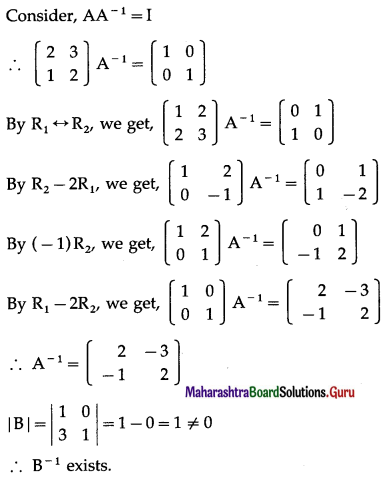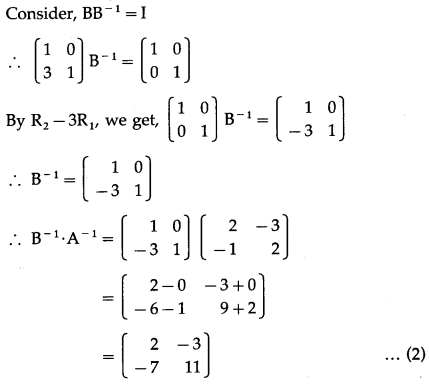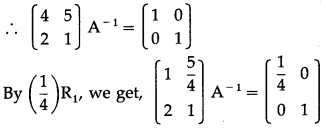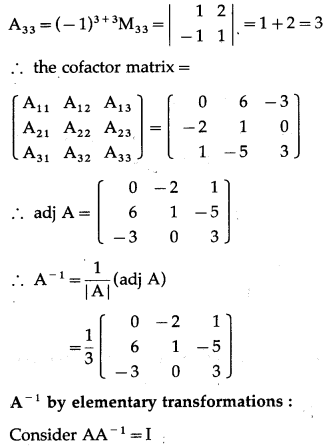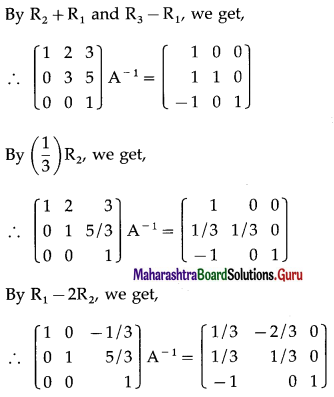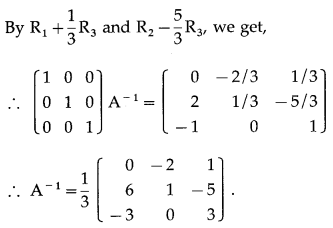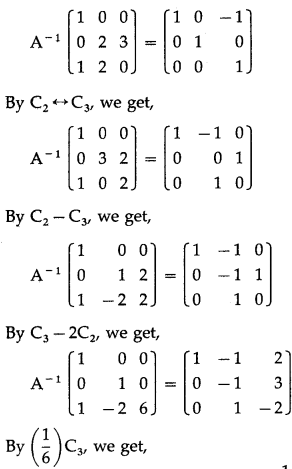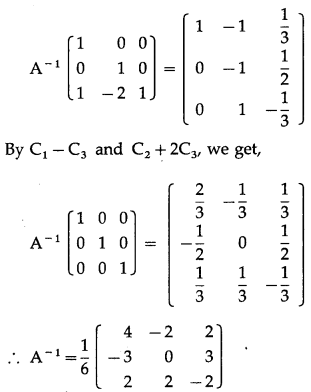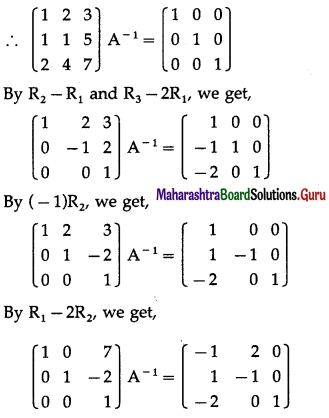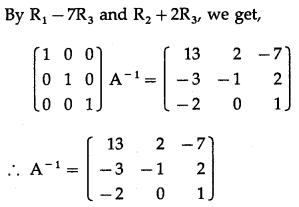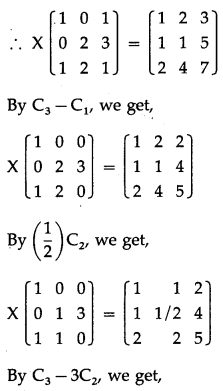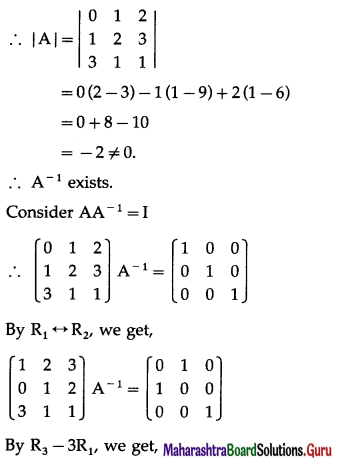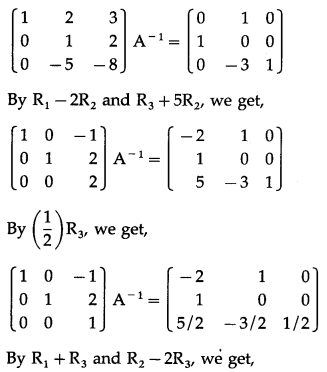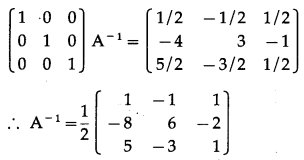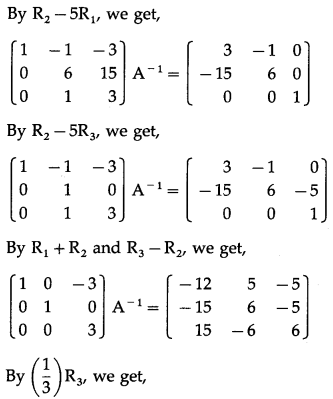Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Miscellaneous Exercise 3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Miscellaneous Exercise 3
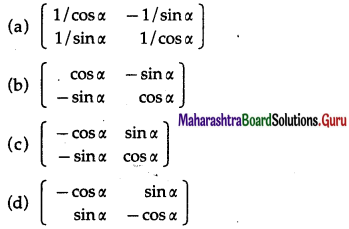
I) Select the correct option from the given alternatives.
Question 1.
The principal of solutions equation sinθ = \(\frac{-1}{2}\) are ________.

Solution:
(b) \(\frac{7 \pi}{6}, \frac{11 \pi}{6}\)
Question 2.
The principal solution of equation cot θ = \(\sqrt {3}\) ___________.

Solution:
(a) \(\frac{\pi}{6}, \frac{7 \pi}{6}\)
Question 3.
The general solution of sec x = \(\sqrt {2}\) is __________.
(a) 2nπ ± \(\frac{\pi}{4}\), n ∈ Z
(b) 2nπ ± \(\frac{\pi}{2}\), n ∈ Z
(c) nπ ± \(\frac{\pi}{2}\), n ∈ Z
(d) 2nπ ± \(\frac{\pi}{3}\), n ∈ Z
Solution:
(a) 2nπ ± \(\frac{\pi}{4}\), n ∈ Z
Question 4.
If cos pθ = cosqθ, p ≠ q rhen ________.
(a) θ = \(\frac{2 n \pi}{p \pm q}\)
(b) θ = 2nπ
(c) θ = 2nπ ± p
(d) nπ ± q
Solution:
(a) θ = \(\frac{2 n \pi}{p \pm q}\)

Question 5.
If polar co-ordinates of a point are \(\left(2, \frac{\pi}{4}\right)\) then its cartesian co-ordinates are ______.
(a) (2, \(\sqrt {2}\) )
(b) (\(\sqrt {2}\), 2)
(c) (2, 2)
(d) (\(\sqrt {2}\) , \(\sqrt {2}\))
Solution:
(d) (\(\sqrt {2}\) , \(\sqrt {2}\))
Question 6.
If \(\sqrt {3}\) cosx – sin x = 1, then general value of x is _________.
(a) 2nπ ± \(\frac{\pi}{3}\)
(b) 2nπ ± \(\frac{\pi}{6}\)
(c) 2nπ ± \(\frac{\pi}{3}-\frac{\pi}{6}\)
(d) nπ + (-1)n\(\frac{\pi}{3}\)
Solution:
(c) 2nπ ± \(\frac{\pi}{3}-\frac{\pi}{6}\)
Question 7.
In ∆ABC if ∠A = 45°, ∠B = 60° then the ratio of its sides are _________.
(a) 2 : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1
(b) \(\frac{\pi}{2}\) : 2 : \(\frac{\pi}{3}\) + 1
(c) 2 \(\frac{\pi}{2}\) : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\)
(d) 2 : 2 \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1
Solution:
(a) 2 : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1

Question 8.
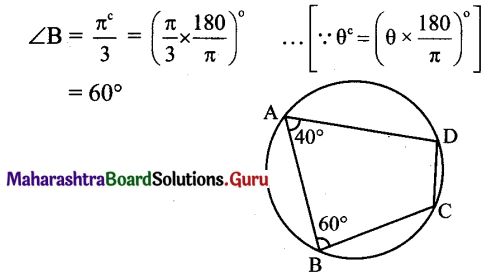
In ∆ABC, if c2 + a2 – b2 = ac, then ∠B = __________.
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{2}\)
(d) \(\frac{\pi}{6}\)
Solution:
(b) \(\frac{\pi}{3}\)
Question 9.
In ABC, ac cos B – bc cos A = ____________.
(a) a2 – b2
(b) b2 – c2
(c) c2 – a2
(d) a2 – b2 – c2
Solution:
(a) a2 – b2
Question 10.
If in a triangle, the are in A.P. and b : c = \(\sqrt {3}\) : \(\sqrt {2}\) then A is equal to __________.
(a) 30°
(b) 60°
(c) 75°
(d) 45°
Solution:
(c) 75°

Question 11.
cos-1\(\left(\cos \frac{7 \pi}{6}\right)\) = ________.

Question 12.
The value of cot (tan-1 2x + cot-1 2x) is __________.
(a) 0
(b) 2x
(c) π + 2x
(d) π – 2x
Solution:
(a) 0
Question 13.
The principal value of sin-1\(\left(-\frac{\sqrt{3}}{2}\right)\) is ____________.
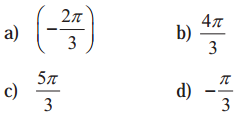
Solution:
(d) \(-\frac{\pi}{3}\)

Question 14.
If sin-1\(\frac{4}{5}\) + cos-1\(\frac{,12}{13}\) = sin-1 ∝, then ∝ = _____________.
(a) \(\frac{63}{65}\)
(b) \(\frac{62}{65}\)
(c) \(\frac{61}{65}\)
(d) \(\frac{60}{65}\)
Solution:
(a) \(\frac{63}{65}\)
Question 15.
If tan-1(2x) + tan-1(3x) = \(\frac{\pi}{4}\), then x = ________.
(a) -1
(b) \(\frac{1}{6}\)
(c) \(\frac{2}{6}\)
(d) \(\frac{3}{2}\)
Solution:
(b) \(\frac{1}{6}\)
Question 16.
2 tan-1\(\frac{1}{3}\) + tan-1\(\frac{1}{7}\) = ______.
(a) tan-1\(\frac{4}{5}\)
(b) \(\frac{\pi}{2}\)
(c) 1
(d) \(\frac{\pi}{4}\)
Solution:
(d) \(\frac{\pi}{4}\)

Question 17.
tan (2 tan-1\(\left(\frac{1}{5}\right)-\frac{\pi}{4}\)) = ______.
(a) \(\frac{17}{7}\)
(b) \(-\frac{17}{7}\)
(c) \(\frac{7}{17}\)
(d) \(-\frac{7}{17}\)
Solution:
(d) \(-\frac{7}{17}\)

Question 18.
The principal value branch of sec-1 x is __________.
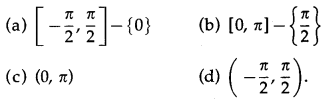
Solution:
(b) [0, π] – {\(\frac{\pi}{2}\)}
Question 19.
cos[tan-1\(\frac{1}{3}\) + tan-1\(\frac{1}{2}\)] = ________.
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{\pi}{4}\)
Solution:
(a) \(\frac{1}{\sqrt{2}}\)

Question 20.
If tan θ + tan 2θ + tan 3θ = tan θ∙tan 2θ∙tan 3θ, then the general value of the θ is _______.
(a) nπ
(b) \(\frac{n \pi}{6}\)
(c) nπ ± \(\frac{n \pi}{4}\)
(d) \(\frac{n \pi}{2}\)
Solution:
(b) \(\frac{n \pi}{6}\)
[Hint: tan(A + B + C) = \(\frac{\tan A+\tan B+\tan C-\tan A \cdot \tan B \cdot \tan C}{1-\tan A \cdot \tan B-\tan B \cdot \tan C-\tan C \cdot \tan A}\)
Since , tan θ + tan 2θ + tan 3θ = tan θ ∙ tan 2θ ∙ tan 3θ,
we get, tan (θ + 2θ + 3θ) = θ
∴ tan6θ = 0
∴ 6θ = nπ, θ = \(\frac{n \pi}{6}\).]
Question 21.
If any ∆ABC, if a cos B = b cos A, then the triangle is ________.
(a) Equilateral triangle
(b) Isosceles triangle
(c) Scalene
(d) Right angled
Solution:
(b) Isosceles triangle
II: Solve the following
Question 1.
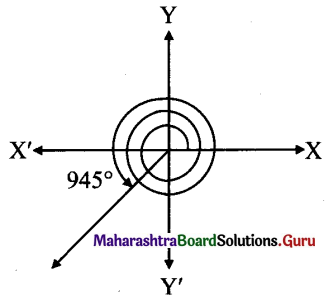
Find the principal solutions of the following equations :
(i) sin2θ = \(-\frac{1}{2}\)
Solution:
sin2θ = \(-\frac{1}{2}\)
Since, θ ∈ (0, 2π), 2∈ ∈ (0, 4π)

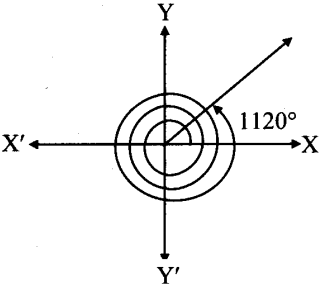
(ii) tan3θ = -1
Solution:
Since, θ ∈ (0, 2π), 3∈ ∈ (0, 6π)
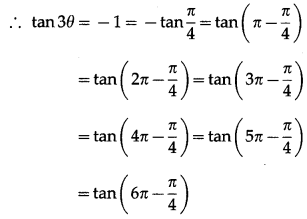
… [∵ tan(π – θ) = tan(2π – θ) = tan(3π – θ)
= tan (4π – θ) = tan (5π – θ) = tan (6π – θ) = -tan θ]
∴ tan3θ = tan\(\frac{3 \pi}{4}\) = tan\(\frac{7 \pi}{4}\) = tan\(\frac{11 \pi}{4}\) = tan\(\frac{15 \pi}{4}\)

(iii) cotθ = 0
Solution:
cotθ = 0
Since θ ∈ (0, 2π),
cotθ = 0 = cot \(\frac{\pi}{2}\) = cot (π + \(\frac{\pi}{2}\) …[∵ cos(π + θ) = cotθ]
∴ cotθ = cot\(\frac{\pi}{2}\) = cot\(\frac{3 \pi}{2}\)
∴ θ = \(\frac{\pi}{2}\) or θ = \(\frac{3 \pi}{2}\)
Hence, the required principal solutions are \(\left\{\frac{\pi}{2}, \frac{3 \pi}{2}\right\}\)

Question 2.
Find the principal solutions of the following equations :
(i) sin2θ = \(-\frac{1}{\sqrt{2}}\)
Solution:
(ii) tan5θ = -1
Solution:
(iii) cot2θ = 0
Solution:
Question 3.
Which of the following equations have no solutions ?
(i) cos 2θ = \(\frac{1}{3}\)
Solution:
cos 2θ = \(\frac{1}{3}\)
Since \(\frac{1}{3}\) ≤ cosθ ≤ 1 for any θ
cos2θ = \(\frac{1}{3}\) has solution
(ii) cos2 θ = -1
Solution:
cos2θ = -1
This is not possible because cos2θ ≥ 0 for any θ.
∴ cos2θ = -1 does not have any solution.
(iii) 2 sinθ = 3
Solution:
2 sin θ = 3 ∴ sin θ = \(\frac{3}{2}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 2 sin θ = 3 does not have any solution.
(iv) 3 sin θ = 5
Solution:
3 sin θ = 5
∴ sin θ = \(\frac{5}{3}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 3 sin θ = 5 does not have any solution.
Question 4.
Find the general solutions of the following equations :
(i) tanθ = \(-\sqrt {x}\)
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z.
Now, tanθ = \(-\sqrt {x}\)
∴ tanθ = tan\(\frac{\pi}{3}\) …[∵ tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ tanθ = tan\(\left(\pi-\frac{\pi}{3}\right)\) …[∵ tan(π – θ) = -tanθ]
∴ tanθ = tan\(\frac{2 \pi}{3}\)
∴ the required general solution is
θ = nπ + \(\frac{2 \pi}{3}\), n ∈ Z.
(ii) tan2θ = 3
Solution:
The general solution of tan2θ = tan2∝ is
θ = nπ ± ∝, n ∈ Z.
Now, tan2θ = 3 = (\(\sqrt {x}\))2
∴ tan2θ = (tan\(\frac{\pi}{3}\))2 …[∵ tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ tan2θ = tan2\(\frac{\pi}{3}\)
∴ the required general solution is
θ = nπ ± \(\frac{\pi}{3}\), n ∈ Z.
(iii) sin θ – cosθ = 1
Solution:
∴ cosθ – sin θ = -1


(iv) sin2θ – cos2θ = 1
Solution:
sin2θ – cos2θ = 1
∴ cos2θ – sin2θ = -1
∴ cos2θ = cosπ …(1)
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
∴ the general solution of (1) is given by
2θ = 2nπ ± π, n ∈ Z
∴ θ = nπ ± \(\frac{\pi}{2}\), n ∈ Z

Question 5.
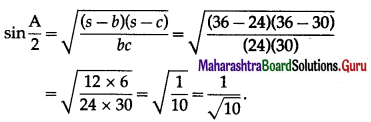
In ∆ABC prove that cos \(\left(\frac{A-B}{2}\right)=\left(\frac{a+b}{c}\right)\) sin \(\frac{C}{2}\)
Solution:
By the sine rule,
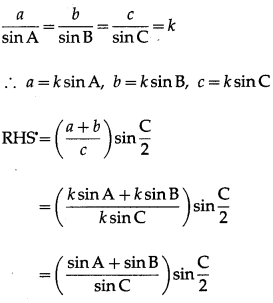
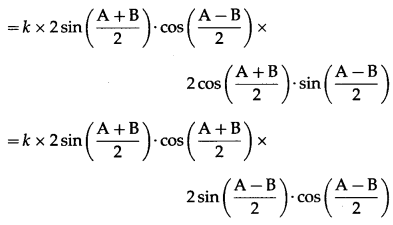
Question 6.
With usual notations prove that \(\frac{\sin (A-B)}{\sin (A+B)}=\frac{a^{2}-b^{2}}{c^{2}}\).
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC

Question 7.
In ∆ABC prove that (a – b)2 2cos2\(\frac{\mathrm{C}}{2}\) + (a + b)2 sin2\(\frac{\mathrm{C}}{2}\) = c2.
Solution:
LHS (a – b)2 2cos2\(\frac{\mathrm{C}}{2}\) + (a + b)2 sin2\(\frac{\mathrm{C}}{2}\)
= (a2 + b2 – 2ab) cos2\(\frac{\mathrm{C}}{2}\) + (a2 + b2 + 2ab) sin\(\frac{\mathrm{C}}{2}\)2
= (a2 + b2) cos2\(\frac{\mathrm{C}}{2}\) – 2ab cos2\(\frac{\mathrm{C}}{2}\) + (a2 + b2) sin2\(\frac{\mathrm{C}}{2}\) + 2ab sin2\(\frac{\mathrm{C}}{2}\)
= (a2 + b2) (cos2\(\frac{\mathrm{C}}{2}\) + sin2\(\frac{\mathrm{C}}{2}\)) – 2ab(cos2\(\frac{\mathrm{C}}{2}\) – sin2\(\frac{\mathrm{C}}{2}\))
= a2 + b2 – 2ab cos C
= c2 = RHS.

Question 8.
In ∆ABC if cosA = sin B – cos C then show that it is a right angled triangle.
Solution:
cos A= sin B – cos C
∴ cos A + cos C = sin B

∴ A – C = B
∴ A = B + C
∴ A + B + C = 180° gives
A + A = 180°
∴ 2A = 180 ∴ A = 90°
∴ ∆ ABC is a rightangled triangle.
Question 9.
If \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\) then show that a2, b2, c2, are in A.P.
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) = \(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sin B = kb,sin C = kc
Now, \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\)
∴ sinA∙sin(B – C) = sinC∙sin(A -B)
∴ sin [π – (B + C)] ∙ sin (B – C)
= sin [π – (A + B)]∙sin (A – B) … [∵ A + B + C = π]
∴ sin(B + C) ∙ sin(B – C) = sin (A + B) ∙ sin (A – B)
∴ sin2B – sin2C = sin2A – sin2B
∴ 2 sin2B = sin2A + sin2C
∴ 2k2b2 = k2a2 + k2c2
∴ 2b2 = a2 + c2
Hence, a2, b2, c2 are in A.P.
Question 10.
Solve the triangle in which a = (\(\sqrt {3}\) + 1), b = (\(\sqrt {3}\) – 1) and ∠C = 60°.
Solution:
Given : a = \(\sqrt {3}\) + 1, b = \(\sqrt {3}\) – 1 and ∠C = 60°.
By cosine rule,
c2 = a2 + b2 – 2ab cos C
= (\(\sqrt {3}\) + 1)2 + (\(\sqrt {3}\) – 1)2 – 2(\(\sqrt {3}\) + 1)(\(\sqrt {3}\) – 1)cos60°
= 3 + 1 + 2\(\sqrt {3}\) + 3+ 1 – 2\(\sqrt {3}\) – 2(3 – 1)\(\left(\frac{1}{2}\right)\)
= 8 – 2 = 6
∴ c = \(\sqrt {6}\) …[∵ c > 0)
By sine rule,
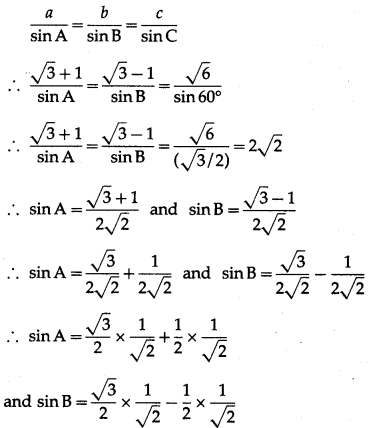
∴ sin A = sin 60° cos 45° + cos 60° sin 45°
and sin B = sin 60° cos 45° – cos 60° sin 45°
∴ sin A = sin (60° + 45°) – sin 105°
and sin B = sin (60° – 45°) = sin 15°
∴ A = 105° and B = 15°
Hence, A = 105°, B 15° and C = \(\sqrt {6}\) units.
Question 11.
In ∆ABC prove the following :
(i) a sin A – b sin B = c sin (A – B)
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC,
LHS = a sin A – b sinB
= ksinA∙sinA – ksinB∙sinB
= k (sin2A – sin2B)
= k (sin A + sin B)(sin A – sin B)
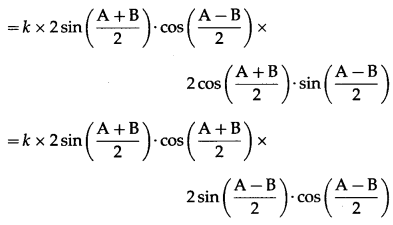
= k × sin (A + B) × sin (A – B)
= ksin(π – C)∙sin(A – B) … [∵ A + B + C = π]
= k sinC∙sin (A – B)
= c sin (A – B) = RHS.
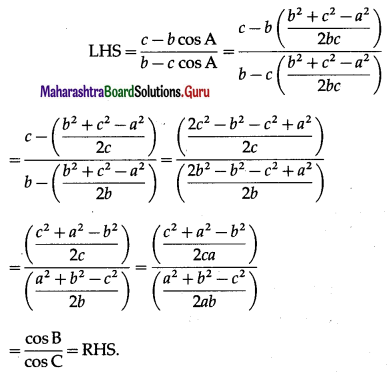
(ii) \(\frac{c-b \cos A}{b-c \cos A}=\frac{\cos B}{\cos C}\).
Solution:
(iii) a2 sin (B – C) = (b2 – c2) sinA
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC
RHS = (b2 – c2) sin A
= (k2sin2B – k2sin2C)sin A
= k2(sin2B – sin2C) sin A
= k2(sin B + sin C)(sin B – sin C) sin A
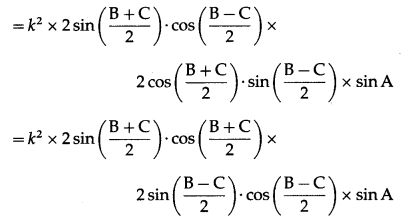
= k2 × sin (B + C) × sin (B – C) × sin A
= k2∙sin(π – A)∙sin(B – C)∙sinA … [∵ A + B + C = π]
= k2sin A∙sin (B – C)∙sin A
= (k sin A)2∙sin (B – C)
= a2sin (B – C) = LHS.
(iv) ac cos B – bc cos A = (a2 – b2).
Solution:
LHS = ac cos B – bc cos A
= ac\(\left(\frac{c^{2}+a^{2}-b^{2}}{2 c a}\right)\) – bc\(\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)\)
=\(\frac{1}{2}\)(c2 + a2 – b2) – \(\frac{1}{2}\)(b2 + c2 – a2)
= \(\frac{1}{2}\)(c2 + a2 – b2 – b2 – c2 + a2)
= \(\frac{1}{2}\)(2a2 – 2b2) = a2 – b2 = RHS.

(v) \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^{2}+b^{2}+c^{2}}{2 a b c}\) .
Solution:
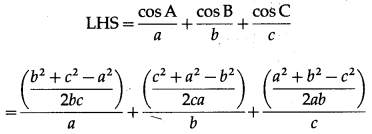
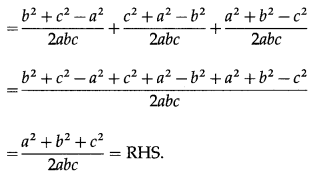
(vi) \(\frac{\cos 2 \mathrm{~A}}{a^{2}}-\frac{\cos 2 \mathrm{~B}}{b^{2}}=\frac{1}{a^{2}}-\frac{1}{b^{2}}\).
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}=\frac{\sin \mathrm{B}}{b}\)
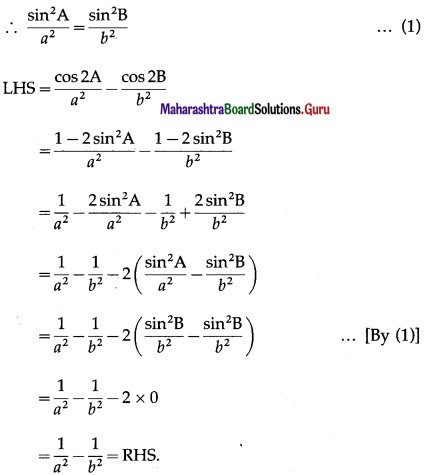
(vii) \(\frac{b-c}{a}=\frac{\tan \frac{B}{2}-\tan \frac{C}{2}}{\tan \frac{B}{2}+\tan \frac{C}{2}}\)
Solution:
By sine rule,
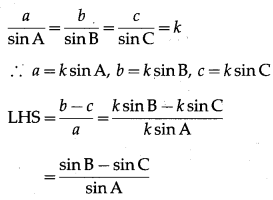
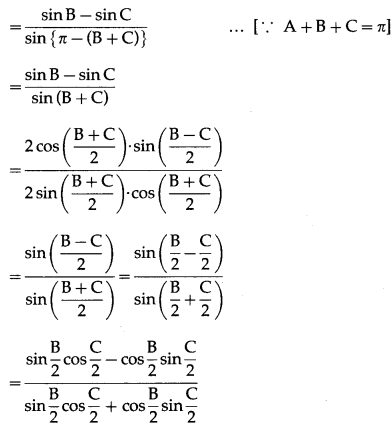
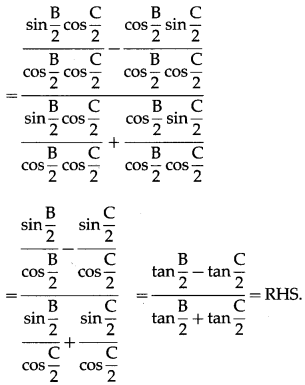
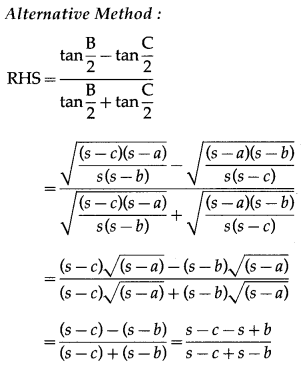
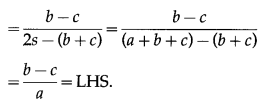
Question 12.
In ∆ABC if a2, b2, c2, are in A.P. then cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are also in A.P.
Question is modified
In ∆ABC if a, b, c, are in A.P. then cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are also in A.P.
Solution:
a, b, c, are in A.P.
∴ 2b = a + c …(1)
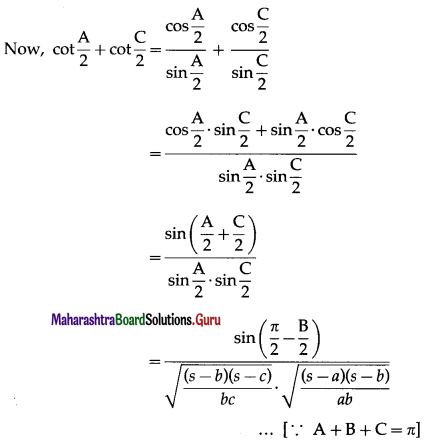
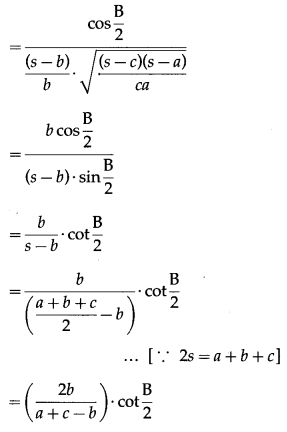
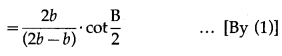
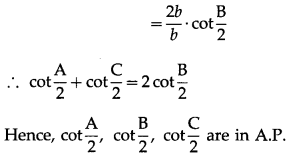
Question 13.
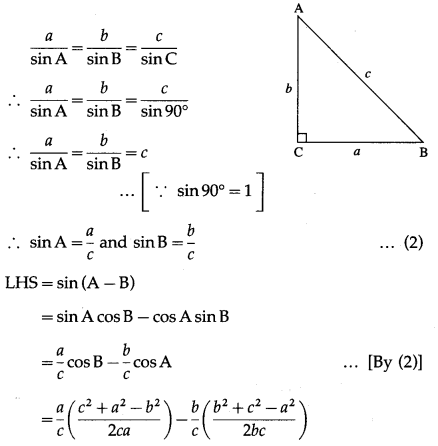
In ∆ABC if ∠C = 90º then prove that sin(A – B) = \(\frac{a^{2}-b^{2}}{a^{2}+b^{2}}\)
Solution:
In ∆ABC, if ∠C = 90º
∴ c2 = a2 + b2 …(1)
By sine rule,
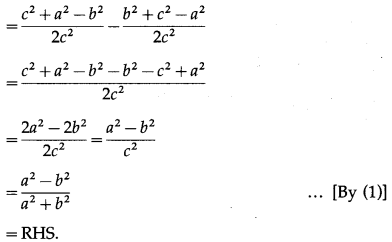
Question 14.
In ∆ABC if \(\frac{\cos A}{a}=\frac{\cos B}{b}\), then show that it is an isosceles triangle.
Solution:
Given : \(\frac{\cos A}{a}=\frac{\cos B}{b}\) ….(1)
By sine rule,
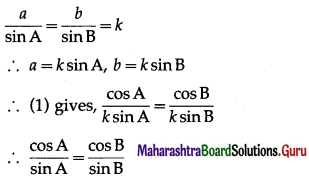
∴ sin A cos B = cos A sinB
∴ sinA cosB – cosA sinB = 0
∴ sin (A – B) = 0 = sin0
∴ A – B = 0 ∴ A = B
∴ the triangle is an isosceles triangle.
Question 15.
In ∆ABC if sin2A + sin2B = sin2C then prove that the triangle is a right angled triangle.
Question is modified
In ∆ABC if sin2A + sin2B = sin2C then show that the triangle is a right angled triangle.
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) = \(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sinB = kb, sin C = kc
∴ sin2A + sin2B = sin2C
∴ k2a2 + k2b2 = k2c2
∴ a2 + b2 = c2
∴ ∆ABC is a rightangled triangle, rightangled at C.

Question 16.
In ∆ABC prove that a2(cos2B – cos2C) + b2(cos2C – cos2A) + c2(cos2A – cos2B) = 0.
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
LHS = a2(cos2B – cos2C) + b2( cos2C – cos2A) + c2(cos2A – cos2B)
= k2sin2A [(1 – sin2B) – (1 – sin2C)] + k2sin2B [(1 – sin2C) – (1 – sin2A)] + k2sin2C[(1 – sin2A) – (1 – sin2B)]
= k2sin2A (sin2C – sin2B) + k2sin2B(sin2A – sin2C) + k2sin2C (sin2B – sin2A)
= k2(sin2A sin2C – sin2Asin2B + sin2A sin2B – sin2B sin2C + sin2B sin2C – sin2A sin2C)
= k2(0) = 0 = RHS.
Question 17.
With usual notations show that (c2 – a2 + b2) tan A = (a2 – b2 + c2) tan B = (b2 – c2 + a2) tan C.
Solution:
By sine rule,
\(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\) = \(\frac{c}{\sin C}\) = k
∴ a = fksinA, b = ksinB, c = ksinC

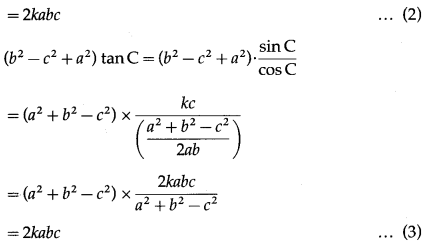
From (1), (2) and (3), we get
(c2 – a2 + b2) tan A = (a2 – b2 + c2) tan B
= (b2 – c2 + a2) tan C.
Question 18.
In ∆ABC, if a cos2\(\frac{C}{2}\) + c cos2\(\frac{A}{2}\) = \(\frac{3 b}{2}\), then prove that a , b ,c are in A.P.
Solution:
a cos2\(\frac{C}{2}\) + c cos2\(\frac{A}{2}\) = \(\frac{3 b}{2}\)
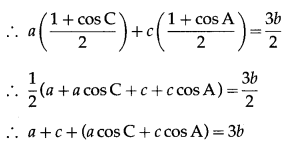
∴ a + c + b = 3b …[∵ a cos C + c cos A = b]
∴ a + c = 2b
Hence, a, b, c are in A.P.

Question 19.
Show that 2 sin-1\(\left(\frac{3}{5}\right)\) = tan-1\(\left(\frac{24}{7}\right)\).
Solution:
Let sin2\(\left(\frac{3}{5}\right)\) = x.

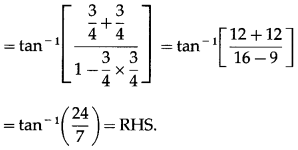

∴ tan-1\(\left(\frac{24}{7}\right)\) = RHS
Question 20.
Show that tan-1\(\left(\frac{1}{5}\right)\) + tan-1\(\left(\frac{1}{7}\right)\) + tan-1\(\left(\frac{1}{3}\right)\) + tan-1\(\left(\frac{1}{8}\right)\) = \(\frac{\pi}{4}\).
Solution:

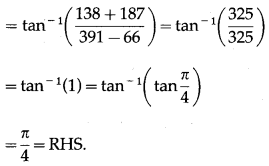
Question 21.
Prove that tan-1\(\sqrt {x}\) = \(\frac{1}{2}\) cos-1\(\left(\frac{1-x}{1+x}\right)\), if x ∈ [0, 1].
Solution:
Let tan-1\(\sqrt {x}\) = y
∴ tan y = \(\sqrt {x}\) ∴ x = tan2y
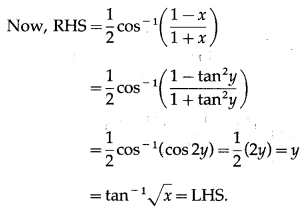
Question 22.
Show that \(\frac{9 \pi}{8}-\frac{9}{4}\) sin-1\(\frac{1}{3}\) = \(\frac{9}{4}\) sin-1\(\frac{2 \sqrt{2}}{3}\).
Question is modified
Show that \(\frac{9 \pi}{8}-\frac{9}{4}\) sin-1\(\left(\frac{1}{3}\right)\) = \(\frac{9}{4}\) sin-1\(\left(\frac{2 \sqrt{2}}{3}\right)\).
Solution:
We have to show that
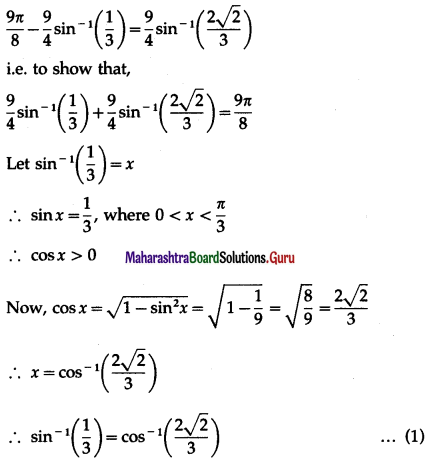
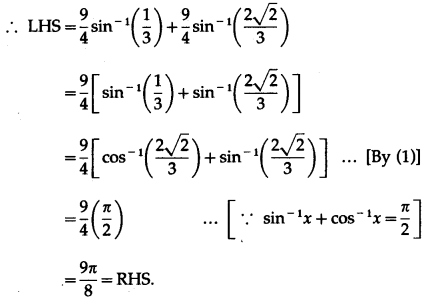

Question 23.
Show that
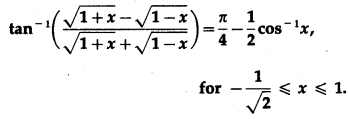
Solution:
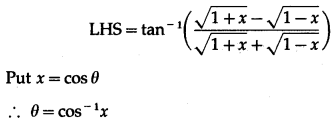
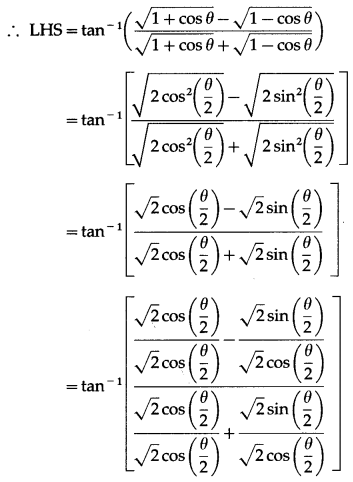
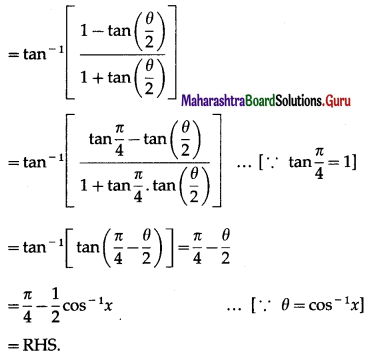
Question 24.
If sin(sin-1\(\frac{1}{5}\) + cos-1x) = 1, then find the value of x.
Solution:
sin(sin-1\(\frac{1}{5}\) = 1
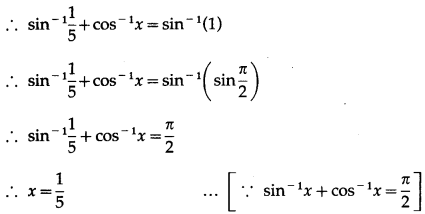
Question 25.
If tan-1\(\left(\frac{x-1}{x-2}\right)\) + tan-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\) then find the value of x.
Solution:
tan-1\(\left(\frac{x-1}{x-2}\right)\) + tan-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\)

∴ x = ±\(\frac{1}{\sqrt{2}}\).
Question 26.
If 2 tan-1(cos x ) = tan-1(cosec x) then find the value of x.
Solution:
2 tan-1(cos x ) = tan-1(cosec x)


Question 27.
Solve: tan-1\(\left(\frac{1-x}{1+x}\right)\) = \(\frac{1}{2}\)(tan-1x), for x > 0.
Solution:
tan-1\(\left(\frac{1-x}{1+x}\right)\) = \(\frac{1}{2}\)(tan-1x)
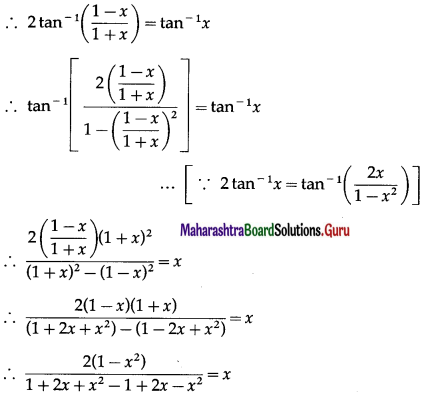
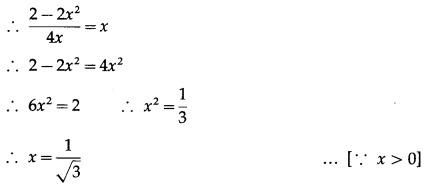
Question 28.
If sin-1(1 – x) – 2sin-1x = \(\frac{\pi}{2}\), then find the value of x.
Solution:
sin-1(1 – x) – 2sin-1x = \(\frac{\pi}{2}\)
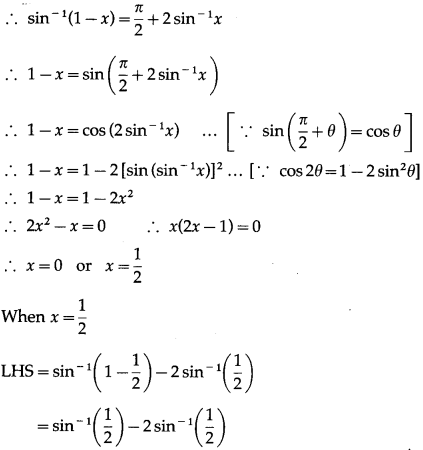
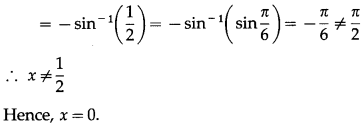
Question 29.
If tan-12x + tan-13x = \(\frac{\pi}{4}\), then find the value of x.
Question is modified
If tan-12x + tan-13x = \(\frac{\pi}{2}\), then find the value of x.
Solution:
tan-12x + tan-13x = \(\frac{\pi}{4}\)
∴ tan-1\(\left(\frac{2 x+3 x}{1-2 x \times 3 x}\right)\) = tan\(\frac{\pi}{4}\), where 2x > 0, 3x > 0
∴ \(\frac{5 x}{1-6 x^{2}}\) = tan\(\frac{\pi}{4}\) = 1
∴ 5x = 1 – 6x2
∴ 6x2 + 5x – 1 = 0
∴ 6x2 + 6x – x – 1 = 0
∴ 6x(x +1) – 1(x + 1) = 0
∴ (x + 1)(6x – 1) = 0
∴ x = -1 or x = \(\frac{1}{6}\)
But x > 0 ∴ x ≠ -1
Hence, x = \(\frac{1}{6}\)
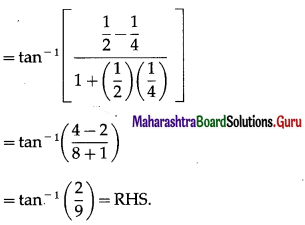
Question 30.
Show that tan-1\(\frac{1}{2}\) – tan-1\(\frac{1}{4}\) = tan-1\(\frac{2}{9}\).
Solution:
LHS = tan-1\(\frac{1}{2}\) – tan-1\(\frac{1}{4}\)

Question 31.
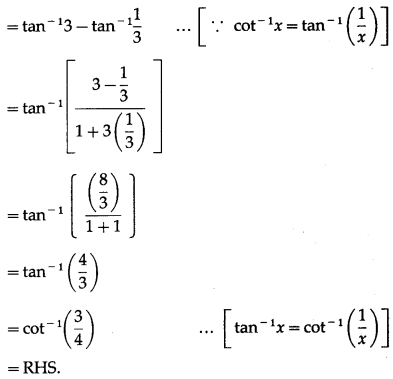
Show that cot-1\(\frac{1}{3}\) – tan-1\(\frac{1}{3}\) = cot-1\(\frac{3}{4}\).
Solution:
LHS = cot-1\(\frac{1}{3}\) – tan-1\(\frac{1}{3}\)
Question 32.
Show that tan-1\(\frac{1}{2}\) = \(\frac{1}{3}\) tan-1\(\frac{11}{2}\).
Solution:
We have to show that

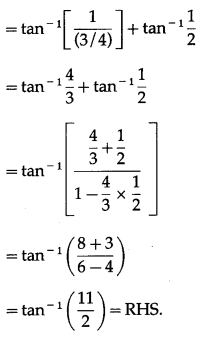

Question 33.
Show that cos-1\(\frac{\sqrt{3}}{2}\) + 2sin-1\(\frac{\sqrt{3}}{2}\) = \(\frac{5 \pi}{6}\)
Solution:

Question 34.
Show that 2cot-1\(\frac{3}{2}\) + sec-1\(\frac{13}{12}\) = \(\frac{\pi}{2}\)
Solution:

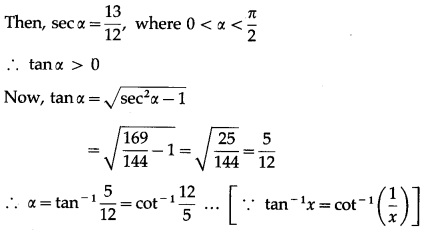

Question 35.
Prove the following :
(i) cos-1 x = tan-1\(\frac{\sqrt{1-x^{2}}}{x}\), if x < 0.
Question is modified
cos-1 x = tan-1\(\left(\frac{\sqrt{1-x^{2}}}{x}\right)\), if x > 0.
Solution:

(ii) cos-1 x = π + tan-1\(\frac{\sqrt{1-x^{2}}}{x}\), if x < 0.
Solution:

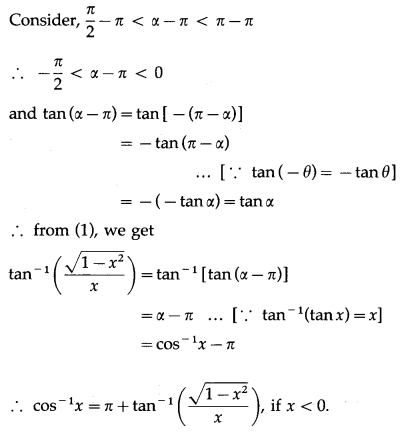

Question 36.
If |x| < 1 , then prove that 2tan-1 x = tan-1\(\frac{2 x}{1-x^{2}}\) = sin-1\(\frac{2 x}{1+x^{2}}\) = cos-1\(\frac{1-x^{2}}{1+x^{2}}\)
Question is modified
If |x| < 1 , then prove that 2tan-1 x = tan-1\(\left(\frac{2 x}{1-x^{2}}\right)\) = sin-1\(\left(\frac{2 x}{1+x^{2}}\right)\) = cos-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
Let tan-1x = y
Then, x = tany

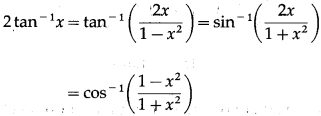
Question 37.
If x, y, z, are positive then prove that tan-1\(\frac{x-y}{1+x y}\) + tan-1\(\frac{y-z}{1+y z}\) + tan-1\(\frac{z-x}{1+z x}\) = 0
Solution:
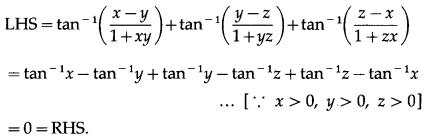
Question 38.
If tan-1 x + tan-1 y + tan-1 z = \(\frac{\pi}{2}\) then, show that xy + yz + zx = 1
Solution:
tan-1 x + tan-1 y + tan-1 z = \(\frac{\pi}{2}\)
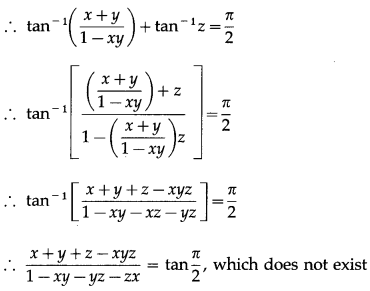
∴ 1 – xy – yz – zx = 0
∴ xy + yz + zx = 1.

Question 39.
If cos-1 x + cos-1 y + cos-1 z = π then show that x2 + y2 + z2 + 2xyz = 1.
Solution:
0 ≤ cos-1x ≤ π and
cos-1x + cos-1y+ cos-1z = 3π
∴ cos-1x = π, cos-1y = π and cos-1z = π
∴ x = y = z = cosπ = -1
∴ x2 + y2 + z2 + 2xyz
= (-1)2 + (-1)2 + (-1)2 + 2(-1)(-1)(-1)
= 1 + 1 + 1 – 2
= 3 – 2 = 1.


![]()


![]()

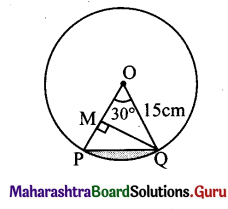
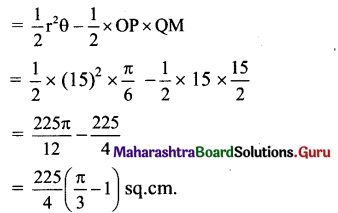
![]()