Prasanna

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 11 Magnetic Materials Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 11 Magnetic Materials

Question 1.
How did a magnet derive its name? What was its ancient use?
Answer:
The characteristic of a magnet to attract iron is called its attractive property. This property was discovered in a rock found in the ancient mineral-rich region of Magnesia (modern Turkey). The word magnet is derived from this Magnesian rock.

The rock when floated on water (by tying it to a piece of wood) or suspended freely was found to align approximately in the north-south direction. Because this directional property was used by some ancient travellers to locate the geographic north, it was also called the leading stone or lodestone.

The Magnesian rock is the naturally magnetized iron ore magnetite (Fe₃O₄). It is hard, black or brownish-black with a metallic luster.

Question 2.
Explain the directional characteristic of a bar magnet.
Answer:
When a bar magnet is suspended so as to rotate freely in a horizontal plane, it comes to rest in approximately the North-South direction.

The end of the magnet directed towards the Earth’s geographic North Pole is called the north-seeking pole or the north pole, and the other end which is directed towards the Earth’s geographic South Pole is called the south-seeking pole or the south pole.

The cause for this alignment is seen when we consider the turning moment on a bar magnet suspended in a uniform magnetic induction \(\vec{B}\), as shown in below figure. The north pole (pole strength + m) and the south pole (pole strength – m) of the bar magnet experience equal and opposite forces of magnitude mB. If the lines of action of these two forces are not the same, they constitute a couple whose effect is to produce rotation.

Question 3.
State the expression for the torque acting on a magnetic dipole in a uniform magnetic field.
Answer:
When a magnetic dipole of magnetic dipole moment \(\vec{M}\) is placed in a uniform magnetic field of induction \(\vec{B}\), it experiences a torque whose magnitude is
τ = MB sin θ
where θ is the smaller angle between the magnetic axis and \(\vec{B}\).
[Note: When the dipole is placed with its axis at right-angles to the field, i.e, θ = 90°,
τ = MB or M = \(\frac{\tau}{B}\)
This is the defining equation for the magnetic dipole moment.]

Question 4.
Derive an expression for the torque acting on a magnetic dipole placed in a region of uniform magnetic induction. Express it in vector form.
Answer:
Consider a magnetic dipole consisting of two point poles of pole strength m a distance 2l apart with its axis inclined at an angle θ to a uniform magnetic field of induction \(\vec{B}\), shown in figure. The magnetic force on the positive (or north) pole is m\(\vec{B}\), while that on the negative (or south) pole is – m\(\vec{B}\). These two forces, equal in magnitude, opposite in direction and separated by a finite distance, constitute a couple which tends to line up the magnetic dipole moment with the field \(\vec{B}\).

The torque of the couple in the clockwise sense in above figure in magnitude, is
τ = (mB) d
where d is the distance between the lines of action of the forces.
∴ τ = (mB)2lsin θ = MB sin θ (∵ m = \(\frac{M}{2 l}\))
Expressed as a vector product,
\(\vec{\tau}=\vec{M} \times \vec{B}\)
The torque has a maximum magnitude, (m2l)B, when sin θ = 1, i.e., when the magnet is perpendicular to the field. The torque vanishes when the magnet is parallel to the field, where sin θ = 0.

Question 5.
A current-carrying coil with magnetic moment \(\vec{M}\) (M = 5 A∙m²) is placed in a uniform magnetic field of induction \(\vec{B}\) (B = 0.2 Wb/m²) such that the angle between \(\vec{M}\) and \(\vec{B}\) is 30°. What is the torque acting on the coil ?
Answer:
τ = MB sin θ = (5) (0.2) sin 30° = 0.5 N∙m is the torque acting on the coil.

Question 6.
Explain what is meant by magnetic potential energy of a bar magnet kept in a uniform magnetic field. Discuss the cases when
(1) θ = 0°
(2) θ = 180°
(3) θ = 90°.
Answer:
A magnet free to rotate in a uniform magnetic field \(\vec{B}\) aligns its dipole moment \(\vec{M}\) with \(\vec{B}\). Work must be done to rotate the magnet from this equilibrium position. The work done is stored as the magnetic potential energy, also called its orientation energy. In a finite angular displacement from 0 to θ, the
magnetic potential energy

1. When θ = 0°, cos θ = cos 0° = 1, U_θ = – MB. At this position, the magnetic moment of the bar magnet is lined up with the field and its magnetic potential energy is minimum. This is its most stable equilibrium position.
2. When θ = 180°, cos θ = cos 180° = – 1, U_θ = MB. At this position, the magnetic moment is antiparallel to the field and its magnetic potential energy is maximum. This is its most unstable position.
3. When θ = 90°, cos θ = cos 90° = 0, U_θ = 0. At this position, the bar magnet is perpendicular to the
   magnetic field. Its magnetic potential energy is zero.

Question 7.
What is the nature of the graph between the magnetic potential energy of a bar magnet kept in a uniform magnetic field and angular position of the magnet ?
OR
Draw a graph of magnetic potential energy as a function of angular displacement.
Answer:

Question 8.
Derive the expression for the time period of angular oscillations of a bar magnet kept in a uniform magnetic field.
Answer:
Consider a bar magnet of magnetic dipole moment \(\vec{M}\), suspended by a light twistless fibre in a uniform magnetic field \(\vec{B}\) in such a way that it is free to rotate in a horizontal plane. In the rest position θ = 0, \(\vec{M}\) is parallel to \(\vec{B}\).

If magnet is given a small angular displacement θ from its rest position and released, the magnet performs angular or torsional oscillations about the rest position.

Let I be the moment of inertia of the bar magnet about the axis of oscillation and α the angular acceleration. The deflecting torque (in magnitude) is
τ_d = Iα = I \(\frac{d^{2} \theta}{d t^{2}}\) …………….. (1)
However, the restoring torque tries to bring back the oscillating bar magnet in the rest position. The restoring torque (in magnitude) is, τ_r = – MB sin θ …………. (2)
The minus sign in Eq. (2) indicates that restoring torque is opposite in direction to the angular deflection.
In equilibrium, both the torques balance each other. From Eqs. (1) and (2),

Eq. (4) represents angular simple harmonic motion.
Writing ω² = \(\frac{M B}{I}\) , the angular frequency ω of the motion is
ω = \(\sqrt{\frac{M B}{I}}\) ………….. (5)
The time period of oscillations of the bar magnet is
T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{I}{M B}}\) ……………… (6)
This is the required expression.

9. Solve the following
Question 1.
Find the magnitude of the magnetic moment of a magnet if a couple exerting torque 0.5 N.m is required to hold the magnet with its axis perpendicular to a uniform magnetic field of induction 2 × 10^-3 T.
Solution:
Data : τ = 0.5 N∙m, B = 2 × 10^-3 T, θ = 90°
τ = MB sin θ
∴ M = \(\frac{\tau}{B \sin \theta}=\frac{0.5 \mathrm{~N} \cdot \mathrm{m}}{\left(2 \times 10^{-3} \mathrm{~T}\right) \sin 90^{\circ}}\)
= 250 A∙m²
The magnitude of the magnetic moment of the magnet is 250 A∙m².

Question 2.
A magnetic dipole of magnetic moment 5 A∙m² is placed in a uniform magnetic field of induction 10^-3 T. Find the magnitude of the maximum torque acting on the dipole.
Solution:
Data : M = 5 A∙m², B = 10^-3 T
Torque, τ = MB sin θ
The magnitude of the torque is maximum when θ = 90°.
∴ τ_max = MB = 5 × 10^-3 N∙m

Question 3.
A bar magnet of magnetic length 0.12 m and pole strength 10 A-m is placed in a uniform magnetic field of induction 3 × 10^-2 tesla. If the angle between the magnetic induction and the magnetic moment is 30°, find the magnitude of the torque acting on the magnet.
Solution:
Data : 2l = 0.12 m, m = 10 A∙m, B = 3 × 10^-2 T,
θ = 30°
The magnitude of the torque,
τ = MB sin θ = m (2l) B sin θ
= (10 A∙m) (0.12 m)(3 × 10^-2 T) sin 30°
= 3.6 × 10^-2 × \(\frac{1}{2}\)
= 1.8 × 10^-2 N∙m

Question 4.
A bar magnet of moment 10 A∙m is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 36 µT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 8C and magnetic potential energy.
Solution:
Data : M = 10 A∙m², B_h = 36µT = 3.6 × 10^-5 T,
θ = 8°
The magnitude of the torque is
τ = MB_h sin θ
= (10) (3.6 × 10^-5) sin 8°
= (36 × 10^-5) (0.1391) = 5.007 × 10^-5 N∙m
The magnetic potential energy of the bar magnet is
U_θ = MB_h cos θ
= (36 × 10^-5) cos 8°
= (36 × 10^-5) (0.99) = 3.564 × 10^-4 J

Question 5.
The time period of angular oscillation of a bar magnet in a horizontal magnetic field is 3.14 s. If the horizontal component of the Earth’s magnetic field at the place is 40 µT and the moment of inertia of the magnet is 10^-4 kg∙m², calculate the magnetic moment of the magnet.
Solution:
Data : T = 3.14 s, B_h = 40 µT = 4 × 10^-5 T,
I = 10^-4 kg∙m²

Question 6.
A bar magnet of moment 10 A∙m² is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 36 µT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 8° and magnetic potential energy.
Solution:
Data : M = 10 A∙m², B_h = 36 µT = 3.6 × 10^-5 T, θ = 8°
The magnitude of the torque is
τ = MB_h sin θ
=(10)(3.6 × 10^-5)sin8°
=(36 × 10^-5)(0.1391) = 5.007 × 10^-5 N∙m
The magnetic potential energy of the bar magnet is
U_θ = MB_h cos θ
=(36 × 10^-5)cos8°
=(36 × 10^-5)(0.99) = 3.564 × 10^-4 J

Question 10.
As the electron revolves in the second Bohr orbit in the hydrogen atom, the corresponding current is (about) 1.3 × 10^-4 A. If the area of the orbit is (about) 1.4 × 10^-19 m², what is the (approximate) equivalent magnetic moment?
Answer:
M = IA = (1.3 × 10^-4)(1.4 × 10^-19)
= 1.82 × 10^-23 A∙m² is the (approximate) equivalent magnetic moment.

Question 11.
What is the magnetic moment of an electron due to its orbital motion?
Answer:
The orbital magnetic moment of an electron, of charge e and revolving with speed v in an orbit of radius r, is \(\frac{1}{2}\) evr.

Question 12.
If the frequency of revolution of a proton (q = 1.6 × 10^-19 C) in a uniform magnetic induction is 10⁶ Hz, what is the corresponding electric current?
Answer:
I = \(\frac{q}{T}\) = qf = (1.6 × 10^-19)(10⁶)
= 1.6 × 10^-13 A
is the corresponding electric current.

Question 13.
The frequency of revolution of the electron in the second Bohr orbit in the hydrogen atom is 8.22 × 10¹⁴ Hz. What is the corresponding electric ’ current? [e = 1.6 × 10^-19 C]
Answer:
I = \(\frac{e}{T}\) = ef
= (1.6 × 10^-19)(8.22 × 10¹⁴)
= 1.315 × 10^-4A
is the corresponding electric current.

Question 14.
A coil has 1000 turns, each of area 0.5 m². What is the magnetic moment of the coil when it carries a current of 1 mA ?
Answer:
Magnetic moment M = NIA
= 1000 × 1 × 10^-3 × 0.5
= 0.5 A∙m²

Question 15.
What is the gyromagnetic ratio of an orbital electron ? State its dimensions and the SI unit.
Answer:
The ratio of the magnitude of the orbital magnetic moment to that of the orbital angular momentum of an electron in an atom is called its gyromagnetic ratio γ₀. If \(\vec{M}_{\mathrm{o}}\) is the orbital magnetic moment of the electron with orbital angular momentum \(\vec{L}_{\mathrm{o}}\),
γ₀ = \(\frac{M_{\mathrm{o}}}{L_{\mathrm{o}}}=\frac{e}{2 m_{\mathrm{e}}}\)
where e and me are the electronic charge and electron mass, respectively.
Dimensions : [γ₀] = \(\frac{[\text { charge }]}{[\text { mass }]}=\frac{[T I]}{[M]}\) = [M^-1TI].
SI unit : The coulomb per kilogram (C/kg).
[Note : γ₀ = 8.794 × 10¹⁰ C/kg. The gyromagnetic ratio of electron spin is nearly twice that of an orbital electron.]

16. Solve the following
Question 1.
A circular coil of 300 turns and diameter 14 cm carries a current of 15 A. What is the magnitude of the magnetic moment associated with the coil?
Solution :
Data : N = 300, d = 14 cm, I = 15 A
r = \(\frac{d}{2}\) = 7 cm = 7 × 10^-2 m
The magnitude of the magnetic moment associated with the coil is
M = NIA = NI(πr²)
= (300)(15)(3.142)(7 × 10^-2)²
= 4500 × 3.142 × 49 × 10^-4
= 69.28 A∙m²

Question 2.
A coil has 300 turns, each of area 0.05 m².
(i) Find the current through the coil for which the magnetic moment of the coil will be 4.5 A∙m².
(ii) It is placed in a uniform magnetic field of induction 0.2 T with its magnetic moment making an angle of 30° with \(\vec{B}\). Calculate the magnitude of the torque experienced by the coil.
Solution:
Data : N = 300, A = 0.05 m², M = 4.5 A∙m², B = 0.2 T, θ = 30°
(i) M = NIA
∴ The current in the coil,
I = \(\frac{M}{N A}=\frac{4.5}{300 \times 0.05}\) = 0.3 A

(ii) The magnitude of the torque,
τ = MB sin θ = 4.5 × 0.2 × sin 30°
= 0.9 × \(\frac{1}{2}\) = 0.45 N∙m

Question 3.
An electron in an atom revolves around the nucleus in an orbit of radius 0.5 Å. Calculate the equivalent magnetic moment if the frequency of revolution of the electron is 10¹⁰ MHz.
Solution:
Data : r = 0.5 Å = 5 × 10^-11 m,
f = 10¹⁰ MHz = 10¹⁶ Hz, e = 1.6 × 10^-19 C
Equivalent current, I = \(\frac{e}{T}\) = ef
The equivalent magnetic moment is
M = IA = ef(πr²)
= (1.6 × 10^-19)(1016)(3.142)(5 × 10^-11)2
= 1.6 × 3.142 × 25 × 10^-25
= 1.257 × 10^-23 A∙m²

Question 4.
Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom. The radius of the orbit is 2.126 Å and the orbital speed of the electron in the orbit is 1.09 × 10⁶ m/s.
Solution:
Data : r = 2.126 Å = 2.126 × 10^-10 m,
v = 1.09 × 10⁶ m/s, e = 1.6 × 10^-19 C
The orbital magnetic dipole moment of the electron,
M₀ = \(\frac{1}{2}\) evr
=(1.6 × 10^-19)(1.09 × 10⁶)(2.126 × 10^-10)
=1.6 × 1.09 × 1.063 × 10^-23
= 1.854 × 10^-23 A∙m²

Question 5.
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Å. If the frequency of revolution of an electron is 9 × 10⁹ MHz, calcu-late the orbital angular momentum. [Charge on an electron = 1.6 × 10^-19 C, gyromagnetic ratio = 8.8 × 10¹⁰ C/kg, π = 3.142]
Solution:
Data : r = 0.53 Å = 0.53 × 10^-10 m,
f = 9 × 10⁹ MHz = 9 × 10¹⁵ Hz, e = 1.6 × 10^-19 C, gyromagnetic ratio = 8.8 × 10¹⁰ C / kg, π = 3.142
Magnetic moment, M₀ =IA = efπr²
= 1.6 × 10^-19 × 9 × 10¹⁵ × 3.142 × (0.53 × 10^-10)²
= 14.4 × 3.142 × (0.53)² × 10^-19 × 10¹⁵× 10²⁰
= 1.272 × 10^-23 A∙m²

Question 6.
The specific charge (charge-to-mass ratio) of an electron is 1.759 × 10¹¹ C/kg.
(i) What is the gyromagnetic ratio of an orbital electron?
(ii) If the measured component of its orbital angular momentum is 2.11 × 10^-34 kg∙m³/s. what Is the associatcd orbital magnetic dipole moment?
Solution:
Data: \(\frac{e}{m_{e}}\) = 1.759 × 10¹¹ C/kg,
L = 2.11 × 10^-34 kg∙m²/s

(i) The gyromag1etic ratio of an orbital electron,
γ₀ = \(\frac{e}{2 m_{\mathrm{e}}}=\frac{1.759 \times 10^{11}}{2}\) =8.795 × 10¹⁰ C/kg

(ii) For the given component of the orbital angular momentum, the associated magnetic dipole moment is
Mo = \(\frac{e}{2m_{e}}\) L₀ = γ₀L₀
= (8.795 × 10¹⁰ )(2.11 × 10^-34)
= 1.856 × 10^-23 A∙m²

Question 7.
An electron performs uniform circuLar motion in a uniform magnetic field of induction 1.2T In a plane perpendicular to the field. Its kinetic energy is 6 × 10^-20 J and its motion is subject only to the magnetic force due to the field. What is the magnetic dipole moment associated with the motion of the electron?
Solution:
Data:B = 1.2T, KE ≡ E_k = 6 × 10^-20 J
The centripetal force on the electron is the magnetic force. If r and e are respectively the radius of the path and linear speed of the electron,

Question 8.
If the magnetic moment of an electron revolving in an orbit of radius 0.4 Å is 9 × 10^-24 A∙m² then find the linear momentum of the electron in that orbit. (e/m = 1.76 × 10¹¹ C/kg]
Solution:
Data: r = 0.5 Å = 5 × 10^-11 m, I = 1.1 × 10^-3 A,
x = 100 Å = 10^-8 m, \(\frac{\mu_{0}}{4 \pi}\) = 10^-7 T∙m/A
The magnitude of the magnetic induction at an axial point of a current loop,

Question 9.
The magnetic moment of an electron revolving in a circular orbit of radius 2.2 Å is 5.024 × 10^-24 A∙m². Calculate the frequency of revolution of the electron in that orbit.
Solution:
Data: d = 0.2 m, B = 4 × 10^-4 T,
2l = 5 cm = 5 × 10^-2 m, A = 2 cm² = 2 × 10^-4 m²,
\(\frac{\mu_{0}}{4 \pi}\) = 10^-7 T∙m/A
The magnitude of the magnetic induction at an axial point of a bar magnet.

Question 17.
Explain magnetization of a material.
Answer:
In an atom, the orbital and spin magnetic moments of its electrons may or may not add up to zero, depending on the electronic configuration. In some materials, their atoms have a net magnetic moment. When such a material is placed in an external magnetic field of induction \(\overrightarrow{B_{0}}\) , the field exerts a torque on each atomic magnet. These torques tend to align the magnetic moments with the applied field. Due to this, the material as a whole acquires a net magnetic moment \(\vec{M}_{\text {net }}\) along \(\overrightarrow{B_{0}}\) and the material is said to be magnetized.

The net magnetic moment per unit volume is called the magnetization \(\vec{M}_{z}\) of the material.
\(\vec{M}_{\mathrm{z}}=\vec{M}_{\text {net }} / V\)
where V is the volume of the material.

Even when the atomic magnetic moment is zero, application of magnetic field induces magnetism in the material. In this case, the magnetization has direction opposite to that of the applied field.

Question 18.
Define magnetization.
State its dimensions and the SI unit.
OR
Define magnetization. State its formula and SI unit.
Answer:
Magnetization : The net magnetic moment per unit volume of a material is called the magnetization of the material.

SI unit: The ampere per metre (A/m).

Question 19.
A bar magnet (volume 1.5 × 10^-5 5m³) has a uniform magnetization of 6000 Aim. What is its magnetic dipole moment?
Answer:
M_z = \(\)
∴ M = M_zV = (6000)(1.5 × 10^-5)
= 9 × 10^-2 A∙m² is the magnetic dipole moment of the magnet.

Question 20.
Define magnetic intensity.
State its dimensions and the SI unit.
Answer:
Magnetic intensity: The magnetic intensity is defined as the magnetic induction in an isotropic medium divided by the permeability of the medium.

The magnetic intensity is a quantitative characteristic of a magnetic field independent of the magnetic properties of the medium. In a medium, it determines the contribution to the magnetic induction in the medium by the external magnetic field.

Dimensions: Within a toroid without a core, which has n windings per unit length carrying a current I, the magnetic intensity, H = nI.
∴ [H] = [n][I] = [L^-1][I] = [L^-1I]
SI unit : The ampere per metre (A/m).
[Note : The magnetic intensity (also called the magnetic field strength), \(\vec{H}\), is defined as
\(\vec{H}=\frac{\vec{B}}{\mu_{0}}-\overrightarrow{M_{z}}\)
where \(\vec{B}\) is the magnetic induction, \(\vec{M}_{z}\) is the magnetization and μ₀ is the permeability of free space.]

Question 21.
What is the magnetic susceptibility of a medium?
Answer:
The magnetic susceptibility of a medium is a dimensionless quantity which signifies the contribution made by the medium when subjected to a magnetic field to the magnetic induction inside the medium. For a material in which the magnetization M_z is proportional to the magnetic intensity H, the magnetic susceptibility of the medium is
χ_m = M_z/H
It is equal to the fractional change in the magnetic induction due to the medium.
Magnetic susceptibility of some materials

Substance	χ	Substance	χ
Silicon	-4.2 × 10-6	Aluminium	2.3 × 10-5
Bismuth	-1.66 × 10-5	Calcium	1.9 × 10-5
Copper	-9.8 × 10-6	Choromium	2.7 × 10-4
Diamond	-2.2 × 10-5	Lithium	2.1 × 10-5
Gold	-3.6 × 10-5	Magnesium	1.2 × 10-5
Lead	-1.7 × 105	Niobium	2.6 × 10-5
Mercury	-2.9 × 10-5	Oxygen (STP)	2.1 × 10-6
Nitrogen	-5.0 × 10-9	Platinum	2.9 ×10-4

Question 22.
Discuss magnetization of a rod of material having net magnetic moment with the help of a solenoid.
OR
Discuss magnetization of an iron rod placed in a solenoid.
OR
Discuss magnetization of a magnetic material placed in a solenoid.
Answer:
Consider an ideal air-cored solenoid carrying a steady current I. The magnitude of the magnetic induction inside the solenoid is
B₀ = \(\frac{\mu_{0} N I}{2 \pi r}\) = μ_onI ………….. (1)
where n = \(\frac{N}{2 \pi r}\) is the number of turns per unit length and p0 is the permeability of free space.

When a core of magnetic material (such as iron) is present, the magnetic field within the solenoid due to the current in the winding magnetizes the material of the core. With the core, the magnetic induction \(\vec{B}\) inside the solenoid is greater than \(\vec{B}_{0}\), so that
B = B₀ + B_m ……………. (2)
where B_m is the contribution of the iron core. B_m is proportional to the magnetization M_z of the material.
B_m = μ_oM_z …………… (3)

While discussing magnetic materials, it is customary to call \(\frac{B_{0}}{\mu_{0}}\) as the magnetizing field or magnetic field intensity, denoted by H, which produces the magnetization.
∴ B₀ = μ_oH …………. (4)
Substituting for B₀ and B_M in Eq. (1),
B = μ₀H + μ₀M_z = μ₀(H + M_z) …………….. (5)
For materials in which the magnetization is pro-portional to the magnetic intensity,
M_z ∝ H or M_z = χ_mH ………. (6)
where the constant of proportionality χ_m is called the magnetic susceptibility.
∴ B = μ₀(H + χ_mH) = μ₀(1 + χ_m)H = μH …………. (7)
where p = μ₀(1 + χ_m) is called the permeability of the material.

[Notes : (1) M_z ∝ H only for diamagnetic and paramagnetic materials. Among ferromagnetic materials, the linear relation in Eq. (6) holds good only for initial magnetization of magnetically softer materials; for magnetically harder materials, M_z is not a single-valued function of H, and depends on the magnetic intensity that the material has been previously exposed to (a phenomenon known as hysteresis). (2) H is defined for convenience; B is more fundamental.]

Question 23.
What is the relation between permeability and magnetic susceptibility of a medium? What is relative permeability of a medium ?
Answer:
If χ_m is the magnetic susceptibility of a medium, the permeability of the medium is
μ = μ₀ (1 + χ_m)
where μ₀ is the permeability of free space.
The ratio of the permeability of a medium to that of free space is called the relative permeability of the medium, denoted by μ_r.
μ_r = μ/μ₀ = 1 + χ_m

Question 24.
Write the relation between relative permeability and magnetic susceptibility.
Answer:
μ_r = 1 – χ_m, where μ_r is the relative permeability and χ_m is the magnetic susceptibility of a substance.

Question 25.
Why do magnetic lines of force prefer to pass through iron than air?
Answer:
The permeability of air (≅ 1.00000037) is negligible relative to that of iron, which typically has μ of several hundreds or thousands. That is, permeability of iron is much more than that of air. Hence, magnetic lines of force prefer to pass through iron than air.

[Note : Air is paramagnetic due to the oxygen it contains. Reference for μ_air: B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, p. 16.]

Question 26.
Is magnetic susceptibility a dimensionless quantity? Why?
Answer:
In a magnetizing field of intensity H, a material for which its magnetization M_z ∝ H, we write . M_z = χ_mH, where the proportionality constant χ_m is called the magnetic susceptibility. Since both magnetization and magnetic intensity have the same dimensions and units, χ_m is a dimensionless quantity.
OR
The relative permeability of a medium,
μ_r = \(\frac{\mu}{\mu_{0}}\) = 1 + χ_m
where μ and χ_m are the permeability and magnetic susceptibility of the medium and μ₀ is the permeability of free space. Hence, both μ₀ and χ_m are dimensionless quantities.

27. Solve the following
Question 1.
A cylindrical magnet 5 cm long has a diameter of 1 cm and a uniform magnetization of 5000 A/m. Find its magnetic dipole moment.
Solution:
Data : L = 5 × 10^-2 m, d = 1 × 10^-2 m,
M_z = 5 × 10³ A/m .
Volume, V = πr²L = \(\frac{\pi d^{2}}{4}\) L
M_z = \(\frac{M}{V}\)
∴ The magnetic dipole moment,

Question 2.
A bar magnet made of steel has magnetic moment 2.5 A∙m² and mass 6.6 × 10^-3 kg. Given that the density of steel is 7.9 × 10³ kg/m³, find the intensity of magnetization of the magnet. (2 marks )
Solution:
Data : M = 2.5 A∙m², m = 6.6 × 10^-3 kg, ρ = 7.9 × 10³ kg/m³
Volume, V = \(\frac{m}{\rho}\)
The intensity of magnetization of the magnet is
M_z = \(\) = M ∙ \(\frac{\rho}{m}\)
= 2.5 x \(\frac{M}{V}\) = 2.992 × 10⁶ A/m
[Note : Intensity of magnetization = magnetization.]

Question 3.
Find the magnetization of a bar magnet of length 10 cm and cross-sectional area 4 cm², if the magnetic moment is 2 A∙m².
Solution:
Data : L = 0.1 m, A = 4 × 10^-4 m², M = 2 A∙m²
Magnetization, M_z = \(\frac{M}{V}\)
= \(\frac{M}{L A}=\frac{2}{(0.1)\left(4 \times 10^{-4}\right)}\)
= \(\frac{10^{4}}{0.2}\) = 5 × 10⁴ A/m

Question 4.
The magnetic susceptibility of annealed iron at saturation is 5500. Find the permeability of annealed iron at saturation.
Solution:
Data : χ_m = 5500, μ₀ = 4π × 10^-7 T∙m/A
Permeability, μ = μ₀(1 + χ_m)
The permeability of annealed iron at saturation is
μ = (4 × 3.142 × 10^-7) (1 + 5500)
= 4 × 3.142 × 5.501 × 10^-4
= 6.914 × 10^-3 T∙m/A

Question 5.
The magnetic induction B and the magnetic intensity H in a material are found to be 1.6 T and 1000 A/m, respectively. Calculate the relative permeability μ_r and the magnetic susceptibility χ_m of the material.
Solution:
Data : B = 1.6 T, H = 1000 A/m,
μ₀ = 4π × 10^-7 T∙m/A
(i) B = μH = μ₀μ_r H
∴ The relative permeability of the material,
μ_r = \(\frac{B}{\mu_{0} H}=\frac{1.6}{\left(4 \times 3.142 \times 10^{-7}\right)\left(10^{3}\right)}\)
= \(\frac{4000}{3.142}\) = 1.273 × 10³

(ii) μ_r = 1 + χ_m
∴ The magnetic susceptibility of the material,
χ_m = μ_r – 1
= 1273 – 1 = 1272 or 1.272 × 10³

Question 6.
An ideal solenoid has a core of relative permeability 500 and its winding has 1000 turns per metre. If a steady current of 1.6 A is passed through its winding, find
(i) the magnetic field strength H
(ii) the magnetization M_z
(iii) the magnetic induction B within the solenoid. Assume that Mz is directly proportional to H and single valued.
Solution:
Data : μ_r = 500, n = 1000 m^-1, I = 1.6 A,
μ₀ = 4π × 10^-7 T∙m/A
(i) The magnetic field strength (or magnetic intensity) of the ideal solenoid,
H = nI
= 1000 × 1.6 = 1.6 × 10³ A/m

(ii) The magnetization of the core,
M_z = χ_mH = (μ_r – 1)H
= (500 – 1) × 1.6 × 10³
= 499 × 1.6 × 10³ = 7.984 × 10⁵ A/m

(iii) The magnetic induction within the core of the solenoid,
B = μ_rμ₀H
= (500) (4 × 3.142 × 10^-7) (1.6 × 10³)
= 32 × 3.142 × 10^-2 = 1.005 T

Question 28.
What is a diamagnetic material? Give two examples.
Answer:
A material which is weakly repelled by a magnet and whose atoms /molecules do not possess a net magnetic’ moment in the absence of an external magnetic field is called a diamagnetic material.

When a diamagnetic material is placed in a uniform magnetic field, it acquires a small net induced magnetic moment directed opposite to the field.

Examples: Bismuth, copper, gold, silver, anti-mony, mercury, water, air, hydrogen, lead, silicon, nitrogen, sodium chloride.

Question 29.
What is diamagnetism?
Answer:
A material which is weakly repelled by a magnet and whose atoms/molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material. When a diamagnetic material is placed in a mag-netic field, it acquires a small net induced magnetic moment directed opposite to the field. The induced magnetism exhibited by such materials is called diamagnetism.

Question 30.
State any four properties of a diamagnetic material.
Answer:
Properties of a diamagnetic material :

1. In the absence of an external magnetic field, the magnetic dipole moment of each atom / molecule of a diamagnetic material is zero.
2. A diamagnetic material is weakly repelled by a magnet.
3. If a thin rod of a diamagnetic material is suspended in a uniform magnetic field, it comes to rest with its length perpendicular to the field.
4. When placed in a nonuniform magnetic field, a diamagnetic material is repelled from the region of strong field.
5. The magnetic susceptibility (χ_m) of a diamagnetic material is small and negative.
6. χ_m is very nearly temperature-independent.
7. The relative permeability (μ_r) of a diamagnetic material is slightly less than 1 and very nearly temperature independent.
8. If a diamagnetic liquid in a watch glass is placed on two closely spaced pole-pieces of a magnet, the liquid accumulates on the sides causing a depression at the centre.
   [ Note : When the pole-pieces are moved apart, the effect is reversed, i.e., the diamagnetic liquid accumulates at the centre, where the magnetic field is weak.]
9. A diamagnetic liquid in a U-tube placed in a magnetic field shows a depression in the arm to which the magnetic field is applied.
10. If a diamagnetic gas is introduced between the pole-pieces of a magnet, it spreads at right angles to the field.

Question 31.
Name two materials that have negative magnetic susceptibility.
Answer:
Copper and gold have negative magnetic susceptibility.

Question 32.
Explain the origin of diamagnetism.
OR
Explain the origin of diamagnetism on the basis of atomic structure.
Answer:
An atomic electron is equivalent to a current loop which has orbital magnetic moment. Further, electron spin gives rise to the spin magnetic moment. The magnetic moment of an atom is equal to the vector sum of the magnetic moments of all its electrons.

The electronic configuration in an atom of a diamagnetic material is such that the vector sum of the orbital and spin magnetic moments of all the electrons is zero. Thus, the atomic magnetic moment is zero. Hence, a diamagnetic material has no inherent magnetic moment associated with it.

When a diamagnetic material is placed in a magnetic field, the orbiting electrons are accelerated or decelerated depending on their sense of revolution. For the electrons that are speeded up, the magnetic moment increases and for those that are slowed down, the magnetic moment decreases. This happens due to induced current as per Lenz’s law. Thus, each atom acquires a net magnetic moment and the diamagnetic material is weakly magnetized. The induced magnetic moment is opposite in direction to the applied field.

Diamagnetism is the weakest magnetic phenomenon. Hence, although diamagnetism is a universal property, it can be detected only in the absence of properties resulting in para- and ferromagnetism.

Question 33.
Explain the diamagnetic behaviour of superconductors.
Answer:
Suppose a superconducting material in its normal phase, not the superconducting phase, is placed in a uniform applied magnetic field of induction \(\vec{B}\) which is weaker than a certain critical magnetic induction \(\vec{B}_{\mathrm{c}}\) for that material. Then, when the temperature is reduced below the critical temperature for the material, it enters into the superconducting phase and the magnetic field is expelled from the interior of the material.

There is no magnetic field inside the material, i.e., the material exhibits perfect diamagnetism. The expulsion of the magnetic field in a superconducting material is called the Meissner effect.

[Notes : (1) What happens is that currents appear on the surface of the material whose magnetic field exactly cancels the applied field inside it. (2) The German physicists Fritz Walther Meissner (1882-1974) and Robert Ochsenfeld (1901-1993) discovered the phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin and lead samples. The Meissner effect is so strong that a magnet can actually be levitated over a material cooled below its superconducting transition temperature T_c.]

Question 34.
What is a paramagnetic material? Give two examples.
Answer:
A material which is weakly attracted by a magnet and whose atoms possess a net magnetic moment with all atomic magnetic moments randomly directed in the absence of an external magnetic field but are capable of being aligned in the direction of the applied magnetic field is called a paramagnetic material.

Examples : Aluminium, platinum, chromium, manganese, sodium, calcium, magnesium, lithium, tungsten, niobium, copper chloride, oxygen.

Question 35.
State any four properties of a paramagnetic material.
Answer:
Properties of a paramagnetic material:

1. Each atom of a paramagnetic material possesses a magnetic dipole moment. However, in the absence of an external magnetic field, the atomic magnetic moments are randomly oriented and hence the resultant magnetization of a paramagnetic material is zero.
2. A paramagnetic material is weakly attracted by a magnet.
3. If a thin rod of a paramagnetic material is sus-pended in a uniform magnetic field, it comes to rest with its length parallel to the field.
4. When placed in a nonuniform magnetic field, a paramagnetic material is attracted towards the region of strong field.
5. The magnetic susceptibility (χ_m) of a paramagnetic material is small and positive.
6. χ_m varies inversely with the absolute temperature T.
7. The relative permeability (μ_r) of a paramagnetic material is slightly greater than 1 and decreases with increasing temperature.
8. If a paramagnetic liquid in a watch glass is placed on two closely spaced pole-pieces of a magnet, it shows a slight rise in the middle.
   [Note : If the pole-pieces are moved apart, the para-magnetic liquid moves away from the centre where the field is weak and gets depressed in the middle.]
9. A paramagnetic liquid in a U-tube placed in a magnetic field shows a rise in the arm to which the magnetic field is applied.

Question 36.
Give one example each of a diamagnetic material and a paramagnetic material.
Answer:
Bismuth is a diamagnetic material and aluminium is a paramagnetic material.

Question 37.
Name two materials that have small and positive magnetic susceptibility.
Answer:
Platinum and Chromium have small and positive magnetic susceptibility.

Question 38.
The relative permeability of two materials are 0.999 and 1.001. Identify the materials.
Answer:
A material with relative permeability μ_r ≤ 1 is diamagnetic while the one with μ_r ≥ 1 is paramagnetic.

Question 39.
Explain the origin of paramagnetism.
OR
Explain the origin of paramagnetism on the basis of atomic structure.
Answer:
Paramagnetism depends on the presence of permanent atomic or molecular magnetic dipole moments. The inherent net atomic magnetic mo-ment results from a particular combination of the spin and orbital magnetic moments of its electrons.

The spin magnetic moments of the electrons in matter are affected by the internal magnetic field created by the magnetic moments of surrounding electrons. This internal field, ~ 10^-2 T to 10^-1 T,
causes the spin magnetic moments to precess about the field direction. At normal temperature; the thermal motion of the electrons produces constant fluctuations in the internal field so that the spin magnetic moments have random directions, from figure (a). In the absence of an external magnetizing field, therefore, a paramagnetic material is not magnetized.

When the applied field strength is greater than that of the internal field, the spin magnetic moments tend to align parallel to the external field direction. But the randomizing effect of thermal agitation prevents complete alignment, from figure (b). Therefore, at room temperature, when a paramagnetic material is placed in a magnetic field, it is weakly magnetized in the direction of the magnetizing field.

If the external field is very large or the temperature is very low, the magnetic dipole moments are effectively aligned parallel to the field so as to have the least magnetic potential energy and the magnetization reaches saturation, from figure (c).

Question 40.
Discuss Curie’s law for paramagnetic material.
OR
State Curie’s law of paramagnetism.
Answer:
Curie’s law : The magnetization of a paramagnetic material is directly proportional to the external magnetic field and inversely proportional to the absolute temperature of the material.

If a paramagnetic material at an absolute temperature T is placed in an external magnetic field of induction \(\overrightarrow{B_{\text {ext }}}\), the magnitude of its magnetization
M_z ∝ \(\frac{B_{\text {ext }}}{T}\) ∴ M_z = C \(\frac{B_{\text {ext }}}{T}\)
where the proportionality constant C is called the Curie constant.

[Notes : (1) The above law, discovered experimentally in 1895 by Pierre Curie (1859-1906) French physicist, is true only for values of B_ext/ T below about 0.5 tesla per kelvin.
(2) [C] = [M_z ∙ T] / [B_ext] = [L^-1I∙] /[MT^-2I^-1]
= [M^-1L^-1T²I²],
where denotes the dimension of temperature.]

Question 41.
Prove that the magnetic susceptibility of a para-magnetic material is inversely proportional to its absolute temperature.
Answer:
Consider a paramagnetic material at an absolute temperature T placed in an external magnetic field of induction \(\vec{B}_{\text {ext }}\). The magnitude of its magnetization is
M_z = C \(\frac{\vec{B}_{\text {ext }}}{T}\) …………. (1)
where the proportionality constant C is called the Curie constant.
Substituting \(\vec{B}_{\text {ext }}\) = μ₀H in Eq. (1),
M_z = C \(\frac{\mu_{0} H}{T}\)
where µ₀ is the permeability of free space and H is the intensity of the magnetizing field.
The magnetic susceptibility of the medium
χ_m = \(\frac{M_{z}}{H}\). Thus, Eq. (2) becomes ti
χ_m = C \(\frac{\mu_{0}}{T}\)
χ_m ∝ \(\frac{1}{T}\)
This is the required expression.

Question 42.
What is a ferromagnetic material? Give two examples.
Answer:
A material which is strongly attracted by a magnet and whose atoms possess a net magnetic moment (largely due to electron spin) which, within a certain temperature range, spontaneously line up parallel to each other by quantum mechanical exchange interaction is called a ferromagnetic material.

Examples : Transition elements (iron, cobalt and nickel), inner transition elements (gadolinium, Gd, and dysprosium, Dy) and their alloys.

[Note : Ferromagnetic behaviour was first explained by Pierre-Ernest Weiss on the basis of domain theory but its satisfactory explanation is given only by quantum mechanics.]

Question 43.
What are domains in a ferromagnetic material ?
OR
Write a short note on domains in a ferromagnetic material.
Answer:
A ferromagnetic material is composed of mosaic of small regions within each of which all the atomic magnetic moments spontaneously line up parallel to each other by quantum mechanical exchange interaction within a certain temperature range. Each such spontaneously magnetized region is called a domain and the common direction of magnetic moment is called the domain axis. A domain is an extremely small region (e.g., a size of about 10^-6 m -10^-4 m) containing a large number (10¹⁰ – 10¹⁷) of atoms. The boundary between adjacent domains with a different orientation of magnetic moment is called a domain wall.

Question 44.
Explain ferromagnetism on the basis of the domain theory.
Answer:
Atoms of a ferromagnetic material have a perms tient non-zero magnetic dipole moment arising mainly from spin magnetic moments of the electrons.

According to the domain theory, a ferromagnetic material is composed of small regions called domains.

A domain is an extremely small region contain Inga large number (something like 10¹⁵ atoms as in common iron) of atoms,

Within each domain, the atomic magnetic moments of nearest-neighbour atoms interact strongly through exchange interaction (a quantum mechanical phenomenon) and align themselves parallel to each other even in the absence of an extemal magnetic field. A domain is. therefore, spontaneously magnetized to saturation.

In an unmagnetized material, however, the directions of magnetization of the different domains are w oriented that the net magnetization is zero.

When an external magnetic field Is applied, the resultant magnetization of the specimen Increases. This is achieved in either of two ways: Either a domain that is favourably oriented grows in size at the expenses of a less favourably oriented domain, or the direction of magnetization of an entire domain changes and aligns along the external magnetic field.

When a weak nagnetic field is applied, favour ably oriented domains grow in size by domain boundary displacement, from figure (b). In strong fields, the domains change their magnetization by domain rotation, from figures. 11.9 (c) and (d). If domains reach perfect alignment, as in from figure 11.9 (d),, the domains may merge into one large domain.

After the external field is removed, it may be energetically favourable for a domain’s direction of magnetizaLion to persist. Then, the specimen has a permanent magnetic dipole moment. This phonomenon, called magnetic remanance, Is the basis of the existence of permanent magnets.

Question 45.
State any four properties of a ferromagnetic material.
Answer:
(1) Each atom of a ferromagnetic material possesses a magnetic moment. A ferromagnetic material is composed of domains each of which is spontaneously magnetized to saturation. In an unmagnetized sample, the magnetic moments of different domains are so oriented that the macroscopic magnetization of the sample is zero.

(2) When a ferromagnetic material is placed in a strong external magnetic field, the domains whose magnetic moments are favourably oriented relative to the external field grow in size such that the sample acquires a nonzero macroscopic magnetization.
(3) A ferromagnetic material retains some magnetization even after it is removed from an external magnetic field. This magnetic retentivity is the basis ‘ of the existence of permanent magnets.

(4) A ferromagnetic material is strongly attracted by a magnet.
(5) A bar magnet, suspended in a uniform magnetic field, comes to rest with its magnetic dipole moment in the direction of the external field.
(6) When placed in a nonuniform magnetic field, a ferromagnetic material is attracted towards the region of strong field.
(7) The magnetic susceptibility (χ_m) and relative permeability (μ_r) of a ferromagnetic material are very high.

Question 46.
Are the (i) diamagnetic materials (ii) paramagnetic materials (iii) ferromagnetic materials attracted or repelled by a magnet?
Answer:
When placed in a nonuniform magnetic field,

1. a diamagnetic material is weakly repelled from’ the region of strong field
2. a paramagnetic material is weakly attracted towards the region of strong field
3. a ferromagnetic material is strongly attracted towards the region of strong field.

Question 47.
Can there be a material which is nonmagnetic?
Answer:
All materials are magnetic. However, only ferromagnetics can have magnetic remanance and exhibit magnetic behaviour even in the absence of an external magnetic field. Diamagnetics and para-magnetics exhibit induced magnetism, i.e., they exhibit magnetic behaviour only in the presence of an external magnetic field.

[Note : A solid solution formed between paramagnetic or diamagnetic metals can be an exception to the general statement that all substances are magnetic. However, the zero value of the susceptibility will be retained only at one temperature, because the susceptibility of the paramagnetic constituent generally changes with temperature. A Cu-Ni alloy with 3.7 wt% Ni has zero susceptibility at room temperature.]

Question 48.
Which magnetic materials have
(i) relative permeability > 1
(ii) relative permeability <1?
Answer:
(i) Both paramagnetic and ferromagnetic materials have relative permeability (μ_r) greater than 1. μ_r is only slightly greater than 1 for a paramagnetic material. μ_r is very high for a ferromagnetic material and is a function of the magnetizing field (also called the magnetic field intensity).

(ii) μ_r is slightly less than 1 for a diamagnetic material.

Question 49.
Draw a graph showing the variation of magnetic susceptibility of a ferromagnetic material with temperature.
Answer:
The magnetic susceptibility of a ferromagnetic material above Curie temperature T_c is given by χ_m = \(\frac{C}{T-T_{\mathrm{c}}}\), where C is the Curie constant. Below figure shows the variation of magnetic susceptibility of a ferromagnetic material with temperature.

[Note : The relation, χ_m = \(\frac{C}{T-T_{\mathrm{c}}}\), is known as Curie-Weiss law. A plot of reciprocal susceptibility versus temperature for a ferromagnetic material is a straight line intercepting the temperature axis at T. At T = T, the susceptibility diverges which implies that one may have a nonzero magnetization in a zero applied field. This exactly corresponds to the definition of the Curie temperature, being the upper limit for having a spontaneous magnetization.].

Question 50.
Distinguish between a diamagnetic material and a paramagnetic material.
Answer:

Diamagnetic material	Paramagnetic material
1. A material whose atoms/ 1. molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material.	1. A material whose atoms possess net magnetic mo­ments that are all randomly directed in the absence of an external magnetic field is called a paramagnetic material.
2. When placed in a nonuni­form magnetic field, a diamagnetic material is weakly repelled from the region of strong field.	2. When placed in a nonuni­form magnetic field, a para­magnetic material is weakly attracted towards the region of strong field.
3.  In an external magnetic j field, it gets weakly magnetized in the direction oppo­site to that of the field.	3.  In an external magnetic field, it gets weakly magne­tized in the same direction as that of the field.
4.  When a rod of a diamagnetic material is suspended in a uniform magnetic field, it comes to rest with its length perpendicular to the direc­tion of the field.	4.  When a rod of a paramag­netic material is suspended in a uniform magnetic field, it comes to rest with its length parallel to the direc­tion of the field.
5.  χm is small, negative and very nearly temperature independent.	5.  χm is small, positive and varies inversely with abso­lute temperature T
6.  μr is slightly less than 1 and very nearly temperature! independent.	6. μr is slightly greater than 1 and decreases with increas­ing temperature.

Question 51.
Distinguish between a paramagnetic material and a ferromagnetic material.
Answer:

A paramagnetic material	A ferromagnetic material
1. The permanent atomic mag­netic moments of a para­magnetic material are all randomly oriented so that, in the absence of an external magnetizing field, the material is unmagnetized.	1. The permanent atomic mag­netic moments of a ferro­magnetic material interact strongly through exchange interaction forming domains which are spontaneously magnetized to saturation
2. It gets weakly magnetized when placed in an external magnetic field.	2. In an unmagnetized ma­terial, the directions of mag­netization of the different domains are so oriented that the net magnetization is zero.
3. Its magnetization becomes zero when the external magnetic field is removed.	3. It retains some magnetiz­ation even after the external magnetic field is removed.
4. Its magnetization in a given external magnetic field increases with decreasing temperature. The magne­tization reaches saturation only if the external field is very large and the tempera­ture is very low.	4. It retains its domain struc­ture only up to a characte­ristic Curie temperature, above which it becomes paramagnetic.
5. χm is small and positive. μr is slightly greater than 1.	5. χm and μr are positive and very high.

Question 52.
Distinguish between a ferromagnetic material and a diamagnetic material.
Answer:

A ferromagnetic material	A diamagnetic material
1. A material whose atoms/molecules possess permanent  magnetic moments which interact strongly through exchange interaction to form magnetic domains, each of which is magnetized to saturation, is called a ferromagnetic material.	1. A material whose atoms/molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material.
2. It gets strongly magnetized in the direction of the field even when placed in a weak magnetic field	2. In an external magnetic field, it gets weakly magnetized in the direction opposite to the field.
3. It retains some magnetiz­ation even after the external magnetic field is removed.	3. Its magnetization becomes zero when the external magnetic field is removed.
4. When placed in a nonuni­form magnetic field, a ferromagnetic material is strongly attracted towards the region of strong field.	4. When placed in a nonuni­form magnetic field, a dia­magnetic material is weakly repelled from the region of strong field.
5. χm and μr are positive and very high.	5. χm is small and negative. μr is slightly less than 1.

53. Solve the following
Question 1.
(5) A toroid (Rowland ring) of mean radius 16 cm has 1000 turns of wire closely wound on a ferromagnetic core of relative permeability 400. What is the magnetic induction B within the core for a magnetizing current of 1 A?
Solution:
Data: r = 16 × 10^-2 m, N = 1000, μ_r = 400, I = 1 A,
μ₀ = 4π × 10^-7 T∙m/A
Magnetic field strength, H = nI = \(\frac{N I}{2 \pi r}\)
∴ The magnetic induction within the core,
B = μ₀μ_rH = μ₀μ_r \(\frac{N I}{2 \pi r}\)
= (4π × 10^-7) (400) \(\frac{1000 \times 1}{2 \pi \times 16 \times 10^{-2}}\)
= \(\frac{8 \times 10^{-2}}{16 \times 10^{-2}}\) = 0.5 T

Question 2.
Find the percentage increase in the magnetic induction B when the space within a current-carrying toroid is filled with aluminium. The magnetic susceptibility of aluminium is 2.1 × 10^-5.
Solution:
Data: χ_m = 2.1 × 10^-5 (positive, since aluminium is paramagnetic)
The percentage increase in the magnetic induction B within the toroid due to the aluminium core

Question 3.
The permeability of a substance at temperature 300 K is 6.284 × 10^-3 SI unit. At what temperature will the susceptibility of that substance increase to 9.998 × 10³?
Solution:
Data: T₁ = 300 K, μ₁ = 6.284 × 10^-3, χ_m2 = 9.998 × 10³, μ₀ = 4π × 10^-7 T∙m/A
Permeability, μ = μ₀(1 + χ_m)
∴ The magnetic susceptibility at temperature T₁,

∴ The required temperature,
T₂ = \(\frac{\chi_{\mathrm{m} 1}}{\chi_{\mathrm{m} 2}}\) × T₁ = \(\frac{4999}{9998}\) × 300 = 150 K

Question 54.
Explain magnetic hysteresis in a ferromagnetic material.
OR
Explain the behaviour of a ferromagnetic material in an external magnetic field with the help of a magnetic hysteresis cycle.
OR
Explain the behaviour of a ferromagnetic material through one cycle of magnetization.
Answer:
A large scale consequence of the magnetic behaviour of a ferromagnetic under different applied magnetic fields can be observed by placing an unmagnetized rod of the material inside a solenoid. A current through the coil establishes the magnetizing field H, which we take as the independent variable. By measuring the voltage induced in a test coil wound alongside, we can determine changes in flux Φ, and hence changes in B inside the rod. B is measured in tesla while H is measured in ampere per metre. Knowing B and H, we can always compute magnetization M. It is however usual to plot B rather than M, as a function of H.

Typical B-H plot during the following operations :
(1) Starting with an unmagnetized rod, B = 0 and H = 0 (Point O), H is increased until it has the value corresponding to point a : Here the rod has reached its saturation magnetization and B remains constant even with further increase in H. The lower part of the curve Oa is governed by domain growth while the upper flattening part is governed by domain rotation.

(2) Reduce H to zero (point b) : the curve does not retrace itself, as shown by the curve ab. This irre-versibility is called hysteresis. It is largely due to the domain boundary movements being partially irreversible. If the current is simply switched off at this point, the rod will have a residual magnetization as indicated by the non-zero value of B, called retentivity or remanence, for H = 0. Essentially now B = μ₀M, i.e., the rod has acquired a permanent magnetization.

(3) Reverse H and increase it in magnitude until it has the value corresponding to point c : Here B is zero. The corresponding reverse magnetizing field H is called coercivity.

(4) Increase H in reverse direction until saturation magnetization is reached (point d).
(5) Reduce H to zero again (point e).
(6) Reverse the current once more until point a is reached again.
The process of taking the magnetic material once through the hysteresis loop abcdefa is called hysteresis cycle.

Question 55.
What is magnetic hysteresis ?
Explain it on the basis of magnetic domains.
Answer:
Magnetic hysteresis is a phenomenon shown by ferromagnetic materials in which the magnetic flux density through a material depends on the applied magnetizing field as well as the previous state of magnetization. Due to retention of its memory of previous state of magnetization, the flux density B lags behind (does not remain in step) with magnetizing field H. This delay in the change of its magnetization M (or equivalently, B) in response to a change in H is called hysteresis.

Hysteresis can be understood through the concept of magnetic domains. Domain boundary displacements and domain rotations are not totally reversible. When the applied magnetizing field H is increased and then decreased back to its initial value, the domains do not return completely to their original configuration but retain some memory or history of their previous alignment.

Question 56.
Define :
(1) retentivity
(2) coercivity.
Answer:

1. Retentivity : The residual magnetic flux density or magnetization in a magnetic material when the magnetizing field intensity is reduced to zero is called retentivity or remanence.
2. Coercivity: The reversed magnetizing field strength required to reduce the remanent magnetic flux density or magnetization in a magnetic material from its remanent value to zero, i.e., to demagnetize the magnetic material completely, is

Question 57.
What is a ‘soft’ magnetic material?
OR
What is meant by a ‘soft’ iron?
Answer:
A soft magnetic material, usually iron-based, has high permeability, low retentivity and low coercivity. In other words, it does not have appreciable hysteresis, i.e., its hysteresis loop is very narrow. Such a material magnetizes and demagnetizes more easily, by small external fields.

Question 58.
What is an electromagnet?
Answer:
An electromagnet is an insulated coil wrapped around a ferromagnetic core (usually a soft iron) of high permeability and low retentivity. When a current is passed through the coil-a solenoid or toroid, the ferromagnetic material magnifies the magnetic field of the coil, the magnification factor being the relative permeability (μ / μ₀) of the core. The magnetic field of the current-carrying coil magnetizes the core material, thereby producing a much larger field than the coil would produce by itself.

Question 59.
What is a magnetically hard material?
Answer:
A ‘hard’ magnetic material, such as ALNICO (an alloy of aluminium, nickel and cobalt), has high permeability, high retentivity and very high coercivity- of the orders of 1 tesla and 10⁴ ampere per metre, respectively. In other words, it has a large zero-field magnetization, and large reverse field needed to demagnetize. Its hysteresis loop is very broad. Such a material can be made into a permanent magnet, that is, its magnetization will persist indefinitely if it is subsequently exposed only to weak magnetic fields.

Question 60.
Distinguish between an electromagnet and a permanent magnet.
Answer:

Electromagnet	Permanent magnet
1. Magnetic field of an electromagnet is retained till there is passage of electric current through the solenoid or coil.	1. Magnetic field is retained for a long period of time.
2. current through the solenoid and the number of turns per unit length of the solenoid.	2. The strength of a permanent magnet depends upon the nature of the material of which it is made.
3. For a good electromagnet, the retentivity and coerciv­ity of the material should be low.	3. For a good permanent mag­ net, the retentivity and co­ercivity of the material should be high.
4. It is usually made of soft ferromagnetic material.	4. It is usually made of hard ferromagnetic material.
5. Poles of an electromagnet can be reversed by revers­ing the direction of electric current.	5. Poles of a permanent mag­net cannot be reversed.

Question 61.
Explain magnetic shielding.
Answer:
The use of a shell or box of magnetic material of high permeability to protect sensitive instruments from stray magnetic fields is called magnetic shielding. The permeability of the material being many order of magnitudes greater than air, the magnetic field lines pass through the shell. The saturation v induction B of the material must be greater than the external field to be shielded. from below figure shows the cross section of a cylindrical or spherical shield in which the central region is the field-free region.

Magnetic shielding is useful for a wide range of applications, from small components inside a set of speakers to large magnetically shielded rooms.

[Note : The most widely used alloy for magnetic shielding purposes is the patented MuMetal^®. Its composition of 80% nickel, 4.5% molybdenum and balance iron gives it high permeability.] .

Multiple Choice Questions

Question 1.
A rectangular bar magnet-with sides l. b and w – h.is mass n and magnetic moment M. It is free to rotate about a vertical axis through its centre of mass such that its faces of area l × b are honzoritaL The period T of angular oscillations of this magnet in a uniform magnetic field B is given by

Answer:
(B) \(\sqrt{\frac{\pi^{2} m\left(l^{2}+b^{2}\right)}{3 M B}}\)

Question 2.
A magnet of moment \(\vec{m}\) is placed in a uniform magnetic field \(\vec{B}\). Which of the following graphs correctly depicts the variation of its orientation energy U_θ i.e., its potential energy due to its orientation θ with \(\vec{B}\)?

Answer:
(D)

Question 3.
The magnetic dipole moment has the dimensions of current
(A) \(\frac{\text { current }}{\text { area }}\)
(B) current × area
(C) \(\frac{\text { area }}{\text { current }}\)
(D) current × length.
Answer:
(B) current × area

Question 4.
The dimensions of magnetic dipole moment are
(A) [L²I]
(B) [LI]
(C) [L^-1I]
(D) [L^-2I]
Answer:
(A) [L²I]

Question 5.
The gyromagnetic ratio of an orbital electron is the ratio of its
(A) charge to mass
(B) magnetic moment to volume
(C) orbital magnetic moment to linear momentum
(D) orbital magnetic moment to orbital angular momentum.
Answer:
(D) orbital magnetic moment to orbital angular momentum.

Question 6.
If \(\vec{M}_{0}, \vec{L}_{0}\) and γ₀ are respectively the magnetic dipole moment, orbital angular momentum and gyrornagnetlc ratio of an orbital electron. Then.

Answer:
(A) \(\vec{M}_{0}=-\gamma_{0} \overrightarrow{L_{0}}\)

Question 7.
Bohr magneton is the magnetic dipole moment of
(A) an orbital electron in the ground state of a Bohr atom
(B) an orbital electron with orbital angular momenturn of \(\frac{h}{2 \pi}\)
(C) the order of 10^-23 J/T
(D) all of the above.
Answer:
(D) all of the above.

Question 8.
A bar magnet 10 cm long has cross-sectional area 2 cm² and magnetic dipole moment of 10 A∙m². The magnetization of its material, assumed to be uniform, is
(A) 5 × 10⁵ A/m
(B) 2 × 10⁵ A/m
(C) 0.5 A/m
(D) 0.2 A/m.
Answer:
(A) 5 × 10⁵ A/m

Question 9.
An iron rod of volume 10^-4 m³ acquires a magnetic moment of 25 A∙m² when placed inside a solenoid whose windings carry a current of 0.5 A. The magnetization of the rod (in A/m), assumed to be uniform, is
(A) 5 × 10^-5
(B) 2.5 × 10^-3
(C) 12.5
(D) 2.5 × 10⁵
Answer:
(D) 2.5 × 10⁵

Question 10.
The dimensions of magnetic intensity are
(A) [LI]
(B) [L²I]
(C) [L^-1I]
(D) [L^-2I].
Answer:
(C) [L^-1I]

Question 11.
The ratio of magnetization to magnetic field induction (M/B) for both diamagnetic and paramagnetic materials is, in the usual notation,
(A) χ_m
(B) \(\frac{\chi_{\mathrm{m}}}{\mu_{0}}\)
(C) µ_r
(D) µ
Answer:
(B) \(\frac{\chi_{\mathrm{m}}}{\mu_{0}}\)

Question 12.
Magnetic susceptibility for vacuum (where there is no matter) is
(A) zero
(B) positive
(C) negative
(D) infinite.
Answer:
(A) zero

Question 13.
Magnetic susceptibility is positive and small for
(A) silver
(B) platinum
(C) mercury
(D) sodium chloride.
Answer:
(B) platinum

Question 14.
The magnetic induction within an ideal solenoid with air core is 5 mT. With an iron core of magnetic susceptibility 500, the induction within changes by
(A) 2.5 T
(B) 25 T
(C) 50 T
(D) 100 T.
Answer:
(A) 2.5 T

Question 15.
The magnetic moment of any atom in an isolated diamagnetic material is
(A) zero
(B) small
(C) large
(D) negative.
Answer:
(A) zero

Question 16.
Which of the following is diamagnetic?
(A) Dysprosium
(B) Gadolinium
(C) Magnesium
(D) Silver
Answer:
(D) Silver

Question 17.
The most exotic diamagnetic materials are
(A) the glasses
(B) the insulators
(C) the superconductors
(D) the semiconductors.
Answer:
(C) the superconductors

Question 18.
A thin, small gIas rod is suspended between the poles of a strung electromagnet. The rod
(A) is strongly repelled by the magnetic field.
(B) orients itself parallel to the magnetic field
(C) orients itself perpendicuLar to the magnetic field
(D) is weakly attracted by the magnetic field
Answer:
(C) orients itself perpendicuLar to the magnetic field

Question 19.
Which of the following is paramagnetic?
(A) Bismuth
(B) Copper
(C) Liq. oxygen
(D) Silver
Answer:
(C) Liq. oxygen

Question 20.
When a parainagnetic material Is placed in a uniform magnetic field,
(A) its atoms acquire a magnetic moment opposite to the magnetic field
(B) the atomic magnetic moments tend to align along the magnetizing field
(C) all the atomic magnetic moments align along the magnetizing field
(D) the sample temporarily becomes ferromagnetic.
Answer:
(B) the atomic magnetic moments tend to align along the magnetizing field

Question 21.
Curte constant is
(A) a universal constant
(B) constant for a given paramagnetic material
(C) constant for a given diamagnetic material
(D) inversely proportional to the absolute temperature
Answer:
(B) constant for a given paramagnetic material

Question 22.
The rare-earth element, gadolinium, is
(A) diamagnetic
(B) paramagnetic
(C) ferromagnetic
(D) nonmagnetic.
Answer:
(C) ferromagnetic

Question 23.
Curie’s law is valid for
(A) diamagnelics
(B) paramagnetics
(C) ferromagnetics
(D) all materials,
Answer:
(B) paramagnetics

Question 24.
Magnetizing and demagnetizing a material that has hysteresis involves
(A) increase in the temperature of the material
(B) a terro-to-para phase change
(C) decrease in the temperature of the material
(D) none of the above.
Answer:
(A) increase in the temperature of the material

Question 25.
The length of a bar magnet is large compared to its width and breadth. The time period of its angular oscillation in a vibration magnetometer is 2s. The magnet is cut along its length into two equal parts and the two parts are then mounted together in the magnetometer with their like poles together. The time period of this combination will be
(A) 2 s
(B) 1 s
(C) \(\frac{1}{2}\) s
(D) \(\frac{1}{\sqrt{2}}\) s
Answer:
(B) 1 s

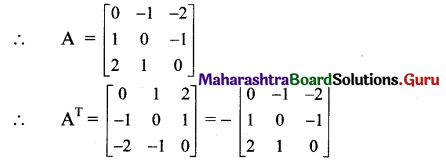
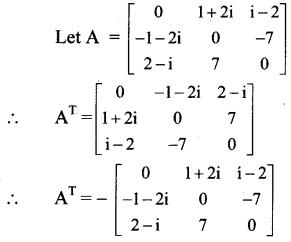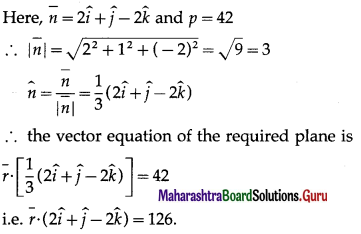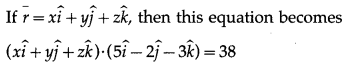Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 4 Business Services Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 4 Business Services

Select the correct option and rewrite the sentences

Question 1.
Principle of utmost good faith is applicable to ………………
(a) Life insurance
(b) Marine insurance
(c) All types of insurance
Answer:
All types of insurance

Question 2.
Insurable interest must exist in ……………..
(a) Life insurance contract only
(b) Marine insurance contract only
(c) Every insurance contract
Answer:
Every insurance contract

Question 3.
Indemnity means ………………….
(a) compensation equal to loss
(b) compensation more than loss
(c) compensation less than loss
Answer:
compensation equal to loss.

Question 4.
In India railways are owned and managed by ………………….
(a) Private companies
(b) Government
(c) Individuals
Answer:
Government

Question 5.
The costliest means of transport is ………………
(a) Rail transport
(b) Water transport
(c) Air transport
Answer:
Airtransport

Question 6.
Road transport is suitable for ……………… distance.
(a) Short
(b) Long
(c) Medium
Answer:
Short

Question 7.
Railway transport is convenient mode of transport for travelling ………………. distance.
(a) Short
(b) Long
(c) Medium
Answer:
Long.

Question 8.
Food Corporation of India is Em exEimple of ……………….
(a) Government warehouse
(b) Duty-paid warehouse
(c) Cold storage warehouse
Answer:
Government warehouse

Question 9.
Duty paid warehouses are located near ………………….
(a) Railway stations
(b) villages
(c) port and dock
Answer:
port and dock.

Question 10.
Postal services are administered by …………………
(a) Private companies
(b) Government of India
(c) Panchayat system
Answer:
Government of India

Question 11.
In case of urgency and to avoid delays ……………… is sent.
(a) Registered post
(b) Speed post
(c) Insured post
Answer:
Speed post

Question 12.
Inland letter card is used for transmission of messages ……………… only.
(a) outside India
(b) within India
(c) within state
Answer:
within India

Question 13.
Communication in the nature of financial statements may be posted by a service provider to the customers at least once in ……………….. days under Bill Mail Service.
(a) 90
(b) 60
(c) 30
Answer:
90

Question 14.
A ………….. is the person named in money order to whom the money is to be paid.
(a) drawee
(b) drawer
(c) payee
Answer:
payee

Question 15.
Under iMO one can transfer money from Rs ………………….. to Rs 50,000 from designated iMO post offices.
(a) 5,000
(b) 1,000
(c) 500
Answer:
1,000.

Question 16.
The types of account under which the amount is kept fixed for specific period is called ……………….
(a) Fixed Deposit Account
(b) Current Account
(c) Recurring Deposit Account
Answer:
Fixed Deposit Account

Question 17.
The account In which a monthly deposit of certain amount Is to be made for a fixed period Is known as ……………….
(a) Savings Account
(b) Current Account
(c) Recurring Deposit Account
Answer:
Recurring Deposit Account

Question 18.
The account suitable for business purpose is ………………….
(a) Savings Account
(b) Current Account
(c) Recurring Account
Answer:
Current Account

Question 19.
The account suitable for creating a saving habit is ………………..
(a) Current Account
(b) Recurring Account
(c) Savings Account
Answer:
Savings Account

Question 20.
There Is no limit on the frequency of withdrawals from a …………………
(a) Savings Account
(b) Fixed Deposit Account
(c) Current Account
Answer:
Current Account.

Match the pairs

Question 1.

Group A	Group B
(A) Life Insurance	(1) Written request by insured
(B) Mitigation of loss	(2) Document contains terms and conditions of insurance contract
(C) Premium	(3) Insurable interest
(D) Policy	(4) Maximise loss
(E) Claim	(5) Transfer of loss from one person to another
(F) Subject-matter of insurance	(6) To minimise the loss
	(7) Owned by Private Companies
	(8) Life, property or cargo of insured
	(9) Demand to compensate the loss occurred
	(10) Payment made by policyholder

Answer:

Group A	Group B
(A) Life Insurance	(3) Insurable interest
(B) Mitigation of loss	(6) To minimise the loss
(C) Premium	(10) Payment made by policyholder
(D) Policy	(2) Document contains terms and conditions of insurance contract
(E) Claim	(9) Demand to compensate the loss occurred
(F) Subject-matter of insurance	(8) Life, property or cargo of insured

Question 2.

Group A	Group B
(A) Air Transport	(1) Suitable for carrying bulky and heavy goods
(B) Pipeline Transport	(2) Connects two places on the hills
(C) Railway Transport	(3) Raigad Ropeway
(D) Road transport	(4) Fastest mode of Transport
(E) Water Transport	(5) Feeder to other Transport
	(6) Petroleum and gas
	(7) Monorail transport
	(8) Door to door service
	(9) Owned by private companies
	(10) Fully owned by foreign companies.

Answer:

Group A	Group B
(A) Air Transport	(4) Fastest mode of Transport
(B) PipelineTransport	(6) Petroleum and gas
(C) Railway Transport	(5) Feeder to other Transport
(D) Road transport	(8) Door to door service
(E) Claim	(1) Suitable for carrying bulky and heavy goods

Question 3.

Group A	Group B
(A) Warehousing	(1) Located at railway station
(B) Cold storage	(2) Stocks the goods on which duty is paid
(C) Warehouse keeper	(3) Owned and managed by Government
(D) Duty paid warehouses	(4) Time utility
(E) Government warehouses	(5) Bond
	(6) Possession utility
	(7) Perishable goods
	(8) Stocks the goods on which duty is not yet paid
	(9) Owned and managed by NGOs
	(10) Operated by manufacturers to profit storage needs

Answer:

Group A	Group B
(A) Warehousing	(4) Time utility
(B) Cold storage	(7) Perishable goods
(C) Warehouse keeper	(5) Bond
(D) Duty paid warehouses	(2) Stocks the goods on which duty is paid
(E) Government warehouses	(3) Owned and managed by Government

Question 4.

Group A	Group B
(A) Reserve Bank of India (RBI)	(1) Recurring deposit account
(B) Overdraft facilities	(2) 12 hours service
(C) ATM	(3) Withdrawals after fixed period of time
(D) Fixed deposit account	(4) Central Bank
(E) Business Service	(5) Current account
	(6) 24 hours service
	(7) Commercial bank
	(8) Withdrawal before fixed period of time
	(9) Intangible in nature
	(10) Tangible in nature

Answer:

Group A	Group B
(A) Reserve Bank of India (RBI)	(4) Central Bank
(B) Overdraft facilities	(5) Current account
(C) ATM	(6) 24 hours service
(D) Fixed deposit account	(3) Withdrawals after fixed period of time
(E) Business Service	(9) Intangible in nature

Give one word/phrase/term for the following sentences

Question 1.
The policy under which cargo is insured for a specific period and voyage.
Answer:
Mixed Policy

Question 2.
The principle of insurance under which the insurer and insured must show complete faith towards each other.
Answer:
Principle of utmost good faith

Question 3.
The type of insurance where the principle of indemnity is not applicable.
Answer:
Life insurance

Question 4.
The person who is protected against certain losses.
Answer:
Insured or Policy Holder

Question 5.
The policy for which the premium is lowest, among all insurance policies.
Answer:
Term insurance policy

Question 6.
The consideration for which the insurer agrees to insure the insured.
Answer:
Premium

Question 7.
This policy is applicable till the departure of the vessel from the port.
Answer:
Part Risk Policy

Question 8.
A policy in which subject matter is insured for a specific voyage irrespective of time involved in it.
Answer:
Voyage policy

Question 9.
Type of marine insurance policy purchased from more than one insurer.
Answer:
Composite marine insurance policy

Question 10.
Policy under which several ships belonging to one owner are insured under the same policy.
Answer:
Fleet Policy or Block Policy.

Question 11.
Mode of transport which helps to get goods and passengers at their doors.
Answer:
Road transport

Question 12.
The mode of transport which connects two places on the hills or across a valley or river.
Answer:
Rope way.

Question 13.
A warehouse where the goods can be stored after the payment of import duty.
Answer:
Duty Paid Warehouse

Question 14.
These warehouses are owned and operated by big manufacturers to fulfil their own storage needs.
Answer:
Private Warehouses

Question 15.
The warehouses which provide storage facilities to general public for certain charges.
Answer:
Public Warehouses

Question 16.
The warehouses which store imported goods until the payment of custom duty.
Answer:
Bonded Warehouses

Question 17.
These warehouses are owned, managed and controlled by co-operative societies.
Answer:
Cooperative Warehouses.

Question 18.
A quick and easy way of transferring personal remittances from abroad to beneficiaries in India.
Answer:
International Money Transfer

Question 19.
A method of exchanging mail between people using electronic devices.
Answer:
e-mail

Question 20.
The process of passing any information from one person to another with the help of some medium.
Answer:
Communication

Question 21.
The postal service which provide complete solutions right from mail preparation to mail delivery useful for small business and large companies.
Answer:
Business Post.

Question 22.
A bank which Is known as banker’s bank.
Answer:
Central bank

Question 23.
The type of bank which issues currency notes In India.
Answer:
Reserve Bank of India

Question 24.
They operate at village level.
Answer:
Primary Credit Societies

Question 25.
It is not allowed to Issue loans and credit cards.
Answer:
Payment Bank

Question 26.
It is an apex institution for financing agricultural and rural sector.
Answer:
National Bank for Agricultural and Rural Development (NABARD)

Question 27.
The type of bank engaged in financing import and export trade and in foreign exchange transactions.
Answer:
Exchange bank.

State whether following statements are True or False

Question 1.
The principle of subrogation is applicable to life insurance contract.
Answer:
False

Question 2.
The principle of utmost good faith is only applicable to life insurance contract.
Answer:
False

Question 3.
Insured must have insurable interest in the subject-matter at the time of taking the policy.
Answer:
True

Question 4.
An individual must always try to minimize the loss by fire as far as possible.
Answer:
True

Question 5.
The Principle of indemnity is applicable to fire insurance.
Answer:
True

Question 6.
Railway transport provides door to door services.
Answer:
False

Question 7.
Water transport is the costliest means of transport.
Answer:
False

Question 8.
Transport is useful in raising standard of living.
Answer:
True

Question 9.
Air transport is suitable for short distances.
Answer:
False

Question 10.
Air transport plays vital role during war or emergency situation.
Answer:
True.

Question 11.
International trade for perishable goods has become possible due to cold storage warehouses.
Answer:
True

Question 12.
In bonded warehouses imported goods on which customs duty is already paid are stocked.
Answer:
False

Question 13.
In duty paid warehouses imported goods on which customs duty is not yet paid are stocked.
Answer:
False

Question 14.
Co-operative warehouses are owned, managed and controlled by individuals and private enterprises to earn rent.
Answer:
False

Question 15.
Warehouses can provide transportation facilities to bulk depositors.
Answer:
True.

Question 16.
Parcel cannot be insured.
Answer:
False

Question 17.
Envelope ensures safety of documents and confidentiality of messages.
Answer:
True

Question 18.
If insured parcel lost in transit, the post office is not responsible to pay the insured amount.
Answer:
False

Question 19.
As a premium, courier service is usually less” expensive than usual mail services.
Answer:
False.

Question 20.
Central bank of the nation cannot accept deposits from the public.
Answer:
True

Question 21.
Overdraft facility Is given to savings account holders.
Answer:
False

Question 22.
Current account Is suitable for business community.
Answer:
True

Question 23.
Debit cards are issued by the bank to non account holders also.
Answer:
False

Question 24.
Real-Time Gross Settlement means payment transaction is not subject to any waiting period.
Answer:
True

Question 25.
The minimum amount to be remitted through RTGS Rs 1.00,000
Answer:
False

Question 26.
Banks never charge any commission for issuing a bank draft.
Answer:
False

Question 27.
Bank issue gift cheques and gold coins to account holders only.
Answer:
False

Find the odd one

Question 1.
Voyage policy, Time policy, Average policy, Mixed policy.
Answer:
Average policy

Question 2.
Specific policy, Composite policy, Comprehensive policy, Excess policy.
Answer:
Composite policy.

Question 3.
Big ships, boats, helicopters, launches
Answer:
helicopters

Question 4.
Aircrafts, tankers, jets, helicopters
Answer:
tankers

Question 5.
Animal carts, motor-cycles, tracks, boats
Answer:
boats

Question 6.
Launches, buses, boats, tankers
Answer:
buses

Question 7.
Fruits, machinery, fish, vegetables
Answer:
machinery

Question 8.
Machinery, cotton, coal, vegetables
Answer:
vegetables.

Question 9.
Storage, advertising, price stabilisation, risk-bearing
Answer:
advertising

Question 10.
Financing, grading and packing, salesmanship, processing.
Answer:
salesmanship.

Question 11.
Inland Letter, Envelope, Business Post, Book Post.
Answer:
Business Post

Question 12.
Electronic Money Transfer, Instant Money order, Bill Mail Service, International Money Transfer.
Answer:
Bill Mail Service

Question 13.
e-post, courier service, internet, email.
Answer:
e-post.

Question 14.
Issue of cheques. locker facility. issue of currency flotes, preparing project report.
Answer:
issue of currency notes

Question 15.
Portfolio management. framing monetary policy, Dematerlalisatlon, Forex transactions.
Answer:
framing monetary policy

Complete the sentences

Question 1.
……………… policy is suitable for small ship owner having only one ship.
Answer:
Single vessel

Question 2.
……………… policy is purchased from more than one insurer.
Answer:
Composite

Question 3.
Insurance is a means of protection from …………………
Answer:
financial loss

Question 4.
………………. is the consideration for which the insurer agrees to insured a person.
Answer:
Premium

Question 5.
……………….. policy is like pension payment scheme.
Answer:
Annuity

Question 6.
ULIP stands for ………………..
Answer:
Unit Linked Insurance Plan.

Question 7.
Road transport is suitable for …………….. distance.
Answer:
short

Question 8.
Road transport is suitable to carry …………….. goods over a short distance.
Answer:
Perishable

Question 9.
Transport system contributes to the rapid development of ………………..
Answer:
industry and commerce

Question 10.
Long distance networks of Pipeline transport are used for ………………
Answer:
petroleum and gas

Question 11.
When the goods and passenger move inside the country, it is known as ……………….. water transport.
Answer:
inland.

Question 12.
Warehouses provide space for ………………
Answer:
storage of goods

Question 13.
Bonded warehouses are under the close supervision of ………………
Answer:
customs authority

Question 14.
The ……………… warehouses are owned and managed by big manufacturers and merchants.
Answer:
private

Question 15.
All duty paid warehouses are ………………
Answer:
public warehouses

Question 16.
……………… warehouses are owned, managed and controlled by the Government.
Answer:
Government

Question 17.
……………… warehouses are owned, managed and controlled by co-operative societies.
Answer:
Co-operative.

Question 18.
The process of passing information from one person to another with the help of some ……………….. is called Communication.
Answer:
Medium

Question 19.
The Department of Post and Telegraph is part of ………………..
Answer:
Ministry of Communication and Information and Technology

Question 20.
Printed books, magazines, etc. can be sent through ………………
Answer:
Book Post

Question 21.
………………. is the service through which customers can send their messages to any address in India.
Answer:
e-post

Question 22.
Courier services are usually employed by ………………..
Answer:
a company

Question 23.
The minimum quantity of articles to be posted ……………….. by Bill Mail Service at a time is
Answer:
5000.

Question 24.
Cash credit is granted under a separate …………………
Answer:
Loan account

Question 25.
ICICI Bank is an example of ……………..
Answer:
PrIvate Sector Bank

Question 26.
The account under which a fixed sum is to be deposited regularly every month is known as ………………
Answer:
Recurring deposit account

Question 27.
The RBI was established in the ……………… year
Answer:
1945

Question 28.
In public sector banks, the majority of capital Is held by …………………
Answer:
Government.

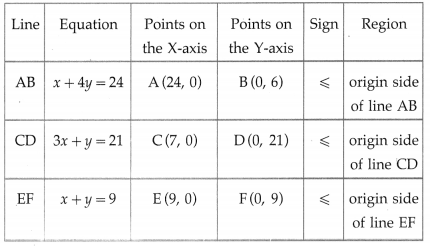
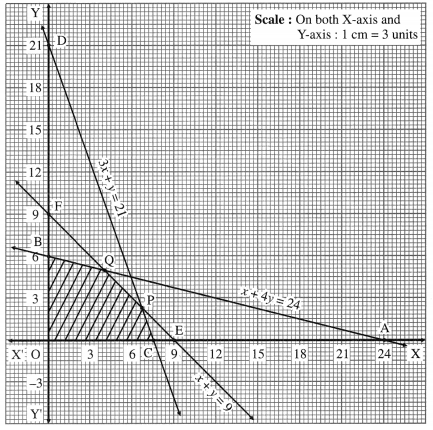
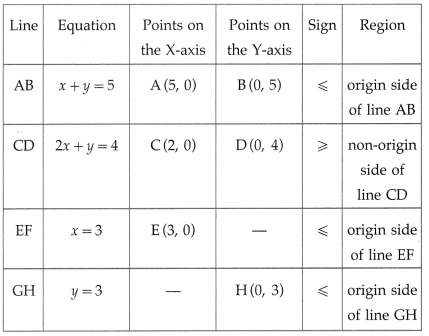
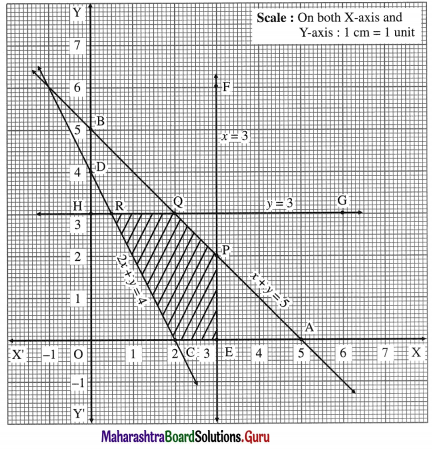
Select the correct option and complete the following table

Question 1.
(Warehousing provides storage facilities on rental basis, Big manufacturers and merchants to fulfil their storage needs, Duty paid warehouses, Bonded warehouses)

Group A	Group B
(1) Private warehouses	—————
(2) ————–	Work under the control of customs authorities
(3) ————–	Useful for importer as proper care of goods is taken after paying customs duty
(4) Public warehouses	————–
(5) Time utility and place utility	——————–

Answer:

Group A	Group B
(1) Private warehouses	Big manufacturers and merchants to fulfil their storage needs
(2) Bonded warehouses	Work under the control of customs authorities
(3) Duty paid warehouses	Useful for importer as proper care of goods is taken after paying customs duty
(4) Public warehouses	Provide storage facilities on rental basis
(5) Time utility and place utility	Warehousing.

Question 2.
(Courier service, ensures safety of documents and confidentiality of messages, Book Post, International Money Transfer, Communication in the nature of financial statements, bills, etc.)

Group A	Group B
(1) Envelope	—————-
(2) —————	Printed books, magazines can be sent at distance places through post.
(3) Bill mail service	—————
(4) —————-	Transferring personal remittances from abroad to beneficiaries in India.
(5) —————-	Exchange of items between two or more persons.

Answer:

Group A	Group B
(1) Envelope	ensures safety of documents and confidentiality of messages
(2) Book Post	Printed books, magazines can be sent at distance places through post.
(3) Bill mail service	Communication in the nature of financial statements, bills, etc.
(4) International Money Transfer	Transferring personal remittances from abroad to beneficiaries in India.
(5) Courier service	Exchange of items between two or more persons.

Question 3.
(Ministry of Shipping, Air transport, movement of people and goods from place to another, Duroto Express and Shatabdi Express, Ministry of Railways, looks after development of surface transport in the country)

Group A	Group B
(1) Transportation	—————
(2) Ministry of Road Transport	————–
(3) ————–	Looks after development of rail transport
(4) Some popular trains	————–
(5) ————–	Mountainous areas where other modes of transport cannot reach
(6) —————-	Looks after development of ocean transport

Answer:

Group A	Group B
(1) Transportation	Movement of people and goods from one place to another
(2) Ministry of Road Transport	Looks after development of surface transport in the country
(3) Ministry of Railways	Looks after development of rail transport
(4) Some popular trains	Duranto express and Shatabdi Express
(5) Air transport	Mountainous areas where other modes of transport cannot reach
(6) Ministry of Shipping	Looks after development of ocean transport

Answer in one sentence

Question 1.
What is Indemnity ?
Answer:
Indemnity means a guarantee or assurance to put the insured in same financial position in which he was immediately before the happening of the uncertain event.

Question 2.
What is Insurance ?
Answer:
insurance is contract between the insured and insurer whereby the insurer agrees to compensate the insured against loss.

Question 3.
What is Child Insurance ?
Answer:
A child insurance policy is a saving cum investment plan that is designed to meet child’s future financial requirements which helps him to pursue his dreams.

Question 4.
What is ULIP policy ?
Answer:
Unit Linked Insurance Policy (ULIP) is the policy which combines the benefits of life insurance policy with mutual funds.

Question 5.
Define warehouse.
Answer:
A warehouse is defined as, an establishment for the storage or accumulation of goods.

Question 6.
What is public warehouses ?
Answer:
A public warehouse is a specialised business establishment that provides storage facilities to the general public on certain charges.

Question 7.
What is Retail Post ?
Answer:
The service under which department of S post offers convenience to the common people by making third party’s products and services available in their areas through selected post offices, e.g. collection of electricity bill, collection of taxes, etc. is called Retail post.

Question 8.
What is e-Post ?
Answer:
e-Post is the service through which customers can send their messages to any address in India with a combination of electronic transmission and physical delivery.

Question 9.
What is Transportation ?
Answer:
Transportation refers to the movement of people, animals and goods from one location to another location.

Question 10.
What is Road Transport ?
Answer:
Road transport are the means that connect people and places on the surface of the land.

Question 11.
What is Rail Transport ?
Answer:
Transportation of passengers and goods on rail lines through trains is called as rail transport.

Question 12.
What is Water Transport ?
Answer:
The movement of passengers and goods on waterways by using various means such as boats, steamers, launches, ships, etc. is called water transport.

Question 13.
What are services ?
Answer:
Services are an act of performance that one party offers to another for certain consideration or without consideration essentially intangible and does not result in the ownership of anything, e.g. services of doctors.

Question 14.
What are business services ?
Answer:
Business services are those services which help business to grow and run It successfully.

Question 15.
What is NABARD ?
Answer:
National Bank for Agriculture and Rural Development (NABARD) Is an apex Institution which provides short term as well as long term credit through regional rural banks to agricultural and rural sector of the Indian economy.

Question 16.
What is overdraft ?
Answer:
Overdraft is a temporary arrangement by which a current accountholder Is allowed to withdraw more money than his own balance up to a certain limit sanctioned by the bank.

Correct the underlined word and rewrite the sentences

Question 1.
Under whole life policy, the insured can receive money from the insurance company.
Answer:
cannot receive

Question 2.
The person who is protected against certain losses is called insurer.
Answer:
insured

Question 3.
Whole life policy is taken for a specific period.
Answer:
Endowment

Question 4.
Fire insurance gives protection against the losses caused due to the dangers of the sea.
Answer:
Marine.

Question 5.
Ministry of Railways looks after the development of water transport throughout the country.
Answer:
Railways

Question 6.
In hilly areas where other modes of transport are not accessible, water transport is important and convenient.
Answer:
Air

Question 7.
Ministry of Road transport looks after development of ocean transport throughout the country.
Answer:
Shipping

Question 8.
Palace on wheels and Maharaja are the examples of popular trains.
Answer:
Luxury

Question 9.
Warehouses are constructed in such a way to maximise risks.
Answer:
Minimise

Question 10.
Warehouses create place utility by preserving the goods till they are demanded.
Answer:
time

Question 11.
A private warehouse is a specialised establishment that provides storage facilities to the general public for certain charges.
Answer:
public

Question 12.
Duty paid warehouses work under the control of customs authorities.
Answer:
Bonded

Question 13.
Bonded warehouses are more useful for re-export of the goods.
Answer:
Duty paid.

Question 14.
Inland letter is used to send message outside India only.
Answer:
within

Question 15.
Printed books, magazines, journals, etc. can be sent through Business Post.
Answer:
Book Post

Question 16.
The minimum quantity of articles to be posted at a time is 1000 in Bill Mail Service.
Answer:
5000

Question 17.
A Drawee is the person named in money order as the person to whom the money is to be paid.
Answer:
A Payee

Question 18.
On can transfer money from INR 1000 to INR 5000 from designated imp post offices.
Answer:
50,000

Question 19.
Services are homogeneous.
Answer:
heterogeneous

Question 20.
All services are transferable in nature.
Answer:
non-transferable

Question 21.
Commercial bank issues currency notes in India.
Answer:
Reserve Bank of India

Question 22.
Export and Import Bank provides financial assistance to common people.
Answer:
Exporters and Importers

Distinguish between.

Question 1.
Private Warehouse and Public Warehouses
Answer:

	Private Warehouse	Public Warehouses
1. Ownership and management	These warehouses are owned and managed by big manufacturers, merchants, a firm or a company.	These warehouses are owned and managed by individuals, firms, co-operative organisations, etc.
2. Purpose	These warehouses are meant for their owners. They Eire not given on rental basis to outsiders.	These warehouses are meant for commercial use. Storage and other facilities are provided to small manufacturers and traders on payment of rent.
3. Location	Private warehouses are located at the places near factory or residence or place which is convenient to their owners.	Public warehouses are generally located near the junctions of railways, highways and waterways.
4. Rules and Regulations	These warehouses Eire not required to work under any rules and regulations. They have to observe general laws of the nation.	These warehouses work under a licence from the government in accordance with the rules and regulations prescribed by the government.
5. Suitability	These warehouses are suitable for large scale manufacturers, wholesalers and retailers who can afford to have their own warehouses.	These warehouses are more suitable for small scale manufacturers, traders or distributors who cannot afford to have their own warehouses.

Question 2.
Government Warehouses and Private Warehouses

	Government Warehouses	Private Warehouses
1. Ownership and management	These warehouses Eire owned, managed and controlled by Central and State governments or public authorities.	These warehouses are owned, managed and controlled by big manufacturers, merchants, a firm or a company.
2. Storage facilities	These warehouses offer storage facilities to the governments, small farmers, businessmen, traders at nominal charges.	These warehouses offer storage facilities to the owners for their own purposes. They are not rented to others.
3. Other services	These warehouses provide all the services for marketing such as classification, standardisation, grading, packing, etc.	These warehouses provide only those services which Eire required by their owners.
4. Rate	The rates charged by these warehouses for storing the goods are usually cheap and low.	Since these warehouses do not give their space on hire to outsiders, the question of charging rent does not arise.
5. Location	These warehouses Eire located at the important transport centres across different states and country.	These warehouses Eire located in the premises of the owners which may be near to their factories or market places.

Question 3.
Road Transport and Water Transport
Answer:

	Road Transport	Water Transport
1. Nature	Road transport represents transport facilities on the ground. It consists of motor transport, carts, etc.	Water transport represents transport facilities in the water. It consists of river, canal and ocean transport.
2. Carrying capacity	It has limited carrying capacity.	It has huge or large carrying capacity.
3. Cost of construction and maintenance	It requires relatively less capital investment in terms of construction of vehicles and roads and their maintenance.	Although no cost is involved in construction of waterways, high cost is involved for construction of ships and ports and also for maintenance of ships and ports
4. Transport charges	Transport charges are not fixed but they Eire usually high due to increase in fuel charges.	Transport charges Eire fixed according to the distance and they Eire relatively the lowest.
5. Door to door service	Road transport provides door to door services to the passengers.	Water transport does not provide door-to-door services to the passengers.
6. Suitability	It is suitable for short distances and for carrying light and perishable goods such as fruits, fish, vegetables, food grains and other consumer goods.	It is suitable for long distance and for carrying heavy and bulky goods such as machinery, cotton, COEQ, etc. in large quantity to any part of the world.
7. Means of transport	It uses animals, animal carts, motor-cycles, trucks, tempos, three-wheelers, buses, motor CEO’S, etc.	It uses launches, boats, tankers, liners, big ships etc.

Question 4.
Water Transport and Air Transport
Answer:

	Water Transport	Air Transport
1. Speed	Water transport is the slowest mode of transport.	Air transport is the fastest mode of transport
2. Carrying capacity	Water transport has huge carrying capacity.	Air transport has limited carrying capacity.
3. Means of transport	Water transport uses big ships, boats, liners, tankers, etc. as means of transport.	Air transport uses aircraft, jets, helicopter, etc. as means of transport.
4. Suitability	Water transport is suitable for carrying heavy Eind bulky goods such as machinery, cotton, coal, etc. in large quantities to any part of the world.	Air transport is suitable to carry light, perishable and valuable goods to any part of the world.
5. Transport charges	Transport charges are fixed according to the distance and they are relatively lowest.	Transport charges are fixed according to the distance and they Eire relatively highest.
6. Origin	Water transport dates back to early historical period.	Air transport commenced at the beginning of the 20th century.
7. Means of transport	It uses animals, animal carts, motor-cycles, trucks, tempos, three-wheelers, buses, motor CEO’S, etc.	It uses launches, boats, tankers, liners, big ships etc.

Question 5.
Savings Account and Fixed Deposit Account
Answer:

	Savings Account	Fixed Deposit Account
1. meaning	A savings account is a type of bank account meant for any regular salaried and wage earners and for making savings	A Fixed Deposit Account is a type of bank account under which a certain fixed amount is deposited for a definite period of time.
2. Mode of withdrawals	Withdrawals are allowed by cheques or withdrawal slips.	No withdrawal is permitted before the date of maturity.
3. Facilities	Passbook balance on SMS, cheque books, etc. are issued to the account holders.	Only Fixed Deposit Receipt (FDR) is issued.
4. Restrictions on withdrawals	There are certain restrictions on the number of withdrawals and the amount to be withdrawn at a time.	Withdrawal or payment can be obtained only on the expiry of the fixed period.
5. Rate of interest	Interest at low rate is paid periodically in this account.	Interest at high rate is paid periodically or at the expiry of period along with principal sum depending upon the time period of deposit.
6. Loan	No loan facility is available on the balance of savings account.	A certain amount by way of loan can be granted against the security of the Fixed Deposit Receipt (FDR).

Question 6.
Loan and Overdraft
Answer:

	Loan	Overdraft
1. Meaning	Loan is an arrangement under which the bank advances an amount against securities for a certain fixed period of time.	Overdraft is a temporary arrangement where a current account holder is allowed to overdraw from the account up to a specified limit.
2. Eligibility	Any account holder (i.e. current, savings or fixed deposit) can get a loan facility.	Only current account holders are eligible for an overdraft facility.
3. Purpose	The purpose of loan is to provide a long-term finance for some project or expansion of business.	The purpose of overdraft is to meet short term working capital requirements.
4.Duration	Loan may be sanctioned for a period such as 1 year, 3 years, 5 years or even more.	Overdraft is generally sanctioned for a short duration from 15 to 60 days.
5. Interest	Interest is calculated on the sanctioned loan amount whether it is withdrawn or not and the rate of interest is a little higher than that of overdraft.	Interest is calculated on the amount actually withdrawn and the rate of interest is lower than that of loan.
6. Repayment	Loan is repaid either in instalments or in lump sum on its due date.	Overdraft amount is adjusted against the amount or cheques deposited in the Current Account.

Arrange in proper order

Question 1.
email, Inland letter, Courier
Answer:
Inland letter, Courier, email.

Explain the following terms/concepts

Question 1.
Insurable interest.
Answer:
(1) A person is said to have insurable interest in the object insured if he is in such a relationship with the object of insurance, that he would stand to benefit monetarily by the continuance of the object insured or would suffer a financial loss by the loss or destruction or absence of the object. Therefore, it is necessary that he should be the owner or the lawful user of the object concerned.

(2) In simple term, insurable interest means – some financial interest in the subject-matter. The insured must have insurable (financial) interest in the subject-matter of insurance. No person can enter into a valid insurance contract unless he has insurable interest in the object insured. A person has insurable interest in his own life and his property. A wife has insurable interest in the life of her husband. Similarly, a businessman has insurable interest in the business property.

Question 2.
E-banking service
Answer:
(1) E-banklng stands for electronic banking. It is also called Virtual banking or Online Banking It is a systern under which all the working of the banks Is done through Internet and computers. With the help of this system. an account holder can deposit the money into the bank or withdraw the money. These funds tram one account to another. He can also get information of his account on the computer itself.

(2) The following-banking services are available to account holders:

• Automated Thller Machine (ATM)
• Credit Cards
• Debit Cards
• Mobile Banking
• National Electronic Fund Transfer (NEFT)
• Real Time Gross Settlement (RTGS). E-banking has made life much easier and banking much faster for both customers and banks.

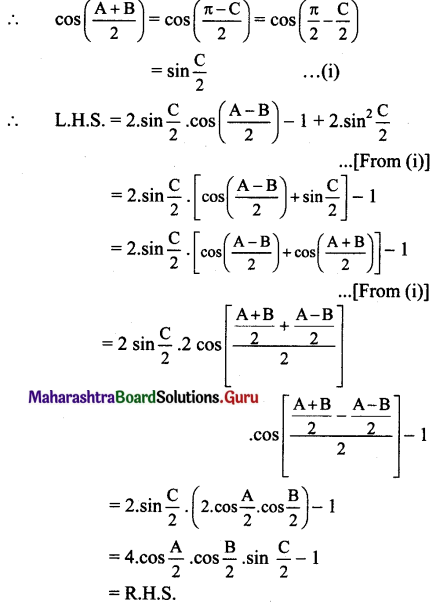
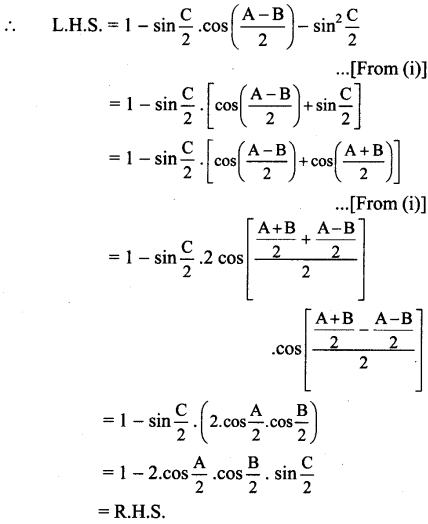
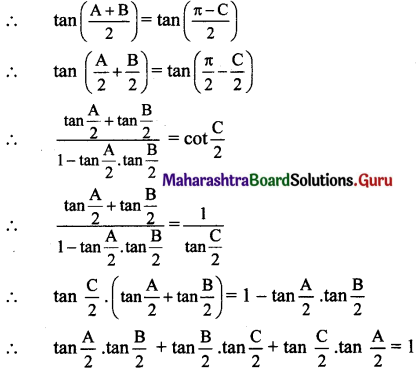
Justify the following statements

Question 1.
The principle of indemnity does not apply to life insurance contract.
Answer:
(1) The principle of indemnity is the controlling principle of insurance according to which the insured shall be compensated for only the actual loss suffered by him.

(2) All insurance contracts except life insurance contracts are the contracts of indemnity. Life insurance contract is, strictly speaking, a contract of assurance and not a contract of indemnity.

(3) In the case of life insurance contract, insurer cannot fully compensate the insured or his legal heir. This is because loss due to death of individual cannot be exactly determined or expressed in terms of money.

(4) Life insurance contract is a contract of assurance by which the insurer agrees to pay a fixed amount on the happening of the contingency.

Question 2.
Transport is useful in raising standard of living.
Answer:
(1) An efficient transportation system helps to develop agriculture by making available better seeds, fertilisers and agricultural equipment.

(2) Transport system also contributes to the rapid development of industry and commerce. The development in agriculture, industry and commerce leads to expansion in employment opportunities. Transport, as an industry by itself, also provides jobs to millions of people all over the country.

(3) By generating employment, transport leads to increase the purchasing power with people. As a result consumption pattern improves and consumption of variety of goods and services increases.

(4) Transport makes products from different regions available in local markets. The people also get variety of new and novel goods and services from any corner of the world at their places. This raises their standard of living.

Question 3.
Railway transport does not provide door to door service.
Answer:
(1) Transportation of passengers and goods from one place to another on the land surface on railway tracks through trains is called Railway Transport. It is the most dependable, cheaper and faster mode of transport to carry goods and passengers over long distances. It occupies an important place in land transport system.

(2) Railway transport requires specially ; prepared rail tracks with signalling systems. Therefore, throughout the country only certain places are fixed between which such tracks Eire laid. So, it runs between two railway stations.

(3) Special platforms are constructed to facilitate the loading and unloading of goods and for the movement of passengers.

(4) Goods and passengers are transported from one station to another by railway and there onward journey in the interior locations is facilitated by road transport. Thus, railways cannot provide door-to-door service in the interior as road transport does.

Question 4.
Current account is suitable for businessman.
Answer:
(1) A current account is a type of bank account in which there are no restrictions on the number of deposits and withdrawals. Therefore, it is suitable for businessmen (traders, hospitals, educational institutions, companies, etc.) as they have numerous day-to-day transactions of depositing amounts or cheques into a bank and issuing cheques for making payments to various parties.

(2) A current account is meant for facilitating, banking transactions of a businessman, such as collection of cheques, remittances to parties, bank overdraft facility, etc. A salaried person has no such transactions and does not require such facilities.

(3) A salaried person is interested in the rate of interest on his savings in the bank account. Banks generally do not pay any interest on the current account balances because they cannot use the current deposits for advancing loans to businessmen. Therefore, a salaried person finds savings account suitable for his limited banking transactions.

(4) The minimum balance to be kept for running the current account is much higher as compared to that for the savings account. A salaried person has a limited income and therefore, cannot afford to keep relatively large sum blocked in his account without earning any interest thereon. Therefore, a current account is suitable for businessman.

Attempt the following

Question 1.
What is fire insurance? Explain the different types of fire insurance policies.
Answer:
[A] Meaning : Fire insurance contract is contract of indemnity against loss or damage to goods or property arising from fire. Any property which is likely to damage due to fire may be insured against fire. Fire insurance also cover the loss caused due to fire, lightning and explosion.

[B] Types : The different types of fire insurance policies are shown in the following:

1. Valued Policy
2. Average Policy
3. Specific Policy
4. Floating Policy
5. Excess Policy
6. Reinstatement Policy
7. Comprehensive Policy
8. Consequential Loss Policy
9. Sprinkler Leakage Policy

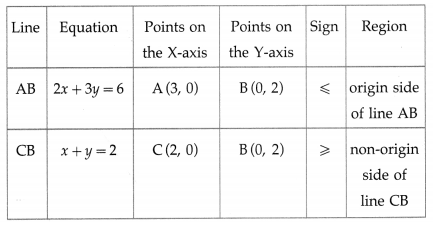
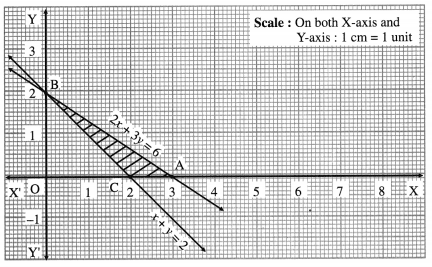
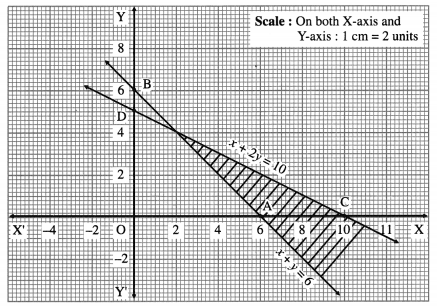
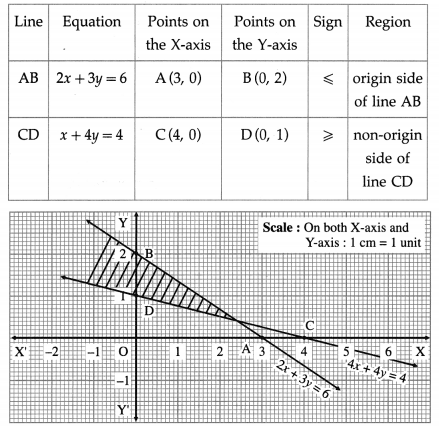
1. Valued Policy : It is a policy under which the value of the property (i.e. subject mater) is ascertained and agreed upon by the insurer and the insured at the time of issue of the policy. The insurer undertakes to pay the agreed value irrespective of amount of loss caused due to fire. This type of policy is taken for those goods whose value is too difficult to calculate at the time of loss by fire, e.g. artwork, paintings, etc.

2. Average Policy : This policy contains an average clause. Under this policy the insurer is liable to pay only that proportion of the actual loss as the insured sum will bear to the full value of the property at the time of the loss, e.g. the machinery of Rs 5,00,000 is insured under fire insurance for Rs 2,00,000, The loss occurred due to fire arrived at Rs 2,50,000. This is because insurance is 40% of actual value of machinery. Hence the claim for loss is also 40% of 2,50,000 i.e. Rs 1,00,000.
Formula to calculate claim:
\(\frac {Value of Policy}{Value of Property}\) × Actual loss
\(\frac {200000}{500000}\) × 250000 = Rs 100000

3. Specific Policy: This type of policy mentions a specific maximum amount payable as compensation in case the insured property is destroyed by fire, irrespective of the market value of the property insured, e.g. a property of the value of Rs 5,00,000 is insured for Rs 3,00,000. The loss occurred due to fire is Rs 1,50,000. Here insurance company will pay Rs 1,50,000 in full as compensation.

4. Floating Policy : This type of policy covers, under one sum and for a single premium, one or several kinds of goods lying in different localities. As the quantity of goods lying at different places fluctuate from time to time, it is convenient to the businessmen to take a policy for one sum and one premium for goods lying at different places.

5. Excess Policy : This type of policy is taken when the market value of stock constantly fluctuates. In such case one policy is taken for a minimum amount below which value of stock never falls and another policy for excess amount by which price fluctuates, e.g. If the value of stock ranges between Rs 5,00,000 and Rs 5,40,000, then one policy will be taken for Rs 5,00,000 and another policy will be taken for Rs 40,000 i.e. for excess amount.

6. Reinstatement Policy : Under this policy, insurer undertakes to replace the property or goods lost by fire or to pay the amount that would be needed to reinstate or replace the damaged or destroyed property. While replacing the property for paying compensation depreciation amount of the property destroyed is not taken into consideration. The rate of premium is usually very high.

7. Comprehensive Policy : This fire insurance policy covers all kinds of risks such as fire explosion, lightning, earthquake, floods, riot, strikes, burglary, etc. under single policy.

8. Consequential Loss Policy : Initially a fire insurance policy was meant for indemnification of loss due to damage of tangible property. The intangible property was not covered by fire insurance. The consequential loss policy now taken for the loss of tangible as well as intangible properties. This policy covers the risk of loss of net profits, payment of standing charges, expenditure in respect of the increased cost of working, etc.

9. Sprinkler Leakage Policy: This policy covers the damage of property caused by an automatic sprinkler system that has leakage or discharged water accidently and not due to fire and smoke. This policy does not cover the discharge or leakage of water due to heat caused by fire, repair, earthquake, war, explosion, etc.

Question 2.
Explain the advantages of air transport.
Answer:
The advantages of air transport are explained as follows:
(1) Fastest means of transport : Among all the means of transport available at present, air transport is the fastest and quickest means of transport.

(2) Vital services : Air transport plays key role during war and emergency situations because it is useful to provide valuable services quickly in affected areas by floods, earthquakes, etc.

(3) Free routes : In case of air transport, it is not necessary to incur any expenditure on the construction of aerial routes. It uses natural and shortest aerial routes.

(4) Less pollution : In comparison to other means of transport like road transport, air transport is less polluting.

(5) Useful in certain areas : Air transport is very useful in carrying passengers, goods and medicines to the areas specially hilly and mountainous areas which are not accessible by any other means.

(6) Market for perishable and costly goods : For speedy transport of perishable good medicines, human organs, diamonds, ornaments, etc. air transport is most suitable and the fastest.

Answer the following.

Question 1.
Explain types of warehouses.
Answer:
The different types of warehouses are:
(1) Private warehouses : The warehouses owned and operated by the big manufacturers and wholesalers for storing their own goods are called private warehouses. Big companies which need large storage capacity on a regular basis, can afford to construct and maintain their own warehouses. Many public sector organisations also have their own private warehouses, e.g. the Food Corporation of India (FCI) has constructed warehouses in different parts of the country for its own use. Usually these warehouses are constructed near to ones business factory or industry for convenience. They have network of warehouses in different parts of the country.

(2) Public warehouses : Warehouses which are established to provide storage facilities to the general public, small manufacturers and traders on rental basis are called public warehouses. These warehouses are owned and managed by an individual or co-operative societies. These warehouses are located near railway junctions, highways, waterways, airport, seaport, etc. They are well guarded and specially designed to protect goods from several types of risks. These warehouses have to obtain licence from the government. They provide warehousing facilities at low cost. Many marketing facilities such as standardisation, grading, labelling, packing, branding, etc. are provided in these warehouses.

(3) Bonded warehouses : Warehouses which are licensed by the government to accept and store imported goods till the customs duties are not paid on such goods are called bonded warehouses. These warehouses are managed and controlled by customs authorities. These warehouses are located near the ports. The importers cannot take possession of goods from such warehouses unless and until the duty on the goods is paid.

The warehouse-keeper is required to give undertaking or ‘Bond’ that without the consent of the customs authorities goods will not be removed from the warehouse. Hence, such warehouses are called ‘Bonded Warehouses’. If an importer is unwilling or unable to pay customs duty immediately, he can withdraw them in instalments and pay customs duty proportionately.

(4) Duty-paid warehouses : The duty-paid warehouses provide the facility of storing the imported goods but not yet sold or transported to importers’ place or godown. These warehouses are owned and managed by the dock authorities only and hence they are also known as public warehouses. These warehouses are located near port and dock areas. They are more useful to importers who re-export the imported goods. The concerned authorities take all the due and reasonable care to ensure their safety. Processing of imported goods such as sorting, re-packing is done in these warehouses.

(5) Government warehouses : Warehouses which are owned, managed and controlled by the Central and State Governments or public authorities are called Government warehouses. These warehouses offer storage facilities to small traders, farmers, businessmen, etc. who are in need of the same on payment of reasonable rent. Central Warehousing Corporation of India (CWC), State Warehousing Corporation (SWC) and Food

(6) Co-operative warehouses : These are warehouses owned, run, managed and controlled by co-operative societies to provide warehousing facilities to the members who are farmers in rural areas. These warehouses are similar to private warehouses but they run on the principle of co-operation. They are used for storing agricultural commodities, consumer goods, raw materials, etc. Farmers, small producers and traders are benefited by such warehouses as they charge at economical rates.

(7) Cold storage warehouses : Cold storage warehouses are largely used to store and preserve perishable goods such as flowers, fish, eggs, meat, vegetables, fruits, medicines, dairy products, etc. These products are kept in cold storage warehouses at very low temperature so that their quality and freshness would remain intact. These warehouses ensure continuous supply of seasonal and perishable products throughout the year. International trade for seasonal and perishable goods such as green peas, mangoes, etc., becomes possible only because of cold storage facilities.

Question 2.
What is rail transport. Explain its advantages and disadvantages.
Answer:
[A] Meaning : Railways are the principal means of transport on land. The mode of transport which carries goods, passengers and materials from one place to another on rail lines through trains is called Railway transport. It runs passenger trains, mail express, goods trains, popular trains and luxury trains. The ministry of railways looks after the development of rail transport in India.

[B] Advantages : The advantages of rail transport are explained as follows:

1. Suitable for long distances : Railway transport is suitable and convenient mode of transport for travelling over long distances.
2. Carriage of heavy and bulky goods : Railway transport is more suitable for the carriage of bulky and heavy goods like engineering goods, coal, cotton, livestock, oil, etc. over long distances.
3. Speedy : Railway transport is more speedy in comparison to road transport.
4. Less affected by adverse weather conditions : Usually railway service is more certain, uniform and regular. It is not much affected by adverse weather conditions such as rains, fogs, floods, etc.
5. Protection to goods : Railway transport protects goods against rains, sun, wind, snow, etc. and ensures safety and security to goods.

[C] Disadvantages : The disadvantages of railway transport are explained as follows:

1. Expensive for short distances : Railway transport is more expensive for carrying goods and passengers over short distances.
2. Non-availability of services in remote part : The services of railway transport are not reachable or available in the remote part of the country.
3. Heavy loss in case of accident : In case of accident, it involves heavy losses of life, goods and materials.
4. Inflexibility : Fixed time schedule of trains, permanent track, definite station and halts, etc. bring certain degree of inflexibility in railway transport.
5. Incomplete service : The railway service is available between the nearest stations only. Railways can not provide door-to-door services. Therefore, railway stations are required to be connected by roads.

Question 3.
What is water transport? Explain the advantages and disadvantages of water transport.
Answer:
[A] Meaning : This is the oldest and cheapest means of transport. The mode of transport which carries goods and passengers on the surface of the water from one port to another by using boats, steamers, launches, ships, etc. is called water transport. When the passengers and goods move within the country, it is known as inland water transport and when the goods and passengers are carried through sea and oceans, it is known as ocean or sea transport. The ministry of shipping takes cares of ocean transport in India.

[B] Advantages : The advantages of water transport are explained as follows:

1. Economical mode of transport : Water transport is suitable and economical mode of transport for carrying heavy and bulky goods over longer distances.
2. Safe mode of transport : It is safe and secured mode of transport in regard to occurrence of accidents.
3. Promotes international trade : Water transport facilitates and promotes international trade and thus helps to widen the market.
4. Free routes : Water transport use waterways which are natural and free of cost route and involve no construction and maintenance costs.
5. More flexibility : Water transport is more flexible in comparison to rail transport.

[C] Disadvantages : The disadvantages of water transport are explained as follows:

1. Absence of door-to-door services : Water transport cannot provide door-to-door service. It carries goods and passengers from one port to another.
2. Affected by adverse weather conditions : It is much affected by adverse weather conditions like heavy rains, cyclone, storms, etc.
3. Low speed : In comparison to other modes of transport, speed of water transport is very slow. Therefore, perishable goods cannot be transported by this mode of transport.
4. Heavy capital expenditure : Heavy investment (capital expenditure) cost is involved in the construction and maintenance of ships, ports, docks, wharves, etc.
5. Hazardous : Water transport is hazardous. There are dangers of storms, cyclone and other perils of sea.

Question 4.
Define Bank. Explain different type of banks.
Answer:
[A] Definition : Bank is a dealer in money and credit. It is a financial institution whose basic activities are to accept deposits and advance, lend money and provide other related services, According to The Indian Banking Regulation Act, 1949, “any company which transacts the business of banking in India.” The term banking is further defined as, “accepting for the purpose of lending or investment of deposits from the public, repayable on demand or otherwise and withdrawable by cheque, draft and order or otherwise.”

[B] Types of Banks:
The different types of banks are shown In the following:

1. Central Bank
2. Commercial Bank
3. Co-operatIve Bank
4. Industrial Development Bank
5. Exchange Bank
6. RegIonal Rural Bank
7. SavIngs Bank
8. Investment Bank
9. Speclalised Bank

The different types of banks are explained below:
1. Central Bank : The central bank in a country is the financial institution at the top (apex) of all the banking institutions operating in the country. In India, The Reserve Bank of India was established in 1945 under a special statute called the Reserve Bank of India Act, 1944. It performs the functions like framing monetary policy, issuing currency notes, acting as a banker to the Government and acting as the banker’s bank to commercial and other banks in India.

2. Commercial Bank : The Commercial bank plays key role in the economic, industrial and social development of a country. It performs broadly two functions such as (i) Primary functions which include accepting deposits and lending money in different forms and (ii) Secondary function which include agency functions and utility functions. The different types of commercial banks in India are as follows:
(i) Public Sector Banks : The banks in which majority of the share capital or stake (interest) is held by the Government of India are called Public Sector Bank, e.g. State Bank of India, Bank of India, etc.

(ii) Private Sector Banks : The banks in which majority of the share capital or stake is held by private individuals are called Private Sector Banks, e.g. Axis Bank, HDFC Bank, etc.

(iii) Foreign Banks : The banks which are registered and have their headquarters in foreign country but operate in different countries including India through their branches established there, are called Foreign banks e.g. Standard Chartered Bank, American Express Bank, HSBC, etc.

3. Co-operative Banks : Co-operative banks are formed, registered and organised under the Indian Co-operative Societies Act and regulated under Banking Regulation Act. These banks are more popular in rural and semi-urban areas. These banks are primarily meant for catering to the financial needs of economically backward people, farmers and small scale units. They operate at three different levels:
(a) Primary Credit Societies : The primary credit societies work at village level. These credit societies collect the savings and surplus money in the form of deposits from members and common people. They are also financed by the State Co¬operative Banks and District Co-operative Banks for the purpose of lending to needy people for productive purpose.

(b) District Central Co-operative Banks : The District Central Co-operative Banks operating at district level and financed by the State Co-operative Bank for the purpose of providing finance to primary credit societies.

(c) State Co-operative Banks : The State Co-operative Banks Eire working at state level. These banks provide funds to District Central Cooperative Banks and Primary Credit Societies to enable them to provide finance to rural and semi urban areas. Apart from this, they also supervise the working of district banks and credit co¬operative societies.

4. Industrial Development Banks : The banks which provide medium and long term equipment, latest technology, expansion and modernisation of business, etc. are called Industrial Development Banks. Industrial Finance ; Corporation of India (IFCI), State Financial Corporations (SFCs), Maharashtra State Finance Corporation (MSFC), etc. are the examples of Industrial Development Banks. These banks perform the following functions:

• Provide medium and long term finance to business organisations for expansion and modernisation.
• Underwriting i.e. giving guarantee to buy shares issued by public limited companies.
• Purchase debentures and bonds.

5. Exchange Banks : An exchange bank specialises in financing import and export trade and in foreign exchange transactions. The American Express Bank, Bank of Tokyo, Barclays Bank, etc. are the examples of Exchange Banks functioning in India. The Exchange Banks perform the following functions:

• Finance foreign trade transactions,
• Issue letter of credit on behalf of importer,
• Discount foreign bills of exchange,
• Remit dividend, interests and profits.

6. Regional Rural Banks : These banks were constituted (established) in 1975 and are sponsored by large public sector banks. 50%, 35% and 15% of the capital of these banks are provided by the Central Government, sponsored banks and State Government respectively. These banks collect (mobilise) funds in the form of deposits from rural and semi-urban areas. They provide loans and advances to small and marginal farmers, agricultural workers, rural artisans for productive purpose.

7. Savings Bank : A savings bank is one which has the main object of inculcating the habit of saving among the community. It collects scattered savings of the community especially from rural areas and invests the same in good securities. In India, Postal Savings Bank is an example of such a bank. Commercial Banks and Co-operative Banks act as savings banks as they have separate savings accounts departments.

8. Investment Bank : Investment banks offer financial and advisory assistance to their customers which usually include business firms and government organisations. These banks provide advice on investment decisions and facilitate mergers and acquisitions by undertaking research. These Banks do not directly deal with the common people.

9. Specialised Banks: The banks which make available to the requirements of the business and provide possible support to set up business activities in specific area are called Specialised Banks. The different types of specialised banks are:
(a) Export Import Bank of India (EXIM Bank) : These banks provide the needed financial assistance and support to the exporters and importers in setting up business for exporting and importing products respectively. They work to expand and promote country’s international trade.

(b) Small Industries Development Bank of India (SIDBI) : SIDBI was established on 2nd April, 1990 under the Act of Parliament of India. Its main function is to act as the main institution for financing, promoting and developing the Micro, Small and Medium Enterprises (MSMEs) as well as co-ordinator of the institutions engaged in similar activities.

(c) National Bank for Agricultural and Rural Development (NABARD) : NABARD has been established to work as an apex institution to finance agricultural and rural sector. It provides long term and short term loans through regional rural banks. It provides loans to financial institutions and not individuals. It is also concerned with the function of policy planning and operations relating to agricultural credit and credit for other activities in rural areas.