Balbharti Maharashtra State Board 12th Chemistry Important Questions Chapter 3 Ionic Equilibria Important Questions and Answers.
Maharashtra State Board 12th Chemistry Important Questions Chapter 3 Ionic Equilibria
Question 1.
What are electrolytes?
Answer:
Electrolytes: The substances which in their aqueous solutions (or in any polar solvents) dissociate or ionize forming positively charged ions (cations) and negatively charged ions (anions) are called electrolytes. For example, NaCl, HCl, etc.
Question 2.
What is an ionic equilibrium?
Answer:
Ionic equilibrium: The equilibrium between ions and unionized molecules of an electrolyte in solution is called an ionic equilibrium.
\(\mathrm{CH}_{3} \mathrm{COOH}_{(\mathrm{aq})} \rightleftharpoons \mathrm{CH}_{3} \mathrm{COO}_{(\mathrm{aq})}^{-}+\mathrm{H}_{(\mathrm{aq})}^{+}\)
Question 3.
What are the types of electrolytes?
Answer:
There are two types of electrolytes as follows :
(a) Strong electrolyte The electrolytes which ionise completely or almost completely are called strong electrolytes. For example, NaCl, HCl, H2SO4, etc.
(b) Weak electrolytes: The electrolytes which dissociate to a less extent are called weak electrolytes. For example, CH3COOH, NH4OH, etc.
Question 4.
Define degree of dissociation.
Answer:
Degree of dissocsavIt is defined as a fraction of total number of moles of an electrolyte that dissociate into its ions at equilibrium.
It is denoted by a and represented by,
![]()
OR α = \(\frac{\text { Per cent dissociation }}{100}\)
∴ Per cent dissociation = α × 100
![]()
Question 5.
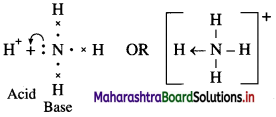
Define acid and base. Give examples.
Answer:
Acid : A hydrogen containing substance which gives H+ ions in aqueous solution is called an acid. For example, HCl, CH3COOH, etc.
\(\mathrm{HCl}_{(\mathrm{aq})} \longrightarrow \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-}\)
Base : A substance that contains OH group and produces hydroxide ions (OH–) in aqueous solution is called a base.
\(\mathrm{NaOH}_{(\mathrm{aq})} \longrightarrow \mathrm{Na}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-}\)
Question 6.
What are the limitations of Arrhenius acid-base theory ?
Answer:
Limitations of Arrhenius theory :
- This theory is applicable only for aqueous solutions and not for non-aqueous solutions.
- It fails to explain the acidic nature of non-hydrogen compounds like BF3, AlCl2, FeCl3, etc.
- It fails to explain the basic nature of non-hydroxy compounds like NH3, amines, Na2CO3, KCN, aniline, etc. in their aqueous solutions.
- It does not explain role of solvent or existence of H3O+ in an aqueous solution of an acid.
Question 7.
Explain neutralisation reaction according to Arrhenius theory.
Answer:
Neutralisation reaction : According to Arrhenius theory neutralisation is a reaction between an acid and a base in their aqueous solutions produciijg salt and unionised water.
\(\mathrm{HCl}_{(\mathrm{aq})}+\mathrm{NaOH}_{(\mathrm{aq})} \rightarrow \mathrm{NaCl}_{(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
Since strong acid, strong base and salt dissociate completely, the above reaction is represented as,
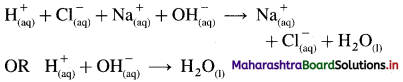
Hence, according to Arrhenius theory neutralisation reaction is defined as a reaction between H+ ions and OH– ions forming unionised water molecules.
Question 8.
Explain Bronsted-Lowry theory of acids and bases.
Answer:
Acid : According to Bronsted-Lowry theory acid is a substance that donates a proton (H+) to another substance.
Base : According to this theory base is a substance that accepts a proton (H+) from another substance. For example,
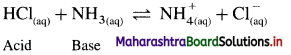
Since HCl donates a proton it is an acid while NH3 accepts a proton it is a base.
Question 9.
For each of the following reactions, identify the Lowry-Bronsted conjugate acid-base pairs :
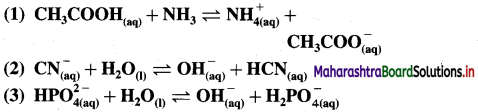
Answer:
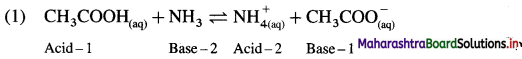
In this Acid-1 (CH3COOH) and Base-1 (CH3COO–) is one acid base conjugate pair while Base-2 (NH3) and Acid-2 \(\mathrm{NH}_{4}^{+}\) is another conjugate pair.
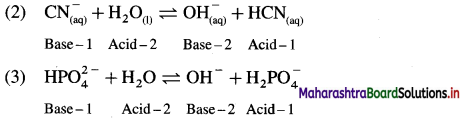
Question 10.
Mention a conjugate acid and a conjugate base for each of the following :
(a) H2O (b) \(\mathrm{HSO}_{4}^{-}\) (C) Br– (d) H2CO3 (e) \(\mathbf{H}_{2} \mathbf{P O}_{4}^{-}\) (f) \(\mathbf{N H}_{4}^{+}\)
Answer:
| Substance | Conjugate acid | Conjugate base |
| (a) H2O | H3O+ | OH– |
| (b) \(\mathrm{HSO}_{4}^{-}\) | H2SO4 | \(\mathrm{SO}_{4}^{-2}\) |
| (c) Br– | HBr | – |
| (d) H2CO3 | – | \(\mathrm{HCO}_{3}^{-}\) |
| (e) \(\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\) | H3PO4 | \(\mathrm{HPO}_{4}^{-2}\) |
| (f) \(\mathrm{NH}_{4}^{+}\) | – | NH3 |
![]()
Question 11.
Identify conjugate acid-base pairs in the following :
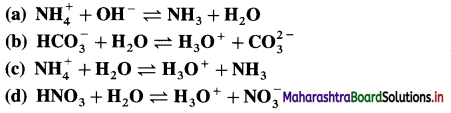
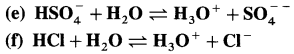
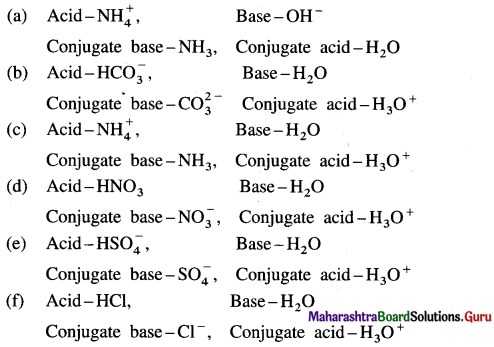
Answer:
Question 12.
Define acids and bases on the basis of Lewis concept. Give examples.
Answer:
Lewis concept of an acid and a base is based on the electronic theory.
Acid : It is defined as any species (molecule or ion) that can accept a pair of electrons. E.g. BF3, AlCl3 and all electron deficient species like cations (K+, Ag+) and molecules having incomplete octet, like BeF2, BF3.
Base : It is defined as any species (molecule or ion) that can donate a pair of electrons. E.g. NH3, C2H5NH2 and all electron rich species like anions (Cl–, OH–) and all molecules with lone pair of electrons.
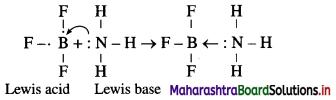
Question 13.
Explain : (A) BF3 is a Lewis acid, (B) NH3 is a Lewis base.
Answer:
(A) According to Lewis theory, an acid is a substance which can accept a pair of electrons.
In BF3 molecule, the octet of B is incomplete, hence it needs two electrons or a pair of electrons to complete its octet. Hence BF3 acts as a Lewis acid.

(B) According to Lewis theory, a base is a substance which can donate a pair of electrons.
In NH3 molecule, nitrogen atom has one lone pair of elctrons to donate.
The reaction between BF3 and NH3 can be represented as,
Question 14.
Classify the following into Lewis acids and bases :
CN–, Cl–, S2-, Cu++, H2O, OH–, BF3, Ag+.
Answer:
(1) Lewis acid : Cu++, BF3, Ag+
(2) Lewis bases : CN–, Cl–, S2-, OH–.
Question 15.
Explain amphoteric nature of water.
Answer:
(1) Since water acts as an acid as well as a base, it is amphoteric in nature.
(2) H2O has a tendency to donate a proton forming OH– as well as has a tendency to accept a proton forming H3O+.
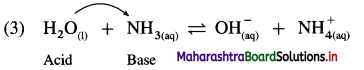
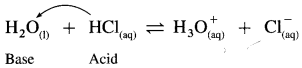
Therefore H2O is amphoteric in nature.
![]()
Question 16.
How are acids and bases classified on the basis of extent of their dissociation?
Answer:
On the basis of extent of dissociation acids and bases are classified as follows :
(1) Strong acids and strong bases : The acids and bases which dissociate to a greater extent or almost completely are called strong acids and strong bases.
\(\mathrm{HCl}_{\text {(aq) }} \longrightarrow \mathrm{H}_{\text {(aq) }}^{+}+\mathrm{Cl}_{\text {(aq) }}^{-}\)
\(\mathrm{NaOH}_{(\mathrm{aq})} \longrightarrow \mathrm{Na}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-}\)
(2) Weak acids and weak bases : The acids and bases which dissociate partially are called weak acids and weak bases. There exists an equilibrium between undissociated molecules and ions in solution.
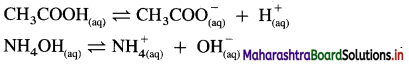
Question 17.
Give examples of (a) strong acids and strong bases, (b) weak acids and bases.
Answer:
(a) Strong acids : HCl, H2SO4
Strong bases : NaOH, KOH
(b) Weak acids : HCOOH, CH3COOH
Weak bases : NH4OH, C2H5NH2
Question 18.
Define and explain dissociation constant of a weak acid.
Answer:
Dissociation constant of a weak acid : It is defined as the equilibrium constant for dissociation equilibrium of a weak acid and denoted by Ka.
Explanation : Consider an aqueous solution of a weak acid HA.
\(\mathrm{HA}_{(\mathrm{aq})} \rightleftharpoons \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{A}_{(\mathrm{aq})}^{-}\)
The equilibrium constant called dissociation constant Ka is represented as,
Ka = \(\frac{\left[\mathrm{H}^{+}\right] \times\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)
Question 19.
Derive the expression of Ostwald’s dilution law in case of a weak acid (HA).
OR
Derive the relationship between degree of dissociation and dissociation constant of a weak acid.
Answer:
Expression of Ostwald’s dilution law in case of a weak acid : Consider the dissociation of a weak acid HA. Let V dm3 of a solution contain one mole of weak acid HA. Then the concentration of a solution is, C = \(\frac{1}{V}\) mol dm3-3. Let α be the degree of dissociation of HA.
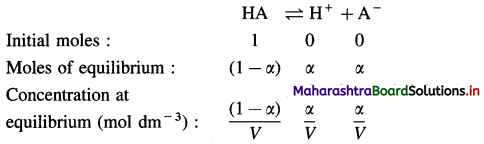
Applying the law of mass action to this dissociation equilibrium, we have,
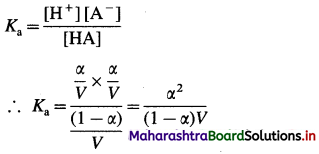
As the acid is weak, a is very small as compared to unity,
∴ (1 – α) ≈ 1.
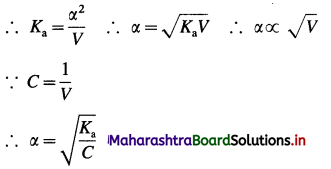
This is an expression for Ostwald’s dilution law. This shows that the degree of dissociation of a weak acid is directly proportional to the volume of solution containing one mole of acid or inversely proportional to square root of its concentration.
Question 20.
Derive the relationship between degree of dissociation and dissociation constant of a weak base.
OR
Derive the expression of Ostwald’s dilution law in case of a weak base.
Answer:
Expression of Ostwald’s dilution law in case of a weak base : Consider the dissociation of a weak base BOH. Let V dm3 of a solution contain one mole of weak base BOH. Then the concentration of a solution is, C = \(\frac{1}{V}\) mol dm-3. Let α be the degree of dissociation of BOH.
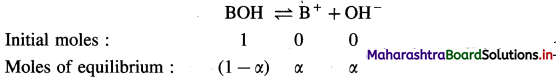
Consentration at equilibrium (mol dm-3) \(\frac{(1-\alpha)}{V} \quad \frac{\alpha}{V} \quad \frac{\alpha}{V}\)
Applying the law of mass action to this dissociation equilibrium, we have,

This is an expression of Ostwald’s dilution law. Thus, the degree of dissociation of a weak base is directly proportional to the square root of the volume of the solution containing one mole of a base or inversely proportional to the square root of its concentration.
![]()
Solved Examples 3.4
Question 21.
Solve the following:
(1) At 298 K, 0.01 M formic acid solution is 1.2% dissociated. Calculate the dissociation constant of formic acid.
Solution :
Given : Concentration of HCOOH = C = 0.01 M
Percent dissociation = 1.2
Dissociation constant = Ka = ?
∴ Degree of dissociation = \(\frac{\text { Percent dissociation }}{100}\)
α = \(\frac{1.2}{100}\)
= 1.2 × 10-2
Ka = Cα2
= 0.01 × (1.2 × 10-2)2
= 1.44 × 10-6
Ans. Dissociation constant = Ka = 1.44 × 10-6
(2) The degree of dissociation of ammonium hydroxide is 0.0232 in 0.5 M solution. What will be the dissociation constant of ammonium hydroxide ?
Solution :
Given : Degree of dissociation = α = 0.0232
Concentration of NH4OH = C = 0.5 M
Dissociation constant = Kb = ?
Kb = Cα2
= 0.5 × (0.0232)2
= 2.692 × 10-4
Ans. Dissociation constant of NH4OH
= Kb = 2.692 × 10-4.
(3) Calculate the hydrogen ion concentration in 0.1 M acetic acid solution when the acetic acid is 2% dissociated in the solution.
Solution : The dissociation of acetic acid is represented below :
CH3COOH ⇌ CH3 – COO– + H+
Given : Dissociation = 2%, C = 0.1 M
[H3O+] = ?
The concentration of hydrogen ion, [H+], is given by the following formula :
[H3O+] = αC
α = Degree of dissociation = \(\frac{\text { Per cent dissociation }}{100}\)
= \(\frac{2}{100}\) = 0.02
[H3O+] = Hydrogen ion concentration = ?
C = Molar concentration of acetic acid
= 0.1 M = 0.1 mol dm-3
∴ [H3O+] = C × α = 0.1 × 0.02
= 0.002 = 2.0 × 10-3 mol dm-3
Ans. Hydrogen ion concentration = 2.0 × 10-3 mol dm-3.
(4) Calculate the percentage dissociation of 0.01 M NH4OH solution. The Kb for NH4OH is 1.75 × 10-5.
Solution :
Given : Concentration of NH4OH = C = 0.01 M
Dissociation constant of NH4OH
= Kb= 1.75 × 10-5
Percentage dissociation = ?
Kb = Cα2

∴ Per cent dissociation = α × 100
= 4.183 × 10-2 × 100
= 4.183
Ans. Dissociation of NH4OH = 4.183%
![]()
(5) 0.01 mole of a weak base is dissolved in 8 dm3 of water. The dissociation constant of the base is 4.0 × 10-10. Calculate the degree of dissociation of the base in the solution.
Solution :
Given : V = 8 dm3; n = 0.01 mole; Kb = 4 × 10-10
α = ?
The degree of dissociation and dissociation constant of a weak base are related to each other by the following formula :
Kb = α2C OR α = \(\sqrt{\frac{K_{b}}{C}}\)
Kb = Dissociation constant of the base = 4.0 × 10-10
α = Degree of dissociation of the base = ?
C = Molar concentration of the base
= 0.01 mole in 8 dm3
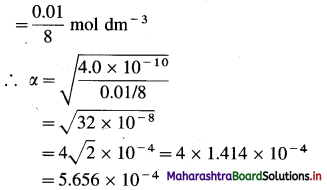
Ans. Degree of dissociation of the base = 5.656 × 10-4
(6) The dissociation constant of benzoic acid (C6H5COOH) is 6.6 × 10-5. Calculate the hydrogen ion concentration of a solution containing 1.22 g of benzoic acid in 2000 mL of water.
Solution :
Given : Ka = 6.6 × 10-5; V = 2000 mL;
W = 1.22 g; [H+] = ?
Molar mass of benzoic acid (C6H5COOH) = 122
The concentration of the solution is 1.22 g benzoic acid in 2000 ml (2 dm3) of solution.
1.22 g = \(\frac{1.22}{122}\) = 0.01 mol
∴ Molar concentration of benzoic acid = \(\frac{0.01}{2}\)
= 0.005 mol dm-3
The dissociation constant and degree of dissociation of a weak acid are,
Ka = α2C OR α = \(\sqrt{\frac{K_{\mathrm{a}}}{C}}\)
α = Degree of dissociation of benzoic acid = ?
C = 0.005 mol dm-3

Since benzoic acid is a monobasic acid, [H+] = aC
∴ [H+] = 0.1149 × 0.005
= 5.745 × 10-4 mol dm-3
Ans. Hydrogen ion concentration
= 5.745 × 10-4 mol dm-3
(7) The degree of dissociation of acetic acid in its 0.1 M solution is 0.0132 at 25 °C. Calculate the degree of dissociation in its 0.01 M solution.
Solution :
Given : C = 0.1 M, α = 0.0132, C’ = 0.01 M,
α = 0.0132, α’= ?
Ka = α2C
C = Molar concentration of acetic acid = 0.1 M
α = Degree of dissociation in 0.1 M solution = 0.0132
∴ α = \(\sqrt{\frac{K_{\mathrm{a}}}{C}}\)
If the concentration is C’, α’ = \(\sqrt{\frac{K_{\mathrm{a}}}{C^{\prime}}}\)

Ans. Degree of dissociation in 0.01 M solution = 4.175 × 10-2
Question 22.
Explain autoionisation of water. Derive a relation for ionic product of water.
Answer:
Pure water ionises to a very less extent. The ionisation equilibrium is represented as follows,
\(\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \rightleftharpoons \mathrm{H}_{3} \mathrm{O}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-}\)
The equilibrium constant K for the above equilibrium is represented as,
K = \(\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}\)
∴ K × [H2O]2 = [H3O+] × [OH–]
Since K and active mass of pure water [H2O] are constant we can write,
K × [H2O] = Kw,
∴ Kw= [H3O+] × [OH–]
where Kw is called ionic product of water. At 25 °C,
Kw= 1 × 10-14.
Question 23.
Define ionic product of water.
Answer:
Ionic product of water : It is defined as the product of molar concentrations of hydronium ions (or hydrogen ions) and hydroxyl ions at equilibrium in pure water at constant temperature.
It is represented as,
Kw = [H3O+] × [OH–]
At 25 °C, Kw= 1 × 10-14.
![]()
Question 24.
Define the following :
(i) pH (2) pOH. (2 marks)
Ans.
(1) pH : The negative logarithm, to the base 10, of the molar concentration of hydrogen ions, H+ is known as the pH of a solution.
PH = -log10 [H+]
(2) pOH : The negative logarithm, to the base 10, of the molar concentration of hydroxyl ions, OH– is known as the pOH of a solution.
pOH = -log10 [OH–]
Question 25.
What are approximate concentrations of H3O+ and OH– in, (a) pure water or neutral solution, (b) acidic solution and (c) basic solution ? Also mention pH values.
Answer:

Question 26.
Write a note on pH scale.
Answer:
Most of the chemical reactions and industrial processes are carried out in aqueous solutions, hence there is a need to know concentration of H+ and OH– ions in the solution.
Sorensen developed a convenient scale to represent the acidic, basic or neutral nature of the solution.
The pH scale is used to express the concentration of H+ and OH– along with pH and pOH of the solution.
According to Sorensen,
pH = -log10 [H+], pOH = -log10 [OH–]
pH + pOH = 14.
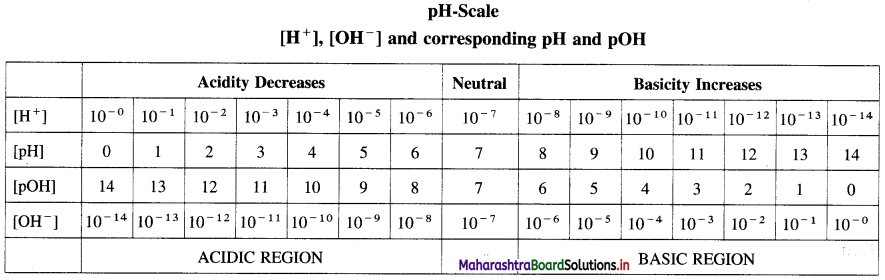
Acids, basic and neutral solutions.
Question 27.
Solve the following :
(1) At 50 °C the value of ionic product of water is 5.5 × 10-14. What are the concentrations of [H3O+] and OH– in a neutral solution at 50°C temperature ?
Solution :
Given : at 50 °C
Ionic product of water = Kw = 5.5 × 10-14
[H3O+] = ? OH– = ?
Water at any temperature will be neutral.
Hence, [H3O+] = [OH–] = x mol dm-3
[H3O+] × [OH–] = Kw
x × x = 5.5 × 10-14
∴ x = 2.345 × 10-7
∴ [H+] = [OH–] = 2.345 × 10-7 M
Ans. Concentrations : [H3O+] = [OH–]
= 2.345 × 10-7 M
(2) The concentration of H+ ion in lemon juice is 2.5 × 10-3 M. Calculate the OH– ion concentration and classify the solution as acidic, basic or neutral.
Solution :
Given : [H3O+] = 2.5 × 10-3 M, Kw = 1 × 10-4
[OH–] = ?
By ionic product of water,
[H3O+] × [OH–] = Kw
∴ [OH–] = \(\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\)
= \(\frac{1 \times 10^{-14}}{2.5 \times 10^{-3}}\)
Ans. Concentration of OH–
= [OH–] = 4 × 10-12 M
Hence the solution of lemon juice is acidic.
(3) Calculate pH and pOH of 0.02 M HCl solution.
Solution :
Given : C = 6.02 M HCl; pH = ? pOH = ?
\(\begin{aligned}
\mathrm{HCl}_{(\mathrm{aq})} \longrightarrow & \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-} \\
& 0.02 \mathrm{M}
\end{aligned}\)
[H+] = [H3O+] = 0.02 M
PH= -log10 [H3O+]
= -log10 0.02
= -(\(\overline{2} .3010\))
= 2 – 0.3010 = 1.699
pH + pOH = 14
∴ pOH = 14 – pH
= 14 – 1.699
= 12.3010
Ans. pH = 1.6990; pOH = 12.3010.
![]()
(4) The pH of a solution is 6.06. Calculate its [H3O+] ion concentration.
Solution :
Given : pH = 6.06, [H3O+] = ?
PH = -log10 [H3O+]
∴ log10 [H3O+] = -pH
∴ [H3O+] = Antilog – pH
= Antilog – 6.06
= Antilog \(\overline{7} .94\)
= 8.714 × 10-7 M
Ans. [H3O+] = 8.714 × 10-7 M.
(5) Calculate number H+ ions present in 1 mL of 0.01 M H2SO4 solution.
Solution :
Given : C = 0.01 M H2SO4; Y = 1 mL
Number of H+ ions = ?
\(\begin{aligned}
\mathrm{H}_{2} \mathrm{SO}_{4(\mathrm{aq})} \longrightarrow & 2 \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{SO}_{4(\mathrm{aq})}^{2-} \\
& 0.01 \times 2 \mathrm{M}
\end{aligned}\)
∵ 1000 mL solution contains 0.02 mol H+
∴ 1 mL solution contains \(\frac{0.02}{1000}\) mol
= 2 × 10-5 mol H+
∴ Number of H+ ions = 2 × 10-5 × 6.022 × 1023
= 1.204 × 1019
Ans. Number of H+ ions = 1.204 × 1019
(6) The pH of a 0.1 M monoacidic base is 11.11. What is the percent dissociation of base ?
Solution :
Given : pH = 11.11; per cent Dissociation of base = ?
c = 0.1 M
\(\begin{gathered}
\mathrm{BOH}_{(\mathrm{aq})} \rightleftharpoons \mathrm{B}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-} \\
c(l-\alpha) \quad c \alpha \quad c \alpha
\end{gathered}\)
pH + pOH = 14
∴ pOH = 14 – pH= 14 – 11.11 = 2.89
POH = -log10 [OH–]
∴ [OH–] = Antilog – pOH
= Antilog – 2.89
= Antilog \(\overline{3} .11\)
= 1.29 × 10-3 M
∵ [OH–] = cα
∴ α = \(\frac{\left[\mathrm{OH}^{-}\right]}{c}=\frac{1.29 \times 10^{-3}}{0.1}\) = 1.29 × 10-2
∴ Per cent dissociation = α × 100
= 1.29 × 10-2 × 100 = 1.29
Ans. Per cent dissociation = 1.29.
(7) Calculate the pH of dedmolar solution of sulphuric add aqueous solution. Assuming complete Ionization of sulphuric add.
Solution:
Given : Concentration of H2SO4 = decimolar
= 0.1 M
H2SO4 → 2H+ + \(\mathrm{SO}_{4}^{-2}\)
∴ [H+] = 2 × 0.1
= 0.2 M
PH = -log10 [H+]
= -log10 0.2 M
= \(-[\overline{1} .3010]\)
= 1 – 0.3010 = 0.6990
Ans. pH of H2SO4 solution = 0.6990.
(8) The pH of a 0.2 M solution of ammonia is 10.78. Calculate (i) OH– ions concentration (ii) the degree of dissociation (iii) the dissociation constant.
Solution :
Given: pH = 10.78, C = 0.02 M, [OH–] = ? Kb = ?
As NH3 is a base,
pOH = 14 – pH
pH = 10.78
∴ pOH = 14 – 10.78 = 3.22
pOH = -log10 [OH–]
∴ 3.22 = -log10 [OH–]
∴ -3.22 = log10 [OH–]
[OH–] = antilog (-3.22)
∴ [OH–] = antilog \((\overline{4} .78)\)
= 6.026 × 10-4 M
As NH4OH is a monoacidic base, [OH–]

(9) NH4OH is 4.3% ionised at 298 K in 0.01 M solution. Calculate the ionization constant and pH of NH4OH.
Solution :
Given : Per cent dissociation = 4.3,
C = 0.01 M, Kb = ?, pH = ?
The degree of dissociation and dissociation constant of NH4OH are related to each other by the formula :
Kb = α2C
Kb = Dissociation constant of NH4OH = ?
α = Degree of dissociation of NH4OH = 4.3%
= 4.3 × 10-2
C = Molar concentration of NH4OH = 0.01 M
∴ Kb = (4.3 × 10-2)2 × 0.01
= 18.49 × 10-4 × 10-2
∴ Kb = 1.849 × 10-5
Since NH4OH is a monoacidic base,
[OH–] = αC
= 4.3 × 10-2 × 0.01
= 4.3 × 10-4 mol dm-3
pOH = -log10 [OH-]
= -log10 4.3 × 10-4
= -[0.6335 – 4] = 3.3665
pH + pOH = 14
pH = 14 – 3.3665 = 10.6335
Ans. Kb = 1.849 × 10-5, pH = 10.6335
![]()
Question 28.
Define hydrolysis.
Answer:
Hydrolysis : A reaction in which the cations or anions or both the ions of a salt react with water to produce acidity or basicity or sometimes neutrality is called hydrolysis.
Question 29.
What are the types of the salts? Give examples.
Answer:
A salt is formed by the reaction between equivalent amounts of an acid and a base. According to the nature of an acid and a base, there are four types of the salts as follows :
(1) Salt of a strong acid and a strong base :
![]()
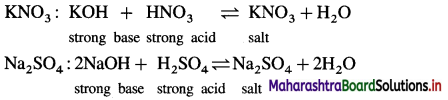
(2 ) Salt of a weak acid and a strong base :
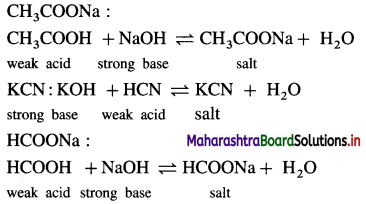
(3) Salt of a strong acid and a weak base :
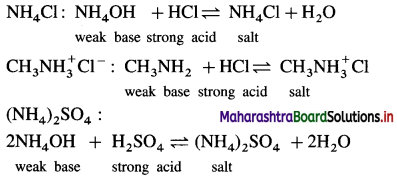
(4) Salt of a weak acid and a weak base : CH3COONH4 :
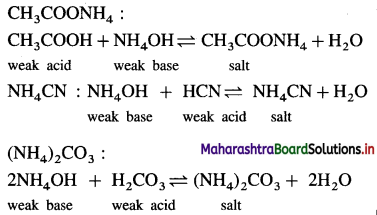
Question 30.
A salt of strong acid and strong base does not undergo hydrolysis. Explain.
OR
An aqueous solution of sodium chloride is neutral. Explain.
Answer:
(1) Sodium chloride is a salt of strong acid HCl and strong base NaOH.
(2) In water, it reacts forming HCl and NaOH.
(3) As both are strong, they dissociate almost completely to liberate H+ and OH– ions, respectively.
(4) H+ and OH– ions combine together to form weakly dissociating H2O. As there are no free H+ ions and OH– ions, the solution is neutral and the salt does not undergo hydrolysis.
NaCl + H2O ⇌ NaOH + HCl
Ionic equation :
Na+ + Cl– +H2O ⇌ Na+ + OH– + H+ + Cl–
H2O ⇌ H+ + OH–
Since the solution contains equal number of H+ and OH– ions, it is neutral.
Hence the salt of strong acid and strong base does not undergo hydrolysis.
Question 31.
Explain the hydrolysis of the salt of strong acid and weak base.
OR
A solution of CuSO4 reacts acidic. Explain.
Answer:
(1) Consider a salt of strong acid and weak base, like CuSO4 obtained from strong acid H2SO4 and weak base Cu(OH)2.
(2) When it is dissolved in water it undergoes hydrolysis as follows :
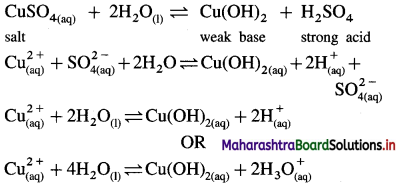
(3) Since [H3O+] > [OH–], the solution is acidic in nature.
Question 32.
Explain the hydrolysis of a salt of weak acid and strong base.
OR
A solution of sodium acetate, CH3COONa reacts basic explain.
Answer:
(1) Consider a salt of weak acid and strong base like CH3COONa. In aqueous solution it undergoes hydrolysis as follows :
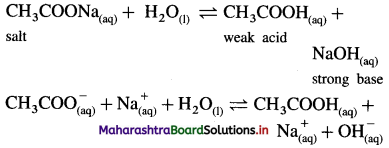
(2) Since the base NaOH is strong, it dissociates completely while acid CH3COOH being weak dissociates partially.
(3) Hence [OH–] > [H3O+] in the solution and the solution reacts basic.
![]()
Question 33.
Explain the hydrolysis of the salt of weak acid and weak base.
Answer:
(1) Consider a salt BA of weak acid (HA) and weak base (BOH).
(2) In aqueous solution it undergoes hydrolysis as follows :
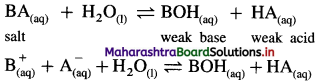
(3) The nature of the solution will depend upon relative strength of weak acid and weak base, hence will depend upon their dissociation constants Ka and Kb.
(i) A salt of weak acid and weak base for which Ka > Kb :
Consider hydrolysis of NH4F.
![]()
Since Ka (7.2 × 10-4) for HF is greater than Kb (1.8 × 10-5) for NH4OH, the acid dissociates partially more than the base, hence, [H3O+] > [OH–] and the solution reacts acidic after hydrolysis.
(ii) A salt of weak acid and weak base for which Ka < Kb :
Consider hydrolysis of NH4CN.
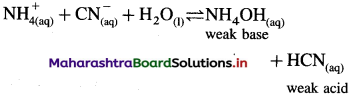
Since Ka (4 × 10-10) for HF is less than Kb (1.8 × 10-5) for NH4OH, the base dissociates more than acid and hence [H3O+] < [OH–] and the solution reacts basic after hydrolysis.
(iii) A salt of weak acid and weak base for which Ka = Kb:
Consider hydrolysis of CH3COONH4.
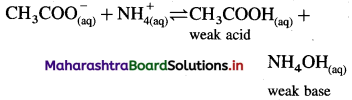
Since Ka = Kb, the weak acid CH3COOH and weak base NH4OH dissociate to the same extent, hence, [H3O+] = [OH–] and the solution reacts neutral after hydrolysis.
Question 34.
Define buffer solution.
OR
What is buffer solution?
Answer:
Buffer solution : It is defined as a solution which resists the change in pH even after the addition of a small amount of a strong acid or a strong base or on dilution or on addition of water.
Question 35.
What are the types of buffer solutions ?
Answer:
These are two types of buffer solutions :
(A) Acidic buffer solution : it is a solution containing a weak acid e.g. (CH3COOH) and its salt of a strong base. e.g. (CH3COONa).
pH of an acidic buffer is given by following Henderson Hasselbalch equation,
pH = \(\mathrm{p} K_{\mathrm{a}}+\log _{10} \frac{[\text { Salt }]}{[\text { Acid }]}\)
where pKa = -log10 Ka
and Ka is the dissociation constant of weak acid.
(B) Basic buffer solutions : It is a solution containing a weak base (e.g. NH4OH) and its salt of strong acid, (e.g. NH4Cl).
pOH of a basic buffer is given by Henderson Hassebalch equation,
pOH = \(\mathrm{p} K_{\mathrm{b}}+\log _{10} \frac{[\text { Salt }]}{[\text { Base }]}\)
where pKb = -log10 Kb
and Kb is the dissociation constant of a weak base.
Question 36.
Explain a buffer action of an acidic buffer.
Answer:
Mechanism of action of an acidic buffer :
(1) An acidic buffer is a mixture of a weak acid and its salt with a strong base. The weak acid dissociates feebly, but the salt dissociates almost completely. Moreover, due to the common ions, largely supplied by the salt, dissociation of the weak acid is further suppressed.
(CH3COOH + CH3COONa) :
CH3COONa(aq) → CH3COO(aq) + \(\mathrm{Na}_{(\mathrm{aq})}^{+}\) (Complete)
(2) When a small quantity of strong acid (H+) is added to this mixture, hydrogen ions combine with acetate ions to form undissociated acetic acid. Thus, addition of an acid does not change the pH of the buffer.
\(\mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{CH}_{3} \mathrm{COO}_{(\mathrm{aq})}^{-} \rightleftharpoons \mathrm{CH}_{3}-\mathrm{COOH}_{(\mathrm{aq})}\)
This removal of added H+ is called reserved basicity.
(3) When a small quantity of a strong base (OH–) is added, the hydroxide ions react with the acid producing the corresponding anions and water. Thus, the concentrations of H+ and OH– in the solution do not change and the pH remains constant.
\(\mathrm{CH}_{3} \mathrm{COOH}_{(\mathrm{aq})}+\mathrm{OH}_{(\mathrm{aq})}^{-} \rightleftharpoons \mathrm{CH}_{3} \mathrm{COO}_{(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
This removal of added OH– is called reserved acidity.
Question 37.
Explain a buffer action of a basic buffer.
Answer:
Mechanism of action of a basic buffer :
(1) A basic buffer solution is a solution containing a weak base and its salt with a strong acid. The weak base dissociates feebly, but the salt dissociates completely. Moreover, due to the presence of the common ion, largely supplied by the salt, the dissociation of the base is further suppressed. (NH4OH + NH4Cl) :
\(\mathrm{NH}_{4} \mathrm{Cl}_{(\mathrm{aq})} \rightarrow \mathrm{NH}_{4(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-}\) (Complete)
(2) When a small quantity of a strong acid is added to the solution, the hydrogen ions combine with the base producing corresponding cations and water. Thus, the addition of an acid does not change the pH of the buffer.
\(\mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{NH}_{4} \mathrm{OH}_{(\mathrm{aq})} \rightleftharpoons \mathrm{NH}_{4(\mathrm{aq})}^{+}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
This removal of added H+ is called reserved basicity.
(3) When a small quantity of a strong base is added, the hydroxide ions combine with \(\mathrm{NH}_{4}^{+}\) ions to form undissociated NH4OH. As a result, the hydrogen or hydroxyl ion concentration does not change. Thus, the pH of the solution does not change.
\(\mathrm{OH}_{(\mathrm{aq})}^{-}+\mathrm{NH}_{4}^{+} \rightleftharpoons \mathrm{NH}_{4} \mathrm{OH}_{(\mathrm{aq})}\)
This removal of added OH– is called reserved acidity.
![]()
Question 38.
What are properties of a buffer solution ?
OR
What are the advantages of a buffer solution ?
Answer:
Properties (or advantages) of a buffer solution :
- The pH of a buffer solution is maintained appreciably constant.
- By addition of a small amount of an acid or a base pH does not change.
- On dilution with water, pH of the solution doesn’t change.
Question 39.
What are the applications of a buffer solution ?
Answer:
Buffer solutions have many applications as follows :
(1) In a biochemical system : Blood in our body has pH 7.36 – 7.42 due to (\(\mathrm{HCO}_{3}^{-}+\mathrm{H}_{2} \mathrm{CO}_{3}\)) and little change of 0.2 pH unit may be fatal. For example, saline solution used in intravenous injection contains a buffer solution maintaining pH of the blood in the required range.
(2) Agriculture : The properties of soil depend upon its pH. The salts present in soil such as phosphates, carbonates, bicarbonates and organic acids impart definite pH to the soil. Depending on pH the fertilizers are selected.
(3) Industry : In many industries, buffer solutions are used to carry out chemical processes very effectively, such as the industries of paper, dye, paints, drugs, ink, etc.
(4) Medicines : Many medicines particularly in the liquid state have a good stability and optimum activity at a definite pH, for which buffer solutions are used. For example penciline preparations are carried out in the presence of a buffer of sodium citrate. A buffer solution of magnesium citrate is prepared by adding citric acid to Mg(OH)2.
(5) Analytical chemistry : In a qualitative analysis, the precipitation of groups, the chemical tests for detection of ions, etc. are carried out at a definite pH. For example, precipitation of cations of IIIA are carried in the presence of a basic buffer of pH 8 – 10 obtained by using NH4OH and NH4Cl.
Solved Examples 3.8
Question 40.
Solve the following :
(1) Calculate the pH of a buffer solution containing 0.1 M CH3COOH and 0.05 M CH3COONa. Dissociation constant of CH3COOH is 1.8 × 10-5 at 25 °C.
Solution :
Given : [CH3COOH] = 0.1 M,
[CH3COONa] = 0.05 M; Ka = 1.8 × 10-5; pH = ?
pKa = -log10 Ka
= -log10 1.8 × 10-5
= -(\(\overline{5} \cdot 2553\))
= 5 – 0.2553
= 4.7447
pH = \(\mathrm{p} K_{\mathrm{a}}+\log _{10} \frac{\left[\mathrm{CH}_{3} \mathrm{COONa}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}\)
= \(4.7447+\log _{10} \frac{0.05}{0.1}\)
= 4.7447 + \((\overline{1} .6990)\)
= 4.7447 + (-1 + 0.6990)
= 4.7447 – 0.3010
= 4.4437
Ans. pH = 4.4437
(2) A buffer solution contains 0.3 M NH4OH and 0.4 M NH4Cl. If Kb for NH4OH is 1.8 × 10-5, calculate pH of the solution.
Solution :
Given : [NH4OH] = 0.3 M; [NH4Cl] = 0.4 M
Kb =1.8 × 10-5; pH = ?
pKb = -log10 Kb
= -log10 1.8 × 10-5
= \(-(\overline{5} .2553)\)
= 4.7447
pOH = \(\mathrm{p} K_{\mathrm{b}}+\log _{10} \frac{[\text { Salt }]}{[\mathrm{Base}]}\)
= \(4.7447+\log _{10} \frac{0.4}{0.3}\)
= 4.7447 + log10 1.333
= 4.7447 + 0.1248
= 4.8695
∵ pH + pOH = 14
∴ pH = 14 – pOH
= 14 – 4.8695
= 9.1305
Ans. pH = 9.1305.
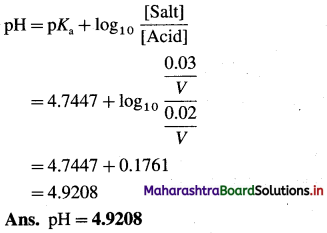
(3) 0.2 dm3 acidic buffer solution contains 1.18 g acetic acid and 2.46 g sodium acetate. If Ka for acetic acid is 1.8 × 10-5 at 25 °C, find pH of the solution.
Solution :

(4) A basic buffer solution contains 0.3 M NH4OH and 0.2 M (NH4)2SO4. If Kb for NH4OH at a certain temperature is 2 × 10-5, what is the pH of the solution ?
Solution :
Given : [NH4OH] = 0.3 M
[NH4+ ] = 2 × 0.2 = 0.4 M
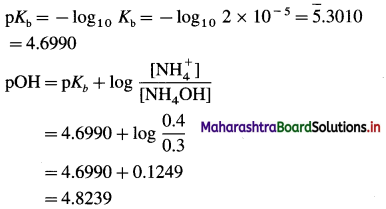
pH + pOH = 14
∴ pH = 14 – pOH = 14 – 4.8239 = 9.1761
Ans. pH = 9.1761
![]()
Question 41.
Define solubility. How is it expressed ?
Answer:
Solubility : It is defined as the maximum amount of a substance in moles, that can be dissolved at constant temperature to give one litre of its saturated solution.
It is expressed in moles per litre or moles per decimeter cube of a saturated solution at given temperature.

Question 42.
Derive a relationship between solubility and solubility product.
Answer:
Consider a saturated solution of a spraingly soluble electrolyte (or salt) AxBy at a given constant temperature. Let S mol dm-3 be the solubility of AxBy.
A following heterogeneous ionic equilibrium exists.

By a law of mass action, the equilibrium constant K will be represented as,
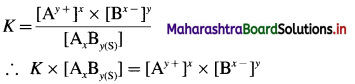
Since the active mass (concentration) of pure solid, AxBy(s) is treated as constant, [AxBy(s)] = K’
K × [AxBy(s)] = K × K’ = K(sp)
Therefore, Ksp = [Ay+]x × [Bx-]y
where Ksp is called solubility product of AxBy.
At equilibrium the concentrations are,
[Ay+] = xS mol dm-3
[Bx-]y = yS mol dm-3
∴ Ksp = [Ay+]x × [Bx-]y
= (xS)x × (yS)y
∴ Ksp = xx.yy.(S)x+y ……….(1)
Hence solubility S is given by,
S = \(\left(\frac{K_{(\mathrm{sp})}}{x^{x} \cdot y^{y}}\right)^{\frac{1}{x+y}} \mathrm{~mol} \mathrm{dm}^{-3}\) …………(2)
The above equations, (1) and (2) give the relationship between solubility and solubility product.
Here x and y represent number of cations and anions respectively from the electrolyte.
Question 43.
Write expression for solubility and solubility product of following sparingly soluble salts : (1) AgBr (2) PbI2 (3) Al(OH)3
Answer:
In general, for a sparingly soluble salt AxBy,
Ksp = xx.yy.(S)x+y
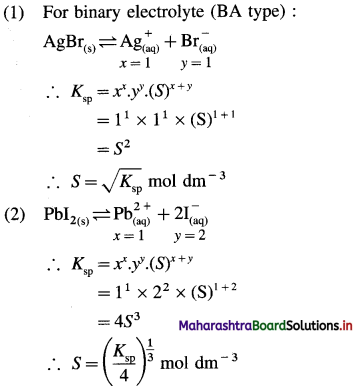
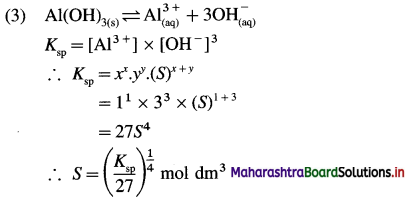
Question 44.
What is ionic product?
Answer:
Ionic product (IP) : It is defined as the product of concentrations in mol dm-3 of ions of an electrolyte in the solution and denoted by IP.
In a saturated solution,
IP = Ksp where Ksp is the solubility product of the electrolyte.
![]()
Solved Examples 3.9
Question 45.
Solve the following :
(1) The solubility of AgBr in water is 1.28 × 10-5 mol/dm3 at 298 K. Calculate the solubility product of AgBr at the same temperature.
Solution :
Given : S = 1.28 × 10-5 mol dm-3; Ksp = ?
AgBr dissociates as,
\(\mathrm{AgBr} \rightleftharpoons \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{Br}_{(\mathrm{aq})}^{-}\)
Ksp = [Ag+] [Br–]
As the solubility of AgBr in water is 1.28 × 10-5 moles/dm3,
[Ag+] = [Br–] = 1.28 × 10-5 mol dm3
∴ Ksp = [1.28 × 10-5] [1.28 × 10-5]
= 1.638 × 10-10
Ans. Solubility product of AgBr = 1.638 × 10-10.
(2) The solubility of lead sulphate is 3.03 × 10-5 kg/dm3. Calculate its solubility product. [Molecular mass of PbSO4 = 303]
Solution :
Given : S = 3.03 × 10-5 kg dm-3, Ksp = ?
Lead sulphate dissociates as
\(\begin{aligned}
&\mathrm{PbSO}_{4} \rightleftharpoons \mathrm{Pb}^{2+}+\mathrm{SO}_{4}^{2-} \\
&\text { (solid) } \quad \text { (aq) } \quad \text { (aq) }
\end{aligned}\)
Molecular weight of PbSO4 = 303
= 303 × 10-3 kg
The solubility of PbSO4 is 3.03 × 10-5 kg/dm3.
Solubility in mol dm-3
Weight of PbSO4 per dm3 Molecular weight 3.03 × 10-5

(3) The solubility product of AgBr is 3.3 × 10-12 at 298 K. What concentration of Br– ion is needed to precipitate AgBr from solution of 0.01 M Ag+?
Solution :
Given : Ksp = 3.3 × 10; [Ag+] = 1 × 10-2 M;
[Br–] = ?
AgBr dissociates as
\(\begin{aligned}
&\mathrm{AgBr} \rightleftharpoons \mathrm{Ag}^{+}+\mathrm{Br}^{-} \\
&\text {(solid) } \quad \text { (aq) } \quad \text { (aq) }
\end{aligned}\)
Ksp = [Ag+] [Br–]
Ksp = Solubility product = 3.3 × 10-12
[Ag+] = Concentration of Ag+
= 0.01 = 1.0 × 10-2 M
[Br–] = Concentration of Br– = ?
∴ 3.3 × 10-12 = 1.0 × 10-2 × [Br–]
∴ [Br–] = 3.3 × 10-10 mol/dm3
Ans. The concentration of Br– required for precipitation of AgBr should be greater than 3.3 × 10-10 mol/dm3.
(4) The solubility product of magnesium hydroxide is 1.4 × 10-11. Calculate the solubility of magnesium hydroxide.
Solution :
Given : Ksp =1.4 × 10-11; S = ?
Magnesium hydroxide dissociates as shown below :
Mg(OH)2 ⇌ Mg2+ + 2(OH)–
Ksp = [Mg2+] [OH–]2
Let the solubility of Mg(OH)2 be S mol dm-3.
∴ [Mg2+] = Concentration of Mg2+ ions
= S mol dm-3
∴ [OH–] = Concentration of OH– ions
= 2S mol dm-3
∴ Ksp = S × (25)2 = 4S3
Ksp = 1.4 × 10-11
∴ 1.4 × 10-11 =4S3
1.4 × 10-11 = 4S3.
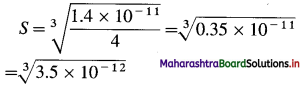
S = 1.518 × 10-4 mol dm-3
Ans. Solubility of Mg(OH)2
= 1.518 × 10-4 mol dm-3
![]()
(5) The solubility of silver chloride is 1.562 × 10-10 mol dm-3 at 298 K. Find its solubility in g dm-3 at the same temperature.
Solution :
Given :
Solubility of AgCl = S = 1.562 × 10-10 mol dm-3
Solubility of AgCl in g dm-3 = ?
Molar mass of AgCl = M = 143.5 g mol-1
Solubility in gram per dm3
= solubility in mol dm-3 × molar mass
= 1.562 × 10-10 × 143.5
= 2.241 × 10-5 g dm-3
Ans. Solubility of AgCl = 2.241 × 10-8 g dm-3
(6) The solubility of PbSO4 in water is 0.038 g dm-3 at room temperature. Calculate its solubility and solubility product at the same temperature. (Atomic weights : Pb = 207.3, S = 32, O = 16)
Solution :
Given : Solubility of PbSO4 = 0.038 g/dm-3
Molar mass of PbSO4 = 303.3 g mol-1
Solubility in mol dm-3 = ?
Ksp =?
Solubility in mol dm-3 = \(\frac{0.038}{303.3}\)
= 1.253 × 10-4 mol dm-3

Ans. S = 1.253 × 10-4 mol dm-3;
Ksp = 1.57 × 10-8
(7) The solubility product of PbS at 298 K is 4.2 × 10-28, The concentration of Pb++ ion is 0.001 M. Calculate S2- ion concentration at which PbS just gets precipitated.
Solution :
Given :
Solubility product of PbS = Ksp = 4.2 × 10-28
Concentration of Pb++ = [Pb++] = 0.001 M
Concentration of S– – = [S– –] = ?
For PbS,
\(\mathrm{PbS}_{(\mathrm{s})} \rightleftharpoons \mathrm{Pb}^{++}+\mathrm{S}^{–}\)
∴ Ksp = [Pb++] × [S– –]
∴ [S–] = \(\frac{K_{\mathrm{sp}}}{\left[\mathrm{Pb}^{++}\right]}\)
= \(\frac{4.2 \times 10^{-28}}{0.001}\)
= 4.2 × 10-25 M
To precipitate Pb++ as PbS, ionic product must be greater than 4.2 × 10-28.
Hence, [S– –] > 4.2 × 10-25 M.
Ans. Concentration of S– – required > 4.2 × 10-25 M
(8) At 298 K, the solubility of silver sulphate is 1.85 × 10-2 mol dm-3. Calculate the solubility product of silver sulphate.
Solution :
Given : Silver sulphate dissociates as follows :
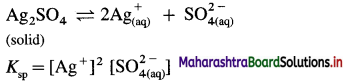
Solubility of Ag2SO4 = 1.85 × 10-2 mol dm-3
Ksp = Solubility product of Ag2SO4 = ?
[Ag+] = Concentration of Ag+ ion
= 2 × 1.85 × 10-2 = 3.70 × 10-2 mol dm-3
[latex]\mathrm{SO}_{4}^{2-}[/latex] = Concentration of \(\mathrm{SO}_{4}^{2-}\)
= 1.85 × 10-2 mol dm-3
∴ Ksp = (3.70 × 10-2)2 × (1.85 × 10-2)
= 13.69 × 10-4 × 1.85 × 10-2
= 25.33 × 10-6
= 2.533 × 10-5
Ans. Solubility product of Ag2SO4
= 2.533 × 10-5
Question 46.
What is common ion?
Answer:
Common ion : An ion common to two electrolytes is called common ion. This is generally applicable to a mixture of a strong and a weak electrolyte. For example, a solution containing weak electrolyte CH3COOH and strong electrolyte salt CH3COONa.
CH3COONa → CH3COO– + Na+;
CH3COOH ⇌ CH3COO– + H+
Hence CH3COOH and CH3COONa have a common ion CH3COO–.
Question 47.
Define the term common ion effect.
Answer:
Common ion effect : The suppression of the degree of dissociation of a weak electrolyte by the addition of a strong electrolyte having an ion in common with the weak electrolyte is called common ion effect. For example, CH3COOH and CH3COONa have common ion CH3COO–.
![]()
Question 48.
Explain common ion effect with suitable example.
Answer:
A weak electrolyte dissociates partially in aqueous solution to produce cations and anions. Equilibrium exists between ions thus formed and the undissociated molecules.
BA ⇌ B+ +A–
For such an equilibrium, the dissociation constant K is defined as
K = \(\frac{\left[\mathrm{B}^{+}\right] \times\left[\mathrm{A}^{-}\right]}{[\mathrm{BA}]}\)
K is constant for the weak electrolyte at a given temperature.
Now, if another electrolyte BC or DA is added to the solution BA, having a common ion either B+ or A–, then the concentration of either B+ or A– is increased. However, as K is always constant, the increase in the concentration of any one of the ions shifts the equilibrium to left. In other words, the dissociation of BA is suppressed. This is called common ion effect. For example, the dissociation of a weak acid CH3COOH is suppressed by adding CH3COONa having common ion CH3COO–.
CH3COOH ⇌ CH3COO– + H+
CH3COONa → CH3COO– + Na+
Question 49.
Explain the common ion effect on dissociation of a weak acid.
Answer:
(1) Consider the dissociation or ionisation of a weak acid, CH3COOH in its solution.
\(\mathrm{CH}_{3} \mathrm{COOH}_{(\mathrm{aq})} \rightleftharpoons \mathrm{CH}_{3} \mathrm{COO}_{(\mathrm{aq})}^{-}+\mathrm{H}_{(\mathrm{aq})}^{+}\)
The dissociation constant Ka for CH3COOH will be,
Ka = \(\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right] \times\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}\)
Ka is constant for CH3COOH at constant temperature.
(2) If a strong electrolyte like salt CH3COONa is added to the solution of CH3COOH, then on dissociation it gives a common ion CH3COO–.
CH3COONa → CH3COO– + Na+
(3) Due to common ion CH3COO–, overall concentration of CH3COO– in the solution is increased, which increases the ratio,
\(\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right] \times\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}\). In order to keep this ratio constant, the concentration of H+ is decreased, by shifting the equilibrium to the left hand side according to Le Chatelier’s principle.
(4) Thus the ionisation of a weak acid is suppressed by a common ion.
Question 50.
Explain the effect of common ion on the dissociation of weak base.
Answer:
(1) Consider the dissociation or ionisation of a weak base, NH4OH in its dilute solution. \(\mathrm{NH}_{4} \mathrm{OH}_{(\mathrm{aq})} \rightleftharpoons \mathrm{NH}_{4(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-}\)
The dissociation constant Kb for NH4OH will be,
\(K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right] \times\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{4} \mathrm{OH}\right]}\)
(2) If a strong electrolyte like salt NH4Cl is added to the solution of NH4OH, then it gives common ion \(\mathrm{NH}_{4}^{+}\).
NH4Cl → \(\mathrm{NH}_{4}^{+}\) + Cl–
(3) Due to common ion \(\mathrm{NH}_{4}^{+}\), overall concentration of \(\mathrm{NH}_{4}^{+}\) is increased, which increases the ratio \(\left[\mathrm{NH}_{4}^{+}\right]\) × [OH–]/[NH4OH],
In order to keep this ratio constant, the equilibrium is shifted to the left hand side which satisfies Le Chatelier’s principle.
(4) Thus the ionisation of a weak base is suppressed by a common ion.
Multiple Choice Questions
Question 51.
Select and write the most appropriate answer from the given alternatives for each subquestion :
1. According to Lowry-Bronsted concept, base is a substance which acts as –
(a) a proton donor
(b) an electron donor
(c) a proton acceptor
(d) an electron acceptor
Answer:
(c) a proton acceptor
2. BF3 is a
(a) Lewis acid
(b) Lewis base
(c) amphoteric compound
(d) Electrolyte only
Answer:
(a) Lewis acid
![]()
3. Which of the following is a conjugate acid-base pair ?
(a) HCl, NaOH
(b) KCN, HCN
(c) NH4Cl, NH4OH
(d) H2SO4, \(\mathrm{HSO}_{4}^{-}\)
Answer:
(d) H2SO4, \(\mathrm{HSO}_{4}^{-}\)
4. The conjugate acid of \(\mathrm{NH}_{2}^{-}\) is
(a) NH3
(b) NH2OH
(c) \(\mathrm{NH}_{4}^{+}\)
(d) N2H4
Answer:
(a) NH3
5. Which of the following molecules is not a Lewis base?
(a) H2O
(b) BF3
(c) NH3
(d) CO
Answer:
(b) BF3
6. In the following reaction
\(\mathrm{HC}_{2} \mathrm{O}_{4(\mathrm{aq})}^{-}+\mathrm{PO}_{4}^{3-} \rightleftharpoons \mathrm{HPO}_{4}^{2-}+\mathrm{C}_{2} \mathrm{CO}_{4}^{2-}\) Which of two are Lowry-Bronsted bases ?
(a) \(\mathrm{HC}_{2} \mathrm{C}_{4}^{-} \text {and } \mathrm{PO}_{4}^{3-}\)
(b) \(\mathrm{HPO}_{4}^{2-} \text { and } \mathrm{C}_{2} \mathrm{O}_{4}^{2-}\)
(c) \(\mathrm{HC}_{2} \mathrm{O}_{4}^{-} \text {and } \mathrm{HPO}_{4}^{2-}\)
(d) \(\mathrm{PO}_{4}^{3-} \text { and } \mathrm{C}_{2} \mathrm{O}_{4}^{2-}\)
Answer:
(d) \(\mathrm{PO}_{4}^{3-} \text { and } \mathrm{C}_{2} \mathrm{O}_{4}^{2-}\)
7. According to the Arrhenius theory,
(a) an acid is a proton donor
(b) an acid is an electron pair acceptor
(c) a hydrogen ion exists freely in an aqueous solution
(d) a hydrogen ion is always hydrated to form a hydrogen ion
Answer:
(c) a hydrogen ion exists freely in an aqueous solution
8. The species which will behave both as a conjugate acid and base is
(a) NH4OH
(b) \(\mathrm{CO}_{3}^{–}\)
(c) \(\mathrm{HSO}_{4}^{-}\)
(d) H2SO4
Answer:
(c) \(\mathrm{HSO}_{4}^{-}\)
![]()
9. According to the Lewis theory, an acid is
(a) nucleophile
(b) an electrophile
(c) a proton acceptor
(d) an electron donor
Answer:
(b) an electrophile
10. If a 0.1 M solution of HCN is 0.01% dissociated, the dissociation constant for HCN is,
(a) 10-3
(b) 10+3
(c) 10-7
(d) 10-9
Answer:
(d) 10-9
11. The pH of decimolar solution KOH is
(a) 1
(b) 4
(c) 10
(d) 13
Answer:
(d) 13
12. Ostwald’s dilution law is applicable in case of dilute solution of
(a) HCl
(b) H2SO4
(c) NaOH
(d) CH3COOH
Answer:
(d) CH3COOH
13. The degree of dissociation of a 0.1 M monobasic acid is 0.4%. Its dissociation constant is
(a) 0.4 × 10-4
(b) 4.0 × 10-4
(c) 1.6 × 10-6
(d) 0.8 × 10-5
Answer:
(c) 1.6 × 10-6
14. The ionic product of water will increase, if
(a) Pressure is decreased
(b) H+ ions are added
(c) OH– ions are added
(d) Temperature is increased
Answer:
(d) Temperature is increased
15. The [OH–] for a weak base of dissociation constant Kb and concentration C is nearly equal to
(a) \(\sqrt{\frac{K_{\mathrm{b}}}{C}}\)
(b) KbC
(c) \(\sqrt{K_{\mathrm{b}} C}\)
(d) \(\frac{C}{K_{\mathrm{b}}}\)
Answer:
(c) \(\sqrt{K_{\mathrm{b}} C}\)
![]()
16. The [H+] for a weak acid of dissociation constant Ka and concentration C is nearly equal to
(a) \(\sqrt{\frac{K_{\mathrm{a}}}{C}}\)
(b) \(\sqrt{K_{\mathrm{a}} C}\)
(c) \(\frac{K_{\mathrm{a}}}{\sqrt{c}}\)
(d) \(\frac{c}{K_{\mathrm{a}}}\)
Answer:
(b) \(\sqrt{K_{\mathrm{a}} C}\)
17. Which of the following solution with same concentration will have highest pH
(a) Al(OH)3
(b) K2CO3
(c) NH4OH
(d) NaOH
Answer:
(d) NaOH
18. 10 ml of 0.1 M H2SO4 is mixed with 20 ml of 0.1 M KOH, the pH of resulting solution will be
(a) 0
(b) 7
(c) 2
(d) 9
Answer:
(b) 7
19. The gastric juice in our stomach contains enough hydrochloric acid to make the hydrogen ion concentration 0.01 mol/dm3. The pH of gastric juice is-
(a) 0.01
(b) 1
(c) 2
(d) 14
Answer:
(c) 2
20. If the hydrogen ion concentration of an acid is decreased ten times, its pH will be
(a) increased by one
(b) decreased by one
(c) remains unchanged
(d) increase by 10
Answer:
(a) increased by one
21. Which of the following metal sulphide is precipitated in an acidic medium ?
(a) NiS
(b) CoS
(c) CuS
(d) MnS
Answer:
(c) CuS
22. The relationship between the solubility and solubility product for silver carbonate is
(a) Ksp = s2
(b) \(\sqrt{K_{\mathrm{sp}}}\) = 4s2
(c) Ksp = 27S4
(d) Ksp = 4s3
Answer:
(d) Ksp = 4s3
23. If ‘S’ is solubility in mol dm-3 and Ksp is solubility product of BA2 type of salt, then relation between them is
(a) S = \(\sqrt{K_{\mathrm{sp}}}\)
(b) Ksp = 4S3
(c) Ksp = S3
(d) S = Ksp
Answer:
(b) Ksp = 4S3
![]()
24. The addition of solid sodium carbonate to pure water results in
(a) an increase in H+ ion concentration
(b) an increase in pH
(c) no change in pH
(d) a decrease in OH– concentration
Answer:
(b) an increase in pH
25. Which of the following salt, when dissolved in water will hydrolyse ?
(a) NaCl
(b) NH4Cl
(c) KCl
(d) Na2SO4
Answer:
(b) NH4Cl
26. A solution of blue vitriol is acidic in nature because
(a) CuSO4 reacts with water
(b) Cu2+ ions reacts with water
(c) SO42- ions reacts with water
(d) CuSO4 removes OH– ions from water
Answer:
(a) CuSO4 reacts with water
27. What is the nature of the solution of salt FeCl3 ?
(a) Acidic
(b) Basic
(c) Neutral
(d) Amphoteric
Answer:
(a) Acidic
28. Which of the following salts does not hydrolyse in water ?
(a) Sodium acetate
(b) Sodium carbonate
(c) Sodium nitrate
(d) Sodium cyanide
Answer:
(c) Sodium nitrate
29. An aqueous solution of magnesium chloride changes blue litmus red due to
(a) the formation of Cl– ions
(b) the formation Mg2+ ions
(c) reaction of Cl– ions with water
(d) hydrolysis of the salt
Answer:
(d) hydrolysis of the salt
30. An aqueous solution of which of the following salts is basic ?
(a) CH3COONa
(b) NH4Cl
(c) KNO3
(d) CuSO4
Answer:
(a) CH3COONa
31. The number of moles of hydroxide ions (OH–) produced from 2 moles of Na2CO3 is
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
![]()
32. The POH value for solution is 4, its hydrogen ion concentration will be
(a) 10-4
(b) 10-10
(c) 1010
(d) 104
Answer:
(b) 10-10
33. If an acid is diluted
(a) pH increases
(b) pH decreases
(c) no change occurs
(d) can vary depending on an acid
Answer:
(a) pH increases
34. pH of a solution is 13. H+ ions present in 1 cm3 of the solution is
(a) 6.023 × 1010
(b) 6.023 × 107
(c) 6.023 × 10-10
(d) 6.023 × 10-7
Answer:
(b) 6.023 × 107
35. pH of blood is maintained constant by mechanism of
(a) common ion effect
(b) buffer
(c) solubility
(d) all of these
Answer:
(b) buffer
36. The pH of 0.05 M solution of dibasic acid is
(a) +1
(b) -1
(c) +2
(d) -2
Answer:
(a) +1
37. The pH of a 0.63% nitric acid solution is (Equivalent weight of nitric acid is 63)
(a) 6
(b) 7
(c) 1
(d) 9
Answer:
(c) 1
38. 100 ml of 0.01 M solution of NaOH is diluted to 1 dm3. What is the pH of the dilute solution?
(a) 12
(b) 11
(c) 2
(d) 3
Answer:
(b) 11
39. If the H+ ion concentration in a solution is 0.01 M, the pOH of the solution is
(a) 12
(b) 10-10
(c) 2
(d) 14
Answer:
(a) 12
![]()
40. If the pH value of a solution is zero, the solution is
(a) a strong acid
(b) a very weak acid
(c) neutral
(d) a base
Answer:
(a) a strong acid
41. The pH of a solution is 5, when the hydroxyl ion concentration is
(a) 10-5 mol/dm3
(b) 10-7 mol/dm3
(c) 10-9 mol/dm3
(d) 10-14 mol/dm3
Answer:
(c) 10-9 mol/dm3
42. The pH of human blood in a normal person is approximately
(a) 4.7
(b) 6.04
(c) 7.40
(d) 8.74
Answer:
(c) 7.40
43. If molarity of NaOH is 3.162 × 10-3 M, its pH is
(a) 8.5
(b) 9.5
(c) 10.5
(d) 11.5
Answer:
(d) 11.5
44. The common ion effect is based on
(a) Sorensen’s principle
(b) Le Chatelier’s principle
(c) Heisenberg’s principle
(d) Freundlich’s principle
Answer:
(b) Le Chatelier’s principle
45. The ion that cannot be precipitated by both HCl and H2S is
(a) Pb2+
(b) Cu2+
(c) Ag+
(d) Ca2+
Answer:
(d) Ca2+
46. The correct representation for solubility product of SnS2 is
(a) [Sn4+] [S2-]2
(b) [Sn4+] [S2-]
(c) [Sn4+] [2S2-]
(d) [Sn4+] [2S2-]
Answer:
(a) [Sn4+] [S2-]2
![]()
47. The solubility product of a salt BA at room temperature is 1.21 × 10-6. Its molar solubility is
(a) 1.21 × 10-3 M
(b) 1.1 × 10-4 M
(c) 1.1 × 10-3 M
(d) 1.21 × 10-2 M
Answer:
(c) 1.1 × 10-3 M
48. Among the following hydroxides, the one which has the lowest value of solubility product at temperature 298 K is,
(a) Mg(OH)2
(b) Ca(OH)2
(c) Ba(OH)2
(d) Be(OH)2
Answer:
(d) Be(OH)2
49. A solution becomes unsaturated when
(a) ionic product = solubility product
(b) ionic product < solubility product
(c) ionic product > solubility product
(d) ionic product ≥ solubility product
Answer:
(b) ionic product < solubility product
50. The solubility product of Fe(OH)3 is
(a) [latex]\mathrm{F}_{\mathrm{e}}^{2+}[/latex] [OH–]3
(b) [latex]\mathrm{F}_{\mathrm{e}}^{3+}[/latex] [OH–]2
(c) [latex]\mathrm{F}_{\mathrm{e}}^{3+}[/latex] [OH–]3
(d) [latex]\mathrm{F}_{\mathrm{e}}^{3+}[/latex]3 [OH–]3
Answer:
(c) [latex]\mathrm{F}_{\mathrm{e}}^{3+}[/latex] [OH–]3
51. The solubility product of PbS in 4.2 × 10-28 at 300 K. The sulphide ions concentration required to precipitate PbS from a solution containing 0.001 M of lead ion is
(a) ≥ 2.1 × 10-14 mol/dm3
(b) ≥ 4.2 × 10-14 mol/dm3
(c) ≥ 4.2 × 10-25 mol/dm3
(d) ≤ 4.2 × 10-28 mol/dm3
Answer:
(c) ≥ 4.2 × 10-25 mol/dm3
52. 0.025 M CH3COOH is dissociated 9.5%. Hence the pH of the solution is
(a) 2.6244
(b) 3.128
(c) 2.988
(d) 2.267
Answer:
(a) 2.6244
53. 0.1 M HCN is dissociated 0.01%. The dissociation constant of HCN is
(a) 1.1 × 10-6
(b) 1 × 10-8
(c) 1 × 10-9
(d) 1 × 10-7
Answer:
(c) 1 × 10-9
![]()
54. The solubility of product of a sparingly soluble salt AB2 is 3.2 × 10-11. If solubility in mol dm-3 is
(a) 4 × 10-4
(b) 3.2 × 10-4
(c) 1 × 10-5
(d) 2 × 10-4
Answer:
(d) 2 × 10-4