Maharashtra Board Class 12 Chemistry Important Questions Chapter 2 Solutions

Balbharti Maharashtra State Board 12th Chemistry Important Questions Chapter 2 Solutions Important Questions and Answers.

Maharashtra State Board 12th Chemistry Important Questions Chapter 2 Solutions

Question 1.
What is solution?
Answer:
The solution is a homogeneous mixture of two or more components or pure substances. When the size of particles of the components is of the order of 10^-10 m, then the solution is called a true solution. E.g. An aqueous solution of sugar.

Question 2.
Explain : (1) Homogeneous solution
(2) Heterogeneous solution.
Answer:
(1) Homogeneous solution : A solution in which solute and solvent form uniform homogeneous one phase due to attraction between their molecules/particles is called homogeneous solution.
E.g. A solution of NaCl or sugar.

(2) Heterogeneous solution : A solution consisting of two or more phases is called a heterogeneous solution. E.g. A colloidal solution of starch.

Question 3.
Define : (1) Solvent (2) Solute.
Answer:
(1) Solvent : The component in which solution formation takes place and which constitutes larger proportion of a solution is called solvent. For example, in an aqueous solution of sugar, water is the solvent.

(2) Solute : In a solution the component which dissolves and constitutes smaller proportion of a solution is called a solute. For example, in a sugar solution, sugar is the solute.

Question 4.
What are the different types of solutions?
Answer:
A solution consists of a solvent and a solute. Since the physical states of a solvent and a solute may be gaseous, liquid or a solid, there are nine types of solutions.

Question 5.
Mention the solvent and solute in the following :
(1) Smoke
(2) Moisture
(3) Alloy
(4) Soda water.
Answer:

Substance	Solvent	Solute
1. Smoke	Gas	Solid
2. Moisture	Gas	Liquid
3. Alloy	Solid	Solid
4. Soda water	Liquid	Gas

Question 6.
What is a saturated solution?
Answer:
A solution which contains the maximum amount of dissolved solute and further the solute can’t be dissolved is called a saturated solution.

There exists a dynamic equilibrium which is represented as,

Question 7.
What is a supersaturated solution?
Answer:
A solution containing a solute more than that required to form a saturated solution at equilibrium is called a supersaturated solution.

When a tiny crystal of a solute is added to supersaturated solution, the excess solute separates out and forms saturated solution.

Question 8.
What is solubility of a solute ?
Answer:
Solubility : It is defined as amount of a solute present per unit volume in its saturated solution at a specific temperature.
It is expressed in mol L^-1 or mol dm^-3.

Question 9.
Explain the factors on which the solubility of a substance (solute) depends.
Answer:
The extent of dissolution of a substance (solute) depends upon the following factors :
(1) Nature of a solute : A solute may be crystalline, amorphous, ionic or covalent. Hence accordingly its tendency to dissolve changes. The substances having similar intermolecular forces tend to dissolve in each other.

(2) Nature of solvents : Solvents are classified as polar and nonpolar. Polar solutes dissolve in polar solvents. For example, ionic compounds dissolve in polar solvent like water. A solvent other than water is called a nonaqueous solvent. For example, C₆H₆, CCl₄, etc. Solutions in these solvents are called nonaqueous solutions.
The solvent may be a gas, a liquid or a solid.

(3) Amount of a solvent : More amount of a solvent, will dissolve more quantity of the solute.

(4) Temperature : Depending on the nature of a solvent and a solute the solubility changes with termperature. The effect depends on the heat of solution, hydration energy, etc. Generally as the temperature increases, solubility of solid increases and that of gases decreases.

(5) Pressure :

• Pressure has no effect on the solubilities of solids and liquids since they are incompressible.
• The effect of pressure is important only for solutions which involve gases as solutes. With the increase in pressure and decrease in temperature, the solubility of gases increases.

Question 10.
Explain with the help of Le Chatelier’s principle the effect of temperature on solubility.
Answer:

1. The effect of temperature on solubility depends on enthalpy of solution.
2. For example, dissolution of KCl in water is an endothermic process since heat is absorbed during dissolution. In according to Le Chatelier’s principle by increasing temperature the solubility of KCl increases.
3. Dissolution of CaCl₂, Li₂SO₄, H₂O in water is an exothermic process since heat is evolved during dissolution. In this, according to Le Chatelier’s principle by increasing the temperature the solubility decreases.

Question 11.
Explain the solubility of gases in liquids.
Answer:

• Gases are soluble in water and other liquids and their solubility depends upon the nature of the gas.
• Non-polar gases like O₂, have less solubility in polar solvents.
• Polar gases like CO₂, NH₃, HCl, etc. are more soluble in polar solvent like water. CO₂ forms H₂CO₃, while NH₃ forms NH₄OH in aqueous solutions.
• The solubility of gases in liquids increases with the increase in pressure and the decrease in temperature.

Question 12.
Why does the solubility of a gas decrease with increase in temperature ?
OR
How does solubility of a gas in water varies with temperature ?
Answer:

• The gases are soluble in water and other liquids.
• According to Charles’ law, the volume of a given mass of a gas increases with the increase in temperature at constant pressure.
• Hence, the volume of the dissolved gas increases with the increase in temperature.
• This enormous increase in volume of the gases cannot be accommodated by the solvent molecules, hence excess of the gases escape out in the form of bubbles.

Therefore, the solubility of gases in liquids decreases with temperature.

Question 13.
Explain the effect of pressure on the solubility of the gases.
OR
State and explain Henry’s law.
Answer:
(1) Since the gases are compressible, their solubility in the liquids is influenced by external pressure of the gas. The solubility of gases increases with the increase in pressure.

(2) Henry’s law : It states that the solubility of a gas. in a liquid at constant temperature is proportional to the pressure of the gas above the solution.
(i) If S is the solubility of a gas in mol dm^-3 at a pressure P and constant temperature then by Henry’s law,
S ∝ P or S = K_H × P
where K_H is called Henry’s law constant.
(ii) If P = 1 atm, then S = K_H.
(iii) If several gases are present, then the solubility of any gas in the mixture is proportional to its partial pressure at given temperature.

(3) Illustration of Henry’s law : In case of aerated or carbonated drink beverage, the bottle is filled by dissolving CO₂ gas at high pressure and then sealed.
Above the liquid surface there is air and undissolved CO₂. Due to high pressure, the amount of dissolved CO₂ is large.

When the cap of the aerated bottle is removed, the pressure on the solution is lowered, hence excess of CO₂ and air escape out in the form of effervescence. Thus by decreasing the pressure, solubility of CO₂ is decreased.

Question 14.
What are the exceptions to Henry’s law? Why ?
Answer:
(1) The gases like NH₃ and CO₂ do not obey Henry’s law.
(2) This is because, these gases react with water,
\(\mathrm{NH}_{3(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \longrightarrow \mathrm{NH}_{4 \text { (aq) }}^{+}+\mathrm{OH}_{(\text {aq })}^{-}\)
CO_2(g) + H₂O(l) → H₂CO_3(aq)
(3) Due to reactions of the gases like NH₃, CO_2(g), they have higher solubilities than expected by Henry’s law.

Question 15.
Oxygen gas is slightly soluble in water but it is highly soluble in blood. Explain.
Answer:
The vital constituent of blood, namely haemoglobin reacts with oxygen increasing the solubility of oxygen.
Haemoglobin + 4O_2(g) → Haemoglobin O₈
This oxygenated blood is circulated to the various parts of body, for the supply of oxygen.

Question 16.
Obtain the units of Henry’s law constant.
Answer:
By Henry’s law, S = K_H × P, where S is solubility of the gas in mol dm^-3, P is the pressure of the gas in atmosphere (or in bar) and K_H is Henry’s law constant.
∴ K_H = \(\frac{S^{\left(\mathrm{mol} \mathrm{dm}^{-3}\right)}}{P_{(\mathrm{atm})}}\) mol dm^-3 atm^-1 or mol dm^-3 bar^-1
Hence the units of Henry’s law constant K_H are mol dm^-3atm^-1.

Solved Examples 2.4

Question 17.
Solve the following :
(1) For a gas, the Henry’s law constant is 1.25 × 10^-3 mol dm^-3 atm^-1 at 25 °C. Calculate the solubility of the given gas at 2.5 atm and 25 °C.
Solution :
Given : Henry’s law constant = K_H
= 1.25 × 10^-3 mol dm^-3 atm^-1
Pressure of the gas = P = 2.5 atm
Solubility of the gas = S = ?
By Henry’s law
S = K_H × P
= 1.25 × 10^-3 mol dm^-3 atm^-1 × 2.5 atm
= 3.125 × 10^-3 mol dm^-3
Ans. Solubility of gas = 3.125 × 10^-3 mol dm^-3

(2) The solubility of dissolved oxygen to 27 °C is 2.6 × 10^-3 mol dm^-3 at 2 atm. Find its solubility at 8.4 atm and 27 °C.
Solution :
Given : Solubility of O₂
= S₁ = 2.6 × 10^-3 mol dm^-3
Initial pressure of O₂ = P₁ = 2 atm
Final pressure of O₂ = P₂ = 8.4 atm
Solubility of O₂ = S₂ = ?
(i) By Henry’s law,
S₁ = K_H × P₁
∴ Henry’s law constant K_H is,
K_H = \(\frac{S_{1}}{P_{1}}=\frac{2.6 \times 10^{-3}}{2}\)
= 1.3 × 10^-3 mol dm^-3 atm^-1
(ii) Now, S₂ = K_H × P₂ = 1.3 × 10^-3 × 8.4
= 10.92 × 10^-3
= 1.092 × 10^-2 mol dm^-3
Ans. Solubility of O₂ = 1.092 × 10^-2 mol dm^-3

(3) Henry’s law constant for the solubility of methane in benzene is 4.27 × 10^-5 mm^-1 Hg mold dm^-3 at constant temperature. Calculate the solubility of methane at 760 mm Hg pressure at same temperature.
Solution :
Given : Henry’s law constant = K_H
= 4.27 × 10^-5mm^-1 Hg mol dm^-3
Pressure of the gas = P = 760 mm Hg
K_H = 4.27 × 10^-5 mm^-1 mol dm^-3
= 4.27 × 10^-5 × 760 atm^-1 mol dm^-3
= 3245 × 10^-5 atm^-1 mol dm^-3
= 3.245 × 10^-2 atm^-1 mol dm^-3
P = 760 mm = \(\frac{760}{760}\) atm = 1 atm
By Henry’s law,
S = K_H × P = 3.245 × 10^-2 atm^-1 mol dm^-3 × 1 atm
= 3.245 × 10^-2 mol dm^-3
Ans. Solubility of methane = 3.245 × 10^-2 mol dm^-3

(4) The solubility of ethane at 25 °C is 0.92 × 10^-3 g dm^-3 at 1000 mm Hg pressure. Calculate Henry’s law constant.
Solution :
Given : Solubility of ethane
= S = 0.92 × 10^-5 g dm^-3
Pressure of ethane = P = 1000 mm Hg
Molar mass of ethane (C₂H₆) = 30 g mol^-1
Henry’s law constant = K_H = ?
S = 0.92 × 10^-3 g dm^-3
= \(\frac{0.92}{30}\) × 10^-3
= 3.067 × 10^-5 mol dm^-3
P = 1000 mm = \(\frac{1000}{760}\)atm = 1.316 atm
By Henry’s law,
S = K_H × P
∴ K_H = \(\frac{S}{P}=\frac{3.067 \times 10^{-5}}{1.316}\)
= 2.33 × 10^-5 mol dm^-3 atm^-1
Ans. Henry’s law constant = K_H
= 2.33 × 10^-5 mol dm^-3 atm^-1

(5) The solubility of nitrogen at 30 °C is 2.5 × 10^-3 g dm^-3 at 760 mm pressure. What will be its solubility in mol dm^-3 at 20,000 mm and same temperature?
Solution :
Given : Initial solubility of N₂ = S₁ =2.5 × 10^-3 g dm^-3
Initial pressure = P₁ = 760 mm
Final pressure = P₂ = 20,000 mm
Final solubility = S₂ in mol dm^-3 = ?
Molar mass of N₂ gas = 28 g mol^-1
S₁ = 2.33 × 10^-5 mol dm^-3
= \(\frac{2.5 \times 10^{-3}}{28}\) mol dm^-3
= 8.93 × 10^-5 mol dm^-3
P₁ = \(\frac{760}{760}\) = 1 atm
P₂ = \(\frac{20,000}{760}\) = 26.32 atm
By Henry’s law,
S₁ = K_H × P₁
∴ K_H = \(\frac{S_{1}}{P_{1}}=\frac{8.93 \times 10^{-5}}{1}\)
= 8.93 × 10^-5 mol dm^-3 atm^-1
S₂ = K_H × P₂ = 8.93 × 10^-5 × 26.32
= 2.35 × 10^-3 mol dm^-3
Ans. Solubility of N₂ gas
= 2.35 × 10^-3 mol dm^-3.

[Alternative method:
S₁ = K_HP₁ and S₂ = K_HP₂
∴ \(\frac{S_{2}}{S_{1}}=\frac{K_{\mathrm{H}} P_{2}}{K_{\mathrm{H}} P_{1}}=\frac{P_{2}}{P_{1}}\)
∴ S₂ = S₁ × \(\frac{P_{2}}{P_{1}}\) = 8.93 × 10^-5 × \(\frac{20,000}{760}\)
= 2.35 × 10^-3 mol dm^-3]

Question 18.
Marine life like fish prefers to stay at lower level in water. Explain.
OR
Explain, why do aquatic animals prefer to stay at lower level of water during summer?
Answer:

1. The solubility of oxygen gas decreases with the increase in temperature.
2. In sea or lake water, the temperature of upper level is higher than the lower level.
3. Therefore the dissolved oxygen content in water is more at lower level than at higher level required for the marine life.

Hence marine life like fish prefers to stay at lower level than upper level of water.

Question 19.
State and explain Raoult’s law.
Answer:
Statement of Raoult’s law : The law states that, at constant temperature, the partial vapour pressure of any volatile component of a solution is equal to the product of vapour pressure of the pure component and the mole fraction of that component in the solution.

Let P₀ and P be the respective vapour pressures of a pure volatile component and a solution. If x₁ is the mole fraction of a solvent then by Raoult’s law,
P = x₁ × P₀.

Explanation : Consider a solution containing two volatile components A and B having mole fractions x₁ and x₂ respectively.
Let \(P_{1}^{0}\) and \(P_{2}^{0}\) be the vapour pressures of pure components (or liquids) A and B respectively.
Then by Raoult’s law, vapour pressure of component A = P₁ = X₁ × \(P_{1}^{0}\), vapour pressure of component B = P₂ = x₂ × \(P_{2}^{0}\).
Here P₁ and P₂ represent partial vapour pressures of the two liquid components in the solution.
Hence the total vapour pressure, P_T of the solution will be,
P_T = P₁ + P₂
∴ P_T = x₁\(P_{1}^{0}\) + x₂\(P_{2}^{0}\)
∵ x₁ + x₂ = 1
∴ x₁ = 1 – x₂
∴ P_T = (1 – x₂)\(P_{1}^{0}\) + x₂\(P_{2}^{0}\)
= \(P_{1}^{0}\) – x₂\(P_{1}^{0}\) + x₂\(P_{2}^{0}\)
= (\(P_{2}^{0}\) – \(P_{1}^{0}\))x₂ + \(P_{1}^{0}\)
With the help of above equation, the vapour pressures of solutions having different concentrations (or mole fractions) can be calculated.

Question 20.
Explain the variation of vapour pressure with mole fraction of a solute in a liquid mixture.
Answer:
Consider a liquid mixture of two liquid components A and B having vapour pressures \(P_{1}^{0}\) and \(P_{2}^{0}\) and mole fractions x₁ and x₂ respectively.
By Raoult’s law, the vapour pressures P₁ and P₂ are,
P₁ = x₁\(P_{1}^{0}\) and P₂ = x₂\(P_{2}^{0}\)
The vapour pressure of the solution is,
P_T = P₁ +P₂ = x₁\(P_{1}^{0}\) + x₂\(P_{2}^{0}\)

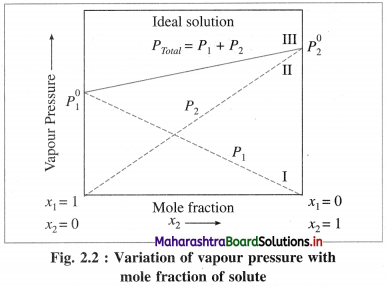
∴ P_T = (\(P_{2}^{0}\) – \(P_{1}^{0}\))x₂ + \(P_{1}^{0}\)
The plot of P_T versus x₂ is a straight line. The plots of P₁ versus x₁, and P₂ versus x₂ are straight lines passing through the origin.
When x₁ = 1, x₂ = 0, P_T = \(P_{1}^{0}\) and when x₁ = 0, x₂ = 1, P_T = \(P_{2}^{0}\) as shown by lines I and II in Fig. 2.2

Question 21.
Explain the composition of vapour phase above a liquid mixture.
Answer:
Consider a liquid mixture of two liquids A and B having vapour pressures \(P_{\mathrm{A}}^{0}\) and \(P_{\mathrm{B}}^{0}\) and mole fractions x₁ and x₂ respectively in the liquid phase.
By Raoult’s law, the vapour pressures of two liquids will be,
P_A = x₁\(P_{\mathrm{A}}^{0}\) and P_B = x₂\(P_{\mathrm{B}}^{0}\)
The total vapour pressure of this liquid mixture is,
P_T = P_A + P_B
P_T = x₁\(P_{\mathrm{A}}^{0}\) + x₂\(P_{\mathrm{B}}^{0}\)
The vapour above liquid surface contains A and B. If y₁ and y₂ are the mole fractions of A and B components respectively in the vapour phase, then by Dalton’s law of partial pressures,
P_A = y₁P_T and P_B = y₂P_T
and total vapour pressure is,
P_T = y₁P_T + y₂P_T.

Question 22.
What are ideal and nonideal solutions ?
Answer:

• Ideal solutions : These are solutions which obey Raoult’s law over an entire range of concentrations at constant temperature.
• Nonideal solutions : These are solutions which do not obey Raoult’s law over the entire range of concentrations.

Question 23.
What are the characteristics of ideal solutions ?
Answer:

• The ideal solutions obey Raoult’s law over entire range of concentrations at constant temperature.
• In the formation of an ideal solution, heat is neither evolved nor absorbed and enthalpy change for mixing is zero, i.e. Δ_mix H = 0.
• In the formation of an ideal solution, there is no volume change on mixing two liquid components and the volume of solution is equal to the sum of volumes of two liquid components. Δ_mix V = 0
• In the ideal solution, solvent-solvent, solute-solute and solvent-solute interactions are comparable.
• The vapour pressure of an ideal solution lies between vapour pressures of two pure components.

Question 24.
Give an example of an ideal solution.
Answer:
A liquid mixture of benzene and toluene which have nearly identical physical properties and inter molecular forces forms an ideal solution.

Question 25.
What are the characteristics of nonideal solutions.
Answer:

• Nonideal solutions do not obey Raoult’s law over the entire range of concentrations.
• The vapour pressures of these solutions may be higher or lower than ideal solutions.
• These solutions exhibit two types of deviations from Raoult’s law namely (a) positive deviation and (b) negative deviation.
• These solutions give azeotropic mixtures.

Question 26.
Explain solutions with positive deviations from Raoult’s law.
Answer:
(i) A solution or a liquid mixture which has higher vapour pressure than theoretically calculated by Raoult’s law or higher than those of pure components is called a nonideal solution with positive deviation.

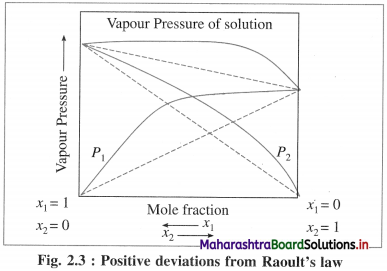
(ii) In these solutions, solute-solvent intermolecular attractions are weaker than those between solvent-solvent and solute-solute interactions.
(iii) For example, solutions of acetone and ethanol, carbon disulphide and acetone, etc.

Question 27.
Explain solutions with negative deviations from Raoult’s law.
Answer:
(1) A solution or a liquid mixture which has lower vapour pressure than theoretically calculated by Raoult’s law or lower than those of pure components is called a nonideal solution with negative deviation.

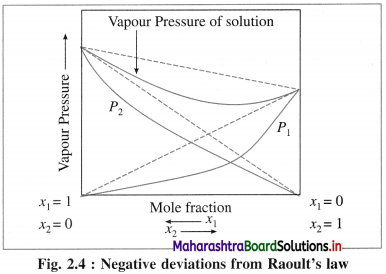
(2) In these solutions, the intermolecular interactions between solvent and solute molecules are stronger than solvent-solvent or solute-solute interactions.
(3) For example, solutions of phenol and aniline, chloroform and acetone, etc.

Solved Examples 2.5

Question 28.
Solve the following :

(1) The vapour pressures of two liquids A and B are 400 mm Hg and 600 mm Hg respectively at 47 °C. A solution is prepared by dissolving 10 g of A of molar mass 60 g mol^-1 in 80 g of B of molar mass 40 g mol^-1. Find the vapour pressure of the solution.
Solution :
Given : \(P_{\mathrm{A}}^{0}\) = 400 mm Hg; \(P_{\mathrm{B}}^{0}\) = 650 mm Hg.
W_A = 10 g and W_B = 80 g.
M_A = 60 g mol^-1; M_B = 40 g mol^-1, P_soln = ?
n_A = \(\frac{W_{\mathrm{A}}}{M_{\mathrm{A}}}=\frac{10}{60}\) = 0.1667 mol
n_B = \(\frac{W_{\mathrm{B}}}{M_{\mathrm{B}}}=\frac{80}{40}\) = 2 mol
Total number of moles = n = n_A + n_B
= 0.1667 + 2
= 2.1667 mol

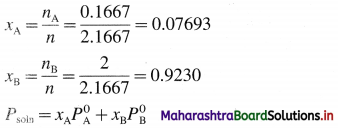
= 0.07693 × 400 + 0.9230 × 600
= 30.772 + 553.8
= 584.572 mm Hg
Ans. Vapour pressure of solution
= P_soln = 584.572 mm Hg

(2) 2.5 mol of a liquid A is mixed with 4.5 mol of liquid B at 25 °C. If the vapour pressures of A and B at 25 °C are 160 mm Hg and 230 mm Hg respectively, calculate the vapour pressure of the liquid mixture.
Solution :
Given : n_A = 2.5 mol; n_B = 4.5 mol,
\(P_{\mathrm{A}}^{0}\) = 160 mm Hg; \(P_{\mathrm{B}}^{0}\) = 230 mm Hg, P_soln = ?
Total number of moles = n = n_A + n_B
= 2.5 + 4.5
= 7.0 mol
Mole fraction of A = x_A = \(\frac{n_{\mathrm{A}}}{n}=\frac{2.5}{7}\) = 0.3571
Mole fraction of B = 1 – x_A = 1 – 0.3571
= 0.6429
\(P_{\text {soln }}=x_{\mathrm{A}} P_{\mathrm{A}}^{0}+x_{\mathrm{B}} P_{\mathrm{B}}^{0}\)
= 0.3571 × 160 + 0.6429 × 230
= 57.136 + 147.9
= 205 mm Hg
Ans. P_soln = 205 mm Hg

(3) The vapour pressures of pure liquids A and B are 400 mm Hg and 650 mm Hg respectively at 330 K. Find the composition of liquid and vapour if total vapour pressure of solution is 600 mm Hg.
Solution :
Given : \(P_{\mathrm{A}}^{0}\) = 400 mm Hg; \(P_{\mathrm{B}}^{0}\) = 650 mm Hg,
P_T = 600 mm Hg, T = 330 K; x_A = ? x_B = ?, y₁ = ? y₂ = ?
(x is mole fraction in liquid phase while y is mole fraction in vapour phase.)
P_T = (\(P_{\mathrm{A}}^{0}\) – \(P_{\mathrm{B}}^{0}\))x_B + \(P_{\mathrm{A}}^{0}\)
600 = (650 – 400)x_B + 400
= 250x_B + 400
∴ x_B = \(\frac{600-400}{250}\) = 0.8
∵ x_A + x_B = 1
∴ x_A = 1 – x_B = 1 – 0.8 = 0.2
The composition of A and B in liquid mixture is, x_A = 0.2 and x_B = 0.8.
If P₁ and P₂ are vapour pressures (or partial pressures) of A and B in vapour phase then by Raoult’s law,
P₁ = x_A × \(P_{\mathrm{A}}^{0}\) = 0.2 × 400 = 80 mm Hg
P₂ = x_B × \(P_{\mathrm{B}}^{0}\) = 0.8 × 650 = 520 mm Hg
If y₁ and y₂ are mole fractions of A and B respectively in vapour phase then, by Dalton’s law,
P₁ = y₁P_T

(or y₂ = 1 – y₁ = 1 – 0.1333 = 0.8667)
Ans. Composition of liquid : x_A = 0.2 and x_B = 0.8
Composition of vapour: y_A = 0.1333 and y_B = 0.8667

(4) A mixture of two liquids A and B have vapour pressures 3.4 × 10⁴ Nm^-2 and 5.2 × 10 Nm^-2. If the mole fractions of A is 0.85, find the vapour pressure of the solution.
Solution:
Given : Vapour pressure of pure liquid A
= \(P_{\mathrm{A}}^{0}\) = 3.4 × 10⁴ Nm^-2
Vapour pressure of pure liquid B
= \(P_{\mathrm{B}}^{0}\) = 5.2 × 10⁴ Nm^-2
Mole fraction of A = x_A = 0.85
Mole fraction of B = x_B = 1 – x_A
= 1 – 0.85
= 0.15
The vapour solution is given by
\(P_{\text {soln }}=X_{A} P_{A}^{0}+X_{B} P_{B}^{0}\)
= 0.85 × 3.4 × 10 + 0.15 × 5.2 × 10⁴
=2.89 × 10⁴ + 0.78 × 10⁴
=(2.89 + 0.78) × 10⁴
P_soln = 3.67 × 10⁴ Nm^-2
Ans. Vapour pressure of a solution = 3.67 × 10⁴ Nm^-2

Question 29.
Define the term colligative property. Give examples.
Answer:
(1) Colligative Property : The property of a solution which depends on the total number of particles of the solute (molecules, ions) present in the solution and does not depend on the nature or chemical composition of solute particles is called colligative property of the solution.

(2) Examples of colligative properties : (a) lowering or relative lowering of vapour pressure of a solution (b) elevation in the boiling point (c) depression in the freezing point (d) osmotic pressure.

Question 30.
Explain and define the term vapour pressure of a liquid.
OR
What is vapour pressure of a liquid?
Answer:

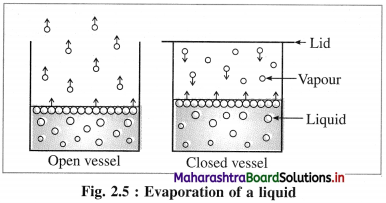
(1) If a volatile liquid is placed in an open vessel, the liquid molecules have a tendency to escape in a gaseous state forming vapour and diffuse into surroundings. Hence evaporation takes place continuously, and no equilibrium is attained.

(2) If a liquid is placed in a closed vessel, the vapour molecules get accumulated on its surface. These vapour molecules are in continuous random motion. They collide with each other, with walls of a container and surface of the liquid, and return to the liquid state. This reverse phenomenon is called condensation.

(3) After some time, rates of evaporation and condensation become equal and an equilibrium is established between liquid and vapour phases. At this stage the vapour exerts a constant pressure called vapour pressure on liquid surface at constant temperature.

(4) Vapour pressure : The pressure exerted by the vapour of a liquid (or solid) when it is in equilibrium with the liquid (or solid) phase at a constant temperature is called the vapour pressure of the liquid (or solid).

(5) The vapour pressure of a liquid increases with the increase in temperature.

Question 31.
Explain the following terms :
(1) Relative vapour pressure of a solution
(2) Lowering of vapour pressure of a solution
(3) Relative lowering of vapour pressure.
Answer:
(1) Relative vapour pressure of a solution : If Po is the vapour pressure of a pure liquid (solvent) and P is the vapour pressure of a solution after adding a nonvolatile solute, then, relative vapour pressure = \(\frac{P}{P_{0}}\).

(2) Lowering of vapour pressure of a solution :
When a nonvolatile solute is added to a pure solvent, the surface area is covered by the solute molecule decreasing the rate of evaporation, hence its vapour pressure decreases. This decrease in vapour pressure is called lowering of vapour pressure.
If P₀ is the vapour pressure of a pure solvent (liquid) and P is the vapour pressure of the solution, where P < P₀, then, (P₀ – P) is the lowering of the vapour pressure.

(3) Relative lowering of vapour pressure : If P₀ and P are the respective vapour pressures of a pure liquid (solvent) and the solution containing a non-volatile solute then P < P₀. Hence, P₀ – P represents the lowering of the vapour pressure due to addition of a nonvolatile solute.
∴ Relative lowering of vapour pressure = \(\frac{P_{0}-P}{P_{0}}=\frac{\Delta P}{P_{0}}\)

Question 32.
State and explain Raoult’s law for solutions of nonvolatile solutes.
Answer:
(a) Statement of Raoult’s law : The law states that the vapour pressure of a solvent over the solution of a nonvolatile solute is equal to the vapour pressure of the pure solvent multiplied by mole fraction of the solvent at constant temperature.

(b) Explanation : Let P0 and P be the vapour pressures of a pure solvent and a solution respectively. If x₁ is the mole fraction of the solvent then Raoult’s law can be represented as,
P = x₁P₀
For a binary solution containing one solute, if x₁ and x₂ are mole fractions of a solvent and a solute respectively then,
x₁ + x₂ = 1
∴ x₁ = 1 – x₂
∴ P = x₁P₀
= (1 – x₂) P₀
= P₀ – x₂P₀
= P₀ – P = x₂P₀
∴ P₀ – P = x₂P₀
∴ x₂ = \(\frac{P_{0}-P}{P_{0}}\)
P₀ – P = ΔP is the lowering of vapour pressure
∴ x₂ = \(\frac{\Delta P}{P_{0}}\)
In the equation, P₀ – P/P₀ is called relative lowering of vapour pressure.
Hence Raoult’s law can also be stated as the relative lowering of vapour pressure is equal to mole fraction of the solute.

Question 33.
Show that relative lowering of vapour pressure is a colligative property.
Answer:
Consider a binary solution containing a nonvolatile solute. If P₀ and P are vapour pressures of a pure solvent and the solution respectively then, Lowering of vapour pressure = ΔP = P₀ – P
Relative lowering of vapour pressure = \(\frac{P_{0}-P}{P_{0}}\)
By Raoult’s law,
\(\frac{P_{0}-P}{P_{0}}=x_{2}\)
where x₂ is mole fraction of the solute. Therefore the relative lowering of vapour pressure is a colligative property.

Question 34.
Explain the variation of vapour pressure with mole fraction of a solvent in solution.
OR
Explain the variation of vapour pressure with the concentration of a solution.
Answer:
The vapour pressure of a pure solvent decreases when a nonvolatile solute is dissolved in it. Consider a pure solvent with vapour pressure P₀ and mole fraction x₁. For a solution containing a non-volatile solute, if x₁ and x₂ are the mole fractions of a solvent and a solute respectively, then x₁ + x₂ = 1 and x₁ < 1.

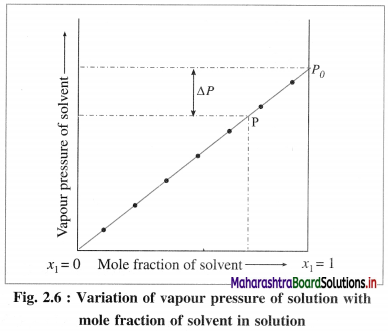
By Raoult’s law, P = x₁ × P₀. As the mole fraction of a solvent in the solution increases the vapour pressure increases as shown in the above figure 2.5. When x₁ becomes equal to 1, the vapour pressure becomes P₀, i.e. the vapour pressure of a pure solvent.

If at any mole fraction of a solvent, the vapour of the solution is P, then the lowering of vapour pressure will be, ΔP = P₀ – P.

Question 35.
Derive a relation between relative lowering of vapour pressure and molar mass of non-volatile solute.
Answer:
Consider a solution in which W₁ gram of a solvent of molar mass (or molecular weight) M₂ contains W₂ gram of a solute of molar mass M₂. Then
number of moles of a solvent = n₁ = \(\frac{W_{1}}{M_{1}}\)
Number of moles of a solute = n₂ = \(\frac{W_{2}}{M_{2}}\)
∴ Total number of moles = n = n₁ + n₂
Mole fraction of the solvent = x₁ = \(\frac{n_{1}}{n}\)
Mole fraction of the solute = x₂ = \(\frac{n_{2}}{n}\)

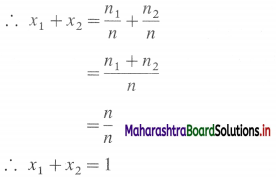
In the case of an ideal solution which is a dilute solution, the concentration and the number of moles of the solute are very low, i.e. n₂ << n₁

If P₀ and P are the vapour pressures of a pure solvent and a solution respectively, then relative lowering of vapour pressure = \(\frac{P_{0}-P}{P_{0}}\)
By Raoult’s law

Hence by measuring the vapour pressure of a pure solvent and a solution, the molar mass of the dissolved nonvolatile substances can be determined.

Solved Examples 2.6 – 2.7

Question 36.
Solve the following :

(1) The vapour pressure of a pure liquid at 298 K is 4 × 10⁴ Nm^-2. When a nonvolatile solute is dissolved the vapour pressure becomes 3.65 × 10⁴ Nm^-2. Calculate (A) relative vapour pressure, (B) lowering of vapour pressure and (C) relative lowering of vapour pressure.
Solution :
Given : P₀ = 4 × 10⁴ Nm^-2
P = 3.65 × 10⁴ Nm^-2
(A) Relative vapour pressure = \(\frac{P}{P_{0}}\)
= \(\frac{3.65 \times 10^{4}}{4 \times 10^{4}}\)
= 0.9125

(B) Lowering of vapour pressure = ΔP = P₀ – P
= 4 × 10⁴ – 3.65 × 10⁴
= (4 – 3.65) × 10⁴
= 0.35 × 10⁴ Nm^-2 = 3.5 × 10³ Nm^-2

(C) Relative lowering of vapour pressure is given by,

Ans. (A) 0.9125 (B) 3.5 × 10³ Nm^-2 (C) 0.0875

(2) A pure liquid has vapour pressure 5.2 × 10⁴ Pa at 298 K. When a solute is dissolved, the mole fraction of it is 0.02 in the solution. Find the vapour pressure of the solution.
Solution :
Given : P₀ = 5.2 × 10⁴ Pa
x₂ = 0.02
P = ?

Ans. Vapour pressure of the solution
= 5.096 × 10⁴ Pa

(3) The vapour pressure of pure benzene is 640 mm of Hg. 2.175 × 10^-3 kg of nonvolatile solute is added to 39 gram of benzene, the vapour pressure of solution is 600 mm of Hg. Calculate molar mass of solute (C = 12, H = 1).
Solution :
Given : P₀ = 640 mm Hg
W₁ = 39 g benzene = 39 × 10^-3 kg
W₂ = 2.175 × 10^-3 kg
P = 600 mm Hg
M₁ = 78 × 10^-3 kg, M₂ = ?

Ans. Molar mass of a solute = 69.6 × 10^-3 kg mol^-1

(4) In an experiment, 18.04 g of mannitol were dissolved in 100 g of water. The vapour pressure of water was lowered by 0.309 mm Hg from 17.535 mm Hg. Calculate the molar mass of mannitol.
Solution :
Given : Mass of a solute (mannitol)
= W₂ = 18.04 g
Mass of a solvent (water) = W₁ = 100 g
Vapour pressure of a solvent (water)
= P₀
= 17.535 mm Hg
Lowering of vapour pressure = ΔP = 0.309 mm Hg
Molar mass of H₂O = M₁ = 18 g mol^-1
Molar mass of solute (mannitol) = M₂ = ?

Ans. Molar mass of mannitol = 184.3 g mol^-1

(5) The vapour pressure of 2.1% solution of a non-electrolyte in water at 100 °C is 755 mm Hg. Calculate the molar mass of the solute.
Solution :
Given : At 100 °C, vapour pressure of water = P₀ = 760 mm Hg
Vapour pressure of the solution = P = 755 mm Hg
Since the solution is 2.1 % by mass,
Mass of solute (nonelectrolyte) = W₂ = 2.1 g
Mass of water = W₁ = 100 – 2.1 = 97.9 g
Molar mass of water = M₁ = 18 g mol^-1
Molar mass of nonelectrolyte = M₂ = ?

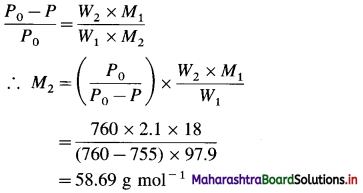
Ans. Molar mass of nonelectrolyte = 58.69 g mol^-1

(6) Calculate the mass of a nonvolatile solute (molar mass 40 × 10^-3 kg/mol) which is dissolved in 114 × 10^-3 kg octane to reduce its vapour pressure to 80%.
Solution :
Given : Molar mass of solute = M₂ =40 × 10^-3 kg mol^-1
Mass of solvent (octane) = W₁ = 114 × 10^-3 kg
If vapour pressure of octane = P₀ = 100
Vapour pressure of solution = P = 80
Molar mass of octane (C₈H₁₈) = 114 × 10^-3 kg mol^-1
Mass of solute = W₂ = ?
In this solution, since the vapour pressure is decreased by greater extent, 100 – 80 = 20% the solution must be concentrated and number of moles of solute must be large so that n₁ + n₂ ≠ n₁
Hence Raoult’s law must be represented as,

∴ Mass of solute dissolved = W
= moles × molar mass = 0.25 × 40 × 10^-3
= 0.01 kg
Ans. Mass of solute dissolved = 0.01 kg

(7) The vapour pressure of water is 16.8 mm Hg at a certain temperature. If the vapour pressure of the solution is 16.78 mm, find the molality of the solution.
Solution :
Given : P₀ = 16.8 mm Hg; P = 16.78 mm Hg
Molar mass of water = M₁ = 18 g mol^-1
Molality of the solution = m = ?

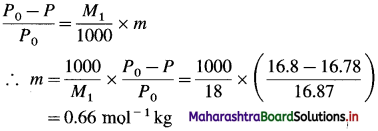
Ans. Molality of the solution = 0.66 m

Question 37.
Explain the effect of temperature on the vapour pressure of a liquid.
Answer:
The vapour pressure of a liquid is the pressure of the vapour in equilibrium with the liquid at a given temperature. The evaporation of a liquid requires thermal energy. Hence, as temperature rises, the vapour pressure rises until it becomes equal to the external pressure, generally the atmospheric pressure, 101.3 kNm^-2 (1 atm). This temperature is called the normal boiling point of the liquid.

Question 38.
What is boiling point of liquid?
OR
Define boiling point.
Answer:
The boiling point of a liquid is defined as the temperature at which the vapour pressure of the liquid becomes equal to the external pressure, i.e., the atmospheric pressure (1 atm), e.g., the boiling point of water at 1 atm is 373 K. m

Question 39.
Explain the elevation in the boiling point of a solution.
Answer:
The elevation in the boiling point of a solution is defined as the difference between the boiling points of the solution and the pure solvents at a given pressure, e.g. If T₀ and T are the boiling points of a pure solvent and a solution, then the elevation in boiling point, ΔT_b = T – T₀. It is a colligative property.

Question 40.
What are the units of molal elevation constant?
Answer:
Boiling point elevation, ΔT_b is given by,
ΔT_b = K_b × m
where m is molality in mol kg^-1 and K_b is molal elevation constant or abullioscopic constant.

∴ K_b has units K kg mol^-1 (or °C kg mol^-1)
Therefore, molal elevation constant is the elevation in boiling point produced by 1 molal solution of a nonvolatile solute.

Question 41.
Derive the relation between molar mass of the solute and boiling point elevation.
Answer:
The boiling point elevation, ΔT_b of a solution is directly proportional to molality (m) of the solution.
∴ ΔT_b ∝ m
ΔT_b = K_b m
where K_b is a proportionality constant
If m = 1 molal, then
ΔT_b = K_b
where K_b is called molal elevation constant.
The molality of the solution is given by,
Number of moles of the solute, m = \(\frac{\text { Number of moles of the solute }}{\text { Weight of the solvent in } \mathrm{kg}}\)
Let W₁ = Weight (in gram) of a solvent,
W₂ = Weight (in gram) of a solute
M₂ = Molecular weight of the solute
Then the molality (m) of the solution is given by

If the weights and molecular weight are expressed in kg, then,
\(\Delta T_{\mathrm{b}}=K_{\mathrm{b}} \times \frac{W_{2}}{W_{1} M_{2}}\)

Question 42.
Define molal elevation constant (Ebullioscopic constant)? Does it depend on the nature of a solute ? What are its units ?
Answer:
(1) Molal elevation constant (Ebullioscopic constant) : It is defined as the elevation in boiling point, produced by dissolving one mole of a solute in 1 kg (or 1000 gram) of a solvent (i.e. 1 molal solution).
The elevation in the boiling point,
ΔT_b is given by ΔT_b = K_b × m
where Kb is molal elevation constant and m is molality of the solution.
∴ When m = 1, ΔT_b = K_b
(2) K_b depends only on the nature of the solvent.
(3) K_b does not depend on the nature of the solute.
(4) It does not depend on concentration of the solution.
(5) The units of molal elevation constant are :
(A) K kg mol^-1 and (B) Km^-1.

Solved Examples 2.8

Question 43.
Solve the following :

(1) Calculate the (i) elevation in the boiling point and (ii) the boiling point of 0.05 m aqueous solution of glucose. (K_b = 0.52 Km^-1)
Solution :
Given : Concentration of the solution = m = 0.05 m
Molal elevation constant = K_b = 1.86 K kg mol^-1
Boiling point of pure water = T₀ = 373 K
Elevation in the boiling point = ΔT_b = ?
Boiling point of solution = T_b = ?

(i) ΔT_b = K_b × m
= 0.52 × 0.05
= 0.026K

(ii) The elevation in the boiling point is given by,
ΔT_b = T_b – T₀
∴ Boiling point of a solution,
T_b = T₀ + ΔT_b
= 373 + 0.026
= 373.026 K
Ans. ΔT_b = 0.026 K, T_b = 373.026 K

(2) 0.18 molal aqueous solution of a substance boils at 373.25 K. Calculate the molal elevation constant of water. (Boiling point of water is 373.15 K)
Solution :
Given : Concentration of solution = m = 0.18 m
Boiling point of water = T₀ = 373.15 K
Boiling of the solution = T_b = 373.25
Molal elevation constant = K_b = ?
Elevation in boiling point = ΔT_b
= T_b – T₀
= 373.25 – 373.15
= 0.1 K
ΔT_b = K_b × m
∴ K_b = \(\frac{\Delta T_{\mathrm{b}}}{m}=\frac{0.1}{0.18}\) = 0.5556 K kg mol^-1
Ans. Molal elevation constant of water
= 0.5556 K kg mol^-1

(3) The boiling point of benzene is 353.23 K. When 1.80 gram of non-volatile solute was dissolved in 90 gram of benzene, the boiling point is raised to 354.11 K. Calculate the molar mass of solute. [K_b for benzene = 2.53 K kg mol^-1]
Solution :
Given : \(T_{b}^{0}\) = 353.23 K; T_b = 354.11 K
W₁ = 90 g; W2 = 1.8 g; K_b = 2.53 K kg mol^-1
Molar mass = M₂ = ?
ΔT_b = T_b – \(T_{b}^{0}\) = 354.11 – 353.23 = 0.88 K

Ans. Molar mass = M₂ = 57.5 g mol^-1

(4) Boiling point of a solvent is 80.2°C. When 0.419 g of the solute of molar mass 252.4 g mol^-1 is dissolved in 75 g of the above solvent, the boiling point of the solution is found to be 80.256 °C. Find the molal elevation constant.
Solution :
Given : T₀ = (273 + 80.2) K
T_b = 273 + 80.256 (K)
W₁ = 75g
W₂ = 0.419 g
M₂ = 252.4 g mol^-1
K_b = ?
ΔT_b = T_b – T₀
= (273 + 80.256) – (273 + 80.2)
= 0.056 K

Ans. K_b = 2.53 K kg mol^-1

(5) 3.795 g of sulphur is dissolved in 100 g of CS₂. This solution boils at 319.81 K. What is the molecular formula of sulphur in solution? Theboiling point of CS₂ is 319.45 K.
(Given that K_b for CS₂ =2.42 K kg mol^-1 and atomic mass of S = 32.)
Solution :
Given : W₂ = 3.795 g; W₁ = 100 g CS₂
T_b = 319.81 K; T₀ = 319.45 K
K_b = 2.42 K kg mol^-1 M₂ = ?
ΔT_b = T_b – T₀ = 319.81 – 319.45 = 0.36 K

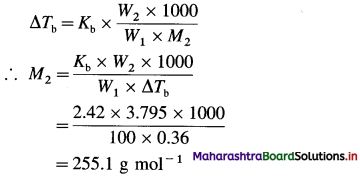
Number of S atoms in molecule = \(\frac{255.1}{32}\)
= 7.972
≅ 8
Ans. Formula of sulphur in CS₂ solution = S₈

(6) Calculate the mass in grams of an impurity of molar mass 100 g mol^-1 which would be required to raise the boiling point of 50 g of chloroform by 0.30°C. (K_b for chloroform = 3.63 K kg mol^-1)
Solution :
Given : M₂ = 100 g mol^-1
W₁ = 50 g chloroform
W₂ = ?
ΔT_b = 0.30°C.
K_b = 3.63 K kg mol^-1

Ans. Weight of impurity = 0.4132 g

(7) A solution containing 0.5126 g of naphthalene (molar mass = 128.17 g mol^-1) in 50.0 g of CCl₄ gives a boiling point elevation of 0.402 °C. While a solution of 0.6216 g of unknown solute in the same mass of the solvent gives a boiling point elevation of 0.647 °C. Find the molar mass of the unknown solute. (K_b for CCl₄ = 5.03 K kg mol^-1 of solvent)
Solution:
Given : For naphthalene solution :
W₂ = 0.5126 g
W₁ = 50 g
M₂ = 128.17 g mol^-1
K_b = 5.03 K kg mol^-1
ΔT_b = 0.402°C
For unknown solute :
W’₁ = 50g
W’₂ = 0.6216 g
ΔT’_b = 0.647°C
M’₂ = ?
For the solution of unknown substance,

Ans. Molecular weight of unknown substance = 96.65 g mol^-1

(8) A solution containing 0.73 g of camphor (molar mass 152 g mol^-1) in 36.8 g of acetone (boiling point 56.3°C) boils at 56.55°C. A solution of 0.564 g of unknown compound in the same weight of acetone boils at 56.46°C. Calculate the molar mass of the unknown compound.
Solution:
Given : Mass of solute = W₂ = 0.73 g camphor
Mass of solvent = W₁ = 36.8 g
Molar Mass of solute = M₂ = 152 g mol^-1
Boiling point of acetone = T₀ = (273 + 56.3) K
Mass of unknown solute = W’₂ = 0.564 g
Mass of solvent = W’₁ = 36.8 g
Boiling point of solution of camphor = T_b = (273 + 56.55) K
Boiling point solution of unknown compound = T’_b = (273 + 56.46) K
Molar mass of unknown compound = M’₂ = ?

For camphor solution,
∴ ΔT_b = T_b – T₀
= (273 + 56.55) – (273 + 56.3)
= 0.25 K

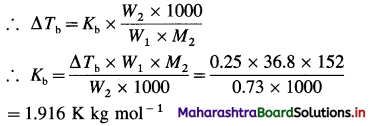
For a solution of unknown compound
ΔT’_b = ΔT’_b – T₀
= (273 + 56.46) – (273 + 56.3)
= 0.16 K

Ans. Molar mass of the compound = 183.5 g mol^-1

(9) 0.12 molal solution of a substance boils at 373.21°K. Calculate molal elevation constant of the solvent.
Solution :
Given : Concentration of solution = m = 0.12
Boiling point of the solution = T_b = 373.21 K
For solvent (water) T₀ = 373.15 K
Molal elevation constant, K_b = ?
ΔT_b = T_b – T₀
= 373.21 – 373.15
= 0.06 K
ΔT_b = K_b × m
∴ K_b = \(\frac{\Delta T_{\mathrm{b}}}{m}\)
= \(\frac{0.06}{0.12}\)
=0.5 K kg mol^-1
Ans. Molal elevation constant = K_b = 0.5 K kg mol^-1

(10) Boiling point of water at 750 mm of Hg is 99.63 °C. How much sucrose must be added to 500 g of water so that it boils at 100 °C? (K_b = 5.02 K kg mol^-1)
Solution :
Given : Boiling point of water = T₀ = 273 + 99.63
= 372.63 K
Boiling point of a solution = T_b = 273 + 100 = 373 K
Mass of a solvent (water) = W₁ = 500 g
Molar mass of sucrose (C₁₂H₂₂O₁₁) = M2
= 342 g mol^-1
K_b = 5.02 K kg mol^-1
Mass of solute (sucrose) = W₂ = ?
ΔT_b = T_b – T₀
= 373 – 372.63
= 0.37 K

Ans. Mass of sucrose required to be added = 12.60 g

(11) A solution of phosphorus prepared by dissolving 0.0175 kg of phosphorus in 0.08 kg of CS₂ has a boiling point 319.87 K. If K_b for CS₂ is 2.4 K kg mol-1 and atomic mass of phosphorus is 31 × 10^-3 kg mol^-1, find the formula of phos-phorus. (Boiling point of CS₂ = 319.45 K)
Solution :
Given : Mass of solvent (CS₂) = W₁ = 0.08 kg
Mass of phosphorus = W₂ = 0.0175 kg
Boiling point of CS₂ = T₀ = 319.45 K
Boiling point of solution = T_b = 319.87 K
Molal elevation constant = K_b = 2.4 K kg mol^-1
Atomic mass of phosphorus = 31 × 10^-3 kg mol^-1
Molecular formula of phosphorus = ?
ΔT_b = T_b – T₀ = 319.87 – 319.45 = 0.42 K

∴ Number of atoms in a molecule of phosphorus = \(\frac{\text { molar mass of phosphorus }}{\text { atomic mass of phosphorus }}\)
= \(\frac {125}{31}\)
= 4.032
≅ 4
Hence the molecular formula of phosphorus is P₄ in CS₂.
Ans. Molecular formula of phosphorus = P₄

(12) Boiling point of water at 750 mm of Hg is 99.63 °C. How much sucrose must be added to 500 g of water so that it boils at 100 °C? (K_b = 0.52 K kg mol^-1)
Solution :
Given : Pressure = P = 750 mm Hg
T₀ = 273 + 99.63 = 372.63 K
T_b = 273 + 100 = 373 K
K_b = 0.52 K kg mol^-1
Molar mass of sucrose (C₁₂H₂₂O₁₁) = 342 × 10^-3 kg mol^-1
W₁ = 500 g = 0.5 kg
Mass of sucrose to be added = W₂ = ?
ΔT_b = T_b – T₀ = 373 – 372.63 = 0.37 K

Ans. Mass of sucrose to be added = 121.7 × 10^-3 kg
= 121.7 g

(13) 35 % (W/W) solution of ethylene glycol in water, an anti-freezer used in automobiles in radiators as a coolant. It lowers freezing point of water to -17.6 °C. Calculate the mole fraction of the components.
Solution :
35% (W/W) means 100 g solution contains 35 g ethylene glycol (CH₂OH-CH₂OH) and 65 g H₂O.
Molar mass of water = 18 g mol^-1
Molar mass of ethylene glycol (CH₂OH-CH₂OH) = 62 g mol^-1
Number of moles of water = n₁ = \(\frac{65}{18}\) = 3.611 mol
Number of moles of ethylene glycol = n₂ = \(\frac{35}{62}\)
= 0.5645 mol
Total moles = n = n₁ + n₂ = 3.611 + 0.5645
= 4.1755 mol
Mole fraction of ethylene glycol = x₂
\(=\frac{n_{2}}{n_{1}}=\frac{0.5645}{4.1755}\) = 0.1352
∴ Mole fraction of water = 1 – x₂ = 1 – 0.1352
= 0.8648
Ans. Mole fraction of water = 0.8648
Mole fraction of ethylene glycol = 0.1352

Question 44.
Define freezing point of a liquid.
Answer:
The freezing point of a liquid is defined as the temperature at which the solid coexists in the equilibrium with the liquid and the vapour pressure of the liquid and the solid are equal.

Question 45.
Explain the depression in the freezing point of a solution.
Answer:
The depression in the freezing point of a solution is defined as the difference between the freezing points of a pure solvent and that of the solution.
If T₀ and T are the respective freezing points of a pure solvent and a solution, then the depression in the freezing point ΔT_f is given by,
ΔT_f = T₀ – T (T < T₀)
The depression in the freezing point (ΔT_f) is a colligative property.

Question 46.
What causes depression in freezing point ?
OR
Explain, freezing point depression as a consequence of vapour pressure lowering.
Answer:
The freezing point of a liquid is the temperature at which the liquid and the solid have the same vapour pressure.

Addition of a nonvolatile solute to a liquid decreases the freezing point, i.e., the freezing point of the solution is less than that of the pure solvent. This is due to the lowering of the vapour pressure of the solvent by the addition of the nonvolatile solute.

When a liquid is cooled from the point A, its vapour pressure decreases and at the point B, it freezes (solidifies).

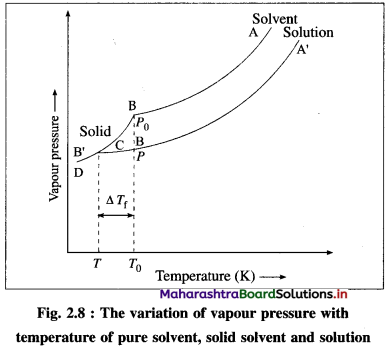
In case of a solution, since the vapour pressure is lowered, the freezing point decreases. Hence, if the solution is cooled from the point A’, it freezes at lower temperature B’, than the pure liquid. This is also due to separation of solvent molecules due to solute molecules decreasing their intermolecular attraction.

If T₀ and T are the freezing points of a pure solvent and the solution, then, the depression in the freezing point is given by,
ΔT_f = T₀ – T.
This depression ΔT_f depends on the lowering of the vapour pressure (P₀ – P). ΔT_f ∝ (P₀ – P), where P₀ and P are the vapour pressures of the pure liquid and the solution.

Question 47.
What is a relationship between freezing point depression and concentration of solute (or solution)?
Answer:
It is observed experimentally that as the concentration of a solution increases, the freezing point of the solution decreases and hence the depression in the freezing point (ΔT_f) increases.

The depression in the freezing point of a solution is directly proportional to the molal concentration (expressed in mol kg^-1) of the solution.
Thus,
ΔT_f ∝ m
where m is the molality of the solution.
∴ ΔT_f = Kfm, where Kf is a constant of proportionality. If m = 1 molal,
ΔT_f = K_f. Hence K_f is called the cryoscopic constant or molal depression constant. K_f is characteristic of the solvent.

Question 48.
What are the units of molal depression constant or cryoscopic constant?
Answer:
The freezing point depression, ΔT_f is given by,
ΔT_f = K_f × m
where m is molality in mol kg^-1 and K_f is molal depression constant or cryoscopic constant.

∴ K_f has unit K kg mol^-1 (or °C kg mol^-1)
Therefore cryoscopic constant is the depression in freezing point produced by 1 molal solution of a nonvolatile solute.

Question 49.
Write the formula to determine molar mass of a solute using freezing point depression method.
Answer:
M₂ = \(\frac{K_{\mathrm{f}} \times W_{2} \times 1000}{W_{1} \times \Delta T_{\mathrm{f}}}\)
where
K_f = Molal depression constant
ΔT_f = Depression in freezing point
W₁ = Mass of a solvent
W₂ = Mass of a solute.
M₂ = Molar mass of solute

Question 50.
Define cryoscopic constant (or molal depression constant).
Answer:
Molal depression constant : It is defined as the depression in freezing point, produced by dissolving one mole of a solute in 1 kg (or 1000 g) of a solvent (i.e. 1 molal solution).

Solved Examples 2.9

Question 51.
Solve the following :

(1) 1.35 g of a substance when dissolved in 55 g acetic acid produced a depression of 0.618°C in a freezing point. Calculate the molar mass of the dissolved substance. (K_f = 3.865 K kg mol^-1)
Solution :
Given : Mass of a solvent = W₁ = 55 g
Mass of a solute = W₂ = 1.35 g
Depression in freezing point = ΔT_f = 0.618 °C
Molal depression constant = K_f = 3.865 K kg mol^-1
Molar mass of a solute = M₂ = ?

Ans. Molar mass of the substance = 153.5 g mol^-1

(2) When certain amount of sucrose is dissolved in 1 kg of water, the freezing point of the solution is found to be 272.8 K. If the molecular mass of sucrose is 342 g mol^-1 and K_f for water is 1.86 K kg mol^-1, calculate the amount of sucrose present in the solution.
Solution :
Given : W₁ = Mass of the solvent = 1 kg
T₀ = Freezing point of pure water = 273 K
T_f = Freezing point of the solution = 272.8 K
ΔT_f = T₀ – T_f = Depression in freezing point
= 273 K – 272.8 K
= 0.2 K
M₂ = Molecular mass of the solute
= 342 × 10^-3 kg mol^-1
K_f = Molal freezing point depression constant for water
= 1.86 K kg mol^-1
W₂ = Mass of the solute = ?
ΔT_f = T₀ – T_f

Ans. Mass of sucrose = 36.78 × 10^-3 kg

(3) The freezing point of a pure solvent is 315 K. On addition of 0.5 mole of urea in 1 kg of the solvent, the freezing point decreases by 3 K. Calculate the molal depression constant for the solvent.
Solution :
Given :
m = Molality of urea = 0.5 m
ΔT_f = Depression in the freezing point = 3 K
K_f = Molal depression constant for the solvent = ?
ΔT_f = K_f × m
∴ K_f = \(\frac{\Delta T_{\mathrm{f}}}{m}\)
= \(\frac{3}{0.5}\)
= 6 K kg mol^-1
Ans. Molal depression constant = 6 K kg mol^-1

(4) The freezing point of pure benzene is 278.4 K. Calculate the freezing point of the solution when 2g of a solute having molecular weight 100 is added to 100 g of benzene. (K_f for benzene = 5.12 K kg mol^-1)
Solution :
Given : K_f for benzene = 5.12 K kg mol^-1
T₀ = Freezing point of the solvent = 278.4 K
W₁ = Mass of the solvent = 100 g = 0.1 kg
W₂ = Mass of the solute = 2g = 2 × 10^-3 kg
M₂ = Molecular mass of the solute = 100 g mol^-1
= 100 × 10^-3 kg mol^-1
T = Freezing point of the solution = ?

Ans. Freezing point of the solution = 277.376 K

(5) 0.635 × 10^-3 kg of a substance of molar mass 190 × 10^-3 kg mol^-1 was dissolved in 30.5 × 10^-3 kg of a solvent. If the depression in the freezing point is 0.62 °C, find the molal depression constant of the solvent.
Solution :
Given : Mass of solvent = W₁ = 30.5 × 10^-3 kg
Mass of solute = W₂ = 0.635 × 10^-3 kg
Depression in freezing point = ΔT_f = 0.62 °C (or K)
Molar mass of the substance = M₂ = 190 × 10^-3 kg mol^-1
Molal depression constant = K_f = ?

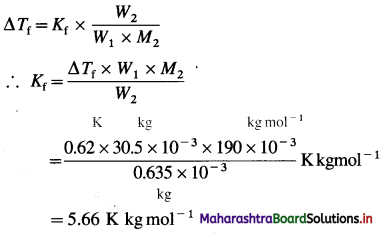
Ans. Molal depression constant = K_f
= 5.66 K kg mol^-1

(6) The boiling point of an aqueous solution is 100.18 °C. Find the freezing point of the solution. (Given : K_b = 0.52 K kg mol^-1, K_f = 1.86 K kg mol^-1)
Solution :
Given : T_b = 100.18 °C + 273 = 373.18 K
K_b = 0.52 K kg mol^-1; K_f = 1.86 K kg mol^-1
Boiling point of water = T₀ = 373 K
T_f = ?
ΔT_b = T_b – T₀ = 373.18 – 373 = 0.18 K
If m is the molality of the solution, then
ΔT_b = K_b × m and ΔT_f = K_f × m

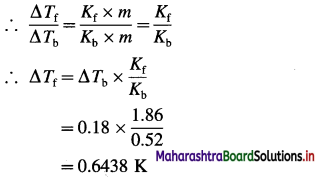
Freezing point of water = T₀ = 273 K
ΔT_f = T₀ – T_f
Hence the freezing point of the solution is,
T_f = T₀ – ΔT_f = 273 – 0.6438 = 272.3562 K
OR Freezing point of solution is -0.6438 °C.
Ans. Freezing point of the solution
= 272.3562 K
= -0.6438 °C

(7) 1.0 × 10^-3 kg of urea when dissolved in 0.0985 kg of a solvent, decreases freezing point of the solvent by 0.211 K. 1.6 × 10^-3 kg of another nonelectrolyte solute when dissolved in 0.086 kg of the same solvent depresses the freezing point by 0.34 K. Calculate the molar mass of the another solute. (Given molar mass of urea = 60)
Solution :
Given : Mass of Urea = W₂ = 1 × 10^-3 kg
Mass of solvent = W₁ = 0.0985 kg
Depression in freezing point = ΔT_f = 0.211 K
Molar mass of urea = M₂ = 60 g mol^-1
= 60 × 10^-3 kg mol^-1
Mass of another solute = W’₂ = 1.6 × 10^-3 kg
Mass of solvent = W’₁ = 0.086 kg
Depression in freezing point = ΔT’_f = 0.34 K
Molar mass of another solute = 60 × 10^-3 kg mol^-1

From urea solution:


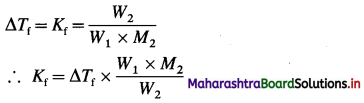
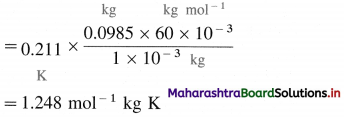
For solution of another solute :

Ans. Molar mass of solute = 68.23 g mol^-1.

Question 52.
What do you understand by the terms :
(1) permeable membrane
(2) semipermeable membrane?
Answer:
(1) Permeable membrane : A membrane which allows free transfer of the solute molecules from a solution of a higher concentration to a solution of a lower concentration through it is called a permeable membrane and the transfer is called diffusion, e.g., a membrane of a paper.

(2) Semipermeable membrane : A membrane which allows free passage of only the solvent molecules but not the large solute molecules or ions of large molecular mass from a solution of a lower concentration (or a pure solvent) to a solution of higher concentration through it, is called a semi-permeable membrane, e.g., parchment paper, complex like Cu₂[Fe(CN)₆], etc.

Question 53.
Define and explain osmosis.
Answer:
(1) Definition : It is defined as a spontaneous uni-directional flow of the solvent molecules from a pure solvent or a dilute solution to the more concentrated solution through a semipermeable membrane.

Example : A flow of water molecules from a dilute solution into a concentrated glucose solution through a parchment paper.

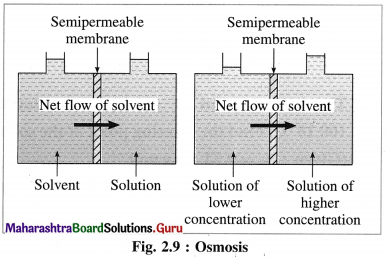
(2) Explanation : Consider a vessel divided into two compartments by a semipermeable membrane. When one compartment is filled with a pure solvent or a dilute solution and another by concentrated solution, there is a spontaneous of solvent molecules to the concentrated solution. This arises due to higher vapour pressure of a pure solvent or dilute solution than concentrated solution.

Question 54.
Explain the relation between osmotic pressure and concentration of solution.
Ans.
(1) Consider V dm³ of a solution in which n₁ moles of a solvent contains n₂ moles of a nonvolatile solute at absolute temperature T.

(2) The osmotic pressure, n of a solution is given by,
π = \(\frac{n R T}{V}\)
R is gas constant having value 0.08206 dm³ atm K^-1 mol^-1 (OR L atm K^-1 mol^-1). Since concentration, C of a solution is in mol dm^-3 or molarity is,
C = \(\frac{n}{V}\) mol dm^-3 or M
∴ π = CRT
(If concentration C is expressed in mol m^-3 and R = 8.314 J K^-1mol^-1, then π will be in SI units, pascals or Nm^-2.)

Question 55.
Explain the terms :
(1) Isotonic solutions
(2) Hypotonic solutions
(3) Hypertonic solutions.
Answer:
(1) Isotonic solutions : The solutions having the same osmotic pressure at a given temperature are called isotonic solutions.

Explanation : If two solutions of substances A and B contain n_A and n_B moles dissolved in volume V (in dm³) of the solutions, then their concentrations are,
C_A = \(\frac{n_{\mathrm{A}}}{V}\) (in mol dm^-3) and
C_B = \(\frac{n_{\mathrm{B}}}{V}\) (in mol dm^-3)
If the absolute temperature of both the solutions is T, then by the van’t Hoff equation,
π_A = C_ARTand π_B = C_BRT where π_A and π_B are their osmotic pressures.
For the isotonic solutions,
π_A = π_B
∴ C_A = C_B
∴ \(\frac{n_{\mathrm{A}}}{V}=\frac{n_{\mathrm{B}}}{V}\)
∴ n_A = n_B
Hence, equal volumes of the isotonic solutions at the same temperature will contain equal number of moles (hence, equal number of molecules) of the substances.

(2) Hypotonic solutions : When two solutions have different osmotic pressures, then the solution having lower osmotic pressure is said to be a hypotonic solution with respect to the other solution.
Explanation : Consider two solutions of the substances A and B having osmotic pressures π_A and π_B. If π_B is less than π_A, then the solution B is a hypotonic solution with respect to the solution A.
Hence, if C_A and C_B are their concentrations, then, C_B < C_A. Hence, for equal volumes of the solutions, n_A < n_A.

(3) Hypertonic solutions : When two solutions have different osmotic pressures, then the solution having higher osmotic pressure is said to be a hypertonic solution with respect to the other solution.
Explanation : Consider two solutions of substances A and B having osmotic pressures π_A and π_B. If π_B is greater than π_A, then the solution B is a hypertonic solution with respect to the solution A.
Hence, if C_A and C_B are their concentrations, then C_B > C_A. Hence, for equal volume of the solutions, n_B > n_A.

Question 56.
Explain colligative properties of electrolytes.
Answer:

• The electrolytic solutions do not exhibit colligative properties similar to nonelectrolytes.
• The colligative properties of electrolytes are higher than those shown by equimolar solutions of nonelectrolytes.
• The molar masses of electrolytes determined by colligative properties are found to be considerably lower than their actual molar masses.

Question 57.
Why are the colligative properties of electrolytic solutions greater than those for non-electrolytic solutions with same concentration ?
Answer:

• The electrolytes in polar solvents or aqueous solutions dissociate into two or more ions whereas nonelectrolytes do not dissociate.
• Consequently the number of particles in electrolytic solutions are considerably higher than equimolar nonelectrolytic solutions.
• Therefore the colligative properties of electrolytes are greater than nonelectrolytes with same concentration in solution.

Question 58.
What is abnormal colligative property? Explain the reasons.
Answer:
Abnormal colligative property : When the experimentally measured colligative property of a solution is different from that calculated theoretically by the van’t Hoff equation or by the laws of osmosis, then the solution is said to have abnormal colligative property.

Explanation : The colligative property depends on the number of solute particles in the solution but it is independent of their nature. Abnormal values of them arise when the dissolved solute undergoes a molecular change like dissociation or association in the solution.
The observed colligative property (or abnormal colligative property ) may be higher or lower than the theoretical value.

(i) Dissociation of the solute molecules : When a solute like an electrolyte is dissolved in a polar solvent like water, it undergoes dissociation, which results in the increase in the number of particles in the solution.

Hence, the observed value of the colligative property becomes higher than the theoretical value, e.g., when one mole of KCl is dissolved in the solution then due to dissociation, KCl → K⁺ + Cl^–, the number of particles increases, hence, the colligative properties like osmotic pressure elevation in the boiling point, etc. increase.

(ii) Association of the solute molecules : When a solute like a nonelectrolyte is dissolved in a nonpolar solvent like benzene, it undergoes association forming molecules of higher molecular mass. Hence, the number of the particles in the solution decreases. Therefore the colligative properties like osmotic pressure, elevation in the boiling point, etc., are lower than the theoretical value, e.g., nA → An.
2CH₃COOH → (CH₃COOH)₂
2C₆H₅COOH → (C₆H₅COOH)₂

Question 59.
Explain abnormal osmotic pressure.
Answer:

• When the experimentally observed osmotic pressure is different than theoretically calculated value by van’t Hoffs equation then it is called abnormal osmotic pressure.
• This arises when the dissolved solute undergoes a molecular change like association or dissociation.

Question 60.
Explain abnormal molecular masses.
Answer:
When the observed molecular masses obtained from their colligative properties of the substances are different (higher or lower) than the theoretical or normal values calculated from their molecular formulae, then they are called abnormal molecular masses.

Question 61.
How is van’t Hoff factor related to molecular mass of the substance ?
Answer:
The van’t Hoff factor is also defined as,
actual moles of particles in solution after


In case of nonelectrolytes, i < 1.
In case of electrolytes, i > 1. For example for KNO₃ and NaCl, i = 2, for Na₂SO₄, CaCl₂, i = 3, etc.

Question 62.
Write modification of expressions of colligative properties with the help of van’t Hoff factor.
Answer:
The modified expressions of colligative properties with the help of van’t Hoff factor i are as follows :
(1) By Raoult’s law :

Question 63.
Obtain a relation between degree of dissociation and molar mass for an electrolyte.
Answer:
Consider an electrolyte AxBy.

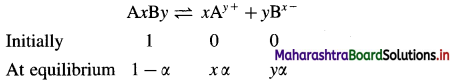
If i is van’t Hoff factor and n is total number of ions produced from dissociation of one mole of electrolyte then, the degree of dissociation α is given by,
α = \(\frac{i-1}{n-1}\)
Now if M_th and M_ob are theoretical arid observed molecular (or molar) masses respectively, then,
i = \(\frac{M_{\mathrm{th}}}{M_{\mathrm{ob}}}\)
∵ α(n – 1) = i – 1

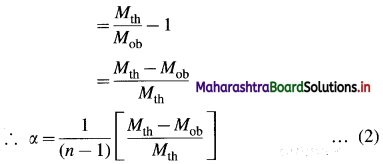
This is a relation between degree of dissociation and molecular masses of the dissolved electrolyte AxBy.

Question 64.
Solve the following :

(1) 300 mL solution at 27 °C contains 0.2 mol of a nonvolatile solute. Calculate osmotic pressure of the solution.
Solution :
Given : V= 300 ml = 0.3 dm³ ;
T= 273 + 27 = 300 K
π = 0.2 mol, π = ?
π = \(\frac{n R T}{V}\)
= \(\frac{0.2 \times 0.08206 \times 300}{0.3}\)
= 16.41 atm
Ans. Osmotic pressure = π = 16.41 atm.

(2) 200 mL solution at 27 °C contains 10 g of a nonvolatile solute of molar mass 65 g mol^-1. What is osmotic pressure of the solution ?
Solution :
Given : V = 200 mL = 0.2 dm³; W = 10 g
M = 65 g mol^-1; T= 273 + 27 = 300 K; π = ?

Ans. Osmotic pressure = π = 18.93 atm.

(3) Calculate the osmotic pressure of 0.2 M glucose solution at 300 K. (R = 8.314 J mol^-1 K^-1)
Solution :
Given : Concentration of the solution
= C = 0.2 M
= 0.2 mol dm^-3
= 0.2 × 10³ mol m^-3
Temperature = T= 300 K
= 8.314 J mol^-1 K^-1
The osmotic pressure, π is given by,
π = CRT
= 0.2 × 10³ × 8.314 × 300
= 4.988 × 10⁵ Nm^-2 (or Pa)
Ans. Osmotic Pressure = 4.988 × 10⁵ Nm^-2

(4) A solution of cane sugar containing 18 g L^-1 has an osmotic pressure 1.25 atm. Calculate the temperature of the solution. (Molar mass of cane sugar = 342, R = 0.082 lit atm mol^-1 K^-1)
Solution:
Given : Amount of cane sugar = W = 18 g L^-1
Osmotic pressure = π = 1.25 atm
Molar mass of cane sugar = M = 342 g mol^-1
Temperature = T = ?
Number of moles of cane sugar
= \(\frac{W}{M}\)
= \(\frac{18}{342}\)
= 0.05263 mol
∴ Concentration of solution = C
= \(\frac{n}{V}\)
= \(\frac{0.05263}{1}\)
= 0.05263 mol lit^-1
π = CRT
∴ T = \(\frac{\pi}{\mathcal{C R}}\)
= \(\frac{1.25}{0.05263 \times 0.08206}\)
= 289.4 K
Ans. Temperature of solution = 289.4 K

(5) Equal volumes of two solutions, one containing glucose and another urea have osmotic pressures 12.6 atm and 23.8 atm at 25 °C. Calculate the ratio of number of moles of urea to glucose.
Solution :
Given : Osmotic pressure of glucose solution = π₁
= 12.6 atm
Osmotic pressure of urea solution = π₂
= 23.8 atm
Number of moles of glucose = n₁
Number of moles of urea = n₂

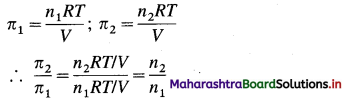
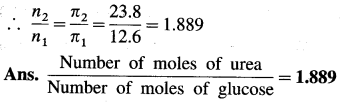
(6) One litre of a solution containing 25 g glucose has osmotic pressure 3.4 atm at 300 K. If by diluting the solution the osmotic pressure becomes 2.0 atm at the same temperature, what would be its concentration ? (Molar mass of glucose = 180)
Solution :
Given : Mass of solute (glucose) = 25 g
Volume of solution = 1.0 L
Osmotic pressure = π₁ = 3.4 atm
After dilution osmotic pressure = π₂ = 2 atm
Final concentration = c₂ = ?
The number of moles of glucose = n = \(\frac{25}{180}\)
= 0.1389 mol
Initial concentration = c₁ = \(\frac{n}{V}\)
= \(\frac{0.1389}{1}\)
At constant temperature, by van’t Hoff-Boyle’s law,

Ans. Concentration of solution = 0.0817 mol L^-1

(7) A solution of a substance having mass 1.8 × 10^-3 kg has the osmotic pressure of 0.52 atm at 280 K. Calculate the molar mass of the substance used.
[Volume = 1 dm³, R = 8.314 JK^-1 mol^-1]
Solution :
Given : W= 1.8 × 10^-3 kg = 1.8 g
π = 0.52 atm; V = 1 dm³
T = 280 K;
Molar mass = M = ?

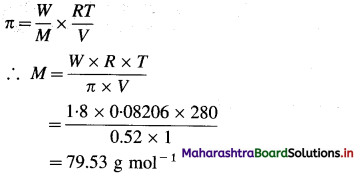
Ans. Molar mass = M = 79.53 g mol^-1

(8) An organic substance (M = 169 gram mol^-1) is dissolved in 2000 cm³ of water. Its osmotic pressure at 12 °C was found to be 0.54 atm. If R = 0.0821 L atm K^-1 mol^-1, calculate the mass of the solute.
Solution :
Given : M = 169 g mol^-1
V = 200 cm3 = 0.2 dm³
T = 273 + 125 = 285 K
π = 0.54 atm
R = 0.0821 L atm K^-1 mol^-1; W = ?

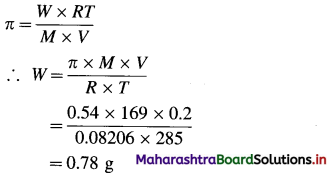
Ans. Mass of solute = 0.78 g

(9) A solution containing 10 g glucose has osmotic pressure 3.84 atm. If 10 g more glucose is added to the same solution, what will be its osmotic pressure. (Temperature remains constant)
Solution :
Given : Mass of glucose = W₁ = 10 g
Mass of more glucose added = W₂ = 10 g
Initial osmotic pressure = π₁ = 3.84 atm
Final osmotic pressure = π₂ = ?
Total mass of glucose in final solution = W₁ + W₂
W’ = 10 + 10
= 20 g

∴ π₂ = \(\pi_{1} \times \frac{W^{\prime}}{W_{1}}\)
= \(3.84 \times \frac{20}{10}\) = 7.68 atm
Ans. Osmotic pressure of the solution = 7.68 atm

(10) A 0.1 m solution of K₂SO₄ in water has freezing point of -0.43 °C. What is the value of van’t Hoff factor if K_f for water is 1.86 K kg mol^-1?
Solution :
Given : m = 0.1 m, ΔT_f = 0 – (-0.43) = 0.43 °C
K_f = 1.86 K kg mol^-1, i = ?
ΔT_f = i × K_f × m
∴ i = \(\frac{\Delta T_{\mathrm{f}}}{K_{\mathrm{f}} \times m}=\frac{0.43}{1.86 \times 0.1}=2.312\)
Ans. van’t Hoff factor = i = 2.312

Multiple Choice Questions

Question 65.
Select and write the most appropriate answer from the given alternatives for each subquestion :

1. A molal solution is one that contains one mole of solute in
(a) one litre of the solvent
(b) 1000 g of the solvent
(c) one litre of the solution
(d) 22.4 litre of solution
Answer:
(b) 1000 g of the solvent

2. 10.0 grams of caustic soda when dissolved in 250 cm³ of water, the resultant molarity of solution is
(a) 0.25 M
(b) 0.5 M
(c) 1.0 M
(d) 0.1 M
Answer:
(c) 1.0 M

3. 5 × 10-3 kg of urea is dissolved in 2 × 10^-2 kg of water. The percentage by weight of urea is
(a) 15%
(b) 20%
(c) 25%
(d) 30%
Answer:
(b) 20%

4. Vapour pressure of solution of a nonvolatile solute is always
(a) equal to the vapour pressure of pure solvent
(b) higher than vapour pressure of pure solvent
(c) lower than vapour pressure of pure solvent
(d) constant
Answer:
(c) lower than vapour pressure of pure solvent

5. According to the Raoult’s law, the relative lowering of vapour pressure is equal to the
(a) mole fraction of solvent
(b) mole fraction of solute
(c) independent of mole fraction of solute
(d) molality of solution
Answer:
(b) mole fraction of solute

6. Partial pressure of solvent in solution of non-volatile solute is given by equation,
(a) P = x₂P⁰
(b) P⁰ = xP
(c) P = x₁P⁰
(d) P⁰ = x₁P
Answer:
(c) P = x₁P⁰

7. When partial pressure of solvent in solution of nonvolatile solute is plotted against its mole fraction, nature of graph is
(a) a straight line passing through origin
(b) a straight line parallel to mole fraction of solvent
(c) a straight line parallel to vapour pressure of solvent
(d) a straight line intersecting vapour pressure axis
Answer:
(a) a straight line passing through origin

8. Colligative property depends only on ………………. in a solution.
(a) Number of solute particles
(b) Number of solvent particles
(c) Nature of solute particles
(d) Nature of solvent particles
Answer:
(a) Number of solute particles

9. Lowering of vapour pressure of solution
(a) is a property of solute
(b) is a property of solute as well as solvent
(c) is a property of solvent
(d) is a colligative property
Answer:
(d) is a colligative property

10. Raoult’s law is not applicable to
(a) solutions of volatile solutes
(b) solutions of electrolytes
(c) dilute solutions
(d) concentrated solutions
Answer:
(d) concentrated solutions

11. The relative lowering of vapour pressure of a solution is proportional to the
(a) mole fraction of the solvent
(b) mole fraction of the solute
(c) amount of the substance
(d) volume of the solvent
Answer:
(b) mole fraction of the solute

12. The vapour pressure of an aqueous solution of glucose at 100 °C is 710 mm Hg. Hence the molality of the solution is
(a) 2.83 m
(b) 3.65 m
(c) 16.47 m
(d) 12.5 m
Answer:
(b) 3.65 m

13. Relative vapour pressure lowering depends only on
(a) Mole fraction of solute
(b) Nature of solvent
(c) Nature of solute
(d) Nature of solute and solvent
Answer:
(a) Mole fraction of solute

14. A solution having mole fraction of a solute equal to 0.05 has vapour pressure 20 × 10³ Nm^-2. Hence the vapour pressure of a pure solvent is
(a) 21.05 × 10³ Nm^-2
(b) 4 × 10⁵ Nm^-2
(c) 1 × 10³ Nm^-2
(d) 2 × 10⁴ Nm^-2
Answer:
(a) 21.05 × 10³ Nm^-2

15. The addition of the nonvolatile solute into the pure solvent ……………..
(a) increases the vapour pressure of solvent
(b) decreases the boiling point of solvent
(c) decreases the freezing point of solvent
(d) increases the freezing point of solvent
Answer:
(c) decreases the freezing point of solvent

16. A solution having the highest vapour pressure is
(a) 1 M Al₂(SO₄)₃
(b) 0.1 M NaNO₃
(c) 1 M BaCl₂
(d) 1 M Ca(NO₃)₂
Answer:
(b) 0.1 M NaNO₃

17. Molal elevation constant is elevation in boiling point produced by
(a) 1 g of solute in 100 g of solvent
(b) 100 g of solute in 1000 g of solvent
(c) 1 mole of solute in one litre of solvent
(d) 1 mole of solute in one kg of solvent
Answer:
(d) 1 mole of solute in one kg of solvent

18. The determination of molar mass from elevation in boiling point is called
(a) cryoscopy
(b) osmometry
(c) ebullioscopy
(d) spectroscopy
Answer:
(c) ebullioscopy

19. Which of the following aqueous solutions will have minimum elevation in boiling point ?
(a) 0.1 M KCl
(b) 0.05 M NaCl
(c) 1 M AIPO₄
(d) 0.1 M MgSO₄
Answer:
(b) 0.05 M NaCl

20. Which of the following solutions shows maximum depression in freezing point ?
(a) 0.5 M Li₂SO₄
(b) 1 M NaCl
(c) 0.5 M Al₂ (SO₄)₃
(d) 0.5 M BaCl₂
Answer:
(c) 0.5 M Al₂ (SO₄)₃

21. If the freezing point of 0.1 m solution is 272.814 K, then the freezing point of 0.2 m solution will be
(a) 545.628 K
(b) 265.64 K
(c) 272.628 K
(d) 0.482 K
Answer:
(c) 272.628 K

22. At a freezing point,
(a) Vapour pressure of a solution = Vapour pressure of a solid
(b) Vapour pressure of a liquid = Vapour pressure of a solid
(c) Vapour pressure of a liquid > Vapour pressure of a solid
(d) Vapour pressure of a solid > Vapour pressure of a liquid
Answer:
(b) Vapour pressure of a liquid = Vapour pressure of a solid

23. In osmosis
(a) solvent molecules pass from high concentration of solute to low concentration
(b) solvent molecules pass from a solution of low concentration of solute to a solution of high concentration of solute
(c) solute molecules pass from low concentration to high concentration
(d) solute molecules pass from high concentration to low concentration
Answer:
(b) solvent molecules pass from a solution of low concentration of solute to a solution of high concentration of solute

24. As temperature increases
(a) Osmotic pressure and vapour pressure decrease
(b) Vapour pressure and osmotic pressure increase
(c) Vapour pressure increases but osmotic pressure decreases
(d) Osmotic pressure increases but vapour pressure decreases
Answer:
(b) Vapour pressure and osmotic pressure increase

25. A mango kept in a salt solution shrinks. Hence the liquid content in mango with respect to the salt solution is
(a) isotonic
(b) hypertonic
(c) hypotonic
(d) equimolar
Answer:
(c) hypotonic

26. The osmotic pressure of 5% glucose solution at 300 K is
(a) 6.93 × 10⁵ Nm^-2
(b) 6.93 × 10² Nm^-2
(c) 6.83 Pa
(d) 6.00 × 10³ Pa
Answer:
(a) 6.93 × 10⁵ Nm^-2

27. 0.1 M solution of A has osmotic pressure xNm^-2 at 300 K. If 200 ml of A and 100 ml of 0.2 M solution of nonreactive solute B are mixed then the osmotic pressure will be
(a) 3x
(b) 0.05 x
(c) 1.33 x
(d) 0.75 x
Answer:
(c) 1.33 x

28. The solution A is twice hypertonic to the solution B at a given temperature. If the solution A contains 8.6 × 10²² molecules, then the number of molecules present in B are,
(a) 8.6 × 10²²
(b) 1.73 × 10²³
(c) 3.24 × 10²²
(d) 4.3 × 10²²
Answer:
(d) 4.3 × 10²²

29. Isotonic solutions are the solutions having the same
(a) surface tension
(b) vapour pressure
(c) osmotic pressure
(d) viscosity
Answer:
(c) osmotic pressure

30. If Kb for water is 0.52 Km^-1, the boiling point of 0.2 m solution of a nonvolatile solute will be
(a) 371.96 K
(b) 373.104 K
(c) 373.52 K
(d) 374.0 K
Answer:
(b) 373.104 K

31. The vapour pressure of water is 15.5 mm at 20 °C. The lowering of vapour pressure of 0.02 m K Br solution will be
(a) 0.0112 mm Hg
(b) 0.0056 mm Hg
(c) 0.056 mm Hg
(d) 0.31 mm Hg
Answer:
(a) 0.0112 mm Hg

32. Which of the following 0.1 M aqueous solutions will exert highest osmotic pressure ?
(a) Al₂(SO₄)₃
(b) Na₂SO₄
(c) MgCl₂
(d) KCl
Answer:
(a) Al₂(SO₄)₃

33. If equimolar solutions of urea, NaCl, sucrose and BaCl₂ have boiling points A, B, C and D, then
(a) A = C < B < D
(b) A = D < B < C
(c) A > B > C < D
(d) A < B < C < D
Answer:
(a) A = C < B < D

34. The molar mass of acetic acid obtained by measuring depression in freezing point is 115.8 gmol^-1. Hence the degree of association is
(a) 0.482
(b) 0.964
(c) 0.883
(d) 1.12
Answer:
(b) 0.964

35. Δ T_b/m for NaBr solution will have value (K_b = 0.52 K kg mol^-1)
(a) 0.52 K mol^-1
(b) 0.104 K kg mol^-1
(c) 1.24 kg mol^-1
(d) 1.04 K kg mol^-1
Answer:
(d) 1.04 K kg mol^-1

36. 0.2 M urea solution can be isotonic with
(a) 0.1 M KBr solution
(b) 0.1 M glucose solution
(c) 0.15 m NaCl solution
(d) 0.2 M KBr solution
Answer:
(a) 0.1 M KBr solution

37. The osmotic pressure of 0.1 M HCl solution at 27 °C will be
(a) 2.46 atm
(b) 0.164 atm
(c) 4.92 atm
(d) 0.0082 atm
Answer:
(c) 4.92 atm

38. If a, b, c and d are the van’t Hoff factors for Na₂SO₄, glucose and K₄[Fe(CN)₆] then
(a) a > b > c
(b) a < b < c
(c) b < a < c
(d) c < a < b
Answer:
(c) b < a < c

39. The osmotic pressure of 0.2 M KCl solution at 310 K is
(a) 10.17 atm
(b) 5.084 atm
(c) 8.36 atm
(d) 12.2 atm
Answer:
(a) 10.17 atm

40. A temperature at which 0.1 M KCl solution will have osmotic pressure 10 atm will be
(a) 408 °C
(b) 263 °C
(c) 310 °C
(d) 337 °C
Answer:
(d) 337 °C

41. 5 % solution of glucose is isotonic with a solution of urea (M = 60). Hence the weight of urea present in the solution is
(a) 1.67 g
(b) 6.0 g
(c) 18.6 g
(d) 1.2 g
Answer:
(a) 1.67 g

42. Abnormal molar mass is produced by
(a) association of solute
(b) dissociation of solute
(c) both association and dissociation of solute
(d) separation by semipermeable membrane
Answer:
(c) both association and dissociation of solute

43. The van’t Hoff factor for an aqueous solution of an electrolyte is
(a) less than 1
(b) zero
(c) greater than 1
(d) equal to 1
Answer:
(c) greater than 1

44. The value of van’t Hoff factor will be minimum for
(a) 0.05 M AlCl₃
(b) 0.2 M NaNO₃
(c) 5.0 M glucose
(d) 0.1 M H₂SO₄
Answer:
(c) 5.0 M glucose

45. van’t Haff factor for K₄[FeC(N)₆] dissociated 10% is
(a) 1.1
(b) 1.4
(c) 0.86
(d) 1.6
Answer:
(b) 1.4