Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 9 Optics Important Questions and Answers.
Maharashtra State Board 11th Physics Important Questions Chapter 9 Optics
Question 1.
Express the speed of EM waves in terms of permittivity and permeability of the medium.
Answer:
In a material medium, the speed of EM waves is given by, c = \(\sqrt{\frac {1}{εµ}}\)
Where, ε = Permittivity and µ = permeability.
These constants depend on the electric and magnetic properties of the medium.
Question 2.
How can one classify commonly observed phenomena of light on the basis of the nature of light?
Answer:
Commonly observed phenomena concerning light can be broadly split into three categories:
- Ray optics or geometrical optics: Ray optics can be used for understanding phenomena like reflection, refraction, double refraction, total internal reflection, etc.
- Wave optics or physical optics: Wave optics explains the phenomena of light such as, interference, diffraction, polarisation, Doppler effect etc.
- Particle nature of light: Particle nature of light can be used to explain phenomena like photoelectric effect, emission of spectral lines, Compton effect etc.
![]()
Question 3.
State the fundamental laws on which ray optics is based.
Answer:
Ray optics is based on the following fundamental laws:
i. Light travels in a straight line in a homogeneous and isotropic medium.
ii. Two or more rays can intersect at a point without affecting their paths beyond that point.
iii. Laws of reflection:
a. Reflected ray lies in the plane formed by incident ray and the normal drawn at the point of incidence and the two rays are on either side of the normal.
b. Angles of incidence and reflection are equal (i = r).
iv. Laws of refraction:
a. Refracted ray lies in the plane formed by incident ray and the normal drawn at the point of incidence; and the two rays are on either side of the normal.
b. Angle of incidence (90 and angle of refraction (62) are related by Snell’s law, given by,
n1 sin θ1 = n2 sin θ2
where, n1, n2 = refractive indices of medium 1 and medium 2 respectively.
Question 4.
Explain Cartesian sign conventions using a graph.
Answer:
According to Cartesian sign conventions:
i. All distances are measured from the optical centre or pole.
ii. Figures should be drawn in such a way that the incident rays travel from left to right. Thus, a real object should be shown to the left and virtual object or image to the right of pole (or optical centre).
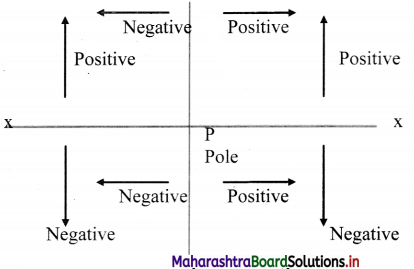
iii. X-axis can be conveniently chosen as the principal axis with origin at the pole.
iv. Distances to the left of the pole are negative and those to the right of the pole are positive.
v. Distances above the principal axis (X-axis) are positive while those below it are negative.
Question 5.
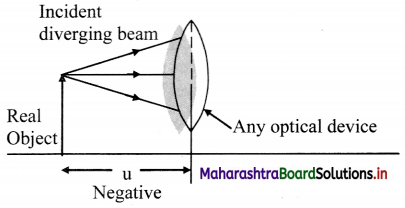
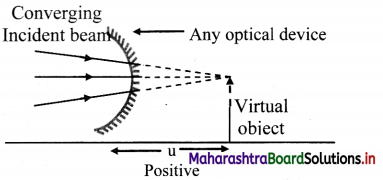
Define and represent in a neat diagram the following terms:
i. Diverging beam
ii. Converging beam
Answer:
i. A diverging beam of light corresponds to rays of light coming from real point object.
ii. A converging beam corresponds to rays of light directed to a virtual point object or image.
Question 6.
Thickness of the glass of a spectacle is 2 mm and refractive index of its glass is 1.5. Calculate time taken by light to cross this thickness. Express your answer with most convenient prefix attached to the unit ‘second’.
Answer:
Speed of light in vacuum, c = 3 × 108 m/s
Given that:
Refractive index, (nglass) = 1.5
Thickness of the glass = 2 mm
= 2 × 10sup>-3 m
∵ Re fractive index (nglass) = \(\frac{\text { speed of light in vacuum }(\mathrm{c})}{\text { speed of light in glass (v) }}\)
∵ v = \(\frac{\mathrm{c}}{\mathrm{n}_{\text {glass }}}=\frac{3 \times 10^{8}}{1.5}\) = 2 × 108 m/s
As v = \(\frac {s}{t}\)
time taken (t) to cross the thickness (s),
t = \(\frac{\mathrm{s}}{\mathrm{v}}=\frac{2 \times 10^{-3}}{2 \times 10^{8}}\) = 1 × 10-11 s
Most convenient unit to express this small time is nano second. (1 ns = 10-9 s)
∴ t = 0.01 × 10-9 s = 0.01 ns
Question 7.
Explain the properties of the image formed after reflection of light from a plane surface.
Answer:
- The image of an object kept in front of a plane reflecting surface is virtual and laterally inverted.
- Image is of the same size as that of the object.
- It is situated at the same distance as that of object but on the other side of the reflecting surface.
Question 8.
Explain the formula to find the number of images formed when an object is placed in between two plane mirrors inclined at an angle θ.
Answer:
- If an object is kept between two plane mirrors inclined at an angle θ, multiple images (N) are formed due to multiple reflections from both the mirrors.
- The number of images can be calculated using formula n = \(\frac {360}{θ}\)
- Exact number of images seen (N) depends upon the angle between the mirrors and position of the object.
- When n is an even integer, for all positions of the object the number of images formed are N = n – 1.
- When n is an odd integer:
a. For an object placed at the angle bisector of the mirrors: N = n- 1
b. For an object placed off the angle bisector of the mirrors: N = n - If n is not an integer, N = m, where m is integral part of n.
Question 9.
Define radius of curvature of a spherical mirror.
Answer:
Radius of the sphere of which a mirror is a part is called as radius of curvature of the mirror.
Question 10.
What is the focal length of a spherical mirror? Give its relation with the radius of curvature.
Answer:
i. For a concave mirror focal length is the distance at which parallel incident rays converge. For a convex mirror, it is the distance from where parallel rays appear to be diverging after reflection.
ii. In case of spherical mirrors, half of radius of curvature is focal length of the mirror,
f = \(\frac {R}{2}\)
Question 11.
Show with the help of a ray diagram that focal length of convex mirror is positive while that of concave mirror is negative.
Answer:
i. According to sign conventions, the incident rays are drawn from left of the mirror to the right as shown in the ray diagrams below.
ii. As the rays incident on convex mirror appear to converge at a point on the positive side of the origin, the focal length of the convex mirror is positive.
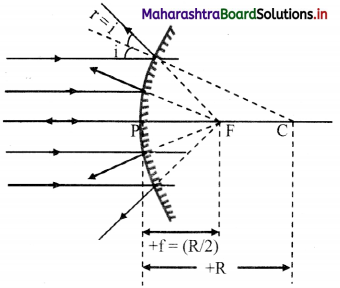
iii. However, in case of concave mirror, the rays converge at a point on negative side of the origin, the focal length of the concave mirror is negative.
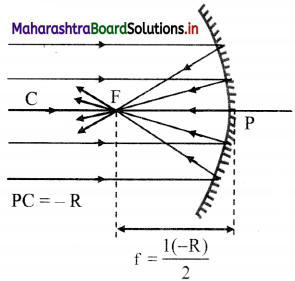
Question 12.
Give relation between focal length, object distance and image distance for a small spherical mirror.
Answer:
For a point object or for a small finite object, the focal length of a small spherical mirror is related to object distance and image distance as,
\(\frac {1}{f}\) = \(\frac {1}{v}\) + \(\frac {1}{u}\)
![]()
Question 13.
What is lateral magnification? How does it vary in different types of spherical mirrors?
Answer:
i. Ratio of linear size of image to that of the object, measured perpendicular to the principal axis, is defined as the lateral magnification.
∴ m = \(\frac {h_2}{h_1}\) = \(\frac {v}{u}\) (for spherical lenses)
m = –\(\frac {v}{u}\) (for spherical mirrors)
ii. For any position of the object, a convex mirror always forms virtual, erect and diminished image. Thus, lateral magnification for convex lens is always m < 1.
iii. In the case of a concave mirror, it depends upon the position of the object.
Question 14.
Complete the following table for a concave mirror?
| Position of object | Position of image | Lateral magnification |
| U = ∞ | v = f | m = 0 |
| u > 2f | ……………. | m < 1 |
| u = f | V = ∞ | ……………… |
| …………… | |v| > |u| | m > 1 |
| 2f > u > f | ……………… | m > 1 |
Answer:
| Position of object | Position of image | Lateral magnification |
| U = ∞ | v = f | m = 0 |
| u > 2f | 2f > v > f | m < 1 |
| u = f | V = ∞ | m = ∞ |
| u < f | |v| > |u| | m > 1 |
| 2f > u > f | v > 2f | m > 1 |
Question 15.
Explain with proper diagram why parabolic mirrors are preferred over spherical one.
Answer:
i. Unlike spherical shape, every point on a parabola is equidistant from a straight line and a point.
ii. Consider given parabola having RS as directrix and F as the focus. Points A, B, C on it are equidistant from line RS and point F.
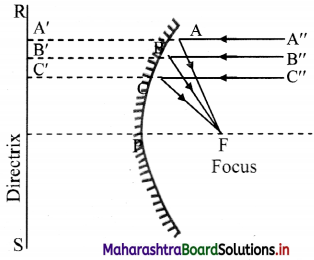
iii. Hence A’A = AF, B’B = BF, C’C = CF, and so on.
iv. If rays of equal optical path converge at a point, that point is the location of real image corresponding to that beam of rays.
v. From figure, the paths A”AA’, B”BB’. C”CC’, etc., are equal paths when mirror is neglected.
vi. If the parabola ABC is a mirror then by definition of parabola the respective optical paths,
A”AF = B”BF = C”CF
vii. Thus, F is the single point focus for entire beam of rays parallel to the axis and there is no spherical aberration.
Hence, parabolic mirrors are preferred over spherical one as there is no spherical aberration.
Question 16.
A small object is kept symmetrically between two plane mirrors inclined at 38°. This angle is now gradually increased to 41°, the object being symmetrical all the time. Determine the number of images visible during the process.
Answer:
The object is kept symmetrically between two plane mirrors. This implies the object is placed at angle bisector.
Thus, for θ = 38°,
n = \(\frac {360}{38}\) = 9.47
As it is not integral, N = 9 (the integral part of n)
∴ For going from 38° to 41°, the mirrors go through angles 39° and 40°. Number of images formed will remain 9 for all angles between 38° and 40°.
For angles > 40°, the n goes on decreasing and when θ = 41°,
n = \(\frac {360}{41}\) = 8.78 i.e., N = 8
Question 17.
A thin pencil of length 20 cm is kept along the principal axis of a concave mirror of curvature 30 cm. Nearest end of the pencil is 20 cm from the pole of the mirror. What will be the size of image of the pencil?
Answer:
For the pencil kept along the principal axis and the end of the pencil closest to pole is at 20 cm,
say, u1 = -20 cm
Flence, the other end of the stick is at distance, u2 = (u1 + 20) = -40 cm from pole of the mirror.
As R = -30 cm, F = \(\frac {R}{2}\) = -15 cm

∴ v2 = -24 cm
Here, negative signs indicate that images are formed on the left of the mirror.
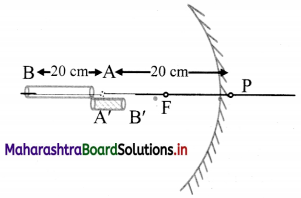
The length of the image formed is given by,
v = v2 – v1 = -24 – (-60) = 36 cm.
Question 18.
An object is placed at 15 cm from a convex mirror having radius of curvature 20 cm. Find the position and kind of image formed by it.
Answer:
Given: u = – 15 cm,
f = \(\frac {R}{2}\) = + \(\frac {20}{2}\) = + 10cm
To find: Nature and position of image (v)
Formula: \(\frac {1}{v}\) + \(\frac {1}{u}\) = \(\frac {1}{f}\)
Calculation:
From formula,
∴ \(\frac {1}{v}\) = \(\frac {1}{f}\) – \(\frac {1}{u}\)
= \(\frac {1}{+10}\) – \(\frac {1}{-15}\) = \(\frac {1}{10}\) + \(\frac {1}{15}\)
= \(\frac {2+3}{30}\) = \(\frac {5}{30}\) = \(\frac {1}{6}\)
∴ v = 6 cm
Question 19.
Prove that refractive index of a glass slab is given by the formula,
n = \(\frac {Real depth}{Apparent depth}\)
Answer:
i. Consider a plane parallel slab of a transparent medium of refractive index n.
ii. A point object O at real depth R appears to be at I at apparent depth A, when seen from outside (air).
iii. Consider incident ray OA and OB as shown in figure.
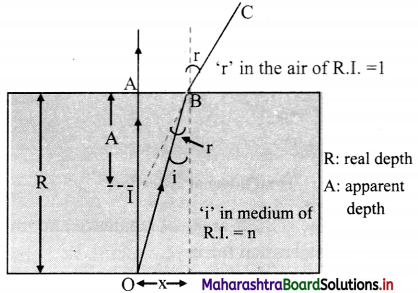
iv. Assuming i and r to be very small, we can write,
tan r = \(\frac {x}{A}\) ≈ sin r and tan i = \(\frac {x}{R}\) ≈ sin i
v. According to Snell’s law, for a ray travelling from denser medium to rarer medium,
n = \(\frac{\sin \mathrm{r}}{\sin \mathrm{i}} \approx \frac{\left(\frac{\mathrm{x}}{\mathrm{A}}\right)}{\left(\frac{\mathrm{x}}{\mathrm{D}}\right)}=\frac{\mathrm{R}}{\mathrm{A}}=\frac{\text { Real depth }}{\text { Apparent depth }}\)
Question 20.
The depth of a pond is 10 m. What is the apparent depth for a person looking normally to the water surface? nwater = 4/3.
Answer:
Given: Real depth of pond, dreal = 10 m,
nw = \(\frac {4}{3}\)
To find: Apparent depth
Formula: n = \(\frac {Realdepth}{Apparent depth}\)
Calculation: From formula,
∴ Apparent depth = \(\frac {Realdepth}{n}\) = \(\frac {10}{(\frac{4}{3})}\)
= \(\frac {10×3}{4}\) = 7.5 m
Question 21.
A crane flying 6 m above a still, clear water lake sees a fish underwater. For the crane, the fish appears to be 6 cm below the water surface. How much deep should the crane immerse its beak to pick that fish?
For the fish, how much above the water surface does the crane appear? Refractive index of water = 4/3.
Answer:
For crane, apparent depth of fish = 6 cm,
Given that refractive index (nw) = \(\frac {4}{3}\)
nw = \(\frac {Realdepth}{Apparent depth}\)
∴ Apparent depth = \(\frac {4}{3}\) × 6 = 8 cm
Similarly, for fish, real height of crane = 6 m and
\(\frac{\mathrm{n}_{\mathrm{air}}}{\mathrm{n}_{\mathrm{w}}}=\frac{1}{\mathrm{n}_{\mathrm{w}}}=\frac{\text { Real height }}{\text { Apparent height }}\)
\(\frac {3}{4}\) = \(\frac {6}{Apparent height}\)
i.e., Apparent height = \(\frac {4×6}{3}\) = 8 m
Question 22.
Write a short note on Periscope.
Answer:
i. Instrument used to see the objects on the surface of a water body from inside of water is called periscope.
ii. It consists of two right angled prisms. The incident rays of light are reflected twice through these prisms.
iii. Total internal reflections occur inside these prisms and a clear view of the surface of water is obtained.
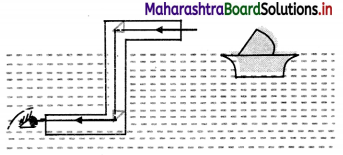
Question 23.
A ray of light passes from glass (ng = 1.52) to water (nw = 1.33). What is the critical angle of incidence?
Answer:
Given: ng = 1.52, nw = 1.33
To find: Critical angle (ic)
formula: sin ic = \(\frac {n_2}{n_1}\) = \(\frac {n_w}{n_g}\)
Calculation:
From formula,
ic = sin-1 (\(\frac {1.33}{1.52}\)) = sin-1 (0.875) = 61°2′
Question 24.
There is a tiny LED bulb at the center of the bottom of a cylindrical vessel of diameter 6 cm. Height of the vessel is 4 cm. The beaker is filled completely with an optically dense liquid. The bulb is visible from any inclined position but just visible if seen along the edge of the beaker. Determine refractive index of the liquid.
Answer:
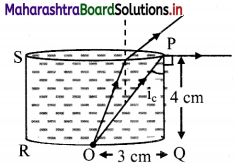
As the bulb is just visible from the edge, the angle of incidence formed by ray OP must be equal to critical angle.
∴ refractive index (n) = \(\frac {1}{sin i_c}\)
From Figure,
tan ic = \(\frac {PQ}{OQ}\) = \(\frac {4}{3}\)
∴ sin ic = \(\frac {OQ}{OP}\) = \(\frac {3}{5}\)
∴ nliquid = \(\frac {5}{3}\)
Question 25.
What are convex and concave lenses? For which condition, convex lens will have negative focal length?
Answer:
- A lens is said to be convex if it is thicker in the middle and narrowing towards the periphery. According to Cartesian sign convention, its focal length is positive.
- Convex lens is visualized to be internal cross section of two spheres (or one sphere or a plane surface).
- A lens is concave if it is thicker at periphery and narrows down towards centre and has negative focal length.
- Concave lens is visualized to be external cross section of two spheres.
- For lenses of material optically rarer than the medium in which those are kept, convex lenses will have negative focal length and they will diverge the incident rays.
Question 26.
Which lenses can be considered as thin lenses?
Answer:
Lenses for which the maximum thickness is at least 50 times smaller than all the other distances are considered as thin lenses.
Question 27.
Give the expression for the focal length of combination of lenses when
i. Lenses are kept in contact with each other
ii. Two lenses kept at a distance d apart from each other.
Answer:
i. For thin lenses kept in contact:
\(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}_{1}}+\frac{1}{\mathrm{f}_{2}}+\frac{1}{\mathrm{f}_{3}}\) + ………
ii. For two lenses kept distance d apart:
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}-\frac{d}{f_{1} f_{2}}\)
Question 28.
An object is placed infront of a convex surface separating two media of refractive index 1.1 and 1.5. The radius of curvature is 40 cm. Where is the image formed when an object is placed at 220 cm from the refracting surface?
Solution:
Given: n1 = 1.1, n2 = 1.5, R = + 40 cm,
u = -220 cm
To find: Position of image (v)
Formula: \(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\)
Calculation: From formula,

Question 29.
A glass paper-weight (n = 1.5) of radius 3 cm has a tiny air bubble trapped inside it. Closest distance of the bubble from the surface is 2 cm. Where will it appear when seen from the other end (from where it is farthest)?
Answer:
From figure, distance OR = 2 cm
∴ Distance OP = 4 cm
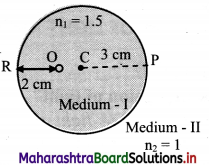
According to sign conventions,
OP = u = -4 cm and CP = R = -3 cm
For refraction at curved surface,

Question 30.
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
Answer:
Given: n = 1.55, f = 20 cm,
R1 = R and R2 = – R
(By sign convention)
To Find: Radius of curvature (R)
Formula: \(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
Calculation: From formula,
\(\frac {1}{20}\) = (1.55 – 1) \(\left[\frac{1}{R}-\left(-\frac{1}{R}\right)\right]=0.55 \times \frac{2}{R}\)
∴ R = \(\frac {1.10}{1}\) × 20 = 22 cm
![]()
Question 31.
A dense glass double convex lens (n = 2) designed to reduce spherical aberration has |R1| : |R2| = 1:5. If a point object is kept 15 cm in front of this lens, it produces its real image at 7.5 cm. Determine R1 and R2.
Answer:
Given: |R1| : |R2| = 1 : 5, u = -15 cm,
v = +7.5 cm, n = 2
To Find: Radii of curvature of double convex lens (R1) and (R2)
Formula:
i. \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}\)
ii. \(\frac {1}{f}\) = (n – 1) \(\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
Calculation: From formula (i),
\(\frac{1}{f}=\frac{1}{7.5}-\frac{1}{(-15)}=\frac{1}{5}\)
∴ f = +5 cm
Substituting this value in formula (ii), we get,
\(\frac{1}{5}=(2-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
∴ \(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}=\frac{1}{5}\)
By sign conventions,
\(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\left(-\mathrm{R}_{2}\right)}=\frac{1}{5}\) ………….. (1)
Also \(\frac{\left|R_{1}\right|}{\left|R_{2}\right|}=\frac{1}{5}\)
∴ |R2| = 5 |R1| …………… (2)
Substituting in equation (1),
∴ \(\frac{1}{R_{1}}-\frac{1}{\left(-5 R_{1}\right)}=\frac{1}{5}\)
∴ \(\frac {6}{5R_1}\) = \(\frac {1}{5}\)
∴ R1 = 6 cm
Using in equation (2),
R2 = 5 × 6 = 30 cm
Question 32.
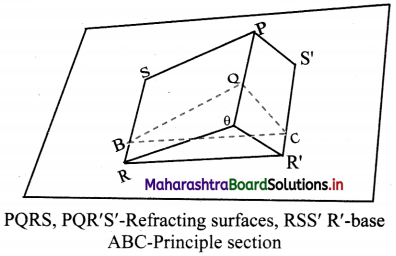
Why are prism preferred for dispersion over two parallel surfaces? Explain its construction in brief.
Answer:
i. In case of two parallel surfaces, for dispersion to be easily detectable, they must be separated over a large distance.
ii. In order to have appreciable and observable dispersion, two parallel surfaces are not useful. In such case we use prisms, in which two refracting surfaces inclined at an angle.
iii. Commonly used prisms have three rectangular surfaces forming a triangle.
iv. Two of which take part in refraction at a time. The one, not involved in refraction is called base of the prism.
v. Any section of prism perpendicular to the base is called principal section of the prism. Commonly all the rays considered during refraction lie in this plane.
Question 33.
Draw neat labelled diagrams showing refraction of a monochromatic light and white light through a prism.
Answer:
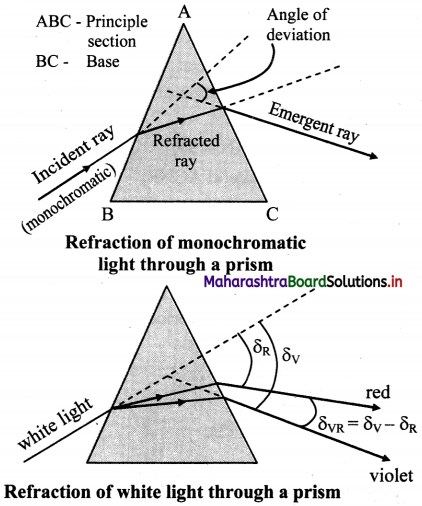
Question 34.
For a prism prove that i + e = A + δ where the symbols have their usual meanings.
Answer:
i. Consider a principal section ABC of a prism of absolute refractive index n kept in air as shown in figure.
ii. Let A be the refracting angle of prism and surface BC be the base.
iii. A monochromatic ray PQ obliquely strikes first reflecting surface AB such that, angle of incidence ∠PQM at Q is i.
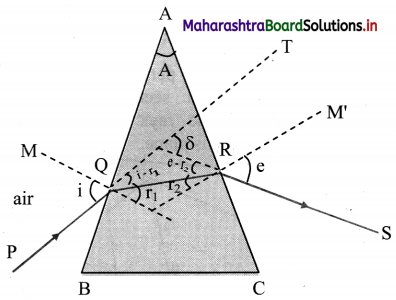
iv. After refraction at Q, the ray deviates towards the normal and strikes second refracting surface AC at R which is the point of emergence.
v. Angles of refraction at Q (∠NQR) and at R (∠QRN) are r1 and r2 respectively.
vi. After R. the ray deviates away from normal and finally emerges along RS making e as the angle of emergence.
vii. Emergent ray RS meets an extended incident ray QT at X if traced backward. In this case, ∠TXS gives the angle of deviation.
viii. From figure,
∠AQN = ∠ARN = 90°
∴ From quadrilateral AQNR,
A + ∠QNR = 180° ………. (1)
From ∆ QNR,
r1 + r2 + ∠QNR = 180° ………. (2)
∴ A = r1 + r2 ……… (3)
ix. Angle δ forms an exterior angle for ∆ XQR.
∴ ∠XQR + ∠XRQ = δ
∴ (i – r1) + (e – r2) = δ
∴ (i + e) – (r1 + r2) = δ
From equation (3),
δ = i + e – A
∴ i + .e = A + δ
Question 35.
Explain δ versus i curve for refraction of light through a prism.
Answer:
i. Variation of angle of incidence i with angle of deviation δ is as shown in figure.
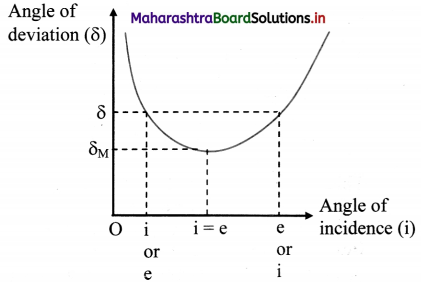
ii. It shows that, with increasing values of i, the angle of deviation δ decreases initially to a certain minimum (δm) value and then increases.
iii. The curve shown in the figure is not a symmetric parabola, but the slope in the part towards right is less.
iv. Except at δ = δm there are two values of i for any given δ. From principle of reversibility of light, we can conclude that if one of these values is i, the other must be e and vice versa. Thus at δ = δm, we have i = e.
Question 36.
Show that, at condition of minimum deviation, n = \(\frac{\sin \left(\frac{\mathbf{A}+\boldsymbol{\delta}_{\mathrm{m}}}{\mathbf{2}}\right)}{\sin \left(\frac{\mathbf{A}}{\mathbf{2}}\right)}\)
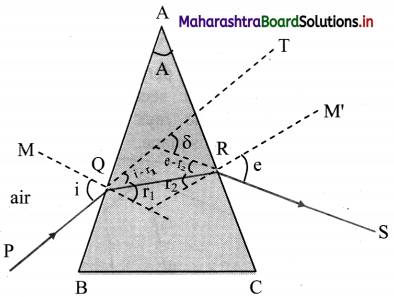
i. For every angle of deviation except angle of minimum deviation, there are two values of angle of incidence.
ii. However, at angle of minimum deviation there is only one corressponding angle of incidence.
iii. From principle of reversibility in path PQRS, the values of i and e are interchangeable for every δ. Thus, at minimum deviation, i = e.
iv. This implies the angles of refraction r1 and r2 are also equal. Also, A = r1 + r2
∴ A = 2 r i.e., r = \(\frac {A}{2}\) ……. (1)
v. In case of minimum deviation, QR is parallel to base BC and the figure is symmetric.
vi. Using i + e = A + δ,
i + i = A + δm
∴ i = \(\frac {A+δ_m}{2}\) …………….(2)
vii. According to Snell’s law,
n = \(\frac {sin i}{sin r}\)
Thus, using equations (1) and (2),
n = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_{\mathrm{m}}}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\)
This is the prism formula.
Question 37.
For grazing emergence of a ray in a prism, find out minimum possible values for angle of incidence (i) and angle of refraction (r1) for commonly used glass prism.
Answer:
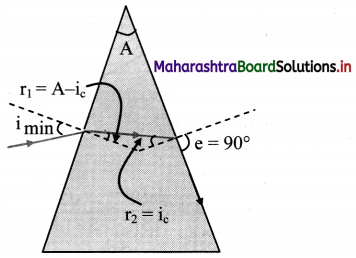
i. At the point of emergence in prism, the ray travels from a denser medium into rarer.
Thus, if r2 = sin-1 (\(\frac {1}{n}\)) is the critical angle, the angle of emergence e = 90°. This is called grazing emergence.
ii. Angle of prism A is constant for a given prism and A = r1 + r2. Hence the corresponding r1 and i will have their minimum possible values.
iii. For commonly used glass prisms,
n = 1.5 (r2)max = sin-1 (\(\frac {1}{n}\)) = sin-1 (\(\frac {1}{1.5}\)) = 41.49°
iv. If, prism is symmetric (equilateral),
A = 60°
∴ r1 = 60° – 41°49′ = 18°11′
∴ n = 1.5 = \(\frac{\sin \left(\mathrm{i}_{\min }\right)}{\sin \left(18^{\circ} 11^{\prime}\right)}\)
sin (imin) = 1.5 × sin (18°11′)
∴ iimin = 27°55′ ≅ 28°.
![]()
Question 38.
Derive the formula for angle of deviation for thin prisms.
OR
Show that in a thin prism, for small angles of incidence, angle of deviation is constant (independent of angle of incidence).
Answer:
For thin prisms (refracting angle < sin 10°). sin θ ≈ θ
∴ Refractive index, n = \(\frac{\sin \mathrm{i}}{\sin \mathrm{r}_{1}} \approx \frac{\mathrm{i}}{\mathrm{r}_{1}}\)
Also n = \(\frac{\sin e}{\sin \mathrm{r}_{2}} \approx \frac{\mathrm{e}}{\mathrm{r}_{2}}\)
∴ i ≈ n r1 and e ≈ nr2
ii. Substituting this in, i + e = A + δ, we get,
i + e = n (r1 + r2) = nA = A + δ
∴ S = A(n – 1)
A and n are constant for a given prism. Thus, for a thin prism, for small angles of incidence, angle of deviation is constant (independent of angle of incidence).
Question 39.
Give the expression for mean deviation for a beam of white light.
Answer:
For a beam of white light, yellow colour is practically chosen to be the mean colour for violet and red.
This gives mean deviation as,
δVR = \(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\) ≈ δY = A(nY – 1)
Where, nY = refractive index for yellow colour.
Question 40.
A fine beam of white light is incident upon the longer side of a plane parallel glass slab of breadth 5 cm at angle of incidence 60°. Calculate lateral deviation of red and violet rays and lateral dispersion between them as they emerge from the opposite side. Refractive indices of the glass for red and violet are 1.51 and 1.53 respectively.
Answer:
As shown in figure,
VM = LV = lateral deviation for violet colour,
RT = LR = lateral deviation for red colour,
∴ Lateral dispersion between these colours, LVR = LV – LR
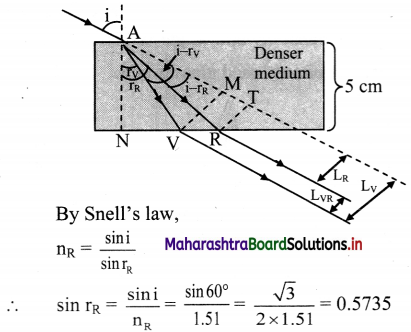
∴ rR = sin-1 (0.5735) ≈ 35°
Similarly,
sin rV = \(\frac{\sin 60^{\circ}}{1.53}=\frac{\sqrt{3}}{2 \times 1.53}=\frac{1.732}{3.06}\)
= antilog {log (1.732) – log (3.06)}
= antilog {0.2385 – 0.4857}
= antilog 11.7528}
= 0.5659
∴ sin rV = 0.566
∴ rV = sin-1 (0.566) = 34°28′
∴ Angle of deviation for red colour
= i – rR = 60° – 35° = 25°
and that for violet colur = i – rV = 60° – 34°28′
= 25°32′
From figure, in ∆ANR,
AR = \(\frac{\mathrm{AN}}{\cos \mathrm{r}_{\mathrm{R}}}=\frac{5}{\cos \left(35^{\circ}\right)}=\frac{5}{0.8192}\) = 6.104 cm
Similarly ∆ANV,
AV = \(\frac{\mathrm{AN}}{\cos \mathrm{r}_{\mathrm{V}}}=\frac{5}{\cos \left(34^{\circ} 28^{\prime}\right)}=\frac{5}{0.8244}\) = 6.065 cm
∴ For red colour, LR = RT = AR [sin(i – rR)]
= AR [sin (25°)]
= 6.104 × 0.4226
= 2.58 cm
For violet colour, LV = VM
= AV [sin (i – rV)]
= AV × sin (25° 32′)
= 6.065 × 0.431
= 2.61 cm
∴ LVR = LV – LR = 2.61 – 2.58 = 0.03 cm
= 0.3 mm
Question 41.
For a glass (n = 1.5) prism having refracting angle 60°, determine the range of angle of incidence for which emergent ray is possible from the opposite surface and the corresponding angles of emergence. Also calculate the angle of incidence for which i = e. How much is the corresponding angle of minimum deviation?
Answer:
For an equilateral prism of glass, the minimum angle of incidence for which the emergent ray just emerges is imin = 27° 55′. Corresponding angle of emergence is, emax = 90°.
From the principle of reversibility of light, imax = 90° and emin = 27°55′
Also, for equilateral glass prism at minimum deviation,

Also, from prism formula,
i + e = A + δ
At minimum deviation,
∴ i + i = 60 + 37°10′ = 97°10′
∴ i = 48°35′
Question 42.
For a dense flint glass prism of refracting angle 10°, obtain angular deviation for extreme colours and dispersive power of dense flint glass. (nred = 1.712, nviolet = 1.792)
Answer:
Given: A = 10°, nR = 1.712, nV = 1.792
To find:
i. Angular deviation for extreme colours (δV and δR)
ii. Dispersive power of flint glass (ω)
Formulae:
i. δ = A(n – 1)
ii. ω = \(\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)}\)
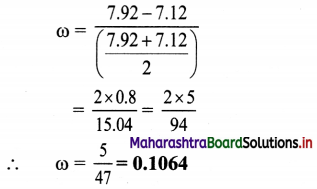
Question 43.
The refractive indices of the material of the prism for red and yellow colour are 1.620 and 1.635 respectively. Calculate the angular dispersion and dispersive power, if refracting angle is 8°.
Solution:
Given: nR = 1.620, nY = 1.635, A = 8°
To find:
i. Angular dispersion (δV – δR)
ii. Dispersive power (ω)
Formulae:
i. δv – δr = A(nV – nR)
ii. ω = \(\frac{\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}}{\mathrm{n}_{\mathrm{Y}}-1}\)
Calculation: Since, nY = \(\frac {n_V+n_R}{2}\)
∴ nV = 2nY – nR
nV = 2 × 1.635 – 1.620 = 3.27 – 1.620
∴ nV = 1.65
From formula (i),
δV – δR = 8(1.65 – 1.620)
= 8 × 0.03 = 0.24°
∴ δV – δR = 0.24°
From formula (ii),
ω = \(\frac{1.65-1.620}{1.635-1}=\frac{0.03}{0.635}\) = 0.0472
Question 44.
What could be the possible reasons for the upward bending of the light ray during hot days?
Answer:
Possible reasons for the upward bending at the road could be:
i. Angle of incidence at the road is glancing. At glancing incidence, the reflection coefficient is very large which causes reflection.
ii. Air almost in contact with the road is not steady. The non-uniform motion of the air bends the ray upwards and once it has bent upwards, it continues to do so.
![]()
Question 45.
State some properties of rainbow.
Answer:
- It is seen during rains and on the opposite side of the Sun.
- It is seen only during mornings and evenings and not throughout the day.
- In the commonly seen rainbow red arch is outside and violet is inside.
- In the rarely occurring concentric secondary rainbow, violet arch is outside and red is inside.
- It is in the form of arc of a circle.
- Complete circle can be seen from a higher altitude, i.e. from an aeroplane.
- Total internal reflection is not possible in this case.
Question 46.
Why is total internal reflection not possible during formation of a rainbow ?
Answer:
i. For total internal reflection, the angle of incidence in the denser medium must be greater than critical angle for the given pair of media.
ii. The relative refractive index of air with the water drop is just less than 1 and hence the critical angle is almost equal to 90°.
iii. Angle of incidence i in air, at the water drop, can’t be greater than 90°.
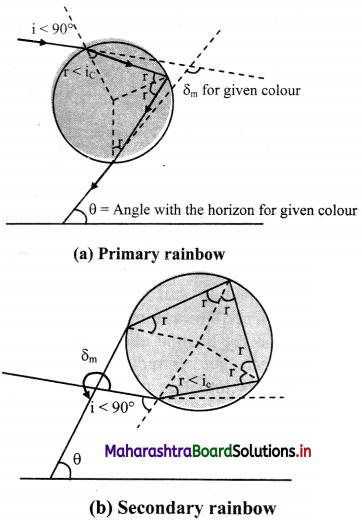
iv. As a result, angle of refraction r in water will always be less than the critical angle.
v. The figures shown indicates that this angle r itself acts as an angle of incidence at any point for one or more internal reflections. But this does not indicate the total internal reflection.
Question 47.
Rainbow is seen only for a definite angle range with respect to the ground. Justify.
Answer:
i. For clear visibility of rainbow, a beam must have enough intensity.
ii. The curve for angle of deviation and angle of incidence is almost parallel to X-axis near minimum deviation i.e., for majority of angles of incidence in this range, the angle of deviation is nearly the same and those rays form a beam of enough intensity.
iii. Rays beyond this range suffer wide angular dispersion and thus will not have enough intensity for visibility. Hence, the rainbow is seen only for a definite angle range with respect to the ground for which the intensity of the beam is enough for the visibility.
Question 48.
How is the range of angles for which rainbows can be observed calculated?
Answer:
i. Angle of deviation for the final emergent ray, can be shown to be equal to δ = π + 2i – 4r for primary rainbow and δ = 2π + 2i – 6r for the secondary rainbow.
ii. Using these relations along with Snell’s law, sin i = n sin r, derivatives of angle of deviation (δ) is obtained.
iii. Second derivative of δ comes out to be negative, which shows that it is the minima condition.
iv. Equating first derivative to zero corresponding values of i and r are obtained. Thus, from the figures shown, the corresponding angles θR and θV at the horizontal are obtained. These angles give the visible angular position for the rainbow.
Question 49.
When can one see complete circle of a rainbow? Explain in detail.
Answer:
i. Figure given below illustrates formation of primary and secondary rainbows with their common centre O. It is the point where the line joining the sun and the observer meets the Earth when extended.
ii. P is location of the observer. Different colours of rainbows are seen on arches of cones of respective angles.
iii. Smallest half angle refers to the cone of violet colour of primary rainbow, which is 41°.
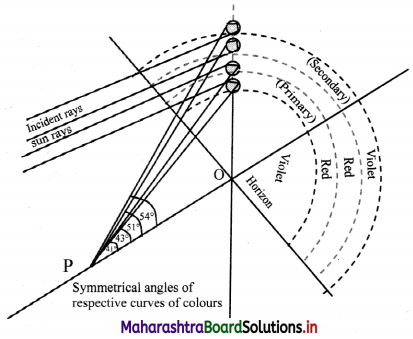
iv. As the Sun rises, the relative position of common centre of the rainbows with respect to observer shifts down. Hence as the Sun comes up, smaller and smaller part of the rainbows will be seen. If the Sun is above 41°, violet arch of primary rainbow cannot be seen.
v. Beyond 53°, no rainbows will be visible. That is why rainbows are visible only during mornings and evenings and in the shape of a bow.
vi. However, if observer moves up (may be in an aeroplane), the line PO itself moves up making lower part of the arches visible. After a certain minimum elevation, entire circle for all the cones can be visible.
Question 50.
Define following terms:
i. Longitudinal chromatic aberration
ii. Circle of least confusion
iii. Transverse chromatic aberration
Answer:
i. Longitudinal chromatic aberration:
Due to different refractive indices and angle of deviations, violet and red colours of a white light converge at different focal points, fV and fR. The distance between fV and fR is measured as the longitudinal chromatic aberration.
ii. Circle of least confusion:
In presence of aberration the image is not a single point but always a circle. At particular location on the screen, this circle has minimum diameter. This is called circle of least confusion.
iii. Transverse chromatic aberration:
Radius of the circle of least confusion is called the transverse chromatic aberration.
Question 51.
After Cataract operation, a person is recommended with concavo-convex spectacles of curvatures 10 cm and 50 cm. Crown glass of refractive indices 1.51 for red and 1.53 for violet colours is used for this. Calculate the lateral chromatic aberration occurring due to these glasses.
Answer:
For a concavo-convex lens, with convex shape facing the object, both the radii of curvature are positive as shown in the figure.
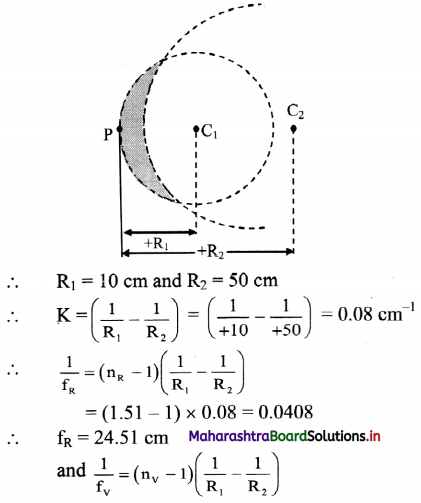
= (1.53 – 1) × 0.08 = 0.0424
∴ fv = 23.58 cm
∴ Longitudinal (lateral) chromatic aberration
= fV – fR = 24.51 – 23.58 = 0.93 cm
Question 52.
Why do we need optical instruments for?
Answer:
i. Due to the limitation for focusing the eye lens it is not possible to take an object closer than a certain distance. This distance is called least distance of distance vision D. For a normal, unaided human eye D = 25cm.
ii. If an object is brought closer than this, we cannot see it clearly.
iii. If an object is too small the corresponding visual angle from 25 cm is not enough to see it and if we bring it closer than that, its image on the retina is blurred.
iv. Also, the visual angle made by cosmic objects far away from us such as stars is too small to make out minor details and we cannot bring those closer.
v. In such cases we need optical instruments like microscope and telescopes to observe these things clearly.
![]()
Question 53.
A convex lens has focal length of 2.0 cm. Find its magnifying power if image is formed at DDV.
Answer:
Given: f = 2 cm, v = D = 25 cm
To find: Magnifying power (M.P.)
Formula: M.P = 1 + \(\frac {D}{f}\)
Calculation:
From formula,
M.P = 1 + \(\frac {25}{2}\)
M.P. = 1 + 12.5 = 13.5
Question 54.
A magnifying glass of focal length 10 cm is used to read letters of thickness 0.5 mm held 8 cm away from the lens. Calculate the image size. How big will the letters appear? Can you read the letters if held 5 cm away from the lens? If yes, of what size would the letters appear? If no, why not?
Answer:
Given that, f = +10 cm, u = -8 cm,
From thin lens formula,
\(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}\)
∴ \(\frac{1}{10}=\frac{1}{\mathrm{v}}-\frac{1}{-8}\)
∴ v = 40 cm
Magnification of a lens is,
m = \(\frac {v}{u}\) = \(\frac {Object size h-i}{Object size h-0}\)
∴ \(\frac {40}{8}\) = \(\frac {h_1}{0.5}\)
∴ h1 = 2.5 cm
This implies the height of the image is 5 times that of the object.
Magnifying power,
M = \(\frac {D}{u}\) = \(\frac {25}{8}\) = 3.125
∴ Image will appear to be 3.125 times bigger,
i.e., 3.125 × 0.5 = 1.5625 cm
For u = -5 cm, v will be -10 cm
For an average human being to see clearly, the image must be at or beyond 25 cm. Thus it will not possible to read the letters if held 5 cm away from the lens.
Question 55.
A compound microscope has a magnification of 15. If the object subtends an angle of 0.5° to eye, what will be the angle subtended by the image at the eye?
Answer:
Given: M.P = 15, α = 0.5°
To Find: Angle(β)
Formula: M.P = \(\frac {β}{α}\)
Calculation:
From formula,
β = M.P × α = 15 × 0.5 = 7.5°
Question 56.
A compound microscope has a magnifying power of 40. Assume that the final image is formed at DDV(25 cm). If the focal length of eyepiece 10 cm, calculate the magnification produced by objective.
Answer:
M.P = 40, D = 25 cm, fe = 10 cm
To Find: Magnification (m0)
Formula: M.P = m0 × Me
Calculation:
From the formula,

Question 57.
The pocket microscope used by a student consists of eye lens of focal length 6.25 cm and objective of focal length 2 cm. At microscope length 15 cm, the final image appears biggest. Estimate distance of the object from the objective and magnifying power of the microscope.
Answer:
Given: fe = 6.25 cm, f0 = 2 cm, L = 15 cm
As image appears biggest, Ve = -25 cm.
To find:
i. Distance of object from objective (u0)
ii. Magnifying power (M)
Formula:
i. \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}\)
ii. L = |v0| + |ue|
iii. M = \(\left(\frac{v_{o}}{u_{o}}\right)\left(\frac{D}{u_{e}}\right)\)
Calculation: For eyelens, using formula (i),
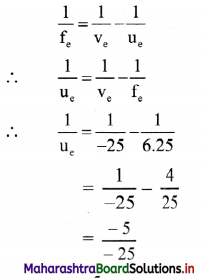
∴ ue = 5 cm
From formula (ii),
|v0| = L – |ue|
= 15 – 5 = 10 cm
Using formula (i) for objective,

Question 58.
Focal length of the objective of an astronomical telescope is 1 m. Under normal adjustment, length of the telescope is 1.05 m. Calculate focal length of the eyepiece and magnifying power under normal adjustment.
Answer:
Given: f0 = 1 m, L = 1.05 m
To find:
i. Focal length of eyepiece (fe)
Magnifying power under normal adjustment (M)
Formula:
i. L = f0 + fe
ii. M = \(\frac {f_0}{f_e}\)
Calculation. From formula (i),
fe = L – f0 = 1.05 – 1 = 0.05 m
From formula (ii),
M = \(\frac {1}{0.05}\) = 20
Question 59.
Magnifying power of an astronomical telescope is 12 and the image is formed at D.D.V. If the focal length of the objective is 90 cm, what is the focal length of the eyepiece?
Answer:
Given: M.P = 12, v = D, f0 = 90 cm,
To find: Focal length of eye piece (fe)
Formula: M.P = \(\frac {f_0}{f_e}\) (1 + \(\frac {f_e}{D}\))
Calculation:
From formula.
12 = \(\frac {90}{f_e}\) (1 + \(\frac {f_e}{25}\))
∴ fe = 10.71 cm
![]()
Question 60.
Two convex lenses of an astronomical telescope have focal length 1.3 m and 0.05 m respectively. Find the magnifying power and the length of the telescope.
Answer:
Given: f0 = 1.3 m, fe = 0.05 m
To find:
i. Magnifying power of telescope (M.P.)
ii. Length of telescope (L)
Formulae:
i. M.P = \(\frac {f_0}{f_e}\)
ii. L = f0 + fe
Calculation: From formula (i),
M.P = \(\frac {1.3}{0.05}\) = 26
From formula (ii),
L = 1.3 + 0.05 = 1.35 m
Question 61.
What is the angle of deviation of reflected ray if ray of light is incident on a plane mirror at an incident angle θ?
Answer: When a ray of light is incident on a plane mirror at an angle θ, the reflected ray gets deviated by an angle of (π – 2θ).
Question 62.
Does nature of the image depend upon size of the mirror?
Answer:
No, nature of the image is independent of size of the mirror.
Question 63.
If a convex mirror is held in air and then dipped in oil, then what will be the change in its focal length?
Answer:
Focal length of spherical mirrors are independent of the medium.
Question 64.
When ray of light falls normally on a mirror, its angle of incidence is 90°. True or false? Justify your answer.
Answer:
False, when light falls normally on a mirror, its angle of incidence is zero degree.
Question 65.
In one of the performances, a magician keeps a gold ring beneath a thick glass slab (µ = \(\frac {3}{2}\)) Then he keeps a flask filled with water (µ = \(\frac {4}{3}\)), over the slab. Now when spectators one by one observe from the open end of the flask, the ring disappears at a certain angle of viewing.
i. What could be the reason behind the disappearance?
ii. At what angle of viewing the ring vanishes?
Answer:
i. The ring disappears due to total internal reflection of the light at water-air interface.
ii. aµw = \(\frac {4}{3}\)
sin ic = \(\frac {1}{µ}\)
∴ ic = sin-1 (\(\frac {1}{_aµ_w}\)) = sin-1 (\(\frac {3}{4}\)) = 48.6°
Hence, for angle of viewing for which angle of incidence of ring from water to air is greater that 48.6°, the ring will vanish.
Question 66.
Why dispersion of light is not observed in glass slab but it is observed in prism?
Answer:
When a light passes from one medium to another, at one interface, it changes its speed. The glass slab and prism both have two glass-air interfaces. Hence, the light undergoes refraction twice in both the cases. When the two interfaces are parallel to each other, although the colours are separated at first interface, they all travel the same path after refracting from second interface. However, in prism, the two interfaces are not parallel. Therefore, the colours separated at first interface do not travel the same path after second refraction but emerge out at different wavelengths producing spectrum.
Question 67.
A prism manufacturer is planning to build a dispersive prism out of following materials with the refracting angles as given.
i. Glass (µ = 1.5), A = 60°
ii. Plastic (µ = 1.4), A = 90°
iii. Fluorite (µ = 1.45), A = 64°
If he desires to give the prism following relations of i and δ, then which of the above combinations can be used to construct the prism?
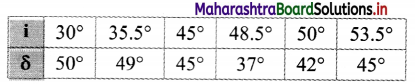
Answer:
From the given values of i and δ, δm = 37°
From prism formula, µ = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_{\mathrm{m}}}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\)
i. For Glass (µ = 1.5), A = 60°;
µ = \(\frac{\sin \left(\frac{60^{\circ}+37^{\circ}}{2}\right)}{\sin \left(30^{\circ}\right)}\)
= 1.5
Hence, this combination can be used for fabricating the desired prism.
ii. For Plastic (µ = 1.4), A = 90°;
µ = \(\frac{\sin \left(\frac{90^{\circ}+37^{\circ}}{2}\right)}{\sin \left(45^{\circ}\right)}\)
= 1.26
As Ppiastic = 1-4, this combination cannot be used.
iii. For Fluorite (µ = 1.45), A = 64°
µ = \(\frac{\sin \left(\frac{64^{\circ}+37^{\circ}}{2}\right)}{\sin \left(32^{\circ}\right)}\)
= 1.45
Hence, this combination can also be used for fabrication of prism.
Question 68.
Find the refractive index of material of following prism if the ray of light incident at angle 45° suffers minimum deviation through the prism.

Answer:

A = 60°
Also, ray of light suffers minimum deviation.
∴ 2i = A + δm
∴ δm = 2i – A = 90° – 60° = 30°
From prism formula,
µ = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_{\mathrm{m}}}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\)
= \(\frac{\sin \left(\frac{60^{\circ}+30^{\circ}}{2}\right)}{\sin \left(30^{\circ}\right)}\)
= √2
Hence, refractive index of material of prism is √2.
Multiple Choice Questions
Question 1.
Time taken by light to cross a glass slab of thickness 4 mm and refractive index 3 is
(A) 4 × 10-11 s
(B) 2 × 10-11 ns
(C) 16 × 10-11 s
(D) 8 × 10-10 s
Answer:
(A) 4 × 10-11 s
![]()
Question 2.
If mirrors are inclined to each other at an angle of 90°, the total number of images seen for a symmetric position of an object will be
(A) 3
(B) 4
(C) 5
(D) 3 or 4
Answer:
(A) 3
Question 3.
In case of a convex mirror, the image formed is
(A) always on opposite side, virtual, erect.
(B) always on the same side, virtual, erect.
(C) always on opposite side, real, inverted.
(D) dependent on object distance.
Answer:
(A) always on opposite side, virtual, erect.
Question 4.
A glass slab is placed in the path of a beam of convergent light. The point of convergence of light
(A) moves towards the glass slab.
(B) moves away from the glass slab.
(C) remains at the same point.
(D) undergoes a lateral shift.
Answer:
(A) moves towards the glass slab.
Question 5.
For a person seeing an object placed in optically rarer medium,
(A) apparent depth of the object is more than real depth
(B) apparent depth is smaller than the real depth.
(C) apparent depthe might be smaller or greater depending on the position of the person.
(D) nothing can be concluded about the depth of object from given data.
Answer:
(A) apparent depth of the object is more than real depth
Question 6.
Light travels from a medium of refractive index µ1 to another of refractive index µ2 (µ1 > µ2). For total internal reflection of light, which is NOT true?
(A) Light must travel from medium of refractive index µ1 to µ2.
(B) Angle of incidence must be greater than the critical angle.
(C) There is no refraction of light.
(D) Light must travel from the medium of refractive index µ2 to µ1.
Answer:
(D) Light must travel from the medium of refractive index µ2 to µ1.
Question 7.
Optical fibre is based on which of the following phenomenon?
(A) Reflection.
(B) Refraction.
(C) Total internal reflection.
(D) Dispersion.
Answer:
(C) Total internal reflection.
Question 8.
Commonly used glass have refractive index of 1.5. What is the critical angle for such glass?
(A) 49°
(B) 42°
(C) 45°
(D) 40°
Answer:
(B) 42°
Question 9.
If the refractive index of water is 4/3 and that of glass slab is 5/3. Then the critical angle of incidence for which a light ray tending to go from glass to water is totally reflected, is
(A) sin-1 (\(\frac {3}{4}\))
(B) sin-1 (\(\frac {3}{5}\))
(C) sin-1 (\(\frac {2}{3}\))
(D) sin-1 (\(\frac {4}{5}\))
Answer:
(D) sin-1 (\(\frac {4}{5}\))
Question 10.
While deriving prism formula, which of the following condition is NOT satisfied?
(A) I = e
(B) r1 = r2
(C) r = \(\frac {A}{2}\)
(D) δm = i + e + r
Answer:
(D) δm = i + e + r
Question 11.
If the critical angle for the material of a prism is C and the angle of the prism is A, then there will be no emergent ray when
(A) A < 2 C
(B) A = 2 C
(C) A > 2 C
(D) A < \(\frac {C}{2}\)
Answer:
(C) A > 2 C
![]()
Question 12.
Chromatic aberrations is caused due to
(A) spherical shape of lens
(B) spherical shape of mirrors
(C) angle of deviation for violet light being more than that for red light.
(D) refractive index for violet light being less than that for red light
Answer:
(C) angle of deviation for violet light being more than that for red light.
Question 13.
In normal adjustment, magnifying powser of a astronomical telescope is given by
(A) \(\frac {D}{f_0}\) \(\frac {L}{f_e}\)
(B) \(\frac {L}{D}\) \(\frac {f_e}{f_0}\)
(C) \(\frac {f_0}{f_e}\)
(D) \(\frac {f_e}{f_0}\)
Answer:
(C) \(\frac {f_0}{f_e}\)