Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 8 Sound Important Questions and Answers.
Maharashtra State Board 11th Physics Important Questions Chapter 8 Sound
Question 1.
State the different types of waves.
Answer:
- Waves that require a material medium for their propagation are called mechanical waves. Example: Sound waves, string waves, seismic waves, etc.
- Waves that do not require a material medium for their propagation are called electromagnetic waves. Example: Light waves, radio waves, y-rays, etc.
- The wave associated with any object when it is in motion is called a matter-wave.
- Waves in which a disturbance created at one place travel to distant points and keeps travelling unless stopped by an external force are known as travelling or progressive waves.
- Waves are also of stationary type.
![]()
Question 2.
Define the following terms. Give their SI units.
i. Period
ii. Frequency
iii. Velocity
Answer:
i. Period (T):
The time taken by the particle of a medium to complete one vibration is called period of the wave.
SI unit: second (s)
ii. Frequency (n):
The number of vibrations performed by a particle per second is called frequency of a wave.
SI unit: hertz (Hz)
iii. Velocity (v):
The distance covered by a wave per unit time is called the velocity of the wave.
SI unit: m/s
Question 3.
State the properties that should be possessed by a medium for a mechanical wave to propagate through it.
Answer:
- The medium must be continuous and elastic so that it can regain its original state as soon as the deforming forces are removed.
- The medium should possess inertia. It must be capable of storing energy and transferring it in the form of waves.
- The frictional resistance of the medium should be negligible to avoid damped oscillations.
Question 4.
What are two types of progressive waves? State two characteristics of progressive waves.
Answer:
Progressive waves are classified into two types:
a. Transverse progressive waves
b. Longitudinal progressive waves.
Characteristics of progressive waves:
1. All the vibrating particles of medium have same amplitude, period and frequency.
2.. State of oscillation i.e., phase changes from particle to particle.
Question 5.
A violin string emits sound of frequency 510 Hz. How far will the sound waves reach when string completes 250 vibrations? The velocity of sound is 340 m/s.
Answer:
Given: n = 510 Hz, v = 340 m/s,
number of vibrations = 250
To find: Distance
Formula: v = nλ
Calculation:
From formula,
λ = \(\frac {v}{n}\) = \(\frac {340}{510}\) = \(\frac {2}{3}\) m
Distance covered in 1 vibration = \(\frac {2}{3}\) m
∴ Distance covered in 250 vibration
= \(\frac {2}{3}\) × 250 = 166.7 m 3
Answer: The distance covered by sound waves is 166.7 m
Question 6.
The speed of sound in air is 330 m/s and that in glass is 4500 m/s. What is the ratio of the wavelength of sound of a given frequency in the two media?
Answer:
Given: vair = 330 m/s, vglass = 4500 m/s
To find: \(\frac {λ_{air}}{λ_{glass}}\)
Formula: v = nλ
Calculation: From formula,
vair = n λair
vglass = n λglass
∴ \(\frac {λ_{air}}{λ_{glass}}\) = \(\frac {v_{air}}{v_{glass}}\) = \(\frac {330}{4500}\) = 7.33 × 10-2
Question 7.
The velocity of sound in gas is 498 m/s and in air is 332 m/s. What is the ratio of wavelength of sound waves in gas to air?
Answer:
vg = 498 m/s, va = 332 m/s
To find: Ratio of wavelengths (\(\frac {λ_g}{λ_a}\))
Formula: v = nλ
Calculation:
Frequency of sound wave remains same.
From formula,
For gas λg = \(\frac {v_g}{n}\) and for air λag = \(\frac {v_a}{n}\)
∴ \(\frac {v_g}{v_a}\) = \(\frac {v_g}{v_a}\) = \(\frac {498}{332}\) = \(\frac {3}{2}\)
∴ \(\frac {v_g}{v_a}\) = 3 : 2
Question 8.
A human ear responds to sound waves of frequencies in the range of 20 Hz to 20 kHz. What are the corresponding wavelengths, if the speed of sound in air is 330 m/s? Answer:
Given: v1 = vg = 330 m/s, n1 = 20 Hz,
n2 = 20 kHz = 20 × 10³ Hz
To find: Wavelength (λ1 and λ2)
Formula: v = nλ
Calculation:
From formula,
λ1 = \(\frac {v_1}{n_1}\) = \(\frac {330}{20}\) = 16.5 m
λ2 = \(\frac {v_2}{n_2}\) = \(\frac {330}{20×10^3}\) = 16.5 × 10-3 = 0.0165 m
Question 9.
A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (i) the reflected sound, (ii) the transmitted sound? Speed of sound in air is 340 m s-1 and in water is 1486 m s-1
Answer:
Given: n = 1000 kHz = 106 Hz,
va = 340 m/s,
vw = 1486 m/s
To find: Reflected wavelength (λR),
Transmitted wavelength (λT),
Formula: v = nλ
Calculation:
In different medium, frequency of sound wave remains same.
From formula,
Sound is reflected in air,
i. ∴ λR = \(\frac {v_a}{n}\) = \(\frac {330}{10^6}\) = 3.4 × 10-4 m
Sound is transmitted in water,
ii. ∴ λT = \(\frac {v_w}{n}\) = \(\frac {1486}{10^6}\) = 1.486 × 10-3 m
![]()
Question 10.
The wavelength of a sound note is 1 m in air and 2.5 m in a liquid. Find the speed of sound in the liquid, if the speed of the sound in air is 330 m/s.
Answer:
Given: λa = 1 m, λl = 2.5 m, va = 330 m/s,
To find: Speed of sound (vl)
Formula: v = nλ
Calculation:
From formula,
Since the frequency n remains the same,
va = nλa and vl = nλl
∴ \(\frac {v_l}{v_a}\) = \(\frac {λ_l}{λ_a}\)
∴ vl = va \(\frac {λ_l}{λ_a}\) = 330 × \(\frac {2.5}{1}\) = 825 m/s
Question 11.
Define a polarised wave.
Answer:
A wave in which the vibrations of all the particles along the path of a wave are constrained to a single plane is called a polarised wave.
Question 12.
Write down the main characteristics of longitudinal waves.
Answer:
Characteristics of longitudinal waves:
- All the particles of medium in the path of wave vibrate in a direction parallel to the direction of propagation of wave with same period and amplitude.
- When longitudinal wave passes through a medium, the medium is divided into alternate compressions (high pressure zone) and rarefactions (low pressure zone).
- A compression and adjacent rarefaction form one cycle of a longitudinal wave. The distance between any two consecutive points having same phase (successive compression or rarefactions) is called wavelength of the wave.
- For propagation of longitudinal waves, the medium should possess the property of elasticity of volume (bulk modulus). Thus, longitudinal waves can travel through solids, liquids and gases. Longitudinal wave cannot travel through vacuum or empty space.
- The compressions and rarefactions advance in the medium and are responsible for transfer of energy.
- When longitudinal wave advances through medium, there is periodic variations in pressure and density along the path of wave and with time.
- Since the direction of vibration of particles and direction of propagation of wave are same or parallel, longitudinal waves cannot be polarised.
Question 13.
State the mathematical expression for a transverse progressive wave travelling along the positive and negative x-axis.
Answer:
i. Consider a transverse progressive wave whose particle position is described by x and displacement from equilibrium position is described by y.
Such a sinusoidal wave can be written as follows:
∴ y (x, t) = a sin (kx – ωt + ø) ……… (1)
where a, k, ω and ø are constants,
y (x, t) = displacement as a function of position (x) and time (t)
a = amplitude of the wave,
ω = angular frequency of the wave
(kx0 – ωt + ø) = argument of the sinusoidal wave and is the phase of the particle at x at time t.
ii. At a particular instant, t = t0,
y (x, t0) = a sin (kx – ωt0 + ø)
= a sin (kx + constant)
Thus at t = t0, shape of wave as a function of x is a sine wave.
iii. At a fixed location x = x0
y(x0, t) = a sin (kx0 – ωt + ø)
= a sin (constant – ωt)
Hence the displacement y, at x = x0 varies as a sine function.
iv. This means that the particles of the medium, through which the wave travels, execute simple harmonic motion around their equilibrium position.
v. For (kx – ωt + ø) to remain constant, x must increase in the positive direction as time t increases. Thus, the equation (1) represents a wave travelling along the positive x axis.
vi. Similarly, a wave travelling in the direction of the negative x axis is represented by,
y(x, t) = a sin (kx + ωt +ø) …….(2)
Question 14.
Explain the Laplace’s correction to the Newton’s formula for the velocity of sound in air.
Answer:
Laplace’s correction:
Laplace suggested that the compression or rarefaction takes place too rapidly. Heat produced during compression and lost during rarefaction does not get sufficient time for dissipation. Due to this, the whole heat content remains same. Thus, it is an adiabatic process.
According to Laplace, E is the adiabatic modulus of elasticity of air medium which is given by,
E = γP ….(1)
where P = pressure of the air medium γ = ratio of specific heat of air at constant pressure (cp) and specific heat of air at constant volume (cv). i.e., γ = cp/cv.
iii. Using equation, v = \(\sqrt{\frac {E}{ρ}}\), we have velocity of sound in air,
v = \(\sqrt{\frac {γP}{ρ}}\), …. [From equation (1)]
For air, γ = 1.41
At NTP, P = 0.76 × 13600 × 9.8 N/m²
ρ = 1.293 kg/m³.
∴ v = \(\sqrt{\frac {1.41×0.76×13600×9.8}{1.293}}\) = 332.35 m/s
This value is in close agreement with the experimental value.
Question 15.
What is the effect of temperature on the velocity of sound in air?
Answer:
Effect of temperature on velocity of sound:
i. Let v0 and v be the velocity of sound in air at T0 and T Kelvin respectively. Let ρ0 and p be the densities of gas at temperature T0 and T respectively.
ii. Considering the number of moles n = 1 for the gas, we have,
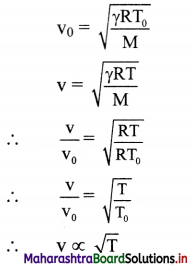
iii. From above formula, we can conclude that velocity of sound in air increases with increase in temperature.
Question 16.
Show that for 1 °C rise in temperature, the velocity of sound in air increases by 0.61 m/s.
Answer:
Let v0 = velocity of sound at 0 °C or 273 K
v = velocity of sound at t °C or (273 + 1) K
we have, v ∝ √T

Hence, velocity of sound increases by 0.61 m/s when temperature increases by 1 °C.
Question 17.
Suppose you are listening to an out-door live concert sitting at a distance of 150 m from the speakers. Your friend is listening to the live broadcast of the concert in another country and the radio signal has to travel 3000 km to reach him. Who will hear the music first and what will be the time difference between the two? Velocity of light = 3 × 108 m/s and that of sound is 330 m/s.
Answer:
Distance between me and the speakers
(s1) = 150 m, distance radio signal has to travel (S2) = 3000 km, vsound 330 m/s, vlight = 3 × 108 m/s
Time taken by sound to reach me,
= \(\frac {s_1}{v_sound}\) = \(\frac {150}{330}\) = 0.4546 s
Time taken by the broadcasted sound (done by
EM waves = \(\frac {s_2}{v_light}\) = \(\frac {3000km}{30×10^5km/s}\) = \(\frac {3×1^30}{3×10^5}\) = 10-2 s
∴My friend will hear the sound first.
The time difference will be = 0.4546 – 0.01
= 0.4446 s.
![]()
Question 18.
Consider a closed box of rigid walls so that the density’ of the air inside it is constant. On heating, the pressure of this enclosed air is increased from P0 to P. It is now observed that sound travels 1.5 times faster than at pressure P0. Calculate P/P0.
Answer:
Given: vP = 1.5 vP0
To find: Ratio of pressure (\(\frac {p}{p_0}\))

Question 19.
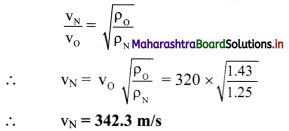
The densities of nitrogen and oxygen at NTP are 1.25 kg/m³ and 1.43 kg/m³ respectively. If the speed of sound in oxygen at NTP is 320 m/s, calculate the speed in nitrogen, under the same conditions of temperature and pressure, (γ for both the gases is 1.4)
Answer:
Given: ρN = 1.25 kg/m³, ρ = 1.43 kg/m³,
v0 = 320 m/s,
To find: Speed in nitrogen (vN)
Formula: v = (\(\sqrt{\frac {γP}{ρ}}\) )
Calculation: From formula,
Question 20.
Find the temperature at which the velocity of sound in air will be 1.5 times its velocity at 0 °C
Answer:
Given: \(\frac {p}{p_0}\) = 1.5, T0 = 0 °C = 273 K
To find: Temperature (T)
Formula: \(\frac {v}{v_0}\) = \(\sqrt{\frac {T}{T_0}}\)
Calculation:
From formula,
\(\frac {T}{T_0}\) = (\(\frac {v}{v_0}\))²
∴ T = T0 (\(\frac {v}{v_0}\))²
∴ T = 273 (1.5)² = 614.25 K = 341.25 °C
Question 21.
The velocity of sound in air at 27 °C is 340 m/s. Calculate the velocity of sound in air at 127 °C.
Answer:
Given: T1 = 27 °C = 27 + 273 = 300 K,
v1 = 340 m/s,
T2 = 127 °C = 127 + 273 = 400 K
To find: Velocity (v2)
Formula: \(\frac {v_1}{v_2}\) = \(\sqrt{\frac {T_1}{T_2}}\)
Calculation: From formula,
v2 = v1 \(\sqrt{\frac {T_2}{T_1}}\) = 340, \(\sqrt{\frac {400}{300}}\)
= 340 × 1.1547
∴ v2 = 392.6 m/s
Question 22.
The wavelength of a note is 27 m in air when the temperature is 27 °C. What is the wavelength when the temperature is increased to 37 °C?
Answer:
Given: λ1 = 27 m,
T1 = 27 °C = 273 + 27 = 300 K,
T2 = 37 °C = 273 + 37 = 310 K
To find: Wavelength (λ2)

Question 23.
We cannot hear an echo at every place. Give reason.
Answer:
- Echo of sound depends upon the temperature of the surrounding and distance between source and reflecting surface.
- To hear a distinct echo at 22 °C, the minimum distance required between the source of sound and reflecting surface should be 17.2 metre.
- The velocity of sound depends on the temperature of air. Thus, the minimum distance will change with temperature. Hence, we cannot hear an echo at every place.
Question 24.
Write a short note on reverberation.
Answer:
- Reverberation is the phenomenon in which sound waves are reflected multiple times causing a single sound to be heard more than once.
- Sound wave gets reflected multiple times if the distance between reflecting surface and source of sound is less than 15 m.
- During reverberation, the time interval between the successive reflections of a sound is small.
- As a result, the reflected sound waves overlap and produce a continuously increasing loud sound which is at times difficult to understand. Measures to decrease reverberation:
- Reverberation can be decreased by making the walls and roofs rough and by using curtains in the hall to avoid reflection of sound.
- Chairs and wall surfaces should be covered with sound absorbing materials.
- Porous cardboard sheets, perforated acoustic tiles, gypsum boards, thick curtains etc. should be used on the ceilings and walls.
Question 25.
Define acoustics.
Answer:
The branch of physics which deals with the study of production, transmission and reception of sound is called acoustics.
Question 26.
State the conditions that must be satisfied for proper acoustics in an auditorium along-with their remedies.
Answer:
i. Acoustics of an auditorium should be such that the sound is heard sufficiently loudly at all the points in the auditorium. The surface behind the speaker should be parabolic with the speaker at its focus for uniform distribution of sound in the auditorium. Reflection of sound helps to maintain good loudness through the entire auditorium.
ii. Echoes and reverberations should be reduced. More absorptive reflecting surfaces and full auditoriums help in reducing echoes.
iii. Unnecessary focusing of sound, poor audibility zone or region of silence should be avoided. Curved surface of the wall or ceiling should be avoided for this purpose.
iv. Echelon effect which arises due to the mixing of sound produced in the hall by the echoes of sound produced in front of regular structure like stairs should be reduced. Stair type construction in the hall must be avoided for this purpose.
v. To avoid outside stray sound from entering, the auditorium should be sound-proof when closed.
vi. Inside fittings, seats, etc. should not produce any sound for proper acoustics. Air conditioners instead of fans and soft action door closers should be used.
Question 27.
State the applications of acoustics observed in nature.
Answer:
Application of acoustics in nature:
i. Bats apply the principle of acoustics to locate objects. They emit short ultrasonic pulses of frequency 30 kHz to 150 kHz. The resulting echoes give them information about location of the obstacle. This helps the bats to fly in even in total darkness of caves.
ii. Dolphins navigate underwater with the help of an analogous system. They emit subsonic frequencies which can be about 100 Hz. They can sense an object about 1.4 m or larger.
![]()
Question 28.
State the medical applications of acoustics.
Answer:
i. High pressure and high amplitude shock waves are used to split kidney stones into smaller pieces without invasive surgery. A reflector or acoustic lens is used to focus a produced shock wave so that as much of its energy as possible converges on the stone. The resulting stresses in the stone causes the stone to break into small pieces which can then be removed easily.
ii. Ultrasonic imaging uses reflection of ultrasonic waves from regions in the interior of body. It is used for prenatal (before the birth) examination, detection of anomalous conditions like tumour etc. and the study of heart valve action.
iii. Ultrasound at a very high-power level, destroys selective pathological tissues which is helpful in treatment of arthritis and certain type of cancer.
Question 29.
State the underwater applications of acoustics.
Answer:
- SONAR (Sound Navigational Ranging) is a technique for locating objects underwater by transmitting a pulse of ultrasonic sound and detecting the reflected pulse.
- The time delay between transmission of a pulse and the reception of reflected pulse indicates the depth of the object.
- Motion and position of submerged objects like submarine can be measured with the help of this system.
Question 30.
State the applications of acoustics in environmental and geological studies.
Answer:
i. Acoustic principle has important application to environmental problems like noise control. The quiet mass transit vehicle is designed by studying the generation and propagation of sound in the motor’s wheels and supporting structures.
ii. Reflected and refracted elastic waves passing through the Earth’s interior can be measured by applying the principles of acoustics.
iii. This is useful in studying the properties of the Earth. Principles of acoustics are applied to detect local anomalies like oil deposits etc. making it useful for geological studies.
Question 31.
A man shouts loudly close to a high wall. He hears an echo. If the man is at 40 m from the wall, how long after the shout will the echo be heard? (speed of sound in air = 330 m/s)
Answer:
Given s = 40m, v = 330 m/s
To Find: time (t)
Formula: Time = distance \(\frac {distence}{speed}\)
Calculation:
The distance travelled by the sound wave
= 2 × distance from man to wall.
= 2 × 40 = 80 m.
From formula,
∴ Time taken to travel the distance
\(\frac {distence}{speed}\) = \(\frac {80}{30}\) = 0.24 s
Question 32.
Write a short note on pitch of sound note.
Answer:
- Pitch refers to the sharpness or shrillness of sound.
- Increase in frequency of sound results in increase in the pitch and the sound is said to be sharper.
- Tone refers to a single frequency of a wave.
- A note may contain single or multiple tones.
- High frequency is generally referred as high pitch or high tone.
- Generally, speech of the men is of low pitch (shrill) and that of the women is of high pitch (sharp). Tones of an acoustic guitar are sharper than that of a base guitar. Sound of table is sharper than that of a dagga.
Question 33.
Write a short note on quality (timbre) of sound note.
Answer:
i. Timbre of a sound refers to the quality of the sound which depends upon the mixture of tones and overtones in the sound. Same sound played on different musical instruments feels significantly different and the musical instrument from which the sound generated can be easily identified.
Question 34.
Write a short note on loudness of sound.
OR
Explain how loudness affects the characteristics of sound.
Answer:
Loudness:
i. Loudness depends upon the intensity of vibration.
ii. Intensity of a wave is proportional to square of the amplitude (I ∝ A²) and is measured in the (SI) unit ofW/m²
iii. The human response to intensity is not linear, i.e., a sound of double intensity is louder but not doubly loud.
iv. Under ideal conditions, for a perfectly healthy human ear, the least audible intensity is I0 = 10-12 W/m².
v. Loudness of a sound of intensity I (measured in unit bel) is given by,
L2 = log10 (\(\frac {I}{I_0}\)) ………….. (1)
vi. Decibel is the commonly used unit for loudness.
vii. As, 1 decibel or 1 dB = 0.1 bel.
∴ 1 bel = 10 dB. Thus, loudness in dB is 10 times loudness in bel.
∴ LdB = 10Lbel = 10 log10 (\(\frac {I}{I_0}\))
For sound of least audible intensity I0
LdB = 10 log10 (\(\frac {I_0}{I_0}\)) = 10 log10 (1) = 0 ………… (2)
This corresponds to threshold of hearing.
viii. For sound of 10 dB,
10 = 10 log10 (\(\frac {I}{I_0}\))
∴ (\(\frac {I}{I_0}\)) = 10 1 or I = 10 I0
For sound of 20 dB,
20 = 10 log10 (\(\frac {I}{I_0}\))
= (\(\frac {I}{I_0}\)) = 10² or I = 100 I0 and so on.
ix. This implies, loudness of 20 dB sound is felt double that of 10 dB, but its intensity is 10 times that of the 10 dB sound. Similarly, 40 dB sound is left twice as loud as 20 dB sound but its intensity is 100 times as that of 20 dB sound and 10000 times that of 10 dB sound. This is the power of logarithmic or exponential scale. If we move away from a (practically) point source, the intensity of its sound varies inversely with square of the distance, i.e., I ∝ \(\frac {1}{r^2}\).
Question 35.
When heard independently, two sound waves produce sensations of 60 dB and 55 dB respectively. How much will the sensation be if those are sounded together, perfectly in phase?
Answer:
L1 = 60 dB = 10 log10 \(\frac {I_1}{I_0}\)
∴ \(\frac {I_1}{I_0}\) = 106
∴ I1 = 106I0
Similarly, I2 = 105.5 I0
As the waves combine perfectly in phase, the vector addition of their amplitudes will be given by A² = (A1 + A2)² = A\(_1^2\) + A\(_2^2\) + 2A1, A2 As intensity is proportional to square of the amplitude.
∴ I = I1 + I2 + 2\(\sqrt {I_1I_2}\) = 105 I0 (101 +100.5 + 2\(\sqrt {10^{1.5}}\))
= 105I0(10 + 3.1623 +2 × 100.75)
= 24.41 × 105I0 = 2.441 × 106I0
∴ L = 10 log10 (\(\frac {I}{I_0}\)) = 10 log10 (2.441 × 106)
= 10[log10 (2.441) + log10(106)]
= 10(0.3876 + 6)
L = 63.876 dB ~ 64 dB
![]()
Question 36.
The noise level in a class-room in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student outputs same sound energy per second, what will be the noise level if the number of students is increases to 100?
Answer:
Loudness of sound is given as,
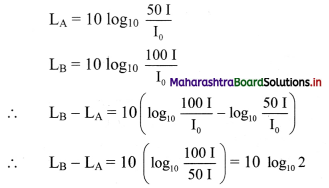
∴ LB – LA = 0.301 × 10 = 3.01
∴ LB = LA + 3.01 = 53.01 dB
Question 37.
Calculate the decibel increase if there is a two-fold increase in the intensity of a wave. (Given: log10 2 = 0.3010)
Answer:
L = 10 log10 \(\frac {I}{I_0}\) decibel
L’ = 10 log10 \(\frac {2I}{I_0}\) decibel
L’ – L = 10 (log10 \(\frac {2I}{I_0}\) – log10 (\(\frac {I}{I_0}\))
= 10 log10 2
= 10 × 0.3010
∴ L’ – L = 3.01 dB
Question 38.
Derive the expression for apparent frequency when listener is stationary and source is moving away from the listener.
Answer:
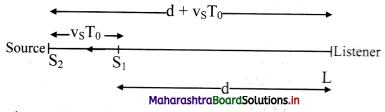
i. Consider a source of sound S moving away from a stationary listener L with velocity vs. Let the speed of sound with respect to the medium be v (always positive). The listener uses a detector for counting each wave crest that reaches it.
ii. Let at t = 0, the source at point Si which is at a distance d from the listener, emit a crest. This crest reaches the listener at time t1, given as, t1 = d/v. …………(1)
iii. Let T0 be the time period at which the waves are emitted.
At t = T0, distance travelled by the source away from the stationary listener to reach point S2 = vsT0.
∴ Distance of point S2 from the listener = d + vsT0.
At S2, The source emits second crest. This crest reaches the listener at t2, given as,
t2 = T0 + (\(\frac {d+v_sT_0}{v}\)) …………. (2)
iv. Similarly, the time taken by the (p+1)th crest (where, p is an integer, p = 1, 2, 3,…), emitted by the source at time pT0, to reach the listener is given as,
tp+1 = pT0 + (\(\frac {d+pv_sT_0}{v}\)) …………. (3)
∴ the listener’s detector counts p crests in the time interval,
tp+1 – t1 = pT0 + (\(\frac {d+pv_sT_0}{v}\)) – \(\frac {d}{v}\)
The period of wave as recorded by the listener is,

Where, n = frequency recorded by the listener (apparent frequency)
n0 = frequency emitted by the source (actual frequency).
This is the expression for apparent frequency when the listener is stationary and the source is moving away from the listener.
Question 39.
Derive an expression for apparent frequency when listener is stationary and source is moving towards the listener.
Answer:
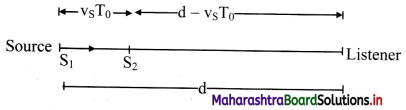
i. Consider a source of sound S moving towards a stationary listener L with velocity vs. Let the speed of sound with respect to the medium be v (always positive). The listener use a detector for counting each wave crest that reaches it.
ii. Let at t = 0, the source at point S1 which is at a distance d from the listener, emit a Crest. This crest reaches the listener at time t1, given as,
∴ t1 = d/v. ……….(1)
iii. Let T0 be the time period at which the waves are emitted.
At t = T0, distance travelled by the source away from the stationary listener to reach point S2 = vsT0.
Distance of S2 from the listener = d – vsT0.
At S2, The source emits second crest. This crest reaches the listener at
t2 = T0 + (\(\frac {d-v_sT_0}{v}\)) ………….. (2)
iv. Similarly, the time taken by the (p+1)th crest (where, p = 1,2,3,…), emitted by the source at time pT0, to reach the listener is given as,
tp+1 = pT0 + (\(\frac {d-pv_sT_0}{v}\)) ……………. (3)
∴ the listener’s detector counts p crests in the time interval,
tp+1 – t1 = pT0 + (\(\frac {d-pv_sT_0}{v}\)) – \(\frac {d}{v}\)
∴ the period of wave as recorded by the listener is,
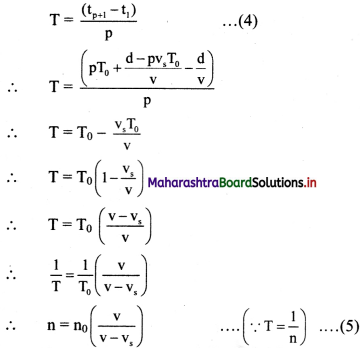
Where, n = frequency recorded by the listener (apparent frequency)
n0 = frequency emitted by the source (actual frequency).
This is the expression for apparent frequency when the listener is stationary and the source is moving towards the listener.
Question 40.
Derive the expression for apparent frequency when the source is stationary and the listener is moving towards the source.
Answer:
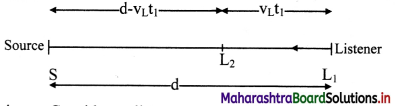
i. Consider a listener approaching a stationary source S with velocity vL as shown in figure. Let the speed of sound with respect to the medium be v (always positive).
ii. Let at time t = 0, the source emits the first wave when the listener L1 is at an initial distance d from the source.
At time t = t1 the listener receives the first wave at the position L2.
Distance travelled by the listener towards the stationary source during time t1 = vLt1.
Distance travelled by the sound wave during time t1 = d – vLt1
∴ time taken by the sound wave to travel this distance, t1 = \(\frac {d-v_Lt_1}{v}\)
∴ t1 = \(\frac {d}{v+v_L}\) ………….. (1)
iii. Let at time t = T0 (time period of the waves emitted by the source), the source emits a second wave.
At t = t2, the listener receives the second wave. Distance travelled by the listener towards the stationary source during time t2 = vLt2.
Distance travelled by the sound wave during time t2 = d – vLt2
∴ time taken by the sound wave to travel this distance = \(\frac {d-v_Lt_2}{v}\)
However, this time should be counted after T0, as the second wave was emitted at t = T0.
∴ t2 = T0 + \(\frac {d-v_Lt_2}{v}\)
∴ t2 = \(\frac {vT_0+d}{v+v_L}\) …………. (2)
iv. Similarly, for the third wave, we get,
t3 = 2T0 + \(\frac {d-v_Lt_3}{v}\)
∴ t3 = \(\frac {2vT_0+d}{v+v_L}\) …………. (3)
v. Extending this argument to the (p + 1)th wave, we get,
tp+1 = pT0 + \(\frac {d-v_Lt_{p+1}}{v}\)
∴ tp+1 = \(\frac {pvT_0+d}{v+v_L}\) …………. (4)
vi. The observed or recorded period T is the time duration between instances of receiving successive waves.

This is the expression for apparent frequency when the source is stationary and the listener is moving towards the source.
![]()
Question 41.
Derive the expression for apparent frequency when the source is stationary and the listener is moving away from the source.
Answer:
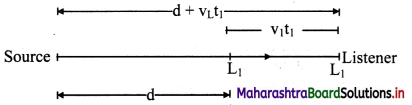
i. Consider a listener moving away a stationary source S with velocity VL. Let the speed of sound with respect to the medium be y (always positive).
ii. Let at time t = 0, the source emits the first wave when the listener L1 is at an initial distance d from the source.
At time t = t1 the listener receives the first wave at the position L2.
Distance travelled by the listener away from the stationary source during time t1 = vLt1.
Distance travelled by the sound wave during time t1 = d + vLt1
∴ time taken by the sound wave to travel this distance,
t1 = \(\frac {d+v_Lt_1}{v}\)
∴ t1 = \(\frac {d}{v-v_L}\) ………….. (1)
iii. Let at time t = T0 (time period of the waves emitted by the source), the source emits a second wave.
At t = t2, the listener receives the second wave. Distance travelled by the listener away from the stationary source during time t2 = vLt2.
∴ Distance travelled by the sound wave during time t2 = d + vLt2.
∴ time taken by the sound wave to travel this distance = \(\frac {d+v_Lt_2}{v}\)
However, this time should be counted after T0, as the second wave was emitted at t = T0.
∴ t2 = T0 \(\frac {d+v_Lt_2}{v}\) ………….. (2)
∴ t2 = \(\frac {vT_0+d}{v-v_L}\)
iv. Similarly for the third wave, we get
t3 = 2T0 \(\frac {d+v_Lt_3}{v}\)
∴ t3 = \(\frac {2vT_0+d}{v-v_L}\) …………..(3)
v. Extending this argument to the (p + 1)th wave, we get,
tp+1 = pT0 + \(\frac {d+v_Lt_{p+1}}{v}\)
∴ tp+1 = \(\frac {pvT_0+d}{v-v_L}\) …………..(4)
vi. The observed or recorded period T is the time duration between instances of receiving successive waves.
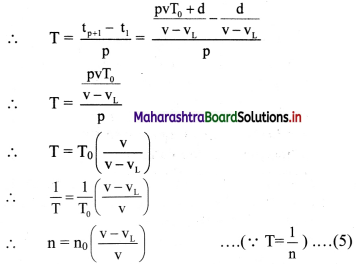
This is the expression for apparent frequency when the source is stationary and the listener is moving away from the source.
Question 42.
State the common properties between Doppler effect of sound and light.
Answer:
i. The recorded frequency is different than the emitted frequency in case of relative motion between listener (or observer) and source (of sound or light waves).
ii. In case of relative approach, recorded frequency > emitted frequency.
iii. In case of relative recede, recorded frequency < emitted frequency.
iv. For values of listener velocity (vL) or source velocity (vs) much smaller then wave speed (speed of sound or light).
n = n0 (1±\(\frac {v_r}{v}\))
Where, vr = relative velocity
n = actual frequency of the source
n0 = apparent frequency of the source
v = velocity of sound in air.
(upper sign is used during relative approach and lower sign is during relative recede.)
v. If velocities of source and observer (listener) are along different lines, their respective components along the line joining them should be chosen for longitudinal Doppler effect and the same mathematical treatment is applicable.
Question 43.
State the major difference between Doppler effects of sound and light.
Answer:
- Speed of light being absolute, only relative velocity between the observer and the source matter irrespective of who is in motion. However, for obtaining exact Doppler shift for sound waves, it is absolutely important to know who is in motion.
- In case of light, classical and relativistic Doppler effects are different while sound only has classical doppler effect.
- Presence of wind affects the velocity of sound which affects the Doppler shift in sound.
Question 44.
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s-1 (b) recedes from the platform with a speed of 10 m s-1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s-1.
Answer:
Given: vs = 10 m/s, v = 340 m/s, n0 = 400 Hz
Apparent frequency (n), velocity of sound (vs) in each case
Formulae:
i. n = n0 (\(\frac {v}{v-v_s}\))
ii. n = n0 \(\frac {v}{v+v_s}\)
Calculation:
a. As the train approaches the platform, using formula (i),
n = 400 (\(\frac {340}{340-10}\)) = 421.12 Hz
b. As the train recedes from the platform, using formula (ii),
n = 400 (\(\frac {340}{340+10}\)) = 388.57 Hz
ii. The relative motion of source and observer results in the apparent change in the frequency but has no effect on the speed of sound. Hence, the speed of sound remains unchanged in both the cases.
Question 45.
A train blows a whistle of frequency 640 Hz in air. Find the difference in apparent frequencies of the whistle for a stationary observer, when the train moves towards and away from the observer with the speed of 72 km/hour. (Speed of sound in air = 340 m/s)
Answer:
Given: vs = 72 km/ hr = 20 m/s, n0 = 640 Hz,
v = 340 m/s
To find: Difference in apparent frequencies
(nA – n’A)
Formulae:
i. When the train moves towards the stationary observer then,
nA = n0 (\(\frac {v}{v-v_s}\))
ii. When the train moves away the stationary observer then,
n’A = n0 (\(\frac {v}{v+v_s}\))
Calculation: From formula (i),
nA = 640 (\(\frac {340}{340-20}\))
∴ nA = 680 Hz
From formula (ii),
n’A = 640 (\(\frac {340}{340+20}\))
∴ n’A = 604.4 Hz
Difference between nA and n’A
= nA – n’A = 75.6 Hz
Question 46.
The speed limit for a vehicle on road is 120 km/hr. A policeman detects a drop of 10% in the pitch of horn of a car as it passes him. Is the policeman justified in punishing the car driver for crossing the speed limit? (Given: Velocity of sound=340 m/s).
Answer:
Given: Speed limit, vL = 120 km/hr
n’A = nA – \(\frac {10}{100}\) nA = 0.9 nA
Velocity of sound, v = 340 m/s
To Find: Velocity of source (vs)
i. nA = (\(\frac {v}{v-v_s}\))n
ii. n’A = (\(\frac {v}{v+v_s}\))n
Calculation:
Dividing formula (i) by (ii),

Question 47.
A stationary source produces a note of frequency 350 Hz. An observer in a car moving towards the source measures the frequency of sound as 370 Hz. Find the speed of the car. What will be the frequency of sound as measured by the observer in the car if the car moves away from the source at the same speed? (Assume speed of sound = 340 m/s)
Answer:
Given: n0 = 350 Hz, v = 340 m/s,
nA = 370 Hz
To find: Speed (vL), Frequency (nA)
Formulae:
i. When the car moves towards the stationary source then,
nA = n0 (\(\frac {v+v_s}{v}\))
ii. When the car moves away from the stationary source then,
nA = n0 (\(\frac {v-v_L}{v}\))
Calculation: From formula (i),
370 = 35o (\(\frac {340+v_L}{340}\))
∴ 359.43 =340 +vL
∴ vL = 19.43 m/s
From formula (ii),
∴ nA = 35o (\(\frac {340-20}{340}\)) = \(\frac {35}{34}\) × 320
∴ nA = 329.41 Hz
![]()
Question 48.
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with a speed of 10 m s-1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s-1? The speed of sound in still air can be taken as 340 m s-1.
Answer:
Blowing of wind changes the velocity of sound. As the wind is blowing in the direction of sound, effective speed of sound ve = v + vw = 340 + 10 = 350 m/s
As the source and listener both are at rest, frequency is unchanged, i.e., n = 400 Hz.
∴ wavelength, λ = \(\frac {v_e}{n}\) = \(\frac {350}{400}\) = 0.875 m
For still air, vw = 0 and ve = v = 340 m/s
Also, as observer runs towards the stationary train vL = 10 m/s and vs = 0
The frequency now heard by the observer,
n = n0 (\(\frac {v+v_L}{v}\)) = 400 (\(\frac {340+10}{340}\))
= 411.76 Hz
As the source is at rest, wavelength does not change i.e., λ’ = λ = 0.875 m
Comparing the answers, it can be stated that, the situations in two cases are different.
Question 49.
A SONAR system fixed in a submarine operates at a frequency 40 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h-1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 m s-1.
Answer:
Frequency of SONAR (source)
n = 40 kHz = 40 × 10³ Hz
Speed of sound waves, v = 1450 m s-1
Speed of the listener, vL = 360 km h-1
= 360 × \(\frac {5}{18}\) ms-1
= 100 m s-1
Since, the source is at rest and the observer moves towards the source (SONAR).
We have,
n = n0 (\(\frac {v+v_L}{v}\)) = 40 × 10³ × (\(\frac {1450+100}{14540}\))
∴ n = 4.276 × 10⁴ Hz
This frequency n’ is reflected by the enemy ship and is observed by the SONAR (which now acts as observer). Therefore, in this case vs = 100 m s-1
Apparent frequency,
n = n0 (\(\frac {v}{v-v_s}\))
= 4.276 × 10⁴ × (\(\frac {1450}{1450-100}\)) = 4.59 × 10⁴ Hz
∴ n = 45.9 kHz
Question 50.
A rocket is moving at a speed of 220 m s-1 towards a stationary target. While moving, it emits a wave of frequency 1200 Hz. Some of the sound reaching the target gets reflected back to the rocket as an echo. Calculate (i) the frequency of the sound as detected by the target and (ii) the frequency of the echo as detected by the rocket (velocity of sound = 330 m/s)
Answer:
Given: vs = 220 m/s, vL = 0 m/s, n = 1200 Hz
To find: Apparent frequency (n)
i. n = n0 (\(\frac {v}{v-v_s}\))
ii. n = n0 \(\frac {v+v_L}{v}\)
Calculation: For first case, observer is stationary and source i.e., rocket is moving towards the target.
Hence, using formula (i),
frequency of sound as detected by the target,
n = 1200 (\(\frac {330}{330-220}\)) = 3600 Hz
For second case, target acts as a source with frequency 3600 Hz as it is the source of echo. While rocket detector acts as an observer. This means, vs = 0 and VL = 220 m/s
Using formula (ii),
frequency of echo as detected by the rocket,
n = 3600 (\(\frac {330+220}{330}\)) = 600 Hz
Question 51.
A bat is flying about in a cave, navigating via ultrasonic beeps. Assume that the sound emission frequency of the bat is 40 kHz. During one fast swoop directly towards a flat wall surface, the bat is moving at 0.03 times the speed of sound in air. What frequency does the bat hear reflected off the wall?
Answer:
Here, frequency of sound emitted by bat,
n = 40 kHz
Velocity of bat, vs = 0.03 v
where v is velocity of sound.
The bat is moving towards the flat wall. This is the case of source in motion and the observer at rest.
Therefore, the frequency of sound reflected at the wall is,
n = ns (\(\frac {v}{v-v_s}\)) = n × (\(\frac {v}{v-0.03v}\))
= n × \(\frac {1}{0.97}\) = \(\frac {n}{0.97}\)
The frequency n’ is reflected by the wall and is again received by the bat moving towards the wall. This is the case of an observer moving towards the source with velocity vL = 0.03 v.
The frequency observed by bat,
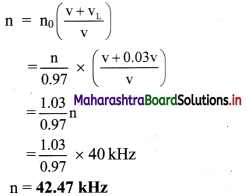
Question 52.
A bat, flying at velocity VB = 12.5 m/s, is followed by a car running at velocity Vc = 50 m/s. Actual directions of the velocities of the car and the bat are as shown in the figure below, both being in the same horizontal plane (the plane of the figure). To detect the car, the bat radiates ultrasonic waves of frequency 36 kHz. Speed of sound at surrounding temperature is 350 m/s.
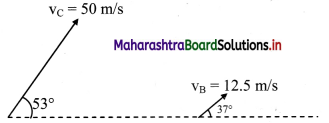
There is an ultrasonic frequency detector fitted in the car. Calculate the frequency recorded by this detector. The ultrasonic waves radiated by the bat are reflected by the car. The bat detects these waves and from the detected frequency, it knows about the speed of the car. Calculate the frequency of the reflected waves as detected by the bat. (sin 37° = cos 53° ~ 0.6, sin 53° = cos 37° ~ 0.8)
Answer:
The components of velocities of the bat and the car, along the line joining them, are
vc cos 53° ~ 50 × 0.6 = 30 m s-1 and
vB cos 37° ~ 12.5 × 0.8 = 10 m s-1
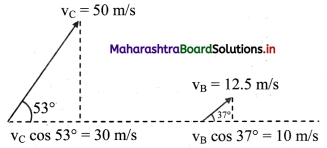
Doppler shifted frequency n = n0 (\(\frac {v±v_1}{v±v_s}\))
upper signs to be used during approach, lower signs during recede.
Case I: Frequency radiated by the bat
n0 = 36 × 10³ Hz,
The source (bat) is receding, while the listener (car) is approaching
vS = vB cos 37° = 10 m/s and
VL = vC cos 53° = 30 m/s
∴ Frequency detected by the detector in the car,
n = n0 (\(\frac {v+v_L}{v+v_s}\))
∴ n = 36 × 10³ (\(\frac {350+30}{350+10}\)) = 36 × 10³ × \(\frac {38}{36}\)
∴ n = 38 × 10³ Hz = 38 kHz
Case II: The car is the source.
Emitted frequency by the car, is given as,
n0 = 38 × 10³ Hz,
Car, the source, is approaching the listener (bat).
Now bat-the listener is receding while car the source is approaching,
∴ vs = vc cos 53° = 30 m/s
∴ vL = vB cos 37° = 10 m/s
∴ n = n0 (\(\frac {v-v_L}{v-v_s}\))
∴ n = 38 × 10³ (\(\frac {350-10}{350-30}\)) = 38 × 10³ × \(\frac {34}{33}\)
= 39.15 × 10³ Hz
∴ n = 39.15 kHz
![]()
Question 53.
Source of sound is placed at one end of a copper bar of length 1 km. Two sounds are heard at the other end at an interval of 2.75 seconds, (speed of sound in air = 330 m/s)
i. Why do we hear two sounds?
ii. Find the velocity of sound in copper.
Answer:
i. Two sounds are heard because sound travels through air as well as through copper.
ii. In air, t1 = \(\frac {distence}{time}\) = \(\frac {1000}{330}\) = 3.03 s
As the time interval is 2.75 seconds and sound travels faster in copper.
∴ In copper, t2 = 3.03 – 2.75 = 0.28 s
∴ velocity of sound in copper = \(\frac {1000}{0.28}\) = 3571 m/s
Question 54.
If all the persons mentioned in the table below are listening to a match commentary on the same channel at their respective locations positioning at same distance from television, then will they hear the same line of the commentary at same instant of time? Justify your answer.
| Name of a person | Location | Humidity |
| Aijun | Bangalore | 65 % |
| Virendra | Hyderabad | 56% |
| Vikas | Delhi | 54% |
| Nilesh | Mumbai | 75% |
Answer:
As the order of humidity for the above locations is Mumbai > Bangalore > Hyderabad > Delhi.
As velocity of sound increases with increase in humidity, the order of velocity of sound at their respective locations is Mumbai > Bangalore > Hyderabad > Delhi.
Hence, the order of persons who would listen the line of commentary first to last is Nilesh, Arjun, Virendra, Vikas.
Question 55.
Speed of sound is greater during day than at night. True or False? Justify your answer.
Answer:
True. At night, the amount of CO2 in atmosphere increases the density of atmosphere. Since, Speed of sound is inversely proportional to the square root of density. Hence, speed of sound is greater during day than in night.
Question 56.
Case I: During summer (33 °C), Prakash was waiting for a train at the platform, train arrived tt seconds after he heard train’s whistle.
Case II: During winter (19 °C), train arrived t2 seconds after Prakash heard the sound of train’s whistle.
i. Will t2 be equal to t1? Justify your answer.
ii. Calculate the velocity of sound in both the cases.
(velocity of sound in air at 0 °C = 330 m/s)
Answer:
i. Velocity of sound is directly proportional to square root of absolute temperature.
Hence, whistle’s sound will be first heard by Prakash in summer than in winter.
Therefore, the time interval between sound and train reaching Prakash in summer will be more than in winter.
i.e.,t1 > t2
ii. When t = 33 °C
∴ v1 = v0 + 0.61t
= 330 + 0.61 × 33
∴ v1 = 350.13 m/s
When t = 19 °C
v2 = v0 + 0.61t
= 330 + 0.61 × 19
v2 = 341.59 m/s
Question 57.
You are at a large outdoor concert, seated 300 m from speaker system. The concert is also being broadcast live. Consider a listener 5000 km away who receives the broadcast. Who will hear the music first, you or listener and by what time difference? (Speed of light = 3 × 108 m/s and speed of sound in air = 343 m/s)
Answer:
s1 = 300 m,
v1 = 343 m/s,
∴ t1 = \(\frac {s_1}{v_1}\) = \(\frac {300}{343}\) = 0.8746 s
Now,
s2 = 5000 km = 5 × 106 m,
v2 = c = 3 × 108 m/s
∴ t2 = \(\frac {s_2}{c}\) = \(\frac {5×10^6}{3×10^8}\) = 0.0167 s
∴ t2 < t1
∴ Listener will hear the music first.
Time difference = t1 – t2
= 0.8746 – 0.0167
= 0.8579 s
The listener will hear the music first, about 0.8579 s before the person present at the concert.
Question 58.
When a source of sound moves towards a stationary observer, then the pitch increases. Give reason.
Answer:
When a source of sound moves towards a stationary observer, then the increase in pitch is due to actual or apparent change in wavelength. When the source of sound moves towards an observer at rest, waves get compressed and the effective velocity of sound waves relative to source becomes less than the actual velocity. Hence the wavelength of sound waves an decreases which results into increase in pitch.
Question 59.
In the examples given below, state if the wave motion is transverse, longitudinal or a combination of both?
- Light waves travelling from Sun to Earth.
- ultrasonic waves in air produced by a vibrating quartz crystal.
- Waves produced by a motor boat sailing in water.
Answer:
- Light waves (from Sun to Earth) are electromagnetic waves which are transverse in nature.
- Ultrasonic waves in air are basically sound waves of frequency greater than the audible frequencies. Therefore, these waves are longitudinal.
- The water surface is cut laterally and pushed backwards by the propeller of motor boat. Therefore, the waves produced are a mixture of longitudinal and transverse waves.
![]()
Question 60.
Internet my friend
Answer:
https://hyperphysics.phys-astr.gsu.edu/ hbase/hframe.html
[Students are expected to visit the above mentioned website and collect more information about sound.]
Multiple Choice Questions
Question 1.
Water waves are …………….
(A) longitudinal
(B) transverse
(C) both longitudinal and transverse
(D) neither longitudinal nor transverse
Answer:
(C) both longitudinal and transverse
Question 2.
Sound travels fastest in ……………..
(A) water
(B) air
(C) steel
(D) kerosene oil
Answer:
(C) steel
Question 3.
At room temperature, velocity of sound in air at 10 atmospheric pressure and at 1 atmospheric pressure will be in the ratio ……………..
(A) 10 : 1
(B) 1 : 10
(C) 1 : 1
(D) cannot say
Answer:
(C) 1 : 1
Question 4.
In a gas, velocity of sound varies directly as ………………
(A) square root of isothermal elasticity.
(B) square of isothermal elasticity.
(C) square root of adiabatic elasticity.
(D) adiabatic elasticity.
Answer:
(C) square root of adiabatic elasticity.
Question 5.
At a given temperature, velocity of sound in oxygen and in hydrogen has the ratio …………………
(A) 4 : 1
(B) 1 : 4
(C) 1 : 1
(D) 2 : 1
Answer:
(B) 1 : 4
Question 6.
With decrease in water vapour content in air, velocity of sound …………………..
(A) increases
(B) decreases
(C) remains constant
(D) cannot say
Answer:
(B) decreases
Question 7.
The temperature at which speed of sound in air becomes double its value at 0 °C is ……………….
(A) 546 °C
(B) 819 °C
(C) 273 °C
(D) 1092 °C
Answer:
(B) 819 °C
Question 8.
The velocity of sound in air at NTP is 330 m/s. What will be its value when temperature is doubled and pressure is halved?
(A) 330 m/s
(B) 165 m/s
(C) 330 √2 m/s
(D) \(\frac {330}{√2}\) m/s
Answer:
(D) \(\frac {330}{√2}\) m/s
Question 9.
A series of ocean waves, each 5.0 m from crest to crest, moving past the observer at a rate of 2 waves per second have wave velocity
(A) 2.5 m/s
(B) 5.0 m/s
(C) 8.0 m/s
(D) 10.0 m/s
Answer:
(D) 10.0 m/s
![]()
Question 10.
A radio station broadcasts at 760 kHz. What is the wavelength of the station?
(A) 395 m
(B) 790 m
(C) 760 m
(D) 197.5 m
Answer:
(A) 395 m
Question 11.
If the bulk modulus of water is 2100 MPa, what is the speed of sound in water?
(A) 1450 m/s
(B) 2100 m/s
(C) 0.21 m/s
(D) 21 m/s
Answer:
(A) 1450 m/s
Question 12.
If speed of sound in air at 0°C is 331 m/s. What will be its value at 35° C?
(A) 331 m/s
(B) 366 m/s
(C) 351.6 m/s
(D) 332 m/s.
Answer:
(C) 351.6 m/s
Question 13.
For a progressive wave, in the usual notation
(A) v = λT
(B) n = \(\frac {v}{λ}\)
(C) T = λv
(D) λ = \(\frac {1}{n}\)
Answer:
(B) n = \(\frac {v}{λ}\)
Question 14.
At normal temperature, for an echo to be heard the reflecting surface should be at a minimum distance of ………………. m.
(A) 34.4
(B) 17.2
(C) 10
(D) 20
Answer:
(B) 17.2
Question 15.
In a transverse wave, are regions of negative displacement.
(A) rarefactions
(B) compressions
(C) crests
(D) troughs
Answer:
(D) troughs
Question 16.
If pressure of air gets doubled at constant temperature then velocity of sound in air ……………….
(A) gets doubled
(B) remains unchanged
(C) √2 times initial velocity
(D) becomes half
Answer:
(B) remains unchanged
Question 17.
Wave motion has ……………………
(A) single periodicity.
(B) double periodicity.
(C) only periodicity in space.
(D) only periodicity in time.
Answer:
(B) double periodicity.
Question 18.
The speed of the mechanical wave depends upon ………………
(A) elastic properties of the medium only.
(B) density of the medium only.
(C) elastic properties and density of the medium
(D) initial speed.
Answer:
(C) elastic properties and density of the medium
Question 19.
Longitudinal waves CANNOT be …………………
(A) reflected
(B) refracted
(C) scattered
(D) polarised
Answer:
(D) polarised
Question 20.
Wavelength of the transverse wave is 30 cm. If the particle at some instant has displacement 2 cm, find the displacement of the particle 15 cm away at the same instant.
(A) 2 cm
(B) 17 cm
(C) -2 cm
(D) -17 cm
Answer:
(C) -2 cm
Question 21.
The wavelength of sound in air is 1.5 m and that in liquid is 2 m. If the velocity of sound in air is 330 m/s, the velocity of sound in liquid is
(A) 330 m/s
(B) 440 m/’s
(C) 495 m/s
(D) 660 m/s
Answer:
(B) 440 m/’s
Question 22.
The velocity of sound in a gas is 340 m/s at the pressure P, what will be the velocity of the gas when only pressure is doubled and temperature same?
(A) 170 m/s
(B) 243 m/s
(C) 340 m/s
(D) 680 m/s
Answer:
(C) 340 m/s
Question 23.
Choose the correct statement.
(A) For 1 °C rise in temperature, velocity of sound increases by 0.61 m/s.
(B) For 1 °C rise in temperature, velocity of sound decreases by 0.61 m/s.
(C) For 1 °C rise in temperature, velocity of sound decreases by \(\frac {1}{273}\) m/s.
(D) For 1 °C rise in temperature, velocity of sound increases by \(\frac {1}{273}\) m/s.
Answer:
(A) For 1 °C rise in temperature, velocity of sound increases by 0.61 m/s.
Question 24.
A sound note emitted from a certain source has a velocity of 300 m/s in air and 1050 m/s in water. If the wavelength of sound note in air is 2 m, the wavelength in water is …………
(A) 2 m
(B) 6 m
(C) 7 m
(D) 12 m
Answer:
(C) 7 m
Question 25.
A thunder clap was heard 6 seconds after a lightening flash was seen. If the speed of sound in air is 340 m/s at the time of observation, the distance of the listener from the thunder clap is ………………
(A) 56.6 m
(B) 346 m
(C) 1020 m
(D) 2040 m
Answer:
(D) 2040 m
Question 26.
The speed of sound in air at NTP is 330 m/s. The period of sound wave of wavelength 66 cm is …………………
(A) 0.2 s
(B) 0.1
(C) 0.1 × 10-2 s
(D) 0.2 × 10-2 s
Answer:
(D) 0.2 × 10-2 s
Question 27.
If the velocity of sound in hydrogen is 1248 m/s, the velocity of sound in oxygen is [Given: MO = 32 and MH = 2]
(A) 1248 m/s
(B) 624 m/s
(C) 312 m/s
(D) 300 m/s
Answer:
(C) 312 m/s
![]()
Question 28.
If the source is moving away from the observer, then the apparent frequency …………..
(A) will increase
(B) will remain the same
(C) will be zero
(D) will decrease
Answer:
(D) will decrease
Question 29.
The working of SONAR is based on …………………
(A) resonance
(B) speed of a star
(C) Doppler effect
(D) speed of rotation of sun
Answer:
(C) Doppler effect
Question 30.
The formula for speed of a transverse wave on a stretched spring is ……………… (m = linear mass density, T = tension in Spring)
(A) v = \(\sqrt{\frac {m}{T}}\)
(B) v = \(\sqrt{\frac {T}{m}}\)
(C) v = (\(\frac {m}{T}\))\(\frac {3}{2}\)
(D) v = (\(\frac {T}{m}\))\(\frac {3}{2}\)
Answer:
(B) v = \(\sqrt{\frac {T}{m}}\)