Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 8 Binomial Distribution Ex 8.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 8 Binomial Distribution Ex 8.1
Question 1.
A die is thrown 6 times. If ‘getting an odd number’ is a success, find the probability of
(i) 5 successes
(ii) at least 5 successes
(iii) at most 5 successes.
Solution:
Let X = number of successes, i.e. number of odd numbers.
p = probability of getting an odd number in a single throw of a die
∴ p = \(\frac{3}{6}=\frac{1}{2}\) and q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Given: n = 6
∴ X ~ B(6, \(\frac{1}{2}\))
The p.m.f. of X is given by

Hence, the probability of 5 successes is \(\frac{3}{32}\).
(ii) P(at least 5 successes) = P[X ≥ 5]
= p(5) + p(6)
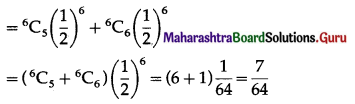
Hence, the probability of at least 5 successes is \(\frac{7}{64}\).
(iii) P(at most 5 successes) = P[X ≤ 5]
= 1 – P[X > 5]

Hence, the probability of at most 5 successes is \(\frac{63}{64}\).
![]()
Question 2.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
Solution:
Let X = number of doublets.
p = probability of getting a doublet when a pair of dice is thrown
∴ p = \(\frac{6}{36}=\frac{1}{6}\) and
q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Given: n = 4
∴ X ~ B(4, \(\frac{1}{6}\))
The p.m.f. of X is given by

Hence, the probability of two successes is \(\frac{25}{216}\).
Question 3.
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?
Solution:
Let X = number of defective items.
p = probability of defective item
∴ p = 5% = \(\frac{5}{100}=\frac{1}{20}\)
and q = 1 – p = 1 – \(\frac{1}{20}\) = \(\frac{19}{20}\)
∴ X ~ B(10, \(\frac{1}{20}\))
The p.m.f. of X is given by
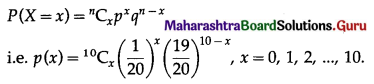
P(sample of 10 items will include not more than one defective item) = P[X ≤ 1]

Hence, the probability that a sample of 10 items will include not more than one defective item = 29\(\left(\frac{19^{9}}{20^{10}}\right)\).
![]()
Question 4.
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards, find the probability that
(i) all the five cards are spades
(ii) only 3 cards are spades
(iii) none is a spade.
Solution:
Let X = number of spade cards.
p = probability of drawing a spade card from a pack of 52 cards.
Since there are 13 spade cards in the pack of 52 cards.
∴ p = \(\frac{13}{52}=\frac{1}{4}\) and
q = 1 – p = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
Given: n = 5
∴ X ~ B(5, \(\frac{1}{4}\))
The p.m.f. of X is given by
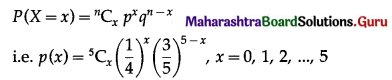
(i) P(all five cards are spade)
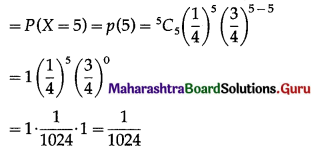
Hence, the probability of all the five cards are spades = \(\frac{1}{1024}\)
(ii) P(only 3 cards are spade) = P[X = 3]
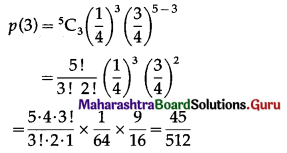
Hence, the probability of only 3 cards are spades = \(\frac{45}{512}\)
(iii) P(none of cards is spade) = P[X = 0]
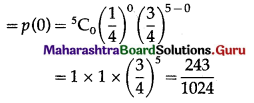
Hence, the probability of none of the cards is a spade = \(\frac{243}{1024}\)
Question 5.
The probability of a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one, will fuse after 150 days of use.
Solution:
Let X = number of fuse bulbs.
p = probability of a bulb produced by a factory will fuse after 150 days of use.
∴ p = 0.05
and q = 1 – p = 1 – 0.05 = 0.95
Given: n = 5
∴ X ~ B(5, 0.05)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e. p(x) = \({ }^{5} C_{x}(0.05)^{x}(0.95)^{5-x}\), x = 0, 1, 2, 3, 4, 5
(i) P(none of a bulb produced by a factory will fuse after 150 days of use) = P[X = 0]
= p(0)
= \({ }^{5} \mathrm{C}_{0}(0.05)^{0}(0.95)^{5-0}\)
= 1 × 1 × (0.95)5
= (0.95)5
Hence, the probability that none of the bulbs will fuse after 150 days = (0.95)5.
(ii) P(not more than one bulb will fuse after 150 days of j use) = P[X ≤ 1]
= p(0) + p(1)
= \({ }^{5} \mathrm{C}_{0} \cdot(0.05)^{0}(0.95)^{5-0}+{ }^{5} \mathrm{C}_{1}(0.05)^{1}(0.95)^{4}\)
= 1 × 1 × (0.95)5 + 5 × (0.05) × (0.95)4
= (0.95)4 [0.95 + 5(0.05)]
= (0.95)4 (0.95 + 0.25)
= (0.95)4 (1.20)
= (1.2) (0.95)4
Hence, the probability that not more than one bulb will fuse after 150 days = (1.2)(0.95)4.
(iii) P(more than one bulb fuse after 150 days)
= P[X > 1]
= 1 – P[X ≤ 1]
= 1 – (1.2)(0.95)4
Hence, the probability that more than one bulb fuse after 150 days = 1 – (1.2)(0.95)4.
(iv) P(at least one bulb fuse after 150 days)
= P[X ≥ 1]
= 1 – P[X = 0]
= 1 – p(0)
= 1 – \({ }^{5} C_{0}(0.05)^{0}(0.95)^{5-0}\)
= 1 – 1 × 1 × (0.95)5
= 1 – (0.95)5
Hence, the probability that at least one bulb fuses after 150 days = 1 – (0.95)5.
![]()
Question 6.
A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
Solution:
Let X = number of balls marked with digit 0.
p = probability of drawing a ball from 10 balls marked with the digit 0.
∴ p = \(\frac{1}{10}\)
and q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
The p.m.f. of X is given by
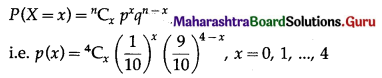
P(none of the ball marked with digit 0) = P(X = 0)

Hence, the probability that none of the bulb marked with digit 0 is \(\left(\frac{9}{10}\right)^{4}\)
Question 7.
On a multiple-choice examination with three possible answers for each of the five questions. What is the probability that a candidate would get four or more correct answers just by guessing?
Solution:
Let X = number of correct answers.
p = probability that a candidate gets a correct answer from three possible answers.
∴ p = \(\frac{1}{3}\) and q = 1 – p = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
Given: n = 5
∴ X ~ B(5, \(\frac{1}{3}\))
The p.m.f. of X is given by
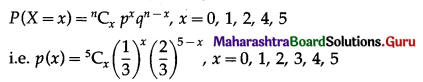
P(four or more correct answers) = P[X ≥ 4]
= p(4) + p(5)
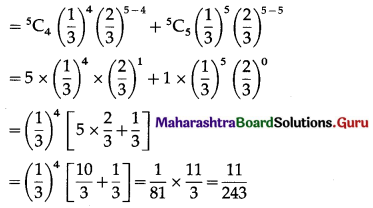
Hence, the probability of getting four or more correct answers = \(\frac{11}{243}\).
![]()
Question 8.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \(\frac{1}{100}\), find the probability that he will win a prize
(i) at least once
(ii) exactly once
(iii) at least twice.
Solution:
Let X = number of winning prizes.
p = probability of winning a prize
∴ p = \(\frac{1}{100}\)
and q = 1 – p = 1 – \(\frac{1}{100}\) = \(\frac{99}{100}\)
Given: n = 50
∴ X ~ B(50, \(\frac{1}{100}\))
The p.m.f. of X is given by
\(P(X=x)={ }^{n} C_{x} p^{x} q^{n-x}\)
i.e., p(x) = \({ }^{50} \mathrm{C}_{x}\left(\frac{1}{100}\right)^{x}\left(\frac{99}{100}\right)^{50-x}\), x = 0, 1, 2,… 50
(i) P(a person wins a prize at least once)

Hence, probability of winning a prize at least once = 1 – \(\left(\frac{99}{100}\right)^{50}\)
(ii) P(a person wins exactly one prize) = P[X = 1] = p(1)

Hence, probability of winning a prize exactly once = \(\frac{1}{2}\left(\frac{99}{100}\right)^{49}\)
(iii) P(a persons wins the prize at least twice) = P[X ≥ 2]
= 1 – P[X < 2]
= 1 – [p(0) + p(1)]

Hence, the probability of winning the prize at least twice = 1 – 149\(\left(\frac{99^{49}}{100^{50}}\right)\).
Question 9.
In a box of floppy discs, it is known that 95% will work. A sample of three of the discs is selected at random. Find the probability that (i) none (ii) 1 (iii) 2 (iv) all 3 of the sample will work.
Solution:
Let X = number of working discs.
p = probability that a floppy disc works
∴ p = 95% = \(\frac{95}{100}=\frac{19}{20}\)
and q = 1 – p = 1 – \(\frac{19}{20}\) = \(\frac{1}{20}\)
Given: n = 3
∴ X ~ B(3, \(\frac{19}{20}\))
The p.m.f. of X is given by
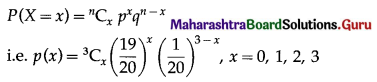
(i) P(none of the floppy discs work) = P(X = 0)
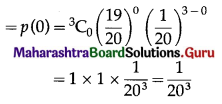
Hence, the probability that none of the floppy disc will work = \(\frac{1}{20^{3}}\).
(ii) P(exactly one floppy disc works) = P(X = 1)

Hence, the probability that exactly one floppy disc works = 3\(\left(\frac{19}{20^{3}}\right)\)
(iii) P(exactly two floppy discs work) = P(X = 2)
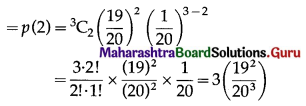
Hence, the probability that exactly 2 floppy discs work = 3\(\left(\frac{19^{2}}{20^{3}}\right)\)
(iv) P(all 3 floppy discs work) = P(X = 3)
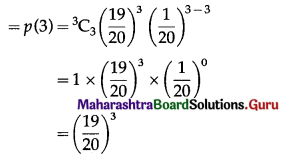
Hence, the probability that all 3 floppy discs work = \(\left(\frac{19}{20}\right)^{3}\).
![]()
Question 10.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solution:
Let X = number of sixes.
p = probability that a die shows six in a single throw
∴ p = \(\frac{1}{6}\)
and q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Given: n = 6
∴ X ~ B(6, \(\frac{1}{6}\))
The p.m.f. of X is given by


Hence, probability of throwing at most 2 sixes = \(\frac{7}{3}\left(\frac{5}{6}\right)^{5}\).
Question 11.
It is known that 10% of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective?
Solution:
Let X = number of defective articles.
p = probability of defective articles.
∴ p = 10% = \(\frac{10}{100}=\frac{1}{10}\)
and q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
Given: n = 12
∴ X ~ B(12, \(\frac{1}{10}\))
The p.m.f. of X is given by

Hence, the probability of getting 9 defective articles = \(22\left(\frac{9^{3}}{10^{11}}\right)\)
![]()
Question 12.
Given X ~ B(n, P)
(i) If n = 10 and p = 0.4, find E(x) and Var(X).
(ii) If p = 0.6 and E(X) = 6, find n and Var(X).
(iii) If n = 25, E(X) = 10, find p and SD(X).
(iv) If n = 10, E(X) = 8, find Var(X).
Solution:
(i) Given: n = 10 and p = 0.4
∴ q = 1 – p = 1 – 0.4 = 0.6
∴ E(X) = np = 10(0.4) = 4
Var(X) = npq = 10(0.4)(0.6) = 2.4
Hence, E(X) = 4, Var(X) = 2.4.
(ii) Given: p = 0.6, E (X) = 6
E(X) = np
6 = n(0.6)
n = \(\frac{6}{0.6}\) = 10
Now, q = 1 – p = 1 – 0.6 = 0.4
∴ Var(X) = npq = 10(0.6)(0.4) = 2.4
Hence, n = 10 and Var(X) = 2.4.
(iii) Given: n = 25, E(X) = 10
E(X) = np
10 = 25p
p = \(\frac{10}{25}=\frac{2}{5}\)
∴ q = 1 – p = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Var(X) = npq = \(25 \times \frac{2}{5} \times \frac{3}{5}\) = 6
∴ SD(X) = √Var(X) = √6
Hence, p = \(\frac{2}{5}\) and S.D.(X) = √6.
![]()
(iv) Given: n = 10, E(X) = 8
E(X) = np
8 = 10p
p = \(\frac{8}{10}=\frac{4}{5}\)
q = 1 – p = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Var(X) = npq = \(10\left(\frac{4}{5}\right)\left(\frac{1}{5}\right)=\frac{8}{5}\)
Hence, Var(X) = \(\frac{8}{5}\).