Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Probability Distributions Miscellaneous Exercise 7 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 7 Probability Distributions Miscellaneous Exercise 7
(I) Choose the correct option from the given alternatives:
Question 1.
P.d.f. of a c.r.v. X is f(x) = 6x(1 – x), for 0 ≤ x ≤ 1 and = 0, otherwise (elsewhere) If P(X < a) = P(X > a), then a =
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{4}\)
Answer:
(b) \(\frac{1}{2}\)
Question 2.
If the p.d.f. of a c.r.v. X is f(x) = 3(1 – 2x2), for 0 < x < 1 and = 0, otherwise (elsewhere), then the c.d.f. of X is F(x) =
(a) 2x – 3x2
(b) 3x – 4x3
(c) 3x – 2x3
(d) 2x3 – 3x
Answer:
(c) 3x – 2x3
![]()
Question 3.
If the p.d.f. of a c.r.v. X is f(x) = \(\frac{x^{2}}{18}\), for -3 < x < 3 and = 0, otherwise, then P(|X| < 1) =
(a) \(\frac{1}{27}\)
(b) \(\frac{1}{28}\)
(c) \(\frac{1}{29}\)
(d) \(\frac{1}{26}\)
Answer:
(a) \(\frac{1}{27}\)
Question 4.
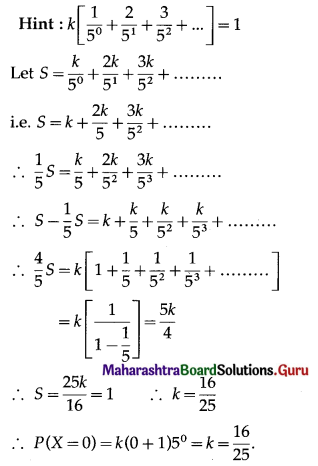
If p.m.f. of a d.r.v. X takes values 0, 1, 2, 3, … which probability P(X = x) = k(x +1) . 5-x, where k is a constant, then P(X = 0) =
(a) \(\frac{7}{25}\)
(b) \(\frac{16}{25}\)
(c) \(\frac{18}{25}\)
(d) \(\frac{19}{25}\)
Answer:
(b) \(\frac{16}{25}\)
Question 5.
If p.m.f. of a d.r.v. X is P(X = x) = \(\frac{\left({ }^{5} \mathrm{C}_{x}\right)}{2^{5}}\), for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise. If a = P(X ≤ 2) and b = P(X ≥ 3), then
(a) a < b
(b) a > b
(c) a = b
(d) a + b
Answer:
(c) a = b
Question 6.
If p.m.f. of a d.r.v. X is P(X = x) = \(\frac{x}{n(n+1)}\), for x = 1, 2, 3, ……, n and = 0, otherwise, then E(X) =
(a) \(\frac{n}{1}+\frac{1}{2}\)
(b) \(\frac{n}{3}+\frac{1}{6}\)
(c) \(\frac{n}{2}+\frac{1}{5}\)
(d) \(\frac{n}{1}+\frac{1}{3}\)
Answer:
(b) \(\frac{n}{3}+\frac{1}{6}\)
![]()
Question 7.
If p.m.f. of a d.r.v. X is P(x) = \(\frac{c}{x^{3}}\), for x = 1, 2, 3 and = 0, otherwise (elsewhere), then E(X) =
(a) \(\frac{343}{297}\)
(b) \(\frac{294}{251}\)
(c) \(\frac{297}{294}\)
(d) \(\frac{294}{297}\)
Answer:
(b) \(\frac{294}{251}\)
Question 8.
If the d.r.v. X has the following probability distribution:

then P(X = -1) =
(a) \(\frac{1}{10}\)
(b) \(\frac{2}{10}\)
(c) \(\frac{3}{10}\)
(d) \(\frac{4}{10}\)
Answer:
(a) \(\frac{1}{10}\)
Question 9.
If the d.r.v. X has the following probability distribution:

then k =
(a) \(\frac{1}{7}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{10}\)
Answer:
(d) \(\frac{1}{10}\)
Question 10.
Find the expected value of X for the following p.m.f.

(a) 0.85
(b) -0.35
(c) 0.15
(d) -0.15
Answer:
(b) -0.35
![]()
(II) Solve the following:
Question 1.
Identify the random variable as either discrete or continuous in each of the following. If the random variable is discrete, list its possible values:
(i) An economist is interested in the number of unemployed graduates in the town of population 1 lakh.
(ii) Amount of syrup prescribed by a physician.
(iii) The person on a high protein diet is interesting to gain weight in a week.
(iv) 20 white rats are available for an experiment. Twelve rats are males. A scientist randomly selects 5 rats, the number of female rats selected on a specific day.
(v) A highway-safety group is interested in studying the speed (in km/hr) of a car at a checkpoint.
Solution:
(i) Let X = number of unemployed graduates in a town.
Since the population of the town is 1 lakh, X takes the finite values.
∴ random variable X is discrete.
Range = {0, 1, 2, …, 99999, 100000}.
(ii) Let X = amount of syrup prescribed by a physician.
Then X takes uncountable infinite values.
∴ random variable X is continuous.
(iii) Let X = gain of weight in a week
Then X takes uncountable infinite values
∴ random variable X is continuous.
(iv) Let X = number of female rats selected on a specific day.
Since the total number of rats is 20 which includes 12 males and 8 females, X takes the finite values.
∴ random variable X is discrete.
Range = {0, 1, 2, 3, 4, 5}
(v) Let X = speed of .the car in km/hr.
Then X takes uncountable infinite values
∴ random variable X is continuous.
Question 2.
The probability distribution of discrete r.v. X is as follows:

(i) Determine the value of k.
(ii) Find P(X ≤ 4), P(2 < X < 4), P(X ≥ 3).
Solution:
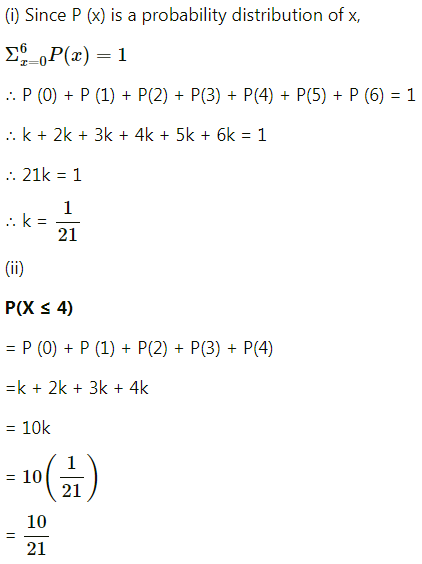
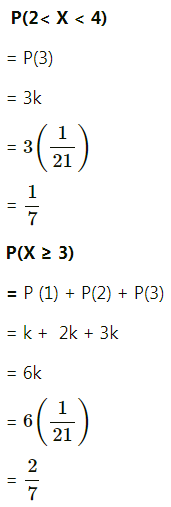
![]()
Question 3.
The following is the probability distribution of X:

Find the probability that
(i) X is positive
(ii) X is non-negative
(iii) X is odd
(iv) X is even.
Solution:
(i) P(X is positive) = P(X = 1) + P(X = 2) + P(X = 3)
= 0.25 + 0.15 + 0.1
= 0.50
(ii) P(X is non-negative)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= 0.20 + 0.25 + 0.15 + 0.1
= 0.70
(iii) P(X is odd)
= P(X = -3) + P(X = -1) + P(X = 1) + P(X = 3)
= 0.05 + 0.15 + 0.25 + 0.1
= 0.55
(iv) P(X is even)
= P(X = -2) + P(X = 0) + P(X = 2)
= 0.10 + 0.20 + 0.15
= 0.45.
Question 4.
The p.m.f. of a r.v. X is given by P(X = x) = x = \(\frac{{ }^{5} \mathrm{C}_{\mathrm{x}}}{2^{5}}\), for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise. Then show that P(X ≤ 2) = P(X ≥ 3).
Solution:
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
= \(\frac{{ }^{5} \mathrm{C}_{0}}{2^{5}}+\frac{{ }^{5} \mathrm{C}_{1}}{2^{5}}+\frac{{ }^{5} \mathrm{C}_{2}}{2^{5}}\)
= \(\frac{{ }^{5} \mathrm{C}_{5}}{2^{5}}+\frac{{ }^{5} \mathrm{C}_{4}}{2^{5}}+\frac{{ }^{5} \mathrm{C}_{3}}{2^{5}}\) ………[latex]{ }^{n} \mathrm{C}_{r}={ }^{n} \mathrm{C}_{n-r}[/latex]
= P(X = 5) + P(X = 4) + P(X = 3)
= P(X ≥ 3)
∴ P(X ≤ 2) = P(X ≥ 3).
![]()
Question 5.
In the p.m.f. of r.v. X

Find a and obtain c.d.f. of X.
Solution:
For p.m.f. of a r.v. X
\(\sum_{i=1}^{5} P(X=x)=1\)
∴ P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 1
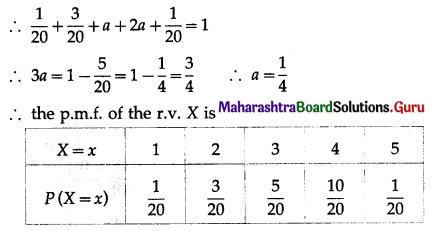
Let F(x) be the c.d.f. of X.
Then F(x) = P(X ≤ x)
∴ F(1) = P(X ≤ 1) = P(X = 1) = \(\frac{1}{20}\)
F(2) = P(X ≤ 2) = P(X = 1) + P (X = 2)
\(=\frac{1}{20}+\frac{3}{20}=\frac{4}{20}=\frac{1}{5}\)
P(3) = P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)
\(=\frac{1}{20}+\frac{3}{20}+\frac{5}{20}=\frac{9}{20}\)
F(4) = P(X ≤ 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
\(=\frac{1}{20}+\frac{3}{20}+\frac{5}{20}+\frac{10}{20}=\frac{19}{20}\)
F(5) = P(X ≤ 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)
\(=\frac{1}{20}+\frac{3}{20}+\frac{5}{20}+\frac{10}{20}+\frac{1}{20}=\frac{20}{20}=1\)
Hence, the c.d.f. of the random variable X is as follows:

Question 6.
A fair coin is tossed 4 times. Let X denote the number of heads obtained. Write down the probability distribution of X. Also, find the formula for p.m.f. of X.
Solution:
When a fair coin is tossed 4 times then the sample space is
S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THHT, THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT}
∴ n(S) = 16
X denotes the number of heads.
∴ X can take the value 0, 1, 2, 3, 4
When X = 0, then X = {TTTT}
∴ n (X) = 1
∴ P(X = 0) = \(\frac{n(X)}{n(S)}=\frac{1}{16}=\frac{{ }^{4} \mathrm{C}_{0}}{16}\)
When X = 1, then
X = {HTTT, THTT, TTHT, TTTH}
∴ n(X) = 4
∴ P(X = 1) = \(\frac{n(X)}{n(S)}=\frac{4}{16}=\frac{{ }^{4} C_{1}}{16}\)
When X = 2, then
X = {HHTT, HTHT, HTTH, THHT, THTH, TTHH}
∴ n(X) = 6
∴ P(X = 2) = \(\frac{n(X)}{n(S)}=\frac{6}{16}=\frac{{ }^{4} \mathrm{C}_{2}}{16}\)
When X = 3, then
X = {HHHT, HHTH, HTHH, THHH}
∴ n(X) = 4
∴ P(X = 3) = \(\frac{n(X)}{n(S)}=\frac{4}{16}=\frac{{ }^{4} C_{3}}{16}\)
When X = 4, then X = {HHHH}
∴ n(X) = 1
∴ P(X = 4) = \(\frac{n(X)}{n(S)}=\frac{1}{16}=\frac{{ }^{4} \mathrm{C}_{4}}{16}\)
∴ the probability distribution of X is as follows:
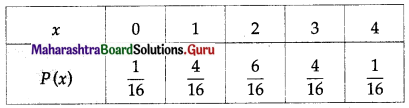
Also, the formula for p.m.f. of X is
P(x) = \(\frac{{ }^{4} \mathrm{C}_{x}}{16}\), x = 0, 1, 2, 3, 4 and = 0, otherwise.
![]()
Question 7.
Find the probability distribution of the number of successes in two tosses of a die, where success is defined as
(i) number greater than 4
(ii) six appear on at least one die.
Solution:
When a die is tossed two times, we obtain (6 × 6) = 36 number of observations.
Let X be the random variable, which represents the number of successes.
Here, success refers to the number greater than 4.
P(X = 0) = P(number less than or equal to 4 on both the tosses)
= \(\frac{4}{6} \times \frac{4}{6}=\frac{16}{36}=\frac{4}{9}\)
P(X = 1) = P(number less than or equal to 4 on first toss and greater than 4 on second toss) + P(number greater than 4 on first toss and less than or equal to 4 on second toss)
= \(\frac{4}{6} \times \frac{2}{6}+\frac{4}{6} \times \frac{2}{6}\)
= \(\frac{8}{36}+\frac{8}{36}\)
= \(\frac{16}{36}\)
= \(\frac{4}{9}\)
P(X = 2) = P(number greater than 4 on both the tosses)
= \(\frac{2}{6} \times \frac{2}{6}=\frac{4}{36}=\frac{1}{9}\)
Thus, the probability distribution is as follows:

(ii) Here, success means six appears on at least one die.
P(Y = 0) = P(six appears on none of the dice) = \(\frac{5}{6} \times \frac{5}{6}=\frac{25}{36}\)
P(Y = 1) = P(six appears on none of the dice x six appears on at least one of the dice ) + P(six appears on none of the dice x six appears on at least one of the dice)
= \(\frac{1}{6} \times \frac{5}{6}+\frac{1}{6} \times \frac{5}{6}=\frac{5}{36}+\frac{5}{36}=\frac{10}{36}\)
P(Y = 2) = P(six appears on at least one of the dice) = \(\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}\)
Thus, the required probability distribution is as follows:
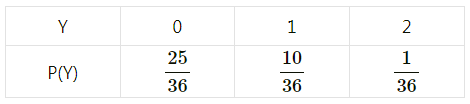
Question 8.
A random variable X has the following probability distribution:

Determine:
(i) k
(ii) P(X > 6)
(iii) P(0 < X < 3).
![]()
Question 9.
The following is the c.d.f. of a r.v. X:

Find
(i) p.m.f. of X
(ii) P( -1 ≤ X ≤ 2)
(iii) P(X ≤ X > 0).
Solution:
(i) From the given table
F(-3) = 0.1, F(-2) = 0.3, F(-1) = 0.5
F(0) = 0.65, f(1) = 0.75, F(2) = 0.85
F(3) = 0.9, F(4) = 1
P(X = -3) = F(-3) = 0.1
P(X = -2) = F(-2) – F(-3) = 0.3 – 0.1 = 0.2
P(X = -1) = F(-1) – F(-2) = 0.5 – 0.3 = 0.2
P(X = 0) = F(0) – F(-1) = 0.65 – 0.5 = 0.15
P(X = 1) = F(1) – F(0) = 0.75 – 0.65 = 0.1
P(X = 2) = F(2) – F(1) = 0.85 – 0.75 = 0.1
P(X = 3) = F(3) – F(2) = 0.9 – 0.85 = 0.1
P(X = 4) = F(4) – F(3) = 1 – 0.9 = 0.1
∴ the p.m.f of X is as follows:

(ii) P(-1 ≤ X ≤ 2) = P(X = -1) + P(X = 0) + P(X = 1) + P(X = 2)
= 0.2 + 0.15 + 0.1 + 0.1
= 0.55
(iii) (X ≤ 3) ∩ (X > 0)
= { -3, -2, -1, 0, 1, 2, 3} n {1, 2, 3, 4}
= {1, 2, 3}

Question 10.
Find the expected value, variance, and standard deviation of the random variable whose p.m.f’s are given below:
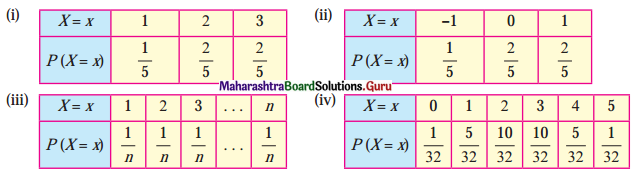
Solution:
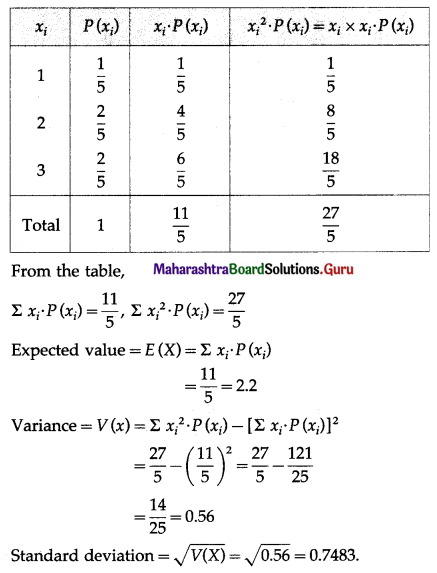
(i) We construct the following table to find the expected value, variance, and standard deviation:
(ii) We construct the following table to find the expected value, variance, and standard deviation:
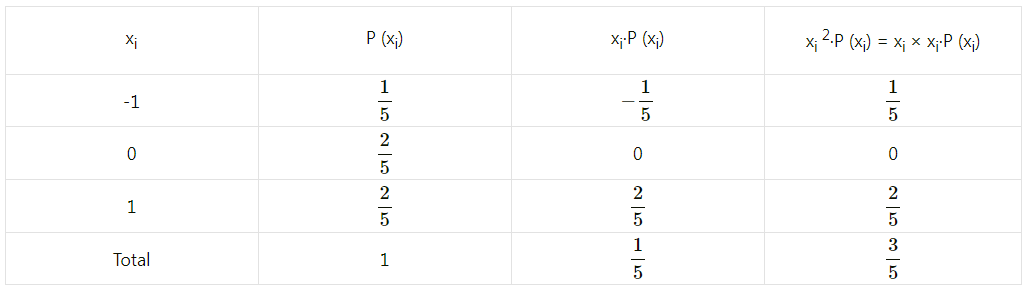
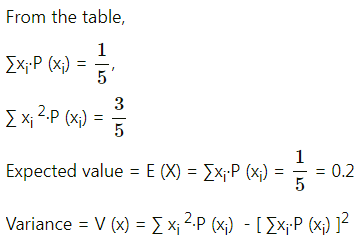
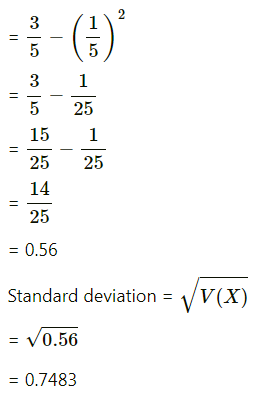
(iii) We construct the following table to find the expected value, variance, and standard deviation:
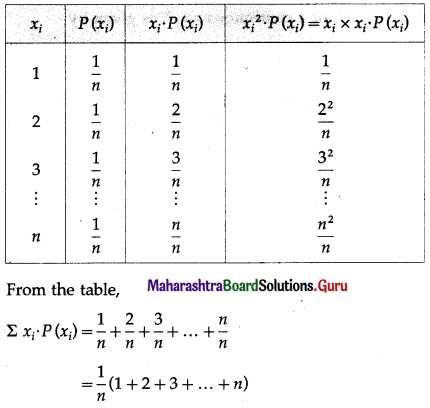


(iv) We construct the following table to find the expected value, variance, and standard deviation:
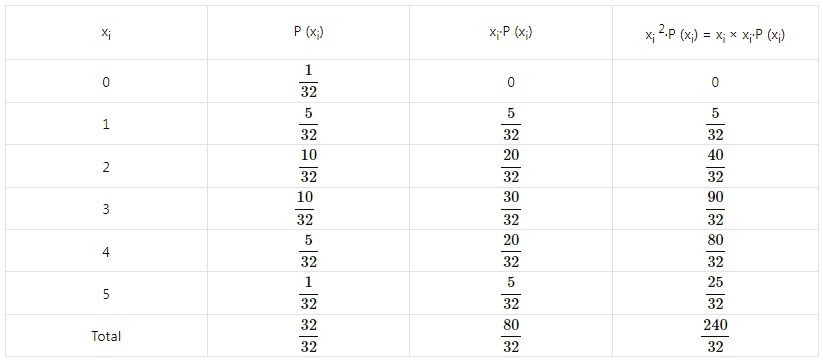
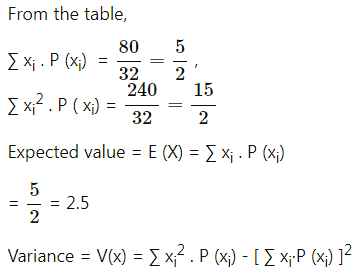

![]()
Question 11.
A player tosses two wins. He wins ₹ 10 if 2 heads appear, ₹ 5 if 1 head appears and ₹ 2 if no head appears. Find the expected winning amount and variance of the winning amount.
Solution:
When a coin is tossed twice, the sample space is
S = {HH, HT, TH, HH}
Let X denote the amount he wins.
Then X takes values 10, 5, 2.
P(X = 10) = P(2 heads appear) = \(\frac{1}{4}\)
P(X = 5) = P(1 head appears) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
P(X = 2) = P(no head appears) = \(\frac{1}{4}\)
We construct the following table to calculate the mean and the variance of X:
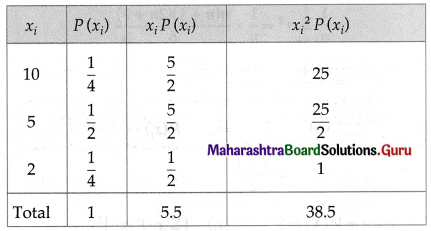
From the table Σxi . P(xi) = 5.5, \(\Sigma x_{i}^{2} \cdot P\left(x_{i}\right)\) = 38.5
E(X) = Σxi . P(xi) = 5.5
Var(X) = \(\Sigma x_{i}^{2} \cdot P\left(x_{i}\right)\) – [E(X)]2
= 38.5 – (5.5)2
= 38.5 – 30.25
= 8.25
∴ Hence, expected winning amount = ₹ 5.5 and variance of winning amount = ₹ 8.25.
Question 12.
Let the p.m.f. of r.v. X be P(x) = \(\frac{3-x}{10}\), for x = -1, 0, 1, 2 and = 0, otherwise.
Calculate E(X) and Var(X).
Solution:
P(X) = \(\frac{3-x}{10}\)
X takes values -1, 0, 1, 2
P(X = -1) = P(-1) = \(\frac{3+1}{10}=\frac{4}{10}\)
P(X = 0) = P(0) = \(\frac{3-0}{10}=\frac{3}{10}\)
P(X = 1) = P(1) = \(\frac{3-1}{10}=\frac{2}{10}\)
P(X = 2) = P(2) = \(\frac{3-2}{10}=\frac{1}{10}\)
We construct the following table to calculate the mean and variance of X:
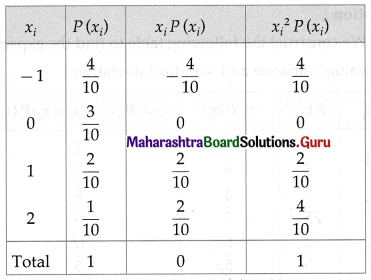
From the table
ΣxiP(xi) = 0 and \(\Sigma x_{i}{ }^{2} \cdot P\left(x_{i}\right)\) = 1
E(X) = ΣxiP(xi) = 0
Var(X) = \(\Sigma x_{i}{ }^{2} \cdot P\left(x_{i}\right)\) – [E(X)]2
= 1 – 0
= 1
Hence, E(X) = 0, Var (X) = 1.
![]()
Question 13.
Suppose the error involved in making a certain measurement is a continuous r.v. X with p.d.f.
f(x) = k(4 – x2), -2 ≤ x ≤ 2 and = 0 otherwise.
Compute
(i) P(X > 0)
(ii) P(-1 < X < 1)
(iii) P(X < -0.5 or X > 0.5).
Solution:
(i) P(X > 0)
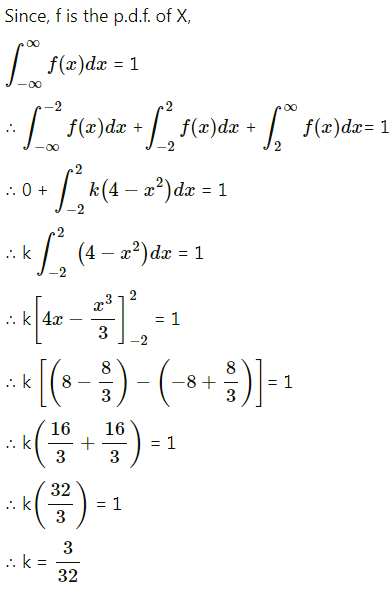
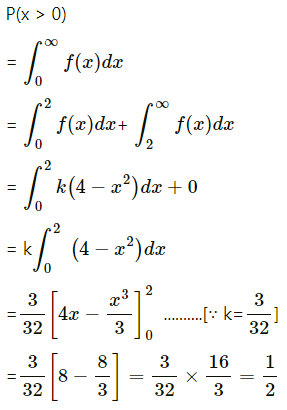
(ii) P(-1 < X < 1)
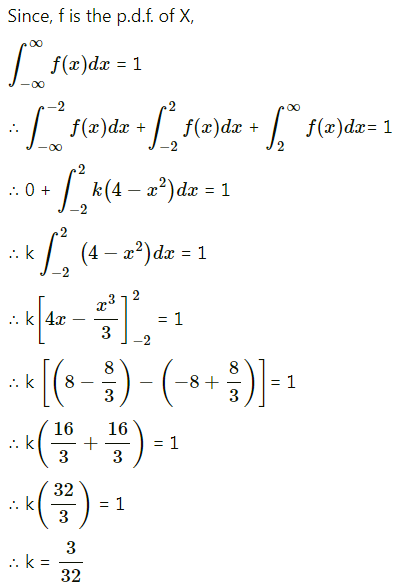
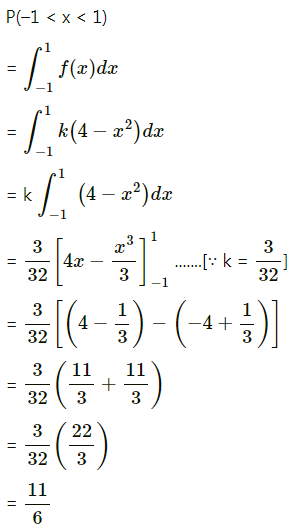
(iii) P(X < -0.5 or X > 0.5)
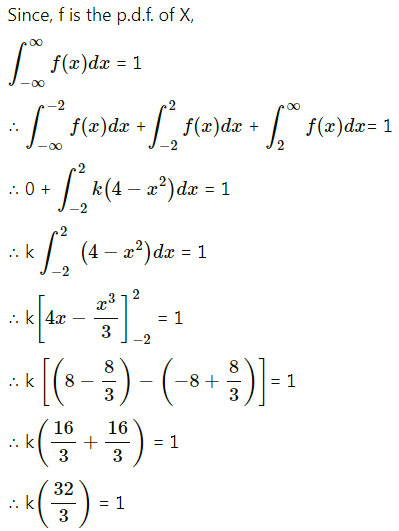
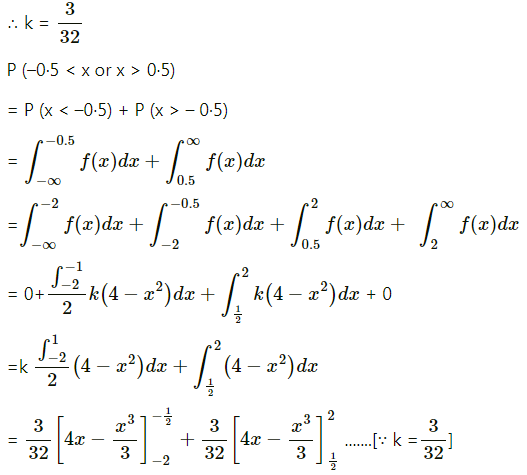
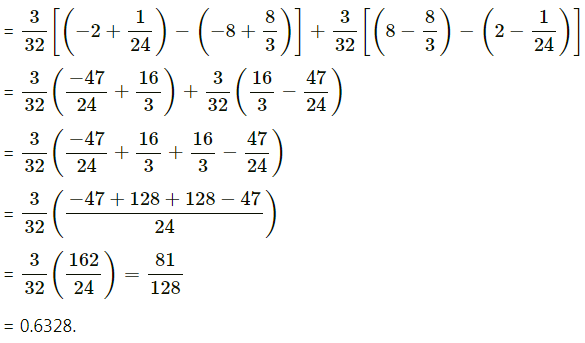
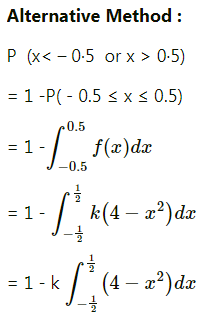
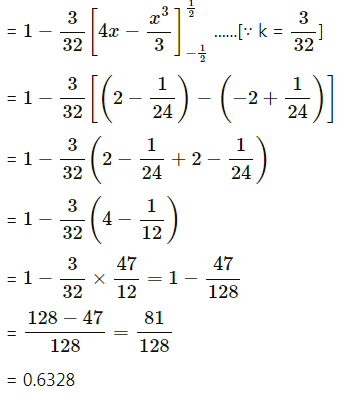
Question 14.
The p.d.f. of a continuous r.v. X is given by f(x) = \(\frac{1}{2 a}\), for 0 < x < 2a and = 0, otherwise. Show that P( X < \(\frac{a}{2}\)) = P(X > \(\frac{3a}{2}\))
Solution:


![]()
Question 15.
The p.d.f. of r.v. X is given by f(x) = \(\frac{k}{\sqrt{x}}\), for 0 < x < 4 and = 0, otherwise. Determine k. Determine c.d.f. of X and hence find P(X ≤ 2) and P(X ≤ 1).
Solution:
Since f is p.d.f. of the r.v. X,

