Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Ex 4.3
Question 1.
Find the joint equation of the pair of lines:
(i) Through the point (2, -1) and parallel to lines represented by 2x2 + 3xy – 9y2 = 0
Solution:
The combined equation of the given lines is
2x2 + 3 xy – 9y2 = 0
i.e. 2x2 + 6xy – 3xy – 9y2 = 0
i.e. 2x(x + 3y) – 3y(x + 3y) = 0
i.e. (x + 3y)(2x – 3y) = 0
∴ their separate equations are
x + 3y = 0 and 2x – 3y = 0
∴ their slopes are m1 = \(\frac{-1}{3}\) and m2 = \(\frac{-2}{-3}=\frac{2}{3}\).
The slopes of the lines parallel to these lines are m1 and m2, i.e. \(-\frac{1}{3}\) and \(\frac{2}{3}\).
∴ the equations of the lines with these slopes and through the point (2, -1) are
y + 1 = \(-\frac{1}{3}\) (x – 2) and y + 1 = \(\frac{2}{3}\)(x – 2)
i.e. 3y + 3= -x + 2 and 3y + 3 = 2x – 4
i.e. x + 3y + 1 = 0 and 2x – 3y – 7 = 0
∴ the joint equation of these lines is
(x + 3y + 1)(2x – 3y – 7) = 0
∴ 2x2 – 3xy – 7x + 6xy – 9y2 – 21y + 2x – 3y – 7 = 0
∴ 2x2 + 3xy – 9y2 – 5x – 24y – 7 = 0.
(ii) Through the point (2, -3) and parallel to lines represented by x2 + xy – y2 = 0
Solution:
Comparing the equation
x2 + xy – y2 = 0 … (1)
with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = 1, b = -1
Let m1 and m2 be the slopes of the lines represented by (1).

The slopes of the lines parallel to these lines are m1 and m2.
∴ the equations of the lines with these slopes and through the point (2, -3) are
y + 3 = m1(x – 2) and y + 3 = m2(x – 2)
i.e. m1(x – 2) – (y + 3) = 0 and m2(x – 2) – (y + 3) = 0
∴ the joint equation of these lines is
[m1(x – 2) – (y + 3)][m2(x – 2) – (y + 3)] = 0
∴ m1m2(x – 2)2 – m1(x – 2)(y + 3) – m2(x – 2)(y + 3) + (y + 3)2 = o
∴ m1m2(x – 2)2 – (m1 + m2)(x – 2)(y + 3) + (y + 3)3 = 0
∴ -(x – 2)2 – (x – 2)(y + 3) + (y + 3)2 = 0 …… [By (2)]
∴ (x – 2)2 + (x – 2)(y + 3) – (y + 3)2 = 0
∴ (x2 – 4x + 4) + (xy + 3x – 2y – 6) – (y2 + 6y + 9) = 0
∴ x2 – 4x + 4 + xy + 3x – 2y – 6 – y2 – 6y – 9 = 0
∴ x2 + xy – y2 – x – 8y – 11 = 0.
![]()
Question 2.
Show that equation x2 + 2xy+ 2y2 + 2x + 2y + 1 = 0 does not represent a pair of lines.
Solution:
Comparing the equation
x2 + 2xy + 2y2 + 2x + 2y + 1 = 0 with
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we get,
a = 1, h = 1, b = 2, g = 1, f = 1, c = 1.
The given equation represents a pair of lines, if
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|\) = 0 and h2 – ab ≥ 0
Now, D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 1 (2 – 1) – 1(1 – 1) + 1 (1 – 2)
= 1 – 0 – 1 = 0
and h2 – ab = (1)2 – 1(2) = -1 < 0
∴ given equation does not represent a pair of lines.
Question 3.
Show that equation 2x2 – xy – 3y2 – 6x + 19y – 20 = 0 represents a pair of lines.
Solution:
Comparing the equation
2x2 – xy – 3y2 – 6x + 19y – 20 = 0
with ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we get,
a = 2, h = \(-\frac{1}{2}\), b = -3, g = -3, f = \(\frac{19}{2}\), c = -20.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
2 & -\frac{1}{2} & -3 \\
-\frac{1}{2} & -3 & \frac{19}{2} \\
-3 & \frac{19}{2} & -20
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & -1 & -6 \\
-1 & -6 & 19 \\
-6 & 19 & -40
\end{array}\right|\)
= \(\frac{1}{8}\)[4(240 – 361) + 1(40 + 114) – 6(-19 – 36)]
= \(\frac{1}{8}\)[4(-121) + 154 – 6(-55)]
= \(\frac{11}{8}\)[4(-11) + 14 – 6(-5)]
= \(\frac{1}{8}\)(-44 + 14 + 30) = 0
Also h2 – ab = \(\left(-\frac{1}{2}\right)^{2}\) – 2(-3) = \(\frac{1}{4}\) + 6 = \(\frac{25}{4}\) > 0
∴ the given equation represents a pair of lines.
![]()
Question 4.
Show the equation 2x2 + xy – y2 + x + 4y – 3 = 0 represents a pair of lines. Also find the acute angle between them.
Solution:
Comparing the equation
2x2 + xy — y2 + x + 4y — 3 = 0 with
ax2 + 2hxy + by2 + 2gx + 2fy + c — 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2, c = – 3.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lrr}
2 & \frac{1}{2} & \frac{1}{2} \\
\frac{1}{2} & -1 & 2 \\
\frac{1}{2} & 2 & -3
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & 1 & 1 \\
1 & -2 & 4 \\
1 & 4 & -6
\end{array}\right|\)
= \(\frac{1}{8}\)[4(12 —16) — 1( —6 — 4) + 1(4 + 2)]
= \(\frac{1}{8}\)[4( – 4) – 1(-10) + 1(6)]
= \(\frac{1}{8}\)(—16 + 10 + 6) = 0
Also, h2 – ab = \(\left(\frac{1}{2}\right)^{2}\) – 2(-1) = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
∴ the given equation represents a pair of lines. Let θ be the acute angle between the lines
∴ tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\)
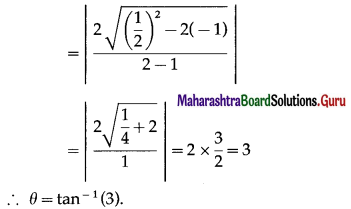
Question 5.
Find the separate equation of the lines represented by the following equations :
(i) (x – 2)2 – 3(x – 2)(y + 1) + 2(y + 1)2 = 0
Solution:
(x – 2)2 – 3(x – 2)(y + 1) + 2(y + 1)2 = 0
∴ (x – 2)2 – 2(x – 2)(y + 1) – (x – 2)(y + 1) + 2(y + 1)2 = 0
∴ (x – 2) [(x – 2) – 2(y + 1)] – (y + 1)[(x – 2) – 2(y + 1)] = 0
∴ (x – 2)(x – 2 – 2y – 2) – (y + 1)(x – 2 – 2y – 2) = 0
∴ (x – 2)(x – 2y – 4) – (y + 1)(x – 2y – 4) = 0
∴ (x – 2y – 4)(x – 2 – y – 1) = 0
∴ (x – 2y – 4)(x – y – 3) = 0
∴ the separate equations of the lines are
x – 2y – 4 = 0 and x – y – 3 = 0.
Alternative Method :
(x – 2)2 – 3(x – 2)(y + 1) + 2(y + 1)2 = 0 … (1)
Put x – 2 = X and y + 1 = Y
∴ (1) becomes,
X2 – 3XY + 2Y2 = 0
∴ X2 – 2XY – XY + 2Y2 = 0
∴ X(X – 2Y) – Y(X – 2Y) = 0
∴ (X – 2Y)(X – Y) = 0
∴ the separate equations of the lines are
∴ X – 2Y = 0 and X – Y = 0
∴ (x – 2) – 2(y + 1) = 0 and (x – 2) – (y +1) = 0
∴ x – 2y – 4 = 0 and x – y – 3 = 0.
![]()
(ii) 10(x + 1)2 + (x + 1)( y – 2) – 3(y – 2)2 = 0
Solution:
10(x + 1)2 + (x + 1)( y – 2) – 3(y – 2)2 = 0 …(1)
Put x + 1 = X and y – 2 = Y
∴ (1) becomes
10x2 + xy – 3y2 = 0
10x2 + 6xy – 5xy – 3y2 = 0
2x(5x + 3y) – y(5x + 3y) = 0
(2x – y)(5x + 3y) = 0
5x + 3y = 0 and 2x – y = 0
5x + 3y = 0
5(x + 1) + 3(y – 2) = 0
5x + 5 + 3y – 6 = 0
∴ 5x + 3y – 1 = 0
2x – y = 0
2(x + 1) – (y – 2) = 0
2x + 2 – y + 2 = 0
∴ 2x – y + 4 = 0
Question 6.
Find the value of k if the following equations represent a pair of lines :
(i) 3x2 + 10xy + 3y2 + 16y + k = 0
Solution:
Comparing the given equation with
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0,
we get, a = 3, h = 5, b = 3, g = 0, f= 8, c = k.
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af2 – bg2 – ch2 = 0
∴ (3)(3)(k) + 2(8)(0)(5) – 3(8)2 – 3(0)2 – k(5)2 = 0
∴ 9k + 0 – 192 – 0 – 25k = 0
∴ -16k – 192 = 0
∴ – 16k = 192
∴ k= -12.
![]()
(ii) kxy + 10x + 6y + 4 = 0
Solution:
Comparing the given equation with
ax2 + 2 hxy + by2 + 2gx + 2fy + c = 0,
we get, a = 0, h = \(\frac{k}{2}\), b = 0, g = 5, f = 3, c = 4
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af2 – bg2 – ch2 = 0
∴ (0)(0)(4) + 2(3)(5)\(\left(\frac{k}{2}\right)\) – 0(3)2 – 0(5)2 – 4\(\left(\frac{k}{2}\right)^{2}\) = 0
∴ 0 + 15k – 0 – 0 – k2 = 0
∴ 15k – k2 = 0
∴ -k(k – 15) = 0
∴ k = 0 or k = 15.
If k = 0, then the given equation becomes
10x + 6y + 4 = 0 which does not represent a pair of lines.
∴ k ≠ o
Hence, k = 15.
(iii) x2 + 3xy + 2y2 + x – y + k = 0
Solution:
Comparing the given equation with
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0,
we get, a = 1, h = \(\frac{3}{2}\), b = 2, g = \(\frac{1}{2}\), f= \(-\frac{1}{2}\), c = k.
Now, given equation represents a pair of lines.
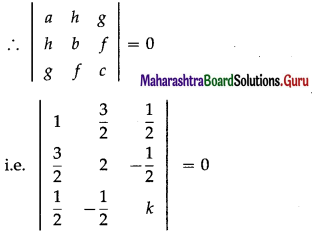
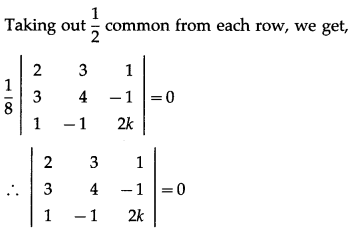
∴ 2(8k – 1) – 3(6k + 1) + 1(-3 – 4) = 0
∴ 16k – 2 – 18k – 3 – 7 = 0
∴ -2k – 12 = 0
∴ -2k = 12 ∴ k = -6.
![]()
Question 7.
Find p and q if the equation px2 – 8xy + 3y2 + 14x + 2y + q = 0 represents a pair of perpendicular lines.
Solution:
The given equation represents a pair of lines perpendicular to each other
∴ (coefficient of x2) + (coefficient of y2) = 0
∴ p + 3 = 0 p = -3
With this value of p, the given equation is
– 3x2 – 8xy + 3y2 + 14x + 2y + q = 0.
Comparing this equation with
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we have,
a = -3, h = -4, b = 3, g = 7, f = 1 and c = q.
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
-3 & -4 & 7 \\
-4 & 3 & 1 \\
7 & 1 & q
\end{array}\right|\)
= -3(3q – 1) + 4(-4q – 7) + 7(-4 – 21)
= -9q + 3 – 16q – 28 – 175
= -25q – 200= -25(q + 8)
Since the given equation represents a pair of lines, D = 0
∴ -25(q + 8) = 0 ∴ q= -8.
Hence, p = -3 and q = -8.
Question 8.
Find p and q if the equation 2x2 + 8xy + py2 + qx + 2y – 15 = 0 represents a pair of parallel lines.
Solution:
The given equation is
2x2 + 8xy + py2 + qx + 2y – 15 = 0
Comparing it with ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we get,
a = 2, h = 4, b = p, g = \(\frac{q}{2}\), f = 1, c = – 15
Since the lines are parallel, h2 = ab
∴ (4)2 = 2p ∴ P = 8
Since the given equation represents a pair of lines
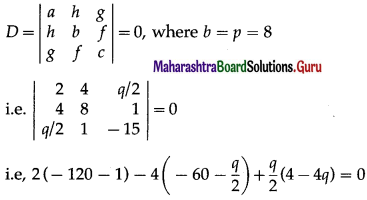
i.e. – 242 + 240 + 2q + 2q – 2q2 = 0
i.e. -2q2 + 4q – 2 = 0
i.e. q2 – 2q + 1 = 0
i.e. (q – 1)2 = 0 ∴ q – 1 = 0 ∴ q = 1.
Hence, p = 8 and q = 1.
Question 9.
Equations of pairs of opposite sides of a parallelogram are x2 – 7x+ 6 = 0 and y2 – 14y + 40 = 0. Find the joint equation of its diagonals.
Solution:
Let ABCD be the parallelogram such that the combined equation of sides AB and CD is x2 – 7x + 6 = 0 and the combined equation of sides BC and AD is y2 – 14y + 40 = 0.
The separate equations of the lines represented by x2 – 7x + 6 = 0, i.e. (x – 1)(x – 6) = 0 are x – 1 = 0 and x – 6 = 0.
Let equation of the side AB be x – 1 = 0 and equation of side CD be x – 6 = 0.
The separate equations of the lines represented by y2 – 14y + 40 = 0, i.e. (y – 4)(y – 10) = 0 are y – 4 = 0 and y – 10 = 0.
Let equation of the side BC be y – 4 = 0 and equation of side AD be y – 10 = 0.
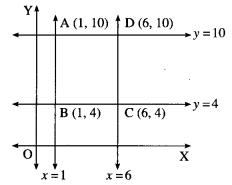
Coordinates of the vertices of the parallelogram are A(1, 10), B(1, 4), C(6, 4) and D(6, 10).
∴ equation of the diagonal AC is
\(\frac{y-10}{x-1}\) = \(\frac{10-4}{1-6}\) = \(\frac{6}{-5}\)
∴ -5y + 50 = 6x – 6
∴ 6x + 5y – 56 = 0
and equation of the diagonal BD is
\(\frac{y-4}{x-1}\) = \(\frac{4-10}{1-6}\) = \(\frac{-6}{-5}\) = \(\frac{6}{5}\)
∴ 5y – 20 = 6x – 6
∴ 6x – 5y + 14 = 0
Hence, the equations of the diagonals are 6x + 5y – 56 = 0 and 6x – 5y + 14 = 0.
∴ the joint equation of the diagonals is (6x + 5y – 56)(6x – 5y + 14) = 0
∴ 36x2 – 30xy + 84x + 30xy – 25y2 + 70y – 336x + 280y – 784 = 0
∴ 36x2 – 25y2 – 252x + 350y – 784 = 0.
![]()
Question 10.
∆OAB is formed by lines x2 – 4xy + y2 = 0 and the line 2x + 3y – 1 = 0. Find the equation of the median of the triangle drawn from O.
Solution:
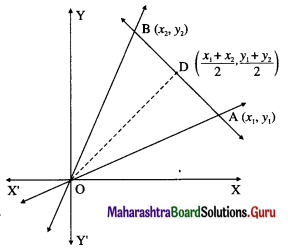
Let D be the midpoint of seg AB where A is (x1, y1) and B is (x2, y2).
Then D has coordinates \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\).
The joint (combined) equation of the lines OA and OB is x2 – 4xy + y2 = 0 and the equation of the line AB is 2x + 3y – 1 = 0.
∴ points A and B satisfy the equations 2x + 3y – 1 = 0
and x2 – 4xy + y2 = 0 simultaneously.
We eliminate x from the above equations, i.e.,
put x = \(\frac{1-3 y}{2}\) in the equation x2 – 4xy + y2 = 0, we get,
∴ \(\left(\frac{1-3 y}{2}\right)^{2}\) – 4\(\left(\frac{1-3 y}{2}\right)\)y + y2 = 0
∴ (1 – 3y)2 – 8(1 – 3y)y + 4y2 = 0
∴1 – 6y + 9y2 – 8y + 24y2 + 4y2 = 0
∴ 37y2 – 14y + 1 = 0
The roots y1 and y2 of the above quadratic equation are the y-coordinates of the points A and B.
∴ y1 + y2 = \(\frac{-b}{a}=\frac{14}{37}\)
∴ y-coordinate of D = \(\frac{y_{1}+y_{2}}{2}=\frac{7}{37}\).
Since D lies on the line AB, we can find the x-coordinate of D as
2x + 3\(\left(\frac{7}{37}\right)\) – 1 = 0
∴ 2x = 1 – \(\frac{21}{37}=\frac{16}{37}\)
∴ x = \(\frac{8}{37}\)
∴ D is (8/37, 7/37)
∴ equation of the median OD is \(\frac{x}{8 / 37}=\frac{y}{7 / 37}\),
i.e., 7x – 8y = 0.
![]()
Question 11.
Find the co-ordinates of the points of intersection of the lines represented by x2 – y2 – 2x + 1 = 0.
Solution:
Consider, x2 – y2 – 2x + 1 = 0
∴ (x2 – 2x + 1) – y2 = 0
∴ (x – 1)2 – y2 = 0
∴ (x – 1 + y)(x – 1 – y) = 0
∴ (x + y – 1)(x – y – 1) = 0
∴ separate equations of the lines are
x + y – 1 = 0 and x – y +1 = 0.
To find the point of intersection of the lines, we have to solve
x + y – 1 = 0 … (1)
and x – y + 1 = 0 … (2)
Adding (1) and (2), we get,
2x = 0 ∴ x = 0
Substituting x = 0 in (1), we get,
0 + y – 1 = 0 ∴ y = 1
∴ coordinates of the point of intersection of the lines are (0, 1).