Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Probability Ex 7.4 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Probability Ex 7.4
Question 1.
Two dice are thrown simultaneously, if at least one of the dice shows a number 5, what is the probability that sum of the numbers on two dice is 9?
Solution:
When two dice are thrown simultaneously, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let A be the event that at least one die shows number 5.
∴ A = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
∴ n(A) = 11
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{11}{36}\)
Let B be the event that sum of the numbers on two dice is 9.
∴ B = {(3, 6), (4, 5), (5, 4), (6, 3)}
Also, A ∩ B = {(4, 5), (5, 4)}
∴ n(A ∩ B) = 2
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{2}{36}\)
∴ Probability of sum of numbers on two dice is 9, given that one dice shows number 5, is given by
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{\frac{2}{36}}{\frac{11}{36}}=\frac{2}{11}\)
![]()
Question 2.
A pair of dice is thrown. If sum of the numbers is an even number, what is the probability that it is a perfect square?
Solution:
When two dice are thrown simultaneously, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let A be the event that sum of the numbers is an even number.
∴ A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)}
∴ n(A) = 18
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{18}{36}\)
Let B be the event that sum of outcomes is a perfect square.
∴ B = {(1, 3), (2, 2), (3, 1), (3, 6), (4, 5), (5, 4), (6, 3)}
Also, A n B= {(1, 3), (2, 2), (3, 1)}
∴ n(A ∩ B) = 3
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{3}{36}\)
∴ Probability of sum of the numbers is a perfect square, given that sum of numbers is an even number, is given by
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{\frac{3}{36}}{\frac{18}{36}}=\frac{3}{18}=\frac{1}{6}\)
Question 3.
A box contains 11 tickets numbered from 1 to 11. Two tickets are drawn at random with replacement. If the sum is even, find the probability that both the numbers are odd.
Solution:
Two tickets can be drawn from 11 tickets with replacement in 11 × 11 = 121 ways.
∴ n(S) = 121
Let A be the event that the sum of two numbers is even.
The event A occurs, if either both the tickets with odd numbers or both the tickets with even numbers are drawn.
There are 6 odd numbers (1, 3, 5, 7, 9, 11) and 5 even numbers (2, 4, 6, 8, 10) from 1 to 11.
∴ n(A) = 6 × 6 + 5 × 5
= 36 + 25
= 61
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{61}{121}\)
Let B be the event that the numbers tickets drawn are odd
∴ n(B) = 6 × 6 = 36
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{36}{121}\)
Since 6 odd numbers are common between A and B.
∴ n(A ∩ B) = 6 × 6 = 36
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{36}{121}\)
∴ Probability of both the numbers are odd, given that sum is even, is given by
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{\frac{36}{121}}{\frac{61}{121}}=\frac{36}{61}\)
![]()
Question 4.
A card is drawn from a well-shuffled pack of 52 cards. Consider two events A and B as
A: a club card is drawn.
B: an ace card is drawn.
Determine whether events A and B are independent or not.
Solution:
One card can be drawn out of 52 cards in 52C1 ways.
∴ n(S) = 52C1
Let A be the event that a club card is drawn.
1 club card out of 13 club cards can be drawn in 13C1 ways.
∴ n(A) = 13C1
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}\)
Let B be the event that an ace card is drawn.
An ace card out of 4 aces can be drawn in 4C1 ways.
∴ n(B) = 4C1
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{4} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}\)
Since 1 card is common between A and B
∴ n(A ∩ B) = 1C1
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{1} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{1}{52}\) …….(i)
∴ P(A) × P(B) = \(\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}} \times \frac{{ }^{4} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{13 \times 4}{52 \times 52}=\frac{1}{52}\) …….(ii)
From (i) and (ii), we get
P(A ∩ B) = P(A) × P(B)
∴ A and B are independent events.
Question 5.
A problem in statistics is given to three students A, B, and C. Their chances of solving the problem are 1/3, 1/4, and 1/5 respectively. If all of them try independently, what is the probability that,
(i) problem is solved?
(ii) problem is not solved?
(iii) exactly two students solve the problem?
Solution:
Let A be the event that student A can solve the problem.
B be the event that student B can solve the problem.
C be the event that student C can solve problem.
∴ P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{4}\), P(C) = \(\frac{1}{5}\)
∴ P(A’) = 1 – P(A) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
P(B’) = 1 – P(B) = 1 – \(\frac{1}{4}\) = \(\frac{5}{4}\)
P(C’) = 1 – P(C) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Since A, B, C are independent events
∴ A’, B’, C’ are also independent events
(i) Let X be the event that problem is solved.
Problem can be solved if at least one of the three students solves the problem.
P(X) = P(at least one student solves the problem)
= 1 – P(no student solved problem)
= 1 – P(A’ ∩ B’ ∩ C’)
= 1 – P(A’) P(B’) P(C’)
= 1 – \(\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}\)
= 1 – \(\frac{2}{5}\)
= \(\frac{3}{5}\)
(ii) Let Y be the event that problem is not solved
∴ P(Y) = P(A’ ∩ B’ ∩ C’)
= P(A’) P(B’) P(C’)
= \(\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}\)
= \(\frac{2}{5}\)
(iii) Let Z be the event that exactly two students solve the problem.
∴ P(Z) = P(A ∩ B ∩ C’) ∪ P(A ∩ B’ ∩ C) ∪ P(A’ ∩ B ∩ C)
= P(A) . P(B) . P(C’) + P(A) . P(B’) . P(C) + P(A’) . P(B) . P(C)
= \(\left(\frac{1}{3} \times \frac{1}{4} \times \frac{4}{5}\right)+\left(\frac{1}{3} \times \frac{3}{4} \times \frac{1}{5}\right)+\left(\frac{2}{3} \times \frac{1}{4} \times \frac{1}{5}\right)\)
= \(\frac{4}{60}+\frac{3}{60}+\frac{2}{60}\)
= \(\frac{3}{20}\)
![]()
Question 6.
The probability that a 50-year old man will be alive till age 60 is 0.83 and the probability that a 45-year old woman will be alive till age 55 is 0.97. What is the probability that a man whose age is 50 and his wife whose age is 45 will both be alive for the next 10 years?
Solution:
Let A be the event that man will be alive at 60.
∴ P(A) = 0.83
Let B be the event that a woman will be alive at 55.
∴ P(B) = 0.97
A ∩ B = Event that both will be alive.
Also, A and B are independent events
∴ P(both man and his wife will be alive) = P(A ∩ B)
= P(A) . P(B)
= 0.83 × 0.97
= 0.8051
Question 7.
In an examination, 30% of the students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subjects I and subject II. A student is selected at random, what is the probability that the student
(i) has failed in the subject I, if it is known that he is failed in subject II?
(ii) has failed in at least one subject?
(iii) has failed in exactly one subject?
Solution:
Let A be the event that the student failed in Subject I
B be the event that the student failed in Subject II
Then P(A) = 30% = \(\frac{30}{100}\)
P(B) = 20% = \(\frac{20}{100}\)
and P(A ∩ B) = 10% = \(\frac{10}{100}\)
(i) P (student failed in Subject I, given that he has failed in Subject II) = P(A/B)
\(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}=\frac{\left(\frac{10}{100}\right)}{\left(\frac{20}{100}\right)}=\frac{10}{20}=\frac{1}{2}\)
(ii) P(student failed in at least one subject) = P(A ∪ B)
= P(A) + P(B) – P(A ∩ B)
= \(\frac{30}{100}+\frac{20}{100}-\frac{10}{100}\)
= 0.40
(iii) P(student failed in exactly one subject) = P(A) + P(B) – 2P(A ∩ B)
= \(\frac{30}{100}+\frac{20}{100}-2\left(\frac{10}{100}\right)\)
= 0.30
Question 8.
One-shot is fired from each of the three guns. Let A, B, and C denote the events that the target is hit by the first, second and third gun respectively. Assuming that A, B, and C are independent events and that P(A) = 0.5, P(B) = 0.6, and P(C) = 0.8, then find the probability that at least one hit is registered.
Solution:
A be the event that first gun hits the target
B be the event that second gun hits the target
C be the event that third gun hits the target
P(A) = 0.5, P(B) = 0.6, P(C) = 0.8
∴ P(A’) = 1 – P(A) = 1 – 0.5 = 0.5
∴ P(B’) = 1 – P(B) = 1 – 0.6 = 0.4
∴ P(C’) = 1 – P(C) = 1 – 0.8 = 0.2
Now A, B, C are independent events
∴ A’, B’, C are also independent events.
∴ P (at least one hit is registered)
= 1 – P(no hit is registered)
= 1 – P(A’ ∩ B’ ∩ C’)
= 1 – P(A’) P(B’) P(C’)
= 1 – (0.5) (0.4) (0.2)
= 1 – 0.04
= 0.96
![]()
Question 9.
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that
(i) first is white and second is black?
(ii) one is white and the other is black?
Solution:
Total number of balls = 10 + 15 = 25
Let S be an event that two balls are drawn at random without replacement in succession
∴ n(S) = 25C1 × 24C1 = 25 × 24
(i) Let A be the event that the first ball is white and the second is black.
First white ball can be drawn from 10 white balls in 10C1 ways
and second black ball can be drawn from 15 black balls in 15C1 ways.
∴ n(A) = 10C1 × 15C1
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{10} \mathrm{C}_{1} \times{ }^{15} \mathrm{C}_{1}}{25 \times 24}=\frac{10 \times 15}{25 \times 24}=\frac{1}{4}\)
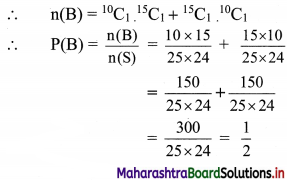
Question 10.
An urn contains 4 black, 5 white, and 6 red balls. Two balls are drawn one after the other without replacement, what is the probability that at least one ball is black?
Solution:
Total number of balls in the urn = 4 + 5 + 6 = 15
Two balls can be drawn without replacement in 15C2 = \(\frac{15 \times 14}{1 \times 2}\) = 105 ways
∴ n(S) = 105
Let A be the event that at least one ball is black
i.e., 1 black and 1 non-black or 2 black and 0 non-black.
1 black ball can be drawn out of 4 black balls in 4C1 = 4 ways
and 1 non-black ball can be drawn out of remaining 11 non-black balls in 11C1 = 11 ways
∴ 1 black and 1 non black ball can be drawn in 4 × 11 = 44 ways
Also, 2 black balls can be drawn from 4 black balls in 4C2 = \(\frac{4 \times 3}{1 \times 2}\) = 6 ways
∴ n(A) = 44 + 6 = 50
∴ Required probability = P(A) = \(\frac{n(A)}{n(S)}=\frac{50}{105}\) = \(\frac{10}{21}\)
Alternate Solution:
Total number of balls = 15
Required probability = 1 – P(neither of two balls is black)
Balls are drawn without replacement
Probability of first non-black ball drawn = \(\frac{11}{15}\)
Probability of second non-black ball drawn = \(\frac{10}{14}\)
Probability of neither of two balls is black = \(\frac{11}{15} \times \frac{10}{14}=\frac{11}{21}\)
Required probability = 1 – \(\frac{11}{21}\) = \(\frac{10}{21}\)
![]()
Question 11.
Two balls are drawn from an urn containing 5 green, 3 blue, 7 yellow balls one by one without replacement. What is the probability that at least one ball is blue?
Solution:
Total number of balls in the urn = 5 + 3 + 7 = 15
Out of these 12 are non-blue balls.
Two balls can be drawn from 15 balls without replacement in 15C2
= \(\frac{15 \times 14}{1 \times 2}\)
= 105 ways.
∴ n(S) = 105
Let A be the event that at least one ball is blue,
i.e., 1 blue and other non-blue or both are blue.
∴ n(A) = 3C1 × 12C1 + 3C2
= 3 × 12 + 3
= 36 + 3
= 39
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{39}{105}=\frac{13}{35}\)
Alternate solution:
Total number of balls in the urn = 15
Required probability = 1 – P(neither of two balls is blue)
Balls are drawn one by one without replacement.
Probability of first non-blue ball drawn = \(\frac{12}{15}\)
Probability of second non-blue ball drawn = \(\frac{11}{14}\)
Probability of neither of two ball is blue = \(\frac{12}{15} \times \frac{11}{14}=\frac{22}{35}\)
∴ Required probability = 1 – \(\frac{22}{35}\) = \(\frac{13}{35}\)
Question 12.
A bag contains 4 blue and 5 green balls. Another bag contains 3 blue and 7 green balls. If one ball ¡s drawn from each bag, what is the Probability that two balls are of the same colour?
Solution:
Let A be the event that a blue ball is drawn from each bag.
Probability of drawing one blue ball out of 4 blue balls where there are a total of 9 balls in the first bag and that of drawing one blue ball out of 3 blue balls where there are a total of 10 balls in the second bag is
P(A) = \(\frac{4}{9} \times \frac{3}{10}\)
Let B be the event that a green ball is drawn from each bag.
Probability of drawing one green ball out of 5 green balls where there are a total of 9 balls in the first bag and that of drawing one green ball out of 7 green balls where there are a total of 10 balls in the second bag is
P(B) = \(\frac{5}{9} \times \frac{7}{10}\)
Since both, the events are mutually exclusive and exhaustive events
∴ P(that both the balls are of the same colour) = P(both are of blue colour) or P(both are of green colour)
= P(A) + P(B)
= \(\frac{4}{9} \times \frac{3}{10}+\frac{5}{9} \times \frac{7}{10}\)
= \(\frac{12}{90}+\frac{35}{90}\)
= \(\frac{47}{90}\)
![]()
Question 13.
Two cards are drawn one after the other from a pack of 52 cards with replacement. What is the probability that both the cards are drawn are face cards?
Solution:
Two cards are drawn from a pack of 52 cards with replacement.
∴ n(S) = 52 × 52
Let A be the event that two cards drawn are face cards.
First card from 12 face cards is drawn with replacement in 12C1 = 12 ways
and second face card is drawn from 12 face card in 12C1 = 12 ways after replacement.
∴ n(A) = 12 × 12
∴ P(that both the cards drawn are face cards) = P(A)
= \(\frac{n(A)}{n(S)}=\frac{12 \times 12}{52 \times 52}=\frac{9}{169}\)