Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Probability Miscellaneous Exercise 7 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Probability Miscellaneous Exercise 7
Question 1.
From a group of 2 men (M1, M2) and three women (W1, W2, W3), two persons are selected. Describe the sample space of the experiment. If E is the event in which one man and one woman are selected, then which are the cases favourable to E?
Solution:
Let S be the sample space of the given event.
∴ S = {(M1, M2), (M1, W1), (M1, W2), (M1, W3), (M2, W1), (M2, W2), (M2, W3), (W1, W2) (W1, W3), (W2, W3)}
Let E be the event that one man and one woman are selected.
∴ E = {(M1, W1), (M1, W2), (M1, W3), (M2, W1), (M2, W2), (M2, W3)}
Here, the order is not important in which 2 persons are selected e.g. (M1, M2) is the same as (M2, M1)
![]()
Question 2.
Three groups of children contain respectively 3 girls and 1 boy, 2 girls and 2 boys and 1 girl and 3 boys. One child is selected at random from each group. What is the chance that the three selected consist of 1 girl and 2 boys?
Solution:
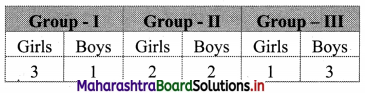
Let G1, G2, G3 denote events for selecting a girl,
and B1, B2, B3 denote events for selecting a boy from 1st, 2nd and 3rd groups respectively.
Then P(G1) = \(\frac{3}{4}\), P(G2) = \(\frac{2}{4}\), P(G3) = \(\frac{1}{4}\)
P(B1) = \(\frac{1}{4}\), P(B2) = \(\frac{2}{4}\), P(B3) = \(\frac{3}{4}\)
Where G1, G2, G3, B1, B2 and B3 are mutually exclusive events.
Let E be the event that 1 girl and 2 boys are selected
∴ E = (G1 ∩ B2 ∩ B3) ∪ (B1 ∩ G2 ∩ B3) ∪ (B1 ∩ B2 ∩ G3)
∴ P(E) = P(G1 ∩ B2 ∩ B3) + P(B1 ∩ G2 ∩ B3) + P(B1 ∩ B2 ∩ G3)
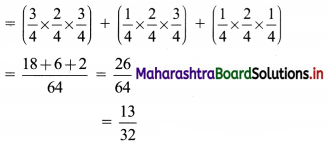
Question 3.
A room has 3 sockets for lamps. From a collection of 10 light bulbs, 6 are defective. A person selects 3 at random and puts them in every socket. What is the probability that the room, will be lit?
Solution:
Total number of bulbs = 10
Number of defective bulbs = 6
∴ Number of non-defective bulbs = 4
3 bulbs can be selected out of 10 light bulbs in 10C3 ways.
∴ n(S) = 10C3
Let A be the event that room is lit.
∴ A’ is the event that the room is not lit.
For A’ the bulbs should be selected from the 6 defective bulbs.
This can be done in 6C3 ways.
∴ n(A’) = 6C3
∴ P(A’) = \(\frac{\mathrm{n}\left(\mathrm{A}^{\prime}\right)}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{6} \mathrm{C}_{3}}{{ }^{10} \mathrm{C}_{3}}\)
∴ P(Room is lit) = 1 – P(Room is not lit)

Question 4.
There are 2 red and 3 black balls in a bag. 3 balls are taken out at random from the bag. Find the probability of getting 2 red and 1 black ball or 1 red and 2 black balls.
Solution:
There are 2 + 3 = 5 balls in the bag and 3 balls can be drawn out of these in
5C3 = \(\frac{5 \times 4 \times 3}{1 \times 2 \times 3}\) = 10 ways.
∴ n(S) = 10
Let A be the event that 2 balls are red and 1 ball is black
2 red balls can be drawn out of 2 red balls in 2C2 = 1 way
and 1 black ball can be drawn out of 3 black balls in 3C1 = 3 ways.
∴ n(A) = 2C2 × 3C1 = 1 × 3 = 3
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{3}{10}\)
Let B be the event that 1 ball is red and 2 balls are black
1 red ball out of 2 red balls can be drawn in 2C1 = 2 ways
and 2 black balls out of 3 black balls can be drawn in 3C2 = \(\frac{3 \times 2}{1 \times 2}\) = 3 ways.
∴ n(B) = 2C1 × 3C2 = 2 × 3 = 6
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{6}{10}\)
Since A and B are mutually exclusive and exhaustive events
∴ P(A ∩ B) = 0
∴ Required probability = P(A ∪ B) = P(A) + P(B)
= \(\frac{3}{10}+\frac{6}{10}\)
= \(\frac{9}{10}\)
![]()
Question 5.
A box contains 25 tickets numbered 1 to 25. Two tickets are drawn at random. What is the probability that the product of the numbers is even?
Solution:
Two tickets can be drawn out of 25 tickets in 25C2 = \(\frac{25 \times 24}{1 \times 2}\) = 300 ways.
∴ n(S) = 300
Let A be the event that product of two numbers is even.
This is possible if both numbers are even, or one number is even and other is odd.
As there are 13 odd numbers and 12 even numbers from 1 to 25.
∴ n(A) = 12C2 + 12C1 × 13C1
= \(\frac{12 \times 11}{1 \times 2}\) + 12 × 13
= 66 + 156
= 222
∴ Required probability = P(A)
= \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}\)
= \(\frac{222}{300}\)
= \(\frac{37}{50}\)
Question 6.
A, B and C are mutually exclusive and exhaustive events associated with the random experiment. Find P(A), given that
P(B) = \(\frac{3}{2}\) P(A) and P(C) = \(\frac{1}{2}\) P(B)
Solution:
P(B) = \(\frac{3}{2}\) P(A) and P(C) = \(\frac{1}{2}\) P(B)
Since A, B, C are mutually exclusive and exhaustive events,

Question 7.
An urn contains four tickets marked with numbers 112, 121, 122, 222, and one ticket is drawn at random. Let Ai (i = 1, 2, 3) be the event that ith digit of the number of the ticket drawn is 1. Discuss the independence of the events A1, A2, and A3.
Solution:
One ticket can be drawn out of 4 tickets in 4C1 = 4 ways.
∴ n(S) = 4
According to the given information,
Let A1 be the event that 1st digit of the number of tickets is 1
A2 be the event that the 2nd digit of the number of tickets is 1
A3 be the event that the 3rd digit of the number of tickets is 1
∴ A1 = {112, 121, 122}, A2 = {112}, A3 = {121}

∴ A1, A2, A3 are not pairwise independent
For mutual independence of events A1, A2, A3
We require to have
P(A1 ∩ A2 ∩ A3) = P(A1) P(A2) P(A3)
and P(A1) P(A2) = P(A1 ∩ A2),
P(A2) P(A3) = P(A2 ∩ A3),
P(A1) P(A3) = P(A1 ∩ A3)
∴ From (iii),
A1, A2, A3 are not mutually independent.
Question 8.
The odds against a certain event are 5 : 2 and the odds in favour of another independent event are 6 : 5. Find the chance that at least one of the events will happen.
Solution:
Let A and B be two independent events.
Odds against A are 5 : 2
∴ the probability of occurrence of event A is given by
P(A) = \(\frac{2}{5+2}=\frac{2}{7}\)
Odds in favour of B are 6 : 5
∴ the probability of occurrence of event B is given by
P(B) = \(\frac{6}{6+5}=\frac{6}{11}\)
∴ P(at least one event will happen) = P(A ∪ B)
= P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) P(B) ……[∵ A and B are independent events]
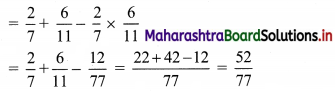
Question 9.
The odds against a husband who is 55 years old living till he is 75 is 8 : 5 and it is 4 : 3 against his wife who is now 48, living till she is 68. Find the probability that
(i) the couple will be alive 20 years hence
(ii) at least one of them will be alive 20 years hence.
Solution:
Let A be the event that husband would be alive after 20 years.
Odds against A are 8 : 5
∴ the probability of occurrence of event A is given by
P(A) = \(\frac{5}{8+5}=\frac{5}{13}\)
∴ P(A’) = 1 – P(A)
= 1 – \(\frac{5}{13}\)
= \(\frac{8}{13}\)
Let B be the event that wife would be alive after 20 years.
Odds against B are 4 : 3
∴ the probability of occurrence of event B is given by
P(B) = \(\frac{3}{4+3}=\frac{3}{7}\)
∴ P(B’) = 1 – P(B)
= 1 – \(\frac{3}{7}\)
= \(\frac{4}{7}\)
Since A and B are independent events
∴ A’ and B’ are also independent events
(i) Let X be the event that both will be alive after 20 years.
∴ P(X) = (A ∩ B)
∴ P(X) = P(A) . P(B)
= \(\frac{5}{13} \times \frac{3}{7}\)
= \(\frac{15}{91}\)
(ii) Let Y be the event that at least one will be alive after 20 years.
∴ P(Y) = P(at least one would be alive)
= 1 – P(both would not be alive)
= 1 – P(A’ ∩ B’)
= 1 – P(A’). P(B’)
= 1 – \(\frac{8}{13} \times \frac{4}{7}\)
= 1 – \(\frac{32}{91}\)
= \(\frac{59}{91}\)
![]()
Question 10.
Two throws are made, the first with 3 dice and the second with 2 dice. The faces of each die are marked with the number 1 to 6. What is the probability that the total in the first throw is not less than 15 and at the same time the total in the second throw is not less than 8?
Solution:
When 3 dice are thrown, then the sample space S1 has 6 × 6 × 6 = 216 sample points.
∴ n(S1) = 216
Let A be the event that the sum of the numbers is not less than 15.
∴ A = {(3, 6, 6), (4, 5, 6), (4, 6, 5), (4, 6, 6), (5, 4, 6), (5, 5, 5), (5, 5, 6), (5, 6, 4), (5, 6, 5), (5, 6, 6), (6, 3, 6), (6, 4, 5), (6, 4, 6), (6, 5, 4), (6, 5, 5), (6, 5, 6), (6, 6, 3), (6, 6, 4), (6, 6, 5), (6, 6, 6)}
∴ n(A) = 20
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}\left(\mathrm{S}_{1}\right)}=\frac{20}{216}=\frac{5}{54}\)
When 2 dice are thrown, the sample space S2 has 6 × 6 = 36 sample points.
∴ n(S2) = 36
Let B be the event that sum of numbers is not less than 8.
∴ B = {(2, 6), (3, 5), (3,6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(B) = 15
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}\left(\mathrm{S}_{2}\right)}=\frac{15}{36}=\frac{5}{12}\)
A ∩ B = Event that the total in the first throw is not less than 15 and at the same time the total in the second throw is not less than 8.
∴ A and B are independent events
∴ P(A ∩ B) = P(A) . P(B)
= \(\frac{5}{54} \times \frac{5}{12}\)
= \(\frac{25}{648}\)
Question 11.
Two-thirds of the students in a class are boys and the rest are girls. It is known that the probability of a girl getting first class is 0.25 and that of a boy getting is 0.28. Find the probability that a student chosen at random will get first class.
Solution:
Let A be the event that student chosen is a boy
B be the event that student chosen is a girl
C be the event that student gets first class
∴ P(A) = \(\frac{2}{3}\), P(B) = \(\frac{1}{3}\)
Probability of student getting first class, given that student is boy
Probability of student getting first class given that student is a girl, is
P(C/A) = 0.28 = \(\frac{28}{100}\)
and P(C/B) = 0.25 = \(\frac{25}{100}\)
∴ Required probability = P((A ∩ C) ∪ (B ∩ C))
Since A ∩ C and B ∩ C are mutually exclusive events
∴ Required probability = P(A ∩ C) + P(B ∩ C)
= P(A) . P(C/A) + P(B) . P(C/B)
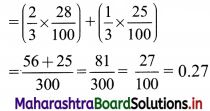
Question 12.
A number of two digits is formed using the digits 1, 2, 3,……, 9. What is the probability that the number so chosen is even and less than 60?
Solution:
The number of two digits can be formed from the given 9 digits in 9 × 9 = 81 different ways.
∴ n(S) = 81
Let A be the event that the number is even and less than 60.
Since the number is even, the unit place of two digits can be filled in 4P1 = 4 different ways by any one of the digits 2, 4, 6, 8.
Also the number is less than 60, so tenth place can be filled in 5P1 = 5 different ways by any one of the digits 1, 2, 3, 4, 5.
∴ n(A) = 4 × 5 = 20
∴ Required probability = P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{20}{81}\)
![]()
Question 13.
A bag contains 8 red balls and 5 white balls. Two successive draws of 3 balls each are made without replacement. Find the probability that the first drawing will give 3 white balls and the second drawing will give 3 red balls.
Solution:
Total number of balls = 8 + 5 = 13.
3 balls can be drawn out of 13 balls in 13C3 ways.
∴ n(S) = 13C3
Let A be the event that all 3 balls drawn are white.
3 white balls can be drawn out of 5 white balls in 5C3 ways.
∴ n(A) = 5C3
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{{ }^{5} C_{3}}{{ }^{13} C_{3}}=\frac{5 \times 4 \times 3}{13 \times 12 \times 11}=\frac{5}{143}\)
After drawing 3 white balls which are not replaced in the bag, there are 10 balls left in the bag out of which 8 are red balls.
Let B be the event that the second draw of 3 balls are red.
∴ Probability of drawing 3 red balls, given that 3 white balls have been already drawn, is given by
P(B/A) = \(\frac{{ }^{8} \mathrm{C}_{3}}{{ }^{10} \mathrm{C}_{3}}=\frac{8 \times 7 \times 6}{10 \times 9 \times 8}=\frac{7}{15}\)
∴ Required probability = P(A ∩ B)
= P(A) . P(B/A)
= \(\frac{5}{143} \times \frac{7}{15}\)
= \(\frac{7}{429}\)
Question 14.
The odds against student X solving a business statistics problem are 8 : 6 and the odds in favour of student Y solving the same problem are 14 : 16
(i) What is the chance that the problem will be solved, if they try independently?
(ii) What is the probability that neither solves the problem?
Solution:
(i) Let A be the event that X solves the problem B be the event that Y solves the problem.
Since the odds against student X solving the problem are 8 : 6
∴ Probability of occurrence of event A is given by
P(A) = \(\frac{6}{8+6}=\frac{6}{14}\)
and P(A’) = 1 – P(A)
= 1 – \(\frac{6}{14}\)
= \(\frac{8}{14}\)
Also, the odds in favour of student Y solving the problem are 14 : 16
∴ Probability of occurrence of event B is given by
P(B) = \(\frac{14}{14+16}=\frac{14}{30}\) and
P(B’) = 1 – P(B)
= 1 – \(\frac{14}{30}\)
= \(\frac{16}{30}\)
Now A and B are independent events.
∴ A’ and B’ are independent events.
∴ A’ ∩ B’ = Event that neither solves the problem
= P(A’ ∩ B’)
= P(A’) . P(B’)
= \(\frac{8}{14} \times \frac{16}{30}\)
= \(\frac{32}{105}\)
A ∪ B = the event that the problem is solved
∴ P(problem will be solved) = P(A ∪ B)
= 1 – P(A ∪ B)’
= 1 – P(A’ ∩ B’)
= 1 – \(\frac{32}{105}\)
= 1 – \(\frac{73}{105}\)
![]()
(ii) P (neither solves the problem) = P(A’ ∩ B’)
= P(A’) P(B’)
= \(\frac{8}{14} \times \frac{16}{30}\)
= \(\frac{32}{105}\)