Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Correlation Ex 5.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 5 Correlation Ex 5.1
Question 1.
Draw a scatter diagram for the data given below and interpret it.

Solution:
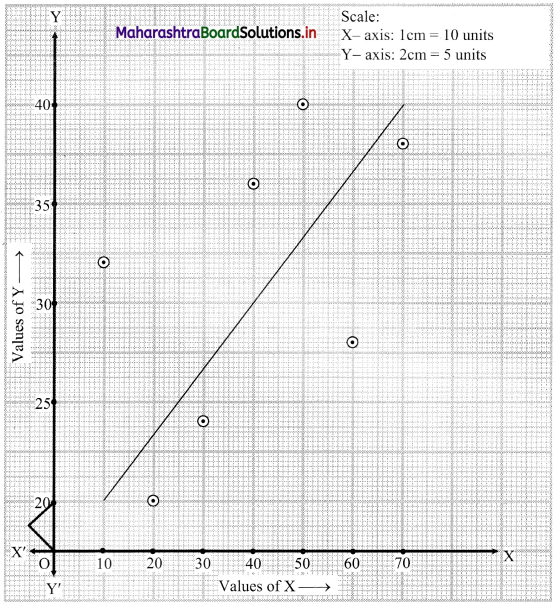
Since all the points lie in a band rising from left to right.
Therefore, there is a positive correlation between the values of X and Y respectively.
Question 2.
For the following data of marks of 7 students in Physics (x) and Mathematics (y), draw scatter diagram and state the type of correlation.

Solution:
We take marks in Physics on X-axis and marks in Mathematics on Y-axis and plot the points as below.
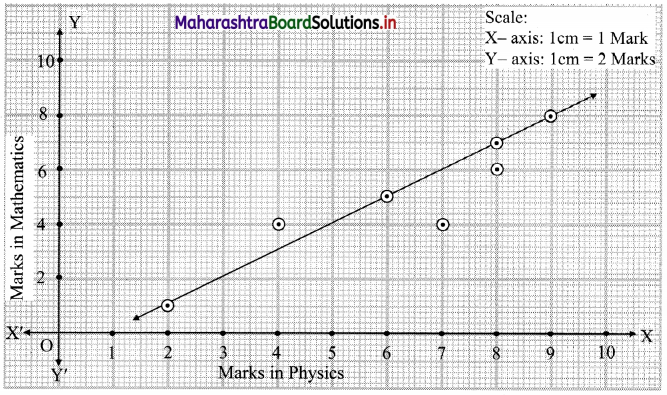
We get a band of points rising from left to right. This indicates the positive correlation between marks in Physics and marks in Mathematics.
Question 3.
Draw a scatter diagram for the data given below. Is there any correlation between Aptitude score and Grade points?
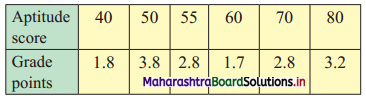
Solution:
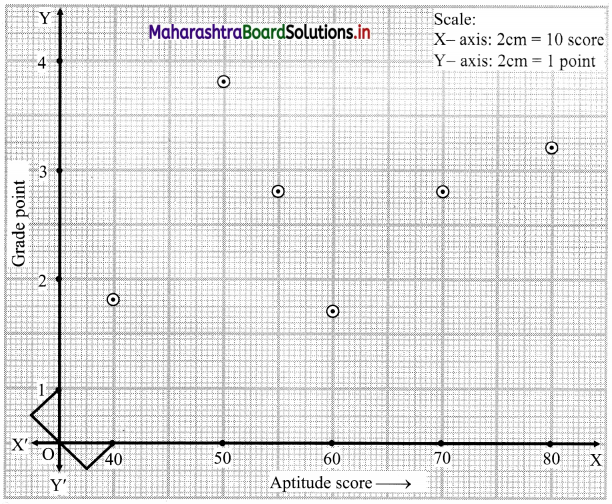
The points are completely scattered i.e., no trend is observed.
∴ there is no correlation between Aptitude score (X) and Grade point (Y).
Question 4.
Find correlation coefficient between x andy series for the following data:
n = 15, \(\bar{x}\) = 25, \(\bar{y}\) = 18, σx = 3.01, σy = 3.03, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 122
Solution:
Here, n = 15, \(\bar{x}\) = 25, \(\bar{y}\) = 18, σx = 3.01, σy = 3.03, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 122
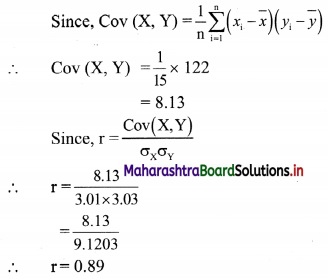
Question 5.
The correlation coefficient between two variables x and y are 0.48. The covariance is 36 and the variance of x is 16. Find the standard deviation of y.
Solution:
Given, r = 0.48, Cov(X, Y) = 36
Since \(\sigma_{X}^{2}\) = 16
∴ σx = 4

∴ the standard deviation of y is 18.75.
Question 6.
In the following data, one of the values of y is missing. Arithmetic means of x and y series are 6 and 8 respectively. (√2 = 1.4142)

(i) Estimate missing observation.
(ii) Calculate correlation coefficient.
Solution:
(i) Let X = xi, Y = yi and missing observation be ‘a’.
Given, \(\bar{x}\) = 6, \(\bar{y}\) = 8, n = 5
∴ 8 = \(\frac{35+a}{5}\)
∴ 40 = 35 + a
∴ a = 5
(ii) We construct the following table:


Question 7.
Find correlation coefficient from the following data. [Given: √3 = 1.732]
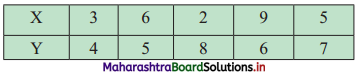
Solution:
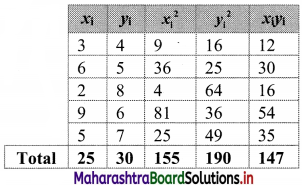
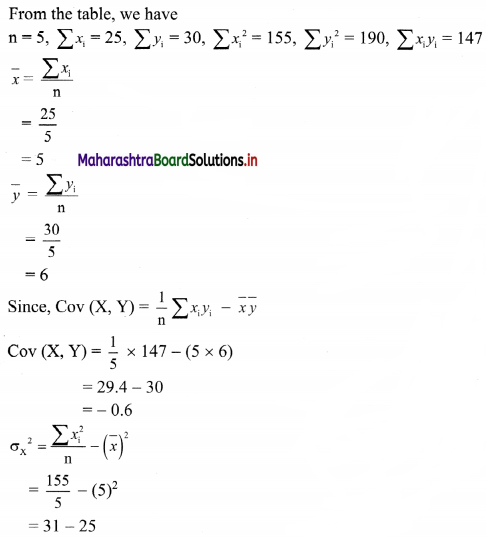

Question 8.
The correlation coefficient between x and y is 0.3 and their covariance is 12. The variance of x is 9, find the standard deviation of y.
Solution:
Given, r = 0.3, Cov(X, Y) = 12,
\(\sigma_{X}^{2}\) = 9
∴ \(\sigma_{\mathrm{X}}\) = 3
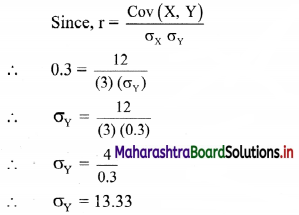
∴ the standard deviation of y is 13.33.