Maharashtra Board 11th Commerce Maths Solutions Chapter 5 Correlation Miscellaneous Exercise 5

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Correlation Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 5 Correlation Miscellaneous Exercise 5

Question 1.
Two series of x and y with 50 items each have standard deviations of 4.8 and 3.5 respectively. If the sum of products of deviations of x and y series from respective arithmetic means is 420, then find the correlation coefficient between x and y.
Solution:

Question 2.
Find the number of pairs of observations from the following data,
r = 0.15, σ_y = 4, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 12, \(\Sigma\left(x_{i}-\bar{x}\right)^{2}\) = 40.
Solution:
Given, r = 0.15, σ_y = 4, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 12, \(\Sigma\left(x_{i}-\bar{x}\right)^{2}\) = 40

Question 3.
Given that r = 0.4, σ_y = 3, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 108, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)^{2}\) = 900. Find the number of pairs of observations.
Solution:
Given, r = 0.4, σ_y = 3, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)\left(y_{\mathrm{i}}-\bar{y}\right)\) = 108, \(\sum\left(x_{\mathrm{i}}-\bar{x}\right)^{2}\) = 900

Question 4.
Given the following information, Σ\(x_{\mathrm{i}}^{2}\) = 90, Σx_iy_i = 60, r = 0.8, σ_y = 2.5, where x_i and y_i are the deviations from their respective means, find the number of items.
Solution:
Here, Σ\(x_{\mathrm{i}}^{2}\) = 90, Σx_iy_i = 60, r = 0.8, σ_y = 2.5
Here, x_i and y_i are the deviations from their respective means.
∴ If X_i, Y_i are elements of x and y series respectively, then
X_i – \(\bar{x}\) = x_i and Y_i – \(\bar{y}\) = y_i
∴ Σx_iy_i = \(\Sigma\left(\mathrm{X}_{\mathrm{i}}-\bar{x}\right)\left(\mathrm{Y}_{\mathrm{i}}-\bar{y}\right)\) = 60, \(\sum x_{\mathrm{i}}^{2}=\sum\left(\mathrm{X}_{\mathrm{i}}-\bar{x}\right)^{2}\) = 90

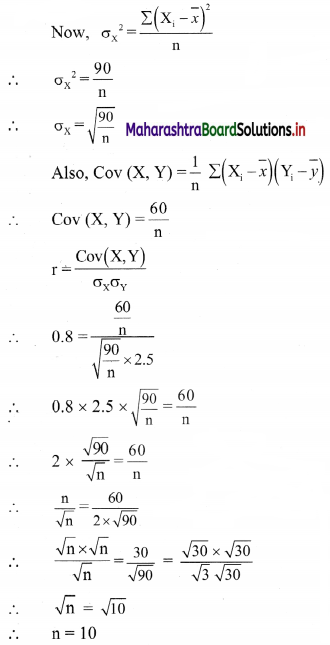
Question 5.
A sample of 5 items is taken from the production of a firm. The length and weight of 5 items are given below. [Given: √0.8823 = 0.9393]

Calculate the correlation coefficient between length and weight and interpret the result.
Solution:
Let length = x_i (in cm), Weight = y_i (in gm)


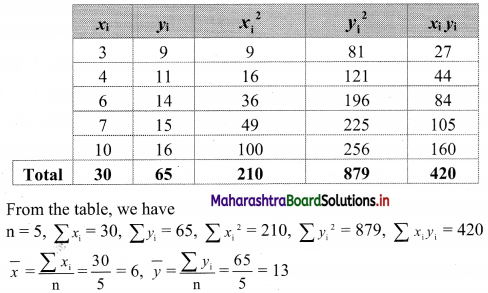
∴ the value of r indicates a high degree of positive correlation between length and weight of items.

Question 6.
Calculate the correlation coefficient from the following data and interpret it.

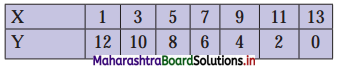
Solution:


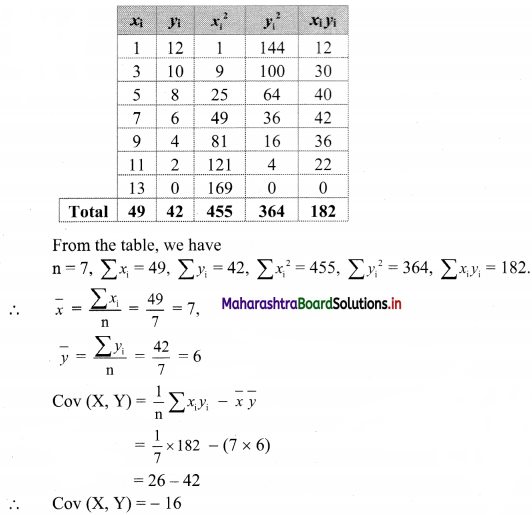
∴ the value of r indicates a perfect negative correlation between x and y.

Question 7.
Calculate the correlation coefficient from the following data and interpret it.

Solution:



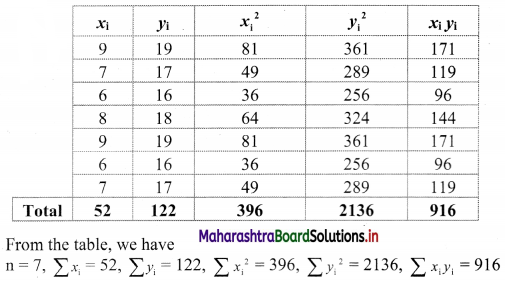
∴ the value of r indicates a perfect positive correlation between x and y.

Question 8.
If the correlation coefficient between X and Y is 0.8, what is the correlation coefficient between
(i) 2X and Y
(ii) \(\frac{X}{2}\) and Y
(iii) X and 3Y
(iv) X – 5 and Y – 3
(v) X + 7 and Y + 9
(vi) \(\frac{X-5}{7}\) and \(\frac{Y-3}{8}\)?
Solution:
The correlation coefficient remains unaffected by the change of origin and scale.
i.e., if u_i = \(\frac{x_{i}-\mathrm{a}}{\mathrm{h}}\) and v_i = \(\frac{y_{i}-\mathrm{b}}{\mathrm{k}}\), then Corr(U, V) = ±Corr(X, Y).
according to the same or opposite signs of h and k.
(i) u_i = \(\frac{2\left(x_{i}-0\right)}{1}\), v_i = \(\frac{y_{i}-0}{1}\)
Here, h = 1 and k = 1 are of the same signs.
∴ Corr (U, V) = Corr (X, Y) = 0.8

(ii) u_i = \(\frac{x_{i}-0}{2}\), v_i = \(\frac{y_{\mathrm{i}}-0}{1}\)
Here, h = 2 and k = 1 are of the same signs.
∴ Corr (U, V) = Corr (X, Y) = 0.8

(iii) Corr (X, 3Y) = Corr (X, Y) = 0.8

(iv) Corr (X – 5, Y – 3) = Corr(X, Y) = 0.8

(v) Corr (X + 7, Y + 9) = Corr(X, Y) = 0.8

(vi) Corr(\(\frac{X-5}{7}, \frac{Y-3}{8}\)) = Corr(X, Y) = 0.8

Question 9.
In the calculation of the correlation coefficient between the height and weight of a group of students of a college, one investigator took the measurements in inches and pounds while the other investigator took the measurements in cm. and kg. Will they get the same value of the correlation coefficient or different values? Justify your answer.
Solution:
The coefficient of correlation is a ratio of covariance and standard deviations.
Since covariance and standard deviations are independent of units of measurement.
∴ coefficient of correlation is also independent of units of measurement.
∴ values of coefficient of correlation obtained by first and second investigators are the same.