Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Miscellaneous Exercise 4 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Miscellaneous Exercise 4
Question 1.
Following data gives the coded price (X) and demand (Y) of a commodity.
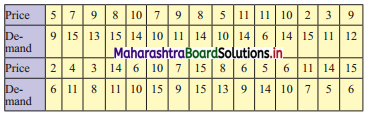
Classify the data by taking classes 0 – 4, 5 – 9, etc. for X and 5 – 8, 9 – 12, etc. for Y.
Also find
(i) marginal frequency distribution of X and Y.
(ii) conditional frequency distribution of Y when X is less than 10.
Solution:
Given, X = coded price
Y = demand
Bivariate frequency table can be prepared by taking class intervals 0 – 4, 5 – 9,… etc for X and 5 – 8, 9 – 12,… etc for Y.
Bivariate frequency distribution is as follows.
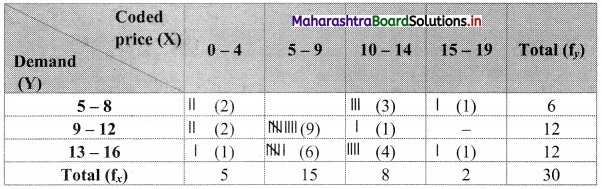
(i) Marginal frequency distribution of X:

Marginal frequency distribution of Y:

(ii) Conditional frequency distribution of Y when X < 10:

![]()
Question 2.
Following data gives the age in years and marks obtained by 30 students in an intelligence test.
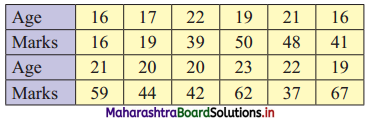
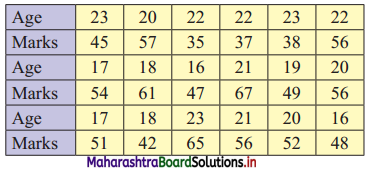
Prepare a bivariate frequency distribution by taking class intervals 16 – 18, 18 – 20,…,etc. for age and 10 – 20, 20 – 30,…, etc. for marks.
Find
(i) marginal frequency distributions.
(ii) conditional frequency distribution of marks obtained when age of students is between 20 – 22.
Solution:
Let X = Age in years
Y = Marks
Bivariate frequency table can be prepared by taking class intervals 16 – 18, 18 – 20,…, etc for X and 10 – 20, 20 – 30,…, etc for Y.
Bivariate frequency distribution is as follows:
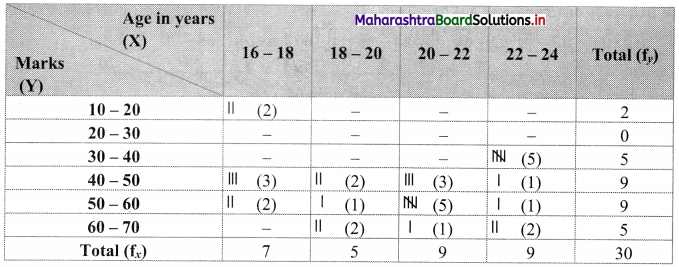
(i) Marginal frequency distribution of X:

Marginal frequency distribution of Y:

(ii) Conditional frequency distribution of Y when X is between 20 – 22:

Question 3.
Following data gives Sales (in Lakh ?) and Advertisement Expenditure (in Thousand ₹) of 20 firms.
(115, 61) (120, 60) (128, 61) (121, 63) (137, 62) (139, 62) (143, 63) (117, 65) (126, 64) (141, 65) (140, 65) (153, 64) (129, 67) (130, 66) (150, 67) (148, 66) (130, 69) (138, 68) (155, 69) (172, 68)
(i) Construct a bivariate frequency distribution table for the above data by taking classes 115 – 125, 125 – 135, ….etc. for sales and 60 – 62, 62 – 64, …etc. for advertisement expenditure.
(ii) Find marginal frequency distributions
(iii) Conditional frequency distribution of Sales when the advertisement expenditure is between 64 – 66 (Thousand ₹)
(iv) Conditional frequency distribution of advertisement expenditure when the sales are between 125 – 135 (lakh ₹)
Solution:
(i) Let X = Sales (in lakh ₹)
Y = Advertisement Expenditure (in Thousand ₹)
Bivariate frequency table can be prepared by taking class intervals 115 – 125, 125 – 135, …. etc for X and 60 – 62, 62 – 64, ….etc for Y.
Bivariate frequency distribution is as follows:
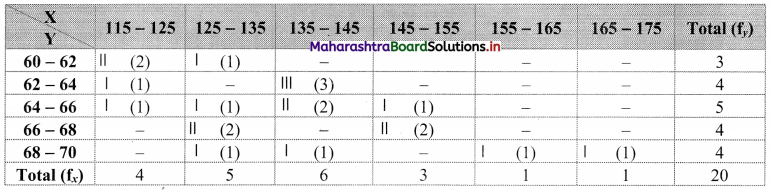
(ii) Marginal frequency distribution of X:

Marginal frequency distribution of Y:

(ii) Conditional frequency distribution of X when Y is between 64 – 66:

(iii) Conditional frequency distribution of Y when X is between 125 – 135:

![]()
Question 4.
Prepare a bivariate frequency distribution for the following data, taking class intervals for X as 35 – 45, 45 – 55, …. etc and for Y as 115 – 130, 130 – 145, … etc where, X denotes the age in years and Y denotes blood pressure for a group of 24 persons.
(55, 151) (36, 140) (72, 160) (38, 124) (65, 148) (46, 130) (58, 152) (50, 149) (38, 115) (42, 145) (41, 163) (47, 161) (69, 159) (60, 161) (58, 131) (57, 136) (43, 141) (52, 164) (59, 161) (44, 128) (35, 118) (62, 142) (67, 157) (70, 162)
Also find
(i) Marginal frequency distribution of X.
(ii) Conditional frequency distribution of Y when X < 45.
Solution:
Given X = Age in years
Y = Blood pressure
Bivariate frequency table can be prepared by taking class intervals 35 – 45, 45 – 55, …, etc for X and 115 – 130, 130 – 145, ….., etc for Y.
Bivariate frequency distribution is as follows:
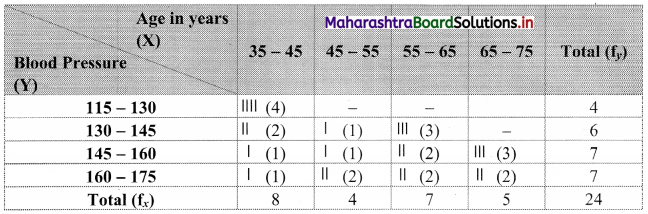
(i) Marginal frequency distribution of X:

(ii) Conditional frequency distribution of Y when X < 45:

Question 5.
Thirty pairs of values of two variables X and Y are given below. Form a bivariate frequency table. Also find marginal frequency distributions of X and Y.
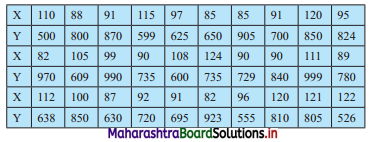
Solution:
Bivariate frequency table can be prepared by taking class intervals 80 – 90, 90 – 100, etc for X and 500 – 600, 600 – 700, …., etc for Y.
Bivariate frequency distribution is as follows:
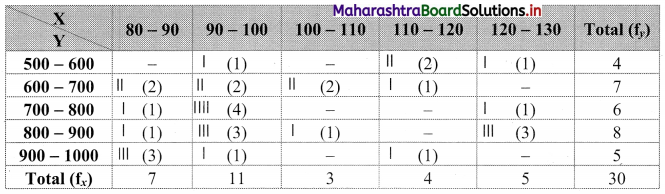
Marginal frequency distribution of X:

Marginal frequency distribution of Y

Question 6.
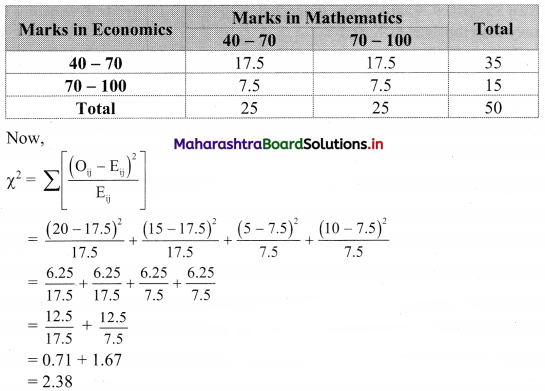
The following table shows how the samples of Mathematics and Economics scores of 25 students are distributed:
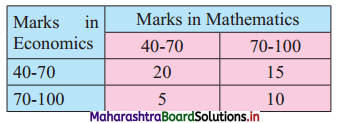
Find the value of ϰ2 statistic.
Solution:
Table of observed frequencies.
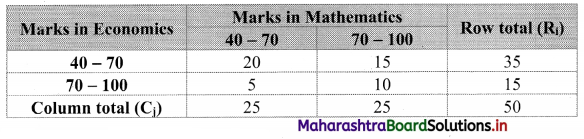
Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{35 \times 25}{50}\) = 17.5
E12 = \(\frac{35 \times 25}{50}\) = 17.5
E21 = \(\frac{15 \times 25}{50}\) = 7.5
E22 = \(\frac{15 \times 25}{50}\) = 7.5
Table of expected frequencies.
![]()
Question 7.
Compute ϰ2 statistic from the following data:
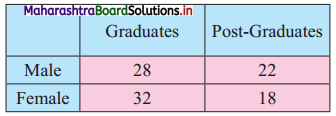
Solution:
Table of observed frequencies.
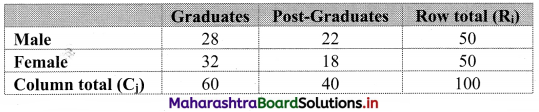
Expected frequencies are given by
Eij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E11 = \(\frac{50 \times 60}{100}\) = 30
E12 = \(\frac{50 \times 40}{100}\) = 20
E21 = \(\frac{50 \times 60}{100}\) = 30
E22 = \(\frac{50 \times 40}{100}\) = 20
Table of expected frequencies.
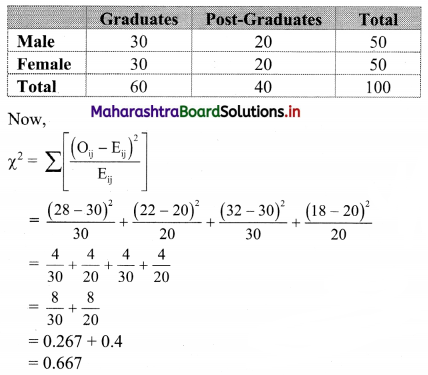
Question 8.
The attitude of 250 employees towards a proposed policy of the company is as observed in the following table. Calculate ϰ2 statistic.
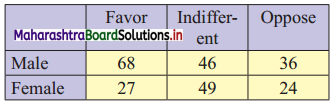
Solution:
Table of observed frequencies

Expected frequencies are given by
Eij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E11 = \(\frac{150 \times 95}{250}\) = 57
E12 = \(\frac{150 \times 95}{250}\) = 57
E13 = \(\frac{150 \times 60}{250}\) = 36
E21 = \(\frac{100 \times 95}{250}\) = 38
E22 = \(\frac{100 \times 95}{250}\) = 38
E23 = \(\frac{100 \times 60}{250}\) = 24
Table of observed frequencies.

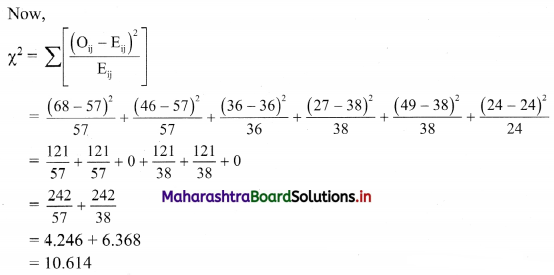
Question 9.
In a certain sample of 1000 families, 450 families are consumers of tea. Out of 600 Hindu families, 286 families consume tea. Calculate ϰ2 statistic.
Solution:
The given data can be arranged in the following table.

Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{600 \times 450}{1000}\) = 270
E12 = \(\frac{600 \times 550}{1000}\) = 330
E21 = \(\frac{400 \times 450}{1000}\) = 180
E22 = \(\frac{400 \times 550}{1000}\) = 220
Table of expected frequencies.
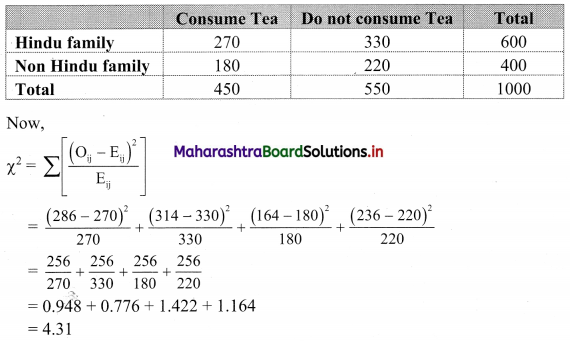
![]()
Question 10.
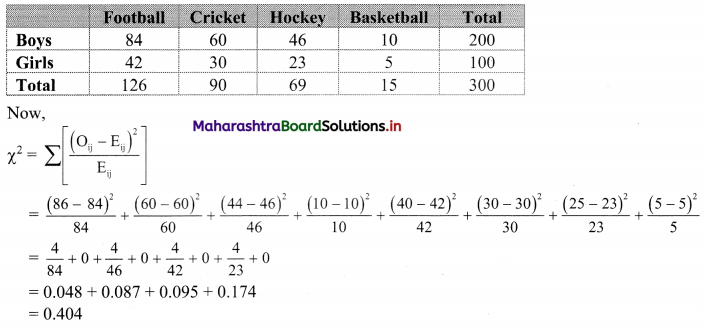
A sample of boys and girls were asked to choose their favourite sport, with the following results. Find the value of ϰ2 statistic.
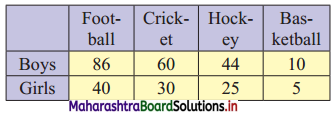
Solution:
Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{200 \times 126}{300}\) = 84
E12 = \(\frac{200 \times 90}{300}\) = 60
E13 = \(\frac{200 \times 69}{300}\) = 46
E14 = \(\frac{200 \times 15}{300}\) = 10
E21 = \(\frac{100 \times 126}{300}\) = 42
E22 = \(\frac{100 \times 90}{300}\) = 30
E23 = \(\frac{100 \times 69}{300}\) = 23
E24 = \(\frac{100 \times 15}{300}\) = 5
Table of expected frequencies.