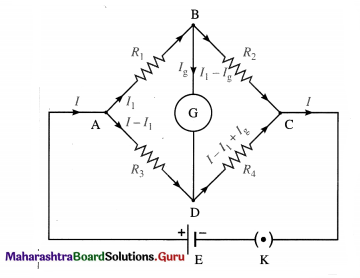
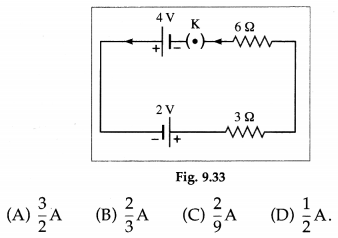
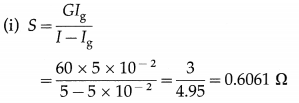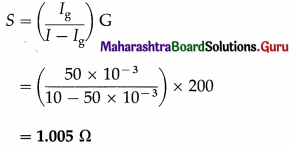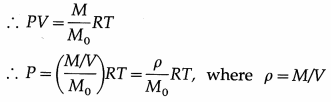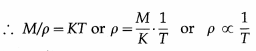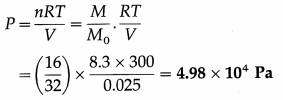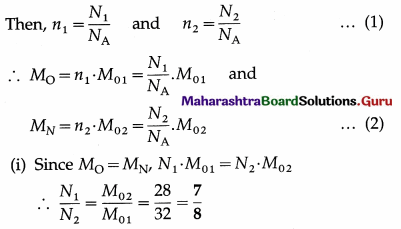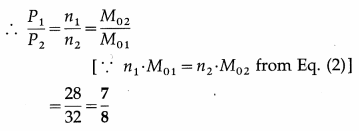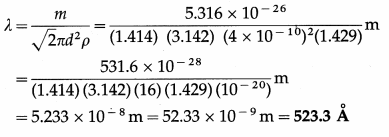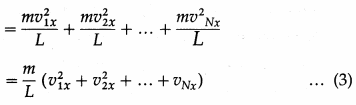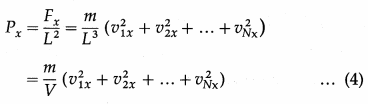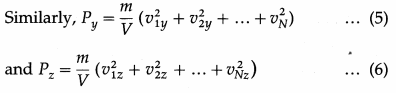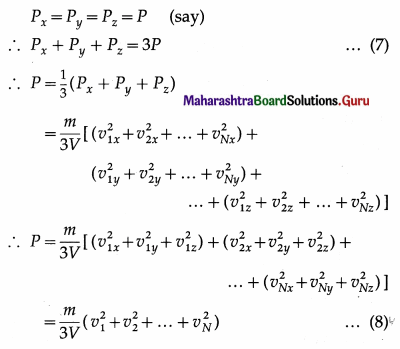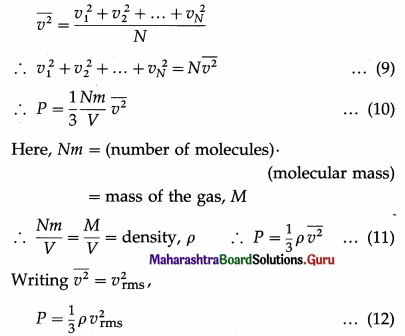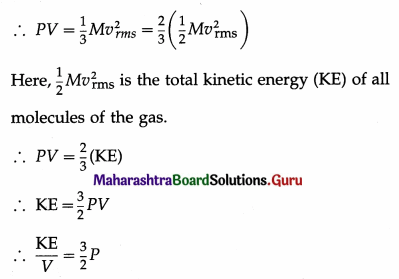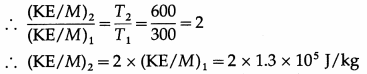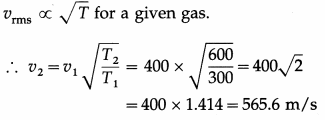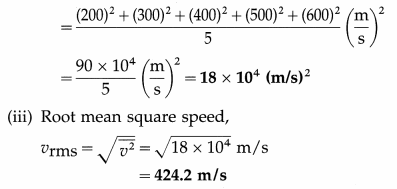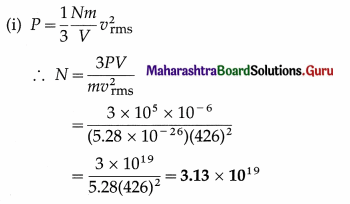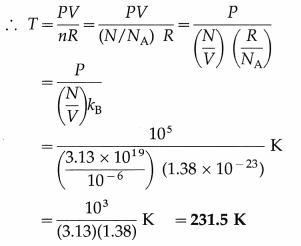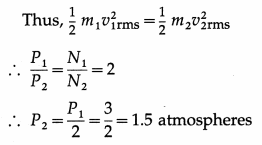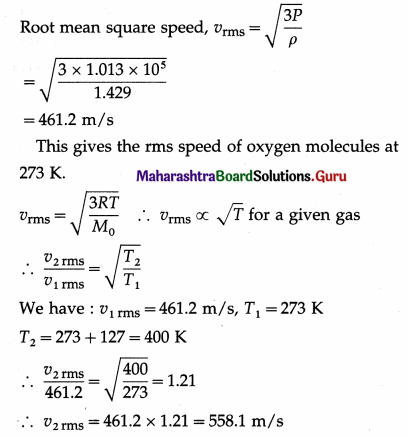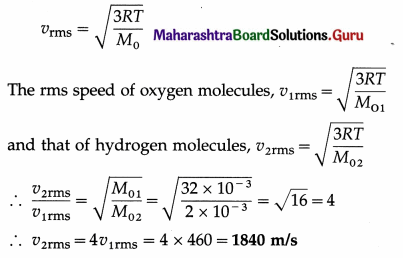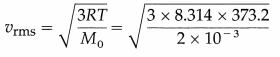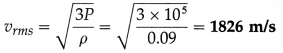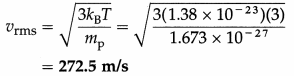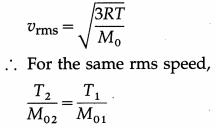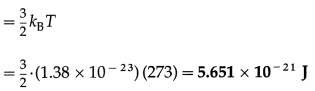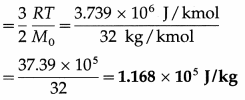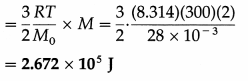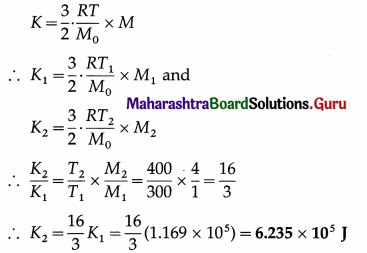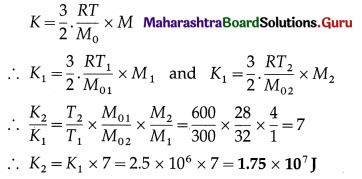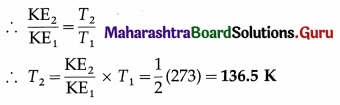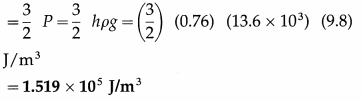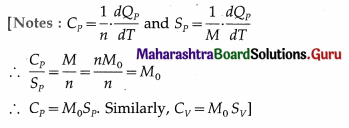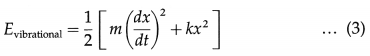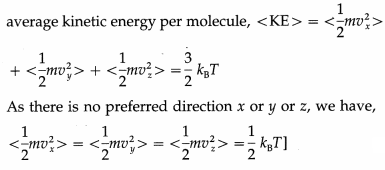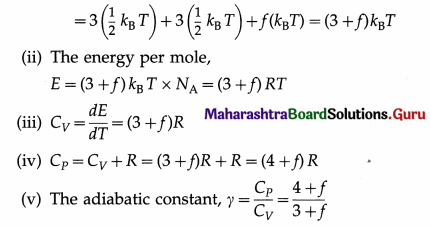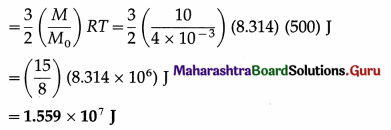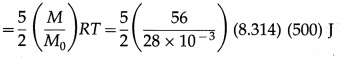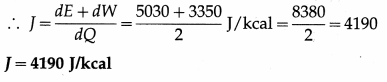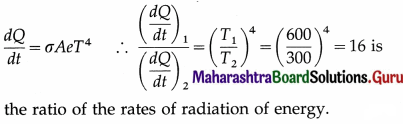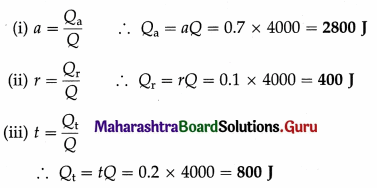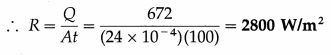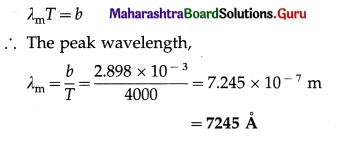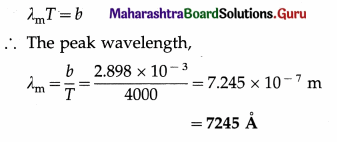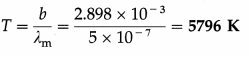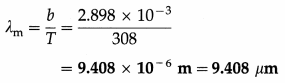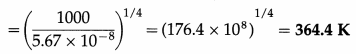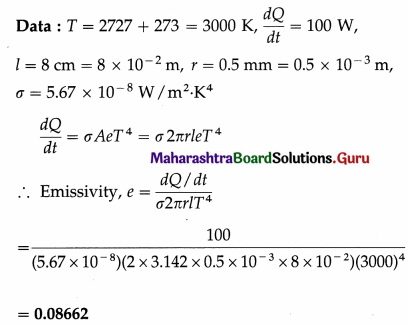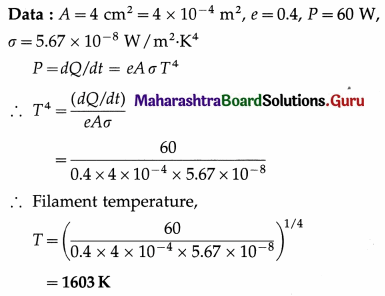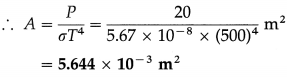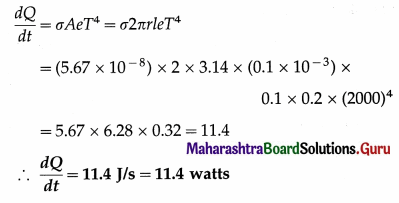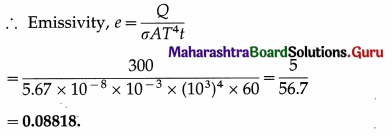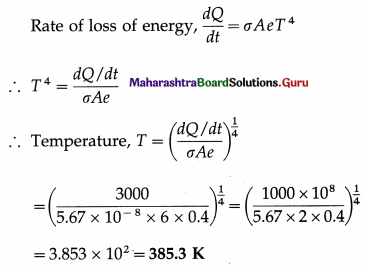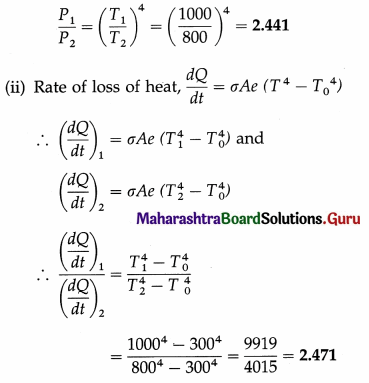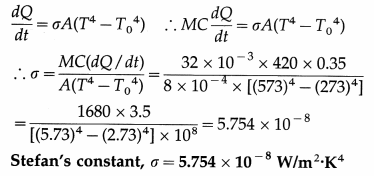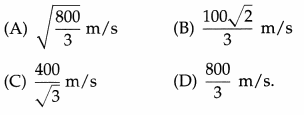Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 3 Kinetic Theory of Gases and Radiation Important Questions and Answers.
Maharashtra State Board 12th Physics Important Questions Chapter 3 Kinetic Theory of Gases and Radiation
Question 1.
What is an ideal or perfect gas ? Explain.
Answer:
An ideal or perfect gas is a gas which obeys the gas laws (Boyle’s law, Charles’ law and Gay-Lussac’s law) at all pressures and temperatures. An ideal gas cannot be liquefied by application of pressure or lowering the temperature.
A molecule of an ideal gas is an ideal particle having only mass and velocity. Its structure and size are ignored. Also, intermolecular forces are zero except during collisions.
Question 2.
Derive the ideal gas equation, PV = nRT.
OR
Derive the equation of state for an ideal gas
Answer:
Let P1, V1 and T1 be the pressure, volume and absolute temperature (thermodynamic temperature) of n moles of a gas (assumed to be ideal).
Suppose the gas is heated at constant pressure (P1) so that its temperature becomes T and volume becomes V2. Then by Charles’ law,\(\frac{V_{2}}{V_{1}}\) = \(\frac{T}{T_{1}}\).
∴ T = \(\frac{V_{2}}{V_{1}}\)T1 … (1)
Now, suppose that the gas is heated at constant volume (V2) so that its temperature becomes T2 and pressure becomes P2. Then by Gay—Lussac’s law,
\(\frac{P_{2}}{P_{1}}\) = \(\frac{T_{2}}{T}\)
∴ T = \(\frac{P_{1}}{P_{2}}\)T2 … (2)
From equations (1) and (2), we get,
\(\frac{V_{2}}{V_{1}}\)T1 = \(\frac{P_{1}}{P_{2}}\)T2
∴ \(\frac{P_{2} V_{2}}{T_{2}}\) = \(\frac{P_{1} V_{1}}{T_{1}}\)
When pressure and temperature are constant, V ∝ n. Hence, in general, we can write \(\frac{P V}{T}\) = nR, where R is a proportionality constant, called the universal gas constant.
Thus, PV = nRT for an ideal gas. This is the equation of state for an ideal gas.
[ Note : By Boyle’s law, for a fixed mass of gas at constant temperature, PV = constant. Writing PV ∝ nT, we get PV = nRT.]

Question 3.
Express the ideal gas equation in terms of
(i) the Avogadro number
(ii) The Boltzmann constant.
Answer:
In the usual notation, PV = nRT;
(i) Now, the number of moles, n = \(\frac{N}{N_{\mathrm{A}}}\), where N is the number of molecules corresponding to n moles of the gas and NA is the Avogadro number.
∴ PV = \(\frac{N}{N_{\mathrm{A}}}\)RT
(ii) PV = \(\frac{N}{N_{\mathrm{A}}}\)RT = N(\(\frac{R}{N_{\mathrm{A}}}\))T
= NkBT, where kB = \(\frac{R}{N_{\mathrm{A}}}\) is the Boltzmann constant.
Question 4.
Express the ideal gas equation in terms of the density of the gas.
Answer:
In the usual notation, PV = nRT. Now, the number of moles n = \(\frac{M}{M_{0}}\), where M is the mass of the gas M0 corresponding to n moles and M0 is the molar mass of the gas.
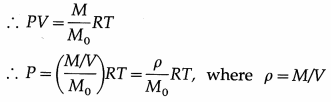
is the density of the gas.
Notes :
(1) Charles’ law : At a constant pressure, the volume of a fixed mass of gas is directly proportional to its absolute temperature (thermodynamic temperature).
If V is the volume of n moles of an ideal gas at a pressure P and T denotes its absolute temperature, P and n remaining constant,
V ∝ T or \(\frac{V}{T}\) = constant
The law was deduced experimentally in 1787 by Jacques Alexandre Cesar Charles (1746 -1823), French physicist.
From Charles’ law, V = KT, where K is a constant which depends on the mass and pressure. If M and ρ are the mass and mass per unit volume of a gas, V = M/ρ.
Charles’ law was properly established only after the publication in 1802 of more accurate experimental results by Joseph Gay-Lussac (1778-1850), French chemist. Hence, the law is also known as Gay-Lussac’s law.
(2) The Boltzmann constant is the ratio of the molar gas constant (R) to the Avogadro constant (Avogadro number) (NA). Its symbol is kB or k.
kB = 1.380 648 8(13) × 10-23 JK-1
It is a fundamental physical constant relating the average energy of a molecule (at the microscopic level) with temperature (a state variable, at the macroscopic level). It can be called the gas constant per molecule. It is named after Ludwig Eduard Boltzmann (1844-1906), Austrian physicist.
Question 5.
State the basic assumptions of the kinetic theory of gases.
Answer:
The basic assumptions of the kinetic theory of an ideal gas :
- A gas of a pure material consists of an extremely large number of identical molecules.
- A gas molecule behaves as an ideal particle, i.e., it has mass but its structure and size can be ignored as compared with the intermolecular separation in a dilute gas and the dimensions of the container.
- The molecules are in constant random motion with various velocities and obey Newton’s laws of motion.
- Intermolecular forces can be ignored on the average so that the only forces between the molecules and the walls of the container are contact forces during collisions. It follows that between successive collisions, a gas molecule travels in a straight line with constant speed.
- The collisions are perfectly elastic conserving total momentum and kinetic energy, and the duration of a collision is very small compared to the time interval between successive collisions.
Notes :
(1) The walls of the container holding the gas are assumed to be rigid and infinitely massive so that they do not move. (2) Assumption (2) allows us to ignore intermolecular collisions because if they are truly point like (i.e., of negligible extent) they cannot make contact with each other. Therefore, the only collisions we consider are those with the walls of the container. If these collisions are perfectly elastic [by assumption (5)], they only change the direction of the velocity of a gas molecule and a gas molecule possesses only kinetic energy by assumption
(4). The kinetic theory of gases was developed by Daniel Bernoulli (1700 – 82), Swiss mathematician, Rudolf Clausius (1822 – 88), German theoretical physicist, James Clerk Maxwell (1831-79), British physicist, Ludwig Eduard Boltzmann, Josiah Willard Gibbs (1839-1903), US physical chemist.]
Question 6.
Distinguish between an ideal gas and a real gas.
Answer:
| Ideal Gas | Real Gas |
| 1. Molecules of an ideal gas behave as ideal particles, i.e., they are like geometrical points without size and structure. | 1. Molecules of a real gas have finite size and structure. |
| 2. Molecules of an ideal gas have only translational motion. | 2. Polyatomic molecules have in general, translational, vibrational and rotational motion. |
| 3. There are no intermolecular forces in this case. | 3. Intermolecular forces are non-zero in this case. |
| 4. An ideal gas cannot be liquefied. | 4. A real gas can be liquefied and also solidified in many cases, by application of pressure and reducing temperature. |
| 5. There are no intermolecular collisions in this case. | 5. There are intermolecular collisions in this case, and under normal conditions the collision frequency is very high. |
| 6. In the absence of intermolecular forces, the internal energy of the gas is only kinetic. | 6. Due to the intermolecular forces, the internal energy of the gas is (potential energy + kinetic energy.) |
Question 7.
The pressure exerted by a certain mass of enclosed gas at 300 K is 5 × 104 Pa. What will be the pressure exerted by the gas at 600 K if the volume of the gas is kept constant ?
Answer:
Here, P ∝ T ∴\(\frac{P_{2}}{P_{1}}\) = \(\frac{T_{2}}{T_{1}}\) = \(\frac{600}{300}\) = 2
∴ P2 = 2P1 = 2 × 5 × 104 Pa = 105 Pa is the required pressure.
Question 8.
Solve the following :
Question 1.
16 g of oxygen occupy 0.025 m3 at 27 °C. Find the pressure exerted by it.
[Molar mass of oxygen = 32 g/mol, universal gas constant R = 8.3 J/mol.K]
Solution :
Data : M = 16 g, M0 = 32 g/mol, V = 0.025 m3,
T = 27 °C = (273 + 27) K = 300 K,R = 8.3 J/mol.K
PV = nRT, where number of moles, n = \(\frac{M}{M_{0}}\)
∴ The pressure exerted by the gas,
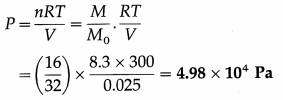
[Note : 1 Pa = 1 N/m2]
Question 2.
Two tanks of equal volume contain equal masses of oxygen and nitrogen at 127 °C. Find the ratio of
(i) the number of molecules of the gases
(ii) the pressure exerted by the gases in the two tanks. [Molar mass of oxygen = 32 g/mol, molar mass of nitrogen = 28 g/mol]
Solution :
Data : M0 = MN (equal masses of the two gases), equal volumes and the same temperature,
M01 (Oxygen) = 32 g/ mol,
M02(nitrogen) = 28 g/mol
Let N1 and N2 be the number of molecules of oxygen and nitrogen, n1 and n2 the respective number of moles, and NA the Avogadro number.
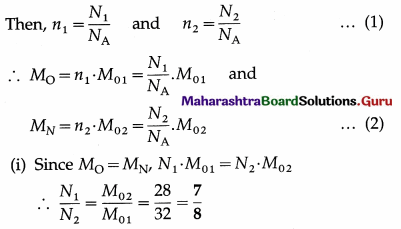
This is the ratio of the number of oxygen-molecules to that of nitrogen.
(ii) Using the ideal gas equation, PV = nRT,
P1 = n1\(\frac{R T}{V}\) and P2 = n2\(\frac{R T}{V}\) … (3)
since the gases occupy the same volume V and are at the same temperature T.
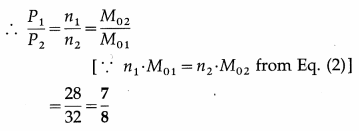
This is the corresponding pressure ratio.

Question 3.
A room is to be prepared for a birthday party filled with helium balloons. Some balloons are filled to occupy 0.240 m3 when the pressure inside them is 0.038 atm and the constant temperature of the room is 70 °F. With what pressure should the larger balloons be filled with helium so that they occupy 0.400 m3 ?
Solution :
Data : V1 = 0.240 m3, P1 = 0.038 atm, temperature = 70 °F, V2 = 0.400 m3
At constant temperature, by Boyle’s law,
P2V2 = P1V1
∴ Hence, the pressure of helium inside the larger balloons,
∴ P2 = \(\frac{P_{1} V_{1}}{V_{2}}\) = \(\frac{(0.038)(0.240)}{0.400}\)
= 0.038 × 0.6 = 0.0228 atm
Question 4.
Determine the pressure exerted by 4 grams of hydrogen occupying a volume of 16 litres at 10 °C. (R = 8.314 J/mol.K, molar mass of hydrogen = 2 g/mol)
Solution :
Data : Mass of hydrogen = 4 grams,
V = 16 litres = 16 × 10-3 m3,
T = 273 + 10 = 283 K, M0 = 2 g/mol,
R = 8.314 J/mol.K
Number of moles (n) = \(\frac{\text { mass }}{M_{0}}\) = \(\frac{4}{2}\) = 2
PV = nRT ∴ P = \(\frac{n R T}{V}\) = \(\frac{2 \times 8.314 \times 283}{16 \times 10^{-3}}\)
P = 2.941 × 105 N/m2
This is the pressure exerted by the gas.
Question 5.
Find the number of molecules per m3 of a gas at STP.
[Given : 1 atmosphere = 1.013 × 105 N/m2 NA = 6.022 × 1023 per mole, R = 8.314 J/mol.K]
Solution :
Data : P = 1.013 × 105 N/m2,
NA = 6.022 × 1023 per mole,
R = 8.314 J/mol.K, T = 273 K
Number of molecules per m3,
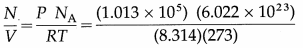
= 2.688 × 1025 molecules/m3
[ Note : STP means Standard temperature (0°C) and pressure (1 atmosphere).]
Question 6.
Explain the concept of free path of a gas molecule. Define free path and mean free path. State the expression for mean free path.
Answer:
Molecules of a real gas’ are not point like particles. For simplicity, molecules are assumed to be spherical. Because of their finite size, two molecules collide with each other when they come within a molecular diameter of each other, strictly speaking, within the sphere of influence of each molecule.
The molecular collisions, though perfectly elastic, result in significant changes in the speeds and
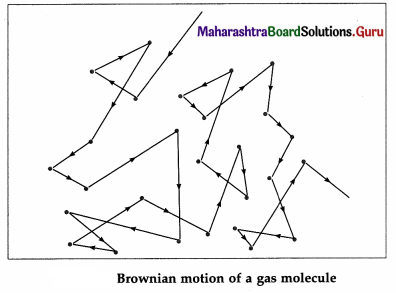
directions of motion of the molecules. Hence, every molecule follows a zigzag path, with abrupt changes in its speed and direction of motion at short and random time intervals. This is called Brownian motion.
Free path : The straight line path of a molecule, i.e., the distance covered by it between successive collisions, is called a free path.
Mean free path : The average distance travelled by a gas molecule between successive collisions, the average being taken over a large number of free paths (or collisions) is called the mean free path.
Maxwell, on the basis of the law of distribution of molecular speeds, obtained the formula for the mean free path (λ) as λ = \(\frac{1}{\sqrt{2} \pi d^{2}(N / V)}\), where N is the number of molecules in volume V of the gas and d is the diameter of a molecule.
[Note : Brownian motion is named after Robert Brown (1773-1858), British botanist, who, in 1827, observed under the microscope the random movement of pollen grains suspended in water. ]
Question 7.
Express the mean free path of a gas molecule in terms of pressure and temperature.
Answer:
In the usual notation, the mean free path of a gas molecule,

Question 8.
Express the mean free path of a gas molecule in terms of the density of the gas
Answer:
In the usual notation, the mean free path of a gas molecule,
λ = \(\frac{1}{\sqrt{2} \pi d^{2}(N / V)}\)
Density, ρ, of the gas = \(\frac{\text { mass }}{\text { volume }}\)
= \(\frac{m N}{V}\), where m is the molecular mass.
∴ \(\frac{N}{V}\) = \(\frac{\rho}{m}\)
∴ λ = \(\frac{m}{\sqrt{2} \pi d^{2} \rho}\)
Question 9.
State the factors on which the mean free path of a gas molecule depends.
Answer:
The mean free path of a gas molecule depends upon the number of molecules per unit volume of the gas and molecular diameter.
Question 10.
What happens to the mean free path of a gas molecule if there is
- increase in temperature at constant pressure
- increase in pressure at constant temperature?
Answer:
- The mean free path increases,
- The mean free path decreases.
Question 9.
Solve the following :
Question 1.
Calculate the mean free path of a gas molecule if the molecular diameter is 5A and the number of molecules per unit volume of the gas is 2 × 1024 per m3. Compare it with molecular diameter.
Solution :
Data : d = 5Å = 5 × 10-10m, \(\frac{N}{V}\) = 2 × 1024 per m3

[Note : 1Å = 10-10m, 1 nm = 10-9 m = 10 Å]
Question 2.
If the mean free path of a gas molecule under certain conditions is 5000Å and the molecular speed is 500 mIs, find
(i) the time interval between successive collisions
(ii) the collision frequency (number of collisions per unit time) of a gas molecule.
Solution :
Data : λ = 5000 Å = 5000 × 10-10 m
= 5 × 10-7 m, v = 500 m/s
(i) speed (v) = \(\frac{\text { distance }(\lambda)}{\text { time }(T)}\)
∴ The time interval between successive collisions of a gas molecule, T = \(\frac{\lambda}{v}\)
= \(\frac{5 \times 10^{-7} \mathrm{~m}}{500 \mathrm{~m} / \mathrm{s}}\) = 10-9 s
(ii) The collision frequency (number of collisions per unit time) of a gas molecule,
f = \(\frac{1}{T}\) = \(\frac{1}{10^{-9} \mathrm{~s}}\) = 109 collisions per second
Question 3.
Calculate the mean free path of a gas molecule with diameter 4 Å if the pressure of the gas is 1.013 × 105 N/m2 and the temperature is 27° C. (The Boltzmann constant, kB = 1.38 × 10-23 J/K)
Solution :
Data : d = 4 Å = 4 × 10-10m, P = 1.013 × 105 N/m2, T = (273 + 27) K = 300 KB = 1.38 × 10-23 J/K
The mean free path of a gas molecule,

Question 4.
Find the mean free path of a gas molecule if the diameter of a molecule is 4 A, the mass of a molecule is 5.316 × 10-26 kg and density of the gas is 1.429 kg/m3.
Solution :
Data : d = 4 Å = 4 × 10-10 m, m = 5.316 × 10-26 kg, ρ = 1.429 kg/m3
The mean free path of a gas molecule,
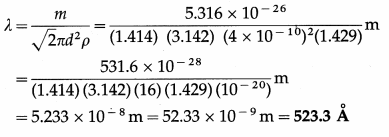
Question 5.
The mean free path of a gas molecule is 60 nm when the density of the gas is 1.2 kg/m3. What will be the mean free path if the density is reduced to 0.8 kg/m3 ?
Solution :
Data : λ1 = 60 nm, ρ1 = 1.2 kg/m3, ρ2 = 0.8 kg/m3
λ = \(\frac{m}{\sqrt{2} \pi d^{2} \rho}\)
∴ \(\frac{\lambda_{2}}{\lambda_{1}}\) = \(\frac{\rho_{1}}{\rho_{2}}\) as m and d are not changed.
∴ λ2 = \(\lambda_{1} \frac{\rho_{1}}{\rho_{2}}\) = 60\(\left(\frac{1.2}{0.8}\right)\) nm = 90 nm
This is the required quantity.
Question 10.
What is the origin of pressure exerted by a gas on the walls of a container?
Answer:
The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on a wall by all the molecules, per unit wall area, is the gas pressure on the wall.
Question 11.
Define
(1) the mean (or average) speed
(2) the mean square speed
(3) the root-mean-square speed of gas molecules. State the expressions for the same.
Answer:
(1) Mean (or average) speed of molecules of a gas : The mean speed of gas molecules is defined as the arithmetic mean of the speeds of all molecules of the gas at a given temperature.
(2) Mean square speed of molecules of a gas : The mean square speed of gas molecules is defined as the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.
(3) Root-mean-square speed of molecules of a gas : The root-mean-square (rms) speed of gas molecules is defined as the square root of the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.
If there are N molecules in an enclosed pure gas and v1, v2, v3, …, vN are the speeds of different molecules,
- the mean speed, \(\bar{v}\) = \(\frac{v_{1}+v_{2}+\ldots+v_{N}}{N}\)
- the mean square speed,
\(\overline{v^{2}}\) = \(\frac{v_{1}^{2}+v_{2}^{2}+\ldots+v_{N}^{2}}{N}\) - the rms speed, vrms = \(\sqrt{\overline{v^{2}}}\)
[Note : The mean square velocity is numerically equal to the mean square speed. Similarly, the rms velocity is numerically equal to the rms speed. But in random motion, the mean velocity would be statistically zero, but the mean speed cannot be zero. ]
Question 12.
On the basis of the kinetic theory of gases, derive an expression for the pressure exerted by the gas.
Answer:
The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on the wall by all the molecules, per unit wall area, is the gas pressure on the wall.
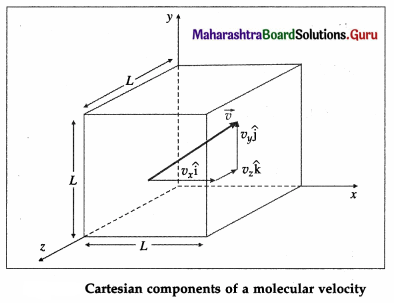
Consider a very dilute gas at a steady-state temperature enclosed in a cubical container of side L. The coordinate axes are aligned with the edges of this cube, as shown in above figure. Suppose that there are N molecules in the container, each of mass m. Consider a molecule moving with velocity \(\).
\(\overrightarrow{v_{1}}\) = \(v_{1 x} \hat{\mathbf{i}}\) + \(v_{1 y} \hat{\mathrm{j}}\) + \(v_{1 z} \hat{\mathbf{k}}\) …. (1)
where v, v1x and v1z are the velocity components along the x-, y- and z-axes, respectively, so that
\(v_{1}^{2}\) = \(v_{1 x}^{2}\) + \(v_{1 y}^{2}\) + \(v_{1 z}^{2}\)
The change in momentum of the molecule on collision with the right wall
= final momentum – initial momentum
= (-m|v1x|) – m|v1x| = -2m|v1x|
Assuming the collision to be elastic, the change in momentum of the right wall due to this collision is 2m|v1x|.
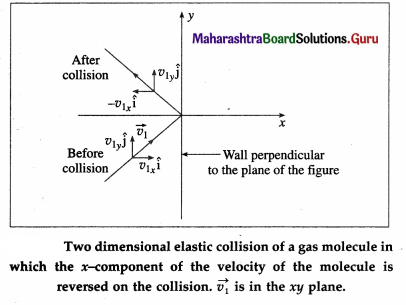
Since the distance between the right and left walls is L, the time between successive collisions with the right wall is,
∆t = \(\frac{2 L}{\left|v_{1 x}\right|}\)
Therefore, the frequency with which the molecule collides with the right wall is \(\frac{\left|v_{1 x}\right|}{2 L}\).
∴ Rate of change of momentum of the right wall = (change in momentum in one collision)
(frequency of collision)
= (2m|v1x|).\(\frac{\left|v_{1 x}\right|}{2 L}\) = \(\frac{m v_{1 x}^{2}}{L}\) …. (2)
By Newton’s second law of motion, this is the force f1x exerted by the molecule on the right wall.
Thus, the net force on the right wall by all the N molecules is
Fx = f1x + f2x + … + fNx
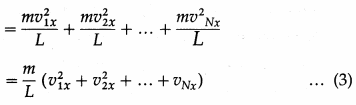
The pressure Px exerted by all the molecules on a wall perpendicular to the x-axis is
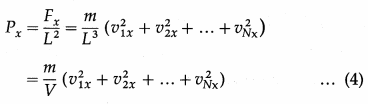
where V = L3 is the volume of the container.
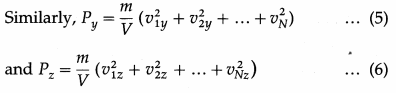
As pressure is the same in all directions,
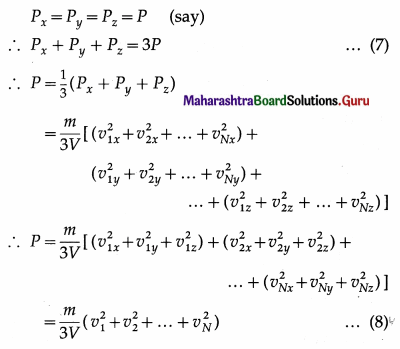
By definition, the mean square speed of the gas molecules is
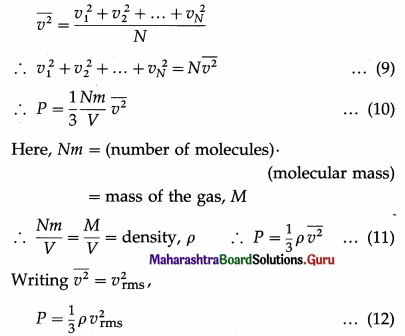
where vrms is the root-mean-square speed of molecules of the gas at a given temperature. Equation (12) gives the pressure exerted by an ideal gas in terms of its density and the root-mean-square speed of its molecules.

Question 13.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is \(\frac{3}{2}\)P.
Answer:
According to the kinetic theory of gases, the pressure P exerted by the gas is
P = \(\frac{1}{3} \rho v_{r m s}^{2}\) = \(\frac{1}{3} \frac{M}{V} v_{\mathrm{rms}}^{2}\)
where vrms is the rms speed (root-mean-square speed) of the gas molecules; M, V and ρ are the mass, volume and density of the gas, respectively.
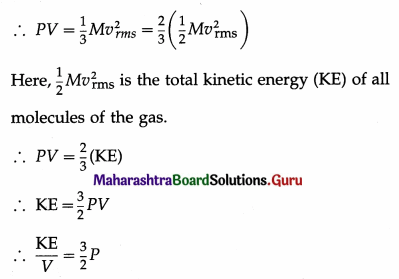
Thus, the kinetic energy per unit volume of an ideal gas is \(\frac{3}{2}\)P.
Question 14.
What is the kinetic energy per unit volume of a gas if the gas pressure is 105 N/m2?
Answer:
Kinetic energy per unit volume of a gas
= \(\frac{3}{2}\)P = \(\frac{3}{2}\) × 105 = 1.5 × 105 J/m3.
Question 15.
Assuming the expression for the pressure exerted by an ideal gas, prove that (1) the kinetic energy per mole of the gas = \(\frac{3}{2}\)RT (2) the rms speed of a gas molecule, urms = \(\sqrt{3 R T / M_{0}}\).
OR
Assuming the expression for the pressure exerted by an ideal gas, show that the rms speed of a gas molecule is directly proportional to the square root of its absolute temperature.
OR
Show that the rms velocity of gas molecules is directly proportional to the square root of its absolute temperature.
Answer:
According to the kinetic theory of gases, the pressure P exerted by a gas is
ρ = \(\frac{1}{3} \rho v_{\mathrm{rms}}^{2}\) = \(\frac{1}{3} \frac{M}{V} v_{\mathrm{rms}}^{2}\)
∴ PV = \(\frac{1}{3} m v_{\mathrm{rms}}^{2}\)
where vrms is the rms speed (root-mean-square speed) of the gas molecules; M, V and ρ are the mass,
volume and density of the gas, respectively. If there are n moles of the gas and M0 is the molar mass,
M = nM0, so that PV = \(\frac{1}{3} n M_{0} v_{\mathrm{rms}}^{2}\) … (1)
The equation of state of an ideal gas is
PV = nRT … (2)
where T is the absolute temperature of the gas and R is the molar gas constant.
From Eqs. (1) and (2), we get,

where the term on the left-hand side is the kinetic energy of one mole of the gas.
∴ Kinetic energy per mole of the gas = \(\frac{3}{2}\)RT… (5)
From Eq. (3),

In Eq. (6), R and M0 are constant so that vrms ∝ \(\sqrt{T}\). Thus, the rms speed of a gas molecule is directly proportional to the square root of the absolute temperature of the gas.
Question 16.
The rms speed of oxygen molecules at a certain temperature is 400 m/s. What is the rms speed of nitrogen molecules at the same temperature ?
[M01 (oxygen) = 32 × 10-3 kg/mol,
M02 (nitrogen) = 28 × 10-3 kg/mol]
Answer:

Question 17.
The kinetic energy per unit mass of a certain gas at 300 K is 1.3 × 105 J/kg. What will be the kinetic energy per unit mass of the gas at 600 K ?
Answer:
KE per unit mass of a gas (KE/M) ∝ T
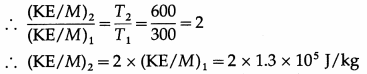
This is the required quantity.
Question 18.
Prove that the kinetic energy per molecule of an ideal gas is \(\frac{3}{2}\)KBT.
Give the interpretation of temperature according to the kinetic theory of gases.
Answer:
Consider n moles of an ideal gas in a container of volume V. If m is the mass of a gas molecule and vrms is the root-mean-square speed of the gas molecules then, by the kinetic theory, the pressure exerted by the gas is

Therefore, the kinetic energy per molecule of an ideal gas is directly proportional to its absolute temperature.
This equation is the relation between the kinetic per molecule of a gas and the absolute temperature which is the macroscopic parameter of the gas. The absolute temperature of a gas is a measure of the kinetic energy per molecule of the gas. This result is called the kinetic intepretation of temperature, i.e., the interpretation of temperature according to the kinetic theory of gases.
Question 19.
The rms speed of molecules of a certain gas at 300 K is 400 m/s. What will be the rms speed if the gas is heated to 600 K?
Answer:
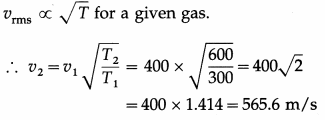
gives the required rms speed.
Question 20.
State Boyle’s law. Deduce it on the basis of the kinetic theory of an ideal gas.
OR
Deduce Boyle’s law using the expression for pressure exerted by an ideal gas.
Answer:
Boyle’s law : At a constant temperature, the pressure exerted by a fixed mass of gas is inversely proportional to its volume. If P and V denote the pressure and volume of a fixed mass of gas, then, PV = constant at a constant temperature, for a fixed mass of gas.
According to the kinetic theory of gases, the pressure exerted by the gas is
P = \(\frac{1}{3} \frac{N m v_{\mathrm{rms}}^{2}}{V}\)
where N is the number of molecules of the gas, m is the mass of a single molecule, vrms is the rms speed of the molecules and V is the volume occupied by the gas.
∴ PV = (\(\frac{1}{2}\)mv2rms) × \(\frac{2}{3}\) N
= (KE of a gas molecule) \(\frac{2}{3}\) N … (1)
For a fixed mass of gas, N is constant. Further, intermolecular forces are ignored so that the corresponding potential energy of the gas molecules may be assumed to be zero. Therefore, \(\frac{1}{2} m v_{\mathrm{rms}}^{2}\) is the total energy of a gas molecule and N\(\left(\frac{1}{2} m v_{\mathrm{rms}}^{2}\right)\) is the total energy of the gas molecules, which is proportional to the absolute temperature of the gas. Then, the right-hand side of EQ. (1) will be constant if its temperature is constant. Hence, it follows that PV = constant for a fixed mass of gas at constant temperature, which is Boyle’s law.
Question 21.
Solve the following :
Question 1.
The speeds of five molecules are 200 m/s, 300 m/s, 400 m/s, 500 m/s and 600 m/s respectively. Find
(i) the mean speed
(ii) the mean square speed
(iii) the root mean square speed of the molecules.
Solution :
Data : v1 = 200 m/s, v2 = 300 m/s, v3 = 400 m/s,. v5 = 500 m/s, v6 = 600 m/s
(i) Mean speed,

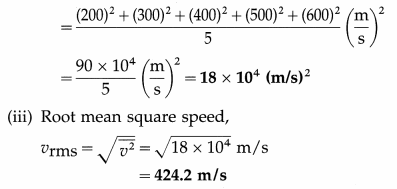
Question 2.
Find the number of molecules in 1 cm3 of oxygen at a pressure of 105 N/m2 if the rms speed of oxygen molecules is 426 m/s. What is the temperature of the gas? (Mass of an oxygen molecule = 5.28 × 10-26 kg, kB = 1.38 × 10-23 J/K)
Solution :
Data : m = 5.28 × 10-26 kg, vrms = 426 m/s,
V = 1 cm3 = 10-6 m3, P = 105 Pa, kB = 1.38 × 10-23 J/K
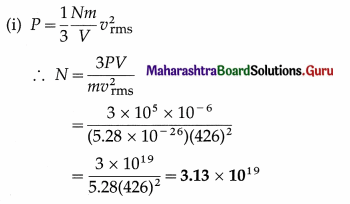
This is the number of molecules in 1 cm3 of oxygen under given conditions.
(ii) PV = nRT
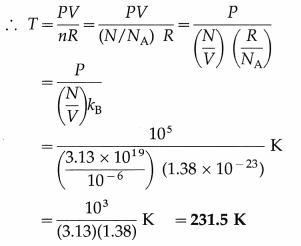
This is the required temperature.
Question 3.
A cylinder filled with hydrogen at 400 K exerts a pressure of 3 atmospheres. If hydrogen is replaced by an equal mass of helium at the same temperature, find the
(i) relative number of molecules of hydrogen and helium occupying the cylinder
(ii) pressure exerted by helium. (Molar mass of hydrogen = 2 g/mol, molar mass of helium = 4 g/mol)
Solution:
Let the subscript 1 refer to hydrogen and the subscript 2 to helium.
From the data in the example,
T = 400 K, P1 = 3 atmospheres, molar mass of hydrogen, M1 = 2 g/mol
Molar mass of helium, M2 = 4 g/mol
∴ \(\frac{M_{2}}{M_{1}}\) = \(\frac{4}{2}\) = 2
(i) Since both the gases have the same mass, N1m1 = N2m2, where is the mass of a molecule of hydrogen and m2 is the mass of a molecule of helium.

∴ P2 = \(\frac{2}{3}\) × \(\frac{N_{2}}{V}\) × \(\left(\frac{1}{2} m_{2} v_{2 \mathrm{rms}}^{2}\right)\)
As the temperature is the same in both the cases, the average kinetic energy of gas molecules will be the same in both the cases.
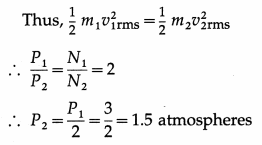
Pressure exerted by helium,
P2 = 1.5 atmospheres

Question 4.
Calculate the rms speed of oxygen molecules at 127 °C. (Density of oxygen at STP = 1.429 kg/m3 and one atmosphere = 1.013 × 105 N/m2)
Solution:
By the data, ρ = 1.429 kg/m3,
P = 1.013 × 105N/m2
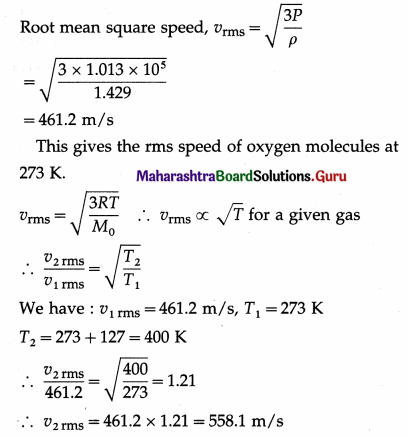
The root mean square speed of oxygen molecules at 127° C = 558.1 m/s.
Question 5.
At what temperature will helium molecules have the same rms speed as that of hydrogen molecules at STP ? (Molar mass of hydrogen = 2 g/mol, molar mass of helium = 4 g/mol)
Solution :
Data : M01 (hydrogen) = 2 g/mol
M02 (helium) = 4 g/mol, T1 (hydrogen) = 273 K,
vrms (hydrogen) = v2rms (helium)

The temperature of helium = 546 K = 273 °C
Question 6.
Compute the temperature at which the rms speed of nitrogen molecules is 831 m/s. [Universal gas constant, R = 8310 J/kmol K, molar mass of nitrogen = 28 kg/kmol]
Solution :
Data : vrms = 831 m/s, R = 8310 J/kmol.K,
M0 = 28 kg/kmol

This is the required temperature.
Question 7.
If the rms speed of oxygen molecules at STP is 460 m/s, determine the rms speed of hydrogen molecules at STP. [Molar mass of oxygen = 32 g/mol, molar mass of hydrogen = 2 g/mol]
Solution :
Data : vrms (oxygen) = 460 m/s, same temperature, M01 (oxygen) = 32 × 10-3 kg/mol,
M02 (hydrogen) = 2 × 10-3 kg/mol
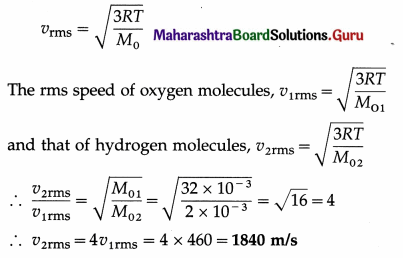
This is the rms speed of hydrogen molecules at STP.
Question 8.
Calculate the rms speed of helium atoms at 27 °C. [Density of helium at STP = 0.1785 kg/m3, one atmosphere = 1.013 × 105 Pa]
Solution :
Data : ρ = 0.1785 kg/m3, P = 1.013 × 105 Pa,
T0 = 273 K, T = (273 + 27) = 300 K
The rms speed of helium atoms at STP,

Question 9.
Determine the pressure of oxygen at 0°C if the density of oxygen at STP = 1.44 kg/m3 and the rms speed of the molecules at STP = 456.4 m/s.
Solution :
Data : ρ = 1.44 kg/m3, vrms = 456.4 m/s
The pressure of oxygen,
P = \(\frac{1}{3} \rho v_{\mathrm{rms}}^{2}\)
= \(\frac{1}{2}\)(1.44)(456.4)2 = 9.98 × 104 Pa
Question 10.
Calculate the rms speed of hydrogen molecules at 373.2K. [Molar mass of hydrogen, M0 = 2 × 10-3 kg/mol, R = 8.314 J/mol.K]
Solution :
Data : T = 373.2 K, M0 = 2 × 10-3 kg/mol,
R = 8.314 J/mol.K
The rms speed of hydrogen molecules,
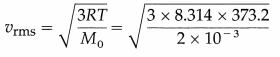
= 2157 m/s = 2.157 km/s
Question 11.
Find the rms speed of hydrogen molecules if its pressure is 105 Pa and density is 0.09 kg/m3.
Solution :
Data : ρ = 0.09 kg/m3, P = 105 Pa
The rms speed of hydrogen molecules,
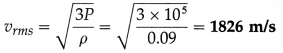
Question 12.
The temperature of matter in interstellar space has an average value of about 3 K. Find the rms speed of a proton in the space. [mp = 1.673 × 10-27 kg, kB = 1.38 × 10-23 J/K]
Solution :
Data : T = 3 K, mp = 1.673 × 10-27 kg, kB = 1.38 × 10-23 J/K
The rms speed of a proton in interstellar space,
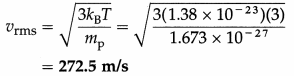
Question 13.
Find the temperature at which
(i) the rms speed
(ii) the average kinetic energy of the molecules of an ideal gas are double their respective values at STP.
Solution:
Data : T0 = 273 K, v = 2v0 (rms speeds),
KE = 2KE0 (average kinetic energies)
(i) vrms ∝ \(\sqrt{\mathrm{T}}\) for a given gas.
∴\(\frac{v}{v_{\mathrm{o}}}\) = \(\sqrt{\frac{T}{T_{0}}}\)
∴\(\sqrt{\frac{T}{T_{0}}}\) = 2
∴ Temperature, T = 4T0 = 4 × 273 = 1092 K
(ii) Average Kinetic Energy ∝ T
∴ \(\frac{\mathrm{KE}}{\mathrm{KE}_{0}}\) = \(\frac{T}{T_{0}}\)
∴ Temperature, T = 2T0 = 2 × 273 = 546 K
Question 14.
At what temperature is the rms speed of an argon atom equal to that of a helium atom at – 20 °C ? [Atomic mass of Ar = 39.9 amu, atomic mass of He = 4.0 amu]
Solution :
Data : T1 = -20 °C = 273 – 20 = 253 K,
M01 (He) = 4 amu, M02 (Ar) = 39.9 amu
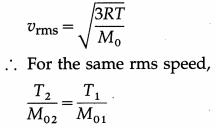
∴ T2 = \(\frac{M_{02}}{M_{01}}\) T1 = \(\frac{39.9}{4} \times 253\)
= 2523 K
This is the required temperature.
Question 15.
Calculate the kinetic energy
(i) per mole
(ii) per unit mass
(iii) per molecule of nitrogen at STP. [Molar mass of nitrogen = 28 × 10-3 kg/mol, R = 8.314 J/mol.K, kB = 1.38 × 10-23 J/K]
Solution :
Data : T = 273 K, M0 = 28 × 10-3 kg/mol,
R = 8.314 J/mol.K, kB = 1.38 × 10-23 J/K
(i) The KE per mole = \(\frac{3}{2}\)RT
= \(\frac{3}{2}\)(8.314)(273) = 3.404 × 103 J/mol
(ii) The KE per unit mass = \(\frac{3}{2} \frac{R T}{M_{0}}\)
= \(\frac{3}{2} \cdot \frac{(8.314)(273)}{28 \times 10^{-3}}\) = 1.216 × 105 J/kg
(iii) The KE per molecule
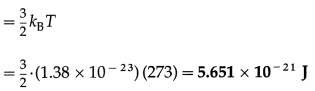
Question 16.
Calculate the average molecular kinetic energy
(i) per kilomole
(ii) per kilogram of oxygen at 27 °C. [R = 8310 J/kmol.K, Avogadro’s number = 6.02 × 1026 molecules/kmol]
Solution :
Data : T = 273 + 27 = 300 K, M0 = 32 kg / kmol,
R = 8310 J/kmol.K
(i) The average molecular kinetic energy per kilomole of oxygen
= \(\frac{3}{2}\) RT = \(\frac{3}{2}\) (8310) (300)
= 4155 × 900 = 3739 × 1000
= 3.739 × 106 J/kmol
(ii) The average molecular kinetic energy per unit mass of oxygen
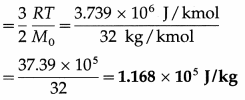
Question 17.
Calculate the kinetic energy of 10 grams of argon molecules at 127 °C. [Universal gas constant R = 8310 J/kmol.K, atomic weight of argon = 40]
Solution:
Data : M = 10 g = 10 × 10-3 kg, T = 273 + 127 = 400 K,R = 8310 J/kmol.K, M0 = 40 kg/kmol Kinetic energy per unit mass
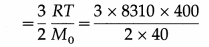
= 15 × 8310 = 1.247 × 105 J/kg
∴ The kinetic energy of 1 × 10-3 kg of argon at 127°C = 1.247 × 105 × 10 × 10-3
= 1247 J
Question 18.
Calculate the kinetic energy of 2 kg of nitrogen at 300 K. [Molar mass of nitrogen = 28 × 10-3 kg/mol, R = 8.314 J/mol.K]
Solution :
Data : Mass of nitrogen, M = 2 kg, T = 300 K,
M0 = 28 × 10-3 kg/mol, R = 8.314 J/mol.K
Kinetic energy per kg = \(\frac{3}{2} \frac{R T}{M_{0}}\)
∴ The kinetic energy of 2 kg of nitrogen
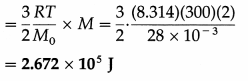
Question 19.
The kinetic energy of 1 kg of oxygen at 300 K is 1.169 × 105 J. Find the kinetic energy of 4 kg of oxygen at 400 K.
Solution :
Data : Masses of oxygen, M1 = 1 kg and M2 = 4 kg, T1 = 300 K, T2 = 400 K, kinetic energy,
K1 = 1.169 × 105 J
Kinetic energy of a given mass (M) of a gas,
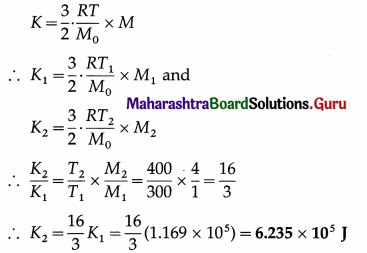
This is the kinetic energy of 4 kg of oxygen at 400 K.
Question 20.
The kinetic energy per unit mass of nitrogen at 300 K is 2.5 × 106J/kg. Find the kinetic energy of 4 kg of oxygen at 600 K. [Molar mass of nitrogen = 28 kg/kmol, molar mass of oxygen = 32 kg/kmol]
Solution:
Data : T1 = 300 K, K1 = 2.5 × 106 J/kg,
M1 (nitrogen) = 1 kg, M2(oxygen) = 4 kg,
M01 (nitrogen) = 28 kg/kmol, T2 = 600 K,
M02(oxygen) = 32 kg/kmol
Kinetic energy of a given mass M of a gas,
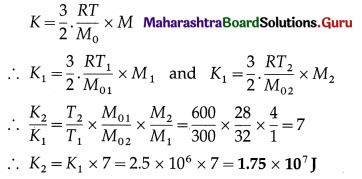
This is the required quantity.
Question 21.
The pressure of a gas in a 0.1 litre container is 200 kPa and the KE per molecule is 6 × 10-21J. Find the number of gas molecules in the container. How many moles are in the container? [Avogadro number = 6.022 × 1023 mol-1]
Solution:
Data : V = 0.1 litre = 10-4 m3, P = 200 kPa
= 2 × 105 Pa, KE per molecule = 6 × 10-21 J,
NA = 6.022 × 1023 mol-1
The KE per molecule of a gas = \(\frac{3}{2}\)kBT

Question 22.
At what temperature will the average kinetic energy of a gas be exactly half of its value at NTP ?
Solution :
Data : KE2/KE1 = 1/2, T1 = 273K
Average molecular kinetic energy per mole of the gas = \(\frac{3}{2}\)RT
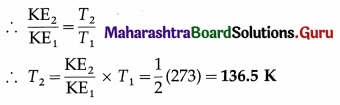
This is the required temperature.

Question 23.
Find the kinetic energy per unit volume of nitrogen at a pressure of 76 cm of mercury. Hence, find the kinetic energy of 10 cm3 of the gas under the same condition. Take ρ (mercury) = 13.6 g/cm3 and g = 9.8 m/s2.
Solution :
Data :h = 76 cm = 0.76 m, ρ = 13.6 g/cm3 = 13.6 × 103 kg/m3, g = 9.8 m/s2,
V = 10 cm3 = 10 × 10-6 cm3
(i) The kinetic energy per unit volume of nitrogen
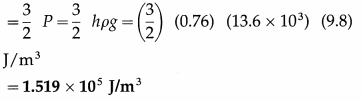
(ii) The kinetic energy of 10 cm3 of the gas = \(\frac{3}{2}\) PV= (1.519 × 105) (10 × 10-6)
= 1.519 J
Question 22.
What is meant by degrees of freedom ? Explain the degrees of freedom for
(i) an atom
(ii) a diatomic molecule.
Answer:
The concept of degrees of freedom as used in the kinetic theory specifies the number of independent ways in which an atom or molecule can take up energy. It depends only on the possibilities of motion of the atom or molecule.
Gas molecules of all types have x-, y- and z-components of velocity that are entirely independent of one another. Thus, they have three ways to move in translation, i.e., three degrees of translational freedom.
An atom (or a monatomic molecule, i.e., a molecule containing a single atom, e.g., He) treated as a point mass, has no rotational motion. Hence, it has only three degrees of translational freedom.
A diatomic molecule, in addition to translation, can rotate about axes perpendicular to the line connecting the atoms, as shown in below figure, but not about that line itself. Therefore, it has only two degrees of rotational freedom.
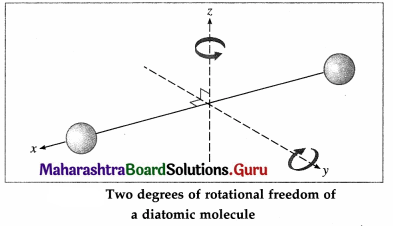
Further, the two atoms may oscillate alternately toward and away from one another along the line joining them, as if connected by a spring. As a, i harmonic oscillator can have potential energy as well as kinetic energy, a diatomic molecule is regarded to have two degrees of vibrational freedom. Thus, at high enough temperatures, a diatomic molecule has seven degrees of freedom : three of translation, and two each of rotation and vibration.
Notes :
(1) That a monatomic gas molecule does not have rotational energy, and that a diatomic molecule does not have a third rotational degree of freedom corresponding to rotation about the line joining the atoms, are explained by quantum theory.
(2) Also according to quantum theory, rotational and oscillatory motions begin at certain higher temperatures. For a molecule of a diatomic gas (like hydrogen), only translation is possible at very low temperatures (below about 100 K). As the temperature increases, rotational motion can begin; so that, at room temperature, a diatomic molecule has only five degrees of freedom-behaving like a pair of atoms rigidly connected like a dumbbell. Oscillatory motion can begin only at quite high temperatures substantially above room temperature (usually of the order of thousands of kelvin).
Question 23.
Derive Mayer’s relation between the molar specific heat of a gas at constant pressure and that at constant volume.
OR
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
Answer:
Consider a cylinder of volume V containing n moles of an ideal gas at pressure P, fitted with a piston of area A. Suppose, the gas is heated at constant pressure which raises its temperature by dT. The gas exerts a total force F = PA on the piston which moves outward a small distance dx.
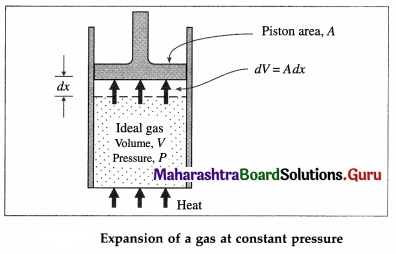
dW = Fdx = PAdx = PdV … (1)
where Adx = dV is the increase in volume of the gas during the expansion. dW is the work done by the gas on the surroundings as a result of the expansion. If the heat supplied to the gas is dQP and the increase in its internal energy is dE then, by the first law of thermodynamics,
dQP = dE + dW=dE + PdV
If CP is the molar specific heat capacity of the gas at constant pressure, dQP = nCP dT.
∴ nCPdT = dE + PdV …(2)
On the other hand, if the gas was heated at constant volume (instead of at constant pressure) from the initial state such that its temperature increases by the same amount dT, then dW=0. Since the internal energy of an ideal gas depends only on the temperature, the increase in internal would again be dE. If dQv was the heat supplied to the gas in this case, by the first law of thermodynamics and the definition of molar specific heat capacity at constant volume (CV),

This is Mayer’s relation between CP and CV.
Here, heat and work are expressed in the same units. If heat is expressed in calorie or kilo calorie and work is expressed in erg or joule, the above relation becomes
CP – CV = \(\frac{R}{J}\) …. (7)
Where J is the mechanical equivalent of heat.
Question 24.
Express Mayer’s relation in terms of the principal specific heats, SP and SV.
Answer:
Mayer’s relation : CP – CV = R. Let M0 = molar mass of the gas, SP = specific heat of the gas at constant pressure and SV = specific heat of the gas at constant volume.
Now, CP = M0SP and CV = M0SV
∴ M0Sp – M0SV = R
∴ SP – SV = \(\frac{R}{M_{0}}\) when heat and work are expressed
in the same units. If heat is expressed in calorie or kilo calorie and work is expressed in erg or joule, we
get,
Sp – Sv = \(\frac{R}{M_{0} J}\), where J is the mechanical equivalent of heat.
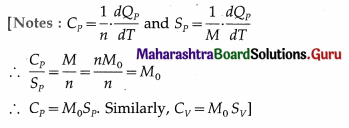
Question 25.
Explain : Each translational and rotational degree of freedom contributes only one quadratic term to the energy but one vibrational mode contributes two quadratic terms.
Answer:
With three translational degrees of freedom, the average translational energy per molecule of a gas is
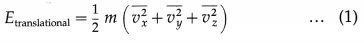
where m is the mass of the molecule and vx, vy and vz are the x-, y- and z-components of the molecular velocity.
A diatomic molecule has two rotational degrees of freedom. If ω1 and ω2 are the angular speeds about the two axes and I1 and I2 are the corresponding moments of inertia, the rotational energy of a diatomic molecule,
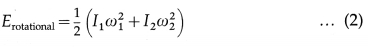
A diatomic molecule is regarded to have two degrees of vibrational freedom for the vibrational mode in which the two atoms vibrate relative to, and without affecting, the centre of mass of the molecule. Comparing this system with a vibrating body of mass m connected to a spring of force constant k, the vibrational energy has two terms corresponding to the kinetic and potential energies :
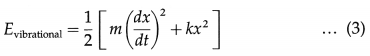
where x is the displacement from the mean position.
From Eqs. (1), (2) and (3), each translational and rotational degree of freedom contributes only one quadratic term to the average energy of a gas molecule while one vibrational mode contributes two quadratic terms.
[ Note : For a gas at an absolute temperature T, the
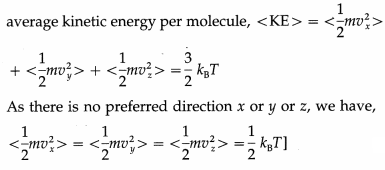
Question 26.
Explain the degrees of freedom a polyatomic molecule can have. Hence write the expressions for
(i) the energy per molecule
(ii) the energy per mole
(iii) CV
(iv) CP
(v) the adiabatic constant, for a polyatomic gas.
Answer:
A polyatomic molecule has three degrees of translational freedom like any particle. Each molecule can also rotate about its centre of mass with an angular velocity components along each of the three axes. Therefore, each molecule has three degrees of rotational freedom. Additionally, if the molecule is soft at high enough temperatures, it can vibrate easily with many different frequencies, say, f, because there are many interatomic bonds. Hence, it has 2f degrees of vibrational freedom. Then, according to the law of equipartition of energy, for each degree of freedom of translation and rotation,
the molecule has the average energy \(\frac{1}{2}\)kBT, but for each frequency of vibration the average energy is kBT, since each vibration involves potential energy and kinetic energy. kB is the Boltzmann constant and T is the thermodynamic temperature.
(i) The energy per molecule
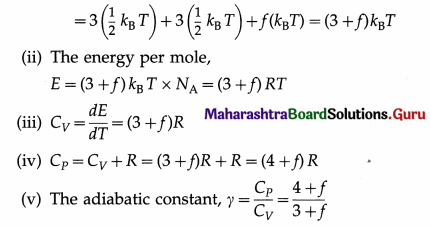
[Note : As /increases, y decreases.]
Question 27.
The top of a cloud of smoke holds together for hours. Why?
Answer:
According to the law of equipartition of energy, the smoke particles have the same average kinetic energy of random motion as the air molecules. But smoke particles have a much larger mass than air molecules and therefore move slowly, i.e., the average speed of diffusion of smoke particles is small. Hence, in the absence of significant turbulence in the atmosphere, a smoke cloud is relatively stable.

Question 28.
Solve the following :
Question 1.
Find the kinetic energy per molecule of a monatomic gas at 300 K.
Solution :
Data : T = 300 K, kB = 1.38 × 10-23 J/K
The kinetic energy per molecule of the gas
= \(\frac{3}{2}\)kBT
= \(\frac{3}{2}\) (1.38 × 10-23) (300) J/molecule
= (4.5) (1.38 × 10-21) J/molecule
= 6.21 × 10-21 J/molecule
[Note : Here, the number of degrees of freedom is 3.]
Question 2.
Find the kinetic energy of two moles of a mon-atomic gas at 400 K.
Solution :
Data : n = 2, T = 400 K, R = 8.314 J/mol.K
The kinetic energy of two moles of the gas
= \(\frac{3}{2}\)nRT = \(\frac{3}{2}\)(2) (8.314) (400) J
= (12) (8.314 × 102) J
= 9.977 × 103 J.
Question 3.
Find the kinetic energy of 10 kg of a monatomic gas at 500 K if the molar mass of the gas is 4 × 10-3 kg/mol.
Solution :
Data : M = 10 kg, M0 = 4 × 10-3 kg/mol, T = 500 K, R = 8.314 J/mol.K.
The kinetic energy of 10 kg of the gas
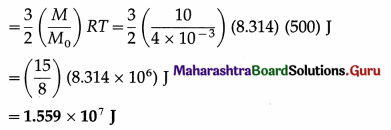
Question 4.
Find the kinetic energy per molecule of a diatomic gas at 300 K.
Solution :
Data : T = 300 K, kB = 1.38 × 10-23 J/K
The kinetic energy per molecule of the gas
= \(\frac{5}{2}\) kBT = \(\frac{5}{2}\)(1.38 × 10-23) (300) J/molecule
= (7.5) (1.38 × 10-23) J/molecule
= 1.035 × 10-22 J/molecule.
[Note : Here, the number of degrees of freedom is 5.]
Question 5.
Find the kinetic energy of four moles of a diatomic gas at 400 K.
Solution :
Data : n = 4, T = 400 K, R = 8.314 J/mol.K
The kinetic energy of four moles of the gas
= \(\frac{5}{2}\)nRT = \(\left(\frac{5}{2}\right)\) (8.314) (400) J
= (40)(8.314 × 102) J
= 3.326 × 104 J
Question 6.
Find the kinetic energy of 56 kg of a diatomic gas at 500 K if the molar mass of the gas is 28 × 10-3 kg/mol.
Solution :
Data : M = 56 kg, M0 = 28 × 10-3 kg/mol, T = 500 K, R = 8.314 J/mol.K
The kinetic energy of 56 kg of the gas
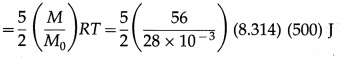
= 25(8.314 × 105)
= 2.079 × 107 J
Question 7.
When two kilocalories of heat are supplied to a system, the internal energy of the system increases by 5030 J and the work done by the gas against the external pressure is 3350 J. Calculate J, the mechanical equivalent of heat.
Solution :
Data : From the data in the example,
dQ = 2 kcal, dE = 5030 J, dW = 3350 J.
dQ = \(\frac{d E+d W}{J}\), where J = mechanical equivalent of heat
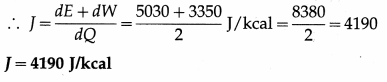
Question 8.
Find the increase in the internal energy of a gas of mass 10 grams when it is heated from 300 K to 305 K.
Given : SV = 0.16 kcal/kg.K, J = 4186 J/kcal
Solution :
Data : M = 10 grams = 10 × 10-3 kg,
SV = 0.16 kcal/kg.K, J = 4186 J/kcal
Rise in the temperature of the gas,
∆T = 305 – 300 = 5K
∆E = J SV M∆T = (4186)(0.16)(10 × 10-3) × (5) J
= 33.49 J
The increase in the internal energy of the gas, ∆E = 33.49 J
Question 9.
The molar specific heat of helium at constant volume is 12.5 J/mol.K. Find its molar specific heat at constant pressure. Take R = 8.31 J/mol.K.
Solution :
Data : CV = 12.5 J/mol.K, R = 8.31 J/mol.K
The molar specific heat of helium at constant press-ure,
CP = CV + R = (12.5 + 8.31) J/mol.K
= 20.81 J/mol.K.
Question 10.
Find the principal specific heats of helium and hence the universal gas constant. Given : CP = 20.81 J/mol.K, CV = 12.5 J/mol.K. M0 (He) = 4 × 10-3 kg/mol.
Solution :
Data : CP = 20.81 J/mol.K, CV = 12.5 J/mol.K,
M0 = 4 × 10-3 kg/mol.
(i) The specific heat of helium at constant pressure,

[Note : R = CP – CV = (20.81 – 12.5) J/mol.K = 8.31 J/mol.K. The difference between the two values of R is due to the approximation involved in calculation.]
Question 11.
The molar specific heat of nitrogen at constant volume is 4.952 cal/mol.K and that at constant pressure is 6.933 cal/mol.K. Find the mechanical equivalent of heat. Take R = 8.31 J/mol.K.
Solution :
Data : CV = 4.952 cal/mol.K, CP = 6.933 cal/mol.K, R = 8.31 J/mol.K
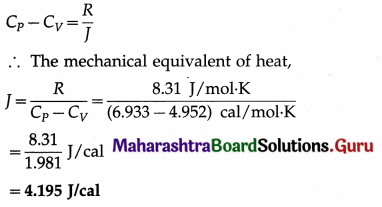
Question 29.
Name and define the modes of heat transfer.
Answer:
The three modes of heat transfer are conduction, convection and radiation.
- Conduction is the mode of heat transfer within a body or between two bodies in contact, from a region of high temperature to a region of lower temperature without the migration of the particles of the medium.
- Convection is the mode of heat transfer from one part of a fluid to another by the migration of the particles of the fluid.
- Radiation is the mode of heat transfer by electromagnetic waves / quanta.
Question 30.
What is thermal radiation or heat radiation? State its characteristic properties.
Answer:
Radiation is the mode of heat transfer or in general, energy transfer by electromagnetic waves / quanta. Thermal radiation or heat radiation is the radiation produced by thermal agitation of the particles of a body, and its spectrum, i.e., frequency distribution or wavelength distribution, is continuous from the far infrared to the extreme ultraviolet region depending on the temperature of the body.
Properties :
- Thermal radiations are electromagnetic waves/ quanta extending from the far infrared to the extreme ultraviolet region. In this spectrum, the infrared waves (wavelengths ranging from about 700 nm to about 1 mm) are sensed as heat.
- They have the same speed in free space as that of light, nearly 3 × 108 m/s, which makes radiation the most rapid mode of heat transfer.
- They exhibit all the optical phenomena of light, viz., reflection, absorption, refraction, interference, diffraction and polarization.
- Radiation incident on a body is, in general, partly reflected, partly, absorbed and partly transmitted.
- Thermal radiation obeys the inverse-square law of intensity, i.e., the intensity at a point is inversely proportional to the square of its distance from a point source of radiation.
Question 31.
Define the coefficients of absorption, reflection and transmission. Obtain the relation between them.
Answer:
- The coefficient of absorption or absorptive power or absorptivity of a body is the ratio of the quantity of radiant energy absorbed by the body to the quantity of radiant energy incident on the body in the same time.
- The coefficient of reflection or reflectance or reflective power of the surface of a body is the ratio of the quantity of radiant energy reflected by the surface to the quantity of radiant energy incident on the surface in the same time.
- The coefficient of transmission or transmittance or transmissive power of a body is the ratio of the quantity of radiant energy transmitted by the body to the quantity of radiant energy incident on the body in the same time.
Let Q be the quantity of radiant energy incident on a body and Qa, Qr and Qt be the quantities of radiant energy absorbed, reflected and transmitted by the body respectively, in the same time. Since the total energy is conserved, we have,

Hence, a + r + t = 1
This is the required relation.
[Note : The coefficients of absorption, reflection and transmission are, respectively, the measures of the ability of the body or material to absorb, reflect or transmit radiation.
They are dimensionless quantities and have no units. They depend on the material and physical conditions of the body as well as on the frequency of the incident radiation.]
Question 32.
If for a certain body, under certain conditions, the coefficient of absorption is 0.2 and the coefficient of reflection is 0.5, what will be the coefficient of transmission ?
Answer:
In the usual notation, a + r +1 = 1
Hence, the coefficient of transmission of the body = 1 – (a + r) = 1 – (0.2 + 0.5) = 1 – 0.7 = 0.3.
Question 33.
Give four exmaples of
- athermanous substance
- diathermanous substances.
Answer:
- Water, wood, iron, copper, moist air, benzene are athermanous substances.
- Quartz, sodium chloride, hydrogen, oxygen, dry air, carbon tetrachloride are diathermanous substances.

Question 34.
A substance may be athermanous or diathermanous for certain wavelength ranges while good absorber for other wavelength ranges. Explain.
Answer:
For interaction of light with matter, it is necessary to consider the atomic nature of matter. Interaction of an atom with light depends on the frequency or equivalently on the photon energy.
An atom absorbs light if the photon’s energy equals one of the excitation energies of the atom. In the dense atomic neighbourhood of ordinary gases at pressures above 100 Pa, solids and liquids, the discrete atomic energy states widen into bands. Thus, bulk matter, depending on its nature, possesses absorption bands in specific regions within the electromagnetic frequency spectrum.
Radiant energy of other frequencies is elastically scattered so that the material is transparent at these frequencies.
[Note : Colourless, transparent materials have their absorption bands outside the visible region of the spectrum, which is why they are, in fact, colourless and transparent. Glasses have absorption bands in the ultraviolet region (~ 100 nm-200 nm), where they become opaque. At even longer wavelengths of radiowaves glass is again transparent. In comparison, a stained glass has absorption band in the visible region where it absorbs out a particular range of frequencies, transmitting the complementary colour. Semiconductors, such as ZnSe, CdTe, GaAs and Ge, which are opaque in the visible region of the spectrum are highly transparent in the infrared region (2 µm to 30 µm).]
Question 35.
In Fery’s blackbody, the hole is the blackbody but not the inner coated or outer sphere alone. Explain.
Answer:
Any space which is almost wholly closed – e.g., an empty closed tin can with a tiny hole punched-approximates to a blackbody. The hole is a good absorber and looks black because any light which enters through it is almost completely absorbed after multiple reflections inside. This absorption is quickened in Fery’s blackbody by the inner coat of lampblack. Thus, the hole acts as a perfect absorber.
Also, the relative intensities of radiation at different wavelengths is determined only by the temperature of the blackbody, not by the nature of its surfaces. This is so because the radiation coming out from a small part of the inner surface is made up of
- the radiation emitted by that area
- the radiation from other parts reflected at that area. Since the hole in Fery’s blackbody is very small, the radiations from the inner surface are well mixed up by reflection before they can escape. Hence, when Fery’s blackbody is placed in a high-temperature bath of fused salts, the hole serves as the source of blackbody radiation.
The outer surface of Fery’s blackbody is made highly reflective and lampblack too has a small coefficient of reflection. Hence, neither of them alone is a blackbody.
Question 36.
What is
(i) a cavity radiator
(ii) cavity radiation?
Answer:
(i) A cavity radiator is a block of material with internal cavity. The inner and outer surfaces of the block are connected by a small hole. Most of the radiant energy entering the block through the hole cannot escape from the hole. The block, therefore, acts almost like a blackbody.
(ii) When the cavity radiator is heated to high temperature, radiation coming out from the hole resembles blackbody radiation. It is called cavity radiation. It depends only on the temperature of the radiator and not on the shape and size of the cavity as well as the material of the walls of the cavity.
Question 37.
‘If r = 1, then it is a white body’. Is this true ? Explain.
Answer:
No.
Since a + r + t = l,a = 0 and t = 0 for r = 1. Therefore, by Kirchhoff’s law, e = a = 0 which is impossible as every body at temperature above 0 K does emit radiant energy, and T = 0 K is impossible.
A blackbody being a full radiator, when heated to high enough temperature it would emit thermal radiation at all the wavelengths and thus appear white. A perfect reflector (r = 1), on the other hand, is a poor emitter and thus would not necessarily appear white when heated.
Question 38.
State and explain Prevost’s theory of exchange of heat.
Answer:
In 1792, Pierre Prevost put forward a theory of exchange of heat. According to this theory, all bodies at all temperatures above the absolute zero temperature (0 K) radiate thermal energy to the surroundings and at the same time receive radiant energy from the surroundings. Thus, there is continuous exchange of radiant energy between a body and its surroundings.
The quantity of radiant energy (thermal energy) emitted by a body per unit time depends upon the nature of the emitting surface, the area of the surface and the temperature of the surface. The quantity of radiant energy absorbed by a body per unit time depends upon the nature of the absorbing surface, the area of the surface and the time rate at which the radiant energy is incident on the body.
If the time rate of emission of thermal energy is greater than the time rate of absorption of thermal energy, the temperature of the body falls. If the emission rate is less than the absorption rate, the temperature of the body increases. If the emission rate equals the absorption rate, the temperature of the body remains constant.
[Note : A body appears red if its temperature is around 800 °C, and white hot if its temperature is around 3000 °C]
Question 39.
Define
(1) emissive power or radiant power
(2) coefficient of emission of a body
Answer:
(1) Emissive power or radiant power of a body (symbol, R) : The emissive power or radiant power of a body at a given temperature is defined as the quantity of radiant energy emitted by the body per unit time per unit surface area of the body at that temperature.
(2) Coefficient of emission (or emissivity) of a body (symbol, e) : The coefficient of emission (or emissivity) of a body is defined as the ratio of the emissive power of the body (R) to the emissive power of a perfect blackbody (Rb) at the same temperature as that of the body.
e = \(\frac{R}{R_{\mathrm{b}}}\)
[Note : The SI unit and dimensions of emissive power are the watt per square metre (W/m2 Or Js-1m-2) and [M1L°T-3]. The coefficient of emission is a dimensionless and unitless quantity. For a perfect blackbody, e = 1 and for a perfect reflector, e = 0.]
Question 40.
If the emissive power of a certain body at a certain temperature is 2000 W/m2 and the emissive power of a perfect blackbody at the same temperature is 10000 W/m2, what is the coefficient of emission of the body?
Answer:
The coefficient of emission of the body,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{2000}{1000}\) = 0.2
Question 41.
State the characteristics of blackbody radiation spectrum.
Answer:
Characteristics of blackbody radiation spectrum :
- The emissive power Rλ for every wavelength λ increases with increasing temperature.
- Each curve has a characteristic form with a maximum for Rλ at a certain wavelength λm.
- λm depends on the absolute temperature of the body and, with increasing temperature, shifts towards shorter wavelengths, i.e., towards the ultraviolet end of the spectrum.
- λmT = a constant.
- The area under each curve gives the total radiant power per unit area of a blackbody at that temperature and is proportional to T4, (Stefan-Boltzmann law).
Notes :
- Experimental work on the distribution of energy in blackbody radiation, was carried out by German physicists Otto Lummer (1860-1925), Wilhelm Wien (1864-1928) and Ernst Pringsheim (1859-1917).
- Explanation of the radiation spectrum, given by Wien on the basis of thermodynamics could account only for the short wavelength region. The formula obtained by Rayleigh and Jeans, on the basis of the equipartition of energy could account only for long wavelength region. Planck’s empirical formula, put forward in 1900, could account for the entire spectrum.
Question 42.
State the significance of Wien’s displacement law.
Answer:
Significance :
- It can be used to estimate the surface temperature of stars.
- It explains the common observation of the change of colour of a solid on heating-from dull red (longer wavelengths) to yellow (smaller wavelengths) to white (all wavelengths in the visible region).
Question 43.
Explain the Stefan-Boltzmann law.
Answer:
The power per unit area radiated from the surface of a blackbody at an absolute temperature T is its emissive power or radiant power Rb at that temperature. According to the Stefan-Boltzmann law,
Rb ∝ T4 ∴ Rb = σT4
where the constant a is called Stefan’s constant.
If A is the surface area of the body, its radiant power, i.e., energy radiated per unit time, is AσT4.
[Note : This law was deduced by Josef Stefan (1835-93), Austrian physicist, from the experimental results obtained by John Tyndall (1820-93), British physicist. The theoretical derivation of this law is due to Boltzmann in 1884. Hence, the law is known as the Stefan- Boltzmann law.


Question 44.
What is the emissive power of a perfect black-body at 1000 K? (σ = 5.67 × 10-8 W/m2.K4)
Answer:
Rb = σT4 = 5.67 × 10-8 × (103)4
= 5.67 × 104\(\frac{\mathrm{W}}{\mathrm{m}^{2}}\) is the required emissive power.
Question 45.
In the above case (Question 43), if the body is not a perfect blackbody and e = 0.1, what will be the emissive power?
Answer:
R = eRh = 0.1 × 5.67 × 104 = 5.67 × 103\(\frac{\mathrm{W}}{\mathrm{m}^{2}}\)
Question 46.
Derive an expression for the net rate of loss of heat per unit area by a perfect blackbody in a cooler surroundings.
Answer:
Consider a perfect blackbody at absolute temperature T. We assume its surroundings also to act as a perfect blackbody at absolute temperature T0, where T0 < T.
The power per unit area radiated from the surface of a blackbody at temperature T is its emissive power Rb at that temperature. According to the Stefan-Boltzmann law,
Rb = σT4
where σ is the Stefan constant.
At the same time, the body absorbs radiant energy from the surroundings. The radiant energy absorbed per unit time per unit area by the black-body is \(\sigma T_{0}^{4}\).
Therefore, the net rate of loss of radiant energy per unit area by the blackbody is σ(T4 – \(T_{0}^{4}\)).
[Note : If the body at temperature T has emissivity e < 1, (i.e., it is not a perfect blackbody) the net rate of loss of radiant energy per unit area is eσ(T4 – \(T_{0}^{4}\)).]
Question 47.
Compare the rates of radiation of energy by a metal sphere at 600 K and 300 K.
Answer:
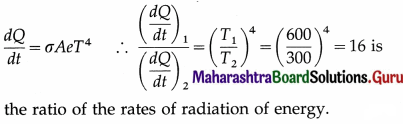
Question 48.
Solve the following :
Question 1.
Radiant energy is incident on a body at the rate of 2000 joules per minute. If the reflection coefficient of the body is 0.1 and its transmission coefficient is 0.2, find the radiant energy
(i) absorbed
(ii) reflected
(iii) transmitted by the body in 2 minutes.
Solution :
Data : r = 0.1, t = 0.2
a + r + t = 1
∴ a = 1 – r – f = 1 – 0.1 – 0.2 = 0.7
Radiant energy incident per minute on the body is 2000 J. Hence, in 2 minutes, the radiant energy (Q) incident on the body is 4000 J. Let Qa, Qr and Qt be the quantities of radiant energy absorbed, reflected and transmitted in 2 minutes by the body, respectively.
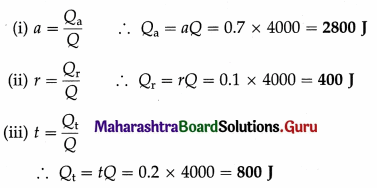
Question 2.
Heat is incident at the rate of 10 watts on a completely opaque body having emissivity 0.8. Find the quantity of radiant heat reflected by it in 1 minute.
Answer:
Data : e = 0.8, time =1 min =60 s, \(\frac{d Q}{d t}\)= 10 W
For a completely opaque body, t =0.
Also, a = e = 0.8
a + r + t = 1
∴ 0.8 + r + 0 = 1
∴ r = 1 – 0.8 = 0.2
Total radiant heat incident on the body in 1 minute
Q = \(\left(\frac{d Q}{d t}\right)\) × time = 10 × 60 = 600J
∴ The quantity of radiant heat reflected by the body in 1 minute is
Qr = rQ = 0.2 × 600 = 120J
Question 3.
A metal cube of side 2 cm emits 672 J of heat in 100 s at a certain temperature. Calculate its emissive power (radiant power) at that temperature.
Solution :
Data : L = 2 cm = 2 × 10-2 m, Q = 672 J, t = 100 s
The surface area of the cube is
A = 6L2 = 6(2 × 10-2)2 = 24 × 10-4 m2
The energy radiated by the cube is Q = RAt
where R ≡ emissive power (radiant power).
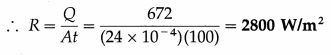
Question 4.
The energy of 6000 J is radiated in 5 minutes by a body of surface area 100 cm2. Find the emissive power (radiant power) of the body.
Solution :
Data : Q = 6000 J, t = 5 minutes = 5 × 60 s = 300 s,
A = 10 cm2 = 10 × 10-4 m2 = 10-3 m2
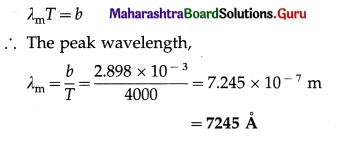
Emissive power (radiant power), R = \(\frac{Q}{A t}\)
= \(\frac{6000}{10^{-3} \times 300}\)
= 2000 J/m2.s 2000 W/m2
Question 5.
An ordinary body A and a perfect blackbody B are maintained at the same temperature. If the radiant power of A is 2 × 104 W/m2 and that of B is 5 × 104 W/m2, what is the coefficient of emission (emissivity) of A ?
Solution :
Data : R = 2 × 104 W/m2, Rb = 5 × 104 W/m2
The coefficient of emission (emissivity) of A,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{2 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}}{5 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}}\) = 0.4
Question 6.
A body of surface area 100 cm2 radiates energy 3000 J in 10 minutes at a certain constant temperature. The radiant power of a perfect blackbody maintained at the same temperature is 2500 W/m2. Find the the radiant power and emissivity of the body.
Solution:
Data : A = 100 cm2 = 100 × 10-4m2 = 10-2m2, t = 10 minutes = 10 × 60 s = 600 s, Q = 3000 J.
Rb = 2500 W/m2.
(i) The radiant power of the body,
R = \(\frac{Q}{A t}\) = \(\frac{3000 \mathrm{~J}}{\left(10^{-2} \mathrm{~m}^{2}\right)(600 \mathrm{~s})}\)
= 5 × 102 W/m2
(ii) The emissivity of the body,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{500 \mathrm{~W} / \mathrm{m}^{2}}{2500 \mathrm{~W} / \mathrm{m}^{2}}\) = 0.2
Question 7.
For a certain body, the coefficient of absorption (absorptive power, absorptivity) is 0.4. The body is maintained at a constant temperature. The radiant power of a perfect blackbody maintained at the same temperature is 5 × 104 W/m2. Find the radiant power of the body at that temperature.
Solution:
Data: a = 0.4, Rb = 5 × 104 W/m2
As the emissivity, e = a,
we have, e = 0.4
∴ R = eRb = (0.4) (5 × 104 W/m2)
= 2 × 104 W/m2
This is the required quantity.
Question 8.
Calculate the wavelength in angstrom at which the emissive power is maximum for a blackbody heated to 3727 °C.
[Wien’s constant, b = 2.898 × 10-3 m.K]
Solution :
Data : T = 3727 °C = 3727 + 273 = 4000 K,
b = 2.898 × 10-3 m.K
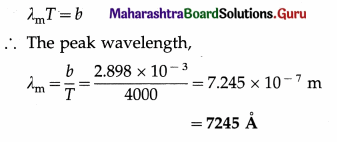
Question 9.
The maximum radiant power of the Sun is at wavelength 500 nm. The Wien displacement law constant is 2.898 × 10-3 m.K. Estimate the temperature of the surface of the Sun. Assume the Sun to be a blackbody radiator.
Solution :
Data : λm = 500 nm = 5 × 107 m, b = 2.898 × 10-3 m.K
By Wien’s displacement law,
λmT = b
∴ The estimated surface temperature of the Sun,
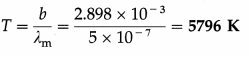

Question 10.
What is the peak wavelength of the radiation emitted by a blackbody at 35 °C ? [Wien’s displace-ment law constant, b = 2.898 × 10-3 m.K]
Solution :
Data : t = 35 °C, b = 2.898 × 10-3 m.K
The absolute temperature of the blackbody,
T = t + 273 = 35 + 273 = 308 K
By Wien’s displacement law, λmT = b
∴ The peak wavelength,
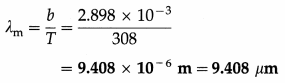
Question 11.
Calculate the emissive power of a perfect black-body at 127°C.
Solution:
Data: T = 127°C = (127 + 273) K = 400 K,
= 5.67 × 10-8 W/m2.K4
Emissive power, Rb = σT4
= 5.67 × 10-8 × (400)4
= 1.452 × 103 W/m2
Question 12.
What is the temperature at which a blackbody radiates heat at the rate of 1 kilowatt per square metre?
Solution :
Data : Rb = 1 kW/m2 = 1000 W/m2,
σ = 5.67 × 10-8 W/m2K4
Rb = σT4
∴ Temperature, T = \(\left(\frac{R_{\mathrm{b}}}{\sigma}\right)^{1 / 4}\)
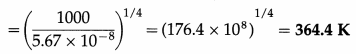
Question 13.
A perfect blackbody, maintained at 27 °C, radiates energy at the rate of 551.1 W. Find the surface area of the body.
Solution :
Data : dQ/dt = 551.1 W,
T = 27 °C = (27 + 273) K = 300 K,
σ = 5.67 × 10-8 W/m2.K4
Let A be the surface area of the body. Energy radiated per unit time,

Question 14.
Calculate the energy radiated in two minutes by a perfect black sphere of radius 2 cm, maintained at 427 °C.
Solution :
Data : T = 427 °C = (427 + 273) K = 700 K, r = 2 cm = 0.02 m, σ = 5.67 × 10-8 W/m2.K4, t = 2 minutes = 120 seconds
∴ A = 4πr2 = 4 × 3.142 × (0.02)2 = 5.027 × 10-3 m2
Energy radiated in time t = AσT4t
∴ Energy radiated in 120 seconds
= 5.027 × 10-3 × 5.67 × 10-8 × (700)4 × 120 J
= 8.212 × 103 J
Question 15.
The temperature of the filament of a 100 watt electric lamp is 2727 °C. Calculate its emissivity if the length of the filament is 8 cm and its radius is 0.5 mm.
Solution :
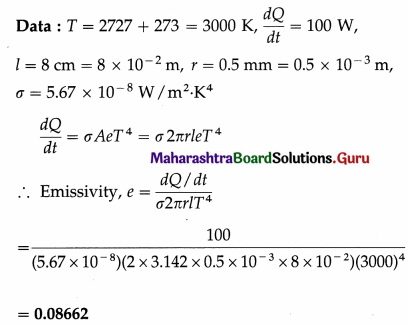
Question 16.
A 60 watt electric bulb loses its energy entirely by radiation from the surface of its filament. If the surface area of the filament is 4 cm2 and its coefficient of emission is 0.4, calculate the temperature of the filament.
Solution :
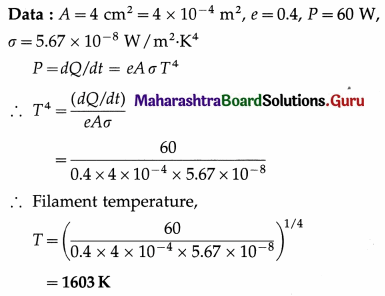
Question 17.
Energy is emitted from a hole in an electric furnace at the rate of 20 watts when the furnace is at 227 °C. Find the area of the hole.
Solution :
Data : T = 227 °C = (227 + 273) K = 500 K,
P = 20 W, σ = 5.67 × 10-8 W/m2.K4
Let A be the area at the hole. Then,
P = AσT4
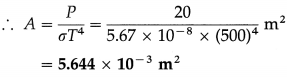
Question 18.
A body of surface area 10 cm2 and temperature 727 °C emits 300 J of energy per minute. Find its emissivity.
Solution :
Data : A = 10 cm2 = 10 × 10-4m2 = 10-3m2,
T = 273 + 727 = 1000 K, Q = 300 J,

Question 19.
A pinhole is made in a hollow sphere of radius 5 cm whose inner wall is at 727 °C. Find the power radiated per unit area. [Stefan’s constant, a = 5.7 × 10-8J/m2.s.K4, emissivity (e) = 0.2]
Solution :
Data : r = 5 × 10-2m, T = 727 + 273 = 1000 K, e = 0.2,
σ = 5.7 × 10-2 J/m2.s.K4
The power radiated per unit area, i.e., emissive power,
R = eσT4
= (0.2) (5.7 × 10-8) (103)4
= 1.14 × 10-8 × 1012 = 1.14 × 104 W/m2

Question 20.
A body of surface area 400 cm2 and absorption coefficient 0.5 radiates energy 1.5 kcal in 2 minutes when the temperature of the body is kept constant. Find the temperature of the body. (Given : J = 4186 J/kcal, σ = 5.67 × 10-8 J/s.m.K4)
Solution :
Data : A = 400 cm2 = 400 × 10-4 4 m2
= 4 × 10-2 m2, absorption coefficient, a = 0.8
But a = e ∴ e = 0.8, J = 4186 J/kcal
Q = 1.5 kcal = 1.5 × 4186 J = 6279 J,
t = 2 minutes = 120 s, σ = 5.67 × 10-8 J/s.m. K4
Energy radiated, Q = σ AeT4t
∴ 6279 = (5.67 × 10-8) × (4 × 10-2) × 0.8 × T4 × 120
∴ T4 = \(\frac{6279 \times 10^{8}}{21.77}\) = 288.4 × 108
∴ T = 4.121 × 102 K
This is the temperature of the body.
Question 21.
The filament of an evacuated light bulb has length 10 cm, diameter 0.2 mm and emissivity 0.2. Calculate the power it radiates at 2000 K. (a = 5.67 × 10-8 W/m2.K4)
Solution :
Data : 1 = 10 cm = 0.1 m, d = 0.2 mm
∴ r = 0.1 mm = 0.1 × 10-3 m, e = 0.2,
T = 2000 K, σ = 5.67 × 10-3 W/m2.K4
Surface area of the filament, A = 2πrl
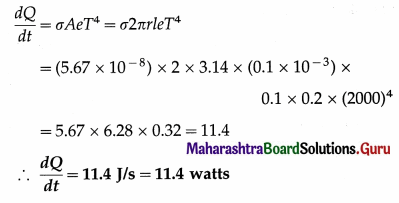
This is the required quantity.
Question 22.
A body of surface area 10 cm2 and temperature 727 °C emits 300 J of energy per minute. Find its emissivity.
Solution :
Data : A = 10 cm2 = 10 × 10-4 m2 = 10-3 m2,
T = 273 + 727 = 1000 K, Q = 300 J,
t = 1 minute = 60 s, σ = 5.67 × 10-8 J/m2.s.K4
Q = σAeT4t
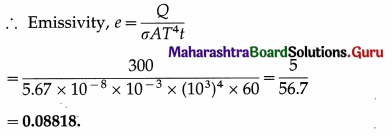
Question 23.
A metal cube of each side of length 1 m loses all its energy at the rate of 3000 watts. If the emissivity of the material of the cube is 0.4, estimate its temperature.
Solution :
Data : L = 1 m, e = 0.4, \(\frac{d Q}{d t}\) = 3000 W, dt
a = 5.67 × 10-8 W/m2.K4
Surface area of the cube, A = 6L2 = 6 m2
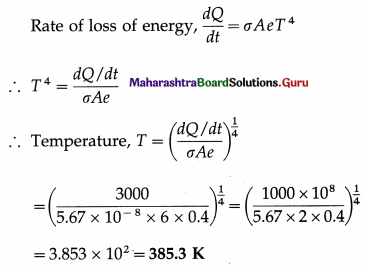
Question 24.
Assuming the Stefan-Boltzmann law, compare the rate of radiation from a metal ball at 727 °C with its rate of radiation at 527 °C. Also compare its rate of loss of heat at the two temperatures, if the temperature of the surroundings is 27 °C. Solution :
Data : T0 = 273 + 27 = 300 K,
T1 = 273 + 727 = 1000 K, T2 = 273 + 527 = 800 K
(i) Rate of radiation (radiant power),
P = σAeT4
If P1 and P2 are the radiant powers at the temperatures T1 and T2, respectively,
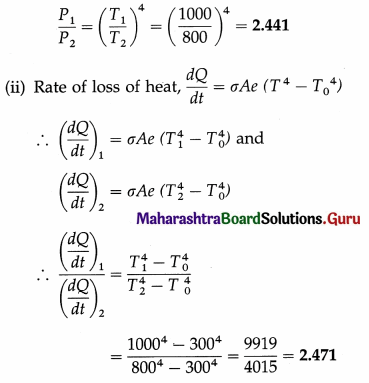
Question 25.
A black body at 1000°c radiates 14.89 watt per square centimetre of its surface. The surfaceof a certain star radiates 10 kW per square centimetre. Assuming that the star’s surface behaves as a perfect blackbody, estimate its temperature.
Solution:
Data: T1 = 273 + 1000 = 1273K,
R1 = 14.89 watt/cm2 = 14.89 × 104 watt/m2,
R2 = 10 kW/cm2 = 107 watt/cm2
Emissive power of a blackbody, R = σT4
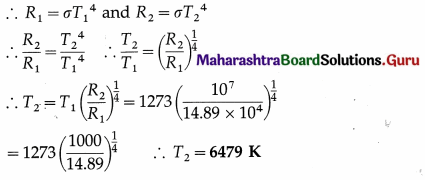
∴ This is the temperature of the star’s surface.
Question 26.
A blackbody with initial temperature of 300 °C is allowed to cool inside an evacuated enclosure surrounded by melting ice at the rate of 0.35 °C/second. If the mass, specific heat and surface area of the body are 32 grams, 0.10 cal/g °C and 8 cm2 respectively, calculate Stefan’s constant. (Take J = 4200 j/kcal.)
Solution :
Data : T = 273 + 300 = 573 K, T0 = 273 K,
\(\frac{d Q}{d t}\) = 0.35 °C/s = 0.35 K/s, at
M = 32 g = 32 × 10-3 kg, A = 8 cm2 = 8 × 10-4 m2 C = 0.10 cal/g.°C = 0.10 kcal/kg.K = 420 j/kg.K
since J = 4200 J/kcal
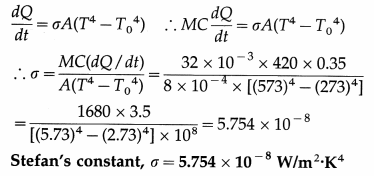
Question 27.
A blackbody at 327 °C, when suspended in a black enclosure at 27 °C, loses heat at a certain rate. Find the temperature of the body at which its rate of loss of heat by radiation will be half of the above rate. Assume that the other conditions remain unchanged.
Solution :
Data : T1 = 273 + 327 = 600 K, T0 = 273 + 27 = 300 K,

Question 49.
Choose the correct option.
Question 1.
The rms speed of a gas molecule is directly proportional to
(A) its absolute temperature
(B) the square root of its absolute temperature
(C) the square of its absolute temperature
(D) its molar mass.
Answer:
(B) the square root of its absolute temperature
Question 2.
Temperature remaining constant, if you double the number of molecules in a box, the pressure will
(A) remain unchanged
(B) double
(C) become one-half
(D) quadruple.
Answer:
(B) double
Question 3.
The pressure P of an ideal gas having volume V is \(\frac{2 E}{3 V}\). Then E is
(A) translational kinetic energy
(B) rotational kinetic energy
(C) vibrational kinetic energy
(D) potential energy.
Answer:
(A) translational kinetic energy
Question 4.
According to the kinetic theory of gases, at a given temperature, molecules of all gases have the same
(A) rms speed
(B) momentum
(C) energy
(D) most probable speed.
Answer:
(C) energy

Question 5.
The kinetic energy per molecule of a gas at temperature T is
(A) \(\frac{3}{2} R T\)
(B) \(\frac{3}{2} k_{\mathrm{B}} T\)
(C) \(\frac{2}{3} R T\)
(D) \(\frac{3}{2} \frac{R T}{M_{0}}\)
Answer:
(B) \(\frac{3}{2} k_{\mathrm{B}} T\)
Question 6.
When the temperature of an enclosed gas is increased by 2 °C, its pressure increases by 0.5%. The initial temperature of the gas was
(A) 250 K
(B) 275 K
(C) 300 K
(D) 400 K.
Answer:
(D) 400 K.
Question 6.
For a given gas at 800 K, the rms speed of the ‘ molecules is
(A) four times the rms speed at 200 K
(B) half the rms speed at 200 K
(C) twice the rms speed at 200 K
(D) twice the rms speed at 400 K.
Answer:
(C) twice the rms speed at 200 K
Question 7.
If the absolute temperature of a gas becomes three times the initial absolute temperature, the rms speed of the gas molecules
(A) becomes \(\frac{1}{3}\) times the initial rms speed
(B) becomes \(\frac{1}{\sqrt{3}}\) times the initial rms speed
(C) becomes \(\sqrt{3}\) times the initial rms speed
(D) becomes 3 times the initial rms speed.
Answer:
(C) becomes \(\sqrt{3}\) times the initial rms speed
Question 8.
An ideal gas occupies 2 m3 at a pressure of 2 atm. Taking 1 atm = 105 Pa, the energy density of the gas is
(A) 3 × 105 J/m3
(B) 1.5 × 105 J/m3
(C) 300 J/m3
(D) 150 J/m3.
Answer:
(A) 3 × 105 J/m3
Question 9.
An ideal gas is confined to a cylinder with a movable piston. As it is heated to twice its initial absolute temperature, the gas is allowed to expand freely against the atmospheric pressure. The average thermal energy of the molecules
(A) quadruples
(B) doubles
(C) increases by a factor of \(\sqrt{2}\)
(D) remains unchanged.
Answer:
(B) doubles
Question 10.
Equal volumes of hydrogen and oxygen (relative molar masses 2 and 32, respectively) in separate containers are equimolar and exert equal pressure. The rms speeds of hydrogen and oxygen molecules are in the ratio
(A) 1 : 32
(B) 1 : 16
(C) 1 : 4
(D) 4 : 1.
Answer:
(D) 4 : 1.
Question 11.
At what temperature will the rms velocity of a gas molecule be double its value at NTP ?
A) 273 °C
(B) 546 °C
(C) 819 °C
(D) 1092 °C.
Answer:
(C) 819 °C
Question 12.
The rms speed of the molecules of a gas is 200 m/s at 27 °C and 1 atmosphere pressure. The rms speed at 127 °C and double the pressure is
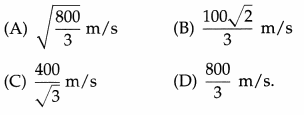
Answer:
(C) \(\frac{400}{\sqrt{3}}\) m/s
Question 13.
The temperature at which helium molecules have the same rms speed as hydrogen molecules at STP is
[MoH = MoHe = 4g/mol]
A) 1092 K
(B) 546 K
(C) 300 K
(D) 273 K.
Answer:
(B) 546 K
Question 14.
The number of degrees of freedom for a rigid diatomic molecule is
(A) 3
(B) 5
(C) 6
(D) 7
Answer:
(B) 5
Question 15.
For polyatomic molecules having / vibrational modes, the ratio of two specific heats is
Answer:
(C) \(\frac{4+f}{3+f}\)
Question 16.
A nonlinear triatomic molecule has …… degree(s) of freedom of rotational motion.
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
(D) 3
Question 17.
The wavelength range of thermal radiation is
(A) from 4000 Å to 7000 Å
(B) from 7700 Å to 4 × 106 Å
(C) from 106 Å to 108 Å
(D) from 4 × 10-12 Å to 4 × 108 Å.
Answer:
(B) from 7700 Å to 4 × 106 Å
Question 18.
The coefficient of reflection of a perfectly opaque body is 0.16. Its coefficient of emission is
(A) 0.94
(B) 0.84
(C) 0.74
(D) 0.64.
Answer:
(B) 0.84
Question 19.
Which of the following materials is diathermanous ?
(A) Wax
(B) Glass
(C) Quartz
(D) Porcelain
Answer:
(C) Quartz
Question 20.
Which of the following substances is opaque to radiant energy?
(A) Carbon tetrachloride
(B) Sodium chloride
(C) Benzene
(D) Potassium bromide
Answer:
(C) Benzene
Question 21.
The substance which allows heat radiations to pass through it is
(A) iron
(B) water vapour
(C) wood
(D) dry air.
Answer:
(D) dry air.
Question 22.
A perfect blackbody is the one that
(A) absorbs all incident radiation
(B) reflects all incident radiation
(C) transmits all incident radiation
(D) both reflects and transmits incident radiation.
Answer:
(A) absorbs all incident radiation
Question 23.
The conical projection in Fery’s blackbody is
(A) used to support the spheres
(B) used to transmit incident radiation to outer sphere
(C) used to prevent reflected radiation to escape outside
(D) used for all of the above purposes.
Answer:
(C) used to prevent reflected radiation to escape outside
Question 24.
The emissive power of a body is
(A) the energy emitted by the body in a given time
(B) the radiant energy emitted by the body per unit area of the body
(C) the radiant energy emitted by the body per unit time
(D) the radiant energy emitted by the body per unit time per unit area of the body.
Answer:
(D) the radiant energy emitted by the body per unit time per unit area of the body.
Question 25.
The dimensions of emissive power are
(A) [M1L-2T-3]
(B) [M1L2T-3]
(C) [M1L0T-3]
(D) [M1L0-2]
Answer:
(C) [M1L0T-3]
Question 26.
The emissive power per wavelength interval Rλ of a blackbody at an absolute temperature T1 is maximum at λ1 = 1.1 µm. At an absolute temperature T2, its Rλ is maximum at λ2 = 0.55 µm. Then, \(\frac{T_{1}}{T_{2}}\) is equal to
(A) \(\frac{1}{2}\)
(B) 1
(C) 2
(D) 4.
Answer:
(A) \(\frac{1}{2}\)
Question 27.
The temperature of the photosphere of the Sun is about 6000 K. Wien’s displacement law constant is 2.898 × 10-3 m.K. The photosphere has maximum emissive power at wavelength
(A) 483 nm
(B) 496.7 nm
(C) 4830 nm
(D) 4967 nm.
Answer:
(A) 483 nm
Question 28.
A sphere and a cube made of the same metal have equal volumes, identical surface characteristics and are at the same temperature. If they are allowed to cool in identical surroundings, the ratio of their rates of loss of heat will be
(A) \(\frac{4 \pi}{3}\) : 1
(B) 1 : 1
(C) \(\left(\frac{\pi}{6}\right)^{\frac{2}{3}}\) : 1
(D) \(\left(\frac{\pi}{6}\right)^{\frac{1}{3}}\) : 1
Answer:
(D) \(\left(\frac{\pi}{6}\right)^{\frac{1}{3}}\) : 1
Question 29.
If the absolute temperature of a blackbody is increased by a factor 3, the energy radiated by it per unit time per unit area will increase by a factor of
(A) 9
(B) 27
(C) 81
(D) 243.
Answer:
(C) 81

Question 30.
Two spheres P and Q, having radii 8 cm and 2 cm, and of the same surface characteristics are maintained at 127 °C and 527 °C, respectively. The ratio of the radiant powers of P to Q is
(A) 0.0039
(B) 0.0156
(C) 1
(D) 2.
Answer:
(C) 1
Question 31.
Two copper spheres of radii 6 cm and 12 cm, respectively, are suspended in an evacuated enclosure. Each of them is at a temperature of 15 °C above the surroundings. The ratio of their rate of loss of heat is
(A) 2 : 1
(B) 1 : 4
(C) 1 : 8
(D) 8 : 1.
Answer:
(B) 1 : 4
Question 32.
The peak of the radiation spectrum of a blackbody occurs at 2 µn. Taking Wien’s displacement law constant as 2.9 × 10-3 m.K, the approximate temperature of the blackbody is
(A) 15 K
(B) 150 K
(C) 750 K
(D) 1500 K.
Answer:
(D) 1500 K.
Question 33.
The light from the Sun is found to have a maximum intensity near the wavelength of 470 nm. Assuming the surface of the Sun as a blackbody, the temperature of the Sun is [Wien’s constant b = 2.898 × 10-3 m.K]
(A) 5800 K
(B) 6050 K
(C) 6166 K
(D) 6500 K.
Answer:
(C) 6166 K
Question 34.
The amount of energy radiated per unit time by a body does not depend upon the
(A) nature of its surface
(B) area of its surface
(C) mass of the body
(D) temperature difference of the surface and surroundings.
Answer:
(C) mass of the body
Question 35.
Two gases exert pressure in the ratio 3 : 2 and their densities are in the ratio 2 : 3. Then the ratio of their rms speeds is
(A) 2 : 3
(B) 3 : 2
(C) 2 : 1
(D) 1 : 2.
Answer:
(B) 3 : 2
Question 36.
Find the wavelength at which a blackbody radiates maximum energy, if its temperature is 427 °C.
[Wien’s constant b = 2.898 × 10-3 m.K]
(A) 0.0414 × 10-6 m
(B) 4.14 × 10-6 m
(C) 41.4 × 10-6 m
(D) 414 × 10-6 m
Answer:
(B) 4.14 × 10-6 m
Question 37.
If the total kinetic energy per unit volume of gas enclosed in a container is E, the pressure exerted by the gas is
(A) E
(B) \(\frac{3}{2}\)E
(C) \(\sqrt{3}\)E
(D) \(\frac{2}{3}\)E.
Answer:
(D) \(\frac{2}{3}\)E.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()