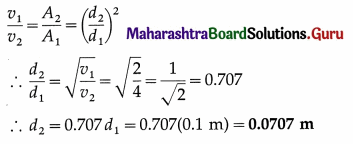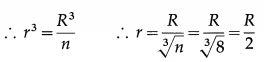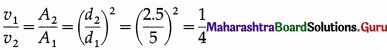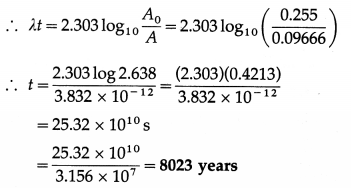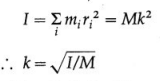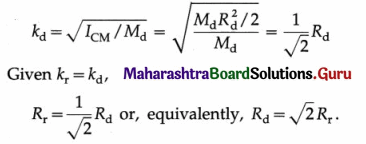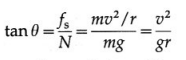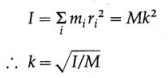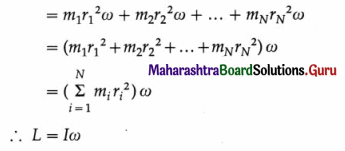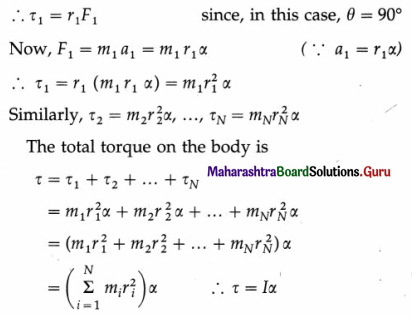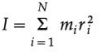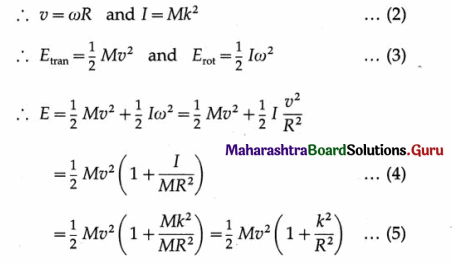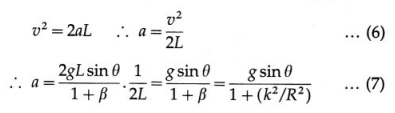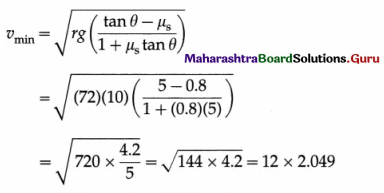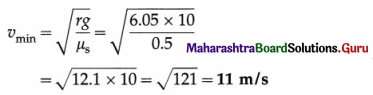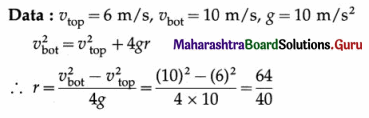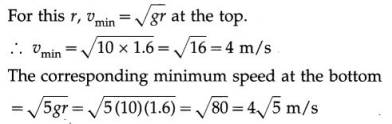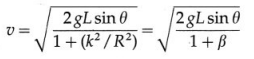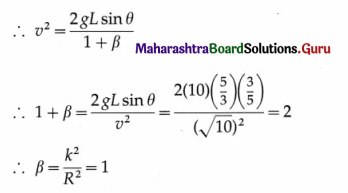Class 12

Balbharti Yuvakbharati English 12th Digest Chapter 4.4 The Sign of Four Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 4.4 The Sign of Four

12th English Digest Chapter 4.4 The Sign of Four Textbook Questions and Answers

CHARACTER:

(A1)

Question (i)
Read the extract again and complete the web by highlighting the qualities of the following characters:


Answer:

Question (ii)
Describe the character of Mary Morstan from Dr. Watson’s point of view.
Answer:
From Dr. Watson’s point of view: When I first saw Mary, she was dressed simply but tastefully. I could see that she was a person of limited means. Her expression was sweet and pleasant, and I could make out that her nature was refined and sensitive. My calculations told me that she was about 27 years old. She was agitated by the mystery surrounding her life. I found her attractive, though her face did not have regular features or a beautiful complexion. Her eyes showed that she was a sympathetic person. I was much impressed by her and attracted to her.

Question (iii)
Sherlock Holmes is the leading character in the extract. Explain.
Answer:
It is Sherlock Holmes who is the detective and the leading character. Mary Morstan had come to ask his advice about a problem that she was facing. Holmes was the one who took the lead and found out about Major Sholto; it was Holmes who analysed the handwriting in the letter that Mary had received. Holmes was sharp, accurate, intelligent and methodical. He had an excellent record of solving cases, and his deductions were always correct. Watson was merely his friend who helped him and kept a record of his cases.

Question (iv)
Dr. Watson, the narrator, is one of the major characters in the novel. Illustrate.
Answer:
Dr. Watson is the narrator. He was present when the case was brought to Holmes by Mary Morstan. He is generally always with Holmes, helping him to solve cases. He accompanied Holmes whenever necessary.

He also kept a record of all the cases that Holmes was a part of. In this extract, he is present when Mary recounts her case, and he accompanies Holmes and Mary to meet the writer of the anonymous letter. (He marries Mary in the end.)

Question (v)
Holmes is always one step ahead of Dr. Watson in solving cases. Elucidate.
Answer:
Where Watson is emotional, simple and trustful, Holmes is sharp, objective and methodical. Holmes is also analytical and notices the little details which give him clues to solving a case. Watson does not, and hence is often on the wrong track. Holmes is the real detective, while Watson is merely his companion. Holmes is always ahead of Watson and solves cases which Watson is not even near to cracking.

PLOT:

(A2)

Question (i)
Arrange the sentences in correct sequence as per their occurrence in the extract.
Answer:

Jumbled Incidents	Correct Sequence
1. Holmes put a revolver in his pocket.	(a) Mary Morstan was a well-dressed young lady.
2. Holmes gave Winwood’s book ‘Martyrdom of Man’ to Dr. Watson.	(b) Mary’s father was an officer in an Indian regiment.
3. Mary received a large and lustrous pearl through the post.	(c) Mary received a large and lustrous pearl through the post.
4. Mary’s father was an officer in an Indian regiment.	(d) Holmes gave Winwood’s book ‘Martyrdom of Man’ to Dr. Watson.
5. Mary Morstan was a well-dressed young lady.	(e) Holmes put a revolver in his pocket.

(ii) Discuss the importance of the following statements from the light of the extract.

Question (a)
The trio-Holmes, Dr. Watson and Mary decide to visit Lyceum Theatre.
Answer:
Mary had received an anonymous letter asking her to be outside the Lyceum Theatre on a particular night at seven o’clock. The letter said that it would be to Mary’s advantage if she came. The letter also mentioned that she could bring two friends with her. However, she did not have any friends who could accompany her, and so she asked Holmes and Watson if they could do so. They agreed. Hence, Holmes, Dr. Watson and Mary decide to visit Lyceum Theatre. This was the first step to solving the case.

Question (b)
Mary received pearls every year on the same day.
Answer:
Major Sholto, Mary’s father’s friend, had cheated Mary’s father of his share in the Agra treasure. When he died, Major Sholto informed his son Thaddeus of this. Though Thaddeus did not have the treasure, he tried to rectify the matter to a certain extent by sending Mary a rare and expensive pearl every year, on the same day as he sent the first one.

Question (c)
Holmes carefully examined the paper given by Mary.
Answer:
Mary had found a curious paper in her father’s desk which no one could understand. Holmes deduced from the colour of the paper that it was an important document. He felt it was related in some way to the mystery on hand. Hence, he examined it carefully to get some clues which would help to solve the mystery.

SETTING:

(A3)

Question (i)
Cite various references (lines) from the extract that tell us about the time and period of the events:
Answer:

Lines	Time and period
1. He disappeared upon the 3rd of December, 1878. – nearly ten years ago.	Mary’s father had disappeared about ten years before she met Holmes and Watson on a particular day.
2. About six years ago – to be exact, upon the 4th of May, 1882 – an advertisement appeared in the Times asking for the address of Miss Mary Morstan. The same day there arrived through the post a small card-board box addressed to me, which I found to contain a very large and lustrous pearl.	Mary first received an expensive and rare pearl six years before she received an anonymous letter/before she came to meet Holmes.
3. This morning I received this letter, which you will perhaps read for yourself.	Mary receives an anonymous letter on the morning of the day on which she consults Holmes.
4. Major Sholto, of Upper Norword, late of the 34th Bombay Infantry, died upon the 28th of April, 1882. Within a week of his death Captain Morstan’s daughter receives a valuable present, which is repeated from year to year.	Mary begins to receive the pearls immediately after Major Sholto’s death.
5. At the Lyceum Theatre the crowds were already thick at the side-entrances. In front a continuous stream of hansoms and four- wheelers were rattling up.	Holmes, Watson and Mary reach the Lyceum Theatre on the evening of the day Mary receives the anonymous letter, as instructed by the writer of the letter. This was in the year 1888.
6. We had hardly done so before the driver whipped up his horse, and we plunged away at a furious pace through the foggy streets.	This happens when Holmes, Watson and Mary are taken by the driver to meet the writer of the anonymous letter, on the evening when Mary receives it.
7. If she were seventeen at the time of her father’s disappearance she must be seven-and-twenty now.	Watson, who is attracted to Mary, calculates that Mary must be twenty -seven years old in 1888 when she meets him and Holmes.
8. In the year 1878 my father, who was senior captain of his regiment, obtained twelve months’ leave and came home.	This was the time, ten years earlier, when Captain Morstan disappeared.

Question (ii)
Explain by citting references from the extract the ways the series of actions moves from London to India.
Answer:
The extract begins when Mary Morstan meets Sherlock Holmes at his house in London. They then meet Thaddeus Sholto in a rundown neighbourhood of London. Thaddeus reveals that his father Major Sholto had mistakenly killed Captain Morstan in London. They then go to Bartholomew Sholto’s house to get the treasure; however, Bartholomew is found dead.

Holmes follows Jonathan Small and Tonga, who have escaped by a steam launch, over the river Thames in London. When Small is captured, he tells them about the time he spent in India, where he was an accomplice in stealing the Agra treasure. Thus, the narration goes to India. Major Sholto and Captain Morstan were also at one time stationed in India.

Question (iii)
The extract begins when Mary Morstan meets Sherlock Holmes at his house. After that Holmes, Dr.Watson and Mary visit some places in London. Explain in detail the various places mentioned in the extract.
Answer:
Holmes, Dr.Watson and Mary were taken down the Strand, which was crowded, badly lit and humid. All kinds of people-sad, happy, old and young could be seen moving about in the dim light. Watson found it eerie and ghostlike, and he felt nervous and depressed. They then reached the Lyceum Theatre, where the crowds were pouring in.

A continuous stream of horse carriages could be seen, with stylish people getting out of them. Near the Lyceum Theatre they were met by a coachman who took them in his coach through Rochester Row and Vincent Square onto Vauxhall Bridge Road. They were on the Surrey side, on the bridge from where they got glimpses of the river Thames with lamps shining on the silent water.

The cab then took them through a maze of streets. Holmes could identify Wordsworth Road, Priory Road, Lark Hall Lane, Stockwell Place, Robert Street and Cold Harbor Lane. They were all rundown places. The cab took them further to a rather grim and shady neighbourhood with dull brick houses and cheap and showy public houses at the corner.

Holmes mentions that this was not a very fashionable or rich neighbourhood. This was followed by rows of two-storied villas each with a small front garden, and then again there were never-ending lines of new brick buildings, which were an extension of the city. The houses in the area were all dark and appeared uninhabited.

At last the cab drew up at the third house in a new terrace, which was also dark except for a light in the kitchen. However, when they knocked the door was opened instantly, and an Oriental figure of a servant clad in a yellow turban, white loose-fitting clothes, and a yellow sash stood there. It was strange to find an Oriental figure framed in the doorway of a cheap suburban house.

Question (iv)
Basically the setting of the extract is in London but it has some references of India, too. Explain how the settings of the extract contribute to the theme of the novel.
Answer:
The setting of the extract is in London, where Mary meets Holmes and Watson to explain her problem. She talks about her father being an officer in an Indian regiment. When he returned to England on leave, he called Mary to meet him at a London hotel, but disappeared mysteriously before she could do so. His only friend in London was a Major Sholto. Holmes finds that Major Sholto was also from the 34th Bombay Infantry.

Mary shows Holmes a piece of paper belonging to her father. The paper was of Indian origin, and three of the names written on it were also Indian. Holmes, Watson and Mary go to meet the anonymous letter writer at a rundown suburban house in London. Later they chase Jonathan Small and Tonga, who were trying to escape by boat on the river Thames. When Jonathan Small was captured, he spoke of being an accomplice in stealing the Agra treasure.

He was sent to the Andaman Islands, where Major Sholto and Captain Morstan were prison guards. At the end of the extract, the door of the anonymous letter writer’s house was opened by an Indian servant. His master used an Indian name to call him. Thus, we have a mingling of incidents both in London as well as in India, where the case had its roots.

Question (v)
Describe in brief the importance of the following places in the extract.
(a) London
(b) Lyceum Theatre
(c) Edinburgh
(d) Agra
(e) Andaman Islands
Answer:
(a) London: The case starts here with Mary Morstan meeting Holmes at his place in London. They go to meet Thaddeus Sholto in London. They also chase Jonathan Small and Tonga in London. Tonga is killed and Small captured. Small then narrates the entire story.

(b) Lyceum Theatre: This is the place near which the writer of the anonymous letter told Mary Morstan to reach if she wished to get justice.

(c) Edinburgh: Mary spent her childhood till she was seventeen at a boarding school in Edinburgh.

(d) Agra: When Jonathan Small was standing guard one night at the Agra fortress, he was overpowered by two Sikh troopers, who forced him to waylay a servant of a Rajah and steal a valuable fortune in pearls and jewels. This was called the ‘Agra treasure’.

(e) Andaman Islands: Jonathan Small was arrested and imprisoned on the Andaman Islands for the robbery of the Agra treasure. After 20 years, Small made a deal with John Sholto and Arthur Morstan, who were the prison guards. Sholto would recover the treasure and in return send a boat to pick up Small and the Sikhs. Sholto double-crossed both Morstan and Small and stole the treasure for himself. Small vowed vengeance and four years later escaped from the Andaman Islands with an islander named Tonga after they both killed a prison guard.

Question (vi)
Complete:
Name the places/cities in India and England which are mentioned/have appeared in the extract. Describe their importance.
Answer:

India	Importance	London	Importance
Andaman Islands	Major Sholto and Captain Morstan were stationed here and in charge of the troops; Jonathan Small was also imprisoned here.	Baker Street	The residence of Sherlock Holmes and Dr. Watson. This was the place which Mary Morstan came to, to consult Holmes.
Agra	Jonathan Small was a gatekeeper at the Agra fortress when he was forced to be an accomplice in the theft of the Rajah’s jewels.	Langham Hotel	This was the place Mary’s father stayed at when he came to London. He invited Mary to the hotel to meet him; but disappeared before her arrival.
Bombay (Now Mumbai)	Major Sholto, and Captain Morstan were both from the regiment ‘the 34th Bombay Infantry’.	Lyceum Theatre	Mary was supposed to meet the writer of the anonymous letter or his messenger at the third pillar from the left outside the Lyceum Theatre.
–	–	River Thames	Jonathan Small, who tried to escape by boat along the river Thames, was captured. His accomplice Tonga was killed.

THEME:

(A4)

Question (i)
Write in brief the theme of the extract.
Answer:
The theme of the extract revolves round the mystery of the disappearance of Mary Morstan’s father, the receipt of expensive pearls by Mary and the mysterious letter received by her. It also involves the journey of Holmes, Watson and Mary Morstan to a strange house to meet the writer of the mysterious letter. The theme of the novel revolves around the Agra treasure.

Question (ii)
Write 4-5 sentences about the meeting of Miss Morstan with Holmes.
Answer:
Miss Morstan met Holmes and Watson at their house in Baker Street. She then discussed with them the mysterious disappearance of her father a few years earlier, the receipt of an expensive pearl every year for the past six years, and the receipt of a mysterious letter that morning asking her to meet the writer of the letter. Miss Morstan was intensely agitated and confused and did not know what to do. She showed Holmes the pearls, the boxes in which they had come and the letter. Then they planned to follow the instructions and meet the writer of the letter.

Question (iii)
Write the central idea of the given extract of the novel, “The Sign of Four”.
Answer:
The central idea is the meeting of Mary Morstan with Holmes and Watson, and her explanation of her problems. It is also about the short trip made by the three to meet I the writer of the mysterious letter. This is Watson’s first meeting with Miss Morstan and his attraction towards her.

Question (iv)
Complete the following giving reasons:
Answer:
(a) Miss Morstan plans to meet Sherlock Holmes to ask his advice about the disappearance of her father, the receipt of expensive pearls and the mysterious letter received by her.

(b) Miss Morstan gives the reference of Mrs. Cecil Forrester because Mrs. Cecil Forrester was her employer, whom Holmes had once helped to solve a domestic complication. Mrs. Forrester had been impressed by his kindness and skill.

(c) It’s a singular case because Miss Morstan’s father had come back to England and contacted her, and had seemed happy. After fixing a meeting ; with her at his hotel, he had suddenly ; disappeared and was never seen again, Even his only friend in town, Major Sholto, had not known either of his ; arrival or disappearance.

(d) Holmes needed some references to find out details about Major Sholto, who was the only friend Mary’s father had in England, and who had said that he did not know about his arrival in England.

(e) Miss Morstan received a pearl every year, when she replied to an advertisement asking for her address, adding that it would be to her advantage.

(f) The coachman confirmed that neither of Miss Morstan’s companion was a police officer because this was the condition made by the writer of the mysterious letter, whom they were going to meet.

LANGUAGE:

(A5)

(i) Elaborate the following lines in the light of the novel/extract, “The Sign of Four”:

Question (a)
“You really are an automaton – a calculating machine”.
Answer:
These words are said by Watson to Holmes when Mary Morstan had left after discussing her case. Watson is attracted to her and full of admiration for her. When he voices his admiration, Holmes says that he had not noticed if she is attractive or not. Watson is indignant and calls him a calculating machine.

Question (b)
“The letter speaks of giving her justice.”
Discuss.
Answer:
These are the words of Holmes to Watson, when they are discussing the letter that Mary Morstan has received from an unknown person. He wondered what was the ‘justice’ that the letter spoke of, and who had done ’ something wrong to Mary that she now needed justice.

Question (c)
“Our quest does not appear to take us to very fashionable regions.”
Answer:
These words are said by Holmes to Watson and Mary Morstan, when they are being driven by the coachman to some strange place. They were going through narrow streets in an unfriendly and grim neighbourhood, which had dull brick rows of houses and cheap and showy public houses at the comer. Holmes mentions that this was not a very fashionable or rich neighbourhood.

Question (ii)
Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, style, significance, etc. of the dialogue.
Answer:

Dialogue	Speaker	To whom it is said	Tone, Style, Significance etc.
1.  “… you have once enabled my employer, Mrs. Cecil Forrester, to unravel a little domestic omplication. She was much impressed by your kindness and skill.”	Miss Morstan	Sherlock Holmes	Polite, cultured. Mary proves her identity, and how she came to know about Sherlock Holmes.
2. “You will, I am sure, excuse me.”	Watson	Miss Morstan and Sherlock Holmes	Polite and courteous; Watson wants to make a good impression on Miss Morstan, and doesn’t want to poke his nose if he is not wanted.
3. “Your statement is most interesting. Has anything else occurred to you?”	Sherlock Holmes	Miss Morstan	Polite tone, acknowledging the story told by Miss Morstan, and trying to get further information.
4. “Are you the parties who come with Miss Morstan?”	A coachman/  messenger sent by the letter-writer.	Sherlock Holmes and Watson	Firm but respectful; cautious and asking for affirmation; shows that the person who had invited Miss Morstan was being very cautious, and checking them out.
5. “The Sahib awaits you.”	Khitmutgar (a male servant)	Miss Morstan, Sherlock Holmes and Watson	Respectful, formal. Shows some connection with the east, especially India.

 

Balbharti Yuvakbharati English 12th Digest Chapter 4.3 Around the World in Eighty Days Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 4.3 Around the World in Eighty Days

12th English Digest Chapter 4.3 Around the World in Eighty Days Textbook Questions and Answers

CHARACTER:

(A1)

Question (i)
One of the following is not a major character of the novel. Choose the correct one and justify.
(Select the correct one.)
(a) Phileas Fogg
(b) Aouda
(c) James Strand
(d) Jean Passepartout
Answer:
James Strand is not a major character of the novel. He was the real bank robber whom Fix was searching for.

Question (ii)
Complete the table highlighting the various traits of the major characters in the extract.
Answer:

1. Phileas Fogg	A solitary person; cared little about the opinions of others; honest, courageous, calm, honourable, proud; he had plenty of self-respect; was unselfish, non-materialistic, obstinate, generous.
2. Aouda	Grateful, loving, concerned, sincere, sweet, noble, unselfish, non-materialistic, generous.
3. Passepartout	Loyal,  faithful, grateful, loving, concerned, unselfish, repentant, conscientious.
4. Detective Fix	Dutiful, stupid, repentant, unimaginative, stubborn.

Question (iii)
Phileas Fogg is as cool as a cucumber whereas Passepartout is as crazy as a loon. Explain the statement by citing some references from the extract.
Answer:
Phileas Fogg was always cool except when he hit the detective Fix. He was cool and calm in prison. Even when he felt that he had lost the wager, he shut himself up in his house quietly without any noise. He was cool when dealing with Passepartout, and also when dealing with Aouda. He could control his emotions and appear to be expressionless. Passepartout, on the other hand was a very emotional and excitable person. He was very repentant when he realized that he could have prevented Fogg’s arrest; he was thrilled when he knew that Fogg was marrying Aouda.

He was tremendously worried about Fogg when he thought that Fogg had lost the wager. Finally, when he came to know that they had reached earlier than they had thought and there was a chance that they could reach the Reform Club in time to win the bet, he became very excited. He rushed back breathlessly to inform Fogg of the fact that it was Saturday and not Sunday.

Question (iv)
Detective Fix tried hard but could not fix the charge of robbery on Fogg. Explain the statement from the point of view of Fix.
Answer:
From the point of view of Detective Fix : Scotland Yard had given only a vague description of the man who had robbed a great sum from the bank of England. I thought that Fogg fitted the description and he was the bank robber. I put obstacles in Fogg’s path just so that I could arrest him whenever I got the warrant from England. The moment we reached Liverpool, I arrested him. However, after arresting him, I found that he was not the guilty person, and the robber had already been arrested in Edinburgh some days earlier.

Fogg was a respectable gentleman living at Saville Row. There was no proof and no evidence against him except that he had been travelling all over the world apparently without any purpose. I was sorry that I arrested him wrongly and I apologized to him.

Question (v)
Describe the character sketch of Aouda from Fogg’s point of view.
Answer:
From Fogg’s point of view: Aouda has had a very difficult time in India. She was nearly killed by her persecutors, but I, Fogg, managed to save her and bring her to England with me. She is a wonderful person and so grateful for what I did. She was even apologetic for having delayed my return – she did not think about the danger she was in from her persecutors! She is very loving. She is not at all money-minded and was ready to marry me even though I did not have a penny to my name. How many will do this? What a compassionate, kind-hearted and generous person! An admirable woman, indeed, and one whom I am proud to have as my wife.

PLOT:

(A2)

Question (i)
Arrange the incidents in correct sequence as per their occurrence in the extract.
(a) Aouda accepted Fogg’s proposal of marriage.
(b) When set free, the first thing that Fogg did was he knocked Fix down.
(c) As a part of duty, Fix arrested Fogg.
(d) At the fifty-seventh second, Fogg entered the Reform Club Saloon.
Answer:
(c) As a part of duty, Fix arrested Fogg.
(b) When set free, the first thing that Fogg did was he knocked Fix down.
(d) At the fifty-seventh second, Fogg entered the Reform Club Saloon.
(a) Aouda accepted Fogg’s proposal of marriage.

Question (ii)
There is a sudden twist in the climax of the novel. Explain by citing some lines and relevant examples from the extract.
Answer:
Fogg and the reader first think that Fogg has lost not only the wager, but also the money and honour that went with it. The following lines tell us this : ‘After having steadily traversed that long journey, overcome a hundred obstacles, braved many dangers, and still found time to do some good on his way, to fail near the goal by a sudden event which he could not have foreseen, and against which he was unarmed; it was terrible!’ The unforeseen event was his arrest and imprisonment by detective Fix, who mistakenly thought he was the bank robber.

However, the twist comes when Passepartout finds out that it is not Sunday but Saturday, and perhaps they can just make it to the Reform Club in time. Just as Fogg’s antagonists are counting the seconds to their win,, Fogg manages to reach the Club and win the wager, giving a happy and thrilling ending to the novel. The following lines tell us this : ‘At the fifty-seventh second the door of the saloon opened; and the pendulum had not beat the sixtieth second when Phileas Fogg appeared, followed by an excited crowd who had forced their way through the club doors, and in his calm voice, said, “Here I am, gentlemen!”’

Question (iii)
Which of the following is an appropriate reason for Phileas Fogg starting his journey around the world?
(a) Fellow members bet Fogg
(b) Fogg bets his fellow members
(c) Fogg wants to marry Aouda
(d) Fogg committed robbery
Ans.
(a) Fellow members bet Fogg

SETTING:

(A3)

Question (i)
Choose from the following options, the means of transport used in the novel and explain the way they help the characters.
(a) Elephant
(b) Horse
(c) Train
(d) Steamer
Answer:
Elephants, trains and steamers were used as a means of transport in the novel. They help the characters go around the world in the allotted time. After overcoming a number of obstacles, they reach London in time to win the wager.

Question (ii)
The beginning of the extract is a scene in the prison at the custom house. From there the novel moves further from one place/spot to another. Pick and explain all the places/spots where the incidents took place.
Answer:
From the prison at the custom house, Fogg and his companions go to Liverpool station to catch a train back to London, where Fogg lives and where the Reform Club is located. Once they reach London, thinking that they had lost the wager, they go to Saville Row, which is Fogg’s residence. The next location is the preacher’s house where Passepartout goes to make arrangements for Fogg’s wedding. The last location is the Reform Club, which Fogg reaches in time to win his wager.

Question (iii)
Most of the setting in the extract is in London. Explain how this is suited to the theme of the novel.
Answer:
Fogg’s residence was in London. The Reform Club, which Fogg frequented on a regular basis and where the all-important wager took place, is also in London. Fogg’s journey starts from London and ends in London. Hence, London is the central place in the novel, and thus this setting is suited to the theme.

(iv) Describe the importance of the following places in the development of the plot and behaviour of the characters.

Question (a)
Liverpool.
Answer:
Liverpool is the place where Fogg disembarks from his steamer, and from where he has to catch a train to London. Liverpool is also the place where he is arrested by Fix and thus misses his train. He arranges a special train in an attempt to reach London on time.

Question (b)
London.
Answer:
Fogg lives in London. The Reform Club, which Fogg frequented on a regular basis, is also in London. Fogg’s accepts the wager in London; his journey starts from London and ends in London. Hence, London is the central place in the novel.

Question (c)
Reform Club.
Answer:
Reform Club is the place which Fogg frequented on a regular basis. It is at the Reform Club that Fogg gets involved in an argument over an article, and where the wager with his fellow club members takes place. It is the place where Fogg was supposed to return before 8.45 p.m. on 21 December, 80 days later. It is the place where his antagonists are waiting anxiously for him, and which he reaches at practically the last second to win his wager.

Question (d)
Saville Row.
Answer:
Phileas Fogg’s residence is in Saville Row.
This is also the place where he takes Aouda.
Fogg has always stayed quietly at this place.
When he returned from his trip around the world and thought he had lost the wager, he remained there so quietly that no one even knew he had returned.

Question (e)
Edinburgh.
Answer:
Detective Fix arrested Phileas Fogg in Liverpool thinking that he was a bank robber. However, the real bank robber, James Strand, had been arrested on 17th December at Edinburgh.

Question (iv)
Select the correct options:
Find from the options, the place which are not mentioned in the extract:
(a) Bombay (Now, Mumbai)
(b) Allahabad
(c) Chennai
(d) Calcutta (Now, Kolkata)
Answer:
Allahabad, Chennai

THEME:

(A4)

Question (i)
Find and explain the significance of various exciting incidents in the extract.
Answer:
The first exciting incident was when Fogg was arrested by Detective Fix and imprisoned in the Custom House. This meant that his return to London would be delayed, for he would have missed his train.

The second exciting incident was his release. This meant that he could perhaps still reach London on time.

The third exciting incident was when he tried to organize a train to London but had problems.

The fourth exciting incident was Aouda’s marriage proposal and Fogg’s acceptance of it. This showed that Aouda was not at all materialistic and extremely grateful to Fogg for what he had done. She was willing to marry Fogg even after knowing that he was penniless.
The fifth exciting incident was when Passepartout, on reaching the clergyman’s house, discovers that it is not Sunday as they had thought but Saturday, and there was a chance that they could still win the wager. The sixth most exciting incident was Fogg’s reaching the Reform Club at the last moment and winning the wager. All the twists and turns and the climax at the end keeps the reader glued to the novel right till the end.

Question (ii)
Write 4-5 sentences on the ‘Time’ theme of the extract.
Answer:
Phileas Fogg has to go around the world in eighty days if he has to win the wager. As he and his companions struggle to do this, time foils their plans in many cases. Fogg gets arrested for no fault of his and loses precious time. He is unable to catch the train from Liverpool, and the special train he arranged too gets delayed. Fogg is afraid that he has lost the bet. However, in the end, Fogg wins the bet with seconds to spare as he gained a day when crossing the International Date Line. His journey through the time zones had gained him a day. The ultimate message is that no one can control time; time will work the way it wants to work, and humans are at its mercy.

Question (iii)
Write 4-5 sentences on the ‘Morality’ theme of the extract.
Answer:
Fogg embarks on his journey to preserve his honour and prove his worth to the men at the Reform Club. He spends nearly all of his money along the way, showing that riches are not what he is truly out for. He is honourable – when he thinks he is penniless, he does not want Aouda to marry him. Aouda, by proposing to him, shows that she is not materialistic. He forgives Passepartout his mistakes. Passepartout shows his loyalty and love for his master at every step.

In the end, when he wins the bet, he divides whatever money is left between Passepartout and Detective Fix, showing that he had no grudges against him. The writer shows that with human effort and willpower enormous obstacles can be overcome. The writer also tells us in the end that Fogg had won something more important than money, by travelling around the world. He had won a charming woman, who made him the happiest of men. The moral at the end is that love and its attainment is more important than all the challenges and money in the world.

Question (iv)
Write the central idea of the given extract of the novel, ‘Around the World in Eighty Days’.
Answer:
The central idea of the given extract is how Fogg ultimately wins the bet even though there are unexpected delays and missed trains. He had unknowingly gained a day when crossing the International Date Line, and hence he was still in time to meet the deadline. The final statement is that love and its attainment is more important than all the challenges and money in the world.

Question (v)
Justice is served/done in the end. Explain.
Answer:
Phileas Fogg is an honourable and compassionate person. He wants to win his wager of going around the world in eighty S days. He struggles against time, as well as the obstacles and delays that come his way. Finally, when he reaches Liverpool and is about to go to London to win his wager, he is arrested because he is wrongly thought to be a bank robber. Throughout this ordeal, Fogg is calm and unshakeable. Even though he thinks he has lost the wager, he does not blame anyone or lose his temper.

He tells Aouda that he cannot marry her and make her live in poverty. Justice is done unexpectedly in the end when he wins the wager. He had unknowingly gained a day when crossing the International Date Line, and hence he was still in time to meet the deadline. In the end, the writer tells us that Fogg had won something more important than money, by travelling around the world. He had won a charming woman, who made him the happiest of men. Thus, justice was done to the quiet and honourable Phileas Fogg.

LANGUAGE:

(A5)

(i) Elaborate the following quotes in the light of the extract of the novel, ‘Around the World in Eighty Days’.

Question (a)
‘Quitters never win and winners never quit’.
Answer:
Even though Fogg loses time due to being wrongly arrested and imprisoned, he makes every effort to reach London on time. He arranges a special train from Liverpool. He does not quit when he feels that there is some faint chance of a win. Later, when Passepartout discovers that it is Saturday and not Sunday, and that there is still a chance of winning, Fogg puts aside everything and rushes headlong to the Reform Club. He does not give up in spite of all the obstacles, and comes out a winner, both in winning the bet and the love of a good woman.

Question (b)
‘Time is the only solution to problems’.
Answer:
The most important theme in the extract is time. Fogg’s wager is a race against time, and his adventures illustrate repeatedly that time is fickle, and either works for or against them. In many cases, time foils their plans, when the delays build up and the train to Liverpool leaves without them. In the end, though, it is time that helps wins Fogg his bet, since they gained a day when crossing the International Date Line. The ultimate message is that no one can control time; time will work the way it wants to work, and humans are at its mercy. Time is the only solution to problems.

Question (ii)
Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, style, significance, etc., of the dialogue.
Answer:

Dialogue	Speaker	Who said to Whom	Tone, Style, Significance etc.
1. “Why do you not curse me? It was my fault that-”	Passepartout	Passepartout to Phileas Fogg	Repentant; thinks himself responsible for not telling Phileas Fogg about Fix earlier
2. “If Phileas Fogg had come in the 7: 23 train, he would have got here by this time. We can, therefore, regard the bet as won.”	Andrew Stuart	Andrew Stuart to the other antagonists at the Reform Club	Nervous and anxious; the men with whom Fogg had the wager were calculating whether he would still meet the deadline.
3. “Sir-forgive me-a most-unfortunate resemblance-robber arrested three days ago-you-are free!”	Detective Fix	Detective Fix to Phileas Fogg	Repentant and apologetic for arresting Phileas Fogg when he was innocent.
4. “Will you pardon me for bringing you to England?”	Phileas Fogg	Phileas Fogg to Aouda	Proud and honourable; asking pardon from Aouda for bringing her to England on false hopes, when he has now become poor.
5. “It is for me to ask that question. You were ruined, but now you are rich again.”	Aouda	Aouda to Phileas Fogg	Honourable and dignified; says this after Fogg wins the wager, and he asks her whether she still wanted to marry him.

 

Balbharti Yuvakbharati English 12th Digest Chapter 4.2 To Sir, with Love Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 4.2 To Sir, with Love

12th English Digest Chapter 4.2 To Sir, with Love Textbook Questions and Answers

Character:

(A1)

Question (i)
From the options given below, choose the name of the teacher and write a couple of lines from the extract in support of your answer.
(a) Denham
(b) Miss Joseph
(c) Sapiano
(d) Dale-Evans
Answer:
Dale-Evans is the teacher. The lines to support this are: The names were called Mr. Weston, Mrs. Dale-Evans, Miss Phillips. Denham and Miss Joseph led the others off the stage and the teachers took their seats.

Question (ii)
Complete the table highlighting the various traits of the major characters in the extract.

Answer:

Question (iii)
The narrator played a crucial role in bringing a significant change in the students. Discuss the statement by citing some references from the extract.
Answer:
The narrator initially had a very difficult time with the students who were disrespectful, ill- mannered and mischievous. They considered him to be an arrogant outsider, unfamiliar with the social environment in which they I have grown up. They harass him from day one; however, they come around after only a few weeks, completely changing both their hygiene and their attitudes towards one another.

This marks the success of the narrator in handling the students in a very amicable way. This is proved on the day of the half-yearly report of the Students’ Council. The narrator’s students allocate tasks in a business-like way. They present their reports confidently and clearly. They are cool and efficient in their work. They are courteous towards each other and the teachers, and they accept the verdict of the teachers. This shows the significant and crucial change brought about by the narrator in his students.

Question (iv)
Femman brought a comic relief in the Students’ Council programme. Explain with an incident.
Answer:
In order to explain a point, Fernman made a signal to someone off-stage. Two students, Welsh and Alison, appeared bearing a skeleton between them, with a sort of gallows. When this arrangement had been set up there was the skeleton hanging from a hook screwed into the top of its skull, gently revolving at the end of a cord. This brought some comic relief to the proceedings, and the students laughed uproariously.

(v) Give a brief character-sketch of –

Question (a)
Denham.
Answer:
Denham is business-like and confident while allocating tasks and fitting in the j programme. He is an important official for the function and sits confidently beside the Head. He courteously addresses the girls as ‘Miss’. While discussing P.T. and Games, he shocks the audience with his views. He is a trained boxer and does not want to do P.T. exercises which he feels are unnecessary for him. His tone is initially blunt, critical and argumentative. However, when Miss Phillips gently replies to his arguments and outwits him, he graciously and politely accepts his defeat.

Question (b)
Miss Joseph.
Answer:
Miss Joseph is business-like and confident while allocating tasks and fitting in the programme. She is an important official for the function. She sits on the stage beside Mr. Florian with composure. She also addresses the audience with confidence.

Question (c)
The Narrator.
Answer:
Ricky Braithwaite, the narrator, is a very sensitive person. He is very upset at the racism that he has to face after serving in the army. He gets a job in a school, and initially has a very difficult time with the students who are disrespectful, ill-mannered and mischievous. They harass him from day one. However, his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts.

Though he was bullied, harassed, mentally and physically tortured many times, he didn’t lose his patience and continued implementing his novel ideas and techniques that helped him to bring a significant change in his students’ lives. On the day of the half-yearly report of the Students’ Council, he is very anxious to see how they behave. When they are business-like, confident, cool and courteous, he feels proud of them.

Question (d)
Miss Dare.
Answer:
Miss Dare spoke about the problems which all humanity has to face in terms of sickness and disease, and of the advantages gained by interchange of knowledge, advice and assistance. Her contribution was something of an anticlimax after Femman’s performance, and she seemed to realise it, but continued with her speech.

Question (e)
Miss Phillips.
Answer:
Miss Phillips, whom everyone had thought to be frilly and brainless, proves while answering Denham’s questions that she is the best-informed of the three teachers on the stage. She intervenes skilfully when the other two teachers are at a loss, without embarrassing them. She speaks coolly, honestly and with authority.

She is very slightly built but she controls her class very well. She tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She confidently asserts that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. Thus, she put ‘ Denham in his place very coolly.

Question (vi)
Compare the following characters:
Answer:
Miss Joseph and Denham:
Miss Joseph and Denham are both business-like and efficient while allocating tasks and fitting in the programme. They are important officials for the function and sit on the stage confidently beside Mr. Florian. Both address the audience with confidence.

However, Denham is blunt, critical and argumentative while discussing the P.T. exercises that everyone has to do in school. He argues with Miss Phillips, but when Miss Phillips pleasantly and coolly puts him in his place, he graciously accepts defeat. He is also courteous in his dealing with the ladies.

Miss Phillips, whom everyone had thought to be frilly and brainless, proved while answering Denham’s questions that she was the best-informed of the three teachers on the stage. She intervened skilfully when the other two teachers were at a loss, without embarrassing them. She spoke coolly, honestly and with authority.

When Denham is blunt, critical and argumentative while discussing the P.T. exercises that everyone has to do in school, she tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She gives her views confidently and puts Denham in his place very coolly. Denham accepts his defeat courteously.

Fernman and Miss Dare:

Fernman is clear, precise and dramatic. He keeps the audience spell-bound by his speech. Miss Dare and Fernman discuss the subject of physiology, with Fernman stealing the show by exhibiting a model of a human skeleton and stressing the class conclusion that “basically all people were the same.” Miss Dare speaks about the problems which all humanity has to face in terms of sickness and disease, and of the advantages gained by interchange of knowledge, advice and assistance.

Her contribution was something of an anticlimax after Fernman’s performance, and she seemed to realise it, but continued with her speech. Fernman was also adroit while questioning the teachers.

The narrator, a teacher, is sensitive, and upset about racism, which has affected him directly. He initially had a very difficult time with the students who were disrespectful, ill-mannered and mischievous. However, he didn’t lose his patience and continued implementing his novel ideas and techniques. This helped him to bring a significant change in his students’ lives. He is very anxious about the students and later proud of their confidence, understanding and behaviour.

The Head of the school, Mr. Florian, addressed the school on the day of the half-yearly report of the Students’ Council. He spoke about the aims and policy of the school and of the important contribution each child could make. He gave praise wherever necessary, but insisted that there was yet a great deal to be done. His remarks showed that he identified himself with the school and everyone in it. At the end he expressed his pride in all the children and his deep appreciation of their efforts.

PLOT:

(A2)

Question (i)
Arrange the incidents in correct sequence as per their occurrence in the extract.
(a) Denham was outwitted by Miss Phillips.
(b) The head of the school closed the proceedings.
(c) Denham asserted that P.T. periods were a waste of time.
(d) The slips were folded and placed in a hat.
(e) Fernman was as usual a trump card.
(f) Denham called out the names of the representatives.
(g) Students’ Council was held every year on November 15th.
Answer:
(g) Students’ Council was held every year on November 15th.
(f) Denham called out the names of the representatives.
(e) Fernman was as usual a trump card.
(d) The slips were folded and placed in a hat.
(c) Denham asserted that P.T. periods were a waste of time.
(a) Denham was outwitted by Miss Phillips.
(b) The head of the school closed the proceedings.

Question (ii)
Describe in brief the purpose of organising the half-yearly report programme of Students’ Council.
Answer:
During the half-yearly report programme of Students’ Council, each class would report, through its representatives, on the studies pursued during the half year which began after Easter. A representative was chosen for each subject. When all the classes had completed their reports a panel of teachers would be invited to occupy the stage and answer questions from the body of the hall on matters arising out of the various reports. Throughout all the reports, the emphasis was on what they understood rather than on what they were expected to learn.

Question (iii)
Write in your words the entire half- yearly report programme of Students’ Council.
Answer:
In the half-yearly report of the Students’ Council, the students report to the faculty and other students on what they have been studying thus far. The representatives of the narrator’s class spoke knowledgeably about their coursework and placed a considerable amount of emphasis on how much they had learnt about different people, cultures, customs, and the importance of international and interracial cooperation.

Miss Joseph and Denham, both students of the narrator’s class, presided over the meeting. Mr. Florian, the headmaster, addressed the meeting with a lengthy presentation. After this, one after another, each class gave a brief report of their progress, through their chosen representatives, on what they had been studying in each subject so far. A panel of teachers was then chosen to answer any questions put by the students.

The lowest class began first; the narrator’s class, being the oldest, was the last to present their report. Miss Joseph began the highest class’s proceedings by clarifying that the common theme underlying all their studies that term was the interdependency of mankind. Potter spoke in the field of math, focusing on how greater understanding in the world is fostered by the use of common weights and measures.

Miss Pegg and Jackson spoke on geography, and Miss Dare and Fernman discussed the subject of physiology, with Fernman stealing the show by exhibiting a model of a human skeleton and stressing the class conclusion that “basically all people are the same.” Miss Dodd reported on history, and Miss Joseph on domestic science. Denham created a stir by speaking on the subject of P.T. and games, complaining that the class ‘was ill-conceived and pointless.’

Mr. Weston, Mrs. Dale-Evans, and Miss Phillips were chosen at random to answer students’ questions. When Denham pursued his inquiry on the necessity of requiring all students to take P.T., Mr. Weston responded quite ridiculously, trying to bluster his way out of the subject, and offering no sensible argument. Unexpectedly, the quiet and hesitant Miss Phillips stepped in and gave a strong defence of the practice. Finally, Denham, knowing that he had been outwitted, had no choice but to respectfully accept his defeat. The narrator was immensely satisfied with the progress of the students of his class.

Question (iv)
Describe the question-answer session that took place at the end of the extract.
Answer:
The questions were mostly from the two top classes. The teachers had no briefing, and were often caught out stammering in their indecision. One of the teachers, Miss Euphemia Phillips proved to be the coolest and best informed of the three teachers on the stage. She dealt with questions put to her with honesty and with authority, and would often intervene skilfully to assist one of the others without causing embarrassment.

While Femman was skillful in his questioning, Denham was blunt in his criticism. He severely criticised the general pattern of P.T. and games. Denham was a trained boxer, and insisted that such exercises were only advantageous if practised daily and for more sustained periods; P.T. twice weekly for twenty minutes was a waste of time, he asserted.

Miss Phillips reminded the school that every subject, including P.T. and games, , had been carefully considered and fitted into the teaching timetable so that each student received maximum benefit from it. The school considered it in terms of the greatest good for the greatest number. She added, hinting at Denham, that while some were fortunate in their own fine physical development and did not really need the few meagre helpings of P.T. and games which the school could offer, there were others for whom the programme was ideally suited. It would be beyond anyone’s powers to please everybody.

She suggested that some of the older boys might even be able to help in that respect. Denham, not put off by these sugary remarks, replied that only the kids who needed it could take it, while the others could have a game of football or something, instead of doing something useless.

This was a difficult question to answer, but Miss Phillips replied pleasantly that it should be considered as much an exercise of the mind as it is of the body. The whole timetable in the school was meant to help them in the world after they left the school, and doing what one was told in spite of not liking it, was part of the training. That answer defeated Denham and he accepted his defeat gracefully.

Question (v)
Describe the discussion that took place between Miss Joseph and Denham.
(There is no discussion between Miss Joseph and Denham.)

SETTING:

(A3)

Question (i)
Identify the event that took place in the extract. Give reason/s to support your answer:
(a) Annual Sports Day on November 15th
(b) Annual Social and Cultural Gathering on November 15th
(c) Half-yearly report of Students’ Council on November 15th
(d) Farewell Programme on November 15th
Answer:
(c) Half-yearly report of Students’ Council on November 15th
The following lines support this:
The half-yearly report of the Students’ Council was on November 15th, and was one of the important days in the calendar of Greenslade School.

Question (ii)
The event in the extract was held at the Choose the correct alternative. Give reason/s to support your answer.
(a) author’s house
(b) auditorium of the school
(c) market
(d) garden
Answer:
(b) auditorium of the school
The following lines support this:
A bell was rung at 10.00 a.m. and everyone trooped into the auditorium to sit together in classes.

Question (iii)
The incidents in the extract occurred at a particular place. Explain the significance of that place in your own words.
Answer:
The extract confines itself to narrating the incidents that take place on the important day of the half-yearly report of the Students’ s Council. This report takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal programme, and the setting is the auditorium, with a stage and a formal atmosphere. This is just right.

Question (iv)
Explain how the setting of the extract contributes to the theme of the novel.
Answer:
One of the themes of the novel is the teacher- student relationship, and the change in the behaviour of the students after the narrator’s patient dealing. The narrator initially had a very difficult time with the students who were disrespectful, ill- mannered and mischievous. He finds that the students belong to a background that is not suitable for learning and for their overall development and progress.

They are in no mood to change their attitude and behaviour. The narrator, with his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts. The narrator is now anxious to see how far his teaching has been effective.

He can judge it from the behaviour and attitude of his students on the important day of the half-yearly report of the Students’ Council. This report takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal programme, and the setting of the auditorium, a stage and a formal atmosphere, is just right. The discussion and the question . and answer session also contributes to the theme.

THEME:

(A4)

Question (i)
‘When the turn of my class came I sat up anxiously’.
Explain the reasons of the narrator’s anxiety hy citing suitable references from the extract.
Answer:
The narrator initially had a very difficult time with the students who were disrespectful, ill-mannered and mischievous. They were in no mood to change their attitude and behaviour. The narrator with his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts. The narrator later grew very fond of his students and wanted them to do well in their lives. He wanted them to shine. He is now anxious to see how far his teaching has been effective.

He can judge it from their behaviour, conduct and attitude on the important day of the half-yearly report of the Students’ Council. He also wanted to see how they would express themselves and how much they had understood during the given period. The programme takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal one. Hence he sat up anxiously when the turn of his class came.

Question (ii)
Select two statements that describe the theme of the extract:
(a) Half-yearly report of the Students’ Council was not an important event for the students and teachers of school.
(b) The writer was immensely pleased to notice the progress of his students.
(c) The students showed a remarkable change in their behaviour and were progressing in all the subjects.
(d) The head of the institution was against I conducting such activities in the school.
Answer:
(b) The writer was immensely pleased to notice the progress of his students.
(c) The students showed a remarkable change in their behaviour and were j progressing in all the subjects.

Question (iii)
The relationship between the teacher and the students is highlighted in the extract. Illustrate with suitable examples from the extract.
Answer:
In the extract, the narrator describes the day on which the half-yearly report of the Students’ Council takes place. It is entirely the students’ affair; the students are given full freedom. Denham and Miss Joseph conduct the whole programme and preside over it. The students and teachers all listen attentively to the reports made by the student representatives on what they have been studying till then. At the end of the students’ presentation, three teachers are chosen at random to answer the students’ questions. They have to answer whatever questions are put to them by the students. Fernman questions them adroitly; Denham is blunt, critical and argumentative.

Two of the teachers are flustered by the questions, which they find difficult to answer. However, Miss Phillips intervenes skilfully when the other two teachers are at a loss without embarrassing them. She speaks coolly, honestly and with authority. Denham counter-questions her; she is cool and pleasant. The programme is serious, formal and frank. It is a democratic set up. There is freedom of expression, fearlessness on the part of students, honesty and analysis of issues.

Question (iv)
Explain in brief the theme of the extract.
Answer:
The theme of the extract is the student- teacher relationship and the proceedings of the half-yearly report of the Students’ Council. The extract shows the improvement in the conduct of the students, the increase in their level of confidence and courtesy. It also shows the freedom and candour in student-teacher interaction in the school.

Question (v)
Describe the atmosphere of the school described in the extract.
Answer:
In the extract, the narrator describes the day on which the half-yearly report of the Students’ Council takes place. Here, the students of the school report to the faculty and other students on what they have been studying thus far. It is entirely the students’ affair; the students conduct the whole programme and preside over it. At the end of the students’ presentation, three teachers are chosen at random to answer the students’ questions.

The programme is serious, formal and frank. The students honestly give their reports and ask questions fearlessly. The selected teachers do their best to answer the critical and blunt questions put to them. It is a democratic set up. There is freedom of expression, honesty, and analysis of issues on that day.

LANGUAGE:

(A4)

(i) Explain the following statements that enrich the language and create a powerful impact.

Question (a)
Miss Phillips is transformed into a very convincing personality.
Answer:
Miss Phillips is earlier considered as ‘frilly and brainless’; but she was the best- informed of the three teachers on the stage, She intervened skilfully when the other two I teachers were at a loss without embarrassing them. She spoke coolly, honestly and with authority. When Denham is blunt, critical and argumentative while discussing the P.T. exercises, she tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training.

She confidently asserted that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. Thus, she put Denham in his place very coolly and pleasantly, and Denham accepted his defeat courteously. The teacher who was considered brainless is transformed into a s . very convincing personality at the end.

Question (b)
There are many features of language that contribute to the smooth sailing of ) the plot.
Answer:
With reference to the extract, the words used by the narrator contribute to the smooth sailing of the plot. Expressions and sentences like ‘the school showed its approval by laughing uproariously’, ‘Fernman was wonderful; he had them eating out of his hand’, ‘frilly and seemingly brainless’ ‘Miss Phillips took the reins and her stock promptly shot up a hundredfold’, ‘sugary remarks’, ‘her baby-blue eyes twinkling in her delight at this crossing of staves’, ‘this frilly, innocent-looking puss had gobbled her canary without leaving the tiniest feather’ lend beauty and interest to the writing. Apt words and expressions have been used to give the reader a compete idea of the situation. The programme has also been described clearly.

(ii) Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, the style, significance etc. of the dialogues:

Question 1.
“Then why do we have to do P.T.? Why don’t they take only the kids who need it?”
Answer:
The speaker is Denham. His tone is initially blunt, critical and argumentative. He is a trained boxer and does not want to do P.T exercises which he feels are unnecessary for him. However, when Miss Phillips gently replies to his arguments and outwits him, he has the grace to accept his defeat. The blunt and critical Denham turns into a gracious loser.

Question 2.
“Let’s say it is as much an exercise of the mind as it is of the body, Denham.”
Answer:
The speaker is Miss Phillips. She answers Denham’s questions coolly, honestly and with authority. She tells him that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She confidently asserted that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. This piece of advice was not meant only for Denham but for the whole school and the reader as well.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 2 Mechanical Properties of Fluids Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 2 Mechanical Properties of Fluids

1) Multiple Choice Questions

i) A hydraulic lift is designed to lift heavy objects of maximum mass 2000 kg. The area of cross-section of piston carrying
the load is 2.25 × 10^-2 m². What is the maximum pressure the piston would have to bear?
(A) 0.8711 × 10⁶ N/m²
(B) 0.5862 × 10⁷ N/m²
(C) 0.4869 × 10⁵ N/m²
(D) 0.3271 × 10⁴ N/m²
Answer:
(A) 0.8711 × 10⁶ N/m²

ii) Two capillary tubes of radii 0.3 cm and 0.6 cm are dipped in the same liquid. The ratio of heights through which the liquid will rise in the tubes is
(A) 1:2
(B) 2:1
(C) 1:4
(D) 4:1
Answer:
(B) 2:1

iii) The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly
(A) 0.9 × 10^-3 J
(B) 0.4 × 10^-3 J
(C) 0.7 × 10^-3 J
(D) 0.5 × 10^-3 J
Answer:
(A) 0.9 × 10^-3 J

iv) Two hail stones with radii in the ratio of 1:4 fall from a great height through the atmosphere. Then the ratio of their terminal velocities is
(A) 1:2
(B) 1:12
(C) 1:16
(D) 1:8
Answer:
(C) 1:16

v) In Bernoulli’s theorem, which of the following is conserved?
(A) linear momentum
(B) angular momentum
(C) mass
(D) energy
Answer:
(D) energy

2) Answer in brief.

i) Why is the surface tension of paints and lubricating oils kept low?
Answer:
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oils must below.

ii) How much amount of work is done in forming a soap bubble of radius r?
Answer:
Let T be the surface tension of a soap solution. The initial surface area of soap bubble = 0
The final surface area of soap bubble = 2 × 4πr²
∴ The increase in surface area = 2 × 4πr^2-
The work done in blowing the soap bubble is W = surface tension × increase in surface area = T × 2 × 4πr² = 8πr²T

iii) What is the basis of the Bernoulli’s principle?
Answer:
Conservation of energy.

iv) Why is a low density liquid used as a manometric liquid in a physics laboratory?
Answer:
An open tube manometer measures the gauge pressure, p — p₀ = hpg, where p₀ is the pressure being measured, p₀ is the atmospheric pressure, h is the difference in height between the manometric liquid of density p in the two arms. For a given pressure p, the product hp is constant. That is, p should be small for h to be large. Therefore, for noticeably large h, laboratory manometer uses a low density liquid.

v) What is an incompressible fluid?
Answer:
An incompressible fluid is one which does not undergo change in volume for a large range of pressures. Thus, its density has a constant value throughout the fluid. In most cases, all liquids are incompressible.

Question 3.
Why two or more mercury drops form a single drop when brought in contact with each other?
Answer:
A spherical shape has the minimum surface area- to-volume ratio of all geometric forms. When two drops of a liquid are brought in contact, the cohesive forces between their molecules coalesces the drops into a single larger drop. This is because, the volume of the liquid remaining the same, the surface area of the resulting single drop is less than the combined surface area of the smaller drops. The resulting decrease in surface energy is released into the environment as heat.

Proof : Let n droplets each of radius r coalesce to form a single drop of radius R. As the volume of the liquid remains constant, volume of the drop = volume of n droplets
∴ \(\frac{4}{3}\)πR³ = n × \(\frac{4}{3}\)πr³
∴ R³ = nr³ ∴ R = \(\sqrt[3]{n}\)r
Surface area of n droplets = n × πR²
Surface area of the drop = 4πR² = n^2/3 × πR²
∴ The change in the surface area = surface area of drop – surface area of n droplets
= πR²(n^2/3 – n)
Since the bracketed term is negative, there is a decrease in surface area and a decrease in surface energy.

Question 4.
Why does velocity increase when water flowing in broader pipe enters a narrow pipe?
Answer:
When a tube narrows, the same volume occupies a greater length, as schematically shown in below figure. A₁ is the cross section of the broader pipe and that of narrower pipe is A₂. By the equation of continuity, V₂ = (A₁/A₂)V₁

Since A₁/A₂ > v₂ > v₁. For the same volume to pass points 1 and 2 in a given time, the speed must be greater at point 2.
The process is exactly reversible. If the fluid flows in the opposite direction, its speed decreases when the tube widens.

Question 5.
Why does the speed of a liquid increase and its pressure decrease when a liquid passes through constriction in a horizontal pipe?
Answer:

Consider a horizontal constricted tube.
Let A₁ and A₂ be the cross-sectional areas at points 1 and 2, respectively. Let v₁ and v₂ be the corresponding flow speeds, ρ is the density of the fluid in the pipeline. By the equation of continuity,
v₁A₁ = v₂A₂ …… (1)
∴ \(\frac{v_{2}}{v_{1}}\) = \(\frac{A_{1}}{A_{2}}\) > 1 (∵ A₁ > A₂)
Therefore, the speed of the liquid increases as it passes through the constriction. Since the meter is assumed to be horizontal, from Bernoulli’s equation we get,

Again, since A₁ > A₂, the bracketed term is positive so that p₁ > p₂. Thus, as the fluid passes through the constriction or throat, the higher speed results in lower pressure at the throat.

Question 6.
Derive an expression of excess pressure inside a liquid drop.
Answer:
Consider a small spherical liquid drop with a radius R. It has a convex surface, so that the pressure p on the concave side (inside the liquid) is greater than the pressure p0 on the convex side (outside the liquid). The surface area of the drop is
A = 4πR² … (1)
Imagine an increase in radius by an infinitesimal amount dR from the equilibrium value R. Then, the differential increase in surface area would be dA = 8πR ∙ dR …(2)
The increase in surface energy would be equal to the work required to increase the surface area :
dW = T∙dA = 8πTRdR …..(3)

We assume that dR is so small that the pressure inside remains the same, equal to p. All parts of the surface of the drop experience an outward force per unit area equal to ρ — ρ₀. Therefore, the work done by this outward pressure-developed force against the surface tension force during the increase in radius dR is
dW = (excess pressure × surface area) ∙ dR
= (ρ – ρ₀) × 4πnR² ∙ dR …..(4)
From Eqs. (3) and (4),
(ρ — ρ₀) × 4πR² ∙ dR = 8πTRdR
∴ ρ – ρ₀ = \(\frac{2 T}{R}\) …… (5)
which is called Laplace’s law for a spherical membrane (or Young-Laplace equation in spherical form).
[Notes : (1) The above method is called the principle of virtual work. (2) Equation (5) also applies to a gas bubble within a liquid, and the excess pressure in this case is also called the gauge pressure. An air or gas bubble within a liquid is technically called a cavity because it has only one gas-liquid interface. A bubble, on the other hand, such as a soap bubble, has two gas-liquid interfaces.]

Question 7.
Obtain an expression for conservation of mass starting from the equation of continuity.
Answer:

Consider a fluid in steady or streamline flow, that is its density is constant. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude. Suppose the velocity is \(\vec{v}_{1}\), at point P and \(\vec{v}_{2}\) at point. Q. If A₁ and A₂ are the cross-sectional areas of the tube at these two points, the volume flux across A₁, \(\frac{d}{d t}\)(V₂) = A₁v₁ and that across A₂, \(\frac{d}{d t}\)(V₂) = A₂v₂
By the equation of continuity of flow for a fluid, A₁v₁ = A₂V₂
i.e., \(\frac{d}{d t}\)(V₁) = \(\frac{d}{d t}\)(V₂)
If ρ₁ and ρ₁ are the densities of the fluid at P and Q, respectively, the mass flux across A₁, \(\frac{d}{d t}\)(m₁) = \(\frac{d}{d t}\)(ρ₁ v₁) = A₁ρ₁v₁
and that across A₂, \(\frac{d}{d t}\)(m₂) = \(\frac{d}{d t}\)(ρ₂V₂) = A₂ρ₂v₂
Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires the mass fluxes to be equal, i.e.,
\(\frac{d}{d t}\)(m₁) = \(\frac{d}{d t}\)(m₂)
i.e., A₁ρ₁v₁ = A₂ρ₂v₂
i. e., Apv = constant
which is the required expression.

Question 8.
Explain the capillary action.
Answer:
(1) When a capillary tube is partially immersed in a wetting liquid, there is capillary rise and the liquid meniscus inside the tube is concave, as shown in below figure.

Consider four points A, B, C, D, of which point A is just above the concave meniscus inside the capillary and point B is just below it. Points C and D are just above and below the free liquid surface outside.

Let P_A, P_B, P_C and P_D be the pressures at points A, B, C and D, respectively.
Now, P_A = P_C = atmospheric pressure
The pressure is the same on both sides of the free surface of a liquid, so that

The pressure on the concave side of a meniscus is always greater than that on the convex side, so that
P_A > P_B
∴ P_D > P_B (∵ P_A = P_D)

The excess pressure outside presses the liquid up the capillary until the pressures at B and D (at the same horizontal level) equalize, i.e., P_B becomes equal to P_D. Thus, there is a capillary rise.

(2) For a non-wetting liquid, there is capillary depression and the liquid meniscus in the capillary tube is convex, as shown in above figure.

Consider again four points A, B, C and D when the meniscus in the capillary tube is at the same level as the free surface of the liquid. Points A and B are just above and below the convex meniscus. Points C and D are just above and below the free liquid surface outside.

The pressure at B (P_B) is greater than that at A (P_A). The pressure at A is the atmospheric pressure H and at D, P_D \(\simeq\) H = P_A. Hence, the hydrostatic pressure at the same levels at B and D are not equal, P_B > P_D. Hence, the liquid flows from B to D and the level of the liquid in the capillary falls. This continues till the pressure at B’ is the same as that D’, that is till the pressures at the same level are equal.

Question 9.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Answer:
Consider a capillary tube of radius r partially immersed into a wetting liquid of density p. Let the capillary rise be h and θ be the angle of contact at the edge of contact of the concave meniscus and glass. If R is the radius of curvature of the meniscus then from the figure, r = R cos θ.

Surface tension T is the tangential force per unit length acting along the contact line. It is directed into the liquid making an angle θ with the capillary wall. We ignore the small volume of the liquid in the meniscus. The gauge pressure within the liquid at a depth h, i.e., at the level of the free liquid surface open to the atmosphere, is
ρ – ρ_o = ρgh …. (1)
By Laplace’s law for a spherical membrane, this gauge pressure is
ρ – ρ_o = \(\frac{2 T}{R}\) ….. (2)
∴ hρg = \(\frac{2 T}{R}\) = \(\frac{2 T \cos \theta}{r}\)
∴ h = \(\frac{2 T \cos \theta}{r \rho g}\) …. (3)
Thus, narrower the capillary tube, the greater is the capillary rise.
From Eq. (3),
T = \(\frac{h \rho r g}{2 T \cos \theta}\) … (4)
Equations (3) and (4) are also valid for capillary depression h of a non-wetting liquid. In this case, the meniscus is convex and θ is obtuse. Then, cos θ is negative but so is h, indicating a fall or depression of the liquid in the capillary. T is positive in both cases.
[Note : The capillary rise h is called Jurin height, after James Jurin who studied the effect in 1718. For capillary rise, Eq. (3) is also called the ascent formula.]

Question 10.
Find the pressure 200 m below the surface of the ocean if pressure on the free surface of liquid is one atmosphere. (Density of sea water = 1060 kg/m³) [Ans. 21.789 × 10⁵ N/m²]
Answer:
Data : h = 200 m, p = 1060 kg/m³,
p₀ = 1.013 × 10⁵ Pa, g = 9.8 m/s²
Absolute pressure,
p = p₀ + hρg
= (1.013 × 10³) + (200)(1060)(9.8)
= (1.013 × 10⁵) + (20.776 × 10⁵)
= 21.789 × 10⁵ = 2.1789 MPa

Question 11.
In a hydraulic lift, the input piston had surface area 30 cm² and the output piston has surface area of 1500 cm². If a force of 25 N is applied to the input piston, calculate weight on output piston. [Ans. 1250 N]
Answer:
Data : A₁ = 30 cm² = 3 × 10^-3 m²,
A₂ = 1500 cm² = 0.15 m², F₁ = 25 N
By Pascal’s law,
\(\frac{F_{1}}{A_{1}}\) = \(\frac{F_{2}}{A_{2}}\)
∴ The force on the output piston,
F₂ = F₁\(\frac{A_{2}}{A_{1}}\) = (25)\(\frac{0.15}{3 \times 10^{-3}}\) = 25 × 50 = 1250 N

Question 12.
Calculate the viscous force acting on a rain drop of diameter 1 mm, falling with a uniform velocity 2 m/s through air. The coefficient of viscosity of air is 1.8 × 10^-5 Ns/m².
[Ans. 3.393 × 10^-7 N]
Answer:
Data : d = 1 mm, v₀ = 2 m / s,
η = 1.8 × 10^-5 N.s/m²
r = \(\frac{d}{2}\) = 0.5 mm = 5 × 10^-4 m
By Stokes’ law, the viscous force on the raindrop is f = 6πηrv₀
= 6 × 3.142 (1.8 × 10^-5 N.s/m² × 5 × 10^-4 m)(2 m/s)
= 3.394 × 10^-7 N

Question 13.
A horizontal force of 1 N is required to move a metal plate of area 10^-2 m² with a velocity of 2 × 10^-2 m/s, when it rests on a layer of oil 1.5 × 10^-3 m thick. Find the coefficient of viscosity of oil. [Ans. 7.5 Ns/m²]
Answer:
Data : F = 1 N, A = 10^-2m², v₀ = 2 × 10^-2 y = 1.5 × 10^-3 m
Velocity gradient, \(\frac{d v}{d y}\) = \(\frac{2 \times 10^{-2}}{1.5 \times 10^{-3}}\) = \(\frac{40}{3}\)s^-1

Question 14.
With what terminal velocity will an air bubble 0.4 mm in diameter rise in a liquid of viscosity 0.1 Ns/m² and specific gravity 0.9? Density of air is 1.29 kg/m³. [Ans. – 0.782 × 10^-3 m/s, The negative sign indicates that the bubble rises up]
Answer:
Data : d = 0.4 mm, η = 0.1 Pa.s, ρ_L = 0.9 × 10³ kg/m³ = 900 kg/m³, ρ_air = 1.29 kg/m³, g = 9.8 m/s².
Since the density of air is less than that of oil, the air bubble will rise up through the liquid. Hence, the viscous force is downward. At terminal velocity, this downward viscous force is equal in magnitude to the net upward force.
Viscous force = buoyant force – gravitational force

Question 15.
The speed of water is 2m/s through a pipe of internal diameter 10 cm. What should be the internal diameter of nozzle of the pipe if the speed of water at nozzle is 4 m/s?
[Ans. 7.07 × 10^-2m]
Answer:
Data : d₁ = 10 cm = 0.1 m, v₁ = 2 m/s, v₂ = 4 m/s
By the equation of continuity, the ratio of the speed is

Question 16.
With what velocity does water flow out of an orifice in a tank with gauge pressure 4 × 10⁵ N/m² before the flow starts? Density of water = 1000 kg/m³. [Ans. 28.28 m/s]
Answer:
Data : ρ — ρ₀ = 4 × 10⁵ Pa, ρ = 10³ kg/m³
If the orifice is at a depth h from the water surface in a tank, the gauge pressure there is
ρ – ρ₀ = hρg … (1)
By Toricelli’s law of efflux, the velocity of efflux,
v = \(\sqrt{2 g h}\) …(2)
Substituting for h from Eq. (1),

Question 17.
The pressure of water inside the closed pipe is 3 × 10⁵ N/m². This pressure reduces to 2 × 10⁵ N/m² on opening the value of the pipe. Calculate the speed of water flowing through the pipe. (Density of water = 1000 kg/m³). [Ans. 14.14 m/s]
Answer:
Data : p₁ = 3 × 10⁵ Pa, v₁ = 0, p₂ = 2 × 10⁵ Pa, ρ = 10³ kg/m³
Assuming the potential head to be zero, i.e., the pipe to be horizontal, the Bernoulli equation is

Question 18.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10^-2 N/m. The angle of contact between water and glass is zero, density of water = 1000 kg/m³, g = 9.8 m/s².
[Ans. 0.1429 m]
Answer:
Data : r = 0.1 mm = 1 × 10^-4m, θ = 0°,
T = 7 × 10^-2 N/m, r = 10³ kg/m³, g = 9.8 m/s²
cos θ = cos 0° = 1

= 0.143 m

Question 19.
An air bubble of radius 0.2 mm is situated just below the water surface. Calculate the gauge pressure. Surface tension of water = 7.2 × 10^-2 N/m.
[Ans. 720 N/m²]
Answer:
Data : R = 2 × 10^-4m, T = 7.2 × 10^-2N/m, p = 10³ kg/m³
The gauge pressure inside the bubble = \(\frac{2 T}{R}\)
= \(\frac{2\left(7.2 \times 10^{-2}\right)}{2 \times 10^{-4}}\) = 7.2 × 10² = 720 Pa

Question 20.
Twenty seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m. [Ans. 1.628 × 10^-7 J = 1.628 erg]
Answer:
Data : r = 1 mm = 1 × 10^-3 m, T = 0.472 J/m²
Let R be the radius of the single drop formed due to the coalescence of 8 droplets of mercury.
Volume of 8 droplets = volume of the single drop as the volume of the liquid remains constant.
∴ 8 × \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)πR³
∴ 8r³ = R³
∴ 2r = R
Surface area of 8 droplets = 8 × 4πr²
Surface area of single drop = 4πR²
∴ Decrease in surface area = 8 × 4πr² – 4πR²
= 4π(8r² – R²)
= 4π[8r² – (2r)²]
= 4π × 4r²
∴ The energy released = surface tension × decrease in surface area = T × 4π × 4r²
= 0.472 × 4 × 3.142 × 4 × (1 × 10^-3)²
= 2.373 × 10^-5 J
The decrease in surface energy = 0.072 × 4 × 3.142 × 18 × (1 × 10^-4)²
= 1.628 × 10^-7 J

Question 21.
A drop of mercury of radius 0.2 cm is broken into 8 identical droplets. Find the work done if the surface tension of mercury is 435.5 dyne/cm. [Ans. 2.189 × 10^-5J]
Answer:
Let R be the radius of the drop and r be the radius of each droplet.
Data : R = 0.2 cm, n = 8, T = 435.5 dyn/cm
As the volume of the liquid remains constant, volume of n droplets = volume of the drop
∴ n × \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)πR³

Surface area of the drop = 4πR²
Surface area of n droplets = n × 4πR²
∴ The increase in the surface area = surface area of n droplets-surface area of drop
= 4π(nr² – R²) = 4π(8 × \(\frac{R^{2}}{4}\) – R²)
= 4π(2 — 1)R² = 4πR²
∴ The work done
= surface tension × increase in surface area
= T × 4πR² = 435.5 × 4 × 3.142 × (0.2)²
= 2.19 × 10² ergs = 2.19 × 10^-5 J

Question 22.
How much work is required to form a bubble of 2 cm radius from the soap solution having surface tension 0.07 N/m.
[Ans. 0.7038 × 10^-3 J]
Answer:
Data : r = 4 cm = 4 × 10^-2 m, T = 25 × 10^-3 N/m
Initial surface area of soap bubble = 0
Final surface area of soap bubble = 2 × 4πr²
∴ Increase in surface area = 2 × 4πr²
The work done
= surface tension × increase in surface area
= T × 2 × 4πr²
= 25 × 10^-3 × 2 × 4 × 3.142 × (4 × 10^-2)²
= 1.005 × 10^-3 J
The work done = 0.07 × 8 × 3.142 × (2 × 10^-2)²
= 7.038 × 10^-4 J

Question 23.
A rectangular wire frame of size 2 cm × 2 cm, is dipped in a soap solution and taken out. A soap film is formed, if the size of the film is changed to 3 cm × 3 cm, calculate the work done in the process. The surface tension of soap film is 3 × 10^-2 N/m. [Ans. 3 × 10^-5 J]
Answer:
Data : A₁ = 2 × 2 cm² = 4 × 10^-4 m²,
A₂ = 3 × 3 cm² =9 × 10^-4 m², T = 3 × 10^-2 N/m
As the film has two surfaces, the work done is W = 2T(A₂ – A₁)
= 2(3 × 10^-2)(9 × 10^-4 × 10^-4)
= 3.0 × 10^-5 J = 30 µJ

12th Physics Digest Chapter 2 Mechanical Properties of Fluids Intext Questions and Answers

Can you tell? (Textbook Page No. 27)

Question 1.
Why does a knife have a sharp edge or a needle has a sharp tip ?
Answer:
For a given force, the pressure over which the force is exerted depends inversely on the area of contact; smaller the area, greater the pressure. For instance, a force applied to an area of 1 mm² applies a pressure that is 100 times as great as the same force applied to an area of 1 cm². The edge of a knife or the tip of a needle has a small area of contact. That is why a sharp needle is able to puncture the skin when a small force is exerted, but applying the same force with a finger does not.

Use your brain power

Question 1.
A student of mass 50 kg is standing on both feet. Estimate the pressure exerted by the student on the Earth. Assume reasonable value to any quantity you need; justify your assumption. You may use g = 10 m/s², By what factor will it change if the student lies on back ?
Answer:
Assume area of each foot = area of a 6 cm × 25 cm rectangle.
∴ Area of both feet = 0.03 m²
∴ The pressure due to the student’s weight
= \(\frac{m g}{A}\) = \(\frac{50 \times 10}{0.03}\) = 16.7 kPa

According to the most widely used Du Bois formula for body surface area (BSA), the student’s BSA = 1.5 m², so that the area of his back is less than half his BSA, i.e., < 0.75 m². When the student lies on his back, his area of contact is much smaller than this. So, estimating the area of contact to be 0.3 m², i.e., 10 times more than the area of his feet, the pressure will be less by a factor of 10 or more, [Du Bois formula : BSA = 0.2025 × W^0.425 × H^0.725, where W is weight in kilogram and H is height in metre.]

Can you tell? (Textbook Page No. 30)

Question 1.
The figures show three containers filled with the same oil. How will the pressures at the reference compare ?

Answer:
Filled to the same level, the pressure is the same at the bottom of each vessel.

Use Your Brain Power (Textbook Page 35)

Question 1.
Prove that equivalent SI unit of surface tension is J/m².
Answer:
The SI unit of surface tension =

Try This (Textbook Page No. 36)

Question 1.
Take a ring of about 5 cm in diameter. Tie a thread slightly loose at two diametrically opposite points on the ring. Dip the ring into a soap solution and take it out. Break the film on any one side of the thread. Discuss what happens.
Answer:
On taking the ring out, there is a soap film stretched over the ring, in which the thread moves about quite freely. Now, if the film is punctured with a pin on one side-side A in below figure-then immediately the thread is pulled taut by the film on the other side as far as it can go. The thread is now part of a perfect circle, because the surface tension on the side F of the film acts everywhere perpendicular to the thread, and minimizes the surface area of the film to as small as possible.

Can You Tell ? (Textbook Page No. 38)

Question 1.
How does a waterproofing agent work ?
Answer:
Wettability of a surface, and thus its propensity for penetration of water, depends upon the affinity between the water and the surface. A liquid wets a surface when its contact angle with the surface is acute. A waterproofing coating has angle of contact obtuse and thus makes the surface hydrophobic.

Brain Teaser (Textbook Page No. 41)

Question 1.
Can you suggest any method to measure the surface tension of a soap solution? Will this method have any commercial application?
Answer:
There are more than 40 methods for determining equilibrium surface tension at the liquid-fluid and solid-fluid boundaries. Measuring the capillary rise (see Unit 2.4.7) is the laboratory method to determine surface tension.

Among the various techniques, equilibrium surface tension is most frequently measured with force tensiometers or optical (or the drop profile analysis) tensiometers in customized measurement setups.
[See https: / / www.biolinscientific.com /measurements /surface-tension]

Question 2.
What happens to surface tension under different gravity (e.g., aboard the International Space Station or on the lunar surface)?
Answer:
Surface tension does not depend on gravity.
[Note : The behaviour of liquids on board an orbiting spacecraft is mainly driven by surface tension phenomena. These make predicting their behaviour more difficult than under normal gravity conditions (i.e., on the Earth’s surface). New challenges appear when handling liquids on board a spacecraft, which are not usually present in terrestrial environments. The reason is that under the weightlessness (or almost weightlessness) conditions in an orbiting spacecraft, the different inertial forces acting on the bulk of the liquid are almost zero, causing the surface tension forces to be the dominant ones.

In this ‘micro-gravity’ environment, the surface tension forms liquid drops into spheres to minimize surface area, causes liquid columns in a capillary rise up to its rim (without over flowing). Also, when a liquid drop impacts on a dry smooth surface on the Earth, a splash can be observed as the drop disintegrates into thousands of droplets. But no splash is observed as the drop hits dry smooth surface on the Moon. The difference is the atmosphere. As the Moon has no atmosphere, and therefore no gas surrounding a falling drop, the drop on the Moon does not splash.
(See http://mafija.fmf.uni-Ij.si/]

Can you tell? (Textbook Page No. 45)

Question 1.
What would happen if two streamlines intersect?
Answer:
The velocity of a fluid molecule is always tangential to the streamline. If two streamlines intersect, the velocity at that point will not be constant or unique.

Activity

Question 1.
Identify some examples of streamline flow and turbulent flow in everyday life. How would you explain them ? When would you prefer a streamline flow?
Answer:
Smoke rising from an incense stick inside a wind-less room, air flow around a car or aeroplane in motion are some examples of streamline flow, Fish, dolphins, and even massive whales are streamlined in shape to reduce drag. Migratory birds species that fly long distances often have particular features such as long necks, and flocks of birds fly in the shape of a spearhead as that forms a streamlined pattern.

Turbulence results in wasted energy. Cars and aeroplanes are painstakingly streamlined to reduce fluid friction, and thus the fuel consumption. (See ‘Disadvantages of turbulence’ in the following box.) Turbulence is commonly seen in washing machines and kitchen mixers. Turbulence in these devices is desirable because it causes mixing. (Also see ‘Advantages of turbulence’ in the following box.) Recent developments in high-speed videography and computational tools for modelling is rapidly advancing our understanding of the aerodynamics of bird and insect flights which fascinate both physicists and biologists.

Use your Brain power (Textbook Page No. 46)

Question 1.
The CGS unit of viscosity is the poise. Find the relation between the poise and the SI unit of viscosity.
Answer:
By Newton’s law of viscosity,
\(\frac{F}{A}\) = η\(\frac{d v}{d y}\)
where \(\frac{F}{A}\) is the viscous drag per unit area, \(\frac{d v}{d y}\) is the velocity gradient and η is the coefficient of viscosity of the fluid. Rewriting the above equation as

SI unit : the pascal second (abbreviated Pa.s), 1 Pa.s = 1 N.m^-2.s
CGS unit: dyne.cm^-2.s, called the poise [symbol P, named after Jean Louis Marie Poiseuille (1799 -1869), French physician].
[Note : Thè most commonly used submultiples are the millipascalsecond (mPa.s) and the centipoise (cP). 1 mPa.s = 1 cP.]

Use your Brain power (Textbook Page No. 49)

Question 1.
A water pipe with a diameter of 5.0 cm is connected to another pipe of diameter 2.5 cm. How would the speeds of the water flow compare ?
Answer:
Water is an incompressible fluid (almost). Then, by the equation of continuity, the ratio of the speeds, is

Do you know? (Textbook Page No. 50)

Question 1.
How does an aeroplane take off?
Answer:
A Venturi meter is a horizontal constricted tube that is used to measure the flow speed through a pipeline. The constricted part of the tube is called the throat. Although a Venturi meter can be used for a gas, they are most commonly used for liquids. As the fluid passes through the throat, the higher speed results in lower pressure at point 2 than at point 1. This pressure difference is measured from the difference in height h of the liquid levels in the U-tube manometer containing a liquid of density ρ_m. The following treatment is limited to an incompressible fluid.

Let A₁ and A₂ be the cross-sectional areas at points 1 and 2, respectively. Let v₁ and v₂ be the corresponding flow speeds. ρ is the density of the fluid in the pipeline. By the equation of continuity,
v₁A₁ = v₂A₂ … (1)
Since the meter is assumed to be horizontal, from Bernoufli’s equation we get,

The pressure difference is equal to ρ_mgh, where h is the differences in liquid levels in the manometer.
Then,

Equation (3) gives the flow speed of an incompressible fluid in the pipeline. The flow rates of practical interest are the mass and volume flow rates through the meter.
Volume flow rate =A₁v₁ and mass flow rate = density × volume flow
rate = ρA₁v₁
[Note When a Venturi meter is used in a liquid pipeline, the pressure difference is measured from the difference in height h of the levels of the same liquid in the two vertical tubes, as shown in the figure. Then, the pressure difference is equal to ρgh.


The flow meter is named after Giovanni Battista Venturi (1746—1822), Italian physicist.]

Question 2.
Why do racer cars and birds have typical shape ?
Answer:
The streamline shape of cars and birds reduce drag.

Question 3.
Have you experienced a sideways jerk while driving a two wheeler when a heavy vehicle overtakes you ?
Answer:
Suppose a truck passes a two-wheeler or car on a highway. Air passing between the vehicles flows in a narrower channel and must increase its speed according to Bernoulli’s principle causing the pressure between them to drop. Due to greater pressure on the outside, the two-wheeler or car veers towards the truck.

When two ships sail parallel side-by-side within a distance considerably less than their lengths, since ships are widest toward their middle, water moves faster in the narrow gap between them. As water velocity increases, the pressure in between the ships decreases due to the Bernoulli effect and draws the ships together. Several ships have collided and suffered damage in the early twentieth century. Ships performing At-sea refueling or cargo transfers performed by ships is very risky for the same reason.

Question 4.
Why does dust get deposited only on one side of the blades of a fan ?
Answer:
Blades of a ceiling/table fan have uniform thickness (unlike that of an aerofoil) but are angled (cambered) at 8° to 12° (optimally, 10°) from their plane. When they are set rotating, this camber causes the streamlines above/behind a fan blade to detach away from the surface of the blade creating a very low pressure on that side. The lower/front streamlines however follow the blade surface. Dust particles stick to a blade when it is at rest as well as when in motion both by intermolecular force of adhesion and due to static charges. However, they are not dislodged from the top/behind surface because of complete detachment of the streamlines.

The lower/front surface retains some of the dust because during motion, a thin layer of air remains stationary relative to the blade.

Question 5.
Why helmets have specific shape?
Answer:
Air drag plays a large role in slowing bike riders (especially, bicycle) down. Hence, a helmet is aerodynamically shaped so that it does not cause too much drag.

Use your Brain power (Textbook Page No. 52)

Question 1.
Does the Bernoulli’s equation change when the fluid is at rest ? How ?
Answer:
Bernoulli’s principle is for fluids in motion. Hence, it is pointless to apply it to a fluid at rest. Nevertheless, for a fluid is at rest, the Bernoulli equation gives the pressure difference due to a liquid column.

For a static fluid, v₁ = v₂ = 0. Bernoulli’s equation in that case is p₁ + ρgh₁ = ρ₂ + ρgh₂

Further, taking h₂ as the reference height of zero, i.e., by setting h₂ = 0, we get p₂ = p₁ + ρgh₁

This equation tells us that in static fluids, pressure increases with depth. As we go from point 1 to point 2 in the fluid, the depth increases by h₁ and consequently, p₂ is greater than p₁ by an amount ρgh₁.

In the case, p₁ = p₀, the atmospheric pressure at the top of the fluid, we get the familiar gauge pressure at a depth h₁ = ρgh₁. Thus, Bernoulli’s equation confirms the fact that the pressure change due to the weight of a fluid column of length h is ρgh.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 3 Kinetic Theory of Gases and Radiation Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 3 Kinetic Theory of Gases and Radiation

1. Choose the correct option.

i) In an ideal gas, the molecules possess
(A) only kinetic energy
(B) both kinetic energy and potential energy
(C) only potential energy
(D) neither kinetic energy nor potential energy
Answer:
(A) only kinetic energy

ii) The mean free path λ of molecules is given by
(A) \(\sqrt{\frac{2}{\pi n d^{2}}}\)
(B) \(\frac{1}{\pi n d^{2}}\)
(C) \(\frac{1}{\sqrt{2} \pi n d^{2}}\)
(D) \(\frac{1}{\sqrt{2 \pi n d^{1}}}\)
where n is the number of molecules per unit volume and d is the diameter of the molecules.
Answer:
(C) \(\frac{1}{\sqrt{2} \pi n d^{2}}\)

iii) If pressure of an ideal gas is decreased by 10% isothermally, then its volume will
(A) decrease by 9%
(B) increase by 9%
(C) decrease by 10%
(D) increase by 11.11%
Answer:
(D) increase by 11.11% [Use the formula P₁V₁ = P₂V₂. It gives \(\frac{V_{2}}{V_{1}}\) = \(\frac{1}{0.9}\) = 1.111 ∴ \(\frac{V_{2}-V_{1}}{V_{1}}\) = 0.1111, i.e., 11.11%

iv) If a = 0.72 and r = 0.24, then the value of t_r is
(A) 0.02
(B) 0.04
(C) 0.4
(D) 0.2
Answer:
(B) 0.04

v) The ratio of emissive power of a perfect blackbody at 1327°C and 527°C is
(A) 4 : 1
(B) 16 : 1
(C) 2 : 1
(D) 8 : 1
Answer:
(B) 16 : 1

2. Answer in brief.

i) What will happen to the mean square speed of the molecules of a gas if the temperature of the gas increases?
Answer:
If the temperature of a gas increases, the mean square speed of the molecules of the gas will increase in the same proportion.
[Note: \(\overline{v^{2}}\) = \(\frac{3 n R T}{N m}\) ∴ \(\overline{v^{2}}\) ∝ T for a fixed mass of gas.]

ii) On what factors do the degrees of freedom depend?
Answer:
The degrees of freedom depend upon
(i) the number of atoms forming a molecule
(ii) the structure of the molecule
(iii) the temperature of the gas.

iii) Write ideal gas equation for a mass of 7 g of nitrogen gas.
Answer:
In the usual notation, PV = nRT.

Therefore, the corresponding ideal gas equation is
PV = \(\frac{1}{4}\)RT.

iv) What is an ideal gas ? Does an ideal gas exist in practice ?.
Answer:
An ideal or perfect gas is a gas which obeys the gas laws (Boyle’s law, Charles’ law and Gay-Lussac’s law) at all pressures and temperatures. An ideal gas cannot be liquefied by application of pressure or lowering the temperature.

A molecule of an ideal gas is an ideal particle having only mass and velocity. Its structure and size are ignored. Also, intermolecular forces are zero except during collisions

v) Define athermanous substances and diathermanous substances.
Answer:

1. A substance which is largely opaque to thermal radiations, i.e., a substance which does not transmit heat radiations incident on it, is known as an athermanous substance.
2. A substance through which heat radiations can pass is known as a diathermanous substance.

Question 3.
When a gas is heated its temperature increases. Explain this phenomenon based on kinetic theory of gases.
Answer:
Molecules of a gas are in a state of continuous random motion. They possess kinetic energy. When a gas is heated, there is increase in the average kinetic energy per molecule of the gas. Hence, its temperature increases (the average kinetic energy per molecule being proportional to the absolute temperature of the gas).

Question 4.
Explain, on the basis of kinetic theory, how the pressure of gas changes if its volume is reduced at constant temperature.
Answer:
The average kinetic energy per molecule of a gas is constant at constant temperature. When the volume of a gas is reduced at constant temperature, the number of collisions of gas molecules per unit time with the walls of the container increases. This increases the momentum transferred per unit time per unit area, i.e., the force exerted by the gas on the walls. Hence, the pressure of the gas increases.

Question 5.
Mention the conditions under which a real gas obeys ideal gas equation.
Answer:
A real gas obeys ideal gas equation when temperature is vey high and pressure is very low.
[ Note : Under these conditions, the density of a gas is very low. Hence, the molecules, on an average, are far away from each other. The intermolecular forces are then not of much consequence. ]

Question 6.
State the law of equipartition of energy and hence calculate molar specific heat of mono-and di-atomic gases at constant volume and constant pressure.
Answer:
Law of equipartition of energy : For a gas in thermal equilibrium at absolute temperature T, the average energy for a molecule, associated with each quadratic term (each degree of freedom), is \(\frac{1}{2}\)k_BT,
where k_B is the Boltzmann constant. OR

The energy of the molecules of a gas, in thermal equilibrium at a thermodynamic temperature T and containing large number of molecules, is equally divided among their available degrees of freedom, with the energy per molecule for each degree of freedom equal to \(\frac{1}{2}\)k_BT, where k_B is the Boltzmann constant.
(a) Monatomic gas : For a monatomic gas, each atom has only three degrees of freedom as there can be only translational motion. Hence, the average energy per atom is \(\frac{3}{2}\)k_BT. The total internal energy per mole of the gas is E = \(\frac{3}{2}\)N_Ak_BT, where N_A is the Avogadro
number.
Therefore, the molar specific heat of the gas at constant volume is
C_V = \(\frac{d E}{d T}\) = \(\frac{3}{2}\)N_Ak_B = \(\frac{3}{2}\)R,
where R is the universal gas constant.
Now, by Mayer’s relation, C_p — C_v = R, where C_p is the specific heat of the gas at constant pressure.
∴ C_P = C_V + R = \(\frac{3}{2}\)R + R = \(\frac{5}{2}\)R

(b) Diatomic gas : Treating the molecules of a diatomic gas as rigid rotators, each molecule has three translational degrees of freedom and two rotational degrees of freedom. Hence, the average energy per molecule is
3(\(\frac{1}{2}\)k_BT) + 2(\(\frac{1}{2}\)k_BT) = \(\frac{5}{2}\)k_BT
The total internal energy per mole of the gas is
E = \(\frac{5}{2}\)N_Ak_BT.
∴ C_V = \(\frac{d E}{d T}\) = \(\frac{5}{2}\)N_Ak_B = \(\frac{5}{2}\)R and
C_P = C_V + R = \(\frac{5}{2}\)R + R = \(\frac{7}{2}\)R
A soft or non-rigid diatomic molecule has, in addition, one frequency of vibration which contributes two quadratic terms to the energy.
Hence, the energy per molecule of a soft diatomic molecule is

Therefore, the energy per mole of a soft diatomic molecule is
E = \(\frac{7}{2}\)k_BT × N_A = \(\frac{7}{2}\) RT
In this case, C_V = \(\frac{d E}{d T}\) = \(\frac{7}{2}\)R and
C_P = C_V + R = \(\frac{7}{2}\)R + R = \(\frac{9}{2}\)R
[Note : For a monatomic gas, adiabatic constant,
γ = \(\frac{C_{p}}{C_{V}}\) = \(\frac{5}{3}\). For a diatomic gas, γ =\(\frac{7}{5}\) or \(\frac{9}{7}\).]

Question 7.
What is a perfect blackbody ? How can it be realized in practice?
Answer:
A perfect blackbody or simply a blackbody is defined as a body which absorbs all the radiant energy incident on it.

Fery designed a spherical blackbody which consists of a hollow double-walled, metallic sphere provided with a tiny hole or aperture on one side, in below figure. The inside wall of the sphere is blackened with lampblack while the outside is silver-plated. The space between the two walls is evacuated to minimize heat loss by conduction and convection.

Any radiation entering the sphere through the aperture suffers multiple reflections where about 97% of it is absorbed at each incidence by the coating of lampblack. The radiation is almost completely absorbed after a number of internal reflections. A conical projection on the inside wall opposite the hole minimizes probability of incident radiation escaping out.

When the sphere is placed in a bath of suitable fused salts, so as to maintain it at the desired temperature, the hole serves as a source of black-body radiation. The intensity and the nature of the radiation depend only on the temperature of the walls.

A blackbody, by definition, has coefficient of absorption equal to 1. Hence, its coefficient of reflection and coefficient of transmission are both zero.

The radiation from a blackbody, called blackbody radiation, covers the entire range of the electromagnetic spectrum. Hence, a blackbody is called a full radiator.

Question 8.
State (i) Stefan-Boltmann law and
(ii) Wein’s displacement law.
Answer:
(i) The Stefan-Boltzmann law : The rate of emission of radiant energy per unit area or the power radiated per unit area of a perfect blackbody is directly proportional to the fourth power of its absolute temperature. OR
The quantity of radiant energy emitted by a perfect blackbody per unit time per unit surface area of the body is directly proportional to the fourth power of its absolute temperature.

(ii) Wien’s displacement law : The wavelength for which the emissive power of a blackbody is maximum, is inversely proportional to the absolute temperature of the blackbody.
OR
For a blackbody at an absolute temperature T, the product of T and the wavelength λ_m corresponding to the maximum radiation of energy is a constant.
λ_mT = b, a constant.
[Notes: (1) The law stated above was stated by Wilhelm Wien (1864-1928) German Physicist. (2) The value of the constant b in Wien’s displacement law is 2.898 × 10^-3 m.K.]

Question 9.
Explain spectral distribution of blackbody radiation.
Answer:
Blackbody radiation is the electromagnetic radiation emitted by a blackbody by virtue of its temperature. It extends over the whole range of wavelengths of electromagnetic waves. The distribution of energy over this entire range as a function of wavelength or frequency is known as the spectral distribution of blackbody radiation or blackbody radiation spectrum.

If R_λ is the emissive power of a blackbody in the wavelength range λ and λ + dλ, the energy it emits per unit area per unit time in this wavelength range depends on its absolute temperature T, the wavelength λ and the size of the interval dλ.

Question 10.
State and prove Kirchoff’s law of heat radiation.
Answer:
Kirchhoff’s law of heat radiation : At a given temperature, the ratio of the emissive power to the coefficient of absorption of a body is equal to the emissive power of a perfect blackbody at the same temperature for all wavelengths.
OR
For a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity.

Theoretical proof: Consider the following thought experiment: An ordinary body A and a perfect black body B are enclosed in an athermanous enclosure as shown in below figure.

According to Prevost’s theory of heat exchanges, there will be a continuous exchange of radiant energy between each body and its surroundings. Hence, the two bodies, after some time, will attain the same temperature as that of the enclosure.

Let a and e be the coefficients of absorption and emission respectively, of body A. Let R and R_b be the emissive powers of bodies A and B, respectively. ;

Suppose that Q is the quantity of radiant energy incident on each body per unit time per unit surface area of the body.

Body A will absorb the quantity aQ per unit time per unit surface area and radiate the quantity R per unit time per unit surface area. Since there is no change in its temperature, we must have,
aQ = R … (1)
As body B is a perfect blackbody, it will absorb the quantity Q per unit time per unit surface area and radiate the quantity R_b per unit time per unit surface area.

Since there is no change in its temperature, we must have,
Q = R_b ….. (2)
From Eqs. (1) and (2), we get,
a = \(\frac{R}{Q}\) = \(\frac{R}{R_{\mathrm{b}}}\) ….. (3)
From Eq. (3), we get, \(\frac{R}{a}\) = R_b OR

By definition of coefficient of emission,
\(\frac{R}{R_{\mathrm{b}}}\) …(4)
From Eqs. (3) and (4), we get, a = e.
Hence, the proof of Kirchhoff ‘s law of radiation.

Question 11.
Calculate the ratio of mean square speeds of molecules of a gas at 30 K and 120 K. [Ans: 1:4]
Answer:
Data : T₁ = 30 K, T₂ = 120 K

This is the required ratio.

Question 12.
Two vessels A and B are filled with same gas where volume, temperature and pressure in vessel A is twice the volume, temperature and pressure in vessel B. Calculate the ratio of number of molecules of gas in vessel A to that in vessel B.
[Ans: 2:1]
Answer:
Data : V_A = 2V_B, T_A = 2T_B, P_A = 2P_B PV = Nk_BT

This is the required ratio.

Question 13.
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one third of their original value and their speeds are doubled, then find the resultant pressure. [Ans: 4/3 P]
Answer:
Data : m₂ = m₁/3, v_{rms 2} = 2v_{rms 1} as the speeds of all molecules are doubled

This is the resultant pressure.

Question 14.
Show that rms velocity of an oxygen molecule is \(\sqrt{2}\) times that of a sulfur dioxide molecule at S.T.P.
Answer:

Question 15.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively)
[Ans: 2184 K]
Answer:
Data : T₂ = 273 K, M₀₁ (oxygen) = 32 × 10^-3 kg/mol, M₀₂ (hydrogen) = 4 × 10^{– 3} kg/mol
The rms speed of oxygen molecules, v₁ = \(\sqrt{\frac{3 R T_{1}}{M_{01}}}\) and that of helium molecules, v₂ = \(\sqrt{\frac{3 R T_{2}}{M_{02}}}\)
When v₁ = v₂,

Question 16.
Compare the rms speed of hydrogen molecules at 127 ºC with rms speed of oxygen molecules at 27 ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively. [Ans: 8: 3]
Answer:
Data : M₀₁ (hydrogen) = 2 g/mol,
M₀₂ (oxygen) = 32 g/mol,
T₁ (hydrogen) = 273 + 127 = 400 K,
T₂ (oxygen) = 273 + 27 = 300 K
The rms speed, v_rms = \(\sqrt{\frac{3 R T}{M_{0}}}\),
where M₀ denotes the molar mass

Question 17.
Find kinetic energy of 5000 cc of a gas at S.T.P. given standard pressure is 1.013 × 10⁵ N/m².
[Ans: 7.598 × 10² J]
Answer:
Data : P = 1.013 × 10⁵ N/m², V = 5 litres
= 5 × 10^-3 m³
E = \(\frac{3}{2}\)PV
= \(\frac{3}{2}\)(1.013 × 10⁵ N/m²) (5 × 10^-3 m³)
= 7.5 × 1.013 × 10² J = 7.597 × 10² J
This is the required energy.

Question 18.
Calculate the average molecular kinetic energy
(i) per kmol
(ii) per kg
(iii) per molecule of oxygen at 127 ºC, given that molecular weight of oxygen is 32, R is 8.31 J mol^-1 K^-1 and Avogadro’s number N_A is 6.02 × 10²³ molecules mol^-1.
[Ans: 4.986 × 10⁶J, 1.558 × 10²J 8.282 × 10^-21 J]
Answer:
Data : T = 273 +127 = 400 K, molecular weight = 32 ∴ molar mass = 32 kg/kmol, R = 8.31 Jmol^-1 K^-1, N_A = 6.02 × 10²³ molecules mol^-1

(i) The average molecular kinetic energy per kmol of oxygen = the average kinetic energy per mol of oxygen × 1000
= \(\frac{3}{2}\)RT × 1000 = \(\frac{3}{2}\) (8.31) (400) (10³)\(\frac{\mathrm{J}}{\mathrm{kmol}}\)
= (600)(8.31)(10³) = 4.986 × 10⁶ J/kmol

(ii) The average molecular kinetic energy per kg of

(iii) The average molecular kinetic energy per molecule of oxygen

Question 19.
Calculate the energy radiated in one minute by a blackbody of surface area 100 cm² when it is maintained at 227ºC. (Take Stefen’s constant σ = 5.67 × 10^-8J m^-2s^-1K^-4)
[Ans: 2126.25 J]
Answer:
Data : t = one minute = 60 s, A = 100 cm²
= 100 × 10^-4 m² = 10^-2 m², T = 273 + 227 = 500 K,
σ = 5.67 × 10^-8 W/m².K⁴
The energy radiated, Q = σAT⁴t
= (5.67 × 10^-8)(10^-2)(500)⁴(60) J
= (5.67)(625)(60)(10^-2)J = 2126 J

Question 20.
Energy is emitted from a hole in an electric furnace at the rate of 20 W, when the temperature of the furnace is 727 ºC. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10^-8 J s^-1 m^-2 K^-4) [Ans: 3.509 × 10^-4m²]
Answer:
Data : \(\frac{Q}{t}\) = 20 W, T = 273 + 727 = 1000 K

Question 21.
The emissive power of a sphere of area 0.02 m² is 0.5 kcal s^-1 m^-2. What is the
amount of heat radiated by the spherical surface in 20 second? [Ans: 0.2 kcal]
Answer:
Data : R = 0.5 kcal s^-1m^-2, A = 0.02 m², t = 20 s Q = RAt = (0.5) (0.02) (20) = 0.2 kcal
This is the required quantity.

Question 22.
Compare the rates of emission of heat by a blackbody maintained at 727ºC and at 227ºC, if the black bodies are surrounded
by an enclosure (black) at 27ºC. What would be the ratio of their rates of loss of heat ?
[Ans: 18.23:1]
Answer:
Data : T₁ = 273 + 727 = 1000 K, T₂ = 273 + 227 = 500 K, T₀ = 273 + 27 = 300 K.
(i) The rate of emission of heat, \(\frac{d Q}{d t}\) = σAT⁴.
We assume that the surface area A is the same for the two bodies.

Question 23.
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λ_max. In which part of the electromagnetic spectrum, does this value lie? (Take Wien’s constant b = 2.897 × 10^-3 m K) [Ans: 1.035 × 10^-5m, infrared region]
Answer:
Data : T = 280 K, Wien’s constant b = 2.897 × 10^-3 m.K
λ_maxT = b

This value lies in the infrared region of the electromagnetic spectrum.
The nature of the curve of blackbody radiation will be the same as shown in above, but the maximum will occur at 1.035 × 10^-5 m.

Question 24.
A small-blackened solid copper sphere of radius 2.5 cm is placed in an evacuated chamber. The temperature of the chamber is maintained at 100 ºC. At what rate energy must be supplied to the copper sphere to maintain its temperature at 110 ºC? (Take Stefan’s constant σ to be 5.670 × 10^-8 J s^-1 m^-2 K^-4 , π = 3.1416 and treat the sphere as a blackbody.)
[Ans: 0.9624 W]
Answer:
Data : r = 2.5 cm = 2.5 × 10^-2 m, T₀ = 273 + 100 = 373 K, T = 273 + 110 = 383 K,
σ = 5.67 × 10^-8 J s^-1 m^-2 k^-4
The rate at which energy must be supplied
σA(T⁴ — T₀⁴) = σ 4πr²(T⁴ – T₀⁴)
= (5.67 × 10^-8) (4) (3.142) (2.5 × 10^-2)² (383⁴ – 373⁴)
= (5.67) (4) (3.142) (6.25) (3.83⁴ – 3.73⁴) × 10^-4
= 0.9624W

Question 25.
Find the temperature of a blackbody if its spectrum has a peak at (a) λ_max = 700 nm (visible), (b) λ_max = 3 cm (microwave region) and (c) λ_max = 3 m (short radio waves) (Take Wien’s constant b = 2.897 × 10^-3 m K). [Ans: (a) 4138 K, (b) 0.09657 K, (c) 0.9657 × 10^-3 K]
Answer:
Data:(a) λ_max = 700nm=700 × 10^-9m,
(b) λ_max = 3cm = 3 × 10^-2 m, (c) λ_max = 3 m, b = 2.897 × 10^-3 m.K
λ_maxT = b

12th Physics Digest Chapter 3 Kinetic Theory of Gases and Radiation Intext Questions and Answers

Remember This (Textbook Page No. 60)

Question 1.
Distribution of speeds of molecules of a gas.
Answer:
Maxwell-Boltzmann distribution of molecular speeds is a relation that describes the distribution of speeds among the molecules of a gas at a given temperature.

The root-mean-square speed v_rms gives us a general idea of molecular speeds in a gas at a given temperature. However, not all molecules have the same speed. At any instant, some molecules move slowly and some very rapidly. In classical physics, molecular speeds may be considered to cover the range from 0 to ∞. The molecules constantly collide with each other and with the walls of the container and their speeds change on collisions. Also the number of molecules under consideration is very large statistically. Hence, there is an equilibrium distribution of speeds.

If dN_v represents the number of molecules with speeds between v and v + dv, dN_v remains fairly constant at equilibrium. We consider a gas of total N molecules. Let r\vdv be the probability that a molecule has its speed between v and v + dv. Then, dN_v = Nη_vdv
so that the fraction, i.e., the relative number of molecules with speeds between v and v + dv is dN_v/N = η_vdv
Below figure shows the graph of η_v against v. The area of the strip with height η_v and width dv gives the fraction dN_v/N.

Remember This (Textbook Page No. 64)

Question 1.
If a hot body and a cold body are kept in vacuum, separated from each other, can they exchange heat ? If yes, which mode of transfer of heat causes change in their temperatures ? If not, give reasons.
Answer:
Yes. Radiation.

Remember This (Textbook Page No. 66)

Question 1.
Can a perfect blackbody be realized in practice ?
Answer:
For almost all practical purposes, Fery’s blackbody is very close to a perfect blackbody.

Question 2.
Are good absorbers also good emitters ?
Answer:
Yes.

Use your brain power (Textbook Page No. 68)

Question 1.
Why are the bottom of cooking utensils blackened and tops polished ?
Answer:
The bottoms of cooking utensils are blackened to increase the rate of absorption of radiant energy and tops are polished to increase the reflection of radiation.

Question 2.
A car is left in sunlight with all its windows closed on a hot day. After some time it is observed that the inside of the car is warmer than outside air. Why ?
Answer:
The air inside the car is trapped and hence is a bad conductor of heat.

Question 3.
If surfaces of all bodies are continuously emitting radiant energy, why do they not cool down to 0 K ?
Answer:
Bodies absorb radiant energy from the surroundings.

Can you tell? (Textbook Page No. 71)

Question 1.
λ_max the wavelength corresponding to maximum intensity for the Sun is in the blue-green region of visible spectrum. Why does the Sun then appear yellow to us ?
Answer:
The colour that we perceive depends upon a number of factors such as absorption and scattering by atmosphere (which in turn depends upon the composition of air) and spectral response of the human eye. The colour may be yellow/orange/ red/white.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 15 Structure of Atoms and Nuclei Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 15 Structure of Atoms and Nuclei

In solving problems, use m_e = 0.00055 u = 0.5110 MeV/c², m_p = 1.00728 u, m_n = 1.00866u, m_H = 1.007825 u, u = 931.5 MeV, e = 1.602 × 10^-19 C, h = 6.626 × 10^-34 Js, ε₀ = 8.854 × 10^-12 SI units and me = 9.109 × 10^-31 kg.

1. Choose the correct option.

i) In which of the following systems will the radius of the first orbit of the electron be the smallest?
(A) hydrogen
(B) singly ionized helium
(C) deuteron
(D) tritium
Answer:
(D) tritium

ii) The radius of the 4th orbit of the electron will be smaller than its 8th orbit by a factor of
(A) 2
(B) 4
(C) 8
(D) 16
Answer:
(B) 4

iii) In the spectrum of hydrogen atom which transition will yield longest wavelength?
(A) n = 2 to n = 1
(B) n = 5 to n = 4
(C) n = 7 to n = 6
(D) n = 8 to n = 7
Answer:
(D) n = 8 to n = 7

iv) Which of the following properties of a nucleus does not depend on its mass number?
(A) radius
(B) mass
(C) volume
(D) density
Answer:
(D) density

v) If the number of nuclei in a radioactive sample at a given time is N, what will be the number at the end of two half-lives?
(A) \(\frac{N}{2}\)
(B) \(\frac{N}{4}\)
(C) \(\frac{3N}{4}\)
(D) \(\frac{N}{8}\)
Answer:
(B) \(\frac{N}{4}\)

2. Answer in brief.

i) State the postulates of Bohr’s atomic model.
Answer:
The postulates of Bohr’s atomic model (for the hydrogen atom) :

1. The electron revolves with a constant speed in acircular orbit around the nucleus. The necessary centripetal force is the Coulomb force of attraction of the positive nuclear charge on the negatively charged electron.
2. The electron can revolve without radiating energy only in certain orbits, called allowed or stable orbits, in which the angular momentum of the electron is equal to an integral multiple of h/2π, where h is Planck’s constant.
3. Energy is radiated by the electron only when it jumps from one of its orbits to another orbit having lower energy. The energy of the quantum of elec-tromagnetic radiation, i.e., the photon, emitted is equal to the energy difference of the two states.

ii) State the difficulties faced by Rutherford’s atomic model.
Answer:
(1) According to Rutherford, the electrons revolve in circular orbits around the atomic nucleus. The circular motion is an accelerated motion. According to the classical electromagnetic theory, an accelerated charge continuously radiates energy. Therefore, an electron during its orbital motion, should go on radiating energy. Due to the loss of energy, the radius of its orbit should go on decreasing. Therefore, the electron should move along a spiral path and finally fall into the nucleus in a very short time, of the order of 10^-16 s in the case of a hydrogen atom. Thus, the atom should be unstable. We exist because atoms are stable.

(2) If the electron moves along such a spiral path, the radius of its orbit would continuously decrease. As a result, the speed and frequency of revolution of the electron would go on increasing. The electron, therefore, would emit radiation of continuously changing frequency, and hence give rise to a con-tinuous spectrum. However, atomic spectrum is a line spectrum.

iii) What are alpha, beta and gamma decays?
Answer:
(a) A radioactive transformation in which an α-particle is emitted is called α-decay.
In an α-decay, the atomic number of the nucleus decreases by 2 and the mass number decreases by 4.
Example : \({ }_{92}^{238} \mathrm{U} \rightarrow{ }_{90}^{234} \mathrm{Th}+{ }_{2}^{4} \alpha\)
Q = [m_u – m_Th – m_α]c²

(b) A radioactive transformation in which a β-particle is emitted is called β-decay.
In a β^–-decay, the atomic number of the nucleus increases by 1 and the mass number remains unchanged.
Example : \({ }_{90}^{234} \mathrm{Th} \rightarrow{ }_{91}^{234} \mathrm{~Pa}+{ }_{-1}^{0} e+\bar{v}_{\mathrm{e}}\)
where \(\bar{v}_{\mathrm{e}}\) is the neutrino emitted to conserve the momentum, energy and spin.
Q = [m_u – m_Th – m_α]c²
In a β⁺-decay, the atomic number of the nucleus decreases by 1 and the mass number remains unchanged.
Example : \(\begin{aligned}
&30 \\
&15
\end{aligned} P \rightarrow{ }_{14}^{30} \mathrm{Si}+{ }_{+1}^{0} e+v_{\mathrm{e}}\)
where v_e is the neutrino emitted to conserve the momentum, energy and spin.
Q = [m_P – m_Si – m_e]c²
[Note : The term fi particle refers to the electron (or positron) emitted by a nucleus.]

A given nucleus does not emit α and β-particles simultaneously. However, on emission of α or β-particles, most nuclei are left in an excited state. A nucleus in an excited state emits a γ-ray photon in a transition to the lower energy state. Hence, α and β-particle emissions are often accompanied by γ-rays.

iv) Define excitation energy, binding energy and ionization energy of an electron in an atom.
Answer:
(1) Excitation energy of an electron in an atom : The energy required to transfer an electron from the ground state to an excited state (a state of higher energy) is called the excitation energy of the electron in that state.

(2) Binding energy of an electron in an atom is defined as the minimum energy that should be provided to an orbital electron to remove it from the atom such that its total energy is zero.

(3) Ionization energy of an electron in an atom is defined as the minimum energy required to remove the least strongly bound electron from a neutral atom such that its total energy is zero.

v) Show that the frequency of the first line in Lyman series is equal to the difference between the limiting frequencies of Lyman and Balmer series.
Answer:
For the first line in the Lyman series,
\(\frac{1}{\lambda_{\mathrm{L} 1}}=R\left(\frac{1}{1^{2}}-\frac{1}{2^{2}}\right)=R\left(1-\frac{1}{4}\right)=\frac{3 R}{4}\)
∴ v_L1 = \(\frac{c}{\lambda_{\mathrm{L} 1}}=\frac{3 R_{c}}{4}\), where v denotes the frequency,
c the speed of light in free space and R the Rydberg constant.
For the limit of the Lyman series,

Hence, the result.

Question 3.
State the postulates of Bohr’s atomic model and derive the expression for the energy of an electron in the atom.
Answer:
The postulates of Bohr’s atomic model (for the hydrogen atom) :
(1) The electron revolves with a constant speed in acircular orbit around the nucleus. The necessary centripetal force is the Coulomb force of attraction of the positive nuclear charge on the negatively charged electron.
(2) The electron can revolve without radiating energy only in certain orbits, called allowed or stable orbits, in which the angular momentum of the electron is equal to an integral multiple of h/2π, where h is Planck’s constant.
(3) Energy is radiated by the electron only when it jumps from one of its orbits to another orbit having lower energy. The energy of the quantum of elec-tromagnetic radiation, i.e., the photon, emitted is equal to the energy difference of the two states.

Consider the electron revolving in the nth orbit around the nucleus of an atom with the atomic number Z. Let m and e be the mass and the charge of the electron, r the radius of the orbit and v the linear speed of the electron.

According to Bohr’s first postulate, centripetal force on the electron = electrostatic force of attraction exerted on the electron by the nucleus
∴ \(\frac{m v^{2}}{r}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Z e^{2}}{r^{2}}\) ……………. (1)
where ε₀ is the permittivity of free space.
∴ Kinetic energy (KE) of the electron
= \(\frac{1}{2} m v^{2}=\frac{Z e^{2}}{8 \pi \varepsilon_{0} r}\) ………….. (2)
The electric potential due to the nucleus of charge +Ze at a point at a distance r from it is
V = \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\mathrm{Ze}}{r}\)
∴ Potential energy (PE) of the electron
= charge on the electron × electric potential
= – e × \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e}{r}=-\frac{Z e^{2}}{4 \pi \varepsilon_{0} r}\) …………….. (3)
Hence, the total energy of the electron in the nth orbit is
E = KE + PE = \(\frac{-Z e^{2}}{4 \pi \varepsilon_{0} r}+\frac{Z e^{2}}{8 \pi \varepsilon_{0} r}\)
∴ E = \(-\frac{Z e^{2}}{8 \pi \varepsilon_{0} r}\) ………….. (4)
This shows that the total energy of the electron in the nth orbit of the atom is inversely proportional to the radius of the orbit as Z, ε₀ and e are constants. The radius of the nth orbit of the electron is
r = \(\frac{\varepsilon_{0} h^{2} n^{2}}{\pi m Z e^{2}}\) …………….. (5)
where h is Planck’s constant.
From Eqs. (4) and (5), we get,
E_n = \(-\frac{Z e^{2}}{8 \pi \varepsilon_{0}}\left(\frac{\pi m Z e^{2}}{\varepsilon_{0} h^{2} n^{2}}\right)=-\frac{m Z^{2} e^{4}}{8 \varepsilon_{0}^{2} h^{2} n^{2}}\) ……………… (6)
This gives the expression for the energy of the electron in the nth Bohr orbit. The minus sign in the expression shows that the electron is bound to the nucleus by the electrostatic force of attraction.
As m, Z, e, ε₀ and h are constant, we get
E_n ∝ \(\frac{1}{n^{2}}\)
i.e., the energy of the electron in a stationary energy state is discrete and is inversely proportional to the square of the principal quantum number.
[ Note : Energy levels are most conveniently expressed in electronvolt. Hence, substituting the values of m, e, £0 and h, and dividing by the conversion factor 1.6 × 10^-19 J/eV,
E_n ≅ \(-\frac{13.6 Z^{2}}{n^{2}}\) (in eV)
For hydrogen, Z = 1
∴ E_n ≅ \(-\frac{13.6}{n^{2}}\) (in eV).

Question 4.
Starting from the formula for energy of an electron in the n^th orbit of hydrogen atom, derive the formula for the wavelengths of Lyman and Balmer series spectral lines and determine the shortest wavelengths of lines in both these series.
Answer:
According to Bohr’s third postulate for the model of the hydrogen atom, an atom radiates energy only when an electron jumps from a higher energy state to a lower energy state and the energy of the
quantum of electromagnetic radiation emitted in this process is equal to the energy difference between the two states of the electron. This emission of radiation gives rise to a spectral line.

The energy of the electron in a hydrogen atom,
when it is in an orbit with the principal quantum
number n, is
E_n = \(-\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2} n^{2}}\)
where m = mass of electron, e = electronic charge, h = Planck’s constant and = permittivity of free space.

Let E_m be the energy of the electron in a hydrogen atom when it is in an orbit with the principal quantum number m and E, its energy in an orbit with the principal quantum number n, n < m. Then
E_m = \(-\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2} m^{2}}\) and E_n = \(-\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2} m^{2}}\)
Therefore, the energy radiated when the electron jumps from the higher energy state to the lower energy state is
E_m – E_n = \(\frac{-m e^{4}}{8 \varepsilon_{0}^{2} h^{2} m^{2}}-\left(-\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2} n^{2}}\right)\)
= \(\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2}}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\)
This energy is emitted in the form of a quantum of radiation (photon) with energy hv, where V is the frequency of the radiation.
∴ E_m – E_n = hv
∴ v = \(\frac{E_{m}-E_{n}}{h}=\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{3}}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\)
The wavelength of the radiation is λ = \(\frac{c}{v^{\prime}}\)
where c is the speed of radiation in free space.
The wave number, \(\bar{v}=\frac{1}{\lambda}=\frac{v}{c}\)
\(\bar{v}=\frac{1}{\lambda}=\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{3} c}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)=R\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\)
where \(R\left(=\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{3} c}\right)\) is a constant called the Ryd berg constant.

This expression gives the wave number of the radiation emitted and hence that of a line in hydrogen spectrum.

For the Lyman series, n = 1,m = 2, 3, 4, ………… ∞
∴ \(\frac{1}{\lambda_{\mathrm{L}}}=R\left(\frac{1}{1^{2}}-\frac{1}{m^{2}}\right)\) and for the shortest wavelength line m this series, \(\frac{1}{\lambda_{\mathrm{Ls}}}=R\left(\frac{1}{1^{2}}\right)\) as m = ∞.
For the Balmer series, n = 2, m = 3, 4, 5, … ∞.
∴ \(\frac{1}{\lambda_{\mathrm{B}}}=R\left(\frac{1}{4}-\frac{1}{m^{2}}\right)\) and for the shortest wavelength line in this series, \(\frac{1}{\lambda_{\mathrm{Bs}}}=R\left(\frac{1}{4}\right)\) as m = ∞
[Note: Johannes Rydberg (1854—1919), Swedish spectroscopist, studied atomic emission spectra and introduced the idea of wave number. The empirical formula \(\bar{v}=\frac{1}{\lambda}=R\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\) where m and n are simple integers, is due to Rydberg. When we consider the finite mass of the nucleus, we find that R varies slightly from element to element.]

Question 5.
Determine the maximum angular speed of an electron moving in a stable orbit around the nucleus of hydrogen atom.
Answer:
The radius of the ,ith Bohr orbit is
r = \(\frac{\varepsilon_{0} h^{2} n^{2}}{\pi m Z e^{2}}\) ………….. (1)
and the linear speed of an electron in this orbit is
ν = \(\frac{Z e^{2}}{2 \varepsilon_{0} n h}\) …………… (2)
where ε ₀ permittivity of free space, h ≡ Planck’s constant, n ≡ principal quantum number, m ≡ electron mass, e electronic charge and Z ≡ atomic number of the atom.
Since angular speed ω = \(\frac{v}{r}\), then from Eqs. (1) and (2), we get,
ω = \(\frac{v}{r}=\frac{Z e^{2}}{2 \varepsilon_{0} n h} \cdot \frac{\pi m Z e^{2}}{\varepsilon_{0} h^{2} n^{2}}=\frac{\pi m Z^{2} e^{4}}{2 \varepsilon_{0}^{2} h^{3} n^{3}}\) ………………. (3)
which gives the required expression for the angular speed of an electron in the nth Bohr orbit.
From Eq. (3), the frequency of revolution of the electron,
f = \(\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \times \frac{\pi m Z^{2} e^{4}}{2 \varepsilon_{0}^{2} h^{3} n^{3}}=\frac{m Z^{2} e^{4}}{4 \varepsilon_{0}^{2} h^{3} n^{3}}\) …………….. (4)
as required.
[Note : From Eq. (4), the period of revolution of the electron, T = \(\frac{1}{f}=\frac{4 \varepsilon_{0}^{2} h^{3} n^{3}}{m Z e^{4}}\). Hence, f ∝ \(\frac{1}{n^{3}}\) and T ∝ n³].

Obtain the formula for ω and continue as follows :

This is required quantity.

Question 6.
Determine the series limit of Balmer, Paschen and Bracket series, given the limit for Lyman series is 912 Å.
Answer:
Data : λ_L∞ = 912 Å

as n = 5 and m = ∞
From Eqs. (1) and (2), we get,
\(\frac{\lambda_{\mathrm{Pa} \infty}}{\lambda_{\mathrm{L} \infty}}=\frac{R_{\mathrm{H}}}{R_{\mathrm{H}} / 9}\) = 9
∴ λ_Pa∞ = 9λ_L∞ = (9) (912) = 8202 Å
\(\frac{\lambda_{\mathrm{Pf} \infty}}{\lambda_{\mathrm{L} \infty}}=\frac{R_{\mathrm{H}}}{R_{\mathrm{H}} / 25}\) = 25
∴ λ_Pf∞ = 25λ_L∞ = (25) (912) = 22800 Å
This is the series limit of the pfund series.

Question 7.
Describe alpha, beta and gamma decays and write down the formulae for the energies generated in each of these decays.
Answer:
(a) A radioactive transformation in which an α-particle is emitted is called α-decay.
In an α-decay, the atomic number of the nucleus decreases by 2 and the mass number decreases by 4.
Example : \({ }_{92}^{238} \mathrm{U} \rightarrow{ }_{90}^{234} \mathrm{Th}+{ }_{2}^{4} \alpha\)
Q = [m_u – m_Th – m_α]c²

(b) A radioactive transformation in which a β-particle is emitted is called β-decay.
In a β^–-decay, the atomic number of the nucleus increases by 1 and the mass number remains unchanged.
Example : \({ }_{90}^{234} \mathrm{Th} \rightarrow{ }_{91}^{234} \mathrm{~Pa}+{ }_{-1}^{0} e+\bar{v}_{\mathrm{e}}\)
where \(\bar{v}_{\mathrm{e}}\) is the neutrino emitted to conserve the momentum, energy and spin.
Q = [m_u – m_Th – m_α]c²
In a β⁺-decay, the atomic number of the nucleus decreases by 1 and the mass number remains unchanged.
Example : \(\begin{aligned}
&30 \\
&15
\end{aligned} P \rightarrow{ }_{14}^{30} \mathrm{Si}+{ }_{+1}^{0} e+v_{\mathrm{e}}\)
where v_e is the neutrino emitted to conserve the momentum, energy and spin.
Q = [m_P – m_Si – m_e]c²
[Note : The term fi particle refers to the electron (or positron) emitted by a nucleus.]

A given nucleus does not emit α and β-particles simultaneously. However, on emission of α or β-particles, most nuclei are left in an excited state. A nucleus in an excited state emits a γ-ray photon in a transition to the lower energy state. Hence, α and β-particle emissions are often accompanied by γ-rays.

Question 8.
Explain what are nuclear fission and fusion giving an example of each. Write down the formulae for energy generated in each of these processes.
Answer:
Nuclear fission is a nuclear reaction in which a heavy nucleus of an atom, such as that of uranium, splits into two or more fragments of comparable size, either spontaneously or as a result of bombardment of a neutron on the nucleus (induced fission). It is followed by emission of two or three neutrons.
The mass of the original nucleus is more than the sum of the masses of the fragments. This mass difference is released as energy, which can be enormous as in the fission of ²³⁵U.
Nuclear fission was discovered by Lise Meitner, Otto Frisch, Otto Hahn and Fritz Strassmann in 1938.

The products of the fission of ²³⁵U by thermal neutrons are not unique. A variety of fission fragments are produced with mass number A ranging from about 72 to about 138, subject to the conservation of mass-energy, momentum, number of protons (Z) and number of neutrons (N). A few typical fission equations are

A type of nuclear reaction in which lighter atomic nuclei (of low atomic number) fuse to form a heavier nucleus (of higher atomic number) with the’ release of enormous amount of energy is called nuclear fusion.

Very high temperatures, of about 107 K to 108 K, are required to carry out nuclear fusion. Hence, such a reaction is also called a thermonuclear reaction.

Example : The D-T reaction, being used in experimental fusion reactors, fuses a deuteron and a triton nuclei at temperatures of about 10⁸ K.

(2) The value of the energy released in the fusion of two deuteron nuclei and the temperature at which the reaction occurs mentioned in the textbook are probably misprints.]

Question 9.
Describe the principles of a nuclear reactor. What is the difference between a nuclear reactor and a nuclear bomb?
Answer:
In a nuclear reactor fuel rods are used to provide a suitable fissionable material such as \(\begin{gathered}
236 \\
92
\end{gathered}\)U. Control rods are used to start or stop the reactor. Moderators are used to slow down the fast neutrons ejected in a nuclear fission to the appropriate lower speeds. Material used as a coolant removes the energy released in the nuclear reaction by converting it into thermal energy for production of electricity.

In a nuclear reactor, a nuclear fission chain reaction is used in a controlled manner, while in a nuclear bomb, the nuclear fission chain reaction is not controlled, releasing tremendous energy in a very short time interval.
[Note : The first nuclear bomb (atomic bomb) was dropped on Hiroshima in Japan on 06 August 1945. The second bomb was dropped on Nagasaki in Japan on 9 August 1945.]

Question 10.
Calculate the binding energy of an alpha particle given its mass to be 4.00151 u.
Answer:
Data : M = 4.00151 u, = 1.00728 u,
m_n = 1.00866 u, 1 u = 931.5 MeV/c²
The binding energy of an alpha particle
(Zm_p + N_n -M)c²
=(2m_p + 2m_n -M)c²
= [(2)(1.00728u) + 2(1.00866 u) – 4.00151 u]c²
= (2.01456 + 2.01732 – 4.00151)(931.5) MeV
= 28.289655 MeV
= 28.289655 × 10⁶ eV × 1.602 × 10^-19 J
= 4.532002731 × 10^-12 J

Question 11.
An electron in hydrogen atom stays in its second orbit for 10^-8 s. How many revolutions will it make around the nucleus in that time?
Answer:
Data : z = 1, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C, ε₀ = 8.85 × 10^-12 C² / N.m², h = 6.63 × 10 ^-34 J.s, n = 2, t = 10^-8 s
The periodic time of the electron in a hydrogen atom,

Let N be the number of revolutions made by the electron in time t. Then, t = NT.
∴ N = \(\frac{t}{T}=\frac{10^{-8}}{3.898 \times 10^{-16}}\) = 2.565 × ⁷

Question 12.
Determine the binding energy per nucleon of the americium isotope \(_{95}^{244} \mathrm{Am}\) , given the mass of \({ }_{95}^{244} \mathrm{Am}\) to be 244.06428 u.
Answer:
Data : Z = 95, N = 244  – 95 = 149,
m_p = 1.00728 u, m_n = 1.00866 u,
M = 244.06428 u, 1 u = 931.5 MeV/c²
The binding energy per nucleon,

= 7.3209 MeV/nucleon

Question 13.
Calculate the energy released in the nuclear reaction \({ }_{3}^{7} \mathrm{Li}\) + p → 2α given mass of \({ }_{3}^{7} \mathrm{Li}\) atom and of helium atom to be 7.016 u and 4.0026 u respectively.
Answer:
Data: M₁ (\({ }_{3}^{7} \mathrm{Li}\) Li atom)= 7.016 u, M₂ (He atom)
= 4.0026 u, m_p = 1.00728 u, 1 u = 931.5 MeV/c²
∆M = M₁ + m_p – 2M₂
= [7.016 + 1.00728 – 2(4.0026)]u
= 0.01808 u = (0.01808)(931.5) MeV/c²
= 16.84152 MeV/c²
Therefore, the energy released in the nuclear reaction = (∆M) c² = 16.84152 MeV

Question 14.
Complete the following equations describing nuclear decays.

Answer:
(a) \({ }_{88}^{226} \mathrm{Ra} \rightarrow{ }_{2}^{4} \alpha+{ }_{86}^{222} \mathrm{Em}\)
Em (Emanation) ≡ Rn (Radon)
Here, α particle is emitted and radon is formed.

(b) \({ }_{8}^{19} \mathrm{O} \rightarrow e^{-}+{ }_{9}^{19} \mathrm{~F}\)
Here, e^– ≡ \({ }_{-1}^{0} \beta\) is emitted and fluorine is formed.

(c) \(\underset{90}{228} \mathrm{Th} \rightarrow{ }_{2}^{4} \alpha+{ }_{88}^{224} \mathrm{Ra}\)
Here, α particle is emitted and radium is formed.

(d) \({ }_{7}^{12} \mathrm{~N} \rightarrow{ }_{6}^{12} \mathrm{C}+{ }_{1}^{0} \beta\)
\({ }_{1}^{0} \beta\) is e⁺ (positron)
Here, β⁺ is emItted and carbon is formed.

Question 15.
Calculate the energy released in the following reactions, given the masses to be \({ }_{88}^{223} \mathrm{Ra}\) : 223.0185 u, \({ }_{82}^{209} \mathrm{~Pb}\) : 208.9811, \({ }_{6}^{14} C\) : 14.00324, \({ }_{92}^{236} \mathrm{U}\) : 236.0456, \({ }_{56}^{140} \mathrm{Ba}\) : 139.9106, \({ }_{36}^{94} \mathrm{Kr}\) : 93.9341, \({ }_{6}^{11} \mathrm{C}\) : 11.01143, \({ }_{5}^{11} \mathrm{~B}\) : 11.0093. Ignore neutrino energy.

Answer:

(a) \({ }_{88}^{223} \mathrm{Ra} \rightarrow{ }_{82}^{209} \mathrm{~Pb}+{ }_{6}^{14} \mathrm{C}\)
The energy released in this reaction = (∆M) c²
= [223.0185 – (208.9811 + 14.00324)j(931 .5) MeV
= 31.820004 MeV

(b) \({ }_{92}^{236} \mathrm{U} \rightarrow{ }_{56}^{140} \mathrm{Ba}+{ }_{36}^{94} \mathrm{Kr}+2 \mathrm{n}\)
The energy released in this reaction =
(∆M) c² = [236.0456 – (139.9106 + 93.9341 + (2)(1 .00866)1(93 1 .5)MeV
= 171.00477 MeV

(c) \({ }_{6}^{11} \cdot \mathrm{C} \rightarrow{ }_{5}^{11} \mathrm{~B}+e^{+}\) + neutrino
The energy released in this reaction = (∆M) c²
= [11.01143 – (11.0093 + O.00055)](931.5) MeV
= 1.47177 MeV

Question 16.
Sample of carbon obtained from any living organism has a decay rate of 15.3 decays per gram per minute. A sample of carbon obtained from very old charcoal shows a disintegration rate of 12.3 disintegrations per gram per minute. Determine the age of the old sample given the decay constant of carbon to be 3.839 × 10^-12 per second.
Answer:
Data: 15.3 decays per gram per minute (living organism), 12.3 disintegrations per gram per minute (very old charcoal). Hence, we have,
\(\frac{A(t)}{A_{0}}=\frac{12.3}{15.3}\), λ = 3.839 × 10^-12 per second

Question 17.
The half-life of \({ }_{38}^{90} \mathrm{Sr}\) is 28 years. Determine the disintegration rate of its 5 mg sample.
Answer:
Data: T_1/2 = 28 years = 28 × 3.156 × 10⁷ s
=8.837 × 10⁸s, M = 5 mg =5 × 10^-3g
90 grams of \({ }_{38}^{90} \mathrm{Sr}\) contain 6.02 × 10²³ atoms
Hence, here, N = \(\frac{\left(6.02 \times 10^{23}\right)\left(5 \times 10^{-3}\right)}{90}\)
= 3.344 × 10¹⁹ atoms
∴ The disintegration rate = Nλ = N\(\frac{0.693}{T_{1 / 2}}\)
= \(\frac{\left(3.344 \times 10^{19}\right)(0.693)}{8.837 \times 10^{8}}\)
= 2.622 × 10¹⁰ disintegrations per second

Question 18.
What is the amount of \({ }_{27}^{60} \mathrm{Co}\) necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
Answer:
Data : Activity = 10.0 mCi = 10.0 × 10^-3 Ci
= (10.0 × 10^-3)(3.7 × 10¹⁰) dis/s = 3.7 × 10⁸ dis/s
T_1/2 = 5.3 years = (5.3)(3.156 × 10⁷) s
= 1.673 × 10⁸ s
Decay constant, λ = \(\frac{0.693}{T_{1 / 2}}=\frac{0.693}{1.673 \times 10^{8}} \mathrm{~s}^{-1}\)
=4.142 × 10^-9 s^-1
Activity = Nλ
∴ N = \(\frac{\text { activity }}{\lambda}=\frac{3.7 \times 10^{8}}{4.142 \times 10^{-9}} \text { atoms }\)
= 8.933 × 10¹⁶ atoms
=60 grams of \({ }_{27}^{60} \mathrm{Co}\) contain 6.02 × 10²³ atoms
Mass of 8.933 × 10¹⁶ atoms of \({ }_{27}^{60} \mathrm{Co}\)
= \(\frac{8.933 \times 10^{16}}{6.02 \times 10^{23}} \times 60 \mathrm{~g}\)
= 8.903 × 10^-6 g = 8.903 µg
This is the required amount.

Question 19.
Disintegration rate of a sample is 10¹⁰ per hour at 20 hrs from the start. It reduces to 6.3 × 10⁹ per hour after 30 hours. Calculate its half life and the initial number of radioactive atoms in the sample.
Answer:
Data : A (t₁) = 10¹⁰ per hour, where t₁ = 20 h,
A (t₂) = 6.3 × 10⁹ per hour, where t₂ = 30 h
A(t) = A₀e^-λt ∴ A(t₁) = A₀e^-λt₁ and A(t₂) = A_oe^-λt₂

∴ 1.587 e^10λ ∴ 10λ =2.3031og₁₀(1.587)
∴ λ = (0.2303)(0.2007) = 0.04622 per hour
The half life of the material, T_1/2 = \(\frac{0.693}{\lambda}=\frac{0.693}{0.04622}\)
= 14.99 hours
Now, A₀ = A (t₁)e^λt₁ = 10¹⁰e^{(0.04622)(20)}
= 10¹⁰ e^0.9244
Let x = e^0.9244 ∴ 2.3031og₁₀x = 0.9244
∴ 1og₁₀x = \(\frac{0.9244}{2.303}\) = 0.4014
∴ x = antilog 0.4014 = 2.52
∴ A₀ = 2.52 × 10¹⁰ per hour
Now A₀ = N₀λ ∴ N₀ = \(\frac{A_{0}}{\lambda}=\frac{2.52 \times 10^{10}}{0.04622}\)
= 5.452 × 10¹¹
This is the initial number of radioactive atoms in the sample.

Question 20.
The isotope ⁵⁷Co decays by electron capture to ⁵⁷Fe with a half-life of 272 d. The ⁵⁷Fe nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for ⁵⁷Co.
(b) If the activity of a radiation source ⁵⁷Co is 2.0 µCi now, how many ⁵⁷Co nuclei does the source contain?
(c) What will be the activity after one year?
Answer:
Data: T_1/2 = 272d = 272 × 24 × 60 × 60s = 2.35 × 10⁷ s,
A₀ = 2.0uCi = 2.0 × 10^-6 × 3.7 × 10¹⁰
= 7.4 × 10⁴ dis/s
t = 1 year = 3.156 × 10⁷ s
(a) T_1/2 = \(\frac{0.693}{\lambda}\) = 0.693 τ ∴ The mean lifetime for
⁵⁷Co = τ = \(\frac{T_{1 / 2}}{0.693}=\frac{2.35 \times 10^{7}}{0.693}\) = 3391 × 10⁷ s
The decay constant for ⁵⁷Co = λ = \(\frac{1}{\tau}\)
= \(\frac{1}{3.391 \times 10^{7} \mathrm{~s}}\)
= 2949 × 10^-8 s^-1

(b)A₀ = N₀A ∴ N₀ = \(\frac{A_{0}}{\lambda}\) = A₀τ
= (7.4 × 10⁴)(3.391 × 10⁷)
= 2.509 × 10¹² nuclei
This is the required number.

(c) A(t) = A₀e^-λt = 2e^{-(2.949 × 10-8)(3.156 × 107)}
= 2e^-0.9307 = 2 / e^0.9307
Let x = e^0.9307 ∴ Iog_ex = 0.9307
∴ 2.303log₁₀x = 0.9307
∴ log₁₀x = \(\frac{0.9307}{2.303}\) = 0.4041
∴ x = antilog 0.4041 = 2.536
∴ A (t) = \(\frac{2}{2.536}\) μCi = 0.7886 μCi

Question 21.
A source contains two species of phosphorous nuclei, \({ }_{15}^{32} \mathrm{P}\) (T_1/2 = 14.3 d) and \({ }_{15}^{32} \mathrm{P}\) (T_1/2 = 25.3 d). At time t = 0, 90% of the decays are from \({ }_{15}^{32} \mathrm{P}\) . How much time has to elapse for only 15% of the decays to be from \({ }_{15}^{32} \mathrm{P}\) ?
Answer:

∴ (0.04846 – 0.02739) t = 2.303 (2.1847 – 0.4771)
∴ t = \(\frac{(2.303)(1.7076)}{0.02107}\) = 186.6 days
This is the required time.

Question 22.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of ¹⁴C averaged about 0.255 Bq per gram of carbon. (a) What fraction of carbon atoms were ¹⁴C? (b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? Half-life of 14C is 5730 years?
Answer:
0.693
Data: T_1/2 = 5730y ∴ λ = \(\frac{0.693}{5730 \times 3.156 \times 10^{7}} \mathrm{~s}^{-1}\)
= 3.832 × 10^-12 s^-1, A = 0.255 Bq per gram of carbon in part (a); M = 500 mg = 500 × 10^-3 g,
174 decays in one hour \(\frac{174}{3600}\) dis/s = 0.04833 dis/s in part (b) (per 500 mg].

(a) A = Nλ ∴ N = \(\frac{A}{\lambda}=\frac{0.255}{3.832 \times 10^{-12}}\)
= 6.654 × 10¹⁰
Number of atoms in 1 g of carbon = \(\frac{6.02 \times 10^{23}}{12}\)
=5.017 × 10²²
\(\frac{5.017 \times 10^{22}}{6.654 \times 10^{10}}\) = 0.7539 × 10¹²
∴ 1 ¹⁴C atom per 0.7539 × 10¹² atoms of carbon
∴ 4 ¹⁴C atoms per 3 × 10¹² atoms of carbon

(b) Present activity per gram = \(\)
= 0.09666 dis/s per gram
A₀ = 0.255 dis/s per gram
Now, A(t) = A₀e^-λt

This is the required quantity.

Question 23.
How much mass of ²³⁵U is required to undergo fission each day to provide 3000 MW of thermal power? Average energy per fission is 202.79 MeV
Answer:
Data: Power = 3000 MW = 3 × 10⁹ J/s
∴ Energy to be produced each day
=3 × 10⁹ × 86400 J each day
= 2.592 × 10¹⁴ J each day
Energy per fission = 202.79 MeV
= 202.79 × 10⁶ × 1.6 × 10^-19 J = 3,245 × 10^-11 J
∴ Number of fissions each day
= \(\frac{2.592 \times 10^{14}}{3.245 \times 10^{-11}}\) × 10²⁴ each day
0.235 kg of ²³⁵U contains 6.02 × 10²³ atoms
7988 x 1024
∴ M = \(\left(\frac{7.988 \times 10^{24}}{6.02 \times 10^{23}}\right)\) (o.235) = 3.118 kg
This is the required quantity.

Question 24.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are \({ }_{12}^{24} \mathrm{Mg}\) (23.98504 u), \({ }_{12}^{25} \mathrm{Mg}\) (24.98584 u) and \({ }_{12}^{26} \mathrm{Mg}\) (25.98259 u). The natural abundance of \({ }_{12}^{24} \mathrm{Mg}\) is 78.99% by mass. Calculate the abundances of other two isotopes.
[Answer: 9.3% and 11.7%]
Answer:
Data : Average atomic mass of magnesium =

12th Physics Digest Chapter 15 Structure of Atoms and Nuclei Intext Questions and Answers

Use your brain power (Textbook Page No. 336)

Question 1.
Why don’t heavy nuclei decay by emitting a single proton or a single neutron?
Answer:
According to quantum mechanics, the probability for these emissions is extremely low.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 1 Rotational Dynamics Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 1 Rotational Dynamics

1. Choose the correct option.

i) When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select correct statement about the directions of its angular velocity and angular acceleration.
(A) Angular velocity upwards, angular acceleration downwards.
(B) Angular velocity downwards, angular acceleration upwards.
(C) Both, angular velocity and angular acceleration, upwards.
(D) Both, angular velocity and angular acceleration, downwards.
Answer:
(A) Angular velocity upwards, angular acceleration downwards.

ii) A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform vertical circular motion, under gravity. Minimum speed of a particle is 5 m/s. Consider following statements.
P) Maximum speed must be 5 5 m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N. Select correct option.
(A) Only the statement P is correct.
(B) Only the statement Q is correct.
(C) Both the statements are correct.
(D) Both the statements are incorrect.
Answer:
(C) Both the statements are correct.

iii) Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
(A) Different objects must have different expressions for their M.I.
(B) When rotating about their central axis, a hollow right circular cone and a disc have the same expression for the M.I.
(C) Expression for the M.I. for a parallelepiped rotating about the transverse axis passing through its centre includes its depth.
(D) Expression for M.I. of a rod and that of a plane sheet is the same about a transverse axis.
Answer:
(B) When rotating about their central axis, a hollow right circular cone and a disc have the same expression for the M.I.

iv) In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is \(\sqrt{2.5}\). Its radius of gyration about a tangent in its plane (in the same unit) must be
(A) \(\sqrt{5}\)
(B) 2.5
(C) 2\(\sqrt{2.5}\)
(D) \(\sqrt{12.5}\)
Answer:
(B) 2.5

v) Consider following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
(A) Only for (P)
(B) Only for (Q)
(C) For both, (P) and (Q)
(D) Neither for (P), nor for (Q)
Answer:
(C) For both, (P) and (Q)

X) A thin walled hollow cylinder is rolling down an incline, without slipping. At any instant, the ratio ”Rotational K.E.:
Translational K.E.: Total K.E.” is
(A) 1:1:2
(B) 1:2:3
(C) 1:1:1
(D) 2:1:3
Answer:
(D) 2:1:3

2. Answer in brief.

i) Why are curved roads banked?
Answer:
A car while taking a turn performs circular motion. If the road is level (or horizontal road), the necessary centripetal force is the force of static friction between the car tyres and the road surface. The friction depends upon the nature of the surfaces in contact and the presence of oil and water on the road. If the friction is inadequate, a speeding car may skid off the road. Since the friction changes with circumstances, it cannot be relied upon to provide the necessary centripetal force. Moreover, friction results in fast wear and tear of the tyres.

To avoid the risk of skidding as well as to reduce the wear and tear of the car tyres, the road surface at a bend is tilted inward, i.e., the outer side of the road is raised above its inner side. This is called banking of road. On a banked road, the resultant of the normal reaction and the gravitational force can act as the necessary centripetal force. Thus, every car can be safely driven on such a banked curve at certain optimum speed, without depending on friction. Hence, a road should be properly banked at a bend.

The angle of banking is the angle of inclination of the surface of a banked road at a bend with the horizontal.

ii) Do we need a banked road for a two wheeler? Explain.
Answer:
When a two-wheeler takes a turn along an unbanked road, the force of friction provides the centripetal force. The two-wheeler leans inward to counteract a torque that tends to topple it outward. Firstly, friction cannot be relied upon to provide the necessary centripetal force on all road conditions. Secondly, the friction results in wear and tear of the tyres. On a banked road at a turn, any vehicle can negotiate the turn without depending on friction and without straining the tyres.

iii) On what factors does the frequency of a conical pendulum depend? Is it independent of some factors?
Answer:
The frequency of a conical pendulum, of string length L and semivertical angle θ, is
n = \(\frac{1}{2 \pi} \sqrt{\frac{g}{L \cos \theta}}\)
where g is the acceleration due to gravity at the place.
From the above expression, we can see that

1. n ∝ \(\sqrt{g}\)
2. n ∝ \(\frac{1}{\sqrt{L}}\)
3. n ∝ \(\frac{1}{\sqrt{\cos \theta}}\)
   (if θ increases, cos θ decreases and n increases)
4. The frequency is independent of the mass of the bob.

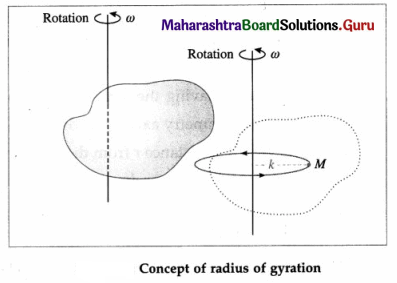
iv) Why is it useful to define radius of gyration?
Answer:
Definition : The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.

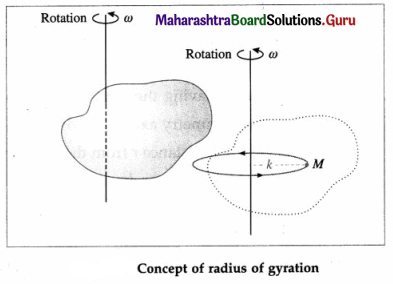
The moment of inertia (MI) of a body about a given rotation axis depends upon

1. the mass of the body and
2. the distribution of mass about the axis of rotation. These two factors can be separated by expressing the MI as the product of the mass (M) and the square of a particular distance (k) from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
   

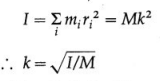
Physical significance : The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.

v) A uniform disc and a hollow right circular cone have the same formula for their M.I., when rotating about their central axes. Why is it so?
Answer:
The radius of gyration of a thin ring of radius Rr about its transverse symmetry axis is
K_r = \(\sqrt{I_{\mathrm{CM}} / M_{\mathrm{r}}}\) = \(\sqrt{R_{\mathrm{r}}^{2}}\) = R_r
The radius of gyration of a thin disc of radius R_d about its transverse symmetry axis is

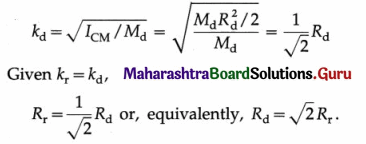
Question 3.
While driving along an unbanked circular road, a two-wheeler rider has to lean with the vertical. Why is it so? With what angle the rider has to lean? Derive the relevant expression. Why such a leaning is not necessary for a four wheeler?
Answer:
When a bicyclist takes a turn along an unbanked road, the force of friction \(\vec{f}_{\mathrm{s}}\) provides the centripetal force; the normal reaction of the road \(\vec{N}\) is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, f_s.h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by \(\vec{N}\) and the weight \(\vec{g}\), mg.a = f_s.h₁

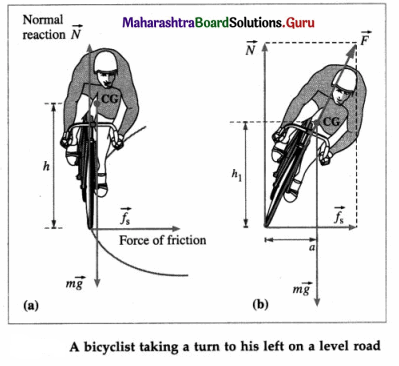
Since the force of friction provides the centripetal force,
f_s = \(\frac{m v^{2}}{r}\)
If the cyclist leans from the vertical by an angle 9, the angle between \(\vec{N}\) and \(\vec{F}\) in above figure.

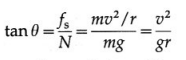
Hence, the cyclist must lean by an angle
θ = tan^-1\(\left(\frac{v^{2}}{g r}\right)\)

When a car takes a turn along a level road, apart from the risk of skidding off outward, it also has a tendency to roll outward due to an outward torque about the centre of gravity due to the friction force. But a car is an extended object with four wheels. So, when the inner wheels just get lifted above the ground, it can be counterbalanced by a restoring torque of the couple formed by the normal reaction (on the outer wheels) and the weight.

Question 4.
Using the energy conservation, derive the expressions for the minimum speeds at different locations along a vertical circular motion controlled by gravity. Is zero speed possible at the uppermost point? Under what condition/s? Also prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the object.
Answer:
In a non uniform vertical circular motion, e.g., those of a small body attached to a string or the loop-the-loop manoeuvers of an aircraft or motorcycle or skateboard, the body must have some minimum speed to reach the top and complete the circle. In this case, the motion is controlled only by gravity and zero speed at the top is not possible.

However, in a controlled vertical circular motion, e.g., those of a small body attached to a rod or the giant wheel (Ferris wheel) ride, the body or the passenger seat can have zero speed at the top, i.e., the motion can be brought to a stop.

Question 5.
Discuss the necessity of radius of gyration. Define it. On what factors does it depend and it does not depend? Can you locate some similarity between the centre of mass and radius of gyration? What can you infer if a uniform ring and a uniform disc have the same radius of gyration?
Answer:
Definition : The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.

The moment of inertia (MI) of a body about a given rotation axis depends upon

1. the mass of the body and
2. the distribution of mass about the axis of rotation. These two factors can be separated by expressing the MI as the product of the mass (M) and the square of a particular distance (k) from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,

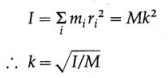
Physical significance : The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.

The centre of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton’s second law of motion, viz.,
\(\vec{F}_{\mathrm{net}}\) = M\(\overrightarrow{\mathrm{a}}_{\mathrm{CM}}\), where \(\vec{F}_{\mathrm{net}}\) is the sum of all the external forces acting on the body or on the individual particles of the system of particles.

Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis of rotation obeys the relation, \(\vec{\tau}_{\mathrm{net}}\) = M\(\vec{\alpha}\), where \(\vec{\tau}_{\text {net }}\) is the sum of all the external torques acting on the body or on the individual particles of the system of particles.

Question 6.
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
Answer:
The theorem of parallel axis is applicable to any body of arbitrary shape. The moment of inertia (MI) of the body about an axis through the centre mass should be known, say, I_CM. Then, the theorem can be used to find the MI, I, of the body about an axis parallel to the above axis. If the distance between the two axes is h,
I = I_CM + Mh² …(1)
The theorem of perpendicular axes is applicable to a plane lamina only. The moment of inertia I_z of a plane lamina about an axis-the z axis- perpendicular to its plane is equal to the sum of its moments of inertia I_x and I_y about two mutually perpendicular axes x and y in its plane and through the point of intersection of the perpendicular axis and the lamina.
I_z = I_x + I_y …. (2)

Question 7.
Derive an expression that relates angular momentum with the angular velocity of a rigid body.
Answer:
Consider a rigid body rotating with a constant angular velocity \(\vec{\omega}\) about an axis through the point O and perpendicular to the plane of the figure. All the particles of the body perform uniform circular motion about the axis of rotation with the same angular velocity \(\vec{\omega}\). Suppose that the body consists of N particles of masses m₁, m₂, …, m_n, situated at perpendicular distances r₁, r₂, …, r_N, respectively from the axis of rotation.

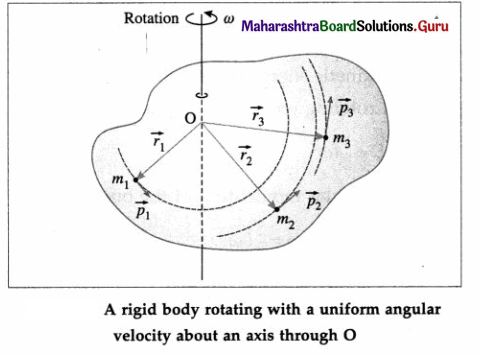
The particle of mass m₁ revolves along a circle of radius r₁, with a linear velocity of magnitude v₁ = r₁ω. The magnitude of the linear momentum of the particle is
p₁ = m₁v₁ = m₁r₁ω
The angular momentum of the particle about the axis of rotation is by definition,
\(\vec{L}_{1}\) = \(\vec{r}_{1}\) × \(\vec{p}_{1}\)
∴ L₁ = r₁p₁ sin θ
where θ is the smaller of the two angles between \(\vec{r}_{1}\) and \(\vec{p}_{1} \text { . }\)
In this case, θ = 90° ∴ sin θ = 1
∴ L₁ = r₁p₁ = r₁m₁r₁ω = m₁r₁²ω
Similarly L₂ = m₂r₂²ω, L₃ = m₃r₃²ω, etc.
The angular momentum of the body about the given axis is
L = L₁ + L₂ + … + L_N

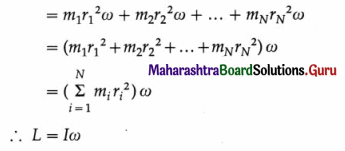
where I = \(\sum_{i=1}^{N} m_{i} r_{i}^{2}\) = moment of inertia of the body about the given axis.
In vector form, \(\vec{L}\) = \(I \vec{\omega}\)
Thus, angular momentum = moment of inertia × angular velocity.
[Note : Angular momentum is a vector quantity. It has the same direction as \(\vec{\omega}\).]

Question 8.
Obtain an expression relating the torque with angular acceleration for a rigid body.
Answer:
A torque acting on a body produces angular acceleration. Consider a rigid body rotating about an axis passing through the point O and perpendicular to the plane of the figure. Suppose that a torque \(\vec{\tau}\) on

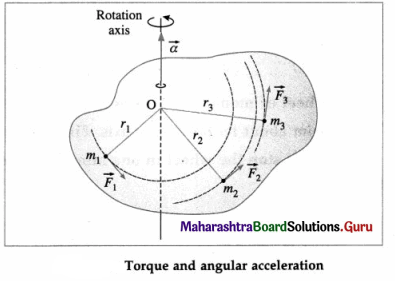
the body produces uniform angular acceleration \(\vec{\alpha}\) along the axis of rotation.
The body can be considered as made up of N particles with masses m₁, m₂, …, m_N situated at perpendicular distances r₁, r₂, …, r_N respectively from the axis of rotation, \(\vec{\alpha}\) is the same for all the particles as the body is rigid. Let \(\vec{F}_{1}\), \(\vec{F}_{2}\), …, \(\vec{F}_{N}\) be the external forces on the particles.
The torque \(\vec{\tau}_{1}\), on the particle of mass m₁, is
\(\vec{\tau}_{1}\) = \(\vec{r}_{1}\) × \(\vec{F}_{1}\)
∴ τ₁ = r₁F₁ sin θ
where θ is the smaller of the two angles between \(\vec{r}_{1}\) and \(\vec{F}_{1} .\)

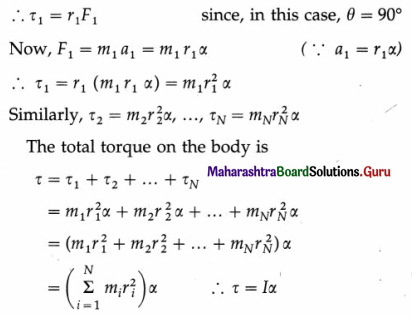
where

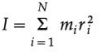
is the moment of inertia of the body about the axis of rotation.
In vector form, \(\vec{\tau}\) = I\(\vec{\alpha}\)
This gives the required relation.
Angular acceleration \(\vec{\alpha}\) has the same direction as the torque \(\vec{\tau}\) and both of them are axial vectors along the rotation axis.

Question 9.
State and explain the principle of conservation of angular momentum. Use a suitable illustration. Do we use it in our daily life? When?
Answer:
Law (or principle) of conservation of angular momentum : The angular momentum of a body is conserved if the resultant external torque on the body is zero.
Explanation : This law (or principle) is used by a figure skater or a ballerina to increase their speed of rotation for a spin by reducing the body’s moment of inertia. A diver too uses it during a somersault for the same reason.

(1) Ice dance :
Twizzle and spin are elements of the sport of figure skating. In a twizzle a skater turns several revolutions while travelling on the ice. In a dance spin, the skater rotates on the ice skate and centred on a single point on the ice. The torque due to friction between the ice skate and the ice is small. Consequently, the angular momentum of a figure skater remains nearly constant.

For a twizzle of smaller radius, a figure skater draws her limbs close to her body to reduce moment of inertia and increase frequency of rotation. For larger rounds, she stretches out her limbs to increase moment of inertia which reduces the angular and linear speeds.

A figure skater usually starts a dance spin in a crouch, rotating on one skate with the other leg and both arms extended. She rotates relatively slowly because her moment of inertia is large. She then slowly stands up, pulling the extended leg and arms to her body. As she does so, her moment of inertia about the axis of rotation decreases considerably,and thereby her angular velocity substantially increases to conserve angular momentum.

(2) Diving :
Take-off from a springboard or diving platform determines the diver’s trajectory and the magnitude of angular momentum. A diver must generate angular momentum at take-off by moving the position of the arms and by a slight hollowing of the back. This allows the diver to change angular speeds for twists and somersaults in flight by controlling her/his moment of inertia. A compact tucked shape of the body lowers the moment of inertia for rotation of smaller radius and increased angular speed. The opening of the body for the vertical entry into water does not stop the rotation, but merely slows it down. The angular momentum remains constant throughout the flight.

Question 10.
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object that rolls without slipping.
Answer:
Consider a symmetric rigid body, like a sphere or a wheel or a disc, rolling on a plane surface with friction along a straight path. Its centre of mass (CM) moves in a straight line and, if the frictional force on the body is large enough, the body rolls without slipping. Thus, the rolling motion of the body can be treated as translation of the CM and rotation about an axis through the CM. Hence, the kinetic energy of a rolling body is
E = E_tran + E_rot ……. (1)

where E_tran and E_rot are the kinetic energies associated with translation of the CM and rotation about an axis through the CM, respectively.

Let M and R be the mass and radius of the body. Let ω, k and i be the angular speed, radius of gyration and moment of inertia for rotation about an axis through its centre, and v be the translational speed of the centre of mass.

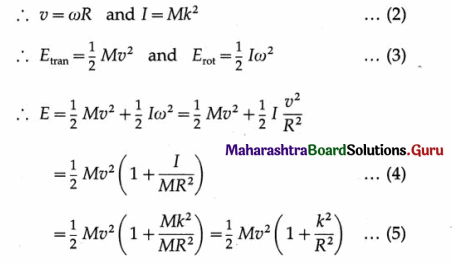
Question 11.
A rigid object is rolling down an inclined plane. Derive expressions for the acceleration along the track and the speed after falling through a certain vertical distance.
Answer:
Consider a circularly symmetric rigid body, like a sphere or a wheel or a disc, rolling with friction down a plane inclined at an angle 9 to the horizontal. If the frictional force on the body is large enough, the body rolls without slipping.
Let M and R be the mass and radius of the body. Let I be the moment of inertia of the body for rotation about an axis through its centre. Let the body start from rest at the top of the incline at a

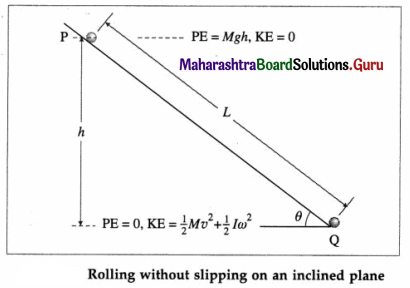
height h. Let v be the translational speed of the centre of mass at the bottom of the incline. Then, its kinetic energy at the bottom of the incline is

Let a be the acceleration of the centre of mass of the body along the inclined plane. Since the body starts from rest,

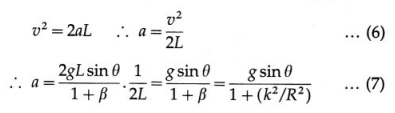
Starting from rest, if t is the time taken to travel the distance L,

[Note : For rolling without slipping, the contact point of the rigid body is instantaneously at rest relative to the surface of the inclined plane. Hence, the force of friction is static rather than kinetic, and does no work on the body. Thus, the force of static friction causes no decrease in the mechanical energy of the body and we can use the principle of conservation of energy.]

Question 12.
Somehow, an ant is stuck to the rim of a bicycle wheel of diameter 1 m. While the bicycle is on a central stand, the wheel
is set into rotation and it attains the frequency of 2 rev/s in 10 seconds, with uniform angular acceleration. Calculate
(i) Number of revolutions completed by the ant in these 10 seconds.
(ii) Time taken by it for first complete revolution and the last complete revolution.
[Ans:10 rev., t_first = \(\sqrt{10}\)s, t_last = 0.5132s]
Answer:
Data : r = 0.5 m, ω₀ = 0, ω = 2 rps, t = 10 s

(i) Angular acceleration (α) being constant, the average angular speed,
ω_av = \(\frac{\omega_{\mathrm{o}}+\omega}{2}\) = \(\frac{0+2}{2}\) = 1 rps
∴ The angular displacement of the wheel in time t,
θ = ω_av ∙ t = 1 × 10 = 10 revolutions

(ii)

The time for the last, i.e., the 10th, revolution is t₁ – t₂ = 10 – 9.486 = 0.514 s

Question 13.
Coefficient of static friction between a coin and a gramophone disc is 0.5. Radius of the disc is 8 cm. Initially the
centre of the coin is 2 cm away from the centre of the disc. At what minimum frequency will it start slipping from there? By what factor will the answer change if the coin is almost at the rim?
(use g = π² m/s²)
[Ans: 2.5 rev/s, n₂ = \(\frac{1}{2}\)n₁]
Answer:
Data : µ_s = 0.5, r₁ = π cm = π × 10^-2 m, r₂ = 8 cm = 8 × 10^-2 m, g = π² m/s²
To revolve with the disc without slipping, the necessary centripetal force must be less than or equal to the limiting force of static friction.

The coin will start slipping when the frequency is

The minimum frequency in the second case will be \(\sqrt{\frac{\pi}{8}}\) times that in the first case.
[ Note The answers given in the textbook are for r₁ = 2 cm.]

Question 14.
Part of a racing track is to be designed for a radius of curvature of 72 m. We are not recommending the vehicles to drive faster than 216 kmph. With what angle should the road be tilted? At what height will its outer edge be, with respect to the inner edge if the track is 10 m wide?
[Ans: θ = tan^-1 (5) = 78.69°, h = 9.8 m]
Answer:
Data : r = 72 m, v₀ = 216 km/h, = 216 × \(\frac{5}{18}\)
= 60 m/s, w = 10 m, g = 10 m/s²
tan θ = \(\frac{v_{\mathrm{o}}^{2}}{r g}\) = \(\frac{(60)^{2}}{72 \times 10}\) = \(\frac{3600}{720}\) = 5
∴ θ = tan^-1 5 = 78°4′
This is the required angle of banking.
sin θ = \(\frac{h}{w}\)
∴ h = w sin θ = (10) sin 78°4′ = 10 × 0.9805
= 9.805 m
This gives the height of the outer edge of the track relative to the inner edge.

Question 15.
The road in the example 14 above is constructed as per the requirements. The coefficient of static friction between the tyres of a vehicle on this road is 0.8, will there be any lower speed limit? By how much can the upper speed limit exceed in this case?
[Ans: v_min ≅ 88 kmph, no upper limit as the road is banked for θ > 45°]
Answer:
Data : r = 72 m, θ = 78 °4′, µ_s = 0.8, g = 10 m/s² tan θ = tan 78°4′ = 5

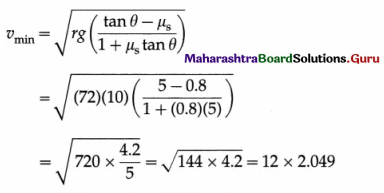
= 24.588 m/s = 88.52 km/h
This will be the lower limit or minimum speed on this track.
Since the track is heavily banked, θ > 45 °, there is no upper limit or maximum speed on this track.

Question 16.
During a stunt, a cyclist (considered to be a particle) is undertaking horizontal circles inside a cylindrical well of radius 6.05 m. If the necessary friction coefficient is 0.5, how much minimum speed should the stunt artist maintain? Mass of the artist is 50 kg. If she/he increases the speed by 20%, how much will the force of friction be?
[Ans: v_min = 11 m/s, f_s = mg = 500 N]
Answer:
Data : r = 6.05 m, µ_s = 0.5, g = 10 m/s², m = 50 kg, ∆v = 20%

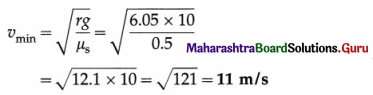
This is the required minimum speed. So long as the cyclist is not sliding, at every instant, the force of static friction is fs = mg = (50)(10) = 500 N

Question 17.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm. Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π ² = 10 )
[Ans: cos θ = 0.8, K.E. = 0.45 J, ∆(P E.) = 0.04 J]
Answer:
Data : L = 0.2 m, m = 0.1 kg, n = \(\frac{75}{60}\) = \(\frac{5}{4}\) rps,
g = 10 m/s², π² = 10,

The increase in gravitational PE,
∆PE = mg(L – h)
= (0.1) (10) (0.2 – 0.16)
= 0.04 J

Question 18.
A motorcyclist (as a particle) is undergoing vertical circles inside a sphere of death. The speed of the motorcycle varies between 6 m/s and 10 m/s. Calculate diameter of the sphere of death. What are the minimum values are possible for these two speeds?
[Ans: Diameter = 3.2 m, (v₁)_min = 4 m/s, (v₂)_min = 4 \(\sqrt{5}\)/m s ]
Answer:

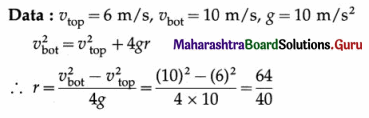
= 1.6 m
The diameter of the sphere of death = 3.2 m.

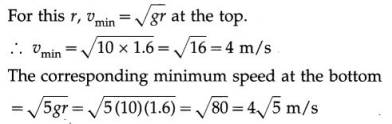
The required minimum values of the speeds are 4 m/s and 4\(\sqrt{5}\) m/s.

Question 19.
A metallic ring of mass 1 kg has moment of inertia 1 kg m² when rotating about one of its diameters. It is molten and remoulded into a thin uniform disc of the same radius. How much will its moment of inertia be, when rotated about its own axis.
[Ans: 1 kg m²]
Answer:
The MI of the thin ring about its diameter,
I_ring = \(\frac{1}{2}\)MR² = 1 kg.m²
Since the ring is melted and recast into a thin disc of same radius R, the mass of the disc equals the mass of the ring = M.
The MI of the thin disc about its own axis (i.e., transverse symmetry axis) is
I_disc = \(\frac{1}{2}\)MR² = I_ring
∴ I_disc = 1 kg.m²

Question 20.
A big dumb-bell is prepared by using a uniform rod of mass 60 g and length 20 cm. Two identical solid thermocol spheres of mass 25 g and radius 10 cm each are at the two ends of the rod. Calculate moment of inertia of the dumbbell when rotated about an axis passing through its centre and perpendicular to the length.
[Ans: 24000 g cm^-2]
Answer:
Data : M_sph = 50 g, R_sph = 10 cm, M_rod = 60 g, L_rod = 20 cm
The MI of a solid sphere about its diameter is
I_sph,CM = \(\frac{2}{5}\)M_sphR_sph
The distance of the rotation axis (transverse symmetry axis of the dumbbell) from the centre of sphere, h = 30 cm.
The MI of a solid sphere about the rotation axis, I_sph = I_{sph, CM} + M_sphh²
For the rod, the rotation axis is its transverse symmetry axis through CM.
The MI of a rod about this axis,
I_rod = \(\frac{1}{12}\) M_rodL²_rod
Since there are two solid spheres, the MI of the dumbbell about the rotation axis is

Question 21.
A flywheel used to prepare earthenware pots is set into rotation at 100 rpm. It is in the form of a disc of mass 10 kg and
radius 0.4 m. A lump of clay (to be taken equivalent to a particle) of mass 1.6 kg falls on it and adheres to it at a certain
distance x from the centre. Calculate x if the wheel now rotates at 80 rpm.
[Ans: x = \(\frac{1}{\sqrt{8}}\)m = 0.35 m]
Answer:
Data : f₁ = 60 rpm = 60/60 rot/s = 1 rot/s,
f₂ = 30 rpm = 30/60 rot/s = \(\frac{1}{2}\) rot/s, ∆E = — 100 J

(i)

This gives the MI of the flywheel about the given axis.

(ii) Angular momentum, L = Iω = I(2πf) = 2πIf
The change in angular momentum, ∆L
= L₂ – L₁ = 2πI(f₂ – f₁)
= 2 × 3.142 × 6.753(\(\frac{1}{2}\) – 1)
= -3.142 × 6.753 = -21.22 kg.m²/s

Question 22.
Starting from rest, an object rolls down along an incline that rises by 3 units in every 5 units (along it). The object gains a speed of \(\sqrt{10}\) m/s as it travels a distance of \(\frac{5}{3}\)m along the incline. What can be the possible shape/s of the object?
[Ans: \(\frac{K^{2}}{R^{2}}\) = 1. Thus, a ring or a hollow cylinder]
Answer:
Data : sin θ = \(\frac{3}{5}\), u = 0, v = \(\sqrt{10}\) m/s, L = \(\frac{5}{3}\)m, g = 10 m/s²


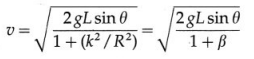
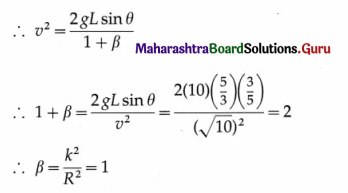
Therefore, the body rolling down is either a ring or a cylindrical shell.

12th Physics Digest Chapter 1 Rotational Dynamics Intext Questions and Answers

Activity (Textbook Page No. 3)

Question 1.
Attach a body of suitable mass to a spring balance so that it stretches by about half its capacity. Now whirl the spring balance so that the body performs a horizontal circular motion. You will notice that the balance now reads more for the same body. Can you explain this ?
Answer:
Due to outward centrifugal force.

Use your brain power (Textbook Page No. 4)

Question 1.
Obtain the condition for not toppling (rollover) for a four-wheeler. On what factors does it depend and how?
Answer:
Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are :

1. the lateral limiting force of static friction \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels-acting along the axis of the wheels and towards the centre of the circular path- which provides the necessary centripetal force,
2. the weight \(m \vec{g}\) acting vertically downwards at the centre of gravity (C.G.)
3. the normal reaction \(\vec{N}\) of the road on the wheels, acting vertically upwards effectively at the C.G. Since maximum centripetal force = limiting force of static friction,
   ma_r = \(\frac{m v^{2}}{r}\) = f_s…. (1)

In a simplified rigid-body vehicle model, we consider only two parameters-the height h of the C.G. above the ground and the average distance b between the left and right wheels called the track width.

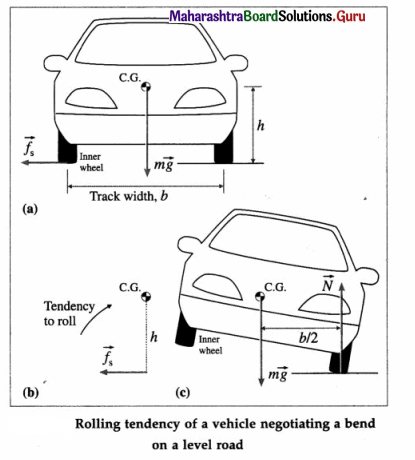
The friction force \(\overrightarrow{f_{s}}\) on the wheels produces a torque \(\tau_{\mathrm{t}}\) that tends to overturn/rollover the car about the outer wheel. Rotation about the front-to-back axis is called roll.
\(\tau_{\mathrm{t}}\) = f_s.h = \(\left(\frac{m v^{2}}{r}\right)\)h … (2)

When the inner wheel just gets lifted above the ground, the normal reaction \(\vec{N}\) of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque \(\tau_{\mathrm{r}}\) which tends to restore the car back on all four wheels
\(\tau_{\mathrm{r}}\) = mg.\(\frac{b}{2}\) …. (3)
The car does not topple as long as the restoring torque \(\tau_{\mathrm{r}}\) counterbalances the toppling torque \(\tau_{\mathrm{t}}\). Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by
\(\left(\frac{m v^{2}}{r}\right)\)h = mg.\(\frac{b}{2}\) ∴ v_max = \(\sqrt{\frac{r b g}{2 h}}\) … (4)

Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force \(m \vec{g}\) passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower centre of gravity.

There will be rollover (before skidding) if \(\tau_{t}\) ≥ \(\tau_{\mathrm{r}}\), that is if

The vehicle parameter ratio, \(\frac{b}{2 h}\), is called the static stability factor (SSF). Thus, the risk of a rollover is low if SSF ≤ µ_s. A vehicle will most likely skid out rather than roll if µ_s is too low, as on a wet or icy road.

Question 2.
Think about the normal reactions. Where are those and how much are those?
Answer:

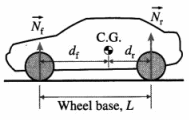
In a simplified vehicle model, we assume the normal reactions to act equally on all the four wheels, i.e., mg/4 on each wheel. However, the C.G. is not at the geometric centre of a vehicle and the wheelbase (i.e., the distance L between its front and rear wheels) affects the weight distribution of the vehicle. When a vehicle is not accelerating, the normal reactions on each pair of front and rear wheels are, respectively,
N_f = \(\frac{d_{\mathrm{r}}}{L}\)mg and N_r = \(\frac{d_{\mathrm{f}}}{L}\) mg
where d_r and d_f are the distances of the rear and front axles from the C.G. [When a vehicle accelerates, additional torque acts on the axles and the normal reactions on the wheels change. So, as is common experience, a car pitches back (i.e., rear sinks and front rises) when it accelerates, and a car pitches ahead (i.e., front noses down). Rotation about the lateral axis is called pitch.]

Question 3.
What is the recommendations on loading a vehicle for not toppling easily?
Answer:
Overloading (or improper load distribution) or any load placed on the roof raises a vehicle’s centre of gravity, and increases the vehicle’s likelihood of rolling over. A roof rack should be fitted by considering weight limits.

Road accidents involving rollovers show that vehicles with higher h (such as SUVs, pickup vans and trucks) topple more easily than cars. Untripped rollovers normally occur when a top-heavy vehicle attempts to perform a panic manoeuver that it physically cannot handle.

Question 4.
If a vehicle topples while turning, which wheels leave the contact with the road? Why?
Answer:
Inner wheels.
Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are :

1. the lateral limiting force of static friction \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels-acting along the axis of the wheels and towards the centre of the circular path- which provides the necessary centripetal force,
2. the weight \(m \vec{g}\) acting vertically downwards at the centre of gravity (C.G.)
3. the normal reaction \(\vec{N}\) of the road on the wheels, acting vertically upwards effectively at the C.G. Since maximum centripetal force = limiting force of static friction,
   ma_r = \(\frac{m v^{2}}{r}\) = f_s…. (1)

In a simplified rigid-body vehicle model, we consider only two parameters-the height h of the C.G. above the ground and the average distance b between the left and right wheels called the track width.

The friction force \(\overrightarrow{f_{s}}\) on the wheels produces a torque \(\tau_{\mathrm{t}}\) that tends to overturn/rollover the car about the outer wheel. Rotation about the front-to-back axis is called roll.
\(\tau_{\mathrm{t}}\) = f_s.h = \(\left(\frac{m v^{2}}{r}\right)\)h … (2)

When the inner wheel just gets lifted above the ground, the normal reaction \(\vec{N}\) of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque \(\tau_{\mathrm{r}}\) which tends to restore the car back on all four wheels
\(\tau_{\mathrm{r}}\) = mg.\(\frac{b}{2}\) …. (3)
The car does not topple as long as the restoring torque \(\tau_{\mathrm{r}}\) counterbalances the toppling torque \(\tau_{\mathrm{t}}\). Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by
\(\left(\frac{m v^{2}}{r}\right)\)h = mg.\(\frac{b}{2}\) ∴ v_max = \(\sqrt{\frac{r b g}{2 h}}\) … (4)

Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force \(m \vec{g}\) passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower centre of gravity.

Question 5.
How does [tendency to] toppling affect the tyres?
Answer:
While turning, shear stress acts on the tyre-road contact area. Due to this, the treads and side wall of a tyre deform. Apart from less control, this contributes to increased and uneven wear of the shoulder of the tyres.

Each wheel is placed under a small inward angle (called camber) in the vertical plane. Under severe lateral acceleration, when the car rolls, the camber angle ensures the complete contact area is in contact with the road and the wheels are now in vertical position. This improves the cornering behavior of the car. Improperly inflated and worn tyres can be especially dangerous because they inhibit the ability to maintain vehicle control. Worn tires may cause the vehicle to slide
sideways on wet or slippery pavement, sliding the vehicle off the road and increasing its risk of rolling over.

Question 6.
What is the recommendation for this?
Answer:
Because of uneven wear of the tyre shoulders, tyres should be rotated every 10000 km-12000 km. To avoid skidding, rollover and tyre-wear, the force of friction should not be relied upon to provide the necessary centripetal force during cornering. Instead, the road surface at a bend should be banked, i.e., tilted inward.

A car while taking a turn performs circular motion. If the road is level (or horizontal road), the necessary centripetal force is the force of static friction between the car tyres and the road surface. The friction depends upon the nature of the surfaces in contact and the presence of oil and water on the road. If the friction is inadequate, a speeding car may skid off the road. Since the friction changes with circumstances, it cannot be relied upon to provide the necessary centripetal force. Moreover, friction results in fast wear and tear of the tyres.

To avoid the risk of skidding as well as to reduce the wear and tear of the car tyres, the road surface at a bend is tilted inward, i.e., the outer side of the road is raised above its inner side. This is called banking of road. On a banked road, the resultant of the normal reaction and the gravitational force can act as the necessary centripetal force. Thus, every car can be safely driven on such a banked curve at certain optimum speed, without depending on friction. Hence, a road should be properly banked at a bend.

The angle of banking is the angle of inclination of the surface of a banked road at a bend with the horizontal.

When a two-wheeler takes a turn along an unbanked road, the force of friction provides the centripetal force. The two-wheeler leans inward to counteract a torque that tends to topple it outward. Firstly, friction cannot be relied upon to provide the necessary centripetal force on all road conditions. Secondly, the friction results in wear and tear of the tyres. On a banked road at a turn, any vehicle can negotiate the turn without depending on friction and without straining the tyres.

Question 7.
Determine the angle to be made with the vertical by a two-wheeler while turning on a horizontal track?
Answer:

When a bicyclist takes a turn along an unbanked road, the force of friction \(\vec{f}_{\mathrm{s}}\) provides the centripetal force; the normal reaction of the road \(\vec{N}\) is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, f_s.h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by \(\vec{N}\) and the weight \(\vec{g}\), mg.a = f_s.h₁

Since the force of friction provides the centripetal force,
f_s = \(\frac{m v^{2}}{r}\)
If the cyclist leans from the vertical by an angle 9, the angle between \(\vec{N}\) and \(\vec{F}\) in above figure.

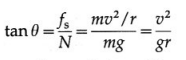
Hence, the cyclist must lean by an angle
θ = tan^-1\(\left(\frac{v^{2}}{g r}\right)\)

When a car takes a turn along a level road, apart from the risk of skidding off outward, it also has a tendency to roll outward due to an outward torque about the centre of gravity due to the friction force. But a car is an extended object with four wheels. So, when the inner wheels just get lifted above the ground, it can be counterbalanced by a restoring torque of the couple formed by the normal reaction (on the outer wheels) and the weight.

Question 8.
We have mentioned about ‘static friction’ between road and tyres. Why is it static friction? What about kinetic friction between road and tyres?
Answer:
When a car takes a turn on a level road, the point of contact of the wheel with the surface is instantaneously stationary if there is no slipping. Hence, the lateral force on the car is the limiting force of static friction between the tyres and road. Lateral forces allow the car to turn. As long as the wheels are rolling, there is lateral force of static friction and longitudinal force of rolling friction. Longtitudinal forces, which act in the direction of motion of the car body (or in the exact opposite direction), control the acceleration or deceleration of the car and therefore the speed of the car. These are the wheel force, rolling friction, braking force and air drag. If the car skids, the friction force is kinetic friction; more importantly, the direction of the friction force then changes abruptly from lateral to that opposite the velocity of skidding and not towards the centre of the curve, so that the car cannot continue in its curved path.

Question 9.
What do you do if your vehicle is trapped on a slippery or sandy road? What is the physics involved?
Answer:
Driving on a country road should be attempted only with a four-wheel drive. However, if you do get stuck in deep sand or mud, avoid unnecessary panic and temptation to drive your way out of the mud or sand because excessive spinning of your tyres will most likely just dig you into a deeper hole. Momentum is the key to getting unstuck from sand or mud. One method is the rocking method-rocking your car backwards and forwards to gain momentum. Your best option is usually to gain traction and momentum by wedging a car mat (or sticks, leaves, gravel or rocks) in front and under your drive wheels. Once you start moving, keep the momentum going until you are on more solid terrain.

Use your brain power (Textbook Page No. 6)

Question 1.
As a civil engineer, you are to construct a curved road in a ghat. In order to calculate the banking angle 0, you need to decide the speed limit. How will you decide the values of speed and radius of curvature at the bend ?
Answer:
For Indian roads, Indian Road Congress (IRC), [IRC-73-1980, Table 2, p.4], specifies the design speed depending on the classification of roads (such as national and state highways, district roads and village roads) and terrain. It is the basic design parameter which determines further geometric design features. For the radius of curvature at a bend, IRC [ibid., Table 16, p.24] specifies the absolute minimum values based on the minimum design speed. However, on new roads, curves should be designed to have the largest practicable radius, generally more than the minimum values specified, to allow for ‘sight distance’ and ‘driver comfort’. To consider the motorist driving within the innermost travel lane, the radius used to design horizontal curves should be measured to the inside edge of the innermost travel lane, particularly for wide road-ways with sharp horizontal curvature.

A civil engineer refers to banking as superelevation e;e = tan θ. IRC fixes e_max = 0.07 for a non-urban road and the coefficient of lateral static friction, µ = 0.15, the friction between the vehicle tyres and the road being incredibly variable. Ignoring the product eµ, from Eq. (6)
e + µ = \(\frac{v^{2}}{g r}\) (where both v and r are in SI units)
= \(\frac{V^{2}}{127 r}\)(where V is in km / h and r is in metre) …. (1)
The sequence of design usually goes like this :

1. Knowing the design speed V and radius r, calculate the superelevation for 75% of design speed ignormg friction : e = \(\frac{(0.75 \mathrm{~V})^{2}}{127 r}\) = \(\frac{V^{2}}{225 r}\)
2. If e < 0.07, consider this calculated value of e in subsequent calculations. If e > 0.07, then take e = e_max = 0.07.
3. Use Eq. (1) above to check the value of µ for e_max = 0.07 at the full value of the design speed V : µ = \(\frac{V^{2}}{127 r}\) – 0.07
   If µ < 0.15, then e = 0.07 is safe. Otherwise, calculate the allowable speed Va as in step 4.
4. \(\frac{V_{\mathrm{a}}^{2}}{127 r}\) = e + p = 0.07 + 0.15
   If V_a > V, then the design speed V is adequate.
   If V_a < V, then speed is limited to V_a with appropriate warning sign.

Use your brain power (Textbook Page No. 7)

Question 1.
If friction is zero, can a vehicle move on the road? Why are we not considering the friction in deriving the expression for the banking angle?
Answer:
Friction is necessary for any form of locomotion. Without friction, a vehicle cannot move. The banking angle for a road at a bend is calculated for optimum speed at which every vehicle can negotiate the bend without depending on friction to provide the necessary lateral centripetal force.

Question 2.
What about the kinetic friction between the road and the lyres?
Answer:
When a car takes a turn on a level road, the point of contact of the wheel with the surface is instantaneously stationary if there is no slipping. Hence, the lateral force on the car is the limiting force of static friction between the tyres and road. Lateral forces allow the car to turn. As long as the wheels are rolling, there is lateral force of static friction and longitudinal force of rolling friction. Longtitudinal forces, which act in the direction of motion of the car body (or in the exact opposite direction), control the acceleration or deceleration of the car and therefore the speed of the car. These are the wheel force, rolling friction, braking force and air drag. If the car skids, the friction force is kinetic friction; more importantly, the direction of the friction force then changes abruptly from lateral to that opposite the velocity of skidding and not towards the centre of the curve, so that the car cannot continue in its curved path.

Use your brain power (Textbook Page No. 12)

Question 1.
What is expected to happen if one travels fast over a speed breaker? Why?
Answer:
The maximum speed with which a car can travel over a road surface, which is in the form of a convex arc of radius r, is \(\sqrt{r g}\) where g is the acceleration due to gravity. For a speed breaker, r is very small (of the order of 1 m). Hence, one must slow down considerably while going over a speed breaker. Otherwise, the car will lose contact with the road and land with a thud.

Question 2.
How does the normal force on a concave suspension bridge change when a vehicle is travelling on it with a constant speed ?
Answer:
At the lowest point, N-mg provides the centripetal force. Therefore, N-mg = \(\frac{m v^{2}}{r}\), so that N = m(g + \(\frac{v^{2}}{r}\)).
Therefore, N increases with increasing v.

Use your brain power (Textbook Page No. 15)

Question 1.
For the point P in above, we had to extend OC to Q to meet the perpendicular PQ. What will happen to the expression for I if the point P lies on OC?
Answer:
There will be no change in the expression for the MI (I) about the parallel axis through O.

Balbharti Yuvakbharati English 12th Digest Chapter 4.1 History of Novel Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 4.1 History of Novel

12th English Digest Chapter 4.1 History of Novel Textbook Questions and Answers

1. Match the columns:

Question 1.
Match the columns:

A	B
1. Murasaki Shikibu	(a) Cervantes
2. Novella	(b) Bankimchandra Chattopadhyaya
3. Don Quixote	(c) Tale of Genji
4. Rajmohan’s Wife	(d) New

Answer:

A	B
1. Murasaki Shikibu	(c) Tale of Genji
2. Novella	(d) New
3. Don Quixote	(a) Cervantes
4. Rajmohan’s Wife	(b) Bankimchandra Chattopadhyaya

2. Pick out the odd element from each group:

Question (i)
Arun Joshi, Vikram Seth, Graham Greene, Kiran Nagarkar
Answer:
Graham Greene (Graham Greene was an English novelist; the others are Indian writers)

Question (ii)
Place, Period, Theme, Climate, Lifestyle
Answer:
Theme (the others are aspects of the setting)

Question (iii)
Theme, Plot, Character, Novella
Answer:
Novella (‘Novella’ is a ‘novel’; the others are the elements of a novel)

3. Complete the following statements:

Question 1.
Complete the following statements:
Answer:
(i) The two types of conflicts that the plot may have are internal (inside the mind of the character) or external (with other characters or entities).
(ii) The word ‘picaresque’ is originated from the Spanish word ‘picaro,’ which means a rogue.
(iii) The epistolary novel presents the narrative through a series of correspondence or other documents like letters or diary entries.
(iv) In the eighteenth century, the middle class could get the time for reading and discussing the novels because the spread of machines helped them in their work and could provide them with some spare time.

4. Write short notes on:

Question 1.
Write short notes on:
(i) Style of the novel
(ii) Stream of consciousness novel
(iii) Novella
(iv) Indian tradition of novels.
Answer:
(i) Style of the novel: The language and the techniques used by the author for the narration of the course of events is known as the ‘style’. An author can use extensive vocabulary and difficult phrases or he may be brief and could write only to the point or he may mix both according to the requirement of his story. He may use linguistic devices like figures of speech to make the narrative effective. All these factors decide the ‘texture’ of the narration and create an impact on the readers.

(ii) Stream of consciousness novel: The phrase ‘Stream of consciousness’ means the flow of thoughts in the minds of the characters. This phrase was coined by William James in his treatise ‘Principles of Psychology.’ (1890). In such a novel, incidents in the plot are in the sequence of their occurrence. The novelist narrates them just as they occur in the minds of the characters. Sometimes they do not make sense; but they truthfully represent the thoughts without any censoring or editing.

(iii) Novella: The word ‘Novella’ which means new is originated from the Italian word ‘novelle’. A Novella is a type of prose fiction which is shorter than a full length novel and longer than short stories. It is a well-structured yet short narrative, often satiric or realistic in tone. Novella usually focuses on one incident or issue with one or two main characters and takes place at a single location. Given below are some of the famous novellas in English:

1. ‘The Heart of Darkness’ by Joseph Conrad
2. ‘The Turn of the Screw’ by Henry James
3. ‘Billy Budd’ by Hermann Melville
4. ‘Death in Venice’ by Thomas Mann
5. ‘Seize The Day’ by Saul Bellow
6. ‘Pearl’ by John Steinbeck

(iv) Indian tradition of novels: Indians have also played a major role in the writing of English Novels. ‘Rajmohan’s Wife’, by Bankim Chandra Chattopadhyaya was the first novel in English written by an Indian. The period after that is marked by a few more navels written by Indian writers. These novels were based on either nationalistic virtues or social issues. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.

Novelists like Anita Desai, Nayantara Sahgal, Arun Joshi and Manohar Malgaonkar changed the current of Indian English novel through their works. Amitav Ghosh, Vikram Seth and Upamanyu Chatterjee improved upon the Indian novel in English by adding new features to it. In recent years, Indian novelists like Salman Rushdie, Arvind Adiga, Arundhati Roy, Kiran Desai and Kiran Nagarkar have come into the limelight. The tradition of the Indian English novel has undergone a vital change since its birth and has undoubtedly a very bright future.

Yuvakbharati English 12th Digest Chapter 4.1 History of Novel Additional Important Questions and Answers

Question 1.
Pick out the statements that are False. Rewrite them correctly:
1. Setting describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘novella’.
3. The struggle between the opposite forces in the story is called ‘conflict.’
4. Theme is the central idea in the novel which can be expressed in a nutshell.
5. The plot and character are affected due to the setting.
6. ‘Plot’ is the narrative style of the author.
Answer:
False statements:
1. Setting describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘novella’.
6. ‘Plot’ is the narrative style of the author.

Corrected statements:
1. Characterization describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘protagonist’.
6. Plot is the course of events that make up the theme.

Question 2.
Rewrite the following statements in chronological order:
1. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.
2. The novel originated as the literary form in England.
3. Indian novelists like Arvind Adiga, Arundhati Roy and Kiran Desai have dazzled with their writing.
4. Many stalwart novelists such as Charles Dickens, Walter Scott became famous.
Answer:
2. The novel originated as the literary form in England.
4. Many stalwart novelists such as Charles Dickens, Walter Scott became famous.
1. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.
3. Indian novelists like Arvind Adiga, Arundhati Roy and Kiran Desai have dazzled with their writing.

Question 3.
List the types of novels.
Answer:
The types of novels are: Realistic
Novel, Picaresque Novel, Historical
Novel, Epistolary Novel, Gothic Novel, Autobiographical Novel, Allegorical Novel, Utopian/Dystopian Novel, Psychological Novel, Stream of Consciousness Novel, Bildungsroman Novel.

Question 4.
Choose the correct options from the brackets and fill in the blanks :
Answer:
1. The characters in the Realistic novel interact with other characters and undergo plausible and everyday experiences. (Realistic/Utopian)
2. A Picaresque novel narrates the adventures of the protagonist, who is an eccentric or a disreputable person, in an episodic form. (Picaresque/Realistic)
3. The Dystopian novel is about an imaginary community or society possessing the ideal qualities. (Dystopian/Picaresque)
4. In the Stream of Consciousness novel, the novelist narrates the character’s thoughts as they enter the mind of the character. (Stream of Consciousness/ Utopian)
5. The Bildungsroman novel is a fictional biography or autobiography which is concerned with the growth of the protagonist’s mind, spirit and character from childhood to adulthood. (Bildungsroman/Gothic)
6. The Gothic novel includes terror, mystery, horror, thriller, supernatural, doom, death or decay or haunted buildings. (Dystopian/Gothic)

Glossary:

1. genre – a style, especially in the arts, that involves a particular set of characteristics,
2. embellishing – decorating.
3. adopted – followed,
4. precursor – something that happened or existed before another thing,
5. profoundly – deeply,
6. elite – upper class.
7. aspirations – ambitions, desires,
8. encompass – include,
9. plenteous – plentiful,
10. stalwart – (here) a person who has achieved great recognition and appreciation,
11. innovative – new and original,
12. pageant – a colourful or impressive procession of people.
13. ameliorate – to make something better,
14. dazzling – shining.
15. satiric – sharp or sarcastic.
16. interweaving – combining; twisting together,
17. thumbnail sketch – brief description,
18. antagonist – a person who is opposed to the hero,
19. laconic – short and crisp.
20. plausible – believable,
21. eccentric – peculiar; crazy; out-of-the-way.
22. disreputable – not respectable.
23. speculative – unproven, unreal,
24. extraterrestrial – of or from outside the earth or its atmosphere.
25. amateur – inexperienced; unprofessional.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 16 Semiconductor Devices Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 16 Semiconductor Devices

1. Choose the correct option

i.
In a BJT, the largest current flow occurs
(A) in the emitter
(B) in the collector
(C) in the base
(D) through CB junction.
Answer:
(A) in the emitter

ii.
A series resistance is connected in the Zener diode circuit to
(A) properly reverse bias the Zener
(B) protect the Zener
(C) properly forward bias the Zener
(D) protect the load resistance.
Answer:
(A) properly reverse bias the Zener

iii.
An LED emits visible light when its
(A) junction is reverse biased
(B) depletion region widens
(C) holes and electrons recombine
(D) junction becomes hot.
Answer:
(C) holes and electrons recombine

iv.
Solar cell operates on the principle of
(A) diffusion
(B) recombination
(C) photovoltaic action
(D) carrier flow.
Answer:
(C) photovoltaic action

v.
A logic gate is an electronic circuit which
(A) makes logical decisions
(B) allows electron flow only in one direction
(C) works using binary algebra
(D) alternates between 0 and 1 value.
Answer:
(A) makes logical decisions

2 Answer in brief.

i.
Why is the base of a transistor made thin and is lightly doped?
Answer:
The base of a transistor is lightly doped than the emitter and is made narrow so that virtually all the electrons injected from the emitter (in an npn tran-sistor) diffuse right across the base to the collector junction without recombining with holes. That is, the base width is kept less than the recombination distance. Also, the emitter is much heavily doped than the base to improve emitter efficiency and common-base current gain a.

ii.
How is a Zener diode different than an ordinary diode?
Answer:
A Zener diode is heavily doped-the doping con-centrations for both p- and n-regions is greater than 1018 cm-3 while those of an ordinary diode are voltage (PIV) of an ordinary diode is higher than a Zener diode and the breakdown occurs by impact ionization (avalanche process). Their I-V characteristics are otherwise similar.

iii.
On which factors does the wavelength of light emitted by a LED depend?
Answer:
The intensity of the emitted light is directly propor-tional to the recombination rate and hence to the diode forward current. The colour of the light emitted by an LED depends on the compound semiconductor material used and its composition (and doping levels) as given below :
Table: Typical semiconductor materials and emitted colours of LEDs

Material	Emitted colour(s)
Gallium arsenide (GaAs), Indium gallium arsenide phosphide (InGaAsP)	Infrared
Aluminum gallium arsenide (AlGaAs)	Deep red, also IR laser
Indium gallium phosphide (InGaP)	Red
Gallium arsenide phosphide (GaAsP), aluminum indium gallium phosphide (AlInGaP)	Orange, red or yellow
Gallium phosphide (GaP)	Green or yellow
Aluminium gallium phosphide (AlGaP), zinc selenide (ZnSe), zinc selenide telluride (ZnSeTe), nitrogen impregnated gallium phosphide (GaP:N)	Green
Indium gallium nitride (InGaN), gallium nitride (GaN), sine sulphide (ZnS)	Blue and violet Longer wave lengths (green and yellow) are obtained by increasing the indium (In) content. Phosphor encapsulation produce white light.
Aluminium gallium nitride (AlGaN)	Ultraviolet

iv.
Why should a photodiode be operated in reverse biased mode?
Answer:
A photodiode is operated in a reverse biased mode because as photodetector or photosensor, it must conduct only when radiation is incident on it. In the reverse biased mode, the dark current for zero illumination is negligibly small—of the order of few picoamperes to nanoamperes. But when illuminated, the photocurrent is several orders of magnitude greater.

v.
State the principle and uses of a solar Cell.
Answer:
A solar cell is an unbiased pn-junction that converts the energy of sunlight directly into electricity with a high conversion efficiency.

Principle : A solar cell works on the photovoltaic effect in which an emf is produced between the two layers of a pn-junction as a result of irradiation.

Question 3.
Draw the circuit diagram of a half wave rectifier. Explain its working. What is the frequency of ripple in its output?
Answer:
A device or a circuit which rectifies only one-half of each. cycle of an alternating voltage is called a half-wave rectifier.
Electric circuit : The alternating voltage to be rectified is applied across the primary coil (P₁P₂) of a transformer. The secondary coil (S₁S₂) of the transformer is connected in series with the junction diode and a load resistance R_L, as shown in below figure. The alternating voltage across the secondary coil is the ac input voltage V_i. The dc voltage across the load resistance is called the output voltage V₀.

Working : Due to the alternating voltage V_i, the p-region of the diode becomes alternatively positive and negative with respect to the n-region.
During the half-cycle when the p-region is positive, the diode is forward biased and conducts. A current I_L passes through the load resistance RL in the direction shown.

During the next half cycle, when the p-region is negative, the diode is reverse biased and the forward current drops to zero.

Thus, the diode conducts only during one-half of the input cycle and thus acts as a half-wave rectifier. The intermittent output voltage V₀ has a fixed polarity but changes periodically with time between zero and a maximum value. I_L is unidirectional. Above figure shows the input and output voltage waveforms.

The pulsating dc output voltage of a half-wave rectifier has the same frequency as the input.

Question 4.
Why do we need filters in a power supply?
Answer:
A rectifier-half-wave or full-wave – outputs a pul-sating dc which is not directly usable in most electronic circuits. These circuits require something closer to pure dc as produced by batteries. Unlike pure dc waveform of a battery, a rectifier output has an ac ripple riding on a dc waveform.

The circuit used in a dc power supply to remove the ripple is called a filter. A filter circuit can produce a very smooth waveform that approximates the waveform produced by a battery. The most common technique used for filtering is a capacitor connected across the output of a rectifier.

Question 5.
Draw a neat diagram of a full wave rectifier and explain it’s working.
Answer:
A device or a circuit which rectifies both halves of each cycle of an alternating voltage is called a full-wave rectifier.
Electric circuit : The alternating voltage to be rectified is applied across the primary coil (P₁P₂) of a transformer with a centre-tapped secondary coil (S₁S₂). The terminals and S2 of the secondary are connected to the two p-regions of two junction diodes D₁ and D₂, respectively. The centre-tap T is connected to the ground. The load resistance RL is connected across the common n-regions and the

P₁P₂, S₁S₂ : Primary and secondary of transformer,
T : Centre-tap on secondary; D₁ D₂ : Junction diodes,
R_L : Load resistance, I_L : Load current,
V_i: AC input voltage, V₀ : DC output voltage
Above Figure : Full-wave rectifier circuit

Working : During one half cycle of the input, terminal S₁ of the secondary is positive while S₂ is negative with respect to the ground (the centre-tap T). During this half cycle, diode D₁ is forward biased and conducts, while diode D₂ is reverse biased and does not conduct. The direction of current Z_L through R_L is in the sense shown.

During the next half cycle of the input voltage, S2 becomes positive while S, is negative with respect to T. Diode D2 now conducts sending a current IL through RL in the same sense as before. Dt now does not conduct. Thus, the current through RL flows in the same direction, i.e., it is unidirectional, for both halves or the full-wave of the input. This is called full-wave rectification.

The output voltage has a fixed polarity but varies periodically with time between zero and a maximum value. Above figure shows the input and output voltage waveforms. The pulsating dc output voltage of a full-wave rectifier has twice frequency of the input.

Question 6.
Explain how a Zener diode maintains constant voltage across a load.
Answer:
Principle : In the breakdown region of a Zener diode, for widely changing Zener current, the voltage across the Zener diode remains almost constant.

Electric circuit : The circuit for regulating or stabilizing the voltage across a load resistance RL against change in load current and supply voltage is shown in above figure. The Zener diode is connected parallel to load Rh such that the current through the Zener diode is from the n to p region. The series resistance Rs limits the current through the diode below the maximum rated value.
From the circuit, I = I_Z + I_L and V = IR_s + V_Z
= (I_Z + I_L)R_s + V_Z
Working: When the input unregulated dc voltage V across the Zener diode is greater than the Zener voltage V_Z in magnitude, the diode works in the Zener breakdown region. The voltage across the diode and load Rh is then V_Z. The corresponding current in the diode is I_Z.

As the load current (I) or supply voltage (V) changes, the diode current (7Z) adjusts itself at constant V_Z. The excess voltage V-V_Zappears across the series resistance Rs.

For constant supply voltage, the supply current I and the voltage drop across R_s remain constant. If the diode is within its regulating range, an increase in load current is accompanied by a decrease in Iz at constant V_Z.
Since the voltage across R_L remains constant at V_Z, the Zener diode acts as a voltage stabilizer or voltage regulator.

Question 7.
Explain the forward and the reverse characteristic of a Zener diode.
Answer:
The forward bias region of a Zener diode is identical to that of a regular diode. There is forward current only after the barrier potential of the pn- junction is overcome. Beyond this threshold or cut in voltage, there is an exponential upward swing.

The typical forward voltage at room temperature with a current of around 1 mA is around 0.6 V.

In the reverse bias condition the Zener diode is an open circuit and only a small reverse saturation current flows as shown with change of scale. At the reverse breakdown voltage there is an abrupt rapid increase in the current-the knee is very sharp, followed by an almost vertical increase in current. The voltage across the Zener diode in the breakdown region is very nearly constant with only a small increase in voltage with increasing current. There is a minimum Zener current, I_Z (min), that places the operating point in the desired breakdown region. At some high current level, I_ZM, the power dissipation of the diode becomes excessive beyond which the diode can be damaged.

Zener diode characteristics

The I-V characteristics of a Zener diode is not totally vertical in the breakdown region. This means that for slight changes in current, there will be a small change in the voltage across the diode. The voltage change for a given change in current is the resistance R_Z of the Zener diode.

Question 8.
Explain the working of a LED.
Answer:
Working :
An LED is forward-biased with about 1.2 V to 3.6 V at 12 mA to 20 mA. Majority carriers electrons from n-type layer and holes from p-type layer are injected into the active layer. Electrons cross the junction into the p-layer. In the active p-layer, some of these excess minority carriers electrons, recombine radiatively with majority carriers, holes, thereby emitting photons. The resulting photon has an energy approximately equal to the bandgap of the active layer material. Modifying the bandgap of the active layer creates photons of diferent energies.

In the energy band diagram this recombination is equivalent to a transition of the electron from a higher energy state in the conduction band to a lower energy state in the valence band. The energy difference is emitted as a photon of energy hv.
[Note : The photons originate primarily in the p-side of the junction which has a bandgap E_Gp narrower than that of the n-side, E_Gn. Thus, with hv < E_Gn, the photons are emitted through the wide-bandgap n-region with essentially no absorption.]

Question 9.
Explain the construction and working of solar cell.
Answer:
Construction :
A simple pn-junction solar cell con-sists of a p-type semiconductor substrate backed with a metal electrode back contact. A thin n-layer (less than 2.5 pm, for silicon) is grown over the p-type substrate by doping with suitable donor impurity. Metal finger electrodes are prepared on top of the n-layer so that there is enough space between the fingers for sunlight to reach the n-layer and, subsequently, the underlying pn-junction.

Working : When exposed to sunlight, the absorption of incident radiation (in the range near-UV to infrared) creates electron-hole pairs in and near the depletion layer.

Consider light of frequency v incident on the pn-junction such that the incident photon energy hv is greater than the band gap energy EG of the semiconductor. The photons excite electrons from the valence band to the conduction band, leaving vacancies or holes in the valence band, thus generating electron-hole pairs.

The photogenerated electrons and holes move towards the n side and p side, respectively. If no external load is connected, these photogenerated charges get collected at the two sides of the junction and give rise to a forward photovoltage. In a closed- circuit, a current I passes through the external load as long as the solar cell is exposed to sunlight.

A solar cell module consists of several solar cells connected in series for a higher voltage output. For outdoor use with higher power output, these modules are connected in different series and parallel combinations to form a solar cell array.

[Note : Currently most of the crystalline solar cells are p-type as described above. This is because of a lower cost of production of p-type. But performance wise, n-type solar cells (a thin p-layer over an n-type substrate by doping with suitable acceptor impurity) can give much better efficiency compared to p-type solar cells.]

Question 10.
Explain the principle of operation of a photodiode.
Answer:
Construction:
A photodiode consists of an n-type silicon substrate with a metal electrode back contact. A thin p-type layer is grown over the n-type substrate by diffusing a suitable acceptor dopant.

The area of the p-layer defines the photodiode active area. An ohmic contact pad is deposited on the active area. The rest of the active area is left open with a protective antireflective coating of silicon nitride to minimize the loss of photons. The nonactive area is covered with an insulating opaque SiO₂ coating.

Depending on the required spectral sensitivity, i.e., the operating wavelength range, typical photodiode materials are silicon, germanium, indium gallium arsenide phosphide (InGaAsP) and indium gallium arsenide (InGaAs), of which silicon is the cheapest while the last two are expensive.

Working : The band gap energy of silicon is E_G = 1.12 eV at room temperature. Thus, photons or particles with energies greater than or equal to 1.12 eV, which corresponds to 110 nm, can transfer electrons from the valence band into the conduction band.

A photodiode is operated in the reverse bias mode which results in a wider depletion region. When operated in the dark (zero illumination), there is a reverse saturation current due solely to the thermally generated minority charge carriers. This is called the dark current. Depending on the minority carrier concentrations, the dark current in an Si photodiode may range from 5 pA to 10 nA.

When exposed to radiation of energy hv ≥ E_G (in the range near-UV to near-IR), electron-hole pairs are created in the depletion region. The electric field in the depletion layer accelerates these photogenerated electrons and holes towards the n side and p side, respectively, constituting a photocurrent l in the external circuit from the p side to the n side. Due to the photogeneration, more charge carriers are available for conduction and the reverse current is increased. The photocurrent is directly propor-tional to the intensity of the incident light. It is independent of the reverse bias voltage.
[Notes : Typical photodiode materials are :
(1) silicon (Si) : low dark current, high speed, good sensitivity between ~ 400 nm and 1000 run (best around 800 nm-900 nm)
(2) germanium (Ge) : high dark current, slow speed, good sensitivity between ~ 900 nm and 1600 nm (best around 1400 nm-1500 nm)
(3) indium gallium arsenide phosphide (InGaAsP) : expensive, low dark current, high speed, good sensitivity between ~ 1000 nm and 1350 nm (best around 1100 nm- 1300 nm)
(4) indium gallium arsenide (InGaAs): expensive, low dark current, high speed, good sensitivity between ~ 900 nm and 1700 nm (best around 1300 nm-1600 nm],

Question 11.
What do you mean by a logic gate, a truth table and a Boolean expression?
Answer:
A logic gate is a basic switching circuit used in digital circuits that determines when an input pulse can pass through to the output. It generates a single output from one or more inputs.

Explanation/Uses :
Any digital computation process consists in performing a sequence of arithmetical operations on the data of the problem. At each stage in the computation, the nature of the operation to be performed is decided partly by the pre-determined program and partly by the outcome of earlier stages in the process. We therefore need switches with multiple inputs to perform logical operations, i.e., the outputs of these switches are determined in specified ways by the condition (binary state) of their inputs. These arrangements are known as logic gates, and mostly they are extension of a simple transistor switch.

(1) Boolean expression : An equation expressing a logical compound statement in Boolean algebra is called a Boolean expression. A Boolean expression for a logic gate expresses the relation between input(s) and output of a logic gate.

(2) Truth table : The table which shows the truth values of a Boolean expression for a logic gate for all possible combinations of its inputs is called the truth table of logic gate.

The truth table contains one row for each input combination. Since a logical variable can assume only two possible values, 0 and 1, there are 2N combinations of N inputs so that the table has 2N rows.
[Note : Boolean algebra is a form of symbolic logic developed in 1847 by George Boole (1815-64) British mathematician.]

Question 12.
What is logic gate? Write down the truth table and Boolean expression for ‘AND’ gate.
Answer:
A logic gate is a basic switching circuit used in digital circuits that determines when an input pulse can pass through to the output. It generates a single output from one or more inputs.

The AND gate : It is a circuit with two or more inputs and one output in which the output signal is HIGH if and only if all the inputs are HIGH simultaneously.

The AND operation represents a logical multiplication.

Below figure shows the 2-input AND gate logic symbol and the Boolean expression and the truth table for the AND function.
Logic symbol:

Truth table:

Boolean expression:
Y = A ∙ B

Question 13.
What are the uses of logic gates? Why is a NOT gate known as an inverter?
Answer:
Explanation/Uses :
Any digital computation process consists in performing a sequence of arithmetical operations on the data of the problem. At each stage in the computation, the nature of the operation to be performed is decided partly by the pre-determined program and partly by the outcome of earlier stages in the process. We therefore need switches with multiple inputs to perform logical operations, i.e., the outputs of these switches are determined in specified ways by the condition (binary state) of their inputs. These arrangements are known as logic gates, and mostly they are extension of a simple transistor switch.

The NOT gate or INVERTER : It is a circuit with one input whose output is HIGH if the input is LOW and vice versa.

The NOT operation outputs an inverted version of the input. Hence, a NOT gate is also known as an INVERTER.

The small invert bubble on the output side of the inverter logic symbol, below figure and the over bar (^–) in the Boolean expression represent the invert function.

Question 14.
Write the Boolean expression for (i) OR gate, (ii) AND gate, and (iii) NAND Gate.
Answer:
(i) The OR gate : It is a circuit with two or more inputs and one output in which the output signal is HIGH if any one or more of the inputs is HIGH.
The OR operation represents a logical addition.
Below figure shows the 2-input OR gate logic sym-bol, and the Boolean expression and the truth table for the OR function.

(ii) The AND gate : It is a circuit with two or more inputs and one output in which the output signal is HIGH if and only if all the inputs are HIGH simultaneously.

The AND operation represents a logical multiplication.

Below figure shows the 2-input AND gate logic symbol and the Boolean expression and the truth table for the AND function.
Logic symbol:

Truth table:

Boolean expression:
Y = A ∙ B

(iii) The NAND gate : It is a circuit with two or more inputs and one output, whose output is HIGH if any one or more of the inputs is LOW; the output is LOW if all the inputs are HIGH.

The NAND gate is a combination of an AND gate followed by a NOT gate so that the truth table of the NAND function is obtained by inverting the outputs of the AND gate.

Question 15.
Why is the emitter, the base and the collector of a BJT doped differently?
Answer:
A BJT being a bipolar device, both electrons and holes participate in the conduction process. Under the forward-biased condition, the majority carriers injected from the emitter into the base constitute the largest current component in a BJT. For these carriers to diffuse across the base region with t negligible recombination and reach the collector junction, these must overwhelm the majority carriers of opposite charge in the base. The total emitter current has two components, that due to majority carriers in the emitter and that due to minority carriers diffused from base into emitter. The ratio of the current component due to the injected majority carriers from the emitter to the total emitter current is a measure of the emitter efficiency. To improve the emitter efficiency and the common-base current gain (a), it can be shown that’ the emitter should be much heavily doped than the base.

Also, the base width is a function of the base- collector voltage. A low doping level of the collector increases the size of the depletion region. This increases the maximum collector-base voltage and reduces the base width. Further, the large depletion region at the collector-base junction-extending mainly into the collector-corresponds to a smaller electric field and avoids avalanche breakdown of the reverse-biased collector-base junction.
[Note : Effective dopant concentrations of (a) npn transistor (b) pnp transistor are shown below.

The base doping is less than the emitter doping but greater than the collector doping. Contrary to the impression stressed in the Board’s and NCERT textbooks, collector doping is typically an order of magnitude lower than base doping. {Ref. : Semiconductor Devices Physics and Technology (3rd Edition), Simon M. Sze and M. K. Lee, p. 125}]

Question 16.
Which method of biasing is used for operating transistor as an amplifier?
Answer:
For use as an amplifier, the transistor should be in active mode. Therefore, the emitter-base junction is forward biased and the collector-base junction is reverse biased. Also, an amplifier uses an emitter bias rather than a base bias.

Question 17.
Define α and β. Derive the relation between then.
Answer:
The dc common-base current ratio or current gain (α_dc) is defined as the ratio of the collector current to emitter current.
α_dc = \(\frac{I_{C}}{I_{\mathrm{E}}}\)
The dc common-emitter current ratio or current gain (β_dc) is defined as the ratio of the collector current to base current.
β_dc = \(\frac{I_{C}}{I_{B}}\)
Since the emitter current I_E = I_B + I_C
\(\frac{I_{\mathrm{E}}}{I_{C}}=\frac{I_{\mathrm{B}}}{I_{\mathrm{C}}}+1\)
∴ \(\frac{1}{\alpha_{\mathrm{dc}}}=\frac{1}{\beta_{\mathrm{dc}}}+1\)
Therefore, the common-base current gain in terms of the common-emitter current gain is
α_dc = \(\frac{\beta_{\mathrm{dc}}}{1+\beta_{\mathrm{dc}}}\)
and the common-emitter current gain in terms of the common-base current gain is
β_dc = \(\frac{\alpha_{\mathrm{dc}}}{1-\alpha_{\mathrm{dc}}}\)
For a transistor, α_dc is close to but always less than 1 (about 0.92 to 0.98) and β_dc ranges from 20 to 200 for most general purpose transistors.

Question 18.
The common-base DC current gain of a transistor is 0.967. If the emitter current is 10mA. What is the value of base current?
Answer:
Data : α_dc = 0.967, I_E = 10 mA
α_dc = \(\frac{I_{C}}{I_{\mathrm{E}}}\) and I_E = I_B + I_C
The collector current,
I_C = α_dcI_E = 0.967 × 10 = 9.67 mA
Therefore, the base current,
I_B = I_E – I_C = 10 – 9.67 = 0.33 mA

Question 19.
In a comman-base connection, a certain transistor has an emitter current of 10mA and collector current of 9.8 mA. Calculate the value of the base current.
Answer:
DATA : I_E = 10 mA, I_C = 9.8 mA
I_E = I_B + I_C
Therefore, the base current,
I_B = I_E – I_C – 10 – 9.8 = 0.2 mA

Question 20.
In a common-base connection, the emitter current is 6.28mA and collector current is 6.20 mA. Determine the common base DC current gain.
Answer:
Data : I_E = 6.28 mA, I_C = 6.20 mA
α_dc = \(\frac{I_{C}}{I_{\mathrm{E}}}\) and β_dc = \(\frac{I_{\mathrm{C}}}{I_{\mathrm{B}}}=\frac{\alpha_{\mathrm{dc}}}{1-\alpha_{\mathrm{dc}}}\)
Common-emitter current gain, α_dc = \(\frac{6.20}{6.28}\) = 0.9873
Therefore, common-base current gain,
β_dc = \(\frac{0.9873}{1-0.9873}=\frac{0.9873}{0.0127}\) = 77.74
OR
I_E = I_B + I_C
∴ I_B = I_E – I_C = 6.28 – 6.20 = 0.08 mA
∴ β_dc = \(\frac{6.20}{0.08}\) = 77.5
[Note : The answer given in the textbook obviously refers to the common-emitter current gain.]

12th Physics Digest Chapter 16 Semiconductor Devices Intext Questions and Answers

Remember this (Textbook Page No. 346)

Question 1.
A full wave rectifier utilises both half cycles of AC input voltage to produce the DC output.
Answer:
A half-wave rectifier rectifies only one half of each cycle of the input ac wave while a full-wave rectifier rectifies both the halves. Hence the pulsating dc output voltage of a half-wave rectifier has the same frequency as the input but that of a full-wave rectifier has double the frequency of the ac input.

Do you know (Textbook Page No. 346)

Question 1.
The maximum efficiency of a full wave rectifier is 81.2% and the maximum efficiency of a half wave rectifier is 40.6%. It is observed that the maximum efficiency of a full wave rectifier is twice that of half wave rectifier.
Answer:
The ratio of dc power obtained at the output to the applied input ac power is known as rectifier efficiency. A half-wave rectifier can convert maximum 40.6% of ac power into dc power, and the remaining power of 59.4% is lost in the rectifier circuit. In fact, 50% power in the negative half cycle is not converted and the remaining 9.4% is lost in the circuit. Hence, a half wave rectifier efficiency is 40.6%. The maximum efficiency of a full-wave rectifier is 81.2%, i.e., twice that of a half-wave rectifier.

Do you know (Textbook Page No. 349)

Question 1.
The voltage stabilization is effective when there is a minimum Zener current. The Zener diode must be always operated within its breakdown region when there is a load connected in the circuit. Similarly, the supply voltage V_s must be greater than V_z.
Answer:
A Zener diode is operated in the breakdown region. There is a minimum Zener current, I_z, that places the desired operating point in the breakdown region. There is a maximum Zener current, I_zM, at which the power dissipation drives the junction temperature to the maximum allowed. Beyond that current the diode can be damaged. Hence, the supply voltage must be greater than V_z and the current-limiting resistor must limit the diode current to less than the rated maxi mum, I_zM.

Remember this (Textbook Page No. 350)

Question 1.
Zener effect occurs only if the diode is heavily doped, because when the depletion layer is thin, breakdown occurs at low reverse voltage and the field strength will be approximately 3 × 10⁷ V/m. It causes an increase in the flow of free carriers and increase in the reverse current.
Answer:
Zener breakdown occurs only in heavily doped pn junctions (doping concentrations for both p- and n-regions greater than 1018 cm3) and can take place only if the electric field in the depletion region of the reverse-biased junction is very high. It is found that the critical field at which tunneling becomes probable, i.e., at which Zener breakdown commences, is approximately 10⁶ V/cm. [“internal Field Emissiot at Narrow Silicon and Germanium PN-Junctions,” Phys. Rev., 118, 425 (1960).]

Can you tell (Textbook Page No. 350)

Question 1.
How does a cell phone charger produce a voltage of 5.0 V form the line voltage of 230V?
Answer:
A phone charger is usually a 5 V power supply. A 4-diode bridge input rectifier rectifies the ac mains voltage a provide a high voltage dc. A transistor chopper switches this on and off at high frequency. This stage is required because this high frequency allows the transformer to be smaller, lighter and much lower in cost.

A small transformer steps this down to a low voltage high-frequency ac. An output rectifier and filter convert this to low-voltage (5 V) dc and smooths out the ripple. A chopper controller provides a feedback to the chopper through an optoisohitor and adjusts the chopping cycle to maintain the output voltage at 5 V.

Question 2.
Why is a resistance connected in series with a Zener diode when used in a circuit?
Answer:
The I-V characteristics in the breakdown region of a Zener diode is almost vertical. That is, the current I_Z can rapidly increase at constant V_Z. To prevent damage due to excessive heating, the Zener current should not exceed the rated maximum current, I_ZM. Hence, a current-limiting resistor R_s is connected in series with the diode.

I_Z and the power dissipated in the Zener diode will be large for I _L = 0 (no-load condition) or when I_L is less than the rated maximum (when R_s is small and R_L is large). The current-limiting resistor R_s is so chosen that the Zener current does not exceed the rated maximum reverse current, I_ZM when there is no load or when the load is very high.
The rated maximum power of a Zener diode is
P_ZM = I_ZM = V_Z

At n-load condition, the current through R is I = I_ZM and the voltage drop across it is V – V_Z, where V is the unregulated source voltage. The diode current will be maximum when V is maxi mum at V_max and I = I_ZM. Then, the minimum value of the series resistance should be
R_{s, min} = \(\frac{V_{\max }-V_{\mathrm{Z}}}{I_{\mathrm{ZM}}}\)

Question 3.
The voltage across a Zener diode does not remain strictly constant with the changes in the Zener current. This is due to R_Z, the Zener impedance, or the internal resistance of the Zener diode. R_Z acts like a small resistance in series with the Zener. Changes in I_Z cause small changes in V_Z .
Answer:
The I-V characteristics of a Zener diode in the breakdown region is not strictly vertical. Its slope is 1/R_Z, where R_Z is the Zener impedance.

Can you know (Textbook Page No. 354)

Question 1.
What is the difference between a photo diode and a solar cell?
Answer:
Both are semiconductor photovoltaic devices. A photodiode is a reverse-biased pn-junction diode while a solar cell is an unbiased pn-junction diode. Photod iodes, however, are optimized for light detection while solar cells are optimized for energy conversion efficiency.

Question 2.
When the intensity of light incident on a photo diode increases, how is the reverse current affected?
Answer:
The photocurrent increases linearly with increasing illuminance, limited by the power dissipation of the photodiode.

Do you know (Textbook Page No. 355)

Question 1.
LED junction does not actually emit that much light so the epoxy resin body is constructed in such a way that the photons emitted by the junction are reflected away from the surrounding substrate base to which the diode is attached and are focused upwards through the domed top of the LED, which itself acts like a lens concentrating the light. This is why the emitted light appears to be brightest at the top of the LED.
Answer:
The pn-junction of an LED is encased in a transparent, hard plastic (epoxy resin), not only for shock protection but also for enhancing the brightness in one direction. Light emitted by the pn-junction is not directional. The hemispherical epoxy lens focuses the light in the direction of the hemispherical part. This is why the emitted light appears to be brightest at the top of the LED.

Question 2.
The current rating of LED is of a few tens of milli-amps. Hence it is necessary to connect a high resistance in series with it. The forward voltage drop of an LED is much larger than an ordinary diode and is around 1.5 to 3.5 volts.
Answer:
Most common LEDs require a forward operating voltage of between approximately 1.2 V (for a standard red LED) to 3.6 V (for a blue LED) with a forward current rating of about 10 mA to 30 mA, with 12 mA to 20 mA being the most common range. Like any diode, the forward current is approximately an exponential function of voltage and the forward resistance is very small. A small voltage change may result in a large change in current. If the current exceeds the rated maximum, an LED may overheat and get destroyed. LEDs are current driven devices and a current-limiting series resistor is required to prevent burning up the LED.

Do you know (Textbook Page No. 356)

Question 1.
White Light LEDs or White LED Lamps:
Shuji Nakamura, a Japanese – born American electronic engineer invented the blue LED. He was awarded the Nobel prize for physics for 2014. He was also awarded the global energy prize in the year 2015. His invention of blue LED made the fabrication of white LED possible.
LED lamps, bulbs, street lighting are becoming very popular these days because of the very high efficiency of LEDs in terms of light output per unit input power(in milliWatts), as compared to the incandescent bulbs. So for general purpose lightings, white light is preferred.
Commercially available white LEDs are normally manufactured by using the technique of wavelength conversion. It is a process which partly or completely converts the radiation of a LED into white light. There are many ways of wavelength conversion. One of these methods uses blue LED and yellow phosphor. In this method of wavelength conversion, a LED which emits blue colour is used to excite a yellow colour phosphor. This results in the emission of yellow and blue light and this mixture of blue and yellow light gives the appearance of white light. This method is the least expensive method for producing white light.
Answer:

The all important blue LEDs
The development of LEDs has made more efficient light sources possible. Creating white light that can be used for lighting requires a combination of red, green and blue light. Blue LEDs proved to be much more difficult to create than red and green LEDs. During the 1980s and 1990s Isamu Akasaki, Hiroshi Amano, and Shuji Nakamura successfully used the difficult-to-handle semiconductor gallium nitride to create efficient blue LEDs. Isamu Akasaki is known for invent ing the bright gallium nitride (CaN) pn-junction blue LED in 1989 and subsequently the high-brightness CaN blue LED.

Using blue LEDs, highly efficient white light sources. became possible by converting part of the blue light emitted from an LED to yellow using a phosphor. To the human eye, the combination of blue and yellow light is perceived as white. A white LED can be created by embedding phosphors in the plastic cap which surrounds a blue LED. Higher quality white light can also be created by mixing blue light with other colors as well, including red and green

Isamu Akasaki, together with Shuji Nakamura and Hiroshi Amano, received the 2014 Nobel Prize in Physics for the invention of efficient blue light-emitting diodes which has enabled bright and energy saving white light sources.

Use your brain power (Textbook Page No. 357)

Question 1.
What would happen if both junctions of a BJT are forward biased or reverse biased?
Answer:
A BJT has four regimes of operation, depending on the four combinations of the applied biases (voltage polarities) to the emitter-base junction and the collector-base junction, as shown in the following table; ‘F’ and ‘R’ indicate forward bias and reverse bias, respectively.

Remember This (Textbook Page No. 358)

Question 1.
The lightly doped, thin base region sandwiched between the heavily doped emitter region and the intermediate doped collector region plays a crucial role in the transistor action.
Answer:
If the two junctions in a BJT are physically close compared with the minority carrier diffusion length (i.e., the distance within which recombination will take place), the careers injected from the emitter can diffuse through the base to reach the base-collector junction. The narrow width of the base is thus crucial for transistor action.

Use your brain power (Textbook Page No. 361)

Question 1.
If a transistor amplifies power, explain why it is not used to generate power.
The term ‘amplification’ is used as an abstraction of the transistor properties so that we have few equations which are useful for a large number of practical problems. Transistors use a small power to control a power supply which can output a huge power. The large output comes from the power supply, while the input signal valves the transistor on and off. The increased power comes from the power supply so that a transistor does not violate the law of conservation of energy.

Maharashtra State Board 12th Std Physics Textbook Solutions Digest

• Chapter 1 Rotational Dynamics
• Chapter 2 Mechanical Properties of Fluids
• Chapter 3 Kinetic Theory of Gases and Radiation
• Chapter 4 Thermodynamics
• Chapter 5 Oscillations
• Chapter 6 Superposition of Waves
• Chapter 7 Wave Optics
• Chapter 8 Electrostatics
• Chapter 9 Current Electricity
• Chapter 10 Magnetic Fields due to Electric Current
• Chapter 11 Magnetic Materials
• Chapter 12 Electromagnetic Induction
• Chapter 13 AC Circuits
• Chapter 14 Dual Nature of Radiation and Matter
• Chapter 15 Structure of Atoms and Nuclei
• Chapter 16 Semiconductor Devices

Maharashtra State Board Class 12 Textbook Solutions