Class 12

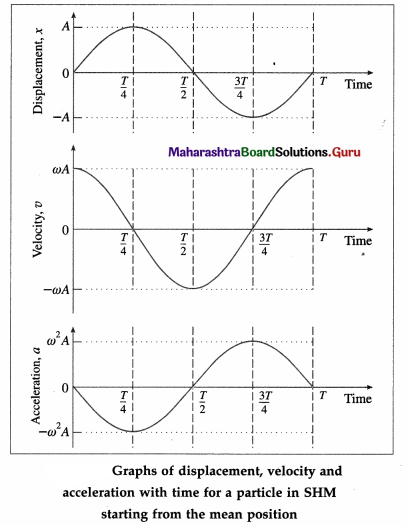
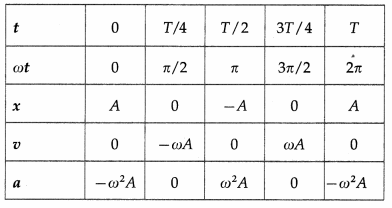
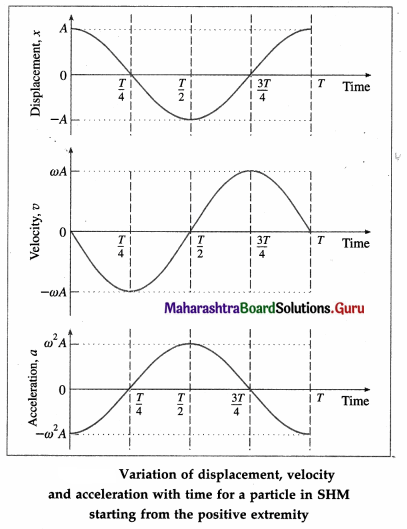
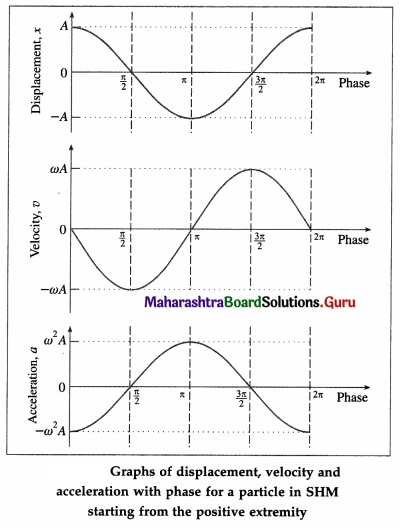
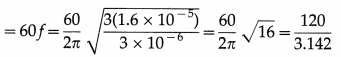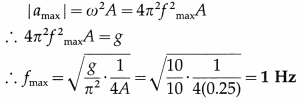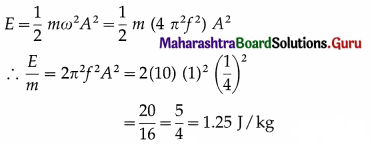Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 11 Magnetic Materials Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 11 Magnetic Materials

1. Choose the correct option.

i) Intensity of magnetic field of the earth at the point inside a hollow iron box is.
(A) less than that outside
(B) more than that outside
(C) same as that outside
(D) zero
Answer:
(D) zero

ii) Soft iron is used to make the core of transformer because of its
(A) low coercivity and low retentivity
(B) low coercivity and high retentivity
(C) high coercivity and high retentivity
(D) high coercivity and low retentivity
Answer:
(A) low coercivity and low retentivity

iii) Which of the following statements is correct for diamagnetic materials?
(A) µ_r < 1
(B) χ is negative and low
(C) χ does not depend on temperature
(D) All of above
Answer:
(D) All of above

iv) A rectangular magnet suspended freely has a period of oscillation equal to T. Now it is broken into two equal halves ( each having half of the original length) and one piece is made to oscillate freely. Its period of oscillation is T′, the ratio of T′ / T is.
(A) \(\frac{1}2 \sqrt{2}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) \(\frac{1}{4}\)
Answer:
(B) \(\frac{1}{2}\)

v) A magnetising field of 360 Am -1 produces a magnetic flux density (B ) = 0.6 T in a ferromagnetic material. What is its permeability in Tm A^-1 ?
(A) \(\frac{1}{300}\)
(B) 300
(C) \(\frac{1}{600}\)
(D) 600
Answer:
(C) \(\frac{1}{600}\)

2 Answer in brief.

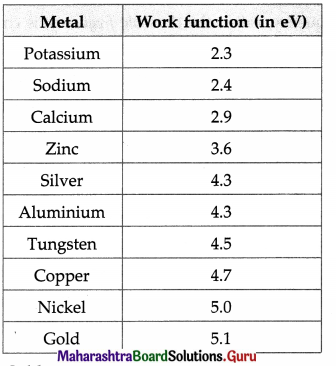
i) Which property of soft iron makes it useful for preparing electromagnet?
Answer:
An electromagnet should become magnetic when a current is passed through its coil but should lose its magnetism once the current is switched off. Hence, the ferromagnetic core (usually iron-based) used for an electromagnet should have high permeability and low retentivity, i.e., it should be magnetically ‘soft’.

ii) What happens to a ferromagnetic material when its temperature increases above curie temperature?
Answer:
A ferromagnetic material is composed of small regions called domains. Within each domain, the atomic magnetic moments of nearest-neighbour atoms interact strongly through exchange interaction, a quantum mechanical phenomenon, and align themselves parallel to each other even in the absence of an external magnetic field. A domain is, therefore, spontaneously magnetized to saturation.

The material retains its domain structure only up to a certain temperature. On heating, the increased thermal agitation works against the spontaneous domain magnetization. Finally, at a certain critical temperature, called the Curie point or Curie temperature, thermal agitation overcomes the exchange forces and keeps the atomic magnetic moments randomly oriented. Thus, above the Curie point, the material becomes paramagnetic. The ferromagnetic to paramagnetic transition is an order to disorder transition. When cooled below the Curie point, the material becomes ferromagnetic again.

iii) What should be retentivity and coercivity of permanent magnet?
Answer:
A permanent magnet should have a large zero-field magnetization and should need a very large reverse field to demagnetize. In other words, it should have a very broad hysteresis loop with high retentivity and very high coercivity.

iv) Discuss the Curie law for paramagnetic material.
Answer:
Curie’s law : The magnetization of a paramagnetic material is directly proportional to the external magnetic field and inversely proportional to the absolute temperature of the material.

If a paramagnetic material at an absolute temperature T is placed in an external magnetic field of induction \(\), the magnitude of its magnetization
M_z ∝ \(\frac{B_{\text {ext }}}{T}\) ∴ M_z = C\(\frac{B_{\text {ext }}}{T}\)
where the proportionality constant C is called the Curie constant.
[Notes : (1) The above law, discovered experimentally in 1895 by Pierre Curie (1859-1906) French physcist, is true only for values of Bext/ T below about 0.5 tesla per kelvin.
(2) [C] = [M_z ∙ T] / [B_ext] = [L^-1I ∙ ] /[MT^-2I^-1]
= [M^-1L^-1T²I²],
where  denotes the dimension of temperature.]

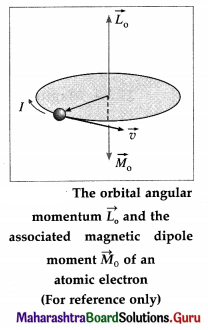
v) Obtain and expression for orbital magnetic moment of an electron rotating about the nucleus in an atom.
Answer:
In the Bohr model of a hydrogen atom, the electron of charge – e performs a uniform circular motion around the positively charged nucleus. Let r, v and T be the orbital radius, speed and period of motion of the electron. Then,
T = \(\frac{2 \pi r}{v}\) …………….. (1)
Therefore, the orbital magnetic moment asso-ciated with this orbital current loop has a magnitude,
I = \(\frac{e}{T}=\frac{e v}{2 \pi r}\) …………… (2)
Therefore, the magnetic dipole moment associated with this electronic current loop has a magnitude
M₀ = current × area of the loop
= I(πr²) = \(\frac{e v}{2 \pi r}\) × πr² = \(\frac{1}{2}\) evr ……………… (3)
Multiplying and dividing the right hand side of the above expression by the electron mass m_e,
M₀ = \(\frac{e}{2 m_{\mathrm{e}}}\) (m_evr) = \(\frac{e}{2 m_{\mathrm{e}}}\) L₀ ……………. (4)
where L₀ = m_evr is the magnitude of the orbital angular momentum of the electron. \(\vec{M}_{0}\) is opposite to \(\vec{L}_{0}\).
∴ \(\vec{M}_{0}=-\frac{e}{2 m_{e}} \overrightarrow{L_{0}}\) ……………. (5)
which is the required expression.

According to Bohr’s second postulate of stationary orbits in his theory of hydrogen atom, the angular momentum of the electron in the nth stationary orbit is equal to n \(\frac{h}{2 \pi}\) , where h is the Planck constant and n is a positive integer. Thus, for an orbital electron,

L₀ = m_evr = \(\frac{nh}{2 \pi}\) …………… (6)
Substituting for L₀ in Eq. (4),
M₀ = \(\frac{e n h}{4 \pi m_{\mathrm{e}}}\)
For n = 1, M₀ = \(\frac{e n h}{4 \pi m_{\mathrm{e}}}\)
The quantity \(\frac{e n h}{4 \pi m_{\mathrm{e}}}\) is a fundamental constant called the Bohr magneton,
µ_B ∙ µ_B = 9.274 × 10^-24 J/T (or A∙m²) = 5.788 × 10^-5 eV/T.
[ Notes : (1) Magnetic dipole moment is conventionally denoted by µ. (2) The magnetic moment of an atom is expressed in terms of Bohr magneton (vµ_B). (3) According to quantum mechanics, an atomic electron also has an intrinsic spin angular momentum and an associated spin magnetic moment of magnitude µ₅. It is this spin magnetic moment that gives rise to magnetism in matter. (4) The total magnetic moment of the atom is the vector sum of its orbital magnetic moment and spin magnetic moment.]

vi) What does the hysteresis loop represents?
Answer:
A magnetic hysteresis loop is a closed curve obtained by plotting the magnetic flux density B of a ferromagnetic material against the corresponding magnetizing field H when the material is taken through a complete magnetizing cycle. The area enclosed by the loop represents the hysteresis loss per unit volume in taking the material through the magnetizing cycle.

vii) Explain one application of electromagnet.
Answer:
Applications of an electromagnet:

1. Electromagnets are used in electric bells, loud speakers and circuit breakers.
2. Large electromagnets are used in junkyard cranes and industrial cranes to lift iron scraps.
3. Superconducting electromagnets are used in MRI and NMR machines, as well as in particle accelerators of cyclotron family.
4. Electromagnets are used in data storage devices such as computer hard disks and magnetic tapes.

Question 3.
When a plate of magnetic material of size 10 cm × 0.5 cm × 0.2 cm (length , breadth and thickness respectively) is located in magnetising field of 0.5 × 10⁴ Am^-1 then a magnetic moment of 0.5 A∙m² is induced in it. Find out magnetic induction in plate.
Answer:
Data : l = 10 cm, b = 0.5 cm, h = 0.2 cm,
H = 0.5 × 10⁴ Am^-1, M = 5 A∙m²
The volume of the plate,
V = 10 × 0.5 × 0.2 = 1 cm² = 10^-6 m²
B = μ₀ (H + M_z) = μ₀ (H + \(\frac{M}{V}\))
The magnetic induction in the plate,
∴ B = 4π × 10^-7 (0.5 × 10⁴ + \(\frac{5}{10^{-6}}\))
= 6.290 T

Question 4.
A rod of magnetic material of cross section 0.25 cm² is located in 4000 Am^-1 magnetising field. Magnetic flux passing through the rod is 25 × 10^-6 Wb. Find out (a) relative permeability (b) magnetic susceptibility and (c) magnetisation of the rod.
Answer:
Data: A = 0.25 cm² = 25 × 10^-6 m²,
H = 4000 A∙m^-1, Φ = 25 × 10^-6 Wb
Magnetic induction is
B = \(\frac{\phi}{A}=\frac{25 \times 10^{-6}}{25 \times 10^{-6}}\) = 1 Wb/m²
(a) B = µ₀µ_rK
∴ The relative permeability of the material,
µ_r = \(\frac{B}{\mu_{0} H}=\frac{1}{4 \times 3.142 \times 10^{-7} \times 4000}\)
= \(\frac{10000}{50.272}\) = 198.91 = 199

(b) µ_r = 1 + χ_m
∴ The magnetic susceptibility of the material,
χ_m = µ_r – 1 = 199 – 1 = 198

(c) χ_m = \(\frac{M_{\mathrm{z}}}{H}\)
The magnetization of the rod,
M_z = χ_mH = 198 × 4000 = 7.92 × 10⁵ A/m

Question 5.
The work done for rotating a magnet with magnetic dipole momentm, through 90° from its magnetic meridian is n times the work done to rotate it through 60°. Find the value of n.
Answer:
Data : θ₀ = 0°, θ₁ = 90°, θ₂ = 60°, W₁ = nW₂
The work done by an external agent to rotate the magnet from θ₀ to θ is
W = MB (cos θ₀ – cos θ)
∴ W1 = MB(cos θ₀ – cosθ₁)
= MB (cos 0° – cos 90°)
= MB (1 – 0)
= MB

∴ W2 = MB (cos 0°- cos 60°)
= MB(1 – \(\frac{1}{2}\))
= 0.5MB
∴ W₁ = 2W₂ = MB
Given W₁ = nW₂. Therefore n = 2.

Question 6.
An electron in an atom is revolving round the nucleus in a circular orbit of radius 5.3 × 10^-11 m, with a speed of 2 × 10⁶ ms^-1 Find the resultant orbital magnetic moment and angular momentum of electron. (charge on electron e = 1.6 × 10^-19 C, mass of electron m_e = 9.1 × 10^-31 kg.)
Answer:
Data: r = 5.3 × 10^-11 m, v = 2 × 10⁶ m/s,
e = 1.6 × 10^-19 C, m_e = 9.1 × 10^-31 kg
The orbital magnetic moment of the electron is
M₀ = \(\frac{1}{2}\) evr
= \(\frac{1}{2}\) (1.6 × 10^-19) (2 × 10⁶) (5.3 × 10^-11)
= 8.48 × 10^-24 A∙m²
The angular momentum of the electron is
L₀ = m_evr
=(9.1 × 10^-31) (2 × 10⁶) (5.3 × 10^-11)
= 96.46 × 10^-36 = 9.646 × 10^-35 kg∙m²/s

Question 7.
A paramagnetic gas has 2.0 × 10²⁶ atoms/m with atomic magnetic dipole moment of 1.5 × 10^-23 A m² each. The gas is at 27° C. (a) Find the maximum magnetization intensity of this sample. (b) If the gas in this problem is kept in a uniform magnetic field of 3 T, is it possible to achieve saturation magnetization? Why? (k_B = 1.38 × 10^-23 JK^-1)[Answer: 3.0× 103 A m-1, No]
(Hint: Find the ratio of Thermal energy of atom of a gas ( 3/2 kBT) and maximum potential energy of the atom (mB) and draw your conclusion)
Answer:
Data: \(\frac{N}{V}\) = 2.0 × 10²⁶ atoms/m³,
μ = 1.5 × 10^-23 Am2, T = 27 + 273 = 300 K,
B = 3T, k^B = 1.38 × 10^-23 J/K, 1 eV = 1.6 × 10^-19 J
(a) The maximum magnetization of the material,
M_z = \(\frac{N}{V}\)μ =(2.0 × 10²⁶) (1.5 ×10^-23)
= 3 × 10³ A/m

(b) The maximum orientation energy per atom is
U_m = -μB cos 180° = μB
= (1.5 × 10^-23) (3) = \(\frac{4.5 \times 10^{-23}}{1.6 \times 10^{-19}}\)
= 2.8 × 10^-4 eV

The average thermal energy of each atom,
E = \(\frac{3}{2}\) k_BT
where k_B is the Botzmann constant.
∴ E = 1.5(1.38 × 10^-23)(300)
= 6.21 × 10^-21 J = \(\frac{6.21 \times 10^{-21}}{1.6 \times 10^{-19}}\)
= 3.9 × 10^-2 eV
Since the thermal energy of randomization is about two orders of magnitude greater than the magnetic potential energy of orientation, saturation magnetization will not be achieved at 300 K.

Question 8.
A magnetic needle placed in uniform magnetic field has magnetic moment of 2 × 10^-2 A m², and moment of inertia of 7.2 × 10^-7 kg m². It performs 10 complete oscillations in 6 s. What is the magnitude of the magnetic field ?
Answer:
Data: M = 2 × 10^-2 A∙m², I = 7.2 × 10^-7 kg∙m²,
T = \(\frac{6}{10}\) = 0.6 S
T = 2π\(\sqrt{\frac{I}{M B}}\)
The magnitude of the magnetic field is
B = \(\frac{4 \pi^{2} I}{M T^{2}}\)
= \(\frac{(4)(3.14)^{2}\left(7.2 \times 10^{-7}\right)}{\left(2 \times 10^{-2}\right)(0.6)^{2}}\)
= 3.943 × 10^-3 T = 3.943 mT

Question 9.
A short bar magnet is placed in an external magnetic field of 700 guass. When its axis makes an angle of 30° with the external magnetic field, it experiences a torque of 0.014 Nm. Find the magnetic moment of the magnet, and the work done in moving it from its most stable to most unstable position.
Answer:
Data : B = 700 gauss = 0.07 tesla, θ = 30°,
τ = 0.014 N∙m
τ = MB sin θ
The magnetic moment of the magnet is
M = \(\frac{\tau}{B \sin \theta}=\frac{(0.014)}{(0.07)\left(\sin 30^{\circ}\right)}\) = 0.4 A∙m²
The most stable state of the bar magnet is for θ = 0°.
It is in the most unstable state when θ = 180°. Thus, the work done in moving the bar magnet from 0° to 180° is
W = MB(cos θ₀ – cos θ)
= MB (cos 0° – cos 180°)
= MB [1 – (-1)]
= 2 MB = (2) (0.4) (0.07)
= 0.056 J
This the required work done.

Question 10.
A magnetic needle is suspended freely so that it can rotate freely in the magnetic meridian. In order to keep it in the horizontal position, a weight of 0.1 g is kept on one end of the needle. If the pole strength of this needle is 20 Am , find the value of the vertical component of the earth’s magnetic field. (g = 9.8 m s^-2)
Answer:
Data: M = 0.2g = 2 × 10^-4kg, q_m = 20 A∙m, g =9.8 m/s²

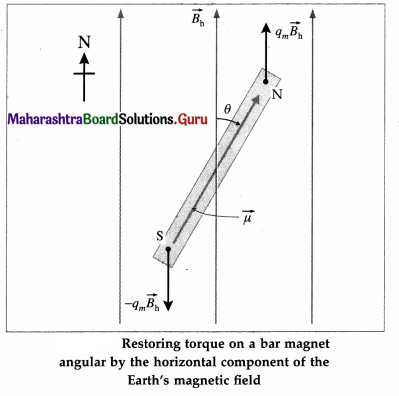
Without the added weight at one end, the needle will dip in the direction of the resultant magnetic field inclined with the horizontal. The torque due to the added weight about the vertical axis through the centre balances the torque of the couple due to the vertical component of the Earth’s magnetic field.
∴ (Mg)\(\left(\frac{L}{2}\right)\) = (q_m B_v) L
The vertical component of the Earth’s magnetic field,
B_v = \(\frac{M g}{2 q_{\mathrm{m}}}=\frac{\left(2 \times 10^{-4}\right)(9.8)}{2(20)}\) = 4.9 × 10^-5 T

Question 11.
The susceptibility of a paramagnetic material is χ at 27° C. At what temperature its susceptibility be \(\frac{\chi}{3}\) ?
Answer:
Data: χ_m1 = χ, T₁ = 27°C = 300 K, χ_m2 = \(\frac{\chi}{3}\)
By Curie’s law,
M_z = C\(\frac{B_{0}}{T}\)
Since M_z = χ_mH = B₀ = μ₀H

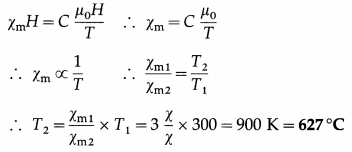
This gives the required temperature.

12th Physics Digest Chapter 11 Magnetic Materials Intext Questions and Answers

Activity (Textbook Page No. 251)

Question 1.
You have already studied in earlier classes that a short bar magnet suspended freely always aligns in North South direction. Now if you try to forcefully move and bring it in the direction along East West and leave it free, you will observe that the magnet starts turning about the axis of suspension. Do you know from where does the torque which is necessary for rotational motion come from? (as studied in rotational dynamics a torque is necessary for rotational motion).
Answer:
Suspend a short bar magnet such that it can rotate freely in a horizontal plane. Let it come to rest along the magnetic meridian. Rotate the magnet through some angle and release it. You will see that the magnet turns about the vertical axis in trying to return back to its equilibrium position along the magnetic meridian. Where does the torque for the rotational motion come from?

Take another bar magnet and bring it near the suspended magnet resting in the magnetic meridian. Observe the interaction between the like and unlike poles of the two magnets facing each other. Does the suspended magnet rotate continuously or rotate through certain angle and remain stable? Note down your observations and conclusions.

Do you know (Textbook Page No. 255)

Effective magneton numbers for iron group ions (No. of Bohr magnetons)

Ion	Electron configuration	Magnetic moment (in terms of /iB)
Fe3 +	[Ar] 3s23p63d5	5.9
Fe2 +	[Ar] 3s23p63d6	5.4
Co2 +	[Ar] 3s23p63d7	4.8
n2+	[Ar] 3s23p63d8	3.2

(Courtsey: Introduction to solid state physics by Charles Kittel, pg. 306 )
These magnetic moments are calculated from the experimental value of magnetic susceptibility. In several ions the magnetic moment is due to both orbital and spin angular momenta.
Answer:
In terms of Bohr magneton (µ_B), the effective magnetic moments of some iron group ions are as follows. In several cases, the magnetic moment is due to both orbital and spin angular momenta.

Ion	Configuration	Effective magnetic moment in terms of Bohr magneton (B.M) (Expreimental values)
Fe3 +	3d5	5.9
Fe2 +	3d6	5.4
Co2 +	3d7	4.8
n2+	3d8	3.2

Remember this (Textbook Page No. 256)

Question 1.
Permeability and Permittivity:
Magnetic Permeability is a term analogous to permittivity in electrostatics. It basically tells us about the number of magnetic lines of force that are passing through a given substance when it is kept in an external magnetic field. The number is the indicator of the behaviour of the material in magnetic field. For superconductors χ = – 1. If you substitute in the Eq. (11.18), it is observed that permeability of material µ = 0. This means no magnetic lines will pass through the superconductor.

Magnetic Susceptibility (χ) is the indicator of measure of the response of a given material to the external applied magnetic field. In other words it indicates as to how much magnetization will be produced in a given substance when kept in an external magnetic field. Again it is analogous to electrical susceptibility. This means when the substance is kept in a magnetic field, the atomic dipole moments either align or oppose the external magnetic field. If the atomic dipole moments of the substance are opposing the field, χ is observed to be negative, and if the atomic dipole moments align themselves in the direction of field, χ is observed to be positive. The number of atomic dipole moments of getting aligned in the direction of the applied magnetic field is proportional to χ. It is large for soft iron (χ >1000).
Answer:
Magnetic permeability is analogous to electric permittivity, both indicating the extent to which a material permits a field to pass through or permeate into the material. For a superconductor, χ = -1 which makes µ = 0, so that a superconductor does not allow magnetic field lines to pass through it.

Magnetic susceptibility (χ). analogous to electrical susceptibility, is a measure of the response of a given material to an applied magnetic field. That is, it indicates the extent of the magnetization produced in the material when it is placed in an external magnetic field. χ is positive when the atomic dipole moments align themselves in the direction of the applied field; χ is negative when the atomic dipole moments align antiparallel to the field. χ is large for soft iron (χ > 1000).

Use your brain power (Textbook Page No. 259)

Question 1.
Classify the following atoms as diamagnetic or paramagnetic.
H, O, Zn, Fe, F, Ar, He
(Hint : Write down their electronic configurations)
Is it true that all substances with even number of electrons are diamagnetic?
Answer:

Atoms	Electronic configuration	No. of Electrons	Diamagnetic/Paramagnetic
H	1s1„	1	Diamagnetic
0	1s22s22p4	8	Paramagnetic
Zn	1s22s22p63s23p63d104s2	30	Diamagnetic
Fe	1s22s22p63s23p64s23d6	26	Neither diamagnetic nor paramagnetic (ferromagnetic)
F	1s22s22p5	9	Paramagnetic
Ar	1s22s22p63s23p6	18	Diamagnetic
He	Is2	2	Diamagnetic

It can be seen that all substances with an even number of electrons are not necessarily diamagnetic.

Do you know (Textbook Page No. 260)

Question 1.
Exchange Interaction: This exchange interaction in stronger than usual dipole-dipole interaction by an order of magnitude. Due to this exchange interaction, all the atomic dipole moments in a domain get aligned with each other. Find out more about the origin of exchange interaction.
Answer:
Exchange Interaction :
Quantum mechanical exchange interaction be-tween two neighbouring spin magnetic moments in a ferromagnetic material arises as a consequence of the overlap between the magnetic orbitals of two adjacent atoms. The exchange interaction in particular for 3d metals is stronger than the dipole-dipole interaction by an order of magnitude. Due to this, all the atomic dipole moments in a domain get aligned with each other and each domain is spontaneously magnetized to saturation. (Quantum mechanics and exchange interaction are beyond the scope of the syllabus.)

Use your brain power (Textbook Page No. 262)

Question 1.
What does the area inside the curve B – H (hysteresis curve) indicate?
Answer:
A magnetic hysteresis loop is a closed curve obtained by plotting the magnetic flux density B of a ferromagnetic material against the corresponding magnetizing field H when the material is taken through a complete magnetizing cycle. The area enclosed by the loop represents the hysteresis loss per unit volume in taking the material through the magnetizing cycle.

Do you know (Textbook Page No. 262)

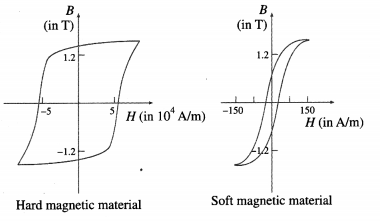
Question 1.
What is soft magnetic material?
Soft ferromagntic materials can be easily magnetized and demagnetized.

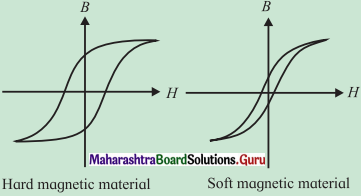
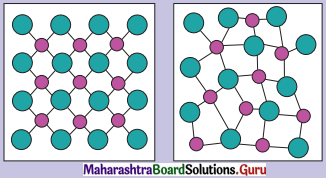
Hysteresis loop for hard and soft ferramagnetic materials.
Answer:
A soft magnetic material, usually iron-based, has high permeability, low retentivity and low coercivity. In other words, it does not have appreciable hysteresis, i.e., its hysteresis loop is very narrow. Such a material magnetizes and demagnetizes more easily, by small external fields.

Do you know (Textbook Page No. 263)

Question 1.
There are different types of shielding available like electrical and accoustic shielding apart from magnetic shielding discussed above. Electrical insulator functions as an electrical barrier or shield and comes in a wide array of materials. Normally the electrical wires used in our households are also shielded. In case of audio recording it is necessary to reduce other stray sound which may interfere with the sound to be recorded. So the recording studios are sound insulated using acoustic material.
Answer:
There are different types of shielding, such as electrical, electromagnetic. magnetic, RF (radio fre quency) and acoustic, to shield a given space or sensitive instrument from unwanted fields of each type.

Maharashtra State Board 12th Std Biology Textbook Solutions Digest

• Chapter 1 Reproduction in Lower and Higher Plants
• Chapter 2 Reproduction in Lower and Higher Animals
• Chapter 3 Inheritance and Variation
• Chapter 4 Molecular Basis of Inheritance
• Chapter 5 Origin and Evolution of Life
• Chapter 6 Plant Water Relation
• Chapter 7 Plant Growth and Mineral Nutrition
• Chapter 8 Respiration and Circulation
• Chapter 9 Control and Co-ordination
• Chapter 10 Human Health and Diseases
• Chapter 11 Enhancement of Food Production
• Chapter 12 Biotechnology
• Chapter 13 Organisms and Populations
• Chapter 14 Ecosystems and Energy Flow
• Chapter 15 Biodiversity, Conservation and Environmental Issues

Maharashtra State Board Class 12 Textbook Solutions

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 1 Solid State Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Chemistry Solutions Chapter 1 Solid State

1. Choose the most correct answer.

Question i.
Molecular solids are
(a) crystalline solids
(b) amorphous solids
(c) ionic solids
(d) metallic solids
Answer:
(b) amorphous solids

Question ii.
Which of the following is n-type semiconductor?
(a) Pure Si
(b) Si doped with As
(c) Si doped with Ga
(d) Ge doped with In
Answer:
(b) Si doped with As

Question iii.
In Frenkel defect
(a) electrical neutrality of the substance is changed.
(b) density of the substance is changed.
(c) both cation and anion are missing
(d) overall electrical neutrality is preserved
Answer:
(d) overall electrical neutrality is preserved

Question iv.
In crystal lattice formed by bcc unit cell the void volume is
(a) 68%
(b) 74%
(c) 32%
(d) 26%
Answer:
(c) 32%

Question v.
The coordination number of atoms in bcc crystal lattice is
(a) 2
(b) 4
(c) 6
(d) 8
Answer:
(d) 8

Question vi.
Which of the following is not correct ?
(a) Four spheres are involved in the formation of tetrahedral void.
(b) The centres of spheres in octahedral voids are at the a pices of a regular tetrahedron.
(c) If the number of atoms is N the number of octahedral voids is 2N.
(d) If the number of atoms is N/2, the number of tetrahedral voids is N.
Answer:
(c) If the number of atoms is N the number of octahedral voids is 2N.

Question vii.
A compound forms hcp structure. Number of octahedral and tetrahedral voids in 0.5 mole of substance is respectively
(a) 3.011 × 10²³, 6.022 × 10²³
(b) 6.022 × 10²³, 3.011 × 10²³
(c) 4.011 × 10²³, 2.011 × 10²³
(d) 6.011 × 10²³, 12.022 × 10²³
Answer:
(a) 3.011 × 10²³, 6.022 × 10²³

Question viii.
Pb has fcc structure with edge length of unit cell 495 pm. Radius of Pb atom is
(a) 205 pm
(b) 185 pm
(c) 260 pm
(d) 175 pm
Answer:
(d) 175 pm

2. Answer the following in one or two sentences.

Question i.
What are the types of particles in each of the four main classes of crystalline solids?
Answer:
The smallest constituents or particles of various solids are atoms, ions or molecules.

Question ii.
Which of the three types of packing used by metals makes the most efficient use of space and which makes the least efficient use ?
Answer:
fcc has the most efficient packing of particles while scc has the least efficient packing.

Question iii.
The following pictures show population of bands for materials having different electrical properties. Classify them as insulator, semiconductor or a metal.

Answer:
Picture A represents metal conductor,
Picture B represents insulator,
Picture C represents semiconductor.

Question iv.
What is a unit cell?
Answer:

• Unit cell : It is the smallest repeating structural unit of a crystalline solid (or crystal lattice) which when repeated in different directions produces the crystalline solid (lattice).
• The crystal is considered to consist of an infinite number of unit cells.
• The unit cell possesses all the characteristics of the crystalline solid.

Question v.
How does electrical conductivity of a semiconductor change with temperature ? Why?
Answer:

• Since the energy difference between valence band and conduction band in semiconductor is not large, the electrons from valence band can be promoted to conduction by heating.
• Hence electrical conductivity of a semiconductor increases with temperature.

Question vi.
The picture represents bands of MOs for Si. Label valence band, conduction band and band gap.

Answer:

Question vii.
A solid is hard, brittle and electrically non-conductor. Its melt conducts electricity. What type of solid is it?
Answer:
A solid crystalline electrolyte like NaCl is hard, brittle and electrically nonconductor. But its melt conducts electricity.

Question viii.
Mention two properties that are common to both hep and ccp lattices.
Answer:
In hcp and ccp crystal lattices coordination number is 12 and packing efficiency is 74%.

Question ix.
Sketch a tetrahedral void.
Answer:

Question x.
What are ferromagnetic substances?
Answer:

1. The substances which possess unpaired electrons and high paramagnetic character and when placed in a magnetic field are strongly attracted and show permanent magnetic moment even when the external magnetic field is removed are said to be ferromagnetic. They can be permanently magnetised.
2. In the solid state, the metal ions of ferromagnetic substance are grouped together into small regions called domains, where each domain acts as a tiny magnet.

For example : Fe, Co, Gd, Ni, CrO₂, etc.

3. Answer the following in brief.

Question i.
What are valence band and conduction band?
Answer:
There are two types of bands of molecular orbitals as follows :

• Valence band : The atomic orbitals with filled electrons from the inner shells form valence bands, where there are no free mobile electrons since they are involved in bonding.
• Conduction band : Atomic orbitals which are partially filled or empty on overlapping form closely placed molecular orbitals giving conduction bands where electrons are delocalised and can conduct, heat and electricity.

Question ii.
Distinguish between ionic solids and molecular solids.
Answer:

Type/ Property	Ionic solids	Molecular solids
1. Particles of unit cell	Cations and anions	Monoatomic or polyatomic molecules
2. Interparticle forces	Electrostatic	London, dipole-dipole forces and/or hydrogen bonds
3. Hardness	Hard and brittle	Soft
4. Melting points	High 600 °C to 3000 °C	Low (-272 °C to 400 °C)
5. Thermal and electrical conductivity	Poor electrical conductors in solid state. Good conductors when melted or dissolved in water.	Poor conductor of heat and electricity
6. Examples	NaCl, CaF2	ice, benzoic acid

Question iii.
Calculate the number of atoms in fcc unit cell.
Answer:
Number of atoms in face-centred cubic (fcc) unit cell :
In this unit cell, there are 8 atoms at 8 corners and 6 atoms at 6 face centres. Each corner contributes 1/8th atom to the unit cell, hence due to 8 corners,
Number of atoms = \(\frac {1}{8}\) × 8 = 1.
Each face centre contributes half of the atom to the unit cell, hence due to 6 face centres,
Number of atoms = \(\frac {1}{2}\) × 6 = 3.
∴ Total number of atoms present in fee unit cell = 1 + 3 = 4.
Hence the volume of the unit cell is equal to the volume of four atoms.

Face centered unit cell

Question iv.
How are the spheres arranged in first layer of simple cubic close-packed structures? How are the successive layers of spheres placed above this layer ?
Answer:
(i) Stacking of square close packed layers :

Stacking of square close packed layers

In this arrangement, the two dimensional AAAA type square closed packed layers are placed one over the other in such a way that the crests of all spheres are in contact with successive layers in all directions. All spheres of different layers are perfectly aligned horizontally and vertically forming unit cells having primitive or simple cubic structure. Since all the layers are identical and if each layer is labelled as layer A, then whole three dimensional crystal lattice will be of AAAA… type.

Each sphere is in contact with six surrounded spheres, hence the coordination number of each sphere is six.

(ii) Stacking of two hexagonal close packed layers :
A close packed three dimensional structure can be generated by arranging hexagonal close packed layers in a particular manner.

In this the spheres of second layer are placed in the depression of the first layer.
In this if first layer is labelled as A then second layer is labelled as B since they are aligned differently.

Two layers of closed packed spheres

In this, all triangular voids of the first layers are not covered by the spheres of the second layer. The triangular voids which are covered by second layer spheres generate tetrahedral void which is surrounded by four spheres. The triangular voids in one layer have above them triangular voids of successive layers.

The overlapping triangular voids from two layers together form an octahedral void which is surrounded by six spheres.

Question v.
Calculate the packing efficiency of metal crystal that has simple cubic structure.
Answer:
Step 1 : Radius of sphere : In simple cubic lattice, the atoms (spheres) are present at eight corners and in contact along the edge in the unit cell.
If ‘a’ is the edge length of the unit cell and ‘r’ is the radius of the atom, then
a = 2r or r = a/2

scc structure

Step 2 : Volume of sphere :
Volume of one particle = \(\frac{4 \pi}{3}\) × r³
= \(\frac{4 \pi}{3}\) × (a/2)³ = \(\frac{\pi a^{3}}{6}\)

Step 3 : Total volume of particles : Since the unit cell contains one particle. Volume occupied by one particle in unit cell = \(\frac{\pi a^{3}}{6}\)

Step 4 : Packing efficiency :
Packing efficiency

∴ Packing efficiency = 52.36%
Percentage of void space = 100 – 52.36
= 47.64%

Question vi.
What are paramagnetic substances? Give examples.
Answer:
(1) The magnetic properties of a substance arise due to the presence of electrons.
(2) An electron while revolving around the nucleus, also spins around its own axis and generates a magnetic moment and magnetic properties.
(3) If an atom or a molecule contains one or more unpaired electrons spinning in same direction, clockwise or anticlockwise, then the substance is associated with net magnetic moment and magnetic properties. They experience a net force of attraction when placed in the magnetic field. This phenomenon is called paramagnetism and the substance is said to be paramagnetic.
For example, O₂, Cu²⁺, Fe³⁺ , Cr³⁺ , NO, etc.

Question vii.
What are the consequences of Schottky defect?
Answer:
Consequences of Schottky defect :

• Since the number of ions (cations and anions) decreases but volume remains unchanged, the density of a substance decreases.
• As the number of missing cations and anions is equal, the electrical neutrality of the compound remains same.
• This defect arises in ionic crystals like NaCl, AgBr, KCl, etc.

Question viii.
Cesium chloride crystallizes in cubic unit cell with Cl^– ions at the corners and Cs⁺ ion in the centre of the cube. How many CsCl molecules are there in the unit cell ?
Answer:
Number of Cs⁺ ion at body centre = 1
Number of Cl^– ions due to 8 comers = 8 × \(\frac {1}{8}\) = 1
Hence unit cell contains 1 CsCl molecule.

Question ix.
Cu crystallizes in fee unit cell with edge length of 495 pm. What is the radius of Cu atom ?
Answer:
Given : a = 495 pm
Radius, r = ?
For fee structure,
radius = r = \(\frac{a}{2 \sqrt{2}}=\frac{495}{2 \times \sqrt{2}}\) = 175 cm.
Radius of Cu atom = 175 pm

Question x.
Obtain the relationship between density of a substance and the edge length of unit cell.
Answer:
(1) Consider a cubic unit cell of edge length ‘a’.
The volume of unit cell = a³

(2) If there are ‘n’ particles per unit cell and the mass of particle is ‘m’, then
Mass of unit cell = m × n.

(3) If the density of the unit cell of the substance is p then
Density of unit cell = \(\frac{\text { Mass of unit cell }}{\text { Volume of unit cell }}\)
ρ = \(\frac{m \times n}{a^{3}}\)

Question 4.
The density of iridium is 22.4 g/cm³. The unit cell of iridium is fcc. Calculate the radius of iridium atom. Molar mass of iridium is 192.2 g/mol.
Answer:
Given : Crystal structure of iridium = fcc
Molar mass of iridium = 192.2 gmol^-1
Density = ρ = 22.4 gcm^-3
Radius of iridium = ?
In fcc structure, there are 8 Ir atoms at 8 comers and 6 Ir atoms at 6 face centres.
∴ Total number of Ir atoms = \(\frac {1}{8}\) × 8 + \(\frac {1}{2}\) × 6
= 1 + 3
= 4
Mass of Ir atom = \(\frac{192.2}{6.022 \times 10^{23}}\)
= 31.92 × 10^-23 g
∴ Mass of 4 Ir atoms = 4 × 31.92 × 10^-23
= 1.277 × 10^-21 g
∴ Mass of unit cell = 1.277 × 10^-21 g
Density of unit cell = \(\frac{\text { Mass of unit cell }}{\text { Volume of unit cell }}\)
22.4 = \(\frac{1.277 \times 10^{-21}}{a^{3}}\)
∴ a³ = \(\frac{1.277 \times 10^{-21}}{22.4}\)
= 57 × 10^-24 cm³
∴ a = (57 × 10^-24)³ = 3.848 × 10^-8 cm
If r is the radius of iridium atom, then for fcc structure,
r = \(\frac{a}{2 \sqrt{2}}\)
= \(\frac{3.848 \times 10^{-8}}{2 \times 1.414}\)
= 1.36 × 10^-8 cm
= 136 pm
Radius of iridium atom = 136 pm

Question 5.
Aluminium crystallizes in cubic close packed structure with unit cell edge length of 353.6 pm. What is the radius of Al atom ? How many unit cells are there in 1.00 cm³ of Al ?
Answer:
Given : Structure of Al
= Cubic close packed structure
= ccp structure
Edge length of unit cell = a = 353.6 pm
= 3.536 × 10^-8 cm
r = ?
Number of unit cells in 1.00 cm³ of Al = ?
Radius of Al atom = r = \(\frac{a}{2 \sqrt{2}}=\frac{353.6}{2 \sqrt{2}}\)
= \(\frac{353.6}{2 \times 1.414}\) = 125 pm
Volume of one unit cell = a³ = (3.536 × 10^-8)³
= 4.421 × 10^-23 cm³
Number of unit cells = \(\frac{1.00}{4.421 \times 10^{-23}}\)
= 2.26 × 10²²
Radius of Al atom = 125 pm
Number of unit cells = 2.26 × 10²²

Question 6.
In an ionic crystalline solid atoms of element Y form hcp lattice. The atoms of element X occupy one third of tetrahedral voids. What is the formula of the compound?
Answer:
In the given hcp lattice, Y atoms are present at 12 corners and 2 face centres.
∴ Number of Y atoms = \(\frac {1}{2}\) × 12 + 2 × \(\frac {1}{2}\) = 3
There are 6 tetrahedral voids, the number of X atoms = \(\frac {1}{3}\) × 6 = 2
∴ Formula of the compound is X₂Y₃.

Question 7.
How are tetrahedral and octahedral voids formed?
Answer:
Tetrahedral void : The vacant space or void among four constituent particles having tetrahedral arrangement in the crystal lattice is called tetrahedral void.

The arrangement of four spheres around the void is tetrahedral. A tetrahedral void is formed when a triangular void made by three coplanar spheres is in contact with fourth sphere above or below it.

Octahedral void : The vacant space or void at the centre of six spheres (or atoms) which are placed octahedrally is called octahedral void.

Question 8.
Third layer of spheres is added to second layer so as to form hcp or ccp structure. What is the difference between the addition of third layer to form these hexagonal close-packed structures?
Answer:

1. In the formation of hexagonal closed-packed (hcp) structure, the first one dimensional row shows depressions between neighbouring atoms.
2. When a second row is arranged so that spheres fit in these depressions then a staggered arrangement is obtained. If the first row is A then the second row is B.
3. When third row is placed in staggered manner in contact with second row then A type arrangement is obtained.
4. Similarly, the spheres in fourth row can be arranged as B type layer. This results in ABAB… type setting of the layers. This gives hexagonal close packing (hcp) structure.

Hexagonal close packing (hcp)

Question 9.
An element with molar mass 27 g/mol forms cubic unit cell with edge length of 405 pm. If density of the element is 2.7 g/cm³, what is the nature of cubic unit cell ? (fcc or ccp)
Answer:
Given : Molar mass = M = 27 g mol^-1
Nature of crystal = cubic unit cell
Edge length = a = 405 pm = 4.05 × 10^-8 cm
Density = ρ = 2.7 g cm^-3
Nature of unit cell = ?

= 3.997
≅ 4
Hence the nature of unit cell = face-centred cubic unit cell
Radius of Al atom = 125 pm
The nature of cubic unit cell is fcc.

Question 10.
An element has a bcc structure with unit cell edge length of 288 pm. How many unit cells and number of atoms are present in 200 g of the element? (1.16 × 10²⁴, 2.32 × 10²⁴)

Question 11.
Distinguish with the help of diagrams metal conductors, insulators and semiconductors from each other.
Answer:
Conductor:

1. A substance which conducts heat and electricity to a greater extent is called conductor.
2. In this, conduction bands and valence bands overlap or are very closely spaced.
3. There is no energy difference or very less energy difference between valence bands and conduction bands.
4. There are free electrons in the conduction bands.
5. The conductance decreases with the increase in temperature.
6. E.g., Metals, alloys.
7. The conducting properties can’t be improved by adding third substance.

Insulator:

1. A substance which cannot conduct heat and electricity under any conditions is called insulator.
2. In this, conduction bands and valence bands are far apart.
3. The energy difference between conduction bands and valence bands is very large.
4. There are no free electrons in the conduction bands and electrons can’t be excited from valence bands to conduction bands due to large energy difference.
5. No effect of temperature on conducting properties.
6. E.g., Wood, rubber, plastics.
7. No effect of addition of any substance.

Semiconductor:

1. A substance that has poor electrical conductance at low temperature but higher conductance at higher temperature is called semiconductor.
2. In this, conduction bands and valence bands are spaced closely.
3. The energy difference between conduction bands and valence bands is small.
4. The electrons can be easily excited from valence bands to conduction bands by heating.
5. Conductance increases with the increase in temperature.
6. E.g., Si, Ge
7. By doping, conducting properties improve. E.g. n-type, p-type semiconductors.

Question 12.
What are n-type semiconductors? Why is the conductivity of doped n-type semiconductor higher than that of pure semiconductor ? Explain with diagram.
Answer:
n-type semiconductor:

• n-type semiconductor contains increased number of electrons in the conduction band.
• When Si semiconductor is doped with 15^th group element phosphorus, P, the new atoms occupy some vacant sites in the lattice in place of Si atoms.
• P has five valence electrons, out of which four are involved in covalent bonding with neighboring Si atoms while one electrons remains free and delocalised.
• These free electrons increase the electrical conductivity of the semiconductor.
• The semiconductors with extra non-bonding free electrons are called n-type semiconductors.

P atom occupying regular site of Si atom

Question 13.
Explain with diagram. Frenkel defect. What are the conditions for its formation? What is its effect on density and electrical neutrality of the crystal?
Answer:

1. Frenkel defect : This defect arises when an ion of an ionic compound is missing from its regular site and occupies interstitial vacant position between lattice points.
2. Cations have smaller size than anions, hence generally cations occupy the interstitial sites.
3. This creates a vacancy defect at its original position and interstitial defect at new position.
4. Frenkel defect is regarded as the combination of interstitial defect and vacancy defect.

Conditions for the formation of Frenkel defect :

1. This defect arises in ionic compounds with a large difference between the sizes of cation and anion.
2. The ionic compounds must have ions with low coordination number.

Consequences of Frenkel defect :

1. Since there is no loss of ions from the crystal lattice, the density of the solid remains unchanged.
2. The crystal remains electrically neutral.
3. This defect is observed in ZnS, AgCl, AgBr, Agl, CaF₂, etc.

Question 14.
What is an impurity defect? What are its types? Explain the formation of vacancies through aliovalent impurity with example.
Answer:
Impurity defect : This defect arises when foreign atoms, that is, atoms different from the host atoms are present in the crystal lattice.

There are two types of impurity defects namely

1. Substitutional defects and
2. Interstitial defects.

(1) Substitutional defects : These defects arises when foreign atoms occupy the lattice sites in place of host atoms, due to their displacements.
Examples : Solid solutions of metals (alloys). For example. Brass in which host atoms are of Cu which are replaced by impurity of Zn atoms. In this Zn atoms occupy regular sites while Cu atoms occupy substituted sites.

Brass

Vacancy through aliovalent impurity :
By addition of impurities of aliovalent ions :

Vacancy through aliovalent ion

When aliovalent ion like Sr²⁺ in small amount is added by additing SrCl₂ to NaCl during its crystallisation, each Sr²⁺ ion (oxidation state 2+) removes 2 Na⁺ ions from their lattice points, to maintain electrical neutrality. Hence one of vacant lattice site is occupied by Sr²⁺ ion while other site remains vacant.

Interstitial impurity defect :

Stainless steel

A defect in solid in which the impurity atoms occupy interstitial vacant spaces of lattice structure is called interstitial impurity defect.

For example, in steel, normal lattice sites are occupied by Fe atoms but interstitial spaces are occupied by carbon atoms.

12th Chemistry Digest Chapter 1 Solid State Intext Questions and Answers

Try this… (Textbook Page No. 1)

Observe the above figure carefully. The two types of circles in this figure represent two types of constituent particles of a solid.

Question 1.
Will you call the arrangement of particles in this solid regular or irregular ?
Answer:
The arrangement of particles in this solid is regular.

Question 2.
Is the arrangement of constituent particles in directions \(\overrightarrow{\mathbf{A B}}\), \(\overrightarrow{\mathbf{C D}}\) and \(\overrightarrow{\mathbf{E F}}\) same or different?
Answer:
\(\overrightarrow{\mathbf{A B}}\) represents arrangement of identical particles of one type.
\(\overrightarrow{\mathbf{C D}}\) represents arrangement of identical particles of another type.
\(\overrightarrow{\mathbf{E F}}\) represents regular arrangement of two different particles in alternate positions.

Use your brain power ! (Textbook Page No. 2)

Question 1.
Identify the arrangements A and B as crystalline or amorphous.

Answer:
Arrangement in image A indicates the substance is crystalline.
Arrangement in image B indicates the substance is amorphous.

Try this… (Textbook Page No. 3)

Question 1.
Graphite is a covalent solid yet soft and good conductor of electricity. Explain.
Answer:

1. Each carbon atom in graphite is sp² hybridised and covalently bonded to other three sp2 hybridised carbon atoms forming σ bonds and the fourth electron in 2p_z orbital of each carbon atom is used in the formation of a π bond. This results in the formation of hexagonal rings in two dimensions.
2. In graphite, the layers consisting of hexagonal carbon network are held together by weak van der Waal’s forces imparting softness.
3. The electrons in π bonds in the ring are delocalised and free to move in the delocalised molecular orbitals giving good electrical conductance.

Use your brain power ! (Textbook Page No. 13)

Question 1.
Which of the three lattices scc, bcc and fcc has the most efficient packing of particles ? Which one has the least efficient packing ?
Answer:
fcc has the most efficient packing of particles while see has the least efficient packing.

Can you think ? (Textbook Page No. 20)

Question 1.
When ZnO is heated it turns yellow and returns back to original white colour on cooling. What could be the reason ?
Answer:
When colourless ZnO is strongly heated, the metal atoms are deposited on crystal surface and anions O^2- migrate to the surface producing vacancies at anion lattice points.

These anions combine with Zn atoms forming ZnO and release electrons.
Zn + O^2- → ZnO + 2e^–

These released electrons diffuse into the crystal and occupy vacant sites of anions and produce F- centres. Due to these colour centres, ZnO turns yellow.

Can you tell ? (Textbook Page No. 23)

Let a small quantity of phosphorus be doped into pure silicon.

Question 1.
Will the resulting material contain the same number of total number of electrons as the original pure silicon ?
Answer:
Total number of electrons in doped silicon will be more than in original silicon.

Question 2.
Will the material be electrically neutral or charged ?
Answer:
Material will be electrically neutral.

Maharashtra State Board 12th Std Chemistry Textbook Solutions Digest

• Chapter 1 Solid State
• Chapter 2 Solutions
• Chapter 3 Ionic Equilibria
• Chapter 4 Chemical Thermodynamics
• Chapter 5 Electrochemistry
• Chapter 6 Chemical Kinetics
• Chapter 7 Elements of Groups 16, 17 and 18
• Chapter 8 Transition and Inner Transition Elements
• Chapter 9 Coordination Compounds
• Chapter 10 Halogen Derivatives
• Chapter 11 Alcohols, Phenols and Ethers
• Chapter 12 Aldehydes, Ketones and Carboxylic Acids
• Chapter 13 Amines
• Chapter 14 Biomolecules
• Chapter 15 Introduction to Polymer Chemistry
• Chapter 16 Green Chemistry and Nanochemistry

Maharashtra State Board Class 12 Textbook Solutions

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 5 Oscillations Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 5 Oscillations

1. Choose the correct option.

i) A particle performs linear S.H.M. starting from the mean position. Its amplitude is A and time period is T. At the instance when its speed is half the maximum speed, its displacement x is
(A) \(\frac{\sqrt{3}}{2}\)A
(B) \(\frac{2}{\sqrt{3}}\)
(C) A/2
(D) \(\frac{1}{\sqrt{2}}\)
Answer:
(A) \(\frac{\sqrt{3}}{2}\)A

ii) A body of mass 1 kg is performing linear S.H.M. Its displacement x (cm) at t (second) is given by x = 6 sin (100t + π/4). Maximum kinetic energy of the body is
(A) 36 J
(B) 9 J
(C) 27 J
(D) 18 J
Answer:
(D) 18 J

iii) The length of second’s pendulum on the surface of earth is nearly 1 m. Its length on the surface of moon should be [Given: acceleration due to gravity (g) on moon is 1/6 th of that on the earth’s surface]
(A) \(\frac{1}{6}\) m
(B) 6 m
(C) \(\frac{1}{36}\) m
(D) \(\frac{1}{\sqrt{6}}\) m.
Answer:
(A) \(\frac{1}{6}\) m

iv) Two identical springs of constant k are connected, first in series and then in parallel. A metal block of mass m is suspended from their combination. The ratio of their frequencies of vertical oscillations will be in a ratio
(A) 1:4
(B) 1:2
(C) 2:1
(D) 4:1
Answer:
(B) 1:2

v) The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
(A) The acceleration is maximum at time T.
(B) The force is maximum at time 3T/4.
(C) The velocity is zero at time T/2.
(D) The kinetic energy is equal to total energy at time T/4.

Answer:
(B) The force is maximum at time 3T/4.

2. Answer in brief.

i) Define linear simple harmonic motion.
Answer:
Definition: Linear simple harmonic motion (SHM) is defined as the linear periodic motion of a body, in which the force (or acceleration) is always directed towards the mean position and its magnitude is proportional to the displacement from the mean position.
OR
A particle is said to execute linear SHM if the particle undergoes oscillations about a point of stable equilibrium, subject to a linear restoring force always directed towards that point and whose magnitude is proportional to the magnitude of the displacement of the particle from that point.
Examples : The vibrations of the tines (prongs) of a tuning fork, the oscillations of the needle of a sewing machine.

ii) Using differential equation of linear S.H.M, obtain the expression for
(a) velocity in S.H.M.,
(b) acceleration in S.H.M.
Answer:
The general expression for the displacement of a particle in SHM at time t is x = A sin (ωt + α) … (1)
where A is the amplitude, ω is a constant in a particular case and α is the initial phase.
The velocity of the particle is

Equation (2) gives the velocity as a function of x.
The acceleration of the particle is
a = \(\frac{d v}{d t}\) = \(\frac{d}{d t}\) [Aω cos (ωt + α) J at at
∴ a = – ω² A sin (ωt + α)
But from Eq. (1), A sin (ωt + α) = x
∴ a = -ω²x … (3)
Equation (3) gives the acceleration as a function of x. The minus sign shows that the direction of the acceleration is opposite to that of the displacement.

iii) Obtain the expression for the period of a simple pendulum performing S.H.M.
Answer:
An ideal simple pendulum is defined as a heavy point mass suspended from a rigid support by a weightless, inextensible and twistless string, and set oscillating under gravity through a small angle in a vertical plane.

In practice, a small but heavy sphere, called the bob, is used. The distance from the point of suspension to the centre of gravity of the bob is called the length of the pendulum.

Consider a simple pendulum of length L₁ – suspended from a rigid support O. When displaced from its initial position of rest through a small angle θ in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in below figure. At B, the forces on the bob are its weight \(m \vec{g}\) and the tension \(\overrightarrow{F_{1}}\) in the string. Resolve \(m \vec{g}\) into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string.

mg cos θ balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position.
Restoring force, F = – mg sin θ
If θ is small and expressed in radian,
sin θ \(\approx\) θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{\mathrm{AB}}{\mathrm{OB}}\) = \(\frac{x}{L}\)
∴ F = – mgθ = -mg\(\frac{x}{L}\) …. (1)
Since m, g and L are constant,
F ∝ (-x) …. (2)

Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM.
Acceleration, a = \(\frac{F}{m}\) = –\(\frac{g}{L}\)x … (3)
Therefore, acceleration per unit displacement
= |\(\frac{a}{x}\)| = \(\frac{g}{L}\) ….. (4)
Period of SHM,

This gives the expression for the period of a simple pendulum.

iv) State the laws of simple pendulum.
Answer:
The period of a simple pendulum at a given place is
T = 2π\(\sqrt{\frac{L}{g}}\)
where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows :

(1) Law of length : The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length.
∴ T ∝\(\sqrt{L}\)
(2) Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity.
∴ T ∝ \(\frac{1}{\sqrt{g}}\)
(3) Law of mass : The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum.
(4) Law of isochronism : The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small.

v) Prove that under certain conditions a magnet vibrating in uniform magnetic field performs angular S.H.M.
Answer:
Consider a bar magnet of magnetic moment μ, suspended horizontally by a light twistless fibre in a region where the horizontal component of the Earth’s magnetic field is B_h. The bar magnet is free to rotate in a horizontal plane. It comes to rest in approximately the North-South direction, along B_h. If it is rotated in the horizontal plane by a small

displacement θ from its rest position (θ = 0), the suspension fibre is twisted. When the magnet is released, it oscillates about the rest position in angular or torsional oscillation.

The bar magnet experiences a torque \(\tau\) due to the field B_h. Which tends to restore it to its original orientation parallel to B_h. For small θ, this restoring torque is
\(\tau\) = – μB_h sin θ = – μB_hμ …. (1)

where the minus sign indicates that the torque is opposite in direction to the angular displacement θ. Equation (1) shows that the torque (and hence the angular acceleration) is directly proportional in magnitude of the angular displacement but opposite in direction. Hence, for small angular displacement, the oscillations of the bar magnet in a uniform magnetic field is simple harmonic.

Question 3.
Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and performing S.H.M.
Answer:
Definition : Angular SHM is defined as the oscillatory motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.
The differential equation of angular SHM is
I\(\frac{d^{2} \theta}{d t^{2}}\) + cθ = 0 ….. (1)
where I = moment of inertia of the oscillating body, \(\frac{d^{2} \theta}{d t^{2}}\) = angular acceleration of the body when its angular displacement is θ, and c = torsion constant of the suspension wire,
∴ \(\frac{d^{2} \theta}{d t^{2}}\) + \(\frac{c}{I}\)θ = 0
Let \(\frac{c}{I}\) = ω², a constant. Therefore, the angular frequency, ω = \(\sqrt{c / I}\) and the angular acceleration,
a = \(\frac{d^{2} \theta}{d t^{2}}\) = -ω²θ … (2)
The minus sign shows that the α and θ have opposite directions. The period T of angular SHM is

This is the expression for the period in terms of torque constant. Also, from Eq. (2),

Question 4.
Show that a linear S.H.M. is the projection of a U.C.M. along any of its diameter.
Answer:
Consider a particle which moves anticlockwise around a circular path of radius A with a constant angular speed ω. Let the path lie in the x-y plane with the centre at the origin O. The instantaneous position P of the particle is called the reference point and the circle in which the particle moves as the reference circle.

The perpendicular projection of P onto the y-axis is Q. Then, as the particle travels around the circle, Q moves to-and-fro along the y-axis. Line OP makes an angle α with the x-axis at t = 0. At time t, this angle becomes θ = ωt + α.
The projection Q of the reference point is described by the y-coordinate,
y = OQ = OP sin ∠OPQ, Since ∠OPQ = ωt + α, y = A sin(ωt + α)
which is the equation of a linear SHM of amplitude A. The angular frequency w of a linear SHM can thus be understood as the angular velocity of the reference particle.

The tangential velocity of the reference particle is v = ωA. Its y-component at time t is v_y = ωA sin (90° – θ) = ωA cos θ
∴ v_y = ωA cos (ωt + α)
The centripetal acceleration of the reference particle is a_r = ω²A, so that its y-component at time t is a_x = a_r sin ∠OPQ
∴ a_x = – ω²A sin (ωt + α)

Question 5.
Draw graphs of displacement, velocity and acceleration against phase angle, for a particle performing linear S.H.M. from (a) the mean position
(b) the positive extreme position. Deduce your conclusions from the graph.
Answer:
Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where ω is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are
x = A sin ωt = A sin\(\left(\frac{2 \pi}{T} t\right)\) (∵ω = \(\frac{2 \pi}{T}\))
v = \(\frac{d x}{d t}\) = ωA cos ωt = ωA cos\(\left(\frac{2 \pi}{T} t\right)\)
a = \(\frac{d v}{d t}\) = -ω² A sin ωt = – ω²A sin\(\left(\frac{2 \pi}{T} t\right)\) as the initial phase α = 0.
Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.

Using the values in the table we can plot graphs of displacement, velocity and acceleration with time.

Conclusions :

1. The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting at the mean position, the x-t and a-t graphs are sine curves. The v-t graph is a cosine curve.
2. There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
3. There is a phase difference of π radians between x and a.

Consider a particle performing linear SHM with amplitude A and period T = 2π/ω, starting from the positive extreme position, where ω is the angular frequency. Its displacement from the mean position (x), velocity (y) and acceleration (a) at any instant (t) are
x = A cos ωt = A cos \(\left(\frac{2 \pi}{T} t\right)\) (∵ω = \(\frac{2 \pi}{T}\))
v = -ωA sin ωt = – ωA sin \(\left(\frac{2 \pi}{T} t\right)\)
a = -ω²A cos ωt = -ω²A cos \(\left(\frac{2 \pi}{T} t\right)\)
Using these expressions, the values of x, y and a at the end of every quarter of a period, starting from t = 0, are tabulated below.

Using these values, we can plot graphs showing the variation of displacement, velocity and acceleration with time.

Conclusions :

1. The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x-t and a-t graphs are cosine curves; the v-t graph is a sine curve.
2. There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
3. There is a phase difference of n radians between x and a.

Explanations :
(1) v-t graph : It is a sine curve, i.e., the velocity is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π/2 rad between a and v.
v is minimum (equal to zero) at the extreme positions (i.e., at x = ± A) and v is maximum ( = ± ωA) at the mean position (x = 0).

(2) a-t graph : It is a cosine curve, i.e., the acceleration is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π rad between v and a. a is minimum (equal to zero) at the mean position (x = 0) and a is maximum ( = \(\mp\)ω²A) at the extreme positions (x = ±A).

Question 6.
Deduce the expressions for the kinetic energy and potential energy of a particle executing S.H.M. Hence obtain the expression for total energy of a particle performing S.H.M and show that the total energy is conserved. State the factors on which total energy depends.
Answer:
Consider a particle of mass m performing linear SHM with amplitude A. The restoring force acting r on the particle is F = – kx, where k is the force constant and x is the displacement of the particle from its mean position.
(1) Kinetic energy : At distance x from the mean position, the velocity is
v = ω\(\sqrt{A^{2}-x^{2}}\)
where ω = \(\sqrt{k / m} .\) The kinetic energy (KE) of the particle is
KE = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) mω² (A² – x²)
= \(\frac{1}{2}\)k(A² – x²) … (1)
If the phase of the particle at an instant t is θ = ωt + α, where α is initial phase, its velocity at that instant is
v = ωA cos (ωt + α)
and its KE at that instant is
KE = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\)mω²A² cos²(ωt + α) ….. (2)
Therefore, the KE varies with time as cos² θ.

(2) Potential energy : The potential energy of a particle in linear SHM is defined as the work done by an external agent, against the restoring force, in taking the particle from its mean position to a given point in the path, keeping the particle in equilibirum.

Suppose the particle in below figure is displaced from P₁ to P₂, through an infinitesimal distance dx against the restoring force F as shown.

The corresponding work done by the external agent will be dW = ( – F)dx = kx dx. This work done is stored in the form of potential energy. The potential energy (PE) of the particle when its displacement from the mean position is x can be found by integrating the above expression from 0 to x.
∴ PE = \(\int\)dW = \(\int_{0}^{x}\) kx dx = \(\frac{1}{2}\) kx² … (3)
The displacement of the particle at an instant t being
x = A sin (wt + α)
its PE at that instant is
PE = \(\frac{1}{2}\)kx² = \(\frac{1}{2}\)kA² sin²(ωt + α) … (4)
Therefore, the PE varies with time as sin²θ.

(3) Total energy : The total energy of the particle is equal to the sum of its potential energy and kinetic energy.
From Eqs. (1) and (2), total energy is E = PE + KE
= \(\frac{1}{2}\)kx² + \(\frac{1}{2}\)k(A² – x²)
= \(\frac{1}{2}\)kx² + \(\frac{1}{2}\)kA² – \(\frac{1}{2}\)kx²
∴ E = \(\frac{1}{2}\)kA² = \(\frac{1}{2}\)mω²A² … (5)
As m is constant, ω and A are constants of the motion, the total energy of the particle remains constant (or its conserved).

Question 7.
Deduce the expression for period of simple pendulum. Hence state the factors on which its period depends.
Answer:
An ideal simple pendulum is defined as a heavy point mass suspended from a rigid support by a weightless, inextensible and twistless string, and set oscillating under gravity through a small angle in a vertical plane.

In practice, a small but heavy sphere, called the bob, is used. The distance from the point of suspension to the centre of gravity of the bob is called the length of the pendulum.

Consider a simple pendulum of length L₁ – suspended from a rigid support O. When displaced from its initial position of rest through a small angle θ in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in below figure. At B, the forces on the bob are its weight \(m \vec{g}\) and the tension \(\overrightarrow{F_{1}}\) in the string. Resolve \(m \vec{g}\) into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string.

mg cos θ balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position.
Restoring force, F = – mg sin θ
If θ is small and expressed in radian,
sin θ \(\approx\) θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{\mathrm{AB}}{\mathrm{OB}}\) = \(\frac{x}{L}\)
∴ F = – mgθ = -mg\(\frac{x}{L}\) …. (1)
Since m, g and L are constant,
F ∝ (-x) …. (2)

Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM.
Acceleration, a = \(\frac{F}{m}\) = –\(\frac{g}{L}\)x … (3)
Therefore, acceleration per unit displacement
= |\(\frac{a}{x}\)| = \(\frac{g}{L}\) ….. (4)
Period of SHM,

This gives the expression for the period of a simple pendulum.

The period of a simple pendulum at a given place is
T = 2π\(\sqrt{\frac{L}{g}}\)
where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows :

(1) Law of length : The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length.
∴ T ∝\(\sqrt{L}\)
(2) Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity.
∴ T ∝ \(\frac{1}{\sqrt{g}}\)

Question 8.
At what distance from the mean position is the speed of a particle performing S.H.M. half its maximum speed. Given path length of S.H.M. = 10 cm. [Ans: 4.33 cm]
Answer:
Data : v = \(\frac{1}{2}\)v_max, 2A = 10 cm
∴ A = 5 cm
v = ω\(\sqrt{A^{2}-x^{2}}\) and v_max = ωA
Since v = \(\frac{1}{2}\)v_max,

This gives the required displacement.

Question 9.
In SI units, the differential equation of an S.H.M. is \(\frac{d^{2} x}{d t^{2}}\) = -36x. Find its frequency and period. Find its frequency and period.
[Ans: 0.9548 Hz, 1.047 s]
Answer:
\(\frac{d^{2} x}{d t^{2}}\) = -36x
Comparing this equation with the general equation,
\(\frac{d^{2} x}{d t^{2}}\) = -ω²x
We get, ω² = 36 ∴ ω = 6 rad/s
ω = 2πf
∴ The frequency, f = \(\frac{\omega}{2 \pi}\) = \(\frac{6}{2(3.142)}\) = \(\frac{6}{6.284}\) = 0.9548 Hz
and the period, T = \(\frac{1}{f}\) = \(\frac{1}{0.9548}\) = 1.047 s

Question 10.
A needle of a sewing machine moves along a path of amplitude 4 cm with frequency 5 Hz. Find its acceleration \(\frac{1}{30}\)s after it has crossed the mean position. [Ans: 34.2 m/s²]
Answer:
Data : A = 4 cm = 4 × 10^-2 m, f = 5Hz, t = \(\frac{1}{30}\)s
ω = 2πf = 2π (5) = 10π rad/s
Therefore, the magnitude of the acceleration,
|a| = ω²x = ω²A sin ωt
= (10π)² (4 × 10²)
= 10π² sin \(\frac{\pi}{3}\) = 10 (9.872)(0.866) = 34.20 m/s²

Question 11.
Potential energy of a particle performing linear S.H.M is 0.1 π² x² joule. If mass of the particle is 20 g, find the frequency of S.H.M. [Ans: 1.581 Hz]
Answer:
Data : PE = 0.1 π² x² J, m = 20 g = 2 × 10^-2 kg
PE = \(\frac{1}{2}\)mω²x² = \(\frac{1}{2}\)m (4π²f²)x²
∴ \(\frac{1}{2}\)m(4π²f²)x² = 0.1 π² x²
∴ 2mf² = 0.1 ∴ f² = \(\frac{1}{20\left(2 \times 10^{-2}\right)}\) = 2.5
∴ The frequency of SHM is f = \(\sqrt{2.5}\) = 1.581 Hz

Question 12.
The total energy of a body of mass 2 kg performing S.H.M. is 40 J. Find its speed while crossing the centre of the path. [Ans: 6.324 cm/s]
Answer:
Data : m = 2 kg, E = 40 J
The speed of the body while crossing the centre of the path (mean position) is v_max and the total energy is entirely kinetic energy.

Question 13.
A simple pendulum performs S.H.M of period 4 seconds. How much time after crossing the mean position, will the displacement of the bob be one third of its amplitude. [Ans: 0.2163 s]
Answer:
Data : T = 4 s, x = A/3
The displacement of a particle starting into SHM from the mean position is x = A sin ωt = A sin \(\frac{2 \pi}{T}\) t

∴ the displacement of the bob will be one-third of its amplitude 0.2163 s after crossing the mean position.

Question 14.
A simple pendulum of length 100 cm performs S.H.M. Find the restoring force acting on its bob of mass 50 g when the displacement from the mean position is 3 cm. [Ans: 1.48 × 10^-2 N]
Answer:
Data : L = 100 cm, m = 50 g = 5 × 10^-2 kg, x = 3 cm, g = 9.8 m/s²
Restoring force, F = mg sin θ = mgθ
= (5 × 10^-2)(9.8)\(\left(\frac{3}{100}\right)\)
= 1.47 × 10^-2 N

Question 15.
Find the change in length of a second’s pendulum, if the acceleration due to gravity at the place changes from 9.75
m/s² to 9.80 m/s². [Ans: Decreases by 5.07 mm]
Answer:
Data : g₁ = 9.75 m/s², g₂ = 9.8 m/s²
Length of a seconds pendulum, L = \(\frac{g}{\pi^{2}}\)

∴ The length of the seconds pendulum must be increased from 0.9876 m to 0.9927 m, i.e., by 0.0051 m.

Question 16.
At what distance from the mean position is the kinetic energy of a particle performing S.H.M. of amplitude 8 cm, three times its potential energy? [Ans: 4 cm]
Answer:
Data : A = 8 cm, KE = 3 PE
KE = \(\frac{1}{2}\) (A² – x²) and PE = \(\frac{1}{2}\)kx²
Given, KE = 3PE.
∴ \(\frac{1}{2}\)k(A² – x²) = 3\(\left(\frac{1}{2} k x^{2}\right)\)
∴ A² – x² = 3x² ∴ 4x² = A²
∴ the required displacement is
x = ±\(\frac{A}{2}\) = ±\(\frac{8}{2}\) = ± 4 cm

Question 17.
A particle performing linear S.H.M. of period 2π seconds about the mean position O is observed to have a speed of \(b \sqrt{3}\) m/s, when at a distance b (metre) from O. If the particle is moving away from O at that instant, find the
time required by the particle, to travel a further distance b. [Ans: π/3 s]
Answer:
Data : T = 2πs, v = b\(\sqrt{3}\) m/s at x = b

∴ Assuming the particle starts from the mean position, its displacement is given by
x = A sin ωt = 2b sin t
If the particle is at x = b at t = t₁,
b = 2b sint₁ ∴ t₁ = sin^-1 \(\frac{1}{2}\) = \(\frac{\pi}{6}\)s
Also, with period T = 2πs, on travelling a further distance b the particle will reach the positive extremity at time t₂ = \(\frac{\pi}{2}\)s.
∴ The time taken to travel a further distance b from x = b is t₂ – t₁ = \(\frac{\pi}{2}\) – \(\frac{\pi}{6}\) = \(\frac{\pi}{3}\)s.

Question 18.
The period of oscillation of a body of mass m₁ suspended from a light spring is T. When a body of mass m₂ is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m₁ and m₂ [Ans: 1/3]
Answer:

This gives the required ratio of the masses.

Question 19.
The displacement of an oscillating particle is given by x = asinωt + bcosωt where a, b and ω are constants. Prove that the particle performs a linear S.H.M. with amplitude A = \(\sqrt{a^{2}+b^{2}}\)
Answer:
x = asinωt + bcosωt
Let a = A cos φ and b = A sin φ, so that
A² = a² + b² and tan φ = \(\frac{b}{a}\)
∴ x = A cos φ sin ωt + A sin φ cos ωt
∴ x = A sin (ωt + φ)
which is the equation of a linear SHM with amplitude A = \(\sqrt{a^{2}+b^{2}}\) and phase constant φ = tan^-1 \(\frac{b}{a}\), as required.

Question 20.
Two parallel S.H.M.s represented by x₁ = 5sin (4πt + \(\frac{\pi}{3}\)) cm and x₂ = 3sin(4πt + π/4) cm are superposed on a particle. Determine the amplitude and epoch of the resultant S.H.M. [Ans: 7.936 cm, 54° 23′]
Answer:
Data: x₁ = 5 sin (4πt + \(\frac{\pi}{3}\)) = A₁ sin(ωt + α),
x₂ = 3 sin (4πt + \(\frac{\pi}{4}\)) = A₂ sin(ωt + β)
∴ A₁ = 5 cm, A₂ = 3 cm, α = \(\frac{\pi}{3}\) rad, β = \(\frac{\pi}{4}\) rad
(i) Resultant amplitude,

(ii) Epoch of the resultant SHM,

Question 21.
A 20 cm wide thin circular disc of mass 200 g is suspended to a rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π³ ≈ 31)
[Ans: 0.04133 N m]
Answer:
Data: R = 10cm = 0.1 m, M = 0.2 kg, θ_m = 60° = \(\frac{\pi}{3}\) rad, T = 1 s, π³ ≈ 31
The Ml of the disc about the rotation axis (perperdicular through its centre) is
I = \(\frac{1}{2}\)MR² = (0.2)(0.1)² = 10^-3 kg.m²
The period of torsional oscillation, T = 2π\(\sqrt{\frac{I}{c}}\)
∴ The torsion constant, c = 4πr²\(\frac{I}{T^{2}}\)
The magnitude of the maximum restoring torque,

Question 22.
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10^-5 Wb/m². The magnet has moment of inertia 3 × 10^-6 kgm² and magnetic moment 3 A m². [Ans:38.19 osc/min.]
Answer:
Data : B = 1.6 × 10^-5 T, I = 3 × 10^-6kg/m²,
µ = 3 A.m²
The period of oscillation, T = 2π \(\sqrt{\frac{I}{\mu B_{\mathrm{h}}}}\)
∴ The frequency of oscillation is
f = \(\frac{1}{2 \pi}\)\(\sqrt{\frac{\mu B}{I}}\)
∴ The number of oscillations per minute

= 38.19 per minute

Question 23.
A wooden block of mass m is kept on a piston that can perform vertical vibrations of adjustable frequency and amplitude. During vibrations, we don’t want the block to leave the contact with the piston. How much maximum frequency is possible if the amplitude of vibrations is restricted to 25 cm? In this case, how much is the energy per unit mass of the block? (g ≈ π² ≈ 10 m s^-2)
[Ans: n_max = 1/s, E/m = 1.25 J/kg]
Answer:
Data : A = 0.25 m, g = π² = 10 m/s²
During vertical oscillations, the acceleration is maximum at the turning points at the top and bottom. The block will just lose contact with the piston when its apparent weight is zero at the top, i. e., when its acceleration is a_max = g, downwards.

This gives the required frequency of the piston.

12th Physics Digest Chapter 5 Oscillations of Waves Intext Questions and Answers

Can you tell? (Textbook Page No. 112)

Question 1.
Why is the term angular frequency (ω) used here for a linear motion ?
Answer:
A linear SHM is the projection of a UCM on a diameter of the circle. The angular speed co of a particle moving along this reference circle is called the angular frequency of the particle executing linear SHM.

Can you tell? (Textbook Page No. 114)

Question 1.
State at which point during an oscillation the oscillator has zero velocity but positive acceleration ?
Answer:
At the left extreme, i.e., x = – A, so that a = – ω²x = – ω²(- A) = ω²A = a_max

Question 2.
During which part of the simple harmonic motion velocity is positive but the displacement is negative, and vice versa ?
Answer:
Velocity v is positive (to the right) while displacement x is negative when the particle in SHM is moving from the left extreme towards the mean position. Velocity v is negative (to the left) while displacement x is positive when the particle in SHM is moving from the right extreme towards the mean position.

Can you tell? (Textbook page 76)

Question 1.
To start a pendulum swinging, usually you pull it slightly to one side and release. What kind of energy is transferred to the mass in doing this?
Answer:
On pulling the bob of a simple pendulum slightly to one side, it is raised to a slightly higher position. Thus, it gains gravitational potential energy.

Question 2.
Describe the energy changes that occur when the mass is released.
Answer:
When released, the bob oscillates in SHM in a vertical plane and the energy oscillates back and forth between kinetic and potential, going completely from one form of energy to the other as the pendulum oscillates. In the case of undamped SHM, the motion starts with all of the energy as gravitational potential energy. As the object starts to move, the gravitational potential energy is converted into kinetic energy, becoming entirely kinetic energy at the equilibrium position. The velocity becomes zero at the other extreme as the kinetic energy is completely converted back into gravitational potential energy,
and this cycle then repeats.

Question 3.
Is/are there any other way/ways to start the oscillations of a pendulum? Which energy is supplied in this case/cases?
Answer:
The bob can be given a kinetic energy at its equilibrium position or at any other position of its path. In the first case, the motion starts with all of the energy as kinetic energy. In the second case, the motion starts with partly gravitational potential energy and partly kinetic energy.

Can you tell? (Textbook Page No. 109)

Question 1.
Is the motion of a leaf of a tree blowing in the wind periodic ?
Answer:
The leaf of a tree blowing in the wind oscillates, but the motion is not periodic. Also, its displacement from the equilibrium position is not a regular function of time.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 1 Introduction to Corporate Finance Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 1 Introduction to Corporate Finance

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
_____________ is related to money and money management.
(a) Production
(b) Marketing
(c) Finance
Answer:
(c) Finance

Question 2.
Finance is the management of _____________ affairs of the company.
(a) monetary
(b) marketing
(c) production
Answer:
(a) monetary

Question 3.
Corporation finance deals with the acquisition and use of _____________ by business corporation.
(a) goods
(b) capital
(c) land
Answer:
(b) capital

Question 4.
Company has to pay _____________ to government.
(a) taxes
(b) dividend
(c) interest
Answer:
(a) taxes

Question 5.
_____________ refers to any kind of fixed assets.
(a) Authorised capital
(b) Issued capital
(c) Fixed capital
Answer:
(c) Fixed capital

Question 6.
_____________ refers to the excess of current assets over current liabilities.
(a) Working capital
(b) Paid-up capital
(c) Subscribed capital
Answer:
(a) Working capital

Question 7.
Manufacturing industries have to invest _____________ amount of funds to acquire fixed assets.
(a) huge
(b) less
(c) minimal
Answer:
(a) huge

Question 8.
When the population is increasing at a high rate, certain manufacturers find this as an opportunity to _____________ business.
(a) close
(b) expand
(c) contract
Answer:
(b) expand

Question 9.
The sum of all _____________ is gross working capital.
(a) expenses
(b) current assets
(c) current liabilities
Answer:
(b) current assets

Question 10.
_____________ means mix up of various sources of funds in desired proportion.
(a) Capital budgeting
(b) Capital structure
(c) Capital goods
Answer:
(b) Capital structure

1B. Match the pairs:

Question 1.

Answer:

Group ‘A’	Group ‘B’
(a) Capital budgeting	(6) Investment decision
(b) Fixed capital	(5) Fixed assets
(c) Working capital	(1) Sum of current assets
(d) Capital structure	(9) Mix up various sources of funds
(e) Corporate finance	(2) Deals with acquisition and use of capital

1C. Write a word or term or a phrase that can substitute each of the following statements:

Question 1.
A key determinant of the success of any business function.
Answer:
Finance

Question 2.
The decision of the finance manager ensures that the firm is well-capitalized.
Answer:
Financing decision

Question 3.
The decision of the finance manager to deploy the funds in a systematic manner.
Answer:
Investment decision

Question 4.
Capital is needed to acquire fixed assets that are used for a longer period of time.
Answer:
Fixed capital

Question 5.
The sum of current assets.
Answer:
Gross working capital

Question 6.
The excess of current assets over current liabilities.
Answer:
Networking capital

Question 7.
The process of converting raw material into finished goods.
Answer:
Production cycle

Question 8.
The boom and recession cycle in the economy.
Answer:
Economic Trend

Question 9.
The ratio of different sources of funds in the total capital.
Answer:
Capital Structure

Question 10.
The internal source of financing.
Answer:
Retained earnings

1D. State whether the following statements are True or False:

Question 1.
Finance is related to money and money management.
Answer:
True

Question 2.
The business firm gives a green signal to the project only when it is profitable.
Answer:
True

Question 3.
Corporate finance brings coordination between various business activities.
Answer:
True

Question 4.
Fixed capital is also referred as circulating capital.
Answer:
False

Question 5.
Working capital stays in the business almost permanently.
Answer:
False

Question 6.
The business will require huge funds if assets are acquired on a lease basis.
Answer:
False

Question 7.
The business dealing in luxurious products will require a huge amount of working capital.
Answer:
True

Question 8.
A firm with large-scale operations will require more working capital.
Answer:
True

Question 9.
Liberal credit policy creates a problem of bad debt.
Answer:
True

Question 10.
Financial institutions and banks cater to the working capital requirement of the business.
Answer:
True

1E. Find the odd one.

Question 1.
Land and Building, Plant and Machinery, Cash.
Answer:
Cash

Question 2.
Debenture Capital, Equity Share Capital, Preference Share Capital.
Answer:
Debenture Capital

Question 3.
Fixed Capital, Capital Structure, Working Capital.
Answer:
Capital Structure

1F. Complete the sentences.

Question 1.
Initial planning of capital requirement is made by _____________
Answer:
entrepreneur

Question 2.
When there is boom in economy, sales will _____________
Answer:
increase

Question 3.
The process of converting raw material into finished goods is called _____________
Answer:
production cycle

Question 4.
During recession period sales will _____________
Answer:
decrease

1G. Select the correct option from the bracket.

Question 1.

(To have the right amount of capital, deploy funds in a systematic manner, fixed capital, working capital, capital structure, carry dividend at a fixed rate)
Answer:

Group ‘A’	Group ‘B’
(a) Financing decision	(1) To have the right amount of capital
(b) Fixed capital	(2) Longer period of time
(c) Investment decision	(3) Deploy funds in a systematic manner
(d) Working capital	(4) Circulating capital
(e) Combination of various sources of funds	(5) capital structure

1H. Answer in one sentence.

Question 1.
Define corporate finance.
Answer:
Corporate finance deals with the raising and using of finance by a corporation.

Question 2.
What is fixed capital?
Answer:
Fixed capital is the capital that is used for buying fixed assets that are used for a longer period of time in the business eg. Capital for plant and machinery etc.

Question 3.
What is working capital?/Define working capital.
Answer:
Working capital is the capital that is used to carry out day-to-day business activities and takes into consideration all current assets of the company.
Eg: for building up inventories.

Question 4.
What is the production cycle?
Answer:
The process of converting raw material into finished goods is called the production cycle.

Question 5.
Define capital structure.
Answer:
Capital structure means to mix up various sources of funds in the desired proportion. To decide capital structure means to decide upon the ratio of different types of capital.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
Finance is needed to pay dividends to debenture holders.
Answer:
Finance is needed to pay interest to debenture holders.

Question 2.
When there is a recession in the economy sales will increase.
Answer:
When there is a boom in the economy sales will increase.

Question 3.
Share is an acknowledgment of a loan raised by the company.
Answer:
A debenture is an acknowledgment of a loan raised by a company.

Question 4.
Equity shares carry dividends at a fixed rate.
Answer:
Preference shares carry dividends at a fixed rate.

2. Explain the following terms/concepts.

Question 1.
Financing decision
Answer:
A financing decision is a right decision that is made by a finance manager of any corporation ensuring that the firm is well capitalized with the right combination of debt and equity, having access to multiple choices of sources of financing.

Question 2.
Investment decision
Answer:
Investment decisions mean capital budgeting i.e. finding investments and deploying them successfully in the business for greater profits.

Question 3.
Fixed capital
Answer:
Fixed capital is the capital that is used for buying fixed assets that are used for a longer period of time in the business. These assets are not meant for. resale. Examples of fixed capital are capital used for purchasing land and building, furniture, plant, and machinery, etc.

Question 4.
Working Capital
Answer:
Working capital is the capital that is used to carry out day-to-day business activities. It takes into consideration all current assets, of the company. It also refers to ‘Gross Working Capital’.
Examples of working capital are

• for building up inventories.
• for financing receivables.
• for covering day-to-day operating expenses.

3. Study the following case/situation and express your opinion.

1. The management of ‘Maharashtra State Road Transport Corporation’ wants to determine the size of working capital.

Question (a).
Being a public utility service provider will it need less working capital or more?
Answer:
MSRTC being a public utility service provider will need less working capital because of a continuous flow of cash from there, customers thus liabilities are taken care of.

Question (b).
Being a public utility service provider, will it need more fixed capital?
Answer:
Being a public utility service provider MSRTC will need a huge amount of funds to acquire fixed assets thus it will need more fixed capital.

Question (c).
Give one example of a public utility service that you come across on a day-to-day basis.
Answer:
The Indian Railways.

2. A company is planning to enhance its production capacity and is evaluating the possibility of purchasing new machinery whose cost is ₹ 2 crore or has alternative of machinery available on a lease basis.

Question (a).
What type of asset is machinery?
Answer:
Machinery is a Fixed Asset.
A fixed asset may be held for 5, 10 or 20 years and more. But if assets are acquired on a lease or rental basis, then less amount of funds for fixed assets will be needed for business.

Question (b).
Capital used for the purchase of machinery is fixed capital or working capital.
Answer:
Capital used for the purchase of machinery is fixed capital.

Question (c).
Does the size of a business determine the fixed capital requirement?
Answer:
Yes. Where a business firm is set up to carry on large-scale operations, its fixed capital requirements are likely to be high.

4. Distinguish between the following.

Question 1.
Fixed Capital and Working Capital
Answer:

Points	Fixed Capital	Working Capital
1. Meaning	Fixed capital refers to any kind of physical asset, a portion of total capital that is invested in fixed assets.	Working capital refers to the sum of current assets or gross working capital.
2. Nature	It stays in the business almost permanently.	Working capital is circulatory capital. It keeps changing.
3. Purpose	It is invested in fixed assets such as land, building, equipment, etc.	Working capital is invested in short-term assets such as cash, account receivable, inventory, etc.
4. Sources	Fixed capital funding can come from selling shares, debentures, bonds, long-term loans, etc.	Working capital can be funded with short-term loans, deposits, trade credit, etc.
5. Objectives of investors	Investors invest money in fixed capital hoping to make a future profit.	Investors invest money in working capital for getting immediate returns.
6. Risk	Investment in fixed capital implies more risk.	Investment in working capital is less risky. Eg. Land, building, plant and machinery
7. Decisions	Decisions relating to fixed capital investment are generally made by top-level management. Eg. Cash, bills receivable, inventories, cash at the bank	Decisions relating to working capital needs are generally made by middle-level or lower-level management.

5. Answer in brief:

Question 1.
Define capital structure and state its components.
Answer:
Definition: R.H. Wessel “The long term sources of funds employed in a business enterprise.”
John H. Hampton “A firm’s capital structure is the relation between the debt and equity securities that make up the firm’s financing of its assets.” Thus, the term capital structure means security mix. It refers to the proportion of different securities raised by a firm for long-term finance.

Components/Parts of Capital Structure:
There are four basic components of capital structure. They are as follows:
(i) Equity Share Capital:

• It is the basic source of financing activities of the business. Equity share capital is provided by equity shareholders.
• They buy equity shares and help a business firm to raise necessary funds. They bear the ultimate risk associated with ownership.
• Equity shares carry dividends at a fluctuating rate depending upon profit.

(ii) Preference Share Capital:

• Preference shares carry preferential rights as to payment of dividends and have priority over equity shares for return of capital when the company is liquidated.
• These shares carry dividends at a fixed rate.
• They enjoy limited voting rights.

(iii) Retained earnings:

• It is an internal source of financing.
• It is nothing but ploughing back of profit.

(iv) Borrowed capital: It comprises of the following:

• Debentures: A debenture is an acknowledgment of a loan raised by the company. The company has to pay interest at an agreed rate.
• Term Loan: Term loans are provided by the bank and other financial institutions. They carry fixed rate of interest.

Question 2.
State any four factors affecting fixed capital requirements?
Answer:
(i) Nature of business:

• The nature of business certainly plays a role in determining fixed capital requirements. They need to invest a huge amount of money in fixed assets.
• e.g. Rail, road, and other public utility services have large fixed investments.
• Their working capital requirements are nominal because they supply services and not the product.
• They deal in cash sales only.

(ii) Size of business:
The size of a business also affects fixed capital needs. A general rule applies that the bigger the business, the higher the need for fixed capital. The size of the firm, either in terms of its assets or sales, affects the need for fixed capital.

(iii) Scope of business:
Some business firms that manufacture the entire range of their production would require a huge investment in fixed capital. However, those companies that are labour intensive and who do not use the latest technology may require less fixed capital and vice versa.

(iv) Extent of lease or rent:
Companies who take their assets on a lease basis or on a rental basis will require less amount of funds for fixed assets. On the other side, firms that purchase assets will naturally require more fixed capital in the initial stages.

Question 3.
What are Corporate Finance and State’s two decisions which are basic of corporate finance?
OR
Write short note on Corporate Finance
Answer:
Corporate finance deals with the raising and using of finance by a corporation. It includes various financial activities like capital structuring and making investment decisions, financial planning, capital formation, and foreign capital, etc. Even financial organisations and banks play a vital role in corporate financing.

Henry Hoagland expresses, “Corporate Finance deals primarily with the acquisition and use of capital by the business corporation”.

Following two decisions are the basis of corporate finances:
(i) Financing decision:
Every business firm must carefully estimate its capital needs i.e. working capital and fixed capital. The firm needs to mobilize funds from the right sources also maintaining the right combination of debt capital and equity capital. For this balance, a company may go for or raise equity capital or even opt for borrowed funds by way of debentures, public deposits term loans, etc. to raise funds.

(ii) Investment decision:
Once the capital needs are accessed, the finance manager needs to take correct decisions regarding the use of the funds in a systematic manner, productively, using effective cost control measures to generate high profits. Finding investments through proper decisions and using them successfully in business is called ‘capital budgeting

6. Justify the following statements.

Question 1.
The firm has multiple choices of sources of financing.
Answer:

• Business firms require finance in terms of working capital and fixed capital.
• Funds are required at different stages of business.
• The company can raise funds from various sources i.e. from internal and external sources.
• Internal sources could be cash inflows on sales turnover, income from investments, and retained earnings.
• External sources can be obtained for short-term requirements through cash credit, overdraft trade credit, discounting bills of Exchange issues of commercial paper, etc.
• For long-term needs, a firm can meet its financing needs through the issue of shares, debentures, bonds, public deposits, etc. Thus, it is rightly said that the firm has multiple choices of sources of financing.

Question 2.
There are various factors affecting the requirements of fixed capital.
Answer:

• Fixed capital being long-term capital is required for the development and expansion of the company.
• The nature and size of a business have a great impact on fixed capital. Manufacturing businesses require huge fixed capital whereas trading organizations like retailers require less fixed capital.
• Methods of acquiring assets on rentals or on a lease/installment basis will require less amount of fixed assets.
• If fixed assets are available at low prices and concessional rates then it would reduce the need for investment in fixed assets.
• International conditions and economic trends like a boom period will require high investment in fixed assets and a recession will lead to less requirement.
• Similarly, consumer preferences, competition, and highly demanded goods and services will require a large amount of fixed capital. E.g. Mobile phones. Thus, it is rightly said that there are various factors affecting the requirements of fixed capital.

Question 3.
Fixed capital stays in the business almost permanently.
Answer:
Factors determining fixed capital requirements are:

• Fixed capital refers to capital invested for acquiring fixed assets.
• These assets are not meant for resale.
• Fixed capital is capital used for purchasing land and building, furniture, plant, and machinery, etc.
• Such cap al is usually required at the time of the establishment of a new company.
• Existing companies may also need such capital for their expansion and development, replacement of equipment, etc.
• Modern industrial processes require the increased use of heavy automated machinery. Thus, it is rightly said that fixed capital stays in the business almost permanently.

Question 4.
Capital structure is composed of owned funds and borrowed funds.
Answer:

• Capital structure means to mix up of various sources of funds in desired proportions.
• To decide capital structures means to decide upon the ratio of different types of capital.
• A firm’s capital structure is the relation between the debt and equity securities that make up the firm’s financing of its assets.
• The capital structure is composed of own funds which include share capital, free serves, and surplus, and borrowed funds which represent debentures, bank loans, and long-term loans provided by financial institutions.
• Thus capital structure = Equity share capital + preference share capital + reserves + debentures.
• Thus, it is rightly said that capital structure is composed of owned funds and borrowed funds.

Question 5.
There are various factors affecting the requirement of working capital.
Answer:

• The nature and size of a business affect the requirement of working capital. Trading or merchandising firms and big retail enterprises need a large amount of capital compared to small firms which need a small amount of working capital.
• If the period of the production cycle is longer then the firm needs more amount of working capital. If the manufacturing cycle is short, it requires less working capital.
• During the boom period sales will increase leading to increased investment in stocks, thus requiring additional working capital and during the recession, it is vice versa.
• Along with the expansion and growth of the firm or company in terms of sales and fixed assets, the requirement of working capital increases.
• If there is proper coordination, communication, and co-operation between production and sales departments then the requirement of working capital is less.
• A liberal credit policy increases the possibility of bad debts and in such cases, the requirement of working capital is high, whereas a firm making cash sales requires less working capital.

7. Answer the following questions.

Question 1.
Discuss the importance of Corporate Finance?
Answer:
Corporate finance deals with the raising and utilizing of finance by a corporation. It also deals with capital structuring and making investment decisions, financial planning of capital, and the money market. The finance manager should ensure that:
The firm has adequate finance and it’s being utilized effectively;
Generate minimum return for its owners.

The importance of Corporate Finance are as follows:
(i) Helps in decision making:
Most important decisions of business enterprises are made on the basis of availability of funds, as without finance any function of business enterprise is difficult to be performed independently. Obtaining the funds from the right sources at a lower cost and productive utilization of funds would lead to higher profits. Thus corporate finance plays a significant role in the decision-making process.

(ii) Helps in raising capital for a project:
A new business venture needs to raise capital. Business firms can raise funds by issuing shares, debentures, bonds or even by taking loans from the banks.

(iii) Helps in Research and Development
Research and Development need to be undertaken by firms for growth and expansion of business and to enjoy a competitive advantage. Research and development mostly involve lengthy and detailed technical work for the execution of projects. Through surveys and market analysis etc. companies may have to upgrade old products or develop new products to face competition and attract consumers. Thus the availability of adequate finance helps to generate high efficiency.

(iv) Helps in the smooth running of the business firm:
A smooth flow of corporate finance is important to pay the salaries of employees on time, pay loans, and purchase the required raw materials. At the same time finance is needed for sales promotion of existing products and more so for the launch of new products effectively.

(v) Brings co-ordination between various activities:
Corporate finance plays a significant role in the coordination and control of all activities in an organization. Production activity requires adequate finance for the purchase of raw materials and meeting other day-to-day financial requirements for the smooth running of the production unit. If the production increases, sales will also increase by contributing the income of the concern and profit to increase.

(vi) Promotes expansion and diversification:
Corporate finance provides money for the purchase of modern machines and sophisticated technology. Modern machines and technology help to improve the performance of the firm in terms of profits. It also helps the firm to expand and diversify the business.

(vii) Managing risk:
Companies have to manage several risks such as sudden fall in sales, loss due to natural calamity, loss due to workers strikes, change in government policies, etc. Financial aids help in such situations to manage such risks.

(viii) Replace old assets:
Assets like plants and machinery have become old and outdated over the years. Finance is required to purchase new assets or replace the old assets with new assets having new technology and features.

(ix) Payment of dividend and interest:
Finance is needed to pay the dividend to shareholders, interest to creditors, bank, etc.

(x) Payment of taxes/fees:
The company has to pay taxes to the government such as Income tax, Goods and Service Tax (GST), and fees to the Registrar of Companies on various occasions. Finance is needed for paying these taxes and fees.

Question 2.
Discuss the factors determining working capital requirements?
Answer:
Working Capital = Current Assets – Current Liabilities.
In other words, it is also called ‘Circulating Capital’. Also, refer to ‘GROSS WORKING CAPITAL.’ Management needs to determine the size of working capital with reference to the economic environment and other aspects within the business firm.

Factors determining/influencing working capital requirements are as follows:
(i) Nature of Business:
The working capital requirements are highly influenced by the nature of the business. Trading/ merchandising forms concerned with the distribution of goods require a huge amount of working capital to maintain a large stock of the variety of goods to meet customers’ demands are extend credit facilities to attract them. Whereas public utility concerns have to maintain small working capital because of a continuous flow of cash from their customers.

(ii) Size of business:
The size of a business also affects the requirements of working capital. Size of the firm refers to the scale of operation i.e. a firm with large scale operations will require more working capital and vice versa.

(iii) Volume of Sales:
The volume of sales and the size of the working capital have a direct relationship with each other. If the volume of sales increases there is an increase in the amount of working capital.

(iv) Production cycle:
The process of converting raw material into finished goods is called the ‘production cycle’. If the production cycle period is longer, the firm needs more amount of working capital. If the manufacturing cycle is short, it requires less working capital.

(v) Business cycle:
When there is a boom in the economy, sales will increase resulting in to increase in investment in stock. This will require additional working capital. During a recession period, sales will decline and consequently, the need for working capital will also decrease.

(vi) Terms of purchases and sales:
If credit terms of purchase are favourable and terms of sales are less liberal, then the requirement of cash will be less. Thus, the working capital requirement will be reduced.
A firm that enjoys more credit facilities needs less working capital. On the other hand, if a firm does not get proper credit for purchases and adopts a liberal credit policy for sales if requires more working capital.

(vii) Credit Control:
Credit control includes the factors such as volume of credit sales, the terms of credit sales, the collection policy etc. A firm with a good credit control policy will have more cash flow reducing the working capital requirement. Whereas if the firm’s credit policy is liberal there would be more requirements of the working capital.

(viii) Growth and Expansion:
Those firms which are growing and expanding at a rapid pace need more working capital compared to those firms which are stable in their growth.

(ix) Management ability:
The requirement of working capital is reduced if there is proper coordination in the production and distribution of goods. A firm stocking on heavy inventory calls for a higher level of working capital.

(x) External factors:
If the financial institutions and banks provide funds to the firm as and when required, the need for working capital is reduced.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 13 AC Circuits Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 13 AC Circuits

1. Choose the correct option.

i) If the RMS current in a 50 Hz AC circuit is 5A, the value of the current \(\frac{1}{300}\) seconds after its value becomes zero is
(A) 5\(\sqrt {2}\) A
(B) 5\(\sqrt{\frac{3}{2}}\) A
(C) \(\frac{5}{6}\) A
(D) \(\frac{5}{\sqrt{2}}\) A
Answer:
(B) 5\(\sqrt{\frac{3}{2}}\) A

ii) A resistor of 500 Ω and an inductance of 0.5 H are in series with an AC source which is given by V = 100 \(\sqrt {2}\) sin (1000t). The power factor of the combination
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(\frac{1}{\sqrt{3}}\)
(C) 0.5
(D) 0.6
Answer:
(A) \(\frac{1}{\sqrt{2}}\)

iii) In a circuit L, C & R are connected in series with an alternating voltage of frequency f. the current leads the voltage by 450. The value of C is

Answer:
(B) \(\frac{1}{2 \pi f(2 \pi f L-R)}\)

iv) In an AC circuit, e and i are given by e = 150 sin (150t) V and i = 150 sin (150 t + \(\frac{\pi}{3}\)) A. the power dissipated in the circuit is
(A) 106W
(B) 150W
(C) 5625W
(D) Zero
Answer:
(C) 5625W

v) In a series LCR circuit the phase difference between the voltage and the current is 45°. Then the power factor will be
(A) 0.607
(B) 0.707
(C) 0.808
(D) 1
Answer:
(B) 0.707

2. Answer in brief.

i) An electric lamp is connected in series with a capacitor and an AC source is glowing with a certain brightness. How does the brightness of the lamp change on increasing the capacitance ?
Answer:
Impedance, Z = \(\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}\), where R is the resistance of the lamp, w is the angular frequency of AC and C is the capacitance of the capacitor connected in series with the AC source and the lamp. When C is increased, \(\) decreases. Hence, Z increases.
Power factor, cos Φ = \(\frac{R}{Z}\)
As Z increases, the power factor decreases.
Now, the average power over one cycle,
P_av = v_rms i_rms cos Φ
= V_rms \(\left(\frac{V_{\mathrm{rms}}}{Z}\right)\) cos Φ
= \(\frac{V_{\mathrm{rms}}^{2}}{\mathrm{Z}} \cos \phi\)
∴ P_av decreases as Z increases and cos Φ decreases.
As the current through the lamp \(\left(\frac{V_{\mathrm{rms}}}{Z}\right)\) decreases, the brightness of the lamp will decrease when C is increased.

ii) The total impedance of a circuit decreases when a capacitor is added in series with L and R. Explain why ?
Answer:
For an LR circuit, the impedance,
Z_LR = \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}}\), where X_L is the reactance of the inductor.
When a capacitor of capacitance C is added in series with L and R, the impedance,
Z_LCR = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\) because in the case of an inductor the current lags behind the voltage by a phase angle of \(\frac{\pi}{2}\) rad while in the case of a capacitor the current leads the voltage by a phase angle of \(\frac{\pi}{2}\) rad. The decrease in net reactance decreases the total impedance (Z_LCR < Z_LR).

iii) For very high frequency AC supply, a capacitor behaves like a pure conductor. Why ?
Answer:
The reactance of a capacitor is X_C = \(\frac{1}{2 \pi f C}\), where f is the frequency of the AC supply and C is the capacitance of the capacitor. For very high frequency, f, X_C is very small. Hence, for very high frequency AC supply, a capacitor behaves like a pure conductor.

iv) What is wattless current ?
Answer:
The current that does not lead to energy consumption, hence zero power consumption, is called wattless current.
In the case of a purely inductive circuit or a purely capacitive circuit, average power consumed over a complete cycle is zero and hence the corresponding alternating current in the circuit is called wattless current.
[Note : In this case, the power factor is zero.]

v) What is the natural frequency of L C circuit ? What is the reactance of this circuit at this frequency
Answer:
The natural frequency of LC circuit is \(\frac{1}{2 \pi \sqrt{L C}}\) ,
where L is the inductance and C is the capacitance. The reactance of this circuit at this frequency is

Question 3.
In a series LR circuit X_L = R and power factor of the circuit is P₁. When capacitor with capacitance C such that X_L = X_C is put in series, the power factor becomes P₂. Calculate P₁ / P₂ .
Answer:
For a series LR circuit, power factor,

Question 4.
When an AC source is connected to an ideal inductor show that the average power supplied by the source over a complete cycle is zero.
Answer:
In an AC circuit containing only an ideal inductor, the current i lags behind the emf e by a phase angle of \(\frac{\pi}{2}\) rad. Here, for e = e₀ sin ωt, we have, i = i₀ sin(ωt – \(\frac{\pi}{2}\))
Instantaneous power, P = ei
= (e₀ sin ωt) [i₀ (sin ωt cos \(\frac{\pi}{2}\) – cos ωt sin \(\frac{\pi}{2}\))]
= – e₀i₀ sin ωt cos ωt as cos \(\frac{\pi}{2}\) = 0 and sin \(\frac{\pi}{2}\) = 1.
Average power over one cycle,


= e_rms i_rms cos Φ = e_rms i_rms (\(\frac{R}{Z}\)), where the impedance Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\).
∴ P_av = 0, i.e., the circuit does not dissipate power.

Question 5.
Prove that an ideal capacitor in an AC circuit does not dissipate power
Answer:
In an AC circuit containing only an ideal inductor, the current i lags behind the emf e by a phase angle of \(\frac{\pi}{2}\) rad. Here, for e = e₀ sin ωt, we have, i = i₀ sin(ωt – \(\frac{\pi}{2}\))
Instantaneous power, P = ei
= (e₀ sin ωt) [i₀ (sin ωt cos \(\frac{\pi}{2}\) + cos ωt sin \(\frac{\pi}{2}\))]
= – e₀i₀ sin ωt cos ωt as cos \(\frac{\pi}{2}\) = 0 and sin \(\frac{\pi}{2}\) = 1.
Average power over one cycle, P_av


= e_rms i_rms cos Φ = e_rms i_rms (\(\frac{R}{Z}\)), where the impedance Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\).
∴ P_av = 0, i.e., the circuit does not dissipate power.

Question 6.
(a) An emf e = e₀ sin ωt applied to a series L – C – R circuit derives a current I = I₀ sinωt in the circuit. Deduce the expression for the average power dissipated in the circuit.
(b) For circuits used for transporting electric power, a low power factor implies large power loss in transmission. Explain.
Answer:
(a) Instantaneous power,
P = ei
= (e₀ sin ωt) [i₀ (sin ωt ± Φ)]
= e₀i₀ sin ωt(sin ωt cos Φ ± cos ωt sin Φ)
= e₀i₀ sin² ωt ± e₀i₀ sin Φ sin ωt cos ωt
Average power over one cycle,


= e_rms i_rms cos Φ = e_rms i_rms (\(\frac{R}{Z}\)), where the impedance Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\).

(b) P_av = e_rms i_rms cos Φ
The factor cos Φ is called as power factor. For circuits used for transporting electric power, a low power factor means the power available on transportation is much less than e_rms i_rms It means there is significant loss of power during transportation.

Question 7.
A device Y is connected across an AC source of emf e = e₀ sinωt. The current through Y is given as i = i₀ sin(ωt + π/2)
a) Identify the device Y and write the expression for its reactance.
b) Draw graphs showing variation of emf and current with time over one cycle of AC for Y.
c) How does the reactance of the device Y vary with the frequency of the AC ? Show graphically
d) Draw the phasor diagram for the device Y.
Answer:
(a) The device Y is a capacitor. Its reactance is X_c = \(\frac{1}{\omega C}\),
where ω is the angular frequency of the applied emf and C is the capacitance of the capacitor.

(b)

(c) X_C = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\). Thus X_C ∝ \(\frac{1}{f}\), where f is the frequency of AC. Suppose C = \(\left(\frac{1000}{2 \pi}\right)\) pF
For f= 100 Hz, X_C = 1 × 10⁷Ω = 10MΩ;
for f = 200 Hz, X_C = 5 MΩ;
for f = 300 Hz, X_C = \(\frac{10}{3}\) MΩ;
for f = 400 Hz, X_C = 2.5 MΩ
for f = 500 Hz, X_C = 2 MΩ and so on

(d)

The phasor representing the peak emf (e₀) makes an angle (ωt) in an anticlockwise direction with respect to the horizontal axis. As the current leads the voltage by 90°, the phasor representing the peak current (i₀) is turned 90° anticlockwise with respect to the phasor representing emf e₀. The projections of these phasors on the vertical axis give instantaneous values of e and i.

Question 8.
Derive an expression for the impedance of an LCR circuit connected to an AC power supply.
Answer:
Figure shows an inductor of inductance L, capacitor of capacitance C, resistor of resistance R, key K and source (power supply) of alternating emf (e) connected to form a closed series circuit.

We assume the inductor, capacitor and resistor to be ideal. As these are connected in series, at any instant, they carry the same current i = i₀ sin ωt. The voltage across the resistor, e_R = Ri, is in phase with the current. The voltage across the inductor, e_L = X_Li, leads the current by \(\frac{\pi}{2}\) rad and that across the capacitor, e_C = X_Ci, lags behind the current by \(\frac{\pi}{2}\) rad. This is shown in the phasor diagram.

is the effective resistance of the circuit. It is called the impedance.

Question 9.
Compare resistance and reactance.
Answer:
(1) Resistance is opposition to flow of charges (current) and appears in a DC circuit as well as in an AC circuit.
The term reactance appears only in an AC circuit. It occurs when an inductor and/or a capacitor is used.

(2) In a purely resistive circuit, current and voltage are always in phase.
When reactance is not zero, there is nonzero phase difference between current and voltage.

(3) Resistance does not depend on the frequency of AC.
Reactance depends on the frequency of AC. In case of an inductor, reactance increases linearly with frequency. In case of a capacitor, reactance decreases as frequency of AC increases; it is inversely proportional to frequency.

(4) Resistance gives rise to production of Joule heat in a component.
In a circuit with pure reactance, there is no production of heat.

Question 10.
Show that in an AC circuit containing a pure inductor, the voltage is ahead of current by π/2 in phase.
Answer:
Figure 13.8 shows an AC source, generating a voltage e = e₀ sin ωt, connected to a key K and a pure inductor of inductance L to form a closed circuit.

On closing the key K, an emf is induced in the inductor as the magnetic flux linked with it changes with time. This emf opposes the applied emf and according to the laws of electromagnetic induction by Faraday and Lenz, we have,
e’ = -L\(\frac{d i}{d t}\) ………………. (1)
where e’ is the induced emf and i is the current through the inductor. To maintain the current; e and e’ must be equal in magnitude and opposite in direction.

According to Kirchhoff’s voltage law, as the resistance of the inductor is assumed to be zero, we

where C is the constant of integration. C must be time independent and have the dimension of current. As e oscillates about zero, i also oscillates about zero and hence there cannot be any time independent component of current.
∴ C = 0. ∴ i = –\(\frac{e_{0}}{\omega L}\)cos ωt = – \(\frac{e_{0}}{\omega L}\)sin(\(\frac{\pi}{2}\) – ωt)
∴ i = \(\frac{e_{0}}{\omega L}\) sin(ωt – \(\frac{\pi}{2}\)) ……………. (3)
as sin (-θ) = – sin θ
From Eq. (3), i_peak = i₀ = \(\frac{e_{0}}{\omega L}\)
∴ i = i₀ sin(ωt – \(\frac{\pi}{2}\)) ………………. (4)
Comparison of this equation with e = e₀ sin ωt shows that e leads i by \(\frac{\pi}{2}\) rad, i.e., the voltage is ahead of current by \(\frac{\pi}{2}\) rad in phase.

Question 11.
An AC source generating a voltage e = e₀ sinωt is connected to a capacitor of capacitance C. Find the expression for the current i flowing through it. Plot a graph of e and i versus ωt.
Answer:
Figure 13.12 shows an AC source, generating a voltage e = e₀ sin ωt, connected to a capacitor of capacitance C. The plates of the capacitor get charged due to the applied voltage. As the alternating voltage is reversed in each half cycle, the

capacitor is alternately charged and discharged. If q is the charge on the capacitor, the corresponding potential difference across the plates of the capacitor is V = \(\frac{q}{C}\) ∴ q = CV. q and V are functions of time, with V = e = e₀ sin ωt. The instantaneous current in the circuit is i = \(\frac{d q}{d t}=\frac{d}{d t}\)(CV) = C \(\frac{d v}{d t}\) = C \(\frac{d}{d t}\) (e₀ sin ωt) = ωC e₀ cos ωt
∴ i = \(\frac{e_{0}}{(1 / \omega C)} \sin \left(\omega t+\frac{\pi}{2}\right)=i_{0} \sin \left(\omega t+\frac{\pi}{2}\right)\)
where i₀ = \(\frac{e_{0}}{(1 / \omega C)}\) is the peak value of the current.

Table gives the values of e and i for different values of cot and Fig shows graphs of e and i versus ωt. i leads e by phase angle of \(\frac{\pi}{2}\) rad.

Question 12.
If the effective current in a 50 cycle AC circuit is 5 A, what is the peak value of current? What is the current 1/600 sec.after if was zero ?
Answer:
Data : f = 50 Hz, i_rms = 5 A, t = \(\frac{1}{600}\) s
The peak value of the current,
i₀ = i_rms\(\sqrt {2}\) = (5)(1.414) = 7.07 A
= i₀sin (2πft)
= 7.07 sin [2π(5o) (\(\frac{1}{600}\))]
= 7.07 sin (\(\frac{\pi}{6}\)) = (7.07)(0.5)
= 3.535 A
This is the required current.

Question 13.
A light bulb is rated 100W for 220 V AC supply of 50 Hz. Calculate (a) resistance of the bulb. (b) the rms current through the bulb.
Answer:
Data: Power (V_rms i_rms) = 100 W, V_rms = 220V,
f = 50 Hz
The rms current through the bulb,
i_rms = \(\frac{\text { power }}{V_{\mathrm{rms}}}=\frac{100}{220}\) = 0.4545 A
The resistance of the bulb,
R = \(\frac{V_{\mathrm{rms}}}{i_{\mathrm{rms}}}=\frac{220}{(100 / 220)}\) = (22) (22) = 484 Ω

Question 14.
A 15.0 µF capacitor is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak)
in the circuit. If the frequency is doubled, what will happen to the capacitive reactance and the current.
Answer:
Data : C = 15 µF = 15 × 10-6 F, V_rms = 220V, f = 50 Hz,
The capacitive reactance = \(\frac{1}{2 \pi f C}\)

If the frequency is doubled, the capacitive reactance will be halved and the current will be doubled.

Question 15.
An AC circuit consists of only an inductor of inductance 2 H. If the current is represented by a sine wave of amplitude 0.25 A and frequency 60 Hz, calculate the effective potential difference across the inductor (π = 3.142)
Answer:
Data : L = 2H, i₀ = 0.25 A, f = 60 Hz, π = 3.142
ωL = 2πfL = 2(3.142)(60)(2) = 754.1 Ω
The effective potential difference across the inductor = ωLi_rms = ωL \(\frac{i_{0}}{\sqrt{2}}\)
= \(\frac{(754.1)(0.25)}{1.414}\) = 133.3 V

Question 16.
Alternating emf of e = 220 sin 100 πt is applied to a circuit containing an inductance of (1/π) henry. Write an equation for instantaneous current through the circuit. What will be the reading of the AC galvanometer connected in the circuit?
Answer:
Data: e = 220 sin 100 πt, L = (\(\frac{1}{\pi}\))H
Comparing e = 220 sin 100 πt with
e = e₀ sin ωt, we get
ω = 100 π ∴ ωL = (100 π) (\(\frac{1}{\pi}\)) = 100 Ω
∴ The instantaneous current through the circuit
= i = \(\frac{e_{0}}{\omega L}\) sin(100 πt – \(\frac{\pi}{2}\))
= \(\frac{220}{100}\) sin (100 πt – \(\frac{\pi}{2}\)) = 2.2 sin (100 πt – \(\frac{\pi}{2}\)) in ampere [assuming that e is in volt.]
i_rms = \(\frac{i_{0}}{\sqrt{2}}=\frac{2.2}{1.414}\) = 1.556 A is the reading of the AC galvanometer connected in the circuit.

Question 17.
A 25 µF capacitor, a 0.10 H inductor and a 25Ω resistor are connected in series with an AC source whose emf is given by e = 310 sin 314 t (volt). What is the frequency, reactance, impedance, current and phase angle of the circuit?
Answer:
Data: C = 25 µF = 25 × 10^-6F, L = 0.10H, R = 25 Ω ,
e = 310 sin (314 t) [volt]
Comparing e = 310 sin (314 t) with
e = e₀ sin (2πft), we get,
the frequency of the alternating emf as

cos Φ = \(\frac{R}{Z}=\frac{25}{99.2}\) = 0.2520
∴ The phase angle, Φ = cos^-1(0.2520) = 75.40° = 1.316 rad

Question 18.
A capacitor of 100 µF, a coil of resistance 50Ω and an inductance 0.5 H are connected in series with a 110 V-50Hz source. Calculate the rms value of current in the circuit.
Answer:
Data : C = 100 µF = 100 × 10^-6 F = 10^-4 F,
R = 50 Ω, L = 0.5H, f = 50 Hz, V_rms = 110 V
∴ ωL = 2πfL = 2 (3.142)(50)(0.5) = 157.1 Ω

2500 + 15700 = 18200 Ω²
∴ Impedance, Z = \(\sqrt {18200}\) Ω = 134.9 Ω
The rms value of the current in the circuit,
i_rms = \(\frac{V_{\mathrm{rms}}}{\mathrm{Z}}=\frac{110}{134.9} \mathrm{~A}\)
= 0.8154 A

Question 19.
Find the capacity of a capacitor which when put in series with a 10Ω resistor makes the power factor equal to 0.5. Assume an 80V-100Hz AC supply.
Answer:
Data : R = 10 Ω, power factor = 0.5, f = 100 Hz
Power factor = \(\frac{1}{2 \pi f C R}\)
∴ 0.5 = \(\frac{1}{2(3.142)(100) C(10)}\)
∴ C = \(\frac{1}{3.142 \times 10^{3}}\)
= \(\frac{10 \times 10^{-4}}{3.142}\)
= 3.182 × 10^-4 F
This is the capacity of the capacitor.

Question 20.
Find the time required for a 50 Hz alternating current to change its value from zero to the rms value.
Answer:
Data : f = 50 Hz, i = \(\frac{i_{0}}{\sqrt{2}}\) ∴ \(\frac{i}{i_{0}}=\frac{1}{\sqrt{2}}\)
i = i₀ sinωt
∴ sinωt = \(\frac{i}{i_{0}}=\frac{1}{\sqrt{2}}\)
∴ ωt = \(\frac{\pi}{4}\) rad
∴ 2πft = \(\frac{\pi}{4}\)
∴ t = \(\frac{1}{8 f}=\frac{1}{8(50)}=\frac{1}{400}\)
= \(\frac{1000 \times 10^{-3}}{400}\) = 2.5 × 10^-3 s
This is the required time.

Question 21.
Calculate the value of capacitance in picofarad, which will make 101.4 micro henry inductance to oscillate with frequency of one megahertz.
Answer:
Data : f_r = 10⁶ Hz, L = 101.4 × 10^-6 H

= \(\frac{10000 \times 10^{-10}}{4(3.142)^{2}(101.4)}\) = 2.497 × 10^-10 F
= 249.7 × 10^-12 F = 249.7 picofarad
This is the value of the capacity.

Question 22.
A 10 µF capacitor is charged to a 25 volt of potential. The battery is disconnected and a pure 100 m H coil is connected across the capacitor so that LC oscillations are set up. Calculate the maximum current in the coil.
Answer:
Data: C = 10 µF = 10 × 10^-6F = 10^-5F,
L = 100mH = 100 × 10^-3 H = 10^-1 H, V = 25V
For reference, see the solved example (8) above.
\(\frac{1}{2}\)CV² = \(\frac{1}{2}\)Li²
∴i² = \(\frac{C}{L} V^{2}=\frac{10^{-5}}{10^{-1}}(25)^{2}\)
∴i = 25 × 10^-2 A = 0.25 A
This is the maximum current in the coil.

Question 23.
A 100 µF capacitor is charged with a 50 V source supply. Then source supply is removed and the capacitor is connected across an inductance, as a result of which 5A current flows through the inductance. Calculate the value of the inductance.
Answer:
Data: C = 100 µF = 100 × 10^-6 F = 10^-4 F,
V = 50V, i = 5A
The energy stored in the electric field in the capacitor
= \(\frac{1}{2}\)CV²
The energy stored in the magnetic field in the inductor = \(\frac{1}{2}\)Li²
Here, \(\frac{1}{2}\)CV² = \(\frac{1}{2}\)Li²
∴ L = C\(\frac{V^{2}}{i^{2}}\)
∴ L = C\(\left(\frac{V}{i}\right)^{2}=10^{-4}\left(\frac{50}{5}\right)^{2}\) = 10^-4 × 10²
= 10^-2H
This is the value of the inductance.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions Digest

• Chapter 1 Introduction to Corporate Finance
• Chapter 2 Sources of Corporate Finance
• Chapter 3 Issue of Shares
• Chapter 4 Issue of Debentures
• Chapter 5 Deposits
• Chapter 6 Correspondence with Members
• Chapter 7 Correspondence with Debentureholders
• Chapter 8 Correspondence with Depositors
• Chapter 9 Depository System
• Chapter 10 Dividend and Interest
• Chapter 11 Financial Market
• Chapter 12 Stock Exchange

Maharashtra State Board Class 12 Textbook Solutions

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 4 Thermodynamics Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 4 Thermodynamics

1. Choose the correct option.

i) A gas in a closed container is heated with 10J of energy, causing the lid of the container to rise 2m with 3N of force. What is the total change in the internal energy of the system?
(A) 10J
(B) 4J
(C) -10J
(D) – 4J
Answer:
(B) 4J

ii) Which of the following is an example of the first law of thermodynamics?
(A) The specific heat of an object explains how easily it changes temperatures.
(B) While melting, an ice cube remains at the same temperature.
(C) When a refrigerator is unplugged, everything inside of it returns to room temperature after some time.
(D) After falling down the hill, a ball’s kinetic energy plus heat energy equals the initial potential energy.
Answer:
(B) While melting, an ice cube remains at the same temperature. [Here, ∆u = 0, W = Q]
(C) When a refrigerator is unplugged, everything inside of it returns to room temperature after some time.
(D) After falling down the hill, a ball’s kinetic energy plus heat energy equals the initial potential energy.

iii) Efficiency of a Carnot engine is large when
(A) T_H is large
(B) T_C is low
(C) T_H – T_C is large
(D) T_H – T_C is small
Answer:
(A) T_H is large
(B) T_C is low
(C) T_H – T_C is large
[η = \(\frac{T_{\mathrm{H}}-T_{\mathrm{c}}}{T_{\mathrm{H}}}\) = 1 – \(\frac{T_{\mathrm{c}}}{T_{\mathrm{H}}}\)]

iv) The second law of thermodynamics deals with transfer of:
(A) work done
(B) energy
(C) momentum
(D) mass
Answer:
(B) energy

v) During refrigeration cycle, heat is rejected by the refrigerant in the :
(A) condenser
(B) cold chamber
(C) evaporator
(D) hot chamber
Answer:
closed tube[See the textbook]

2. Answer in brief.

i) A gas contained in a cylinder surrounded by a thick layer of insulating material is quickly compressed.
(a) Has there been a transfer of heat?
(b) Has work been done?
Answer:
(a) There is no transfer of heat.
(b) The work is done on the gas.

ii) Give an example of some familiar process in which no heat is added to or removed form a system, but the temperature of the system changes.
Answer:
Hot water in a container cools after sometime. Its temperature goes on decreasing with time and after sometime it attains room temperature.
[Note : Here, we do not provide heat to the water or remove heat from the water. The water cools on exchange of heat with the surroundings. Recall the portion covered in chapter 3.]

iii) Give an example of some familiar process in which heat is added to an object, without changing its temperature.
Answer:

1. Melting of ice
2. Boiling of water.

iv) What sets the limits on efficiency of a heat engine?
Answer:
The temperature of the cold reservoir sets the limit on the efficiency of a heat engine.
[Notes : (1) η = 1 – \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\)
This formula shows that for maximum efficiency, T_C should be as low as possible and T_H should be as high as possible.
(2) For a Carnot engine, efficiency
η = 1 – \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\).η → 1 T_C → 0.]

v) Why should a Carnot cycle have two isothermal two adiabatic processes?
Answer:
With two isothermal and two adiabatic processes, all reversible, the efficiency of the Carnot engine depends only on the temperatures of the hot and cold reservoirs.
[Note : This is not so in the Otto cycle and Diesel cycle.]

3. Answer the following questions.

i) A mixture of hydrogen and oxygen is enclosed in a rigid insulting cylinder. It is ignited by a spark. The temperature and the pressure both increase considerably. Assume that the energy supplied by the spark is negligible, what conclusions may be drawn by application of the first law of thermodynamics?
Answer:
The internal energy of a system is the sum of potential energy and kinetic energy of all the constituents of the system. In the example stated above, conversion of potential energy into kinetic energy is responsible for a considerable rise in pressure and temperature of the mixture of hydrogen and oxygen ignited by the spark.

ii) A resistor held in running water carries electric current. Treat the resistor as the system
(a) Does heat flow into the resistor?
(b) Is there a flow of heat into the water?
(c) Is any work done?
(d) Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
Answer:
(a) Heat is generated into the resistor due to the passage of electric current. In the usual notation, heat generated = I2Rt.
(b) Yes. Water receives heat from the resistor.

Here, I = current through the resistor, R = resistance of the resistor, t = time for which the current is passed through the resistor, M = mass of the water, S = specific heat of water, T = rise in the temperature of water, P = pressure against which the work is done by the water, ∆u= increase in the volume of the water.

iii) A mixture of fuel and oxygen is burned in a constant-volume chamber surrounded by a water bath. It was noticed that the temperature of water is increased during the process. Treating the mixture of fuel and oxygen as the system,
(a) Has heat been transferred ?
(b) Has work been done?
(c) What is the sign of ∆u ?
Answer:
(a) Heat has been transferred from the chamber to the water bath.
(b) No work is done by the system (the mixture of fuel and oxygen) as there is no change in its volume.
(c) There is increase in the temperature of water. Therefore, ∆u is positive for water.
For the system (the mixture of fuel and oxygen), ∆u is negative.

iv) Draw a p-V diagram and explain the concept of positive and negative work. Give one example each.
Answer:
Consider some quantity of an ideal gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.

Suppose the gas is allowed to expand by moving the piston outward extremely slowly. There is decrease in pressure of the gas as the volume of the gas increases. Below figure shows the corresponding P-V diagram.

In this case, the work done by the gas on its surroundings,
W = \(\int_{V_{\mathrm{i}}}^{V_{\mathrm{f}}} P d V\) (= area under the curve) is positive as the volume of the gas has increased from V_i to V_f.
Let us now suppose that starting from the same

initial condition, the piston is moved inward extremely slowly so that the gas is compressed. There is increase in pressure of the gas as the volume of the gas decreases. Figure shows the corresponding P-V diagram.
In this case, the work done by the gas on its surroundings, W = \(\int_{V_{\mathrm{i}}}^{V_{\mathrm{f}}} P d V\) (= area under the curve) is negative as the volume of the gas has decreased from V_i to V_f.

v) A solar cooker and a pressure cooker both are used to cook food. Treating them as thermodynamic systems, discuss the similarities and differences between them.
Answer:
Similarities :

1. Heat is added to the system.
2. There is increase in the internal energy of the system.
3. Work is done by the system on its environment.

Differences : In a solar cooker, heat is supplied in the form of solar radiation. The rate of supply of heat is relatively low.

In a pressure cooker, usually LPG is used (burned) to provide heat. The rate of supply of heat v is relatively high.

As a result, it takes very long time for cooking when a solar cooker is used. With a pressure cooker, it does not take very long time for cooking.
[Note : A solar cooker can be used only when enough solar radiation is available.]

Question 4.
A gas contained in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 5 litres to a volume of 10 litres. In doing so it absorbs 400 J of thermal energy from its surroundings. Determine the change in internal energy of system. [Ans: -106.5 J]
Answer:
Data : P = 1 atm = 1.013 × 10⁵ Pa, V₁ = 5 litres = 5 × 10^-3 m³ V₂ = 10 litres = 10 × 10^-3 m³, Q = 400J.
The work done by the system (gas in this case) on its surroundings,
W = P(V₂ – V₁)
= (1.013 × 10⁵ Pa) (10 × 10^-3 m³ – 5 × 10^-3 m³)
= 1.013 (5 × 10²)J = 5.065 × 10²J
The change in the internal energy of the system, ∆u = Q – W = 400J – 506.5J = -106.5J
The minus sign shows that there is a decrease in the internal energy of the system.

Question 5.
A system releases 130 kJ of heat while 109 kJ of work is done on the system. Calculate the change in internal energy.
[Ans: ∆U = 21 kJ]
Answer:
Data : Q = -130kj, W= – 109kJ
∆u = Q – W = – 130kJ – ( – 109kJ)
= (-130 + 104) kJ = – 26 kj.
This is the change (decrease) in the internal energy.

Question 6.
Efficiency of a Carnot cycle is 75%. If temperature of the hot reservoir is 727ºC, calculate the temperature of the cold reservoir. [Ans: 23ºC]
Data : η = 75% = 0.75, T_H = (273 + 727) K = 1000 K
η = 1 – \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\) ∴ \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\) = 1 – η
∴ T_C = T_C(1 – η) = 1000 K (1 – 0.75)
= 250K = (250 – 273)°C
= -23 °C
This is the temperature of the cold reservoir.

Question 7.
A Carnot refrigerator operates between 250K and 300K. Calculate its coefficient of performance. [Ans: 5]
Answer:
Data : T_C = 250 K, T_H = 300 K
K = \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}-T_{\mathrm{C}}}\) = \(\frac{250 \mathrm{~K}}{300 \mathrm{~K}-250 \mathrm{~K}}\) = \(\frac{250}{50}\) = 5
This is the coefficient of performance of the refrigerator.

Question 8.
An ideal gas is taken through an isothermal process. If it does 2000 J of work on its environment, how much heat is added to it? [Ans: 2000J]
Answer:
Data : W = 2000 J, isothermal process
In this case, the change in the internal energy of the gas, ∆u, is zero as the gas is taken through an isothermal process.
Hence, the heat added to it,
Q = ∆ u + W = 0 + W = 200J

Question 9.
An ideal monatomic gas is adiabatically compressed so that its final temperature is twice its initial temperature. What is the ratio of the final pressure to its initial pressure? [Ans: 5.656]
Answer:
Data : T_f = 2T_i, monatomic gas ∴ γ = 5/3


This is the ratio of the final pressure (P_f) to the initial pressure (P_i).

Question 10.
A hypothetical thermodynamic cycle is shown in the figure. Calculate the work done in 25 cycles.

[Ans: 7.855 × 10⁴ J]
Answer:


25 cycles
The work done in one cycle, \(\oint\)PdV
= πab = (3.142) (2 × 10^-3 m³) (5 × 10⁵ Pa)
= 3.142 × 10³J
Hence, the work done in 25 cycles
= (25) (3.142 × 10³ J) = 7.855 × 10⁴J

Question 11.
The figure shows the V-T diagram for one cycle of a hypothetical heat engine which uses the ideal gas. Draw the p-V diagram and P-V diagram of the system. [Ans: (a)]

[Ans: (b)]
Answer:
(a) P-V diagram (Schematic)

ab: isobaric process,
bc : isothermal process,
cd : isobaric process,
da : isothermal process
\(\frac{P_{\mathrm{a}} V_{\mathrm{a}}}{T_{\mathrm{a}}}\) = \(\frac{P_{\mathrm{b}} V_{\mathrm{b}}}{T_{\mathrm{b}}}\) = \(\frac{P_{\mathrm{c}} V_{\mathrm{c}}}{T_{\mathrm{c}}}\) = \(\frac{P_{\mathrm{d}} V_{\mathrm{d}}}{T_{\mathrm{d}}}\) = nR

(b) P—T diagram (Schematic)

Question 12.
A system is taken to its final state from initial state in hypothetical paths as shown figure. Calculate the work done in each case.

[Ans: AB = 2.4 × 10⁶ J, CD = -8 × 10⁵ J, BC and DA zero, because constant volume change]
Answer:

Data: P_A = P_B = 6 × 10⁵ Pa, P_C = P_D = 2 × 10⁵ Pa V_A = V_D = 2 L, V_B = V_C6 L, 1 L = 10^-3m³
(i) The work done along the path A → B (isobaric process), W_AB = P_A (V_B – V_A) = (6 × 10⁵ Pa)(6 – 2)(10^-3 m³) = 2.4 × 10³ J
(ii) W_BC = zero as the process is isochoric (V = constant).
(iii) The work done along the path C → D (isobaric process), W_CD = P_C (V_D – V_C)
= (2 × 10⁵ Pa) (2 – 6) (10^-3m³) = -8 × 10²J
(iv) W_DA = zero as V = constant.

12th Physics Digest Chapter 4 Thermodynamics Intext Questions and Answers

Can you tell? (Textbook Page No. 76)

Question 1.
Why is it that different objects kept on a table at room temperature do not exchange heat with the table ?
Answer:
The objects do exchange heat with the table but there is no net transfer of energy (heat) as the objects and the table are at the same temperature.

Can you tell? (Textbook Page No. 77)

Question 1.
Why is it necessary to make a physical contact between a thermocouple and the object for measuring its temperature ?
Answer:
For heat transfer to develop thermoemf.

Can you tell? (Textbook Page No. 81)

Question 1.
Can you explain the thermodynamics involved in cooking food using a pressure cooker ?
Answer:
Basically, heat is supplied by the burning fuel causing increase in the internal energy of the food (system), and the system does some work on its surroundings. In the absence of any data about the components of food and their thermal and chemical properties, we cannot evaluate changes in internal energy and work done.

Use your brain power (Textbook Page No. 85)

Question 1.
Verify that the area under the P-V curve has dimensions of work.
Answer:
Area under the P-V curve is \(\int_{V_{\mathrm{i}}}^{V_{\mathrm{f}}} P d V\), where P is the pressure and V is the volume.

Use your brain power (Textbook Page No. 91)

Question 1.
Show that the isothermal work may also be expressed as W = nRT ln\(\left(\frac{\boldsymbol{P}_{\mathrm{i}}}{\boldsymbol{P}_{\mathrm{f}}}\right)\),
Answer:
In the usual notation,
W = nRT In \(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\) and P_i V_i = P_f V_f = nRT in an isothermal process
∴ \(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\) = \(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\) and W = nRT ln \(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\)

Use your brain power (Textbook Page No. 94)

Question 1.
Why is the P-V curve for an adiabatic process steeper than that for an isothermal process ?
Answer:
Adiabatic process : PV^γ = constant
∴ V^γdP + γPV^γ-1 dV = 0
∴ \(\frac{d P}{d V}\) = – \(\frac{\gamma P}{V}\)
Isothermal process : PV = constant
∴ pdV + VdP = 0 ∴ \(\frac{d P}{d V}\) = \(\frac{P}{-V}\)
Now, γ > 1

∴ \(\frac{d P}{d V}\) is the slope of the P – V curve.
∴The P – V curve for an adiabatic process is steeper than that for an isothermal process.

Question 2.
Explain formation of clouds at high altitude.
Answer:
As the temperature of the earth increases due to absorption of solar radiation, water from rivers, lakes, oceans, etc. evaporates and rises to high altitude. Water vapour forms clouds as water molecules come together under appropriate conditions. Clouds are condensed water vapour and are of various type, names as cumulus clouds, nimbostratus clouds, stratus clouds and high-flying cirrus clouds.

Can you tell? (Textbook Page No. 95)

Question 1.
How would you interpret Eq. 4.21 (Q = W) for a cyclic process ?
Answer:
It means ∆ u = 0 for a cyclic process as the system returns to its initial state.

Question 2.
An engine works at 5000 rpm, and it performs 1000 J of work in one cycle. If the engine runs for 10 min, how much total work is done by the engine ?
Answer:
The total work done by the engine = (1000 J/cycle) (5000 cycles/min) (10 min) = 5 × 10⁷ J.

Do you know? (Textbook Page No. 101)

Question 1.
Capacity of an air conditioner is expressed in tonne. Do you know why?
Answer:
Before refrigerator and AC were invented, cooling was done by using blocks of ice. When cooling machines were invented, their capacity was expressed in terms of the equivalent amount of ice melted in a day (24 hours). The same term is used even today.
(Note : 1 tonne = 1000 kg = 2204.6 pounds, 1 ton (British) = 2240 pounds = 1016.046909 kg, 1 ton (US) = 2000 pounds = 907.184 kg.]

Use your brain power (Textbook Page No. 105)

Question 1.
Suggest a practical way to increase the efficiency of a heat engine.
Answer:
The efficiency of a heat engine can be increased by choosing the hot reservoir at very high temperature and cold reservoir at very low temperature.

Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 14 Dual Nature of Radiation and Matter Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Physics Solutions Chapter 14 Dual Nature of Radiation and Matter

1. Choose the correct answer.

i) A photocell is used to automatically switch on the street lights in the evening when the sunlight is low in intensity. Thus it has to work with visible light. The material of the cathode of the photocell is
(A) zinc
(B) aluminum
(C) nickel
(D) potassium
Answer:
(D) potassium

ii) Polychromatic (containing many different frequencies) radiation is used in an experiment on the photoelectric effect. The stopping potential
(A) will depend on the average wavelength
(B) will depend on the longest wavelength
(C) will depend on the shortest wavelength
(D) does not depend on the wavelength
Answer:
(C) will depend on the shortest wavelength

iii) An electron, a proton, an α-particle and a hydrogen atom are moving with the same kinetic energy. The associated de Broglie wavelength will be longest for
(A) electron
(B) proton
(C) α-particle
(D) hydrogen atom
Answer:
(A) electron

iv) If N_Red and N_Blue are the number of photons emitted by the respective sources of equal power and equal dimensions in unit time, then
(A) N_Red < N_Blue
(B) N_Red = N_Blue
(C) N_Red > N_Blue
(D) N_Red ≈ N_Blue
Answer:
(C) N_Red > N_Blue

v) The equation E = pc is valid
(A) for all sub-atomic particles
(B) is valid for an electron but not for a photon
(C) is valid for a photon but not for an electron
(D) is valid for both an electron and a photon
Answer:
(C) is valid for a photon but not for an electron

2. Answer in brief.

i) What is photoelectric effect?
Answer:
The phenomenon of emission of electrons from a metal surface when electromagnetic radiation of appropriate frequency is incident on it is known as photoelectric effect.

ii) Can microwaves be used in the experiment on photoelectric effect?
Answer:
No

iii) Is it always possible to see photoelectric effect with red light?
Answer:
No

iv) Using the values of work function given in Table 14.1, tell which metal will require the highest frequency of incident radiation to generate photocurrent.

Answer:
Gold.
[ Note : W₀ = hv₀, where h is Planck’s constant. The larger the work function (W₀), the higher is the threshold frequency (v₀). ]

v) What do you understand by the term wave-particle duality? Where does it apply?
Answer:
Depending upon experimental conditions or structure of matter, electromagnetic radiation and material particles exhibit wave nature or particle nature. This is known as wave-particle duality.

It applies to all phenomena. The wave nature and particle nature are liked by the de Broglie relation λ = h/p, where λ is the wavelength of matter waves, also called de Broglie waves / Schrodinger waves, p is the magnitude of the momentum of a particle or quantum of radiation and h is the universal constant called Planck’s constant.

[Note : It is the smallness of h (= 6.63 × 10^-34 J∙s) that is very significant in wave-particle duality.]

Question 3.
Explain the inverse linear dependence of stopping potential on the incident wavelength in a photoelectric effect experiment.
Answer:
We have V₀e = \(\frac{h c}{\lambda}\) – Φ, where V₀ is the stopping potential, e is the magnitude of the charge on the electron, h is Planck’s constant, c is the speed of light in free space, λ is the wavelength of the electromagnetic radiation incident on a metal surface and Φ is the work function for the metal, h, c and e are constants. Φ is constant for a particular metal.
Hence, it follows that as \(\frac{1}{\lambda}\) increases, V₀ increases.
The plot of V₀ verses \(\frac{1}{\lambda}\) is linear. This is because the energy associated with a quantum of radiation (photon) is directly proportional to the frequency of radiation and hence inversely proportional to the wavelength of radiation.

Question 4.
It is observed in an experiment on photoelectric effect that an increase in the intensity of the incident radiation does not change the maximum kinetic energy of the electrons. Where does the extra energy of the incident radiation go? Is it lost? State your answer with explanatory reasoning.
Answer:
When electromagnetic radiation with frequency greater than the threshold frequency is incident on a metal surface, there is emission of electrons. It is observed that not every incident photon is effective in liberating an electron. In fact, the number of electrons emitted per second is far less than the number of photons incident per second. The photons that are not effective in liberation of electrons are reflected (or scattered) or absorbed resulting in rise in the temperature of the metal surface. The maximum kinetic energy of a photoelectron depends on the frequency of the incident radiation and the threshold frequency for the metal. It has nothing to do with the intensity of the incident radiation. The increase in intensity results in increase in the number of electrons emitted per second.

Question 5.
Explain what do you understand by the de Broglie wavelength of an electron. Will an electron at rest have an associated de Broglie wavelength? Justify your answer.
Answer:
Under certain conditions an electron exhibits wave nature. Waves associated with a moving electron are called matter waves or de Broglie waves or- Schrodinger waves. The de Broglie wavelength of these matter waves is given by X = h/p, where h is Planck’s constant and p is the magnitude of the momentum of the electron.

If an electron is at rest, its momentum would be zero, and hence the corresponding de Broglie wavelength would be infinite indicating absence of a matter wave. However, according to quantum mechanics/wave mechanics, this is not possible.

Question 6.
State the importance of Davisson and Germer experiment.
Answer:
The Davisson and Germer experiment directly indicated the wave nature of material particles and quantitatively verified the de Broglie hypothesis for the existence of matter waves.

[Note : The aim of the experiment was not to verify wave like properties of electrons. The realisation came only later, an example of serendipity.]

[Note : Like X-rays, electrons exhibit wave nature under suitable conditions. When the wavelength of matter waves associated with moving electrons is comparable to the inter-atomic spacing in a crystal, electrons show diffraction effects. In 1927, Sir George Thomson (1892 – 1975), British physicist, with his student Alex Reid, observed electron diffraction with a metal foil. It is found that neutrons, atoms, molecules, Œ-particles, etc. show wave nature under suitable conditions.]

Question 7.
What will be the energy of each photon in monochromatic light of frequency 5 × 10¹⁴ Hz?
Answer:
Data: y = 5 × 10¹⁴ Hz, h = 6.63 × 10^-34 Js,
1eV=1.6 × 10^-19 J
The energy of each photon,
E = hv = (6.63 × 10^-34 J.s)(5 × 10¹⁴ Hz)
= 3.315 × 10^-19 J
= \(\frac{3.315 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 2.072 eV

Question 8.
Observations from an experiment on photoelectric effect for the stopping potential by varying the incident frequency were plotted. The slope of the linear curve was found to be approximately 4.1 × 10^-15 V s. Given that the charge of an electron is 1.6 × 10^-19 C, find the value of the Planck’s constant h.
Answer:
Data : Slope=4.1 × 10^-15 V∙s, e = 1.6 ×10^-19 C
V₀e = hv – hv₀
∴ V₀ =\(\left(\frac{h}{e}\right) v-\left(\frac{h v_{0}}{e}\right)\)
∴ Slope = \(\frac{h}{e}\) ∴ Planck’s constant,
h = (slope) (e)=(4.1 × 10^-15 V∙s)(1.6 × 10^-19 C)
= 6.56 × 10 34J. (as 1 V = \(\frac{1 \mathrm{~J}}{1 \mathrm{C}}\))

Question 9.
The threshold wavelength of tungsten is 2.76 × 10^-5 cm. (a) Explain why no photoelectrons are emitted when the wavelength is more than 2.76 × 10^-5 cm.(b) What will be the maximum kinetic energy of electrons ejected in each of the following cases
(i) if ultraviolet radiation of wavelength λ = 1.80 × 10^-5 cm and
(ii) radiation of frequency 4 × 10¹⁵ Hz is made incident on the tungsten surface.
Answer:
Data: λ₀ = 2.76 × 10^-5 cm = 2.76 × 10^-7 m,
λ =1.80 × 10^-5 cm = 1.80 × 10^-7 m,
v = 4 × 10¹⁵ Hz, h = 6.63 × 10^-34 J∙s,c = 3 × 10⁸ m/s
(a) For λ > λ₀, v < v₀ (threshold frequency).
∴ hv < hv₀. Hence, no photoelectrons are emitted.

(b) Maximum kinetic energy of electrons ejected
= hc\(\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)\)
=(6.63 × 10^-34)(3 × 10⁸)\(\left(\frac{10^{7}}{1.8}-\frac{10^{7}}{2.76}\right)\)J
= (6.63 × 10^-19)(0.5555 – 0.3623)
= (6.63)(0.1932 × 10^-19)J = 1.281 × 10^-19 J
= \(\frac{1.281 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 0.8006 eV

(c) Maximum kinetic energy of electrons ejected
= hv – \(\frac{h c}{\lambda_{0}}\)
=(6.63 × 10^-34(4 × 10¹⁵) – \(\frac{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{2.76 \times 10^{-7}}\)
= 26.52 × 10^-19 – 7.207 × 10^-19
= 19.313 × 10^-19 J
= \(\frac{19.313 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 12.07eV

Question 10.
Photocurrent recorded in the micro ammeter in an experimental set-up of photoelectric effect vanishes when the retarding potential is more than 0.8 V if the wavelength of incident radiation is 4950 Å. If the source of incident radiation is changed, the stopping potential turns out to be 1.2 V. Find the work function of the cathode material and the wavelength of the second source.
Answer:
Data: V₀ = 0.8 V, λ = 4950 Å = 4.950 × 10^-7 m,
V₀‘ = 1.2V, h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s.
(i) V₀e = hv – Φ = \(\frac{h c}{\lambda}\) – Φ
∴ The work function of the cathode material,

Question 11.
Radiation of wavelength 4500 Å is incident on a metal having work function 2.0 eV. Due to the presence of a magnetic field B, the most energetic photoelectrons emitted in a direction perpendicular to the field move along a circular path of radius 20 cm. What is the value of the magnetic field B?
Answer:
Data: λ = 4500Å = 4.5 × 10^-7 m,
Φ = 2.0eV = 2 × 1.6 × 10^-19 J = 3.2 × 10^-19 J,
h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s,
r = 20 cm = 0.2 m, e= 1.6 × 10^-19 C,
m = 9.1 × 10^-31kg

This is the value of the magnetic field.

Question 12.
Given the following data for incident wavelength and the stopping potential obtained from an experiment on photoelectric effect, estimate the value of Planck’s constant and the work function of the cathode material. What is the threshold frequency and corresponding wavelength? What is the most likely metal used for emitter?

Answer:
Data: λ = 2536Å = 2.536 × 10^-7 m,
λ’ = 3650Å = 3.650 ×10^-7 m, V₀ = 1.95V, V₀‘ = 0.5V,
c = 3 × 10⁸ mIs, e = 1.6 × 10^-19 C

(i) V₀e = \(\frac{h c}{\lambda}\) – Φ and V₀‘e =\(\frac{h c}{\lambda^{\prime}}\) – Φ
∴ (V₀ – V₀‘)e = hc\(\left(\frac{1}{\lambda}-\frac{1}{\lambda^{\prime}}\right)\)
∴ (1.95 – 0.5(1.6 × 10^-19)
= h (3 × 10⁸\(\left(\frac{10^{7}}{2.536}-\frac{10^{7}}{3.650}\right)\)
∴ 2.32 × 10^-19 = h(3 × 10¹⁵)(0.3943 – 0.2740)
∴ h = \(\frac{2.32 \times 10^{-34}}{0.3609}\) = 6.428 × 10^-34 J∙s
This is the value of Planck’s constant.

(ii) Φ = \(\frac{h c}{\lambda}\) – V₀e

This is the work function of the cathode material.

(iii) Φ = hv₀
∴ The threshold frequency, v₀ = \(\frac{\phi}{h}\)
= \(\frac{4.484 \times 10^{-19} \mathrm{~J}}{6.428 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}\) = 6.976 × 10¹⁴ Hz

(iv) v₀ = \(\frac{c}{\lambda_{\mathrm{o}}}\) ∴ The threshold frequency, λ₀ = \(\frac{c}{v_{\mathrm{o}}}\)
= \(\frac{3 \times 10^{8}}{6.976 \times 10^{14}}\) = 4.300 × 10^-7 m = 4300 Å

(v) The most likely metal used for emitter : calcium

Question 13.
Calculate the wavelength associated with an electron, its momentum and speed
(a) when it is accelerated through a potential of 54 V
Answer:
Data : V = 54 V, m = 9.1 × 10^-31 kg, e
e = 1.6 × 10^-19 C, h = 6.63 × 10^-34 J.s, KE = 150 eV
(a) We assume that the electron is initially at rest.
∴ Ve = \(\frac{1}{2}\)mv²
∴ v = \(\sqrt{\frac{2 V e}{m}}=\sqrt{\frac{2(54)\left(1.6 \times 10^{-19}\right)}{9.1 \times 10^{-31}}}\)
= \(\sqrt{19 \times 10^{12}}\) = 4.359 × 10⁶ m/5
This is the speed of the electron.
p = mv = (9.1× 10^-31)(4.359 × 10⁶)
= 3.967 × 10^-24 kg∙m/s
This is the momentum of the electron. The wavelength associated with the electron,
λ = \(\frac{h}{p}=\frac{6.63 \times 10^{-34}}{3.967 \times 10^{-24}}\) = 1.671 × 10^-10 m
= 1.671 Å = 0.1671 nm

(b) when it is moving with kinetic energy of 150 eV.
Answer:
As KE ∝ \(\sqrt{V}\), we get
\(\frac{v^{\prime}}{v}=\sqrt{\frac{150}{54}}\) = 1.666
∴ v’ = 1.666v = (1.666)(4.356 × 10⁶)
= 7.262 × 10⁶ m/s
This is the speed of the electron.
p’ = mv’’=(9.1 × 10^-31)(7.262 × 10⁶)
= 6.608 × 10^-24 kg∙m/s
This is the momentum of the electron. The
wavelength associated with the electron,
λ = \(\frac{h}{p^{\prime}}=\frac{6.63 \times 10^{-34}}{6.608 \times 10^{-24}} \) = 1.003 × 10^-10 m
= 1.003 Å = 0.1003 nm

Question 14.
The de Broglie wavelengths associated with an electron and a proton are same. What will be the ratio of
(i) their momenta
(ii) their kinetic energies?
Answer:
Data : λ (electron) = λ (proton)
m (proton) = 1836 m (electron)
(i) λ = \(\frac{h}{p}\) As λ (electron) = λ (proton),
\(\frac{p(\text { electron })}{p \text { (proton) }}\) = 1, where p denotes the magnitude of momentum.

(ii) Assuming v «c,
KE = \(\frac{1}{2}\)mv² = \(\frac{1}{2} \frac{m^{2} v^{2}}{m}=\frac{p^{2}}{2 m}\)
∴ \(\frac{\mathrm{KE} \text { (electron) }}{\mathrm{KE} \text { (proton) }}=\frac{m \text { (proton) }}{m \text { (electron) }}\) = 1836 as p is the same for the electron and the proton.

Question 15.
Two particles have the same de Broglie wavelength and one is moving four times as fast as the other. If the slower particle
is an α-particle, what are the possibilities for the other particle?
Answer:
Data : λ₁ = λ₂, v₁ = 4v₂
λ = \(\frac{h}{p}=\frac{h}{m v}\) ∴ λ₁ = \(\frac{h}{m_{1} v_{1}}\), λ₂ = \(\frac{h}{m_{2} v_{2}}\)
∴ m₁ = m₂ \(\frac{v_{2}}{v_{1}}\) = m₂\(\left(\frac{1}{4}\right)=\frac{m_{2}}{4}\)
As particle 2 is the a-particle, particle 1 (having the mass \(\frac{1}{4}\) times that of the a-particle) may be a proton or neutron.

Question 16.
What is the speed of a proton having de Broglie wavelength of 0.08 Å?
Answer:
Data : λ = 0.08 Å = 8 × 10^-12m, h = 6.63 × 10^-34 J∙s, m = 1.672 × 10^-27 kg
λ = \(\frac{h}{m v}\) ∴ v = \(\frac{h}{\lambda m}=\frac{6.63 \times 10^{-34}}{\left(8 \times 10^{-12}\right)\left(1.672 \times 10^{-27}\right)}\)
∴ v = 4.957 × 10⁴ m/s
This is the speed of the proton.

Question 17.
In nuclear reactors, neutrons travel with energies of 5 × 10^-21 J. Find their speed and wavelength.
Answer:
Data : KE = 5 × 10^-21 J, m = 1.675 × 10^-27 kg, h = 6.63 × 10^-34 J∙s
KE = \(\frac{1}{2}\) mv² = 5 × 10^-21 J
∴ v = \(\sqrt{\frac{2 \mathrm{KE}}{m}}=\sqrt{\frac{(2)\left(5 \times 10^{-21}\right)}{1.675 \times 10^{-27}}}\)
= 2.443 × 10³ m/s
This is the speed of the neutrons. The de Broglie wavelength associated with the neutron,
λ = \(\frac{h}{m v}=\frac{6.63 \times 10^{-34}}{\left(1.675 \times 10^{-27}\right)\left(2.443 \times 10^{3}\right)}\)
= 1.620 × 10^-10 m = 1.620 Å

Question 18.
Find the ratio of the de Broglie wavelengths of an electron and a proton when both are moving with the (a) same speed, (b) same energy and (c) same momentum? State which of the two will have the longer wavelength in each case?
Answer:
Data: m_p = 1836 m_e

12th Physics Digest Chapter 14 Dual Nature of Radiation and Matter Intext Questions and Answers

Remember This (Textbook Page No. 316)

Question 1.
Is solar cell a photocell?
Answer:
Yes

Remember This (Textbook Page No. 317)

Question 1.
Can you estimate the de Broglie wavelength of the Earth?
Answer:
Taking the mass of the Earth as (about) 6 × 10²⁴ kg, and the linear speed of the earth around the Sun as (about) 3 × 10⁴ m/s, we have, the de Brogue wave length of the Earth as
λ = \(\frac{h}{p}=\frac{h}{M v}=\frac{6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(6 \times 10^{24} \mathrm{~kg}\right)\left(3 \times 10^{4} \mathrm{~m} / \mathrm{s}\right)}\)
= 3.683 × 10^-63 m (extremely small)

Question 2.
The expression p = E/c defines the momentum of a photon. Can this expression be used for momentum of an electron or proton?
Answer:
No

Remember This (Textbook Page No. 319)

Diffraction results described above can be produced in the laboratory using an electron diffraction tube as shown in figure. It has a filament which on heating produces electrons. This filament acts as a cathode. Electrons are accelerated to quite high speeds by creating large potential difference between the cathode and a positive electrode. On its way, the beam of electrons comes across a thin sheet of

graphite. The electrons are diffracted by the atomic layers in the graphite and form diffraction rings on the phosphor screen. By changing the voltage between the cathode and anode, the energy, and therefore the speed, of the electrons can be changed. This will change the wavelength of the electrons and a change will be seen in the diffraction pattern. By increasing the voltage, the radius of the diffraction rings will decrease. Try to explain why?
Answer:
When the accelerating voltage is increased, the kinetic energy and hence the momentum of the electron increases. This decreases the de Brogue wavelength of the electron. Hence, the radius of the diffraction ring decreases.

Remember This (Textbook Page No. 320)

Question 1.
On what scale or under which circumstances are the wave nature of matter apparent?
Answer:
When the de Brogue wavelength of a particle such as an electron, atom, or molecule is comparable to the interatomic spacing in a crystal, the wave nature of matter is revealed in diffraction/interference.