Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 6 Chemical Kinetics Textbook Exercise Questions and Answers.
Maharashtra State Board Class 12 Chemistry Solutions Chapter 6 Chemical Kinetics
1. Choose the most correct option.
Question i.
The rate law for the reaction aA + bB → P is rate = k[A] [B]. The rate of reaction doubles if
a. concentrations of A and B are both doubled.
b. [A] is doubled and [B] is kept constant
c. [B] is doubled and [A] is halved
d. [A] is kept constant and [B] is halved.
Answer:
b. [A] is doubled and [B] is kept constant
![]()
Question ii.
The order of the reaction for which the units of rate constant are mol dm-3 s-1 is
a. 1
b. 3
c. 0
d. 2
Answer:
c. 0
Question iii.
The rate constant for the reaction 2N2O5(g) → 2N2O4(g) + O2(g) is 4.98 × 10-4 s-1. The order of reaction is
a. 2
b. 1
c. 0
d. 3
Answer:
b. 1
Question iv.
Time required for 90 % completion of a certain first order reaction is t. The time required for 99.9 % completion will be
a. t
b. 2t
c. t/2
d. 3t
Answer:
d. 3t
Question v.
Slope of the graph ln[A]t versus t for first order reaction is
a. -k
b. k
c. k/2. 303
d. -k/2. 303
Answer:
a. -k
Question vi.
What is the half life of a first order reaction if time required to decrease concentration of reactant from 0.8 M to 0.2 M is 12 h?
a. 12 h
b. 3 h
c. 1.5 h
d. 6 h
Answer:
d. 6 h
Question vii.
The reaction, 3ClO3Θ ClO3Θ + 2 ClΘ occurs in two steps,
(i) 2 ClO– → ClO2Θ
(ii) ClO2Θ + ClOΘ → ClO3Θ + ClΘ
The reaction intermediate is
a. ClΘ
b. ClO2Θ
c. ClO3Θ
d. ClOΘ
Answer:
b. ClO2Θ
Question viii.
The elementary reaction O2(g) + O(g) → 2O2(g) is
a. unimolecular and second order
b. bimolecular and first order
c. bimolecular and second order
d. unimolecular and first order
Answer:
c. bimolecular and second order
![]()
Question ix.
Rate law for the reaction, 2NO + Cl2 → 2 NOCl is rate = k[NO2]2[Cl2]. Thus k would increase with
a. increase of temperature
b. increase of concentration of NO
c. increase of concentration of Cl2
d. increase of concentrations of both Cl2 and NO
Answer:
a. increase of temperature
Question x.
For an endothermic reaction, X ⇌ Y. If E f is activation energy of the forward reaction and Er that for reverse reaction, which of the following is correct?
a. Ef = Er
b. Ef < Er
c. Ef > Er
d. ∆H = Ef – Er is negative
Answer:
(c) Ef → Er
2. Answer the following in one or two sentences.
Question i.
For the reaction,
N2(g) + 3 H2(g) → 2NH3(g), what is the relationship among \(\frac{\mathrm{d}\left[\mathrm{N}_{2}\right]}{\mathrm{dt}}\)\(\frac{\mathrm{d}\left[\mathrm{H}_{2}\right]}{\mathrm{dt}} \text { and } \frac{\mathrm{d}\left[\mathrm{NH}_{3}\right]}{\mathrm{dt}} ?\)
Answer:
N2(g) + 3H2(g) → 2NH3(g)
From the above reaction, when 1 mole of N2 reacts, 3 moles of H2 are consumed and 2 moles of NH3 are formed.
If the instantaneous rate R of the reaction is represented in terms of rate of the consumption of N2 then, \(R=-\frac{d\left[\mathrm{~N}_{2}\right]}{d t}\)
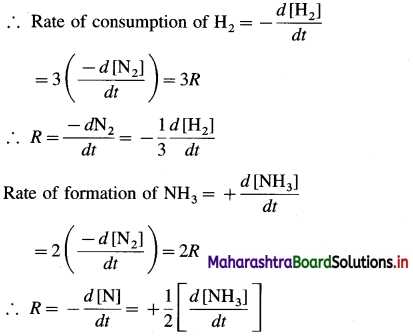
Hence the rate of reaction in terms of concentration changes in N2, H2 and NH3 may be represented as,
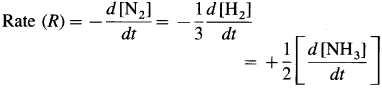
Question ii.
For the reaction,
CH3Br(aq) + OH-(aq) → CH3OHΘ (aq) +BrΘ (aq), rate law is rate = k[CH3Br][OHΘ]
a. How does reaction rate changes if [OHΘ] is decreased by a factor of 5?
b. What is change in rate if concentrations of both reactants are doubled?
Solution :
Given :
(a) Rate = R = k [CH3Br] x [OH–]
If R1 and R2 are initial and final rates of reaction then,

Rate will be increased 4 time.
![]()
Question iii.
What is the relationship between coeffients of reactants in a balanced equation for an overall reaction and exponents in rate law. In what case the coeffients are the exponents?
Answer:
Explanation : Consider the following reaction, aA + bB → products
If the rate of the reaction depends on the concentrations of the reactants A and B, then, by rate law,
R α [A]a [B]b
∴ R = k [A]a [Bb
where [A] = concentration of A and
[B] = concentration of B
The proportionality constant k is called the velocity constant, rate constant or specific rate of the reaction.
a and b are the exponents or the powers of the concentrations of the reactants A and B respectively when observed experimentally.
The exponents or powers may not be necessarily a and b but may be different x and y depending on experimental observations. Then the rate R will be,
R = k [A]x [B]y
For example, if x = 1 and y = 2, then,
R = k [A] x [B]2
Question iv.
Why all collisions between reactant molecules do not lead to a chemical reaction?
Answer:
(i) Collisions of reactant molecules : The basic re-quirements of a reaction is that the reacting species (atoms, ions or molecules) must come together and collide for a reaction to occur. Therefore the rate of the reaction shall depend on the rate and frequency of collisions which increase with the amount of reacting species and temperature.
However it is observed that the rate of reaction is very low as compared to the rate of collisions between reacting species in gaseous phase or liquid phase. This suggests that all the collisions are not fruitful leading to a reaction. Hence it is necessary to consider another factor like energy of colliding species along with collision frequency.
(ii) Energy requirement (Activation energy) : The colliding molecules must possess a certain mini-mum energy called activation energy required far breaking and making bonds resulting in the reaction. This implies that the colliding molecules must have energy equal to or greater than the activation energy. The colliding molecules with less energy do not react.
(iii) Orientation of reactant molecules : The concept of activation energy is satisfactory in case of simple molecules or ions but not in case of complex or higher polyatomic molecules. It is observed that the rates of reaction are less as compared to the rates of collisions between activated molecules with activation energy.
This suggests that in addition, the colliding molecules must have proper orientations relative to each other during collisions. For example, consider the reaction, A – B-l-C → A + B – C. For the reaction to occur, C must collide with B while collisions with A will not be fruitful. Since B has to bond with C.
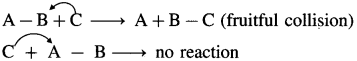
Question v.
What is the activation energy of a reaction?
Answer:
Activation energy : The energy required to form activated complex or transition state from the reactant molecules is called activation energy.
OR
The height of energy barrier in the energy profile diagram is called activation energy.
Question vi.
What are the units for rate constants for zero order and second order reactions if time is expressed in seconds and concentration of reactants in mol/L?
Answer:
(a) For a zero order reaction, the rate constant has units, molL-1s-1.
(b) For second order reaction,
Rate = k x [Reactant]2
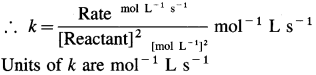
![]()
Question vii.
Write Arrhenius equation and explain the terms involved in it.
Answer:
Arrhenius equation is represented as k = A x e-Ea/RT
where
k = Rate constant at absolute temperature T
Ea = Energy of activation R = Gas constant
A = Frequency factor or pre-exponential factor.
Question viii.
What is the rate determining step?
Answer:
Many chemical reactions take place in a series of elementary steps. Among many steps of the reaction, one of the steps is the slowest step compared to other steps.
Rate determining step : The slowest step in the reaction mechanism which involves many steps is called the rate-determining step.
Question ix.
Write the relationships between rate constant and half life of fist order and zeroth order reactions.
Answer:
(a) For first order reaction, half-life period t1/2 is, \(t_{1 / 2}=\frac{0.693}{k}\) where k is the rate constant.
(b) For zeroth-order reaction, half half period (t1/2) is, \(t_{1 / 2}=\frac{[\mathrm{A}]_{0}}{2 k}\) where k is the rate constant and [A]0 is initial concentration of the reactant.
Question x.
How do half lives of the fist order and zero order reactions change with initial concentration of reactants?
Answer:
(A) For the first order reaction, half life, t1/2 is given by, \(t_{1 / 2}=\frac{0.693}{k}\) where k is rate constant. Hence it is independent of initial concentration of the reactant.
(B) Zero order reaction,
\(t_{1 / 2}=\frac{[\mathrm{A}]_{0}}{2 k}\) where [A]0 is initial concentration of the reactant.
Hence, half life period increases with the increase in concentration of the reactant.
3. Answer the following in brief.
Question i.
How instantaneous rate of reaction is determined?
Answer:
(1) The instantaneous rate is expressed as an infinite¬simal change in concentration (- dc) of the reactant with the infinitesimal change in time (dt).
For a reaction, A → B, let an infinitesimal change in A be – dc in time dt, then Rate \(=\frac{d[\mathrm{~A}]}{d t}\).
Hence, it is represented as,
∴ Instantaneous rate \(=-\frac{d[\mathrm{~A}]}{d t}\)
The negative sign indicates a decrease in the concentration of A.
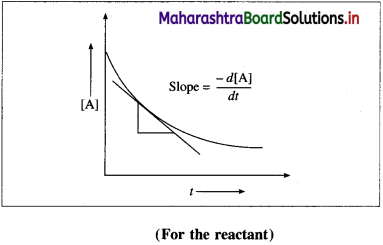
It is obtained by drawing a tangent to the curve obtained by plotting the concentration against the time. Hence, the slope at a given point represents the instantaneous rate of the reaction.
(2) The instantaneous rate can also be expressed as an infinitesimal change (or increase) in the concentration of the product with the infinitesimal change in time (dt).
Let dB be an infinitesimal change in the concentration of product B in time dt, then Rate \(=\frac{d[\mathrm{~B}]}{d t}=\frac{d x}{d t}\).
![]()
Hence,
Instantaneous rate \(=\frac{d x}{d t}\)
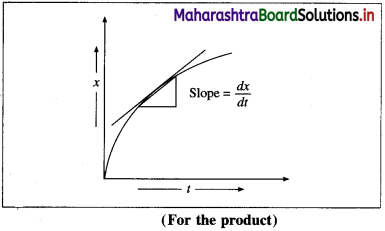
It is obtained from the slope of the curve obtained by plotting the concentration of the product against time.
The instantaneous rate is more useful in obtaining the rate law integrated equations.
Question ii.
Distinguish between order and molecularity of a reaction.
Answer:
| Order | Molecularity |
| 1. It is the sum of the exponents to which the concentration terms in rate law expression are raised. | 1. ¡t is the number of molecules (or atoms or ions) of the reaCtants taking part in the elementary reaction. |
| 2. It is experimentally determined and indicates the dependence of the reaction rate on the concentration of particular reactants. | 2. It is the oretical property and indicátes the number of molecules of reactant in each step of the reaction. |
| 3. It may have values that are integer, fractional, or zero. | 3. It is always an integer. |
| 4. Its value depends upon experimental conditions. | 4. Its value does not depend upon experimental conditions. |
| 5. It is the property of elementary and complex reactions. | 5. It is the property of elementary reactions only. |
| 6. Rate law expression describes the order of the reaction. | 6. Rate law does not describe molecularity. |
Question iii.
A reaction takes place in two steps,
1. NO(g) + Cl2(g) NOCl2(g)
2. NOCl2(g) + NO(g) → 2NOCl(g)
a. Write the overall reaction.
b. Identify reaction intermediate.
c. What is the molecularity of each step?
Solution :
Given :
(1) NO(g) + Cl2(g) → NOCl2(g)
(2) NOCl2(g) + NO(g) → 2NOCl(g)
(a) Overall reaction is obtained by adding both the reactions
2NO(g) + Cl2(g) → 2NOCl2(g)
(b) The reaction intermediate is NOCl2, since it is formed in first step and consumed in the second step.
(c) Since the first step is a slow and rate determining step, the molecularity is two.
Since the second step is a fast step its molecularity is not considered.
Question iv.
Obtain the relationship between the rate constant and half-life of a fist order reaction.
Answer:
Consider the following reaction,
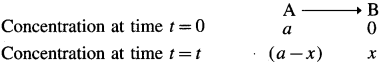
If [A]0 and [A]t are the concentrations of A at start and after time t, then [A]0 = a and [A]t = a – x.
The velocity constant or the specific rate constant k for the first order reaction can be represented as,
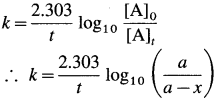
where, a is the initial concentration of the reactant A, x is the concentration of the product B after time t, so that (a – x) is the concentration of the reactant A after time t.
![]()
Half-life of a reaction : The time required to reduce the concentration of the reactant to half of its initial value is called the half-life period or the half-life of the reaction.
If t1/2 is the half-life of a reaction, then at t = t1/2, x = a/2, hence a – x = a – a/2 = a/2

Hence, for a first order reaction, the half-life of the reaction is independent of the initial concentration of the reactant.
Question v.
How will you represent zeroth-order reaction graphically?
Answer:
(1) A graph of concentration against time : In case of a zero-order reaction, the rate of reaction is independent of the concentration of the reactant. The concentration [A]t of the reactant at a time t is given by
[A]t = – kt + [A]0 (y = – mx + c)
where [A]0 is the initial concentration of the reactant and k is a rate constant.
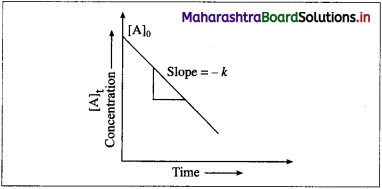
Hence in case of zero order reaction, when the concentration of the reactant is plotted against time, a straight line with the slope equal to – k is obtained. The concentration of the reactants de-crease with time. The intercept on the concentration axis gives the initial concentration, [A]0.
(2) A graph of rate of a reaction against the concen-tration of the reactant: Rate of a zero order reaction is independent of the concentration of the reactant.
![]()
Rate, R = k [A]0 = k
Hence even if the concentration of the reactant decreases, the rate of the reaction remains constant.
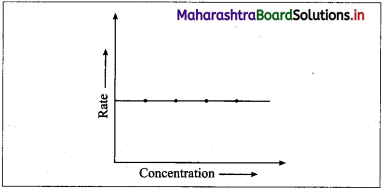
Therefore if the rate of a zero order reaction is plotted against concentration, then a straight line with zero slope is obtained indicating, no change in the rate of the reaction with a change in the concentration of the reactants.
(3) A graph of half-life period against concentration : The half-life period of a zero-order reaction is given by, \(t_{1 / 2}=\frac{[\mathrm{A}]_{0}}{2 k}\) where [A]0 is initial con-centration of the reactant and k is the rate constant. Hence the half-life period is directly proportional to the concentration.
When a graph of t1/2 is plotted against concentration, a straight line passing through origin is obtained, and the slope gives \(\frac{1}{2 k}\), where k is the rate constant.

Question vi.
What are pseudo-fist order reactions? Give one example and explain why it is pseudo-fist order.
Answer:
Pseudo-first-order reaction : A reaction which has higher-order true rate law but is experimentally found to behave as first order is called pseudo first order reaction.
Explanation : Consider an acid hydrolysis reaction of an ester like methyl acetate.
CH3COOCH3(aq) + H2O(1) \(\stackrel{\mathrm{H}_{(\mathrm{aq})}^{+}}{\longrightarrow}\) CH3COOH(aq) + CH3OH(aq)
Since the reaction involves two substances, ester and water, it is a bimolecular reaction and the true rate law should be, Rate = k’ [CH3COOCH3] x [H2O]
Hence the reaction is expected to follow second order kinetics. However experimentally it is found that the reaction follows first order kinetics.
This is because solvent water being in a large excess, its concentration remains constant. Hence, [H2O] = constant = k”
Rate = k [CH3COOCH3] x [H2O]
= k [CH3COOCH3] x k”
= k’ x k” x [CH3COOCH3]
If k’ x k” = k, then Rate = k [CH3COOCH3],
This indicates that second-order true rate law is forced into first order rate law. Therefore this bimolecular reaction which appears of second order is called pseudo first order reaction.
Question vii.
What are the requirements for the colliding reactant molecules to lead to products?
Answer:
Collisions of reactant molecules : The basic requirements of a reaction is that the reacting species (atoms, ions or molecules) must come together and collide for a reaction to occur. Therefore the rate of the reaction shall depend on the rate and frequency of collisions which increase with the amount of reacting species and temperature.
![]()
However it is observed that the rate of reaction is very low as compared to the rate of collisions between reacting species in gaseous phase or liquid phase. This suggests that all the collisions are not fruitful leading to a reaction. Hence it is necessary to consider another factor like energy of colliding species along with collision frequency.
Energy requirement (Activation energy) : The colliding molecules must possess a certain minimum energy called activation energy required far breaking and making bonds resulting in the reaction. This implies that the colliding molecules must have energy equal to or greater than the activation energy. The colliding molecules with less energy do not react.
Orientation of reactant molecules : The concept of activation energy is satisfactory in case of simple molecules or ions but not in case of complex or higher polyatomic molecules. It is observed that the rates of reaction are less as compared to the rates of collisions between activated molecules with activation energy.
This suggests that in addition, the colliding molecules must have proper orientations relative to each other during collisions. For example, consider the reaction, A – B + C → A + B – C. For the reaction to occur, C must collide with B while collisions with A will not be fruitful. Since B has to bond with C.
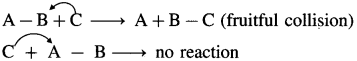
Question viii.
How catalyst increases the rate of reaction? Explain with the help of a potential energy diagram for catalyzed and uncatalyzed reactions.
Answer:
(i) A catalyst is a substance, when added to the reactants, increases the rate of the reaction without being consumed. For example, the decomposition of KClO3 in the presence of small amount of MnO2 is very fast but very slow in the absence of MnO2.
2KClO3(s) \(\frac{\mathrm{MnO}_{2}}{\Delta}\) 2KCl(s) + 3O2(g)
(ii) The phenomenon of catalysed reaction is called catalysis and depends on nature of the catalyst. In heterogeneous catalysis, the reactant molecules are adsorbed on the solid catalyst surface while in case of homogeneous catalysis, the catalyst reacts with one of the reactants, forms intermediate and decomposes reforming original catalyst and the products.
(iii) The catalyst provides alternative and lower energy path or mechanism for the reaction.
(iv) In the presence of the catalyst, the activation energy of the reaction is lowered. The height of activation energy barrier is less than that in the uncatalysed reaction.
(v) Due to lowering of energy of activation, (Ea) the number of molecules possessing Ea increases, hence the rate of the reaction increases.
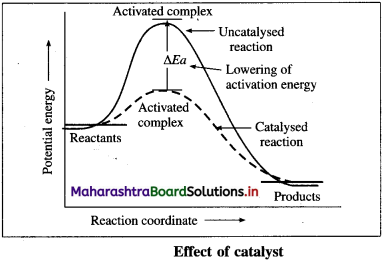
(vi) The rate constant = k = A x e-Ea/RT where A is a frequency factor and hence the rates of the catalysed reaction are higher than those of un-catalysed reactions.
(vii) The catalyst does not change the extent of the reaction but hastens the reaction.
(viii) The catalyst enters the reaction but does not appear in the balanced equation since it is consumed in one step and regenerated in the another.
Question ix.
Explain with the help of the Arrhenius equation, how does the rate of reaction changes with (a) temperature and (b) activation energy.
Answer:
(a) By Arrhenius equation, k = Ax e-Ea/RT where k is rate constant, A is a frequency factor and Ed is energy of activation at temperature T. As Ea increases, the rate constant and rate of the reaction decreases.
(b) As temperature increases Ea/RT decreases but due to negative sign, k and rate increase with the increase in temperature.
![]()
Question x.
Derive the integrated rate law for first order reaction.
Answer:
Consider following gas phase reaction,
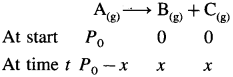
Let initial pressure of A be P0 at t = 0. If after time t the pressure of a A decreases by jc then the partial pressures of the substances will be, PA = PQ – x; PB = x and Pc = x
Total pressure will be,
PT + P0 – x + x + x = Po + x
∴ x = PT – Pn
The partial pressures at time t will be,
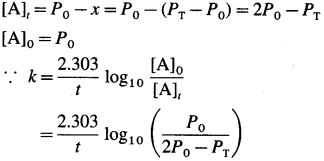
Question xi.
How will you represent first-order reactions graphically.
Answer:
(1) A graph of rate of a reaction and concentration : The differential rate law for first-order reaction, A → Products is represented as, Rate = [/latex]-\frac{d[\mathrm{~A}]}{d t}=k[\mathrm{~A}]\(
∴ Rate = k x [A]t (y = mx). When the rate of a first order reaction is plotted against concentration, [A]t, a straight line graph is obtained.
With the increase in the concentration [A]t, rate R, increases. The slope of the line gives the value of rate constant k.
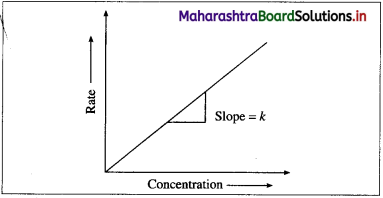
(2) A graph of concentration against time : When the concentration of the reactant is plotted against time t, a curve is obtained. The concentration [A], of the reactant decreases exponentially with time. The variation in the concentration can be represented as,

where [A]0 and [A]t are initial and final concentrations the reactant and k is the rate constant. The time required to complete the first order reaction is infinity.
(3) A graph of log10 (a – x) against time t :
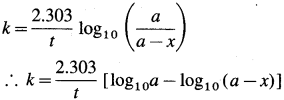

When log10(a – x) is plotted against time t, a straight line with negative slope is obtained, from which the velocity constant k can be calculated.
![]()
(4) A graph of half-life period and concentration : The half-life period, t1/2 of a first order reaction is given by, where k is the rate constant.
For the given reaction at a constant temperature, t1/2 is constant and independent of the concentration of the reactant.
Hence when a graph of t1/2 is plotted against concentration, a straight line parallel to the concentration axis (slope = zero) is obtained.

(5) A graph of log10 [latex]\left(\frac{a}{a-x}\right)\) against time : The rate constant, for a first order reaction is represented as,  where [A0] and [A]t are the respective initial and final concentrations of the reactant after time t.
where [A0] and [A]t are the respective initial and final concentrations of the reactant after time t.


When \(\log _{10}\left(\frac{a}{a-x}\right)\) is plotted against time t, a straight line graph passing through the origin is obtained and the slope gives the value of k/2.303. From this slope, the rate constant can be calculated.
Question xii.
Derive the integrated rate law for the first order reaction, A(g) → B(g) + C(g) in terms of pressure.
Answer:
Consider following gas phase reaction,
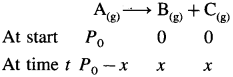
Let initial pressure of A be P0 at t = 0. If after time t the pressure of a A decreases by jc then the partial pressures of the substances will be, PA = PQ – x; PB = x and Pc = x
Total pressure will be,
PT + P0 – x + x + x = Po + x
∴ x = PT – Pn
The partial pressures at time t will be,
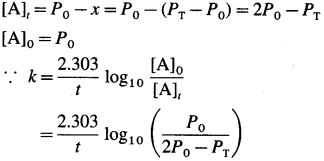
![]()
Question xiii.
What is zeroth-order reaction? Derive its integrated rate law. What are the units of rate constant?
Answer:
Definition : Zero order reaction : A reaction in which the rate of the reaction does not depend on the concentration of any reactant taking part in the reaction is called zero order reaction.
Consider a zero order reaction, A → Products
The rate of the reaction is, Rate \(=\frac{-d[\mathrm{~A}]}{d t}\)
By rate law,
Rate = k x [A]0 = k
∴ – d[A] = k x dt
If [A]0 is the initial concentration of the reactant A at t = 0 and [A]t is the concentration of A present after time t, then by integrating above equation,

This is the integrated rate law expression for rate constant for zero order reaction.
∴ k x t = [A]0 – [A]t
∴ [A]t = – kt + A0
For a zero order reaction :
The rate of reaction is R = k [A]0 = k
Hence, the velocity constant k has the unit of the rate of the reaction, i.e., mol dm-3 s-1.
Question xiv.
How will you determine activation energy: (a) graphically using Arrhenius equation (b) from rate constants at two different temperatures?
Answer:
(a) By Arrhenius equation,
Rate constant = = A x e-Ea/RT where A is a fre-quency factor.
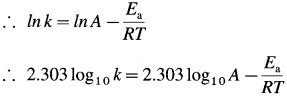
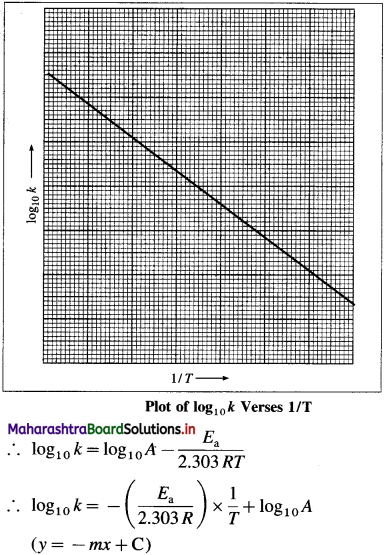
![]()
When log10k is plotted against 1/T a straight line with negative slope is obtained. From the slope of the graph, energy of activation Ea, is obtained as follows :
Slope = \(\frac{E_{\mathrm{a}}}{2.303 R}\)
∴ Ea = 2303R x sloPe
(b) For the given reaction, rate constants k1 and k2 are measured at two different temperatures T1 and T2 respectively. Then \(\log _{10} \frac{k_{2}}{k_{1}}=\frac{E_{\mathrm{a}}\left(T_{2}-T_{1}\right)}{2.303 R \times T_{1} \times T_{2}}\) where Ea is the energy of activation.
Hence by substituting appropriate values, energy of activation Ea for the reaction is determined.
Question xv.
Explain graphically the effect of temperature on the rate of reaction.
Answer:
(i) It has been observed that the rates of chemical reactions increase with the increase in temperature.
(ii) The kinetic energy of the molecules increases with the increase in temperature. The fraction of molecules possessing minimum energy barrier,
i. e. activation energy Ea increases with increase in temperature.
(iii) Hence the fraction of colliding molecules that possess kinetic energy (Ea) also increases, hence the rate of the reaction increases with increase in temperature.
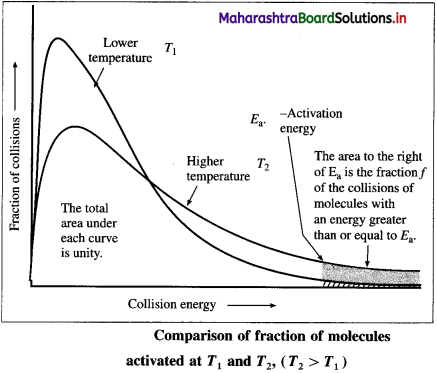
(iv) The above figure shows that the area that represents the fraction of molecules with kinetic energy exceeding Ea is greater at higher temperature T2 than at lower temperature T1. This explains that the rate of the reaction increases at higher temperature.
(v) The shaded area to the right of activation energy Ea represents fraction of collisions of activated molecules having energy Ea or greater.
Question xvi.
Explain graphically the effect of catalyst on the rate of reaction.
Answer:
(i) The phenomenon of catalysed reaction is called catalysis and depends on nature of the catalyst. In heterogeneous catalysis, the reactant molecules are adsorbed on the solid catalyst surface while in case of homogeneous catalysis, the catalyst reacts with one of the reactants, forms intermediate and decomposes reforming original catalyst and the products.
(ii) The catalyst provides alternative and lower energy path or mechanism for the reaction.
(iii) In the presence of the catalyst, the activation energy of the reaction is lowered. The height of activation energy barrier is less than that in the uncatalysed reaction.
![]()
Question xvii.
For the reaction 2A + B → products, find the rate law from the following data.
| [A]/M | [A]/M | rate/M s-1 |
| 0.3 | 0.05 | 0.15 |
| 0.6 | 0.05 | 0.30 |
| 0.6 | 0.2 | 1.20 |
Solution :
Given : 2A + B → Products
Rates : R1 = 0.15 Ms-1 R2 = 0.3 Ms-1
[A]1 = 0.3 M [A]2 = 0.6 M
[B]1 = 0.05 M [B]2 = 0.05 M
(i) If order of the reaction in A is x and in B is y then, by rate law,

∴ y = 1. Hence the reaction has order one in B.
The order of overall reaction = n = nA + nB = 1 + 1 = 2

Answer:
(i) Rate law : Rate = fc [A] x [B]
Rate constant = k = 10M-1s-1
Order of the reaction = 2
![]()
4. Solve
Question i.
In a first order reaction, the concentration of reactant decreases from 20 mmol dm-3 to 8 mmol dm-3 in 38 minutes. What is the half life of reaction? (28.7 min)
Solution :
Given: [A]0 =20 mmol dm-3;
[A]t=8 mmol dm-3; t=38 mm;

Answer:
Half life period = 28.74 min
Question ii.
The half life of a first order reaction is 1.7 hours. How long will it take for 20% of the reactant to react? (32.9 min)
Solution :
Given : t1/2 = 1.7 hr; [A]0 = 100;
[A]t = 100 – 20 = 80; t =?
\(t_{1 / 2}=\frac{0.693}{k}\)

Answer:
Time required = t = 32.86 min
![]()
Question iii.
The energy of activation for a first order reaction is 104 kJ/mol. The rate constant at 25 0C is 3.7 × 10-5 s-1. What is the rate constant at 300C? (R = 8.314 J/K mol) (7.4 × 10-5)
Solution :

Answer:
k2 = 7.382 x 10-5 s-1
Question iv.
What is the energy of activation of a reaction whose rate constant doubles when the temperature changes from 303 K to 313 K? (54.66 kJ/mol)
Solution :
Given : k2 = 2kt, T1 = 303 K; T2 = 313 K; Ea = ?

Answer:
Energy of activation = Ea = 54.66 kJ
Question v.
The rate constant of a reaction at 5000C is 1.6 × 103 M-1 s-1. What is the frequency factor of the reaction if its activation energy is 56 kJ/mol. (9.72 × 106 M-1 s-1)
Solution :

Answer:
Frequency factor = A = 9.727 x 106 M-1s-1
![]()
Question vi.
Show that time required for 99.9% completion of a first order reaction is three times the time required for 90% completion.
Solution :
Given : For 99.9 % completion, if [A]0 = 100,

If t1 and t2 are the times required for 99.9 % and 90 % completion of reaction respectively, then
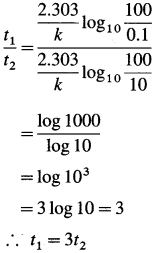
Answer:
Time required for 99.9 % completion of a first order reaction is three time the time required for 90 % completion of the reaction.
Question vii.
A first order reaction takes 40 minutes for 30% decomposition. Calculate its half life. (77.66 min)
Solution :

Answer:
Half life period = 77.70 min.
![]()
Question viii.
The rate constant for the first order reaction is given by log10 k = 14.34 – 1.25 × 104 T. Calculate activation energy of the reaction. (239.3 kJ/mol)
Solution :
Given : log10 k = 14.34 – \(\frac{1.25 \times 10^{4}}{T}\) ……………………. (1)
From Arrhenius equation we can write,
\(\log _{10} k=\log _{10} A-\frac{E_{\mathrm{a}}}{2.303 R \times T}\) ……………………. (2)
By comparing equations (1) and (2),
\(\frac{E_{\mathrm{a}}}{2.303 \times R}\) = 1.25 x 104
∴ Ea = 1.25 x 104 x 2.303 x R
= 1.25 x 104 x 2.303 x 8.314
= 23.93 x 104 = 239.3 kJ mol-1
[Note : Frequency factor A may also be calculated as follows : log10 A = 14.34
∴ A = Antilog 14.34 = 2.188 x 104
Answer:
Energy of activation = Ea = 239.3 kJ mol-1.
Question ix.
What fraction of molecules in a gas at 300 K collide with an energy equal to activation energy of 50 kJ/mol? (2 × 10-9)
Solution :
Given : T = 300 K; Ea = 50 kJ mol-1
= 50 x 103 mol-1
The fraction of molecules undergoing fruitful collisions is

Answer:
Fraction of molecules undergoing collision = 2 x 10-9
Activity :
1. If you wish to determine the reaction order and rate constant for the reaction, 2AB2 → A2 + 2B2.
a) What data would you collect?
b) How would you use these data to determine whether the reaction is zeroth or first order?
2. The activation energy for two reactions are Ea and E’a with Ea > E’a. If the temperature of reacting system increases from T1 to T2, predict which of the following is correct?
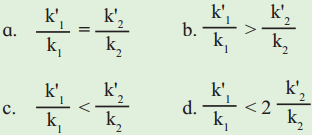
k values are rate constants at lower temperatures and k values at higher temperatures.
12th Chemistry Digest Chapter 6 Chemical Kinetics Intext Questions and Answers
(Textbook Page No 121)
Question 1.
Write the expressions for rates of reaction for :
2N2O5(g) → 4NO2(g) + O2(g)?
Answer:
For the given reaction, Rate of reaction =
\(=R=-\frac{1}{2} \frac{d\left[\mathrm{~N}_{2} \mathrm{O}_{5}\right]}{d t}\)
\(\begin{aligned}
&=+\frac{1}{4} \frac{d\left[\mathrm{NO}_{2}\right]}{d t} \\
&=+\frac{d\left[\mathrm{O}_{2}\right]}{d t}
\end{aligned}\)
![]()
Problem 6.1: (Textbook Page No 121)
Question 1.
For the reaction,
\(\mathbf{3 I}_{(a q)}^{-}+\mathbf{S}_{2} \mathbf{O}_{8(a q)}^{2-} \longrightarrow \mathbf{I}_{3(\text { (aq) }}^{-}+2 \mathbf{S O}_{4(\mathrm{aq})}^{2-}\)
Calculate (a) the rate of formation of I3–,
(b) the rates of consumption of 1 and S2O and (c) the overall rate of reaction if the rate of formation of \(\mathrm{SO}_{4}^{2-}\) is 0.O22 moles dm-3 sec-1.
Answer:
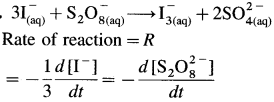

∴ (a) Rate of formation of \(\mathrm{I}_{3}^{-}\) = 0.011 mol dm-3 s-1
(b) Rate of consumption of I– = 0.033 mol dm-3 s-1
(c) Rate of consumption of \(\mathrm{S}_{2} \mathrm{O}_{8}^{2-}\) = 0.011 mol dm-3 s-1
(d) Overall rate of reaction = Rate of consumption of reactant = Rate of formation of product
Try this….. (Textbook Page No 122)
Question 1.
For the reaction :
NO2(g) + CO(g) → NO(g) + CO2(g), the rate of reaction is experimentally found to be proportional to the square of the concentration of NO2 and independent that of CO. Write the rate law.
Answer:
Since the rate of the reaction is proportional to [NO2]2 and [CO]0, the rate law is R = k[NO2]2 x [CO]0
∴ R = k[NO2]2.
![]()
Try this….. (Textbook Page No 124)
Question 1.
The reaction,
CHCl3(g) + Cl2(g) → CCl4(g) + HCl(g) is first order in CHCl3 and 1/2 order in Cl2. Write the rate law and overall order of reaction.
Answer:
Since the reaction is first order in CHCl3 and 1/2 order in Cl2, the rate law for the reaction will be, Rate = k[CHCl3] X [Cl2]1/2
The overall order (n) of the reaction will be, n = l + = \(\frac{1}{2}=\frac{3}{2}\)
Use your brain power! (Textbook Page No 124)
Question 1.
The rate of the reaction 2A + B → 2C + D is 6 x 10-4 mol dm-3 s-1 when [A] =[B] = O.3 mol dm-3 If the reaction is of first order in A and zeroth order in B, what is the rate constant?
Answer:
For the reaction,
2A + B → 2C + D,

(Problem 6.7) (Textbook Page No 126)
Question 1.
A reaction occurs in the following steps :
(i) NO2(g) + F2(g) → NO2F(g) + F(g) (slow)
(ii) F(g) + NO2(g) → NO2F(g) (fast)
(a) Write the equation of overall reaction.
(b) Write down rate law.
(c) Identify the reaction intermediate.
Solution :
(a) The addition of two steps gives the overall reaction as
2NO2(g) + F2(g) → 2NO2 F(g)
(b) Step (i) is slow. The rate law of the reaction is predicted from its stoichiometry. Thus, rate = k [NO2] [F2]
(c) F is produced in step (i) and consumed in step (ii) hence F is the reaction intermediate.
![]()
Try this….. (Textbook Page No 126)
Question 1.
A complex reaction takes place in two steps :
(i) NO(g) + O3(g) → NO3(g) + O(g)
(ii) NO3(g) + O(g) → NO2(g) + O2(g)
The predicted rate law is rate = k [NO] [O3]. Identify the rate-determining step. Write the overall reaction. Which is the reaction inter-mediate? Why?
Answer:
(i) NO(g) + O3(g) → NO3(g) + O(g)
(ii) NO3(g) + O(g) → NO2(g) + O2(g)
(a) The first step is slow and rate determining step since the rate depends on concentrations of NO(g) and O3(g). (Given : Rate = k [NO] x [O])
(b) The overall reaction is the combination of two steps.
NO(g) + O3(g) → NO2(g) + O2(g)
(c) NO3(g) and O(g) are reaction intermediates. They are formed in first step (i) and removed in the second step (ii).
Try this….. (Textbook Page No 129)
Question 1.
The half-life of a first-order reaction is 0.5 min. Calculate (a) time needed for the reactant to reduce to 20% and (b) the amount decomposed in 55 s.
Answer:

Try this….. (Textbook Page No 123)
Question 1.
For the reaction 2A + 2B → 2C + D, if concentration of A is doubled at constant [B] the rate increases by a factor of 4. If the concentration of B is doubled with [A] being constant the rate is doubled. Write the rate law of the reaction.
Answer:
Rate = R1 = k[A]x [B]y
When concentration of A = [2A] and

Hence order with respect to A is 2 and with respect to B is 1. By rate law,
Rate = A: [A]2 [B]
![]()
Question 2.
The rate law for the reaction A + B → C is found to be rate = k [A]2 x [B]. The rate constant of the reaction at 25 °C is 6.25 M-2 S-1. What is the rate of reaction when [A] = 1.0 mol dm-3 and [B] = 0.2 mol dm-3?
Answer:
Rate = k x [A]2 x [B]
= 6.25 x 12 x 0.2
Rate = 1.25 x 102 mol dm-3 s-1