Class 12

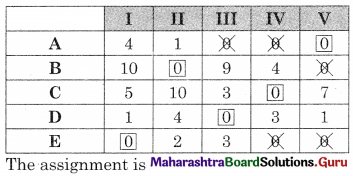
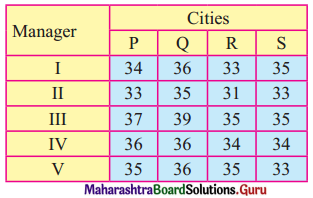
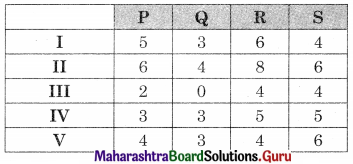
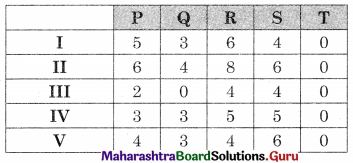
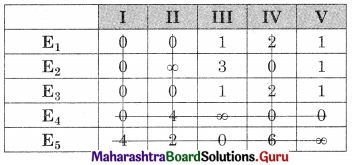
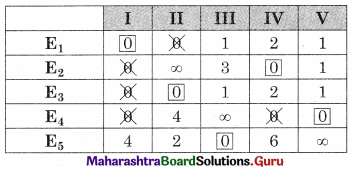
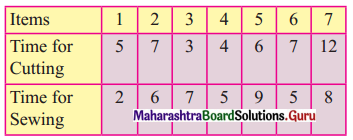
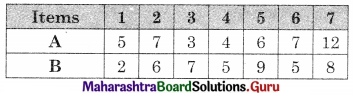
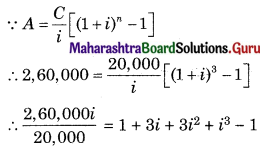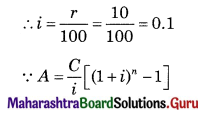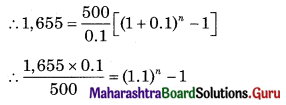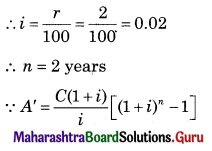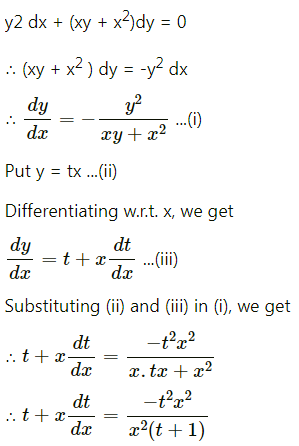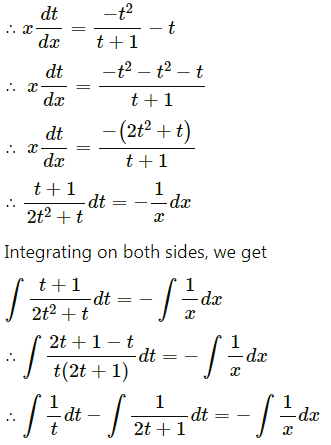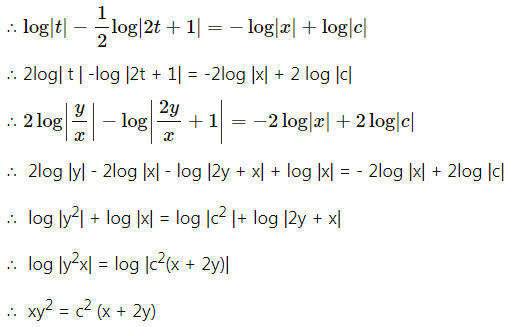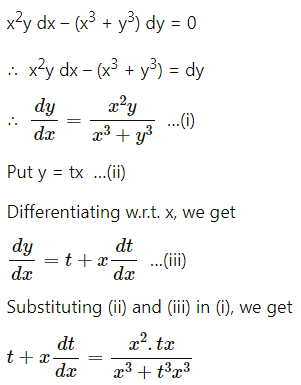Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 1 Commission, Brokerage and Discount Ex 1.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Commission, Brokerage and Discount Ex 1.1

Question 1.
An agent charges a 12% commission on the sales. What does he earn if the total sale amounts to ₹ 48,000? What does the seller get?
Solution:
Rate of commission = 12%
Total sales = ₹ 48,000
Agent’s commission = \(\frac {12}{100}\) × 48,000
= ₹ 5,760
Amount received by the seller = Total sales – commission
= ₹ 8,000 – ₹ 5760
= ₹ 2,240

Question 2.
A salesman receives a 3% commission on sales up to ₹ 50,000 and a 4% commission on sales over ₹ 50,000. Find his total income on the sale of ₹ 2,00,000.
Solution:
Total sales = ₹ 2,00,000
Rate of commission upto ₹ 50,000 = 3%
= \(\frac{3}{100}\) × 50,000
= ₹ 1,500
Rate of commission on the sales over ₹ 50,000 = 4%
Sales over ₹ 50,000 is 2,00,000 – 50,000 = ₹ 1,50,000
Commission on sales over ₹ 50,000 = \(\frac{4}{100}\) × 1,50,000 = ₹ 6,000
His total income = ₹ 1,500 + ₹ 6,000 = ₹ 7,500

Question 3.
Ms. Saraswati was paid ₹ 88,000 as commission on the sale of computers at the rate of 12.5%. If the price of each computer was ₹ 32,000, how many computers did she sell?
Solution:
Total commission = ₹ 88,000
Rate of commission = 12.5%
Let the number of computers sold be x
since price of each computer = ₹ 32,000
Total sales = ₹ 32,000x
Total commission = 12.5% of total sales
88,000 = \(\frac{12.5}{100}\) × 32,000x
= \(\frac{125}{1000}\) × 32,000x
x = \(\frac{88,000}{125 \times 32}\)
x = 22

Question 4.
Anita is allowed 6.5% commission on the total sales made by her, plus, a bonus of \(\frac{1}{2}\)% on the sale over ₹ 20,000. If her total commission amounts to ₹ 3,400. Find the sales made by her.
Solution:
Let the total sales made by Anita be ₹ x
Rate of commission = 6.5% of total sales
= \(\frac{6.5}{100} \times x\)
= \(\frac{65 x}{1,000}\)
= \(\frac{13 x}{200}\)

Question 5.
Priya gets a salary of ₹ 15,000 per month and a commission of 8% on sales over ₹ 50,000. If she gets ₹ 17,400 in a certain month. Find the sales made by her in that month.
Solution:
Let the total sales made by Priya be ₹ x
Salary of Priya = ₹ 15,000
Commission = Total earning – salary
= ₹ 17,400 – ₹ 15,000
= ₹ 2,400
Commission = 8% on the sales over ₹ 50,000
2400 = \(\frac{8}{100}\) (x – 50000)
\(\frac{2,400 \times 100}{8}\) = x – 50,000
30,000 = x – 50,000
30,000 + 50,000 = x
∴ x = ₹ 80,000

Question 6.
The income of the broker remains unchanged though the rate of commission is increased from 4% to 5%. Find the percentage reduction in the value of the business.
Solution:
Let the original value of business be ₹ 100
Original rate of commission = 4%
∴ Original commission = \(\frac{4}{100}\) × 100 = ₹ 4
Let the new value of business be ₹ x
The new rate of commission = 5%
∴ New commission = \(\frac{5}{100}\) × x = \(\frac{x}{20}\)
Given, original income = New income
4 = \(\frac{x}{20}\)
∴ x = ₹ 80
Thus there is 20% reduction in the value of the business.

Question 7.
Mr. Pavan is paid a fixed weekly salary plus commission based on a percentage of sales made by him. If on the sale of ₹ 68,000 and ₹ 73,000 in two successive weeks, he received in all ₹ 9,880 and ₹ 10,180. Find his weekly salary and the rate of commission paid to him.
Solution:
Let the weekly salary of Mr. Pavan be ₹ x and the rate of commission paid to him be y%
Income = Weekly salary + Commission on the sales
∴ 9,880 = x + \(\frac{y}{100}\) × 68,000
i.e. 9,880 = x + 680y …….(1)
Also, 10,180 = x + \(\frac{y}{100}\) × 73,000
i.e 10,180 = x + 730y ………(2)
Subtracting (1) from (2), we get
50y = 300
∴ y = 6
Substituting y = 6 in equation (1)
9,880 = x + 680(6) ‘
∴ 9,880 – 4,080 = x
∴ x = 5,800
Weekly salary = ₹ 5,800
Rate of commission = 6%

Question 8.
Deepak’s salary was increased from ₹ 4,000 to ₹ 5,000. The sales being the same, due to a reduction in the rate of commission from 3% to 2%, his income remained unchanged. Find his sales.
Solution:
Let Deepak’s total sales be ₹ x
Original salary of Deepak = ₹ 4,000
Original rate of commission = 3%
His new salary = ₹ 5,000
New rate of commission = 2%
Original income = New income (given)
4000 + \(\frac{3 x}{100}\) = 5000 + \(\frac{2 x}{100}\)
\(\frac{3 x}{100}-\frac{2 x}{100}\) = 5,000 – 4,000
\(\frac{x}{100}\) = 1000
x = ₹ 1,00,000
∴ His total sales = ₹ 1,00,000

Question 9.
An agent is paid a commission of 7% on cash sales and 5% on credit sales made by him. If on the sale of ₹ 1,02,000 the agent claims a total commission of ₹ 6,420, find his cash sales and credit sales.
Solution:
Total Sales = ₹ 1,02,000
Let cash sales ₹ x
∴ Credit sales = ₹ (1,02,000 – x)
Agent’s commission on cash sales = 7%
= \(\frac{7}{100}\) × x
= \(\frac{7x}{100}\)
Commission on credit sales = 5%
= \(\frac{5}{100}\)(1,02,000 – x)
Given, Total commission = ₹ 6,420
∴ \(\frac{7x}{100}\) + \(\frac{5}{100}\)(1,02,000 – x) = 6420
∴ \(\frac{7x}{100}\) + 5100 – \(\frac{5x}{100}\) = 6,420
∴ \(\frac{2x}{100}\) = 6,420 – 5,100
∴ \(\frac{2x}{100}\) = 1320
∴ x = ₹ 66,000
∴ Cash sales = ₹ 66,000
∴ Credit sales = 1,02000 – 66,000 = ₹ 36,000

Question 10.
Three cars were sold through an agent for ₹ 2,40,000, ₹ 2,22,000 and ₹ 2,25,000 respectively. The rates of the commission were 17.5% on the first, 12.5% on the second. If the agent overall received 14% commission on the total sales, find the rate of commission paid on the third car.
Solution:
Total selling price of three cars = 2,40,000 + 2,22,000 + 2,25,000 = ₹ 6,87,000
Commission on total sales = 14%
= \(\frac{14}{100}\) × 6,87,000
= ₹ 96,180
Selling price of first car = ₹ 2,40,000
Rate of commission = 17.5% = \(\frac{17.5}{100}\) × 2,40,000
∴ Commission on first car = ₹ 42,000
Selling price of second car = ₹ 2,22,000
Rate of commission = 12.5% = \(\frac{12.5}{100}\) × 2,22,000
∴ Commission on second car = ₹ 27,750
Selling price of third car = ₹ 2,25,000
Let the rate of commission be x%
Commission on third car = \(\frac{x}{100}\) × 2,25,000
96,180 – (42,000 + 27,750) = \(\frac{x}{100}\) × 2,25,000
\(\frac{26,430 \times 100}{2,25,000}\) = x
∴ x = 11.75
∴ Rate of commission on the third car = 11.75%

Question 11.
Swatantra Distributors allows a 15% discount on the list price of the washing machines. Further 5% discount is giver for cash payment. Find the list price of the washing machine if it was sold for the net amount of ₹ 38,356.25.
Solution:
Let the list price of the washing machine be ₹ 100
Trade discount = 15% = \(\frac{15}{100}\) × 100 = ₹ 15
∴ Invoice price =100 – 15 = ₹ 85
Cash discount = 5% = \(\frac{5}{100}\) × 85 = ₹ 4.25
∴ Net price = 85 – 4.25 = ₹ 80.75
Thus if List price is 100 than Net price is 80.75
if List price is x than Net price is 38,356.25.
∴ x = \(\frac{38356.25 \times 100}{80.75}\)
∴ x = ₹ 47,500
The list price of the washing machine is ₹ 47,500

Question 12.
A bookseller received ₹ 1,530 as a 15% commission on the list price. Find the list price of the books.
Solution:
Let the list price of the books be ₹ x
Rate of commission = 15%
Book seller’s commission = ₹ 1,530
∴ \(\frac{15}{100}\) × x = 1,530
∴ x = \(\frac{1,530 \times 100}{15}\)
∴ x = ₹ 10,200

Question 13.
A retailer sold a suit for ₹ 8,832 after allowing an 8% discount on market price and a further 4% cash discount. If he made 38% profit, find the cost price and the market price of the suit.
Solution:
Let the marked price of the suit be ₹ 100
Trade discount = 8% = \(\frac{8}{100}\) × 100 = ₹ 8
Invoice price = 100 – 8 = ₹ 92
Cash discount = 4% = \(\frac{4}{100}\) × 92 = ₹ 3.68
∴ Net price = 92 – 3.68 = ₹ 88.32
Thus if list price is 100 then net price is 88.32, if list price is x then net price is 8,832
∴ x = \(\frac{8,832 \times 100}{88.32}\)
∴ x = ₹ 10,000
The retailer made 38% profit.
Let the CP of the suit be ₹ 100
∴ SP of the suit = 100 + 38 = ₹ 138
Thus if the SP of the suit is ₹ 138 then its CP is ₹ 100
If the SP of the suit is 88.32 then its
CP = \(\frac{88.32 \times 100}{138}\) = ₹ 6400

Question 14.
An agent charges 10% commission plus 2% delcredere. If he sells goods worth ₹ 37,200, find his total earnings.
Solution:
Total sales = ₹ 37,200
Rate of commission = 10%
Agents commission = \(\frac{4}{100}\) × 37200 = ₹ 3720
Rate of delcredere = 2%
Amount of delcredere = \(\frac{2}{100}\) × 37,200 = ₹ 744
Total earning of the agent = ₹ 3,720 + ₹ 744 = ₹ 4,464

Question 15.
A whole seller allows a 25% trade discount and 5% cash discount. What will be the net price of an article marked at ₹ 1600?
Solution:
Marked price of the article = ₹ 1,600
Trade discount = 25%
= \(\frac{25}{100}\) × 1,600
= ₹ 400
∴ Invoice price = 1,600 – 400 = ₹ 1,200
Cash discount = 5%
= \(\frac{5}{100}\) × 1,200
= ₹ 60
∴ Net price = 1,200 – 60 = ₹ 1,140

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.4

Question 1.
If X has Poisson distribution with m = 1, then find P(X ≤ 1) given e^-1 = 0.3678.
Solution:
∵ m = 1
∵ X follows Poisson Distribution

= e^-m × 1 + e^-m × 1
= e^-1 + e^-1
= 2 × e^-1
= 2 × 0.3678
= 0.7356

Question 2.
If X ~ P(\(\frac{1}{2}\)), then find P(X = 3) given e^-0.5 = 0.6065.
Solution:

Question 3.
If X has Poisson distribution with parameter m and P(X = 2) = P(X = 3), then find P(X ≥ 2). Use e^-3 = 0.0497
Solution:
∵ X follows Poisson Distribution

Question 4.
The number of complaints which a bank manager receives per day follows a Poisson distribution with parameter m = 4. Find the probability that the manager receives (i) only two complaints on a given day, (ii) at most two complaints on a given day. Use e^-4 = 0.0183.
Solution:
∵ m = 1
∵ X ~ P(m = 4)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
X = No. of complaints recieved
(i) P(Only two complaints on a given day)

(ii) P(Atmost two complaints on a given day)
P(X ≤ 2) = p(0) + p(1) + p(2)
= \(\frac{e^{-4} \times 4^{0}}{0 !}+\frac{e^{-4} \times 4^{1}}{1 !}\) + 0.1464
= e^-4 + e^-4 × 4 + 0.1464
= e^-4 [1 + 4] + 0.1464
= 0.0183 × 5 + 0.1464
= 0.0915 + 0.1464
= 0.2379

Question 5.
A car firm has 2 cars, which are hired out day by day. The number of cars hired on a day follows a Poisson distribution with a mean of 1.5. Find the probability that
(i) no car is used on a given day.
(ii) some demand is refused on a given day, given e^-1.5 = 0.2231.
Solution:
Let X = No. of demands for a car on any day
∴ No. of cars hired
n = 2
m = 1.5
∵ X ~ P(m = 1.5)

Question 6.
Defects on plywood sheets occur at random with an average of one defect per 50 sq. ft. Find the probability that such a sheet has (i) no defect, (ii) at least one defect. Use e^-1 = 0.3678.
Solution:
∵ X = No. of defects on a plywood sheet
∵ m = -1
∵ X ~ P(m = -1)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
(i) P(No defect)
P(X = 0) = \(\frac{e^{-1} \times 1^{0}}{0 !}\)
= e^-1
= 0.3678

(ii) P(At least one defect)
P(X ≥ 1) = 1 – P(X < 1)
= 1 – p(0)
= 1 – 0.3678
= 0.6322

Question 7.
It is known that, in a certain area of a large city, the average number of rats per bungalow is five. Assuming that the number of rats follows Poisson distribution, find the probability that a randomly selected bungalow has
(i) exactly 5 rats
(ii) more than 5 rats
(iii) between 5 and 7 rats, inclusive. Given e^-5 = 0.0067.
Solution:
X = No. of rats
∵ m = 5
∴ X ~ P(m = 5)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
(i) P(Exactly five rats)

(ii) P(More than five rats)
P(X > 5) = 1 – P(X ≤ 5)

(iii) P(between 5 and 7 rats, inclusive)
P(5 ≤ x ≤ 7) = p(5) + p(6) + p(7)

= 0.0067 × 3125 × 0.02
= 0.0067 × 62.5
= 0.42

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.3

Question 1.
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of (i) 2 successes (ii) at least 3 successes (iii) at most 2 successes.
Solution:
X: Getting an odd no.
p: Probability of getting an odd no.
A die is thrown 4 times
∴ n = 4
∵ p = \(\frac{3}{6}=\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
∵ X ~ B(3, \(\frac{1}{2}\))
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
(i) P(Two Successes)

(ii) P(Atleast 3 Successes)

(iii) P(Atmost 2 Successes)

Question 2.
A pair of dice is thrown 3 times. If getting a doublet is considered a success, find the probability of two successes.
Solution:
n: No. of times die is thrown = 3
X: No. of doublets
p: Probability of getting doublets
Getting a doublet means, same no. is obtained on 2 throws of a die
There are 36 outcomes
No. of doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)

Question 3.
There are 10% defective items in a large bulk of items. What is the probability that a sample of 4 items will include not more than one defective item?
Solution:
n: No of sample items = 4
X: No of defective items
p: Probability of getting defective items
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
X ~ B(4, 0.1)
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} \mathrm{q}^{n-x}\)
P(Not include more than 1 defective)
P(X ≤ 1) = p(0) + p(1)
= ⁴C₀ (0.1)⁰ (0.9)⁴ + ⁴C₁ (0.1)¹ (0.9)^4-1
= 1 × 1 × (0.9)⁴ + 4 × 0.1 × (0.9)³
= (0.9)³ [0.9 + 0.4]
= (0.9)³ × 1.3
= 0.977

Question 4.
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Find the probability that (i) all the five cards are spades, (ii) only 3 cards are spades, (iii) none is a spade.
Solution:
X: No. of spade cards
Number of cards drawn
∴ n = 5
p: Probability of getting spade card

(i) P(All five cards are spades)

(ii) P(Only 3 cards are spades)

(iii) P(None is a spade)

Question 5.
The probability that a bulb produced by a factory will use fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of (i) X = 0, (ii) X ≤ 1, (iii) X > 1, (iv) X ≥ 1.
Solution:
X : No. of bulbs fuse after 200 days of use
p : Probability of getting fuse bulbs
No. of bulbs in a sample
∴ n = 5
∴ p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
∵ X ~ B(5, 0.2)
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
(i) P(X = 0) = ⁵C₀ (0.2)⁰ (0.8)^5-0
= 1 × 1 × (0.8)⁵
= (0.8)⁵

(ii) P(X ≤ 1) = p(0) + p(1)
= ⁵C₀ (0.2)⁰ (0.8)^5-0 + ⁵C₁ (0.2)¹ (0.8)^5-1
= 1 × 1 × (0.8)⁵ + 5 × 0.2 × (0.8)⁴
= (0.8)⁴ [0.8 + 1]
= 1.8 × (0.8)⁴

(iii) P(X > 1) = 1 – [p(0) + p(1)]
= 1 – 1.8 × (0.8)⁴

(iv) P(X ≥ 1) = 1 – p(0)
= 1 – (0.8)⁵

Question 6.
10 balls are marked with digits 0 to 9. If four balls are selected with replacement. What is the probability that none is marked 0?
Solution:
X : No. of balls drawn marked with the digit 0
n : No. of balls drawn
∴ n = 4
p : Probability of balls marked with 0.
∴ p = \(\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
p(x) = \({ }^{n} C_{x} p^{x} q^{n-x}\)
P(None of the ball is marked with digit 0)

Question 7.
In a multiple-choice test with three possible answers for each of the five questions, what is the probability of a candidate getting four or more correct answers by random choice?
Solution:
n: No. of Questions
∴ n = 5
X: No. of correct answers by guessing
p: Probability of getting correct answers

Question 8.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solution:
X : No. of sixes in 6 throws
n : No. of times dice thrown
∴ n = 6
p : Probability of getting six
∴ p = \(\frac{1}{6}\)
∴ q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
∵ X ~ B(6, \(\frac{1}{6}\))
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
P(At most 2 sixes)
P(X ≤ 2) = p(0) + p(1) + p(2)

Question 9.
Given that X ~ B(n, p),
(i) if n = 10 and p = 0.4, find E(X) and Var(X).
(ii) if p = 0.6 and E(X) = 6, find n and Var(X).
(iii) if n = 25, E(X) = 10, find p and Var(X).
(iv) if n = 10, E(X) = 8, find Var(X).
Solution:
∵ X ~ B (n, p), E(X) = np, V(X) = npq, q = 1 – p
(i) E(X) = np = 10 × 0.4 = 4
∵ q = 1 – p = 1 – 0.4 = 0.6
V(X) = npq = 10 × 0.4 × 0.6 = 2.4

(ii) ∵ p = 0.6
∴ q = 1 – p = 1 – 0.6 = 0.4
E(X) = np
∴ 6 = n × 0.6
∴ n = 10
∴ V(X) = npq = 10 × 0.6 × 0.4 = 2.4

(iii) E(X) = np
∴ 10 = 25 × p
∴ p = 0.4
∴ q = 1, p = 1 – 0.4 = 0.6
∴ S.D.(X) = √V(X)
= \(\sqrt{n p q}\)
= \(\sqrt{25 \times 0.4 \times 0.6}\)
= √6
= 2.4494

(iv) ∵ E(X) = np
∴ 8 = 10p
∴ p = 0.8
∴ q = 1 – p = 1 – 0.8 = 0.2
∵ V(X) = npq = 10 × 0.8 × 0.2 = 1.6

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.2

Question 1.
Check whether each of the following is p.d.f.
(i) \(f(x)= \begin{cases}x & \text { for } 0 \leq x \leq 1 \\ 2-x & \text { for } 1<x \leq 2\end{cases}\)
Solution:
Given function is
f(x) = x, 0 ≤ x ≤ 1
Each f(x) ≥ 0, as x ≥ 0.


∴ The given function is a p.d.f. of x.

(ii) f(x) = 2 for 0 < x < 1
Solution:
Given function is
f(x) = 2 for 0 < x < 1 Each f(x) > 0,

∴ The given function is not a p.d.f.

Question 2.
The following is the p.d.f. of a r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
Find (i) P(X < 1.5), (ii) P(1 < X < 2), (iii) P(X > 2)
Solution:

Question 3.
It is felt that error in measurement of reaction temperature (in Celsius) in an experiment is a continuous r.v. with p.d.f.
\(f(x)= \begin{cases}\frac{x^{3}}{64} & \text { for } 0 \leq x \leq 4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Verify whether f(x) is a p.d.f.
(ii) Find P(0 < X ≤ 1).
(iii) Find the probability that X is between 1 and 3.
Solution:
(i) f(x) is p.d.f. of r.v. X if
(a) f(x) ≥ 0, ∀ x ∈ R
(b) \(\int_{0}^{4} f(x) d x\) = 1

Question 4.
Find k, if the following function represents the p.d.f. of a r.v. X.
(i) \(f(x)= \begin{cases}k x & \text { for } 0<x<2 \\ 0 & \text { otherwise }\end{cases}\)
Also find P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)]
Solution:

(ii) \(f(x)= \begin{cases}k x(1-x) & \text { for } 0<x<1 \\ 0 & \text { otherwise }\end{cases}\)
Also find (a) P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)], (b) P[X < \(\frac{1}{2}\)]
Solution:
We know that

Question 5.
Let X be the amount of time for which a book is taken out of the library by a randomly selected student and suppose that X has p.d.f.
\(f(x)= \begin{cases}0.5 x & \text { for } 0 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Calculate (i) P(X ≤ 1), (ii) P(0.5 ≤ X ≤ 1.5), (iii) P(X ≥ 1.5).
Solution:
Given p.d.f. of X is f(x) = 0.5x for 0 ≤ x ≤ 2
∴ Its c.d.f. F(x) is given by

(i) P(X < 1) = F(1)
= 0.25(1)²
= 0.25

(ii) P(0.5 < X < 1.5) = F(1.5) – F(0.5)
= 0.25(1.5)² – 0.25(0.5)²
= 0.25[2.25 – 0.25]
= 0.25(2)
= 0.5

(iii) P(X ≥ 1.5) = 1 – P(X ≤ 1.5)
= 1 – F(1.5)
= 1 – 0.25(1.5)²
= 1 – 0.25(2.25)
= 1 – 0.5625
= 0.4375

Question 6.
Suppose X is the waiting time (in minutes) for a bus and its p.d.f. is given by
\(f(x)=\left\{\begin{array}{cl}
\frac{1}{5} & \text { for } 0 \leq x \leq 5 \\
0 & \text { otherwise }
\end{array}\right.\)
Find the probability that (i) waiting time is between 1 and 3 minutes, (ii) waiting time is more than 4 minutes.
Solution:
p.d.f. of r.v. X is given by
f(x) = \(\frac{1}{5}\) for 0 ≤ x ≤ 5
This is a constant function.
(i) Probability that waiting time X is between 1 and 3 minutes

(ii) Probability that waiting time X is more than 4 minutes

Question 7.
Suppose error involved in making a certain measurement is a continuous r.v. X with p.d.f.
\(f(x)= \begin{cases}k\left(4-x^{2}\right) & \text { for }-2 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Compute (i) P(X > 0), (ii) P(-1 < X < 1), (iii) P(X < -0.5 or X > 0.5)
Solution:
Since given f(x) is a p.d.f. of r.v. X
Since -2 ≤ x ≤ 2
∴ x² ≤ 4
∴ 4 – x² ≥ 0
∴ k(4 – x²) ≥ 0
∴ k ≥ 0 [∵ f(x) ≥ 0]

Question 8.
Following is the p.d.f. of a continuous r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Find an expression for the c.d.f. of X.
(ii) Find F(x) at x = 0.5, 1.7, and 5.
Solution:
The p.d.f. of a continuous r.v. X is
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) c.d.f. of continuous r.v. X is given by

(ii) F(0.5) = \(\frac{(0.5)^{2}}{16}=\frac{0.25}{16}=\frac{1}{64}\) = 0.015
F(1.7) = \(\frac{(1.7)^{2}}{16}=\frac{2.89}{16}\) = 0.18
For any of x greater than or equal to 4, F(x) = 1
∴ F(5) = 1

Question 9.
The p.d.f. of a continuous r.v. X is
\(f(x)=\left\{\begin{array}{cl}
\frac{3 x^{2}}{8} & \text { for } 0<x<2 \\
0 & \text { otherwise }
\end{array}\right.\)
Determine the c.d.f. of X and hence find (i) P(X < 1), (ii) P(X < -2), (iii) P(X > 0), (iv) P(1 < X < 2).
Solution:
The p.d.f. of a continuous r.v. X is

Question 10.
If a r.v. X has p.d.f.
\(f(x)= \begin{cases}\frac{c}{x} & \text { for } 1<x<3, c>0 \\ 0 & \text { otherwise }\end{cases}\)
Find c, E(X) and V(X). Also find f(x).
Solution:
The p.d.f. of r.v. X is
f(x) = \(\frac{c}{x}\), 1 < x < 3, c > 0
For p.d.f. of X, we have

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.1

Question 1.
Let X represent the difference between a number of heads and the number of tails obtained when a coin is tossed 6 times. What are the possible values of X?
Solution:
∵ A coin is tossed 6 times
S = {6H and 0T, 5H and 1T, 4H and 2T, 3H and 3T, 2H and 4T, 1H and 5T, 0H and 6T}
X: Difference between no. of heads and no. of tails.
X = 6 – 0 = 6
X = 5 – 1 = 4
X = 4 – 2 = 2
X = 3 – 3 = 0
X = 2 – 4 = -2
X = 1 – 5 = -4
X = 0 – 6 = -6
X = {-6, -4, -2, 0, 2, 4, 6}

Question 2.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes the number of black balls drawn. What are the possible values of X?
Solution:
S : Two bolts are drawn from the Urn
S = {RR, RB, BR, BB}
X : No. of black balls
∴ X = {0, 1, 2}

Question 3.
Determine whether each of the following is a probability distribution. Give reasons for your answer.
(i)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.4 + 0.4 + 0.2
= 1
∴ The function is a p.m.f.

(ii)

Solution:
Here, p(3) = -0.1 < 0
∴ P(X = x) ≯ 0, ∀ x
∴ The function is not a p.m.f.

(iii)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.1 + 0.6 + 0.3
= 1
∴ The function is a p.m.f.

(iv)

Solution:
Here, P(Z = z) ≥ 0, ∀ z and
\(\sum_{x=-1}^{3} \mathrm{P}(\mathrm{Z}=z)\) = p(-1) + p(0) + p(1) + p(2) + p(3)
= 0.05 + 0 + 0.4 + 0.2 + 0.3
= 0.95
≠ 1
∴ The function is not a p.m.f.

(v)

Solution:
Here, P(Y = y) ≥ 0, ∀ y and
\(\sum_{x=-1}^{2} \mathrm{P}(\mathrm{Y}=y)\) = p(-1) + p(0) + p(1)
= 0.1 + 0.6 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.

(vi)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{0} \mathrm{P}(X=x)\) = p(-2) + p(-1) + p(0)
= 0.3 + 0.4 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.

Question 4.
Find the probability distribution of
(i) number of heads in two tosses of a coin,
(ii) number of trails in three tosses of a coin,
(iii) number of heads in four tosses of a coin.
Solution:
(i) S: Coin is tossed two times
S = {HH, HT, TH, TT}
n(S) = 4
X: No. of heads
Range of X = {0, 1, 2}
p.m.f. Table

(ii) S: 3 coin are tossed
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
X: No. of heads
Range of X = {0, 1, 2, 3}
p.m.f. Table

(iii) S: Four coin are tossed
S = {HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
n(S) = 16
X: No. of heads
Range of X = {0, 1, 2, 3, 4}
p.m.f. Table

Question 5.
Find the probability distribution of the number of successes in two tosses of a die if successes are defined as getting a number greater than 4.
Solution:
S = A die is tossed 2 times
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
X = No. getting greater than 4
Range of X = {0, 1, 2}
p(0) = \(\frac{16}{36}=\frac{4}{9}\)
p(1) = \(\frac{16}{36}=\frac{4}{9}\)
p(2) = \(\frac{4}{36}=\frac{1}{9}\)

Question 6.
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
Solution:
Total no. of bulbs = 30
No. of defective bulbs = 6
A sample of 4 bulbs are drawn from 30 bulbs.
∴ n(S) = \({ }^{30} \mathrm{C}_{4}\)
∴ No. of non-defective bulbs = 24
Let X = No. of defective bulbs drawn in sample of 4 bulbs.

Question 7.
A coin is biased so that the head is 3 times as likely to occur as the tail. Find the probability distribution of a number of tails in two tosses.
Solution:
Here, the head is 3 times as likely to occur as the tail.
i.e., If 4 times coin is tossed, 3 times there will be a head and 1 time there will be the tail.
∴ p(H) = \(\frac{3}{4}\) and p(T) = \(\frac{1}{4}\)
Let X : No. of tails in two tosses.
And coin is tossed twice.
∴ X = {0, 1, 2}
For X = 0,
p(0) = p(both heads)
= p(H) × p(H)
= \(\frac{3}{4} \times \frac{3}{4}\)
= \(\frac{9}{16}\)
For X = 1,
p(1) = p(HT or TH)
= p(HT) + p(TH)
= p(H) × p(T) + p(T) × p(H)
= \(\frac{3}{4} \times \frac{1}{4}+\frac{1}{4} \times \frac{3}{4}\)
= \(\frac{6}{16}\)
For X = 2,
p(2) = p(both tails)
= p(T) × p(T)
= \(\frac{1}{4} \times \frac{1}{4}\)
= \(\frac{1}{16}\)
The probability distribution of the number of tails in two tosses is

Question 8.
A random variable X has the following probability distribution:

Determine (i) k, (ii) P(X < 3), (iii) P(0 < X < 3), (iv) P(X > 4).
Solution:
(i) It is a p.m.f. of r.v. X
∴ Σp(x) = 1
∴ p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) = 1
∴ k + 2k + 2k + 3k + k² + 2k² + (7k² + k) = 1
∴ 10k² + 9k = 1
∴ 10k² + 9k – 1 = 0
∴ 10k² + 10k – k – 1 = 0
∴ 10k(k + 1) – (k + 1) = 0
∴ (10k – 1)(k + 1) = 0
∴ 10k – 1 = 0 or k + 1 = 0
∴ k = \(\frac{1}{10}\) or k = -1
but k = -1 is not accepted
∴ k = \(\frac{1}{2}\) is accepted

(ii) P(X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iii) P(0 < X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iv) P(X > 4) = p(5) + p(6) + p(7)
= k² + 2k² + (7k² + k)
= 10k² + k
= \(10\left(\frac{1}{10}\right)^{2}+\frac{1}{10}\)
= \(\frac{2}{10}\)
= \(\frac{1}{5}\)

Question 9.
Find expected value and variance of X using the following p.m.f.

Solution:

E(X) = Σxp = -0.05
V(X) = Σx²p – (Σxp)²
= 2.25 – (-0.05)²
= 2.25 – 0.0025
= 2.2475

Question 10.
Find expected value and variance of X, the number on the uppermost face of a fair die.
Solution:
S : A fair die is thrown
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
X: No obtained on uppermost face of die
Range of X = {1, 2, 3, 4, 5, 6}

E(X) = Σxp = \(\frac{21}{6}=\frac{7}{2}\) = 3.5
V(X) = Σx²p – (Σxp)²
= \(\frac{91}{6}\) – (3.5)²
= 15.17 – 12.25
= 2.92

Question 11.
Find the mean of the number of heads in three tosses of a fair coin.
Solution:
S : A coin is tossed 3 times
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Range of X = {0, 1, 2, 3}

∴ Mean = E(X) = Σxp = \(\frac{12}{8}=\frac{3}{2}\) = 1.5

Question 12.
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Solution:
S : Two dice are thrown
S = {(1, 1), (1, 2), (1, 3), ……, (6, 6)}
n(S) = 36
Range of X = {0, 1, 2}
First 6 positive integers are 1, 2, 3, 4, 5, 6
X = Larger two numbers selected
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36

∴ E(X) = Σxp = \(\frac{12}{36}=\frac{1}{3}\)

Question 13.
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers. Find E(X).
Solution:
First 6 positive integers are 1, 2, 3, 4, 5, 6
X : The larger of the selected two numbers
S = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
n(S) = 30

E(X) = Σxp = \(\frac{140}{30}=\frac{14}{3}\) = 4.67

Question 14.
Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance of X.
Solution:
S : Two fair dice are rolled
S = {(1, 1), (1, 2), (1, 4), ……, (6, 6)}
n(S) = 36
X : Sum of the two numbers.
Range of X = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}


V(X) = Σx²p – (Σxp)²
= \(\frac{1952}{36}-\left(\frac{252}{36}\right)^{2}\)
= 54.22 – (7)²
= 5.22
SD(X) = √V(X) = √5.22 = 2.28

Question 15.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. If X denotes the age of a randomly selected student, find the probability distribution of X. Find the mean and variance of X.
Solution:

Question 16.
70% of the member’s favour and 30% oppose a proposal in a meeting. The random variable X takes the value 0 if a member opposes the proposal and the value 1 if a member is in favour. Find E(X) and V(X).
Solution:

E(X) = Σxp = 0.7
V(X) = Σx²p – (Σxp)²
= 0.7 – (0.7)²
= 0.7 – 0.49
= 0.21

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Ex 2.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Insurance and Annuity Ex 2.1

Question 1.
Find the premium on a property worth ₹ 25,00,000 at 3% if
(i) the property is fully insured
(ii) the property is insured for 80% of its value.
Solution:
Case-1
Property value = ₹ 25,00,000
Rate of Premium = 3%
Policy Value = ₹ 25,00,000
∴ Amount of Premium = 3% × 25,00,000 = ₹ 75,000
Case-2
Property Value = ₹ 25,00,000
Policy value = 80% × 25,00,000 = ₹ 20,00,000
Rate of Premium = 3%
∴ Amount of Premium = 3% × 20,00,000 = ₹ 60,000

Question 2.
A shop is valued at ₹ 3,60,000 for 75% of its value. If the rate of premium is 0.9%, find the premium paid by the owner of the shop. Also, find the agents commission if the agent gets commission at 15% of the premium.
Solution:
Property Value = ₹ 3,60,000
Policy Value = 75% × 3,60,000 = ₹ 2,70,000
Rate of Premium = 0.9%
∴ Amount of Premium = 0.9% × 2,70,000 = ₹ 2,430
Rate of Commission = 15%
∴ Amount of Commission = 15% × 2,430 = ₹ 364.5

Question 3.
A person insures his office valued at ₹ 5,00,000 for 80% of its value. Find the rate of premium if he pays ₹ 13,000 as premium. Also, find agent’s commission at 11%.
Solution:
Property Value = ₹ 5,00,000
Policy Value = 80% × 5,00,000 = ₹ 4,00,000
Amount of Premium = ₹ 13000
Let the rate of Premium be x%
Amount of premium = Rate × Policy Value
∴ 13000 = x% × 4,00,000
∴ \(\frac{13,000}{4,00,000}=\frac{x}{100}\)
∴ \(\frac{13,000 \times 100}{4,00,000}\) = x
∴ x = 3.25%
Rate of commission = 11%
∴ Amount of Commission = 11% × 13,000 = ₹ 1,430

Question 4.
A building is insured for 75% of its value. The annual premium at 0.70 percent amounts to ₹ 2625. If the building is damaged to the extent of 60% due to fire, how much can be claimed under the policy?
Solution:
Let the Property Value of building be ₹ x
Policy Value = 75% × x = 0.75x
Rate of Premium = 0.70%
Amount of Policy = Rate × Policy Value
2625 = 0.70% × 0.75x
\(\frac{2625}{0.75}\) = 0.70% × x
3520 = \(\frac{0.70}{100}\) × x
\(\frac{3500 \times 100}{0.70}\) = x
x = ₹ 5,00,000
∴ Damage = 60% × Property Value
= \(\frac{60}{100}\) × 5,00,000
= ₹ 3,00,000
∴ Policy Value = 0.75 × 3,00,000 = ₹ 2,25,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,25,000}{5,00,000}\) × 3,00,000
= ₹ 1,35,000

Question 5.
A stock worth ₹ 7,00,000 was insured for ₹ 4,50,000. Fire burnt stock worth ₹ 3,00,000 completely and damaged there remaining stock to the extent of 75% of its value. What amount can be claimed undertaken policy?
Solution:
Property Value = ₹ 7,00,000
Policy Value = ₹ 4,50,000
Complete Loss = 3,00,000
Partial loss = 75% × [7,00,000 – 3,00,000]
= \(\frac{75}{100}\) × 4,00,000
= ₹ 3,00,000
∴ Total loss = ₹ 3,00,000 + ₹ 3,00,000 = ₹ 6,00,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{4,50,000}{7,00,000}\) × 6,00,000
= ₹ 3,85,714.29

Question 6.
A cargo of rice was insured at 0.625 % to cover 80% of its value. The premium paid was ₹ 5,250. If the price of rice is ₹ 21 per kg. find the quantity of rice (in kg) in the cargo.
Solution:
Let Property Value be ₹ x
Policy Value = 80% × x = ₹ 0.8x
Rate of Policy = 0.625%
Amount of Premium = Rate × Policy value
∴ 5250 = 0.625% × 0.8x
∴ 5250 = 0.005x
∴ x = \(\frac{5250}{0.005}\)
∴ x = ₹ 10,50,000
Rate of Rice = ₹ 21/kg
∴ Quantity of Rice (in kg) = \(\frac{\text { Total value }}{\text { Rate of Rice }}\)
= \(\frac{10,50,000}{21}\)
= 50,000 kgs

Question 7.
60,000 articles costing ₹ 200 per dozen were insured against fire for ₹ 2,40,000. If 20% of the articles were burnt and 7,200 of the remaining articles were damaged to the extent of 80% of their value, find the amount that can be claimed under the policy.
Solution:
No of articles = 60,000
Cost of articles = ₹ 200/dozen
∴ Property of Value = \(\frac{60,000}{12}\) × 200 = ₹ 1o,oo,ooo
∴ Policy Value = ₹ 2,40,000
Complete Loss = 20% × 10,00,000 = ₹ 2,00,000
Partial loss = \(\frac{7200}{12}\) × 200 × 80% = ₹ 96,000
∴ Total loss = 2,00,000 + 96,000 = ₹ 2,96,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,40,000}{10,00,000}\) × 2,96,000
= ₹ 71,040

Question 8.
The rate of premium is 2% and other expenses are 0.075%. A cargo worth ₹ 3,50,100 is to be insured so that all its value and the cost of insurance will be recovered in the event of total loss.
Solution:
Let the Policy Value of Cargo be ₹ 100 which includes insurance and other expenses
∴ Property Value = 100 – [2 + 0.075] = ₹ 97.925
If Policy Value is ₹ 100, then Property Value is ₹ 97.925
If Property Value is ₹ 3,50,100
Then policy Value = \(\frac{100 \times 3,50,100}{97.925}\) = ₹ 3,57,518.51

Question 9.
A property worth ₹ 4,00,000 is insured with three companies. A, B, and C. The amounts insured with these companies are ₹ 1,60,000, ₹ 1,00,000 and ₹ 1,40,000 respectively. Find the amount recoverable from each company in the event of a loss to the extent of ₹ 9,000.
Solution:
Property Value = ₹ 4,00,000
Loss = ₹ 9,000
Total Value of Policies = 1,60,000 + 1,00,000 + 1,40,000 = ₹ 4,00,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
Claim of company A = \(\frac{1,60,000}{40,000}\) × 9,000 = ₹ 3,600
Claim of company B = \(\frac{1,00,000}{4,00,000}\) × 9,000 = ₹ 2,250
Claim of company C = \(\frac{1,40,000}{4,00,000}\) × 9,000 = ₹ 3,150

Question 10.
A car valued at ₹ 8,00,000 is insured for ₹ 5,00,000. The rate of premium is 5% less 20%. How much will the owner bear including the premium if value of the ear is reduced to 60% of its original value.
Solution:
Property Value = ₹ 8,00,000
Policy Value = ₹ 5,00,000
Rate of Premium = 5% less 20%
= 5% – 20% × 5%
= (5 – 1)%
= 4%
Amount of Premium = 4% × 5,00,000 = ₹ 20,000
Loss = [100 – 60]% × Property Value
= 40% × 8,00,000
= ₹ 3,20,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{5,00,000}{8,00,000}\) × 3,20,000
= ₹ 2,00,000
Loss bear by owner = Loss – claim + Premium
= 3,20,000 – 2,00,000 + 20,000
= ₹ 1,40,000

Question 11.
A shop and a godown worth ₹ 1,00,000 and ₹ 2,00,000 respectively were insured through an agent who was paid 12% of the total premium. If the shop was insured for 80% and the godown for 60% of their respective values, find the agent’s commission, given that the rate of premium was 0.80% less 20%.
Solution:
Rate of Premium = 0.80% Less 20%
= 0.80% – 20% × 0.80%
= (0.80 – 0.16)%
= 0.64%
For Shop
Property Value = ₹ 1,00,000
Policy Value = 80% × 1,00,000 = ₹ 80,000
Premium = 0.64% × 80,000 = ₹ 512
For Godown
Property Value = ₹ 2,00,000
Policy Value = 60% × 2,00,000 = ₹ 1,20,000
Premium = 0.64% × 1,20,000 = ₹ 768
∴ Total Premium = 512 + 768 = ₹ 1,280
Rate of Commission = 12%
∴ Agent Commission = 12% × 1,280 = ₹ 153.6

Question 12.
The rate of premium on a policy of ₹ 1,00,000 is ₹ 56 per thousand per annum. A rebate of ₹ 0.75 per thousand is permitted if the premium is paid annually. Find the net amount of premium payable if the policy holder pays the premium annually.
Solution:
Policy Value = ₹ 1,00,000
Rate of Premium = ₹ 56 per thousand p.a
Rate of Rebate = ₹ 0.75 per thousand p.a
Premium is paid annually
∴ Net rate of = 56 – 0.75 = ₹ 55.25 per thousand p.a.
∴ Net Amount ot Premium = \(\frac{1,00,000}{1000}\) × 55.25 = ₹ 5,525

Question 13.
A warehouse valued at ₹ 40,000 contains goods worth ₹ 2,40,000. The warehouse is insured against fire for ₹ 16,000 and the goods to the extent of 90% of their value. Goods worth ₹ 80,000 are completely destroyed, while the remaining goods are destroyed to 80% of their value due to a fire. The damage to the warehouse is to the extent of ₹ 8,000. Find the total amount that can be claimed.
Solution:
For Warehouse
Property Value = ₹ 40,000
Policy Value = ₹ 16,000
Loss = ₹ 8,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{16,000}{40,000}\) × 8,000
= ₹ 3,200
For Goods
Property Value = ₹ 2,40,000
Policy Value = 90% × 2,40,000 = ₹ 2,16,000
Complete Loss = 80,000
Partial Loss = 80% × (2,16,000 – 80,000)
= 80% × 1,36,000
= ₹ 1,08,800
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,16,000}{24,000}\) × 1,08,800
= ₹ 97,920
∴ Total Claim = 3,200 + 97,920 = ₹ 1,01,120

Question 14.
A person takes a life policy for ₹ 2,00,000 for a period of 20 years. He pays premium for 10 years during which bonus was declared at an average rate of ₹ 20 per year per thousand. Find the paid up value of the policy if he discontinuous paying premium after 10 years.
Solution:
Policy Value = ₹ 2,00,000
Rate of Bonus = ₹ 20 Per thousand p.a.
Total Bonus = \(\frac{2,00,000 \times 20}{1,000}\) = ₹ 4,000
∴ Bonus for 10 years = 4,000 × 10 = ₹ 40,000
Period of Policy = 20 years
∴ Amount of Premium = \(\frac{2,00,000}{20}\) = ₹ 10,000 p.a.
∴ Total Premium for 10 years = 10,000 × 10 = ₹ 1,00,000
∴ Paid up Value of Policy = Total premium + Total Bonus
= 1,00,000 + 40,000
= ₹ 1,40,000

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1

(I) Choose the correct alternative.

Question 1.
An agent who gives a guarantee to his principal that the party will pay the sale price of goods is called
(a) Auctioneer
(b) Del Credere Agent
(c) Factor
(d) Broker
Answer:
(b) Del Credere Agent

Question 2.
An agent who is given the possession of goods to be sold is known as
(a) Factor
(b) Broker
(c) Auctioneer
(d) Del Credere Agent
Answer:
(a) Factor

Question 3.
The date on which the period of the bill expires is called
(a) Legal Due Date
(b) Grace Date
(c) Nominal Due Date
(d) Date of Drawing
Answer:
(c) Nominal Due Date

Question 4.
The payment date after adding 3 days of grace period is known as
(a) The legal due date
(b) The nominal due date
(c) Days of grace
(d) Date of drawing
Answer:
(a) The legal due date

Question 5.
The sum due is also called as
(a) Face value
(b) Present value
(c) Cash value
(d) True discount
Answer:
(a) Face value

Question 6.
P is the abbreviation of
(a) Face value
(b) Present worth
(c) Cash value
(d) True discount
Answer:
(b) Present worth

Question 7.
Banker’s gain is the simple interest on
(a) Banker’s discount
(b) Face Value
(c) Cash value
(d) True discount
Answer:
(d) True discount

Question 8.
The marked price is also called as
(a) Cost price
(b) Selling price
(c) List price
(d) Invoice price
Answer:
(c) List price

Question 9.
When only one discount is given then
(a) List price = Invoice price
(b) Invoice price = Net selling price
(c) Invoice price = Cost price
(d) Cost price = Net selling price
Answer:
(b) Invoice price = Net selling price

Question 10.
The difference between the face value and present worth is called
(a) Banker’s discount
(b) True discount
(c) Banker’s gain
(d) Cash value
Answer:
(b) True discount

(II) Fill in the blanks.

Question 1.
A person who draws the bill is called ____________
Answer:
Drawee

Question 2.
An ____________ is an agent who sells the goods by auction.
Answer:
Auctioneer

Question 3.
Trade discount is allowed on the ____________ price.
Answer:
Catalogue/List

Question 4.
The banker’s discount is also called ____________.
Answer:
Commercial Discount

Question 5.
The banker’s discount is always ____________ than the true discount.
Answer:
higher

Question 6.
The diffrence between the banker’s discount and the true discount is called ____________.
Answer:
bankers gain

Question 7.
The date by which the buyer is legally allowed to pay the amount is known as ____________.
Answer:
legal due date

Question 8.
A ____________ is an agent who brings together the buyer and the seller.
Answer:
broker

Question 9.
If buyer is allowed both trade and cash discounts, ____________ discount is fist calculated on ____________ price.
Answer:
Trade, Catalogue/List

Question 10.
____________ = List price (catalogue Price) – Trade Discount.
Answer:
Invoice Price

(III) State whether each of the following is True or False.

Question 1.
A broker is an agent who gives a guarantee to the seller that the buyer will pay the sale price of goods.
Answer:
False

Question 2.
A cash discount is allowed on the list price.
Answer:
False

Question 3.
Trade discount is allowed on catalogue price.
Answer:
True

Question 4.
The buyer is legally allowed 6 days grace period.
Answer:
False

Question 5.
The date on which the period of the bill expires is called the nominal due date.
Answer:
True

Question 6.
The difference between the banker’s discount and true discount is called sum due.
Answer:
False

Question 7.
The banker’s discount is always lower than the true discount.
Answer:
False

Question 8.
The banker’s discount is also called a commercial discount.
Answer:
True

Question 9.
In general cash, the discount is more than trade discount.
Answer:
False

Question 10.
A person can get both, trade discount and a cash discount.
Answer:
True

(IV) Solve the following problems.

Question 1.
A salesman gets a commission of 6.5% on the total sales made by him and a bonus of 1% on sales over ₹ 50,000. Find his total income on a turnover of ₹ 75,000.
Solution:
Rate of commission = 6.5% on the total sales
∴ Commission on a turnover of ₹ 75,000
= \(\frac{6.5}{100}\) × 75,000
= ₹ 4,875
Rate of bonus = 1% on sales over ₹ 50,000
∴ Amount of bonus = \(\frac{1}{100}\) × (75,000 – 50,000) = ₹ 250
∴ Total income of the sales man = ₹ 4,875 + ₹ 250 = ₹ 5,125

Question 2.
A shop is sold at 30% profit, the amount of brokerage at the rate of \(\frac{3}{4}\)% amounts to ₹ 73,125. Find the cost of the shop.
Solution:
Rate of brokerage = \(\frac{3}{4}\)%
Amount of brokerage = ₹ 73,125
Let the selling price of the shop be ₹ 100 then the brokerage = ₹ \(\frac{3}{4}\)
Thus, if the amount of brokerage is ₹ \(\frac{3}{4}\) then the selling price of the shop is ₹ 100
If the amount of brokerage is ₹ 73,125, then the selling price of the shop is = 73125 × \(\frac{4}{3}\) × 100 = ₹ 97,50,000
The shop is sold at 30% profit
∴ If the cost of the shop is ₹ 100, then it is sold at ₹ 130
Thus, if the shop is sold at ₹ 130, then its cost price is ₹ 100
If the shop is sold at ₹ 97,50,000 then its cost price is = \(\frac{97,50,000 \times 100}{130}\) = ₹ 75,00,000
Then, the cost of the shop is ₹ 75,00,000

Question 3.
A merchant gives 5% commission and 1.5% delcredere to his agents. If the agent sells goods worth ₹ 30,600 how much does he get? How much does the merchant receive?
Solution:
Rate of commission = 5%
Total sales = ₹ 30,600
Amount of commission = \(\frac{5}{100}\) × 30,600
Rate of delcredere = 1.5%
= \(\frac{1.5}{100}\) × 30,600
= ₹ 459
Thus, the agents gets 1,530 + 459 = ₹ 1,989
And the merchant receives = 30,600 – 1,989 = ₹ 28,611

Question 4.
After deducting commission at 7\(\frac{1}{2}\)% on first ₹ 50,000 and 5% on the balance of sales made by him, an agent remits ₹ 93,750 to his principal. Find the value of goods sold by him.
Solution:
Rate of commission = 7\(\frac{1}{2}\)% on first ₹ 50,000
= \(\frac{7.5}{100}\) × 50,000
= ₹ 3,750
Let the total sales be ₹ x
Rate of commission on the balance sales = 5%
Commission on the balance sales = \(\frac{5}{100}\) × (x – 50000) = \(\frac{x}{20}\) – 2,500
Total commission = 3750 + \(\frac{x}{20}\) – 2,500 = \(\frac{x}{20}\) + 1,250
Now, the amount to be remitted to the principal = Value of goods sold – Commission of the agent
= x – (\(\frac{x}{20}\) + 1250)
= \(\frac{19x}{20}\) – 1250
The agents remits ₹ 93,750 to his principal
∴ \(\frac{19x}{20}\) – 1,250 = 93,750
∴ \(\frac{19x}{20}\) = 95,000
∴ x = ₹ 1,00,000
Thus, the value of the goods sold by the agent is ₹ 1,00,000

Question 5.
The present worth of ₹ 11,660 due 9 months hence is ₹ 11,000. Find the rate of interest.
Solution:
Given, PW = ₹ 11,000, SD = ₹ 11,660
n = \(\frac{9}{12}\) year = \(\frac{3}{4}\) year
We have,

∴ The rate of interest is 8% p.a.

Question 6.
An article is marked at ₹ 800, a trader allows a discount of 2.5% and gains 20% on the cost. Find the cost price of the article?
Solution:
Marked price of the article = ₹ 800
Rate of discount = 2.5%
Amount of discount = \(\frac{2.5}{100}\) × 800 = ₹ 20
∴ Selling price of the article = 800 – 20 = ₹ 780
Now, given, gain = 20%
Let cost price of the article be ₹ 100, then
The selling price of the article is ₹ 120
Thus if cost price of the articles is ₹ x
Then the selling price is ₹ 780
∴ x = \(\frac{780 \times 100}{120}\)
∴ x = 650
∴ Cost price of the article is ₹ 650

Question 7.
A salesman is paid a fixed monthly salary plus commission on the sales. If on sale of ₹ 96,000 and ₹ 1,08,000 in two successive months he receives in all ₹ 17,600 and ₹ 18,800 respectively. Find his monthly salary and rate of commission paid to him.
Solution:
Let the monthly salary of the salesman be ₹ x
And the rate of commission be y%
Income = monthly salary + commission on the sales
17600 = x + \(\frac{y}{100}\) × 96,000
∴ 17600 = x + 960y ………(1)
and 18800 = x + \(\frac{y}{100}\) × 108000
∴ 18,800 = x + 1080y ………(2)
Subtracting equation (1) from equation (2), we get
1,200 = 120y
∴ y = 10
Substituting y = 10 in (1), we get
17,600 = x + 960(10)
∴ x = 17,600 – 9,600 = 8,000
∴ Salary of the salesman = ₹ 8,000
Rate of commission = 10%

Question 8.
A merchant buys some mixers at a 15% discount on catalogue price. The catalogue price is ₹ 5,500 per price of the mixer. The freight charges amount to 2\(\frac{1}{2}\)% on the catalogue price. The merchant sells each mixer at a 5% discount on the catalogue price. His net profit is ₹ 41,250, Find the number of mixers.
Solution:
Catalogue price of a mixer = ₹ 5,500
Trade discount = 15% on catalogue price
= \(\frac{15}{100}\) × 5,500
= ₹ 825
Freight charges = 2\(\frac{1}{2}\)% of the catalogue price
= \(\frac{5}{2} \times \frac{1}{100} \times 5,500\)
= ₹ 137.5
∴ Cost price of a mixer for the merchant = 5,500 – 825 + 137.5 = 4,812,5
Catalogue price = ₹ 5,500
Rate of discount = 5%
∴ Selling price of one mixer = 5500 – \(\frac{5}{100}\) × 5,500 = ₹ 5,225
∴ Profit on one mixer = 5,225 – 4,812.5 = ₹ 412.5
Now, total profit = ₹ 41,250
∴ Number of mixers = \(\frac{41,250}{412.5}\) = 100
Thus the number of mixers is 100.

Question 9.
A bill is drawn for ₹ 7,000 on 3rd May for 3 months and is discounted on 25th May at 5.5% Find the present worth.
Solution:
Face value of the bill = ₹ 7,000
Date of drawing = 3rd May
Period = 3 months
Normal due date = 3rd August
Legal due date = 6th August
Rate of interest = 5.5%
Date of discounting = 25th May
Unexpired period (number of days from date of discounting to legal due date)

∴ Bankers discount = 7,000 × \(\frac{73}{365} \times \frac{5.5}{100}\) = ₹ 77
Also PW = SD – BD
= 7,000 – 77
= ₹ 6,923
∴ Present worth is ₹ 6,923

Question 10.
A bill was drawn on 14th April 2005 for ₹ 3,500 and was discounted on 6th July 2005 at 5% per annum. The banker paid ₹ 3,465 for the bill. Find the period of the bill.
Solution:
Face value of the bill = ₹ 3,500
Date of drawing = 14/04/2005
Date of discount = 06/07/2005
Rate of interest = 5%
Cash value = ₹ 3,465
Bankers discount = Face value – Cash value
= 3,500 – 3,465
= ₹ 35
Let the unexpired days be n days
∴ BD = \(\frac{\mathrm{FV} \times n \times r}{365 \times 100}\)
∴ 35 = \(\frac{3,500 \times n \times 5}{365 \times 100}\)
∴ n = 73 days
Thus, legal due date is 73 days from the date of discounting

∴ Legal due date = 17/09/2005
∴ Nominal due date = 14/09/2005
∴ The period of the bill is 5 months

Question 11.
The difference between true discount and banker’s discount on 6 months hence at 4% p.a. is ₹ 80. Find the true discount, banker’s discount, and amount of the bill.
Solution:
BG = BD – TD
∴ BG = ₹ 80
Also BG = \(\frac{\mathrm{TD} \times n \times r}{100}\)
∴ 80 = \(\frac{\mathrm{TD} \times 6 \times 4}{12 \times 100}\)
∴ TD = \(\frac{80 \times 100}{2}\)
∴ TD = ₹ 4,000
Now BD = TD + BG
= 4,000 + 80
= ₹ 4,080
Also, BD = \(\frac{\mathrm{FV} \times n \times r}{100}\)
∴ 4,080 = \(\frac{\mathrm{FV} \times 6 \times 4}{12 \times 100}\)
∴ FV = \(\frac{4,080 \times 100}{2}\)
∴ FV = ₹ 2,04,000
Amount of the bill = ₹ 2,04,000

Question 12.
A manufacturer makes a clear profit of 30% on the cost after allowing a 35% discount. If the cost of production rises by 20%, by what percentage should he reduce the rate of discount so as to make the same rate of profit keeping his list prices unaltered.
Solution:
Rate of discount = 35%
Let the list price be ₹ 100.
Then discount at 35% = ₹ 35
∴ Net selling price = 100 – 35 = ₹ 65 ……..(1)
The manufacturer makes a clear profit of 30% on the cost after allowing a 35% Discount.
Let the cost be ₹ 100.
Then selling price at 30% profit is 100 + 30 = ₹ 130.
Thus, if the net selling price is ₹ 130, then the cost price is ₹ 100.
But, the net selling price is ₹ 130, then the cost price is ₹ 65 ……[from (1)]
∴ The cost price is \(\frac{65}{130} \times 100\) = ₹ 50
Hence, we have,

Now, the cost of production has increased by 20%.
Let the old cost price be ₹ 100.
∴ The new cost price is ₹ 120.
But, the old cost price is ₹ 50.
∴ The new cost price is = \(\frac{50}{100} \times 120\) = ₹ 60.
The old net price is ₹ 65.
Now 20% of ₹ 65 = \(\frac{20}{100} \times 65\) = ₹ 13
∴ New net price = 65 + 13 = ₹ 78
Hence, we have

Now, 100 – 78 = ₹ 22
Thus, the rate of discount should be reduced by 22%, The original rate of discount is 35%.
Hence, the reduction in discount should be (35 – 22)% = 13%
so as to make the same rate of profit, keeping the list price unaltered.

Question 13.
A trader offers a 25% discount on the catalogue price of the radio and yet makes a 20% profit. If he gains ₹ 160 per radio, what must be the catalogue price of the radio?
Solution:
Rate of discount = 25% on the catalogue price of a radio.
Let the catalogue price of the radio be ₹ 100.
Then, the discount on a radio = ₹ 25.
Net selling price = 100 – 25 = ₹ 75.
He makes a profit of 20%.
Let the cost price be ₹ 100.
Then, at 20% profit, net selling price = ₹ 120.
Thus, if net SP is ₹ 120, then cost price is ₹ 100.
But, the net SP is ₹ 75.
∴ The cost price is \(\frac{75}{120}\) × 100 = \(\frac{750}{12}\) = ₹ 62.50
∴ Profit on a radio set = 75 – 62.5 = ₹ 12.50
Thus, if the profit on a radio set is ₹ 12.50 then its catalogue price is ₹ 100.
But the profit on a radio set is ₹ 160.
∴ The catalogue price of radio = \(\frac{160}{12.50}\) × 100
= 12.80 × 100
= ₹ 1,280
∴ Thus, the catalogue price of the radio is ₹ 1280

Question 14.
A bill of ₹ 4,800 was drawn on 9th March 2006 at 6 months and was discounted on 19th April 2006 for 6\(\frac{1}{4}\)% p.a. How much does the banker charge and how much does the holder receive?
Solution:
Face value of the bill = ₹ 4.800
Date of drawing = 09/03/2006
Period of the bill = 6 months
Normal due date = 09/09/2006
Legal due date = 12/09/2006
Rate of discount = 6\(\frac{1}{4}\)% = 6.25%
Now, for the unexpired

Thus the banker charges ₹ 120
Amount received by the holder = 4,800 – 120 = ₹ 4,680

Question 15.
A bill of ₹ 65,700 drawn on July 10 for 6 months was discounted for ₹ 65,160 at 5% p.a. On what day was the bill discounted?
Solution:
BD = FV – Cash value
= 65,700 – 65,160
= ₹ 540
Let the unexpired days be x days
BD = \(\frac{\mathrm{FV} \times n \times r}{100}\)
∴ 540 = \(\frac{65,700 \times x \times 5}{365 \times 100}\)
∴ x = 60 days
The unexpired days = 60 days
Date-of drawing = 10th July
Period of the bill = 6 months
Nominal due date = 10th January (next year)
Legal due date = 13th January (next year)
Then the date of discount is 60 days before, the legal due date

∴ The date of discounting is 14th November

Question 16.
An agent sold a car and charged a 3% commission on the sale value. If the owner of the car received ₹ 48,500, find the sale value of the car. If the agent charged 2% from the buyer, find his total remuneration.
Solution:
Let the sale value of the car be ₹ x
Rate of commission of the agent = 3%
Since the owner received ₹ 48,500 after agent has charged his commission
x – \(\frac{3 x}{100}\) = 48500
∴ \(\frac{97 x}{100}\) = 48500
∴ x = \(\frac{48,500 \times 100}{97}\)
∴ x = ₹ 50,000
∴ Sale value of the car = ₹ 50,000
Against commission received from the owner = \(\frac{3}{100}\) × 50,000 = ₹ 1500
Against commission received from the buyer = \(\frac{2}{100}\) × 50,000 = ₹ 1000
∴ Agents total remuneration = 1,500 + 1,000 = ₹ 2,500

Question 17.
An agent is paid a commission of 4% on cash sales and 6% on credit sales made by him. If on the sale of ₹ 51,000 the agent claims a total commission of ₹ 2,700, find the sales made by him for cash and on credit.
Solution:
Total sales = ₹ 51,000
Let eash sales be ₹ x
∴ Credit sales = ₹ (51,000 – x)
Agent’s commission on cash sales = 4%
= \(\frac{4}{100}\) × x
= \(\frac{4x}{100}\)
Commission on credit sales = 6%
= \(\frac{6}{100}\)(51,000 – x)
Given total commission = ₹ 2,700

∴ Cash sales = ₹ 18,000
∴ Credit sales = 51,000 – 18,000 = ₹ 33,000

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Ex 2.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Insurance and Annuity Ex 2.2

Question 1.
Find the accumulated (future) value of annuity of ₹ 800 for 3 year at interest rate 8% compounded annually. [Given: (1.08)³ = 1.2597]
Solution:
∵ C = ₹ 800
∵ n = 3 years
∵ r = 8% p.a.

∴ A = 10,000[(1.08)³ – 1]
∴ A = 10,000[1.2597 – 1]
∴ A = 10,000 × 0.2597
∴ A = ₹ 2,597

Question 2.
A person invested ₹ 5,000 every year in finance company that offered him interest compounded at 10% p.a., what is the amount accumulated after 4 years? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ C = ₹ 5,000
∵ r = 10% p.a.

= 50,000[(1.1)⁴ – 1]
= 50,000[1.4641 – 1]
= 50,000 × 0.4641
= ₹ 23,205

Question 3.
Find the amount accumulated after 2 years if a sum of ₹ 24,000 is invested every six months at 12% p.a. compounded half yearly. [Given: (1.06)⁴ = 1.2625]
Solution:
∵ C = ₹ 24,000
∵ n = 2 years
But invested half yearly
∴ n = 2 × 2 = 4
∵ r = 12% p.a. compounded half yearly

= 4,00,000[(1.06)⁴ – 1]
= 4,00,000[1.2625 – 1]
= 4,00,000 × 0.2625
= ₹ 1,05,000

Question 4.
Find the accumulated value after 1 year of an annuity immediate in which ₹ 10,000 are invested every quarter at 16% p.a. compounded quarterly. [Given: (1.04)⁴ = 1.1699]
Solution:
∵ C = ₹ 10,000
∵ n = 1 year
But invested every quarterly
∴ n = 1 × 4 = 4
∴ r = 16% p.a. compounded quarterly

= 2,50,000 [1.1699 – 1]
= 2,50,000 × 0.1699
= ₹ 42,475

Question 5.
Find the present value of an annuity immediate of ₹ 36,000 p.a. for 3 years at 9% p.a. compounded annually. [Given: (1.09)^-3 = 0.7722]
Solution:
∵ C = ₹ 36,000
∵ n = 3 years
∵ r = 9% p.a.

= 4,00,000 × 0.2278
= ₹ 91,120

Question 6.
Find the present value of ordinary annuity of ₹ 63,000 p.a. for 4 years at 14% p.a. compounded annually. [Given: (1.14)^-4 = 0.5921]
Solution:
∵ C = ₹ 63,000
∵ n = 4 years
∵ r = 14% p.a.

= 4,50,000[1 – 0.5921]
= 4,50,000 × 0.4079
= ₹ 1,83,555

Question 7.
A lady plans to save for her daughter’s marriage. She wishes to accumulate a sum of ₹ 4,64,100 at the end of 4 years. What amount should she invest every year if she get an interest of 10%p.a. compounded annually? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ A = ₹ 4,64,100
∵ n = 4 years
∵ r = 10% p.a.

∴ 46,410 = C[1.4641 – 1]
∴ 46,410 = C × 0.4641
∴ \(\frac{46,410}{0.4641}\) = C
∴ C = ₹ 1,00,000

Question 8.
A person wants to create a fund of ₹ 6,96,150 after 4 years at the time of his retirement. He decides to invest a fixed amount at the end of every year in a bank that offers him interest of 10% p.a. compounded annually. What amount should he invest every year? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ A = ₹ 6,96,150
∵ n = 4 years
∵ r = 10% p.a

∴ 69,615 = C[1.4641 – 1]
∴ 69,615 = C × 0.4641
∴ \(\frac{69,615}{0.4641}\) = C
∴ C = ₹ 1,50,000

Question 9.
Find the rate of interest compounded annually if an annuity immediate at ₹ 20,000 per year amounts to ₹ 2,60,000 in 3 years.
Solution:
∵ C = ₹ 20,000
∵ A = ₹ 2,60,000
∵ n = 3 years

∴ 13i = 3i + 3 i² + i³
∴ 13i = i(3 + 3i + i²)
∴ 13 = 3 + i + i²
∴ i² + 3i + 3 – 13 = 0
∴ i² + 3i – 10 = 0
∴ (i + 5) (i – 2) = 0
∴ i + 5 = 0 or i – 2 = 0
∴ i = -5 or i = 2
∵ Rate of interest cannot be negative
∴ i = 2 is accepted
∴ \(\frac{r}{100}\) = 2
∴ r = 200% p.a.

Question 10.
Find the number of years for which an annuity of ₹ 500 is paid at the end of every years, if the accumulated amount works out to be ₹ 1,655 when interest is compounded annually at 10% p.a.
Solution:
∵ C = 7500
∵ A = 71,655
∵ r = 10% p.a.


∴ 0.331 + 1 = (1.1)ⁿ
∴ 1.331 = (1.1)ⁿ
∴ (1.1)³ = (1.1)ⁿ
∴ n = 3 years

Question 11.
Find the accumulated value of annuity due of ₹ 1,000 p.a. for 3 years at 10% p.a. compounded annually. [Given: (1.1)³ = 1.331]
Solution:
∵ C = ₹ 1,000
∵ n = 3 years
∵ r = 10% p.a.

∴ A’ = 10,000 × 1.1[(1.1)³ – 1]
∴ A’ = 11,000 [1.331 – 1]
∴ A’ = 11,000 × 0.331
∴ A’ = ₹ 3,641

Question 12.
A person plans to put ₹ 400 at the beginning of each year for 2 years in a deposit that gives interest at 2% p.a. compounded annually. Find the amount that will be accumulated at the end of 2 years. [Given: (1.02)² = 1.0404]
Solution:
∵ C = ₹ 400
∵ r = 2% p.a.


= 20,000 (1.02) (1.0404 – 1)
= 20,400 [0.0404]
= ₹ 824.16

Question 13.
Find the present value of an annuity due of ₹ 600 to be paid quarterly at 32% p.a. compounded quarterly. [Given (1.08)^-4 = 0.7350]
Solution:
∵ C = ₹ 600
∵ n = 1 year
∴ But invested every quarterly
∴ n = 1 × 4 = 4
∵ r = 32% p.a. compounded quarterly

= 7,500(1.08) [1 – 0.7350]
= 8,100 [0.2650]
= ₹ 2,146.5

Question 14.
An annuity immediate is to be paid for some years at 12% p.a. The present value of the annuity is ₹ 10,000 and the accumulated value is ₹ 20,000. Find the amount of each annuity payment.
Solution:
∵ r = 12% p.a.
∴ i = \(\frac{r}{100}=\frac{12}{100}\) = 0.12
∵ P = ₹ 10,000
∵ A = ₹ 20,000
∵ \(\frac{1}{P}-\frac{1}{A}=\frac{i}{C}\)

∴ C = 0.12 × 20,000
∴ C = ₹ 2,400

Question 15.
For an annuity immediate paid for 3 years with interest compounded at 10% p.a. the present value is ₹ 24,000. What will be the accumulated value after 3 years? [Given (1.1)³ = 1.331]
Solution:
∵ n = 3 years
∵ P = ₹ 24,000
∵ r = 10% p.a.
∴ i = \(\frac{r}{100}=\frac{10}{100}\) = 0.1
∵ A = P(1 + i)ⁿ
∴ A = 24,000 [1 + 0.1]³
∴ A = 24,000 × (1.1)³
∴ A = 24,000 × 1.331
∴ A = ₹ 31,944

Question 16.
A person sets up a sinking fund in order to have ₹ 1,00,000 after 10 years. What amount should be deposited bi-annually in the account that pays him 5% p.a. compounded semi-annually? [Given: (1.025)²⁰ = 1.675]
Solution:
∴ A = ₹ 1,00,000
∴ n = 10 years
But, invested half yearly
∴ n = 10 × 2 = 20
∵ r = 5% p.a. compounded half yearly
∴ r = \(\frac{r}{2}=\frac{5}{2}\) = 2.5%
∴ i = \(\frac{r}{100}=\frac{2.5}{100}\) = 0.025

∴ 2,500 = C[1.675 – 1]
∴ 2,500 = C × 0.675
∴ \(\frac{2,500}{0.675}\) = C
∴ C = ₹ 3,703.70

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7

(I) Choose the correct alternative.

Question 1.
In sequencing, an optimal path is one that minimizes ___________
(a) Elapsed time
(b) Idle time
(c) Both (a) and (b)
(d) Ready time
Answer:
(c) Both (a) and (b)

Question 2.
If job A to D have processing times as 5, 6, 8, 4 on first machine and 4, 7, 9, 10 on second machine then the optimal sequence is:
(a) CDAB
(b) DBCA
(c) BCDA
(d) ABCD
Answer:
(b) DBCA

Question 3.
The objective of sequence problem is
(a) to find the order in which jobs are to be made
(b) to find the time required for the completing all the job on hand
(c) to find the sequence in which jobs on hand are to be processed to minimize the total time required for processing the jobs
(d) to maximize the cost
Answer:
(c) to find the sequence in which jobs on hand are to be processed to minimize the total time required for processing the jobs

Question 4.
If there are n jobs and m machines, then there will be ___________ sequences of doing the jobs.
(a) mn
(b) m(n!)
(c) n^m
(d) (n!)^m
Answer:
(d) (n!)^m

Question 5.
The Assignment Problem is solved by
(a) Simple method
(b) Hungarian method
(c) Vector method
(d) Graphical method
Answer:
(b) Hungarian method

Question 6.
In solving 2 machine and n jobs sequencing problem, the following assumption is wrong
(a) No passing is allowed
(b) Processing times are known
(c) Handling times is negligible
(d) The time of passing depends on the order of machining
Answer:
(d) The time of passing depends on the order of machining

Question 7.
To use the Hungarian method, a profit maximization assignments problem requires
(a) Converting all profit to opportunity losses
(b) A dummy person or job
(c) Matrix expansion
(d) Finding the maximum number of lines to cover all the zeros in the reduced matrix
Answer:
(a) Converting all profits to opportunity losses

Question 8.
Using the Hungarian method the optimal assignment obtained for the following assignment problem to minimize the total cost is:

(a) 1 – C, 2 – B, 3 – D, 4 – A
(b) 1 – B, 2 – C, 3 – A, 4 – D
(c) 1 – A, 2 – B, 3 – C, 4 – D
(d) 1 – D, 2 – A, 3 – B, 4 – C
Answer:
(a) 1 – C, 2 – B, 3 – D, 4 – A

Question 9.
The assignment problem is said to be unbalanced if
(a) Number of rows is greater than the number of columns
(b) Number of rows is lesser than number of columns
(c) Number of rows is equal to the number of columns
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 10.
The assignment problem is said to be balanced if
(a) Number of rows is greater than the number of columns
(b) Number of rows is lesser than number of columns
(c) Number of rows is equal to the number of columns
(d) If the entry of rows is zero
Answer:
(c) Number of rows is equal to number of columns

Question 11.
The assignment problem is said to be balanced if it is a
(a) Square matrix
(b) Rectangular matrix
(c) Unit matrix
(d) Triangular matrix
Answer:
(a) Square matrix

Question 12.
In an assignment problem if the number of rows is greater than the number of columns then
(a) Dummy column is added
(b) Dummy row is added
(c) Row with cost 1 is added
(d) Column with cost 1 is added
Answer:
(a) Dummy column is added

Question 13.
In a 3 machine and 5 jobs problem, the least of processing times on machines A, B, and C are 5, 1 and 3 hours and the highest processing times are 9, 5 and 7 respectively, then it can be converted to a 2 machine problem if the order of the machines is:
(a) B – A – C
(b) A – B – C
(c) C – B – A
(d) Any order
Answer:
(b) A – B – C

Question 14.
The objective of an assignment problem is to assign
(a) Number of jobs to equal number of persons at maximum cost
(b) Number of jobs to equal number of persons at minimum cost
(c) Only the maximize cost
(d) Only to minimize cost
Answer:
(b) Number of jobs to equal number of persons at minimum cost

(II) Fill in the blanks.

Question 1.
An assignment problem is said to be unbalanced when ___________
Answer:
the number of rows is not equal to the number of columns

Question 2.
When the number of rows is equal to the Number of columns then the problem is said to be ___________ assignment problem.
Answer:
balanced

Question 3.
For solving assignment problem the matrix should be a ___________
Answer:
square matrix

Question 4.
If the given matrix is not a ___________ matrix, the assignment problem is called an unbalanced problem.
Answer:
square

Question 5.
A dummy row(s) or column(s) with the cost elements as ___________ the matrix of an unbalanced assignment problem as a square matrix.
Answer:
zero

Question 6.
The time interval between starting the first job and completing the last, job including the idle time (if any) in a particular order by the given set of machines is called ___________
Answer:
Total elapsed time

Question 7.
The time for which a machine j does not have a job to process to the start of job i is called ___________
Answer:
Idle time

Question 8.
The maximization assignment problem is transformed to minimization problem by subtracting each entry in the table from the ___________ value in the table.
Answer:
maximum

Question 9.
When the assignment problem has more than one solution, then it is ___________ optimal solution.
Answer:
multiple

Question 10.
The time required for printing four books A, B, C, and D is 5, 8, 10, and 7 hours. While its data entry requires 7, 4, 3, and 6 hrs respectively. The sequence that minimizes total elapsed time is ___________
Answer:
A – D – B – C

(III) State whether each of the following is True or False.

Question 1.
One machine – one job is not an assumption in solving sequencing problems.
Answer:
False

Question 2.
If there are two least processing times for machine A and machine B, priority is given for the processing time which has the lowest time of the adjacent machine.
Answer:
True

Question 3.
To convert the assignment problem into a maximization problem, the smallest element in the matrix is deducted from all other elements.
Answer:
False

Question 4.
The Hungarian method operates on the principle of matrix reduction, whereby the cost table is reduced to a set of opportunity costs.
Answer:
True

Question 5.
In a sequencing problem, the processing times are dependent on the order of processing the jobs on machines.
Answer:
False

Question 6.
The optimal assignment is made in the Hungarian method to cells in the reduced matrix that contain a Zero.
Answer:
True

Question 7.
Using the Hungarian method, the optimal solution to an assignment problem is fund when the minimum number of lines required to cover the zero cells in the reduced matrix equals the number of people.
Answer:
True

Question 8.
In an assignment problem, if a number of columns are greater than the number of rows, then a dummy column is added.
Answer:
False

Question 9.
The purpose of a dummy row or column in an assignment problem is to obtain a balance between a total number of activities and a total number of resources.
Answer:
True

Question 10.
One of the assumptions made while sequencing n jobs on 2 machines is: two jobs must be loaded at a time on any machine.
Answer:
False

(IV) Solve the following problems.

Part – I

Question 1.
A plant manager has four subordinates, and four tasks to be performed. The subordinates differ in efficiency and the tasks differ in their intrinsic difficulty. This estimate of the times each man would take to perform each task is given in the effectiveness matrix below.

How should the tasks be allocated, one to a man, as to minimize the total man-hours?
Solution:
The hr matrix is given by

Subtracting row minimum from all values in that row we get

Subtracting column minimum from all values in that column we get

The minimum no. of lines covering ail the zeros (4) is equal to the order of the matrix (4)
∴ The assignment is possible.

The assignment is
A → I, B → III, C → II, D → IV
For the minimum hrs. take the corresponding value from the hr matrix.
Minimum hrs = 7 + 3 + 18 + 9 = 37 hrs

Question 2.
A dairy plant has five milk tankers, I, II, III, IV & V. These milk tankers are to be used on five delivery routes A, B, C, D & E. The distances (in kms) between the dairy plant and the delivery routes are given in the following distance matrix.

How should the milk tankers be assigned to the chilling centre so as to minimize the distance travelled?
Solution:
The distance matrix is given by

Subtracting row minimum from all values in that row we get

Subtracting column minimum from each value in that column we get

The number of lines covering all the zeros (3) is less than the order of the matrix (5) so the assignment is not possible. The modification is required.
The minimum uncovered value (15) is subtracted from uncovered values and added to the values at the intersection. The numbers on the lines remain the same. We get

The minimum lines covering all the zeros (4) are less than the order of the matrix (5) so the assignment is not possible. The modification is required the minimum uncovered value (5) is subtracted from uncovered values and added to the values at the intersection. The numbers on the lines remain the same we get

The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) So assignment is possible.
The assignment is
A → II, B → III, C → V, D → I, E → IV
Total minimum distance is = 120 + 120 + 175 + 40 + 70 = 525 kms.

Question 3.
Solve the following assignment problem to maximize sales:

Solution:
As it is a maximization problem so we need to convert it into a minimization problem.
Subtracting all the values from the maximum value (19) we get

Also, it is an unbalanced problem so we need to add a dummy row (E) with all values zero, we get

Subtracting row minimum from all values in that row we get

Subtracting column minimum from all values in that column we get the same matrix

The minimum number of lines covering all the zero (4) is less than the order of the matrix (5) So assignment is not possible. The modification is required. The minimum uncovered value (2) is subtracted from the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so the assignment is not possible. The modification is required. The minimum uncovered value (1) is subtracted from the uncovered value and added to the values at the intersection. The values on the lines remain the same. We get

The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

The assignment is
A → V, B → II, C → IV, D → III, E → I
No salesman goes to I as E is a dummy row.
For the maximum value take the corresponding values from the original matrix.
We get Maximum value = 15 + 19 + 14 + 17 + 0 = 65 units

Question 4.
The estimated sales (tons) per month in four different cities by five different managers are given below:

Find out the assignment of managers to cities in order to maximize sales.
Solution:
This is a maximizing problem. To convert it into minimizing problem subtract all the values of the matrix from the maximum (largest) value (39) we get

Also as it is an unbalanced problem so we have to add a dummy column (T) with all the values as zero. We get

Subtracting row minimum from all values in that row we get the same matrix
Subtracting column minimum from all values in that column we get

The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so assignments are not possible. The modification is required. The minimum uncovered value (1) is subtracted from the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

So I → S, II → T, III → Q, IV → P, V → R.
As T is dummy manager II is not given any city.
To find the maximum sales we take the corresponding value from the original matrix
Total maximum sales = 35 + 39 + 36 + 35 = 145 tons

Question 5.
Consider the problem of assigning five operators to five machines. The assignment costs are given in the following table.

Operator A cannot be assigned to machine 3 and operator C cannot be assigned to machine 4. Find the optimal assignment schedule.
Solution:
This is a restricted assignment problem, so we assign a very high cost (oo) to the prohibited cells we get

Subtracting row minimum from all values in that row we get.

Subtracting column minimum from all values in that column we get

As the minimum number of lines covering all the zeros (4) is equal to the order of the matrix (5) so the assignment is not possible. The modification is required. The minimum uncovered value (2) is subtracted from all the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

As the minimum number of lines covering all the zeros (5) is equal to the order of the matrix, assignment is the possible

So A → 4, B → 3, C → 2, D → 1, E → 5
For the minimum cost take the corresponding values from the cost matrix we get
Total minimum cost = 3 + 3 + 4 + 3 + 7 = 20 units

Question 6.
A chartered accountant’s firm has accepted five new cases. The estimated number of days required by each of their five employees for each case are given below, where-means that the particular employee can not be assigned the particular case. Determine the optimal assignment of cases of the employees so that the total number of days required to complete these five cases will be minimum. Also, find the minimum number of days.

Solution:
This is a restricted assignment problem so we assign a very high cost (∞) to all the prohibited cells. The day matrix becomes

Subtracting row minimum from all values in that row we get

Subtracting column minimum from all values in that column we get

The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so the assignment is not possible, The modification is required. The minimum uncovered value (1) is subtracted from all the uncovered values and added to the values at the intersection. The values on the lines remain the same, we get

The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

So E₁ → I, E₂ → IV, E₃ → II, E₄ → V, E₅ → III
To find the minimum number of days we take the corresponding values from the day matrix.
Total minimum number of days = 6 + 6 + 6 + 6 + 3 = 27 days

Part – II

Question 1.
A readymade garments manufacture has to process 7 items through two stages of production, namely cutting and sewing. The time taken in hours for each of these items in different stages are given below:

Find the sequence in which these items are to be processed through these stages so as to minimize the total processing time. Also, find the idle time of each machine.
Solution:
Let A = cutting and B = sewing. So we have

Observe min {A, B} = 2 for item 1 for B.

The problem reduces to

Now min {A, B} = 3 for item 3 for A

The problem reduces to

New min {A , B} = 4 for item 4 for A.

The problem reduces to

Now min(A, B} = 5 for item 6 for B

The problem reduces to

Now min {A, B} = 6 for item 5 for A and item 2 for B

Now only 7 is left
∴ The optimal sequence is

Worktable

Total elapsed time = 46 hrs
Idle time for A (cutting) = 46 – 44 = 2 hrs
Idle time for B (Sewing) = 4 hrs

Question 2.
Five jobs must pass through a lathe and a surface grinder, in that order. The processing times in hours are shown below. Determine the optimal sequence of the jobs. Also, find the idle time of each machine.

Solution:
Let A = lathe and B = surface grinder. We have

Observe min {A, B} = 1 for job II for A

The problem reduces to

Now min {A, B} = 2 for job IV for A

The problem reduces to

Now min {A, B} = 3 for job I for B

The problem reduces to

Now min {A, B} = 5 for jobs III and V for A
∴ We have two options

or

We take the first one.
Worktable

Total elapsed time = 21 hrs
Idle time for A (lathe) = 21 – 17 = 4 hrs
Idle time for B (surface grinder) = 3 hrs

Question 3.
Find the sequence that minimizes the total elapsed time to complete the following jobs. Each job is processed in order AB.

Determine the sequence for the jobs so as to minimize the processing time. Find the total elapsed time and the idle time for both machines.
Solution:
Observe min {A, B} = 3 for job VII on B.

The problem reduces to

Now min {A, B} = 4 for job IV on B.

The problem reduces to

Now min {A, B} = 5 for job III & V on A. we have two options

or

We take the first one
The problem reduces to

Now min {A, B} = 5 for job II on A

The problem reduces to

Now min {A, B} = 7 for a job I on B and for job VI on A
∴ The optional sequence is

Worktable

Total elapsed time = 55 units
Idle time for A = 55 – 52 = 3 units
Idle time for B = 9 units.

Question 4.
A toy manufacturing company has five types of toys. Each toy has to go through three machines A, B, C in the order ABC. The time required in hours for each process is given in the following table.

Solve the problem for minimizing the total elapsed time.
Solution:
Min A = 12, Max B = 12
As min A ≥ max B.
The problem can be converted into two machine problems.
Let G and H be two fictitious machines such that G = A + B and H = B + C, We get

Now min {G, H} = 16 for type 3 on G

The problem reduces to

Min (G, H} = 18 for type 1, 4 & 5 on H
We have more than one option, we take

Now only type 2 is left.
∴ The optional sequence is

Worktable

Total elapsed time = 102 hours
Idle time for A = 102 – 84 = 18 hours
Idle time for B = 54 + (102 – 94) = 62 hours
Idle time for C = 38 hours

Question 5.
A foreman wants to process 4 different jobs on three machines: a shaping machine, a drilling machine, and a tapping, the sequence of operations being shaping-drilling-tapping. Decide the optimal sequence for the four jobs to minimize the total elapsed time. Also, find the total elapsed time and the idle time for every machine.

Solution:
The time matrix is

Min A = 8, Max B = 8, as min A ≥ max B.
The problem can be converted into a two-machine problem.
Let G and H be two fictitious machines such that
G = A + B and H = B + C we get

Observe min (G, H} = 12 for job 2 on H

The problem reduces to

Now min {G, H} = 14 for job 3 on G and job 4 on H

Now only job 1 is left.
∴ The optimal sequence is

Worktable

Total elapsed time = 74 min
Idle time for A (shapping) = 74 – 62 = 12 min
Idle time for B (Drilling) = 47 + (74 – 70) = 51 min
Idle time for C (trapping) = 31 min

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

(I) Choose the correct option from the given alternatives:

Question 1.
The order and degree of \(\left(\frac{d y}{d x}\right)^{3}-\frac{d^{3} y}{d x^{3}}+y e^{x}=0\) are respectively.
(a) 3, 1
(b) 1, 3
(c) 3, 3
(d) 1, 1
Answer:
(a) 3, 1

Question 2.
The order and degree of \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]^{\frac{2}{3}}=8 \frac{d^{3} y}{d x^{3}}\) are respectively
(a) 3, 1
(c) 3, 3
(b) 1, 3
(d) 1, 1
Answer:
(c) 3, 3

Question 3.
The differential equation of y = k₁ + \(\frac{k_{2}}{x}\) is
(a) \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
(d) \(x \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
Answer:
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)

Question 4.
The differential equation of y = k₁ e^x + k₂ e^-x is
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
(b) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}+y \frac{d y}{d x}=0\)
(d) \(\frac{d^{2} y}{d x^{2}}+y=0\)
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)

Question 5.
The solution of \(\frac{d y}{d x}\) = 1 is
(a) x + y = c
(b) xy = c
(c) x² + y² = c
(d) y – x = c
Answer:
(d) y – x = c

Question 6.
The solution of \(\frac{d y}{d x}+\frac{x^{2}}{y^{2}}=0\) is
(a) x³ + y³ = 7
(b) x² + y² = c
(c) x³ + y³ = c
(d) x + y = c
Answer:
(c) x³ + y³ = c

Question 7.
The solution of x \(\frac{d y}{d x}\) = y log y is
(a) y = ae^x
(b) y = be^2x
(c) y = be^-2x
(d) y = e^ax
Answer:
(d) y = e^ax

Question 8.
Bacterial increases at a rate proportional to the number present. If the original number M doubles in 3 hours, then the number of bacteria will be 4M in
(a) 4 hours
(b) 6 hours
(c) 8 hours
(d) 10 hours
Answer:
(b) 6 hours

Question 9.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is
(a) x
(b) -x
(c) e^x
(d) e^-x
Answer:
(c) e^x

Question 10.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is e^-x, then its solution is
(a) ye^-x = x + c
(b) ye^x = x + c
(c) ye^x = 2x + c
(d) ye^-x = 2x + c
Answer:
(a) ye^-x = x + c

(II) Fill in the blanks:

Question 1.
The order of highest derivative occurring in the differential equation is called ________ of the differential equation.
Answer:
order

Question 2.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called ________ of the differential equation.
Answer:
degree

Question 3.
A solution of differential equation that can be obtained from the general solution by giving particular values to the arbitrary constants is called _________ solution.
Answer:
particular

Question 4.
Order and degree of a differential equation are always _________ integers.
Answer:
positive

Question 5.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is _________
Answer:
e^-x

Question 6.
The differential equation by eliminating arbitrary constants from bx + ay = ab is _________
Answer:
\(\frac{d^{2} y}{d x^{2}}=0\)

(III) State whether each of the following is True or False:

Question 1.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is e^-x.
Answer:
True

Question 2.
The order and degree of a differential equation are always positive integers.
Answer:
True

Question 3.
The degree of a differential equation is the power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any.
Answer:
True

Question 4.
The order of highest derivative occurring in the differential equation is called the degree of the differential equation.
Answer:
False

Question 5.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called the order of the differential equation.
Answer:
False

Question 6.
The degree of the differential equation \(e^{\frac{d y}{d x}}=\frac{d y}{d x}+c\) is not defined.
Answer:
True

(IV) Solve the following:

Question 1.
Find the order and degree of the following differential equations:
(i) \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given differential equation is \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
∴ \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3}=\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3
∴ order = 3 and degree = 3

(ii) \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
Solution:
The given differential equation is \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ order = 1, degree = 2.

Question 2.
Verify that y = log x + c is a solution of the differential equation \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\).
Solution:
y = log x + c
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{1}{x}+0=\frac{1}{x}\)
∴ x\(\frac{d y}{d x}\) = 1
Differentiating again w.r.t. x, we get
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \times 1=0\)
∴ \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
This shows that y = log x + c is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)

Question 3.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = 1 + x + y + xy
Solution:
\(\frac{d y}{d x}\) = 1 + x + y + xy
∴ \(\frac{d y}{d x}\) = (1 + x) + y(1 + x) = (1 + x)(1 + y)
∴ \(\frac{1}{1+y}\) dy = (1 + x) dx
Integrating, we get
∫\(\frac{1}{1+y}\) dy = ∫(1 + x) dx
∴ log|1 + y| = x + \(\frac{x^{2}}{2}\) + c
This is the general solution.

(ii) \(e^{d y / d x}=x\)
Solution:

∴ from (1), the general solution is
y = x log x – x + c, i.e. y = x(log x – 1) + c.

(iii) dr = ar dθ – θ dr
Solution:
dr = ar dθ – θ dr
∴ dr + θ dr = ar dθ
∴ (1 + θ) dr = ar dθ
∴ \(\frac{d r}{r}=\frac{a d \theta}{1+\theta}\)
On integrating, we get
\(\int \frac{d r}{r}=a \int \frac{d \theta}{1+\theta}\)
∴ log |r| = a log |1 + θ| + c
This is the general solution.

(iv) Find the differential equation of the family of curves y = e^x (ax + bx²), where a and b are arbitrary constants.
Solution:
y = e^x (ax + bx²)
ax + bx² = ye^-x …….(1)
Differentiating (1) w.r.t. x twice and writing \(\frac{d y}{d x}\) as y₁ and \(\frac{d^{2} y}{d x^{2}}\) as y₂, we get


This is the required differential equation.

Question 4.
Solve \(\frac{d y}{d x}=\frac{x+y+1}{x+y-1}\) when x = \(\frac{2}{3}\) and y = \(\frac{1}{3}\).
Solution:

Question 5.
Solve y dx – x dy = -log x dx.
Solution:
y dx – x dy = -log x dx
∴ y dx – x dy + log x dx = 0
∴ x dy = (y + log x) dx
∴ \(\frac{d y}{d x}=\frac{y+\log x}{x}=\frac{y}{x}+\frac{\log x}{x}\)
∴ \(\frac{d y}{d x}-\frac{1}{x} \cdot y=\frac{\log x}{x}\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 6.
Solve y log y \(\frac{d x}{d y}\) + x – log y = 0.
Solution:

Question 7.
Solve (x + y) dy = a² dx
Solution:

Question 8.
Solve \(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\)
Solution:
\(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\) ……..(1)
This is a linear differential equation of the form

This is the general solution.

Question 9.
The rate of growth of the population is proportional to the number present. If the population doubled in the last 25 years and the present population is 1 lakh, when will the city have a population of 400000?
Solution:
Let P be the population at time t years.
Then the rate of growth of the population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\)= k dt
On integrating, we get
\(\int \frac{d P}{P}=k \int d t\)
∴ log P = kt + c
The population doubled in 25 years and present population is 1,00,000.
∴ initial population was 50,000
i.e. when t = 0, P = 50000
∴ log 50000 = k × 0 + c
∴ c = log 50000
∴ log P = kt + log 50000
When t = 25, P = 100000
∴ log 100000 = k × 25 + log 50000
∴ 25k = log 100000 – log 50000 = log(\(\frac{100000}{50000}\))
∴ k = \(\frac{1}{25}\) log 2
∴ log P = \(\frac{t}{25}\) log 2 + log 50000
If P = 400000, then
log 400000 = \(\frac{t}{25}\) log 2 + log 50000
∴ log 400000 – log 50000 = \(\frac{t}{25}\) log 2
∴ log(\(\frac{400000}{50000}\)) = \(\log (2)^{t / 25}\)
∴ log 8 = \(\log (2)^{t / 25}\)
∴ 8 = \((2)^{t / 25}\)
∴ \((2)^{t / 25}\) = (2)³
∴ \(\frac{t}{25}\) = 3
∴ t = 75
∴ the population will be 400000 in (75 – 25) = 50 years.

Question 10.
The resale value of a machine decreases over a 10 years period at a rate that depends on the age of the machine. When the machine is x years old, the rate at which its value is changing is ₹ 2200(x – 10) per year. Express the value of the machine as a function of its age and initial value. If the machine was originally worth ₹ 1,20,000 how much will it be worth when it is 10 years old?
Solution:
Let V be the value of the machine after x years.
Then rate of change of the value is \(\frac{d V}{d x}\) which is 2200(x – 10)
∴ \(\frac{d V}{d x}\) = 2200(x – 10)
∴ dV = 2200(x – 10) dx
On integrating, we get
∫dV = 2200∫(x – 10) dx
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + c
Initially, i.e. at x = 0, V = 120000
∴ 120000 = 2200 × 0 + c = c
∴ c = 120000
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + 120000 …….(1)
This gives value of the machine in terms of initial value and age x.
We have to find V when x = 10.
When x = 10, from (1)
V = 2200[\(\frac{100}{2}\) – 100] + 120000
= 2200 [-50] + 120000
= -110000 + 120000
= 10000
Hence, the value of the machine after 10 years will be ₹ 10000.

Question 11.
Solve y² dx + (xy + x²) dy = 0
Solution:

Question 12.
Solve x²y dx – (x³ + y³) dy = 0
Solution:

Question 13.
Solve yx \(\frac{d y}{d x}\) = x² + 2y²
Solution:

Question 14.
Solve (x + 2y³) \(\frac{d y}{d x}\) = y
Solution:
(x + 2y³) \(\frac{d y}{d x}\) = y
∴ x + 2y³ = y \(\frac{d x}{d y}\)

This is the general solution.

Question 15.
Solve y dx – x dy + log x dx = 0
Solution:
y dx – x dy + log x dx = 0
∴ (y + log x) dx = x dy


This is the general solution.

Question 16.
Solve \(\frac{d y}{d x}\) = log x dx
Solution:
\(\frac{d y}{d x}\) = log x dx
∴ dy = log x dx
On integrating, we get
∫dy = ∫log x . 1 dx
∴ y = (log x) ∫1 dx – \(\int\left[\left\{\frac{d}{d x}(\log x)\right\} \cdot \int 1 d x\right] d x\)
∴ y = (log x) . x – \(\int \frac{1}{x} \cdot x d x\)
∴ y = x log x – ∫1 dx
∴ y = x log x – x + c
This is the general solution.

Question 17.
y log y \(\frac{d x}{d y}\) = log y – x
Solution: