Class 12

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 5.1 गुरुबानी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 5.1 गुरुबानी

12th Hindi Guide Chapter 5.1 गुरुबानी Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) संजाल पूर्ण कीजिए :

उत्तर :

(आ) कृति पूर्ण कीजिए :
(a) आकाश के दीप

उत्तर :

शब्द संपदा

प्रश्न 2.
लिखिए :

उत्तर:

अभिव्यक्ति

प्रश्न 3.
(अ) ‘गुरु बिन ज्ञान न होई उक्ति पर अपने विचार लिखिए।
उत्तर :
ज्ञान की कोई सीमा नहीं है। विभिन्न क्षेत्रों में भिन्न-भिन्न प्रकार के ज्ञान की आवश्यकता होती है। यह ज्ञान हमें किसी-नकिसी व्यक्ति से मिलता है। जिस व्यक्ति से हमें यह ज्ञान मिलता है, वही हमारे लिए गुरु होता है। बचपन में बच्चे का पालन-पोषण कर उसे बड़ा करके बोलने-चालने और बोली-भाषा सिखाने का काम माता करती है। उस समय वह बच्चे की गुरु होती है। बड़े होने पर बच्चे को विद्यालय में शिक्षकों से ज्ञान प्राप्त होता है।

पढ़-लिखकर। जीवन में पदार्पण करने पर हर व्यक्ति को किसी-न-किसी से अपने काम-काज करने का ढंग सीखना पड़ता है। इस तरह के लोग हमारे लिए गुरु के समान होते हैं। मनुष्य गुरुओं से ही सीखकर विभिन्न कलाओं में पारंगत होता है। बड़े-बड़े विद्वान, विचारक, राजनेता,। समाजशास्त्री, वैज्ञानिक, अर्थशास्त्री अपने-अपने गुरुओं से ज्ञान। प्राप्त करके ही महान हुए हैं। अच्छी शिक्षा देने वाला गुरु होता है। गुरु की महिमा अपरंपार है।

गुरु ही हमें गलत या सही में भेद करना सिखाते हैं। वे अपने मार्ग से भटके हुए लोगों को सही मार्ग दिखाते हैं। यह सच है कि गुरु के बिना ज्ञान नहीं होता।

(आ) ‘ईश्वर भक्ति में नामस्मरण का महत्त्व होता है’, इस विषय पर अपना मंतव्य लिखिए।
उत्तर :
ईश्वरभक्ति के अनेक मार्ग बताए गए हैं। उनमें सबसे सरल मार्ग ईश्वर का नाम स्मरण करना है। नाम स्मरण करने का कोई नियम नहीं है। भक्त जहाँ भी हो, चाहे जिस हालत में हो, ईश्वर का नाम स्मरण कर सकता है। अधिकांश लोग ईश्वर भक्ति का यही मार्ग अपनाते हैं।

उठते-बैठते, आते-जाते तथा काम करते हुए नाम स्मरण किया जा सकता है। भजन-कीर्तन भी ईश्वर के नाम स्मरण का ही एक रूप है। ईश्वर भक्ति के इस मार्ग में प्रभु के गुणों का वर्णन किया जाता है। इसमें धार्मिक पूजा-स्थलों में जाने की जरूरत नहीं होती।

गृहस्थ अपने घर में ईश्वर का नाम स्मरण कर उनके गुणों का बखान कर सकता है। इससे नाम स्मरण करने वालों को मानसिक शांति मिलती हैं और मन प्रसन्न होता है। कहा गया है – ‘कलियुग केवल नाम अधारा, सुमिरि-सुमिर नर उतरें पारा।’ इसमें ईश्वर भक्ति में नाम स्मरण का ही महत्त्व बताया गया है।

रसास्वादन

प्रश्न 4.
‘गुरुनिष्ठा और भक्तिभाव से ही मानव श्रेष्ठ बनता है’ इस कथन के आधार पर कविता का रसास्वादन कीजिए।
उत्तर :
गुरु नानक का कहना है कि बिना गुरु के मनुष्य को ज्ञान नहीं मिलता। मनुष्य के अंतःकरण में अनेक प्रकार के मनोविकार होते हैं, जिनके वशीभूत होने के कारण उसे वास्तविकता के दर्शन नहीं होते। वह अहंकार में डूबा रहता है और उसमें गलत-सही का विवेक नहीं रह जाता।

ये मनोविकार दूर होता है गुरु से ज्ञान प्राप्त होने पर। यदि गुरु के प्रति सच्ची श्रद्धा और उनमें पूरा विश्वास हो तो मनुष्य के अंतःकरण के इन विकारों को दूर होने में समय नहीं लगता। मन के विकार दूर हो जाने पर मनुष्य में सबको समान दृष्टि से देखने की भावना उत्पन्न हो जाती है।

उसके लिए कोई बड़ा या छोटा अथवा ऊँच-नीच नहीं रह जाता। उसे मनुष्य में ईश्वर के दर्शन होने लगते हैं। उसके लिए ईश्वर की भक्ति भी सुगम हो जाती है। गुरु नानक ने अपने पदों में इस बात को सरल ढंग से कहा है। … इस तरह गुरु के प्रति सच्ची निष्ठा और भक्ति-भावना से मनुष्य श्रेष्ठ मानव बन जाता है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) गुरु नानक जी की रचनाओं के नाम :
…………………………………………………………
उत्तर :
गुरुग्रंथसाहिब आदि।

(आ) गुरु नानक जी की भाषाशैली की विशेषताएं:
…………………………………………………………
…………………………………………………………
उत्तर :
गुरु नानक जी सहज-सरल भाषा में अपनी बात कहने में माहिर हैं। आपकी काव्य भाषा में फारसी, मुल्तानी, पंजाबी, सिंधी, खड़ी बोली और अरबी भाषा के शब्द समाए हए हैं। आपने पद शैली में रचना की है। ‘पद’ काव्य रचना की गेय शैली है।

प्रश्न 6.
निम्नलिखित वाक्यों में अधोरेखांकित शब्दों का वचन परिवर्तन करके वाक्य फिर से लिखिए :

(1) सत्य का मार्ग सरल है।
उत्तर :
सत्य के मार्ग सरल हैं।

(2) हथकड़ियाँ लगाकर बादशाह अकबर के दरबार को ले चले।
उत्तर :
हथकड़ी लगाकर बादशाह अकबर के दरबार को ले चले।

(3) चप्पे-चप्पे पर काटों की झाड़ियाँ हैं।
उत्तर :
चप्पे-चप्पे पर काँटे की झाड़ी है।

(4) सुकरात के लिए यह जहर का प्याला है।
उत्तर :
सुकरात के लिए ये जहर के प्याले हैं।

(5) रूढ़ि स्थिर है, परंपरा निरंतर गतिशील है।
उत्तर :
रूढ़ियाँ स्थिर हैं, परंपराएँ निरंतर गतिशील हैं।

(6) उनकी समस्त खूबियों-खामियों के साथ स्वीकार कर अपना लें।
उत्तर :
उनकी समस्त खूबी-कमी के साथ स्वीकार कर अपना लें।

(7) वे तो रुपये सहेजने में व्यस्त थे।
उत्तर :
वह तो रुपया सहेजने में व्यस्त था।

(8) ओजोन विघटन के खतरे क्या-क्या हैं?
उत्तर :
ओजोन विघटन का खतरा क्या है?

(9) शब्द में अर्थ छिपा होता है।
उत्तर :
शब्दों में अर्थ छिपे होते हैं।

(10) अभी से उसे ऐसा कोई कदम नहीं उठाना चाहिए।
उत्तर :
अभी से उसे ऐसे कोई कदम नहीं उठाने चाहिए।

Hindi Yuvakbharati 12th Digest Chapter 5.1 गुरुबानी Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)
पदयाश क्र. 1
प्रश्न. निम्नलिखितपद्यांशपढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : गुरु को महत्त्व न देने वाले ऐसे होते हैं –
(1) ……………………………………..
(2) ……………………………………..
(3) ……………………………………..
(4) ……………………………………..
उत्तर :
(1) व्यर्थ ही उगने वाले तिल की झाड़ियों के समान।
(2) केवल ऊपर से फलते-फूलते दिखाई देते हैं।
(3) उनके अंदर गंदगी और मैल भरा होता है।
(4) लोग उनसे किनारा कर लेते हैं।

प्रश्न 2.
उत्तर लिखिए :
(1) मन के लिए यह कहा गया है – ……………………………………..
(2) संसार में ऐसे लोग विरले होते हैं – ……………………………………..
(3) साधक को अपना ध्यान इसमें लगाना है – ……………………………………..
(4) प्रभु के दर्शन के लिए आवश्यक है – ……………………………………..
उत्तर :
(1) दिन-रात भगवान के गुणों का स्मरण करना।
(2) जो एक क्षण भी भगवान का नाम नहीं भूलते।
(3) भगवान में।
(4) साधक को अहंभाव का त्याग करना।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) तन = …………………………….
(2) मसि = …………………………….
(3) मति = …………………………….
(4) विरले = …………………………….
उत्तर :
(1) (1) तन = शरीर।
(2) मसि = स्याही।
(3) मति = बुद्धि।
(4) बिसरे = भूले।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

(2) संजाल पूर्ण कीजिए :

उत्तर :

रसास्वादन। मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर दोहो-पदों का रसास्वादन कीजिए:
उत्तर :
(1) रचना का शीर्षक : गुरुवाणी।
(2) रचनाकार : गुरु नानक
(3) कविता की केंद्रीय कल्पना : प्रस्तुत दोहों-पदों में गुरु के .. महत्त्व, ईश्वर की महिमा तथा प्रभु का नाम स्मरण करने से ईश्वर प्राप्ति की बात कही गई है।

(4) रस-अलंकार :
गगन में थाल, रवि-चंद्र दीपक बने।
तारका मंडल जनक मोती।
धूप मलयानिल, पवनु चैवरो करे।
सकल वनराइ कुलंत जोति।।

यहाँ कहा गया है कि गगन ही थाल है; सूर्य-चंद्रमा ही दीपक हैं; तारका मंडल ही मोती है; मलयानिल ही धूप-गंध है; जंगल की समस्त वनस्पतियाँ फूल हैं। इसलिए रूपक अलंकार है।

(5) प्रतीक विधान : प्रस्तुत कविता में कवि ने गुरु का चिंतन न करने वालों तथा अपने आप को ही ज्ञानी समझने वालों को बिना संरक्षक वाले व्यक्ति कहा गया है। इसके लिए कवि ने निर्जन स्थान पर उगी हुई तिल्ली के पौधे का प्रतीक के रूप में उपयोग किया है।

(6) कल्पना : जीवन में गुरु का महत्त्व, कर्म की महानता तथा प्रभु के नाम का स्मरण ही प्रभु प्राप्ति का मार्ग है।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
नानक गुरु न चेतनी मनि आपणे सुचेत।
छूते तिल बुआड़ जिऊ सुएं अंदर खेत।
खेते अंदर छुट्टया कहु नानक सऊ नाह।
फली अहि फूली अहि बपुड़े भी तन विच स्वाह।

इन पंक्तियों में कवि ने गुरु का महत्त्व न समझने और अपने को ज्ञानी मानने वालों को मरुस्थल में पाई जानेवाली तिल्ली की फली में मिलने वाली राख कहा है, जो बहुत ही सटीक है।

(8) कविता पसंद आने का कारण : गुरु नानक ने इन पंक्तियों में यह बताया है कि कुछ लोग ऐसे होते हैं, जो गुरु को महत्त्व नहीं देते और अपने आप को ही ज्ञानी मान बैठते हैं। गुरु नानक जी ऐसे लोगों की तुलना उस तिल के पौधे से करते हैं, जो किसी निर्जन स्थान पर अपने आप उग आता है और उसको खाद-पानी देने वाला कोई भी नहीं होता। इसलिए उस पौधे का विकास नहीं हो पाता। ऐसे पौधे में फूल भी लगते हैं और फली भी लगती है, पर फली के अंदर दाने नहीं पड़ते, उसमें गंदगी और राख ही होती है। वैसी ही हालत बिना गुरु के मनुष्य की होती है। ऐसे लोगों का मानसिक विकास नहीं हो पाता।

1. अलंकार :

निम्नलिखित काव्य पंक्तियों में प्रयुक्त अलंकार पहचानकर लिखिए :
(1) तरुवर की छायानुवाद सी,
उपमा-सी-भावुकता-सी,
अविदित भावाकुल भाषा-सी,
कटी-छूटी नव कविता-सी।

(2) उदित उदय गिरि मंच पर, रघुवर बाल पतंग।
विकसे संत सरोज सब हरषे लोचन भंग।

(3) जिन दिन देखे वे कुसुम, गई सो बीति बहार।
अब अलि रही गुलाब में, अपत कँटीली डार।

(4) छिप्यो छबीली मुँह लसै नीले अंचल चीर।
मनो कलानिधि झलमले, कालिंदी के तीर।

(5) छाले परिबे के डरनि, सकै न हाथ छुवाय।
झिझकत हिये गुलाब के सँवा सँवावत पाय।
उत्तर :
(1) उपमा अलंकार
(2) रूपक अलंकार
(3) अन्योक्ति अलंकार
(4) उत्प्रेक्षा अलंकार
(5) अतिशयोक्ति अलंकार।

2. रस :

निम्नलिखित काव्य पंक्तियों में प्रयुक्त रस पहचानकर लिखिए :
(1) भूषन बसन बिलोकत सिय के।
प्रेम-बिबस मन, कंप पुलक तनु
नीरज नयन नीर भरे पिय के।
सकुचत, कहत, सुमिरि उर उमगत
सील, सनेह सुगुन गुन तिय के।

(2) लीन्हों उखारि पहार बिसाल
चल्यौ तेहि काल, बिलंब न लायौ।
मारुत नंदन मारुत को, मन को
खगराज को बेगि लजायो।।

(3) रामहि बाम समेत पठै बन,
शोक के भार में भुंजौ भरत्थहि।
जो धनु हाथ धरै रघुनाथ तो
आज अनाथ करौं दशरत्थहि।
उत्तर :
(1) शृंगार रस
(2) अद्भुत रस
(3) रौद्र रस।

3. मुहावरे :

निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :

(1) सिर खपाना।
अर्थ : कठिन परिश्रम करना।
वाक्य : कई साल तक सिर खपाने के बाद आखिरकार उस युवक को सी.ए. की डिग्री मिल ही गई।

(2) उगल देना।
अर्थ : भेद बता देना।
वाक्य : पुलिस का डंडा पड़ते ही चोर ने चुराई गई संपत्ति को छिपाकर रखे जाने के स्थान की बात उगल दी।

(3) कब्र में पैर लटकना।
अर्थ : मरने के समीप होना।
वाक्य : कोरोना के प्रसार से अनेक मरीजों के पैर कब्र में लटक गए हैं।

(4) पापड़ बेलना।
अर्थ : कड़ी मेहनत करना।
वाक्य : आज जो लड़का जिलाधीश के पद पर आसीन है, इस पद तक पहुँचने में इसने बहुत पापड़ बेले हैं।

(5) मरने की फुरसत न होना।
अर्थ : कामों में बहुत व्यस्त होना।
वाक्य : मुनीम जी तो अपने काम में इतने व्यस्त हैं कि उन्हें मरने की भी फुरसत नहीं है।

4. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों को कोष्ठक में सूचित काल में परिवर्तन कीजिए :
(1) वे सभी धर्मों को समान दृष्टि से देखते थे। (सामान्य वर्तमानकाल)
(2) दिन रात महान आरती होती है। (अपूर्ण भूतकाल)
(3) अनहद नाद का वाद्य बज रहा है। (सामान्य भविष्यकाल)
(4) श्रद्धा भक्त की सबसे बड़ी भेंट होगी। (पूर्ण भूतकाल)
(5) तुम्हारे अनेक रंग हैं। (भविष्यकाल)
उत्तर :
(1) वे सभी धर्मों को समान दृष्टि से देखते हैं।
(2) दिन-रात महान आरती हो रही थी।
(3) अनहद नाद का वाद्य बजेगा।
(4) श्रद्धा भक्त की सबसे बड़ी भेंट थी।
(5) तुम्हारे अनेक रंग होंगे।

5. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) गुरू के बिना ग्यान नहीं होता।
(2) उसने भगवान की नाम का माला पहन ली है।
(3) सभी जंगल की वनस्पतियाँ फूल चढ़ा रही है।
(4) श्रद्धा ही भक्त का सबसे बड़ा भेट है।
(5) तू दीन-रात भगवान के गुणों का स्मरण कर।
उत्तर :
(1) गुरु के बिना ज्ञान नहीं होता।
(2) उसने भगवान के नाम की माला पहन ली है।
(3) जंगल की सभी वनस्पतियाँ फूल चढ़ा रही हैं।
(4) श्रद्धा ही भक्त की सबसे बड़ी भेंट है।
(5) तू दिन-रात भगवान के गुणों का स्मरण कर।

गुरुबानी Summary in Hindi

गुरुबानी कवि का परिचय

कवि का नाम : गुरु नानक। (जन्म 15 अप्रैल, 1469; निधन 1539.)

प्रमुख कृतियाँ : गुरुग्रंथसाहिब आदि।

विशेषता : आप सर्वेश्वरवादी हैं और सभी धर्मों को समान दृष्टि से देखते हैं। आपके भावुक व कोमल हृदय ने प्रकृति से एकात्म होकर अनूठी अभिव्यक्ति की है। आप सहज-सरल भाषा द्वारा अपनी बात कहने में सिद्धहस्त हैं।

विधा : दोहे, पद। पदकाव्य रचना की एक गेय शैली है। इसके विकास का मूल स्रोत लोकगीतों की परंपरा रही है। हिंदी साहित्य में ‘पद शैली’ की दो परंपराएँ मिलती हैं – एक संतों की ‘शबद’ और दूसरी ‘कृष्ण भक्तों की परंपरा’।

विषय प्रवेश : मनुष्य के जीवन को उत्तम और सदाचार से परिपूर्ण बनाने के लिए गुरु का मार्गदर्शन अत्यंत आवश्यक होता है। इसी से शिक्षा प्राप्त कर मनुष्य उत्तम कार्य करता है। प्रस्तुत दोहों और पदों में गुरु नानक ने गुरु की महिमा, कर्म की महानता तथा सच्ची शिक्षा आदि के बारे में अपने अमूल्य विचारों से परिचित कराया है। वे गुरु द्वारा दिए गए ज्ञान को शिष्य की सबसे बड़ी पूँजी मानते हैं। उन्होंने प्रभु की महिमा का वर्णन करते हुए नाम स्मरण को प्रभु प्राप्ति का मार्ग बताया है और कर्मकांड और बाह्याडंबर का घोर विरोध किया है।

गुरुबानी कविता (पदों) का सरल अर्थ

(1) नानक गुरु न चेतनी …………………………………….. तन बिच स्वाह।

गुरु नानक कहते हैं कि जो लोग गुरु का चिंतन नहीं करते, गुरु से लापरवाही बरतते हैं और अपने आप को ही ज्ञानी समझते हैं, वे व्यर्थ ही उगने वाली तिल की उन झाड़ियों के समान होते हैं, जिनकी देखभाल करने वाला कोई नहीं होता। वे ऊपर से फलतीफूलती दिखाई देती है, पर उन फलियों के अंदर गंदगी और मैल भरा होता है। लोग ऐसे लोगों से किनारा कर लेते हैं।

(2) जलि मोह धसि …………………………………….. अंत न पारावार।

गुरु नानक कहते हैं कि मोह को जलाकर और घिसकर स्याही बनाओ। अपनी बुद्धि को श्रेष्ठ कागज समझो। प्रेम-भाव की कलम बनाओ। चित को लेखक समझो और गुरु से पूछकर लिखो – नाम की स्तुति। साथ ही यह सच्चाई भी लिखो कि प्रभु का न कोई आदि है और न कोई अंत।

(3) मन रे अहिनिसि …………………………………….. मेले गरु संजोग।

हे मन! तू दिन-रात भगवान के गुणों का स्मरण कर। जिन्हें एक क्षण के लिए भी ईश्वर का नाम नहीं भूलता, संसार में ऐसे लोग विरले ही होते हैं। अपना ध्यान उसी ईश्वर में लगाओ और उसकी ज्योति से तुम भी प्रकाशित हो जाओ। जब तक तुझमें अहंभाव रहेगा, तब तक तुझे प्रभु के दर्शन नहीं हो सकते। जिसने अपने हृदय में भगवान के नाम की माला पहन ली है, उसे ही प्रभु के दर्शन होते हैं।

(4) तेरी गति मिति …………………………………….. दजा और न कोई।

हे प्रभो! अपनी शक्ति के सब रहस्यों को केवल तुम्हीं जानते हो। उनकी व्याख्या कोई दूसरा नहीं कर सकता है। तुम ही अप्रकट रूप भी हो और तुम ही प्रकट रूप भी हो। तुम्हारे अनेक रंग हैं। अनगिनत भक्त, सिद्ध, गुरु और शिष्य तुम्हें ढूँढ़ते फिरते हैं। हे प्रभु! जिन्होंने नाम स्मरण किया उन्हें प्रसाद (भिक्षा) में तुम्हारे दर्शन की प्राप्ति हुई है। प्रभु! तुम्हारे इस संसार के खेल को केवल कोई गुरुमुख ही समझ सकता है। प्रभु! अपने इस संसार में युग-युग से तुम्हीं बिराजमान रहते हो, कोई दूसरा नहीं।।

(5) गगन में थाल …………………………………….. शबद बाजत भेरी। (संसार में दिन-रात महान आरती हो रही है।)

आकाश की थाल में सूर्य और चंद्रमा के दीपक जल रहे हैं। हजारों तारे-सितारे – मोती बने हैं। मलय की खुशबूदार हवा वाला धूप (गुग्गुल) महक रहा है। वायु हवा से चँवर कर रही है। जंगल की सभी वनस्पतियाँ फूल चढ़ा रही हैं। हृदय में अनहद नाद का वाद्य बज रहा है। हे मनुष्य! इस महान आरती के होते हुए तेरी आरती का क्या महत्त्व है। अर्थात भगवान की असली आरती तो मन में उतारी जाती है। श्रद्धा ही भक्त की सबसे बड़ी भेंट है।

गुरुबानी शब्दार्थ

• बूआड़ = बुआई करना
• सउ = ईश्वर
• चितु = चित्त
• गुपता = अप्रकट, गुप्त
• सगल = संपूर्ण
• सुंजे = सूने
• मसु = स्याही
• अहिनिसि = दिन-रात
• जुग = युग
• भेरी = बड़ा ढोल

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 2 निराला भाई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 2 निराला भाई

12th Hindi Guide Chapter 2 निराला भाई Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
लिखिए :

(अ) लेखिका के पास रखे तीन सौ रुपये इस प्रकार समाप्त हो गए :
(1) ……………………………………………
(2) …………………………………………..
(3) ……………………………………………
(4) ……………………………………………
उत्तर :
लेखिका के पास रखे तीन सौ रुपए इस प्रकार समाप्त हो गए –
(1) किसी विद्यार्थी का परीक्षा शुल्क देने के लिए 50 रुपए लिए।
(2) किसी साहित्यिक मित्र को देने के लिए 60 रुपए लिए।
(3) तांगेवाले की माँ को मनीआर्डर करने के लिए 40 रुपए लिए।
(4) दिवंगत मित्र की भतीजी के विवाह के लिए 100 रुपए लिए। तीसरे दिन जमा पैसे समाप्त।

(आ) अतिथि की सुविधा हेतु निराला जी ये चीजें ले आए :
(1) ……………………………………………
(2) ……………………………………………
(3) ……………………………………………
(4) ……………………………………………
उत्तर :
अतिथि की सुविधा हेतु निराला जी ये चीजें ले आए –
(1) नया घड़ा खरीदकर लाए।
(2) उसमें गंगाजल भर लाए।
(3) धोती।
(4) चादर।

शब्द संपदा

प्रश्न 2.
निम्न शब्दों के समानार्थी शब्द लिखिए :
(1) प्रहरी – ……………………………………………
(2) अतिथि – ……………………………………………
(3) प्रयास – ……………………………………………
(4) स्मृति – ……………………………………………
उत्तर :
(1) प्रहरी = द्वारपाल
(2) अतिथि = मेहमान
(3) प्रयास = प्रयत्न
(4) स्मृति = याद

अभिव्यक्ति

प्रश्न 3.
(अ) ‘भाई-बहन का रिश्ता अनूठा होता है, इस विषय पर अपना मत लिखिए।
उत्तर :
एक माता से उत्पन्न भाइयों अथवा भाई-बहनों का रिश्ता निराला होता है। यह रिश्ता अटूट होता है। बचपन में वे साथ-साथ खेलते, बढ़ते और पढ़ते हैं। जीवन में घटने वाली अनेक अच्छी बुरी घटनाओं के साक्षी होते हैं। बड़े होने पर बहन की शादी हो जाने पर उसका नया घर बस जाता है। फिर भी उसका लगाव अपने मायके के परिवार के साथ बना रहता है। जब भी पीहर आने का कोई मौका आता है, वह उसे कभी गँवाना नहीं चाहती।

पीहर में आकर उसे जो खुशी मिलती है, उसका वर्णन नहीं किया जा सकता। रक्षाबंधन के त्योहार पर वह कहीं भी हो, अपने भाई की कलाई पर राखी बाँधने और उसकी आरती उतारने जरूर पहुँचती है। भाई-बहन का यह मिलन अनूठा होता है। भाई भी इस अवसर पर उसे अपनी क्षमता के अनुसार अच्छे-से-अच्छा उपहार देने से नहीं चूकता। यह उनके अटूट प्यार और अनूठे रिश्ते का ही प्रमाण है।

(आ) ‘सभी का आदरपात्र बनने के लिए व्यक्ति का सहृदयी और संस्कारशील होना आवश्यक है’, इस कथन पर अपने विचार लिखिए।
उत्तर :
मनुष्य एक सामाजिक प्राणी है। वह अपने परिवार और समाज में सबके साथ हिल-मिल कर रहना चाहता है। उसे सबके दुख-सुख में शामिल होना अच्छा लगता है। जीवों पर दया करना और मन में करुणा के भाव उत्पन्न होना मनुष्य का स्वाभाविक गुण है। ऐसे व्यक्ति संस्कारशील कहलाते हैं।

ऐसे व्यक्ति का सभी लोग आदर करते हैं और उसे अपना प्यार देते हैं। मगर सब लोग ऐसे नहीं होते। कुछ लोग विभिन्न कारणों से समाज से कटे-कटे रहते हैं और ‘अपनी डफली अपना राग’ विचार वाले होते हैं। वे अपने घमंड में चूर रहते हैं और किसी अन्य की परवाह नहीं करते।

ऐसे लोगों को समाज तो क्या कोई भी पसंद नहीं करता। ऐसे लोगों को समाज में सम्मान नहीं मिलता। इसलिए मनुष्य को सहृदयी और संस्कारशील होना जरूरी है।

पाठ पर आधारित लघूत्तरी प्रश्न –

प्रश्न 4.
(अ) निराला जी की चारित्रिक विशेषताएँ लिखिए।
उत्तर :
निराला जी मानवता के पुजारी थे। उनमें मानवीय गुण कूट-कूट कर भरे हुए थे। उन्हें स्वयं से अधिक दूसरों की अधिक चिंता होती थी। खुद निर्धनता में जीवन बिताते रहे, पर दूसरों के आर्थिक दुखों का भार उठाने के लिए सदा तत्पर रहते थे। आतिथ्य करने में उनका जवाब नहीं था।

अतिथियों को सदा हाथ पर लिये रहते थे। उनके लिए खुद भोजन बनाने और बर्तन माँजने में उन्हें हर्ष होता था। घर में सामान न होने पर अतिथियों के लिए मित्रों से कुछ चीजें माँग लाने में शर्म नहीं करते थे। उदार इतने थे कि अपने उपयोग की वस्तुएँ भी दूसरों को दे देते थे और खुद कष्ट उठाते थे।

साथी साहित्यकारों के लिए उनके मन में बहुत लगाव था। एक बार कवि सुमित्रानंदन पंत के स्वर्गवास की झूठी खबर सुनकर वे व्यथित हो गए थे और उन्होंने पूरी रात जाग कर बिता दी थी।

निराला जी पुरस्कार में मिले धन का भी अपने लिए उपयोग नहीं करते थे। अपनी अपरिग्रही वृत्ति के कारण उन्हें मधुकरी खाने ३ तक की नौबत भी आई थी। इस बात को वे बड़े निश्छल भाव से बताते थे।

उनका विशाल डील-डौल देखने वालों के हृदय में आतंक पैदा कर देता था, पर उनके मुख की सरल आत्मीयता इसे दूर कर देती थी।

निराला जी से अन्याय सहन नहीं होता था। इसके विरोध में उनका हाथ और उनकी लेखनी दोनों चल जाते थे। निराला जी आचरण से क्रांतिकारी थे। वे किसी चीज का विरोध करते हुए कठिन चोट करते थे। पर उसमें द्वेष की भावना नहीं होती थी। निराला जी के प्रशंसक तथा आलोचक दोनों थे। कुछ लोग जहाँ उनकी नम्र उदारता की प्रशंसा करते थे, वहीं कुछ लोग उनके उद्धत व्यवहार की निंदा करते नहीं थकते थे।

निराला जी अपने युग की विशिष्ट प्रतिभा रहे हैं। उनके सामने अनेक प्रतिकूल परिस्थितियाँ आईं पर वे कभी हार नहीं माने।

(आ) निराला जी का आतिथ्य भाव स्पष्ट कीजिए।
उत्तर :
निराला जी में आतिथ्य सत्कार का पुराना संस्कार था। वे अतिथि को देवता के समान मानते थे। अपने अतिथि की सुविधा में कोई कसर बाकी नहीं रखते थे। वे अतिथि को अपने कक्ष में ठहराते थे। उसके लिए स्वयं भोजन तैयार करते थे। बर्तन भी वे खुद माँजते थे। अतिथि सत्कार के लिए आवश्यक सामान घर में न होता तो वे अपने हित-मित्रों से माँगकर ले आते थे, पर अतिथि सेवा में कोई कमी नहीं रखते थे। कई बार तो वे कवयित्री महादेवी वर्मा के यहाँ से भोजन बनाने के लिए लकड़ियाँ तथा घी आदि माँगकर ले आए थे।

निराला जी की आर्थिक स्थिति अच्छी नहीं थी। उनका कक्ष भी सुविधाओं से रहित था, पर अतिथि के लिए उनके दिल में अपार श्रद्धा थी। एक बार प्रसिद्ध कवि मैथिलीशरण गुप्त निराला जी का आतिथ्य ग्रहण करने आए थे। उस समय उन्होंने उनका जो सत्कार किया था वह देखते ही बनता था। निराला जी गुप्त जी के बिछौने का बंडल खुद बगल में दबाकर और दियासलाई की तीली के प्रकाश में तंग सीढ़ियों का मार्ग दिखाते हुए उन्हें अपने कक्ष में ले गए थे।

कक्ष प्रकाश और सुख सुविधा से रहित था, पर निराला जी की विशाल आत्मीयता से भरा हुआ था। वे गुप्त जी की सुविधा के लिए नया घड़ा खरीदकर उसमें गंगाजल ले आए। घर में धोती-चादर जो कुछ मिल सका सब तख्त पर बिछा कर गुप्त जी को प्रतिष्ठित किया था। निराला जी का आतिथ्य भाव अपनी किस्म का निराला था।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) ‘निराला’ जी का मूल नाम – [ ]
(आ) हिंदी के कुछ आलोचकों द्वारा महादेवी वर्मा को दी गई उपाधि – [ ]
उत्तर :
(अ) निराला जी का मूल नाम – सूर्यकांत त्रिपाठी।
(आ) कुछ हिंदी आलोचकों द्वारा महादेवी वर्मा को दी गई उपाधि – [आधुनिक मीरा]

रस

काव्यशास्त्र में आचार्यों ने रस को काव्य की आत्मा माना है। विभाव, अनुभाव, व्यभिचारी (संचारी) भाव और स्थायी भाव रस के अंग हैं और इन अंगों अर्थात तत्त्वों के संयोग से रस की निष्पत्ति होती है।

साहित्यशास्त्र में नौ प्रकार के रस माने गए हैं। कालांतर में अन्य दो रसों को सम्मिलित किया गया है।
रस – स्थायी भाव – रस – स्थायी भाव

• शृंगार – प्रेम
• शांत – शांति
• करुण – शोक
• हास्य – हास
• भयानक – भय
• रौद्र – क्रोध
• बीभत्स – घृणा
• वीर – उत्साह
• अद्भुत – आश्चर्य
• वात्सल्य – ममत्व
• भक्ति – भक्ति

ग्यारहवीं कक्षा की युवकभारती पाठ्यपुस्तक में हमने करुण, हास्य, वीर, भयानक और वात्सल्य रस के लक्षण एवं उदाहरणों का अध्ययन किया है। इस वर्ष हम शेष रसों – रौद्र, बीभत्स, अद्भुत, शृंगार, शांत और भक्ति रस का अध्ययन करेंगे।

रौद्र रस : जहाँ पर किसी के असह्य वचन, अपमानजनक व्यवहार के फलस्वरूप हृदय में क्रोध का भाव उत्पन्न होता है; वहाँ रौद्र रस उत्पन्न होता है। इस रस की अभिव्यंजना अपने किसी प्रिय अथवा श्रद्धेय व्यक्ति के प्रति अपमानजनक, असह्य व्यवहार के प्रतिशोध के रूप में होती है।

उदा. –
(१) श्रीकृष्ण के वचन सुन, अर्जुन क्रोध से जलने लगे।
सब शोक अपना भूलकर, करतल युगल मलने लगे।

(२) कहा – कैकयी ने सक्रोध
दूर हट! दूर हट! निर्बोध!
द्विजिव्हे रस में, विष मत घोल।

बीभत्स रस : जहाँ किसी अप्रिय, अरुचिकर, घृणास्पद वस्तुओं, पदार्थों के प्रसंगों का वर्णन हो, वहाँ बीभत्स रस उत्पन्न होता है।

उदा. –
(१) सिर पर बैठो काग, आँखि दोऊ खात
खींचहि जीभहि सियार अतिहि आनंद उर धारत।
गिद्ध जाँघ के माँस खोदि-खोदि खात, उचारत हैं।
(२) सुडुक, सुडुक घाव से पिल्लू (मवाद) निकाल रहा है,
नासिका से श्वेत पदार्थ निकाल रहा है।

Hindi Yuvakbharati 12th Digest Chapter 2 निराला भाई Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए)
गद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

(1)

उत्तर :

(2)

उत्तर :

प्रश्न 2.
उत्तर लिखिए : निराला जी ने
(1) यह रचा – ………………………………..
(2) यह किया – ………………………………..
उत्तर :
निराला जी ने
(1) यह रचा – दिव्य वर्ण-गंधवाले मधुर गीत।
(2) यह किया – बर्तन मांजने, पानी भरने जैसे कठिन काम।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) कच्चे x ………………………………..
(2) प्रश्न x ………………………………..
(3) कठिन x ………………………………..
(4) जीवन x ………………………………..
उत्तर :
(1) कच्चे x पक्के
(2) प्रश्न – उत्तर
(3) कठिन x सरल
(4) जीवन x मरण।

प्रश्न 2.
गद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए :
(1) ………………………………..
(2) ………………………………..
उत्तर :
(1) वर्ण-गंध
(2) दिन-रात।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
किसी अन्य का कष्ट दूर करने के लिए लुप्त हो गई वस्तुएँ –
(1) …………………………..
(2) …………………………..
उत्तर :
किसी अन्य का कष्ट दूर करने के लिए लुप्त हो गई वस्तुएँ –
(1) रजाई
(2) कोट।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) आदेश = ……………………………….
(2) दुष्कर = ……………………………….
(3) अंतर्धान = ……………………………….
(4) दिवंगत = ……………………………….
उत्तर :
(1) आदेश = हुकम
(3) अंतर्धान = अदृश्य
(2) दुष्कर = कठिन
(4) दिवंगत = मृत।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘निर्बंध उदारता’ के बारे में अपना मत 40 से 50 शब्दों में व्यक्त किजिए।
उत्तर :
मनुष्य ही मनुष्य के काम आता है। किसी के दुखदर्द से सहानुभूति रखना अथवा उसकी आर्थिक मदद करना मनुष्य का धर्म है। इससे जरूरतमंद व्यक्ति को राहत और नैतिक सहयोग मिलता है। अनेक संपन्न व्यक्ति एवं बड़ी-बड़ी संस्थाएँ इस प्रकार का सहयोग देने का कार्य करती हैं। कई साधारण व्यक्ति भी अपनी क्षमता के अनुसार अपने जान-पहचान वाले लोगों की मदद करते हैं।

पर सामान्य लोगों के लिए किसी की आर्थिक सहायता करने की एक सीमा होती है। उसे सबसे पहले अपना घर-बार देखना पड़ता है। अगर कोई व्यक्ति अपनी क्षमता से अधिक उदारता बरतने लगता है, तो उसकी आर्थिक स्थिति अस्त-व्यस्त हो जाती है। ‘अति’ किसी की अच्छी नहीं होती। हर काम अपनी सीमा में ही फबता है। इसलिए निबंध उदारता अनुचित ही नहीं है, यह किसी की भी आर्थिक स्थिति को डाँवाडोल कर सकती है।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : निराला जी का कक्ष ऐसा था –
(1) ………………………….
(2) ………………………….
(3) सुख-सुविधाहीन।
(4) ………………………….
उत्तर :
(1) निराला जी का कक्ष ऐसा था –
(2) कक्ष में जाने का मार्ग तंग सीढ़ियों से होकर था।
(3) प्रकाश रहित था।
(4) सुख-सुविधाहीन।

प्रश्न 2.
अतिथि के लिए निराला जी माँग लिया करते थे –
(1) ………………………….
(2) ………………………….
उत्तर :
अतिथि के लिए निराला जी माँग लिया करते थे
(1) लकड़ियाँ
(2) थोड़ा घी।

प्रश्न 3.
अतिथि देवता के लिए निराला जी शौक से ये करते थे-
(1) ………………………….
(2) ………………………….
उत्तर :
अतिथि देवता के लिए निराला जी शौक से ये करते थे –
(1) अतिथि के लिए भोजन बनाने का काम।
(2) उनके जूठे बर्तन माँजना।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘अतिथि देवो भव’ के बारे में अपने विचार 40 से 50 शब्दों में लिखिए।
उत्तर :
अतिथियों का स्वागत-सत्कार करना हमारे देश के लोगों के संस्कार का एक अंग रहा है। अतिथि के स्वागत में लोग कोई कसर बाकी नहीं रखते। घर में कोई सामान न हो, तो किसी के यहाँ से माँग-जाँच कर ले आने में भी लोग नहीं हिचकते। पर अतिथि की सेवा करने में कोई कसर नहीं रखते।

सुशील अतिथि मेजबान की क्षमता को ध्यान में रखते हैं और उसके साथ पूरा सहयोग करते हैं। मेजबान की तरफ से कहीं कोई कमी भी रह जाती है तो भी उसके साथ सहयोग करते हैं। ऐसे अतिथि मेजबान के लिए देव स्वरूप होते हैं। पर कुछ अतिथि ऐसे होते हैं, जो मेजबान की तरफ से आवभगत में कहीं कोई कमी रह जाने पर उसकी निंदा करने से भी नहीं चूकते।

कुछ अतिथि ‘मान न मान मैं तेरा मेहमान’ की तरह मेजबान के घर आ धमकते हैं और जाने का नाम ही नहीं लेते। ऐसे अतिथि मेजबान के लिए भार स्वरूप होते हैं। जो अतिथि मेजबान की सुविधा-असुविधा का ध्यान रखते हैं, वही अतिथि देव स्वरूप होते हैं।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :
कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
चौखट पूर्ण कीजिए :
(1) गेरू में रंगे हुए वस्त्र।
(2) शरीर पर इस वस्त्र का अभाव था। –
(3) गद्यांश में प्रयुक्त दो वृक्ष।
(4) कवि का गैरिक शरीर ऐसा लगता था। –
उत्तर :
(1) गेरू में रंगे हुए वस्त्र। – [दोनों अधोवस्त्र और उत्तरीय]
(2) शरीर पर इस वस्त्र का अभाव था। – [अंगोछा]
(3) गद्यांश में प्रयुक्त दो वृक्ष। – [नीम-पीपल]
(4) कवि का गैरिक शरीर ऐसा लगता था – [किसी शिखर जैसा।]

प्रश्न 3.
उत्तर लिखिए : कवि के संन्यास से लेखिका को –
(1) लाभ – ………………………….
(2) हानि – ………………………….
उत्तर :
कवि के संन्यास से लेखिका को
(1) लाभ – साबुन के पैसे बचेंगे।
(2) हानि – जाने कहाँ-कहाँ छप्पर डलवाने पड़ेंगे।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदल कर लिखिए :
(1) निधियाँ – ………………………..
(2) वस्त्रों – ………………………..
(3) रोटियाँ – ………………………..
(4) पुत्रौं – ………………………..
उत्तर :
(1) निधियाँ – निधि
(3) रोटियाँ – रोटी
(2) वस्त्रों – वस्त्र
(4) पुत्रौं – पुत्र

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘साधु-संन्यासियों से जनता का मोहभंग’ इस विषय पर 40 से 50 शब्दों में अपना मत व्यक्त कीजिए।
उत्तर :
एक समय था जब लोग साधु-संतों और संन्यासियों का बड़ा सम्मान करते थे। वे समाज में बड़े सम्मान की दष्टि से देखे जाते थे। वे समाज-सुधार और जनता के हित के कार्य किया करते थे और बदले में जनता से कोई अपेक्षा नहीं करते थे। लेकिन हाल में जब से साधु-संन्यासियों के वेष में कुछ ढोंगी लोगों ने साधुसंन्यासियों की जमात को अपने समाज-विरोधी कार्यों से बदनाम कर दिया है, तब से लोगों को इनसे घृणा हो गई है।

ऐसा नहीं है कि सच्चे साधु-संन्यासी हैं ही नहीं। हैं, लेकिन इन ढोंगी साधु संन्यासियों ने उनकी छबि-धूमिल कर दी है। ढोंगी साधु-संन्यासियों के बीच सच्चे साधु-संन्यासियों को पहचानना मुश्किल हो गया है। साधु-संन्यासियों से जनता का मोहभंग ढोंगी साधु-संन्यासियों की जमात के कारण हुआ है। सच्चे साधु-संन्यासियों की जनता आज भी मुरीद है।

गद्यांश क्र. 5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई। सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : निराला जी इस दृष्टि से निराले थे –
(1) ………………………..
(2) जीवन में ………………………..
(3) ………………………..
उत्तर :
निराला जी इस दृष्टि से निराले थे –
(1) अपने शरीर की दृष्टि से।
(2) जीवन में।
(3) अपने साहित्य की दृष्टि से।

प्रश्न 2.
उत्तर लिखिए :
(1) देखने वालों के हृदय में इससे आतंक उत्पन्न होता था –
(2) सत्य दृष्टा ऐसे होते हैं –
(3) अन्याय के प्रतिकार का निराला जी का तरीका –
(4) निराला जी की लेखनी की विशेषता –
उत्तर :
(1) देखने वालों के हृदय में इससे आतंक उत्पन्न होता था – [निराला जी का विशाल डील-डौल देखकर।]
(2) सत्यदृष्टा ऐसे होते हैं – [बालकों जैसे सरल और विश्वासी।]
(3) अन्याय के प्रतिकार का निराला जी का तरीका – [लेखनी के पहले हाथ उठाना।]
(4) निराला जी की लेखनी की विशेषता – [उनकी लेखनी हाथ से अधिक कठोर प्रहार करती थी।]

प्रश्न 3.
संबंध निरूपित कीजिए :
(1) क्रूरता – ………………………..
(2) कायरता – ………………………..
उत्तर :
(1) क्रूरता – वृक्ष की जड़ के अव्यक्त रस में
(2) कायरता – वृक्ष के फल के व्यक्त स्वाद में।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) शरीर = ………………………………………
(2) सत्य = ………………………………………
(3) प्रतिकार = ………………………………………
(3) कठोर = ………………………………………
उत्तर :
(1) शरीर = तन
(2) सत्य = सच्चाई
(3) प्रतिकार = विरोध
(4) कठोर = कड़ा

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘अन्याय सहन करना भी अन्याय है।’ इस विषय पर 40 से 50 . शब्दों में अपने विचार लिखिए।
उत्तर :
सभी मनुष्य समान हैं। किसी को भी किसी के साथ अन्याय करने का अधिकार नहीं है। इसके बावजूद कुछ लोग ऐसे होते हैं, जो अपने से कमजोर व्यक्तियों पर अत्याचार करने से नहीं चूकते। कभी किन्हीं कारणों से जिनके साथ अन्याय होता है, वे उसका विरोध भी नहीं कर पाते।

वे समझते हैं कि विरोध करने का परिणाम उल्टा होगा और अत्याचारी उसे और सताने की कोशिश करेगा। लेकिन यह सोच उचित नहीं है। अन्याय का विरोध न करने से अत्याचारी का मन और बढ़ जाता है। वह समझ जाता है कि उसके अत्याचार का विरोध करने की संबंधित व्यक्ति में शक्ति नहीं है।

इसलिए ऐसे लोगों पर अत्याचार करना अपना अधिकार मान लेता है और वह निडर होकर उन पर अत्याचार करता रहता है। इस तरह अत्याचार सहन करना अपने आप पर अन्याय हो जाता मुक्ति मिल सकती है।

गद्यांश क्र. 6 प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : निराला जी के व्यवहार के बारे में जन-मत –
(1) – …………………………………..
(2) – …………………………………..
उत्तर :
(1) कोई उनकी उदारता की भूरि-भूरि प्रशंसा करता था।
(2) कोई उनके उद्धत व्यवहार की निंदा करते नहीं हारता था।

प्रश्न 2.
संजाल पूर्ण कीजिए :

उत्तर :

प्रश्न 3.
कृति पूर्ण कीजिए :
(1) निराला अपने युग की यह हैं – …………………………………..
(2) उनके जीवन के चारों ओर यह नहीं है – …………………………………..
(3) उनके लिए परिवार के कोंपल यह बन गए – …………………………………..
(4) आर्थिक कारणों से उन्हें यह नहीं मिली – …………………………………..
उत्तर :
(1) विशिष्ट प्रतिमा
(2) परिवार का लौहसार घेरा।
(3) पत्नी वियोग के पतझड़।
(4) अपनी संतान के प्रति कर्तव्य-निर्वाह की सुविधा।

प्रश्न 4.

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त उपसर्गयुक्त शब्द ढूँढ़ कर लिखिए :
(1) …………………………………….
(2) …………………………………….
(3) …………………………………….
(4) …………………………………….
उत्तर :
(1) असफलता
(2) निष्फल
(3) सजातीय
(4) अभिशाप।

व्याकरण

1. मुहावरे :

• निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) आँखों में धूल झोंकना।
अर्थ : धोखा देना।
वाक्य : साइबर क्राइम से अच्छे-अच्छे लोगों की आँखों में धूल झोंककर लाखों रुपए ऐंठ लिए जाते हैं।

(2) आँखें बिछाना।
अर्थ : अति उत्साह से स्वागत करना।
वाक्य : स्वामी जी के दर्शन के लिए श्रद्धालु आँखें बिछाए हुए थे।

(3) कान में कौड़ी डालना।
अर्थ : गुलाम बनाना।
वाक्य : अंग्रेजों ने भारी संख्या में भारतीय मजदूरों के कान में कौड़ी डाल रखा था।

2. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों का काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) कौन बहिन हम जैसे भुक्खड़ को भाई बनाएगी। (सामान्य वर्तमानकाल)
(2) उनके अस्त-व्यस्त जीवन को व्यवस्थित करने के असफल प्रयासों का स्मरण कर मुझे आज भी हँसी आ जाती है। (अपूर्ण भूतकाल)
(3) उनकी व्यथा की सघनता जानने का मुझे एक अवसर मिला था। (पूर्ण वर्तमानकाल)
(4) पंत के साथ तो रास्ता कम अखरता था, पर अब सोचकर ही थकावट होती है। (सामान्य भविष्यकाल)
(5) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण हैं। (पूर्ण भूतकाल)
उत्तर :
(1) कौन बहिन हम जैसे भुक्खड़ को भाई बनाती है।
(2) उनके अस्त-व्यस्त जीवन को व्यवस्थित करने के असफल प्रयासों का स्मरण कर मुझे आज भी हँसी आ रही थी।
(3) उनकी व्यथा की सघनता जानने का मुझे एक अवसर मिला है।
(4) पंत के साथ तो रास्ता कम अखरता था, पर अब सोचकर ही थकावट होगी।
(5) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण थे।

3. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) निराला जी अपनी युग के विशिष्ट प्रतिभा हैं।
(2) सत्य की मार्ग सरल हैं।
(3) मनुष्य जाती की नासमझी की इतिहास क्रूर और लंबा है।
(4) निराला जी अपना शरीर, जीवन और साहित्य सभी में असाधारण है।
(5) उनके जीवन पर संघर्श के जो आघात हैं, वे उनकी हार के नहीं शक्ती के प्रमाणपत्र हैं।
उत्तर :
(1) निराला जी अपने युग की विशिष्ट प्रतिभा हैं।
(2) सत्य का मार्ग सरल है।
(3) मनुष्य जाति की नासमझी का इतिहास क्रूर और लंबा है।
(4) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण हैं।
(5) उनके जीवन पर संघर्ष के जो आघात हैं, वे उनकी हार के नहीं शक्ति के प्रमाणपत्र हैं।

निराला भाई Summary in Hindi

निराला भाई लेखक का परिचय

निराला भाई लेखक का नाम : श्रीमती महादेवी वर्मा। (जन्म 26 मार्च, 1907; निधन 1987.)

प्रमुख कृतियाँ : नीहार, रश्मि, नीरजा, दीपशिखा, सांध्यगीत, यामा (कविता संग्रह), अतीत के चलचित्र, स्मृति की रेखाएँ, मेरा परिवार (रेखाचित्र), श्रृंखला की कड़ियाँ तथा साहित्यकार की आस्था (निबंध)।

विधा : संस्मरण।

विषय प्रवेश : प्रसिद्ध कवि सूर्यकांत त्रिपाठी “निराला’ की गणना हिंदी के श्रेष्ठ कवियों में की जाती है। वे हिंदी साहित्य में छायावादी कवि एवं क्रांतिकारी व्यक्तित्व के रूप में जाने जाते हैं। प्रसिद्ध कवयित्री महादेवी वर्मा एवं निराला जी दोनों का कार्यक्षेत्र प्रयागराज रहा है। इसलिए भी कवयित्री निराला जी को नजदीक से जानती-समझती और उनके व्यक्तित्व से गहराई से परिचित रही हैं।

प्रस्तुत संस्मरण में उन्होंने निराला जी को जिन विभिन्न रूपों में देखा और परखा है, उसे उन्होंने बेबाकी से शब्दांकित किया है। – इस संस्मरण से हमें निराला जी के फक्कड़पन, उनके व्यक्तित्व, उनकी निर्धनता, उदारता, संवेदनशीलता, आतिथ्य सत्कार की भावना तथा पारिवारिक दशा आदि के बारे में अनेक अनछुई बातों की जानकारी मिलती है।

निराला भाई पाठ का सार

कवयित्री महादेवी वर्मा प्रसिद्ध कवि निराला जी के साथ घटित कई घटनाओं की साक्षी रही हैं। उन्होंने उन्हें नजदीक से देखा-समझा है। उन्होंने इस संस्मरण में उनके साथ घटी हुई अनेक घटनाओं और उनके स्वभाव एवं व्यवहार का चित्रण किया है।

निराला जी संवेदनशील उदार, आतिथ्यप्रेमी, सहृदय, फक्कड़ किस्म के और सदा निर्धनता में जीवन बिताने वाले कवि रहे हैं। वे स्पष्टवादी व्यक्ति थे और अपने बारे में सही बात कहने से नहीं चूकते थे। एक बार रक्षाबंधन त्योहार के अवसर पर कवयित्री ने उनकी सूनी कलाइयाँ देखकर इसके बारे में पूछा तो उन्होंने जवाब दिया, “कौन बहन मुझ भुक्खड़ को भाई बनाएगी।”

कवि अपनी उदारता और दूसरों का दुख दूर करने की प्रवृत्ति के कारण सदा तंगी में रहे। वे खुद कष्ट सह लेते थे पर दूसरों का कष्ट दूर करके रहते थे। एक बार तो उन्होंने अपने लिए बनवाई गई रजाई और कोट भी किसी ठिठुरते हुए को दे दिया और खुद काँपते हुए मजे से सर्दियाँ काट दीं।

आर्थिक संकट सदा उनका साथी रहा। इसके कारण वे अपनी मातृविहीन संतान की भी उचित देखभाल न कर पाए। पुत्री के अंतिम क्षणों में असहाय बने रहे और पुत्र को उचित शिक्षा न दे पाए।

एक बार तो उन्होंने कवयित्री को 300 रुपए देकर अपने खर्च का बजट बनाने के लिए कहा था। पर बजट बनते-बनते तक सारे पैसे लेकर जरूरतमंद लोगों को दे डाले।

एक बार प्रसिद्ध कवि मैथिलीशरण गुप्त ने उनका आतिथ्य ग्रहण किया था। जब वे आए तो वे दियासलाई के प्रकाश में उन्हें लेकर तंग सीढ़ियों से होकर अपने सुविधा रहित कक्ष में पहुँचे तो वहाँ ढंग का बिस्तर भी नहीं था। फिर उन्होंने घर में धोती, चादर जो कुछ मिला उसे तख्त पर बिछाकर बड़े प्यार से उन्हें प्रतिष्ठित किया था। अतिथि का सत्कार करने के लिए उन्होंने कवयित्री से एक बार जलावन लकड़ी और घी तक माँग लिया था।

समकालीन साहित्यकारों की व्यथा के बारे में सुनकर वे विचलित हो जाते थे। एक बार सुमित्रानंदन पंत की मृत्यु की झूठी खबर पढ़कर वे बेचैन हो गए थे और सच्चाई जानने के लिए सारी रात जागते हुए इंतजार करते रहे।

एक बार तो उन्होंने अपने दोनों अधोवस्त्र और उत्तरीय गेरू में रंग डाले थे। कवयित्री उनका रूप देखती रह गई थीं। कहने लगे, “अब ठीक है। जहाँ पहुँचे, किसी नीम या पीपल के पेड़ के नीचे बैठ गए। दो रोटियाँ माँग कर खा लीं और गीत लिखने लगे।”

निराला जी के विशाल डील-डौल से देखने वाले के हृदय में आतंक उत्पन्न हो जाता था, पर उनकी आत्मीयता से यह भय तिरोहित हो जाता था।

निराला ऐसे व्यक्तित्व थे जिनके बारे में अलग-अलग व्यक्तियों की अलग-अलग धारणाएँ थीं। कोई उनकी उदारता की प्रशंसा करते नहीं थकता तो कोई उनके उद्धत व्यवहार की निंदा करते नहीं हारता। पर उन्हें समझ पाना हर किसी के वश की बात नहीं थी।

निराला जी अपने युग की विशिष्ट प्रतिभा थे। वे एक विद्रोही साहित्यकार थे। कवयित्री का मानना है कि निराला जी किसी दुर्लभ सीप में ढले सुडौल मोती नहीं थे, वे तो अनगढ़ पारस के भारी शिलाखंड थे। पारस की अमूल्यता दूसरों का मूल्य बढ़ाने में होती है। उसके मूल्य में तो न कोई कुछ जोड़ सकता है, न कुछ घटा सकता है।

निराला भाई शब्दार्थ

• भुक्खड़ = जिसके पास कुछ न हो, कंगाल
• औढरदानी = अत्यंत उदारतापूर्वक दान करने वाला
• अक्षुण्ण = अखंडित
• लौहसार = लोहे का कठघरा
• अछोर = ओर-छोर रहित, असीम
• महाघ = बहुमूल्य
• कुहेलिका = कोहरा, धुंध
• नापित = नाई
• मधुकरी = भोजन की भिक्षा
• डीलडौल = कदकाठी
• कोंपल = नई पत्ती
• अकूल = बिना किनारेवाला
• अनगढ़ = जिसे व्यवस्थित गढ़ा न गया हो
• संसृति = संसार, सृष्टि

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.3

Question 1.
Find the principal values of the following :
(i) sin^-1\(\left(\frac{1}{2}\right)\)
Solution:
The principal value branch of sin^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).
Let sin^-1\(\left(\frac{1}{2}\right)\) = ∝, where \(\frac{-\pi}{2}\) ≤ ∝ ≤ \(\frac{\pi}{2}\)
∴ sin∝ = \(\frac{1}{2}\) = sin\(\frac{\pi}{6}\)
∴ ∝ = \(\frac{\pi}{6}\) …[∵ – \(\frac{\pi}{2}\) ≤ \(\frac{\pi}{6}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of sin^-1\(\left(\frac{1}{2}\right)\) is \(\frac{\pi}{6}\).

(ii) cosec^-1(2)
Solution:
The principal value branch of cosec^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – {0}.
Let cosec^-1(2) = ∝, where \(\frac{-\pi}{2}\) ≤ ∝ ≤ \(\frac{\pi}{2}\), ∝ ≠ 0
∴ cosec^-1 ∝ = 2 = cosec\(\frac{\pi}{6}\)
∴ ∝ = \(\frac{\pi}{6}\) …[∵ –\(\frac{\pi}{2}\) ≤ \(\frac{\pi}{6}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of cosec^-1(2) is \(\frac{\pi}{6}\).

(iii) tan^-1(-1)
Solution:
The principal value branch of tan^-1x is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
Let tan^-1(-1) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ tan∝ = -1 = -tan\(\frac{\pi}{4}\)
∴ tan∝ = tan\(\left(-\frac{\pi}{4}\right)\) …[∵ tan(-θ) = -tanθ]
∴ ∝ = –\(\frac{\pi}{4}\) …[∵ –\(\frac{\pi}{2}\) < \(\frac{-\pi}{4}\) < \(\frac{\pi}{2}\)]
∴ the principal value of tan^-1(-1) is –\(\frac{\pi}{4}\).

(iv) tan^-1(-\(\sqrt {3}\))
Solution:
The principal value branch of tan^-1x is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\).
Let tan^-1(-\(\sqrt {3}\)) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ tan∝ = –\(\sqrt {3}\) = -tan\(\frac{\pi}{3}\)
∴ tan∝ = tan\(\left(-\frac{\pi}{3}\right)\) …[∵ tan(-θ) = -tanθ]
∴ ∝ = –\(\frac{\pi}{3}\) …[∵ –\(\frac{\pi}{2}\) < \(\frac{-\pi}{3}\) < \(\frac{\pi}{2}\)]
∴ the principal value of tan^-1(-\(\sqrt {3}\)) is –\(\frac{\pi}{3}\).

(v) sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\)
Solution:
The principal value branch of sin^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).
Let sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ sin∝ = \(\left(\frac{1}{\sqrt{2}}\right)\) = sin\(\frac{\pi}{4}\)
∴ ∝ = \(\frac{\pi}{4}\) …[∵ –\(\frac{\pi}{2}\) ≤ \(\frac{\pi}{4}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\) is \(\frac{\pi}{4}\).

(vi) cos^-1\(\left(-\frac{1}{2}\right)\)
Solution:
The principal value branch of cos^-1x is (0, π).
Let cos^-1\(\left(-\frac{1}{2}\right)\) = ∝, where 0 ≤ ∝ ≤ π
∴ cos∝ = \(-\frac{1}{2}\) = -cos\(\frac{\pi}{3}\)
∴ cos∝ = cos\(\left(\pi-\frac{\pi}{3}\right)\) …[∵ cos(π – θ) = -cosθ)
∴ cos∝ = cos\(\frac{2 \pi}{3}\)
∴ ∝ = \(\frac{2 \pi}{3}\) …[∵ 0 ≤ \(\frac{2 \pi}{3}\) ≤ π]
∴ the principal value of cos^-1\(\left(-\frac{1}{2}\right)\) is \(\frac{2 \pi}{3}\).

Question 2.
Evaluate the following :
(i) tan^-1(1) + cos^-1\(\left(\frac{1}{2}\right)\) + sin^-1\(\left(\frac{1}{2}\right)\)
Solution:

(ii) cos^-1\(\left(\frac{1}{2}\right)\) + 2 sin^-1\(\left(\frac{1}{2}\right)\)
Solution:

(iii) tan^-1\(\sqrt {3}\) – sec^-1(-2)
Solution:

∴ tan^-1\(\sqrt {3}\) – sec^-1(-2)
= \(\frac{\pi}{3}-\frac{2 \pi}{3}\) …[By (1) and (2)]
= –\(\frac{\pi}{3}\).

(iv) cosec^-1( \(-\sqrt{2}\)) + cot^-1(\(\sqrt{3}\))
Solution:

Question 3.
Prove the following :
(i) sin^-1\(\left(\frac{1}{\sqrt{2}}\right)\) – 3sin^-1\(\left(\frac{\sqrt{3}}{2}\right)\) = –\(-\frac{3 \pi}{4}\)
Question is modified.
sin^-1\(\left(\frac{1}{\sqrt{2}}\right)\) – 3sin^-1\(\left(\frac{\sqrt{3}}{2}\right)\) = –\(\frac{3 \pi}{4}\)
Solution:

(ii) sin^-1\(\left(-\frac{1}{2}\right)\) + cos^-1\(\left(-\frac{\sqrt{3}}{2}\right)\) = cos^-1\(\left(-\frac{1}{2}\right)\)
Solution:

(iii) sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{12}{13}\right)\) = sin^-1\(\left(\frac{56}{65}\right)\)
Solution:

(iv) cos^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{4}{5}\right)\) = \(\frac{\pi}{2}\)
Solution:
Let cos^-1\(\left(\frac{3}{5}\right)\) = x
∴ cosx = \(\left(\frac{3}{5}\right)\), where 0 < x < \(\frac{\pi}{2}\) ∴ sinx > 0

(v) tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{3}\right)\) = \(\frac{\pi}{4}\)
Solution:
LHS = tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{3}\right)\)
= tan^-1\(\left(\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2} \times \frac{1}{3}}\right)\)
= tan^-1\(\left(\frac{3+2}{6-1}\right)\) = tan^-1(1)
= tan^-1\(\left(\tan \frac{\pi}{4}\right)\) = \(\frac{\pi}{4}\)
= RHS.

(vi) 2 tan^-1\(\left(\frac{1}{3}\right)\) = tan^-1\(\left(\frac{3}{4}\right)\)
Solution:

(vii) tan^-1\(\left[\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}\right]\) = \(\frac{\pi}{4}\) + θ if θ ∈ \(\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)\)
Solution:

(viii) tan^-1\(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}=\frac{\theta}{2}\), if θ ∈ (0, π)
Solution:

= \(\frac{\theta}{2}\) …[∵ tan^-1(tanθ) = θ]
= RHS.

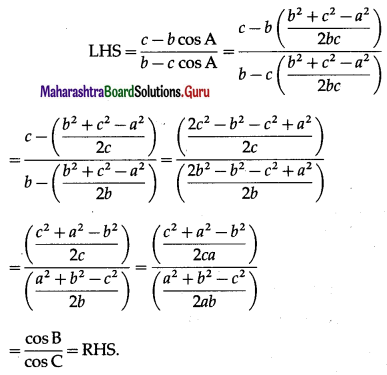
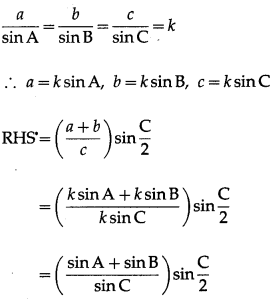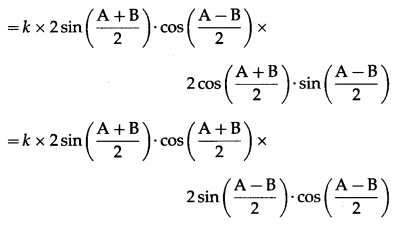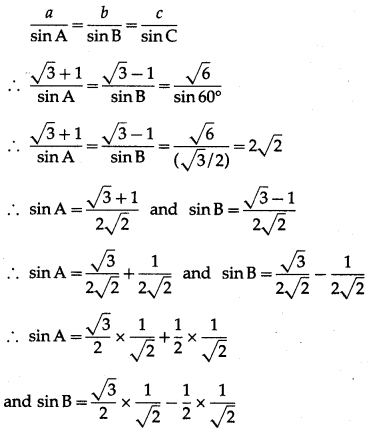Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 4 आदर्श बदला Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 4 आदर्श बदला

12th Hindi Guide Chapter 4 आदर्श बदला Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.

(अ) कृति पूर्ण कीजिए :
साधुओं की एक स्वाभाविक विशेषता – ………………………………
उत्तर :
एक स्थान से दूसरे स्थान पर जाते रहना और भजन तथा भक्तिगीत गाते-बजाते रहना।

(आ) लिखिए :

(a) आगरा शहर का प्रभातकालीन वातावरण –
………………………………………………………………
………………………………………………………………
उत्तर :

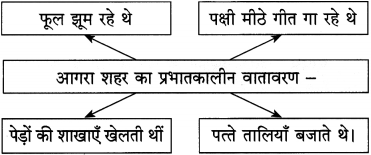
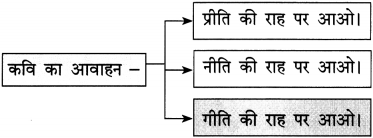
(b) साधुओं की मंडली आगरा शहर में यह गीत गा रही थी –
………………………………………………………………
………………………………………………………………
उत्तर :
सुमर-सुमर भगवान को,
मूरख मत खाली छोड़ इस मन को।

शब्द संपदा

प्रश्न 2.
लिंग बदलिए:

(1) साधु
(2) नवयुवक
(3) महाराज
(4) दास
उत्तर :
(1) साधु – साध्वी
(2) नवयुवक – नवयुवती
(3) महाराज – महारानी
(4) दास – दासी।

अभिव्यक्ति

प्रश्न 3.

(अ) ‘मनुष्य जीवन में अहिंसा का महत्त्व’, इस विषय पर अपने विचार लिखिए।
उत्तर :
हिंसा क्रूरता और निर्दयता की निशानी है। इससे किसी.। का भला नहीं हो सकता। इस संसार के सभी जीव ईश्वर की संतान हैं और समान हैं। सृष्टि में सबको जीने का अधिकार है। कोई कितना भी शक्तिमान क्यों न हो, किसी को उससे उसका जीवन छीनने का अधिकार नहीं है। जब कोई किसी को जीवन दे नहीं सकता तब वह किसी का जीवन ले भी नहीं सकता। बड़े-बड़े मनीषियों और महापुरुषों ने अहिंसा को ही धर्म कहा है – अहिंसा परमोधर्मः।

अहिंसा का अस्त्र सबसे बड़ा माना जाता है। राष्ट्रपिता महात्मा गांधी ने अहिंसा के बल पर शक्तिशाली अंग्रेज सरकार को झुका दिया था और अंग्रेज सरकार देश को आजाद करने पर विवश हो गई थी। जीवन का मूलमंत्र ‘जियो और जीने दो’ है। किसी के प्रति ईर्ष्या की भावना रखना या किसी का नुकसान करना भी एक प्रकार की हिंसा है। इससे हमें बचना चाहिए।

(आ) ‘सच्चा कलाकार वह होता है जो दूसरों की कला का सम्मान करता हैं, इस कथन पर अपना मत व्यक्त कीजिए।
उत्तर :
कलाकार को कोई कला सीखने के लिए गुरु के सान्निध्य में रह कर वर्षों तक तपस्या करनी पड़ती है। कला की छोटीछोटी बारीक बातों की जानकारी करनी पड़ती है। इसके साथ ही निरंतर रियाज करना पड़ता है। गुरु से कला की जानकारियाँ प्राप्त करते-करते अपनी कला में वह प्रवीण होता है।

सच्चा कलाकार किसी कला को सीखने की प्रक्रिया में होने वाली कठिनाइयों से परिचित होता है। इसलिए उसके दिल में अन्य कलाकारों के लिए सदा सम्मान की भावना होती है। वह छोटे-बड़े हर कलाकार को समान समझता है और उनकी कला का सम्मान करता है। सच्चे कलाकार का यही धर्म है। इससे कला को प्रोत्साहन मिलता है और वह फूलती-फलती है।

पाठ पर आधारित लघूत्तरी प्रश्न –

प्रश्न 4.

(अ) ‘आदर्श बदला’ कहानी के शीर्षक की सार्थकता स्पष्ट कीजिए।
उत्तर :
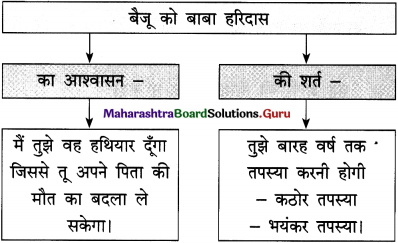
अपने पिता को मृत्युदंड दिए जाने पर बैजू विक्षिप्त हो गया था। और अपनी कुटिया में विलाप कर रहा था। उस समय बाबा हरिदास ने उसकी कुटिया में आकर उसे ढाढ़स बंधाया था। तब बालक बैजू ने बाबा को बताया था कि उसे अब बदले की भूख है। वे उसकी इस भूख को मिटा दें। बाबा हरिदास ने उसे वचन दिया था कि वे उसे ऐसा हथियार देंगे, जिससे वह अपने पिता की मौत का बदला ले सकेगा।

बाबा हरिदास ने बारह वर्षों तक बैजू को संगीत की हर प्रकार की बारीकियाँ सिखाकर उसे पूर्ण गंधर्व के रूप में तैयार कर दिया। मगर इसके साथ ही उन्होंने उससे यह वचन भी ले लिया कि वह इस राग विद्या से किसी को हानि न पहुँचाएगा।

इसके बाद वह दिन भी आया जब बैजू आगरा की सड़कों पर गाता हुआ निकला और उसके पीछे उसकी कला के प्रशंसकों की अपार भीड़ थी। आगरा में गाने के नियम के अनुसार उसे बादशाह के समक्ष पेश किया गया और शर्त के अनुसार तानसेन से उसकी संगीत प्रतियोगिता हुई, जिसमें उसने तानसेन को बुरी तरह परास्त कर दिया। तानसेन बैजू बावरा के पैरों पर गिरकर अपनी जान की भीख माँगने लगा। इस मौके पर बैजू बावरा उससे अपने पिता की मौत का बदला लेकर उसे प्राणदंड दिलवा सकता था। पर उसने ऐसा नहीं किया। बैजू ने तानसेन की जान बख्श दी।

उसने उससे केवल इस निष्ठुर नियम को उड़वा देने के लिए कहा, जिसके अनुसार किसी को आगरे की सीमाओं में गाने और तानसेन की जोड़ का न होने पर मरवा दिया जाता था। इस तरह बैजू बावरा ने तानसेन का गर्व नष्ट कर उसे मुँह की खिलाकर उससे अनोखा बदला लेकर उसे श्रीहीन कर दिया था। यह अपनी तरह का आदर्श बदला था। समूची कहानी इस बदले के आसपास घूमती है। इसलिए ‘आदर्श बदला’ शीर्षक इस कहानी के उपयुक्त है।

(आ) ‘बैजू बावरा संगीत का सच्चा पुजारी है’, इस विचार को स्पष्ट कीजिए।
उत्तर :
सच्चा कलाकार उसे कहते हैं, जिसे अपनी कला से सच्चा लगाव हो। वह अपने गुरु की कही हुई बातों पर अमल करे तथा गुरु से विवाद न करे। इसके अलावा उसे अपनी कला पर अहंकार न हो। बैजू बावरा ने बारह वर्ष तक बाबा हरिदास से संगीत सीखने की कठिन तपस्या की थी।

वह उनका एक आज्ञाकारी शिष्य था। उसकी संगीत शिक्षा पूरी हो जाने के बाद बाबा हरिदास ने जब उससे यह प्रतिज्ञा करवाई कि वह इस राग विद्या से किसी को हानि नहीं पहुँचाएगा, तो भी उसने रक्त का यूंट पी कर इस गुरु आदेश को स्वीकार कर लिया था, जबकि उसे मालूम था कि इससे उसके हाथ में आई हुई प्रतिहिंसा की छुरी कुंद कर दी गई थी। फिर भी गुरु के सामने उसके मुँह से एक शब्द भी नहीं निकला।

बैजू बावरा की संगीत कला की धाक दूर-दूर तक फैल गई थी। है उसके संगीत में जादू का असर था। बैजू बावरा को संगीत ज्ञान है पर तानसेन की तरह कोई अहंकार नही था। बल्कि इसके विपरीत उसके हृदय में दया की भावना थी। गानयुद्ध में तानसेन को पराजित करने पर भी वह अपनी जीत और संगीत का प्रदर्शन नहीं करता।

बल्कि वह तानसेन को जीवनदान दे देता है। वह उससे केवल यह माँग करता है कि वह इस नियम को खत्म करवा दे कि जो कोई आगरा की सीमा के अंदर गाए, वह अगर तानसेन की जोड़ का न हो, तो मरवा दिया जाए। उसकी इस माँग में भी गीत-संगीत की ५ रक्षा करने की भावना निहित है।

इस प्रकार इसमें कोई संदेह नहीं है कि बैजू बावरा संगीत का सच्चा पुजारी था।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.

(अ) सुदर्शन जी का मूल नाम : ……………………………………
उत्तर :
सुदर्शन जी का मूल नाम बदरीनाथ है।

(आ) सुदर्शन ने इस लेखक की लेखन परंपरा को आगे बढ़ाया है : ……………………………………
उत्तर :
सुदर्शन ने मुंशी प्रेमचंद की लेखन परंपरा को आगे बढ़ाया है।

रस

अद्भुत रस : जहाँ किसी के अलौकिक क्रियाकलाप, अद्भुत, आश्चर्यजनक वस्तुओं को देखकर हृदय में विस्मय अथवा आश्चर्य का भाव जाग्रत होता है; वहाँ अद्भुत रस की व्यंजना होती है।

उदा. –

(१) एक अचंभा देखा रे भाई।
ठाढ़ा सिंह चरावै गाई।
पहले पूत पाछे माई।
चेला के गुरु लागे पाई।।

(२) बिनु-पग चलै, सुनै बिनु काना।
कर बिनु कर्म कर, विधि नाना।
आनन रहित सकल रस भोगी।
बिनु वाणी वक्ता, बड़ जोगी।।

शृंगार रस : जहाँ नायक और नायिका अथवा स्त्री-पुरुष की प्रेमपूर्ण चेष्टाओं, क्रियाकलापों का शृंगारिक वर्णन हो; वहाँ शृंगार रस की व्यंजना होती है।

उदा. –
(१) राम के रूप निहारति जानकी, कंकन के नग की परछाही,
यातै सबै सुधि भूलि गई, कर टेकि रही पल टारत नाही।

(२) कहत, नटत, रीझत, खिझत, मिलत, खिलत, लजियात।
भरे भौन में करत हैं, नैननु ही सौं बात।।

शांत रस : (निर्वेद) जहाँ भक्ति, नीति, ज्ञान, वैराग्य, धर्म, दर्शन, तत्त्वज्ञान अथवा सांसारिक नश्वरता संबंधी प्रसंगों का वर्णन हो; वहाँ शांत रस उत्पन्न होता है।

उदा. –
(१) माला फेरत जुग भया, गया न मन का फेर।
कर का मनका डारि कै, मन का मनका फेर।।

(२) माटी कहै कुम्हार से, तू क्या रौंदे मोहे।
एक दिन ऐसा आएगा, मैं रौंदूंगी तोहे।।

भक्ति रस : जहाँ ईश्वर अथवा अपने इष्ट देवता के प्रति श्रद्धा, अलौकिकता, स्नेह, विनयशीलता का भाव हृदय में उत्पन्न होता है; वहाँ भक्ति रस की व्यंजना होती है।

उदा. –
(१) तू दयालु दीन हौं, तू दानि हौं भिखारि।
हौं प्रसिद्ध पातकी, तू पाप पुंजहारि।

(२) समदरसी है नाम तिहारो, सोई पार करो,
एक नदिया इक नार कहावत, मैलो नीर भरो,
एक लोहा पूजा में राखत, एक घर बधिक परो,
सो दुविधा पारस नहीं जानत, कंचन करत खरो।

Hindi Yuvakbharati 12th Digest Chapter 4 आदर्श बदला Additional Important Questions and Answers

गद्यांश क्र. 1
कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए।

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

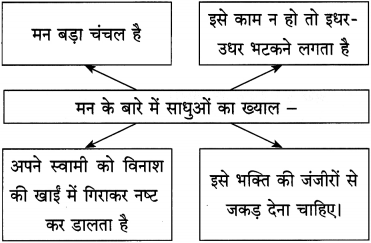
उत्तर :

प्रश्न 2.
साधु इस तरह गाते थे गीत –
(1) ……………………………………..
(2) ……………………………………..
(3) ……………………………………..
(4) ……………………………………..
उत्तर :
(1) कोई ऊँचे स्वर में गाता था।
(2) कोई मुँह में गुनगुनाता था।
(3) सब अपने राग में मगन थे।
(4) उन्हें सुर-ताल की परवाह नहीं थी।

प्रश्न 3.
तानसेन द्वारा बनवाया गया कानून –
(1) ……………………………………..
(2) ……………………………………..
उत्तर :
(1)जो आदमी राग-विद्या में तानसेन की बराबरी न कर सके, है वह आगरे की सीमा में गीत न गाए।
(2) ऐसा आदमी जो आगरे की सीमा में गीत गाए, उसे मौत की सजा दी जाए।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग बदलकर लिखिए :
(1) पत्ते – …………………………………..
(2) स्वामी – …………………………………..
(3) राग – …………………………………..
(4) आदमी – …………………………………..
उत्तर :
(1) पत्ते – पत्तियाँ
(2) स्वामी – स्वामिनी
(3) राग – रागिनी (4) आदमी – औरत

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
साधु-संतों को राग विद्या की जानकारी न होने के कारण मौत की सजा दिया जाना क्या उचित है? इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
साधु-संत दीन-दुनिया से विरक्त ईश्वर आराधना में लीन रहने वाले लोग होते हैं। वे अपने साथी साधु-संतों से सुने-सुनाए भजन-कीर्तन अपने ढंग से गाते हैं। उन्हें राग, छंद और संगीत का समुचित ज्ञान नहीं होता। भजन भी वे अपनी आत्म-संतुष्टि और ईश्वर आराधना के लिए गाते हैं।

उनका उद्देश्य उसे राग में गा कर किसी को प्रसन्न करना नहीं होता। आगरा शहर में बिना सुर-ताल की परवाह किए हुए और बादशाह के कानून से अनभिज्ञ ये साधु गाते हुए जा रहे थे। इन्हें इस जुर्म में पकड़ लिया गया था कि वे आगरा की सीमा में गाते हुए जा रहे हैं। अकबर के मशहूर रागी तानसेन ने यह नियम बनवा दिया था कि जो आदमी राग विद्या में उसकी बराबरी न कर सके वह आगरा की सीमा में न गाए। यदि गाए तो उसे मौत की सजा दी जाए।

अतः इन्हें मौत की सजा दे दी गई। इस तरह साधुओं को मौत की सजा देना उनके साथ बिलकुल अन्याय है। इस तरह के कानून से तानसेन के अभिमान की बू आती है।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

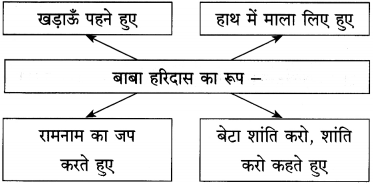
उत्तर :

उत्तर :

प्रश्न 2.
उत्तर लिखिए :

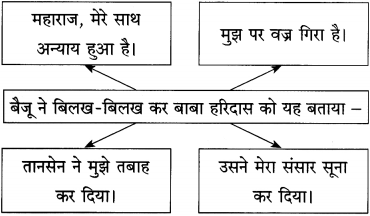
(1) बैजू ने हरिदास के चरणों में और ज्यादा लिपट कर यह कहा –
(i) ……………………………………
(ii) ……………………………………
(iii) ……………………………………
(iv) ……………………………………
उत्तर :
(i) महाराज (मेरी) शांति जा चुकी है।
(ii) अब मुझे बदले की भूख है।
(iii) अब मुझे प्रतिकार की प्यास है।
(iv) आप मेरी प्यास बुझाइए।

(2)

उत्तर :

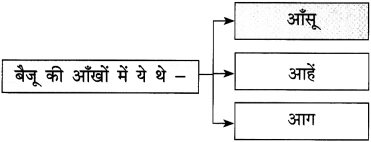
(3)

उत्तर :

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर :

प्रश्न 4.
बैजू ने दिया बाबा हरिदास को यह वचन –
(i) ……………………………………
(ii) ……………………………………
(iii) ……………………………………
(iv) ……………………………………
उत्तर :
(i) मैं बारह जीवन देने को तैयार हूँ।
(ii) मैं तपस्या करूँगा।
(iii) मैं दुख झेलूँगा, मैं मुसीबतें उठाऊँगा।
(iv) मैं अपने जीवन का एक-एक क्षण आपको भेंट कर दूंगा।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग बदल कर लिखिए :
(1) बेटा – ……………………………………
(2) बच्चा – ……………………………………
(3) सेवक – ……………………………………
(4) सूना – ……………………………………
उत्तर :
(1) बेटा – बेटी
(2) बच्चा – बच्ची
(3) सेवक – सेविका
(4) आखिरी = अंतिम।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) संसार = ……………………………………
(2) तबाह = ……………………………………
(3) चरण = ……………………………………
(4) आखिरी = ……………………………………
उत्तर :
(1) संसार = दुनिया
(2) तबाह = बर्बाद
(3) चरण = पाँव
(4) सूना – सूनी।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘बिनु गुरु होय न ज्ञान’ इस कथन के बारे में 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
मनुष्य को बचपन से लेकर अंतिम समय तक विभिन्न . कार्यों को पूर्ण करने के लिए ज्ञान की आवश्यकता होती है। यह ज्ञान विभिन्न रूपों में हमें किसी-न-किसी गुरु से मिलता है। बचपन में बच्चे का पालन-पोषण कर उसे बड़ा करके बोलने-चालने और बोली-भाषा सिखाने का काम माता करती है।

उस समय वह उसकी गुरु होती है। बड़े होने पर विद्यालय में शिक्षकों से बच्चे को ज्ञान की प्राप्ति होती है। तरह-तरह की कलाओं को सीखने के लिए गुरु से ज्ञान प्राप्त करने की आवश्यकता होती है। गुरु से ज्ञान प्राप्त करके ही कलाकार नाम कमाते हैं।

प्रसिद्ध क्रिकेट खिलाड़ी सचिन तेंदुलकर के क्रिकेट के क्षेत्र में महारत हासिल करने में उनके क्रिकेट गुरु रमाकांत आचरेकर का विशेष योगदान रहा है।

इसी तरह छत्रपति शिवाजी महाराज की सफलता में उनके गुरु का काफी योगदान रहा है। गुरु ही हमें सही या गलत में भेद करना सिखाते हैं। वे ही भूले-भटके हओं को सही राह दिखाते हैं। इस तरह गुरु की महिमा अपरंपार है।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
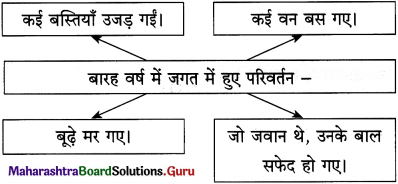
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए : जवान बैजू के संगीत की विशेषताएँ –
(1) …………………………
(2) …………………………
(3) …………………………
(4) …………………………
उत्तर :
(1) उसके स्वर में जादू था और तान में आश्चर्यमयी मोहिनी थी।
(2) गाता था तो पत्थर तक पिघल जाते थे।
(3) पशु-पंछी तक मुग्ध हो जाते थे।
(4) लोग सुनते थे और झूमते थे तथा वाह-वाह करते थे।

प्रश्न 3.
बैजू की राग विद्या की शिक्षा पूरी होने पर हरिदासजी ने यह कहा –
(1) …………………………
(2) …………………………
उत्तर :
(1) वत्स! मेरे पास जो कुछ था, वह मैंने तुझे दे डाला।
(2) अब तू पूर्ण गंधर्व हो गया है।

प्रश्न 4.
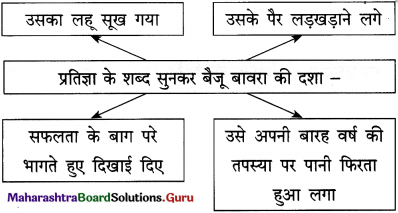
संजाल पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) उजड़ना x ……………………………..
(2) बूढ़े x ……………………………..
(3) कृतज्ञता x ……………………………..
(4) उपकार x ……………………………..
उत्तर :
(1) उजड़ना – बसना
(3) कृतज्ञता – कृतघ्नता
(2) बूढ़े x जवान
(4) उपकार x अपकार।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘कृतज्ञता मनुष्य का उत्तम गुण है’ इस विषय पर 40 से 50 शब्दों में अपना मत लिखिए।
उत्तर :
कृतज्ञता का अर्थ है अपने साथ किसी के द्वारा किए गए किसी अच्छे कार्य के लिए व्यक्ति का एहसान मानना। प्रत्येक मनुष्य के जीवन में कभी-न-कभी ऐसा समय आता है, जब उसे किसी रूप में किसी व्यक्ति से छोटी-बड़ी मदद लेनी पड़ती है अथवा किसी का एहसान लेना पड़ता है। उस समय इस प्रकार की मदद अथवा उपकार करने वाला व्यक्ति हमें किसी फरिश्ते से कम नहीं लगता।

ऐसे समय हमारे मन में उसके प्रति श्रद्धा और सम्मान की भावना जाग उठती है। इसे हम एहसान करने वाले के पैर छू करः अथवा उसे धन्यवाद दे कर प्रदर्शित करते हैं। इतना ही नहीं हम सदा उसके एहसान को याद रखते हैं। कृतज्ञता व्यक्त करने से एहसान करने वाले व्यक्ति को भी प्रसन्नता होती है।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :

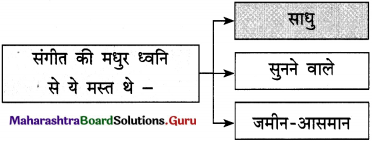
(1) सिपाहियों ने साधु को इस रूप में देखा –
(i) ………………………………..
(ii) ………………………………..
(iii) ………………………………..
(iv) ………………………………..
उत्तर :
(i) साधु के मुँह से तेज की किरणें फूट रही थीं। .
(ii) उन किरणों में जादू था, मोहिनी थी और मुग्ध करने की शक्ति थी।
(iii) उसके मुँह पर सरस्वती का वास था।
(iv) उसके मुँह से संगीत की मधुर ध्वनि की धारा बह रही थी।

(2)

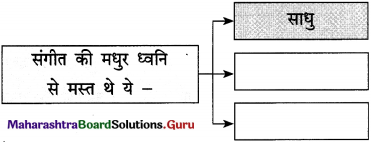
उत्तर :

प्रश्न 2.
कृति पूर्ण कीजिए :

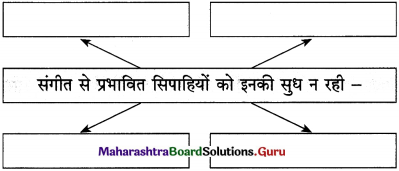
उत्तर :

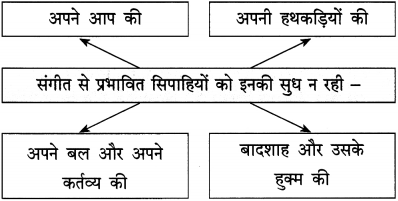
प्रश्न 3.
लिखिए : तानसेन ने नवयुवक (साधु) से यह कहा –
(1) ………………………………..
(2) ………………………………..
(3) ………………………………..
(4) ………………………………..
उत्तर :
(1) शायद आपके सिर पर मौत सवार है।
(2) आप नियम जानते हैं न?
(3) नियम कड़ा है और मेरे दिल में दया नहीं है।
(4) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार हैं।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदल कर लिखिए :
(1) हथकड़ियाँ – ………………………………………
(2) आँखें – ………………………………………
(3) बाजारों – ………………………………………
(4) श्रोता – ………………………………………
उत्तर :
(1) हथकड़ियाँ – हथकड़ी
(2) आँखें – आँख
(3) बाजारों – बाजार
(4) श्रोताँ – श्रोतागण।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘घमंड मनुष्य का सबसे बड़ा शत्रु है’ इस विषय पर अपने विचार 40 से 50 शब्दों में लिखिए।
उत्तर :
मनुष्य के अंदर सद् और असद् दो प्रवृत्तियाँ होती हैं। सद् का अर्थ है अच्छा और असद् का अर्थ है जो अच्छा न हो यानी बुरा। घमंड मनुष्य की बुरी वृत्ति है। घमंडी व्यक्ति को अच्छे और बुरे का विवेक नहीं होता। वह अपने घमंड के नशे में चूर रहता है और अपना भला-बुरा भी भूल जाता है।

घमंडी व्यक्ति को अपनी गलती का अहसास तब होता है, जब उसकी की गई गलतियों का परिणाम उसके सामने आता है। घमंड का परिणाम बहुत बुरा होता है। इसके कारण बड़े-बड़े ज्ञानी पुरुषों को भी मुँह की खानी पड़ती है।

रावण जैसा महाज्ञानी पंडित भी अपने घमंड के कारण अपने कुल परिवार सहित नष्ट हो गया। घमंड मनुष्य का सबसे बड़ा शत्रु है और उसकी मंजिल है दारुण दुख। इसलिए मनुष्य को घमंड का मार्ग त्याग कर प्रेम और सद्गुण का मार्ग अपनाना चाहिए।

गद्यांश क्र. 5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
उत्तर लिखिए :
(1) बैजू बावरा ने अपने सितार के पदों को हिलाया, तो यह हुआ –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
(i) जनता ब्रह्मानंद में लीन हो गई।
(ii) पेड़ों के पत्ते तक निःशब्द हो गए।
(iii) वायु रुक गई।
(iv) सुनने वाले मंत्रमुग्धवत सुधिहीन हुए सिर हिलाने लगे।

प्रश्न 3.
बैजू बावरा की उँगलियाँ जब सितार पर दौड़ी, तब –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
(i) तारों पर राग विद्या निछावर हो रही थी।
(ii) लोगों के मन उछल रहे थे।
(iii) लोग झूम रहे थे, थिरक रहे थे।
(iv) जैसे सारे विश्व की मस्ती वहीं आ गई थी।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द समूहों के लिए गद्यांश में से ढूँढकर एकएक शब्द लिखिए :
(1) ब्रह्म स्वरूप के साक्षात्कार का दर्शन।
(2) जहाँ किसी प्रकार का शब्द न होता हो।
(3) जो होश से रहित हो।
(4) किसी से भी न डरने की भावना।
उत्तर :
(1) ब्रह्मानंद
(2) निःशब्द
(3) सुधिहीन
(4) निर्भयता

गद्यांश क्र. 6
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : गानयुद्ध-स्थल पर दर्शक यह देखकर हैरान रह गए –
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
उत्तर :
(1) कुछ हरिण छलाँगें मारते हुए आए और बैजू बावरा के पास खड़े हो गए।
(2) हरिण संगीत सुनते रहे, सुनते रहे।
(3) हरिण मस्त और बेसुध थे।
(4) बैजू ने सितार रखकर उनके गले में फूलमालाएँ पहनाईं तब उन्हें सुध आई और भाग खड़े हुए।

प्रश्न 2.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 3.
लिखिए : तानसेन ने इस तरह बजाया सितार –
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
उत्तर :
(1) पूर्ण प्रवीणता के साथ।
(2) पूर्ण एकाग्रता के साथ।
(3) वह बजाया, जो कभी न बजाया था।
(4) वह बजाया, जो कभी न बजा सकता था।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित उपसर्ग जोड़कर शब्द बनाकर लिखिए :
(1) अ – …………………………….
(2) बे – …………………………….
(3) निर् – …………………………….
(4) परा – …………………………….
उत्तर
(1) अ – असाधारण
(2) बे – बेसुध
(3) निर् – निरादर
(4) परा – पराजय

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘संगीत का प्रभाव’ विषय पर 40 से 50 शब्दों में अपने विचार व्यक्त कीजिए।
उत्तर :
संगीत ऐसी कला है, जो श्रोताओं को अपनी स्वर लहरियों से आह्लादित कर देती है। संगीत एक गूढ़ विद्या है। संगीत-साधक इसमें जितनी गहराई तक जाता है, उसे उतने ही मोती मिलते हैं। संगीत का आनंद संगीत विशेषज्ञ तो उठाते ही हैं, जिन लोगों में संगीत कला की समझ नहीं होती, वे भी संगीत की स्वर लहरियों को सुन कर झूमने लगते हैं। संगीत की मधुर ध्वनि से लोग अपनी सुध-बुध खो बैठते हैं। संगीत सुनने से मन प्रसन्न होता है।

संगीत तनाव कम करने में सहायक होता है और उससे मानसिक शांति मिलती है।

संगीत का प्रभाव अद्भुत होता है। उससे केवल मनुष्य ही नहीं, वातावरण, पशु-पक्षी, पेड़-पौधे सभी प्रभावित होते हैं। संगीत से पौधों की वृद्धि और दुधारू पशुओं के अधिक दूध देने तक की बातें कही जाती रही हैं। गुणी संगीतकार के संगीत-वादन से वर्षा होने लगती है।

मधुर संगीत से प्रभावित होकर लोगों के मन उछलने लगते हैं, उनके मन थिरकने लगते हैं। लोग मस्ती में डूब जाते हैं। संगीत में जादू-सा प्रभाव होता है। संसार में शायद ही ऐसा कोई प्राणी होगा, जो संगीत की मधुर ध्वनि की धारा में न बह जाता हो।

गद्यांश क्र. 7
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : हरिण बुला पाने में असमर्थ तानसेन की बौखलाहट –
(1) ………………………………..
(2) ………………………………..
(3) ………………………………..
(4) ………………………………..
उत्तर :
(1) उसकी आँखों के सामने मौत नाचने लगी।
(2) उसकी देह पसीना-पसीना हो गई।
(3) लज्जा से उसका मुँह लाल हो गया।
(4) वह खिसिया गया।

प्रश्न 2.
उत्तर लिखिए :

(a) दुबारा बैजू बावरा ने सितार पकड़ा, तो यह हुआ –
(i) …………………………………
(ii) …………………………………
(iii) …………………………………
(iv) …………………………………
उत्तर :
(i) एक बार फिर संगीतलहरी वायुमंडल में लहराने लगी।
(ii) फिर सुनने वाले संगीत-सागर की तरंगों में डूबने लगे।
(iii) हरिण बैजू बावरा के पास फिर आए।
(iv) बैजू ने (उनके गले से) मालाएँ उतार लीं और हरिण छलाँग लगाते चले गए।

(b) अकबर का निर्णय सुन कर तानसेन ने यह किया –
(i) …………………………………
(ii) …………………………………
(iii) …………………………………
(iv) …………………………………
उत्तर :
(i) काँपता हुआ उठा।
(ii) काँपता हुआ आगे बढ़ा।
(iii) काँपता हुआ बैजू बावरा के पाँव में गिर पड़ा।
(iv) उससे गिड़गिड़ाया, ‘मेरे प्राण न लो।’

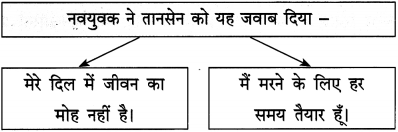
(c) बैजू बावरा ने तानसेन को यह जवाब दिया –
(i) …………………………………
(ii) …………………………………
उत्तर :
(i) मुझे तुम्हारे प्राण लेने की चाह नहीं।
(ii) तुम इस नियम को उड़वा दो कि यदि आगरे की सीमा में गाने वाला तानसेन की जोड़ का न हो, तो उसे मरवा दिया जाए।

(d) बैजू बावरा ने तानसेन को यह पुरानी बात बताई –
(i) …………………………………
(ii) …………………………………
उत्तर :
(i) बारह साल पहले आपने एक बच्चे की जान बचाई (बख्शी ) थी।
(ii) आज उस बच्चे ने आपकी जान बख्शी है।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
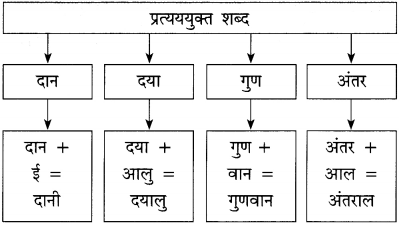
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्द ढूँढ़कर लिखिए : .
(1) ………………………………
(2) ………………………………
(3) ………………………………
(4) ………………………………
उत्तर :
(1) संगीतलहरी – संगीतलहर + ई।
(2) मालाएँ – माला + एँ।
(3) होकर – हो + कर।
(4) दीनता – दीन + ता।

1. मुहावरे :

निम्नलिखित मुहावरों का अर्थ लिखकर अपने वाक्यों में प्रयोग कीजिए :

(1) अगर-मगर करना।
अर्थ : टाल-मटोल करना।
वाक्य : सिपाही ने आरोपी से कहा, अगर-मगर मत करो, सीधे-सीधे मेरे साथ थाने चलो।

(2) अपना राग अलापना।
अर्थ : अपनी ही बातें करते रहना।
वाक्य : श्यामसुंदर की तो आदत है, दूसरे की बात न सुनना और अपना ही राग अलापते रहना।

(3) चाँदी काटना।
अर्थ : बहुत लाभ कमाना।
वाक्य : आजकल जब लोग कोरोना के डर से घरों में दुबके हैं, कुछ सब्जी बेचने वाले चाँदी काट रहे हैं।

(4) कान भरना।
अर्थ : चुगली करना।
वाक्य : मुनीमजी का चपरासी आफिस के अन्य लोगों के बारे में उनके कान भरता रहता है।

(5) जली-कटी सुनाना।
अर्थ : कटु बात करना।
वाक्य : रघु की माँ अकारण अपनी बहू को जली-कटी सुनाती रहती है।

2. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों का काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) प्रकाश की किरणें संसार पर नवीन जीवन की वर्षा कर रही थीं। (सामान्य वर्तमानकाल)
(2) जो जवान थे उनके बाल सफेद हो गए। (सामान्य भविष्यकाल)
(3) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार हैं। (पूर्ण भूतकाल)
(4) बैजू बावरा की उँगलियाँ सितार पर दौड़ रही थीं। (अपूर्ण वर्तमानकाल)
(5) बहुत अच्छा! दोबारा बुलाकर दिखा देता हूँ। (सामान्य भविष्यकाल)
उत्तर :
(1) प्रकाश की किरणें संसार पर नवीन जीवन की वर्षा करती हैं।
(2) जो जवान होंगे उनके बाल सफेद हो जाएंगे।
(3) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार थीं।
(4) बैजू बावरा की उँगलियाँ सितार पर दौड़ रही हैं।
(5) बहुत अच्छा! दोबारा बुलाकर दिखा दूंगा।

3. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्यों को शुद्ध करके लिखिए :
(1) मैं तेरे को वह हथियार दूँगा, जिससे तू तेरे पिता की मौत का बदला ले सकेगा।
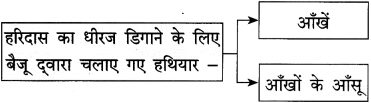
(2) हरिदास की धीरज की दीवार आँसुओं के बौछार न सह सकी।
(3) बैजू हाथों बाँधकर खड़े हो गया।
(4) अब मेरी पास और कुछ नहीं, जो तुजे दूँ।
(5) साधु की प्रार्थना में सर्वसाधारण को भी उसकी जीवन और मृत्यु का तमाशा देखने की आज्ञा दे दी गई थी।
उत्तर :
(1) मैं तुझे वह हथियार दूँगा, जिससे तू अपने पिता की मौत का बदला ले सकेगा।
(2) हरिदास के धीरज की दीवार आँसुओं की बौछार न सह सकी।
(3) बैजू हाथ बाँधकर खड़ा हो गया।
(4) अब मेरे पास और कुछ नहीं जो तुझे दूँ।
(5) साधु की प्रार्थना पर सर्वसाधारण को भी उसके जीवन और मृत्यु का तमाशा देखने की आज्ञा दे दी गई थी।

आदर्श बदला Summary in Hindi

आदर्श बदला लेखक का परिचय

आदर्श बदला लेखक का नाम : सुदर्शन। (मूल नाम : बदरीनाथ) (जन्म 29 मई, 1895, सियालकोट ; निधन 9 मार्च, 1967.)

प्रमुख कृतियाँ : पुष्पलता, सुदर्शन सुधा, तीर्थयात्रा, पनघट (कहानी संग्रह)। सिकंदर, भाग्यचक्र (नाटक)। भागवती (उपन्यास)। आनररी मजिस्ट्रेट (प्रहसन)।

विशेषता : आपने प्रेमचंद की लेखन-परंपरा को आगे बढ़ाया है। आपकी रचनाएँ आदर्शोन्मुख यथार्थवाद को रेखांकित करती हैं। साहित्य को लेकर आपका दृष्टिकोण सुधारवादी रहा है। आपने हिंदी फिल्मों की पटकथाएँ और गीत भी लिखे हैं। आपकी प्रथम कहानी ‘हार की जीत’ हिंदी साहित्य में विशिष्ट स्थान रखती है।

विधा : कहानी। कहानी भारतीय साहित्य की प्राचीन विद्या है। आपकी कहानियों की भाषा सरल, पात्रानुकूल तथा प्रभावोत्पादक हैं। मुहावरों का सटीक प्रयोग, प्रवाहमान शैली कहानी की प्रभावोत्पादकता में वृद्धि करती है।

विषय प्रवेश : बदला लेने वाले व्यक्ति के मन में अकसर क्रोध अथवा हिंसा की भावना प्रमुख होती है। इतना ही नहीं, मौत का बदला मौत से लेने की अनेक घटनाएँ प्रसिद्ध हैं। पर प्रस्तुत कहानी में लेखक ने बदला लेने का अनूठा आदर्श प्रस्तुत किया है। ‘बचपन में बैजू अपने पिता को भजन गाने के अपराध में तानसेन की क्रूरता का शिकार होता हुआ देखता है। परंतु वही बैजू बावरा तानसेन को संगीत-प्रतियोगिता में हरा कर उसे जीवन-दान दे देता है। लेखक ने इस कहानी के माध्यम से बैजू बावरा को आदर्श बदला लेते हुए दर्शाया है।

आदर्श बदला पाठ का सार

आगरा शहर में सुबह-सुबह साधुओं की एक मंडली अपने ढंग से भजन गाते-गुनगुनाते प्रवेश कर रही थी। इस मंडली में एक छोटा बच्चा भी था। साधु अपने राग में मगन थे, तभी राज्य के सिपाहियों ने उन्हें गिरफ्तार कर लिया और उन्हें बादशाह अकबर के सामने पेश कर दिया गया।

अकबर के मशहूर संगीतकार तानसेन ने यह कानून बनवा दिया था कि जो आदमी राग विद्या में उसकी बराबरी न कर सके, वह आगरा की सीमा में गीत न गाए और जो गाए तो उसे मौत की सजा दी जाए। बेचारे साधुओं को इसकी जानकारी नहीं थी। साधु संगीत विद्या से अनभिज्ञ थे। अतः उन्हें मृत्युदंड की सजा हुई। पर उस बच्चे पर दया करके उसे छोड़ दिया गया।

वह बच्चा रोता-तड़पता आगरा की बाजारों से निकल कर जंगल में अपनी कुटिया में पहुँचा और विलाप करता रहा। तभी खड़ाऊँ पहने, हाथ में माला लिए हुए, राम नाम का जप करते हुए बाबा हरिदास कुटिया के अंदर आए और उन्होंने उसे शांत रहने के लिए कहा। पर उस बच्चे के मन में शांति कहाँ थी! उसका तो संसार उजड़ चुका था। तानसेन ने उसे तबाह कर दिया था।

यह बच्चा बैजू बावरा था। उसने अपने साथ हुई सारी दुर्घटना बाबा हरिदास को बताई और अपने बदले की भूख और प्रतिकार की प्यास मिटाने की उनसे प्रार्थना की। E अंत में हरिदास ने उसे आश्वस्त किया कि वे उसे ऐसा हथियार देंगे, जिससे वह अपने पिता का बदला ले सके।

इसके लिए उन्होंने बैजू से बारह वर्ष तक (संगीत की) तपस्या E करने का वचन लिया। बाबा ने बारह वर्ष में बैजू बावरा को वह सब कुछ सिखा दिया, जो उनके पास था। अब बैजू पूर्ण गंधर्व हो गया था। उसके स्वर में जादू था।

लेकिन संगीत-तपस्या पूरी होने के साथ ही बैजू बावरा को बाबा हरिदास के सामने यह प्रतिज्ञा भी करनी पड़ी कि वह इस राग विद्या से किसी को हानि नहीं पहुँचाएगा। इस प्रतिज्ञा से उसे लगा कि प्रतिहिंसा की छुरी हाथ में आई भी तो गुरु ने प्रतिज्ञा लेकर उसे कुंद कर दी।

कुछ दिनों बाद यही सुंदर युवक साधु आगरा के बाजारों में गाता हुआ जा रहा था। लोगों ने सोचा कि इसकी भी मौत आ गई है। वे उसे नगर की रीति की सूचना देने निकले। पर उसके निकट पहुँचने के पहले ही वे उससे मुग्ध होकर अपनी सुधबुध खो बैठे। सिपाही उसे पकड़ने दौड़े तो उसका गीत सुन कर उन्हें अपनी हथकड़ियों की भी सुध न रही। लोग नवयुवक के गीत पर मुग्ध थे। चलते-चलते यह जन-समूह मौत के द्वार यानी तानसेन के महल के सामने था।

तानसेन बाहर निकला और उसने फब्ती कसी, ‘तो शायद आपके सिर पर मौत सवार है।’ यह सुन कर बैजू के होठों पर मुस्कराहट आ गई। उसने कहा, “मैं आपके साथ गान-विद्या पर चर्चा करना चाहता हूँ।” तानसेन ने कहा, “जानते हैं नियम कड़ा है। मेरे दिल में दया नहीं है। मेरी आँखें दूसरों की मौत देखने के लिए हर समय तैयार हैं।” इस पर बैजू बावरा ने कहा, “और मेरे दिल में जीवन का मोह नहीं है। मैं मरने के लिए हर समय तैयार हूँ।”

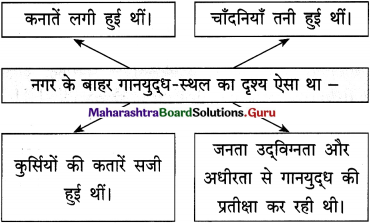
दरबार की ओर से शर्ते सुनाई गई। राग-युद्ध नगर के बाहर वन में आयोजित किया गया था। लगता था वन में नगर बस गया है। बैजू ने सितार उठाया। उसने पदों को हिलाया तो जनता ब्रह्मानंद में लीन हो गई। उसकी उँगलियाँ सितार पर दौड़ने लगीं। लगा, सारे विश्व की मस्ती वहीं आ गई हो। तभी संगीत से प्रभावित होकर कुंछ हरिण छलांगें मारते हुए वहाँ आ पहुँचे। वे संगीत सुनते रहे।

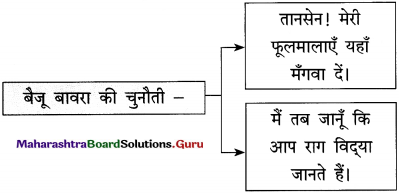
बैजू ने सितार बजाना बंद किया और अपने गले से फूलमालाएँ उतार कर हरिणों को पहना दीं। हरिण चौकड़ी भरते हुए गायब हो गए। बैजू ने तानसेन से कहा, “ तानसेन, मेरी फूलमालाएँ यहाँ मँगवा दें, तब जानूँ कि आप राग-विद्या जानते हैं।”

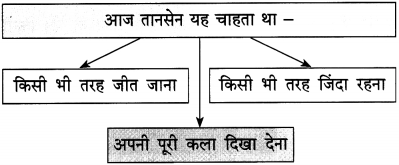
तानसेन सितार हाथ में लेकर बजाने लगा। इतनी एकाग्रता के साथ उसने अपने जीवन में कभी सितार नहीं बजाया था। आज वह अपनी पूरी कला दिखा देना चाहता था। आज वह किसी तरह जीतना चाहता था। आज वह किसी भी तरह जिंदा रहना चाहता था। सितार बजता रहा, पर आज लोगों ने उसे पसंद नहीं किया। तानसेन का शरीर पसीना-पसीना हो गया, पर हरिण न आए। वह खिसिया गया। बोला, “वे हरिण राग की तासीर से नहीं आए थे। हिम्मत है तो दुबारा बुला कर दिखाओ।”

यह सुन कर बैजू ने फिर सितार पकड़ लिया। सितार बजने लगा। वे हरिण फिर बैजू बावरा के पास आ गए। बैजू ने उनके गले से मालाएँ उतार लीं। अकबर ने अपना निर्णय सुना दिया, “बैजू बावरा जीत गया, तानसेन हार गया।’ यह सुन कर तानसेन बैजू बावरा के पाँव में गिर पड़ा और उससे अपने प्राणों की भीख माँगने लगा। बैजू बावरा ने कहा, “मुझे तुम्हारे प्राण लेने की चाह नहीं है। तुम इस निष्ठुर नियम को खत्म करवा दो कि यदि आगरा की सीमा में गाने वाला व्यक्ति तानसेन की जोड़ का न हो, तो उसे मरवा दिया जाए।”

यह सुन कर अकबर ने उसी समय उस नियम को खत्म कर दिया। तानसेन ने बैजू बावरा के चरणों में गिर कर कहा, “मैं यह उपकार जीवन भर नहीं भूलूँगा।’ बैजू बावरा ने उसे याद दिलाया, ‘बारह बरस पहले उसने एक बच्चे की जान बख्शी थी। आज उस बच्चे ने उसकी जान बख्शी है।’

मुहावरे : अर्थ और वाक्य प्रयोग

(1) तूती बोलना।
अर्थ : अधिक प्रभाव होना।
वाक्य : आज उद्योग के क्षेत्र में देश के कुछ घरानों की ही तूती बोलती है।

(2) वाह वाह करना।
अर्थ : प्रशंसा करना।
वाक्य : सितारवादक रविशंकर का सितार वादन सुन कर। श्रोता वाह वाह कर उठते थे।

(3) लहू सूखना।
अर्थ : भयभीत हो जाना।
वाक्य : कोरोना वायरस का नाम सुनते ही लहू सूखने लगता है।

(4) कंठ भर आना।
अर्थ : भावुक हो जाना।
वाक्य : बेटी की बिदाई के समय पिता का कंठ भर आया।

(5) बिलख-बिलख कर रोना।
अर्थ : विलाप करना, जोर-जोर से रोना।
वाक्य : दुर्घटना में घायल पिता की मृत्यु का समाचार सुन कर बेटा बिलख-बिलख कर रोने लगा।

(6) समाँ बँधना।
अर्थ : रंग जमना, वातावरण निर्माण होना।
वाक्य : मदारी ने बंदरों से ऐसा नृत्य करवाया कि समाँ बँध गया।

(7) ब्रह्मानंद में लीन होना।
अर्थ : अलौकिक आनंद का अनुभव करना।
वाक्य : तबलावादक सामताप्रसाद का तबला वादन सुन कर श्रोता ब्रह्मानंद में लीन हो जाते थे।

(8) जान बख्शना।
अर्थ : जीवन दान देना।
वाक्य : डाकुओं ने सेठ की संपत्ति लूट ली, पर उनकी जान बख्श दी।

(9) संसार उजड़ जाना।
अर्थ : सब कुछ व्यर्थ हो जाना।
वाक्य : पति के असामयिक निधन से बेचारी राधा का संसार उजड़ गया।

(10) खरीद लेना।
अर्थ : गुलाम बना लेना।
वाक्य : गाँवों में पहले कुछ लोग मजदूरों को थोड़ा-बहुत कर्ज देकर जैसे उन्हें खरीद ही लेते थे।

(11) रक्त का चूँट पी कर रह जाना।
अर्थ : अपना क्रोध या दुःख प्रकट न होने देना।
वाक्य : मुनीमजी ने बार-बार चपरासी को बुरा-भला कहा, पर वह रक्त का चूंट पी कर रह गया।

(12) पसीना-पसीना होना।
अर्थ : बहुत अधिक परेशान होना।
वाक्य : जंगल से जाते हुए किसान ने हिरन पर झपट्टा मारते हुए चीते को देखा तो वह पसीना-पसीना हो गया।

आदर्श बदला शब्दार्थ

• सुमर = स्मरण करना
• प्रतिकार = बदला, प्रतिशोध
• अवहेलना = अनादर
• चाँदनिया = शामियाना
• नि:शब्द = मौन, चुप
• तासीर = प्रभाव, परिणाम
• खड़ाऊँ = लकड़ी की बनी खूटीदार पादुका
• कुंद = भोथरा, बिना धार का
• कनात = मोटे कपड़े की दीवार या परदा
• उद्विग्नता = घबराहट, आकुलता
• सुधिहीन = बेहोश
• अगाध = अपार, अथाह

आदर्श बदला मुहावरे

• तूती बोलना = अधिक प्रभाव होना
• वाह-वाह करना = प्रशंसा करना
• लहू सूखना = भयभीत हो जाना
• कंठ भर आना = भावुक हो जाना
• बिलख-बिलखकर रोना = विलाप करना/जोर-जोर से रोना
• समाँ बँधना = रंग जमना, वातावरण निर्माण होना
• ब्रह्मानंद में लीन होना = अलौकिक आनंद का अनुभव करना
• जान बख्शना = जीवन दान देना

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Miscellaneous Exercise 3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Miscellaneous Exercise 3

I) Select the correct option from the given alternatives.
Question 1.
The principal of solutions equation sinθ = \(\frac{-1}{2}\) are ________.

Solution:
(b) \(\frac{7 \pi}{6}, \frac{11 \pi}{6}\)

Question 2.
The principal solution of equation cot θ = \(\sqrt {3}\) ___________.

Solution:
(a) \(\frac{\pi}{6}, \frac{7 \pi}{6}\)

Question 3.
The general solution of sec x = \(\sqrt {2}\) is __________.
(a) 2nπ ± \(\frac{\pi}{4}\), n ∈ Z
(b) 2nπ ± \(\frac{\pi}{2}\), n ∈ Z
(c) nπ ± \(\frac{\pi}{2}\), n ∈ Z
(d) 2nπ ± \(\frac{\pi}{3}\), n ∈ Z
Solution:
(a) 2nπ ± \(\frac{\pi}{4}\), n ∈ Z

Question 4.
If cos pθ = cosqθ, p ≠ q rhen ________.
(a) θ = \(\frac{2 n \pi}{p \pm q}\)
(b) θ = 2nπ
(c) θ = 2nπ ± p
(d) nπ ± q
Solution:
(a) θ = \(\frac{2 n \pi}{p \pm q}\)

Question 5.
If polar co-ordinates of a point are \(\left(2, \frac{\pi}{4}\right)\) then its cartesian co-ordinates are ______.
(a) (2, \(\sqrt {2}\) )
(b) (\(\sqrt {2}\), 2)
(c) (2, 2)
(d) (\(\sqrt {2}\) , \(\sqrt {2}\))
Solution:
(d) (\(\sqrt {2}\) , \(\sqrt {2}\))

Question 6.
If \(\sqrt {3}\) cosx – sin x = 1, then general value of x is _________.
(a) 2nπ ± \(\frac{\pi}{3}\)
(b) 2nπ ± \(\frac{\pi}{6}\)
(c) 2nπ ± \(\frac{\pi}{3}-\frac{\pi}{6}\)
(d) nπ + (-1)ⁿ\(\frac{\pi}{3}\)
Solution:
(c) 2nπ ± \(\frac{\pi}{3}-\frac{\pi}{6}\)

Question 7.
In ∆ABC if ∠A = 45°, ∠B = 60° then the ratio of its sides are _________.
(a) 2 : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1
(b) \(\frac{\pi}{2}\) : 2 : \(\frac{\pi}{3}\) + 1
(c) 2 \(\frac{\pi}{2}\) : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\)
(d) 2 : 2 \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1
Solution:
(a) 2 : \(\frac{\pi}{2}\) : \(\frac{\pi}{3}\) + 1

Question 8.
In ∆ABC, if c² + a² – b² = ac, then ∠B = __________.
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{2}\)
(d) \(\frac{\pi}{6}\)
Solution:
(b) \(\frac{\pi}{3}\)

Question 9.
In ABC, ac cos B – bc cos A = ____________.
(a) a² – b²
(b) b² – c²
(c) c² – a²
(d) a² – b² – c²
Solution:
(a) a² – b²

Question 10.
If in a triangle, the are in A.P. and b : c = \(\sqrt {3}\) : \(\sqrt {2}\) then A is equal to __________.
(a) 30°
(b) 60°
(c) 75°
(d) 45°
Solution:
(c) 75°

Question 11.
cos^-1\(\left(\cos \frac{7 \pi}{6}\right)\) = ________.

Question 12.
The value of cot (tan^-1 2x + cot^-1 2x) is __________.
(a) 0
(b) 2x
(c) π + 2x
(d) π – 2x
Solution:
(a) 0

Question 13.
The principal value of sin^-1\(\left(-\frac{\sqrt{3}}{2}\right)\) is ____________.

Solution:
(d) \(-\frac{\pi}{3}\)

Question 14.
If sin^-1\(\frac{4}{5}\) + cos^-1\(\frac{,12}{13}\) = sin^-1 ∝, then ∝ = _____________.
(a) \(\frac{63}{65}\)
(b) \(\frac{62}{65}\)
(c) \(\frac{61}{65}\)
(d) \(\frac{60}{65}\)
Solution:
(a) \(\frac{63}{65}\)

Question 15.
If tan^-1(2x) + tan^-1(3x) = \(\frac{\pi}{4}\), then x = ________.
(a) -1
(b) \(\frac{1}{6}\)
(c) \(\frac{2}{6}\)
(d) \(\frac{3}{2}\)
Solution:
(b) \(\frac{1}{6}\)

Question 16.
2 tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{7}\) = ______.
(a) tan^-1\(\frac{4}{5}\)
(b) \(\frac{\pi}{2}\)
(c) 1
(d) \(\frac{\pi}{4}\)
Solution:
(d) \(\frac{\pi}{4}\)

Question 17.
tan (2 tan^-1\(\left(\frac{1}{5}\right)-\frac{\pi}{4}\)) = ______.
(a) \(\frac{17}{7}\)
(b) \(-\frac{17}{7}\)
(c) \(\frac{7}{17}\)
(d) \(-\frac{7}{17}\)
Solution:
(d) \(-\frac{7}{17}\)

Question 18.
The principal value branch of sec^-1 x is __________.

Solution:
(b) [0, π] – {\(\frac{\pi}{2}\)}

Question 19.
cos[tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{2}\)] = ________.
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{\pi}{4}\)
Solution:
(a) \(\frac{1}{\sqrt{2}}\)

Question 20.
If tan θ + tan 2θ + tan 3θ = tan θ∙tan 2θ∙tan 3θ, then the general value of the θ is _______.
(a) nπ
(b) \(\frac{n \pi}{6}\)
(c) nπ ± \(\frac{n \pi}{4}\)
(d) \(\frac{n \pi}{2}\)
Solution:
(b) \(\frac{n \pi}{6}\)
[Hint: tan(A + B + C) = \(\frac{\tan A+\tan B+\tan C-\tan A \cdot \tan B \cdot \tan C}{1-\tan A \cdot \tan B-\tan B \cdot \tan C-\tan C \cdot \tan A}\)
Since , tan θ + tan 2θ + tan 3θ = tan θ ∙ tan 2θ ∙ tan 3θ,
we get, tan (θ + 2θ + 3θ) = θ
∴ tan6θ = 0
∴ 6θ = nπ, θ = \(\frac{n \pi}{6}\).]

Question 21.
If any ∆ABC, if a cos B = b cos A, then the triangle is ________.
(a) Equilateral triangle
(b) Isosceles triangle
(c) Scalene
(d) Right angled
Solution:
(b) Isosceles triangle

II: Solve the following
Question 1.
Find the principal solutions of the following equations :
(i) sin2θ = \(-\frac{1}{2}\)
Solution:
sin2θ = \(-\frac{1}{2}\)
Since, θ ∈ (0, 2π), 2∈ ∈ (0, 4π)

(ii) tan3θ = -1
Solution:
Since, θ ∈ (0, 2π), 3∈ ∈ (0, 6π)

… [∵ tan(π – θ) = tan(2π – θ) = tan(3π – θ)
= tan (4π – θ) = tan (5π – θ) = tan (6π – θ) = -tan θ]
∴ tan3θ = tan\(\frac{3 \pi}{4}\) = tan\(\frac{7 \pi}{4}\) = tan\(\frac{11 \pi}{4}\) = tan\(\frac{15 \pi}{4}\)

(iii) cotθ = 0
Solution:
cotθ = 0
Since θ ∈ (0, 2π),
cotθ = 0 = cot \(\frac{\pi}{2}\) = cot (π + \(\frac{\pi}{2}\) …[∵ cos(π + θ) = cotθ]
∴ cotθ = cot\(\frac{\pi}{2}\) = cot\(\frac{3 \pi}{2}\)
∴ θ = \(\frac{\pi}{2}\) or θ = \(\frac{3 \pi}{2}\)
Hence, the required principal solutions are \(\left\{\frac{\pi}{2}, \frac{3 \pi}{2}\right\}\)

Question 2.
Find the principal solutions of the following equations :
(i) sin2θ = \(-\frac{1}{\sqrt{2}}\)
Solution:

(ii) tan5θ = -1
Solution:

(iii) cot2θ = 0
Solution:

Question 3.
Which of the following equations have no solutions ?
(i) cos 2θ = \(\frac{1}{3}\)
Solution:
cos 2θ = \(\frac{1}{3}\)
Since \(\frac{1}{3}\) ≤ cosθ ≤ 1 for any θ
cos2θ = \(\frac{1}{3}\) has solution

(ii) cos² θ = -1
Solution:
cos2θ = -1
This is not possible because cos2θ ≥ 0 for any θ.
∴ cos2θ = -1 does not have any solution.

(iii) 2 sinθ = 3
Solution:
2 sin θ = 3 ∴ sin θ = \(\frac{3}{2}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 2 sin θ = 3 does not have any solution.

(iv) 3 sin θ = 5
Solution:
3 sin θ = 5
∴ sin θ = \(\frac{5}{3}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 3 sin θ = 5 does not have any solution.

Question 4.
Find the general solutions of the following equations :
(i) tanθ = \(-\sqrt {x}\)
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z.
Now, tanθ = \(-\sqrt {x}\)
∴ tanθ = tan\(\frac{\pi}{3}\) …[∵ tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ tanθ = tan\(\left(\pi-\frac{\pi}{3}\right)\) …[∵ tan(π – θ) = -tanθ]
∴ tanθ = tan\(\frac{2 \pi}{3}\)
∴ the required general solution is
θ = nπ + \(\frac{2 \pi}{3}\), n ∈ Z.

(ii) tan²θ = 3
Solution:
The general solution of tan²θ = tan²∝ is
θ = nπ ± ∝, n ∈ Z.
Now, tan²θ = 3 = (\(\sqrt {x}\))²
∴ tan²θ = (tan\(\frac{\pi}{3}\))² …[∵ tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ tan²θ = tan²\(\frac{\pi}{3}\)
∴ the required general solution is
θ = nπ ± \(\frac{\pi}{3}\), n ∈ Z.

(iii) sin θ – cosθ = 1
Solution:
∴ cosθ – sin θ = -1

(iv) sin²θ – cos²θ = 1
Solution:
sin²θ – cos²θ = 1
∴ cos²θ – sin²θ = -1
∴ cos2θ = cosπ …(1)
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
∴ the general solution of (1) is given by
2θ = 2nπ ± π, n ∈ Z
∴ θ = nπ ± \(\frac{\pi}{2}\), n ∈ Z

Question 5.
In ∆ABC prove that cos \(\left(\frac{A-B}{2}\right)=\left(\frac{a+b}{c}\right)\) sin \(\frac{C}{2}\)
Solution:
By the sine rule,

Question 6.
With usual notations prove that \(\frac{\sin (A-B)}{\sin (A+B)}=\frac{a^{2}-b^{2}}{c^{2}}\).
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC

Question 7.
In ∆ABC prove that (a – b)² 2cos²\(\frac{\mathrm{C}}{2}\) + (a + b)² sin²\(\frac{\mathrm{C}}{2}\) = c².
Solution:
LHS (a – b)² 2cos²\(\frac{\mathrm{C}}{2}\) + (a + b)² sin²\(\frac{\mathrm{C}}{2}\)
= (a² + b² – 2ab) cos²\(\frac{\mathrm{C}}{2}\) + (a² + b² + 2ab) sin\(\frac{\mathrm{C}}{2}\)²
= (a² + b²) cos²\(\frac{\mathrm{C}}{2}\) – 2ab cos²\(\frac{\mathrm{C}}{2}\) + (a² + b²) sin²\(\frac{\mathrm{C}}{2}\) + 2ab sin²\(\frac{\mathrm{C}}{2}\)
= (a² + b²) (cos²\(\frac{\mathrm{C}}{2}\) + sin²\(\frac{\mathrm{C}}{2}\)) – 2ab(cos²\(\frac{\mathrm{C}}{2}\) – sin²\(\frac{\mathrm{C}}{2}\))
= a² + b² – 2ab cos C
= c² = RHS.

Question 8.
In ∆ABC if cosA = sin B – cos C then show that it is a right angled triangle.
Solution:
cos A= sin B – cos C
∴ cos A + cos C = sin B

∴ A – C = B
∴ A = B + C
∴ A + B + C = 180° gives
A + A = 180°
∴ 2A = 180 ∴ A = 90°
∴ ∆ ABC is a rightangled triangle.

Question 9.
If \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\) then show that a², b², c², are in A.P.
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) = \(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sin B = kb,sin C = kc
Now, \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\)
∴ sinA∙sin(B – C) = sinC∙sin(A -B)
∴ sin [π – (B + C)] ∙ sin (B – C)
= sin [π – (A + B)]∙sin (A – B) … [∵ A + B + C = π]
∴ sin(B + C) ∙ sin(B – C) = sin (A + B) ∙ sin (A – B)
∴ sin²B – sin²C = sin²A – sin²B
∴ 2 sin²B = sin²A + sin²C
∴ 2k²b² = k²a² + k²c²
∴ 2b² = a² + c²
Hence, a², b², c² are in A.P.

Question 10.
Solve the triangle in which a = (\(\sqrt {3}\) + 1), b = (\(\sqrt {3}\) – 1) and ∠C = 60°.
Solution:
Given : a = \(\sqrt {3}\) + 1, b = \(\sqrt {3}\) – 1 and ∠C = 60°.
By cosine rule,
c² = a² + b² – 2ab cos C
= (\(\sqrt {3}\) + 1)² + (\(\sqrt {3}\) – 1)² – 2(\(\sqrt {3}\) + 1)(\(\sqrt {3}\) – 1)cos60°
= 3 + 1 + 2\(\sqrt {3}\) + 3+ 1 – 2\(\sqrt {3}\) – 2(3 – 1)\(\left(\frac{1}{2}\right)\)
= 8 – 2 = 6
∴ c = \(\sqrt {6}\) …[∵ c > 0)
By sine rule,

∴ sin A = sin 60° cos 45° + cos 60° sin 45°
and sin B = sin 60° cos 45° – cos 60° sin 45°
∴ sin A = sin (60° + 45°) – sin 105°
and sin B = sin (60° – 45°) = sin 15°
∴ A = 105° and B = 15°
Hence, A = 105°, B 15° and C = \(\sqrt {6}\) units.

Question 11.
In ∆ABC prove the following :
(i) a sin A – b sin B = c sin (A – B)
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC,
LHS = a sin A – b sinB
= ksinA∙sinA – ksinB∙sinB
= k (sin²A – sin²B)
= k (sin A + sin B)(sin A – sin B)

= k × sin (A + B) × sin (A – B)
= ksin(π – C)∙sin(A – B) … [∵ A + B + C = π]
= k sinC∙sin (A – B)
= c sin (A – B) = RHS.

(ii) \(\frac{c-b \cos A}{b-c \cos A}=\frac{\cos B}{\cos C}\).
Solution:

(iii) a² sin (B – C) = (b² – c²) sinA
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
∴ a = ksinA, b = ksinB, c = ksinC
RHS = (b² – c²) sin A
= (k²sin²B – k²sin²C)sin A
= k²(sin²B – sin²C) sin A
= k²(sin B + sin C)(sin B – sin C) sin A

= k² × sin (B + C) × sin (B – C) × sin A
= k²∙sin(π – A)∙sin(B – C)∙sinA … [∵ A + B + C = π]
= k²sin A∙sin (B – C)∙sin A
= (k sin A)²∙sin (B – C)
= a²sin (B – C) = LHS.

(iv) ac cos B – bc cos A = (a² – b²).
Solution:
LHS = ac cos B – bc cos A
= ac\(\left(\frac{c^{2}+a^{2}-b^{2}}{2 c a}\right)\) – bc\(\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)\)
=\(\frac{1}{2}\)(c² + a² – b²) – \(\frac{1}{2}\)(b² + c² – a²)
= \(\frac{1}{2}\)(c² + a² – b² – b² – c² + a²)
= \(\frac{1}{2}\)(2a² – 2b²) = a² – b2 = RHS.

(v) \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^{2}+b^{2}+c^{2}}{2 a b c}\) .
Solution:

(vi) \(\frac{\cos 2 \mathrm{~A}}{a^{2}}-\frac{\cos 2 \mathrm{~B}}{b^{2}}=\frac{1}{a^{2}}-\frac{1}{b^{2}}\).
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}=\frac{\sin \mathrm{B}}{b}\)

(vii) \(\frac{b-c}{a}=\frac{\tan \frac{B}{2}-\tan \frac{C}{2}}{\tan \frac{B}{2}+\tan \frac{C}{2}}\)
Solution:
By sine rule,

Question 12.
In ∆ABC if a², b², c², are in A.P. then cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are also in A.P.
Question is modified
In ∆ABC if a, b, c, are in A.P. then cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are also in A.P.
Solution:
a, b, c, are in A.P.
∴ 2b = a + c …(1)

Question 13.
In ∆ABC if ∠C = 90º then prove that sin(A – B) = \(\frac{a^{2}-b^{2}}{a^{2}+b^{2}}\)
Solution:
In ∆ABC, if ∠C = 90º
∴ c² = a² + b² …(1)
By sine rule,

Question 14.
In ∆ABC if \(\frac{\cos A}{a}=\frac{\cos B}{b}\), then show that it is an isosceles triangle.
Solution:
Given : \(\frac{\cos A}{a}=\frac{\cos B}{b}\) ….(1)
By sine rule,

∴ sin A cos B = cos A sinB
∴ sinA cosB – cosA sinB = 0
∴ sin (A – B) = 0 = sin0
∴ A – B = 0 ∴ A = B
∴ the triangle is an isosceles triangle.

Question 15.
In ∆ABC if sin²A + sin²B = sin²C then prove that the triangle is a right angled triangle.
Question is modified
In ∆ABC if sin²A + sin²B = sin²C then show that the triangle is a right angled triangle.
Solution:
By sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) = \(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sinB = kb, sin C = kc
∴ sin²A + sin²B = sin²C
∴ k²a² + k²b² = k²c²
∴ a² + b² = c²
∴ ∆ABC is a rightangled triangle, rightangled at C.

Question 16.
In ∆ABC prove that a²(cos²B – cos²C) + b²(cos²C – cos²A) + c²(cos²A – cos²B) = 0.
Solution:
By sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\) = k
LHS = a²(cos²B – cos²C) + b²( cos²C – cos²A) + c²(cos²A – cos²B)
= k²sin²A [(1 – sin²B) – (1 – sin²C)] + k²sin²B [(1 – sin²C) – (1 – sin²A)] + k²sin²C[(1 – sin²A) – (1 – sin²B)]
= k²sin²A (sin²C – sin²B) + k²sin²B(sin²A – sin²C) + k²sin²C (sin²B – sin²A)
= k²(sin²A sin²C – sin²Asin²B + sin²A sin²B – sin²B sin²C + sin²B sin²C – sin²A sin²C)
= k²(0) = 0 = RHS.

Question 17.
With usual notations show that (c² – a² + b²) tan A = (a² – b² + c²) tan B = (b² – c² + a²) tan C.
Solution:
By sine rule,
\(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\) = \(\frac{c}{\sin C}\) = k
∴ a = fksinA, b = ksinB, c = ksinC


From (1), (2) and (3), we get
(c² – a² + b²) tan A = (a² – b² + c²) tan B
= (b² – c² + a²) tan C.

Question 18.
In ∆ABC, if a cos²\(\frac{C}{2}\) + c cos²\(\frac{A}{2}\) = \(\frac{3 b}{2}\), then prove that a , b ,c are in A.P.
Solution:
a cos²\(\frac{C}{2}\) + c cos²\(\frac{A}{2}\) = \(\frac{3 b}{2}\)

∴ a + c + b = 3b …[∵ a cos C + c cos A = b]
∴ a + c = 2b
Hence, a, b, c are in A.P.

Question 19.
Show that 2 sin^-1\(\left(\frac{3}{5}\right)\) = tan^-1\(\left(\frac{24}{7}\right)\).
Solution:
Let sin²\(\left(\frac{3}{5}\right)\) = x.



∴ tan^-1\(\left(\frac{24}{7}\right)\) = RHS

Question 20.
Show that tan^-1\(\left(\frac{1}{5}\right)\) + tan^-1\(\left(\frac{1}{7}\right)\) + tan^-1\(\left(\frac{1}{3}\right)\) + tan^-1\(\left(\frac{1}{8}\right)\) = \(\frac{\pi}{4}\).
Solution:

Question 21.
Prove that tan^-1\(\sqrt {x}\) = \(\frac{1}{2}\) cos^-1\(\left(\frac{1-x}{1+x}\right)\), if x ∈ [0, 1].
Solution:
Let tan^-1\(\sqrt {x}\) = y
∴ tan y = \(\sqrt {x}\) ∴ x = tan²y

Question 22.
Show that \(\frac{9 \pi}{8}-\frac{9}{4}\) sin^-1\(\frac{1}{3}\) = \(\frac{9}{4}\) sin^-1\(\frac{2 \sqrt{2}}{3}\).
Question is modified
Show that \(\frac{9 \pi}{8}-\frac{9}{4}\) sin^-1\(\left(\frac{1}{3}\right)\) = \(\frac{9}{4}\) sin^-1\(\left(\frac{2 \sqrt{2}}{3}\right)\).
Solution:
We have to show that

Question 23.
Show that

Solution:

Question 24.
If sin(sin^-1\(\frac{1}{5}\) + cos^-1x) = 1, then find the value of x.
Solution:
sin(sin^-1\(\frac{1}{5}\) = 1

Question 25.
If tan^-1\(\left(\frac{x-1}{x-2}\right)\) + tan^-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\) then find the value of x.
Solution:
tan^-1\(\left(\frac{x-1}{x-2}\right)\) + tan^-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\)

∴ x = ±\(\frac{1}{\sqrt{2}}\).

Question 26.
If 2 tan^-1(cos x ) = tan^-1(cosec x) then find the value of x.
Solution:
2 tan^-1(cos x ) = tan^-1(cosec x)

Question 27.
Solve: tan^-1\(\left(\frac{1-x}{1+x}\right)\) = \(\frac{1}{2}\)(tan^-1x), for x > 0.
Solution:
tan^-1\(\left(\frac{1-x}{1+x}\right)\) = \(\frac{1}{2}\)(tan^-1x)

Question 28.
If sin^-1(1 – x) – 2sin^-1x = \(\frac{\pi}{2}\), then find the value of x.
Solution:
sin^-1(1 – x) – 2sin^-1x = \(\frac{\pi}{2}\)

Question 29.
If tan^-12x + tan^-13x = \(\frac{\pi}{4}\), then find the value of x.
Question is modified
If tan^-12x + tan^-13x = \(\frac{\pi}{2}\), then find the value of x.
Solution:
tan^-12x + tan^-13x = \(\frac{\pi}{4}\)
∴ tan^-1\(\left(\frac{2 x+3 x}{1-2 x \times 3 x}\right)\) = tan\(\frac{\pi}{4}\), where 2x > 0, 3x > 0
∴ \(\frac{5 x}{1-6 x^{2}}\) = tan\(\frac{\pi}{4}\) = 1
∴ 5x = 1 – 6x²
∴ 6x² + 5x – 1 = 0
∴ 6x² + 6x – x – 1 = 0
∴ 6x(x +1) – 1(x + 1) = 0
∴ (x + 1)(6x – 1) = 0
∴ x = -1 or x = \(\frac{1}{6}\)
But x > 0 ∴ x ≠ -1
Hence, x = \(\frac{1}{6}\)

Question 30.
Show that tan^-1\(\frac{1}{2}\) – tan^-1\(\frac{1}{4}\) = tan^-1\(\frac{2}{9}\).
Solution:
LHS = tan^-1\(\frac{1}{2}\) – tan^-1\(\frac{1}{4}\)

Question 31.
Show that cot^-1\(\frac{1}{3}\) – tan^-1\(\frac{1}{3}\) = cot^-1\(\frac{3}{4}\).
Solution:
LHS = cot^-1\(\frac{1}{3}\) – tan^-1\(\frac{1}{3}\)

Question 32.
Show that tan^-1\(\frac{1}{2}\) = \(\frac{1}{3}\) tan^-1\(\frac{11}{2}\).
Solution:
We have to show that

Question 33.
Show that cos^-1\(\frac{\sqrt{3}}{2}\) + 2sin^-1\(\frac{\sqrt{3}}{2}\) = \(\frac{5 \pi}{6}\)
Solution:

Question 34.
Show that 2cot^-1\(\frac{3}{2}\) + sec^-1\(\frac{13}{12}\) = \(\frac{\pi}{2}\)
Solution:

Question 35.
Prove the following :
(i) cos^-1 x = tan^-1\(\frac{\sqrt{1-x^{2}}}{x}\), if x < 0.
Question is modified
cos^-1 x = tan^-1\(\left(\frac{\sqrt{1-x^{2}}}{x}\right)\), if x > 0.
Solution:

(ii) cos^-1 x = π + tan^-1\(\frac{\sqrt{1-x^{2}}}{x}\), if x < 0.
Solution:

Question 36.
If |x| < 1 , then prove that 2tan^-1 x = tan^-1\(\frac{2 x}{1-x^{2}}\) = sin^-1\(\frac{2 x}{1+x^{2}}\) = cos^-1\(\frac{1-x^{2}}{1+x^{2}}\)
Question is modified
If |x| < 1 , then prove that 2tan^-1 x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\) = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\) = cos^-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
Let tan^-1x = y
Then, x = tany

Question 37.
If x, y, z, are positive then prove that tan^-1\(\frac{x-y}{1+x y}\) + tan^-1\(\frac{y-z}{1+y z}\) + tan^-1\(\frac{z-x}{1+z x}\) = 0
Solution:

Question 38.
If tan^-1 x + tan^-1 y + tan^-1 z = \(\frac{\pi}{2}\) then, show that xy + yz + zx = 1
Solution:
tan^-1 x + tan^-1 y + tan^-1 z = \(\frac{\pi}{2}\)

∴ 1 – xy – yz – zx = 0
∴ xy + yz + zx = 1.

Question 39.
If cos^-1 x + cos^-1 y + cos^-1 z = π then show that x² + y² + z² + 2xyz = 1.
Solution:
0 ≤ cos^-1x ≤ π and
cos^-1x + cos^-1y+ cos^-1z = 3π
∴ cos^-1x = π, cos^-1y = π and cos^-1z = π
∴ x = y = z = cosπ = -1
∴ x² + y² + z² + 2xyz
= (-1)² + (-1)² + (-1)² + 2(-1)(-1)(-1)
= 1 + 1 + 1 – 2
= 3 – 2 = 1.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.1

Question 1.
Find the principal solutions of the following equations :
(i) cos θ= \(\frac{1}{2}\)
Solution:
We know that, cos\(\frac{\pi}{3}\) = \(\frac{1}{2}\) and cos (2π – θ) = cos θ
∴ cos\(\frac{\pi}{3}\) = cos(2π – \(\frac{\pi}{3}\)) = cos\(\frac{5 \pi}{3}\)
∴ cos\(\frac{\pi}{3}\) = cos\(\frac{5 \pi}{3}\) = \(\frac{1}{2}\), where
0 < \(\frac{\pi}{3}\) < 2π and 0 < \(\frac{5 \pi}{3}\) < 2π
∴ cos θ = \(\frac{1}{2}\) gives cos θ = cos\(\frac{\pi}{3}\) = cos\(\frac{5 \pi}{3}\)
∴ θ = \(\frac{\pi}{3}\) and θ = \(\frac{5 \pi}{3}\)
Hence, the required principal solutions are
θ = \(\frac{\pi}{3}\) and θ = \(\frac{5 \pi}{3}\)

(ii) sec θ = \(\frac{2}{\sqrt{3}}\)
Solution:

(iii) cot θ = \(\sqrt {3}\)
Solution:
The given equation is cot θ = \(\sqrt {3}\) which is same as tan θ = \(\frac{1}{\sqrt{3}}\).
We know that,

Hence, the required principal solution are
θ = \(\frac{\pi}{6}\) and θ = \(\frac{7 \pi}{6}\).

(iv) cot θ = 0.
Solution:

Question 2.
Find the principal solutions of the following equations:
(i) sinθ = \(-\frac{1}{2}\)
Solution:
We know that,
sin\(\frac{\pi}{6}\) = \(\frac{1}{2}\) and sin (π + θ) = -sinθ,
sin(2π – θ) = -sinθ

Hence, the required principal solutions are
θ = \(\frac{7\pi}{6}\) and θ = \(\frac{11 \pi}{6}\).

(ii) tanθ = -1
Solution:
We know that,
tan\(\frac{\pi}{4}\) = 1 and tan(π – θ) = -tanθ,
tan(2π – θ) = -tanθ

Hence, the required principal solutions are
θ = \(\frac{3\pi}{4}\) and θ = \(\frac{7 \pi}{4}\).

(iii) \(\sqrt {3}\) cosecθ + 2 = 0.
Solution:

Question 3.
Find the general solutions of the following equations :
(i) sinθ = \(\frac{1}{2}\)
Solution:
(i) The general solution of sin θ = sin ∝ is
θ = nπ + (-1 )ⁿ∝, n ∈ Z
Now, sinθ = \(\frac{1}{2}\) = sin\(\frac{\pi}{6}\) …[∵ sin\(\frac{\pi}{6}\) = \(\frac{1}{2}\)]
∴ the required general solution is
θ = nπ + (-1)ⁿ\(\frac{\pi}{6}\), n ∈ Z.

(ii) cosθ = \(\frac{\sqrt{3}}{2}\)
Solution:
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
Now, cosθ = \(\frac{\sqrt{3}}{2}\) = cos\(\frac{\pi}{6}\) …[∵ cos\(\frac{\pi}{6}\) = \(\frac{\sqrt{3}}{2}\)]
∴ the required general solution is
θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z.

(iii) tanθ = \(\frac{1}{\sqrt{3}}\)
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z
Now, tan θ = \(\frac{1}{\sqrt{3}}\) = tan\(\frac{\pi}{6}\) …[tan\(\frac{\pi}{6}\) = \(\frac{1}{\sqrt{3}}\)]
∴ the required general solution is
θ = nπ + \(\frac{\pi}{6}\) , n ∈ Z.

(iv) cotθ = 0.
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z
Now, cot θ = 0 ∴ tan θ does not exist
∴ tanθ = tan\(\frac{\pi}{2}\) [∵ tan\(\frac{\pi}{2}\) does not exist]
∴ the required general solution is
θ = nπ + \(\frac{\pi}{2}\), n ∈ Z.

Question 4.
Find the general solutions of the following equations:
(i) secθ = \(\sqrt {2}\)
Solution:
The general solution of cos θ = cos ∝ is
θ = nπ ± ∝, n ∈ Z.
Now, secθ = \(\sqrt {2}\) ∴ cosθ = \(\frac{1}{\sqrt{2}}\)
∴ cosθ = cos\(\frac{\pi}{4}\) ….[cos\(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)]
∴ the required general solution is
θ = 2nπ ± \(\frac{\pi}{4}\), n ∈ Z.

(ii) cosecθ = –\(\sqrt {2}\)
Solution:
The general solution of sinθ = sin∝ is

(iii) tanθ = -1
Solution:
The general solution of tanθ = tan∝ is

Question 5.
Find the general solutions of the following equations :
(i) sin 2θ = \(\frac{1}{2}\)
Solution:
The general solution of sin θ = sin ∝ is
θ = nπ + (-1)ⁿ∝, n ∈ Z

(ii) tan \(\frac{2 \theta}{3}\) = \(\sqrt {3}\)
Solution:
The general solution of tan θ = tan ∝ is

(iii) cot 4θ = -1
Solution:
The general solution of tan θ = tan ∝ is

Question 6.
Find the general solutions of the following equations :
(i) 4 cos²θ = 3
Solution:
The general solution of cos²θ = cos² ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 cos²θ = 3

(ii) 4 sin²θ = 1
Solution:
The general solution of sin²θ = sin² ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 sin²θ = 3

(iii) cos 4θ = cos 2θ
Solution:
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
∴ the general solution of cos 4θ = cos 2θ is given by
4θ = 2nπ ± 2θ, n ∈ Z
Taking positive sign, we get
4θ = 2nπ + 2θ, n ∈ Z
∴ 2θ = 2nπ, n ∈ Z
∴ θ = nπ, n ∈ Z
Taking negative sign, we get
4θ = 2nπ – 2θ, n ∈ Z
∴ 6θ = 2nπ, n ∈ Z
∴ θ = \(\frac{n \pi}{3}\), n ∈ Z
Hence, the required general solution is
θ = \(\frac{n \pi}{3}\), n ∈ Z or ∴ θ = nπ, n ∈ Z.
Alternative Method:
cos 4θ = cos 2θ
∴ cos4θ – cos 20 = 0
∴ -2sin\(\left(\frac{4 \theta+2 \theta}{2}\right)\)∙sin\(\left(\frac{4 \theta-2 \theta}{2}\right)\) = 0
∴ sin3θ∙sinθ = 0
∴ either sin3θ = 0 or sin θ = 0
The general solution of sin θ = 0 is
θ = nπ, n ∈ Z.
∴ the required general solution is given by
3θ = nπ, n ∈ Z or θ = nπ, n ∈ Z
i.e. θ = \(\frac{n \pi}{3}\), n ∈ Z or θ = nπ, n ∈ Z.

Question 7.
Find the general solutions of the following equations :
(i) sinθ = tanθ
Solution:
sin θ = tan θ
∴ sin θ = \(\frac{\sin \theta}{\cos \theta}\)
∴ sin θ cos θ = sin θ
∴ sin θ cos θ – sinθ = 0
∴ sin θ (cos θ – 1) = θ
∴ either sinθ = 0 or cosθ – 1 = 0
∴ either sin θ = 0 or cos θ = 1
∴ either sinθ = 0 or cosθ = cosθ …[∵ cos0 = 1]
The general solution of sinθ = 0 is θ = nπ, n ∈ Z and cos θ = cos ∝ is θ = 2nπ ± ∝, where n ∈ Z.
∴ the required general solution is given by
θ = nπ, n ∈ Z or θ = 2nπ ± 0, n ∈ Z
∴ θ = nπ, n ∈ Z or θ = 2nπ, n ∈ Z.

(ii) tan³θ = 3tanθ
Solution:
tan³θ = 3tanθ
∴ tan³θ – 3tanθ = 0
∴ tan θ (tan²θ – 3) = 0
∴ either tan θ = 0 or tan²θ – 3 = 0
∴ either tanθ = 0 or tan²θ = 3
∴ either tan θ = 0 or tan²θ = (\(\sqrt {3}\) )³
∴ either tan θ = 0 or tan²θ = (tan\(\frac{\pi}{3}\))³ …[tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ either tanθ = 0 or tan²θ = tan²\(\frac{\pi}{3}\)
The general solution of
tanθ = 0 is θ = nπ, n ∈ Z and
tan²θ = tan²∝ is θ = nπ ± ∝, n ∈ Z.
∴ the required general solution is given by
θ = nπ, n ∈ Z or θ = nπ ± \(\frac{\pi}{3}\), n ∈ Z.

(iii) cosθ + sinθ = 1.
Solution:
cosθ + sinθ = 1

Question 8.
Which of the following equations have solutions ?
(i) cos 2θ = -1
Solution:
cos 2θ = -1
Since -1 ≤ cos θ ≤ 1 for any θ,
cos 2θ = -1 has solution.

(ii) cos²θ = -1
Solution:
cos²θ = -1
This is not possible because cos²θ ≥ 0 for any θ.
∴ cos²θ = -1 does not have any solution.

(iii) 2 sinθ = 3
Solution:
2 sin θ = 3 ∴ sin θ = \(\frac{3}{2}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 2 sin θ = 3 does not have any solution.

(iv) 3 tanθ = 5
Solution:
3tanθ = 5 ∴ tanθ = \(\frac{5}{3}\)
This is possible because tan θ is any real number.
∴ 3tanθ = 5 has solution.

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 1 नवनिर्माण Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 1 नवनिर्माण

12th Hindi Guide Chapter 1 नवनिर्माण Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

प्रश्न 1.
(अ) कृति पूर्ण कीजिए :

बल इसके लिए होता है ↓
(a) …………………………………….
(b) …………………………………….
उत्तर :
(a)

(b)

(आ) जिसे मंजिल का पता रहता है वह :

(a) …………………………………….
(b) …………………………………….
उत्तर :
(a) सब के बल बनना – सब की मदद करना।
(b) पथ के संकट सहना – मंजिल पर पहुँचने की कोशिश में होने वाला कष्ट सहन करना।

शब्द संपदा

प्रश्न 2.
निम्नलिखित शब्दों से उपसर्गयुक्त शब्द तैयार कर उनका अर्थपूर्ण वाक्य में प्रयोग कीजिए :

(a) नीति – …………………………………….
(b) बल – …………………………………….
उत्तर :
(a) उपसर्गयुक्त शब्द – अनीति।
वाक्य : अनीति के मार्ग पर नहीं चलना चाहिए।

(b) उपसर्गयुक्त शब्द – आजीवन।
वाक्य : कुछ पाठक पुस्तकालयों के आजीवन सदस्य होते हैं।

अभिव्यक्ति

प्रश्न 3.
(अ) ‘धरती से जुड़ा रहकर ही मनुष्य अपने लक्ष्य को प्राप्त कर सकता है’, इस विषय पर अपना मत प्रकट कीजिए।
उत्तर :
लक्ष्य का अर्थ है निर्धारित उद्देश्य, जिसे प्राप्त करने के लिए गंभीरता पूर्वक नजर रखी जाए और उसे अर्जित करने के लिए यथासंभव प्रयास किया जाए। हर व्यक्ति का अपने-अपने है ढंग से लक्ष्य निर्धारण करने और उसे अर्जित करने का अपना तरीका होता है। कोई इसे हल्के-फुल्के ढंग से लेता है और बड़े से बड़ा लक्ष्य निर्धारित कर लेता है। ऐसे लक्ष्य क्षमता की कमी है और अपर्याप्त साधन के अभाव में कभी पूरे नहीं हो पाते। जो व्यक्ति अपनी क्षमता और अपने पास उपलब्ध साधनों के अनुसार लक्ष्य का निर्धारण और उसकी पूर्ति के लिए तन-मन-धन से प्रयास करता है, वह व्यक्ति अपने लक्ष्य को प्राप्त करने में अवश्य सफल होता है। ऐसे दूरदर्शी व्यक्ति जमीन से जुड़े हुए होते हैं और समझ-बूझ कर अपना लक्ष्य निर्धारित करते तथा उसके निरंतर प्रयासरत रहते हैं।

(आ) ‘समाज का नवनिर्माण और विकास नर-नारी के सहयोग से ही संभव है’, इसपर अपने विचार लिखिए।
उत्तर :
हमारा समाज विभिन्न प्रकार की कुरीतियों और समस्याओं से भरा हुआ है। अनेक समाज सुधारकों के कठिन परिश्रम के बावजूद आज भी हमारे समाज में अनेक प्रकार की विषमताएँ व्याप्त हैं। असमानता, जातीयता, सांप्रदायिकता, प्रांतीयता, अस्पृश्यता आदि समस्याओं के कारण समाज के नर-नारी दोनों समान रूप से व्यथित हैं। जब तक हमारे समाज से ये बुराइयाँ दूर नहीं होती, तब तक समाज का नव निर्माण और विकास होना असंभव है। नर-नारी दोनों रथ के दो पहियों के समान हैं। बिना दोनों के सहयोग से आगे बढ़ना मुश्किल है। समाज की अनेक समस्याएँ ऐसी हैं, जिनके बारे में नारी को नर से अधिक जानकारियाँ होती हैं। नर-नारी दोनों कंधे से कंधा मिलाकर समाज उत्थान के कार्य में जुटेंगे, तभी समाज का . नव निर्माण और विकास संभव हो सकता है।

रसास्वादन

प्रश्न 4.
निम्नलिखित मुद्दों के आधार पर चतुष्पादियों का रसास्वादन कीजिए :
(1) रचनाकार का नाम – …………………………………….
(2) पसंद की पंक्तियाँ – …………………………………….
(3) पसंद आने के कारण – …………………………………….
(4) कविता का केंद्रीय भाव – …………………………………….
उत्तर :
(1) रचना का शीर्षक : नव निर्माण।
(2) रचनाकार : त्रिलोचन (मूलनाम – वासुदेव सिंह)
(3) कविता की केंद्रीय कल्पना : प्रस्तुत कविता में संघर्ष करने, अत्याचार, विषमता तथा निर्बलता पर विजय पाने का आवाहन किया गया है तथा समाज में समानता, स्वतंत्रता एवं मानवता की स्थापना की बात कही गई है।
(4) रस-अलंकार :
(5) प्रतीक विधान : कविता में विश्वास और प्रेरणा की मात्रा दर्शाने के लिए ‘आकाश’ तथा नर-नारी द्वारा नए समाज की रचना करने का कठिन कार्य करने के लिए ‘काँटों के ताज’ लेने जैसे प्रतीकों का सुंदर प्रयोग किया गया है।
(6) कल्पना : दबे-कुचले लोगों के प्रति आशावाद एवं उत्थान के स्वर बुलंद करना।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की । पंक्तियाँ इस प्रकार हैं :
जिसको मंजिल का पता रहता है,
पथ के संकट को वही सहता है,
एक दिन सिद्धि के शिखर पर बैठ
अपना इतिहास वही कहता है।

(8) कविता पसंद आने का कारण : प्रस्तुत पंक्तियों में यह बात कही गई है कि एक बार अपने लक्ष्य का निर्धारण कर लेने के बाद मनुष्य को हर समय उसको पूरा करने के काम में जी-जान से लग जाना चाहिए। फिर मार्ग में कितनी भी कठिनाइयाँ क्यों न आएँ, उन्हें सहते हुए निरंतर आगे ही बढ़ते रहना चाहिए। एक दिन ऐसे व्यक्ति को सफलता मिलकर ही रहती है। ऐसे ही व्यक्ति लोगों के आदर्श बन जाते हैं। लोग उनका गुणगान करते है और उनसे प्रेरणा लेते हैं।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) चतुष्पदी के लक्षण लिखिए।
……………………………………………
……………………………………………
उत्तर :
चतुष्पदी चौपाई की भाँति चार चरणों वाला छंद होता है। इसके प्रथम, द्वितीय तथा चतुर्थ चरण में पंक्तियों के तुक मिलते हैं। तीसरे चरण का तुक नहीं मिलता। प्रत्येक चतुष्पदी भाव और विचार की दृष्टि से अपने आप में पूर्ण होती है और कोई चतुष्पदी किसी दूसरी से संबंधित नहीं होती।

(आ) त्रिलोचन जी के दो काव्य संग्रहों के नाम
……………………………………………
उत्तर :
त्रिलोचन जी के कुल पाँच काव्य संग्रह हैं –

• धरती
• दिगंत
• गुलाब और बुलबुल
• उस जनपद का कवि हूँ
• सब का अपना आकाश।

Hindi Yuvakbharati 12th Digest Chapter 1 नवनिर्माण Additional Important Questions and Answers

निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए :

1. अतिथि आए है, घर में सामान नहीं है।
   ……………………………………………
2. परंतु अम्यान भी अपराध है।
   ……………………………………………
3. उसके सत्य का पराजय हो जाता है।
   ……………………………………………
4. प्रेरणा और ताकद बनकर परस्पर विकास मे सहभागी बनें।
   ……………………………………………
5. दिलीप अपने माँ-बाप की इकलौती संतान थी।
   ……………………………………………
6. आप इस शेष लिफाफे को खोलकर पढ़ लीजिए।
   ……………………………………………
7. उसमें फुल बिछा दें।
   ……………………………………………
8. कहाँ खो गई है आप।
   ……………………………………………
9. एक मैं सफल सूत्र संचालक के रूप में प्रसिद्ध हो गया।
   ……………………………………………
10. चलते-चलते हमारे बीच का अंतर कम हो गया था।
    ……………………………………………

उत्तर :

1. अतिथि आए हैं, घर में सामान नहीं है।
2. परंतु अज्ञान भी अपराध है।
3. उसका सत्य पराजित हो जाता है।
4. प्रेरणा और ताकत बनकर परस्पर विकास में सहभागी बनें।
5. दिलीप अपने माता-पिता की इकलौती संतान था।
6. शेष आप इस लिफाफे को खोल कर पढ़ लीजिए।
7. उसमें फूल बिछा दें।
8. कहाँ खो गई हैं आप?
9. मैं एक सफल सूत्र संचालक के रूप में प्रसिद्ध हो गया।
10. हमारे बीच का अंतर चलते-चलते कम हो गया था।

Hindi Yuvakbharati 12th Textbook Solutions Chapter 1 नवनिर्माण Additional Important Questions and Answers

कृति-स्वाध्याय एवं उत्तर
पद्यांश क्र. 1
कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
प्रश्न. निम्नलिखित पद्यांश पढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
ऐसे दो प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द हों :

(a) उत्तर लिखिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द के अर्थ वाले दो शब्द पद्यांश से ढूँढ कर लिखिए :

उत्तर :

प्रश्न 2.
निम्नलिखित शब्दों के शब्द-युग्म बना कर लिखिए :
(1) तोड़ – ……………………………..
(2) काम – ……………………………..
(3) जाना – ……………………………..
(4) आकाश – ……………………………..
उत्तर :
(1) तोड़ – जोड़
(2) काम – काज
(3) जाना – आना
(4) आकाश – पाताल।

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए :
(1) विश्वास x ……………………………..
(2) अँधेरा x ……………………………..
(3) सत्य x ……………………………..
(4) सामने x ……………………………..
उत्तर :
(1) विश्वास – अविश्वास
(2) अँधेरा x उजाला
(3) सत्य x असत्य
(4) सामने x पीछे।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के उपसर्गयुक्त शब्द तैयार कर उनका अर्थपूर्ण वाक्यों में प्रयोग कीजिए :
*(1) बल
(2) न्याय।
उत्तर :
(1) शब्द : निर् + बल = निर्बल।
वाक्य : निर्बल को सताना नहीं चाहिए।

(2)शब्द : अ + न्याय = अन्याय।
वाक्य : किसी व्यक्ति का अपनी बात कहने का अधिकार छीनना उसके साथ अन्याय करना है।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) सिद्धि – …………………….
(2) इतिहास – …………………….
(3) मंजिल – …………………….
(4) पथ – …………………….
उत्तर :
(1) सिद्धि – स्त्रीलिंग।
(2) इतिहास – पुल्लिंग।
(3) मंजिल – स्त्रीलिंग।
(4) पथ – पुल्लिंग।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘मानव सेवा ही सच्ची सेवा है’ इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
सेवा करने का अर्थ है किसी को प्रसन्न करने का प्रयत्न करना। दूसरों का दुख दूर करना सेवा का उद्देश्य है। दीनदुखी हमारे समाज के अंग हैं। अपनी जरूरतों की पूर्ति के लिए वे समाज से ही अपेक्षा रखते हैं। उनकी सेवा-सहायता करना समाज का कर्तव्य है। मानव सेवा विविध रूपों में की जा सकती है। पीड़ित व्यक्ति को बचाया जा सकता है। जिसके साथ अन्याय हो रहा है उसे न्याय दिलाया जा सकता है। निर्धन रोगियों को उनके इलाज का खर्च दिया जा सकता है। गरीब परिवार की कन्याओं के विवाह के लिए आर्थिक मदद की जा सकती है। अनेक संतों और समाज सेवियों ने अपना जीवन ही मानव सेवा को अर्पित कर दिया। दीनदुखियों की सेवा कर हम उनके चेहरों पर खुशी ला सकते हैं। इस तरह मानव सेवा ही सच्ची सेवा है।

पद्यांश क्र. 3
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए :
(1) आज नर-नारी –
(i) इस तरह निकलेंगे – ………………………..
(ii) यह लेंगे – ………………………..
(iii) दोनों की विशेषताएँ – ………………………..
(iv) दोनों रचना करेंगे – ………………………..
उत्तर :
(i) इस तरह निकलेंगे – साथ-साथ।
(ii) यह लेंगे – काँटों का ताज।
(iii) दोनों की विशेषताएँ – संगी हैं, सहचर हैं।
(iv) दोनों रचना करेंगे – समाज की।

प्रश्न 3.
लिखिए –
(i) काँटों का ताज लेंगे, यानी क्या?
(ii) ‘गीत मेरा भविष्य गाएगा’ से कवि का तात्पर्य?
उत्तर :
(i) महत्त्वपूर्ण जिम्मेदारियाँ सँभालेंगे।
(ii) भविष्य में (जब वर्तमान अतीत हो जाएगा तब) लोग वर्तमान की प्रशंसा करेंगे।

प्रश्न 4.
वर्तमान का कथन –
(i) ………………………..
(ii) ………………………..
(iii) ………………………..
(iv) ………………………..
उत्तर :
(i) अतीत अच्छा था।
(ii) प्राण के पथ का गीत अच्छा था।
(iii) मेरा गीत भविष्य गाएगा।
(iv) अतीत का भी गीत अच्छा था।

प्रश्न 5.
दो ऐसे प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द हों :
(1) समाज की
(2) भविष्य।
उत्तर :
(1) नर-नारी किसकी रचना करेंगे?
(2) वर्तमान के गीत कौन गाएगा?

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के युग्म-शब्द बना कर लिखिए :
(1) ……………………………… मीत
(2) साथ – ………………………………
(3) संगी – ………………………………
(4) अच्छा – ………………………………
उत्तर :
(1) हित – मीत
(2) साथ – साथ
(3) संगी – साथी
(4) अच्छा – बुरा।

रसास्वादन मुद्दों के आधार पर

कृतिपत्रिका के प्रश्न 2 (इ) के लिए

निम्नलिखित मुद्दों के आधार पर ‘नव निर्माण’ कविता का रसास्वादन कीजिए।

रसास्वादन अर्थ के आधार पर

प्रश्न 1.
अन्याय, अत्याचार से दीन-दुखियों को मुक्ति दिलाने के लिए उनका बल बन जाना ही बलवान व्यक्तियों के बल का सही उपयोग हैं। इस कथन के आधार पर ‘नव निर्माण’ कविता का रसास्वादन कीजिए।
उत्तर :
कवि त्रिलोचन द्वारा चतुष्पदी छंद में रचित कविता ‘नव निर्माण’ का मूलतत्त्व जीवन में संघर्ष करना बताया गया है। हमारे समाज में व्याप्त अन्याय, अत्याचार, विषमता आदि का बोलबाला है। कवि इन बुराइयों पर काबू पाने के लिए लोगों को बल और साहस एकत्र करने का आवाहन करते हैं। यह सर्व विदित है कि ये सारी बुराइयाँ कुछ लोगों द्वारा अपने शारीरिक एवं आर्थिक बल का दुरुपयोग करने के कारण पनपती हैं। इसलिए इन पर विजय पाने का मार्ग भी बल का प्रयोग ही है। यहाँ बल प्रयोग से कवि का आशय किसी के विरुद्ध बल का अनावश्यक प्रयोग करने से न होकर सताए हुए, दबाए हुए बलहीन लोगों का बल बन कर दिखाने से है। बलहीन निरीह व्यक्तियों पर होने वाला अन्याय और अत्याचार तभी रुक सकता है और तभी उन्हें समाज में समानता का दर्जा मिल सकता है और वे निर्बलता पर विजय प्राप्त कर सकेंगे। इसी बात को कवि अपनी कविता में बिना किसी लाग-लपेट के सीधे-सादे सरल शब्दों में इस प्रकार कहते हैं –

बल नहीं होता सताने के लिए,
वह है पीड़ित को बचाने के लिए।
बल मिला है, तो बल बनो सबके,
उठ पड़ो न्याय दिलाने के लिए।

कवि ने इस कविता में अपनी बात कहने के लिए न कहीं रसअलंकार वाली शृंगारिक भाषा का प्रयोग किया है और न ही उन्हें अपनी बात कहने के लिए दुरुहता के मायाजाल में ही फँसना पड़ा है। कविता के शाब्दिक शरीर के रूप में सरल शब्दों की अमिघा शक्ति तथा कविता का प्रसाद गुण कविता में व्यक्त भावों को सरलतापूर्वक आत्मसात करने में प्रमुख भूमिका निभाते हैं।

व्याकरण

1. अलंकार :

प्रश्न 1.
निम्नलिखित पंक्तियों में उद्धृत अलंकार पहचानकर उसका नाम लिखिए :
(1) हाय फूल-सी कोमल बच्ची। हुई राख की थी ढेरी।
(2) मैया मैं तो चंद्र खिलौना लैहों।
(3) इस काल मारे क्रोध के तनु काँपने उनका लगा। मानो हवा के जोर से सोता हुआ सागर जगा।
उत्तर :
(1) उपमा अलंकार।
(2) रूपक अलंकार।
(3) उत्प्रेक्षा अलंकार।

2. रस :

प्रश्न 1.
निम्नलिखित पंक्तियों में उद्धृत रस पहचानकर उसका नाम लिखिए :
(1) उस काल मारे क्रोध के तन काँपने उनका लगा।
मानो हवा के जोर से सोता हुआ सागर जगा।
उत्तर :
रौद्र रस

प्रश्न 2.
काहु न लखा सो चरित बिसेरवा। सो स्वरूप नृपकन्या देखा। मर्कट बदन भयंकर देही। देखत हृदय क्रोध भा तेही। जेहि दिसि बैठे नारद फूली। सो दिसि तेहिन विलोकी भूली। पुनि पुनि मुनि उकसहिं अकुलाहीं। देखि दशा हर गान मुसुकाहीं।
उत्तर :
हास्य रस।

3. मुहावरे :

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) अपना उल्लू सीधा करना।
अर्थ : अपना स्वार्थ सिद्ध करना।
वाक्य : रमेश से समाज के हित की उम्मीद करना व्यर्थ है, वह हमेशा अपना उल्लू सीधा करने में लगा रहता है।

(2) दिन दूना रात चौगुना बढ़ना।
अर्थ : दिन प्रतिदिन अधिक उन्नति करना।
वाक्य : जब से मुनीम जी की सलाह से सेठ करोड़ीमल ने काम-काज शुरू किया है, तब से उनका धंधा दिन दूना रात चौगुना बढ़ता जा रहा है।

4. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों के साथ दी गई सूचना के अनुसार काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) तुमने मुझे विश्वास दिया है। (अपूर्ण वर्तमानकाल)
(2) राह में अँधेरा है। (सामान्य भविष्यकाल)
(3) नर-नारी साथ निकलेंगे। (पूर्ण भूतकाल)
उत्तर :
(1) तुम मुझे विश्वास दे रहे हो।
(2) राह में अँधेरा होगा।
(3) नर-नारी साथ निकले थे।

नवनिर्माण Summary in Hindi

नवनिर्माण कवि का परिचय

नवनिर्माण कवि का नाम : त्रिलोचन। वास्तविक नाम वासुदेव सिंह। (जन्म 20 अगस्त, 1917; निधन 2007.)

प्रमुख कृतियाँ : धरती, दिगंत, गुलाब और बुलबुल, उस जनपद का कवि हूँ, सब का अपना आकाश (कविता संग्रह); देशकाल (कहानी संग्रह) तथा दैनंदिनी (डायरी) आदि।

विशेषता : काव्यक्षेत्र में प्रयोग धर्मिता के समर्थक। समाज के दबे-कुचले वर्ग को संबोधित करने वाले साहित्य के रचयिता।

विधा : चतुष्पदी। इस विधा में चार चरणों वाला छंद होता है। यह चौपाई की तरह होता है। इसके प्रथम, द्वितीय और चतुर्थ चरण में तुकबंदी होती है। भाव और विचार की दृष्टि से प्रत्येक चतुष्पदी अपने आप में पूर्ण होती है।

विषय प्रवेश : प्रस्तुत पद्य पाठ में कुल आठ चतुष्पदियाँ दी गई हैं। ये सभी चतुष्पदियाँ भाव एवं विचार की दृष्टि से अपने आप में पूर्ण है। इन चतुष्पदियों में आशावादी दृष्टिकोण प्रस्तुत किया गया है। कवि ने इनके माध्यम से संघर्ष करने तथा अन्याय, अत्याचार, विषमता और निर्बलता पर विजय पाने का आवाहन किया है।

नवनिर्माण चतुष्पदियों का सरल अर्थ

(1) तुमने विश्वास ……………………………….. आकाश दिया है मुझको।
मनुष्य के जीवन में किसी का विश्वास प्राप्त करने तथा किसी से प्रोत्साहन पाने का बड़ा महत्त्व होता है। इनके बल पर मनुष्य बड़े-बड़े काम कर डालता है।

कवि कहते हैं कि, तुमने मुझे जो विश्वास और प्रेरणा दी है वह मेरे लिए बहुत ही महत्त्वपूर्ण है। इन्हें देकर तुमने मुझे असीम संसार दे दिया है। पर मैं इन्हें इस तरह सँभाल कर अपने पास रखूगा कि मैं आकाश में न उहूँ और मेरे पाँव हमेशा जमीन पर रहें। अर्थात मुझे अपनी मर्यादा का हमेशा ध्यान रहे।

(2) सूत्र यह तोड़ ……………………………….. छोड़ नहीं सकते।

कवि मनुष्य के बारे में कहते हैं कि वह चाहे कितना ही बड़ा क्यों न हो जाए, आकाश में उड़ानें भरता हो या अन्य कहीं उड़ कर चला जाए, पर अंत में उसे अपनों के बीच यानी धरती पर तो आना ही पड़ता है। कवि कहते हैं कि, यह बात शाश्वत सत्य है। इस सच्चाई को कोई नियम तोड़-मरोड़ कर झूठा साबित नहीं कर सकता। अर्थात मनुष्य कितना भी आडंबर क्यों न कर ले, पर वह अपनी वास्तविकता को छोड़ नहीं सकता।

(3) सत्य है ……………………………….. सामने अँधेरा है।
कवि संघर्ष करने का आवाहन करते हुए कहते हैं कि आपकी राह अँधेरों से भरी हुई है; भले यह बात सच हो या आपकी प्रगति के द्वार को अवरुद्ध करने के लिए तरह-तरह की कठिनाइयाँ रास्ते में आ रही हों, तब भी आपको संघर्ष के मार्ग पर रुकना नहीं है।

अँधेरे में भी आगे ही आगे बढ़ते जाना है, क्योंकि इसके अलावा आपके सामने और कोई चारा भी तो नहीं है। कवि का कहने का तात्पर्य यह है कि संघर्ष करना जारी रखना चाहिए। संघर्ष से ही सफलता का मार्ग प्रशस्त होता है।

(4) बल नहीं होता ……………………………….. “दिलाने के लिए।

कवि कहते हैं कि मनुष्य को निरर्थक कार्यों के लिए अपने बल का प्रयोग नहीं करना चाहिए। उसका प्रयोग सार्थक कार्यों के लिए होना चाहिए। वे कहते हैं कि मनुष्य के पास बल किसी असहाय, पीड़ित व्यक्ति को सताने के लिए नहीं होता। बल्कि वह किसी असहाय या पीड़ित व्यक्ति की रक्षा करने के लिए होता है। कवि बलवान व्यक्तियों को संबोधित करते हुए कहते हैं, यदि ईश्वर ने तुम्हें शक्ति प्रदान की है, तो तुम सभी कमजोर लोगों के बल बन ३ कर उनको न्याय दिलाने के काम में लग जाओ। तभी तुम्हारे बल की सार्थकता है।

(5) जिसको मंजिल ……………………………….. वही कहता है।

कवि कहते हैं कि जिस व्यक्ति को अपनी सफलता की मंजिल की जानकारी हो जाती है, वह व्यक्ति अपने मार्ग में आने वाली परेशानियों से नहीं डरता। वह हँसते-हँसते इन परेशानियों को झेल लेता है। ऐसे व्यक्तियों को ही जीवन में सफलता मिलती है। इस तरह सफलता के शिखर पर पहुँचने वाले व्यक्ति समाज के लिए इतिहास बन जाते हैं और लोग उससे प्रेरणा लेते हैं।

(6) प्रीति की राह ……………………………….. चले आओ।
कवि प्यार-मोहब्बत और अच्छे आचार-व्यवहार को अपनाने की बात करते हुए लोगों का आवाहन करते हैं कि वे सब के साथ प्यार-मोहब्बत से रहें और सब के साथ अच्छा व्यवहार करें। यही सब के लिए अपनाने वाला सही मार्ग है। वे कहते हैं कि सब को हँसते-गाते जीवन जीने का मार्ग अपनाना चाहिए।

(7) साथ निकलेंगे ……………………………….. “समाज नर-नारी।
कवि स्त्री-पुरुष समानता की बात करते हुए कहते हैं कि स्त्री पुरुष दोनों एक साथ मिल कर विकट समस्याओं को सुलझाने का कार्य करेंगे। दोनों इस दिशा में कंधे से कंधा मिलाकर काम करेंगे और नए समाज की रचना करेंगे, जिसमें सब को समानता का अधिकार मिले।

(8) वर्तमान बोला……………………………….. गीत अच्छा था।

कवि वर्तमान और अतीत की बात करते हुए कहते हैं कि वर्तमान के अनुसार बीता हुआ समय अच्छा था। उस समय जीवन पथ में साथ निभाने वाले अच्छे मित्र थे। वर्तमान कहता है कि भविष्य में (जब हम अतीत हो जाएँगे और) लोग हमारा भी गुणगान करेंगे। वैसे अतीत भी गुणगान करने लायक था।

नवनिर्माण शब्दार्थ

• व्योम = आकाश
• सहचर = साथ-साथ चलने वाला, मित्र
• सिद्धि = सफलता
• मीत = मित्र, दोस्त

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2B Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Matrices Miscellaneous Exercise 2B

I) Choose the correct answer from the given alternatives in each of the following questions :
Question 1.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right)\), adj = \(\left(\begin{array}{ll}
4 & a \\
-3 & b
\end{array}\right)\) then the values of a and b are,
(a) a = – 2, b = 1
(b) a = 2, b = 4
(c) a = 2, b = –1
(d) a = 1, b = –2
Solution:
(a) a = – 2, b = 1

Question 2.
The inverse of \(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\) is

Solution:
\(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\)

Question 3.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
2 & 1
\end{array}\right)\) and A(adj A) = k 1, then the value of k is
(a) 1
(b) -1
(c) 0
(d) -3
Solution:
(d) -3 [Hint : A(adj A) = |A| ∙ I]

Question 4.
If A = \(\left(\begin{array}{ll}
2 & -4 \\
3 & 1
\end{array}\right)\), then the adjoint of matrix A is

Solution:\(\left(\begin{array}{ll}
1 & 4 \\
-3 & 2
\end{array}\right)\)

Question 5.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right)\) and A(adj A) = kI, then the value of k is
(a) 2
(b) -2
(c) 10
(d) -10
Solution:
(b) -2

Question 6.
If A = \(\left(\begin{array}{rr}
\lambda & 1 \\
-1 & -\lambda
\end{array}\right)\), then A^-1 does not exist if λ = ………..
(a) 0
(b) ± 1
(c) 2
(d) 3
Solution:
(b) ± 1

Question 7.
If A = \(\left[\begin{array}{ll}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) then A^-1 = ….

Solution:
\(\left[\begin{array}{rr}
\cos \alpha & -\sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)

Question 8.
If F (∝) = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\) where ∝ ∈ R then [F(∝)]^-1 is =
(a) F(-∝)
(b) F(∝^-1)
(c) F(2∝)
(d) None of these
Solution:
(a) F(-∝)

Question 9.
The inverse of A = \(\left[\begin{array}{lll}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\)
(a) I
(b) A
(c) A’
(d) -I
Solution:
(b) A

Question 10.
The inverse of a symmetric matrix is
(a) Symmetric
(b) Non-symmetric
(c) Null matrix
(d) Diagonal matrix
Solution:
(a) Symmetric

Question 11.
For a 2 × 2 matrix A, if A(adjA) = \(\left(\begin{array}{ll}
10 & 0 \\
0 & 10
\end{array}\right)\) then determinant A equals
(a) 20
(b) 10
(c) 30
(d) 40
Solution:
(b) 10

Question 12.
If A² = \(-\frac{1}{2}\left[\begin{array}{cc}
1 & -4 \\
-1 & 2
\end{array}\right]\) then A =

Solution:
\(-\frac{1}{2}\left[\begin{array}{cc}
2 & 4 \\
1 & 1
\end{array}\right]\)

II) Solve the following equations by the methods of inversion.
(i) 2x – y = -2 , 3x + 4y = 5
Solution:
The given equations can be written in the matrix form as :



By equality of matrices,
x = \(-\frac{5}{11}\), y = \(\frac{12}{11}\) is the required solution.

(ii) x + y + z = 1, 2x + 3y + 2z = 2 and ax + ay + 2az = 4, a ≠ 0.
Solution:
The given equations can be written in the matrix form as :

= 1(6a – 2a) – 1(4a – 2a) + 1(2a – 3a)
= 4a – 2a – a = a ≠ 0 ∴ A^-1 exists.
Consider AA^-1 = I

(iii) 5x – y +4z = 5, 2x + 3y + 5z = 2 and 5x – 2y + 6z = -1
Solution:
The given equations can be written in the matrix form as :

= 5(18 + 10) + 1 (12 – 25) + 4( -4 – 15)
= 140 – 13 – 76 = 51 #0
∴ A^-1 exists.
Now, we have to find the cofactor matrix


Now, premultiply AX = B by A^-1, we get,
A^-1(AX) = A^-1B
∴ (A^-1A)X = A^-1B
∴ IX = A^-1B
∴ X = \(\frac{1}{51}\left[\begin{array}{rrr}
28 & -2 & -17 \\
13 & 10 & -17 \\
-19 & 5 & 17
\end{array}\right]\left[\begin{array}{r}
5 \\
2 \\
-1
\end{array}\right]\)

By equality of matrices,
x = 3, y = 2, z = -2 is the required solution.

(iv) 2x + 3y = -5, 3x + y = 3
Solution:

(v) x + y + z = -1, y + z = 2 and x + y – z = 3
Solution:
The given equations can be written in the matrix form as :

= 1(-1 – 1) – 1 (0 – 1) + 1(0 – 1)
= -2 + 1 – 1 = -2 ≠ 0 ∴ A^-1 exists.
Consider AA^-1 = I


Now, premultiply AX = B by A^-1, we get,
A^-1(AX) = A^-1B
∴ (A^-1A)X = A^-1B
∴ IX = A^-1B

∴ by equality of the matrices, x= -3, y = 4, z = -2 is the required solution.

Question 2.
Express the following equation in matrix from and solve them by the method of reduction.
(i) x – y + z = 1, 2x – y = 1, 3x + 3y – 4z = 2
Solution:
The given equations can be written in the matrix form as :


By equality of matrices,
x – y + z = 1 ……(1)
y – 2z = -1 …..(2)
5z = 5 ….(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
y – 2 = -1 ∴ y = 1
Substituting y = 1, z = 1 in (1), we get,
x – 1 + 1 = 1
∴ x = 1
Hence, x = 1, y = 1, z = 1 is the required solution.

(ii) x + y = 1, y + z = \(\frac{5}{3}\), z + x = \(\frac{4}{3}\).
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
x + y = 1 ……(1)
y + z = \(\frac{5}{3}\) …(2)
2z = 2 ……..(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
y + 1 = \(\frac{5}{3}\) ∴ y = \(\frac{2}{3}\)
Substituting y = \(\frac{2}{3}\) in (1), we get,
x + \(\frac{2}{3}\) = 1 ∴ x = \(\frac{1}{3}\)
Hence, x = \(\frac{1}{3}\), y = \(\frac{2}{3}\), z = 1 is the required solution.

(iii) 2x – y + z = 1, x + 2y + 3z = 8 and 3x + y – 4z = 1
Solution:
The given equations can be written in the matrix form as :

∴ \(\left[\begin{array}{r}
x+2 y+3 z \\
0-5 y-5 z \\
0+0-8 z
\end{array}\right]\) = \(\left[\begin{array}{r}
8 \\
-15 \\
-8
\end{array}\right]\)
By equality of matrices,
x + 2y + 3z = 8 …..(1)
-5y – 5z = -15 ….(2)
-8z = -8 …..(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
-5y – 5 = -15
-5y = -10
∴ y = 2
Substituting y = 2, z = 1 in (1), we get,
x + 4 + 3 = 8 ∴ x = 1
Hence, x = 1, y = 2, z = 1 is the required solution.

(iv) x + y + z = 6, 3x – y + 3z =10 and 5x + 5y – 4z = 3.
Solution:

(v) x + 2y + z = 8, 2x + 3y – z =11 and 3x – y – 2z = 5
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
x + 2y + z = 8 … (1)
-y – 3z = -5 … (2)
16z = 16 … (3)
From (3), z = 1
Substituting z = 1 in (2), we get,
-y – 3 = -5, ∴ y = 2
Substituting y = 2, z = 1 in (1), we get,
x + 4 + 1 = 8 ∴ x = 3
Hence, x = 3, y = 2, z = 1 is the required solution.

(vi) x + 3y + 2z = 6, 3x – 2y + 5z =5 and 2x – 3y + 6z = 7.
Solution:
The given equations can be written in the matrix form as :


By equality of matrices,
x + 3y + 2z = 6 …(1)
y + \(\frac{3}{2}\) z = 4 …(2)
\(\frac{31}{2}\)z = 31 …..(3)
From (3), z = 2
Substituting z = 2 in (2), we get,
y + \(\frac{3}{2}\)z = 4
y + \(\frac{3}{2}\)(2) = 4
y + 3 = 4
y = 1
Substituting y = 1, z = 2 in (2), we get,
x + 3y + 2z = 6
x + 3(1) + 2(2) = 6
x + 3 + 4 = 6
x = -1
Hence, x = -1, y = 1, z = 2 is the required solution.

Question 3.
The sum of three numbers is 6. If we multiply third number by 3 and add it to the second number we get 11. By adding first and the third numbers we get a number which is double the second number. Use this information and find a system of linear equations. Find the three numbers using matrices.
Solution:
Let the three numbers be x, y and z. According to the given conditions,
x + y + z = 6.
3z + y = 11, i.e., y + 3z = 11 and x + z = 2y,
i.e., x – 2y + z = 0
Hence, the system of the linear equations is
x + y + z = 6
y + 3z = 11
x – 2y + z = 0
These equations can be written in the matrix form as :

By equality of matrices,
x + y + z = 6 …(1)
y + 3z = 11 …(2)
-3y = -6 …(3)
From (3), y = 2
Substituting y = 2 in (2), we get,
2 + 3z = 11
∴ 3z = 9 ∴ z = 3
Put y = 2, z — 3 in (1), we get,
x + 2 + 3 = 6 ∴ x = 1
∴ x = 1, y = 2, z = 3
Hence, the required numbers are 1, 2 and 3.

Question 4.
The cost of 4 pencils, 3 pens and 2 books is ₹ 150. The cost of 1 pencil, 2 pens and 3 books is ₹ 125. The cos of 6 pencils, 2 pens and 3 books is ₹ 175. Fild the cost of each item by using Matrices.
Solution:
Let the cost of 1 pencil, 1 pen and 1 book be ₹x, ₹ y, ₹ z respectively.
According to the given conditions,
4x + 3y + 2z = 150
x + 2y + 3z = 125
6x + 2y + 3z = 175
The equations can be written in matrix form as :

By equality of matrices,
x + 2y + 3z = 125 …(1)
-5y – 10z = -350 …(2)
5z = 125 …(3)
From (3), z = 25
Substituting z = 25 in (2), we get
-5y – 10(25) = -350
∴ -5y = -350 + 250 = -100
∴ y = 20
Substituting y = 20, z = 25 in (1), we get
x + 2(20) + 3(25) = 125
∴ x = 125 – 40 – 75 = 10
∴ x = 10, y = 20, z = 25
Hence, the cost of 1 pencil is ₹ 10, 1 pen is ₹ 20 and 1 book is ₹ 25.

Question 5.
The sum of three numbers is 6. Thrice the third number when added to the first number, gives 7. On adding three times first number to the sum of second and third number, we get 12. Find the three numbers by using Matrices.
Solution:
Let the numbers be x, y and z.
According to the given conditions,
x + y + z = 6
3z + x = 7, i.e., x + 3z = 7
and 3x + y + z = 12
Hence, the system of linear equations is
x + y + z = 6
x + 3z = 7
3x + y + z = 12
These equations can be written in matrix form as :

By equality of matrices,
x + y + z = 6 …(1)
-y + 2z = 1 …(2)
-3y = -5 …(3)
From (3), y = \(\frac{5}{3}\)
Substituting y = \(\frac{5}{3}\) in (2), we get,
–\(\frac{5}{3}\) + 2z = 1
∴ 2z = 1 + \(\frac{5}{3}\) = \(\frac{8}{3}\)
∴ z = \(\frac{4}{3}\)
Substituting y =\(\frac{5}{3}\), z = \(\frac{5}{3}\) in (1), we get,
x + \(\frac{5}{3}+\frac{4}{3}\) = 6
∴ x = 3
∴ x = 3, y = \(\frac{5}{3}\), z = \(\frac{4}{3}\)
Hence, the required numbers are 3, \(\frac{5}{3}\) and \(\frac{4}{3}\).

Question 6.
The sum of three numbers is 2. If twice the second number is added to the sum of first and third number, we get 1 adding five times the first number to the sum of second and third we get 6. Find the three numbers by using matrices.
Solution:
Let the three numbers be x, y and z.
According to the question,
x + y + 2
x + 2y + z = 1
5x + y + z = 6
The given system of equations can be written in matrix form as follows:

Question 7.
An amount of ₹ 5000 is invested in three types of investments, at interest rates 6%, 7%, 8% per annum respectively. The total annual income from these investimest is ₹ 350. If the total annual income from first two investment is ₹ 70 more than the income from the third, find the amount of each investment using matrix method.
Solution:
Let the amounts in three investments by ₹ x, ₹ y and ₹ z respectively.
Then x + y + z = 5000
Since the rate of interest in these investments are 6%, 7% and 8% respectively, the annual income of the three investments are \(\frac{6 x}{100}\), \(\frac{7 y}{100}\) and \(\frac{8 z}{100}\) respectively.
According to the given conditions,
\(\frac{6 x}{100}+\frac{7 y}{100}+\frac{8 z}{100}\) = 350
i.e. 6x + 7y + 8z = 35000
Also, \(\frac{6 x}{100}+\frac{7 y}{100}\) = \(\frac{8 z}{100}\) + 70
i.e. 6x + 7y – 8z = 7000
Hence, the system of linear equation is
x + y + z = 5000
6x + 7y + 8z = 35000
6x + 7y – 8z = 7000
These equations can be written in matrix form as :


By equality of matrices,
x + y + z = 5000 …(1)
y + 2z = 5000 …(2)
-16z = -28000 ….(3)
From (3), z = 1750
Substituting z = 1750 in (2), we get,
y + 2(1750) = 5000
∴ y = 5000 – 3500 = 1500
Substituting y = 1500, z = 1750 in (1), we get,
x + 1500 + 1750 = 5000
∴ x = 5000 – 3250 = 1750
∴ x = 1750, y = 1500, z = 1750
Hence, the amounts of the three investments are ₹ 1750, ₹ 1500 and ₹ 1750 respectively.

Question 8.
The sum of the costs of one ook each of Mathematics, Physics and Chemistry is ₹ 210. Total cost of a mathematics book, 2 physics books, and a chemistry book is ₹ 240 Also the total cost of a Mathematics book, 3 physics book and chemistry books is Rs. 300/-. Find the cost of each book, using Matrices.
Solution:

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.2

Question 1.
Find the Cartesian co-ordinates of the point whose polar co-ordinates are :
(i) \(\left(\sqrt{2}, \frac{\pi}{4}\right)\)
Solution:
Here, r = \(\sqrt {2}\) and θ = \(\frac{\pi}{4}\)
Let the cartesian coordinates be (x, y)
Then, x = rcosθ = \(\sqrt {2}\)cos\(\frac{\pi}{4}\) = \(\sqrt{2}\left(\frac{1}{\sqrt{2}}\right)\) = 1
y = rsinθ = \(\sqrt {2}\)sin\(\frac{\pi}{4}\) = \(\sqrt{2}\left(\frac{1}{\sqrt{2}}\right)\) = 1
∴ the cartesian coordinates of the given point are (1, 1).

(ii) \(\left(4, \frac{\pi}{2}\right)\)
Solution:

(iii) \(\left(\frac{3}{4}, \frac{3 \pi}{4}\right)\)
Solution:
Here, r = \(\frac{3}{4}\) and θ = \(\frac{3 \pi}{4}\)
Let the cartesian coordinates be (x, y)

(iv) \(\left(\frac{1}{2}, \frac{7 \pi}{3}\right)\)
Solution:
Here, r = \(\frac{1}{2}\) and θ = \(\frac{7 \pi}{4}\)
Let the cartesian coordinates be (x, y)


∴ the cartesian coordinates of the given point are \(\left(\frac{1}{4}, \frac{\sqrt{3}}{4}\right)\)

Question 2.
Find the of the polar co-ordinates point whose Cartesian co-ordinates are.
(i) \((\sqrt{2}, \sqrt{2})\)
Solution:
Here x = \(\sqrt {2}\) and y = \(\sqrt {2}\)
∴ the point lies in the first quadrant.
Let the polar coordinates be (r, θ)
Then, r² = x² + y² = (\(\sqrt {2}\) )² + (\(\sqrt {2}\) )² = 2 + 2 = 4
∴ r = 2 … [∵ r > 0]
cos θ = \(\frac{x}{r}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)
and sin θ = \(\frac{y}{r}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)
∴ tan θ = 1
Since the point lies in the first quadrant and
0 ≤ θ ≤ 2π, tan θ = 1 = tan\(\frac{\pi}{4}\)
∴ θ = \(\frac{\pi}{4}\)
∴ the polar coordinates of the given point are \(\left(2, \frac{\pi}{4}\right)\).

(ii) \(\left(0, \frac{1}{2}\right)\)
Solution:
Here x = 0 and y = \(\frac{1}{2}\)
the point lies on the positive side of Y-axis. Let the polar coordinates be (r, θ)
Then, r² = x² + y² = (0)² + \(\left(\frac{1}{2}\right)^{2}=0+\frac{1}{4}=\frac{1}{4}\)
∴ r = \(\frac{1}{2}\) …[∵ r > 0]
cosθ = \(\frac{x}{r}=\frac{0}{(1 / 2)}\) = 0
and sin θ = \(\frac{y}{r}=\frac{(1 / 2)}{(1 / 2)}\) = 1
Since, the point lies on the positive side of Y-axis and 0 ≤ θ ≤ 2π
cosθ = 0 = cos\(\frac{\pi}{2}\) and sinθ = 1 = sin\(\frac{\pi}{2}\)
∴ θ = \(\frac{\pi}{2}\)
∴ the polar coordinates of the given point are \(\left(\frac{1}{2}, \frac{\pi}{2}\right)\).

(iii) \((1,-\sqrt{3})\)
Solution:
Here x = 1 and y = \(-\sqrt{3}\)
∴ the point lies in the fourth quadrant.
Let the polar coordinates be (r, θ).
Then, r² = x² + y² = (1)² + (\(-\sqrt {3}\) )² = 1 + 3 = 4
∴ r = 2 … [∵ r > 0]

∴ the polar coordinates of the given point are \(\left(2, \frac{5 \pi}{3}\right)\).

(iv) \(\left(\frac{3}{2}, \frac{3 \sqrt{3}}{2}\right)\)
Solution:

Question 3.
In ∆ABC, if ∠A = 45º, ∠B = 60º then find the ratio of its sides.
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\)
∴ \(\frac{a}{b}=\frac{\sin A}{\sin B}\) and \(\frac{b}{c}=\frac{\sin B}{\sin C}\)
∴ a : b : c = sinA : sinB : sinC
Given ∠A = 45° and ∠B = 60°
∵ ∠A + ∠B + ∠C = 180°
∴ 45° + 60° + ∠C = 180°
∴ ∠C = 180° – 105° = 75°

Question 4.
In ∆ABC, prove that sin \(\left(\frac{\mathbf{B}-\mathbf{C}}{2}\right)=\left(\frac{\boldsymbol{b}-\boldsymbol{c}}{a}\right)\) cos \(\frac{A}{2}\).
Solution:
By the sine rule,

Question 5.
With usual notations prove that 2 \(\left\{a \sin ^{2} \frac{C}{2}+c \sin ^{2} \frac{A}{2}\right\}\) = a – b + c.
Solution:

Question 6.
In ∆ABC, prove that a³sin(B – C) + b³sin(C – A) + c³sin(A – B) = 0
Solution:
By the sine rule,
\(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\) = \(\frac{c}{\sin C}\) = k
∴ a = k sin A, b = k sin B, c = k sin C
LHS = a³sin (B – C) + b³sin (C – A) + c³sin (A – B)
= a³(sin B cos C – cos B sin C) + b³(sinCcos A – cos C sin A) + c³(sinAcosB – cos A sin B)

= \(\frac{1}{2 k}\) [a²(a² + b² – c²) – a²(a² + c² – b²) + b²(b² + c² – a²) – b²(a² + b² – c²) + c²(c² + a² – b²) – c²(b² + c² – a²)]
= \(\frac{1}{2 k}\) [a⁴ + a²b² – a²c² – a⁴ – a²c² + a²b² + b⁴ + b²c² – a²b² – a²b² – b⁴ + b²c² + c⁴ + a²c² – b²c² – b²c² – c⁴ + a²c²]
= \(\frac{1}{2 k}\)(0) = 0 = RHS.

Question 7.
In ∆ABC, if cot A, cot B, cot C are in A.P. then show that a², b², c² are also in A.P
Solution:
By the sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) =\(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sin B = kb, sin C = kc …(1)
Now, cot A, cotB, cotC are in A.P.
∴ cotC – cotB = cotB – cot A
∴ cotA + cotC = 2cotB

Question 8.
In ∆ABC, if a cos A = b cos B then prove that the triangle is right angled or an isosceles traingle.
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = k
a = k sin A and b = k sin B
∴ a cos A = b cos B gives
k sin A cos A = k sin B cos B
∴ 2 sin A cos A = 2 sin B cos B
∴ sin 2A = sin 2B ∴ sin 2A – sin 2B = 0
∴ 2 cos (A + B)∙sin (A -B) = 0
∴ 2cos (π – C)∙sin(A – B) = 0 … [∵ A + B + C = π]
∴ -2 cos C∙sin (A – B) = 0
∴ cos C = 0 OR sin(A -B) = 0
∴ C = 90° OR A – B = 0
∴ C = 90° OR A = B
∴ the triangle is either rightangled or an isosceles triangle.

Question 9.
With usual notations prove that 2(bc cos A + ac cos B + ab cos C) = a² + b² + c².
Solution:
LHS = 2 (bc cos A + ac cos B + ab cos C)
= 2bc cos A + 2ac cos B + 2ab cos C
= 2bc \(\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)\) + 2ac\(\left(\frac{c^{2}+a^{2}-b^{2}}{2 c a}\right)\) + 2ab\(\left(\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)\) …(By cosine rule]
= b² + c² – a² + c² + a² – b² + a² + b² – c² = a² + b² + c² = RHS.

Question 10.
In △ABC, if a = 18, b = 24, c = 30 then find the values of
(i) cos A
Solution:
Given : a = 18, b = 24 and c = 30
∴ 2s = a + b + c = 18 + 24 + 30 = 72 ∴ s = 36

(ii) sin\(\frac{A}{2}\)
Solution:

(iii) cos\(\frac{A}{2}\)
Solution:

(iv) tan\(\frac{A}{2}\)
Solution:

(v) A(△ABC)
Solution:

(iv) sin A.
Solution:

Question 11.
In △ABC prove that (b + c – a) tan \(\frac{A}{2}\) = (c + a – b) tan\(\frac{B}{2}\) = (a + b – c) tan\(\frac{C}{2}\).
Solution:
(b + c – a) tan \(\frac{A}{2}\)

Question 12.
In △ABC prove that sin \(\frac{A}{2}\)∙sin \(\frac{A}{2}\)∙sin \(\frac{A}{2}\) = \(\frac{[A(\triangle A B C)]^{2}}{a b c s}\)
Solution:
LHS = sin \(\frac{A}{2}\)∙sin \(\frac{B}{2}\)∙sin \(\frac{C}{2}\)

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2A Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Matrices Miscellaneous Exercise 2A

Question 1.
If A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\) then reduce it to I₃ by using column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right|\)
= 1(1 – 0) – 0 + 0 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By C₁ – 2C₂, we get, A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
-3 & 3 & 1
\end{array}\right]\)
By C₁ + 3C₃ and C₂ – 3C₃, we get,
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I₃.

Question 2.
If A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\), then reduce it to I₃ by using row transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 2 (0 – 1) – 1(1 – 1) + 3 (1 – 0)
= -2 – 0 + 3 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\)
By R₁ – R₂, we get,

By R₁ – R₃ and By R₂ – R₃, we get
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I₃.

Question 3.
Check whether the following matrices are invertible or not:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exists.

(ii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right|\) = 1 – 1 = 0.
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(iii) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right|\) = 3 – 6 = -3 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(iv) \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right|\) = 30 – 30 = 0.
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(v) \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{cc}
\sec \theta & \tan \theta \\
\tan \theta & \sec \theta
\end{array}\right|\)
= sec²θ – tan²θ = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(vii) \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Solution:
let A = \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right|\)
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9 = 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(viii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right|\)
= 1 (-3 -6) – 2 (6 – 3) + 3 (4 + 1)
= -9 – 6 + 15 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(ix) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right|\)
= 1(32 – 30) – 2(24 – 20) + 3(18 – 16)
= 2 – 8 + 6 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

Question 4.
Find AB, if A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
1 & -2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -1 \\
1 & 2 \\
1 & -2
\end{array}\right]\) Examine whether AB has inverse or not.
Solution:

∴ A is a non-singular matrix.
Hence, (AB)^-1 exist.

Question 5.
If A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is a nonsingular matrix then find A^-1 by elementary row transformations.
Hence, find the inverse of \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\)
Solution:
Since A is a non-singular matrix, then find A^-1 by using elementary row transformations.
We write AA^-1 = I

Comparing \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) with \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\),
we get, x = 2, y = 1, z = -1
∴ \(\frac{1}{x}\) = \(\frac{1}{2}\), \(\frac{1}{y}\) = \(\frac{1}{1}\) = 1, \(\frac{1}{z}\) = \(\frac{1}{-1}\) = -1
\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) is \(\left(\begin{array}{rrr}
\frac{1}{2} & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right)\).

Question 6.
if A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) and X is a 2 × 2 matrix such that AX = I , then find X.
Solution:
We will reduce the matrix A to the identity matrix by using row transformations. During this pro¬cess, I will be converted to the matrix X.
We have AX = I.

Question 7.
Find the inverse of each of the following matrices (if they exist).
(i) \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right|\) = 3 + 2 = 5 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(ii) \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right|\) = -2 – 1 = -3 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(iii) \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right|\) = 7 – 6 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(iv) \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right|\) = 14 + 15 = 29 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(v) \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right|\) = 8 – 7 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(vi) \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right|\) = -21 + 20 = -1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(vii) \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right|\)
= 2(4 + 6) +3(4 – 9) + 3(-4 – 6)
= 20 – 15 – 30 = -25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(viii) \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right|\)
= 1(0 + 25) + 3(0 + 10) + 2(-15 – 0)
= 25 + 30 -30
= 25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(ix) \(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A =\(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right|\)
= 2(3 – 0) – 0 – 1(5 – 0)
= 6 – 0 – 5 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I


∴ A^-1 = \(\left[\begin{array}{lll}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\)

(x) \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
∴ A^-1 = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
= 1\(\left|\begin{array}{ll}
-2 & 1 \\
3 & 0
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & 1 \\
-1 & 1
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & -2 \\
-1 & 3
\end{array}\right|\)
|A| = 1(0 – 3) – 2(0 + 1) – 2(0 – 2)
= -3 – 2 + 4
= -1 ≠ 0
∴ A^-1 exists.
We have
AA^-1 = I


∴ A^-1 = \(\left[\begin{array}{lll}
3 & 6 & 2 \\
1 & 2 & 1 \\
2 & 5 & 2
\end{array}\right]\)

Question 8.
Find the inverse of A = \(\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right]\) by
(i) elementary row transformations
Solution:
|A| = \(\left|\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right|\)
= cosθ (cosθ – 0) + sinθ (sinθ – 0) + 0
= cos²θ + sin²θ = 1 ≠ 0
∴ A^-1 exists.
(i) Consider AA^-1 = I

(ii) elementary column transformations
Solution:
Consider A^-1A = I

Question 9.
If A = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\) find AB and (AB)^-1. Verify that (AB)^-1 = B^-1A^-1
Solution:
AB = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\)




From (1) and (2), (AB)^-1 = B^-1 ∙ A^-1.

Question 10.
If A = \(\left[\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right]\), then show that A^-1 = \(\frac{1}{6}\)(A – 5I)
Solution:
|A| = \(\left|\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right|\) = 4 – 10 = -6 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

Question 11.
Find matrix X such that AX = B, where A = \(\left[\begin{array}{ll}
1 & 2 \\
-1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
0 & 1 \\
2 & 4
\end{array}\right]\)
Solution:
AX = B

Question 12.
Find X, if AX = B where A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\).
Solution:
AX = B

Question 13.
If A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
4 & 1 \\
3 & 1
\end{array}\right]\) and C = \(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\) then find matrix X such that AXB = C.
Solution:
AXB = C
∴ \(\left(\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right)(\mathrm{XB})\) =\(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\)
First we perform the row transformations.

Question 14.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by adjoint method.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix
= [A_ij]_3×3 where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = \(\left|\begin{array}{ll}
1 & 5 \\
4 & 7
\end{array}\right|\) = 7 – 20 = -13
A₁₂ = (-1)¹⁺²M₁₂ = \(\left|\begin{array}{ll}
1 & 5 \\
2 & 7
\end{array}\right|\) = -(7 – 10) = 3

Question 15.
Find the inverse of \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by adjoint method.
Solution:
where A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\)
|A| = 1(2 – 6) – 0(0 – 3) + 1(0 – 2)
|A| = -4 – 2
|A| = -6 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix
= [A_ij]3×3, where A_ij = (-1)^i+jM_ij

Question 16.
Find A^-1 by adjoint method and by elementary transformations if A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\)
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right|\)
= 1(4 – 4) – 2(-4 – 2) + 3(-2 – 1)
= 0 + 12 – 9 = 3 ≠ 0
∴ A^-1 exists.
A^-1by adjoint method :
We have to find the cofactor matrix
= [A_ij]_3×3, where A_ij = (-1)^i+j M_ij

Question 17.
Find the inverse of A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by elementary column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right|\)
= 1 (2 – 6) – 0 + 1 (0 – 2)
= -4 – 2= -6 ≠ 0
∴ A^-1 exists.
Consider A^-1A = I
∴ A^-1\(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
By C₃ – C₁, we get,

Question 18.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by elementary row transformations.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

Question 19.
Show with usual notations that for any matrix A = [a_ij]_3×3
(i) a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃ = 0
Solution:
A = [a_ij]_3×3 = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
(i) A₂₁ = (-1)²⁺¹M₂₁ = \(-\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|\)
= -(a₁₂a₃₃ – a₁₃a₃₂)
= -a₁₂a₃₃ + a₁₃a₃₂
A₂₂ = (-1)²⁺²M₂₂ = \(\left|\begin{array}{ll}
a_{11} & a_{13} \\
a_{31} & a_{33}
\end{array}\right|\)
= a₁₁a₃₃ – a₁₃a₃₁
A₂₃ = (-1)²⁺³M₂₃ = \(-\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{31} & a_{32}
\end{array}\right|\)
= -(a₁₁a₃₂ – a₁₂a₃₁)
= -a₁₁a₃₂+ a₁₂a₃₁
∴ a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃
= a₁₁(-a₁₂₃₃ + a₁₃a₃₂) + a₁₂(a₁₁a₃₃ – a₁₃a₃₁) + a₁₃(-a₁₁a₃₂ + a₁₂a₃₁)
= -a₁₁a₁₂a₃₃ + a₁₁a₁₃a₃₂ + a₁₁a₁₂a₃₃ – a₁₂a₁₃a₃₁ – a₁₁a₁₃a₃₂ + a₁₂a₁₃a₃₁
= 0

(ii) a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = |A|
Solution:

Question 20.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\), then find a matrix X such that XA= B.
Solution:
Consider XA = B