Class 12

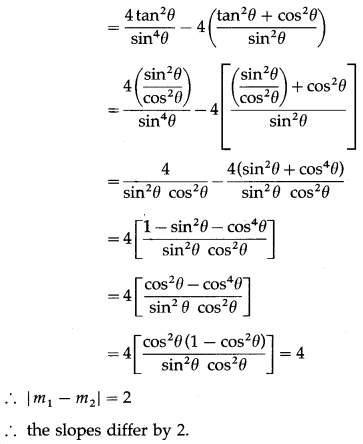
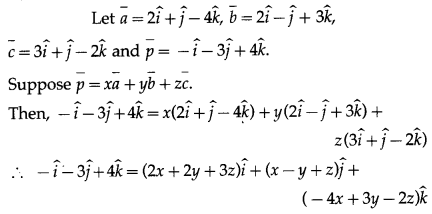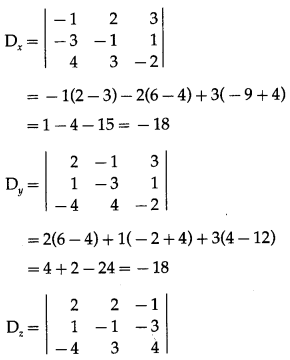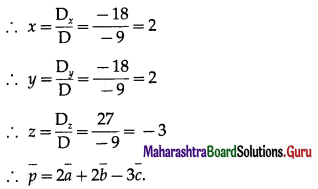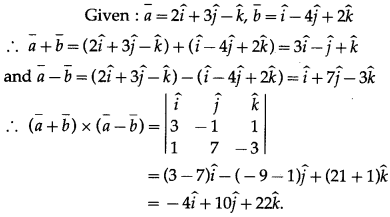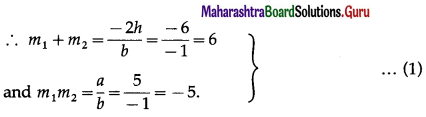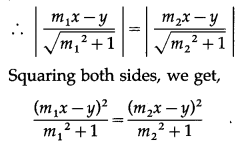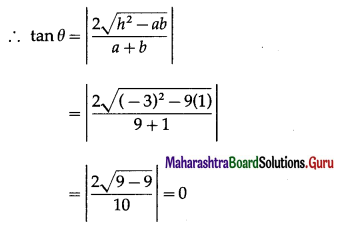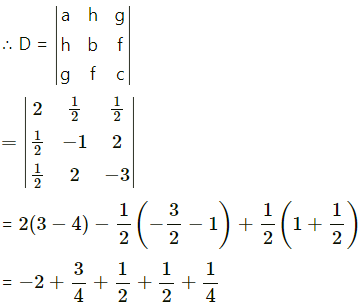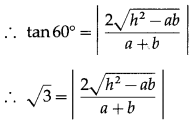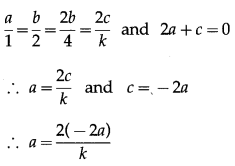Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 10 ओजोन विघटन का संकट Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 10 ओजोन विघटन का संकट

12th Hindi Guide Chapter 10 ओजोन विघटन का संकट Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
लिखिए :
(अ) ओजोन गैस की विशेषताएं :
(a) …………………………………………
(b) …………………………………………
उत्तर :
(a) ओजोन गैस नीले रंग की होती है।
(b) यह प्रकृति में तीक्ष्ण और विषैली होती है और मानव स्वास्थ्य के लिए हानिकारक होती है।

(आ) ओजोन विघटन के दुष्प्रभाव :
(c) …………………………………………
(d) …………………………………………
उत्तर :
(c) ओजोन विघटन के कारण अंतरिक्ष से आने वाली पराबैंगनी किरणों से धरती के तापमान में वृद्धि होगी।
(d) अनेकानेक प्रकार की त्वचा संबंधी व्याधियाँ फैलेंगी। त्वचा के कैंसर के रोगियों की संख्या लाखों में होगी।

शब्द संपदा

प्रश्न 2.
कृदंत बनाइए:

(a) कहना – [ ]
(b) बैठना – [ ]
(c) लगना – [ ]
(d) छीजना – [ ]
उत्तर :
(a) कहना – कथन
(b) बैठना – बैठक
(c) लगना – लगाव
(d) छीजना – छीजन।

अभिव्यक्ति

प्रश्न 3.
(अ) भौतिक विकास के कारण उत्पन्न होने वाली समस्याओं के बारे में अपने विचार व्यक्त कीजिए।
उत्तर :
एक समय था जब धरती का बहुत बड़ा भाग घने जंगलों से ढका हुआ था। परंतु समय के साथ बढ़ती जनसंख्या, शहरीकरण, औद्योगिक विकास के कारण वनों को बहुत तेजी से काटा गया। हजारों-लाखों वर्षों से संचित वन रूपी संपत्ति को हमने समाप्त कर दिया है। आए दिन बढ़ते उद्योग-धंधों के परिणामस्वरूप वायुमंडल में कार्बन-डाइऑक्साइड, सल्फर डाइऑक्साइड, नाइट्रोजन ऑक्साइड जैसी जहरीली गैसें बढ़ती जा रही हैं। ऑक्सीजन की कमी होने लगी है। हवा में अवांछित गैसों की उपस्थिति से मनुष्यों को गंभीर समस्याओं का सामना करना पड़ रहा है। इससे दमा, खाँसी, त्वचा संबंधी रोग उत्पन्न हो रहे हैं। वायु प्रदूषण के कारण जीन अपरिवर्तन, आनुवंशकीय रोग तथा त्वचा के कैंसर के खतरे बढ़ रहे हैं। वायु प्रदूषण से अम्लीय वर्षा के खतरे बढ़े हैं, क्योंकि बारिश के पानी में सल्फर डाइऑक्साइड, नाइट्रोजन ऑक्साइड, जैसी जहरीली गैसों के घुलने की संभावना बढ़ी है।

(आ) ‘पर्यावरण रक्षा में हमारा योगदान’, इस विषय पर लिखिए।
उत्तर :
आज पूरी दुनिया पर्यावरण प्रदूषण से पीड़ित है। पर्यावरण प्रदूषण अर्थात हवा में ऐसी अवांछित गैसों, धूल के कणों आदि की उपस्थिति, जो लोगों तथा प्रकृति दोनों के लिए खतरे का कारण बन जाए। वायु प्रदूषण का एक बड़ा कारण है औद्योगिक इकाइयों से निकलने वाला धुआँ तथा रसायन। पर्यावरण की रक्षा में अपना योगदान देते हुए हमें प्लास्टिक का प्रयोग कम-से-कम करना चाहिए। रिसाइकल किए जा सकने वाली चीजों को फेंक नहीं देना चाहिए। जैसे अखबार, कागज, गत्ते, काँच आदि। पेट्रोल, डीजल आदि के उपयोग में कमी करनी चाहिए। पर्यावरण की रक्षा करना हम सबका कर्तव्य है। पर्यावरण है तो हमारा जीवन है।

पाठ पर आधारित लघूत्तरी प्रश्न

प्रश्न 4.
(अ) ओजोन विघटन संकट से बचने के लिए किए गए अंतर्राष्ट्रीय प्रयासों को संक्षेप में लिखिए।
उत्तर :
ओजोन विघटन संकट पर विचार करने के लिए अनेक देशों की पहली बैठक 1985 में विएना में हुई। बाद में सितंबर 1987 में कनाडा के मांट्रियल शहर में बैठक हुई, जिसमें दुनिया के 48 देशों ने भाग लिया था। इसके तहत यह प्रावधान रखा गया कि 1995 तक सभी देश सी एफ सी की खपत में 50 प्रतिशत की कटौती तथा 1997 तक 85 प्रतिशत की कटौती करेंगे। सन 2010 तक सभी देश सी एफ सी का इस्तेमाल एकदम बंद कर देंगे। इस दौरान विकसित देश नए प्रशीतकों की खोज में विकासशील देशों की आर्थिक मदद करेंगे।

(आ) ‘क्लोरो फ्लोरो कार्बन (सी.एफ.सी.) नामक यौगिक की खोज प्रशीतन के क्षेत्र में क्रांतिकारी उपलब्धि रही स्पष्ट कीजिए।
उत्तर :
सन 1930 से पहले प्रशीतन के लिए अमोनिया और सल्फर डाइऑक्साइड गैसों का इस्तेमाल किया जाता था, जो अत्यंत तीक्ष्ण होने के कारण मानव स्वास्थ्य के लिए हानिकारक थीं। तीस के दशक में क्लोरो फ्लोरो कार्बन (सी. एफ. सी.) नामक यौगिक की खोज प्रशीतन के क्षेत्र में क्रांतिकारी उपलब्धि रही। ये रसायन रंगहीन, गंधहीन, अक्रियाशील होने के साथ ही अज्वलनशील होने के कारण आदर्श प्रशीतक माने गए। परिणामस्वरूप बड़े पैमाने पर सी एफ सी यौगिकों का उत्पादन होने लगा और घरेलू कीटनाशक, प्रसाधन सामग्री, दवाएँ, रंग-रोगन, यहाँ तक कि रेफ्रिजिरेटर और एयरकंडिशनर में इनका खूब इस्तेमाल होने लगा।

अलंकार
अतिशयोक्ति : जहाँ पर लोक सीमा अथवा लोकमान्यता का अतिक्रमण करके किसी विषय का वर्णन किया जाता है, वहाँ पर अतिशयोक्ति अलंकार माना जाता है। अतिशयोक्ति शब्द दो शब्दों से मिलकर बना है। अतिशय+उक्ति अर्थात् अत्यंत बढ़ा-चढ़ाकर कही गई बात।

उदा. –
(१) पत्रा ही तिथि पाइयों, वाँ घर के चहुँ पास
नितप्रति पून्यो रहयो, आनन-ओप उजास

(२) हनुमंत की पूँछ में लग न पाई आग।
लंका सगरी जल गई, गए निशाचर भाग।।

(३) पड़ी अचानक नदी अपार।
घोड़ा उतरे कैसे पार।।
राणा ने सोचा इस पार।
तब तक चेतक था उस पार।।

दृष्टांत : दृष्टांत का अर्थ है उदाहरण। किसी बात की सत्यता प्रमाणित करने के लिए उसी ढंग की कोई दूसरी बात कही जाती है जिससे पूर्व कथन की प्रामाणिकता सिद्ध हो जाए; वहाँ दृष्टांत अलंकार होता है।
उदा. –
(१) करत-करत अभ्यास के, जड़मति होत सुजान।
रसरी आवत जात है, सिल पर पड़त निसान।।

(२) सबै सहायक सबल कै, कोउ न निबल सहाय।
पवन जगावत आग ही, दीपहिं देत बुझाय।।

(३) एक म्यान में दो तलवारें, कभी नहीं रह सकती हैं
किसी और पर प्रेम पति का, नारियाँ नहीं सह सकती हैं।

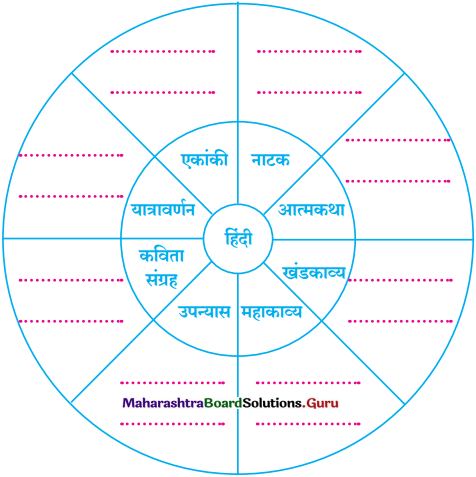
हिंदी की साहित्यिक विधाओं के अनुसार रचनाओं के नाम लिखिए। (अतिरिक्त अध्ययन हेतु)

Hindi Yuvakbharati 12th Digest Chapter 10 ओजोन विघटन का संकट Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए
गद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

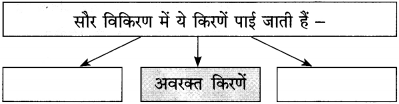
उत्तर :

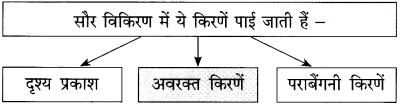
प्रश्न 2.
निम्नलिखित शब्दों के लिए परिच्छेद में प्रयुक्त शब्द ढूँढ़कर लिखिए :
(1) भयानक = ………………………………………..
(2) महत्त्वपूर्ण = ………………………………………..
(3) अप्रभावित = ………………………………………..
(4) संपूर्ण = ………………………………………..
उत्तर :
(1) भयानक = भयावह
(2) महत्त्वपूर्ण = अहम
(3) अप्रभावित = अछूती
(4) संपूर्ण = समूची।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द परिच्छेद में से ढूँढ़कर लिखिए :
(1) अनिल = ………………………………………..
(2) नीर = ………………………………………..
(3) जगत = ………………………………………..
(4) निर्मल = ………………………………………..
उत्तर :
(1) अनिल = हवा
(3) जगत = दुनिया
(2) नीर = पानी
(4) निर्मल = स्वच्छ।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘बढ़ते हुए प्रदूषण को रोकने के उपाय’ विषय पर अपने विचार 40 से 50 शब्दों में लिखिए।
उत्तर :
प्रदूषण एक प्रकार का धीमा जहर है, जो हवा, पानी, धूल आदि के माध्यम से न केवल मनुष्य, बल्कि पेड़-पौधों, पशुपक्षियों, वनस्पतियों को भी नष्ट कर देता है। इसे रोकने के लिए कारखानों की स्थापना शहरी क्षेत्र से दूर, चिमनियों की ऊँचाई अधिक और उनमें फिल्टर का प्रयोग करना चाहिए, जिससे अवशिष्ट पदार्थ और गैसें अधिक मात्रा में वायु में न मिल पाएँ। शहरों, औद्योगिक इकाइयों एवं सड़कों के किनारे अधिक से अधिक वृक्ष लगाने चाहिए।

ये पौधे प्रदूषण नियंत्रक का काम करते हैं। कारखानों से निकले अवशिष्ट पदार्थों को नदी, तालाब व झीलों में न डाला जाए। जिन तालाबों का जल पीने के काम में लाया जाता है, उसमें कपड़े, जानवर आदि नहीं धोने चाहिए। वनों की अनियंत्रित कटाई पर रोक लगाई जानी चाहिए। कृषि के लिए जैविक खाद, प्लास्टिक के स्थान पर कागज व कपड़े के थैलों का प्रयोग करें। पुन:पयोग, रिचार्ज और रिसायकल जैसी आदतों को अपनाना चाहिए। घर में टीवी, संगीत साधनों की हल्की आवाज, कार के हॉर्न, शादी-विवाह में बैंड-बाजा, पटाखे, लाउडस्पीकर के प्रयोग पर रोक लगाई जाए।

प्रदूषण संबंधी सभी कानूनों का कड़ाई से पालन करें।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढकर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
नाम लिखिए :
(1) सी एफ सी नामक यौगिक का आविष्कारक
(2) 1930 से पहले प्रशीतन के लिए इस्तेमाल की जाने वाली गैसें –
उत्तर :
(1) सी एफ सी नामक यौगिक का आविष्कारक — थॉमस भिडले
(2) 1930 से पहले प्रशीतन के लिए इस्तेमाल की जाने वाली गैसें – अमोनिया और सल्फर डाइऑक्साइड

प्रश्न 2.
परिणाम लिखिए : पराबैंगनी किरणें धरती की सतह पर आएँ तो –
उत्तर :
पराबैंगनी किरणें धरती की सतह पर आएँ तो इन्सान के साथ ही जीवमंडल के तमाम दूसरे जीव-जंतुओं को भारी नुकसान हो सकता है। मनुष्यों में अनेक रोग हो सकते हैं।

प्रश्न 3.
घटना के अनुसार वाक्यों का उचित क्रम लगाकर लिखिए :
(1) हमारे कारनामों से प्राकृतिक संतुलन चरमरा गया है।
(2) इससे प्रशीतन प्रौद्योगिकी में एक क्रांति-सी आ गई।
(3) वायुमंडल में स्थित ओजोन की परत हमें घातक किरणों से बचाती है।
(4) विकास की अंधी दौड़ में हमने संसाधनों का अंधाधुंध इस्तेमाल किया है।
उत्तर :
(1) वायुमंडल में स्थित ओजोन की परत हमें घातक किरणों से बचाती है।
(2) विकास की अंधी दौड़ में हमने संसाधनों का अंधाधुंध इस्तेमाल किया है।
(3) हमारे कारनामों से प्राकृतिक संतुलन चरमरा गया है।
(4) इससे प्रशीतन प्रौद्योगिकी में एक क्रांति-सी आ गई। ..

कृति 2 : (शब्द संपदा)

प्रश्न 1.
परिच्छेद में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए :
(1) ……………………………….
(2) ……………………………….
(3) ……………………………….
(4) ……………………………….
उत्तर :
(1) रंग-रोगन
(2) जीव-जंतु
(3) पेड़-पौधे
(4) फलती-फूलती।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘विकास की अंधी दौड़ में आज का मनुष्य संतुष्ट होना भूल गया है’, इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
संतोष और असंतोष का भाव मानव जीवन में बहुत महत्त्व रखता है। ईश्वर ने मनुष्य के साथ-साथ संसार की समस्त वस्तुओं को भी बनाया है। प्रकृति का प्रत्येक जीव इन वस्तुओं का उपयोग करता है और संतुष्ट रहता है। केवल मनुष्य ही है, जो कभी संतुष्ट नहीं होता। इसका कारण एक ही है कि पशु-पक्षी कल की ? चिंता न करके केवल वर्तमान में जीते हैं।

भविष्य के लिए संग्रह है तथा अधिक-से-अधिक सुविधाओं को प्राप्त करने का भाव ही दुख का कारण है। वही दुख मन में असंतोष पैदा करता है। मनुष्य को जो भी प्राप्त हो जाता है, उससे अधिक पाने के लिए वह और व्यग्र है हो जाता है। यह चक्र अनवरत रूप से चलता रहता है। ऐसे व्यक्ति बिरले ही होते हैं, जो अपनी उपलब्धियों से संतुष्ट होना सीख लेते हैं। यही दुनिया के सबसे सुखी लोग हैं।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

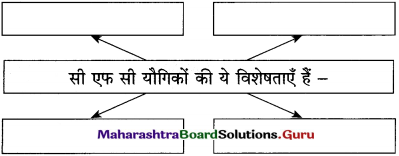
उत्तर :

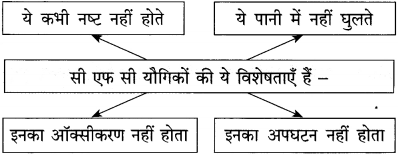
प्रश्न 2.
वाक्य सही करके लिखिए :
(1) सबसे पहले एक अमेरिकी वैज्ञानिक थॉमस मिडले ने बताया कि सी एफ सी यौगिक धरती की ओजोन परत को नष्ट कर चुके हैं।
(2) अमोनिया और सल्फर डाइऑक्साइड यौगिक इस्तेमाल में आने के बाद वायुमंडल में पराबैंगनी किरणों के संपर्क में आते हैं।
उत्तर :
(1) सबसे पहले एक अमेरिकी वैज्ञानिक एफ एस रोलैंड ने बताया कि सी एफ सी यौगिक धरती की ओजोन परत को नष्ट कर चुके हैं।
(2) सी एफ सी यौगिक इस्तेमाल में आने के बाद वायुमंडल में पराबैंगनी किरणों के संपर्क में आते हैं।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द परिच्छेद में से ढूँढ़कर लिखिए :
(1) अवगुण x ………………………….
(2) अंधकार x ………………………….
(3) नीचे x ………………………….
(4) भारी x ………………………….
उत्तर :
(1) अवगुण x गुण
(2) अंधकार – प्रकाश
(3) नीचे x ऊपर
(4) भारी x हल्के।

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर :

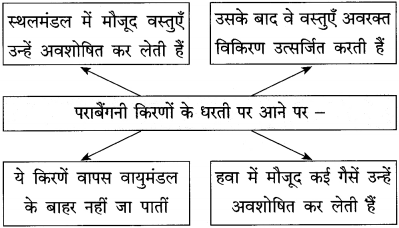
प्रश्न 2.
सहसंबंध जोड़कर अर्थपूर्ण वाक्य बनाइए :
(1) तापवृद्धि से जलवायु में – भूमंडल में काफी परिवर्तन आया है।
(2) ग्रीनहाउस के प्रभाव के कारण – के चलते इन्सानी सभ्यता संकटापन्न है।
(3) विगत एक सदी के दौरान – जबर्दस्त बदलाव आ सकता है।
(4) ओजोन विघटन के व्यापक दुष्प्रभावों – आज धरती का तापमान निरंतर बढ़ रहा है।
उत्तर :
(1) तापवृद्धि से जलवायु में जबर्दस्त बदलाव आ सकता है।
(2) ग्रीनहाउस के प्रभाव के कारण आज धरती का तापमान निरंतर बढ़ रहा है।
(3) विगत एक सदी के दौरान भूमंडल में काफी परिवर्तन आया है।
(4) ओजोन विघटन के व्यापक दुष्प्रभावों के चलते इन्सानी सभ्यता संकटापन्न है।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्दों से मूल शब्द और प्रत्यय अलग कीजिए।
(1) ……………………………..
(2) ……………………………..
(3) ……………………………..
(4) ……………………………..
उत्तर :
(1) विकसित – विकास + इत।
(2) हिस्सेदारी – हिस्से + दारी।
(3) अंतिम – अंत + इम।
(4) विकासशील – विकास + शील।

साहित्य संबंधी सामान्य ज्ञान
कृतिपत्रिका के प्रश्न 1 (ई) के लिए

प्रश्न 1.
हिंदी की साहित्यिक विधाओं के अनुसार रचनाओं के नाम लिखिए :
उत्तर :
(1) एकांकी :
(अ) रीढ़ की हड्डी
(ब) महाभारत की साँझ

(2) नाटक :
(अ) ध्रुवस्वामिनी
(ब) अंधेर नगरी

(3) आत्मकथा :
(अ) सत्य के प्रयोग
(ब) तरुण के स्वप्न

(4) खंडकाव्य :
(अ) उर्वशी
(ब) राम की शक्तिपूजा

(5) महाकाव्य :
(अ) रामचरित मानस
(ब) कामायनी

(6) उपन्यास :
(अ) गोदान
(ब) सुनीता

(7) कविता संग्रह :
(अ) यामा
(ब) कितनी नावों में कितनी बार

(8) यात्रा वर्णन :
(अ) मेरी तिब्बत यात्रा
(ब) पैरों में पंख बाँधकर

मुहावरे

निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) रोटियाँ तोड़ना
अर्थ : मुफ्त में खाना।
वाक्य : कमलेश छह महीने से तो अपने ससुर की रोटियाँ तोड़ रहा है।

(2) वीरगति को प्राप्त होना
अर्थ : युद्ध में वीरतापूर्वक मृत्यु पाना।
वाक्य : राजपूत राजा युद्ध क्षेत्र में पीठ दिखाने के बजाय वीरगति को प्राप्त होना श्रेयस्कर मानते थे।

(3) स्वाँग भरना
अर्थ : किसी की नकल उतारना।
वाक्य : वह बहुरूपिया विश्व के बड़े-बड़े राजनेताओं का स्वाँग भरता हैं।

(4) हवा लगना
अर्थ : असर होना।
वाक्य : उसे गाँव से शहर आए हुए केवल चार महीने हुए हैं, पर अब उसे शहर की हवा लग गई है।

(5) हवाई किले बनाना
अर्थ : बहुत अधिक कल्पना करना।
वाक्य : भोलाराम की तो आदत ही है, हवाई किले बनाने की।

(6) दाई से पेट छिपाना
अर्थ : भेद जानने वाले से सच्ची बात छिपाना।
वाक्य : अरे यजमान! मैंने ही तुम्हारी जन्म-कुंडली बनाई थी। मुझसे अपनी उम्र कम बताकर दाई से पेट छिपाना चाहते हो।

काल परिवर्तन

प्रश्न 1.
निम्नलिखित वाक्यों का कोष्ठक में सूचित काल में परिवर्तन कीजिए :
(1) वृद्धाश्रम के प्रबंधक का फोन सुनकर मैं हैरान रह गया। (पूर्ण भूतकाल)
(2) मौसी को ऐसी हालत में देखकर मैं रोने लगा था। (सामान्य भविष्यकाल)
(3) मैं किसी वृद्धाश्रम में जाना चाहती हूँ। (अपूर्ण वर्तमानकाल)
(5) साधुओं की एक मंडली शहर के अंदर दाखिल हुई। (सामान्य वर्तमानकाल)
उत्तर :
(1) वृद्धाश्रम के प्रबंधक का फोन सुनकर मैं हैरान रह गया था।
(2) मौसी को ऐसी हालत में देखकर मैं रो रहा था।
(3) मैं किसी वृद्धाश्रम में जाना चाहूँगी।
(4) समूची परिस्थिति का तंत्र चरमरा रहा है।
(5) साधुओं की एक मंडली शहर के अंदर दाखिल होती है।

वाक्य शुद्धिकरण

प्रश्न 2.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) त्वचा के कैंसर के रोगी की मात्रा लाखों में होगी।
(2) वतर्मान युग विग्यान का युग है।
(3) बहूत देर तक दोनों रोते रही।
(4) तुमहारा पत्र पाकर खुसी हुई।
(5) मिट्ठी भी आज प्रदूशण से अछूती नहीं रही।
उत्तर :
(1) त्वचा के कैंसर के रोगियों की संख्या लाखों में होगी।
(2) वर्तमान युग विज्ञान का युग है।
(3) बहुत देर तक दोनों रोते रहे।
(4) तुम्हारा पत्र पाकर खुशी हुई।
(5) मिट्टी भी आज प्रदूषण से अछूती नहीं रही।

ओजोन विघटन का संकट Summary in Hindi

ओजोन विघटन का संकट लेखक का परिचय

ओजोन विघटन का संकट  लेखक का नाम : डॉ कृष्ण कुमार मिश्र। (जन्म 15 मार्च, 1966.)

ओजोन विघटन का संकट  प्रमुख कृतियाँ : लोक विज्ञान, समकालीन रचनाएँ, विज्ञान-मानव की यशोगाथा, जल-जीवन का आधार आदि।

ओजोन विघटन का संकट  विशेषता : हिंदी साहित्य में विज्ञान संबंधी लेखन कार्य में विशेष पहचान। आपने विज्ञान को लोकप्रिय बनाने और जनमानस तक पहुँचाने का उल्लेखनीय कार्य किया है। लोक विज्ञान के अनेक विषयों पर हिंदी में व्यापक लेखन किया है। विज्ञान से संबंधित आपकी अनेक मौलिक एवं अनूदित पुस्तकें प्रकाशित हुई हैं। डॉ कृष्ण कुमार मिश्र विज्ञान लेखन की समकालीन पीढ़ी के सशक्त लेखक हैं।

ओजोन विघटन का संकट  विधा : विज्ञान संबंधी लेख।

ओजोन विघटन का संकट  विषय प्रवेश : प्रस्तुत निबंध में लेखक बता रहे हैं कि मनुष्य अपनी सुविधाओं के लिए, जीवन को आरामदायक बनाने के लिए दिन-रात नए-नए आविष्कार करता रहता है। इन नवीन खोजों के कारण पर्यावरण दिन-ब-दिन प्रदूषित होता जा रहा है। हमारी स्वार्थी प्रवृत्ति के चलते सूर्य से आने वाली हानिकारक पराबैंगनी किरणों को रोकने के लिए पर्यावरण में विद्यमान ओजोन परत को क्षति पहुँच रही है। आज हालात की यह माँग है कि ओजोन को होने वाली क्षति को हम रोकें ताकि इस सृष्टि को विनाश से बचाया जा सके।

ओजोन विघटन का संकट  पाठ का सार

आज का युग विज्ञान और प्रौद्योगिकी का युग है। पूरी दुनिया में भौतिक विकास की होड़ लगी हुई है। विकास की इस दौड़ ने जिन समस्याओं को जन्म दिया है, इनमें प्रदूषण की समस्या चिंतनीय है। हवा, पानी, मिट्टी सभी प्रदूषण की गिरफ्त में आ चुके हैं। इनमें भी पर्यावरणीय प्रदूषण बहुत बड़े संकट का रूप ले चुका है।

पर्यावरण में विद्यमान अनेक गैसों में एक गैस है ओजोन। यह गैस मानव स्वास्थ्य के लिए तो हानिकारक है, परंतु वायुमंडल में मौजूद यही गैस हमारी रक्षा भी करती है। यह गैस धरती के वायुमंडल में 15 से 20 किलोमीटर की ऊँचाई तक पाई जाती है।

यह ओजोन गैस बाह्य अंतरिक्ष से आने वाली पराबैंगनी किरणों को अवशोषित करके उन्हें धरती पर आने से रोकती है। यदि ये किरणें धरती की सतह तक चली आएँ तो एक ओर तो धरती के तापमान में वृद्धि होगी, दूसरी ओर त्वचा संबंधी अनेकानेक व्याधियाँ फैलेंगी। वायुमंडल में स्थित ओजोन की परत हमें इन घातक किरणों से बचाती है।

विकास की दौड़ का हिस्सा बनकर हमने सभी संसाधनों का अंधाधुंध इस्तेमाल किया है। जिसके कारण प्राकृतिक संतुलन चरमरा गया है। दैनिक जीवन में कीटनाशक, प्रसाधन सामग्री, दवाएँ, रंग-रोगन, फ्रिज तथा एयरकंडिशनिंग में प्रशीतन का अहम स्थान है। सन 1930 से पहले प्रशीतन के लिए अमोनिया और सल्फर डाइऑक्साइड गैसों का इस्तेमाल किया जाता था, जो अत्यंत तीक्ष्ण होने के कारण मानव स्वास्थ्य के लिए हानिकारक थीं।

तीस के दशक में क्लोरो फ्लोरो कार्बन (सी एफ सी) नामक यौगिक की खोज हुई। रंगहीन, गंधहीन, अक्रियाशील और अज्वलनशील होने के कारण बड़े पैमाने पर सी एफ सी यौगिकों का उत्पादन होने लगा और घरेलू कीटनाशक, प्रसाधन सामग्री, दवाएँ, रंग-रोगन, यहाँ तक कि रेफ्रिजिरेटर और एयरकंडिशनर में इनका खूब इस्तेमाल होने लगा। 1974 में एक अमेरिकी वैज्ञानिक एफ एस रोलैंड ने बताया कि सी एफ सी यौगिक धरती की ओजोन परत को नष्ट कर चुके हैं। क्योंकि सी एफ सी यौगिक इस्तेमाल में आने के बाद वायुमंडल में पराबैंगनी किरणों के संपर्क में आते हैं।

ओजोन विघटन संकट पर विचार करने के लिए अनेक देशों की पहली बैठक 1985 में विएना में हुई। बाद में सितंबर 1987 में कनाडा के मांट्रियल शहर में बैठक हुई, जिसमें दुनिया के 48 देशों ने भाग लिया था। इसके तहत यह प्रावधान रखा गया कि 1995 तक सभी देश सी एफ सी की खपत में 50 प्रतिशत की कटौती तथा 1997 तक 85 प्रतिशत की कटौती करेंगे। सन 2010 तक सभी देश सी एफ सी का इस्तेमाल एकदम बंद कर देंगे। इस दौरान विकसित देश नए प्रशीतकों की खोज में विकासशील देशों की आर्थिक मदद करेंगे।

ओजोन विघटन का संकट  मुहावरे : अर्थ और वाक्य प्रयोग

(1) होड़ मचना।
अर्थ : किसी क्षेत्र में एक-दूसरे से आगे बढ़ जाने की इच्छा।
वाक्य : आज के दौर में जिधर भी नजर दौड़ाओ युवाओ में एक प्रकार की होड़ मची है।

(2) नसीब होना।
अर्थ : प्राप्त होना।
वाक्य : महँगाई के कारण गरीब को दिन-रात मेहनत करने पर भी दो वक्त का भोजन नसीब नहीं होता।

(3) फलना-फूलना।
अर्थ : विकास होना।
वाक्य : माता-पिता अपनी संतान को फलते-फूलते देखकर सदैव प्रसन्न होती है।

ओजोन विघटन का संकट  शब्दार्थ

• सामरिक = युद्ध से संबंधित
• विघटन = अलगाव/तोड़ना
• प्रशीतक = फ्रीज
• यौगिक = दो या अधिक तत्त्वों से बना हुआ
• मुहैया = पूर्ति करना, पहुँचाना
• दोहन = अनियंत्रित उपयोग
• सांद्र = घना, स्निग्ध
• प्रशीतन = ठंडा करने की प्रक्रिया
• छीजना = क्षय होना, घट जाना
• ऊसर = बंजर, अनुपजाऊ

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 13 कनुप्रिया Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 13 कनुप्रिया

12th Hindi Guide Chapter 13 कनुप्रिया Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) कृति पूर्ण कीजिए :

(a) कनुप्रिया की तन्मयता के गहरे क्षण सिर्फ – ………………………………………………
उत्तर :
कनुप्रिया की तन्मयता के गहरे क्षण सिर्फ –

• भावावेश थे।
• सुकोमल कल्पनाएँ थीं।
• रँगे हुए अर्थहीन शब्द थे।
• आकर्षक शब्द थे।

(b) कनुप्रिया के अनुसार यही युद्ध का सत्य स्वरूप है – ………………………………………………
उत्तर :

• टूटे रथ, जर्जर पताकाएँ।
• हारी हुई सेनाएँ, जीती हुई सेनाएँ।
• नभ को कँपाते हुए युद्ध घोष, क्रंदन-स्वर।
• भागे हुए सैनिकों से सुनी हुई अकल्पनीय, अमानुषिक घटनाएँ।

प्रश्न 2.
कनुप्रिया के लिए वे अर्थहीन शब्द जो गली-गली सुनाई देते हैं – ………………………………………………
उत्तर :
कनुप्रिया के लिए वे अर्थहीन शब्द जो गली-गली सुनाई देते हैं – कर्म, स्वधर्म, निर्णय, दायित्व।

(आ) कारण लिखिए :

(a) कनुप्रिया के मन में मोह उत्पन्न हो गया है।
उत्तर :
कनुप्रिया के मन में मोह उत्पन्न हो गया है – (कनुप्रिया कल्पना करती है कि वह अर्जुन की जगह है।) क्योंकि कनु के द्वारा समझाया जाना उसे बहुत अच्छा लगता है।

(b) आम की डाल सदा-सदा के लिए काट दी जाएगी।
उत्तर :
आम्रवृक्ष की डाल सदा-सदा के लिए काट दी जाएगी – क्योंकि कृष्ण के सेनापतियों के वायुवेग से दौड़ने वाले रथों की ऊँची-ऊँची गगनचुंबी ध्वजाओं में यह नीची डाल अटकती हैं।

अभिव्यक्ति

प्रश्न 3.
(अ) ‘व्यक्ति को कर्मप्रधान होना चाहिए’, इस विषय पर अपना मत लिखिए।
उत्तर :
संसार में दो तरह के लोग होते हैं। एक कर्म करने वाले लोग और दूसरे भाग्य के भरोसे बैठे रहने वाले लोग। बड़े-बड़े महापुरुष, वैज्ञानिक, उद्योगपति, शिक्षाविद, देश के कर्णधार तथा बड़े-बड़े अधिकारी अपने कार्यों के बल पर ही महान कहलाए। कर्म करने वाले व्यक्ति ही अपने परिश्रम के फल की उम्मीद कर सकते हैं। हाथ पर हाथ रखकर भगवान के भरोसे बैठे रहने वालों का कोई काम पूरा नहीं होता।

निष्क्रिय बैठे रहने वाले लोग भूल जाते हैं कि भाग्य भी संचित कर्मों का फल ही होता है। किसान को अपने खेत में काम करने के बाद ही अन्न की प्राप्ति होती है। व्यापारी को बौद्धिक श्रम करने के बाद ही व्यवसाय में लाभ होता है। कहा भी गया है कि ‘कर्म प्रधान विश्व करि राखा। जो जस करे सो तस फल चाखा।’ इस प्रकार कर्म सफलता की ओर ले जाने वाला मार्ग है।

(आ) ‘वृक्ष की उपयोगिता’, इस विषय पर अपने विचार लिखिए।
उत्तर :
वृक्ष मनुष्यों के पुराने साथी रहे हैं। प्राचीन काल में जब मनुष्य जंगलों में रहा करता था, तब वह अपनी सुरक्षा के लिए पेड़ों पर अपना घर बनाता था। पेड़ों से प्राप्त फल-फूल और जड़ों पर उसका जीवन आधारित था। पेड़ों की छाया धूप और वर्षा से उसकी मदद करती है। पेड़ों की हरियाली मनुष्य का मन प्रसन्न करती है। अब भी मनुष्य जहाँ रहता है, अपने आसपास फलदार और छायादार वृक्ष लगाता है।

वृक्ष मनुष्य के लिए बहुत उपयोगी होते हैं। अनेक औषधीय वृक्षों से मनुष्यों को औषधियाँ मिलती हैं। वृक्ष वातावरण से कार्बन डाइऑक्साइड सोखते हैं और ऑक्सीजन छोड़ते हैं, जिससे हमें साँस लेने के लिए शुद्ध वायु मिलती है। पेड़ों का सबसे बड़ा फायदा वर्षा कराने में होता है। जहाँ पेड़ों की बहुतायत होती है, वहाँ अच्छी वर्षा होती है। पेड़ों से ही फर्नीचर बनाने वाली तथा इमारती लकड़ियाँ मिलती हैं। इस तरह पेड़ हमारे लिए हर दृष्टि से उपयोगी होते हैं।

पाठ पर आधारित लघूत्तरी प्रश्न

प्रश्न 4.
(अ) ‘कवि ने राधा के माध्यम से आधुनिक मानव की व्यथा को शब्दबद्ध किया है, इस कथन को स्पष्ट कीजिए।
उत्तर :
‘कनुप्रिया’ काव्य में राधा अपने प्रियतम कृष्ण के ‘महाभारत’ युद्ध के महानायक के रूप में अपने से दूर चले जाने से व्यथित है। वह इस बात को लेकर तरह-तरह की कल्पनाएँ करती है। कभी अपनी व्यथा व्यक्त करती है, तो कभी अपने प्रिय की उपलब्धि पर गर्व करके संतोष कर लेती है।

यह व्यथा केवल राधा की ही नहीं है। उन परिवारों के मातापिता की भी है, जिनके बेटे अपने परिवारों के साथ नौकरी व्यवसाय के सिलसिले में अपनी गृहस्थी के प्रति अपना दायित्व निभाने के लिए अपने माता-पिता से दूर रहते हैं। उनसे विछोह की व्यथा उन्हें भोगनी पड़ती है। भोले माता-पिता को लाख माथापच्ची करने पर भी समझ में यह नहीं आता कि सालों-साल तक उनके बेटे माता-पिता को आखिर दर्शन क्यों नहीं देते हैं।

पर वहीं उनको यह संतोष और गर्व भी होता है कि उनका बेटा वहाँ बड़े पद पर है, जो उसे उनके साथ रहने पर नसीब नहीं होता। इसी तरह किसी एहसान फरामोश के प्रति एहसान करने वाले व्यक्ति के मन में उत्पन्न होने वाली भावनाओं में भी राधा के माध्यम से आधुनिक मानव की व्यथा व्यक्त होती है।

(आ) राधा की दृष्टि से जीवन की सार्थकता बताइए।
उत्तर :
राधा के लिए जीवन में प्यार सर्वोपरि है। वह वैरभाव अथवा युद्ध को निरर्थक मानती है। कृष्ण के प्रति राधा का प्यार निश्छल और निर्मल है। राधा ने सहज जीवन जीया है और उसने चरम तन्मयता के क्षणों में डूबकर जीवन की सार्थकता पाई है। अतः वह जीवन की समस्त घटनाओं और व्यक्तियों को केवल प्यार की कसौटी पर ही कसती है। वह तन्मयता के क्षणों में अपने सखा कृष्ण की सभी लीलाओं का अनुमान करती है।

वह केवल प्यार को सार्थक तथा अन्य सभी बातों को निरर्थक मानती है। महाभारत के युद्ध के महानायक कृष्ण को संबोधित करते हुए वह कहती है कि मैं तो तुम्हारी वही बावरी सखी हूँ, तुम्हारी मित्र हूँ। मैंने तुमसे सदा स्नेह ही पाया है और मैं स्नेह की ही भाषा समझती हूँ।

राधा कृष्ण के कर्म, स्वधर्म, निर्णय तथा दायित्व जैसे शब्दों को । सुनकर कुछ नहीं समझ पाती। वह राह में रुक कर कृष्ण के अधरों की कल्पना करती है… जिन अधरों से उन्होंने प्रणय के शब्द पहली बार उससे कहे थे। उसे इन शब्दों में केवल अपना ही राधन्… राधन्… राधन्… नाम सुनाई देता है।

इस प्रकार राधा की दृष्टि से जीवन की सार्थकता प्रेम की पराकाष्ठा में है। उसके लिए इसे त्याग कर किसी अन्य का अवलंबन करना नितांत निरर्थक है।

रसास्वादन

प्रश्न 5.
‘कनुप्रिया’ काव्य का रसास्वादन कीजिए।
उत्तर :
(1) रचना का शीर्षक : कनुप्रिया। (विशेष अध्ययन के लिए)
(2) रचनाकार : डॉ. धर्मवीर भारती।
(3) कविता की केंद्रीय कल्पना : इस कविता में राधा और कृष्ण के तन्मयता के क्षणों के परिप्रेक्ष्य में कृष्ण को महाभारत युद्ध के महानायक के रूप में तौला गया है। राधा कृष्ण के वर्तमान रूप से चकित है। वह उनके नायकत्व रूप से अपरिचित है। उसे तो कृष्ण अपनी तन्मयता के क्षणों में केवल प्रणय की बातें करते दिखाई देते हैं।
(4) रस-अलंकार :
(5) प्रतीक विधान : राधा कनु को संबोधित करते हुए कहती है कि मेरे प्रेम को तुमने साध्य न मानकर साधन माना है। इस लीला क्षेत्र से युद्ध क्षेत्र तक की दूरी तटा करने के लिए तुमने मुझे ही सेतु बना दिया। यहाँ लीला क्षेत्र और युद्ध क्षेत्र को जोड़ने के लिए सेतु जैसे प्रतीक का प्रयोग किया गया है।
(6) कल्पना : प्रस्तुत काव्य-रचना में राधा और कृष्ण के प्रेम
और महाभारत के युद्ध में कृष्ण की भूमिका को अवचेतन मन वाली राधा के दृष्टिकोण से चित्रित किया गया है।
(7) पसंद की पंक्तियाँ तथा प्रभाव : दुख क्यों करती है पगली, क्या हुआ जो/कनु के वर्तमान अपने/तेरे उन तन्मय क्षणों की कथा से/ अनभिज्ञ हैं/उदास क्यों होती है नासमझ/कि इस भीड़भाड़ में/ है तू और तेरा प्यार नितांत अपरिवर्तित/छूट गए हैं। गर्व कर बावरी/कौन है जिसके महान प्रिय की/अठारह अक्षौहिणी सेनाएँ हों? इन पंक्तियों में राधा को अवचेतन मन वाली राधा सांत्वना है देती है।

(8) कविता पसंद आने का कारण : कवि ने इन पंक्तियों में राधा के अवचेतन मन में बैठी राधा के द्वारा चेतनावस्था में स्थित राधा को यह सांत्वना दिलाई है कि यदि कृष्ण युद्ध की हड़बड़ाहट में तुमसे और तुम्हारे प्यार से अपरिचित होकर तुमसे दूर चले गए हैं तो तुम्हें उदास नहीं होना चाहिए।

तुम्हें तो इस बात पर गर्व होना चाहिए। क्योंकि किसके महान है प्रेमी के पास अठारह अक्षौहिणी सेनाएँ हैं। केवल तुम्हारे प्रेमी के पास ही न।

Hindi Yuvakbharati 12th Digest Chapter 13 कनुप्रिया Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 3 (अ) के लिए
पद्यांश क्र. 1
प्रश्न. निम्नलिखितपद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए :
ऐसा है राधा का सेतु जिस्म –
(1) …………………………………….
(2) …………………………………….
(3) …………………………………….
(4) …………………………………….
उत्तर :
ऐसा है राधा का सेतु जिस्म –
(1) सोने के पतले गुंथे तारों वाले पुल-सा
(2) निर्जन
(3) निरर्थक
(4) काँपता-सा।

कृति 2 : (आकलन)

प्रश्न 1.
उत्तर : लिखिए :
(1) पद्यांश में प्रयुक्त एक सुंदर वृक्ष का नाम – …………………………………….
(2) सैनिकों की गणना करने के काम आने वाला शब्द – …………………………………….
(3) इन्हें पथ से अलग हटकर खड़ी होने की सलाह – …………………………………….
(4) आकाश ऐसा था – …………………………………….
उत्तर :
(1) कदंब।
(2) अक्षौहिणी।
(3) राधा को।
(4) धूल भरा।

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर :

पद्यांश क्र. 2
प्रश्न. निम्नलिखितपद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कारण लिखिए :
आज राधा उस पथ से दूर हट जाए – ……………………………………………
उत्तर :
आज राधा उस पथ से दूर हट जाए – क्योंकि आज उस पथ से द्वारिका की युद्धोन्मत्त सेनाएँ गुजर रही हैं।

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर :

कृति 2 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :
(1) कनु सबसे ज्यादा इसका है – …………………………………………
(2) राधा इसके रोम-रोम से परिचित है – …………………………………………
(3) अगणित सैनिक इसके हैं – …………………………………………
(4) राधा को ये बिलकुल नहीं पहचानते – …………………………………………
उत्तर :
(1) राधा का।
(2) कनु (कृष्ण) के।
(3) कनु (कृष्ण) के।
(4) कनु (कृष्ण) के सैनिक।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘धार्मिक दृष्टि से पवित्र माने जाने वाले वृक्ष’ विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
यों तो हर प्रकार के वृक्ष मनुष्य के काम आते हैं, पर कुछ वृक्ष ऐसे होते है, जिन्हें धार्मिक दृष्टि से पवित्र माना जाता है। उनमें से कुछ वृक्षों की पूजा-अर्चना की जाती है और कुछ वृक्षों की पत्तियों का उपयोग धार्मिक कार्यों के लिए किया जाता है। पीपल और नीम के वृक्षों में क्रमशः भगवान शंकर और देवी जी का बास मानकर इन वृक्षों में श्रद्धालु जल छोड़ते हैं। वट पूर्णिमा को सुहागन स्त्रियाँ पति के दीर्घायु के लिए वट वृक्ष की पूजा करती हैं।

अशोक की पत्तियों का शुभ अवसर पर तोरण बनाकर मंडपों आदि को सजाया जाता है। आम का वृक्ष तो शुभ माना ही जाता है। पूजा में कलश पर रखने के लिए आम की पल्लव अनिवार्य होती है। आम की पत्तियाँ तोरण बनाने के काम में आती हैं। इसके अलावा आम की लकड़ी हवन के काम भी आती है।

छोटे पौधों में तुलसी पवित्र मानी जाती है। पूजा में तुलसी- पत्र और पान की पत्तियों का उपयोग भी आवश्यक होता है।

इसी तरह नारियल के वृक्ष को भी पवित्र माना जाता है। नारियल और सुपारी के बिना कोई महत्त्वपूर्ण धार्मिक कार्य संपन्न नहीं होता। इस तरह धार्मिक दृष्टि से पवित्र माने जाने वाले वृक्षों का बहुत महत्त्व है।

पद्यांश क्र. 3
प्रश्न. निम्नलिखित पद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर : लिखिए :
(1) कनुप्रिया (राधा) को उदास नहीं होना चाहिए – ……………………………………..
(2) कनुप्रिया (राधा) को गर्व करना चाहिए – ……………………………………..
उत्तर :
(1) कनुप्रिया (राधा) को उदास नहीं होना चाहिए – कि भीड़भाड़ में वह और उसका प्यार नितांत अपरिचित छूट गए हैं।
(2) कनुप्रिया (राधा) को गर्व करना चाहिए – कि उसके प्रिय के अठारह अक्षौहिणी सेनाएँ हैं।

कृति 2 : (आकलन)

प्रश्न 2.
कनु (कृष्ण) के अनुसार युद्ध सत्य –
उत्तर :
कनु (कृष्ण) के अनुसार युद्ध सत्य –

• पाप-पुण्य
• धर्म-अधर्म
• न्याय-दंड
• क्षमाशीलता।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘प्राचीन काल एवं आधुनिक काल की सेनाओं के बारे में 40 से 50 शब्दों में अपने विचार व्यक्त कीजिए।
उत्तर :
प्राचीन काल में आज की तरह तकनीकी विकास नहीं हुआ था। इसलिए सेनाओं के पास आज की तरह द्रुत गति से मारक और विनाशक अस्त्र-शस्त्र नहीं थे। प्राचीन काल की सेनाएँ पैदल सैनिकों पर आधारित होती थीं। उनमें पैदल सेना, अश्व सेना, गज सेना आदि प्रमुख थीं। राजा और सामंत लड़ाई के समय रथों का प्रयोग करते थे। सेनाओं के पास धनुष-बाण, भाले, तलवारें, कटार-बी तथा गदा जैसे हथियार होते थे।

लड़ाइयाँ अधिकतर आमने-सामने होती थीं। इसलिए सैनिकों की संख्या बहुत अधिक होती थी। आज की सेनाएँ आधुनिक हथियारों से लैस होती हैं। ये थल सेना, जल सेना तथा वायु सेना में बँटी होती हैं। इनके पास अत्यधिक तेज गति से मार करने वाले हथियार होते हैं। थल सेना के पास आधुनिक राइफलें, विकसित तकनीक वाले दूर-दूर तक मार करने वाले टैंक, गोला-बारूद, हजारों मील दूर तक मार करने वाली मिसाइलें होती हैं।

वायु सेना के पास आवाज की गति से तेज चलने वाले फाइटर विमान, तरह-तरह के संहारक बम तथा जल सेना के पास अनेक युद्धक जहाजें तथा पनडुब्बियाँ होती हैं, जो क्षण भर में भारी विनाश कर सकती हैं। इस तरह प्राचीन काल की सेनाओं और आधुनिक काल की सेनाओं में जमीन-आसमान का अंतर हैं।

पढ्यांश क्र. 4
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.

उत्तर :

कृति 2 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :
(1) कनुप्रिया कनु से इनकी तरह सब कुछ समझना चाहती है सार्थकता – ………………………………
(2) कनुप्रिया की तन्मयता के गहरे क्षण – ………………………………
(3) कनुप्रिया के लिए वे सारे शब्द तब अर्थहीन हैं – ………………………………
उत्तर :
(1) कनुप्रिया कनु से इनकी तरह सब कुछ समझना चाहती है सार्थकता – अर्जुन की तरह।
(2) कनुप्रिया की तन्मयता के गहरे क्षण – रँगे हुए अर्थहीन आकर्षक शब्द।
(3) कनुप्रिया के लिए वे सारे शब्द तब अर्थहीन हैं – जब वे कनु के काँपते अधरों से नहीं निकलते।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘युद्ध विनाश एवं शांति विकास का कारण होता है’ इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
युद्ध कोई नहीं चाहता, क्योंकि युद्ध का परिणाम बहुत भयानक होता है। लेकिन कभी-कभी स्थितियाँ ऐसी हो जाती हैं कि न चाहकर भी युद्ध करना पड़ता है। युद्ध में दोनों पक्षों की भारी क्षति होती है। अनेक सैनिक मारे जाते हैं, जिनके कारण अनेक और अस्त्र-शस्त्रों की व्यवस्था करने में भारी आर्थिक क्षति होती है। विकास कार्यों में लगने वाला धन युद्ध के खर्च में लग जाता है। इससे देश का आर्थिक ढाँचा चरमरा जाता है।

युद्ध का परिणाम आने वाली पीढ़ियों को वर्षों तक भोगना पड़ता है। किसी देश के लिए शांति का समय विकास का समय होता है। इससे युद्ध पर होने वाले अनावश्यक खर्च से बचत होती है। देश का धन विकास कार्यों पर खर्च होता है। इसका लाभ देश की जनता को मिलता है।

इससे शासक वर्ग और शासित जनता दोनों खुशहाल होते हैं। रोजगार के अवसर प्राप्त होते हैं और लोग संपन्न बनते हैं। युद्ध और शांति एक-दूसरे के विरोधी हैं। इस तरह युद्ध से विनाश और शांति से विकास होता है।

पद्यांश क्र. 5
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कारण लिखिए :
कन का तेज कनुप्रिया के मूर्च्छित संवेदन को धधका रहा है – ………………………………………..
उत्तर :
कनु का तेज कनुप्रिया के मूर्च्छित संवेदन को धधका रहा है – क्योंकि वह कनु को अपलक देख रही है और उनके हर शब्द को वह अँजुरी बनाकर बूंद-बूंद उन्हें पी रही है।

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :
(1) कनु के फूलों की तरह झरते हुए शब्द कनुप्रिया को इस तरह सुनाई पड़ते हैं – ………………………………………..
(2) कनुप्रिया के लिए कनु के सभी शब्दों के केवल एक अर्थ – ………………………………………..
उत्तर :
(1) राधन्, राधन्, राधन्।
(2) मैं … मैं … मैं …।

प्रश्न 2.
कृति पूर्ण कीजिए : जब कनु राधा को समझाते हैं, तो उसे यह लगता है –
(1) ………………………………………..
(2) ………………………………………..
(3) ………………………………………..
(4) ………………………………………..
उत्तर :
(1) जैसे युद्ध रुक गया है।
(2) जैसे सेनाएँ स्तब्ध खड़ी रह गई हैं।
(3) जैसे इतिहास की गति रुक गई है।
(4) समझाया जाना उसे (राधा को) अच्छा लगता है।

रसास्वादन अर्थ के आधार पर

प्रश्न 1.
‘कनुप्रिया में लेखक ने राधा के मन की व्यथा का सुंदर चित्रण किया है’ इस कथन के आधार पर कविता का रसास्वादन कीजिए।
उत्तर :
डॉ. धर्मवीर भारती लिखित काव्य ‘कनुप्रिया’ आधुनिक मूल्यों वाला नया काव्य है। महाभारत की पृष्ठभूमि पर लिखी गई इस कृति में कनुप्रिया यानी राधा के मानसिक संघर्ष के प्रसंग व्यक्त हुए हैं। कवि ने राधा के माध्यम से कृष्ण को संबोधित करते हुए उनसे कई प्रश्न पुछवाए और उनके जवाब भी राधा से दिलवाए हैं। इस काव्य में कई प्रसंग बहुत सुंदर ढंग से पिरोए गए हैं।

अवचेतन मन में बैठी राधा चेतनास्थित राधा से कहती है कि ‘वह आम्र की डाल जिसका सहारा लेकर कृष्ण वंशी बजाया करते थे अब काट डाली जाएगी, क्योंकि वह कृष्ण के सेनापतियों के रथों की ध्वजाओं में अटकती है।’ या ‘चारों दिशाओं से, उत्तर को उड़-उड़ कर जाते हुए, गिद्धों को क्या तुम बुलाते हो (जैसे बुलाते थे भटकी हुई गायों को)’। इन पंक्तियों में कवि ने राधा के अपने मन की व्यथा व्यक्त की है।

कवि ने नई कविता के मुक्त छंदों में सीधे-सादे सरल शब्दों में राधा के मन की बात कही है। प्रस्तुत कविता में प्रसाद गुण की प्रमुखता है और समूचे काव्य में अतुकांत छंदों का प्रयोग किया गया है, जो नई कविता की अपनी विशेषता है।

कनुप्रिया Summary in Hindi

कनुप्रिया कवि का परिचय

कनुप्रिया कवि का नाम :
डॉ. धर्मवीर भारती। (जन्म 25 दिसंबर, 1926; निधन 4 सितंबर, 1997.)

कनुप्रिया प्रमुख कृतियाँ :
गुनाहों का देवता, सूरज का सातवाँ घोड़ा (उपन्यास); सात गीत वर्ष, ठंडा लोहा, कनुप्रिया (कविता संग्रह), मुर्दो का गाँव, चाँद और टूटे हुए लोग, ऑस्कर वाइल्ड की कहानियाँ, बंद गली का आखिरी मकान (कहानी संग्रह), नदी प्यासी थी (एकांकी), अंधा युग, सृष्टि का आखिरी आदमी (काव्य नाटक), सिद्ध साहित्य (साहित्यिक समीक्षा), एक समीक्षा, मानव मूल्य और साहित्य, कहानी अकहानी, पश्यंती (निबंध) आदि।

कनुप्रिया विशेषता :
आधुनिक काल के रचनाकारों में डॉ. धर्मवीर भारती मूर्धन्य साहित्यकार के रूप में प्रतिष्ठित हैं। ‘कनुप्रिया’ आपकी अनोखी और अद्भुत कृति है। डॉ. धीरेंद्र वर्मा के निर्देशन में सिद्ध साहित्य’ पर शोध प्रबंध, जिसका हिंदी साहित्य अनुसंधान के इतिहास में विशेष स्थान है। टाइम्स ऑफ इंडिया पब्लिकेशन के प्रकाशन ‘धर्मयुग’ के वर्षों तक संपादक। आपको पद्मश्री, व्यास सम्मान तथा कई अन्य राष्ट्रीय पुरस्कारों से अलंकृत किया गया है।

कनुप्रिया विधा :
पद्य (नई कविता)।

कनुप्रिया विषय प्रवेश :
‘कनुप्रिया’ राधा और कृष्ण के प्रेम और महाभारत की कथा से संबंधित कृति है। कृति में बताया गया है कि प्रेम सर्वोपरि है और युद्ध का अवलंब करना निरर्थक है। राधा कृष्ण से महाभारत युद्ध को लेकर कई प्रश्न पूछती है। महाभारत युद्ध में हुई जीत-हार, कृष्ण की भूमिका, युद्ध का उद्देश्य, युद्ध की भयावहता, सैन्य संहार आदि बातों से संबंधित राधा का कृष्ण से हुआ तर्कसंगत संवाद इस काव्य में चार चाँद लगा देता है।

कनुप्रिया कविता का सरल अर्थ

सेतु : मैं

राधा कहती है, “हे कनु (कृष्ण) नीचे की घाटी से ऊपर के शिखरों पर जिसे जाना था, वह चला गया। (लेकिन बलि मेरी ही चढ़ी) मेरे ही सिर पर पैर रख मेरी बाहों से इतिहास तुम्हें ले गया।” हे कनु, इस लीला क्षेत्र से उठकर युद्ध क्षेत्र तक की अलंघ्य दूरी तय करने के लिए क्या तुमने मुझे ही सेतु बना दिया?

अब इन शिखरों और मृत्यु-घाटियों के बीच बने इस सोने के पतले और गुंथे हुए तारों से बने पुल की तरह मेरा यह सेतु-रूपी शरीर काँपता हुआ निर्जन और निरर्थक रह गया है। जिसे जाना था वह चला गया।

अमंगल छाया

अवचेतन मन में बैठी हुई राधा अपने चेतन मन वाली राधा को संबोधित करते हुए कहती है, हे राधा! यमुना के घाट से ऊपर आते समय कदंब के पेड़ के नीचे खड़े कनु को देवता समझकर प्रणाम करने के लिए तुम जिस मार्ग से लौटती थी, हे बावरी! आज तुम उस मार्ग से होकर मत लौटना।

ये उजड़े हुए कुंज, रौंदी हुई लताएँ, आकाश में छाई हुई धूल, क्या तुम्हें यह आभास नहीं दे रहे हैं कि आज उस मार्ग से कृष्ण की अठारह अक्षौहिणी सेनाएँ युद्ध में भाग लेने जा रही हैं!

हे बावरी! आज तू उस मार्ग से दूर हटकर खड़ी हो जा। लताकुंज की ओट में अपने घायल प्यार को छुपा ले। क्योंकि आज इस गाँव से द्वारिका की उन्मत्त सेनाएँ युद्ध के लिए जा रही हैं।

हे राधा! मैं मानती हूँ कि कन्हैया सबसे अधिक तुम्हारा अपना है। मैं मानती हूँ कि तुम कृष्ण के रोम-रोम से परिचित हो। मैं मानती हूँ कि ये असंख्य सैनिक तुम्हारे उसके (कन्हैया के) हैं, पर तू यह जान ले कि ये सैनिक तुझे बिलकुल नहीं पहचानते हैं। इसलिए हे बावरी! इस मार्ग से दूर हट जा।

यह आम की डाल तुम्हारे कन्हैया की अत्यंत प्रिय थी। जब तक तू (यहाँ) नहीं आती थी, सारी शाम कन्हैया इस डाल पर टिककर बंशी में तेरा नाम भर-भरकर तुम्हें टेरा करता था।

आज यह आम की डाल सदा-सदा के लिए काट दी जाएगी। इसका कारण यह है कि कृष्ण के सेनापतियों के तेज गति वाले रथों की ऊँची-ऊँची पताकाओं में यह डाल उलझती है… अटकती है। इतना ही नहीं, रास्ते के किनारे यह छायादार पवित्र अशोक का पेड़ भी आज टुकड़े-टुकड़े कर दिया जा सकता है। अगर इस गाँव के लोग सेनाओं के स्वागत में (इस वृक्ष की पत्तियों के) तोरण नहीं बनाएँगे, तो शायद यह गाँव उजाड़ दिया जाएगा।

अरे पगली! दुखी क्यों होती है। क्या हुआ, यदि आज के कृष्ण तुम्हारे साथ पहले बिताए हुए तन्मयता के गहरे क्षणों को भूल चुक हैं।

हे राधे! तू उदास क्यों होती है कि इस भीड़भाड़ में तुम्हें और तुम्हारे प्यार को पहचानने वाला कोई नहीं है।

राधे, तुम्हें तो गर्व होना चाहिए। क्योंकि किसके महान प्रेमी के पास अठारह अक्षौहिणी सेनाएँ हैं। (केवल तुम्हारे ही प्रेमी के पास न!)

एक प्रश्न

राधा अपने कनु (कृष्ण) को संबोधित करते हुए कहती है कि मेरे महान कनु, मान लो… क्षणभर के लिए मैं इस बात को स्वीकार कर लूँ कि मेरे वे तन्मयता वाले सारे गहरे क्षण केवल मेरे भावावेश थे… मेरी कोमल कल्पनाएँ थीं… केवल बनावटी, निरर्थक और आकर्षक शब्द थे।

मान लो, एक क्षण के लिए मैं यह स्वीकार कर लूँ कि तुम्हारा महाभारत का यह युद्ध पाप-पुण्य, धर्म-अधर्म, न्याय-दंड तथा क्षमा-शील वाला है। इसलिए इस युद्ध का होना इस युग की सच्चाई है। फिर भी कनु, मैं क्या करूँ? मैं तो वही तुम्हारी बावरी मित्र हूँ।

मुझे तो केवल उतना ही ज्ञान मिला है, जितना तुमने मुझे दिया है। तुम्हारे दिए हुए समस्त ज्ञान को समेट कर भी मैं तुम्हारे इतिहास, तुम्हारे उदात्त और महान कार्यों को समझ नहीं पाई हूँ।

कनु, अपनी यमुना नदी, जिसमें मैं अपने आप को घंटों निहारा करती थी, अब उसमें हथियारों से लदी हुई असंख्य नौकाएँ रोज-रोज न जाने कहाँ जाती हैं? नदी की धारा में बह-बह कर आने वाले टूटे हुए रथ और फटी हुई पताकाएँ किसकी हैं?

हे कनु, युद्ध क्षेत्र से हारी हुई सेनाएँ, जीती हुई सेनाएँ, गगनभेदी युद्ध घोष, विलाप के स्वर और युद्ध क्षेत्र से भागे हुए सैनिकों के मुँह से सुनी हुई युद्ध की अकल्पनीय और अमानवीय घटनाएँ, … क्या यह सब सार्थक है? गिद्ध जो चारों दिशाओं से उड़-उड़ कर उत्तर : दिशा की ओर जा रहे हैं, हे कनु, क्या इन्हें तुम बुलाते हो? (जैसे तुम भटकी हुई गायों को बुलाते थे।)

हे कनु, मैंने अब तक तुमसे जितनी समझ पाई है, उस समझ को बटोर कर भी मैं यह जान पाई हूँ कि और भी बहुत कुछ है तुम्हारे पास, जिसका कोई भी अर्थ मेरी समझ में नहीं आता।

हे कनु, जिस तरह तुमने युद्ध क्षेत्र में अर्जुन को युद्ध का प्रयोजन और उसकी सार्थकता समझाई थी, वैसे मुझे भी समझा दो कि सार्थकता क्या है? राधा कहती है कि मान लो कि मेरी तन्मयता के गहरे क्षण रंगे हुए, अर्थहीन परंतु आकर्षक शब्द थे, तो तुम्हारी दृष्टि से सार्थक क्या है? इस सार्थकता को तुम मुझे कैसे समझाओगे?

शब्द – अर्थहीन

…शब्द, शब्द, शब्द! राधा कहती है, मेरे लिए इन शब्दों की कोई कीमत नहीं है। हे कनु, जो शब्द मेरे पास बैठकर तुम्हारे काँपते हुए होठों से नहीं निकलते वे सभी शब्द मेरे लिए अर्थहीन हैं, निरर्थक हैं। वह कहती हैं कि कर्म, स्वधर्म, निर्णय और दायित्व जैसे शब्द मैंने भी गली-गली में सुने हैं। अर्जुन ने इन शब्दों में भले ही कुछ पाया हो, हे कनु! इन शब्दों को सुनकर मैं कुछ भी नहीं पायी। मैं रास्ते में ठहरकर तुम्हारे उन होठों की कल्पना करती हूँ । जिन होठों से तुमने प्रणय के शब्द पहली बार कहे होंगे।

मैं कल्पना करती हूँ कि अर्जुन की जगह मैं हूँ और मेरे मन में मोह उत्पन्न हो गया है। मुझे कुछ पता नहीं है, युद्ध कौन-सा है और मैं किसके पक्ष में हूँ। मुझे कुछ पता नहीं कि समस्या क्या है और लड़ाई किस बात की है। लेकिन मेरे मन में मोह उत्पन्न हो गया है। क्योंकि तुम्हारा समझाना मुझे बहुत अच्छा लगता है। जब तुम मुझे समझा रहे हो तो सेनाएँ स्तब्ध खड़ी रह गई हैं और इतिहास की गति रुक गई है। और तुम मुझे समझा रहे हो।

तुम कर्म, स्वधर्म, निर्णय, दायित्व जैसे जिन शब्दों को कहते हो, ये मेरे लिए बिलकुल अर्थहीन हैं। कनु, मैं इन सबसे हट करके एकटक तुम्हें देख रही हूँ। तुम्हारे प्रत्येक शब्द को अँजुरी बनाकर मैं बूंद-बूंद तुम्हें पी रही हूँ। तुम्हारा तेज, तुम्हारा व्यक्तित्व जैसे मेरे शरीर के एक-एक मूर्छित संवेदन को दहका रहा है। लगता है तुम्हारे जादू भरे होठों से शब्द रजनीगंधा के फूलों की तरह झर रहे हैं – एक के बाद एक।

कनु कनु, स्वधर्म, निर्णय और दायित्व आदि जो शब्द तुम्हारे मुँह से निकलते हैं, वे शब्द मुझ तक आते-आते बदल जाते हैं। मुझे ये शब्द राधन्, राधन्, राधन् के रूप में सुनाई देते हैं। तुम्हारे द्वारा कहे जाने वाले शब्द असंख्य हैं, उनकी गणना नहीं की जा सकती। पर मेरे लिए उनका अर्थ केवल एक ही है – मैं … मैं … केवल मैं। है फिर बताओ कनु, इन शब्दों से तुम मुझे इतिहास कैसे समझाओगे!

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 5 Vectors Ex 5.1

Question 1.
The vector \(\bar{a}\) is directed due north and \(|\bar{a}|\) = 24. The vector \(\bar{b}\) is directed due west and \(|\bar{b}|\) = 7. Find \(|\bar{a}+\bar{b}|\).
Solution:

Let \(\overline{\mathrm{AB}}\) = \(\bar{a}\), \(\overline{\mathrm{BC}}\) = \(\bar{b}\)
Then \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{BC}}\) = a + b
Given : \(|\bar{a}|\) = \(|\overline{\mathrm{AB}}|\) = l(AB) = 24 and
\(|\bar{b}|\) = \(|\overline{\mathrm{BC}}|\) = l(BC) = 7
∴ ∠ABC = 90°
∴ [l(AC)]² = [l(AB)]² + [l(BC)]²
= (24)² + (7)² = 625
∴ l(AC) = 25 ∴ \(|\overline{\mathrm{AC}}|\) = 25
∴ \(|\bar{a}+\bar{b}|\) = \(|\overline{\mathrm{AC}}|\) = 25.

Question 2.
In the triangle PQR, \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\) and \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\). The mid-point of PR is M. Find following vectors in terms of \(\bar{a}\) and \(\bar{b}\).
(i) \(\overline{\mathrm{PR}}\)
Solution:

Given : \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\), \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\)
(i) \(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PQ}}\) + \(\overline{\mathrm{QR}}\)
= 2\(\bar{a}\) + 2\(\bar{a}\).

(ii) \(\overline{\mathrm{PM}}\)
Solution:
∵ M is the midpoint of PR
∴ \(\overline{\mathrm{PM}}\) = \(\frac{1}{2} \overline{\mathrm{PR}}\) = \(\frac{1}{2}\)[2\(\bar{a}\) + 2\(\bar{b}\)]
= \(\bar{a}\) + \(\bar{b}\).

(iii) \(\overline{\mathrm{QM}}\)
Solution:
\(\overline{\mathrm{RM}}\) = \(\frac{1}{2}(\overline{\mathrm{RP}})\) = \(-\frac{1}{2} \overline{\mathrm{PR}}\) = \(-\frac{1}{2}\)(2\(\bar{a}\) + 2\(\bar{b}\))
= –\(\bar{a}\) – \(\bar{b}\)
∴ \(\overline{\mathrm{QM}}\) = \(\overline{\mathrm{QR}}\) + \(\overline{\mathrm{RM}}\)
= 2\(\bar{b}\) – \(\bar{a}\) – \(\bar{b}\)
= \(\bar{b}\) – \(\bar{a}\).

Question 3.
OABCDE is a regular hexagon. The points A and B have position vectors \(\bar{a}\) and \(\bar{b}\) respectively, referred to the origin O. Find, in terms of \(\bar{a}\) and \(\bar{b}\) the position vectors of C, D and E.
Solution:

Given : \(\overline{\mathrm{OA}}\) = \(\bar{a}\), \(\overline{\mathrm{OB}}\) = \(\bar{a}\) Let AD, BE, OC meet at M.
Then M bisects AD, BE, OC.
\(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{AO}}\) + \(\overline{\mathrm{OB}}\) = –\(\overline{\mathrm{OA}}\) + \(\overline{\mathrm{OB}}\) = –\(\bar{a}\) + \(\bar{b}\) = \(\bar{b}\) – \(\bar{a}\)
∵ OABM is a parallelogram

Hence, the position vectors of C, D and E are 2\(\bar{b}\) – 2\(\bar{a}\), 2\(\bar{b}\) – 3\(\bar{a}\) and \(\bar{b}\) – 2\(\bar{a}\) respectively.

Question 4.
If ABCDEF is a regular hexagon, show that \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{AC}}\) + \(\overline{\mathrm{AD}}\) + \(\overline{\mathrm{AE}}\) + \(\overline{\mathrm{AF}}\) = 6\(\overline{\mathrm{AO}}\), where O is the center of the hexagon.
Solution:

ABCDEF is a regular hexagon.
∴ \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{ED}}\) and \(\overline{\mathrm{AF}}\) = \(\overline{\mathrm{CD}}\)
∴ by the triangle law of addition of vectors,

Question 5.
Check whether the vectors \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), + \(-3 \hat{i}+3 \hat{j}+2 \hat{k}\), + \(3 \hat{i}+4 \hat{k}\) form a triangle or not.
Solution:
Let, if possible, the three vectors form a triangle ABC
with \(\overline{A B}\) = \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), \(\overline{B C}\) = \(3 \hat{i}+3 \hat{j}+2 \hat{k}\), \(\overline{A C}\) = \(3 \hat{i}+4 \hat{k}\)
Now, \(\overline{A B}\) + \(\overline{B C}\)
= \((2 \hat{i}+2 \hat{j}+3 \hat{k})\) + \((-3 \hat{i}+3 \hat{j}+2 \hat{k})\)
= \(-\hat{i}+5 \hat{j}+5 \hat{k} \neq 3 \hat{i}+4 \hat{k}\) = \(\overline{\mathrm{AC}}\)
Hence, the three vectors do not form a triangle.

Question 6.
In the figure 5.34 express \(\bar{c}\) and \(\bar{d}\) in terms of \(\bar{a}\) and \(\bar{b}\). Find a vector in the direction of \(\bar{a}\) = \(\hat{i}-2 \hat{j}\) that has magnitude 7 units.

Solution:
\(\overline{\mathrm{PQ}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SQ}}\)
∴ \(\bar{a}\) = \(\bar{c}\) – \(\bar{d}\) … (1)
\(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SR}}\)
∴ \(\bar{b}\) = \(\bar{c}\) + \(\bar{d}\) … (2)
Adding equations (1) and (2), we get
\(\bar{a}\) + \(\bar{b}\) = (\(\bar{c}\) – \(\bar{d}\)) + (\(\bar{c}\) + \(\bar{d}\)) = 2\(\bar{c}\)

Question 7.
Find the distance from (4, -2, 6) to each of the following :
(a) The XY-plane
Solution:
Let the point A be (4, -2, 6).
Then,
The distance of A from XY-plane = |z| = 6

(b) The YZ-plane
Solution:
The distance of A from YZ-plane = |x| = 4

(c) The XZ-plane
Solution:
The distance of A from ZX-plane = |y| = 2

(d) The X-axis
Solution:
The distance of A from X-axis
= \(\sqrt{y^{2}+z^{2}}\) = \(\sqrt{(-2)^{2}+6^{2}}\) = \(\sqrt{40}\) = \(2 \sqrt{10}\)

(e) The Y-axis
Solution:
The distance of A from Y-axis
= \(\sqrt{z^{2}+x^{2}}\) = \(\sqrt{6^{2}+4^{2}}\) = \(\sqrt{52}\) = \(2 \sqrt{13}\)

(f) The Z-axis
Solution:
The distance of A from Z-axis
= \(\sqrt{x^{2}+y^{2}}\) = \(\sqrt{4^{2}+(-2)^{2}}\) = \(\sqrt{20}\) = \(2 \sqrt{5}\)

Question 8.
Find the coordinates of the point which is located :
(a) Three units behind the YZ-plane, four units to the right of the XZ-plane and five units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located 3 units behind the YZ- j plane, 4 units to the right of XZ-plane and 5 units , above the XY-plane,
x = -3, y = 4 and z = 5
Hence, coordinates of the required point are (-3, 4, 5)

(b) In the YZ-plane, one unit to the right of the XZ-plane and six units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located in the YZ plane, x = 0. Also, the point is one unit to the right of XZ-plane and six units above the XY-plane.
∴ y = 1, z = 6.
Hence, coordinates of the required point are (0, 1, 6).

Question 9.
Find the area of the triangle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Solution:
Let A = (1, 1, 0), B = (1, 0, 1), C = (0, 1, 1)

Question 10.
If \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\) and initial point A ≡ (1, 5, ,0). Find the terminal point B.
Solution:
Let \(\bar{a}\) and \(\bar{b}\) be the position vectors of A and B.
Given : A = (1, 5, 0) .’. \(\bar{a}\) = \(\hat{i}+5 \hat{j}\)
Now, \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) – \(\bar{a}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) = \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \(\bar{a}\)
= \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \((\hat{i}+5 \hat{j})\)
= \(3 \hat{i}+\hat{j}+7 \hat{k}\)
Hence, the terminal point B = (3, 1, 7).

Question 11.
Show that the following points are collinear :
(i) A (3, 2, -4), B (9, 8, -10), C (-2, -3, 1).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
A = (3, 2, -4), B = (9, 8, -10) and C = (-2, -3, 1) respectively.

∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.

(ii) P (4, 5, 2), Q (3, 2, 4), R (5, 8, 0).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
P = (4, 5, 2), Q = (3, 2, 4), R = (5, 8, 0) respectively.

= 2.\(\overline{\mathrm{AB}}\) …[By (1)]
∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.

Question 12.
If the vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear, then find the value of q.
Solution:
The vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear
∴ the coefficients of \(\hat{i}, \hat{j}, \hat{k}\) are proportional

Question 13.
Are the four points A(1, -1, 1), B(-1, 1, 1), C(1, 1, 1) and D(2, -3, 4) coplanar? Justify your answer.
Solution:
The position vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{d}\) of the points A, B, C, D are

By equality of vectors,
y = -2 ….(1)
2x – 2y = 2 … (2)
3y = 0 … (3)
From (1), y = -2
From (3), y = 0 This is not possible.
Hence, the points A, B, C, D are not coplanar.

Question 14.
Express \(-\hat{i}-3 \hat{j}+4 \hat{k}\) as linear combination of the vectors \(2 \hat{i}+\hat{j}-4 \hat{k}\), \(2 \hat{i}-\hat{j}+3 \hat{k}\) and \(3 \hat{i}+\hat{j}-2 \hat{k}\).
Solution:

By equality of vectors,
2x + 2y + 3 = -1
x – y + z = -3
-4x + 3y – 2z = 4
We have to solve these equations by using Cramer’s Rule
D = \(\left|\begin{array}{rrr}
2 & 2 & 3 \\
1 & -1 & 1 \\
-4 & 3 & -2
\end{array}\right|\)
= 2(2 – 3) – 2(-2 + 4) + 3(3 – 4)
= -2 – 4 – 3 = -9 ≠ 0

= 2(-4 + 9) – 2(4 – 12) – 1(3 – 4)
= 10 + 16 + 1 = 27

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 5 Vectors Ex 5.4

Question 1.
If \(\bar{a}\) = \(2 \hat{i}+3 \hat{j}-\hat{k}\), \(\bar{b}\) = \(\hat{i}-4 \hat{j}+2 \hat{k}\) find (\(\bar{a}\) + \(\bar{b}\)) × (\(\bar{a}\) – \(\bar{b}\))
Solution:

Question 2.
Find a unit vector perpendicular to the vectors \(\hat{j}+2 \hat{k}\) and \(\hat{i}+\hat{j}\).
Solution:
Let \(\bar{a}\) = \(\hat{j}+2 \hat{k}\), \(\bar{b}\) = \(\hat{i}+\hat{j}\)

Question 3.
If \(\bar{a} \cdot \bar{b}\) = \(\sqrt {3}\) and \(\bar{a} \times \bar{b}\) = \(2 \hat{i}+\hat{j}+2 \hat{k}\), find the angle between \(\bar{a}\) and \(\bar{b}\).
Solution:
Let θ be the angle between \(\bar{a}\) and \(\bar{b}\)

∴ θ = 60°.

Question 4.
If \(\bar{a}\) = \(2 \hat{i}+\hat{j}-3 \hat{k}\) and \(\bar{b}\) = \(\hat{i}-2 \hat{j}+\hat{k}\), find a vector of magnitude 5 perpendicular to both \(\bar{a}\) and \(\bar{b}\).
Solution:
Given : \(\bar{a}\) = \(2 \hat{i}+\hat{j}-3 \hat{k}\) and \(\bar{b}\) = \(\hat{i}-2 \hat{j}+\hat{k}\)

∴ unit vectors perpendicular to both the vectors \(\bar{a}\) and \(\bar{b}\).

∴ required vectors of magnitude 5 units
= ±\(\frac{5}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\)

Question 5.
Find
(i) \(\bar{u}\)∙\(\bar{v}\) if \(|\bar{u}|\) = 2, \(|\vec{v}|\) = 5, \(|\bar{u} \times \bar{v}|\) = 8
Solution:
Let θ be the angle between \(\bar{u}\) and \(\bar{v}\).
Then \(|\bar{u} \times \bar{v}|\) = 8 gives
\(|\bar{u}||\bar{v}|\) sin θ = 8
∴ 2 × 5 × sin θ = 8

(ii) \(|\bar{u} \times \bar{v}|\) if \(|\bar{u}|\) = 10, \(|\vec{v}|\) = 2, \(\bar{u} \cdot \bar{v}\) = 12
Solution:
Let θ be the angle between \(\bar{u}\) and \(\bar{v}\).
Then \(\bar{u} \cdot \bar{v}\) = 12 gives
\(|\bar{u} \| \bar{v}|\)cos θ = 12
∴ 10 × 2 × cos θ = 12

Question 6.
Prove that 2(\(\bar{a}\) – \(\bar{b}\)) × 2(\(\bar{a}\) + \(\bar{b}\)) = 8(\(\bar{a}\) × \(\bar{b}\))
Solution:

Question 7.
If \(\bar{a}\) = \(\hat{i}-2 \hat{j}+3 \hat{k}\), \(\bar{b}\) = \(4 \hat{i}-3 \hat{j}+\hat{k}\), and \(\bar{c}\) = \(\hat{i}-\hat{j}+2 \hat{k}\), verify that \(\bar{a}\) × (\(\bar{b}\) + \(\bar{c}\)) = \(\bar{a}\) × \(\bar{b}\) + \(\bar{a}\) × \(\bar{c}\)
Solution:
Given : \(\bar{a}\) = \(\hat{i}-2 \hat{j}+3 \hat{k}\), \(\bar{b}\) = \(4 \hat{i}-3 \hat{j}+\hat{k}\), \(\bar{c}\) = \(\hat{i}-\hat{j}+2 \hat{k}\)

Question 8.
Find the area of the parallelogram whose adjacent sides are the vectors \(\bar{a}\) = \(2 \hat{i}-2 \hat{j}+\hat{k}\) and \(\bar{b}\) = \(\hat{i}-3 \hat{j}-3 \hat{k}\).
Solution:
Given : \(\bar{a}\) = \(2 \hat{i}-2 \hat{j}+\hat{k}\), \(\bar{b}\) = \(\hat{i}-3 \hat{j}-3 \hat{k}\)

Area of the parallelogram whose adjacent sides are \(\bar{a}\) and \(\bar{b}\) is \(|\bar{a} \times \bar{b}|\) =\(\sqrt {146}\) sq units.

Question 9.
Show that vector area of a quadrilateral ABCD is \(\frac{1}{2}\) (\(\overline{A C}\) × \(\overline{B D}\)), where AC and BD are its diagonals.
Solution:
Let ABCD be a parallelogram.
Then \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{BC}}\)

Question 10.
Find the area of parallelogram whose diagonals are determined by the vectors \(\bar{a}\) = \(3 i-\hat{j}-2 \hat{k}\), and \(\bar{b}\) = \(-\hat{i}+3 \hat{j}-3 \hat{k}\)
Solution:
Given: \(\bar{a}\) = \(3 i-\hat{j}-2 \hat{k}\), \(\bar{b}\) = \(-\hat{i}+3 \hat{j}-3 \hat{k}\)

Question 11.
If \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) are four distinct vectors such that \(\bar{a} \times \bar{b}=\bar{c} \times \bar{d}\) and \(\bar{a} \times \bar{c}=\bar{b} \times \bar{d}\), prove that \(\bar{a}\) – \(\bar{d}\) is parallel to \(\bar{b}\) – \(\bar{c}\).
Solution:
\(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) are four distinct vectors

Question 12.
If \(\bar{a}\) = \(\hat{i}+\hat{j}+\hat{k}\) and, \(\bar{c}\) = \(\hat{j}-\hat{k}\), find a vector \(\bar{b}\) satisfying \(\bar{a}\) × \(\bar{b}\) = \(\bar{c}\) and \(\bar{a} \cdot \bar{b}\) = 3
Solution:
Given \(\bar{a}\) = \(\hat{i}+\hat{j}+\hat{k}\), \(\bar{c}\) = \(\hat{j}-\hat{k}\)

By equality of vectors,
z – y = 0 ….(2)
x – z = 1 ……(3)
y – x = -1 ……(4)
From (2), y = z.
From (3), x = 1 + z
Substituting these values of x and y in (1), we get
1 + z + z + z = 3 ∴ z = \(\frac{2}{3}\)
∴ y = z = \(\frac{2}{3}\)
∴ x = 1 + z =1 + \(\frac{2}{3}=\frac{5}{3}\)

Question 13.
Find \(\bar{a}\), if \(\bar{a} \times \hat{i}+2 \bar{a}-5 \hat{j}=\overline{0}\).
Solution:

By equality of vectors
2x = 0 i.e. x = 0
2y + z – 5 = 0 … (1)
2z – y = 0 … (2)
From (2), y = 2z
Substituting y = 2z in (1), we get
4z + z = 5 ∴ z = 1
∴ y = 2z = 2(1) = 2
∴ x = 0, y = 2, z = 1
∴ \(\bar{a}=2 \hat{j}+\hat{k}\)

Question 14.
If \(|\bar{a} \cdot \bar{b}|\) = \(|\bar{a} \times \bar{b}|\) and \(\bar{a} \cdot \bar{b}\) < 0, then find the angle between \(\bar{a}\) and \(\bar{b}\)
Solution:
Let θ be the angle between \(\bar{a}\) and \(\bar{b}\).
Then \(|\bar{a} \cdot \bar{b}|\) = \(|\bar{a} \times \bar{b}|\) gives

Hence, the angle between \(\bar{a}\) and \(\bar{b}\) is \(\frac{3 \pi}{4}\).

Question 15.
Prove by vector method that sin (α + β) = sinα∙cosβ+cosα∙sinβ.
Solution:

Let ∠XOP and ∠XOQ be in standard position and m∠XOP = -α, m∠XOQ = β.
Take a point A on ray OP and a point B on ray OQ such that
OA = OB = 1.
Since cos (-α) = cos α
and sin (-α) = -sin α,
A is (cos (-α), sin (-α)),
i.e. (cos α, – sin α)
B is (cos β, sin β)

The angle between \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) is α + β.
Also \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) lie in the XY-plane.
∴ the unit vector perpendicular to \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) is \(\bar{k}\).
∴ \(\overline{\mathrm{OA}}\) × \(\overline{\mathrm{OB}}\) = [OA∙OB sin (α + β)]\(\bar{k}\)
= sin(α + β)∙\(\bar{k}\) …(2)
∴ from (1) and (2),
sin (α + β) = sin α cos β + cos α sin β.

Question 16.
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are
(i) -2, 1, -1 and -3, -4, 1
Solution:
Let a, b, c be the direction ratios of the vector which is perpendicular to the two lines whose direction ratios are -2, 1, -1 and -3, -4, 1
∴ -2a + b – c = 0 and -3a – 4b + c = 0

∴ the required direction ratios are -3, 5, 11
Alternative Method:
Let \(\bar{a}\) and \(\bar{b}\) be the vectors along the lines whose direction ratios are -2, 1, -1 and -3, -4, 1 respectively.
Then \(\bar{a}\) = \(-2 \hat{i}+\hat{j}-\hat{k}\) and \(\bar{b}\) = \(-3 \hat{i}-4 \hat{j}+\hat{k}\)
The vector perpendicular to both \(\bar{a}\) and \(\bar{b}\) is given by

Hence, the required direction ratios are -3, 5, 11.

(ii) 1, 3, 2 and -1, 1, 2
Solution:

Question 17.
Prove that two vectors whose direction cosines are given by relations al + bm + cn = 0 and fmn + gnl + hlm = 0 are perpendicular if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\) = 0
Solution:
Given, al + bm + cn = 0 …(1)
and fmn + gnl + hlm = 0 …..(2)
From (1), n = \(-\left(\frac{a l+b m}{c}\right)\) …..(3)
Substituting this value of n in equation (2), we get
(fm + gl)∙[latex]-\left(\frac{a l+b m}{c}\right)[/latex] + hlm = 0
∴ -(aflm + bfm² + agl² + bglm) + chlm = 0
∴ agl² + (af + bg – ch)lm + bfm² = 0 … (4)
Note that both l and m cannot be zero, because if l = m = 0, then from (3), we get
n = 0, which is not possible as l² + m² + n² = 1.
Let us take m # 0.
Dividing equation (4) by m², we get
ag\(\left(\frac{l}{m}\right)^{2}\) + (af + bg – ch)\(\left(\frac{l}{m}\right)\) + bf = 0 … (5)
This is quadratic equation in \(\left(\frac{l}{m}\right)\).
If l₁, m₁, n₁ and l₂, m₂, n₂ are the direction cosines of the two lines given by the equation (1) and (2), then \(\frac{l_{1}}{m_{1}}\) and \(\frac{l_{2}}{m_{2}}\) are the roots of the equation (5).
From the quadratic equation (5), we get

i.e. if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\) = 0.

Question 18.
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and point A.
Solution:

Let M be the foot of the perpendicular drawn from B to the line joining O and A.
Let M = (x, y, z)
OM has direction ratios x – 0, y – 0, z – 0 = x, y, z
OA has direction ratios 1 – 0, 2 – 0, 3 – 0 = 1, 2, 3
But O, M, A are collinear.
∴ \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) = k …(Let)
∴ x = k, y = 2k, z = 3k
∴ M = (k, 2k, 3k)
∵ BM has direction ratios
k – 4, 2k – 5, 3k – 6
BM is perpendicular to OA
∴ (l)(k – 4) + 2(2k – 5) + 3(3k – 6)
∴ = k – 4 + 4k – 10 + 9k – 18 = 0
∴ 14k = 32
∴ k = \(\frac{16}{7}\)
∴ M = (k, 2k, 3k) = (\(\frac{16}{7}, \frac{32}{7}, \frac{48}{7}\))

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.4

Question 1.
Maximize : z = 11x + 8y subject to x ≤ 4, y ≤ 6,
x + y ≤ 6, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and ED whose equations are x = 4, y = 6 and x + y = 6 respectively.


The feasible region is shaded portion OAPDO in the graph.
The vertices of the feasible region are O (0, 0), A (4, 0), P and D (0, 6)
P is point of intersection of lines x + y = 6 and x = 4.
Substituting x = 4 in x + y = 6, we get
4 + y = 6 ∴ y = 2 ∴ P is (4, 2).
∴ the corner points of feasible region are O (0, 0), A (4, 0), P(4, 2) and D(0 ,6).
The values of the objective function z = 11x + 8y at these vertices are
z (O) = 11(0) + 8(0) = 0 + 0 = 0
z(a) = 11(4) + 8(0) = 44 + 0 = 44
z (P) = 11(4) + 8(2) = 44 + 16 = 60
z (D) = 11(0) + 8(2) = 0 + 16 = 16
∴ z has maximum value 60, when x = 4 and y = 2.

Question 2.
Maximize : z = 4x + 6y subject to 3x + 2y ≤ 12,
x + y ≥ 4, x, y ≥ 0.
Solution:
First we draw the lines AB and AC whose equations are 3x + 2y = 12 and x + y = 4 respectively.


The feasible region is the ∆ABC which is shaded in the graph.
The vertices of the feasible region (i.e. corner points) are A (4, 0), B (0, 6) and C (0, 4).
The values of the objective function z = 4x + 6y at these vertices are
z(a) = 4(4) + 6(0) = 16 + 0 = 16
z(B) = 4(0)+ 6(6) = 0 + 36 = 36
z(C) = 4(0) + 6(4) = 0 + 24 = 24
∴ has maximum value 36, when x = 0, y = 6.

Question 3.
Maximize : z = 7x + 11y subject to 3x + 5y ≤ 26
5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 3x + 5y = 26 and 5x + 3y = 30 respectively.


The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (6, 0), p and B(0, \(\frac{26}{5}\))
The vertex P is the point of intersection of the lines
3x + 5y = 26 … (1)
and 5x + 3y = 30 … (2)
Multiplying equation (1) by 3 and equation (2) by 5, we get
9x + 15y = 78
and 25x + 15y = 150
On subtracting, we get
16x = 72 ∴ x = \(\frac{72}{16}=\frac{9}{2}\) = 4.5
Substituting x = 4.5 in equation (2), we get
5(4.5) + 3y = 30
22.5 + 3y = 30
∴ 3y = 7.5 ∴ y = 2.5
∴ P is (4.5, 2.5)
The values of the objective function z = 7x + 11y at these corner points are
z (O) = 7(0) + 11(0) = 0 + 0 = 0
z (C) = 7(6) + 11(0) = 42 + 0 = 42
z (P) = 7(4.5) + 11 (2.5) = 31.5 + 27.5 = 59.0 = 59
z(B) = 7(0) + 11\(\left(\frac{26}{5}\right)=\frac{286}{5}\) = 57.2
∴ z has maximum value 59, when x = 4.5 and y = 2.5.

Question 4.
Maximize : z = 10x + 25y subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3, x + y ≤ 5 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x = 3, y = 3 and x + y = 5 respectively.


The feasible region is OAPQDO which is shaded in the i graph.
The vertices of the feasible region are O (0, 0), A (3, 0), P, Q and D(0, 3).
t P is the point of intersection of the lines x + y = 5 and x = 3.
Substituting x = 3 in x + y = 5, we get
3 + y = 5 ∴ y = 2
∴ P is (3, 2)
Q is the point of intersection of the lines x + y = 5 and y = 3
Substituting y = 3 in x + y = 5, we get
x + 3 = 5 ∴ x = 2
∴ Q is (2, 3)
The values of the objective function z = 10x + 25y at these vertices are
z(O) = 10(0) + 25(0) = 0 + 0 = 0
z(a) = 10(3) + 25(0) = 30 + 0 = 30
z(P) = 10(3) + 25(2) = 30 + 50 = 80
z(Q) = 10(2) + 25(3) = 20 + 75 = 95
z(D) = 10(0)+ 25(3) = 0 + 75 = 75
∴ z has maximum value 95, when x = 2 and y = 3.

Question 5.
Maximize : z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21,
x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.


The feasible region is OCPQBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (7, 0), P, Q and B (0, 6).
P is the point of intersection of the lines
3x + y = 21 … (1)
and x + y = 9 … (2)
On subtracting, we get 2x = 12 ∴ x = 6
Substituting x = 6 in equation (2), we get
6 + y = 9 ∴ y = 3
∴ P = (6, 3)
Q is the point of intersection of the lines
x + 4y = 24 … (3)
and x + y = 9 … (2)
On subtracting, we get
3y = 15 ∴ y = 5
Substituting y = 5 in equation (2), we get
x + 5= 9 ∴ x = 4
∴ Q = (4, 5)
∴ the corner points of the feasible region are 0(0,0), C(7, 0), P (6, 3), Q (4, 5) and B (0, 6).
The values of the objective function 2 = 3x + 5y at these corner points are
z(O) = 3(0)+ 5(0) = 0 + 0 = 0
z(C) = 3(7) + 5(0) = 21 + 0 = 21
z(P) = 3(6) + 5(3) = 18 + 15 = 33
z(Q) = 3(4) + 5(5) = 12 + 25 = 37
z(B) = 3(0)+ 5(6) = 0 + 30 = 30
∴ z has maximum value 37, when x = 4 and y = 5.

Question 6.
Minimize : z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3,
x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 5x + y = 5 and x + y = 3 respectively.


The feasible region is XCPBY which is shaded in the graph.
The vertices of the feasible region are C (3, 0), P and B (0, 5).
P is the point of the intersection of the lines
5x + y = 5
and x + y = 3
On subtracting, we get
4x = 2 ∴ x = \(\frac{1}{2}\)
Substituting x = \(\frac{1}{2}\) in x + y = 3, we get
\(\frac{1}{2}\) + y = 3
∴ y = \(\frac{5}{2}\) ∴ P = \(\left(\frac{1}{2}, \frac{5}{2}\right)\)
The values of the objective function z = 7x + y at these vertices are
z(C) = 7(3) + 0 = 21
z(B) = 7(0) + 5 = 5
∴ z has minimum value 5, when x = 0 and y = 5.

Question 7.
Minimize : z = 8x + 10y subject to 2x + y ≥ 7, 2x + 3y ≥ 15,
y ≥ 2, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are 2x + y = 7, 2x + 3y = 15 and y = 2 respectively.


The feasible region is EPQBY which is shaded in the graph. The vertices of the feasible region are P, Q and B(0,7). P is the point of intersection of the lines 2x + 3y = 15 and y = 2.
Substituting y – 2 in 2x + 3y = 15, we get 2x + 3(2) = 15
∴ 2x = 9 ∴ x = 4.5 ∴ P = (4.5, 2)
Q is the point of intersection of the lines
2x + 3y = 15 … (1)
and 2x + y = 7 … (2)
On subtracting, we get
2y = 8 ∴ y = 4
∴ from (2), 2x + 4 = 7
∴ 2x = 3 ∴ x = 1.5
∴ Q = (1.5, 4)
The values of the objective function z = 8x + 10y at these vertices are
z(P) = 8(4.5) + 10(2) = 36 + 20 = 56
z(Q) = 8(1.5) + 10(4) = 12 + 40 = 52
z(B) = 8(0) +10(7) = 70
∴ z has minimum value 52, when x = 1.5 and y = 4

Question 8.
Minimize : z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4,
3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 2y = 3, x + 4y = 4 and 3x + y = 3 respectively.


The feasible region is XCPQFY which is shaded in the graph.
The vertices of the feasible region are C (4, 0), P, Q and F(0, 3).
P is the point of intersection of the lines x + 4y = 4 and x + 2y = 3
On subtracting, we get
2y = 1 ∴ y = \(\frac{1}{2}\)
Substituting y = \(\frac{1}{2}\) in x + 2y = 3, we get
x + 2\(\left(\frac{1}{2}\right)\) = 3
∴ x = 2
∴ P = (2, \(\frac{1}{2}\))
Q is the point of intersection of the lines
x + 2y = 3 … (1)
and 3x + y = 3 ….(2)
Multiplying equation (1) by 3, we get 3x + 6y = 9
Subtracting equation (2) from this equation, we get
5y = 6
∴ y = \(\frac{6}{5}\)
∴ from (1), x + 2\(\left(\frac{6}{5}\right)\) = 3
∴ x = 3 – \(\frac{12}{5}=\frac{3}{5}\)
Q ≡ \(\left(\frac{3}{5}, \frac{6}{5}\right)\)
The values of the objective function z = 6x + 21y at these vertices are
z(C) = 6(4) + 21(0) = 24
z(P) = 6(2) + 21\(\left(\frac{1}{2}\right)\)
= 12 + 10.5 = 22.5
z(Q)= 6\(\left(\frac{3}{5}\right)\) + 21\(\left(\frac{6}{5}\right)\)
= \(\frac{18}{5}+\frac{126}{5}=\frac{144}{5}\) = 28.8
2 (F) = 6(0) + 21(3) = 63
∴ z has minimum value 22.5, when x = 2 and y = \(\frac{1}{2}\).

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4

I : Choose correct alternatives.
Question 1.
If the equation 4x² + hxy + y² = 0 represents two coincident lines, then h = _________.
(A) ± 2
(B) ± 3
(C) ± 4
(D) ± 5
Solution:
(C) ± 4

Question 2.
If the lines represented by kx² – 3xy + 6y² = 0 are perpendicular to each other then _________.
(A) k = 6
(B) k = -6
(C) k = 3
(D) k = -3
Solution:
(B) k = -6

Question 3.
Auxiliary equation of 2x² + 3xy – 9y² = 0 is _________.
(A) 2m² + 3m – 9 = 0
(B) 9m² – 3m – 2 = 0
(C) 2m² – 3m + 9 = 0
(D) -9m² – 3m + 2 = 0
Solution:
(B) 9m² – 3m – 2 = 0

Question 4.
The difference between the slopes of the lines represented by 3x² – 4xy + y² = 0 is _________.
(A) 2
(B) 1
(C) 3
(D) 4
Solution:
(A) 2

Question 5.
If the two lines ax² +2hxy+ by² = 0 make angles α and β with X-axis, then tan (α + β) = _____.
(A) \(\frac{h}{a+b}\)
(B) \(\frac{h}{a-b}\)
(C) \(\frac{2 h}{a+b}\)
(D) \(\frac{2 h}{a-b}\)
Solution:
(D) \(\frac{2 h}{a-b}\)

Question 6.
If the slope of one of the two lines \(\frac{x^{2}}{a}+\frac{2 x y}{h}+\frac{y^{2}}{b}\) = 0 is twice that of the other, then ab:h² = ___.
(A) 1 : 2
(B) 2 : 1
(C) 8 : 9
(D) 9 : 8
Solution:
(D) 9 : 8

Question 7.
The joint equation of the lines through the origin and perpendicular to the pair of lines 3x² + 4xy – 5y² = 0 is _________.
(A) 5x² + 4xy – 3y² = 0
(B) 3x² + 4xy – 5y² = 0
(C) 3x² – 4xy + 5y² = 0
(D) 5x² + 4xy + 3y² = 0
Solution:
(A) 5x² + 4xy – 3y² = 0

Question 8.
If acute angle between lines ax² + 2hxy + by² = 0 is, \(\frac{\pi}{4}\) then 4h² = _________.
(A) a² + 4ab + b²
(B) a² + 6ab + b²
(C) (a + 2b)(a + 3b)
(D) (a – 2b)(2a + b)
Solution:
(B) a² + 6ab + b²

Question 9.
If the equation 3x² – 8xy + qy² + 2x + 14y + p = 1 represents a pair of perpendicular lines then
the values of p and q are respectively _________.
(A) -3 and -7
(B) -7 and -3
(C) 3 and 7
(D) -7 and 3
Solution:
(B) -7 and -3

Question 10.
The area of triangle formed by the lines x² + 4xy + y² = 0 and x – y – 4 = 0 is _________.
(A) \(\frac{4}{\sqrt{3}}\) Sq. units
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
(C) \(\frac{16}{\sqrt{3}}\) Sq. units
(D)\(\frac{15}{\sqrt{3}}\) Sq. units
Solution:
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
[Hint : Area = \(\frac{p^{2}}{\sqrt{3}}\), where p is the length of perpendicular from the origin to x – y – 4 = 0]

Question 11.
The combined equation of the co-ordinate axes is _________.
(A) x + y = 0
(B) x y = k
(C) xy = 0
(D) x – y = k
Solution:
(C) xy = 0

Question 12.
If h² = ab, then slope of lines ax² + 2hxy + by² = 0 are in the ratio _________.
(A) 1 : 2
(B) 2 : 1
(C) 2 : 3
(D) 1 : 1
Solution:
(D) 1 : 1
[Hint: If h² = ab, then lines are coincident. Therefore slopes of the lines are equal.]

Question 13.
If slope of one of the lines ax² + 2hxy + by² = 0 is 5 times the slope of the other, then 5h² = _________.
(A) ab
(B) 2 ab
(C) 7 ab
(D) 9 ab
Solution:
(D) 9 ab

Question 14.
If distance between lines (x – 2y)² + k(x – 2y) = 0 is 3 units, then k =
(A) ± 3
(B) ± 5\(\sqrt {5}\)
(C) 0
(D) ± 3\(\sqrt {5}\)
Solution:
(D) ± 3\(\sqrt {5}\)
[Hint: (x – 2y)² + k(x – 2y) = 0
∴ (x – 2y)(x – 2y + k) = 0
∴ equations of the lines are x – 2y = 0 and x – 2y + k = 0 which are parallel to each other.
∴ \(\left|\frac{k-0}{\sqrt{1+4}}\right|\) = 3
∴ k = ± 3\(\sqrt {5}\)

II. Solve the following.
Question 1.
Find the joint equation of lines:
(i) x – y = 0 and x + y = 0
Solution:
The joint equation of the lines x – y = 0 and
x + y = 0 is
(x – y)(x + y) = 0
∴ x² – y² = 0.

(ii) x + y – 3 = 0 and 2x + y – 1 = 0
Solution:
The joint equation of the lines x + y – 3 = 0 and 2x + y – 1 = 0 is
(x + y – 3)(2x + y – 1) = 0
∴ 2x² + xy – x + 2xy + y² – y – 6x – 3y + 3 = 0
∴ 2x² + 3xy + y² – 7x – 4y + 3 = 0.

(iii) Passing through the origin and having slopes 2 and 3.
Solution:
We know that the equation of the line passing through the origin and having slope m is y = mx. Equations of the lines passing through the origin and having slopes 2 and 3 are y = 2x and y = 3x respectively.
i.e. their equations are
2x – y = 0 and 3x – y = 0 respectively.
∴ their joint equation is (2x – y)(3x – y) = 0
∴ 6x² – 2xy – 3xy + y² = 0
∴ 6x² – 5xy + y² = 0.

(iv) Passing through the origin and having inclinations 60° and 120°.
Solution:
Slope of the line having inclination θ is tan θ .
Inclinations of the given lines are 60° and 120°
∴ their slopes are m₁ = tan60° = \(\sqrt {3}\) and
m₂ = tan 120° = tan (180° – 60°)
= -tan 60° = –\(\sqrt {3}\)
Since the lines pass through the origin, their equa-tions are
y = \(\sqrt {3}\)x and y= –\(\sqrt {3}\)x
i.e., \(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0
∴ the joint equation of these lines is
(\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ 3x² – y² = 0.

(v) Passing through (1, 2) amd parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0
∴ the equations of the lines passing through (1, 2) and parallel to the coordinate axes are x = 1 and y =1
i.e. x – 1 = 0 and y – 2 0
∴ their combined equation is
(x – 1)(y – 2) = 0
∴ x(y – 2) – 1(y – 2) = 0
∴ xy – 2x – y + 2 = 0

(vi) Passing through (3, 2) and parallel to the line x = 2 and y = 3.
Solution:
Equations of the lines passing through (3, 2) and parallel to the lines x = 2 and y = 3 are x = 3 and y = 2.
i.e. x – 3 = 0 and y – 2 = 0
∴ their joint equation is
(x – 3)(y – 2) = 0
∴ xy – 2x – 3y + 6 = 0.

(vii) Passing through (-1, 2) and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 respectively.
Slopes of the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 are \(-\frac{1}{2}\) and \(-\frac{3}{-4}=\frac{3}{4}\) respectively.
∴ slopes of the lines L₁and L₂ are 2 and \(\frac{-4}{3}\) respectively.
Since the lines L₁ and L₂ pass through the point (-1, 2), their equations are
∴ (y – y₁) = m(x – x₁)
∴ (y – 2) = 2(x + 1)
⇒ y – 1 = 2x + 2
⇒ 2x – y + 4 = 0 and
∴ (y – 2) = \(\left(\frac{-4}{3}\right)\)(x + 1)
⇒ 3y – 6 = (-4)(x + 1)
⇒ 3y – 6 = -4x + 4
⇒ 4x + 3y – 6 + 4 = 0
⇒ 4x + 3y – 2 = 0
their combined equation is
∴ (2x – y + 4)(4x + 3y – 2) = 0
∴ 8x² + 6xy – 4x – 4xy – 3y² + 2y + 16x + 12y – 8 = 0
∴ 8x² + 2xy + 12x – 3y² + 14y – 8 = 0

(viii) Passing through the origin and having slopes 1 + \(\sqrt {3}\) and 1 – \(\sqrt {3}\)
Solution:
Let l₁ and l₂ be the two lines. Slopes of l₁ is 1 + \(\sqrt {3}\) and that of l₂ is 1 – \(\sqrt {3}\)
Therefore the equation of a line (l₁) passing through the origin and having slope is
y = (1 + \(\sqrt {3}\))x
∴ (1 + \(\sqrt {3}\))x – y = 0 ..(1)
Similarly, the equation of the line (l₂) passing through the origin and having slope is
y = (1 – \(\sqrt {3}\))x
∴ (1 – \(\sqrt {3}\))x – y = 0 …(2)
From (1) and (2) the required combined equation is

∴ (1 – 3)x² – 2xy + y² = 0
∴ -2x² – 2xy + y² = 0
∴ 2x² + 2xy – y² = 0
This is the required combined equation.

(ix) Which are at a distance of 9 units from the Y – axis.
Solution:
Equations of the lines, which are parallel to the Y-axis and at a distance of 9 units from it, are x = 9 and x = -9
i.e. x – 9 = 0 and x + 9 = 0

∴ their combined equation is
(x – 9)(x + 9) = 0
∴ x² – 81 = 0.

(x) Passing through the point (3, 2), one of which is parallel to the line x – 2y = 2 and other is perpendicular to the line y = 3.
Solution:
Let L₁ be the line passes through (3, 2) and parallel to the line x – 2y = 2 whose slope is \(\frac{-1}{-2}=\frac{1}{2}\)
∴ slope of the line L₁ is \(\frac{1}{2}\).
∴ equation of the line L₁ is
y – 2 = \(\frac{1}{2}\)(x – 3)
∴ 2y – 4 = x – 3 ∴ x – 2y + 1 = 0
Let L₂ be the line passes through (3, 2) and perpendicular to the line y = 3.
∴ equation of the line L₂ is of the form x = a.
Since L₂ passes through (3, 2), 3 = a
∴ equation of the line L₂ is x = 3, i.e. x – 3 = 0
Hence, the equations of the required lines are
x – 2y + 1 = 0 and x – 3 = 0
∴ their joint equation is
(x – 2y + 1)(x – 3) = 0
∴ x² – 2xy + x – 3x + 6y – 3 = 0
∴ x² – 2xy – 2x + 6y – 3 = 0.

(xi) Passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18 respectively.
Slopes of the lines x + 2y = 19 and 3x + y = 18 are \(-\frac{1}{2}\) and \(-\frac{3}{1}\) = -3 respectively.
Since the lines L₁ and L₂ pass through the origin, their equations are
y = 2x and y = \(\frac{1}{3}\)x
i.e. 2x – y = 0 and x – 3y = 0
∴ their combined equation is
(2x – y)(x – 3y) = 0
∴ 2x² – 6xy – xy + 3y² = 0
∴ 2x² – 7xy + 3y² = 0.

Question 2.
Show that each of the following equation represents a pair of lines.
(i) x² + 2xy – y² = 0
Solution:
Comparing the equation x² + 2xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 2, i.e. h = 1 and b = -1
∴ h² – ab = (1)² – 1(-1) = 1 + 1=2 > 0
Since the equation x² + 2xy – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(ii) 4x² + 4xy + y² = 0
Solution:
Comparing the equation 4x² + 4xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 4, i.e. h = 2 and b = 1
∴ h² – ab = (2)² – 4(1) = 4 – 4 = 0
Since the equation 4x² + 4xy + y² = 0 is a homogeneous equation of second degree and h² – ab = 0, the given equation represents a pair of lines which are real and coincident.

(iii) x² – y² = 0
Solution:
Comparing the equation x² – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 0, i.e. h = 0 and b = -1
∴ h² – ab = (0)² – 1(-1) = 0 + 1 = 1 > 0
Since the equation x² – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(iv) x² + 7xy – 2y² = 0
Solution:
Comparing the equation x² + 7xy – 2y² = 0
a = 1, 2h = 7 i.e., h = \(\frac{7}{2}\) and b = -2
∴ h² – ab = \(\left(\frac{7}{2}\right)^{2}\) – 1(-2)
= \(\frac{49}{4}\) + 2
= \(\frac{57}{4}\) i.e. 14.25 = 14 > 0
Since the equation x² + 7xy – 2y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(v) x² – 2\(\sqrt {3}\) xy – y² = 0
Solution:
Comparing the equation x² – 2\(\sqrt {3}\) xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h= -2\(\sqrt {3}\), i.e. h = –\(\sqrt {3}\) and b = 1
∴ h² – ab = (-\(\sqrt {3}\))² – 1(1) = 3 – 1 = 2 > 0
Since the equation x² – 2\(\sqrt {3}\)xy – y² = 0 is a homo¬geneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

Question 3.
Find the separate equations of lines represented by the following equations:
(i) 6x² – 5xy – 6y² = 0
Solution:
6x² – 5xy – 6y² = 0
∴ 6x² – 9xy + 4xy – 6y² = 0
∴ 3x(2x – 3y) + 2y(2x – 3y) = 0
∴ (2x – 3y)(3x + 2y) = 0
∴ the separate equations of the lines are
2x – 3y = 0 and 3x + 2y = 0.

(ii) x² – 4y² = 0
Solution:
x² – 4y² = 0
∴ x² – (2y)² = 0
∴(x – 2y)(x + 2y) = 0
∴ the separate equations of the lines are
x – 2y = 0 and x + 2y = 0.

(iii) 3x² – y² = 0
Solution:
3x² – y² = 0
∴ (\(\sqrt {3}\) x)² – y² = 0
∴ (\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ the separate equations of the lines are
\(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0.

(iv) 2x² + 2xy – y² = 0
Solution:
2x² + 2xy – y² = 0
∴ The auxiliary equation is -m² + 2m + 2 = 0
∴ m² – 2m – 2 = 0

m₁ = 1 + \(\sqrt {3}\) and m₂ = 1 – \(\sqrt {3}\) are the slopes of the lines.
∴ their separate equations are
y = m₁x and y = m₂x
i.e. y = (1 + \(\sqrt {3}\))x and y = (1 – \(\sqrt {3}\))x
i.e. (\(\sqrt {3}\) + 1)x – y = 0 and (\(\sqrt {3}\) – 1)x + y = 0.

Question 4.
Find the joint equation of the pair of lines through the origin and perpendicular to the lines
given by :
(i) x² + 4xy – 5y² = 0
Solution:
Comparing the equation x² + 4xy – 5y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 4, b= -5
Let m₁ and m₂ be the slopes of the lines represented by x² + 4xy – 5y² = 0.

Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\frac{4}{5}\)xy – \(\frac{1}{5}\)y² = 0 …[By (1)]
∴ 5x² + 4xy – y² = 0

(ii) 2x² – 3xy – 9y² = 0
Solution:
Comparing the equation 2x² – 3xy – 9y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 2, 2h = -3, b = -9
Let m₁ and m₂ be the slopes of the lines represented by 2x² – 3xy – 9y² = 0
∴ m₁ + m₂ =\(\frac{-2 h}{b}=-\frac{3}{9}\) and m₁m₂ = \(\frac{a}{b}=-\frac{2}{9}\) …(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\left(-\frac{3}{9}\right)\)xy + \(\left(-\frac{2}{9}\right)\)y² = 0 …[By (1)]
∴ 9x² – 3xy – 2y² = 0

(iii) x² + xy – y² = 0
Solution:
Comparing the equation x²+ xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 1, b = -1
Let m₁ and m₂ be the slopes of the lines represented by x² + xy – y² = 0
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-1}{-1}\) and m₁m₂ = \(\frac{\mathrm{a}}{\mathrm{b}}=\frac{1}{-1}\) = -1 ..(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂) + m₁m₂y² = 0
∴ x² + 1xy + (-1)y² = 0 …[By (1)]
∴ x² + xy – y² = 0

Question 5.
Find k if
(i) The sum of the slopes of the lines given by 3x² + kxy – y² = 0 is zero.
Solution:
Comparing the equation 3x² + kxy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 3, 2h = k, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 3x² + kxy – y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-k}{-1}\) = k
Now, m₁ + m₂ = 0 … (Given)
∴ k = 0.

(ii) The sum of slopes of the lines given by 2x² + kxy – 3y² = 0 is equal to their product.
Question is modified.
The sum of slopes of the lines given by x² + kxy – 3y² = 0 is equal to their product.
Solution:
Comparing the equation x² + kxy – 3y² = 0, with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = k, b = -3
Let m₁ and m₂ be the slopes of the lines represented by x² + kxy – 3y² = 0.
∴ m₁ + m₂ = \(-\frac{2 h}{b}=\frac{-k}{-3}=\frac{k}{3}\)
and m₁m₂ = \(\frac{a}{b}=\frac{1}{-3}=\frac{-1}{3}\)
Now, m₁ + m₂ = m₁m₂ … (Given)
∴ \(\frac{k}{3}=\frac{-1}{3}\)
∴ k = -1.

(iii) The slope of one of the lines given by 3x² – 4xy + ky² = 0 is 1.
Solution:
The auxiliary equation of the lines given by 3x² – 4xy + ky² = 0 is km² – 4m + 3 = 0.
Given, slope of one of the lines is 1.
∴ m = 1 is the root of the auxiliary equation km² – 4m + 3 = 0.
∴ k(1)² – 4(1) + 3 = 0
∴ k – 4 + 3 = 0
∴ k = 1.

(iv) One of the lines given by 3x² – kxy + 5y² = 0 is perpendicular to the 5x + 3y = 0.
Solution:
The auxiliary equation of the lines represented by 3x² – kxy + 5y² = 0 is 5m² – km + 3 = 0.
Now, one line is perpendicular to the line 5x + 3y = 0, whose slope is \(-\frac{5}{3}\).
∴ slope of that line = m = \(\frac{3}{5}\)
∴ m = \(\frac{3}{5}\) is the root of the auxiliary equation 5
5m² – km + 3 = 0.
∴ 5\(\left(\frac{3}{5}\right)^{2}\) – k\(\left(\frac{3}{5}\right)\) + 3 = 0
∴ \(\frac{9}{5}-\frac{3 k}{5}\) + 3 = 0
∴ 9 – 3k + 15 = 0
∴ 3k = 24
∴ k = 8.

(v) The slope of one of the lines given by 3x² + 4xy + ky² = 0 is three times the other.
Solution:
3x² + 4xy + ky² = 0
∴ divide by x²

∴ y = mx
∴ \(\frac{\mathrm{y}}{\mathrm{x}}\) = m
put \(\frac{\mathrm{y}}{\mathrm{x}}\) = m in equation (1)
Comparing the equation km² + 4m + 3 = 0 with ax² + 2hxy+ by² = 0, we get,
a = k, 2h = 4, b = 3
m₁ = 3m₂ ..(given condition)
m₁ + m₂ = \(\frac{-2 h}{k}=-\frac{4}{k}\)
m₁m₂ = \(\frac{a}{b}=\frac{3}{k}\)
m₁ + m₂ = \(-\frac{4}{\mathrm{k}}\)
4m₂ = \(-\frac{4}{\mathrm{k}}\) …(m₁ = 3m₂)
m₂ = \(-\frac{1}{\mathrm{k}}\)
m₁m₂ = \(\frac{3}{k}\)
\(3 \mathrm{~m}_{2}^{2}=\frac{3}{\mathrm{k}}\) …(m₁ = 3m₂)
\(3\left(-\frac{1}{\mathrm{k}}\right)^{2}=\frac{3}{\mathrm{k}}\) …(m₂ = \(-\frac{1}{k}\))
\(\frac{1}{k^{2}}=\frac{1}{k}\)
k² = k
k = 1 or k = 0

(vi) The slopes of lines given by kx² + 5xy + y² = 0 differ by 1.
Solution:
Comparing the equation kx² + 5xy +y² = 0 with ax² + 2hxy + by²
a = k, 2h = 5 i.e. h = \(\frac{5}{2}\)
m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{5}{1}\) = -5
and m₁m₂ = \(\frac{a}{b}=\frac{k}{1}\) = k
the slope of the line differ by (m₁ – m₂) = 1 …(1)
∴ (m₁ – m₂)² = (m₁ + m₂)² – 4m₁m₂
(m₁ – m₂)² = (-5)² – 4(k)
(m₁ – m₂)² = 25 – 4k
1 = 25 – 4k ..[By (1)]
4k = 24
k = 6

(vii) One of the lines given by 6x² + kxy + y² = 0 is 2x + y = 0.
Solution:
The auxiliary equation of the lines represented by 6x² + kxy + y² = 0 is
m² + km + 6 = 0.
Since one of the line is 2x + y = 0 whose slope is m = -2.
∴ m = -2 is the root of the auxiliary equation m² + km + 6 = 0.
∴ (-2)² + k(-2) + 6 = 0
∴ 4 – 2k + 6 = 0
∴ 2k = 10 ∴ k = 5

Question 6.
Find the joint equation of the pair of lines which bisect angle between the lines given by x² + 3xy + 2y² = 0
Solution:
x² + 3xy + 2y² = 0
∴ x² + 2xy + xy + 2y² = 0
∴ x(x + 2y) + y(x + 2y) = 0
∴ (x + 2y)(x + y) = 0
∴ separate equations of the lines represented by x² + 3xy + 2y² = 0 are x + 2y = 0 and x + y = 0.
Let P (x, y) be any point on one of the angle bisector. Since the points on the angle bisectors are equidistant from both the lines,

the distance of P (x, y) from the line x + 2y = 0
= the distance of P(x, y) from the line x + y = 0

∴ 2(x + 2y)² = 5(x + y)²
∴ 2(x² + 4xy + 4y²) = 5(x² + 2xy + y²)
∴ 2x² + 8xy + 8y² = 5x² + 10xy + 5y²
∴ 3x² + 2xy – 3y² = 0.
This is the required joint equation of the lines which bisect the angles between the lines represented by x² + 3xy + 2y² = 0.

Question 7.
Find the joint equation of the pair of lies through the origin and making equilateral triangle with the line x = 3.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the line x = 3.
∴ OA and OB make an angle of 30° and 150° with the positive direction of X-axis
∴ slope of OA = tan 30° = 1/\(\sqrt {3}\)
∴ equation of the line OA is y = \(\frac{1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = x ∴ x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= – tan 30°= -1/\(\sqrt {3}\)
∴ equation of the line OB is y = \(\frac{-1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = -x ∴ x + \(\sqrt {3}\)y = 0
∴ required combined equation of the lines is
(x – \(\sqrt {3}\)y) (x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

Question 8.
Show that the lines x² – 4xy + y² = 0 and x + y = 10 contain the sides of an equilateral triangle. Find the area of the triangle.
Solution:
We find the joint equation of the pair of lines OA and OB through origin, each making an angle of 60° with x + y = 10 whose slope is -1.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
Also, tan 60° = \(\left|\frac{m-(-1)}{1+m(-1)}\right|\)
∴ \(\sqrt {3}\) = \(\left|\frac{m+1}{1-m}\right|\)
Squaring both sides, we get,
3 = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ 3(1 – 2m + m²) = m² + 2m + 1
∴ 3 – 6m + 3m² = m² + 2m + 1
∴ 2m² – 8m + 2 = 0
∴ m² – 4m + 1 = 0
∴ \(\left(\frac{y}{x}\right)^{2}\) – 4\(\left(\frac{y}{x}\right)\) + 1 = 0 …[By (1)]
∴ y² – 4xy + x² = 0
∴ x² – 4xy + y\left(\frac{y}{x}\right) = 0 is the joint equation of the two lines through the origin each making an angle of 60° with x + y = 10
∴ x² – 4xy + y² = 0 and x + y = 10 form a triangle OAB which is equilateral.
Let seg OM ⊥^r line AB whose question is x + y = 10

Question 9.
If the slope of one of the lines represented by ax² + 2hxy + by² = 0 is three times the other then prove that 3h² = 4ab.
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.
∴ m₁ + m₂ = \(-\frac{2 h}{b}\) and m₁m₂ = \(\frac{a}{b}\)
We are given that m₂ = 3m₁
∴ m₁ + 3m₁ = \(-\frac{2 h}{b}\) 4m₁ = \(-\frac{2 h}{b}\)
∴ m₁ = \(-\frac{h}{2 b}\) …(1)
Also, m₁(3m₁) = \(\frac{a}{b}\) ∴ 3m₁² = \(\frac{a}{b}\)
∴ 3\(\left(-\frac{h}{2 b}\right)^{2}\) = \(\frac{a}{b}\) ….[By (1)]
∴ \(\frac{3 h^{2}}{4 b^{2}}=\frac{a}{b}\)
∴ 3h² = 4ab, as b ≠0.

Question 10.
Find the combined equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.
Solution:
Comparing the equation 5x² + 6xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 5, 2h = 6, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 5x² + 6xy – y² = 0.

The separate equations of the lines are
y = m₁x and y = m₂x, where m1 ≠ m2
i.e. m₁x – y = 0 and m₁x – y = 0.
Let P (x, y) be any point on one of the bisector of the angles between the lines.
∴ the distance of P from the line m₁x – y = 0 is equal to the distance of P from the line m₂x – y = 0.

∴ (m₂² + 1)(m₁x – y)² = (m₁² + 1)(m₂x – y)²
∴ (m₂² + 1)(m₁²x² – 2m₁xy + y²) = (m₁² + 1)(m₂²x² – 2m₂xy + y²)
∴ m₁²m₂²x² – 2m₁m₁²y²xy + m₂²y² + m₁²x² – 2m₁²xy + y²
= m₁²m₂²x² – 2m₁²m₂xy + m₁²y² + m₂²x² – 2m₂xy + y²
∴ (m₁² – m₂²)x² + 2m₁m₂(m₁ – m₂)xy – 2(m₁ – m₂)xy – (m₁² – m₂²)y² = 0
Dividing throughout by m₁ – m₂ (≠0), we get,
(m₁ + m₂)x² + 2m₁m₂xy – 2xy – (m₁ + m₂)y² = 0
∴ 6x² – 10xy – 2xy – 6y² = 0 …[By (1)]
∴ 6x² – 12xy – 6y² = 0
∴ x² – 2xy – y² = 0
This is the joint equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.

Question 11.
Find a, if the sum of the slopes of the lines represented by ax² + 8xy + 5y² = 0 is twice their product.
Solution :
Comparing the equation ax² + 8xy + 5y² = 0 with ax² + 2hxy + by² = 0,
we get, a = a, 2h = 8, b = 5
Let m₁ and m₂ be the slopes of the lines represented by ax² + 8xy + 5y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{8}{5}\)
and m₁m₂ = \(\frac{a}{b}=\frac{a}{5}\)
Now, (m₁ + m₂) = 2(m₁m₂)
\(-\frac{8}{5}\) = \(2\left(\frac{a}{5}\right)\)
a = -4

Question 12.
If the line 4x – 5y = 0 coincides with one of the lines given by ax² + 2hxy + by² = 0, then show that 25a + 40h +16b = 0.
Solution :
The auxiliary equation of the lines represented by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0
Given that 4x – 5y = 0 is one of the lines represented by ax² + 2hxy + by² = 0.
The slope of the line 4x – 5y = 0 is \(\frac{-4}{-5}=\frac{4}{5}\)
∴ m = \(\frac{4}{5}\) is a root of the auxiliary equation bm² + 2hm + a = 0.
∴ b\(\left(\frac{4}{5}\right)^{2}\) + 2h\(\left(\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}+\frac{8 h}{5}\) + a = 0
∴ 16b + 40h + 25a = 0 i.e.
∴ 25a + 40h + 16b = 0

Question 13.
Show that the following equations represent a pair of lines. Find the acute angle between them :
(i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 9, h = -3, b = 1, g = 9, f = -3 and c = 8.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
9 & -3 & 9 \\
-3 & 1 & -3 \\
9 & -3 & 8
\end{array}\right|\)
= 9(8 – 9) + 3(-24 + 27) + 9(9 – 9)
= 9(-1) + 3(3) + 9(0)
= -9 + 9 + 0 = 0
and h² – ab = (-3)² – 9(1) = 9 – 9 = 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

∴ tan θ = tan0°
∴ θ = 0°.

(ii) 2x² + xy – y² + x + 4y – 3 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy+ c = 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2 and c = -3

= -2 + 1 + 1
= -2 + 2= 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

∴ tan θ = tan 3
∴ θ = tan^-1(3)

(iii) (x – 3)² + (x – 3)(y – 4) – 2(y – 4)² = 0.
Solution :
Put x – 3 = X and y – 4 = Y in the given equation, we get,
X² + XY – 2Y² = 0
Comparing this equation with ax² + 2hxy + by² = 0, we get,
a = 1, h = \(\frac{1}{2}\), b = -2
This is the homogeneous equation of second degreeand h² – ab = \(\left(\frac{1}{2}\right)^{2}\) – 1(-2)
= \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
Hence, it represents a pair of lines passing through the new origin (3, 4).
Let θ be the acute angle between the lines.

∴ tanθ = 3 ∴ θ = tan^-1(3)

Question 14.
Find the combined equation of pair of lines through the origin each of which makes angle of 60° with the Y-axis.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

Question 15.
If lines representedby ax² + 2hxy + by² = 0 make angles of equal measures with the co-ordinate
axes then show that a = ± b.
OR
Show that, one of the lines represented by ax² + 2hxy + by² = 0 will make an angle of the same measure with the X-axis as the other makes with the Y-axis, if a = ± b.
Solution:

Let OA and OB be the two lines through the origin represented by ax² + 2hxy + by² = 0.
Since these lines make angles of equal measure with the coordinate axes, they make angles ∝ and \(\frac{\pi}{2}\) – ∝ with the positive direction of X-axis or ∝ and \(\frac{\pi}{2}\) + ∝ with thepositive direction of X-axis.
∴ slope of the line OA = m₁ = tan ∝
and slope of the line OB = m₂
= tan(\(\frac{\pi}{2}\) – ∝) or tan(\(\frac{\pi}{2}\) + ∝)
i.e. m₂ = cot ∝ or m₂ = -cot ∝
∴ m₁m₂ – tan ∝ x cot ∝ = 1
OR m₁m₂ = tan ∝ (-cot ∝) = -1
i.e. m₁m₂ = ± 1
But m₁m₂ = \(\frac{a}{b}\)
∴ \(\frac{a}{b}\)= ±1 ∴ a = ±b
This is the required condition.

Question 16.
Show that the combined equation of a pair of lines through the origin and each making an angle of ∝ with the line x + y = 0 is x² + 2(sec 2∝) xy + y² = 0.
Solution:
Let OA and OB be the required lines.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
It makes an angle ∝ with x + y = 0 whose slope is -1. m +1
∴ tan ∝ = \(\left|\frac{m+1}{1+m(-1)}\right|\)
Squaring both sides, we get,
tan²∝ = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ tan²∝(1 – 2m + m²) = m² + 2m + 1
∴ tan²∝ – 2m tan²∝ + m²tan²∝ = m² + 2m + 1
∴ (tan²∝ – 1)m² – 2(1 + tan²∝)m + (tan²∝ – 1) = 0

∴ y² + 2xysec2∝ + x² = 0
∴ x² + 2(sec2∝)xy + y² = 0 is the required equation.

Question 17.
Show that the line 3x + 4y+ 5 = 0 and the lines (3x + 4y)² – 3(4x – 3y)² =0 form an equilateral triangle.
Solution:
The slope of the line 3x + 4y + 5 = 0 is \(\frac{-3}{4}\)
Let m be the slope of one of the line making an angle of 60° with the line 3x + 4y + 5 = 0. The angle between the lines having slope m and m₁ is 60°.

On squaring both sides, we get,
3 = \(\frac{(4 m+3)^{2}}{(4-3 m)^{2}}\)
∴ 3 (4 – 3m)² = (4m + 3)²
∴ 3(16 – 24m + 9m²) = 16m² + 24m + 9
∴ 48 – 72m + 27m² = 16m² + 24m + 9
∴ 11m² – 96m + 39 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
11\(\left(\frac{y}{x}\right)^{2}\) – 96\(\left(\frac{y}{x}\right)\) + 39 = 0
∴ \(\frac{11 y^{2}}{x^{2}}-\frac{96 y}{x}\) + 39 = 0
∴ 11y² – 96xy + 39x² = 0
∴ 39x² – 96xy + 11y² = 0.
∴ 39x² – 96xy + 11y² = 0 is the joint equation of the two lines through the origin each making an angle of 60° with the line 3x + 4y + 5 = 0.
The equation 39x² – 96xy + 11y² = 0 can be written as :
-39x² + 96xy – 11y² = 0
i.e., (9x² – 48x²) + (24xy + 72xy) + (16y² – 27y²) = 0
i.e. (9x² + 24xy + 16y²) – (48x² – 72xy + 27y²) = 0
i.e. (9x² + 24xy + 16y²) – 3(16x² – 24xy + 9y²) = 0
i.e. (3x + 4y)² – 3(4x – 3y)² = 0
Hence, the line 3x + 4y + 5 = 0 and the lines
(3x + 4y)² – 3(4x – 3y)² form the sides of an equilateral triangle.

Question 18.
Show that lines x² – 4xy + y² = 0 and x + y = \(\sqrt {6}\) form an equilateral triangle. Find its area and perimeter.
Solution:
x² – 4xy + y² = 0 and x + y = \(\sqrt {6}\) form a triangle OAB which is equilateral.
Let OM be the perpendicular from the origin O to AB whose equation is x + y = \(\sqrt {6}\)

In right angled triangle OAM,
sin 60° = \(\frac{\mathrm{OM}}{\mathrm{OA}}\) ∴ \(\frac{\sqrt{3}}{2}\) = \(\frac{\sqrt{3}}{\mathrm{OA}}\)
∴ OA = 2
∴ length of the each side of the equilateral triangle OAB = 2 units.
∴ perimeter of ∆ OAB = 3 × length of each side
= 3 × 2 = 6 units.

Question 19.
If the slope of one of the lines given by ax² + 2hxy + by² = 0 is square of the other then show that a²b + ab² + 8h³ = 6abh.
Solution:
Let m be the slope of one of the lines given by ax² + 2hxy + by² = 0.
Then the other line has slope m²

Multiplying by b³, we get,
-8h³ = ab² + a²b – 6abh
∴ a²b + ab² + 8h³ = 6abh
This is the required condition.

Question 20.
Prove that the product of lengths of perpendiculars drawn from P (x₁, y₁) to the lines repersented by ax² + 2hxy + by² = 0 is \(\left|\frac{a x_{1}^{2}+2 h x_{1} y_{1}+b y_{1}^{2}}{\sqrt{(a-b)^{2}+4 h^{2}}}\right|\)
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.
∴ m¹ + m² = \(-\frac{2 h}{b}\) and m¹m² = \(\frac{a}{b}\) …(1)
The separate equations of the lines represented by
ax² + 2hxy + by² = 0 are
y = m₁x and y = m₂x
i.e. m₁x – y = 0 and m₂x – y = 0
Length of perpendicular from P(x₁, ₁) on

Question 21.
Show that the difference between the slopes of lines given by (tan²θ + cos²θ )x² – 2xytanθ + (sin²θ )y² = 0 is two.
Solution:
Comparing the equation (tan²θ + cos²θ)x² – 2xy tan θ + (sin²θ) y² = 0 with ax² + 2hxy + by² = 0, we get,
a = tan²θ + cos²θ, 2h = -2 tan θ and b = sin2θ
Let m₁ and m₂ be the slopes of the lines represented by the given equation.

Question 22.
Find the condition that the equation ay² + bxy + ex + dy = 0 may represent a pair of lines.
Solution:
Comparing the equation
ay² + bxy + ex + dy = 0 with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 0, H = \(\frac{b}{2}\), B = a,G = \(\frac{e}{2}\), F = \(\frac{d}{2}\), C = 0
The given equation represents a pair of lines,

i.e. if bed – ae² = 0
i.e. if e(bd – ae) = 0
i.e. e = 0 or bd – ae = 0
i.e. e = 0 or bd = ae
This is the required condition.

Question 23.
If the lines given by ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1 then show that (3a + b)(a + 3b) = 4h².
Solution:
Since the lines ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1, the angle between the lines ax² + 2hxy + by² = 0 is 60°.

∴ 3(a + b)² = 4(h² – ab)
∴ 3(a² + 2ab + b²) = 4h² – 4ab
∴ 3a² + 6ab + 3b² + 4ab = 4h²
∴ 3a² + 10ab + 3b² = 4h²
∴ 3a² + 9ab + ab + 3b² = 4h²
∴ 3a(a + 3b) + b(a + 3b) = 4h²
∴ (3a + b)(a + 3b) = 4h²
This is the required condition.

Question 24.
If line x + 2 = 0 coincides with one of the lines represented by the equation x² + 2xy + 4y + k = 0 then show that k = -4.
Solution:
One of the lines represented by
x² + 2xy + 4y + k = 0 … (1)
is x + 2 = 0.
Let the other line represented by (1) be ax + by + c = 0.
∴ their combined equation is (x + 2)(ax + by + c) = 0
∴ ax² + bxy + cx + 2ax + 2by + 2c = 0
∴ ax² + bxy + (2a + c)x + 2by + 2c — 0 … (2)
As the equations (1) and (2) are the combined equations of the same two lines, they are identical.
∴ by comparing their corresponding coefficients, we get,

∴ 1 = \(\frac{-4}{k}\)
∴ k = -4.

Question 25.
Prove that the combined equation of the pair of lines passing through the origin and perpendicular to the lines represented by ax² + 2hxy + by² = 0 is bx² – 2hxy + ay² = 0
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.

Now, required lines are perpendicular to these lines.
∴ their slopes are and \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(-\frac{1}{m_{1}}\)x and y = \(-\frac{1}{m_{2}}\)x
i.e. m₁y= -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x²\(\frac{-2 h}{b}\)x + \(\frac{a}{b}\)y² = 0
∴ bx² – 2hxy + ay² = 0.

Question 26.
If equation ax² – y² + 2y + c = 1 represents a pair of perpendicular lines then find a and c.
Solution:
The given equation represents a pair of lines perpendicular to each other.
∴ coefficient of x² + coefficient of y² = 0
∴ a – 1 = 0 ∴ a = 1
With this value of a, the given equation is
x² – y² + 2y + c – 1 = 0
Comparing this equation with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 1, H = 0, B = -1, G = 0, F = 1, C = c – 1
Since the given equation represents a pair of lines,
D = \(\left|\begin{array}{ccc}
A & H & G \\
H & B & F \\
G & F & C
\end{array}\right|\) = 0
∴ \(\left|\begin{array}{rrr}
1 & 0 & 0 \\
0 & -1 & 1 \\
0 & 1 & c-1
\end{array}\right|\) = 0
∴ 1(-c + 1 – 1) – 0 + 0 = 0
∴ -c = 0
∴ c = 0.
Hence, a = 1, c = 0.

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 8 सुनो किशोरी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 8 सुनो किशोरी

12th Hindi Guide Chapter 8 सुनो किशोरी Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) अंतर स्पष्ट कीजिए :

रूढ़ि	परंपरा
(1) ……………………..	(1) ……………………..
(2) ……………………..	(2) ……………………..

उत्तर :

रूढ़ि	परंपरा
(1) रूढ़ि स्थिर होती है।	(1) परंपरा निरंतर गतिशील है।
(2) रूढ़ि ऐसी रीति-नीति है, जो समय के साथ अपना अर्थ खो चुकी है।	(2) परंपरा समय के साथ बहती धारा है, जो अनुपयोगी हो गए मूल्यों को छोड़कर उपयोगी मूल्यों के साथ आगे बढ़ती है।

(आ) कारण लिखिए :
(1) सुगंधा का पत्र पाकर लेखिका को खुशी हुई …………………………………..
(2) पश्चिमी मूल्य रूपी फल हमारे किसी काम के नहीं होंगे …………………………………..
उत्तर :
(1) सुगंधा का पत्र पाकर लेखिका को खुशी हुई क्योंकि सुगंधा लेखिका की पुत्री थी।
(2) रूढ़ि अर्थात ऐसी रीतियाँ, जो समय के साथ अनुपयोगी हो गई हैं, जिनका पालन करके समाज पिछड़ रहा हो, उन्हें हमें छोड़ देना चाहिए। जैसे बाल विवाह, पर्दा प्रथा, बहुविवाह प्रथा आदि।

शब्द संपदा

प्रश्न 2.
शब्द युग्म को पाठ के आधार पर पूर्ण कीजिए :
(1) क्षत – …………………………………..
(2) आदान – …………………………………..
(3) सूझ – …………………………………..
(4) सोच – …………………………………..
उत्तर :
(1) क्षत – विक्षत
(2) आदान – प्रदान
(3) पुरानी – जर्जर
(4) कहने – सुनने

अभिव्यक्ति

प्रश्न 3.
(अ) विद्यार्थी जीवन में मित्रता का महत्त्व’, इस विषय पर अपना मंतव्य लिखिए।
उत्तर :
विद्यार्थी जीवन स्वतंत्र जीवन होता है। यह ऐसा महत्त्वपूर्ण समय होता है, जिसमें विद्यार्थी चाहे तो अच्छा इनसान बन सकता है और बिगड़ना चाहे तो बिगड़ सकता है। यह ऐसी अवस्था है, जब एक युवा या युवती के विकास में उसके संगीसाथियों का बहुत अधिक प्रभाव होता है।

यदि इस समय अच्छे विद्यार्थियों से मित्रता होगी, तो वह भविष्य में अच्छा ही रहेगा और यदि उसकी संगति बुरे विद्यार्थियों से होगी तो उस पर भी बुरी संगत का असर होगा और वह भी अपने लक्ष्य से भटक जाएगा। सच्चा मित्र हमारे सुख-दुख में सदैव हमारा साथ देता है।

हमारी उलझनों, परेशानियों को दूर करने में हमारी सहायता करता है।

(आ) ‘युवा पीढ़ी किस ओर’, इस विषय पर अपने विचार लिखिए।
उत्तर :
युवा वर्ग किसी भी समाज व देश के लिए आशा की किरण होता है। देशवासी युवाओं में देश का भविष्य देखते हैं। परंतु आज की युवा पीढ़ी अपनी संस्कृति, अपने मूल्यों को तो काट फेंकना चाहती है परंतु पश्चिमी संस्कृति के पीछे दीवानी हो रही है।

युवा पीढ़ी कर्तव्य-पालन के समय विदेशों के उदाहरण दिया करती है। वहाँ युवक-युवती प्रारंभ से ही अपनी अलग गृहस्थी बसा लेते हैं। परंतु ये लोग इस तथ्य को नकार देते हैं कि वहाँ बहुत छोटी अवस्था से ही किशोर-किशोरी स्वावलंबी हो जाते हैं।

वे अपने पोषण के लिए माता-पिता पर निर्भर नहीं करते। प्रत्येक संस्कृति के जीवन-मूल्य अलग होते हैं। भारतीय युवाओं को यह तथ्य समझना चाहिए।

पाठ पर आधारित लघूत्तरी प्रश्न

प्रश्न 4.
(अ) ‘उड़ो बेटी, उड़ो ! पर धरती पर निगाह रखकर’, इस पंक्ति में निहित सुगंधा की माँ के विचार स्पष्ट कीजिए।
उत्तर :
उड़ो बेटी, उड़ो पर धरती पर निगाह रखकर के द्वारा लेखिका का कहना है कि सपने देखना, उन्हें पूरा करने का प्रयास करना प्रत्येक व्यक्ति का अधिकार है। परंतु हमें अपनी महान सभ्यता, अपनी संस्कृति व अपने जीवन मूल्यों को कभी भी नहीं भूलना चाहिए।

अपनी धरती से, अपनी जड़ों से कटकर कोई भी व्यक्ति लंबे समय तक सुखी नहीं रह पाता। जीवन में ऐसे अनेक अवसर आते हैं, जब पीछे छोड़ दिए गए रिश्ते और लोग हमें याद आते हैं और हमें व्याकुल कर जाते हैं।

(आ) पाठ के आधार पर रूढ़ि-परंपरा तथा मूल्यों के बारे में लेखिका के विचार स्पष्ट कीजिए।
उत्तर :
समय के साथ अपना अर्थ खो चुकी या वर्तमान प्रगतिशील समाज को पीछे ले जाने वाली समाज की कोई भी रीति-नीति रूढ़ि है। रूढ़ि स्थिर होती है। जबकि परंपरा समय के साथ अनुपयोगी हो गए मूल्यों को छोड़ती और उपयोगी मूल्यों को जोड़ती निरंतर बहती धारा परंपरा है। परंपरा गतिशील है।

एक निरंतर बहता निर्मल प्रवाह, जो हर सड़ी-गली रूढ़ि को किनारे फेंकता और हर भीतरी-बाहरी, देशी-विदेशी उपयोगी मूल्य को अपने में समेटता चलता है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) आशारानी व्होरा जी के लेखन कार्य का प्रमुख उद्देश्य – …………………………………..
उत्तर :
विभिन्न क्षेत्रों में अग्रणी रही महिलाओं के जीवन संघर्ष को चित्रित करना और वर्तमान नारी वर्ग के सम्मुख उनके आदर्श प्रस्तुत करना।

(आ) आशारानी व्होरा जी की रचनाएँ – …………………………………..
उत्तर :

• भारत की प्रथम महिला
• स्वतंत्रता सेनानी लेखिकाएँ
• क्रांतिकारी किशोरी
• स्वाधीनता सेनानी
• लेखक पत्रकार

प्रश्न 6.
कोष्ठक में दी गई सूचना के अनुसार अर्थ के आधार पर वाक्य परिवर्तन करके फिर से लिखिए :
(1) मनुष्य जाति की नासमझी का इतिहास क्रूर और लंबा है। (प्रश्नात्मक वाक्य)
(2) दया निर्बल थी, वह इतना भार सहन न कर सकी। (निषेधात्मक वाक्य)
(3) अपनी समस्याओं पर माँ से खुलकर बात करके उनसे सलाह (प्रश्नात्मक वाक्य)
(4) मेरे साथ न्याय नहीं हुआ है। (विधि वाक्य)
(5) शेष आप इस लिफाफे को खोलकर पढ़ लीजिए। (आज्ञार्थक वाक्य)
(6) ऐसे समय वह तुम्हारी बात न सुने। (विधि वाक्य) (7) वे निरर्थक हैं तो फिर सार्थक क्या है? (विधानार्थक वाक्य)
(8) मैं तुम्हें खिलौना समझता रहा और तुम साँप निकले। (विस्मयादिबोधक वाक्य)
(9) इस क्षेत्र में भी रोजगार की भरपूर संभावनाएं हैं। (निषेधात्मक वाक्य)
(10) आप भी तो एक विख्यात फीचर लेखक हैं। (विस्मयादिबोधक वाक्य)
उत्तर:
(1) क्या मनुष्य जाति की नासमझी का इतिहास क्रूर और लंबा है?
(2) दया सबल नहीं थी, वह इतना भार सहन न कर सकी।
(3) क्या अपनी समस्याओं पर माँ से खुलकर बात करके उनसे . सलाह लेती है?
(4) मेरे साथ न्याय करें।
(5) शेष आप इस लिफाफे को खोलकर पढ़ो।
(6) ऐसे समय वह तुम्हारी बात सुने।
(7) वे निरर्थक हैं।
(8) अच्छा मैं तुम्हें खिलौना समझता रहा और तुम साँप निकले।
(9) इस क्षेत्र में रोजगार की भरपूर संभावनाएँ नहीं हैं।
(10) आप एक विख्यात फीचर लेखक हैं!

Hindi Yuvakbharati 12th Digest Chapter 8 सुनो किशोरी Additional Important Questions and Answers

(कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए)
गद्यांश क्र. 1

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों में उपसर्ग लगाकर नए शब्दों को वाक्यों में प्रयोग कीजिए:
(1) पसंद – …………………………………………….
(2) अधिकार – …………………………………………….
उत्तर :
(1) पसंद – ना + पसंद, नापसंद।
वाक्य : मुझे किसी की भी निंदा सुनना सख्त नापसंद है।

(2) अधिकार – अन + अधिकार, अनधिकार।
वाक्य : हमें दूसरों के मामलों में अनधिकार घुसपैठ नहीं करनी चाहिए।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘पश्चिमी सभ्यता का अंधानुकरण समाज के लिए हानिप्रद’ विषय पर अपना मत व्यक्त कीजिए।
उत्तर :
आज भारतीय पश्चिमी सभ्यता के जाल में दिन-ब-दिन इस सीमा तक फँसते जा रहे हैं कि अपनी संस्कृति को भूल रहे हैं। पश्चिम से आई हर चीज, चाहे वह उनका बोलने-चलने का ढंग हो या कपड़े पहनने का तरीका, वहाँ का खान-पान हो या वहाँ के त्योहार, आज हम सभी को अपनाने में अपनी शान समझते हैं, बिना यह सोचे कि वह हमारे देश, हमारे समाज और हमारी जलवायु के अनुकूल है भी या नहीं।

पश्चिमी सभ्यता सदा से ही खाओ, पियो और आनंद मनाओ के सिद्धांत को मानती आई है। आज पश्चिमी सभ्यता का अनुकरण करके हम दुख के भागी बन रहे हैं। समाज में चारों ओर अराजकता फैल रही है। इसके परिणामस्वरूप ही आज हमारे महान देश में वृद्धाश्रमों की संख्या बढ़ती जा रही है। हमें पश्चिमी सभ्यता का आकर्षण छोड़कर अपनी संस्कृति, परंपराओं और मूल्यों का अनुसरण करना चाहिए।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई। सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :
(1) नई पीढ़ी इन्हें काट फेंकना चाहती है –
(2) नए मूल्यों के निर्माण का यह अभी नई पीढ़ी में नहीं आया है –
(3) आज नहीं तो कल, ये भरहराकर गिरेंगे ही –
(4) पश्चिमी मूल्यों के ये हमारे किसी काम के नहीं है –
उत्तर :
(1) पुराने मूल्यों को
(2) दम-खम
(3) जर्जर मूल्य
(4) फल।

प्रश्न 2.
कारण लिखिए : पश्चिमी मूल्य रूपी फल हमारे किसी काम के नहीं होंगे –
उत्तर :
जिस प्रकार हर पौधे को पनपने, फलने-फूलने के लिए विशेष प्रकार, की भूमि की आवश्यकता होती है, हर पौधा हर स्थान पर नहीं पनप सकता, उसी प्रकार हर देश व संस्कृति और समाज के मूल्य भी अलग होते हैं। पश्चिमी सभ्यता का अंधानुकरण भारतीय समाज के लिए अग्राह्य होगा।

प्रश्न 3.
वाक्य पूर्ण कीजिए :
(1) यह पगडंडी काटने का साहस ही पहले जरूरी है, …………………………………
(2) नए मूल्यों का निर्माण करना है तो नए ज्ञान-विज्ञान को …………………………………
उत्तर :
(1) यह पगडंडी काटने का साहस ही पहले जरूरी है, नई चौड़ी राह उसी में से खुलती दिखाई देगी।
(2) नए मूल्यों का निर्माण करना है तो नए ज्ञान-विज्ञान को पहले अपनी धरती पर टिकाना होगा।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) निर्मल x ………………………….
(2) निर्माण x ………………………….
(3) धरती x ………………………….
(4) स्थिर x ………………………….
उत्तर :
(1) निर्मल x मलिन
(2) निर्माण x ध्वंस
(3) धरती x आकाश
(4) स्थिर x अस्थिर।

प्रश्न 2.
शब्द युग्म को पाठ के आधार पर पूर्ण कीजिए :
(1) सोच – ………………………….
(2) रीति – ………………………….
(3) दम – ………………………….
(4) ज्ञान – ………………………….
उत्तर :
(1) सोच – समझ
(2) रीति – नीति
(3) दम – खम
(4) ज्ञान – विज्ञान।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘पुरानी परंपराओं का त्याग करना ही उचित है’ विषय पर अपना मत व्यक्त कीजिए।
उत्तर :
कोई भी प्रक्रिया लगातार प्रयोगों से गुजरने के बाद परंपरा का रूप ले लेती है। साथ ही उसमें परिवर्तन की गुंजाइश भी रहती है। परंतु जो बातें, परंपराएँ कल समाज के हित के लिए बनाई गई थीं, बदलती परिस्थितियों में पहले के समान हितकारक हों, आवश्यक नहीं है। अतः हमें ऐसी परंपराओं का मोह त्याग देना चाहिए। जैसे बाल विवाह का प्रचलन मुस्लिम काल में शायद आवश्यक रहा हो, परंतु कालांतर में यह परंपरा एक कुरीति के रूप में सामने आई और है इसके विरोध में 1929 में बाल विवाह अधिनियम बनाया गया। जो है समाज और देश पुरानी परंपराओं से चिपके रहते हैं, उनकी उन्नति है रुक जाती है और वे समय से पिछड़ जाते हैं।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई है सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
परिच्छेद से दो ऐसे प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित हों :
(1) क्रांति की
(2) पछतावा।
उत्तर :
(1) किसकी बड़ी-बड़ी बातें करना आसान है?
(2) जब पानी सिर से गुजर चुका होता है, तब क्या होता है?

प्रश्न 2.
वाक्य सही करके लिखिए :
(1) उस स्थिति में की गई यह कथित क्रांति कठिन भी होगी और असफल भी।
(2) मेरी राय में तुम्हें और तुम्हारी दोस्त को धैर्य से प्रतीक्षा करनी चाहिए।
उत्तर :
(1) उस स्थिति में की गई यह कथित क्रांति न कठिन होगी और न असफल।
(2) मेरी राय में रचना को और उसके दोस्त को धैर्य से प्रतीक्षा करनी चाहिए।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) हस्तक्षेप – ………………………………
(2) लगाव – ………………………………
(3) क्रांति – ………………………………
(4) प्रेरणा – ………………………………
उत्तर :
(1) हस्तक्षेप – पुल्लिंग
(2) लगाव – पुल्लिंग
(3) क्रांति – स्त्रीलिंग
(4) प्रेरणा – स्त्रीलिंग।

प्रश्न 2.
निम्नलिखित जोड़ियों में से विशेषण और विशेष्य की सही जोड़ियाँ बनाकर लिखिए :
(1) निहायत – भावनाएँ
(2) नासमझ – किशोरी
(3) भावुक – मूर्खता
(4) रोमानी – उम्र।
उत्तर :
(1) निहायत – मूर्खता
(3) भावुक – किशोरी
(2) नासमझ – उम्र
(4) रोमानी – भावनाएँ।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई। सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
परिणाम लिखिए : सुगंधा रचना का साथ छोड़ देगी ……………………………
उत्तर :
सुगंधा रचना का साथ छोड़ देगी तो वह और टूट जाएगी। अकेली पड़कर वह उधर ही जाने के लिए कदम बढ़ा लेगी, जिधर जाने से सुगंधा उसे रोकना चाहती है।

प्रश्न 3.
सहसंबंध जोड़कर अर्थपूर्ण वाक्य बनाइए :
(1) यदि तुम्हें लगे कि लड़का निर्दोष है, निश्छल है तो – दोनों को पढ़ाई के अंत तक प्रतीक्षा करने का परामर्श दे , सकती हो।
(2) एक शुभचिंतक सहेली के नाते – वह अपनी बड़ी बहन या भाभी से निर्देशन ले।
(3) यदि उसकी माँ इस योग्य न हो तो – उसका मन टटोलो और उसे प्यार से समझाओ।
(4) उसका मूड देखकर – तुम्हें उसे इसलिए अकेले नहीं छोड़ देना है कि वह तुम्हारी बात नहीं सुनती।
उत्तर :
(1) यदि तुम्हें लगे कि लड़का निर्दोष है, निश्छल है तो दोनों को पढ़ाई के अंत तक प्रतीक्षा करने का परामर्श दे, सकती हो।
(2) एक शुभचिंतक सहेली के नाते तुम्हें उसे इसलिए अकेले नहीं छोड़ देना है कि वह तुम्हारी बात नहीं सुनती।
(3) यदि उसकी माँ इस योग्य न हो तो ऐसे समय वह अपनी बड़ी बहन या भाभी से निर्देशन ले।
(4) उसका मूड देखकर उसका मन टटोलो और उसे प्यार से समझाओ।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
परिच्छेद में प्रयुक्त उपसर्गयुक्त शब्दों से मूल शब्द और उपसर्ग अलग कीजिए और उन उपसर्गों से दो-दो नए शब्द बनाइए:
(1) ………………………………….
(2) ………………………………….
(3) ………………………………….
(4) ………………………………….
उत्तर :
(1) अडिग – अ + डिग, (1) अधर्म – (2) असत्य।
(2) अनहोनी – अन + होनी, (1) अनपढ़ – (2) अनजान।
(3) हमदर्द – हम + दर्द, (1) हमशक्ल – (2) हमउम्र।
(4) निर्दोष – निर् + दोष, (1) निर्जन – (2) निर्बल।

प्रश्न 2.
शब्द युग्म को पाठ के आधार पर पूर्ण कीजिए :
(1) सूझ – ………………………………….
(2) बेटा – ………………………………….
उत्तर :
(1) सूझ – समझ
(2) बेटा – बेटी।।

मुहावरे

प्रश्न 1.
निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) कागजी घोड़े दौड़ाना
अर्थ : लिखा-पढ़ी करना।
वाक्य : आजकल के जमाने में केवल कागजी घोड़े दौड़ाने से काम नहीं बनता।

(2) खाला का घर
अर्थ : आसान काम।
वाक्य : गाँव के लोग दस-पाँच किलोमीटर पैदल चल लेना खाला का घर समझते हैं।

(3) खाल मोटी होना
अर्थ : बेशर्म होना।
वाक्य : घोटाला करने वाले राजनीतिज्ञों की खाल मोटी होती है।

(4) गिरगिट की तरह रंग बदलना
अर्थ : अवसरवादी होना।
वाक्य : आजकल के कुछ नेता अवसर देखकर गिरगिट की तरह रंग बदल लेते हैं।

(5) घोड़े बेचकर सोना
अर्थ : निश्चित होकर सोना।
वाक्य : दिनभर सड़क बनाने वाले मजदूर रात को ऐसे सो रहे थे, मानो घोड़े बेचकर सो रहे हों।

(6) चोली दामन का साथ होना
अर्थ : घनिष्ठ संबंध होना।
वाक्य : प्राचीनकाल की गुरुकुल शिक्षा प्रणाली में गुरु-शिष्य का चोली दामन का साथ होता था।

(7) कन्नी काटना।
अर्थ : निकल जाना।
वाक्य : बड़ा बेटा और बहू पहले ही माँ-बाप से कन्नी काट चुके थे।

काल परिवर्तन

प्रश्न 1.
निम्नलिखित वाक्यों को कोष्ठक में सूचित काल में परिवर्तन कीजिए :
(1) नए मूल्यों के निर्माण का दम-खम अभी उसमें नहीं आया है। (अपूर्ण वर्तमानकाल)
(2) ये बातें बेटा-बेटी के लिए समान रूप से लागू होती हैं। (सामान्य भविष्यकाल)
(3) मैं इसके परिणाम की प्रतीक्षा करूँगी। (अपूर्ण भूतकाल)
उत्तर :
(1) नए मूल्यों के निर्माण का दम-खम अभी उसमें नहीं आ रहा है।
(2) ये बातें बेटा-बेटी के लिए समान रूप से लागू होंगी।
(3) मैं इसके परिणाम की प्रतीक्षा कर रही थी।

वाक्य शुद्धिकरण

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) हमें पुरानी-झर्झर रूढ़ियों को तोड़णा है।
(2) में इसके परिणाम की प्रतीक्छा करूँगी।
(3) दोस अकेली रचना का है बी नहीं।
उत्तर :
(1) हमें पुरानी-जर्जर रूढ़ियों को तोड़ना है।
(2) मैं इसके परिणाम की प्रतीक्षा करूँगी।
(3) दोष अकेली रचना का है भी नहीं।

सुनो किशोरी Summary in Hindi

सुनो किशोरी लेखक का परिचय

सुनो किशोरी लेखक का नाम : आशारानी व्होरा। (जन्म 7 अप्रैल, 1921; निधन 2009.)

सुनो किशोरी प्रमुख कृतियाँ : भारत की प्रथम महिलाएँ, स्वतंत्रता सेनानी लेखिकाएँ, क्रांतिकारी किशोरी, स्वाधीनता सेनानी, लेखक-पत्रकार आदि।

सुनो किशोरी विशेषता : आपने आधुनिक हिंदी साहित्य में नारी विषयक लेखन को समृद्ध किया। लेखन में नई धारा को जन्म। विभिन्न क्षेत्रों में अग्रणी रही. महिलाओं के जीवन संघर्ष को चित्रित किया और वर्तमान नारी वर्ग के सम्मुख उनके आदर्श प्रस्तुत किए।

सुनो किशोरी विधा : पत्र शैली में लिखा गया निबंध।

सुनो किशोरी विषय प्रवेश : प्रस्तुत पाठ पत्र शैली में लिखा गया है। लेखिका अपनी पुत्री को रूढ़ि और परंपरा का अंतर बताते हुए कह रही है कि हमें जीवन में ऊँचा उठने का प्रयास अवश्य करना चाहिए परंतु अपनी संस्कृति, अपनी सभ्यता से कटकर नहीं। साथ ही लेखिका का यह भी कहना है कि किशोरियों की शंकाओं, परेशानियों, प्रश्नों, दुश्चिंताओं आदि के समाधान के लिए एक माँ या एक अच्छी सखी को मार्गदर्शिका के रूप में कार्य करना चाहिए।

सुनो किशोरी पाठ का सार

लेखिका की पुत्री सुगंधा की किशोरी सखी रचना ने अभी कॉलेज में प्रवेश लिया है। वहाँ वह एक सहपाठी की ओर आकर्षित हो जाती है। अभी लड़का और लड़की दोनों की आयु कम है। लेखिका अपनी पुत्री को उसे उचित मार्गदर्शन देने की प्रेरणा दे रही है। साथ ही सखी का साथ न छोड़ने का भी परामर्श देती है। किशोर अवस्था। में बच्चे अपने साथियों पर कहीं अधिक विश्वास करते हैं।

सुनो किशोरी मुहावरे : अर्ध औ२ वाक्य प्रयोग

(1) धरती पर निगाह रखना।
अर्थ : वास्तविकता से जुड़े रहना।
वाक्य : हमें प्रगति की राह पर निरंतर आगे बढ़ते हुए भी धरती पर निगाह रखनी चाहिए।

(2) फलीभूत होना।
अर्थ : फल में परिणत होना, परिणाम निकल आना।
वाक्य : सोनल के भारतीय प्रशासनिक सेवा में चुने जाने पर है उसके माता-पिता की आशाएँ फलीभूत हुईं।

(3) राह का रोड़ा बनना।
अर्थ : उन्नति में बाधा बनना।
वाक्य : कुछ लोग दूसरों को आगे बढ़ता नहीं देख सकते। जब देखो, वे किसी-न-किसी की राह का रोड़ा बने रहते हैं।

(4) कन्नी काटना।
अर्थ : निकल जाना।
वाक्य : कामचोर विजय का जरा-से काम को क्या कह दिया, झट कन्नी काट ली।

(5) आगाह करना।
अर्थ : सूचित करना।
वाक्य : मौसम विभाग ने संपूर्ण महाराष्ट्र को मूसलाधार वर्षा के लिए आगाह किया है।

सुनो किशोरी शब्दार्थ

• डैना = पंख
• अवांछित = जिसकी इच्छा न की गई हो
• भरहराकर = तेजी से
• निहायत = अत्याधिक, पूरी तरह से
• जुनून = पागलपन, उन्माद
• अंतर्मुखी होना = अपने भीतर झाँककर सोचना
• निजात = छुटकारा
• आगाह करना = सूचित करना,
• यथार्थ = सच्चाई/वास्तविकता
• क्षत-विक्षत = बुरी तरह से घायल, लहू-लुहान
• बुनियादी = मौलिक
• भर्त्सना = अनुचित काम के लिए बुरा-भला कहना
• अल्हड़ = भोला-भाला
• राजदार = भेद जानने वाला/भेदिया
• मंशा = इच्छा
• निश्छल = छल रहित

सुनो किशोरी मुहावरे

• धरती पर निगाह रखना = वास्तविकता से जुड़े रहना
• राह का रोड़ा बनना = उन्नति में बाधा बनना
• फलीभूत होना = फल में परिणत होना, परिणाम निकल आना
• कन्नी काटना = बचकर निकल जाना

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 7 पेड़ होने का अर्थ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 7 पेड़ होने का अर्थ

12th Hindi Guide Chapter 7 पेड़ होने का अर्थ Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) लिखिए : पेड़ का बुलंद हौसला सूचित करने वाली दो पंक्तियाँ :
(a) ……………………………………………..
(b) ……………………………………………..
उत्तर :
(a) भेड़िया, बाघ, शेर की दहाड़ पेड़ किसी से नहीं डरता है।
(b) पेड़ रात भर तूफान से लड़ा है।

(आ) कृति पूर्ण कीजिए :

उत्तर :

शब्द संपदा

प्रश्न 2.
निम्नलिखित भिन्नार्थक शब्दों का अर्थपूर्ण वाक्य में प्रयोग कीजिए :
(१) साँस – सास
……………………………………………
……………………………………………
(२) ग्रह – गृह
……………………………………………
……………………………………………
(३) आँचल-अंचल
……………………………………………
……………………………………………
(४) कुल-कूल
……………………………………………
……………………………………………
उत्तर :
(1) साँस – सच कहा गया है कि जब तक साँस है, तब तक आशा नहीं छोड़नी चाहिए।
सास – अपने गुणों के कारण रुचि सास की बहुत लाड़ली है।

(2) ग्रह – संपूर्ण सौर मंडल में शनि सबसे सुंदर ग्रह है।
गृह – आलोक ने गृह-प्रवेश के अवसर पर बड़ी शानदार पार्टी दी।

(3) आँचल – अनन्या सात साल की हो गई है पर अभी भी माँ का आँचल पकड़े उसके पीछे-पीछे घूमती रहती है।
अंचल – भाई की पोस्टिंग चंबल अँचल में होने पर घर के सभी लोग बहुत चिंतित हुए।

(4) कुल – रामचंद्र जी सूर्य कुल के सूर्य थे।
कूल – नदी के कूल पर ठंडी हवा मन को मोह रही थी।

अभिव्यक्ति

प्रश्न 3.

(अ) ‘पेड़ मनुष्य का परम हितैषी’, इस विषय पर अपना मंतव्य लिखिए।
उत्तर :
पेड़ मनुष्य का परम हितैषी है। प्रकृति की ओर से धरती को दिया गया अनमोल उपहार है पेड़। सभी प्रकार की वनस्पतियाँ, फल, फूल, अनाज, लकड़ी, खनिज सभी हमें पेड़ों से ही मिलते हैं। पेड़ हमें इमारती लकड़ी, ईंधन, पशुओं के लिए चारा, औषधि, लाख, गोंद, पत्ते आदि देते हैं।

हम जो विषैली वायु बाहर छोड़ते हैं, वृक्ष उसे ग्रहण करके स्वच्छ और स्वास्थ्यवर्धक वायु हमें प्रदान करते हैं और हमें जीवन देते हैं। पेड़ वर्षा कराने में भी सहायक होते हैं। हमें अपने जीवन में वृक्षों के महत्त्व को समझना चाहिए।

(आ) ‘भारतीय संस्कृति में पेड़ का महत्त्व’, इस विषय पर अपने विचार व्यक्त कीजिए।
उत्तर :
भारतीय संस्कृति में आदि काल से पेड़ों का महत्त्वपूर्ण स्थान रहा है। पेड़ों को देवताओं का स्थान दिया गया है। पेड़ों की पूजा की जाती थी। उनके साथ मनुष्यों के समान आत्मीयता बरती जाती थी। पीपल के पेड़ की पूजा-अर्चना की जाती थी।

स्त्रियाँ उपवास करके उसकी परिक्रमा करती थी और जल अर्पण करती थी। इसी प्रकार केले के पेड़ के पूजन की भी प्रथा थी। तुलसी का पौधा तो आज भी अत्यंत पवित्र माना जाता है। बेल के पेड़ के पत्ते भगवान शंकर के मस्तक पर चढ़ाए जाते हैं।

वातावरण की शुद्धता के लिए पेड़ अत्यंत आवश्यक हैं क्योंकि हम जो विषैली वायु बाहर छोड़ते हैं, पेड़ उसे ग्रहण करके स्वच्छ और स्वास्थ्यवर्धक वायु हमें प्रदान करते हैं और हमें जीवन देते हैं।

रसास्वादन

प्रश्न 4.
‘पेड़ हौसला है, पेड़ दाता है’, इस कथन के आधार पर संपूर्ण कविता का रसास्वादन कीजिए।
उत्तर :
पेड़ होने का अर्थ कविता में कवि डॉ. मुकेश गौतम पेड़ के माध्यम से मनुष्य को मानवता, परोपकार आदि मानवोचित गुणों की प्रेरणा दे रहा है। मनुष्य जरा-सी प्रतिकूल परिस्थिति आने पर या किसी कार्य में मनचाही सफलता न मिलने पर हौसला खो बैठता है। पेड़ भयंकर आँधी-तूफान का सामना करता है, घायल होकर टेढ़ा हो जाता है, परंतु वह अपना हौसला नहीं छोड़ता।

पेड़ के हौसले के कारण शाखों में स्थित घोंसले में चिड़िया के चहचहाते छोटे-छोटे बच्चे सारी रात भयंकर तूफान चलते रहने के बाद भी सुरक्षित रहते हैं। सचमुच पेड़ का हौसला बहुत बड़ा है। पेड़ बहुत बड़ा दाता है। पेड़ की जड़, तना, शाखाएँ, पत्ते, फूल, फल और बीज अर्थात पेड़ का कोई भी भाग अनुपयोगी नहीं होता। अपने स्वार्थ के लिए पेड़ पर कुल्हाड़ी चलाने वालों, उसे काटने वालों के किसी भी दुर्व्यवहार व अत्याचार का पेड़ कभी बदला लेने का नहीं सोचता। वह तो जीवन भर देता ही रहता है।

हम श्वासोच्छ्वास के माध्यम से जो विषैली वायु बाहर छोड़ते हैं, पेड़ उसे स्वच्छ करके हमें स्वास्थ्यवर्धक वायु प्रदान करता है। पेड़ रोगों के लिए विभिन्न प्रकार की औषधियाँ देता है। मनुष्य समाज में किसी की शवयात्रा हो या कोई शुभ कार्य, या फिर किसी की बारात, पेड़ सभी को पुष्पों की सौगात देता है।

पेड़ कवि को कागज, कलम तथा स्याही, पेड़ वैद्य और हकीम को विभिन्न रोगों के लिए दवाएँ तथा शासन और प्रशासन के लोगों को कुरसी, मेज और आसन देता है। वास्तव में देखा जाए तो पेड़ की ऐसी कोई भी वस्तु नहीं है, जो मनुष्य के काम न आती हो।

पेड़ संत के समान है, जो दूसरों को देते ही हैं, किसी से कुछ भी अपेक्षा नहीं रखते। वास्तविकता तो यह है कि पेड़ दधीचि है। जिस प्रकार दधीचि ने देवताओं की रक्षा के लिए वज्रास्त्र बनाने के लिए जीते-जी अपनी अस्थियाँ भी दान कर दी थीं, उसी प्रकार पेड़ बिना किसी स्वार्थ के जीवन भर देता ही रहता है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) नयी कविता का परिचय – ……………………………………………..
उत्तर :
नयी कविता में काव्य क्षेत्र में नए भाव बोध को व्यक्त करने के लिए शिल्प पक्ष और भाव पक्ष के स्तर पर नए प्रयोग किए गए। नए प्रतीकों, उपमानों और प्रतिमानों को ढूँढ़ा गया। परिणामस्वरूप नयी कविता आज के मनुष्य के व्यस्त जीवन का दर्पण और आस-पास की सच्चाई की तस्वीर बनकर उभरी।

(आ) डॉ. मुकेश गौतम जी की रचनाएँ – ……………………………………………..
उत्तर :

• अपनों के बीच
• सतह और शिखर
• सच्चाइयों के रू-ब-रू
• वृक्षों के हक में
• लगातार कविता
• प्रेम समर्थक हैं पेड़
• इसकी क्या जरूरत थी (कविता संग्रह)

अलंकार

उत्प्रेक्षा : जहाँ पर उपमेय में उपमान की संभावना प्रकट की जाए या उपमेय को ही उपमान मान लिया जाए; वहाँ उत्प्रेक्षा अलंकार होता है।
उत् – + प्र + ईक्षा – अर्थात् प्रकट रूप से देखना।
इस अलंकार में मानो, जनु – जानहुँ, मनु – मानहुँ जैसे शब्दों का प्रयोग किया जाता है।

1. सोहत ओढ़े पीत पट श्याम सलोने गात।
   मनों नीलमनि शैल पर, आतप पर्यो प्रभात।।
2. उस क्रोध के मारे तनु उसका काँपने लगा।
   मानो हवा के जोर से सोता हुआ सागर जगा।।
3. लता भवन ते प्रगट भए तेहि अवसर दोउ भाइ।
   निकसे जनु जुग विमल बिंधु, जलद पटल बिलगाइ।।
4. जान पड़ता है नेत्र देख बड़े-बड़े।
   हीरकों में गोल नीलम हैं जड़े।।
5. झूठे जानि न संग्रही, मन मुँह निकसै बैन।
   याहि ते मानहुँ किए, बातनु को बिधि नैन।।

Hindi Yuvakbharati 12th Digest Chapter 7 पेड़ होने का अर्थ Additional Important Questions and Answers.

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)
पद्यांश क्र. 1 प्रश्न. निम्नलिखितपद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
वाक्य पूर्ण कीजिए :
(1) पेड़ किसी के पाँव
(2) आदमी एक पेड़ जितना
उत्तर :
(1) पेड़ किसी के पाँव नहीं पड़ता है।
(2) आदमी एक पेड़ जितना बड़ा कभी नहीं हो सकता।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द के वचन बदलकर लिखिए :
(1) साँस – …………………………….
(2) कमरे – …………………………….
(3) हौसला – …………………………….
(4) आँधी – …………………………….
उत्तर :
(1) साँस – साँसें
(2) अर्थ – आर्थिक
(3) हौसला – हौसले
(4) तूफान – तूफानी।

प्रश्न 2.
निम्नलिखित शब्दों में प्रत्यय लगाकर नए शब्द बनाइए :
(1) आदमी – …………………………….
(2) अर्थ – …………………………….
(3) बड़ा – …………………………….
(4) तूफान – …………………………….
उत्तर :
(1) आदमी – आदमियत
(3) बड़ा – बड़प्पन
(2) कमरे – कमरा
(4) आँधी – आँधियाँ।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘हालात से भागने की बजाय उसका सामना करना ही बेहतर है’ इस विषय पर अपना मत स्पष्ट कीजिए।
उत्तर :
कहा जाता है कि मनुष्य परिस्थितियों के हाथ में एक कठपुतली के समान होता है। यह भी कहा जाता है कि जब रेतीला तूफान आता है तो शुतुरमुर्ग अपनी गरदन रेत में गड़ा लेता है और समझता है कि खतरा टल गया। परंतु खतरा टलता नहीं है। ऐसा ही स्वभाव अनेक व्यक्तियों का भी होता है।

जब भी प्रतिकूल परिस्थितियाँ सामने आ जाती हैं, ऐसे लोग उनका सामना करने की बजाय अपना उद्देश्य ही बदल लेते हैं। ऐसा करना उचित नहीं है। स्थिति से भागने के बजाय डटकर उसका सामना करना चाहिए।

आज नहीं तो कल सफलता अवश्य मिलेगी। हमें पेड़ से सीख लेनी चाहिए। कैसा ही भयंकर आँधी-तूफान हो, पेड़ हार नहीं मानता, डटा रहता है।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :
(1) पेड़ करता है – [ ]
(2) पेड़ देता है – [ ]
उत्तर :
(1) पेड़ करता है – सभी का स्वागत
(2) पेड़ देता है – सभी को विदाई

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का लिंग बदलकर लिखिए :
(1) चिड़िया – …………………………………….
(2) शेर – …………………………………….
(3) पहाड़ – …………………………………….
(4) बाघ – …………………………………….
उत्तर :
(1) चिड़िया – चिड़ा
(2) शेर – शेरनी
(3) पहाड़ – पहाड़ी
(4) बाघ – बाघिन।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) पेड़ = …………………………………….
(2) हवा = …………………………………….
(3) पहाड़ = …………………………………….
(4) राहगीर = …………………………………….
उत्तर :
(1) पेड़ = तरु
(2) हवा = अनिल
(3) पहाड़ = पर्वत
(4) राहगीर = यात्री।

पद्यांश क्र. 3
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कविता की पंक्तियों को उचित क्रमानुसार लिखकर प्रवाह तख्ता पूर्ण कीजिए:
(1) वृक्ष के पास ऐसी एक भी चीज नहीं है
(2) हमेशा देता आया है मनुष्य का साथ
(3) हमारे लिए ही तो है पेड़ की हर एक चीज
(4) सभी के लिए देता है पुष्पों की सौगात
उत्तर :
(1) हमारे लिए ही तो है पेड़ की हर एक चीज
(2) सभी के लिए देता है पुष्पों की सौगात
(3) हमेशा देता आया है मनुष्य का साथ
(4) वृक्ष के पास ऐसी एक भी चीज नहीं है

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के भिन्न अर्थों को वाक्यों द्वारा स्पष्ट कीजिए :
(1) जड़
(2) तना
(3) फल।
उत्तर :
(1) जड़ :

• अर्थ : वृक्ष का मूल।
  वाक्य : वृक्ष अपनी जड़ के द्वारा धरती से पोषक तत्त्व ग्रहण करता है।
• अर्थ : मूर्ख।
  वाक्य : मनीश को दर्शन की बातें क्या समझ आएँगी, वह है तो बिलकुल जड़ है।

(2) तना :

• अर्थ : पेड़ का जमीन से ऊपर का मोटा भाग।
  वाक्य : तने के कारण ही पेड़ खड़ा रहता है।
• अर्थ : अकड़ा हुआ।
  वाक्य : धीरज जाने अपने आपको क्या समझता है, हर समय तना रहता है।

(3) फल :

• अर्थ : खाने का फल।
  वाक्य : हमें अपने भोजन में मौसमी फलों का समावेश अवश्य करना चाहिए।
• अर्थ : परिणाम।
  वाक्य : परीक्षा-फल के दिन मंदिरों में छात्र-छात्राओं की भीड़ लग जाती है।

प्रश्न 2.
पद्यांश में प्रयुक्त विलोम शब्दों की जोड़ियों को वाक्य में प्रयोग कीजिए :
(1) ……………………………… वाक्य :
(2) ……………………………… वाक्य :
उत्तर :

1. सुबह-शाम।
   वाक्य : मेरी माँ सुबह-शाम नियमपूर्वक मंदिर जाती है।
2. दिन-रात।
   वाक्य : नेहा ने मेडिकल की प्रवेश परीक्षा की तैयारी के लिए दिन-रात एक कर दिया।

रसास्वादन मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दो के आधार पर पेड़ होने का अर्थ’ कविता का रसास्वादन कीजिए :
उत्तर :
(1) रचना का शीर्षक : पेड़ होने का अर्थ।
(2) रचनाकार : डॉ. मुकेश गौतम।

(3) कविता की केंद्रीय कल्पना : सब कुछ दूसरों को देकर जीवन की सार्थकता सिद्ध करना। पेड़ मनुष्य का बहुत बड़ा शिक्षक है। पेड़ मनुष्य का हौसला बढ़ाता है। वह उसे समाज के प्रति जिम्मेदारी का निर्वाह करना सिखाता है। पेड़ ने भारतीय संस्कृति को जीवित रखा है और उसने मानव को संस्कारशील बनाया है।

(4) रस-अलंकार :

(5) प्रतीक विधान : कवि ने पेड़ को परोपकार के लिए अपना सर्वस्व न्योछावर करते हुए दर्शाया है। कवि ने इस तरह के महान त्यागी के लिए महर्षि दधीचि जैसे महान दाता तथा संत का प्रतीक के रूप में सटीक उपयोग किया है।

(6) कल्पना : पेड़ आदि काल से मनुष्य का सबसे बड़ा शिक्षक, उसका हौसला बढ़ाने वाला तथा समाज के प्रति उसको अपनी जिम्मेदारियाँ निभाने का बोध कराने वाला रहा है। उसने भारतीय संस्कृति को जीवित रखने और मनुष्य को संस्कारशील बनाने का काम किया है।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
राह में गिरा देता है फूल,
और करता है इशारा उसे आगे बढ़ने का।

(8) कविता पसंद आने का कारण : प्रस्तुत कविता में कवि ने पेड़ के माध्यम से मनुष्य को मानवता, परोपकार जैसे मानवोचित गुणों की प्रेरणा दी है।

अलंकार

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में निहित अलंकार पहचानकर उसका नाम लिखिए :
(1) चरन-कमल बंदी हरिराई।
(2) पीपर पात सरिस मन डोला।
(3) हनुमान की पूँछ में लगन न पाई आग।
लंका सगरी जल गई, गए निसाचर भाग।
उत्तर :
(1) रूपक अलंकार।
(2) उपमा अलंकार।
(3) अतिशयोक्ति अलंकार।

रस

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में निहित रस पहचानकर उसका नाम लिखिए :
(1) अखिल भुवन चर, अचर सब, हरि मुख में लख मातु।
चकित भई, गद्गद वचन, विकसित दृग पुलकातु।
(2) सुनहूँ राम जेहि शिवधनु तोरा।
सहसबाहु सम सो रिपु मोरा।
(3) मेरे तो गिरधर गोपाल, दूसरो न कोई।
जाके सिर मोर मुकुट, मेरो पति सोई।
उत्तर :
(1) अद्भुत रस
(2) रौद्र रस
(3) शांत रस।

मुहावरे

प्रश्न 1.
निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) आसमान पर थूकना
अर्थ : अशोभनीय कार्य करना।
वाक्य : जिनके माता-पिता अपने बच्चों को अच्छे संस्कार नहीं देते, उनके बच्चे आसमान पर थूकने वाले हों, तो ताज्जुब नहीं।

(2) उल्टी गंगा बहाना
अर्थ : उल्टा काम करना।
वाक्य : जब देखो तब ये सज्जन उल्टी गंगा ही बहाते हैं।

(3) एक लाठी से हाँकना
अर्थ : सबके साथ समान व्यवहार करना।
वाक्य : कुछ लोग अच्छे-बुरे सबको एक ही लाठी से हाँकने की कोशिश करते हैं।

(4) चार चाँद लगाना
अर्थ : शोभा बढ़ाना।
वाक्य : उस विद्वान की शालीनता उनके व्यक्तित्व में चार चाँद लगा रही थी।

(5) कोल्हू का बैल
अर्थ : बहुत परिश्रम करने वाला।
वाक्य : मुनीम जी की बात और है, वे तो कोल्हू के बैल

(6) कौड़ी-कौड़ी का मोहताज
अर्थ : अत्यंत निर्धन होना।
वाक्य : गनेश शेठ अपने जमाने में इस बाजार के सबसे बड़े सेठ थे, पर उनके बेटे ऐसे नालायक निकले कि आज वे कौड़ी-कौड़ी के मोहताज हो गए हैं।

काल परिवर्तन

प्रश्न 1.
निम्नलिखित वाक्यों को कोष्ठक में सूचित काल में परिवर्तन कीजिए :
(1) कवि पेड़ को देख रहा था। (सामान्य भूतकाल)
(2) पेड़ सभी का स्वागत करता है। (अपूर्ण वर्तमानकाल)
(3) किशोरी का पत्र पाकर खुशी हुई। (सामान्य भविष्यकाल)
उत्तर :
(1) कवि ने पेड़ को देखा।
(2) पेड़ सभी का स्वागत कर रहा है।
(3) किशोरी का पत्र पाकर खुशी होगी।

वाक्य शुद्धिकरण

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) मनुश्य पेड़ जितना बड़ा कबी नहीं हो सकता।
(2) पेड़ पर चहचाते हुए चिड़िया के बच्चों की घोंसला है।
(3) ओझोन गैस मानव स्वास्थ के लिए हानिकारक होती है।
उत्तर :
(1) मनुष्य पेड़ जितना बड़ा कभी नहीं हो सकता।
(2) पेड़ पर चहचहाते हुए चिड़िया के बच्चों का घोंसला है।
(3) ओजोन गैस मानव स्वास्थ्य के लिए हानिकारक होती है।

पेड़ होने का अर्थ Summary in Hindi

पेड़ होने का अर्थ कवि का परिचय

कवि का नाम : डॉ. मुकेश गौतम। (जन्म 1 जुलाई, 1970.)

पेड़ होने का अर्थ कवि परिचय : डॉ. मुकेश गौतम ने आधुनिक कवियों में अपनी विशिष्ट पहचान बनाई है। आज के मनुष्य की समस्याएँ और प्रकृति के साथ होने वाला क्रूर अत्याचार आपकी कविता में प्रखरता से उभरता है। सामाजिक सरोकार की भावना आपके काव्य का मुख्य स्वर है।

प्रमुख कृतियाँ : अपनों के बीच, सतह और शिखर, सच्चाइयों के रू-ब-रू, वृक्षों के हक में, लगातार कविता, प्रेम समर्थक हैं पेड़, इसकी क्या जरूरत थी (कविता संग्रह) आदि।

विशेषता : आधुनिक भावबोध की सहज-सीधे रूप में अभिव्यक्ति। हास्य-व्यंग्य का सफल मंचन। भावों और विचारों का प्रभावशाली ढंग से संप्रेषण।

विधा : नई कविता

पेड़ होने का अर्थ टिप्पणियाँ

दधीचि : दधीचि एक महान ऋषि थे। कहा जाता है कि एक बार वृत्रासुर नामक राक्षस देवलोक पर अधिकार करने के लिए सभी देवताओं को तरह-तरह से परेशान कर रहा था। उसके अत्याचार बढ़ते ही जाते थे। ब्रह्मा जी ने देवताओं को बताया कि वृत्रासुर को मारने का एक ही उपाय है। वह है पृथ्वीवासी आत्म-त्यागी महर्षि दधीचि की अस्थियों से बना वज्र। देवराज इंद्र के कहने पर महर्षि ने बिना किसी हिचकिचाहट के उसी समय समाधि लगाई और अपनी देह त्याग दी।

विषय प्रवेश : पेड़ और मनुष्य का नाता आदि काल से रहा है। पेड़ मनुष्ये का बहुत बड़ा शिक्षक है। पेड़ मनुष्य का हौसला बढ़ाता है, समाज के प्रति जिम्मेदारी का निर्वाह करना सिखाता है। पेड़ ने भारतीय संस्कृति को जीवित रखा है और मानव को संस्कारशील बनाया है।

पेड़ होने का अर्थ कविता का सरल अर्थ

(1) आदमी पेड़ नहीं हो सकता ………………………………………….. हालात से लड़ता है।

प्रस्तुत कविता में कवि पेड़ के माध्यम से मनुष्य को मानवता, परोपकार आदि मानवोचित गुणों की प्रेरणा दे रहा है। कवि अपने कमरे में खिड़की के पास बैठा है। वह बाहर खड़े पेड़ को देखता है तो पेड़ का हौसला, उसकी दान की प्रवृत्ति कवि को सोचने पर विवश कर देती है। अनगिनत विचार उसके मस्तिष्क में उठने लगते हैं। कवि कहते हैं, मनुष्य कितना भी बड़ा क्यों हो जाए, वह पेड़ जैसा कभी नहीं बन सकता।

पेड़ के हौसले से मनुष्य को सीख लेनी चाहिए। पेड़ जबसे जन्म लेता है अर्थात जब वह कोमल-सा अंकुर होता है, तब से जीवनपर्यंत किसी का आश्रय वह नहीं लेता। कैसा भी आँधी-तूफान आए या सामने कोई कैसा भी बड़े-से-बड़ा, प्रतापी राजा आ जाए, पेड़ कभी किसी के सामने नहीं झुकता।

जब तक पेड़ जीवित रहता है, जैसी भी परिस्थिति हो, एक ही स्थान पर खड़े-खड़े उसका डटकर सामना करता है। जबकि मनुष्य का स्वभाव है कि शक्तिशाली व्यक्ति या स्वार्थपूर्ति करने वाले के पैरों में नाक रगड़ने से भी वह नहीं कतराता। साथ ही जरा-सी प्रतिकूल परिस्थिति आने पर या किसी कार्य में मनचाही सफलता न मिलने पर हौसला खो बैठता है।

(2) जहाँ भी खड़ा है ………………………………………….. पेड़ बहुत बड़ा हौसला है।

कवि कहते हैं, पेड़ जहाँ भी खड़ा हो, चाहे सड़क पर हो, किसी झील के किनारे हो या फिर पहाड़ के ऊपर हो, उसकी मनोस्थिति एक जैसी रहती है। पेड़ के सामने भेड़िया, बाघ जैसे हिंसक पशु आ जाएँ या शेर दहाड़ने लगे, पेड़ किसी से नहीं डरता। जबकि मनुष्य हिंसक पशु के सामने आने पर डर से ही मर जाता है। पेड़ मनुष्य के समान न कभी किसी की हत्या करता है, न ही आत्महत्या।

इसके विपरीत पेड़ थके हुए यात्रियों को ठंडी हवा देता है, शीतल छाया देता है। यही नहीं पेड़, राहगीरों के समक्ष पुष्प वर्षा करके मानो उन्हें अपनी राह पर आगे बढ़ते रहने की प्रेरणा देता है। पेड़ के समीप जो भी आता है, पेड़ सभी का स्वागत करता है। यात्री जब थकान उतरने के बाद पेड़ के नीचे से उठकर चल देते हैं, तो पेड़ सभी को विदा भी करता है। कवि कहते हैं कि गाँव के रास्ते में मुस्कुराता पेड़ जाने कबसे टेढ़ा खड़ा है।

पहले वह पेड़ टेढ़ा नहीं था। वह पूरी रात तेज तूफान का सामना करता रहा। पेड़ घायल हो गया, इसी के कारण टेढ़ा भी हो गया, परंतु उसने अपना हौसला नहीं छोड़ा। पेड़ की शाखों में एक घोंसले में चिड़िया के चहचहाते छोटे-छोटे बच्चे थे। सारी रात भयंकर तूफान चलते रहने के बाद भी पेड़ के हौसले के कारण वह छोटा-सा घोंसला सुरक्षित है। सचमुच पेड़ का हौसला बहुत बड़ा है।

(3) दाता है पेड़ ………………………………………….. पेड़ संत है, दधीचि है।

पेड़ बहुत बड़ा दाता है। पेड़ के फलों के गुणों से तो सभी परिचित हैं, परंतु इसके साथ ही पेड़ की जड़, तना, शाखाएँ हों या पत्ते, फूल और बीज, पेड़ का कोई भी भाग अनुपयोगी नहीं होता। मानव समाज में ऐसे भी लोग हैं, जो पेड़ को पूजते हैं। दूसरी ओर अपने स्वार्थ के लिए पेड़ पर कुल्हाड़ी चलाने वाले, उसे काटने वालों की भी कमी नहीं है। लेकिन पेड़ मनुष्य के किसी भी दुर्व्यवहार पर कभी भी आँसू नहीं गिराता।

मानव पेड़ पर कैसा भी अत्याचार क्यों न करे, पेड़ उससे कभी बदला लेने का नहीं सोचता। वह तो जीवन भर देता ही रहता है। हम श्वासोच्छ्वास के माध्यम से जो विषैली वायु बाहर छोड़ते हैं, पेड़ उसे स्वच्छ करके हमें स्वास्थ्यवर्धक वायु प्रदान करता है। पेड़ रोगों के लिए विभिन्न प्रकार की औषधियाँ देता है।

मनुष्य समाज में किसी की शवयात्रा हो या कोई शुभ कार्य, या फिर किसी की बारात, पेड़ सभी को सजावट के लिए पुष्पों की सौगात देता है। जब से सृष्टि का आरंभ हुआ है, अनादि काल से पेड़ हमेशा मनुष्य को देता ही आया है। पेड़ कवि को कागज, कलम तथा स्याही प्रदान करता है।

पेड़ वैद्य और हकीम को विभिन्न रोगों के लिए दवाएँ देता है। पेड़ शासन और प्रशासन के लोगों को कुरसी, मेज और आसन देता है। वास्तव में देखा जाए तो पेड़ की ऐसी कोई भी वस्तु नहीं है, जो मनुष्य के काम न आती हो। पेड़ संत के समान है, जो दूसरों को देते ही हैं, किसी से कुछ भी अपेक्षा नहीं रखते।

वास्तविकता तो यह है कि पेड़ दधीचि है। जिस प्रकार दधीचि ने देवताओं की रक्षा के लिए वज्रास्त्र बनाने के लिए जीते-जी अपनी अस्थियाँ भी दान कर दी थीं, उसी प्रकार पेड़ बिना किसी स्वार्थ के जीवन भर देता ही रहता है।

पेड़ होने का अर्थ शब्दार्थ

• ढूँठ = फूल-पत्ते विहीन सूखा पेड़
• सौगात = भेंट, उपहार

पेड़ होने का अर्थ टिप्पणी

• दधीचि : एक ऋषि जिन्होंने वृत्रासुर का वध करने हेतु अस्त्र बनाने के लिए इंद्र को अपनी हड्डियाँ दी थीं।

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 6 पाप के चार हथियार Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 6 पाप के चार हथियार

12th Hindi Guide Chapter 6 पाप के चार हथियार Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) कृति पूर्ण कीजिए:

(1) पाप के चार हथियार ये हैं –
(a) …………………………………………………..
(b) …………………………………………………..
(c) …………………………………………………..
(d) …………………………………………………..
उत्तर :
पाप के चार हथियार ये हैं –
उपेक्षा
निंदा
हत्या
श्रद्धा

(2) जॉर्ज बर्नार्ड शॉ का कथन – ………………………………………………………
………………………………………………………………………………
………………………………………………………………………………
उत्तर :
जॉर्ज बर्नार्ड शॉ का कथन – जॉर्ज बर्नार्ड शॉ कहते हैं कि लोग उनकी बातों को दिल्लगी समझकर उड़ा देते हैं। लोग उनकी उपेक्षा करते हैं और उनकी बातों पर गौर नहीं करते।

शब्द संपदा

प्रश्न 2.
शब्दसमूह के लिए एक शब्द लिखिए :

(a) जिसे व्यवस्थित न गढ़ा गया हो – ………………………………….
(b) निंदा करने वाला – ………………………………….
(c) देश के लिए प्राणों का बलिदान देने वाला – ………………………………….
(d) जो जीता नहीं जाता – ………………………………….
उत्तर
(1) जिसे व्यवस्थित न गढ़ा गया हो – अनगढ़
(2) निंदा करने वाला – निंदक
(3) देश के लिए प्राणों का बलिदान देने वाला – शहीद
(4) जो जीता नहीं जाता – अजेय

अभिव्यक्ति

प्रश्न 3.
(अ) ‘समाज सुधारक समाज में व्याप्त बुराइयों को पूर्णत: समाप्त करने में विफल रहे’, इस कथन पर अपना मत प्रकट कीजिए।
उत्तर :
संसार में अनेक महान समाज सुधारक हुए हैं। वे अपने समाजसुधार के कार्यों से अपना नाम अमर कर गए हैं। हर युग में अनेक समाज सुधारक समाज को सुधारने का कार्य करते रहे हैं, पर समाज में व्याप्त बुराइयों की तुलना में उनकी संख्या नगण्य है। इसके अलावा समाज सुधारकों को जनता का पर्याप्त सहयोग भी नहीं मिल पाता। इसलिए वे अपने कार्य में पूर्णतः सफल नहीं हो पाते।

इतना ही नहीं, भिन्न-भिन्न कारणों से समाज विरोधी तत्त्व भी अपने स्वार्थ के कारण समाज सुधारकों के दुश्मन बन जाते हैं। इससे समाज सुधारकों के कार्य में केवल अड़चनें ही नहीं आतीं, बल्कि उनकी जान पर भी बन आती है।

इसलिए समाज सुधारकों के लिए समाज में व्याप्त बुराइयों को पूरी तरह समाप्त करना संभव नहीं हो पाया। आए दिन लोगों के प्रति होने वाले अन्याय और अत्याचार की घटनाएँ इस बात का सबूत हैं कि समाजसुधारक समाज में व्याप्त बुराइयों को पूर्णतः समाप्त करने में विफल रहे हैं।

(आ) ‘लोगों के सक्रिय सहभाग से ही समाज सुधारक का कार्य सफल हो सकता हैं’, इस विषय पर अपने विचार स्पष्ट कीजिए।
उत्तर :
समाज सुधार कोई छोटा-मोटा काम नहीं है। इसका दायरा विशाल है। इस कार्य को करने का बीड़ा उठाने वाले को इस कार्य में निरंतर रत रहना पड़ता है। किसी भी अकेले व्यक्ति के वश का यह काम नहीं है। इस कार्य को सुचारु रूप से संपन्न करने के लिए समाज सुधारक को समाज के प्रतिनिधियों एवं निष्ठावान कार्यकर्ताओं का सहयोग लेना आवश्यक होता है। समाज में तरहतरह की विकृतियाँ होती हैं।

उनके बारे में जानकारी करने और उन्हें १ दूर करने के लिए समाज के लोगों का सहयोग प्राप्त करना अत्यंत आवश्यक होता है। इसके अतिरिक्त किसी भी सामाजिक बुराई के पीछे विभिन्न कारणों से कुछ लोगों का स्वार्थ भी होता है। ऐसे लोगों से निपटे बिना उसे दूर नहीं किया जा सकता।

बिना लोगों के सक्रिय सहयोग से ऐसे समाज विरोधी तत्त्वों से पार पाना संभव, नहीं हो पाता। इसलिए इन सभी बातों को ध्यान में रखकर समाज ३ सुधारक को लोगों का सक्रिय सहयोग लेना आवश्यक है। लोगों ३ के सक्रिय सहयोग से ही वह अपने कार्य में सफल हो सकता है।

पाठ पर आधारित लघूत्तरी प्रश्न –

प्रश्न 4.
(अ) ‘पाप के चार हथियार पाठ का संदेश लिखिए।
उत्तर :
‘पाप के चार हथियार’ पाठ में लेखक कन्हैयालाल मिश्र ‘प्रभाकर’ ने एक ज्वलंत समस्या की ओर ध्यान आकर्षित किया है। संसार में चारों ओर पाप, अन्याय और अत्याचार व्याप्त है, फिर भी कोई संत, महात्मा, अवतार, पैगंबर या सुधारक इससे मुक्ति का मार्ग बताता है, तो लोग उसकी बातों पर ध्यान नहीं देते और उसकी अवहेलना करते हैं। उसकी निंदा करते हैं। इतना ही नहीं, इस प्रकार के कई सुधारकों को तो अपनी जान तक गँवा देनी पड़ी है।

लेकिन यही लोग सुधारकों, महात्माओं की मृत्यु के पश्चात उनके स्मारक और मंदिर बनाते हैं और उनके विचारों और कार्यों का गुणगान करते नहीं थकते। जो लोग सुधारक के जीवित रहते उसकी बातों को अनसुना करते रहे, उसकी निंदा करते रहे और उसकी जान के दुश्मन बने रहे, उसकी मृत्यु के पश्चात उन्हीं लोगों के मन में उसके लिए श्रद्धा की भावना उमड़ पड़ती है और वे उसके स्मारक और मंदिर बनाने लगते हैं।

इस प्रकार लेखक ने ‘पाप के चार हथियार’ के द्वारा यह संदेश दिया है कि सुधारकों और महात्माओं के जीते जी उनके विचारों पर ध्यान देने और उन पर अमल करने से ही समस्याओं का समाधान होता है, न कि स्मारक और मंदिर बनाने से।

(आ) ‘पाप के चार हथियार निबंध का उददेश्य स्पष्ट कीजिए।
उत्तर :
संसार में पाप, अत्याचार और अन्याय का बोलबाला रहा है और आज भी वह वैसा ही है। इससे लोगों को मुक्ति दिलाने के लिए अनेक महापुरुषों, सुधारकों, समाज सेवकों एवं संतमहात्माओं ने अथक प्रयास किया, पर वे अपने प्रयास में सफल नहीं हो पाए। उल्टे उन्हें समाज के लोगों की उपेक्षा तथा निंदा आदि का शिकार होना पड़ा और कुछ लोगों को अपनी जान भी गँवानी पड़ी।

पर देखा यह गया है कि जीते जी जिन सुधारकों और महापुरुषों को समाज का सहयोग नहीं मिला और उनकी अवहेलना होती रही, मरने के बाद उनके स्मारक और मंदिर भी बने और लोगों ने उन्हें भगवान-सुधारक कह कर वंदनीय भी बताया। यहाँ लेखक यह कहना चाहते हैं कि मरणोपरांत सुधारक का स्मारक-मंदिर बनना सुधारक और उसके प्रयासों दोनों की पराजय है।

अच्छा तो तब होता, जब लोग सुधारक के जीते जी उसके विचारों को अपनाते और पाप, अत्याचार और अन्याय जैसी बुराइयों के खिलाफ संघर्ष में उसका सहयोग करते और समाज से इन बुराइयों के दूर होने में सहायक बनते। इससे सुधारक समाज को पाप, अन्याय, भ्रष्टाचार और अत्याचार जैसी बुराइयों से मुक्ति दिलाने में सफल हो सकता था। लोगों को सुधारक की उपेक्षा, निंदा अथवा उनके खिलाफ षड्यंत्र रचने के बजाय उनके अभियान में अपना पूरा सहयोग देना चाहिए। तभी समाज से ये बुराइयाँ दूर हो सकती हैं। यही इस पाठ का उद्देश्य है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) कन्हैयालाल मिश्र ‘प्रभाकर’ जी के निबंध संग्रहों के नाम लिखिए –
उत्तर :
कन्हैयालाल मिश्र ‘प्रभाकर’जी के निबंध संग्रहों के नाम हैं –
(1) जिंदगी मुस्कुराई
(2) बाजे पायलिया के घूघरू
(3) जिंदगी लहलहाई
(4) महके आँगन – चहके द्वार।

(आ) लेखक कन्हैयालाल मिश्र ‘प्रभाकर’ जी की भाषाशैली –
उत्तर :
कन्हैयालाल मिश्रजी कथाकार, निबंधकार एवं पत्रकार थे। आपकी भाषा मँजी हुई, सहज-सरल और मुहावरेदार है, जो कथ्य को दृश्यमान और सजीव बना देती है। आपके लेखन में तत्सम शब्दों का प्रयोग भारतीय चिंतन-मनन को अधिक प्रभावशाली बना देता है। आप एक सफल निबंधकार थे। आप में अपने विषय को प्रखरता से प्रस्तुत करने की सामर्थ्य है।

प्रश्न 6.
रचना के आधार पर निम्न वाक्यों के भेद पहचानिए :
(1) संयोग से तभी उन्हें कहीं से तीन सौ रुपये मिल गए।
(2) यह वह समय था, जब भारत में अकबर की तूती बोलती थी।
(3) सुधारक होता है करुणाशील और उसका सत्य सरल विश्वासी।
(4) फिर भी सावधानी तो अपेक्षित है ही।
(5) यह तस्वीर निःसंदेह भयावह है लेकिन इसे किसी भी तरह अतिरंजित नहीं कहा जाना चाहिए।
(6) आप यहीं प्रतीक्षा कीजिए।
(7) निराला जी हमें उस कक्ष में ले गए, जो उनकी कठोर साधना का मूक साक्षी रहा है।
(8) लोगों ने देखा और हैरान रह गए।
(9) सामने एक बोर्ड लगा था, जिस पर अंग्रेजी में लिखा था।
(10) ओजोन एक गैस है, जो ऑक्सीजन के तीन परमाणुओं से मिलकर बनी होती है।
उत्तर :
(1) सरल वाक्य
(2) मिश्र वाक्य
(3) संयुक्त वाक्य
(4) सरल वाक्य
(5) मिश्र वाक्य
(6) सरल वाक्य
(7) मिश्र वाक्य
(8) संयुक्त वाक्य
(9) मिश्र वाक्य
(10) मिश्र वाक्य।

Hindi Yuvakbharati 12th Digest Chapter 6 पाप के चार हथियार Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए
गद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
शब्दों को उचित वर्ग में लिखिए :
पीड़ित वर्ग – पीड़क वर्ग

जीवन में दोष	संसार में पाप
व्यवस्था में अन्याय	व्यवहार में अत्याचार

उत्तर :

जीवन में दोष	व्यवस्था में अन्याय
संसार में पाप	व्यवहार में अत्याचार

प्रश्न 2.
उत्तर लिखिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विलोम शब्द लिखिए :
(1) नैतिक x …………………………..
(2) पाप x …………………………..
(3) सत्य x …………………………..
(4) असफल x …………………………..
उत्तर :
(1) नैतिक x अनैतिक
(3) सत्य x असत्य
(2) पाप x पुण्य
(4) असफल x सफल।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए : गद्यांश में आए पाप के दो नारे –
(1) …………………………
(2) …………………………
उत्तर :
(1) अजी बेवकूफ है, लोगों को बेवकूफ बनाना चाहता है।
(2) ओह, मैं तुम्हें खिलौना समझता रहा और तुम साँप निकले। पर मैं साँप को जीता नहीं छोडूंगा – पीस डालूँगा।

प्रश्न 3.
आकृति पूर्ण कीजिए :
(1) सुधारक के सत्य की स्थिति –
(i) उपेक्षा की रगड़ से – कुछ तेज हो जाता है।
(i) निंदा की रगड़ से –
(iii) हत्या के घर्षण से –
उत्तर :
(i) उपेक्षा की रगड़ से – कुछ तेज हो जाता है।
(ii) निंदा की रगड़ से – और भी प्रखर हो जाता है।
(iii) हत्या के घर्षण से – प्रचंड हो उठता है।

प्रश्न 4.

उत्तर :

प्रश्न 5.

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त उपसर्गयुक्त शब्द ढूँढ़कर लिखिए :
(1) …………………………………
(2) …………………………………
(3) …………………………………
(4) …………………………………
उत्तर :
(1) विद्रोह
(2) प्रतिनिधि
(3) असह्य
(4) प्रलाप।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :
(1) पाप सत्य पर यह फेंकता है – [ ]
(2) पाप का ब्रह्मास्त्र – [ ]
(3) अब पाप का नारा यह होता है – [ ]
(4) अब पाप सुधारक की यह लगता है – [ ]
उत्तर :
ब्रह्मास्त्र
श्रद्धा
सत्य की जय! सुधारक की जय
चरण वंदना

प्रश्न 2.
कृति पूर्ण कीजिए :

उत्तर :

उत्तर :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
पद्यांश से ढूँढ़कर प्रत्यययुक्त शब्द लिखिए और शब्द और प्रत्यय अलग करके लिखिए :
(1) ………………………………
(2) ………………………………
(3) ………………………………
(4) ………………………………
उत्तर :
(1) तोलकर – तोल + कर
(2) विश्वासी – विश्वास + ई
(3) वंदनीय – वंदन + ईय
(4) अजेयता – अजेय + ता।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) चरण – ………………………………
(2) सुधारक – ………………………………
(3) वाणी – ………………………………
(4) पराजय – ………………………………
उत्तर :
(1) चरण – पुल्लिंग
(2) सुधारक – पुल्लिंग
(3) वाणी – स्त्रीलिंग
(4) पराजय – स्त्रीलिंग।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘स्मारकों और समाधियों का उद्देश्य’ विषय पर 40 से 50 शब्दों में अपने विचार व्यक्त कीजिए।
उत्तर :
स्मारक और समाधियाँ महापुरुषों, मनीषियों, विचारकों, समाज सुधारकों, राजनेताओं तथा शहीदों के अद्भुत कार्यों को ध्यान में रखकर उन्हें सम्मान देने, याद रखने तथा उनके कार्यों से प्रेरणा लेने के उद्देश्य से बनाए जाते हैं। इससे आने वाली पीढ़ियाँ उन्हें याद रखती हैं और उनके कार्यों से प्रेरणा लेती हैं।

पर ऐसा बहुत कम देखा जाता है। अकसर इनके प्रति लोगों में श्रद्धा की भावना होती है। वे इनके दर्शन कर इन्हें श्रद्धांजलि भी देते हैं, पर इनके कार्यों से प्रेरणा लेने की बात उनके मन में कम ही आती है। इन महापुरुषों, मनीषियों, विचारकों, समाज सुधारकों, राजनेताओं तथा शहीदों को सच्ची श्रद्धांजलि उनके कार्यों से प्रेरणा लेकर समाज और देश के विकास के लिए कार्य करना है।

स्मारकों एवं समाधियों की स्थापना के पीछे यही भावना छिपी होती है और लोगों के मन में भी यही भावना होनी चाहिए।

मुहावरे

निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) दाल न गलना।
अर्थ : चतुराई काम न आना।
वाक्य : आफिस के कई लोगों ने उस ईमानदार कर्मचारी को निकलवाने की बड़ी कोशिश की, पर उनकी दाल न गली।

(2) गड़े मुरदे उखाड़ना।
अर्थ : पुरानी कटु बातों को याद करना।
वाक्य : बुढ़िया अकसर अपने बेटों से गड़े मुरदे उखाड़ने की भाषा में ही बोला करती थी।

(3) फूंक फूंक कर पाँव रखना।
अर्थ : अति सावधानी बरतना।
वाक्य : सेठ मटरूमल को जब से धंधे में भारी घाटा उठाना पड़ा है, तब से वे लेन-देन में फूंक फूंक कर पाँव रखते हैं।

(4) आठ-आठ आँसू रोना।
अर्थ : बहुत अधिक रोना।
वाक्य : बुढ़िया का इकलौता बेटा जब से विदेश में नौकरी करने गया है, तब से वह उसकी याद में आठ-आठ आँसू रोती रहती है।

(5) रंग में भंग होना।
अर्थ : प्रसन्नता के वातावरण में विघ्न पड़ना।
वाक्य : कोरोना के लॉक डाउन के कारण मेरे दोस्त नलिन के विवाह समारोह के उत्सव में रंग में भंग हो गया।

काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों का काल परिवर्तन कर के वाक्य फिर से लिखिए :
(1) इसमें संसार का एक बहुत बड़ा सत्य कह दिया गया है। (पूर्ण भूतकाल)
(2) शॉ के इन शब्दों में अहंकार की पैनी धार है। (सामान्य भविष्यकाल)
(3) इसे वे क्यों नहीं बदल पाए? (सामान्य वर्तमानकाल)
(4) सुधारक का सत्य निंदा की रगड़ से और भी प्रखर हो जाता है। (अपूर्ण भूतकाल)
(5) इस वेग में वह पिस जाएगा। (पूर्ण भूतकाल)
उत्तर :
(1) इसमें संसार का एक बहुत बड़ा सत्य कह दिया गया था।
(2) शॉ के इन शब्दों में अहंकार की पैनी धार होगी।
(3) इसे वे क्यों नहीं बदल पाते?
(4) सुधारक का सत्य निंदा की रगड़ से और भी प्रखर हो रहा था।
(5) इस वेग में वह पिस गया था।

वाक्य शुद्धिकरण

प्रश्न 1.
निम्नलिखित वाक्यों को शुद्ध करके लिखिए :
(1) वह स्वरग का अमरित है।
(2) समाज की पाप विवश हो जाती है।
(3) पाप के पास चार शस्त्रे है।
(4) वे मुझे बर्दास्त नई कर सकते।
(5) ये नारा ऊँचे उठता रहता है।
उत्तर :
(1) वह स्वर्ग का अमृत है।
(2) समाज का पाप विवश हो जाता है।
(3) पाप के पास चार शस्त्र हैं।
(4) वे मुझे बर्दाश्त नहीं कर सकते।
(5) यह नारा ऊँचा उठता रहता है।

पाप के चार हथियार Summary in Hindi

पाप के चार हथियार लेखक का परिचय

पाप के चार हथियार लेखक का नाम : कन्हैयालाल मिश्र ‘प्रभाकर’। (जन्म : 26 सितंबर, 1906; निधन : 1995.)

प्रमुख कृतियाँ : ‘धरती के फूल’ (कहानी संग्रह)। ‘जिंदगी मुस्कुराई’, ‘बाजे पायलिया के घूघरू’, ‘जिंदगी लहलहाई’, ‘महके आँगन – चहके द्वार’ (निबंध संग्रह), ‘दीप जले शंख बजे’, ‘माटी हो गई सोना’ (संस्मरण एवं रेखाचित्र) आदि।

पाप के चार हथियार विशेषता : कथाकार, निबंधकार, पत्रकार तथा स्वतंत्रता सेनानी। आपने पत्रकारिता में स्वतंत्रता के स्वर को ऊँचा उठाया। आपका संपूर्ण साहित्य मूलतः सामाजिक सरोकारों का शब्दांकन है। आप पद्मश्री सम्मान से विभूषित हैं।

पाप के चार हथियार विधा : निबंध। निबंध का अर्थ है विचारों को भाषा में व्यवस्थित रूप से बाँधना। इसमें वैचारिकता का अधिक महत्त्व होता है तथा विषय को सहजता से रखने का सामर्थ्य होता है।

पाप के चार हथियार विषय प्रवेश : संसार भर के अनेक संतों, महात्माओं, महापुरुषों, विचारकों, दार्शनिकों तथा समाज सुधारकों ने मनुष्य जाति को पाप, अपराध तथा दुष्कर्मों से मुक्त कराने के लिए अथक प्रयास किया है, पर आज तक संसार में अन्याय, अत्याचार, भ्रष्टाचार, पाप और दुष्कर्मों का अंत नहीं हो पाया है। इसका कारण यह है कि लोगों को इन संतों, महात्माओं और समाज सुधारकों के प्रति श्रद्धा तो होती है, पर वे उनके द्वारा व्यक्त विचारों को अपने आचरण में गंभीरतापूर्वक नहीं उतारते। ऐसा क्यों होता है? लेखक ने प्रस्तुत निबंध में यही बताने का प्रयास किया है।

पाप के चार हथियार पाठ का सार

संसार में सदा से पाप, अपराध, अन्याय, अत्याचार, दुष्कर्म एवं भ्रष्टाचार का बोलबाला रहा है। संसार के कई महापुरुषों, विचारकों, सुधारकों एवं संतों ने मानव जाति को इनसे मुक्ति दिलाने के लिए अथक प्रयास किए हैं, पर यह समस्या आज भी पहले जैसे सर्वत्र व्याप्त है। इसका मुख्य कारण रहा है विचारकों तथा सुधारकों को लोगों का सहयोग न मिलना। इनकी कही गई बातों पर ध्यान न देना। उनके विचारों को आचरण में न उतारना। यही कारण है कि सुधारक अपने उद्देश्य में सफल नहीं हो पाते।

लेखक कहते हैं कि बुराइयों के विरुद्ध सुधारक की बातें लोगों को किसी पागल व्यक्ति की बकवास लगती हैं, जिन्हें वे सुनना ही नहीं चाहते। यदि कभी एकाध बात सुन लेते हैं, तो उसकी निंदा करते नहीं थकते और उस पर लोगों को बेवकूफ बनाने का आरोप लगाने लगते हैं। लेखक कहते हैं कि जब सुधारक का स्वर कुछ प्रखर हो जाता है, तो सामाजिक बुराइयों के लिए यह स्थिति कठिन हो जाती है और ऐसे में सुधारक की हत्या भी हो जाती है। वे कहते हैं कि सुकरात, ईसा और दयानंद की हत्या इसी तरह हुई थी।

लेकिन इसके बाद स्थिति में एकदम बदलाव आ जाता है। सुधारक के विचारों का विरोध करने वाले लोगों के मन में उसके प्रति श्रद्धा उमड़ पड़ती है। इसके बाद उसे भगवान, तीर्थकर, अवतार, पैगंबर और संत, महाप्रभु की संज्ञा दी जाने लगती है। अब वह लोगों के लिए सामान्य सुधारक न रहकर विशिष्ट व्यक्ति हो जाता है। उसके स्मारक और मंदिर बनने लगते हैं।

उसकी प्रशंसा होने लगती है। लेखक कहते हैं कि यहीं सुधारक और उसके सिद्धांत की पराजय हो जाती है। यही कारण है कि अनेक महापुरुषों, विचारकों, सुधारकों एवं संतों द्वारा इन सामाजिक बुराइयों को दूर करने के लिए किए गए प्रयास सफल न हो पाए।

पाप के चार हथियार मुहावरे : अर्थ और वाक्य प्रयोग

(1) ढाँचा डगमगा उठना।
अर्थ : आधार हिल उठना।
वाक्य : कभी-कभी किसी व्यक्ति द्वारा कोई गलत निर्णय ले लेने के कारण किसी परिवार अथवा पूरे समाज का ढाँचा डगमगा उठता है।

(2) लहर को ऊपर से उतार देना।
अर्थ : सिर झुका कर संकट को गुजरने देना।
वाक्य : कोरोना संकट देश की अर्थव्यवस्था को डगमगा देने वाला है, पर हमारी सरकार इस लहर को ऊपर से उतार देने का सफल प्रयास कर रही है।

(3) गले के नीचे उतरना।
अर्थ : स्वीकार करना।
वाक्य : महाराष्ट्र और कर्नाटक के सीमा विवाद का फैसला ऐसा होना चाहिए, जो दोनों राज्यों की सरकारों और जनता के गले उतरने वाला हो।

(4) विवश होना।
अर्थ : लाचार होना।
वाक्य : कोरोना के प्रकोप से बचने के लिए हर आदमी लॉक डाउन के समय अपने घर में रहने के लिए विवश है।

टिप्पणियाँ

• जॉर्ज बर्नार्ड शॉ : आपका जन्म 26 जुलाई, 1856 को आयलैंड में हुआ। आपको साहित्य का नोबल पुरस्कार प्राप्त हुआ है। शॉ महान नाटककार, कुशल राजनीतिज्ञ तथा समीक्षक रह चुके हैं। पिग्मॅलियन, डॉक्टर्स डायलेमा, मॅन ऐंड सुपरमॅन, सीझर ऐंड क्लिओपॅट्रा आपके प्रसिद्ध नाटक हैं।
• तीर्थंकर : जैन धर्मियों के 24 उपास्य मुनि।
• सुकरात (सॉक्रेटिस) : युनानी दार्शनिक सुकरात का जन्म ढाई हजार वर्ष पहले एथेन्स में हुआ। वे युवकों से संवाद स्थापित कर उन्हें सोचने की दिशा में प्रवृत्त करते थे। आप प्रसिद्ध विचारक प्लेटो के गुरु थे।
• दयानंद : आर्य समाज के संस्थापक स्वामी दयानंद सरस्वती समाजसुधारक के रूप में जाने जाते हैं। आपको योगशास्त्र तथा वैद्यकशास्त्र का भी ज्ञान था।
• ब्रह्मास्त्र : पुराणों के अनुसार एक प्रकार का अस्त्र जो मंत्र द्वारा चलाया जाता था।

पाप के चार हथियार शब्दार्थ

• खूबियों का पुंज = विशेषताओं का गुच्छा
• पीड़क = पीड़ा पहुँचाने वाला
• एकांगी = एक पक्षीय
• पैने = तीखे/धारदार
• बखान = वर्णन
• लोकोत्तर = सामान्य लोगों से ऊपर/विशिष्ट
• अजेय = जिसे जीता न जा सके
• अंबार = ढेर
• विडंबना = उपहास
• प्रलाप = निरर्थक बात, बकवास
• शहादत = बलिदान
• उपसंहार = सार, निष्कर्ष
• फलितार्थ = सारांश/निचोड़/तात्पर्य
• खंडित = भग्न, टूटा हुआ

पाप के चार हथियार मुहावरे

• ढाँचा डगमगा उठना = आधार हिल उठना
• लहर को ऊपर से उतार देना = सिर झुकाकर संकट को गुजरने देना
• गले के नीचे उतरना = स्वीकार होना
• विवश होना = लाचार होना

(टिप्पणियाँ)

• जॉर्ज बर्नार्ड शॉ : आपका जन्म २६ जुलाई १८५६ को आयर्लंड में हुआ। आपको साहित्य का नोबल पुरस्कार प्राप्त हुआ है। शॉ महान नाटककार, कुशल राजनीतिज्ञ तथा समीक्षक रह चुके हैं। पिग्मैलियन, डॉक्टर्स डाइलेमा, मॅन एंड सुपरमैन, सीझर अँड क्लियोपैट्रा आपके प्रसिद्ध नाटक हैं।
• तीर्थंकर : जैन धर्मियों के २४ उपास्य मुनि।
• सुकरात (सॉक्रेटिस) : यूनानी दार्शनिक सुकरात का जन्म ढाई हजार वर्ष पहले एथेन्स में हुआ। युवकों से संवाद स्थापित कर उन्हें सोचने की दिशा में प्रवृत्त करते थे। आप प्रसिद्ध विचारक प्लेटो के गुरु थे।
• दयानंद : आर्य समाज के संस्थापक स्वामी दयानंद सरस्वती समाजसुधारक के रूप में जाने जाते हैं। आपको योगशास्त्र तथा वैद्यकशास्त्र का भी ज्ञान था।
• ब्रह्मास्त्र : पुराणों के अनुसार एक प्रकार का अमोध अस्त्र जो मंत्र द्वारा चलाया जाता था।

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 9 चुनिंदा शेर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 9 चुनिंदा शेर

12th Hindi Guide Chapter 9 चुनिंदा शेर Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) लिखिए :

(a) परिंदों को यह शिकायत है –
उत्तर :
परिंदों को यह शिकायत है, हे मालिक कभी तो हमारी बात सुनो। ऐसा प्रतीत होता है कि जो दाना आपकी कृपा से हमें प्राप्त होता है, उसमें भी कीड़े लगे हैं।

(b) नदी के प्रति उत्तरदायित्व –
उत्तर :
नदी के प्रति उत्तरदायित्व – हमारी संस्कृति में नदी को माता के रूप में पूजा जाता है। नदी मानव सभ्यता के लिए जीवनदायिनी का काम करती है। इस नदी रूपी माता के लिए हमारा भी कुछ उत्तरदायित्व है। हमें नदी को स्वच्छ रखना चाहिए। कूड़ा-कचरा, रसायन नदी में नहीं डालने चाहिए।

(आ) परिणाम लिखिए :
(a) पानी सर से गुजर जाएगा तो – ………………………………………….
उत्तर :
पानी सर से गुजर जाएगा तो – पानी सर से गुजर जाने का अर्थ है परिस्थिति का हाथों से निकल जाना। ऐसी स्थिति आने पर या तो व्यक्ति बिलकुल हताश हो जाता है या विद्रोही बनकर न करने योग्य कार्य भी कर गुजरता है।

(b) कवि जिंदगी के सवालों में खो गए – ………………………………………….
उत्तर :
कवि जिंदगी के सवालों में खो गए तब ऐसा हआ कि कवि के सवालों के जवाब उनके उजालों में खो गए।

शब्द संपदा

प्रश्न 2.
पाठ में आए चार उर्दू शब्द और उनके हिंदी अर्थ :
(1) ………………… = …………………
(2) ………………… = …………………
(3) ………………… = …………………
(4) ………………… = …………………
उत्तर :
(1) खुशबू – सुगंध
(2) परिंदे – पक्षी
(3) ख्वाब – स्वप्न
(4) जिंदगी – जीवन।

अभिव्यक्ति

प्रश्न 3.
(अ) ‘आकाश के तारे तोड़ लाना’, इस मुहावरे को स्पष्ट कीजिए।
उत्तर :
आकाश के तारे तोड़ लाना मुहावरे का अर्थ है असंभव काम करना। जब कोई व्यक्ति किसी ऐसे कार्य की पूर्ति कर दे, जिसे कर पाना असंभव माना जा रहा हो तब उसके इस असंभव कार्य के लिए उपर्युक्त मुहावरे का प्रयोग किया जाता है। असीमित कठिनाइयों से भरा कोई काम, जिसे कर पाने में सभी असहज हों, वह कार्य विशेष कर पाना सभी को असंभव लगे, तब यह मुहावरा दोहराया जाता है। जैसे – तुम्हें क्या लगता है कि नलिन कुछ कर नहीं सकता। अरे… समय आने पर वह आकाश के तारे भी तोड़कर ला सकता है।

(आ) ‘क्रांति कभी भी अपने-आप नहीं आती; वह लाई जाती हैं, इस कथन पर अपने विचार लिखिए।
उत्तर :
क्रांति अर्थात बदलाव लाना। बदलाव शासन व्यवस्था के प्रति हो सकता है या फिर किसी सामाजिक प्रथा के विरोध में। क्रांति कभी भी अपने-आप नहीं आती। क्रांति के लिए मानव को ही प्रयास करना पड़ता है। कोई व्यवस्था अथवा रूढ़ि भले ही जर्जर हो चुकी हो, समाज के विकास के लिए अहितकर बन रही हो।

अगर हम उसे बदलने के लिए क्रांतिकारी कदम नहीं उठाएँगे, तो हमारा समाज प्रगति नहीं कर पाएगा, कूपमंडूक बना रहेगा। इतिहास साक्षी है कि जब-जब मानव ने नए सिद्धांतों को, नई खोजों को अपनाया, समाज निरंतर विकास के मार्ग पर आगे बढ़ता रहा।

रसास्वादन

प्रश्न 4.
(अ) कवि की भावुकता और संवेदनशीलता को समझते हुए ‘चुनिंदा शेर’ का रसास्वादन कीजिए।
उत्तर :
कवि अपनी जिंदगी में आई परेशानियों से अप्रभावित हुए बिना उनका इस प्रकार सामना करते रहे कि वहीं से मानो उजाले फूट पड़े। सारी परेशानियाँ इस प्रकार समाप्त हो गईं मानो कभी थीं ही नहीं। हर सुबह हमारे लिए एक नया संदेश लेकर आती है। रात्रि के घोर अंधकार में जुगनू द्वारा फैलाए गए हल्के से प्रकाश में भी आशा की एक किरण छिपी होती है। कवि नित्य नए सपने देखता था, जागती आँखों के सपने।

वह नहीं जानता था कि उसके सपनों में, उसके विचारों में क्रांति का बीज छिपा है। उसके द्वारा आसमान पर लिखे गए सपने एक दिन क्रांति का रूप ले लेंगे। हँसी और आँसू मनुष्य के जीवन के दो अंग हैं। परंतु आज हर मनुष्य अपने जीवन की विसंगतियों से इस कदर त्रस्त है कि वह नहीं चाहता कि दूसरा कोई भी अपने आँसुओं से उसका कंधा भिगोए। अतः हमें अपने चेहरे पर एक मुखौटा लगाकर अपने आँसुओं को हँसी से छिपा लेना चाहिए।

ईश्वर फकीरों, साधुओं और समाज की भलाई की इच्छा रखने वाले लोगों को ऐसी शक्ति प्रदान करता है कि उनके मुख से निकले आशीर्वाद सच होने लगते हैं। ऐसे लोगों की आँखें मानो करुणा और स्नेह बरसाती रहती हैं। हर मनुष्य की सहनशक्ति की एक सीमा होती है। प्रतिकूल परिस्थितियों, असफलताओं और अन्याय को सहन करने की शक्ति जिस दिन समाप्त हो जाएगी, उस व्यक्ति का विवेक उसका साथ छोड़ देगा।

वह दिन बस विद्रोह का दिन होगा। जीवन में निरंतर मिलती निराशाओं के कारण आँखों से आँसू इस प्रकार बहते रहते हैं मानो बाढ़ आ गई हो। कभी-कभी तो ऐसा प्रतीत होता है कि यह जीवन नहीं, बल्कि अषाढ़ का महीना है और निरंतर बादल बरस रहे हैं। एक मेहनतकश इन्सान जेठ मास की कड़कती हुई धूप में नंगे पाँव डामर की जलती सड़क पर चला जा रहा है। उसके पैरों की उँगलियाँ जल रही हैं।

साथ ही दिलोदिमाग में निराशा और हताशा की आँधियाँ चल रही हैं, बिजलियाँ घुमड़ रही हैं। मनुष्य की साँसें निश्चित हैं अर्थात प्रत्येक मनुष्य अपने जीवन में कितना आयुष्य पाएगा, कितनी साँसें ले पाएगा, यह पूर्वनिश्चित है। कवि को ऐसा महसूस होता है मानो उनकी साँसें उनकी अपनी नहीं हैं। अपनी साँसों पर उनका कोई अधिकार नहीं है। इस संसार में अनगिनत लोग ऐसे हैं, जिनमें से किसी का सिर खुला है, तो किसी के पैर चादर से बाहर हैं।

ये लोग अपनी आवश्यकताओं की पूर्ति भी नहीं कर पाते। हे ईश्वर ऐसा कुछ करो कि सभी लोगों को आवश्यकता की हर चीज मिले। सभी अपना भरण-पोषण उचित ढंग से कर सकें। कल भूख और बीमारी के कारण जिस मजदूर की साँसें बंद हो गई, जो इस निर्मोही दुनिया को छोड़कर चला गया, वह अनपढ़ था, निरक्षर था। परंतु उसके भी अनगिनत सपने थे। सपने देखने के लिए किसी भी प्रकार की साक्षरता की आवश्यकता नहीं होती। वह रोज अपनी इच्छाओं, आकांक्षाओं को मानो किताब में लिखता रहता था।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) कैलाश सेंगर जी की प्रसिद्ध रचनाओं के नाम – ……………………………………
उत्तर :

• सूरज तुम्हारा है (गजल संग्रह)
• यहाँ आदमी नहीं, जूते भी चलते हैं
• सुबह होने का इंतजार (कहानी संग्रह)
• अभी रात बाकी है (अनूदित साहित्य)

(आ) गजल इस भाषा का लोकप्रिय काव्य प्रकार है – ……………………………………
उत्तर :
उर्दू

प्रश्न 6.
कोष्ठक में दी गई सूचना के अनुसार काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) एक-एक क्षण आपको भेंट कर देता हूँ। (सामान्य भविष्यकाल)
(2) बैजू का लहू सूख गया है। (सामान्य भूतकाल)
(3) मन बहुत दुखी हुआ था। (अपूर्ण भूतकाल)
(4) पढ़-लिखकर नौकरी करने लगा। (पूर्ण भूतकाल)
(5) यात्रा की तिथि भी आ गई। (सामान्य वर्तमानकाल)
(6) मैं पता लगाकर आता हूँ। (सामान्य भविष्यकाल)
(7) गर्ग साहब ने अपने वचन का पालन किया। (सामान्य भविष्यकाल)
(8) मौसी कुछ नहीं बोल रही थी। (अपूर्ण वर्तमानकाल)
(9) सुधारक आते हैं। (पूर्ण भूतकाल)
(10) प्रकाश उसमें समा जाता है। (सामान्य भूतकाल)
उत्तर :
(1) एक-एक क्षण आपको भेंट कर दूंगा।
(2) बैजू का लहू सूख गया।
(3) मन बहुत दुखी हो रहा था।
(4) पढ़-लिखकर नौकरी करने लगा था।
(5) यात्रा की तिथि भी आ जाती है।
(6) मैं पता लगाकर आऊँगा।
(7) गर्ग साहब अपने वचन का पालन करेंगे।
(8) मौसी कुछ नहीं बोल रही है।
(9) सुधारक आए थे।
(10) प्रकाश उसमें समा जाता था।

Hindi Yuvakbharati 12th Digest Chapter 9 चुनिंदा शेर Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
पद्यांश क्र. 1

प्रश्न. निम्नलिखितपद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
निम्नलिखित शब्दों के लिए पद्यांश में प्रयुक्त शब्द ढूँढ़कर लिखिए :
(1) पक्षी – ………………………………………….
(2) सपना – ………………………………………….
(3) कला – ………………………………………….
(4) क्रांति – ………………………………………….
उत्तर :
(1) पक्षी – परिंदे
(2) सपना – ख्वाब
(3) कला – हुनर
(4) क्रांति – इन्कलाब

कृति 2 : (शब्द संपदा)

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द पद्यांश में से ढूँढ़कर लिखिए :
(1) निशा = कवि जिंदगी के सवालों में खो गए तब ऐसा हआ कि कवि के सवालों के जवाब उनके उजालों में खो गए।
(2) कुसुम = कवि जिंदगी के सवालों में खो गए तब ऐसा हआ कि कवि के सवालों के जवाब उनके उजालों में खो गए।
(3) प्रश्न = कवि जिंदगी के सवालों में खो गए तब ऐसा हआ कि कवि के सवालों के जवाब उनके उजालों में खो गए।
(4) स्वामी = कवि जिंदगी के सवालों में खो गए तब ऐसा हआ कि कवि के सवालों के जवाब उनके उजालों में खो गए।
उत्तर :
(1) निशा = रात
(2) कुसुम = फूल
(3) प्रश्न = सवाल
(4) स्वामी = मालिक।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
पद्यांश से दो ऐसे प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित हों :
(1) किताब
(2) अपनी साँस।
उत्तर :
(1) मजदूर रोज क्या लिखता था?
(2) कवि को क्या पराए धन-सी लगती है?

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का वचन बदलकर लिखिए :
(1) किताब – ……………………………….
(2) नदी – ……………………………….
(3) आँखों – ……………………………….
(4) उँगलियाँ – ……………………………….
उत्तर :
(1) किताब – किताबें
(2) नदी – नदियाँ
(3) आँखों – आँख
(4) उँगलियाँ – उँगली।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) साँस – ……………………………….
(2) कंगन – ……………………………….
(3) सड़क – ……………………………….
(4) चादर – ……………………………….
उत्तर :
(1) साँस – स्त्रीलिंग
(2) कंगन – पुल्लिंग
(3) सड़क – स्त्रीलिंग
(4) चादर – स्त्रीलिंग।

रसास्वादन मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर शेरों का रसास्वादन कीजिए :
उत्तर :
(1) रचना का शीर्षक : चुनिंदा शेर।
(2) रचनाकार : कैलाश सेंगर।
(3) कविता की केंद्रीय कल्पना : प्रस्तुत कविता में कवि की रचनाओं की प्रभावशीलता, परेशानियों से घबराए बिना उनका सामना करना, सुखद भविष्य के सपने देखना, उन्हें प्राप्त करने का प्रयास करने, आँसुओं को हँसी से छिपा लेना, त्याग और तपस्या के महत्त्व, समाज की भलाई की इच्छा, मनुष्य की सहन शक्ति की सीमा, विद्रोह, मेहनतकश इनसान के दिलोदिमाग में चलने वाली निराशा और हताशा की आँधियों का उल्लेख किया गया है। साथ ही इच्छा व्यक्त की गई है।
(4) रस-अलंकार :
(5) प्रतीक विधान : चट्टानी रातों को जुगनू से वह सँवारा करती है’ पंक्तियों में आशा की एक किरण के लिए जुगनू का प्रतीक के रूप में प्रयोग किया गया है।
(6) कल्पना : सामाजिक विषमता, अव्यवस्था तथा आम आदमियों की विवशताओं को अभिव्यक्त किया गया है।
(7) पसंद की पंक्तियाँ तथा प्रभाव : इसमें लाशें भी मिला करती हैं, तुम जरा देख-भाल तो लेते। इसको माँ कहके पूजनेवालों, इस नदी को खंगाल तो लेते। नदियों को माँ की तरह पूजनेवालों के लिए इन पंक्तियों में नदियोंको साफ-सुथरा रखने का आँख खोलनेवाला संदेश दिया गया है।
(8) कविता पसंद आने का कारण : इन पंक्तियों में कवि जलप्रदूषण रोकने की प्रेरणा दे रहे हैं। नदी मानव सभ्यता के लिए जीवन दायिनी का काम करती है। हमें नदी को स्वच्छ रखना चाहिए। कूड़ा-करकट, रसायन आदि नदी में नहीं डालने चाहिए।

अलंकार

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में निहित अलंकार पहचानकर उसका नाम लिखिए :
(1) नहिं पराग, नहिं मधुर मधु, नहिं विकास इहिं काल।
अलि कलि ही सौं बिंध्यौ, आगे कौन हवाल।।
(2) सिर फट गया उसका, मानो अरुण रंग का घड़ा।
(3) वन शारदी चंदिका चादर ओढ़े।
उत्तर :
(1) अन्योक्ति अलंकार
(2) उत्प्रेक्षा अलंकार
(3) रूपक अलंकार।

रस

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में निहित रस पहचानकर है उसका नाम लिखिए :
(1) बतरस लालच लाल की मुरली धरी लुकाय।
सौंह करै, भौंहन हँसै, दै न कहि नटि जाय।।

(2) एक भरोसो, एक बल, एक आस विश्वास।
एक राम घनश्याम हित, चातक तुलसीदास।।

(3) आँखें निकाल उड़ जाते, क्षण भर उड़कर आ जाते।
शव जीभ खींचके कौवे, चुभला-चुभलाकर खाते।।
उत्तर :
(1) शृंगार रस
(2) भक्ति रस
(3) वीभत्स रस।

मुहावरे

प्रश्न 1.
निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :

(1) चोर की दाढ़ी में तिनका
अर्थ : अपराधी का भयभीत और सशंकित रहना।
वाक्य : दरोगा साहब को चोर की दाढ़ी में तिनका के है सिद्धांत पर अपराधियों को पकड़ने में समय नहीं लगता था।

(2) डकार तक न लेना
अर्थ : सब कुछ हजम कर लेना।
वाक्य : भ्रष्टाचार में लिप्त लोग करोड़ों रुपए खाकर बैठ जाते हैं और डकार तक नहीं लेते।

(3) पाँचों ऊँगलियाँ घी में होना
अर्थ : चहुँ ओर लाभ होना।
वाक्य : जब तक नरेश अपने नाना के साथ कोलकाता में धंधा करता था, तब तक उसकी पाँचों ऊँगलियाँ घी में होती थी।

(4) पोंगा होना
अर्थ : नासमझ होना।
वाक्य : भोलाराम की बात मत करो, वह तो पोंगा है पोंगा।

(5) बात का धनी
अर्थ : वचन का पक्का।
वाक्य : सेठ जेठामल गुस्सैल जरूर हैं, पर बात के धनी हैं।

(6) मूंछ उखाड़ना
अर्थ : घमंड चूर-चूर कर देना।
वाक्य : गोल्डन समारा अखाड़े के बाहर दारा सिंह को बढ़-चढ़कर चुनैतियाँ दे रहा था, पर अखाड़े में उतरा, तो दारा सिंह ने पटक-पटक कर उसकी मूंछ उखाड़ ली।

वाक्य शुद्धिकरण

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) यहाँ तक की मिट्टी प्रदूषन से अछूती नहीं रही।
(2) निराला जी अपने युग की विशिष्ठ प्रतीभा हैं।
(3) चारों तरफ खुशिया जूमती थीं।
उत्तर :
(1) यहाँ तक कि मिट्टी भी प्रदूषण से अछूती नहीं रही।।
(2) निराला जी अपने युग की विशिष्ट प्रतिभा हैं।
(3) चारों तरफ खुशियाँ झूमती थीं।

चुनिंदा शेर Summary in Hindi

चुनिंदा शेर कवि का परिचय

चुनिंदा शेर कवि का नाम : कैलाश सेंगरय। (जन्म 16 फरवरी, 1954.)

चुनिंदा शेर प्रमुख कृतियाँ : सूरज तुम्हारा है (गजल संग्रह), यहाँ आदमी नहीं, जूते भी चलते हैं, सुबह होने का इंतजार (कहानी संग्रह), अभी रात बाकी है (अनूदित साहित्य) आदि।

चुनिंदा शेर विशेषता : कैलाश सेंगर जी की कविताएँ सहज-सरल भाषा में लिखी गई हैं, जिनमें आम आदमी की जिंदगी में व्याप्त वेदना, भावना आदि की अभिव्यक्ति है। गजल, गीत, कविता, कहानी, नाटक और पत्रकारिता के क्षेत्र में आपका योगदान उल्लेखनीय है। कथानक के तीखेपन और मौलिक प्रयोगों के कारण कैलाश सेंगर अत्यंत लोकप्रिय हैं। विधा उर्दू कविता का लोकप्रिय प्रकार गजल है। इस विधा की लोकप्रियता के फलस्वरूप हिंदी साहित्य में भी इसने अपनी जगह बना ली है और प्रेम की भावभूमि से हटकर यथार्थ की जमीन पर खड़ी है।

चुनिंदा शेर विषय प्रवेश : प्रस्तुत गजलों में सामाजिक विषमता, अव्यवस्था, आम आदमी की विवशताओं को विभिन्न चित्र शब्दों के माध्यम से अभिव्यक्त किया गया है।

चुनिंदा शेर कविता का सरल अर्थ

(1) गजलों से खुशबू …………………………………………. हुनर देता है।

कैलाश जी का यह मानना है कि कवि अपनी गजलों से, अपनी कविताओं से खुशबू फैलाने में सक्षम होता है। वह अपनी कृतियों से चट्टानों पर भी फूल खिला सकता है अर्थात असंभव कार्य को संभव करके दिखा सकता है, क्रांति ला सकता है।

परिंदे ईश्वर से शिकायत कर रहे हैं कि हे मालिक कभी तो हमारी बात भी सुनो। ऐसा प्रतीत होता है कि जो दाना आपकी कृपा से हमें प्राप्त होता है, उसमें भी कीड़े लगे हैं। अर्थात आपकी कृपा भी अब प्रदूषित हो गई है।

कवि जिंदगी में आई परेशानियों से अप्रभावित हुए बिना उनका इस प्रकार सामना करते रहे कि वहीं से मानो उजाले फूट पड़े। सारी परेशानियाँ इस प्रकार समाप्त हो गईं मानो कभी थी ही नहीं।

कवि कहते हैं कि ऐसा प्रतीत होता है कि हर सुबह हमारे लिए एक नया संदेश लेकर आती है। रात्रि के घोर अंधकार में जुगनू है द्वारा फैलाए गए हल्के से प्रकाश में भी आशा की एक किरण छिपी होती है।

कवि नित्य नए सपने देखता था, जागती आँखों के सपने। वह नहीं जानता था कि उसके सपनों में, उसके विचारों में क्रांति का बीज छिपा है। उसके द्वारा आसमान पर लिखे गए सपने एक दिन क्रांति का रूप ले लेंगे।

हँसी और आँसू मनुष्य के जीवन के दो अंग हैं। परंतु आज है हर मनुष्य अपने जीवन की विसंगतियों से इस कदर त्रस्त है कि वह नहीं चाहता कि दूसरा कोई भी अपने आँसुओं से उसका कंधा भिगोए। अतः अच्छा यही रहेगा कि अपने चेहरे पर एक मुखौटा लगाया जाए और अपने आँसुओं को हँसी से छिपा लिया जाए।

कवि त्याग और तपस्या के महत्त्व पर प्रकाश डालते हुए कहते हैं कि ईश्वर फकीरों, साधुओं और समाज की भलाई की इच्छा रखने वाले लोगों को ऐसी शक्ति प्रदान करता है कि उनके मुख से निकले आशीर्वाद सच होने लगते हैं। ऐसे लोगों की आँखें मानो करुणा और स्नेह बरसाती रहती हैं।

(2) इसमें लाशें भी मिला करती हैं …………………………………………. इक किताब लिखता था।

कवि कहते हैं कि हमारी संस्कृति में नदी को माता के रूप में पूजा जाता है। नदी मानव सभ्यता के लिए जीवन दायिनी का काम करती है। इस नदी रूपी माता के लिए हमारा भी कुछ उत्तरदायित्व है। इसमें लोग लाशें तक बहा देते हैं। हमें नदी को स्वच्छ रखना चाहिए। कूड़ा-कचरा, रसायन आदि नदी में नहीं डालने चाहिए।

कवि कहते हैं कि हर मनुष्य की सहन शक्ति की एक सीमा होती है। प्रतिकूल परिस्थितियों, असफलताओं और अन्याय को सहन करने की शक्ति जिस दिन समाप्त हो जाएगी, उस व्यक्ति का विवेक उसका साथ छोड़ देगा, वह दिन बस विद्रोह का दिन होगा।

कवि कहते हैं कि जीवन में निरंतर मिलती निराशाओं के कारण आँखों से आँसू इस प्रकार बहते रहते हैं मानो बाढ़ आ गई हो। कभी-कभी तो ऐसा प्रतीत होता है कि यह जीवन नहीं, बल्कि अषाढ़ का महीना है और निरंतर बादल बरस रहे हैं।

एक मेहनतकश इन्सान का वर्णन करते हुए कवि कहते हैं कि वह जेठ मास की कड़कती हुई धूप में नंगे पाँव डामर की जलती सड़क पर चला जा रहा है। उसके पैरों की उँगलियाँ जल रही हैं। साथ ही दिलोदिमाग में निराशा और हताशा की आँधियाँ चल रही हैं, बिजलियाँ घुमड़ रही हैं।

कवि कहते हैं कि मनुष्य की साँसें निश्चित हैं अर्थात प्रत्येक मनुष्य अपने जीवन में कितना आयुष्य पाएगा, कितनी साँसें ले पाएगा, यह पूर्वनिश्चित है। कवि को ऐसा महसूस होता है मानो उनकी साँसें उनकी अपनी नहीं हैं। अपनी साँसों की संख्या पर उनका कोई अधिकार नहीं है। ठीक उसी प्रकार जैसे किसी दूसरे की धन-संपत्ति पर हमारा अधिकार नहीं होता। या जैसे हम आवश्यकता पड़ने पर अपने कंगन या अन्य कोई आभूषण किसी महाजन के पास गिरवी रख देते हैं। उसी प्रकार हमारी साँसें भी हमारी अपनी नहीं है।

कवि सृष्टि को बनाने वाले जीवनदाता से कहता है कि इस संसार में अनगिनत लोग ऐसे हैं, जिनमें किसी का सिर खुला है, तो किसी के पैर चादर से बाहर हैं। ये लोग अपनी आवश्यकताओं की पूर्ति भी नहीं कर पाते। हे ईश्वर ऐसा कुछ करो कि सभी लोगों को आवश्यकता की हर चीज मिले। सभी अपना भरण-पोषण उचित ढंग से कर सकें।

कवि कहते हैं कि कल भूख और बीमारी के कारण जिस मजदूर की साँसें बंद हो गईं, जो इस निर्मोही दुनिया को छोड़कर चला गया, वह अनपढ़ था, निरक्षर था। परंतु उसके भी अनगिनत सपने थे। सपने देखने के लिए किसी भी प्रकार की साक्षरता की आवश्यकता नहीं होती। वह रोज अपनी इच्छाओं, आकांक्षाओं को मानो किताब में लिखता रहता था।

चुनिंदा शेर मुहावरे : अर्थ और वाक्य प्रयोग

(1) चट्टानों पर फूल खिलना।
अर्थ : कड़ी मेहनत से खुशहाली पाना।
वाक्य : हिमानी ऐसी दृढनिश्चयी है कि यदि वह ठान ले तो चट्टानों पर फूल खिला सकती है।

(2) सिर से पानी गुजर जाना।
अर्थ : कष्ट या संकट का पराकाष्ठा तक पहुँच जाना, संयम अथवा सहने की शक्ति समाप्त हो जाना।
वाक्य : आए दिन सेठ की गालियाँ सुन-सुनकर गोपाल को लगा कि अब तो सिर से पानी गुजर गया और वह मालिक को टका-सा जवाब देकर नौकरी छोड़कर चला गया।