Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4
I : Choose correct alternatives.
Question 1.
If the equation 4x2 + hxy + y2 = 0 represents two coincident lines, then h = _________.
(A) ± 2
(B) ± 3
(C) ± 4
(D) ± 5
Solution:
(C) ± 4
Question 2.
If the lines represented by kx2 – 3xy + 6y2 = 0 are perpendicular to each other then _________.
(A) k = 6
(B) k = -6
(C) k = 3
(D) k = -3
Solution:
(B) k = -6
Question 3.
Auxiliary equation of 2x2 + 3xy – 9y2 = 0 is _________.
(A) 2m2 + 3m – 9 = 0
(B) 9m2 – 3m – 2 = 0
(C) 2m2 – 3m + 9 = 0
(D) -9m2 – 3m + 2 = 0
Solution:
(B) 9m2 – 3m – 2 = 0
Question 4.
The difference between the slopes of the lines represented by 3x2 – 4xy + y2 = 0 is _________.
(A) 2
(B) 1
(C) 3
(D) 4
Solution:
(A) 2
![]()
Question 5.
If the two lines ax2 +2hxy+ by2 = 0 make angles α and β with X-axis, then tan (α + β) = _____.
(A) \(\frac{h}{a+b}\)
(B) \(\frac{h}{a-b}\)
(C) \(\frac{2 h}{a+b}\)
(D) \(\frac{2 h}{a-b}\)
Solution:
(D) \(\frac{2 h}{a-b}\)
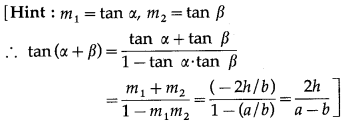
Question 6.
If the slope of one of the two lines \(\frac{x^{2}}{a}+\frac{2 x y}{h}+\frac{y^{2}}{b}\) = 0 is twice that of the other, then ab:h2 = ___.
(A) 1 : 2
(B) 2 : 1
(C) 8 : 9
(D) 9 : 8
Solution:
(D) 9 : 8
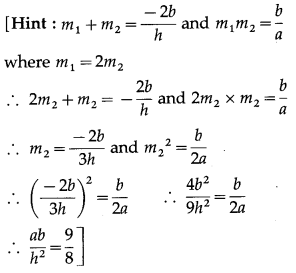
Question 7.
The joint equation of the lines through the origin and perpendicular to the pair of lines 3x2 + 4xy – 5y2 = 0 is _________.
(A) 5x2 + 4xy – 3y2 = 0
(B) 3x2 + 4xy – 5y2 = 0
(C) 3x2 – 4xy + 5y2 = 0
(D) 5x2 + 4xy + 3y2 = 0
Solution:
(A) 5x2 + 4xy – 3y2 = 0
Question 8.
If acute angle between lines ax2 + 2hxy + by2 = 0 is, \(\frac{\pi}{4}\) then 4h2 = _________.
(A) a2 + 4ab + b2
(B) a2 + 6ab + b2
(C) (a + 2b)(a + 3b)
(D) (a – 2b)(2a + b)
Solution:
(B) a2 + 6ab + b2
![]()
Question 9.
If the equation 3x2 – 8xy + qy2 + 2x + 14y + p = 1 represents a pair of perpendicular lines then
the values of p and q are respectively _________.
(A) -3 and -7
(B) -7 and -3
(C) 3 and 7
(D) -7 and 3
Solution:
(B) -7 and -3
Question 10.
The area of triangle formed by the lines x2 + 4xy + y2 = 0 and x – y – 4 = 0 is _________.
(A) \(\frac{4}{\sqrt{3}}\) Sq. units
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
(C) \(\frac{16}{\sqrt{3}}\) Sq. units
(D)\(\frac{15}{\sqrt{3}}\) Sq. units
Solution:
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
[Hint : Area = \(\frac{p^{2}}{\sqrt{3}}\), where p is the length of perpendicular from the origin to x – y – 4 = 0]
Question 11.
The combined equation of the co-ordinate axes is _________.
(A) x + y = 0
(B) x y = k
(C) xy = 0
(D) x – y = k
Solution:
(C) xy = 0
![]()
Question 12.
If h2 = ab, then slope of lines ax2 + 2hxy + by2 = 0 are in the ratio _________.
(A) 1 : 2
(B) 2 : 1
(C) 2 : 3
(D) 1 : 1
Solution:
(D) 1 : 1
[Hint: If h2 = ab, then lines are coincident. Therefore slopes of the lines are equal.]
Question 13.
If slope of one of the lines ax2 + 2hxy + by2 = 0 is 5 times the slope of the other, then 5h2 = _________.
(A) ab
(B) 2 ab
(C) 7 ab
(D) 9 ab
Solution:
(D) 9 ab
Question 14.
If distance between lines (x – 2y)2 + k(x – 2y) = 0 is 3 units, then k =
(A) ± 3
(B) ± 5\(\sqrt {5}\)
(C) 0
(D) ± 3\(\sqrt {5}\)
Solution:
(D) ± 3\(\sqrt {5}\)
[Hint: (x – 2y)2 + k(x – 2y) = 0
∴ (x – 2y)(x – 2y + k) = 0
∴ equations of the lines are x – 2y = 0 and x – 2y + k = 0 which are parallel to each other.
∴ \(\left|\frac{k-0}{\sqrt{1+4}}\right|\) = 3
∴ k = ± 3\(\sqrt {5}\)
![]()
II. Solve the following.
Question 1.
Find the joint equation of lines:
(i) x – y = 0 and x + y = 0
Solution:
The joint equation of the lines x – y = 0 and
x + y = 0 is
(x – y)(x + y) = 0
∴ x2 – y2 = 0.
(ii) x + y – 3 = 0 and 2x + y – 1 = 0
Solution:
The joint equation of the lines x + y – 3 = 0 and 2x + y – 1 = 0 is
(x + y – 3)(2x + y – 1) = 0
∴ 2x2 + xy – x + 2xy + y2 – y – 6x – 3y + 3 = 0
∴ 2x2 + 3xy + y2 – 7x – 4y + 3 = 0.
(iii) Passing through the origin and having slopes 2 and 3.
Solution:
We know that the equation of the line passing through the origin and having slope m is y = mx. Equations of the lines passing through the origin and having slopes 2 and 3 are y = 2x and y = 3x respectively.
i.e. their equations are
2x – y = 0 and 3x – y = 0 respectively.
∴ their joint equation is (2x – y)(3x – y) = 0
∴ 6x2 – 2xy – 3xy + y2 = 0
∴ 6x2 – 5xy + y2 = 0.
(iv) Passing through the origin and having inclinations 60° and 120°.
Solution:
Slope of the line having inclination θ is tan θ .
Inclinations of the given lines are 60° and 120°
∴ their slopes are m1 = tan60° = \(\sqrt {3}\) and
m2 = tan 120° = tan (180° – 60°)
= -tan 60° = –\(\sqrt {3}\)
Since the lines pass through the origin, their equa-tions are
y = \(\sqrt {3}\)x and y= –\(\sqrt {3}\)x
i.e., \(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0
∴ the joint equation of these lines is
(\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ 3x2 – y2 = 0.
![]()
(v) Passing through (1, 2) amd parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0
∴ the equations of the lines passing through (1, 2) and parallel to the coordinate axes are x = 1 and y =1
i.e. x – 1 = 0 and y – 2 0
∴ their combined equation is
(x – 1)(y – 2) = 0
∴ x(y – 2) – 1(y – 2) = 0
∴ xy – 2x – y + 2 = 0
(vi) Passing through (3, 2) and parallel to the line x = 2 and y = 3.
Solution:
Equations of the lines passing through (3, 2) and parallel to the lines x = 2 and y = 3 are x = 3 and y = 2.
i.e. x – 3 = 0 and y – 2 = 0
∴ their joint equation is
(x – 3)(y – 2) = 0
∴ xy – 2x – 3y + 6 = 0.
(vii) Passing through (-1, 2) and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0.
Solution:
Let L1 and L2 be the lines passing through the origin and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 respectively.
Slopes of the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 are \(-\frac{1}{2}\) and \(-\frac{3}{-4}=\frac{3}{4}\) respectively.
∴ slopes of the lines L1and L2 are 2 and \(\frac{-4}{3}\) respectively.
Since the lines L1 and L2 pass through the point (-1, 2), their equations are
∴ (y – y1) = m(x – x1)
∴ (y – 2) = 2(x + 1)
⇒ y – 1 = 2x + 2
⇒ 2x – y + 4 = 0 and
∴ (y – 2) = \(\left(\frac{-4}{3}\right)\)(x + 1)
⇒ 3y – 6 = (-4)(x + 1)
⇒ 3y – 6 = -4x + 4
⇒ 4x + 3y – 6 + 4 = 0
⇒ 4x + 3y – 2 = 0
their combined equation is
∴ (2x – y + 4)(4x + 3y – 2) = 0
∴ 8x2 + 6xy – 4x – 4xy – 3y2 + 2y + 16x + 12y – 8 = 0
∴ 8x2 + 2xy + 12x – 3y2 + 14y – 8 = 0
![]()
(viii) Passing through the origin and having slopes 1 + \(\sqrt {3}\) and 1 – \(\sqrt {3}\)
Solution:
Let l1 and l2 be the two lines. Slopes of l1 is 1 + \(\sqrt {3}\) and that of l2 is 1 – \(\sqrt {3}\)
Therefore the equation of a line (l1) passing through the origin and having slope is
y = (1 + \(\sqrt {3}\))x
∴ (1 + \(\sqrt {3}\))x – y = 0 ..(1)
Similarly, the equation of the line (l2) passing through the origin and having slope is
y = (1 – \(\sqrt {3}\))x
∴ (1 – \(\sqrt {3}\))x – y = 0 …(2)
From (1) and (2) the required combined equation is
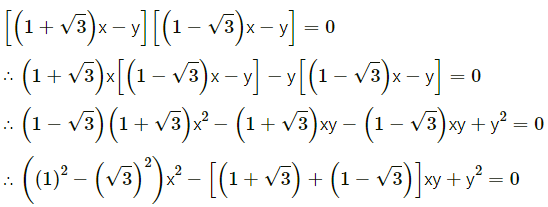
∴ (1 – 3)x2 – 2xy + y2 = 0
∴ -2x2 – 2xy + y2 = 0
∴ 2x2 + 2xy – y2 = 0
This is the required combined equation.
(ix) Which are at a distance of 9 units from the Y – axis.
Solution:
Equations of the lines, which are parallel to the Y-axis and at a distance of 9 units from it, are x = 9 and x = -9
i.e. x – 9 = 0 and x + 9 = 0
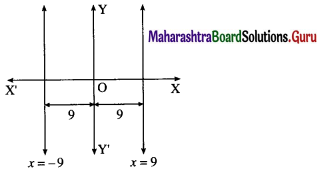
∴ their combined equation is
(x – 9)(x + 9) = 0
∴ x2 – 81 = 0.
(x) Passing through the point (3, 2), one of which is parallel to the line x – 2y = 2 and other is perpendicular to the line y = 3.
Solution:
Let L1 be the line passes through (3, 2) and parallel to the line x – 2y = 2 whose slope is \(\frac{-1}{-2}=\frac{1}{2}\)
∴ slope of the line L1 is \(\frac{1}{2}\).
∴ equation of the line L1 is
y – 2 = \(\frac{1}{2}\)(x – 3)
∴ 2y – 4 = x – 3 ∴ x – 2y + 1 = 0
Let L2 be the line passes through (3, 2) and perpendicular to the line y = 3.
∴ equation of the line L2 is of the form x = a.
Since L2 passes through (3, 2), 3 = a
∴ equation of the line L2 is x = 3, i.e. x – 3 = 0
Hence, the equations of the required lines are
x – 2y + 1 = 0 and x – 3 = 0
∴ their joint equation is
(x – 2y + 1)(x – 3) = 0
∴ x2 – 2xy + x – 3x + 6y – 3 = 0
∴ x2 – 2xy – 2x + 6y – 3 = 0.
(xi) Passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18.
Solution:
Let L1 and L2 be the lines passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18 respectively.
Slopes of the lines x + 2y = 19 and 3x + y = 18 are \(-\frac{1}{2}\) and \(-\frac{3}{1}\) = -3 respectively.
Since the lines L1 and L2 pass through the origin, their equations are
y = 2x and y = \(\frac{1}{3}\)x
i.e. 2x – y = 0 and x – 3y = 0
∴ their combined equation is
(2x – y)(x – 3y) = 0
∴ 2x2 – 6xy – xy + 3y2 = 0
∴ 2x2 – 7xy + 3y2 = 0.
![]()
Question 2.
Show that each of the following equation represents a pair of lines.
(i) x2 + 2xy – y2 = 0
Solution:
Comparing the equation x2 + 2xy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = 2, i.e. h = 1 and b = -1
∴ h2 – ab = (1)2 – 1(-1) = 1 + 1=2 > 0
Since the equation x2 + 2xy – y2 = 0 is a homogeneous equation of second degree and h2 – ab > 0, the given equation represents a pair of lines which are real and distinct.
(ii) 4x2 + 4xy + y2 = 0
Solution:
Comparing the equation 4x2 + 4xy + y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 4, 2h = 4, i.e. h = 2 and b = 1
∴ h2 – ab = (2)2 – 4(1) = 4 – 4 = 0
Since the equation 4x2 + 4xy + y2 = 0 is a homogeneous equation of second degree and h2 – ab = 0, the given equation represents a pair of lines which are real and coincident.
(iii) x2 – y2 = 0
Solution:
Comparing the equation x2 – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = 0, i.e. h = 0 and b = -1
∴ h2 – ab = (0)2 – 1(-1) = 0 + 1 = 1 > 0
Since the equation x2 – y2 = 0 is a homogeneous equation of second degree and h2 – ab > 0, the given equation represents a pair of lines which are real and distinct.
![]()
(iv) x2 + 7xy – 2y2 = 0
Solution:
Comparing the equation x2 + 7xy – 2y2 = 0
a = 1, 2h = 7 i.e., h = \(\frac{7}{2}\) and b = -2
∴ h2 – ab = \(\left(\frac{7}{2}\right)^{2}\) – 1(-2)
= \(\frac{49}{4}\) + 2
= \(\frac{57}{4}\) i.e. 14.25 = 14 > 0
Since the equation x2 + 7xy – 2y2 = 0 is a homogeneous equation of second degree and h2 – ab > 0, the given equation represents a pair of lines which are real and distinct.
(v) x2 – 2\(\sqrt {3}\) xy – y2 = 0
Solution:
Comparing the equation x2 – 2\(\sqrt {3}\) xy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h= -2\(\sqrt {3}\), i.e. h = –\(\sqrt {3}\) and b = 1
∴ h2 – ab = (-\(\sqrt {3}\))2 – 1(1) = 3 – 1 = 2 > 0
Since the equation x2 – 2\(\sqrt {3}\)xy – y2 = 0 is a homo¬geneous equation of second degree and h2 – ab > 0, the given equation represents a pair of lines which are real and distinct.
![]()
Question 3.
Find the separate equations of lines represented by the following equations:
(i) 6x2 – 5xy – 6y2 = 0
Solution:
6x2 – 5xy – 6y2 = 0
∴ 6x2 – 9xy + 4xy – 6y2 = 0
∴ 3x(2x – 3y) + 2y(2x – 3y) = 0
∴ (2x – 3y)(3x + 2y) = 0
∴ the separate equations of the lines are
2x – 3y = 0 and 3x + 2y = 0.
(ii) x2 – 4y2 = 0
Solution:
x2 – 4y2 = 0
∴ x2 – (2y)2 = 0
∴(x – 2y)(x + 2y) = 0
∴ the separate equations of the lines are
x – 2y = 0 and x + 2y = 0.
(iii) 3x2 – y2 = 0
Solution:
3x2 – y2 = 0
∴ (\(\sqrt {3}\) x)2 – y2 = 0
∴ (\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ the separate equations of the lines are
\(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0.
![]()
(iv) 2x2 + 2xy – y2 = 0
Solution:
2x2 + 2xy – y2 = 0
∴ The auxiliary equation is -m2 + 2m + 2 = 0
∴ m2 – 2m – 2 = 0
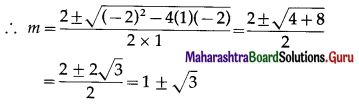
m1 = 1 + \(\sqrt {3}\) and m2 = 1 – \(\sqrt {3}\) are the slopes of the lines.
∴ their separate equations are
y = m1x and y = m2x
i.e. y = (1 + \(\sqrt {3}\))x and y = (1 – \(\sqrt {3}\))x
i.e. (\(\sqrt {3}\) + 1)x – y = 0 and (\(\sqrt {3}\) – 1)x + y = 0.
Question 4.
Find the joint equation of the pair of lines through the origin and perpendicular to the lines
given by :
(i) x2 + 4xy – 5y2 = 0
Solution:
Comparing the equation x2 + 4xy – 5y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = 4, b= -5
Let m1 and m2 be the slopes of the lines represented by x2 + 4xy – 5y2 = 0.
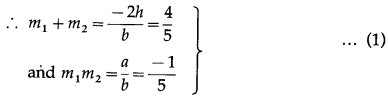
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\frac{4}{5}\)xy – \(\frac{1}{5}\)y2 = 0 …[By (1)]
∴ 5x2 + 4xy – y2 = 0
![]()
(ii) 2x2 – 3xy – 9y2 = 0
Solution:
Comparing the equation 2x2 – 3xy – 9y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 2, 2h = -3, b = -9
Let m1 and m2 be the slopes of the lines represented by 2x2 – 3xy – 9y2 = 0
∴ m1 + m2 =\(\frac{-2 h}{b}=-\frac{3}{9}\) and m1m2 = \(\frac{a}{b}=-\frac{2}{9}\) …(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y)(x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\left(-\frac{3}{9}\right)\)xy + \(\left(-\frac{2}{9}\right)\)y2 = 0 …[By (1)]
∴ 9x2 – 3xy – 2y2 = 0
(iii) x2 + xy – y2 = 0
Solution:
Comparing the equation x2+ xy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = 1, b = -1
Let m1 and m2 be the slopes of the lines represented by x2 + xy – y2 = 0
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-1}{-1}\) and m1m2 = \(\frac{\mathrm{a}}{\mathrm{b}}=\frac{1}{-1}\) = -1 ..(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y)(x + m2y) = 0
∴ x2 + (m1 + m2) + m1m2y2 = 0
∴ x2 + 1xy + (-1)y2 = 0 …[By (1)]
∴ x2 + xy – y2 = 0
![]()
Question 5.
Find k if
(i) The sum of the slopes of the lines given by 3x2 + kxy – y2 = 0 is zero.
Solution:
Comparing the equation 3x2 + kxy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 3, 2h = k, b = -1
Let m1 and m2 be the slopes of the lines represented by 3x2 + kxy – y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-k}{-1}\) = k
Now, m1 + m2 = 0 … (Given)
∴ k = 0.
(ii) The sum of slopes of the lines given by 2x2 + kxy – 3y2 = 0 is equal to their product.
Question is modified.
The sum of slopes of the lines given by x2 + kxy – 3y2 = 0 is equal to their product.
Solution:
Comparing the equation x2 + kxy – 3y2 = 0, with ax2 + 2hxy + by2 = 0, we get,
a = 1, 2h = k, b = -3
Let m1 and m2 be the slopes of the lines represented by x2 + kxy – 3y2 = 0.
∴ m1 + m2 = \(-\frac{2 h}{b}=\frac{-k}{-3}=\frac{k}{3}\)
and m1m2 = \(\frac{a}{b}=\frac{1}{-3}=\frac{-1}{3}\)
Now, m1 + m2 = m1m2 … (Given)
∴ \(\frac{k}{3}=\frac{-1}{3}\)
∴ k = -1.
(iii) The slope of one of the lines given by 3x2 – 4xy + ky2 = 0 is 1.
Solution:
The auxiliary equation of the lines given by 3x2 – 4xy + ky2 = 0 is km2 – 4m + 3 = 0.
Given, slope of one of the lines is 1.
∴ m = 1 is the root of the auxiliary equation km2 – 4m + 3 = 0.
∴ k(1)2 – 4(1) + 3 = 0
∴ k – 4 + 3 = 0
∴ k = 1.
![]()
(iv) One of the lines given by 3x2 – kxy + 5y2 = 0 is perpendicular to the 5x + 3y = 0.
Solution:
The auxiliary equation of the lines represented by 3x2 – kxy + 5y2 = 0 is 5m2 – km + 3 = 0.
Now, one line is perpendicular to the line 5x + 3y = 0, whose slope is \(-\frac{5}{3}\).
∴ slope of that line = m = \(\frac{3}{5}\)
∴ m = \(\frac{3}{5}\) is the root of the auxiliary equation 5
5m2 – km + 3 = 0.
∴ 5\(\left(\frac{3}{5}\right)^{2}\) – k\(\left(\frac{3}{5}\right)\) + 3 = 0
∴ \(\frac{9}{5}-\frac{3 k}{5}\) + 3 = 0
∴ 9 – 3k + 15 = 0
∴ 3k = 24
∴ k = 8.
(v) The slope of one of the lines given by 3x2 + 4xy + ky2 = 0 is three times the other.
Solution:
3x2 + 4xy + ky2 = 0
∴ divide by x2
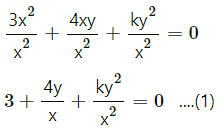
∴ y = mx
∴ \(\frac{\mathrm{y}}{\mathrm{x}}\) = m
put \(\frac{\mathrm{y}}{\mathrm{x}}\) = m in equation (1)
Comparing the equation km2 + 4m + 3 = 0 with ax2 + 2hxy+ by2 = 0, we get,
a = k, 2h = 4, b = 3
m1 = 3m2 ..(given condition)
m1 + m2 = \(\frac{-2 h}{k}=-\frac{4}{k}\)
m1m2 = \(\frac{a}{b}=\frac{3}{k}\)
m1 + m2 = \(-\frac{4}{\mathrm{k}}\)
4m2 = \(-\frac{4}{\mathrm{k}}\) …(m1 = 3m2)
m2 = \(-\frac{1}{\mathrm{k}}\)
m1m2 = \(\frac{3}{k}\)
\(3 \mathrm{~m}_{2}^{2}=\frac{3}{\mathrm{k}}\) …(m1 = 3m2)
\(3\left(-\frac{1}{\mathrm{k}}\right)^{2}=\frac{3}{\mathrm{k}}\) …(m2 = \(-\frac{1}{k}\))
\(\frac{1}{k^{2}}=\frac{1}{k}\)
k2 = k
k = 1 or k = 0
![]()
(vi) The slopes of lines given by kx2 + 5xy + y2 = 0 differ by 1.
Solution:
Comparing the equation kx2 + 5xy +y2 = 0 with ax2 + 2hxy + by2
a = k, 2h = 5 i.e. h = \(\frac{5}{2}\)
m1 + m2 = \(\frac{-2 h}{b}=-\frac{5}{1}\) = -5
and m1m2 = \(\frac{a}{b}=\frac{k}{1}\) = k
the slope of the line differ by (m1 – m2) = 1 …(1)
∴ (m1 – m2)2 = (m1 + m2)2 – 4m1m2
(m1 – m2)2 = (-5)2 – 4(k)
(m1 – m2)2 = 25 – 4k
1 = 25 – 4k ..[By (1)]
4k = 24
k = 6
(vii) One of the lines given by 6x2 + kxy + y2 = 0 is 2x + y = 0.
Solution:
The auxiliary equation of the lines represented by 6x2 + kxy + y2 = 0 is
m2 + km + 6 = 0.
Since one of the line is 2x + y = 0 whose slope is m = -2.
∴ m = -2 is the root of the auxiliary equation m2 + km + 6 = 0.
∴ (-2)2 + k(-2) + 6 = 0
∴ 4 – 2k + 6 = 0
∴ 2k = 10 ∴ k = 5
![]()
Question 6.
Find the joint equation of the pair of lines which bisect angle between the lines given by x2 + 3xy + 2y2 = 0
Solution:
x2 + 3xy + 2y2 = 0
∴ x2 + 2xy + xy + 2y2 = 0
∴ x(x + 2y) + y(x + 2y) = 0
∴ (x + 2y)(x + y) = 0
∴ separate equations of the lines represented by x2 + 3xy + 2y2 = 0 are x + 2y = 0 and x + y = 0.
Let P (x, y) be any point on one of the angle bisector. Since the points on the angle bisectors are equidistant from both the lines,
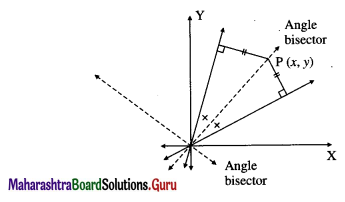
the distance of P (x, y) from the line x + 2y = 0
= the distance of P(x, y) from the line x + y = 0
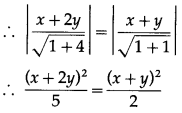
∴ 2(x + 2y)2 = 5(x + y)2
∴ 2(x2 + 4xy + 4y2) = 5(x2 + 2xy + y2)
∴ 2x2 + 8xy + 8y2 = 5x2 + 10xy + 5y2
∴ 3x2 + 2xy – 3y2 = 0.
This is the required joint equation of the lines which bisect the angles between the lines represented by x2 + 3xy + 2y2 = 0.
Question 7.
Find the joint equation of the pair of lies through the origin and making equilateral triangle with the line x = 3.
Solution:
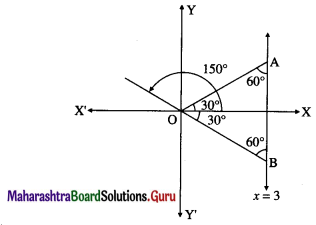
Let OA and OB be the lines through the origin making an angle of 60° with the line x = 3.
∴ OA and OB make an angle of 30° and 150° with the positive direction of X-axis
∴ slope of OA = tan 30° = 1/\(\sqrt {3}\)
∴ equation of the line OA is y = \(\frac{1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = x ∴ x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= – tan 30°= -1/\(\sqrt {3}\)
∴ equation of the line OB is y = \(\frac{-1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = -x ∴ x + \(\sqrt {3}\)y = 0
∴ required combined equation of the lines is
(x – \(\sqrt {3}\)y) (x + \(\sqrt {3}\)y) = 0
i.e. x2 – 3y2 = 0.
Question 8.
Show that the lines x2 – 4xy + y2 = 0 and x + y = 10 contain the sides of an equilateral triangle. Find the area of the triangle.
Solution:
We find the joint equation of the pair of lines OA and OB through origin, each making an angle of 60° with x + y = 10 whose slope is -1.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
Also, tan 60° = \(\left|\frac{m-(-1)}{1+m(-1)}\right|\)
∴ \(\sqrt {3}\) = \(\left|\frac{m+1}{1-m}\right|\)
Squaring both sides, we get,
3 = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ 3(1 – 2m + m2) = m2 + 2m + 1
∴ 3 – 6m + 3m2 = m2 + 2m + 1
∴ 2m2 – 8m + 2 = 0
∴ m2 – 4m + 1 = 0
∴ \(\left(\frac{y}{x}\right)^{2}\) – 4\(\left(\frac{y}{x}\right)\) + 1 = 0 …[By (1)]
∴ y2 – 4xy + x2 = 0
∴ x2 – 4xy + y\left(\frac{y}{x}\right) = 0 is the joint equation of the two lines through the origin each making an angle of 60° with x + y = 10
∴ x2 – 4xy + y2 = 0 and x + y = 10 form a triangle OAB which is equilateral.
Let seg OM ⊥r line AB whose question is x + y = 10
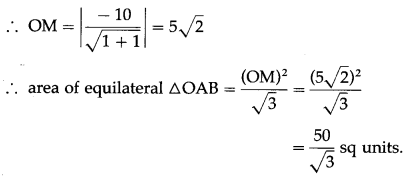
![]()
Question 9.
If the slope of one of the lines represented by ax2 + 2hxy + by2 = 0 is three times the other then prove that 3h2 = 4ab.
Solution:
Let m1 and m2 be the slopes of the lines represented by ax2 + 2hxy + by2 = 0.
∴ m1 + m2 = \(-\frac{2 h}{b}\) and m1m2 = \(\frac{a}{b}\)
We are given that m2 = 3m1
∴ m1 + 3m1 = \(-\frac{2 h}{b}\) 4m1 = \(-\frac{2 h}{b}\)
∴ m1 = \(-\frac{h}{2 b}\) …(1)
Also, m1(3m1) = \(\frac{a}{b}\) ∴ 3m12 = \(\frac{a}{b}\)
∴ 3\(\left(-\frac{h}{2 b}\right)^{2}\) = \(\frac{a}{b}\) ….[By (1)]
∴ \(\frac{3 h^{2}}{4 b^{2}}=\frac{a}{b}\)
∴ 3h2 = 4ab, as b ≠0.
Question 10.
Find the combined equation of the bisectors of the angles between the lines represented by 5x2 + 6xy – y2 = 0.
Solution:
Comparing the equation 5x2 + 6xy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 5, 2h = 6, b = -1
Let m1 and m2 be the slopes of the lines represented by 5x2 + 6xy – y2 = 0.
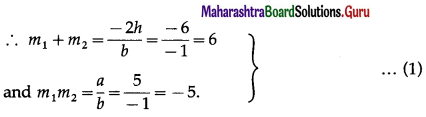
The separate equations of the lines are
y = m1x and y = m2x, where m1 ≠ m2
i.e. m1x – y = 0 and m1x – y = 0.
Let P (x, y) be any point on one of the bisector of the angles between the lines.
∴ the distance of P from the line m1x – y = 0 is equal to the distance of P from the line m2x – y = 0.
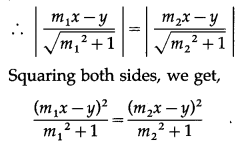
∴ (m22 + 1)(m1x – y)2 = (m12 + 1)(m2x – y)2
∴ (m22 + 1)(m12x2 – 2m1xy + y2) = (m12 + 1)(m22x2 – 2m2xy + y2)
∴ m12m22x2 – 2m1m12y2xy + m22y2 + m12x2 – 2m12xy + y2
= m12m22x2 – 2m12m2xy + m12y2 + m22x2 – 2m2xy + y2
∴ (m12 – m22)x2 + 2m1m2(m1 – m2)xy – 2(m1 – m2)xy – (m12 – m22)y2 = 0
Dividing throughout by m1 – m2 (≠0), we get,
(m1 + m2)x2 + 2m1m2xy – 2xy – (m1 + m2)y2 = 0
∴ 6x2 – 10xy – 2xy – 6y2 = 0 …[By (1)]
∴ 6x2 – 12xy – 6y2 = 0
∴ x2 – 2xy – y2 = 0
This is the joint equation of the bisectors of the angles between the lines represented by 5x2 + 6xy – y2 = 0.
![]()
Question 11.
Find a, if the sum of the slopes of the lines represented by ax2 + 8xy + 5y2 = 0 is twice their product.
Solution :
Comparing the equation ax2 + 8xy + 5y2 = 0 with ax2 + 2hxy + by2 = 0,
we get, a = a, 2h = 8, b = 5
Let m1 and m2 be the slopes of the lines represented by ax2 + 8xy + 5y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=-\frac{8}{5}\)
and m1m2 = \(\frac{a}{b}=\frac{a}{5}\)
Now, (m1 + m2) = 2(m1m2)
\(-\frac{8}{5}\) = \(2\left(\frac{a}{5}\right)\)
a = -4
Question 12.
If the line 4x – 5y = 0 coincides with one of the lines given by ax2 + 2hxy + by2 = 0, then show that 25a + 40h +16b = 0.
Solution :
The auxiliary equation of the lines represented by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0
Given that 4x – 5y = 0 is one of the lines represented by ax2 + 2hxy + by2 = 0.
The slope of the line 4x – 5y = 0 is \(\frac{-4}{-5}=\frac{4}{5}\)
∴ m = \(\frac{4}{5}\) is a root of the auxiliary equation bm2 + 2hm + a = 0.
∴ b\(\left(\frac{4}{5}\right)^{2}\) + 2h\(\left(\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}+\frac{8 h}{5}\) + a = 0
∴ 16b + 40h + 25a = 0 i.e.
∴ 25a + 40h + 16b = 0
![]()
Question 13.
Show that the following equations represent a pair of lines. Find the acute angle between them :
(i) 9x2 – 6xy + y2 + 18x – 6y + 8 = 0
Solution:
Comparing this equation with
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we get,
a = 9, h = -3, b = 1, g = 9, f = -3 and c = 8.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
9 & -3 & 9 \\
-3 & 1 & -3 \\
9 & -3 & 8
\end{array}\right|\)
= 9(8 – 9) + 3(-24 + 27) + 9(9 – 9)
= 9(-1) + 3(3) + 9(0)
= -9 + 9 + 0 = 0
and h2 – ab = (-3)2 – 9(1) = 9 – 9 = 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.
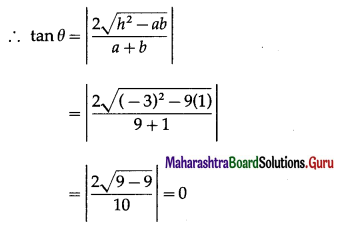
∴ tan θ = tan0°
∴ θ = 0°.
(ii) 2x2 + xy – y2 + x + 4y – 3 = 0
Solution:
Comparing this equation with
ax2 + 2hxy + by2 + 2gx + 2fy+ c = 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2 and c = -3
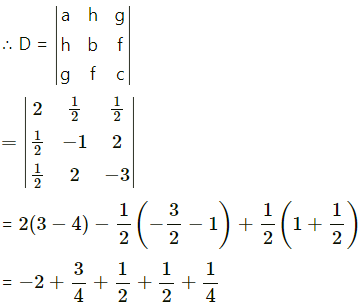
= -2 + 1 + 1
= -2 + 2= 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.
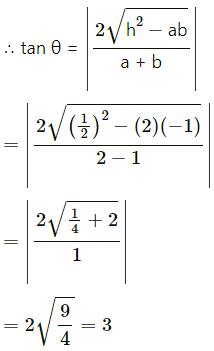
∴ tan θ = tan 3
∴ θ = tan-1(3)
(iii) (x – 3)2 + (x – 3)(y – 4) – 2(y – 4)2 = 0.
Solution :
Put x – 3 = X and y – 4 = Y in the given equation, we get,
X2 + XY – 2Y2 = 0
Comparing this equation with ax2 + 2hxy + by2 = 0, we get,
a = 1, h = \(\frac{1}{2}\), b = -2
This is the homogeneous equation of second degreeand h2 – ab = \(\left(\frac{1}{2}\right)^{2}\) – 1(-2)
= \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
Hence, it represents a pair of lines passing through the new origin (3, 4).
Let θ be the acute angle between the lines.

∴ tanθ = 3 ∴ θ = tan-1(3)
![]()
Question 14.
Find the combined equation of pair of lines through the origin each of which makes angle of 60° with the Y-axis.
Solution:
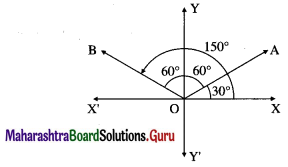
Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x2 – 3y2 = 0.
Question 15.
If lines representedby ax2 + 2hxy + by2 = 0 make angles of equal measures with the co-ordinate
axes then show that a = ± b.
OR
Show that, one of the lines represented by ax2 + 2hxy + by2 = 0 will make an angle of the same measure with the X-axis as the other makes with the Y-axis, if a = ± b.
Solution:
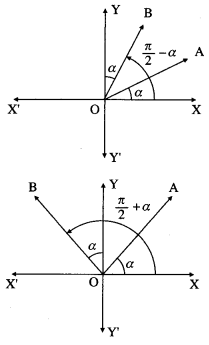
Let OA and OB be the two lines through the origin represented by ax2 + 2hxy + by2 = 0.
Since these lines make angles of equal measure with the coordinate axes, they make angles ∝ and \(\frac{\pi}{2}\) – ∝ with the positive direction of X-axis or ∝ and \(\frac{\pi}{2}\) + ∝ with thepositive direction of X-axis.
∴ slope of the line OA = m1 = tan ∝
and slope of the line OB = m2
= tan(\(\frac{\pi}{2}\) – ∝) or tan(\(\frac{\pi}{2}\) + ∝)
i.e. m2 = cot ∝ or m2 = -cot ∝
∴ m1m2 – tan ∝ x cot ∝ = 1
OR m1m2 = tan ∝ (-cot ∝) = -1
i.e. m1m2 = ± 1
But m1m2 = \(\frac{a}{b}\)
∴ \(\frac{a}{b}\)= ±1 ∴ a = ±b
This is the required condition.
![]()
Question 16.
Show that the combined equation of a pair of lines through the origin and each making an angle of ∝ with the line x + y = 0 is x2 + 2(sec 2∝) xy + y2 = 0.
Solution:
Let OA and OB be the required lines.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
It makes an angle ∝ with x + y = 0 whose slope is -1. m +1
∴ tan ∝ = \(\left|\frac{m+1}{1+m(-1)}\right|\)
Squaring both sides, we get,
tan2∝ = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ tan2∝(1 – 2m + m2) = m2 + 2m + 1
∴ tan2∝ – 2m tan2∝ + m2tan2∝ = m2 + 2m + 1
∴ (tan2∝ – 1)m2 – 2(1 + tan2∝)m + (tan2∝ – 1) = 0
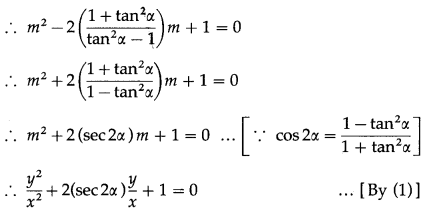
∴ y2 + 2xysec2∝ + x2 = 0
∴ x2 + 2(sec2∝)xy + y2 = 0 is the required equation.
Question 17.
Show that the line 3x + 4y+ 5 = 0 and the lines (3x + 4y)2 – 3(4x – 3y)2 =0 form an equilateral triangle.
Solution:
The slope of the line 3x + 4y + 5 = 0 is \(\frac{-3}{4}\)
Let m be the slope of one of the line making an angle of 60° with the line 3x + 4y + 5 = 0. The angle between the lines having slope m and m1 is 60°.

On squaring both sides, we get,
3 = \(\frac{(4 m+3)^{2}}{(4-3 m)^{2}}\)
∴ 3 (4 – 3m)2 = (4m + 3)2
∴ 3(16 – 24m + 9m2) = 16m2 + 24m + 9
∴ 48 – 72m + 27m2 = 16m2 + 24m + 9
∴ 11m2 – 96m + 39 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
11\(\left(\frac{y}{x}\right)^{2}\) – 96\(\left(\frac{y}{x}\right)\) + 39 = 0
∴ \(\frac{11 y^{2}}{x^{2}}-\frac{96 y}{x}\) + 39 = 0
∴ 11y2 – 96xy + 39x2 = 0
∴ 39x2 – 96xy + 11y2 = 0.
∴ 39x2 – 96xy + 11y2 = 0 is the joint equation of the two lines through the origin each making an angle of 60° with the line 3x + 4y + 5 = 0.
The equation 39x2 – 96xy + 11y2 = 0 can be written as :
-39x2 + 96xy – 11y2 = 0
i.e., (9x2 – 48x2) + (24xy + 72xy) + (16y2 – 27y2) = 0
i.e. (9x2 + 24xy + 16y2) – (48x2 – 72xy + 27y2) = 0
i.e. (9x2 + 24xy + 16y2) – 3(16x2 – 24xy + 9y2) = 0
i.e. (3x + 4y)2 – 3(4x – 3y)2 = 0
Hence, the line 3x + 4y + 5 = 0 and the lines
(3x + 4y)2 – 3(4x – 3y)2 form the sides of an equilateral triangle.
![]()
Question 18.
Show that lines x2 – 4xy + y2 = 0 and x + y = \(\sqrt {6}\) form an equilateral triangle. Find its area and perimeter.
Solution:
x2 – 4xy + y2 = 0 and x + y = \(\sqrt {6}\) form a triangle OAB which is equilateral.
Let OM be the perpendicular from the origin O to AB whose equation is x + y = \(\sqrt {6}\)
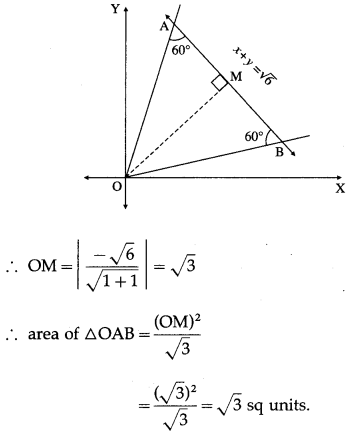
In right angled triangle OAM,
sin 60° = \(\frac{\mathrm{OM}}{\mathrm{OA}}\) ∴ \(\frac{\sqrt{3}}{2}\) = \(\frac{\sqrt{3}}{\mathrm{OA}}\)
∴ OA = 2
∴ length of the each side of the equilateral triangle OAB = 2 units.
∴ perimeter of ∆ OAB = 3 × length of each side
= 3 × 2 = 6 units.
Question 19.
If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is square of the other then show that a2b + ab2 + 8h3 = 6abh.
Solution:
Let m be the slope of one of the lines given by ax2 + 2hxy + by2 = 0.
Then the other line has slope m2
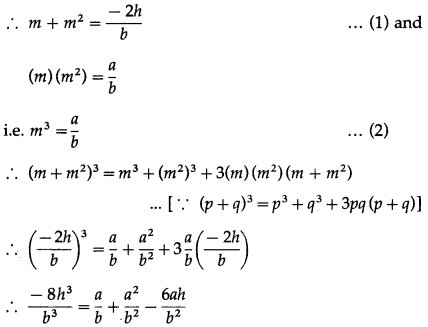
Multiplying by b3, we get,
-8h3 = ab2 + a2b – 6abh
∴ a2b + ab2 + 8h3 = 6abh
This is the required condition.
Question 20.
Prove that the product of lengths of perpendiculars drawn from P (x1, y1) to the lines repersented by ax2 + 2hxy + by2 = 0 is \(\left|\frac{a x_{1}^{2}+2 h x_{1} y_{1}+b y_{1}^{2}}{\sqrt{(a-b)^{2}+4 h^{2}}}\right|\)
Solution:
Let m1 and m2 be the slopes of the lines represented by ax2 + 2hxy + by2 = 0.
∴ m1 + m2 = \(-\frac{2 h}{b}\) and m1m2 = \(\frac{a}{b}\) …(1)
The separate equations of the lines represented by
ax2 + 2hxy + by2 = 0 are
y = m1x and y = m2x
i.e. m1x – y = 0 and m2x – y = 0
Length of perpendicular from P(x1, 1) on

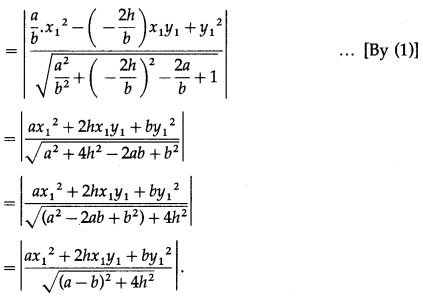
![]()
Question 21.
Show that the difference between the slopes of lines given by (tan2θ + cos2θ )x2 – 2xytanθ + (sin2θ )y2 = 0 is two.
Solution:
Comparing the equation (tan2θ + cos2θ)x2 – 2xy tan θ + (sin2θ) y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = tan2θ + cos2θ, 2h = -2 tan θ and b = sin2θ
Let m1 and m2 be the slopes of the lines represented by the given equation.
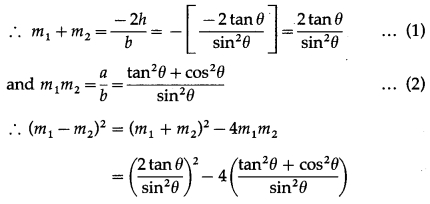
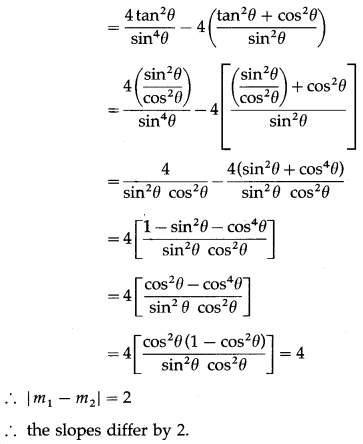
Question 22.
Find the condition that the equation ay2 + bxy + ex + dy = 0 may represent a pair of lines.
Solution:
Comparing the equation
ay2 + bxy + ex + dy = 0 with
Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0, we get,
A = 0, H = \(\frac{b}{2}\), B = a,G = \(\frac{e}{2}\), F = \(\frac{d}{2}\), C = 0
The given equation represents a pair of lines,

i.e. if bed – ae2 = 0
i.e. if e(bd – ae) = 0
i.e. e = 0 or bd – ae = 0
i.e. e = 0 or bd = ae
This is the required condition.
Question 23.
If the lines given by ax2 + 2hxy + by2 = 0 form an equilateral triangle with the line lx + my = 1 then show that (3a + b)(a + 3b) = 4h2.
Solution:
Since the lines ax2 + 2hxy + by2 = 0 form an equilateral triangle with the line lx + my = 1, the angle between the lines ax2 + 2hxy + by2 = 0 is 60°.
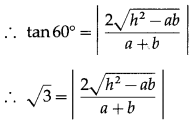
∴ 3(a + b)2 = 4(h2 – ab)
∴ 3(a2 + 2ab + b2) = 4h2 – 4ab
∴ 3a2 + 6ab + 3b2 + 4ab = 4h2
∴ 3a2 + 10ab + 3b2 = 4h2
∴ 3a2 + 9ab + ab + 3b2 = 4h2
∴ 3a(a + 3b) + b(a + 3b) = 4h2
∴ (3a + b)(a + 3b) = 4h2
This is the required condition.
![]()
Question 24.
If line x + 2 = 0 coincides with one of the lines represented by the equation x2 + 2xy + 4y + k = 0 then show that k = -4.
Solution:
One of the lines represented by
x2 + 2xy + 4y + k = 0 … (1)
is x + 2 = 0.
Let the other line represented by (1) be ax + by + c = 0.
∴ their combined equation is (x + 2)(ax + by + c) = 0
∴ ax2 + bxy + cx + 2ax + 2by + 2c = 0
∴ ax2 + bxy + (2a + c)x + 2by + 2c — 0 … (2)
As the equations (1) and (2) are the combined equations of the same two lines, they are identical.
∴ by comparing their corresponding coefficients, we get,
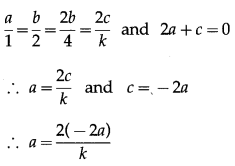
∴ 1 = \(\frac{-4}{k}\)
∴ k = -4.
Question 25.
Prove that the combined equation of the pair of lines passing through the origin and perpendicular to the lines represented by ax2 + 2hxy + by2 = 0 is bx2 – 2hxy + ay2 = 0
Solution:
Let m1 and m2 be the slopes of the lines represented by ax2 + 2hxy + by2 = 0.

Now, required lines are perpendicular to these lines.
∴ their slopes are and \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(-\frac{1}{m_{1}}\)x and y = \(-\frac{1}{m_{2}}\)x
i.e. m1y= -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y)(x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2\(\frac{-2 h}{b}\)x + \(\frac{a}{b}\)y2 = 0
∴ bx2 – 2hxy + ay2 = 0.
![]()
Question 26.
If equation ax2 – y2 + 2y + c = 1 represents a pair of perpendicular lines then find a and c.
Solution:
The given equation represents a pair of lines perpendicular to each other.
∴ coefficient of x2 + coefficient of y2 = 0
∴ a – 1 = 0 ∴ a = 1
With this value of a, the given equation is
x2 – y2 + 2y + c – 1 = 0
Comparing this equation with
Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0, we get,
A = 1, H = 0, B = -1, G = 0, F = 1, C = c – 1
Since the given equation represents a pair of lines,
D = \(\left|\begin{array}{ccc}
A & H & G \\
H & B & F \\
G & F & C
\end{array}\right|\) = 0
∴ \(\left|\begin{array}{rrr}
1 & 0 & 0 \\
0 & -1 & 1 \\
0 & 1 & c-1
\end{array}\right|\) = 0
∴ 1(-c + 1 – 1) – 0 + 0 = 0
∴ -c = 0
∴ c = 0.
Hence, a = 1, c = 0.