Class 11

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.2

Question 1.
First, 6 faced die which is numbered 1 to 6 is thrown, then a 5 faced die which is numbered 1 to 5 is thrown. What is the probability that sum of the numbers on the upper faces of the dice is divisible by 2 or 3?
Solution:
When a 6 faced die and a 5 faced die are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4,4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
∴ n(S) = 30
Let event A: The sum of the numbers on the upper faces of the dice is divisible by 2.
A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4)}
∴ n(A) = 15
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{15}{30}\)
Let event B: Sum of the numbers on the upper faces of the dice is divisible by 3.
B = {(1, 2), (1, 5), (2, 1), (2, 4), (3, 3), (4, 2), (4, 5), (5, 1), (5, 4), (6, 3)}
∴ n(B) = 10
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{10}{30}\)
Now,
A ∩ B = {(1, 5), (2,4), (3, 3), (4, 2), (5, 1)}
∴ n(A ∩ B) = 5
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{5}{30}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{15}{30}+\frac{10}{30}-\frac{5}{30}\)
= \(\frac{20}{30}\)
= \(\frac{2}{3}\)

Question 2.
A card is drawn from a pack of 52 cards. What is the probability that,
(i) card is either red or black?
(ii) card is either black or a face card?
Solution:
One card can be drawn from the pack of 52 cards in \({ }^{52} \mathrm{C}_{1}\) = 52 ways.
∴ n(S) = 52
The pack of 52 cards consists of 26 red and 26 black cards.
(i) Let event A: A red card is drawn.
∴ Red card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26ways
∴ n(A) = 26
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{26}{52}\)
Let event B: A black card is drawn.
∴ Black card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26 ways.
∴ n(B) = 26
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{26}{52}\)
Since A and B are mutually exclusive events,
P(A ∩ B) = 0
∴ Required probability
P(A ∪ B) = P(A) + P(B)
= \(\frac{26}{52}+\frac{26}{52}\)
= 1

(ii) Let event A: A black card is drawn.
∴ Black card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26 ways.
n(A) = 26
n(A) 26 n(S) ~ 52
Let event B: A face card is drawn.
There are 12 face cards in the pack of 52 cards.
∴ 1 face card can be drawn in \({ }^{12} \mathrm{C}_{1}\) = 12 ways.
∴ n(B) = 12
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{12}{52}\)
There are 6 black face cards.
∴ n(A ∩ B) = 6
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{6}{52}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{26}{52}+\frac{12}{52}-\frac{6}{52}\)
= \(\frac{32}{52}\)
= \(\frac{8}{13}\)

Question 3.
A girl is preparing for National Level Entrance exam and State Level Entrance exam for professional courses. The chances of her cracking National Level exam is 0.42 and that of State Level exam is 0.54. The probability that she clears both the exams is 0.11. Find the probability that
(i) she cracks at least one of the two exams.
(ii) she cracks only one of the two.
(iii) she cracks none.
Solution:
Let event A: The girl cracks the National Level exam.
∴ P(A) = 0.42
Let event B: The girl cracks the State Level exam.
∴ P(B) = 0.54
Also, P(A ∩ B) = 0.11
(i) P(the girl cracks at least one of the two exams)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.42 + 0.54 – 0.11
= 0.85

(ii) P(the girl cracks only one of the two exams)
= P(A) – P(B) – 2P(A ∩ B)
= 0.42 + 0.54 – 2(0.11)
= 0.74

(iii) P(the girl cracks none of the exams)
= P(A’ ∩ B’)
= P(A ∪ B)’
= 1 – P(A ∪ B)
= 1 – 0.85
= 0.15

Question 4.
A bag contains 75 tickets numbered from 1 to 75. One ticket is drawn at random. Find the probability that,
(i) number on the ticket is a perfect square or divisible by 4.
(ii) number on the ticket is a prime number or greater than 40.
Solution:
Out of the 75 tickets, one ticket can be drawn in \({ }^{75} \mathrm{C}_{1}\) = 75 ways.
∴ n(S) = 75
(i) Let event A: The number on the ticket is a perfect square.
∴ A = {1, 4, 9, 16, 25, 36, 49, 64}
∴ n(A) = 8
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{75}\)
Let event B: The number on the ticket is divisible by 4.
∴ B = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72}
∴ n(B) = 18
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{18}{75}\)
Now, A ∩ B = {4, 16, 36, 64}
∴ n(A ∩ B) = 4
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{4}{75}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{8}{75}+\frac{18}{75}-\frac{4}{75}\)
= \(\frac{22}{75}\)

(ii) Let event A: The number on the ticket is a prime number.
∴ A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73}
∴ n(A) = 21
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{21}{75}\)
Let event B: The number is greater than 40.
∴ B = {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75}
∴ n(B) = 35
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{35}{75}\)
Now,
A ∩ B = {41, 43, 47, 53, 59, 61, 67, 71, 73}
∴ n(A ∩ B) = 9
∴ n(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{9}{75}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{21}{75}+\frac{35}{75}-\frac{9}{75}\)
= \(\frac{47}{75}\)

Question 5.
The probability that a student will pass in French is 0.64, will pass in Sociology is 0.45 and will pass in both is 0.40. What is the probability that the student will pass in at least one of the two subjects?
Solution:
Let event A: The student will pass in French.
∴ P(A) = 0.64
Let event B: The student will pass in Sociology.
∴ P(B) = 0.45
Also, P(A ∩ B) = 0.40
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.64 + 0.45 – 0.40
= 0.69

Question 6.
Two fair dice are thrown. Find the probability that the number on the upper face of the first die is 3 or sum of the numbers on their upper faces is 6.
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: The number on the upper face of the first die is 3.
∴ A = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)}
∴ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}\)
Let event B: Sum of the numbers on their upper faces is 6.
∴ B = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
∴ n(B) = 5
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{5}{36}\)
Now, A ∩ B = {(3, 3)}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{1}{36}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{36}+\frac{5}{36}-\frac{1}{36}\)
= \(\frac{10}{36}\)
= \(\frac{5}{18}\)

Question 7.
For two events A and B of a sample space S, if P(A) = \(\frac{3}{8}\), P(B) = \(\frac{1}{2}\) and P(A ∪ B) = \(\frac{5}{8}\). Find the value of the following.
(a) P(A ∩ B)
(b) P(A’ ∩ B’)
(c) P(A’ ∪ B’)
Solution:
Here, P(A) = \(\frac{3}{8}\), P(B) = \(\frac{1}{2}\), P(A ∪ B) = \(\frac{5}{8}\)
(a) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{3}{8}+\frac{1}{2}-\frac{5}{8}\)
= \(\frac{1}{4}\)

(b) P(A’ ∩ B’) = P(A ∪ B)’
= 1 – P(A ∪ B)
= 1 – \(\frac{5}{8}\)
= \(\frac{3}{8}\)

(c) P(A’ ∪ B’) = P(A ∩ B)’
= 1 – P(A ∩ B)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)

Question 8.
For two events A and B of a sample space S, if P(A ∪ B) = \(\frac{5}{6}\), P(A ∩ B) = \(\frac{1}{3}\) and P(B’) = \(\frac{1}{3}\), then find P(A).
Solution:
Here, P(A ∪ B) = \(\frac{5}{6}\), P(A ∩ B) = \(\frac{1}{3}\), P(B’) = \(\frac{1}{3}\)
P(B) = 1 – P(B’)
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
\(\frac{5}{6}\) = P(A) + \(\frac{2}{3}-\frac{1}{3}\)
∴ \(\frac{5}{6}\) = P(A) + \(\frac{1}{3}\)
∴ P(A) = \(\frac{5}{6}-\frac{1}{3}\) = \(\frac{1}{2}\)

Question 9.
A bag contains 5 red, 4 blue and an unknown number m of green balls. If the probability of getting both the balls green, when two balls are selected at random is \(\frac{1}{7}\), find m.
Solution:
Total number of balls in the bag = 5 + 4 + m = 9 + m
Two balls are selected from (9 + m) balls in \({ }^{9+m} \mathrm{C}_{2}\) ways.
∴ n(S) = \({ }^{9+m} \mathrm{C}_{2}\)
Let event A: The two balls selected are green.
∴ 2 balls can be selected from m balls in \({ }^{\mathrm{m}} \mathrm{C}_{2}\) ways.
∴ n(A) = \({ }^{\mathrm{m}} \mathrm{C}_{2}\)

(9 + m)(8 + m) = 7m(m – 1)
72 + 9m + 8m + m2 = 7m2 – 7m
6m2 – 24m – 72 = 0
m2 – 4m – 12 = 0
(m – 6)(m + 2) = 0
m = 6 or m = -2
Since number of balls cannot be negative, m ≠ -2
∴ m = 6

Question 10.
From a group of 4 men, 4 women and 3 children, 4 persons are selected at random. Find the probability that,
(i) no child is selected.
(ii) exactly 2 men are selected.
Solution:
The group consists of 4 men, 4 women and 3 children, i.e., 4 + 4 + 3 = 11 persons.
4 persons are to be selected from this group.
∴ 4 persons can be selected from 11 persons in \({ }^{11} \mathrm{C}_{4}\) ways.
∴ n(S) = \({ }^{11} \mathrm{C}_{4}\)
(i) Let event A: No child is selected.
∴ 4 persons can be selected from 4 men and 4 women, i.e., from 8 persons in \({ }^{8} \mathrm{C}_{4}\) ways.
∴ n(A) = \({ }^{8} \mathrm{C}_{4}\)

(ii) Let event B: Exactly 2 men are selected.
∴ 2 men are selected from 4 men in \({ }^{4} \mathrm{C}_{2}\) ways, and remaining 2 persons are selected from 7 persons (i.e., 4 women and 3 children) in \({ }^{7} \mathrm{C}_{2}\) ways.

Question 11.
A number is drawn at random from the numbers 1 to 50. Find the probability that it is divisible by 2 or 3 or 10.
Solution:
One number can be drawn at random from the numbers 1 to 50 in \({ }^{50} \mathrm{C}_{1}\) = 50 ways.
∴ n(S) = 50
Let event A: The number drawn is divisible by 2.
∴ A = {2, 4, 6, 8, 10, …, 48, 50}
∴ n(A) = 25
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{25}{50}\)
Let event B: The number drawn is divisible by 3.
B = {3, 6, 9, 12, …, 48}
∴ n(B) = 16
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{16}{50}\)
Let event C: The number drawn is divisible by 10.
C = {10, 20, 30, 40, 50}
∴ n(C) = 5
∴ P(C) = \(\frac{n(C)}{n(S)}=\frac{5}{50}\)
Now, A ∩ B = {6, 12, 18, 24, 30, 36, 42, 48}
∴ n(A ∩ B) = 8
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{8}{50}\)
B ∩ C = {30}
∴ n(B ∩ C) = 1
∴ P(B ∩ C) = \(\frac{\mathrm{n}(\mathrm{B} \cap \mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{1}{50}\)
A ∩ C = {10, 20, 30, 40, 50}
∴ n(A ∩ C) = 5
∴ P(A ∩ C) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{5}{50}\)
A ∩ B ∩ C = {30}
∴ n(A ∩ B ∩ C) = 1
∴ P(A ∩ B ∩C) = \(\frac{n(A \cap B \cap C)}{n(S)}=\frac{1}{50}\)
∴ P(the number is divisible by 2 or 3 or 10)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
= \(\frac{25}{50}+\frac{16}{50}+\frac{5}{50}-\frac{8}{50}-\frac{1}{50}-\frac{5}{50}+\frac{1}{50}\)
= \(\frac{33}{50}\)

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.5

Question 1.
If odds in favour of X solving a problem are 4 : 3 and odds against Y solving the same problem are 2 : 3. Find the probability of:
(i) X solving the problem
(ii) Y solving the problem
Solution:
(i) Odds in favour of X solving a problem are 4 : 3.
∴ The probability of X solving the problem is
P(X) = \(\frac{4}{4+3}=\frac{4}{7}\)

(ii) Odds against Y solving the problem are 2 : 3.
∴ The probability of Y solving the problem is
P(Y) = 1 – P(Y’)
= 1 – \(\frac{2}{2+3}\)
= 1 – \(\frac{2}{5}\)
= \(\frac{3}{5}\)

Question 2.
The odds against John solving a problem are 4 to 3 and the odds in favour of Rafi solving the same problem are 7 to 5. What is the chance that the problem is solved when both of them try it?
Solution:
The odds against John solving a problem are 4 to 3.
Let event P(A’) = P (John does not solve the problem)
= \(\frac{4}{4+3}\)
= \(\frac{4}{7}\)
So, the probability that John solves the problem
P(A) = 1 – P(A’) = 1 – \(\frac{4}{7}\) = \(\frac{3}{7}\)
Similarly, Let P(B) = P(Rafi solves the problem)
Since the odds in favour of Rafi solving the problem are 7 to 5,
P(B) = \(\frac{7}{7+5}\) = \(\frac{7}{12}\)
Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Since A, B are independent events,
P(A ∩ B) = P(A) . P(B)
∴ Required probability = P(A) + P(B) – P(A) . P(B)

Question 3.
The odds against student X solving a statistics problem are 8 : 6 and odds in favour of student Y solving the same problem are 14 : 16. Find the chance that
(i) the problem will be solved if they try it independently.
(ii) neither of them solves the problem.
Solution:
The odds against X solving a problem are 8 : 6.
Let P(X’) = P(X does not solve the problem) = \(\frac{8}{8+6}\) = \(\frac{8}{14}\)
So, the probability that X solves the problem
P(X) = 1 – P(X’) = 1 – \(\frac{8}{14}\) = \(\frac{6}{14}\)
Similarly, let P(Y) = P(Y solves the problem)
Since odds in favour of Y solving the problem are 14 : 16,
P(Y) = \(\frac{14}{14+16}=\frac{14}{30}\)
So, the probability that Y does not solve the problem
P(Y’) = 1 – P(Y)
= 1 – \(\frac{14}{30}\)
= \(\frac{16}{30}\)
(i) Required probability
P(X ∪ Y) = P(X) + P(Y) – P(X ∩ Y)
Since X and Y are independent events,
P(X ∩ Y) = P(X) . P(Y)
∴ Required probability = P(X) + P(Y) – P(X) . P(Y)
= \(\frac{6}{14}+\frac{14}{30}-\frac{6}{14} \times \frac{14}{30}\)
= \(\frac{73}{105}\)

(ii) Required probability = P(X’ ∩ Y’)
Since X and Y are independent events, X’ and Y’ are also independent events.
∴ Required probability = P(X’) . P(Y’)
= \(\frac{8}{14} \times \frac{16}{30}\)
= \(\frac{32}{105}\)

Question 4.
The odds against a husband who is 60 years old, living till he is 85 are 7 : 5. The odds against his wife who is now 56, living till she is 81 are 5 : 3. Find the probability that
(i) at least one of them will be alive 25 years hence.
(ii) exactly one of them will be alive 25 years hence.
Solution:
The odds against her husband living till he is 85 are 7 : 5.
Let P(H’) = P(husband dies before he is 85) = \(\frac{7}{7+5}=\frac{7}{12}\)
So, the probability that the husband would be alive till age 85
P(H) = 1 – P(H’) = 1 – \(\frac{7}{12}\) = \(\frac{5}{12}\)
Similarly, P(W’) = P(Wife dies before she is 81)
Since the odds against wife will be alive till she is 81 are 5 : 3.
∴ P(W’) = \(\frac{5}{5+3}=\frac{5}{8}\)
So, the probability that the wife would be alive till age 81
P(W) = 1 – P(W’) = 1 – \(\frac{5}{8}\) = \(\frac{3}{8}\)
(i) Required probability
P(H ∪ W) = P(H) + P(W) – P(H ∩ W)
Since H and W are independent events,
P(H ∩ W) = P(H) . P(W)
∴ Required probability = P(H) + P(W) – P(H) . P(W)
= \(\frac{5}{12}+\frac{3}{8}-\frac{5}{12} \times \frac{3}{8}\)
= \(\frac{40+36-15}{96}\)
= \(\frac{61}{96}\)

(ii) Required probability = P(H ∩ W’) + P(H’ ∩ W)
Since H and W are independent events, H’ and W’ are also independent events.
∴ Required probability = P(H) . P(W’) + P(H’) . P(W)
= \(\frac{5}{12} \times \frac{5}{8}+\frac{7}{12} \times \frac{3}{8}\)
= \(\frac{25+21}{96}\)
= \(\frac{46}{96}\)
= \(\frac{23}{48}\)

Question 5.
There are three events A, B, and C, one of which must, and only one can happen. The odds against event A are 7 : 4 and odds against event B are 5 : 3. Find the odds against event C.
Solution:
Since odds against A are 7 : 4,
P(A) = \(\frac{4}{7+4}=\frac{4}{11}\)
Since odds against B are 5 : 3,
P(B) = \(\frac{3}{5+3}=\frac{3}{8}\)
Since only one of the events A, B and C can happen,
P(A) + P(B) + P(C) = 1
\(\frac{4}{11}\) + \(\frac{3}{8}\) + P(C) = 1
∴ P(C) = 1 – (\(\frac{4}{11}\) + \(\frac{3}{8}\))
= 1 – \(\left(\frac{32+33}{88}\right)\)
= \(\frac{23}{88}\)
∴ P(C’) = 1 – P(C)
= 1 – \(\frac{23}{88}\)
= \(\frac{65}{88}\)
∴ Odds against the event C are P(C’) : P(C)
= \(\frac{65}{88}\) : \(\frac{23}{88}\)
= 65 : 23

Question 6.
In a single toss of a fair die, what are the odds against the event that number 3 or 4 turns up?
Solution:
When a fair die is tossed, the sample space is
S = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6
Let event A: 3 or 4 turns up.
∴ A = {3, 4}
∴ n(A) = 2
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{2}{6}=\frac{1}{3}\)
P(A’) = 1 – P(A) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
∴ Odds against the event A are P(A’) : P(A)
= \(\frac{2}{3}: \frac{1}{3}\)
= 2 : 1

Question 7.
The odds in favour of A winning a game of chess against B are 3 : 2. If three games are to be played, what are the odds in favour of A’s winning at least two games out of the three?
Solution:
Let event A: A wins the game and event B: B wins the game.
Since the odds in favour of A winning a game against B are 3 : 2,
the probability of occurrence of event A and B is given by
P(A) = \(\frac{3}{3+2}=\frac{3}{5}\) and P(B) = \(\frac{2}{3+2}=\frac{2}{5}\)
Let event E: A wins at least two games out of three games.
∴ P(E) = P(A) . P(A) . P(B) + P(A) . P(B) . P(A) + P(B) . P(A) . P(A) + P(A) . P(A) . P(A)

∴ Odds in favour of A’s winning at least two games out of three are P(E) : P(E’)
= \(\frac{81}{125}: \frac{44}{125}\)
= 81 : 44

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 8 Measures of Dispersion Ex 8.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 8 Measures of Dispersion Ex 8.3

Question 1.
The means of two samples of sizes 60 and 120 respectively are 35.4 and 30.9 and the standard deviations are 4 and 5. Obtain the standard deviation of the sample of size 180 obtained by combining the two samples.
Solution:

Question 2.
For certain data, the following information is available.

Obtain the combined standard deviation.
Solution:

Question 3.
Calculate the coefficient of variation of marks secured by a student in the exam, where the marks are:
85, 91, 96, 88, 98, 82
Solution:

Question 4.
Find the coefficient of variation of a sample that has a mean equal to 25 and a standard deviation of 5.
Solution:

Question 5.
A group of 65 students of class XI has their average height as 150.4 cm with a coefficient of variance of 2.5%. What is the standard deviation of their heights?
Solution:
Given, n = 65, \(\bar{x}\) = 150.4, C.V. = 2.5%

∴ The standard deviation of students’ height is 3.76 cm.

Question 6.
Two workers on the same job show the following results:

(i) Regarding the time required to complete the job, which worker is more consistent?
(ii) Which worker seems to be faster in completing the job?
Solution:

(i) Since C.V. (P) < C.V.(Q), Worker P is more consistent regarding the time required to complete the job. (ii) Since \(\overline{\mathrm{p}}>\overline{\mathrm{q}}\),
i.e., the expected time for completing the job is less for worker Q.
∴ Worker Q seems to be faster in completing the job.

Question 7.
A company has two departments with 42 and 60 employees respectively. Their average weekly wages are ₹ 750 and ₹ 400. The standard deviations are 8 and 10 respectively.
(i) Which department has a larger bill?
(ii) Which department has larger variability in wages?
Solution:

(i) Since \(\bar{x}_{1}>\bar{x}_{2}\),
i.e., average weekly wages are more for the first department.
∴ The first department has a larger bill.

(ii) Since C.V. (1) < C.V. (2),
second department is less consistent.
∴ The second department has larger variability in wages.

Question 8.
The following table gives the weights of the students of two classes. Calculate the coefficient of variation of the two distributions. Which series is more variable?

Solution:
Let x denote the data of class A and y denote the data of class B.
Calculation of S.D. for class A:



Since C.V. (Y) > C.V.(X),
C.V. (B) > C.V. (A)
∴ Series B is more variable.

Question 9.
Compute the coefficient of variation for team A and team B.

Which team is more consistent?
Solution:
Let f₁ denote no. of goals of team A and f₂ denote no. of goals of team B.




Since C.V. of team A > C.V. of team B,
Team B is more consistent.

Question 10.
Given below is the information about marks obtained in Mathematics and Statistics by 100 students in a class. Which subject shows the highest variability in marks?

Solution:

Since C.V. (S) > C.V. (M),
The subject statistics show higher variability in marks.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.4

Question 1.
There are three bags, each containing 100 marbles. Bag 1 has 75 red and 25 blue marbles. Bag 2 has 60 red and 40 blue marbles and Bag 3 has 45 red and 55 blue marbles. One of the bags is chosen at random and marble is picked from the chosen bag. What is the probability that the chosen marble is red?
Solution:
Let event R: Chosen marble is red.
Let event B_i: ith bag is chosen.
∴ P(B_i) = \(\frac{1}{3}\)
If Bag 1 is chosen, it has 75 red and 25 blue marbles.
∴ Probability that the chosen marble is red under the condition that it is from Bag 1 = P(R/B₁)
= \(\frac{{ }^{75} \mathrm{C}_{1}}{{ }^{100} \mathrm{C}_{1}}\)
= \(\frac{75}{100}\)
= 0.75
Similarly we get,
P(R/B₂) = \(\frac{60}{100}\) = 0.60
P(R/B₃) = \(\frac{45}{100}\) = 0.45
∴ Required probability
P(R) = P(B₁) P(R/B₁) + P(B₂) P(R/B₂) + P(B₃) P(R/B₃)
= \(\frac{1}{3}\)(0.75) + \(\frac{1}{3}\)(0.60) + \(\frac{1}{3}\)(0.45)
= \(\frac{1}{3}\)(1.8)
= 0.60

Question 2.
A box contains 2 blue and 3 pink balls and another box contains 4 blue and 5 pink balls. One ball is drawn at random from one of the two boxes and it is found to be pink. Find the probability that it was drawn from
(i) first box
(ii) second box
Solution:
Let event A₁: The ball is drawn from 1st box and
event A₂: The ball is drawn from the 2nd box.
∴ P(A₁) = \(\frac{1}{2}\), P(A₂) = \(\frac{1}{2}\)
Let event B: The ball drawn is pink.
There are 5 balls in the 1st box, of which 3 are pink.
∴ P(B/A₁) = \(\frac{3}{5}\)
There are 9 balls in the 2nd box, of which 5 are pink.
∴ P(B/A₂) = \(\frac{5}{9}\)
(i) By Bayes’ theorem,
the probability that a pink ball is drawn from the first box, is given by

(ii) By Bayes’ theorem,
the probability that a pink ball is drawn from the second box, is given by

Question 3.
There is a working women’s hostel in a town, where 75% are from neighbouring town. The rest all are from the same town. 48% of women who hail from the same town are graduates and 83% of the women who have come from the neighbouring town are also graduates. Find the probability that a woman selected at random is a graduate from the same town.
Solution:
Let the total number of women be 100.
∴ n(S) = 100
Let event N: Women are from neighbouring town,
event W: Women are from same town and
event G: Women are graduates.
Number of women from neighbouring town,
n(N) = 75
Number of women from same town,
n(W) = 25
∴ P(N) = \(\frac{n(N)}{n(S)}=\frac{75}{100}\) and
P(W) = \(\frac{n(W)}{n(S)}=\frac{25}{100}\)
P(G/N), P(G/W) represent probabilities that woman is graduate given that she is from neighbouring town or same town respectively.
∴ P(G/N) = \(\frac{\mathrm{n}(\mathrm{G} / \mathrm{N})}{\mathrm{n}(\mathrm{S})}=\frac{83}{100}\) and
P(G/W) = \(\frac{\mathrm{n}(\mathrm{G} / \mathrm{W})}{\mathrm{n}(\mathrm{S})}=\frac{48}{100}\)
By Bayes’ theorem, the probability that a women selected at random is a graduate from the same town, is given by

Question 4.
If E₁ and E₂ are equally likely, mutually exclusive and exhaustive events and P(A/E₁) = 0.2, P(A/E₂) = 0.3. Find P(E₁/A).
Solution:
E₁ and E₂ are equally likely, mutually exclusive and exhaustive events.
∴ P(E₁) = P(E₂) = \(\frac{1}{2}\)

Question 5.
Jar I contains 5 white and 7 black balls. Jar II contains 3 white and 12 black balls. A fair coin is flipped; if it is Head, a ball is drawn from Jar I, and if it is Tail, a ball is drawn from Jar II. Suppose that this experiment is done and a white ball was drawn. What is the probability that this ball was in fact taken from Jar II?
Solution:
Let event J₁: Ball drawn from jar I,
event J₂: Ball drawn from jar II.
P(J₁) = P(head) = \(\frac{1}{2}\)
P(J₂) = P(tail) = \(\frac{1}{2}\)
Let event W: Ball drawn is white.
In Jar I, there are total 12 balls, out of which 5 balls are white.
∴ Probability that the ball drawn is white under the condtion that it is drawn from Jar I.
P(W/J₁) = \(\frac{{ }^{5} C_{1}}{{ }^{12} C_{1}}=\frac{5}{12}\)
Similarly, P(W/J₂) = \(\frac{{ }^{3} C_{1}}{{ }^{15} C_{1}}=\frac{3}{15}=\frac{1}{5}\)
Required probability = P(J₂/W)
By Bayes’ theorem,

Question 6.
A diagnostic test has a probability 0.95 of giving a positive result when applied to a person suffering from a certain disease, and a probability 0.10 of giving a (false) positive result when applied to a non-sufferer. It is estimated that 0.5% of the population are sufferers. Suppose that the test is now administered to a person about whom we have no relevant information relating to the disease (apart from the fact that he/she comes from this population). Calculate the probability that:
(i) given a positive result, the person is a sufferer.
(ii) given a negative result, the person is a non-sufferer.
Solution:
Let event T: Test positive
event S: Sufferer
P(S) = \(\frac{0.5}{100}\) = 0.005
∴ P(S’) = 1 – P(S) = 1 – 0.005 = 0.995
Since a probability of getting a positive result when applied to a person suffering from a disease is 0.95 and probability of getting positive result when applied to a non sufferer is 0.10.
∴ P(T/S) = 0.95 and P(T/S’) = 0.10
∴ P(T) = P(S) P(T/S) + P(S’) P(T/S’)
= 0.005 × 0.95 + 0.995 × 0.10
= 0.10425
∴ P(T’) = 1 – P(T) = 1 – 0.10425 = 0.8958
(i) Required probability = P(S/T)
By Bayes’ theorem,

(ii) P(T’/S’) = 1 – 0.1 = 0.9
Required probability = P(S’/T’)
By Bayes’ theorem

Question 7.
A doctor is called to see a sick child. The doctor has prior information that 80% of the sick children in that area have the flu, while the other 20% are sick with measles. Assume that there is no other disease in that area. A well-known symptom of measles is rash. From the past records, it is known that, chances of having rashes given that sick child is suffering from measles is 0.95. However occasionally children with flu also develop rash, whose chance are 0.08. Upon examining the child, the doctor finds a rash. What is the probability that child is suffering from measles?
Solution:
Let the total number of sick children be 100.
∴ n(S) = 100.
Let event A: The child is sick with flu,
event B: The child is sick with measles,
event C: The child is sick with rash.
∴ n(A) = 80 and n(B) = 20
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{80}{100}=\frac{4}{5}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{20}{100}=\frac{1}{5}\)
Since the chances of having rashes, if the child is suffering from measles is 0.95 and the chances of having rashes if the child has flu is 0.08,
P(C/B) = 0.95 = \(\frac{95}{100}\) and
P(C/A) = 0.08 = \(\frac{8}{100}\)
Required probability = P(B/C)
By Bayes’ theorem,

Question 8.
2% of the population have a certain blood disease of a serious form: 10% have it in a mild form; and 88% don’t have it at all. A new blood test is developed; the probability of testing positive is \(\frac{9}{10}\) if the subject has the
serious form, \(\frac{6}{10}\) if the subject has the mild form, and \(\frac{1}{10}\) if the subject doesn’t have the disease. A subject is tested positive. What is the probability that the subject has serious form of the disease?
Solution:
Let event A₁: Disease in serious form,
event A₂: Disease in mild form,
event A₃: Subject does not have disease,
event B: Subject tests positive.
P(A₁) = 0.02, P(A₂) = 0.1, P(A₃) = 0.88
The probability of testing positive is \(\frac{9}{10}\) if the subject has the serious form, \(\frac{6}{10}\) if the subject has the mild form, and \(\frac{1}{10}\) if the subject doesn’t have the disease.
∴ P(B/A₁) = 0.9, P(B/A₂) = 0.6, P(B/A₃) = 0.1
P(B) = P(A₁) P(B/A₁) + P(A₂) P(B/A₂) + P(A₃) P(B/A₃)
= 0.02 × 0.9 + 0.1 × 0.6 + 0.88 × 0.1
= 0.166
Required probability = P(A₁/B)
By Baye’s theorem

Question 9.
A box contains three coins: two fair coins and one fake two-headed coin. A coin is picked randomly from the box and tossed.
(i) What is the probability that it lands head up?
(ii) If happens to be head, what is the probability that it is the two-headed coin?
Solution:
Let event A: Fair coin is tossed,
event B: Fake coin is tossed
and event H: Head occur.
Clearly, a fair coin has one head.
∴ Probability that head occur under the condition that the fair coin is tossed = P(H/A) = \(\frac{1}{2}\)
Fake coin has two heads.
∴ Probability that head occur under the condition that the fake coin is tossed = P(H/B) = 1
n(A) = 2, n(B) = 1, n(S) = 3
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{3}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{3}\)
(i) Required probability
P(H) = P(A) P(H/A) + P(B) P(H/B)
= \(\frac{2}{3} \times \frac{1}{2}+\frac{1}{3} \times 1\)
= \(\frac{1}{3}+\frac{1}{3}\)
= \(\frac{2}{3}\)

(ii) Required probability = P(B/H)
By Baye’s theorem

Question 10.
There are three social media groups on a mobile: Group I, Group II and Group III. The probabilities that Group I, Group II and Group III sending the messages on sports are \(\frac{2}{5}\), \(\frac{1}{2}\) and \(\frac{2}{3}\) respectively. The probability of opening the messages by Group I, Group II and Group III are \(\frac{1}{2}\), \(\frac{1}{4}\) and \(\frac{1}{4}\) respectively. Randomly one of the messages is opened and found a message on sports. What is the probability that the message was from Group III.
Solution:
Let event A: Message sent on sports by group I,
event B: Message sent on sports by group II,
event C: Message sent on sports by group III,
event E: Message is opened.
Given that the probabilities that Group I, Group II and Group III sending the messages on sports are \(\frac{2}{5}\), \(\frac{1}{2}\) and \(\frac{2}{3}\) respectively and the probability of opening the messages by Group I, Group II and Group III are \(\frac{1}{2}\), \(\frac{1}{4}\) and \(\frac{1}{4}\) respectively.
∴ P(A) = \(\frac{2}{5}\)
P(B) = \(\frac{1}{2}\)
P(C) = \(\frac{2}{3}\)
P(E/A) = \(\frac{1}{2}\)
P(E/B) = \(\frac{1}{4}\)
P(E/C) = \(\frac{1}{4}\)
Required probability = P(C/E)
By Baye’s theorem

Question 11.
Mr. X goes to office by Auto, Car and train. The probabilities of him travelling by these modes are \(\frac{2}{7}\), \(\frac{3}{7}\), \(\frac{2}{7}\) respectively. The chances of him being late to the office are \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{4}\) respectively by Auto, Car and train. On one particular day he was late to the office. Find the probability that he travelled by car.
Solution:
Let A, C and T be the events that Mr. X goes to office by Auto, Car and Train respectively.
Let L be event that he is late.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 7 Conic Sections Ex 7.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Conic Sections Ex 7.1

Question 1.
Find co-ordinates of focus, equation of directrix, length of latus rectum and the co-ordinates of end points of latus rectum of the parabola:
(i) 5y² = 24x
(ii) y² = -20x
(iii) 3x² = 8y
(iv) x² = -8y
(v) 3y² = -16x
Solution:
(i) Given equation of the parabola is 5y² = 24x.
⇒ y² = \(\frac{24}{5}\)x
Comparing this equation with y² = 4ax, we get
⇒ 4a = \(\frac{24}{5}\)
⇒ a = \(\frac{6}{5}\)
Co-ordinates of focus are S(a, 0), i.e., S(\(\frac{6}{5}\), 0)
Equation of the directrix is x + a = 0.
⇒ x + \(\frac{6}{5}\) = 0
⇒ 5x + 6 = 0
Length of latus rectum = 4a
= 4(\(\frac{6}{5}\))
= \(\frac{24}{5}\)
Co-ordinates of end points of latus rectum are (a, 2a) and (a, -2a),
⇒ \(\left(\frac{6}{5}, \frac{12}{5}\right)\) and \(\left(\frac{6}{5}, \frac{-12}{5}\right)\)

(ii) Given equation of the parabola is y² = -20x.
Comparing this equation with y² = -4ax, we get
⇒ 4a = 20
⇒ a = 5
Co-ordinates of focus are S(-a, 0), i.e., S(-5, 0)
Equation of the directrix is x – a = 0
⇒ x – 5 = 0
Length of latus rectum = 4a = 4(5) = 20
Co-ordinates of end points of latus rectum are (-a, 2a) and (-a, -2a),
⇒ (-5, 10) and (-5, -10).

(iii) Given equation of the parabola is 3x² = 8y
⇒ x² = \(\frac{8}{3}\) y
Comparing this equation with x² = 4by, we get
⇒ 4b = \(\frac{8}{3}\)
⇒ b = \(\frac{2}{3}\)
Co-ordinates of focus are S(0, b), i.e., S(0, \(\frac{2}{3}\))
Equation of the directrix is y + b = 0,
⇒ y + \(\frac{2}{3}\) = 0
⇒ 3y + 2 = 0
Length of latus rectum = 4b = 4(\(\frac{2}{3}\)) = \(\frac{8}{3}\)
Co-ordinates of end points of latus rectum are (2b, b) and (-2b, b),
⇒ \(\left(\frac{4}{3}, \frac{2}{3}\right)\) and \(\left(-\frac{4}{3}, \frac{2}{3}\right)\).

(iv) Given equation of the parabola is x² = -8y.
Comparing this equation with x² = -4by, we get
⇒ 4b = 8
⇒ b = 2
Co-ordinates of focus are S(0, -b), i.e., S(0, – 2)
Equation of the directrix is y – b = 0, i.e., y – 2 = 0
Length of latus rectum = 4b = 4(2) = 8
∴ Co-ordinates of end points of latus rectum are (2b, -b) and (-2b, -b), i.e., (4, -2) and (-4, -2).

(v) Given equation of the parabola is 3y² = -16x.
⇒ y² = \(-\frac{16}{3}\)x
Comparing this equation withy = -4ax, we get
⇒ 4a = \(\frac{16}{3}\)
⇒ a = \(\frac{4}{3}\)
Co-ordinates of focus are S(-a, 0), i.e., (\(-\frac{4}{3}\), 0)
Equation of the directrix is x – a = 0,
⇒ x – \(-\frac{4}{3}\) = 0
⇒ 3x – 4 = 0
Length of latus rectum = 4a = 4(\(\frac{4}{3}\)) = \(\frac{16}{3}\)
Co-ordinates of end points of latus rectum are (-a, 2a) and (-a, -2a),
i.e., \(\left(-\frac{4}{3}, \frac{8}{3}\right)\) and \(\left(-\frac{4}{3},-\frac{8}{3}\right)\)

Question 2.
Find the equation of the parabola with vertex at the origin, the axis along the Y-axis, and passing through the point (-10, -5).
Solution:
Vertex of the parabola is at origin (0, 0) and its axis is along Y-axis.
Equation of the parabola can be either x² = 4by or x² = -4by
Since the parabola passes through (-10, -5), it lies in 3rd quadrant.
Required parabola is x² = -4by.
Substituting x = -10 and y = -5 in x² = -4by, we get
⇒ (-10)² = -4b(-5)
⇒ b = \(\frac{100}{20}\) = 5
∴ The required equation of the parabola is x² = -4(5)y, i.e., x² = -20y.

Question 3.
Find the equation of the parabola with vertex at the origin, the axis along the X-axis, and passing through the point (3, 4).
Solution:
Vertex of the parabola is at the origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y² = 4ax or y² = -4ax.
Since the parabola passes through (3, 4), it lies in the 1st quadrant.
Required parabola is y² = 4ax.
Substituting x = 3 and y = 4 in y² = 4ax, we get
⇒ (4)² = 4a(3)
⇒ a = \(\frac{16}{12}=\frac{4}{3}\)
The required equation of the parabola is
y² = 4(\(\frac{4}{3}\))x
⇒ 3y² = 16x

Question 4.
Find the equation of the parabola whose vertex is O(0, 0) and focus at (-7, 0).
Solution:
Focus of the parabola is S(-7, 0) and vertex is O(0, 0).
Since focus lies on X-axis, it is the axis of the parabola.
Focus S(-7, 0) lies on the left-hand side of the origin.
It is a left-handed parabola.
Required parabola is y = -4ax.
Focus is S(-a, 0).
a = 7
∴ The required equation of the parabola is y² =-4(7)x, i.e., y² = -28x.

Question 5.
Find the equation of the parabola with vertex at the origin, the axis along X-axis, and passing through the point
(i) (1, -6)
(ii) (2, 3)
Solution:
(i) Vertex of the parabola is at origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y² = 4ax or y² = -4ax.
Since the parabola passes through (1, -6), it lies in the 4th quadrant.
Required parabola is y² = 4ax.
Substituting x = 1 and y = -6 in y² = 4ax, we get
⇒ (-6)² = 4a(1)
⇒ 36 = 4a
⇒ a = 9
∴ The required equation of the parabola is y² = 4(9)x, i.e., y² = 36x.

(ii) Vertex of the parabola is at origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y² = 4ax or y² = -4ax.
Since the parabola passes through (2, 3), it lies in 1st quadrant.
∴ Required parabola is y² = 4ax.
Substituting x = 2 and y = 3 in y² = 4ax, we get
⇒ (3)² = 4a(2)
⇒ 9 = 8a
⇒ a = \(\frac{9}{8}\)
The required equation of the parabola is
y² = 4(\(\frac{9}{8}\))x
⇒ y² = \(\frac{9}{2}\) x
⇒ 2y² = 9x.

Question 6.
For the parabola 3y² = 16x, find the parameter of the point:
(i) (3, -4)
(ii) (27, -12)
Solution:
Given the equation of the parabola is 3y² = 16x.
⇒ y² = \(\frac{16}{3}\)x
Comparing this equation with y² = 4ax, we get
⇒ 4a = \(\frac{16}{3}\)
⇒ a = \(\frac{4}{3}\)
If t is the parameter of the point P on the parabola, then
P(t) = (at², 2at)
i.e., x = at² and y = 2at ………(i)
(i) Given point is (3, -4)
Substituting x = 3, y = -4 and a = \(\frac{4}{3}\) in (i), we get
3 = \(\frac{4}{3}\) t² and -4 = 2(\(\frac{4}{3}\)) t

∴ The parameter of the given point is \(\frac{-3}{2}\)

(ii) Given point is (27, -12)
Substituting x = 27, y = -12 and a = \(\frac{4}{3}\) in (i), we get

∴ The parameter of the given point is \(\frac{-9}{2}\)

Question 7.
Find the focal distance of a point on the parabola y² = 16x whose ordinate is 2 times the abscissa.
Solution:
Given the equation of the parabola is y² = 16x.
Comparing this equation with y² = 4ax, we get
⇒ 4a = 16
⇒ a = 4
Since ordinate is 2 times the abscissa,
y = 2x
Substituting y = 2x in y² = 16x, we get
⇒ (2x)² = 16x
⇒ 4x² = 16x
⇒ 4x² – 16x = 0
⇒ 4x(x – 4) = 0
⇒ x = 0 or x = 4
When x = 4,
focal distance = x + a = 4 + 4 = 8
When x = 0,
focal distance = a = 4
∴ Focal distance is 4 or 8.

Question 8.
Find coordinates of the point on the parabola. Also, find focal distance.
(i) y² = 12x whose parameter is \(\frac{1}{3}\)
(ii) 2y² = 7x whose parameter is -2
Solution:
(i) Given equation of the parabola is y² = 12x.
Comparing this equation with y² = 4ax, we get
⇒ 4a = 12
⇒ a = 3
If t is the parameter of the point P on the parabola, then
P(t) = (at², 2at)
i.e., x = at² and y = 2at ……..(i)
Given, t = \(\frac{1}{3}\)
Substituting a = 3 and t = \(\frac{1}{3}\) in (i), we get
x = 3(\(\frac{1}{3}\))² and y = 2(3)(\(\frac{1}{3}\))
x = \(\frac{1}{3}\) and y = 2
The co-ordinates of the point on the parabola are (\(\frac{1}{3}\), 2)
∴ Focal distance = x + a
= \(\frac{1}{3}\) + 3
= \(\frac{10}{3}\)

(ii) Given equation of the parabola is 2y² = 7x.
⇒ y² = \(\frac{7}{2}\)x
Comparing this equation with y² = 4ax, we get
⇒ 4a = \(\frac{7}{2}\)
⇒ a = \(\frac{7}{8}\)
If t is the parameter of the point P on the parabola, then
P(t) = (at², 2at)
i.e., x = at² and y = 2at …..(i)
Given, t = -2
Substituting a = \(\frac{7}{8}\) and t = -2 in (i), we get
x = \(\frac{7}{8}\)(-2)2 and y = 2(\(\frac{7}{8}\))(-2)
x = \(\frac{7}{2}\) and y = \(\frac{-7}{2}\)
The co-ordinates of the point on the parabola are (\(\frac{7}{2}\), \(\frac{-7}{2}\))
∴ Focal distance = x + a
= \(\frac{7}{2}\) + \(\frac{7}{8}\)
= \(\frac{35}{8}\)

Question 9.
For the parabola y² = 4x, find the coordinates of the point whose focal distance is 17.
Solution:
Given the equation of the parabola is y² = 4x.
Comparing this equation with y² = 4ax, we get
⇒ 4a = 4
⇒ a = 1
Focal distance of a point = x + a
Given, focal distance = 17
⇒ x + 1 = 17
⇒ x = 16
Substituting x = 16 in y² = 4x, we get
⇒ y² = 4(16)
⇒ y² = 64
⇒ y = ±8
∴ The co-ordinates of the point on the parabola are (16, 8) or (16, -8).

Question 10.
Find the length of the latus rectum of the parabola y² = 4ax passing through the point (2, -6).
Solution:
Given equation of the parabola is y² = 4ax and it passes through point (2, -6).
Substituting x = 2 and y = -6 in y² = 4ax, we get
⇒ (-6)² = 4a(2)
⇒ 4a = 18
∴ Length of latus rectum = 4a = 18 units

Question 11.
Find the area of the triangle formed by the line joining the vertex of the parabola x² = 12y to the endpoints of the latus rectum.
Solution:

Given the equation of the parabola is x² = 12y.
Comparing this equation with x² = 4by, we get
⇒ 4b = 12
⇒ b = 3
The co-ordinates of focus are S(0, b), i.e., S(0, 3)
End points of the latus-rectum are L(2b, b) and L'(-2b, b),
i.e., L(6, 3) and L'(-6, 3)
Also l(LL’) = length of latus-rectum = 4b = 12
l(OS) = b = 3
Area of ∆OLL’ = \(\frac{1}{2}\) × l(LL’) × l(OS)
= \(\frac{1}{2}\) × 12 × 3
Area of ∆OLL’ = 18 sq. units

Question 12.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Solution:

Let LOM be the parabolic reflector such that LM is the diameter and ON is its depth.
It is given that ON = 5 cm and LM = 20 cm.
LN = 10 cm
Taking O as the origin, ON along X-axis and a line through O ⊥ ON as Y-axis.
Let the equation of the reflector be y² = 4ax ……(i)
The point L has the co-ordinates (5, 10) and lies on parabola given by (i).
Substituting x = 5 and y = 10 in (i), we get
⇒ 10² = 4a(5)
⇒ 100 = 20a
⇒ a = 5
Focus is at (a, 0), i.e., (5, 0)

Question 13.
Find co-ordinates of focus, vertex, and equation of directrix and the axis of the parabola y = x² – 2x + 3.
Solution:
Given equation of the parabola is y = x² – 2x + 3
⇒ y = x² – 2x + 1 + 2
⇒ y – 2 = (x – 1)²
⇒ (x – 1)² = y – 2
Comparing this equation with X² = 4bY, we get
X = x – 1, Y = y – 2
⇒ 4b = 1
⇒ b = \(\frac{1}{4}\)
The co-ordinates of vertex are (X = 0, Y = 0)
⇒ x – 1 = 0 and y – 2 = 0
⇒ x = 1 and y = 2
The co-ordinates of vertex are (1, 2).
The co-ordinates of focus are S(X = 0, Y = b)
⇒ x – 1 = 0 and y – 2 = \(\frac{1}{4}\)
⇒ x = 1 and y = \(\frac{9}{4}\)
The co-ordinates of focus are (1, \(\frac{9}{4}\))
Equation of the axis is X = 0
x – 1 = 0, i.e., x = 1
Equation of directrix is Y + b = 0
⇒ y – 2 + \(\frac{1}{4}\) = 0
⇒ y – \(\frac{7}{4}\) = 0
⇒ 4y – 7 = 0

Question 14.
Find the equation of tangent to the parabola
(i) y² = 12x from the point (2, 5)
(ii) y² = 36x from the point (2, 9)
Solution:
(i) Given equation of the parabola is y² = 12x.
Comparing this equation with y² = 4ax, we get
⇒ 4a = 12
⇒ a = 3
Equation of tangent to the parabola y² = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (2, 5)
⇒ 5 = 2m + \(\frac{3}{m}\)
⇒ 5m = 2m² + 3
⇒ 2m² – 5m + 3 = 0
⇒ 2m² – 2m – 3m + 3 = 0
⇒ 2m(m – 1) – 3(m – 1) = 0
⇒ (m- 1)(2m – 3) = 0
⇒ m = 1 or m = \(\frac{3}{2}\)
These are the slopes of the required tangents.
By slope point form, y – y₁ = m(x – x₁), the equations of the tangents are
⇒ y – 5 = 1(x – 2) and y – 5 = \(\frac{3}{2}\) (x – 2)
⇒ y – 5 = x – 2 and 2y – 10 = 3x – 6
⇒ x – y + 3 = 0 and 3x – 2y + 4 = 0

(ii) Given equation of the parabola is y² = 36x.
Comparing this equation with y² = 4ax, we get
⇒ 4a = 36
⇒ a = 9
Equation of tangent to the parabola y² = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (2, 9),
⇒ 9 = 2m + \(\frac{9}{m}\)
⇒ 9m = 2m² + 9
⇒ 2m² – 9m + 9 = 0
⇒ 2m² – 6m – 3m + 9 = 0
⇒ 2m(m – 3) – 3(m – 3) = 0
⇒ (m – 3)(2m – 3) = 0
⇒ m = 3 or m = \(\frac{3}{2}\)
These are the slopes of the required tangents.
By slope point form, y – y₁ = m(x – x₁), the equations of the tangents are
⇒ y – 9 = 3(x – 2) and y – 9 = \(\frac{3}{2}\) (x – 2)
⇒ y – 9 = 3x – 6 and 2y – 18 = 3x – 6
⇒ 3x – y + 3 = 0 and 3x – 2y + 12 = 0

Question 15.
If the tangents drawn from the point (-6, 9) to the parabola y² = kx are perpendicular to each other, find k.
Solution:
Given equation of the parabola is y² = kx
Comparing this equation with y² = 4ax, we get
⇒ 4a = k
⇒ a = \(\frac{\mathrm{k}}{4}\)
Equation of tangent to the parabola y² = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (-6, 9),
⇒ 9 = -6m + \(\frac{k}{4m}\)
⇒ 36m = -24m2 + k
⇒ 24m² + 36m – k = 0
The roots m₁ and m₂ of this quadratic equation are the slopes of the tangents.
m₁m₂ = \(\frac{-\mathrm{k}}{24}\)
Since the tangents are perpendicular to each other,
m₁m₂ = -1
⇒ \(\frac{-\mathrm{k}}{24}\) = -1
⇒ k = 24

Alternate method:
We know that, tangents drawn from a point on directrix are perpendicular.
(-6, 9) lies on the directrix x = -a.
⇒ -6 = -a
⇒ a = 6
Since 4a = k
⇒ k = 4(6) = 24

Question 16.
Two tangents to the parabola y² = 8x meet the tangents at the vertex in the points P and Q. If PQ = 4, prove that the equation of the locus of the point of intersection of two tangents is y² = 8(x + 2).
Solution:
Given equation of the parabola is y² = 8x
Comparing this equation with y² = 4ax, we get
⇒ 4a = 8
⇒ a = 2
Equation of tangent to given parabola at A(t₁) is y
t₁ = x + 2\(\mathrm{t}_{1}^{2}\) …….(i)
Equation of tangent to given parabola at B(t₂) is y
t₂ = x + 2\(\mathrm{t}_{2}^{2}\) …..(ii)

A tangent at the vertex is Y-axis whose equation is x = 0.
x-coordinate of points P and Q is 0.
Let P be(0, k₁) and Q be (0, k₂).
Then, from (i) and (ii), we get

∴ Equation of locus of R is y² = 8(x + 2).

Question 17.
Find the equation of common tangent to the parabolas y² = 4x and x² = 32y.
Solution:
Given equation of the parabola is y² = 4x
Comparing this equation with y² = 4ax, we get
⇒ 4a = 4
⇒ a = 1
Let the equation of common tangent be
y = mx + \(\frac{1}{m}\) …..(i)
Substituting y = mx + \(\frac{1}{m}\) in x² = 32y, we get
⇒ x² = 32(mx + \(\frac{1}{m}\)) = 32 mx + \(\frac{32}{m}\)
⇒ mx² = 32 m²x + 32
⇒ mx² – 32 m²x – 32 = 0 ……..(ii)
Line (i) touches the parabola x² = 32y.
The quadratic equation (ii) in x has equal roots.
Discriminant = 0
⇒ (-32m²)² – 4(m)(-32) = 0
⇒ 1024 m⁴ + 128m = 0
⇒ 128m (8m³ + 1) = 0
⇒ 8m³ + 1 = 0 …..[∵ m ≠ 0]
⇒ m³ = \(-\frac{1}{8}\)
⇒ m = \(-\frac{1}{2}\)
Substituting m = \(-\frac{1}{2}\) in (i), we get
⇒ \(y=-\frac{1}{2} x+\frac{1}{\left(-\frac{1}{2}\right)}\)
⇒ \(y=-\frac{1}{2} x-2\)
⇒ x + 2y + 4 = 0, which is the equation of the common tangent.

Question 18.
Find the equation of the locus of a point, the tangents from which to the parabola y² = 18x are such that sum of their slopes is -3.
Solution:
Given equation of the parabola is y² = 18x
Comparing this equation with y² = 4ax, we get
⇒ 4a = 18
⇒ a = \(\frac{9}{2}\)
Equation of tangent to the parabola y² = 4ax having slope m is
⇒ y = mx + \(\frac{a}{m}\)
⇒ y = mx + \(\frac{9}{2m}\)
⇒ 2ym = 2xm² + 9
⇒ 2xm² – 2ym + 9 = 0
The roots m₁ and m₂ of this quadratic equation are the slopes of the tangents.
m₁ + m₂ = \(-\frac{(-2 y)}{2 x}=\frac{y}{x}\)
But, m₁ + m₂ = -3
\(\frac{y}{x}\) = -3
y = -3x, which is the required equation of locus.

Question 19.
The towers of a bridge, hung in the form of a parabola, have their tops 30 metres above the roadway and are 200 metres apart. If the cable is 5 metres above the roadway at the centre of the bridge, find the length of the vertical supporting cable 30 metres from the centre.
Solution:
Let CAB be the cable of the bridge and X’OX be the roadway.
Let A be the centre of the bridge.
From the figure, vertex of parabola is at A(0, 5).
Let the equation of parabola be
x² = 4b(y – 5) …..(i)
Since the parabola passes through (100, 30).
Substituting x = 100 and y = 30 in (i), we get
⇒ 100² = 4b (30 – 5)
⇒ 100² = 4b(25)
⇒ 100² = 100b
⇒ b = 100
Substituting the value of b in (i), we get
x² = 400(y – 5) …..(ii)
Let l metres be the length of vertical supporting cable.
Then P(30, l) lies on (ii).
⇒ 30² = 400(l – 5)
⇒ 900 = 400(l – 5)
⇒ \(\frac{9}{4}\) = l – 5
⇒ l = \(\frac{9}{4}\) + 5
⇒ l = \(\frac{9}{4}\) m = 7.25 m
The length of the vertical supporting cable is 7.25 m.

Question 20.
A circle whose centre is (4, -1) passes through the focus of the parabola x² + 16y = 0. Show that the circle touches the directrix of the parabola.
Solution:
Given equation of the parabola is x² + 16y = 0.
⇒ x² = -16y
Comparing this equation with x² = -4by, we get
⇒ 4b = 16
⇒ b = 4
Focus = S(0, -b) = (0, -4)
Centre of the circle is C(4, -1) and it passes through focus S of the parabola.
Radius = CS
= \(\sqrt{(4-0)^{2}+(-1+4)^{2}}\)
= \(\sqrt{16+9}\)
= 5
Equation of the directrix is y – b = 0, i.e.,y – 4 = 0
Length of the perpendicular from centre C(4, -1) to the directrix
= \(\left|\frac{0(4)+1(-1)-4}{\sqrt{(0)^{2}+(1)^{2}}}\right|\)
= \(\left|\frac{-1-4}{1}\right|\)
= 5
= radius
∴ The circle touches the directrix of the parabola.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 7 Conic Sections Ex 7.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Conic Sections Ex 7.3

Question 1.
Find the length of the transverse axis, length of conjugate axis, the eccentricity, the co-ordinates of foci, equations of directrices, and the length of the latus rectum of the hyperbolae.
(i) \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
(ii) \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=-1\)
(iii) 16x² – 9y² = 144
(iv) 21x² – 4y² = 84
(v) 3x² – y² = 4
(vi) x² – y² = 16
(vii) \(\frac{y^{2}}{25}-\frac{x^{2}}{9}=1\)
(viii) \(\frac{y^{2}}{25}-\frac{x^{2}}{144}=1\)
(ix) \(\frac{x^{2}}{100}-\frac{y^{2}}{25}=1\)
(x) x = 2 sec θ, y = 2√3 tan θ
Solution:
(i) Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 25 and b² = 16
⇒ a = 5 and b = 4
Length of transverse axis = 2a = 2(5) = 10
Length of conjugate axis = 2b = 2(4) = 8
We know that

(ii) Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=-1\)
\(\frac{y^{2}}{16}-\frac{x^{2}}{25}=1\)
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b² = 16 and a² = 25
⇒ b = 4 and a = 5
Length of transverse axis = 2b = 2(4) = 8
Length of conjugate axis = 2a = 2(5) = 10
Co-ordinates of vertices are B(0, b) and B’ (0, -b)
i.e., B(0, 4) and B'(0, -4)
We know that

(iii) Given equation of the hyperbola is 16x² – 9y² = 144.
\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 9 and b² = 16
⇒ a = 3 and b = 4
Length of transverse axis = 2a = 2(3) = 6
Length of conjugate axis = 2b = 2(4) = 8
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}=\frac{\sqrt{9+16}}{3}=\frac{\sqrt{25}}{3}=\frac{5}{3}\)
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S(3(\(\frac{5}{3}\)), 0) and S'(-3(\(\frac{5}{3}\)), 0)
i.e., S(5, 0) and S'(-5, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\)
= \(\pm \frac{3}{\left(\frac{5}{3}\right)}\)
= \(\pm \frac{9}{5}\)
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(16)}{3}=\frac{32}{3}\)

(iv) Given equation of the hyperbola is 21x² – 4y² = 84.
\(\frac{x^{2}}{4}-\frac{y^{2}}{21}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 4 and b² = 21
⇒ a = 2 and b = √21
Length of transverse axis = 2a = 2(2) = 4
Length of conjugate axis = 2b = 2√21
We know that

(v) Given equation of the hyperbola is 3x² – y² = 4.
\(\frac{x^{2}}{\left(\frac{4}{3}\right)}-\frac{y^{2}}{4}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = \(\frac{4}{3}\) and b² = 4

(vi) Given equation of the hyperbola is x² – y² = 16.
\(\frac{x^{2}}{16}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 16 and b² = 16
⇒ a = 4 and b = 4
Length of transverse axis = 2a = 2(4) = 8
Length of conjugate axis = 2b = 2(4) = 8
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}=\frac{\sqrt{16+16}}{4}=\frac{\sqrt{32}}{4}=\frac{4 \sqrt{2}}{4}=\sqrt{2}\)
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S (4√2, 0) and S’ (-4√2, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\)
⇒ x = \(\pm \frac{4}{\sqrt{2}}\)
⇒ x = ± 2√2
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(16)}{4}\) = 8

(vii) Given equation of the hyperbola is \(\frac{y^{2}}{25}-\frac{x^{2}}{9}=1\).
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b² = 25 and a² = 9
⇒ b = 5 and a = 3
Length of transverse axis = 2b = 2(5) = 10
Length of conjugate axis = 2a = 2(3) = 6
Co-ordinates of vertices are B(0, b) and B’ (0, -b),
i.e., B(0, 5) and B’ (0, -5)
We know that

(viii) Given equation of the hyperbola is \(\frac{y^{2}}{25}-\frac{x^{2}}{144}=1\).
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b² = 25 and a² = 144
⇒ b = 5 and a = 12
Length of transverse axis = 2b = 2(5) = 10
Length of conjugate axis = 2a = 2(12) = 24
Co-ordinates of vertices are B(0, b) and B’ (0, -b),
i.e., B(0, 5) and B’ (0, -5)
We know that

(ix) Given equation of the hyperbola is \(\frac{x^{2}}{100}-\frac{y^{2}}{25}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 100 and b² = 25
⇒ a = 10 and b = 5
Length of transverse axis = 2a = 2(10) = 20
Length of conjugate axis = 2b = 2(5) = 10
We know that

(x) Given equation of the hyperbola is x = 2 sec θ, y = 2√3 tan θ.
Since sec² θ – tan² θ = 1,
\(\left(\frac{x}{2}\right)^{2}-\left(\frac{y}{2 \sqrt{3}}\right)^{2}=1\)
\(\frac{x^{2}}{4}-\frac{y^{2}}{12}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a² = 4 and b² = 12
⇒ a = 2 and b = 2√3
Length of transverse axis = 2a = 2(2) = 4
Length of conjugate axis = 2b = 2(2√3) = 4√3
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}\) = \(\frac{\sqrt{4+12}}{2}\) = 2
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S(2(2), 0) and S'(-2(2), 0),
i.e., S(4, 0) and S'(-4, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\).
⇒ x = ±\(\frac{2}{2}\)
⇒ x = ±1
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(12)}{2}\) = 12

Question 2.
Find the equation of the hyperbola with centre at the origin, length of the conjugate axis as 10, and one of the foci as (-7, 0).
Solution:
Given, one of the foci of the hyperbola is (-7, 0).
Since this focus lies on the X-axis, it is a standard hyperbola.
Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of conjugate axis = 2b
Given, length of conjugate axis = 10
⇒ 2b = 10
⇒ b = 5
⇒ b² = 25
Co-ordinates of focus are (-ae, 0)
ae = 7
⇒ a²e² = 49
Now, b² = a²(e² – 1)
⇒ 25 = 49 – a²
⇒ a² = 49 – 25 = 24
The required equation of hyperbola is \(\frac{x^{2}}{24}-\frac{y^{2}}{25}=1\)

Question 3.
Find the eccentricity of the hyperbola, which is conjugate to the hyperbola x² – 3y² = 3
Solution:
Given, equation of hyperbola is x² – 3y² = 3.
\(\frac{x^{2}}{3}-\frac{y^{2}}{1}=1\)
Equation of the hyperbola conjugate to the above hyperbola is \(\frac{y^{2}}{1}-\frac{x^{2}}{3}=1\)
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b² = 1 and a² = 3
Now, a² = b²(e² – 1)
⇒ 3 = 1(e² – 1)
⇒ 3 = e – 1
⇒ e² = 4
⇒ e = 2 …..[∵ e > 1]

Question 4.
If e and e’ are the eccentricities of a hyperbola and its conjugate hyperbola respectively, prove that \(\frac{1}{e^{2}}+\frac{1}{\left(e^{\prime}\right)^{2}}=1\).
Solution:
Let e be the eccentricity of a hyperbola

Question 5.
Find the equation of the hyperbola referred to its principal axes:
(i) whose distance between foci is 10 and eccentricity is \(\frac{5}{2}\)
(ii) whose distance between foci is 10 and length of the conjugate axis is 6.
(iii) whose distance between directrices is \(\frac{8}{3}\) and eccentricity is \(\frac{3}{2}\).
(iv) whose length of conjugate axis = 12 and passing through (1, -2).
(v) which passes through the points (6, 9) and (3, 0).
(vi) whose vertices are (±7, 0) and endpoints of the conjugate axis are (0, ±3).
(vii) whose foci are at (±2, 0) and eccentricity is \(\frac{3}{2}\).
(viii) whose lengths of transverse and conjugate axes are 6 and 9 respectively.
(ix) whose length of transverse axis is 8 and distance between foci is 10.
Solution:
(i) Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Given, eccentricity (e) = \(\frac{5}{2}\)
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a(\(\frac{5}{2}\)) = 5
⇒ a = 2
⇒ a² = 4

(ii) Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of conjugate axis = 2b
Given, length of conjugate axis = 6
⇒ 2b = 6
⇒ b = 3
⇒ b² = 9
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a²e² = 25
Now, b² = a² (e² – 1)
⇒ b² = a² e² – a²
⇒ 9 = 25 – a²
⇒ a² = 25 – 9
⇒ a² = 16
The required equation of hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\)

(iii) Let the required equation of hyperbola be \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\)
Given, eccentricity (e) = \(\frac{3}{2}\)
Distance between directrices = \(\frac{2a}{e}\)
Given, distance between directrices = \(\frac{8}{3}\)

(iv) Let the required equation of hyperbola be
\(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\) ……(i)
Length of conjugate axis = 2b
Given, length of conjugate axis = 12
⇒ 2b = 12
⇒ b = 6 …..(ii)
⇒ b² = 36
The hyperbola passes through (1, -2)
Substituting x = 1 and y = -2 in (i), we get

(v) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) ……(i)
The hyperbola passes through the points (6, 9) and (3, 0).

(vi) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Co-ordinates of vertices are (±a, 0).
Given that, co-ordinates of vertices are (±7, 0)
∴ a = 7
Endpoints of the conjugate axis are (0, b) and (0, -b).
Given, the endpoints of the conjugate axis are (0, ±3).
∴ b = 3
The required equation of hyperbola is \(\frac{x^{2}}{7^{2}}-\frac{y^{2}}{3^{2}}=1\)
i.e., \(\frac{x^{2}}{49}-\frac{y^{2}}{9}=1\)

(vii) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) ……(i)
Given, eccentricity (e) = \(\frac{3}{2}\)
Co-ordinates of foci are (±ae, 0).
Given co-ordinates of foci are (±2, 0)
ae = 2
⇒ a(\(\frac{3}{2}\)) = 2
⇒ a = \(\frac{4}{3}\)
⇒ a² = \(\frac{16}{9}\)

(viii) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of transverse axis = 2a
Given, length of transverse axis = 6
⇒ 2a = 6
⇒ a = 3
⇒ a² = 9
Length of conjugate axis = 2b
Given, length of conjugate axis = 9
⇒ 2b = 9
⇒ b = \(\frac{9}{2}\)
⇒ b² = \(\frac{81}{4}\)
The required equation of hyperbola is
\(\frac{x^{2}}{9}-\frac{y^{2}}{\left(\frac{81}{4}\right)}=1\)
i.e., \(\frac{x^{2}}{9}-\frac{4 y^{2}}{81}=1\)

(ix) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of transverse axis = 2a
Given, length of transverse axis = 8
⇒ 2a = 8
⇒ a = 4
⇒ a² = 16
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a²e² = 25
Now, b² = a² (e² – 1)
⇒ b² = a² e² – a²
⇒ b² = 25 – 16 = 9
The required equation of hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\)

Question 6.
Find the equation of the tangent to the hyperbola.
(i) 3x² – y² = 4 at the point (2, 2√2).
(ii) 3x² – y² = 12 at the point (4, 6)
(iii) \(\frac{x^{2}}{144}-\frac{y^{2}}{25}=1\) at the point whose eccentric angle is \(\frac{\pi}{3}\).
(iv) \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\) at the point in a first quadrant whose ordinate is 3.
(v) 9x² – 16y² = 144 at the point L of the latus rectum in the first quadrant.
Solution:

Question 7.
Show that the line 3x – 4y + 10 = 0 is a tangent to the hyperbola x² – 4y² = 20. Also, find the point of contact.
Solution:
Given equation of the hyperbola is x² – 4y² = 20
\(\frac{x^{2}}{20}-\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a² = 20 and b² = 5
Given equation of line is 3x – 4y + 10 = 0.
y = \(\frac{3 x}{4}+\frac{5}{2}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{3}{4}\) and c = \(\frac{5}{2}\)
For the line y = mx + c to be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we must have

Question 8.
If the line 3x – 4y = k touches the hyperbola \(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\), then find the value of k.
Solution:
Given equation of the hyperbola is
\(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\)
\(\frac{x^{2}}{5}-\frac{y^{2}}{\frac{5}{4}}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 5, b² = \(\frac{5}{4}\)
Given equation of line is 3x – 4y = k
y = \(\frac{3}{4} x-\frac{\mathrm{k}}{4}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{3}{4}\), c = \(-\frac{\mathrm{k}}{4}\)
For the line y = mx + c to be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we must have
c² = a² m² – b²
⇒ \(\left(\frac{-\mathrm{k}}{4}\right)^{2}=5\left(\frac{3}{4}\right)^{2}-\frac{5}{4}\)
⇒ \(\frac{\mathrm{k}^{2}}{16}=\frac{5}{16}(9-4)\)
⇒ \(\frac{\mathrm{k}^{2}}{16}=\frac{5}{16}(5)\)
⇒ k² = 25
⇒ k = ±5

Alternate method:
Given equation of the hyperbola is
\(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\) …….(i)
Given equation of the line is 3x – 4y = k
y = \(\frac{3 x-\mathrm{k}}{4}\)
Substituting this value ofy in (i), we get
\(\frac{x^{2}}{5}-\frac{4}{5}\left(\frac{3 x-\mathrm{k}}{4}\right)^{2}=1\)
⇒ \(\frac{x^{2}}{5}-\frac{4}{5}\left(\frac{9 x^{2}-6 k x+k^{2}}{16}\right)=1\)
⇒ 4x² – (9x² – 6kx + k²) = 20
⇒ 4x² – 9x² + 6kx – k² = 20
⇒ -5x² + 6kx – k² = 20
⇒ 5x² – 6kx + (k² + 20) = 0 …..(ii)
Since, the given line touches the given hyperbola.
The quadratic equation (ii) in x has equal roots.
(-6k)² – 4(5)(k² + 20) = 0
⇒ 36k² – 20k² – 400 = 0
⇒ 16k² = 400
⇒ k² = 25
⇒ k = ±5

Question 9.
Find the equations of the tangents to the hyperbola \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\) making equal intercepts on the co-ordinate axes.
Solution:
Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\).
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a² = 25 and b² = 9
Since the tangents make equal intercepts on the co-ordinate axes,
∴ m = -1
Equations of tangents to the hyperbola \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
⇒ y = -x ± \(\sqrt{25(-1)^{2}-9}\)
⇒ y = -x ± √16
⇒ x + y = ±4

Question 10.
Find the equations of the tangents to the hyperbola 5x² – 4y² = 20 which are parallel to the line 3x + 2y + 12 = 0.
Solution:
Given equation of the hyperbola is 5x² – 4y² = 20
\(\frac{x^{2}}{4}-\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 4 and b² = 5
Slope of the line 3x + 2y + 12 = 0 is \(-\frac{3}{2}\)
Since the given line is parallel to the tangents,
Slope of the required tangents (m) = \(-\frac{3}{2}\)
Equations of tangents to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)

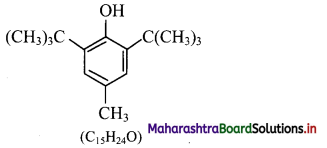
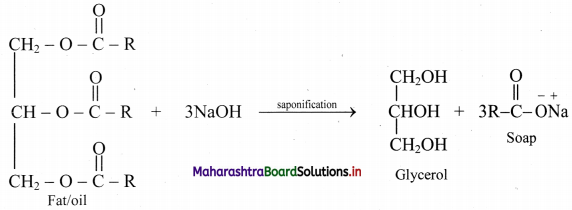
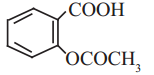
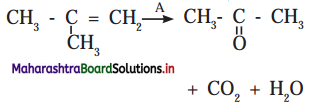
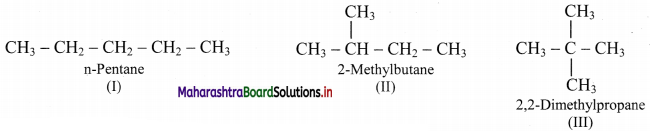
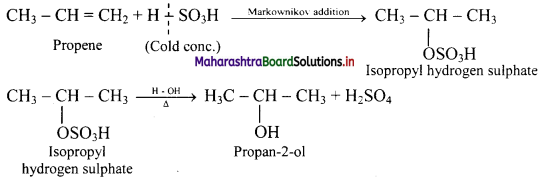
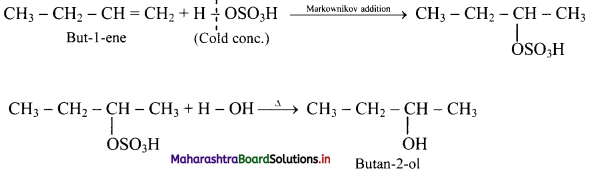
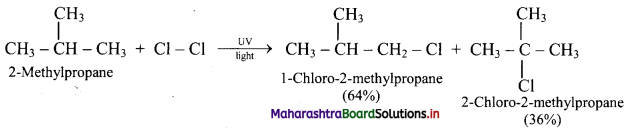
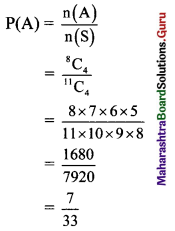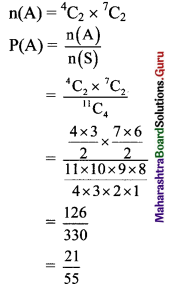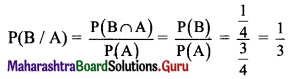Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Miscellaneous Exercise 9 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Miscellaneous Exercise 9

(I) Select the correct answer from the given four alternatives.

Question 1.
There are 5 girls and 2 boys, then the probability that no two boys are sitting together for a photograph is
(A) \(\frac{1}{21}\)
(B) \(\frac{4}{7}\)
(C) \(\frac{2}{7}\)
(D) \(\frac{5}{7}\)
Answer:
(D) \(\frac{5}{7}\)
Hint:
There are 5 girls and 2 boys.
They can be arranged among themselves in \({ }^{7} \mathrm{P}_{7}\) = 7! ways.
∴ Girls can be arranged among themselves in \({ }^{5} \mathrm{P}_{5}\) = 5! ways.
No two boys should sit together.
Let girls be denoted by the letter G.
– G – G – G – G – G –
There are 6 places, marked by ‘-’ where boys can sit.
∴ Boys can be arranged in
\({ }^{6} \mathrm{P}_{2}=\frac{6 !}{(6-2) !}\)
= \(\frac{6 \times 5 \times 4 !}{4 !}\)
= 30 ways.
∴ Required probability = \(\frac{5 ! \times 30}{7 !}=\frac{5 ! \times 30}{7 \times 6 \times 5 !}=\frac{5}{7}\)

Question 2.
In a jar, there are 5 black marbles and 3 green marbles. Two marbles are picked randomly one after the other without replacement. What is the possibility that both the marbles are black?
(A) \(\frac{5}{14}\)
(B) \(\frac{5}{8}\)
(C) \(\frac{5}{7}\)
(D) \(\frac{5}{16}\)
Answer:
(A) \(\frac{5}{14}\)

Question 3.
Two dice are thrown simultaneously. Then the probability of getting two numbers whose product is even is
(A) \(\frac{3}{4}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{5}{7}\)
(D) \(\frac{1}{2}\)
Answer:
(A) \(\frac{3}{4}\)
Hint:
Two dice are thrown.
∴ n(S) = 36
Getting two numbers whose product is even, i.e., one of the two numbers must be even.
Let event A: Getting even number on first dice,
event B: Getting even number on second dice.
n(A) = 18, n(B) = 18, n(A ∩ B) = 9
Required probability = P(A ∩ B)
= \(\frac{n(A)+n(B)-n(A \cap B)}{n(S)}\)
= \(\frac{18+18-9}{36}\)
= \(\frac{3}{4}\)

Question 4.
In a set of 30 shirts, 17 are white and the rest are black. 4 white and 5 black shirts are tagged as ‘PARTY WEAR’. If a shirt is chosen at random from this set, the possibility of choosing a black shirt or a ‘PARTY WEAR’ shirt is
(A) \(\frac{11}{15}\)
(B) \(\frac{13}{30}\)
(C) \(\frac{9}{13}\)
(D) \(\frac{17}{30}\)
Answer:
(D) \(\frac{17}{30}\)
Hint:
17 white + 13 black = 30 shirts
4 white and 5 black are ‘PARTY WEAR’
A: Choosing a black shirt
∴ P(A) = \(\frac{{ }^{13} C_{1}}{{ }^{30} C_{1}}=\frac{13}{30}\)
B: Choosing a ‘PARTY WEAR’ shirt.
∴ P(B) = \(\frac{{ }^{9} \mathrm{C}_{1}}{{ }^{30} \mathrm{C}_{1}}=\frac{9}{30}\)
There are 5 black ‘PARTY WEAR’ shirts.
∴ P(A ∩ B) = \(\frac{{ }^{5} \mathrm{C}_{1}}{{ }^{30} \mathrm{C}_{1}}=\frac{5}{30}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{13}{30}\) + \(\frac{9}{30}\) – \(\frac{5}{30}\)
= \(\frac{17}{30}\)

Question 5.
There are 2 shelves. One shelf has 5 Physics and 3 Biology books and the other has 4 Physics and 2 Biology books. The probability of drawing a Physics book is
(A) \(\frac{9}{14}\)
(B) \(\frac{31}{48}\)
(C) \(\frac{9}{38}\)
(D) \(\frac{1}{2}\)
Answer:
(B) \(\frac{31}{48}\)
Hint:
Let event S₁: First shelve is selected,
event S₂: Second shelve is selected,
event P: Drawing a physics book.
∴ P(S₁) = \(\frac{1}{2}\) and P(S₂) = \(\frac{1}{2}\)
First shelve has 5 physics and 3 biology books, i.e., total 8 books.
∴ P(P/S₁) = \(\frac{{ }^{5} C_{1}}{{ }^{8} C_{1}}=\frac{5}{8}\)
Similarly, P(P/S₂) = \(\frac{{ }^{4} C_{1}}{{ }^{6} C_{1}}=\frac{4}{6}=\frac{2}{3}\)
∴ P(P) = P(S₁) . P(P/S₁) + P(S₂) . P(P/S₂)
= \(\frac{1}{2} \times \frac{5}{8}+\frac{1}{2} \times \frac{2}{3}\)
= \(\frac{31}{48}\)

Question 6.
Two friends A and B apply for a job in the same company. The chances of A getting selected is 2/5 and that of B is 4/7. The probability that both of them get selected is
(A) \(\frac{34}{35}\)
(B) \(\frac{1}{35}\)
(C) \(\frac{8}{35}\)
(D) \(\frac{27}{35}\)
Answer:
(C) \(\frac{8}{35}\)

Question 7.
The probability that a student knows the correct answer to a multiple-choice question is \(\frac{2}{3}\). If the student does not know the answer, then the student guesses the answer. The probability of the guessed answer being correct is \(\frac{1}{4}\). Given that the student has answered the question correctly, the probability that the student knows the correct answer is
(A) \(\frac{5}{6}\)
(B) \(\frac{6}{7}\)
(C) \(\frac{7}{8}\)
(D) \(\frac{8}{9}\)
Answer:
(D) \(\frac{8}{9}\)
Hint:
Let event A: Student knows the correct answer,
event A’: Student guesses the answer,
event B: Answer is correct.
∴ P(A) = \(\frac{2}{3}\), P(A’) = \(\frac{1}{3}\), P(B/A’) = \(\frac{1}{4}\)
Clearly, P(B/A) = 1
Required probability = P(A/B)
= \(\frac{\mathrm{P}(\mathrm{A}) \cdot \mathrm{P}(\mathrm{B} / \mathrm{A})}{\mathrm{P}(\mathrm{A}) \cdot \mathrm{P}(\mathrm{B} / \mathrm{A})+\mathrm{P}\left(\mathrm{A}^{\prime}\right) \mathrm{P}\left(\mathrm{B} / \mathrm{A}^{\prime}\right)}\)
= \(\frac{\frac{2}{3} \times 1}{\frac{2}{3} \times 1+\frac{1}{3} \times \frac{1}{4}}\)
= \(\frac{8}{9}\)

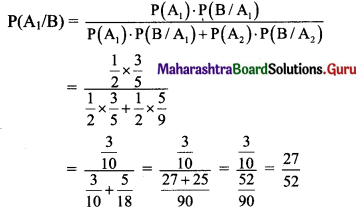
Question 8.
The bag I contain 3 red and 4 black balls while Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II is
(A) \(\frac{33}{68}\)
(B) \(\frac{35}{69}\)
(C) \(\frac{34}{67}\)
(D) \(\frac{35}{68}\)
Answer:
(D) \(\frac{35}{68}\)

Question 9.
A fair die is tossed twice. What are the odds in favour of getting 4, 5, or 6 on the first toss and 1, 2, 3, or 4 on the second toss?
(A) 1 : 3
(B) 3 : 1
(C) 1 : 2
(D) 2 : 1
Answer:
(C) 1 : 2
Hint:
A fair dice is tossed twice.
∴ n(S) = 36
A: Getting 4, 5, or 6 on the first toss and Getting 1, 2, 3, or 4 on the second toss.
∴ A = {(4, 1), (4, 2), (4, 3), (4, 4), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4)}
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{12}{36}=\frac{1}{3}\)
∴ Required answer = P(A) : P(A’) = 1 : 2

Question 10.
The odds against an event are 5 : 3 and the odds in favour of another independent event are 7 : 5. The probability that at least one of the two events will occur is
(A) \(\frac{52}{96}\)
(B) \(\frac{71}{96}\)
(C) \(\frac{69}{96}\)
(D) \(\frac{13}{96}\)
Answer:
(B) \(\frac{71}{96}\)

(II) Solve the following.

Question 1.
The letters of the word ‘EQUATION’ are arranged in a row. Find the probability that
(i) all the vowels are together
(ii) arrangement starts with a vowel and ends with a consonant.
Solution:
The letters of the word EQUATION can be arranged in 8! ways.
∴ n(S) = 8!
There are 5 vowels and 3 consonants.
(i) A: all vowels are together we need to arrange (E, U, A, I, O), Q, T, N
Let us consider all vowels as one unit.
So, there are 4 units, which can be arranged in 4! ways.
Also, 5 vowels can be arranged among themselves in 5! ways.
∴ n(A) = 4! × 5!
Required probability = P(A)
= \(\frac{n(A)}{n(S)}\)
= \(\frac{4 ! \times 5 !}{8 !}\)
= \(\frac{1}{14}\)

(ii) B: arrangement start with a vowel and ends with a consonant.
First and last places can be filled in 5 and 3 ways respectively.
Remaining 6 letters are arranged in 6! Ways.
∴ n(B) = 5 × 3 × 6!
Required probability = P(B)
= \(\frac{n(B)}{n(S)}\)
= \(\frac{5 \times 3 \times 6 !}{8 !}\)
= \(\frac{15}{56}\)

Question 2.
There are 6 positive and 8 negative numbers. Four numbers are chosen at random, without replacement, and multiplied. Find the probability that the product is a positive number.
Solution:
Let event A: Four positive numbers are chosen,
event B: Four negative numbers are chosen,
event C: Two positive and two negative numbers are chosen.
Since four numbers are chosen without replacement,
n(A) = 6 × 5 × 4 × 3 = 360
n(B) = 8 × 7 × 6 × 5 = 1680
In event C, four numbers are to be chosen without replacement such that two numbers are positive and two numbers ate negative. This can be done in following ways:
+ + – – OR + – + – OR + – – + OR – + – + OR – – + + OR – + + –
∴ n(C) = 6 × 5 × 8 × 7 + 6 × 8 × 5 × 7 + 6 × 8 × 7 × 5 + 8 × 6 × 7 × 5 + 6 × 5 × 8 × 7 + 8 × 6 × 5 × 7
= 6 × (8 × 7 × 6 × 5)
=10080
Here, total number of numbers = 14
∴ n(S) = 14 × 13 × 12 × 11 = 24024
Since A, B, C are mutually exclusive events,
Required probability = P(A) + P(B) + P(C)

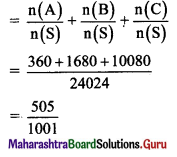
Question 3.
Ten cards numbered 1 to 10 are placed in a box, mixed up thoroughly, and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3, what is the probability that it is an even number?
Solution:
S = {1, 2,…., 10}
∴ n(S) = 10
A: Number is more than 3.
A = {4, 5, 6, 7, 8, 9, 10}
∴ n(A) = 7
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{7}{10}\)
B: Number is even.
B = {2, 4, 6, 8, 10}
∴ A ∩ B = {4, 6, 8, 10}
∴ n(A ∩ B) = 4
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{4}{10}\)
Required probability = P(B/A)
= \(\frac{P(A \cap B)}{P(A)}\)
= \(\frac{\left(\frac{4}{10}\right)}{\left(\frac{7}{10}\right)}\)
= \(\frac{4}{7}\)

Question 4.
If A, B and C are independent events, P(A ∩ B) = \(\frac{1}{2}\), P(B ∩ C) = \(\frac{1}{3}\), P(C ∩ A) = \(\frac{1}{6}\), then find P(A), P(B) and P(C).
Solution:
Since A and B are independent events,
P(A ∩ B) = P(A) . P(B)
∴ P(A) . P(B) = \(\frac{1}{2}\) ……(i)
B and C are independent events.
∴ P(B ∩ C) = P(B) . P(C)
∴ P(B) . P(C) = \(\frac{1}{3}\) ……(ii)
A and C are independent events.
∴ P(A ∩ C) = P(A) . P(C)
∴ P(A) . P(C) = \(\frac{1}{6}\) ……(iii)
Dividing (i) by (ii), we get
\(\frac{\mathrm{P}(\mathrm{A}) \mathrm{P}(\mathrm{B})}{\mathrm{P}(\mathrm{B}) \mathrm{P}(\mathrm{C})}=\frac{\frac{1}{2}}{\frac{1}{3}}\)
P(A) = \(\frac{3}{2}\) P(C) ……(iv)
Substituting equation (iv) in (iii), we get
\(\frac{3}{2}\) P(C) . P(C) = \(\frac{1}{6}\)
[P(C)]² = \(\frac{1}{9}\)
∴ P(C) = \(\frac{1}{3}\)
Substituting P(C) = \(\frac{1}{3}\) in equation (ii), we get P(B) = 1
Substituting P(B) = 1 in equation (i), we get P(A) = \(\frac{1}{2}\)

Question 5.
If the letters of the word ‘REGULATIONS’ be arranged at random, what is the probability that there will be exactly 4 letters between R and E?
Solution:
There are 11 letters in the word ‘REGULATIONS’ which can be arranged among themselves in 11! ways.
∴ n(S) = 11!
Let event A: There will be exactly 4 letters between R and E.
R, E can occur at (1, 6), (2, 7), ….,(6, 11) positions. So, there are 6 possibilities.
Also, R and E can interchange their positions.
So, R, E can be arranged in 2 × 6 = 12 ways.
Remaining 9 letters can be arranged in 9! ways.
∴ n(A) = 12 × 9!
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{12 \times 9 !}{11 !}=\frac{12 \times 9 !}{11 \times 10 \times 9 !}=\frac{6}{55}\)

Question 6.
In how many ways can the letters of the word ARRANGEMENTS be arranged?
(i) Find the chance that an arrangement chosen at random begins with the letters EE.
(ii) Find the probability that the consonants are together.
Solution:
The word ‘ARRANGEMENTS’ has 12 letters in which 2A, 2E, 2N, 2R, G, M, T, S are there.
n(S) = Total number of arrangements = \(\frac{12 !}{2 ! 2 ! 2 ! 2 !}=\frac{12 !}{(2 !)^{4}}\)
(i) A: Arrangement chosen at random begins with the letters EE.
If the first and second places are filled with EE, there are 10 letters left in which 2A, 2N, 2R, G, M, T, S are there.
∴ n(A) = \(\frac{10 !}{2 ! 2 ! 2 !}=\frac{10 !}{(2 !)^{3}}\)

(ii) B: Consonants (G, M, T, S, 2N, 2R) are together.
2A, 2E, and the group containing consonants form total 5 units. Which can be arranged in \(\frac{5 !}{2 ! 2 !}\) ways.
Also, 8 consonants can be arranged among themselves in \(\frac{8 !}{2 ! 2 !}\) ways.

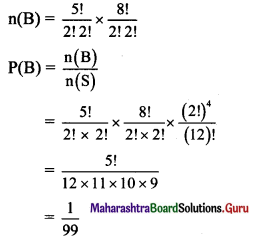
Question 7.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘STATISTICS’. Find the probability that the selected letters are the same.
Solution:
Word ASSISTANT has 2A, I, N, 3S, 2T, and word STATISTICS has A, C, 2I, 3S, 3T.
C and N are uncommon letters.
In the words ASSISTANT, there are 9 letters out of which 2 letters are ‘A’, and in the word STATISTICS, there are 10 letters, out of which 1 letter is A.
∴ Probability of choosing A from both the letters = \(\frac{{ }^{2} C_{1}}{{ }^{9} C_{1}} \times \frac{{ }^{1} C_{1}}{{ }^{10} C_{1}}=\frac{2}{9} \times \frac{1}{10}=\frac{1}{45}\)
Similarly,
Probability of choosing I from both the letters = \(\frac{{ }^{1} \mathrm{C}_{1}}{{ }^{9} \mathrm{C}_{1}} \times \frac{{ }^{2} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}=\frac{1}{9} \times \frac{2}{10}=\frac{1}{45}\)
Probability of choosing S from both the letters = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{9} \mathrm{C}_{1}} \times \frac{{ }^{3} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}=\frac{3}{9} \times \frac{3}{10}=\frac{1}{10}\)
Probability of choosing T from both the letters = \(\frac{{ }^{2} C_{1}}{{ }^{9} C_{1}} \times \frac{{ }^{3} C_{1}}{{ }^{10} C_{1}}=\frac{2}{9} \times \frac{3}{10}=\frac{1}{15}\)
Required probability = \(\frac{1}{45}+\frac{1}{45}+\frac{1}{10}+\frac{1}{15}\) = \(\frac{19}{90}\)

Question 8.
A die is loaded in such a way that the probability of the face with j dots turning up is proportional to j for j = 1, 2,….., 6. What is the probability, in one roil of the die, that an odd number of dots will turn up?
Solution:
According to the given condition, the probability of the face with 1, 2, 3, 4, 5, 6 dots turning up is proportional to 1, 2, 3, 4, 5, 6.
Let k be the common ration of proportionality.
∴ The probabilities of the faces with 1, 2, 3, 4, 5, 6 dots turning up are 1k , 2k, 3k, 4k, 5k, 6k respectively.
Since sum of the probabilities = 1,
k(1 + 2+ ….. + 6) = 1
k(\(\frac{6 \times 7}{2}\)) = 1
k = \(\frac{1}{21}\)
Required probability = P(1) + P(3) + P(5)
= \(\frac{1}{21}+\frac{3}{21}+\frac{5}{21}\)
= \(\frac{9}{21}\)
= \(\frac{3}{7}\)

Question 9.
An urn contains 5 red balls and 2 green balls. A ball is drawn. If it’s green, a red ball is added to the urn, and if it’s red, a green ball is added to the urn. (The original ball is not returned to the urn). Then a second ball is drawn. What is the probability that the second ball is red?
Solution:
A: Event of drawing a red ball and placing a green ball in the urn
B: Event of drawing a green ball and placing a red ball
C: Event of drawing a red ball in the second draw
P(A) = \(\frac{5}{7}\)
P(B) = \(\frac{2}{7}\)
P(C/A) = \(\frac{4}{7}\)
P(C/B) = \(\frac{6}{7}\)
Required probability
P(C) = P(A) P(C/A) + P(B) P(C/B)
= \(\frac{5}{7} \times \frac{4}{7}+\frac{2}{7} \times \frac{6}{7}\)
= \(\frac{32}{49}\)

Question 10.
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5, find the probability that the problem will be solved.
Solution:
The odds against A solving the problems are 4 : 3.
Let P(A’) = P(A does not solve the problem) = \(\frac{4}{4+3}=\frac{4}{7}\)
So, the probability that A solves the problem = P(A) = 1 – P(A’)
= 1 – \(\frac{4}{7}\)
= \(\frac{3}{7}\)
Similarly, let P(B) = P(B solves the problem)
Since odds in favour of B solving the problem are 7 : 5.
∴ P(B) = \(\frac{7}{7+5}=\frac{7}{12}\)
Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Since A and B are independent events.
∴ P(A ∩ B) = P(A) . P(B)
∴ Required probability = P(A) + P(B) – P(A) . P(B)
= \(\frac{3}{7}+\frac{7}{12}-\frac{3}{7} \times \frac{7}{12}\)
= \(\frac{16}{21}\)

Question 11.
If P(A) = P(A/B) = \(\frac{1}{5}\), P(B/A) = \(\frac{1}{3}\), then find
(i) P(A’/B)
(ii) P(B’/A’)
Solution:
Since P(A) = P(A/B) = \(\frac{1}{5}\)
P(A) = \(\frac{1}{5}\)
and \(\frac{P(A \cap B)}{P(B)}=\frac{1}{5}\)
∴ P(A) = \(\frac{1}{5}\) ……(i)
P(B) = 5 P(A ∩ B) ……..(ii)
Since P(B/A) = \(\frac{1}{3}\)
\(\frac{P(A \cap B)}{P(A)}=\frac{1}{3}\)
∴ P(A) = 3 P(A ∩ B) ………(iii)

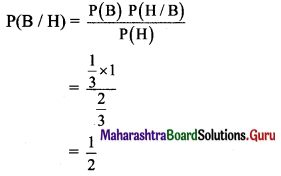
Question 12.
Let A and B be independent events with P(A) = \(\frac{1}{4}\) and P(A ∪ B) = 2P(B) – P(A). Find
(i) P(B)
(ii) P(A/B)
(iii) P(B’/A)
Solution:
A and B are independent events. .
∴ P(A ∩ B) = P(A) × P(B)
(i) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ P(A ∪ B) = P(A) + P(B) – P(A) × P(B)
∴ 2P(B) – P(A) = P(A) + P(B) – P(A) × P(B) ……[∵ P(A ∪ B) = 2P(B) – P(A)]
∴ 2P(B) – \(\frac{1}{4}\) = \(\frac{1}{4}\) + P(B) – \(\frac{1}{4}\) × P(B)
∴ 2P(B) – P(B) + \(\frac{1}{4}\) P(B) = \(\frac{1}{4}\) + \(\frac{1}{4}\)

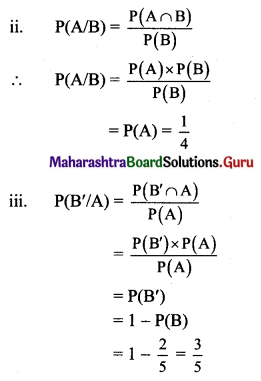
Question 13.
Find the probability that a year selected will have 53 Wednesdays.
Solution:
A leap year comes after 3 years.
∴ The probability of a year being a leap year = \(\frac{1}{4}\)
∴ Probability of a year being a non-leap year = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
In a non-leap year, there are 52 weeks and one extra day, whereas a leap year has 52 weeks and 2 extra days.
∴ 53rd Wednesday’s chance in a non-leap year = \(\frac{1}{7}\)
Two extra days of a leap year can be
(Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat), (Sat, Sun), (Sun, Mon)
∴ There are 2 possibilities of 53rd Wednesday in a leap year.
∴ 53rd Wednesday’s chance in a leap year = \(\frac{2}{7}\)
Required probability = P(a non-leap year and Wednesday) + P(a leap year and Wednesday)
= \(\frac{3}{4} \times \frac{1}{7}+\frac{1}{4} \times \frac{2}{7}\)
= \(\frac{5}{28}\)

Question 14.
The chances of P, Q and R, getting selected as principal of a college are \(\frac{2}{5}\), \(\frac{2}{5}\), \(\frac{1}{5}\) respectively. Their chances of introducing IT in the college are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) respectively. Find the probability that
(a) IT is introduced in the college after one of them is selected as a principal.
(b) IT is introduced by Q.
Solution:
Let event P: P become principal,
event Q: Q become principal,
event R: R become principal,
event E: Subject IT is introduced.
Given, P(P) = \(\frac{2}{5}\)
P(Q) = \(\frac{2}{5}\)
P(R) = \(\frac{1}{5}\)
P(E/P) = \(\frac{1}{2}\)
P(E/Q) = \(\frac{1}{3}\)
P(E/R) = \(\frac{1}{4}\)
(a) Required probability
P(E) = P(P) P(E/P) + P(Q) P(E/Q) + P(R) P(E/R)
= \(\frac{2}{5} \times \frac{1}{2}+\frac{2}{5} \times \frac{1}{3}+\frac{1}{5} \times \frac{1}{4}\)
= \(\frac{1}{5}+\frac{2}{15}+\frac{1}{20}\)
= \(\frac{12+8+3}{60}\)
= \(\frac{23}{60}\)

(b) Required probability = P(Q/E)
By Bayes’ theorem,
P(Q/E) = \(\frac{P(Q) P(E / Q)}{P(E)}\)
= \(\frac{\frac{2}{5} \times \frac{1}{3}}{\frac{23}{60}}\)
= \(\frac{8}{23}\)

Question 15.
Suppose that five good fuses and two defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement What is the probability that we are lucky and find both of the defective fuses in the first two tests?
Solution:
Number of fuses = 5 + 2 = 7
Testing two fuses one-by-one at random, without replacement from 7 can be done in \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) ways.
∴ n(S) = \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) = 7 × 6 = 42
Let event A: Getting defective fuses in the first two tests without replacement.
There are two defective fuses.
∴ n(A) = \({ }^{2} \mathrm{C}_{1} \times{ }^{1} \mathrm{C}_{1}\) = 2 × 1 = 2
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{42}=\frac{1}{21}\)

Question 16.
For three events A, B and C, we know that A and C are independent, B and C are independent, A and B are disjoint, P(A ∪ C) = \(\frac{2}{3}\), P(B ∪ C) = \(\frac{3}{4}\), P(A ∪ B ∪ C) = \(\frac{11}{12}\). Find P(A), P(B) and P(C).
Solution:
Let P(A) = x, P(B) = y, P(C) = z
Since A, B are disjoint,
A ∩ B = Φ and A ∩ B ∩ C = Φ
∴ P(A ∩ B) = 0, P(A ∩ B ∩ C) = 0 ……(i)
Since A and C are independent,
P(A ∩ C) = P(A) P(C) = xz
Since B and C are independent,
P(B ∩ C) = P(B) P(C) = yz
P(A ∪ C) = P(A) + P(C) – P(A ∩ C)
∴ \(\frac{2}{3}\) = x + z – xz ……..(ii)
P(B ∪ C) = P(B) + P(C) – P(B ∩ C)
∴ \(\frac{3}{4}\) = y + z – yz ………(iii)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
\(\frac{11}{12}\) = x + y + z – 0 – yz – zx + 0 …… [From(i)]
= (x + z – xz) + (y + z – yz) – z
= \(\frac{2}{3}+\frac{3}{4}\) – z ……. [From (ii) and (iii)]

Question 17.
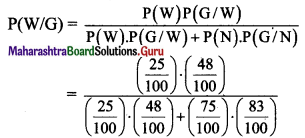
The ratio of boys to girls in a college is 3 : 2 and 3 girls out of 500 and 2 boys out of 50 of that college are good singers. A good singer is chosen. What is the probability that the chosen singer is a girl?
Solution:
Let event S: The student is a good singer,
event B: The student is a boy,
event G: The student is a girl.
Since the ratio of boys to girls is 3 : 2 and 3 girls out of 500 and 2 boys out of 50 are good singers.

Question 18.
A and B throw a die alternatively till one of them gets a 3 and wins the game. Find the respective probabilities of winning. (Assuming A begins the game).
Solution:
Since P(getting 3) = \(\frac{1}{6}\),
P(not getting 3) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
In 1st throw if A gets 3, A wins
∴ P(A win) = \(\frac{1}{6}\)
In 2nd throw by B (i.e., A does not get 3),
∴ P(B wins) = \(\frac{5}{6} \times \frac{1}{6}\)
In 3rd throw by A, P(A wins) = \(\frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}\)
(3rd throw by A shows that B has lost in 2nd throw) and so on.

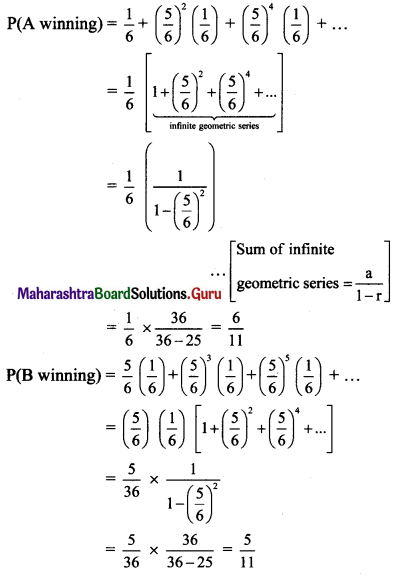
Question 19.
Consider independent trials consisting of rolling a pair of fair dice, over and over. What is the probability that a sum of 5 appears before a sum of 7?
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: The sum is 5 in a trial.
A = {(2, 3), (3, 2), (1, 4), (4, 1)}
∴ P(A) = \(\frac{4}{36}=\frac{1}{9}\)
Let event B: The sum is 7 in a trial.
B = {(2, 5), (5, 2), (3, 4), (4, 3), (1, 6), (6, 1)}
∴ P(B) = \(\frac{6}{36}=\frac{1}{6}\)
Let event C: Neither sum is 5 nor 7.
P(C) = 1 – P(A) – P(B)
= 1 – \(\frac{1}{9}\) – \(\frac{1}{6}\)
= \(\frac{26}{36}\)
Let the sum of 5 appear in the nth trial for the first time and the sum of 7 has not occurred in the first (n – 1) trials.

Question 20.
A machine produces parts that are either good (90%), slightly defective (2%), or obviously defective (8%). Produced parts get passed through an automatic inspection machine, which is able to detect any part that is obviously defective and discard it. What is the probability that the quality of the parts that make it through the inspection machine and get shipped?
Solution:
Let event G: The event that machine produces a good part,
event S: The event that machine produces a slightly defective part,
event D: The event that machine produces an obviously defective part.

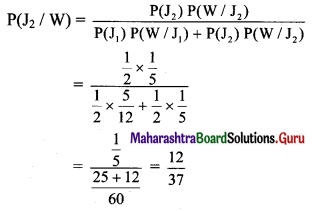
Question 21.
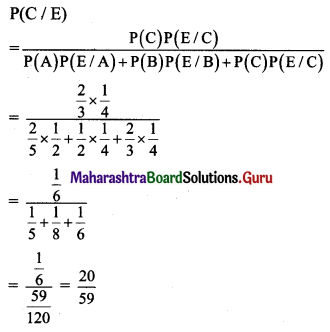
Given three identical boxes, I, II, and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?
Solution:
Let event B₁: Select box I having two gold coins.
event B₂: Selecting box II having two silver coins,
event B₃: Selecting box III having one silver and one gold coin,
event G: Coin is gold.

To find the probability that the other can in the box is also gold. Which is possible only when it is drawn from the box I.
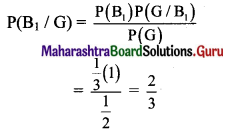
∴ Required probability = P(B₁/G)
By Bayes’ theorem,

Question 22.
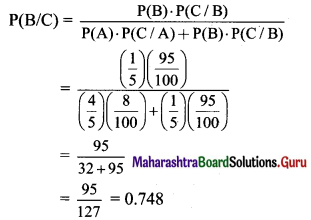
In a factory which manufactures bulbs, machines A, B, and C manufacture respectively 25%, 35% and 40% of the bulbs. Of their outputs, 5, 4, and 2 percent are respectively defective bulbs. A bulb is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by machine B?
Solution:
Let event A: Bulb manufactured by machine A
event B: Bulb manufactured by machine B
event C: Bulb manufactured by machine C
event D: Bulb defective
∴ P(A) = \(\frac{25}{100}\)
P(B) = \(\frac{35}{100}\)
P(C) = \(\frac{40}{100}\)
Machines A, B and C manufacture respectively 25%, 35% and 40% of the bulbs.
Of their outputs, 5, 4, and 2 percent are respectively defective bulbs.

Required probability = P(B/D)
By Bayes’ theorem,

Question 23.
A family has two children. One of them is chosen at random and found that the child is a girl. Find the probability that
(i) both the children are girls.
(ii) both the children are girls given that at least one of them is a girl.
Solution:
A family has two children.
∴ Sample space S = {BB, BG, GB, GG}
(i) A: First child is a girl.
∴ A = {GB, GG}
∴ P(A) = \(\frac{2}{4}=\frac{1}{2}\)
B: Second child is a girl.
∴ B = {BG, GG}
∴ A ∩ B = {GG}
∴ P(A ∩ B) = \(\frac{1}{4}\)
Required probability
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}\)

(ii) A: At least one of the children is a girl.
∴ A = {GG, GB, BG}
∴ P(A) = \(\frac{3}{4}\)
B: both children are girls.
B = {GG}
∴ P(B) = \(\frac{1}{4}\)
Also, A ∩ B = B

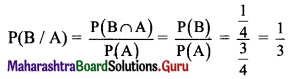
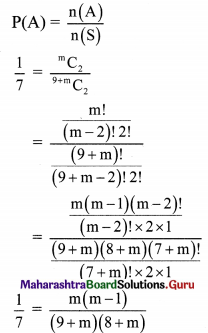
Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.3

Question 1.
A bag contains 3 red marbles and 4 blue marbles. Two marbles are drawn at random without replacement. If the first marble drawn is red, what is the probability that the second marble is blue?
Solution:
Total number of marbles = 3 + 4 = 7
Let event A: The first marble drawn is red.
∴ P(A) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{7} \mathrm{C}_{1}}=\frac{3}{7}\)
Let event B: The second marble drawn is blue.
Since the first red marble is not replaced in the bag, we now have 6 marbles out of which 4 are blue.
∴ Probability that the second marble is blue under the condition that the first red marble is not replaced in the bag = P(B/A) = \(\frac{{ }^{4} \mathrm{C}_{1}}{{ }^{6} \mathrm{C}_{1}}=\frac{4}{6}=\frac{2}{3}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{2}{3} \times \frac{3}{7}\)
= \(\frac{2}{7}\)

Alternate Method:
Total number of marbles = 3 + 4 = 7
Two marbles are drawn at random without replacement.
∴ n(S) = \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) = 7 × 6 = 42
Let event A: The first marble is red and second marble is blue.
First red marble can be drawn from 3 red marbles in \({ }^{3} \mathrm{C}_{1}\) ways and second blue marble can be drawn from 4 blue marbles in \({ }^{4} \mathrm{C}_{1}\) ways.
∴ n(A) = \({ }^{3} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{1}\) = 3 × 4 = 12
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{12}{42}=\frac{2}{7}\)

Question 2.
A box contains 5 green pencils and 7 yellow pencils. Two pencils are chosen at random from the box without replacement. What is the probability that both are yellow?
Solution:
Total number of pencils = 5 + 7 = 12
Let event A: The first pencil chosen is yellow.
∴ P(A) = \(\frac{{ }^{7} \mathrm{C}_{1}}{{ }^{12} \mathrm{C}_{1}}=\frac{7}{12}\)
Let event B: The second pencil chosen is yellow.
Since the first yellow pencil is not replaced in the box, we now have 11 pencils, out of which 6 are yellow.
∴ Probability that the second pencil is yellow under the condition that the first yellow pencil is not replaced in the box = P(B/A)
= \(\frac{{ }^{6} C_{1}}{{ }^{11} C_{1}}\)
= \(\frac{6}{11}\)
Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{6}{11} \times \frac{7}{12}\)
= \(\frac{7}{22}\)

Question 3.
In a sample of 40 vehicles, 18 are red, 6 are trucks, of which 2 are red. Suppose that a randomly selected vehicle is red. What is the probability it is a truck?
Solution:
One vehicle is selected from 40 vehicles.
Let event A: The selected vehicle is red.
There are total of 18 red vehicles.
∴ P(A) = \(\frac{{ }^{18} \mathrm{C}_{1}}{{ }^{40} \mathrm{C}_{1}}=\frac{18}{40}=\frac{9}{20}\)
Let event B: The selected vehicle is a truck.
There are total of 6 trucks.
Since 2 trucks are red, they are common between A and B.
∴ P(A ∩ B) = \(\frac{{ }^{2} \mathrm{C}_{1}}{{ }^{40} \mathrm{C}_{1}}=\frac{2}{40}=\frac{1}{20}\)
∴ Probability that the selected vehicle is a truck under the condition that it is red = P(B/A)
= \(\frac{P(A \cap B)}{P(A)}\)
= \(\frac{\frac{1}{20}}{\frac{9}{20}}\)
= \(\frac{1}{9}\)

Question 4.
From a pack of well-shuffled cards, two cards are drawn at random. Find the probability that both the cards are diamonds when
(i) the first card drawn is kept aside.
(ii) the first card drawn is replaced in the pack.
Solution:
In a pack of 52 cards, there are 13 diamond cards.
Let event A: The first card drawn is a diamond card.
∴ P(A) = \(\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{13}{52}=\frac{1}{4}\)
(i) Let event B: The second card drawn is a diamond card.
Since the first diamond card is kept aside, we now have 51 cards, out of which 12 are diamond cards.
Probability that the second card is a diamond card under the condition that the first diamond card is kept aside in the pack = P(B/A) = \(\frac{{ }^{12} \mathrm{C}_{1}}{{ }^{51} \mathrm{C}_{1}}=\frac{12}{51}=\frac{4}{17}\)
∴ Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{1}{4} \times \frac{4}{17}\)
= \(\frac{1}{17}\)

(ii) Let event B: The second card drawn is a diamond card.
Since the first diamond card is replaced in the pack, we now again have 52 cards, out of which 13 are diamond cards.
∴ Probability that the second card is a diamond card under the condition that the first diamond card is replaced in the pack = P(B/A) = \(\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{13}{52}=\frac{1}{4}\)
Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{1}{4} \times \frac{1}{4}\)
= \(\frac{1}{16}\)

Question 5.
A, B, and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are \(\frac{3}{4}\), \(\frac{1}{2}\) and \(\frac{5}{8}\). Find the probability that the target
(a) is hit exactly by one of them.
(b) is not hit by any one of them.
(c) is hit.
(d) is exactly hit by two of them.
Solution:
Let event A: A can hit the target,
event B: B can hit the target,
event C: C can hit the target.

Since A, B, C are independent events,
A’, B’, C’ are also independent events.
(a) Let event W: Target is hit exactly by one of them.

(b) Let event X: Target is not hit by any one of them.
∴ P(X) = P(A’ ∩ B’ ∩ C’)
= P(A’) P(B’) P(C’)
= \(\frac{1}{4} \times \frac{1}{2} \times \frac{3}{8}\)
= \(\frac{3}{64}\)

(c) Let event Y: Target is hit.
∴ P(Y) = 1 – P(target is not hit by any one of them)
= 1 – \(\frac{3}{64}\)
= \(\frac{61}{64}\)

(d) Let event Z: Target is hit by exactly two of them.

Question 6.
The probability that a student X solves a problem in dynamics is \(\frac{2}{5}\) and the probability that student Y solves the same problem is \(\frac{1}{4}\). What is the probability that
(i) the problem is not solved?
(ii) the problem is solved?
(iii) the problem is solved exactly by one of them?
Solution:
Let event A: Student X solves the problem in dynamics,
event B: Student Y solves the problem in dynamics.
∴ P(A) = \(\frac{2}{5}\), P(B) = \(\frac{1}{4}\)
∴ P(A’) = 1 – P(A) = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
P(B’) = 1 – P(B) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
Since A and B are independent events,
A’ and B’ are also independent events.
(i) Let event C: Problem is not solved.
∴ P(C) = P(A’ ∩ B’)
= P(A’) . P(B’)
= \(\frac{3}{5} \times \frac{3}{4}\)
= \(\frac{9}{20}\)

(ii) Let event D: Problem is solved.
Problem can be solved if at least one of the two students solves the problem.
∴ P(D) = P(at least one student solves the problem)
= 1 – P(no student solves the problem)
= 1 – P(A’ ∩ B’)
= 1 – P(A’) P(B’)
= 1 – \(\frac{3}{5} \times \frac{3}{4}\)
= 1 – \(\frac{9}{20}\)
= \(\frac{11}{20}\)

(iii) Let event E: The problem is solved exactly by one of them.
∴ P(E) = P(A’ ∩ B) ∪ P(A ∩ B’)
= P(A’) . P(B) + P(A) . P(B’)
= \(\left(\frac{3}{5} \times \frac{1}{4}\right)+\left(\frac{2}{5} \times \frac{3}{4}\right)\)
= \(\frac{3}{20}+\frac{6}{20}\)
= \(\frac{9}{20}\)

Question 7.
A speaks truth in 80% of the cases and B speaks truth in 60% of the cases. Find the probability that they contradict each other in narrating an incident.
Solution:
Let event A : A speaks the truth,
event B : B speaks the truth.
∴ P(A) = \(\frac{80}{100}=\frac{4}{5}\)
and P(B) = \(\frac{60}{100}=\frac{3}{5}\)
P(A’) = 1 – P(A) = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
and P(B’) = 1 – P(B) = 1 – \(\frac{3}{5}\) = \(\frac{2}{5}\)
∴ P(A and B contradict each other) = P(A speaks the truth and B lies) + P (A lies and B speaks the truth)
= P(A ∩ B’) + P(A’ ∩ B)
= P(A) P(B’) + P(A’) P(B)
= \(\left(\frac{4}{5} \times \frac{2}{5}\right)+\left(\frac{1}{5} \times \frac{3}{5}\right)\)
= \(\frac{8}{25}+\frac{3}{25}\)
= \(\frac{11}{25}\)

Question 8.
Two hundred patients who had either Eye surgery or Throat surgery were asked whether they were satisfied or unsatisfied regarding the result of their surgery. The following table summarizes their response.

If one person from the 200 patients is selected at random, determine the probability
(a) that the person was satisfied given that the person had Throat surgery.
(b) that person was unsatisfied given that the person had eye surgery.
(c) the person had Throat surgery given that the person was unsatisfied.
Solution:
(a) Let event A: The patient was satisfied,
event B: The patient had throat surgery.
Given, n(S) = 200
n(A ∩ B) = 70
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{70}{200}\)
n(B) = 95
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{95}{200}\)
∴ Required probability = P(A / B)
= \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{\left(\frac{70}{200}\right)}{\left(\frac{95}{200}\right)}\)
= \(\frac{70}{95}\)
= \(\frac{14}{19}\)

Check:
Reduce the sample space to the set of throat patients only.
n(S) = 95
Let E : Patient had satisfactory throat surgery.
n(E) = 70
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{70}{95}=\frac{14}{19}\)

(b) Let event C : The patient was unsatisfied,
event D : The patient had a eye surgery.
Given, n(S) = 200
n(C ∩ D) = 15
∴ P(C ∩ D) = \(\frac{n(C \cap D)}{n(S)}=\frac{15}{200}\)
n(D) = 105
∴ P(D) = \(\frac{105}{200}\)
Required probability = P(C / D)
= \(\frac{P(C \cap D)}{P(D)}\)
= \(\frac{\left(\frac{15}{200}\right)}{\left(\frac{105}{200}\right)}\)
= \(\frac{1}{7}\)

(c) Let event F : The patient had a throat surgery,
event G : The patient was unsatisfied.
Given, n(S) = 200
n(F ∩ G) = 25
∴ P(F ∩ G) = \(\frac{n(F \cap G)}{n(S)}=\frac{25}{200}\)
n(G) = 40
∴ P(G) = \(\frac{n(G)}{n(S)}=\frac{40}{200}\)
∴ Required probability = P(F / G)
= \(\frac{P(F \cap G)}{P(G)}\)
= \(\frac{\left(\frac{25}{200}\right)}{\left(\frac{40}{200}\right)}\)
= \(\frac{5}{8}\)

Question 9.
Two dice are thrown together. Let A be the event ‘getting 6 on the first die’ and B be the event ‘getting 2 on the second die’. Are events A and B independent?
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: Getting 6 on the first die.
∴ A = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
Let event B : Gettting 2 on the second die.
∴ B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
∴ n(B) = 6
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
Now, A ∩ B = {(6, 2)}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{1}{36}\) …..(i)
P(A) × P(B) = \(\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}\) ……..(ii)
From (i) and (ii), we get
P(A ∩ B) = P(A) × P(B)
∴ A and B are independent events.

Question 10.
The probability that a man who is 45 years old will be alive till he becomes 70 is \(\frac{5}{12}\). The probability that his wife who is 40 years old will be alive till she becomes 65 is \(\frac{3}{8}\). What is the probability that, 25 years hence,
(a) the couple will be alive?
(b) exactly one of them will be alive?
(c) none of them will be alive?
(d) at least one of them will be alive?
Solution:
Let event A: The man will be alive till 70.
∴ P(A) = \(\frac{5}{12}\)
Let event B: The wife will be alive till 65.
∴ P(B) = \(\frac{3}{8}\)
∴ P(A’) = 1 – P(A) = 1 – \(\frac{5}{12}\) = \(\frac{7}{12}\)
P(B’) = 1 – P(B) = 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)
Since A and B are independent events,
A’ and B’ are also independent events.
(a) Let event C : Both man and his wife will be alive.
∴ P(C) = P(A ∩ B) = P(A) . P(B)
= \(\frac{5}{12} \times \frac{3}{8}\)
= \(\frac{5}{32}\)

(b) Let event D: Exactly one of them will be alive.
∴ P(D) = P(A’ ∩ B) + P(A ∩ B’)
= P(A’) . P(B) + P(A) . P(B’)
= \(\left(\frac{7}{12} \times \frac{3}{8}\right)+\left(\frac{5}{12} \times \frac{5}{8}\right)\)
= \(\frac{21}{96}+\frac{25}{96}\)
= \(\frac{23}{48}\)

(c) Let event E: None of them will be alive.
∴ P(E) = P(A’ ∩ B’) = P(A’) . P(B’)
= \(\frac{7}{12} \times \frac{5}{8}\)
= \(\frac{35}{96}\)

(d) Let event F: At least one of them will be alive.
∴ P(F) = 1 – P(none of them will be alive)
= 1 – \(\frac{35}{96}\)
= \(\frac{61}{96}\)

Question 11.
A box contains 10 red balls and 15 green balls. Two balls are drawn in succession without replacement. What is the probability that,
(a) the first is red and the second is green?
(b) one is red and the other is green?
Solution:
Total number of balls = 10 + 15 = 25
(a) Let event A: First ball drawn is red.
∴ P(A) = \(\frac{{ }^{10} \mathrm{C}_{1}}{{ }^{25} \mathrm{C}_{1}}=\frac{10}{25}=\frac{2}{5}\)
Let event B: Second ball drawn is green.
Since the first red ball is not replaced in the box, we now have 24 balls, out of which 15 are green.
∴ Probability that the second ball is green under the condition that the first red ball is not replaced in the box = P(B/A) = \(\frac{{ }^{15} \mathrm{C}_{1}}{{ }^{24} \mathrm{C}_{1}}=\frac{15}{24}=\frac{5}{8}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{2}{5} \times \frac{5}{8}\)
= \(\frac{1}{4}\)

(b) To find the probability that one ball is red and the other is green, there are two possibilities:
First ball is red and second ball is green.
OR
The first ball is the green and the second ball is red.
From above, we get
P(First ball is red and second ball is green) = \(\frac{1}{4}\)
Similarly,
P(First ball is green and second ball is red) = \(\frac{{ }^{15} \mathrm{C}_{1}}{{ }^{25} \mathrm{C}_{1}} \times \frac{{ }^{10} \mathrm{C}_{1}}{{ }^{24} \mathrm{C}_{1}}=\frac{15}{25} \times \frac{10}{24}=\frac{1}{4}\)
∴ Required probability = P(First ball is red and second ball is green) + P(First ball is green and second ball is red)
= \(\frac{1}{4}\) + \(\frac{1}{4}\)
= \(\frac{1}{2}\)

Question 12.
A bag contains 3 yellow and 5 brown balls. Another bag contains 4 yellow and 6 brown balls. If one ball is drawn from each bag, what is the probability that,
(a) both the balls are of the same colour?
(b) the balls are of a different colours?
Solution:
(a) Let event A: A yellow ball is drawn from each bag.
Probability of drawing one yellow ball from total 8 balls of first bag and that of drawing one yellow ball out of total 10 balls of second bag is
P(A) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{8} \mathrm{C}_{1}} \times \frac{{ }^{4} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}\) = \(\frac{3}{8} \times \frac{4}{10}=\frac{3}{20}\)
Let event B: A brown ball is drawn from each bag.
Probability of drawing one brown ball out of total 8 balls of first bag and that of drawing one brown ball out of total 10 balls of second bag is
P(B) = \(\frac{{ }^{5} \mathrm{C}_{1}}{{ }^{8} \mathrm{C}_{1}} \times \frac{{ }^{6} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}\) = \(\frac{5}{8} \times \frac{6}{10}=\frac{3}{8}\)
Since both the events are mutually exclusive events,
P(A ∩ B) = 0
∴ P(both the balls are of the same colour) = P(both are of yellow colour) or P(both are of brown colour)
= P(A) + P(B)
= \(\frac{3}{20}+\frac{3}{8}\)
= \(\frac{21}{40}\)

(b) P(both the balls are of different colour) = 1 – P(both the balls are of the same colour)
= 1 – \(\frac{21}{40}\)
= \(\frac{19}{40}\)

Question 13.
An urn contains 4 black, 5 white, and 6 red balls. Two balls are drawn one after the other without replacement. What is the probability that at least one of them is black?
Solution:
Total number of balls in the um = 4 + 5 + 6 = 15
Two balls are drawn from 15 balls without replacement.
∴ n(S) = \({ }^{15} \mathrm{C}_{1} \times{ }^{14} \mathrm{C}_{1}\) = 15 × 14 = 210
Let event A: At least one ball is black.
i.e., the first ball is black, and the second ball is non-black or the first ball is non-black and the second ball is black, or both the first and second balls are black.
∴ n(A) = \({ }^{4} \mathrm{C}_{1} \times{ }^{11} \mathrm{C}_{1}+{ }^{11} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{1}+{ }^{4} \mathrm{C}_{1} \times{ }^{3} \mathrm{C}_{1}\)
= 4 × 11 + 11 × 4 + 4 × 3
= 100
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{100}{210}=\frac{10}{21}\)

Check:
Required probability = 1 – P(no black ball in two balls)
= 1 – \(\frac{{ }^{11} C_{2}}{{ }^{15} C_{2}}=1-\frac{11 \times 10}{15 \times 14}=1-\frac{11}{21}=\frac{10}{21}\)

Question 14.
Three fair coins are tossed. What is the probability of getting three heads given that at least two coins show heads?
Solution:
When three fair coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
∴ n(S) = 8
Let event A: Getting three heads.
∴ A = {HHH}
Let event B: Getting at least two heads.
∴ B = {HHT, HTH, THH, HHH}
∴ n(B) = 4
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{8}\)
Now, A ∩ B = {HHH}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{1}{8}\)
∴ Probability of getting three heads, given that at least two coins show heads, is given by
P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\)
= \(\frac{\frac{1}{8}}{\frac{4}{8}}\)
= \(\frac{1}{4}\)

Question 15.
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards are drawn are face cards?
Solution:
In a pack of52 cards, there are 12 face cards.
Let event A: The first card drawn is a face card.
∴ P(A) = \(\frac{{ }^{12} C_{1}}{{ }^{52} C_{1}}=\frac{12}{52}=\frac{3}{13}\)
Let event B: The second card drawn is a face card.
Since the first card is not replaced in the pack, we now have 51 cards, out of which 11 are face cards.
∴ Probability that the second card is a face card under the condition that the first card is not replaced in the pack = P(B/A) = \(\frac{{ }^{11} C_{1}}{{ }^{51} C_{1}}=\frac{11}{51}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{11}{51} \times \frac{3}{13}\)
= \(\frac{11}{221}\)

Question 16.
Bag A contains 3 red and 2 white balls and bag B contains 2 red and 5 white balls. A bag is selected at random, a ball is drawn and put into the other bag, and then a ball is drawn from that bag. Find the probability that both the balls are drawn are of the same colour.
Solution:
Let event C₁: The first ball drawn is red and from bag A,
event D₁: The first ball drawn is white and from bag A,
event E₁: The first ball drawn is red and from bag B,
event F₁: The first ball drawn is white and from bag B,
event C₂: Second ball drawn is red and from bag B,
event D₂: Second ball drawn is white and from bag B,
event E₂: Second ball drawn is red and from bag A,
event F₂: Second ball drawn is white and from bag A,
event G: Selecting bag A in the first place,
event H: Selecting bag B in the first place.
P(G) = P(H) = \(\frac{1}{2}\)
Let event X: Both the balls drawn are of same colour.
∴ P(X) = P(G) × P (X/G) + P(H) × P(X/H) …….(i)
If bag A is selected in first place, then In bag A, we have 5 balls, out of which 3 are red.
Probability of getting first red ball from bag A = P(C1) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{5} \mathrm{C}_{1}}=\frac{3}{5}\)
Since first red ball is put into the bag B, we now have 8 balls in bag B, out of which 3 are red.
∴ Probability of getting second red ball from bag B.
P(C₂/C₁) = \(\frac{{ }^{3} C_{1}}{{ }^{8} C_{1}}=\frac{3}{8}\)
Similarly, probability of getting first white ball from bag A = P(D₁) = \(\frac{{ }^{2} C_{1}}{{ }^{5} C_{1}}=\frac{2}{5}\)
and probability of getting second white ball form bag B = P(D₂/D₁) = \(\frac{{ }^{6} C_{1}}{{ }^{8} C_{1}}=\frac{6}{8}\)
∴ P(X/G) = P(C₁) P(C₂/C₁) + P(D₁) P(D₂/D₁)
= \(\frac{3}{5} \times \frac{3}{8}+\frac{2}{5} \times \frac{6}{8}\)
= \(\frac{21}{40}\) …..(ii)
Similarly, P(X/H) = P(E₁) P(E₂/E₁) + P(F₁) P(F₂/F₁)
= \(\frac{2}{7} \times \frac{4}{6}+\frac{5}{7} \times \frac{3}{6}\)
= \(\frac{23}{42}\) ………(iii)
From (i), (ii), (iii),
Required probability = \(\frac{1}{2} \times \frac{21}{40}+\frac{1}{2} \times \frac{23}{42}\)
= \(\frac{3604}{6720}\)
= \(\frac{901}{1680}\)

Question 17.
Activity: A bag contains 3 red and 5 white balls. Two balls are drawn at random one after the other without replacement. Find the probability that both the balls are white.
Solution:
Let, event A: The first ball drawn is white
event B: Second ball drawn is white.
P(A) = \(\frac{5}{8}\)
After drawing the first ball, without replacing it into the bag a second ball is drawn from the remaining 7 balls.
∴ P(B/A) = \(\frac{4}{7}\)
∴ P(Both balls are white) = P(A ∩ B)
= P(A) . P(B/A)
= \(\frac{5}{8}\) × \(\frac{4}{7}\)
= \(\frac{5}{14}\)

Question 18.
A family has two children. Find the probability that both the children are girls, given that at least one of them is a girl.
Solution:
A family has two children.
∴ Sample space S = {BB, BG, GB, GG}
∴ n(S) = 4
Let event A: At least one of the children is a girl.
∴ A = {GG, GB, BG}
∴ n(A) = 3
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{4}\)
Let event B: Both children are girls.
∴ B = {GG}
∴ n(B) = 1
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{4}\)
Also, A ∩ B = B
∴ P(A ∩ B) = P(B) = \(\frac{1}{4}\)
∴ Required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{\frac{1}{4}}{\frac{3}{4}}\)
= \(\frac{1}{3}\)

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 16 Chemistry in Everyday Life Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 16 Chemistry in Everyday Life

1. Choose the correct option

Question A.
Oxidative Rancidity is …………….. reaction
a. addition
b. substitution
c. Free radical
d. combination
Answer:
c. Free radical

Question B.
Saponification is carried out by ……………..
a. oxidation
b. alkaline hydrolysis
c. polymerisation
d. Free radical formation
Answer:
b. alkaline hydrolysis

Question C.
Aspirin is chemically named as ……………..
a. Salicylic acid
b. acetyl salicylic acid
c. chloroxylenol
d. thymol
Answer:
b. acetyl salicylic acid

Question D.
Find odd one out from the following
a. dettol
b. chloroxylenol
c. paracetamol
d. trichlorophenol
Answer:
c. paracetamol

Question E.
Arsenic based antibiotic is
a. Azodye
b. prontosil
c. salvarsan
d. sulphapyridine
Answer:
c. salvarsan

Question F.
The chemical used to slow down the browning action of cut fruit is
a. SO₃
b. SO₂
c. H₂SO₄
d. Na₂CO₃
Answer:
b. SO₂

Question G.
The chemical is responsible for the rancid flavour of fats is
a. Butyric acid
b. Glycerol
c. Protein
d. Saturated fat
Answer:
a. Butyric acid

Question H.
Health benefits are obtained by consumption of
a. Saturated fats
b. trans fats
c. monounsaturated fats
d. all of these
Answer:
c. monounsaturated fats

2. Explain the following :

Question A.
Cooking makes food easy to digest.
Answer:

• During the cooking process, high polymers of carbohydrates or proteins are hydrolysed to smaller polymeric units.
• The uncooked food mixture is a heterogeneous suspension which becomes a colloidal matter on cooking.
• As a result, the constituent nutrient molecules present in cooked food are smaller in size and hence, easier to digest, than the uncooked food.

Hence, cooking makes food easy to digest.

Question B.
On cutting some fruits and vegetables turn brown.
Answer:
i. Cutting of fruits and vegetables damage the cells, resulting in release of chemicals.
ii. Depending on the pH of fruits/vegetables, polyphenols are released.
iii. Due to the action of an enzyme, these polyphenols react with oxygen present in the air and get oxidised to form quinones.

iv. Quinones further undergo reactions including polymerization, which results in the formation of brown coloured products called as tannins.
Thus, on cutting, some fruits and vegetables turn brown.

Question C.
Vitmin E is added to packed edible oil.
Answer:

• Vitamin E is a very effective natural antioxidant.
• The phenolic – OH group present in the structure of vitamin E is responsible for its antioxidant activity.
• Also, the long chain of saturated carbon atoms makes it fat soluble.

Therefore, when vitamin E is added to packed edible oil, it prevents the oxidative rancidity of the oil.

Question D.
Browning of cut apple can be prolonged by applying lemon juice.
Answer:

• Browning of cut apple is due to the oxidation of polyphenols at a particular pH to quinones, which further undergoes polymerization to form brown coloured tannins.
• This browning reaction can be prolonged or slowed down by using reducing agents or by changing the pH.
• Applying lemon juice (i.e., citric acid) on the cut apple, lowers the pH at the surface of the apple. This prevents the oxidation reaction. Thus, browning of cut apple can be prolonged by applying lemon juice.

Question E.
A diluted solution (4.8 % w/v) of 2,4,6-trichlorophenol is employed as antiseptic.
Answer:

• 2,4,6-Trichlorophenol (TCP) is more potent antiseptic than phenol.
• It has low corrosive effects as compared to phenol, if used in lower concentrations.

Hence, diluted solution (4.8% w/v) of 2,4,6-trichlorophenol is used as antiseptic.

Question F.
Turmeric powder can be used as antiseptic.
Answer:

• Turmeric powder contains an active ingredient called curcumin.
• Curcumin has antiseptic properties; thus, it is used for wound healing or applied on bruise.

Hence, turmeric powder can be used as antiseptic.

3. Identify the functional groups in the following molecule :

Answer:

4. Give two differences between the following

Question A.
Disinfectant and antiseptic
Answer:

Disinfectant	Antiseptic
1. Disinfectants are applied on non-living surfaces like floors, instruments, sanitary ware, etc. to kill wide range of microorganisms.	1. Antiseptics are applied on the surface of living tissues in order to sterilise them.
2. Disinfectants cannot be applied on wounds.	2. Antiseptics can be directly applied on wounds.
3. p-chloro-o-benzyl phenol	3. Iodine, boric acid, iodoform, dettol, etc.

Question B.
Soap and synthetic detergent
Answer:

Soap	Synthetic detergent
1. Soaps can be broadly classified into two types, i.e., toilet soaps (prepared using KOH) and laundry soaps (prepared using NaOH).	1. Synthetic detergents are of three types, i.e., anionic, cationic and nonionic detergents.
2. Soaps cannot be used in hard water.	2. Synthetic detergents can be used in soft water as well as in hard water.

Question C.
Saturated and unsaturated fats
Answer:

Saturated fats	Unsaturated fats
1. In saturated fat, long chains of tetrahedral carbon atoms in the fatty acid get closely packed together.	1. In unsaturated fats, the presence of one or more C = C bond in long chains of fatty acids, prevent molecules from packing closely together.
2. In saturated fats, the van der Waals forces between long saturated chains are strong. Hence, their melting points are higher than unsaturated fats.	2. In unsaturated fats, the van der Waals forces between long unsaturated chains are weak. Hence, their melting points are lower than saturated fats.

Question D.
Rice flour and cooked rice
Answer:

Rice flour	Cooked rice
1. Rice flour can be stored for a long period of time. It has a long shelf life.	1. Cooked rice cannot be stored for a longer period of time. It has very short shelf life.
2. Rice flour is uncooked food and hence, it is difficult to digest.	2. Cooked rice is easier to digest.

5. Match the pairs.

A group	B group
A. Paracetamol	a. Antibiotic
B. Chloramphenicol	b. Synthetic detergent
C. BHT	c. Soap
D. Sodium stearate	d. Antioxidant
	e. Analgesic

Answer:
A – e,
B – a,
C – d,
D – c

6. Name two drugs which reduce body pain.
Answer:
Aspirin and paracetamol are the two drugs that reduce body pain.

7. Explain with examples

Question A.
Antiseptics
Answer:
i. Antiseptics are used to sterilise surfaces of living tissue when the risk of infection is very high, such as during surgery or on wounds.
ii. Commonly used antiseptics include inorganics like iodine and boric acid or organics like iodoform and some phenolic compounds.

e.g.

• Tincture of iodine (2-3% solution of iodine in alcohol-water mixture) and iodoform serve as powerful antiseptics and is used to apply on wounds.
• A dilute aqueous solution of boric acid is a weak antiseptic used for eyes.
• Various phenols are used as antiseptics. A dilute aqueous solution of phenol (carbolic acid) is used as antiseptic; however, phenol is found to be corrosive in nature. Many chloro derivatives of phenols are more potent antiseptics than the phenol itself. They can be used with much lower concentrations, which reduce their corrosive effects.
• Two of the most common phenol derivatives in use are trichlorophenol (TCP) and chloroxylenol (which is an active ingredient of antiseptic dettol).
• Thymol obtained from oil of thyme (a spice plant) has excellent non-toxic antiseptic properties.

Question B.
Disinfectant
Answer:

• Disinfectants are non-selective antimicrobials.
• They kill a wide range of microorganisms including bacteria.
• They are used on non-living surfaces for example, floors, instruments, sanitary ware, etc.
• Various phenols can be used as disinfectants.
  e.g. p-Chloro-o-benzyl phenol is used as a disinfectant in all-purpose cleaners.

Question C.
Cationic detergents
Answer:
Cationic detergents: These are quaternary ammonium salts having one long chain alkyl group.
e.g. Ethyltrimethylammonium bromide: [CH₃(CH₂)₁₅ – N⁺(CH₃)₃]Br^–

Question D.
Anionic detergents
Answer:
Anionic detergents: These are sodium salts of long chain alkyl sulphonic acids or long chain alkyl substituted benzene sulphonic acids.
e.g. Sodium lauryl sulphate: CH₃(CH₂)₁₀CH₃O\(\mathrm{SO}_{3}^{-}\)Na⁺

Question E.
Non-ionic detergents
Answer:
Nonionic detergents: These are ethers of polyethylene glycol with alkyl phenol or esters of polyethylene glycol with long chain fatty acid.
e.g. a. Nonionic detergent containing ether linkage:

b. Nonionic detergent containing ester linkage: CH₃(CH₂)₁₆ – COO(CH₂CH₂O)_nCH₂CH₂OH

8. Explain : mechnism of cleansing Action of soap with flow chart.
Answer:
The following flow chart shows mechanism of cleansing action of soap:

9. What is meant by broad spectrum antibiotic and narrow spectrum antibiotics?
Answer:
Antibiotics which are effective against wide range of bacteria are known as broad spectrum antibiotics, while antibiotics which are effective against one group of bacteria are known as narrow spectrum antibiotics.

10. Answer in one senetence

Question A.
Name the painkiller obtained from acetylation of salicyclic acid.
Answer:
Aspirin is the pain killer obtained from acetylation of salicylic acid.

Question B.
Name the class of drug often called as painkiller.
Answer:
Analgesics are the class of drug often called as painkiller.

Question C.
Who discovered penicillin?
Answer:
Alexander Fleming discovered penicillin.

Question D.
Draw the structure of chloroxylenol and salvarsan.
Answer:
Structure of chloroxylenol:

Structure of salvarsan:

Question E.
Write molecular formula of Butylated hydroxy toulene.
Answer:
Molecular formula of butylated hydroxytoluene is C₁₅H₂₄O.

Question F.
What is the tincture of iodine ?
Answer:
Tincture of iodine is a 2-3% solution of iodine in alcohol-water mixture.

Question G.
Draw the structure of BHT.
Answer:

Question I.
Write a chemical equation for saponification.
Answer:

Question J.
Write the molecular formula and name of

Answer:
Molecular formula: C₉H₈O₄
Name: Aspirin

11. Answer the following

Question A.
Write two examples of the following.
a. Analgesics
c. Antiseptics
d. Antibiotics
e. Disinfectant
Answer:

No.	Drug type	Examples
i.	Analgesics	Aspirin, paracetamol
ii.	Antiseptics	Dettol, thymol
iii.	Antibiotics	Penicillin, sulphapyridine
iv.	Disinfectant	Phenol, p-Chloro-o-benzyl phenol

Question B.
What do you understand by antioxidant ?
Answer:

• An antioxidant is a substance that delays the onset of oxidant or slows down the rate of oxidation of foodstuff.
• It is used to extend the shelf life of food.
• Antioxidants react with oxygen-containing free radicals and thereby prevent oxidative rancidity.
  e.g. Vitamin E is a very effective natural antioxidant.

Activity :

Collect information about different chemical compounds as per their applications in day-to-day life.
Answer:

No.	Chemical compound	Applications
i.	Vinegar(CH3COOH)	Preservation of food, salad dressing, sauces, etc.
ii.	Magnesium hydroxide [Mg(OH)2]	Common component of antacids (used to relieve heartburn, acid indigestion and stomach upset.)
iii.	Baking soda (NaHCO3)	Cooking, antacid, toothpaste, etc.
iv.	Sodium benzoate (C6H5COONa)	Used as food preservative

[Note: Students can use the above information as reference and collect additional information on their own.]

11th Chemistry Digest Chapter 16 Chemistry in Everyday Life Intext Questions and Answers

Can you recall? (Textbook Page No. 261)

Question i.
What are the components of balanced diet?
Answer:
Carbohydrates, proteins, lipids (fats and oil), vitamins, minerals and water are the components of balanced diet.

Question ii.
Why is food cooked? What is the difference in the physical states of uncooked and cooked food?
Answer:

• Food is cooked in order to make it easy to digest.
• Also, the raw or uncooked food may contain harmful microorganisms which may cause illness. Cooking of food at high temperature kills most of these microorganisms.
• Raw/uncooked food materials like dried pulses, vegetables, meat, etc. are hard and thus, not easily chewable while cooked food is soft and tender, therefore, easily chewable.

Question iii.
What are the chemicals that we come across in everyday life?
Answer:
Detergents, shampoos, medicines, various food flavours, food colours, etc. are different types of chemicals that we come across in everyday life.

Just think (Textbook Page No. 261)

Question i.
Why is food stored for a long time?
Answer:
Food (like various cereals, pulses, pickles) is stored for a long time to make it available in all seasons.

Question ii.
What methods are used for preservation of food?
Answer:
Various physical and chemical methods are used for preservations of food.

• Physical methods like, addition of heat, removal of heat, removal of water, irradiation, etc., are used in order to preserve food.
• Chemical methods like, addition of sugar, salt, vinegar, etc. are employed for preservation of food.

Question iii.
What is meant by quality of food?
Answer:
Food quality can be described in terms of parameters such as flavour, smell, texture, colour and microbial spoilage.

Can you recall? (Textbook Page No. 263)

Question i.
How is Vanaspati ghee made?
Answer:
Vanaspati ghee is prepared by hydrogenation of oils. Hydrogen gas is passed through the oils at about 450 K in the presence of nickel catalyst to form solid edible fats like vanaspati ghee.

Question ii.
What are the physical states of peanut oil, butter, animal fat, Vanaspati ghee at room temperature?
Answer:

Example	Physical state
Peanut oil	Liquid
Butter	Semi-solid
Animal fat	Solid/semi-solid
Vanaspati ghee	Solid/semi-solid

Can you tell? (Textbook Page No. 264)

Question 1.
When is an antipyretic drug used?
Answer:
An antipyretic drug is used to reduce fever (that is, it lowers body temperature when a fever is present).

Question 2.
What type of medicine is applied to a bruise?
Answer:
Antiseptic such as tincture of iodine is applied on a bruise in order to prevent the exposed living tissue from getting infected.

Question 3.
What is meant by a broad spectrum antibiotic?
Answer:
Antibiotics which are effective against wide range of bacteria are known as broad spectrum antibiotic.

Question 4.
What is the active principle ingredient of cinnamon bark?
Answer:
Cinnamaldehyde is the principle active ingredient of cinnamon bark.

Can you tell? (Textbook Page No. 268)

Question i.
Can we use the same soap for bathing as well as cleaning utensils or washing clothes? Why?
Answer:
No, we cannot use the same soap for bathing as well as cleaning utensils or washing clothes due to the following reasons:

• Chemical composition of each type of soap or cleansing material is different.
• Nature, acidity, texture, reactivity towards water (i.e., hard water or soft water), reactivity towards microorganisms, stains are different for each type of soap.
• Depending on these qualities, soaps are classified and used accordingly.
  e.g. pH of soaps used for bathing purpose is different than that of the soap which is used for cleaning utensils.

Thus, we cannot use the same soap for bathing as well as cleaning utensils or washing clothes.

Question ii.
How will you differentiate between soaps and synthetic detergent using borewell water?
Answer:
Borewell water is hard water. Soaps and synthetic detergents react differently with hard water.

1. Soap: Soaps are insoluble in hard water. Borewell water (hard water) contains Ca²⁺ and Mg²⁺ ions. Soaps react with these ions to form insoluble magnesium and calcium salts of fatty acids. These salts precipitate out as gummy substance or form scum.
2. Synthetic detergents: Synthetic detergents can be used in hard water as well. They contain molecules (components) which form soluble calcium and magnesium salts.

Thus, soaps will form scum in borewell water but synthetic detergents will not.

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 15 Hydrocarbons Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 15 Hydrocarbons

1. Choose correct options

Question A.
Which of the following compound has the highest boiling point?
a. n-pentane
b. iso-butane
c. butane
d. neopentane
Answer:
a. n-pentane

Question B.
Acidic hydrogen is present in :
a. acetylene
b. ethane
c. ethylene
d. dimethyl acetylene
Answer:
a. acetylene

Question C.
Identify ‘A’ in the following reaction:

a. KMnO₄/H⁺
b. alkaline KMnO₄
c. dil. H₂SO₄/1% HgSO₄
d. NaOH/H₂O₂
Answer:
a. KMnO₄/H⁺

Question D.
Major product of chlorination of ethyl benzene is :
a. m-chlorethyl benzene
b. p-chloroethyl benzene
c. chlorobenzene
d. o-chloroethylbenzene
Answer:
b. p-chloroethyl benzene

Question E.
1 – chloropropane on treatment with alc. KOH produces :
a. propane
b. propene
c. propyne
d. propyl alcohol
Answer:
b. propene

2. Name the following :

Question A.
The type of hydrocarbon that is used as lubricant.
Answer:
Waxes

Question B.
Alkene used in the manufacture of polythene bags.
Answer:
Ethene

Question C.
The hydrocarbon said to possess carcinogenic property.
Answer:
Benzene

Question D.
What are the main natural sources of alkane?
Answer:
Crude petroleum and natural gas.

Question E.
Arrange the three isomers of alkane with malecular formula C₅H₁₂ in increasing order of boiling points and write their IUPAC names.
Answer:
The three isomers of alkane with molecular formula C₅H₁₂ are as follows:

The increasing order of their boiling point is I > II > III.

Question F.
Write IUPAC names of the products obtained by the reaction of cold concentrated sulphuric acid followed by water with the following compounds.
a. propene
b. but-1-ene
Answer:
a. propene:

b. but-1-ene:

Question G.
Write the balanced chemical reaction for preparation of ethane from
a. Ethyl bromide
b. Ethyl magnesium iodide
Answer:
a. Preparation of ethane from ethyl bromide:

b. Preparation of ethane from ethyl magnesium iodide:

Question H.
How many monochlorination products are possible for
a. 2-methylpropane ?
b. 2-methylbutane ?
Draw their structures and write their IUPAC names.
Answer:
a. Possible monochlorination products for 2-methylpropane:

b. Possible monochlorination products for 2-methylbutane:

Question I.
Write all the possible products for pyrolysis of butane.
Answer:
Possible products for pyrolysis of butane are:

Question J.
Which of the following will exhibit geometical isomerism ?

Answer:
Compound (c) will exhibit geometrical isomerism.

Question K.
What is the action of following on ethyl iodide ?
a. alc. KOH
b. Zn, HCl
Answer:
a. Action of alc. KOH on ethyl iodide:

b. Action of Zn/HCl on ethyl iodide:

Question L.
An alkene ‘A’ an ozonolysis gives 2 moles of ethanal. Write the structure and IUPAC name of ‘A’.
Answer:
Structure of A: CH₃ – CH = CH – CH₃
IUPAC name of A: But-2-ene

Question M.
Acetone and acetaldehyde are the ozonolysis products of an alkene. Write the structural formula of an alkene and give IUPAC name of it.
Answer:
The structural formula of alkene:

IUPAC name is 2-methylbut-2-ene.

Question N.
Write the reaction to convert
a. propene to n-propyl alcohol.
b. propene to isoproyl alcohol.
Answer:
a.

b.

Question O.
What is the action of following on but-2-ene ?
a. dil alkaline KMnO₄
b. acidic KMnO₄
Answer:
a. Action of dil. alkaline KMnO₄ on but-2-ene:

b. Action of acidic KMnO₄ on but-2-ene:

Question P.
Complete the following reaction sequence :

Answer:

Question Q.
Write the balanced chemical reactions to get benzene from
a. Sodium benzoate.
b. Phenol.
Answer:
a. Sodium benzoate:
When anhydrous sodium benzoate is heated with soda lime, it undergoes decarboxylation and gives benzene.

b. Phenol:
When vapours of phenol are passed over heated zinc dust, it undergoes reduction and gives benzene.

Question R.
Predict the possible products of the following reaction.
a. chlorination of nitrobenzene,
b. sulfonation of chlorobenzene,
c. bromination of phenol,
d. nitration of toluene.
Answer:
a. Nitro group is meta directing group. So, chlorination of nitrobenzene gives m-chloronitrobenzene.

b. Chloro group is ortho and para directing group. So, sulphonation of chlorobenzene gives p-chlorobenzene sulphonic acid and o- chlorobenzene sulphonic acid.

c. Phenolic -OH group is ortho and para directing group. So, bromination of phenol gives p-bromophenol and o-bromophenol.

d. Methyl group is ortho and para directing group. So, nitration of toluene gives p-nitrotoluene and o-nitrotoluene.

3. Identify the main product of the reaction

Answer:
a.

b.

c.

d.

4. Read the following reaction and answer the questions given below.

a. Write IUPAC name of the product.
b. State the rule that governs formation of this product.
Answer:
a. IUPAC name of the product: 1 -Bromo-2-methylpropane
b. Anti-Markownikov’s rule/Kharasch effect/peroxide effect: It states that, the addition of HBr to unsymmetrical alkene in the presence of organic peroxide (R-O-O-R) takes place in the opposite orientation to that suggested by Markovnikov’s rule.

5. Identify A, B, C in the following reaction sequence :

Answer:

6. Identify giving reason whether the following compounds are aromatic or not.

Answer:
A.

Compound is non-aromatic since it has 4π electrons and hence, does not obey Huckel rule of aromaticity.

B.

Compound is non-aromatic since it has 4π electrons and hence, does not obey Huckel rule of aromaticity.

C.

Compound is aromatic since it has 6π electrons and hence, obeys Huckel rule of aromaticity.

D.

Compound is aromatic since it has 6n electrons and hence, obeys Huckel rule of aromaticity.

7. Name two reagents used for acylation of benzene.
Answer:
The two reagents used for acylation of benzene are:
i. CH₃COCl (acetyl chloride) and anhydrous AlCl₃
ii. (CH₃CO)₂O (acetic anhydride) and anhydrous AlCl₃

8. Read the following reaction and answer the questions given below.

A. Write the name of the reaction.
B. Identify the electrophile in it.
C. How is this electrophile generated?
Answer:
A. The name of the reaction is Friedel-Craft’s alkylation reaction.
B. The electrophile in the reaction is ⁺CH₃.
C. The electrophile ⁺CH₃ is generated as follows:

Activity:

Prepare chart of hydrocarbons and note down the characteristics.
Answer:

Characteristics of hydrocarbons:

• They are chemical compounds that are formed from only hydrogen and carbon atoms.
• Both ‘C’ and ‘H’ share an electron pair forming covalent bonds.
• One of the special properties of carbon is its ability to form double and triple bonds (unsaturation). Saturated hydrocarbons are alkanes and cycloalkanes while the unsaturated hydrocarbons are the aromatics, alkenes and alkynes.
• All hydrocarbons are insoluble in water, their boiling point increases as the size of alkane increases.
• All hydrocarbons can reach complete oxidation.
• Hydrocarbons are mainly used as fuel for transport and industry.

[Note: Students are expected to collect additional information on hydrocarbons on their own.]

11th Chemistry Digest Chapter 15 Hydrocarbons Intext Questions and Answers

Can you recall? (Textbook Page No. 233)

Question i.
What are hydrocarbons?
Answer:
The compounds which contain carbon and hydrogen as the only elements are called hydrocarbons.

Question ii.
Write structural formulae of the following compounds: propane, ethyne, cyclobutane, ethene, benzene.
Answer:

Do you know? (Textbook Page No. 233)

Question 1.
Why are alkanes called paraffins?
Answer:
i. Alkanes contain only carbon-carbon and carbon-hydrogen single covalent bonds.
ii. They are chemically less reactive and do not have much affinity for other chemicals.
Hence, they are called paraffins.

Internet my friend. (Textbook Page No. 233)

Question 1.
Collect information about hydrocarbon.
Answer:

• In organic chemistry, a hydrocarbon is an organic compound consisting of carbon and hydrogen as the only elements.
• They are examples of group 14 hydrides.
• Alkanes, cycloalkanes, aromatic hydrocarbons are different types of hydrocarbons.
• Most of the hydrocarbons found on earth occur naturally in crude oil.
• They mainly undergo substitution, addition or combustion reactions.
• Most hydrocarbons are flammable and toxic.
• They are the primary energy source in the form of combustible fuel source.

[Note: Students are expected to collect additional information on their own]

Use your brain power! (Textbook Page No. 234)

Question 1.
i. Write the structures of all the chain isomers of the saturated hydrocarbon containing six carbon atoms.
ii. Write IUPAC names of all the above structures.
Answer:
The structural formulae and names of all possible isomers having molecular formula C₆H₁₄ are as follows:

Note:
Alkanes and isomer number

Number of Carbon	Alkane	Number of isomers
1	Methane	No structural isomer
2	Ethane	No structural isomer
3	Propane	No structural isomer
4	Butane	Two
5	Pentane	Three
6	Hexane	Five

Can you recall? (Textbook Page No. 235)

Question i.
What is a catalyst?
Answer:
A catalyst is a substance that can be added to a reaction to increase the reaction rate without getting consumed in the process.
e.g. Ni is used as a catalyst in the catalytic hydrogenation of alkenes or alkynes.

Question ii.
What is addition reaction?
Answer:
When a compound combines with another compound to form a product that contain all the atoms in both the reactants, it is called an addition reaction.

Try this (Textbook Page No. 235)

Question 1.
Transform the following word equation into balanced chemical equation and write at least 3 changes that occur at molecular level during this chemical change.
\(\text { 2-Methylpropene + Hydrogen } \stackrel{\text { catalyst }}{\longrightarrow} \text { Isobutane }\)
Answer:

Three changes which occur at molecular level include:
Step 1: Adsorption of reactants: Reactants (alkene and hydrogen) get adsorbed on the catalytic surface.
Step 2: Formation of a product: Hydrogen atoms are added across the double bond of 2-methylpropene which results in the formation of product isobutane.
Step 3: Desorption: Product formed on the catalytic surface is readily desorbed making catalytic surface available for other molecules.

Use your brain power! (Textbook Page No. 236)

Question 1.
Why are alkanes insoluble in water and readily soluble in organic solvents like chloroform or ether?
Answer:

• The solubility of any substance is governed by the principle of like dissolves like. This means polar compounds are soluble in polar solvents while nonpolar compounds are soluble in nonpolar solvents.
• Alkanes consist of C – C and C – H nonpolar covalent bonds and thus, they are nonpolar in nature, whereas water is a polar solvent.
• The dipole-dipole forces that exist between water molecules is much stronger than the forces of attraction between alkane and water molecules.

Hence, alkanes are insoluble in water and readily soluble in organic solvents like chloroform or ether.

Can you recall? (Textbook Page No. 238)

Question 1.
What is the product which is poisonous and causes air pollution formed by incomplete combustion of alkane?
Answer:
When alkanes are subjected to incomplete combustion, it forms carbon monoxide and carbon (soot).
i. 2CH_4(g) + 3O_2(g) → 2CO_(g) + 4H₂O_(g)
ii. CH_4(g) + O_2(g) → C_(s) + 2H₂O_(l)

Can you recall? (Textbook Page No. 238)

Question i.
What are alkenes?
Answer:
Alkenes are unsaturated hydrocarbons containing at least one carbon-carbon double bond.

Question ii.
Calculate the number of sigma (σ) and pi (π) bonds in 2-methylpropene.
Answer:

Question iii.
Write the structural formula of pent-2-ene.
Answer:

Can you tell? (Textbook Page No. 241)

Question i.
Explain by writing a reaction, the main product formed on heating 2-methylbutan-2-ol with concentrated sulphuric acid.
Answer:

Question ii.
Will the main product in the above reaction show geometrical isomerism?
Answer:
No, the major product, i.e., 2-methylbut-2-ene does not show geometrical (or cis-trans) isomerism.

Can you tell? (Textbook Page No. 244)

Question 1.
Propan-1-ol and 2-methypropan-1-ol are not prepared by hydration method. Why?
Answer:
Propan-1-ol and 2-methylpropan-1-ol cannot be prepared by hydration of propene and 2-methylprop-1-ene because the addition reaction follows Markovnikov’s rule.

Use your brainpower. (Textbook Page No. 244)

Question 1.
On ozonolysis, an alkene forms the following carbonyl compounds. Draw the structure of unknown alkene from which these compounds are formed: HCHO and CH₃COCH₂CH₃
Answer:
The structure of alkene which produces a mixture of HCHO and CH₃COCH₂CH₃ on ozonolysis is

Use your brain power! (Textbook Page No. 245)

Question 1.
Write the structure of monomer from which each of the following polymers are obtained.

Answer:

	Polymer	Monomeric unit
i.	Teflon	CF2 – CF2 Tetrafluoroethene
ii.	Polypropene	H3C – CH = CH2 Propene
iii.	Polyvinyl chloride	H2C = CHCl Vinyl chloride

Can you tell? (Textbook Page No. 246)

Question i.
What are aliphatic hydrocarbons?
Answer:
Aliphatic hydrocarbons are hydrocarbons containing carbon and hydrogen joined together in straight chain or branched chain. They may be saturated (alkanes) or unsaturated (alkenes or alkynes).

Question ii.
Compare the proportion of carbon and hydrogen atoms in ethane, ethene and ethyne. Which compound is most unsaturated with hydrogen?
Answer:
Ethane
C : H = 2 : 6 = 1 : 3
Ethene
C : H = 2 : 4 = 1 : 2
Ethyne
C : H = 2 : 2 = 1 : 1
From the above proportion it is clear that ethyne with 1 : 1 ratio of C : H is most unsaturated with hydrogen (50%) as compared to ethane (25%) and ethene (33.33%).

Can you tell? (Textbook Page No. 247)

Question 1.
Why is sodamide used in dehydrohalogenation of vicinal dihalides to remove HX from alkenyl halide in place of alcoholic KOH?
Answer:

• Sodamide (NaNH₂) is a strong base and hence, helps in complete conversion of alkenyl halide formed in the first step to form alkynes.
• The base (KOH or NaOH) used in first step gives alkynes in poor yield and hence, stronger bases such as NaNH₂ on KNH₂ are used in second step.

Use your brainpower! (Textbook Page No. 247)

Question 1.
Convert: 1-Bromobutane to hex-1-yne
Answer:

Can you tell? (Textbook Page No. 248)

Question 1.
Alkanes and alkenes do not react with lithium amide. Give reason.
Answer:
i. The sp hybrid carbon atom in terminal alkynes is more electronegative than the sp² carbon in ethene or the sp³ carbon in ethane.
ii. Due to high electronegative character of carbon in terminal alkynes, hydrogen atom can be given away as proton (H⁺) to very strong base as shown in the reactions below.

iii. Further, since s-character decreases from sp to sp² to sp³ carbon atom, the relative acidity of alkanes, alkenes and alkynes is in the following order: H – C = C – H > H₂C = CH₂ > H₃C – CH₃
Hence, alkenes and alkanes do not react with lithium amide.

Use your brain power! (Textbook Page No. 248)

Question 1.
Arrange following hydrocarbons in the increasing order of acidic character: propane, propyne, propene.
Answer:
Propyne > propene > propane

Use your brain power! (Textbook Page No. 249)

Question 1.
Convert: 3-Methylbut-l-yne into 3-methylbutan-2-one
Answer:

Can you recall? (Textbook Page No. 249)

Question i.
What are aromatic hydrocarbons?
Answer:
Benzene and all compounds that have structures and chemical properties resembling benzene are called as aromatic hydrocarbons.

Question ii.
What are benzenoid and non-benzenoid aromatics?
Answer:
Benzenoid aromatics are compounds having at least one benzene ring in the structure.
e.g. Benzene, naphthalene, anthracene, phenol, etc.,
Non-benzenoid aromatics are compounds that contain an aromatic ring, other than benzene. e.g. Tropone, etc.

Can you recall? (Textbook Page No. 254)

Question 1.
What is decarboxylation?
Answer:
The reaction which involves removal of a carboxyl group (-COOH) in the form of carbon dioxide (CO₂) is known as decarboxylation reaction.
R – COOH → R – H + CO₂