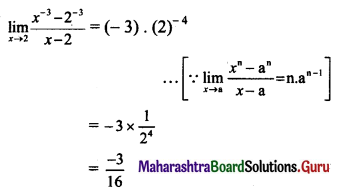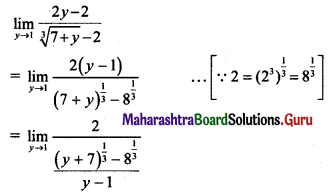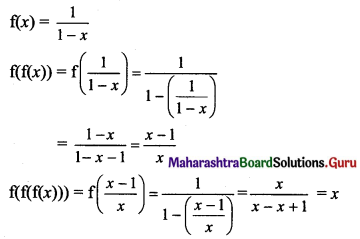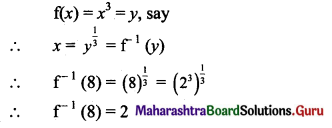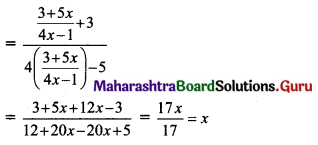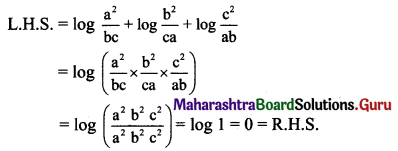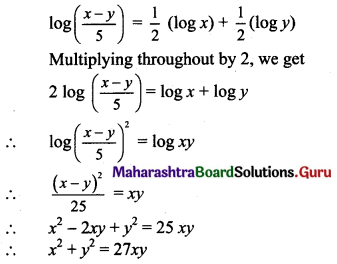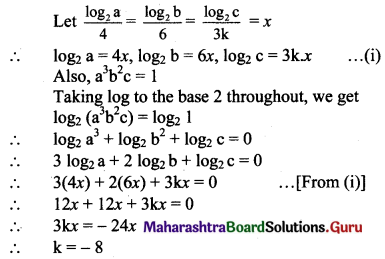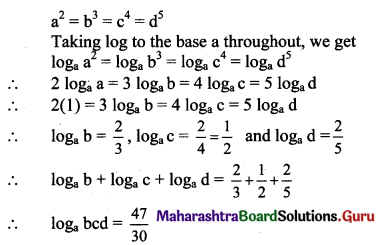Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 6 Functions Miscellaneous Exercise 6 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 6 Functions Miscellaneous Exercise 6
(I) Select the correct answer from the given alternatives.
Question 1.
If log (5x – 9) – log (x + 3) = log 2, then x = ________
(A) 3
(B) 5
(C) 2
(D) 7
Answer:
(B) 5
Hint:
log (5x – 9) – log (x + 3) = log 2
∴ \(\frac{5 x-9}{x+3}\) = 2
∴ 3x = 9 + 6
∴ x = 5
Question 2.
If log10 (log10 (log10 x)) = 0, then x = ________
(A) 1000
(B) 1010
(C) 10
(D) 0
Answer:
(B) 1010
Hint:
log10 log10 log10 x = 0
∴ log10 (log10 (x)) = 100 = 1
∴ log10 x = 101 = 10
∴ x = 1010

Question 3.
Find x, if 2 log2 x = 4
(A) 4, -4
(B) 4
(C) -4
(D) not defined
Answer:
(B) 4
Hint:
2 log2 x = 4, x > 0
∴ log2 (x2) = 4
∴ x2 = 16
∴ x = ±4
∴ x = 4
Question 4.
The equation \(\log _{x^{2}} 16+\log _{2 x} 64=3\) has,
(A) one irrational solution
(B) no prime solution
(C) two real solutions
(D) one integral solution
Answer:
(A), (B), (C), (D)
Hint:
\(\log _{x^{2}} 16+\log _{2 x} 64=3\)
∴ \(\frac{\log 16}{\log x^{2}}+\frac{\log 64}{\log 2 x}=3\)
∴ 4 log 2 [log x + log 2] + (6 log 2) (2 log x) = 3 (2 log x) (log 2 + log x)
Let log 2 = a, log x = t. Then
∴ 4at + 4a2 + 12at = 6at + 6t2
∴ 6t2 – 10at – 4a2 = 0
∴ 3t2 – 5at – 2a2 = 0
∴ (3t + a) (t – 2a) = 0
∴ t = \(-\frac{1}{3}\)a, 2a
∴ log x = \(\log (2)^{-\frac{1}{3}}\), log (22)
∴ x = \(2^{-\frac{1}{3}}\), 4
∴ x = \(\frac{1}{\sqrt[3]{2}}\), 4
Question 5.
If f(x) = \(\frac{1}{1-x}\), then f(f(f(x))) is
(A) x – 1
(B) 1 – x
(C) x
(D) -x
Answer:
(C) x
Hint:
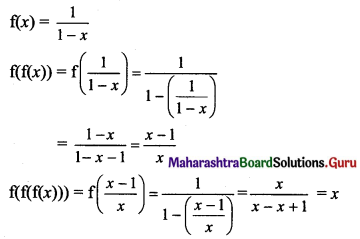
Question 6.
If f: R → R is defined by f(x) = x3, then f-1 (8) is equal to:
(A) {2}
(B) {-2.2}
(C) {-2}
(D) (-2.2)
Answer:
(A) {2}
Hint:
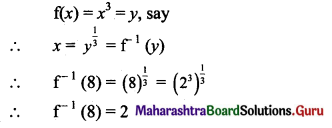
Question 7.
Let the function f be defined by f(x) = \(\frac{2 x+1}{1-3 x}\) then f-1 (x) is:
(A) \(\frac{x-1}{3 x+2}\)
(B) \(\frac{x+1}{3 x-2}\)
(C) \(\frac{2 x+1}{1-3 x}\)
(D) \(\frac{3 x+2}{x-1}\)
Answer:
(A) \(\frac{x-1}{3 x+2}\)
Hint:
f(x) = \(\frac{2 x+1}{1-3 x}\) = y, say. then
2x + 1 = y(1 – 3x)
∴ y – 1 = x(2 + 3y)
∴ x = \(\frac{y-1}{2+3 y}\) = f-1 (y)
∴ f-1 (x) = \(\frac{x-1}{2+3 x}\)

Question 8.
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
(A) -2
(B) 0
(C) 1
(D) 2
Answer:
(B) 0
Hint:
f(x) = 2x2 + bx + c
f(0) = 3
∴ 2(0) + b(0) + c = 3
∴ c = 3 ……..(i)
∴ f(2) = 1
∴ 2(4) + 2b + c = 1
∴ 2b + c = -7
∴ 2b + 3 = -7 …..[From (i)]
∴ b = -5
∴ f(x) = 2x2 – 5x + 3
∴ f(1) = 2(1)2 – 5(1) + 3 = 0
Question 9.
The domain of \(\frac{1}{[x]-x}\), where [x] is greatest integer function is
(A) R
(B) Z
(C) R – Z
(D) Q – {0}
Answer:
(C) R – Z
Hint:
f(x) = \(\frac{1}{[x]-x}=\frac{1}{-\{x\}}\)
For f to be defined, {x} ≠ 0
∴ x cannot be integer.
∴ Domain = R – Z
Question 10.
The domain and range of f(x) = 2 – |x – 5| are
(A) R+, (-∞, 1]
(B) R, (-∞, 2]
(C) R, (-∞, 2)
(D) R+, (-∞, 2]
Answer:
(B) R, (-∞, 2]
Hint:
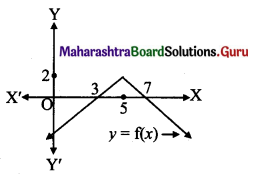
f(x) = 2 – |x – 5|
= 2 – (5 – x), x < 5
= 2 – (x – 5), x ≥ 5
∴ f(x) = x – 3, x < 5
= 7 – x, x ≥ 5
Domain = R,
Range (from graph) = (-∞, 2]
(II) Answer the following:
Question 1.
Which of the following relations are functions? If it is a function determine its domain and range.
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2) (9, 3), (9, -3), (16, 4), (16, -4)}
(iii) {(2, 1), (3, 1), (5, 2)}
Solution:
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
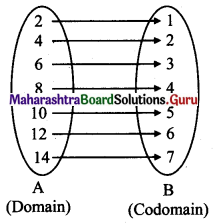
Every element of set A has been assigned a unique element in set B
∴ Given relation is a function
Domain = {2, 4, 6, 8, 10, 12, 14}, Range = {1, 2, 3, 4, 5, 6, 7}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2) (9, 3), (9, -3) (16, 4), (16, -4)}
∵ (1, 1), (1, -1) ∈ the relation
∴ Given relation is not a function.
As element 1 of the domain has not been assigned a unique element of co-domain.
(iii) {(2, 1), (3, 1), (5, 2)}
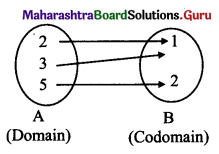
Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {2, 3, 5}, Range = {1, 2}

Question 2.
Find whether the following functions are one-one.
(i) f: R → R defined by f(x) = x2 + 5
(ii) f: R – {3} → R defined by f(x) = \(\frac{5 x+7}{x-3}\) for x ∈ R – {3}
Solution:
(i) f: R → R, defined by f(x) = x2 + 5
Note that f(-x) = f(x) = x2 + 5
∴ f is not one-one (i.e., many-one) function.
(ii) f: R – {3} → R, defined by f(x) = \(\frac{5 x+7}{x-3}\)
Let f(x1) = f(x2)
∴ \(\frac{5 x_{1}+7}{x_{1}-3}=\frac{5 x_{2}+7}{x_{2}-3}\)
∴ 5x1 x2 – 15x1 + 7x2 – 21 = 5x1 x2 – 15x2 + 7x1 – 21
∴ 22(x1 – x2) = 0
∴ x1 = x2
∴ f is a one-one function.
Question 3.
Find whether the following functions are onto or not.
(i) f: Z → Z defined by f(x) = 6x – 7 for all x ∈ Z
(ii) f: R → R defined by f(x) = x2 + 3 for all x ∈ R
Solution:
(i) f(x) = 6x – 7 = y (say)
(x, y ∈ Z)
∴ x = \(\frac{7+y}{6}\)
Since every integer y does not give integer x, f is not onto.
(ii) f(x) = x2 + 3 = y (say)
(x, y ∈ R)
Clearly y ≥ 3 …..[x2 ≥ 0]
∴ All the real numbers less than 3 from codomain R, have not been pre-assigned any element from the domain R.
∴ f is not onto.
Question 4.
Let f: R → R be a function defined by f(x) = 5x3 – 8 for all x ∈ R. Show that f is one-one and onto. Hence find f-1.
Solution:

Question 5.
A function f: R → R defined by f(x) = \(\frac{3 x}{5}\) + 2, x ∈ R. Show that f is one-one and onto. Hence find f-1.
Solution:

Question 6.
A function f is defined as f(x) = 4x + 5, for -4 ≤ x < 0. Find the values of f(-1), f(-2), f(0), if they exist.
Solution:
f(x) = 4x + 5, -4 ≤ x < 0
f(-1) = 4(-1) + 5 = -4 + 5 = 1
f(-2) = 4(-2) + 5 = -8 + 5 = -3
x = 0 ∉ domain of f
∴ f(0) does not exist.
Question 7.
A function f is defined as f(x) = 5 – x for 0 ≤ x ≤ 4. Find the values of x such that
(i) f(x) = 3
(ii) f(x) = 5
Solution:
(i) f(x) = 3
∴ 5 – x = 3
∴ x = 5 – 3 = 2
(ii) f(x) = 5
∴ 5 – x = 5
∴ x = 0

Question 8.
If f(x) = 3x4 – 5x2 + 7, find f(x – 1).
Solution:
f(x) = 3x4 – 5x2 + 7
∴ f(x – 1) = 3(x – 1)4 – 5(x – 1)2 + 7
= 3(x4 – 4C1 x3 + 4C2 x2 – 4C3 x + 4C4) – 5(x2 – 2x + 1) + 7
= 3(x4 – 4x3 + 6x2 – 4x + 1) – 5(x2 – 2x + 1) + 7
= 3x4 – 12x3 + 18x2 – 12x + 3 – 5x2 + 10x – 5 + 7
= 3x4 – 12x3 + 13x2 – 2x + 5
Question 9.
If f(x) = 3x + a and f(1) = 7, find a and f(4).
Solution:
f(x) = 3x + a, f(1) = 7
∴ 3(1) + a = 7
∴ a = 7 – 3 = 4
∴ f(x) = 3x + 4
∴ f(4) = 3(4) + 4 = 12 + 4 = 16
Question 10.
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Solution:
f(x) = ax2 + bx + 2
f(1) = 3
∴ a(1)2 + b(1) + 2 = 3
∴ a + b = 1 ….(i)
f(4) = 42
∴ a(4)2 + b(4) + 2 = 42
∴ 16a + 4b = 40
Dividing by 4, we get
4a + b = 10 …..(ii)
Solving (i) and (ii), we get
a = 3, b = -2
Question 11.
Find composite of f and g:
(i) f = {(1, 3), (2, 4), (3, 5), (4, 6)}
g = {(3, 6), (4, 8), (5, 10), (6, 12)}
(ii) f = {(1, 1), (2, 4), (3, 4), (4, 3)}
g = {(1, 1), (3, 27), (4, 64)}
Solution:
(i) f = {(1, 3), (2, 4), (3, 5), (4, 6)}
g = {(3, 6), (4, 8), (5, 10), (6, 12)}
∴ f(1) = 3, g(3) = 6
f(2) = 4, g(4) = 8
f(3) = 5, g(5)=10
f(4) = 6, g(6) = 12
(gof) (x) = g (f(x))
(gof)(1) = g(f(1)) = g(3) = 6
(gof)(2) – g(f(2)) = g(4) = 8
(gof)(3) = g(f(3)) = g(5) = 10
(gof)(4) = g(f(4)) = g(6) = 12
∴ gof = {(1, 6), (2, 8), (3, 10), (4, 12)}
(ii) f = {(1, 1), (2, 4), (3, 4), (4, 3)}
g = {(1, 1), (3, 27), (4, 64)}
f(1) = 1, g(1) = 1
f(2) = 4, g(3) = 27
f(3) = 4, g(4) = 64
f(4) = 3
(gof) (x) = g(f(x))
(gof) (1) = g(f(1)) = g(1) = 1
(gof) (2) = g(f(2)) = g(4) = 64
(gof) (3) = g(f(3)) = g(4) = 64
(gof) (4) = g(f(4)) = g(3) = 27
∴ gof = {(1, 1), (2, 64), (3, 64), (4, 27)}

Question 12.
Find fog and gof:
(i) f(x) = x2 + 5, g(x) = x – 8
(ii) f(x) = 3x – 2, g(x) = x2
(iii) f(x) = 256x4, g(x) = √x
Solution:
(i) f(x) = x2 + 5, g(x) = x – 8
(fog) (x) = f(g(x))
= f(x – 8)
= (x – 8)2 + 5
= x2 – 16x + 64 + 5
= x2 – 16x + 69
(gof) (x) = g(f(x))
= g(x2 + 5)
= x2 + 5 – 8
= x – 3
(ii) f(x) = 3x – 2, g(x) = x2
(fog) (x) = f(g(x)) = f(x2) = 3x2 – 2
(gof) (x) = g(f(x))
= g(3x – 2)
= (3x – 2)2
= 9x2 – 12x + 4
(iii) f(x) = 256x4, g(x) = √x
(fog) (x) = f(g(x)) = f (√x) = 256 (√x)4 = 256x2
(gof) (x) = g(f(x)) = g(256x4) = \(\sqrt{256 x^{4}}\) = 16x2
Question 13.
If f(x) = \(\frac{2 x-1}{5 x-2}, x \neq \frac{2}{5}\), show that (fof) (x) = x.
Solution:

Question 14.
If f(x) = \(\frac{x+3}{4 x-5}\), g(x) = \(\frac{3+5 x}{4 x-1}\), then show that (fog) (x) = x.
Solution:
f(x) = \(\frac{x+3}{4 x-5}\), g(x) = \(\frac{3+5 x}{4 x-1}\)
(fog)(x) = f(g(x))
= f(\(\frac{3+5 x}{4 x-1}\))
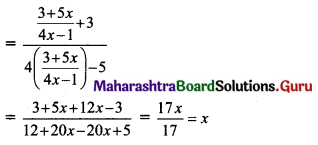
Question 15.
Let f: R – {2} → R be defined by f(x) = \(\frac{x^{2}-4}{x-2}\) and g: R → R be defined by g(x) = x + 2. Examine whether f = g or not.
Solution:
f(x) = \(\frac{x^{2}-4}{x-2}\), x ≠ 2
∴ f(x) = x + 2, x ≠ 2 and g(x) = x + 2,
The domain of f = R – {2}
The domain of g = R
Here, f and g have different domains.
∴ f ≠ g
Question 16.
Let f: R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph.
Solution:
f(x) = x + 5
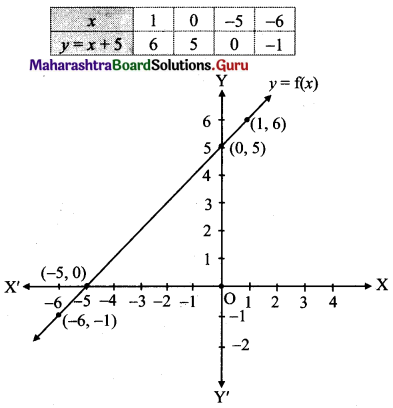
Question 17.
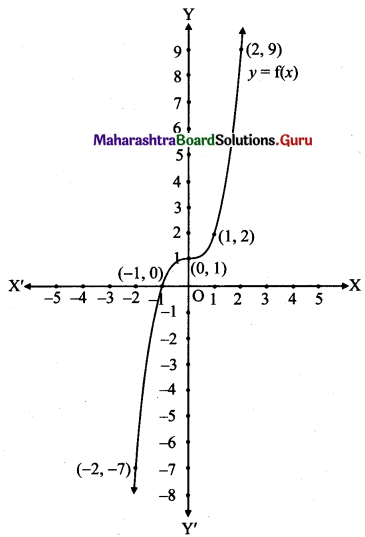
Let f: R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph.
Solution:
Let y = f(x) = x3 + 1

Question 18.
For any base show that log(1 + 2 + 3) = log 1 + log 2 + log 3
Solution:
L.H.S. = log(1 + 2 + 3) = log 6
R.H.S. = log 1 + log 2 + log 3
= 0 + log (2 × 3)
= log 6
∴ L.H.S. = R.H.S.

Question 19.
Find x, if x = \(3^{3 \log _{3} 2}\).
Solution:
x = \(3^{3 \log _{3} 2}\)
= \(3^{\log 3\left(2^{3}\right)}\)
= 23 ….[\(a^{\log _{a} b}\) = b]
= 8
Question 20.
Show that, log|\(\sqrt{x^{2}+1}\) + x| + log|\(\sqrt{x^{2}+1}\) – x| = 0.
Solution:
L.H.S. = log|\(\sqrt{x^{2}+1}\) + x| + log|\(\sqrt{x^{2}+1}\) – x|
= \(\log \left|\left(\sqrt{x^{2}+1}+x\right)\left(\sqrt{x^{2}+1}-x\right)\right|\)
= log|x2 + 1 – x2|
= log 1
= 0
= R.H.S.
Question 21.
Show that \(\log \frac{\mathrm{a}^{2}}{\mathrm{bc}}+\log \frac{\mathrm{b}^{2}}{\mathrm{ca}}+\log \frac{\mathrm{c}^{2}}{\mathrm{ab}}=0\).
Solution:
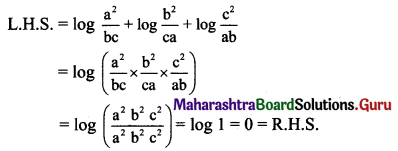
Question 22.
Simplify log (log x4) – log(log x).
Solution:
log (log x4) – log (log x)
= log (4 log x) – log (log x) …..[log mn = n log m]
= log 4 + log (log x) – log (log x) …..[log (mn) = log m + log n]
= log 4
Question 23.
Simplify \(\log _{10} \frac{28}{45}-\log _{10} \frac{35}{324}+\log _{10} \frac{325}{432}-\log _{10} \frac{13}{15}\)
Solution:

Question 24.
If log (\(\frac{a+b}{2}\)) = \(\frac{1}{2}\) (log a + log b), then show that a = b.
Solution:
log (\(\frac{a+b}{2}\)) = \(\frac{1}{2}\) (log a + log b)
∴ 2 log (\(\frac{a+b}{2}\)) = log a + log b
∴ log \(\left(\frac{a+b}{2}\right)^{2}\) = log ab
∴ \(\frac{(a+b)^{2}}{4}\) = ab
∴ a2 + 2ab + b2 = 4ab
∴ a2 + 2ab – 4ab + b2 = 0
∴ a2 – 2ab + b2 = 0
∴ (a – b)2 = 0
∴ a – b = 0
∴ a = b
Question 25.
If b2 = ac. Prove that, log a + log c = 2 log b.
Solution:
b2 = ac
Taking log on both sides, we get
log b2 = log ac
∴ 2 log b = log a + log c
∴ log a + log c = 2 log b

Question 26.
Solve for x, logx (8x – 3) – logx 4 = 2.
Solution:
logx (8x – 3) – logx 4 = 2
∴ \(\log _{x}\left(\frac{8 x-3}{4}\right)\) = 2
∴ x2 = \(\frac{8 x-3}{4}\)
∴ 4x2 = 8x – 3
∴ 4x2 – 8x + 3 = 0
∴ 4x2 – 2x – 6x + 3 = 0
∴ 2x(2x – 1) – 3(2x – 1) = 0
∴ (2x – 1)(2x – 3) = 0
∴ 2x – 1 = 0 or 2x – 3 = 0
∴ x = \(\frac{1}{2}\) or x = \(\frac{3}{2}\)
Question 27.
If a2 + b2 = 7ab, show that \(\log \left(\frac{a+b}{3}\right)=\frac{1}{2} \log a+\frac{1}{2} \log b\)
Solution:
a2 + b2 = 7ab
a2 + 2ab + b2 = 7ab + 2ab
(a + b)2 = 9ab
\(\frac{(a+b)^{2}}{9}\) = ab
\(\left(\frac{a+b}{3}\right)^{2}\) = ab
Taking log on both sides, we get
log \(\left(\frac{a+b}{3}\right)^{2}\) = log (ab)
2 log \(\left(\frac{a+b}{3}\right)\) = log a + log b
Dividing throughout by 2, we get
\(\log \left(\frac{a+b}{3}\right)=\frac{1}{2} \log a+\frac{1}{2} \log b\)
Question 28.
If \(\log \left(\frac{x-y}{5}\right)=\frac{1}{2} \log x+\frac{1}{2} \log y\), show that x2 + y2 = 27xy.
Solution:
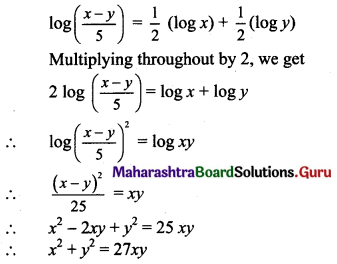
Question 29.
If log3 [log2 (log3 x)] = 1, show that x = 6561.
Solution:
log3 [log2 (log3 x)] = 1
∴ log2 (log3 x) = 31
∴ log3 x = 23
∴ log3 x = 8
∴ x = 38
∴ x = 6561
Question 30.
If f(x) = log(1 – x), 0 ≤ x < 1, show that f(\(\frac{1}{1+x}\)) = f(1 – x) – f(-x).
Solution:

Question 31.
Without using log tables, prove that \(\frac{2}{5}\) < log10 3 < \(\frac{1}{2}\).
Solution:
We have to prove that, \(\frac{2}{5}\) < log10 3 < \(\frac{1}{2}\)
i.e., to prove that \(\frac{2}{5}\) < log10 3 and log10 3 < \(\frac{1}{2}\)
i.e., to prove that 2 < 5 log10 3 and 2 log10 3 < 1
i.e., to prove that 2 log10 10 < 5 log10 3 and 2 log10 3 < log10 10 ……[∵ loga a = 1]
i.e., to prove that log10 102 < log10 35 and log10 32 < log10 10
i.e., to prove that 102 < 35 and 32 < 10
i.e., to prove that 100 < 243 and 9 < 10 which is true
∴ \(\frac{2}{5}\) < log10 3 < \(\frac{1}{2}\)
Question 32.
Show that \(7 \log \left(\frac{15}{16}\right)+6 \log \left(\frac{8}{3}\right)+5 \log \left(\frac{2}{5}\right)+\log \left(\frac{32}{25}\right)\) = log 3
Solution:

Question 33.
Solve : \(\sqrt{\log _{2} x^{4}}+4 \log _{4} \sqrt{\frac{2}{x}}=2\)
Solution:


Question 34.
Find the value of \(\frac{3+\log _{10} 343}{2+\frac{1}{2} \log _{10}\left(\frac{49}{4}\right)+\frac{1}{2} \log _{10}\left(\frac{1}{25}\right)}\)
Solution:

Question 35.
If \(\frac{\log a}{x+y-2 z}=\frac{\log b}{y+z-2 x}=\frac{\log c}{z+x-2 y}\), show that abc = 1.
Solution:
Let \(\frac{\log a}{x+y-2 z}=\frac{\log b}{y+z-2 x}=\frac{\log c}{z+x-2 y}\) = k
∴ log a = k(x + y – 2z), log b = k(y + z – 2x), log c = k(z + x – 2y)
log a + log b + log c = k(x + y – 2z) + k(y + z – 2x) + k(z + x – 2y)
= k(x + y – 2z + y + z – 2x + z + x – 2y)
= k(0)
= 0
∴ log (abc) = log 1 …….[∵ log 1 = 0]
∴ abc = 1

Question 36.
Show that, logy x3 . logz y4 . logx z5 = 60.
Solution:

Question 37.
If \(\frac{\log _{2} \mathrm{a}}{4}=\frac{\log _{2} \mathrm{~b}}{6}=\frac{\log _{2} \mathrm{c}}{3 \mathrm{k}}\) and a3b2c = 1, find the value of k.
Solution:
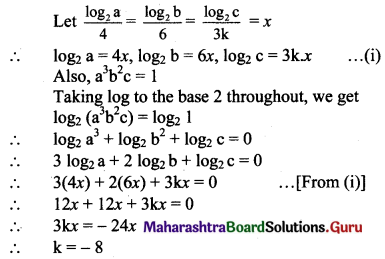
Question 38.
If a2 = b3 = c4 = d5, show that loga bcd = \(\frac{47}{30}\).
Solution:
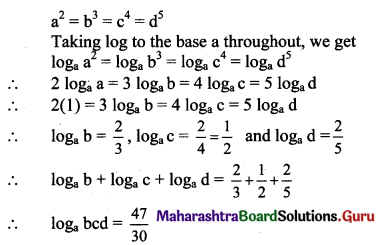
Question 39.
Solve the following for x, where |x| is modulus function, [x] is the greatest integer function, {x} is a fractional part function.
(i) 1 < |x – 1| < 4
(ii) |x2 – x – 6| = x + 2
(iii) |x2 – 9| + |x2 – 4| = 5
(iv) -2 < [x] ≤ 7
(v) 2[2x – 5] – 1 = 7
(vi) [x]2 – 5 [x] + 6 = 0
(vii) [x – 2] + [x + 2] + {x} = 0
(viii) \(\left[\frac{x}{2}\right]+\left[\frac{x}{3}\right]=\frac{5 x}{6}\)
Solution:
(i) 1 < |x – 1| < 4
∴ -4 < x – 1 < -1 or 1 < x – 1 < 4
∴ -3 < x < 0 or 2 < x < 5
∴ Solution set = (-3, 0) ∪ (2, 5)
(ii) |x2 – x – 6| = x + 2 …..(i)
R.H.S. must be non-negative
∴ x ≥ -2 …..(ii)
|(x – 3) (x + 2)| = x + 2
∴ (x + 2) |x – 3| = x + 2 as x + 2 ≥ 0
∴ |x – 3| = 1 if x ≠ -2
∴ x – 3 = ±1
∴ x = 4 or 2
∴ x = -2 also satisfies the equation
∴ Solution set = {-2, 2, 4}
(iii) |x2 – 9| + |x2 – 4| = 5
∴ |(x – 3) (x + 3)| + |(x – 2) ( x + 2)| = 5 ………(i)
Case I: x < -3
Also, x < -2, x < 2, x < 3
∴ (x – 3) (x + 3) > 0 and (x – 2) (x + 2) > 0
Equation (i) reduces to
x2 – 9 + x2 – 4 = 5
∴ 2x2 = 18
∴ x = -3 or 3 (both rejected as x < -3)
Case II: -3 ≤ x < -2
As x < -2, x < 3
∴ (x – 3) (x + 3) < 0, (x – 2) (x + 2) > 0
Equation (i) reduces to
-(x2 – 9) + x2 – 4 = 5
∴ 5 = 5 (true)
-3 ≤ x < -2 is a solution ….(ii)
Case III: -2 ≤ x < 2 As x > -3, x < 3
∴ (x – 3) (x + 3) < 0,
(x – 2) (x + 2) < 0
Equation (i) reduces to
9 – x2 + 4 – x2 = 5
∴ 2x2 = 13 – 5
∴ x2 = 4
∴ x = -2 is a solution …..(iii)
Case IV: 2 ≤ x < 3 As x > -3, x > -2
∴ (x – 3) (x + 3) < 0, (x – 2) (x + 2) > 0
Equation (i) reduces to
9 – x2 + x2 – 4 = 5
∴ 5 = 5 (true)
∴ 2 ≤ x < 3 is a solution ……(iv)
Case V: 3 ≤ x As x > -3, x > -2, x > 2
∴ (x + 3) (x – 3) > 0,
(x – 2) (x + 2) > 0
Equation (i) reduces to
x2 – 9 + x2 – 4 = 5
∴ 2x2 = 18
∴ x2 = 9
∴ x = 3 …..(v)
(x = -3 rejected as x ≥ 3)
From (ii), (iii), (iv), (v), we get
∴ Solution set = [-3, -2] ∪ [2, 3]
(iv) -2 < [x] ≤ 7
∴ -2 < x < 8
∴ Solution set = (-2, 8)

(v) 2[2x – 5] – 1 = 7
∴ [2x – 5] = \(\frac{7+1}{2}\) = 4
∴ [2x] – 5 = 4
∴ [2x] = 9
∴ 9 ≤ 2x < 10
∴ \(\frac{9}{2}\) ≤ x < 5
∴ Solution set = [\(\frac{9}{2}\), 5)
(vi) [x]2 – 5[x] + 6 = 0
∴ ([x] – 3)([x] – 2) = 0
∴ [x] = 3 or 2
If [x] = 2, then 2 ≤ x < 3
If [x] = 3, then 3 ≤ x < 4
∴ Solution set = [2, 4)
(vii) [x – 2] + [x + 2] + {x} = 0
∴ [x] – 2 + [x] + 2 + {x} = 0
∴ [x] + x = 0 …..[{x} + [x] = x]
∴ x = 0
(viii) \(\left[\frac{x}{2}\right]+\left[\frac{x}{3}\right]=\frac{5 x}{6}\)
L.H.S. = an integer
R.H.S. = an integer
∴ x = 6k, where k is an integer
Question 40.
Find the domain of the following functions.
(i) f(x) = \(\frac{x^{2}+4 x+4}{x^{2}+x-6}\)
(ii) f(x) = \(\sqrt{x-3}+\frac{1}{\log (5-x)}\)
(iii) f(x) = \(\sqrt{1-\sqrt{1-\sqrt{1-x^{2}}}}\)
(iv) f(x) = x!
(v) f(x) = \({ }^{5-x} P_{x-1}\)
(vi) f(x) = \(\sqrt{x-x^{2}}+\sqrt{5-x}\)
(vii) f(x) = \(\sqrt{\log \left(x^{2}-6 x+6\right)}\)
Solution:
(i) f(x) = \(\frac{x^{2}+4 x+4}{x^{2}+x-6}=\frac{x^{2}+4 x+4}{(x+3)(x-2)}\)
For f to be defined, x ≠ -3, 2
∴ Domain of f = (-∞, -3) ∪ (-3, 2) ∪ (2, ∞)
(ii) f(x) = \(\sqrt{x-3}+\frac{1}{\log (5-x)}\)
For f to be defined,
x – 3 ≥ 0, 5 – x > 0 and 5 – x ≠ 1
x ≥ 3, x < 5 and x ≠ 4
∴ Domain of f = [3, 4) ∪ (4, 5)
(iii) f(x) = \(\sqrt{1-\sqrt{1-\sqrt{1-x^{2}}}}\)

Equation (i) gives solution set = [-1, 1]
∴ Domain of f = [-1, 1]
(iv) f(x) = x!
∴ Domain of f = set of whole numbers (W)
(v) f(x) = \({ }^{5-x} P_{x-1}\)
5 – x > 0, x – 1 ≥ 0, x – 1 ≤ 5 – x
∴ x < 5, x ≥ 1 and 2x ≤ 6
∴ x ≤ 3
∴ Domain of f = {1, 2, 3}
(vi) f(x) = \(\sqrt{x-x^{2}}+\sqrt{5-x}\)
x – x2 ≥ 0
∴ x2 – x ≤ 0
∴ x(x – 1) ≤ 0
∴ 0 ≤ x ≤ 1 …..(i)
5 – x ≥ 0
∴ x ≤ 5 …..(ii)
Intersection of intervals given in (i) and (ii) gives
Solution set = [0, 1]
∴ Domain of f = [0, 1]
(vii) f(x) = \(\sqrt{\log \left(x^{2}-6 x+6\right)}\)
For f to be defined,
log (x2 – 6x + 6) ≥ 0
∴ x2 – 6x + 6 ≥ 1
∴ x2 – 6x + 5 ≥ 0
∴ (x – 5)(x – 1) ≥ 0
∴ x ≤ 1 or x ≥ 5 …..(i)
[∵ The solution of (x – a) (x – b) ≥ 0 is x ≤ a or x ≥ b, for a < b]
and x2 – 6x + 6 > 0
∴ (x – 3)2 > -6 + 9
∴ (x – 3)2 > 3
∴ x < 3 – √3 0r x > 3 + √3 ……..(ii)
From (i) and (ii), we get
x ≤ 1 or x ≥ 5
Solution set = (-∞, 1] ∪ [5, ∞)
∴ Domain of f = (-∞, 1] ∪ [5, ∞)

Question 41.
(i) f(x) = |x – 5|
(ii) f(x) = \(\frac{x}{9+x^{2}}\)
(iii) f(x) = \(\frac{1}{1+\sqrt{x}}\)
(iv) f(x) = [x] – x
(v) f(x) = 1 + 2x + 4x
Solution:
(i) f(x) = |x – 5|
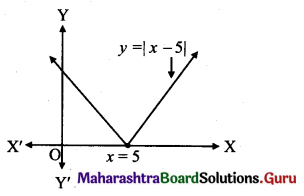
∴ Range of f = [0, ∞)
(ii) f(x) = \(\frac{x}{9+x^{2}}\) = y (say)
∴ x2y – x + 9y = 0
For real x, Discriminant > 0
∴ 1 – 4(y)(9y) ≥ 0
∴ y2 ≤ \(\frac{1}{36}\)
∴ \(\frac{-1}{6}\) ≤ y ≤ \(\frac{1}{6}\)
∴ Range of f = [\(\frac{-1}{6}\), \(\frac{1}{6}\)]
(iii) f(x) = \(\frac{1}{1+\sqrt{x}}\) = y, (say)
∴ √x y + y = 1
∴ √x = \(\frac{1-y}{y}\) ≥ 0
∴ \(\frac{y-1}{y}\) ≤ 0
∴ o < y ≤ 1
∴ Range of f = (0, 1]
(iv) f(x) = [x] – x = -{x}
∴ Range of f = (-1, 0] …..[0 ≤ {x} < 1]
(v) f(x) = 1 + 2x + 4x
Since, 2x > 0, 4x > 0
∴ f(x) > 1
∴ Range of f = (1, ∞)
Question 42.
Find (fog) (x) and (gof) (x)
(i) f(x) = ex, g(x) = log x
(ii) f(x) = \(\frac{x}{x+1}\), g(x) = \(\frac{x}{1-x}\)
Solution:
(i) f(x) = ex, g(x) = log x
(fog) (x) = f(g(x))
= f(log x)
= elog x
= x
(gof) (x) = g(f(x))
= g(ex)
= log (ex)
= x log e
= x …..[∵ log e = 1]
(ii) f(x) = \(\frac{x}{x+1}\), g(x) = \(\frac{x}{1-x}\)

Question 43.
Find f(x), if
(i) g(x) = x2 + x – 2 and (gof) (x) = 4x2 – 10x + 4
(ii) g(x) = 1 + √x and f [g(x)] = 3 + 2√x + x.
Solution:
(i) g(x) = x2 + x – 2
(gof) (x) = 4x2 – 10x + 4
= (2x – 3)2 + (2x – 3) – 2
= g(2x – 3)
= g(f(x))
∴ f(x) = 2x – 3
(gof) (x) = 4x2 – 10x + 4
= (-2x + 2)2 + (-2x + 2) – 2
= g(-2x + 2)
= g(f(x))
∴ f(x) = -2x + 2
(ii) g(x) = 1 + √x
f(g(x)) = 3 + 2√x + x
= x + 2√x + 1 + 2
= (√x + 1)2 + 2
f(√x + 1) = (√x + 1)2 + 2
∴ f(x) = x2 + 2

Question 44.
Find (fof) (x) if
(i) f(x) = \(\frac{x}{\sqrt{1+x^{2}}}\)
(ii) f(x) = \(\frac{2 x+1}{3 x-2}\)
Solution:




![]()









![]()





![]()



![]()



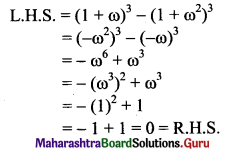

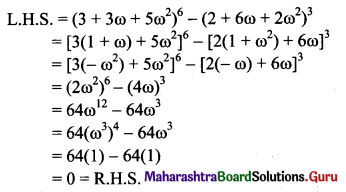

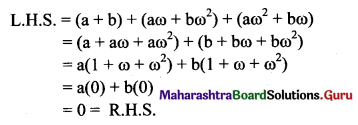





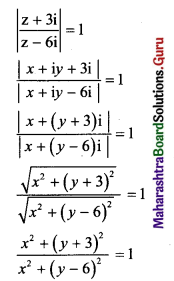



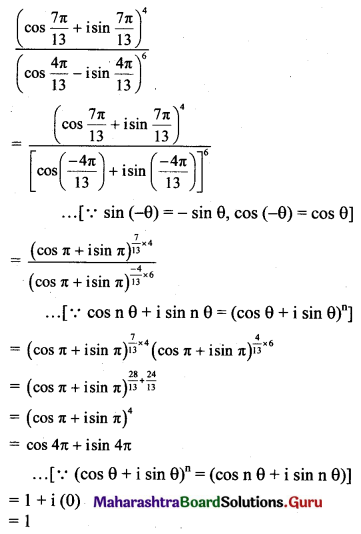





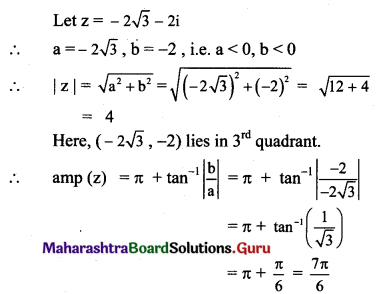







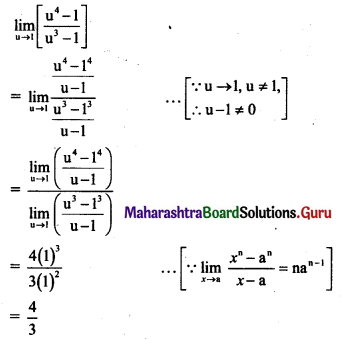



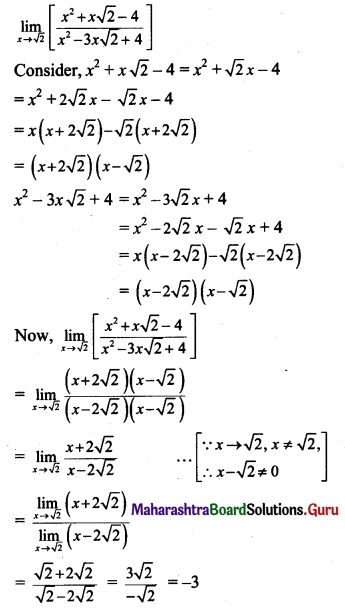

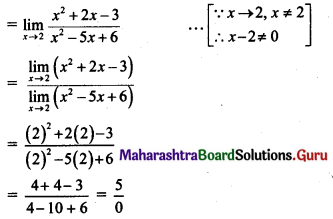









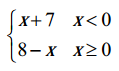
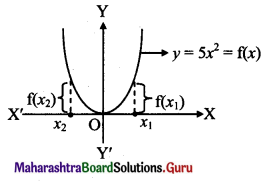
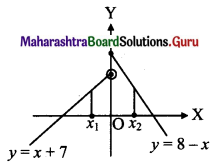
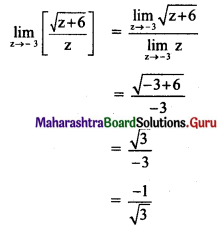
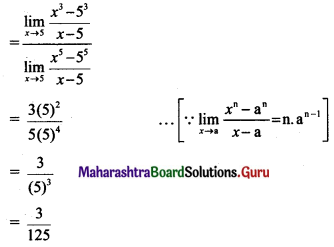
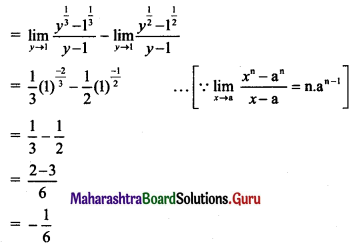
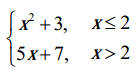 , then find
, then find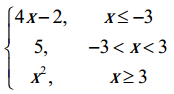 , then find
, then find