Prasanna

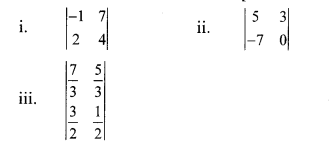
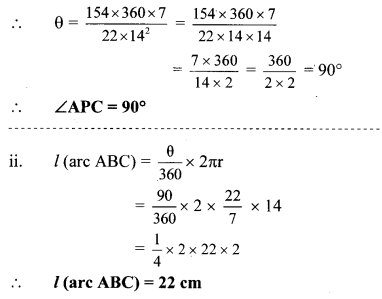
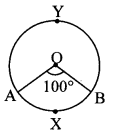
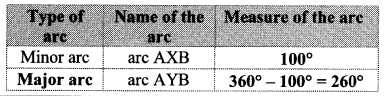
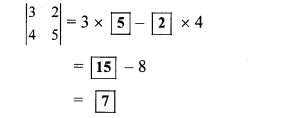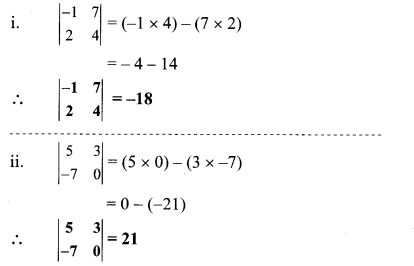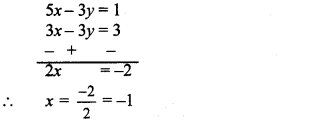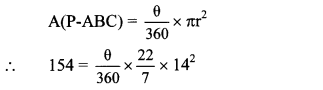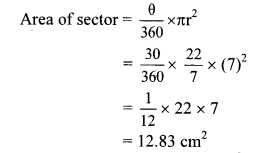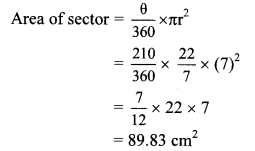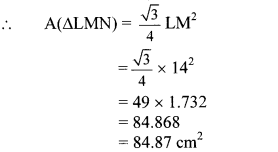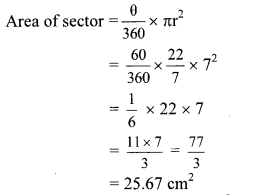Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 3.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.

Practice Set 3.2 Algebra 10th Std Maths Part 1 Answers Chapter 3 Arithmetic Progression

Question 1.
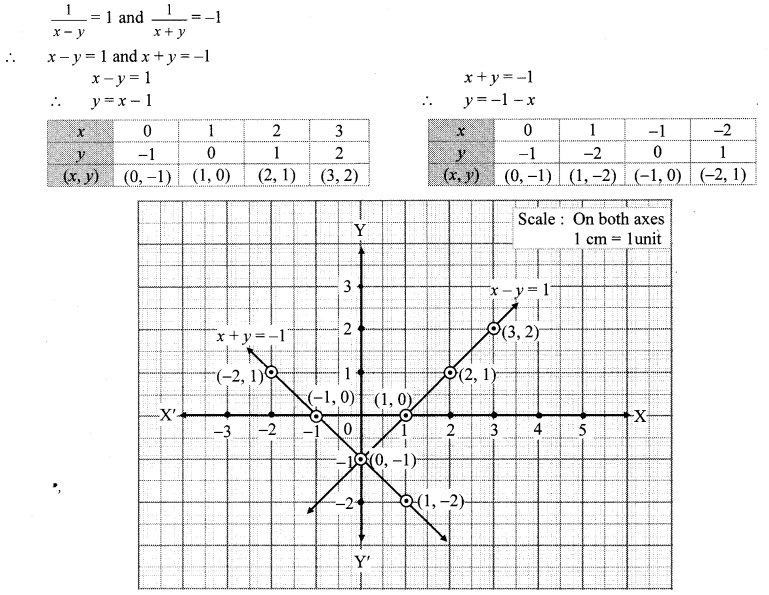
Write the correct number in the given boxes from the following A.P.

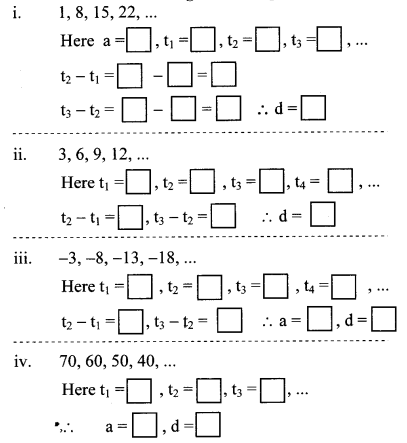
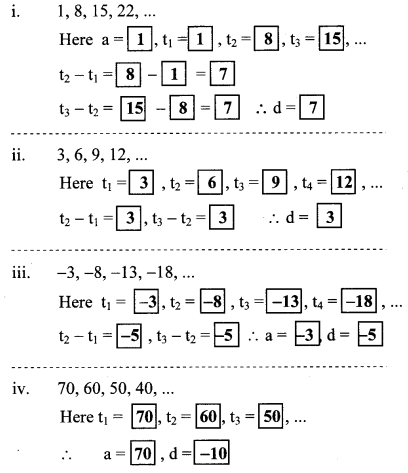
Solution:

Question 2.
Decide whether following sequence is an A.P., if so find the 20^th term of the progression.
-12, -5, 2, 9,16, 23,30,…
Solution:
i. The given sequence is
-12, -5,2, 9, 16, 23,30,…
Here, t₁ = -1₂, t₂ = -5, t₃ = 2, t₄ = 9
∴ t₂ – t₁ – 5 – (-12) – 5 + 12 = 7
t₃ – t₂ = 2 – (-5) = 2 + 5 = 7
∴ t₄ – t₃ – 9 – 2 = 7
∴ t₂ – t₁ = t₃ – t₂ = … = 7 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P.

ii. t_n = a + (n – 1)d
∴ t₂₀ = -12 + (20 – 1)7 …[∵a = -12, d = 7]
= -12 + 19 × 7
= -12 + 133
∴ t₂₀ = 121
∴ 20^th term of the given A.P. is 121.

Question 3.
Given Arithmetic Progression is 12, 16, 20, 24, … Find the 24^th term of this progression.
Solution:
The given A.P. is 12, 16, 20, 24,…
Here, a = 12, d = 16 – 12 = 4 Since,
t_n = a + (n – 1)d
∴ t₂₄ = 12 + (24 – 1)4
= 12 + 23 × 4
= 12 + 92
∴ t₂₄ = 104
∴ 24th term of the given A.P. is 104.

Question 4.
Find the 19th term of the following A.P. 7,13,19,25…..
Solution:
The given A.P. is 7, 13, 19, 25,…
Here, a = 7, d = 13 – 7 = 6
Since, t_n = a + (n – 1)d
∴ t₁₉ = 7 + (19 – 1)6
= 7 + 18 × 6
= 7 + 108
∴ t₁₉ = 115
∴ 19^th term of the given A.P. is 115.

Question 5.
Find the 27^th term of the following A.P. 9,4,-1,-6,-11,…
Solution:
The given A.P. is 9, 4, -1, -6, -11,…
Here, a = 9, d = 4- 9 = -5
Since, t_n = a + (n – 1)d
∴ t₂₇ = 9 + (27 – 1)(-5)
= 9 + 26 × (-5)
= 9 – 130
∴ t₂₇ = -121
∴ 27^th term of the given A.P. is -121.

Question 6.
Find how many three digit natural numbers are divisible by 5.
Solution:
The three digit natural numbers divisible by
5 are 100, 105, 110, …,995
The above sequence is an A.P.
∴ a = 100, d = 105 – 100 = 5
Let the number of terms in the A.P. be n.
Then, t_n = 995
Since, t_n = a + (n – 1)d
∴ 995 = 100 +(n – 1)5
∴ 995 – 100 = (n – 1)5
∴ 895 = (n – 1)5
∴ n – 1 = \(\frac { 895 }{ 5 } \)
∴ n – 1 = 179
∴ n = 179 + 1 = 180
∴ There are 180 three digit natural numbers which are divisible by 5.

Question 7.
The 11th term and the 21st term of an A.P. are 16 and 29 respectively, then find the 41st term of that A.P.
Solution:
Bor an A.P., let a be the first term and d be the common difference,
t₁₁ = 16, t₂₁ = 29 …[Given]
t_n = a + (n – 1)d
∴ t₁₁, = a + (11 – 1)d
∴ 16 = a + 10d
i.e. a + 10d = 16 …(i)
Also, t₂₁ = a + (21 – 1)d
∴ 29 = a + 20d
i.e. a + 20d = 29 …(ii)
Subtracting equation (i) from (ii), we get a

Question 8.
8. 11, 8, 5, 2, … In this A.P. which term is number-151?
Solution:
The given A.P. is 11, 8, 5, 2,…
Here, a = 11, d = 8 – 11 = -3
Let the n^th term of the given A.P. be -151.
Then, t_n = – 151
Since, t_n = a + (n – 1)d
∴ -151= 11 + (n – 1)(-3)
∴ -151 – 11 =(n – 1)(-3)
∴ -162 = (n – 1)(-3)
∴ n – 1 = \(\frac { -162 }{ -3 } \)
∴ n – 1 = 54
∴ n = 54 + 1 = 55
∴ 55th term of the given A.P. is -151.

Question 9.
In the natural numbers from 10 to 250, how many are divisible by 4?
Solution:
The natural numbers from 10 to 250 divisible
by 4 are 12, 16, 20, …,248
The above sequence is an A.P.
∴ a = 12, d = 16 – 12 = 4
Let the number of terms in the A.P. be n.
Then, t_n = 248
Since, t_n = a + (n – 1)d
∴ 248 = 12 + (n – 1)4
∴ 248 – 12 = (n – 1)4
∴ 236 = (n – 1)4
∴ n – 1 = \(\frac { 236 }{ 4 } \)
∴ n – 1 = 59
∴ n = 59 + 1 = 60
∴ There are 60 natural numbers from 10 to 250 which are divisible by 4.

Question 10.
In an A.P. 17^th term is 7 more than its 10th term. Find the common difference.
Solution:
For an A.P., let a be the first term and d be the common difference.
According to the given condition,
t₁₇ = t₁₀ + 7
∴ a + (17 – 1)d = a + (10 – 1)d + 7 …[∵ t_n = a + (n – 1)d]
∴ a + 16d = a + 9d + 7
∴ a + 16d – a – 9d = 7
∴ 7d = 7
∴ d = \(\frac { 7 }{ 7 } \) = 1
∴ The common difference is 1.

Question 1.
Kabir’s mother keeps a record of his height on each birthday. When he was one year old, his height was 70 cm, at 2 years he was 80 cm tall and 3 years he was 90 cm tall. His aunt Meera was studying in the 10th class. She said, “it seems like Kabir’s height grows in Arithmetic Progression”. Assuming this, she calculated how tall Kabir will be at the age of 15 years when he is in 10th! She was shocked to find it. You too assume that Kabir grows in A.P. and find out his height at the age of 15 years. (Textbook pg. no. 63)
Solution:
Height of Kabir when he was 1 year old = 70 cm Height of Kabir when he was 2 years old = 80 cm
Height of Kabir when he was 3 years old = 90 cm The heights of Kabir form an A.P.
Here, a = 70, d = 80 – 70 = 10
We have to find height of Kabir at the age of 15years i.e. t₁₅.
Now, tn = a + (n – 1)d
∴ t₁₅ = 70 + (15 – 1)10
= 70 + 14 × 10 = 70 + 140
∴ t₁₅ = 210
∴ The height of Kabir at the age of 15 years will be 210 cm.

Question 2.
Is 5, 8, 11, 14, …. an A.P.? If so then what will be the 100^th term? Check whether 92 is in this A.P.? Is number 61 in this A.P.? (Textbook pg. no, 62)
Solution:
i. The given sequence is
5, 8,11,14,…
Here, t₁ = 5, t₂ = 8, t₃ = 11, t₄ = 14
∴ t₂ – t₁ = 8 – 5 = 3
t₃ – t₂ = 11 – 8 = 3
t₄ – t₃ = 14 – 11 = 3
∴ t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = 3 = d = constant
The difference between two consecutive terms is constant
∴ The given sequence is an A.P.

ii. t_n = a + (n – 1)d
∴ t₁₀₀ = 5 + (100 – 1)3 …[∵ a = 5, d = 3]
= 5 + 99 × 3
= 5 + 297
∴ t₁₀₀ = 302
∴ 100^th term of the given A.P. is 302.

iii. To check whether 92 is in given A.P., let t_n = 92
∴ t_n = a + (n – 1)d
∴ 92 = 5 + (n – 1)3
∴ 92 = 5 + 3n – 3
∴ 92 = 2 + 3n
∴ 90 = 3n
∴ n = \(\frac { 90 }{ 3 } \) = 30
∴ 92 is the 30th term of given A.P.

iv. To check whether 61 is in given A.P., let t_n = 61
61 = 5 + (n – 1)3
∴ 61 = 5 + 3n – 3
∴ 61 = 2 + 3n
∴ 61 – 2 = 3n
∴ 59 = 3n
∴ n = \(\frac { 59 }{ 3 } \)
But, n is natural number 59
∴ n ≠ \(\frac { 59 }{ 3 } \)
∴ 61 is not in given A.P.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.

Practice Set 2.1 Algebra 10th Std Maths Part 1 Answers Chapter 2 Quadratic Equations

Question 1.
Write any two quadratic equations.
Solution:
i. y² – 7y + 12 = 0
ii. x² – 8 = 0

Question 2.
Decide which of the following are quadratic
i. x² – 7y + 2 = 0
ii. y² = 5y – 10
iii. y² + \(\frac { 1 }{ y } \) = 2
iv. x + \(\frac { 1 }{ x } \) = -2
v. (m + 2) (m – 5) = 03
vi. m³ + 3m² – 2 = 3m³
Solution:
i. The given equation is x² + 5x – 2 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 5, c = -2 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

ii. The given equation is
y² = 5y – 10
∴ y² – 5y + 10 = 0
Here, y is the only variable and maximum index of the variable is 2.
a = 1, b = -5, c = 10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

iii. The given equation is
y² + \(\frac { 1 }{ y } \) = 2
∴ y³ + 1 = 2y …[Multiplying both sides by y]
∴ y³ – 2y + 1 = 0
Here, y is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.

iv. The given equation is
x + \(\frac { 1 }{ x } \) = -2
∴ x² + 1 = -2x …[Multiplying both sides by x]
∴ x² + 2x+ 1 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 2, c = 1 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

v. The given equation is
(m + 2) (m – 5) = 0
∴ m(m – 5) + 2(m – 5) = 0
∴ m² – 5m + 2m – 10 = 0
∴ m² – 3m – 10 = 0
Here, m is the only variable and maximum index of the variable is 2.
a = 1, b = -3, c = -10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

vi. The given equation is
m³ + 3m² – 2 = 3m³
∴ 3m³ – m³ – 3m² + 2 = 0
∴ 2m³ – 3m² + 2 = 0
Here, m is the only variable and maximum
index of the variable is not 2.
∴ The given equation is not a quadratic equation.

Question 3.
Write the following equations in the form ax² + bx + c = 0, then write the values of a, b, c for each equation.
i. 2y = 10 – y²
ii. (x – 1)² = 2x + 3
iii. x² + 5x = – (3 – x)
iv. 3m² = 2m² – 9
v. P (3 + 6p) = – 5
vi. x² – 9 = 13
Solution:
i. 2y – 10 – y²
∴ y² + 2y – 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = 2, c = -10

ii. (x – 1)² = 2x + 3
∴ x² – 2x + 12x + 3
x² – 2x + 1 – 2x – 30
∴ x² – 4x – 2 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = -4, c = -2

iii. x² + 5x = – (3 – x)
∴ x² + 5x = -3 + x
∴ x² + 5x – x + 3 = 0
∴ x² + 4x + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 4, c = 3

iv. 3m² = 2m² – 9
∴ 3m² – 2m² + 9 = 0
∴ m² + 9 = 0
∴ m² + 0m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1, b = 0, c = 9

v. p (3 + 6p) = – 5
∴ 3p + 6p² = -5
∴ 6p² + 3p + 5 = 0
Comparing the above equation with
ap² + bp + c = 0, we get
a = 6, b = 3, c = 5

vi. x² – 9 = 13
∴ x² – 9 – 13 = 0
∴ x² – 22 = 0
∴ x² + 0x – 22 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 0, c = -22

Question 4.
Determine whether the values given against each of the quadratic equation are the roots of the equation.
i. x² + 4x – 5 = 0; x = 1,-1
ii. 2m² – 5m = 0; m = 2, \(\frac { 5 }{ 2 } \)
Solution:
i. The given equation is
x² + 4x – 5 = 0 …(i)
Putting x = 1 in L.H.S. of equation (i), we get
L.H.S. = (1)² + 4(1) – 5 = 1 + 4 – 5 = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation.
Putting x = -1 in L.H.S. of equation (i), we get
L.H.S. = (-1)² + 4(-1) – 5 = 1 – 4 – 5 = -8
∴ LH.S. ≠ R.H.S.
∴ x = -1 ¡s not the root of the given quadratic equation.

ii. The given equation is
2m² – 5m = 0 …(i)
Putting m = 2 in L.H.S. of equation (i), we get
L.H.S. = 2(2)² – 5(2) = 2(4) -10 = 8 – 10 = -2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
Putting m = \(\frac { 5 }{ 2 } \) in L.H.S. of equation (i), we get

Question 5.
Find k if x = 3 is a root of equation kx² – 10x + 3 = 0.
Solution:
x = 3 is the root of the equation kx² – 10x + 3 = 0.
Putting x = 3 in the given equation, we get
k(3)² – 10(3) + 3 = 0
∴ 9k – 30 +3 = 0
∴ 9k – 27 = 0
∴ 9k = 27
∴ k = \(\frac { 27 }{ 9 } \)
∴ k = 3

Question 6.
One of the roots of equation 5m² + 2m + k = 0 is \(\frac { -7 }{ 5 } \) Complete the following activity to find the value of ‘k’.
Solution:

Question 1.
x² + 3x – 5, 3x² – 5x, 5x²; Write the polynomials In the index form. Observe the coefficients and fill in the boxes. (Textbook p. no. 31)
Answer:
Index form of the given polynomials:
x² + 3x – 5, 3x² – 5x + 0, 5x² + 0x + 0
i. Coefficients of x2 are [1], [3] and [5] respectively, and these coefficients are non zero.
ii. Coefficients of x are 3, [-5] and [0] respectively.
iii. Constant terms are [-5], [0] and [0] respectively.
Here, constant terms of second and third polynomial is zero.

Question 2.
Complete the following table (Textbook p. no. 31)

Answer:

Question 3.
Decide which of the following are quadratic equations? (Textbook pg. no. 31)
i. 9y² + 5 = 0
ii. m³ – 5m² + 4 = 0
iii. (l + 2)(l – 5) = 0
Solution:
i. In the equation 9y² + 5 = 0, [y] is the only variable and maximum index of the variable is [2].
∴ It [is] a quadratic equation.

ii. In the equation m³ – 5m² + 4 = 0, [m] is the only variable and maximum index of the variable is not 2.
∴ It [is not] a quadratic equation.

iii. (l + 2)(l – 5) = 0
∴ l(l – 5) + 2(l – 5) = 0
∴ l² – 5l + 2l – 10 = 0
∴ l² – 3l – 10 = 0.
In this equation [l] is the only variable and maximum index of the variable is [2]
∴ it [is] a quadratic equation.

Question 4.
If x = 5 is a root of equation kx² – 14x – 5 = 0, then find the value of k by completing the following activity. (Textbook pg, no. 33)
Solution:

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.5 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Practice Set 1.5 Algebra 10th Std Maths Part 1 Answers Chapter 1 Linear Equations in Two Variables

Question 1.
Two numbers differ by 3. The sum of twice the smaller number and thrice the greater number is 19. Find the numbers.
Solution:
Let the greater number be x and the smaller number be y.
According to the first condition, x – y = 3 …(i)
According to the second condition,
3x + 2y = 19 …(ii)
Multiplying equation (i) by 2, we get
2x – 2y = 6 …(iii)
Adding equations (ii) and (iii), we get

Substituting x = 5 in equation (i), we get
5 – y = 3
∴ 5 – 3 = y
∴ y = 2
∴ The required numbers are 5 and 2.

Question 2.
Complete the following.

Solution:
Opposite sides of a rectangle are equal.
∴ 2x + y + 8 = 4x – y
∴ 8 = 4x – 2x – y – y
∴ 2x – 2y = 8
∴ x – y = 4 …(i)[Dividingboth sides by 2]
Also, x + 4= 2y
∴ x – 2y = -4 …(ii)
Subtracting equation (ii) from (i), we get

Substituting y = 8 in equation (i), we get
x – 8 = 4
∴ x = 4 + 8
∴ x = 12
Now, length of rectangle = 4x – y
= 4(12) – 8
= 48 – 8
∴ Length of rectangle = 40
Breadth of rectangle = 2y = 2(8) = 16
Perimeter of rectangle = 2(length + breadth)
= 2(40 + 16)
= 2(56)
∴ Perimeter of rectangle =112 units
Area of rectangle = length × breadth
= 40 × 16
∴ Area of rectangle = 640 sq. units
∴ x = 12 and y = 8, Perimeter of rectangle is 112 units and area of rectangle is 640 sq. units.

Question 3.
The sum of father’s age and twice the age of his son is 70. If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.
Solution:
Let the present ages of father and son be x years and y years respectively.
According to the first condition,
x + 2y = 70 …(i)
According to the second condition,
2x + y = 95 …(ii)
Multiplying equation (i) by 2, we get
2x + 4y = 140 …(iii)
Subtracting equation (ii) from (iii), we get

Substituting y = 15 in equation (i), we get
x + 2(15) = 7O
⇒ x + 30 = 70
⇒ x = 70 – 30
∴ x = 40
∴ The present ages of father and son are 40 years and 15 years respectively.

Question 4.
The denominator of a fraction is 4 more than twice its numerator. Denominator becomes 12 times the numerator, if both the numerator and the denominator are reduced by 6. Find the fraction.
Solution:
Let the numerator of the fraction be x and the denominator be y.
∴ Fraction = \(\frac { x }{ y } \)
According to the first condition,
y = 2x + 4
∴ 2x – y = -4 …(i)
According to the second condition,
(y – 6)= 12(x – 6)
∴ y – 6 = 12x – 72
∴ 12x – y = 72 – 6
∴ 12x – y = 66 …(ii)
Subtracting equation (i) from (ii), we get

Question 5.
Two types of boxes A, B ,are to be placed in a truck having capacity of 10 tons. When 150 boxes of type A and 100 boxes of type B are loaded in the truck, it weights 10 tons. But when 260 boxes of type A are loaded in the truck, it can still accommodate 40 boxes of type B, so that it is fully loaded. Find the weight of each type of box.
Solution:
Let the weights of box of type A be x kg and that of box of type B be y kg.
1 ton = 1000 kg
∴ 10 tons = 10000 kg
According to the first condition,
150x + 100y = 10000
∴ 3x + 2y = 200 …(i) [Dividing both sides by 50]
According to the second condition,
260x + 40y = 10000
∴ 13x + 2y = 500 …(ii) [Dividing both sides by 20]
Subtracting equation (i) from (ii), we get

∴ The weights of box of type A is 30 kg and that of box of type B is 55 kg.

Question 6.
Out of 1900 km, Vishal travelled some distance by bus and some by aeroplane. Bus travels with average speed 60 km/hr and the average speed of aeroplane is 700 km/hr. It takes 5 hours to complete the journey. Find the distance Vishal travelled by bus.
Solution:
Let the distance Vishal travelled by bus be x km and by aeroplane be y km.
According to the first condition,
x + y = 1900 …(i)
\(\text { Time }=\frac{\text { Distance }}{\text { Speed }} \)
∴ Time required to cover x km by bus = \(\frac { x }{ 60 } \) hr
Time required to cover y km by aeroplane
= \(\frac { y }{ 700 } \) hr
According to the second condition,

Multiplying equation (i) by 6, we get
6x + 6y= 11400 …(iii)
Subtracting equation (iii) from (ii), we get

∴ The distance Vishal travelled by bus is 150 km.

Question 1.
There are some instructions given below. Frame the equations from the information and write them in the blank boxes shown by arrows. (Textbook pg. no. 20)
Answer:

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Problem Set 1 Algebra 10th Std Maths Part 1 Answers Chapter 1 Linear Equations in Two Variables

Choose correct alternative for each of the following questions.

Question 1.
To draw graph of 4x + 5y = 19, find y when x = 1.
(a) 4
(b) 3
(c) 2
(d) -3
Answer:
(b)

Question 2.
For simultaneous equations in variables x and y, D_x = 49, Dy = – 63, D = 7 then what is x?
(a) 7
(b) -7
(c) \(\frac { 1 }{ 7 } \)
(d) \(\frac { -1 }{ 7 } \)
Answer:
(a)

Question 3.
Find the value of

(a) -1
(b) -41
(c) 41
(d) 1
Answer:
(d)

Question 4.
To solvex + y = 3; 3x – 2y – 4 = 0 by determinant method find D.
(a) 5
(b) 1
(c) -5
(d) -1
Answer:
(c)

Question 5.
ax + by = c and mx + n y = d and an ≠ bm then these simultaneous equations have-
(a) Only one common solution
(b) No solution
(c) Infinite number of solutions
(d) Only two solutions.
Answer:
(a)

Question 2.
Complete the following table to draw the graph of 2x – 6y = 3.
Answer:

Question 3.
Solve the following simultaneous equations graphically.
i. 2x + 3y = 12 ; x – y = 1
ii. x – 3y = 1 ; 3x – 2y + 4 = 0
iii. 5x – 6y + 30 = 0; 5x + 4y – 20 = 0
iv. 3x – y – 2 = 0 ; 2x + y = 8
v. 3x + y= 10 ; x – y = 2
Answer:
i. The given simultaneous equations are

The two lines interest at point (3,2).
∴ x = 3 and y = 2 is the solution of the simultaneous equations 2x + 3y = 12 and x – y = 1.

ii. The given simultaneous equations are

The two lines intersect at point (-2, -1).
∴ x = -2 and y = -1 is the solution of the simultaneous equations x – 3y = 1 and 3x – 2p + 4 = 0.

iii. The given simultaneous equations are

The two lines intersect at point (0, 5).
∴ x = 0 and y = 5 is the solution of the simultaneous equations 5x – 6y + 30 = 0 and 5x + 4y – 20 = 0.

iv. The given simultaneous equations are


The two lines intersect at point (2, 4).
∴ x = 2 and y = 4 is the solution of the simultaneous equations 3x – y – 2 = 0 and 2x + y = 8.

v. The given simultaneous equations are

The two lines intersect at point (3, 1).
∴ x = 3 and y = 1 is the solution of the simultaneous equations 3x + y = 10 and x – y = 2.

Question 4.
Find the values of each of the following determinants.

Solution:

Question 5.
Solve the following equations by Cramer’s method.

Solution:
i. The given simultaneous equations are
6x – 3y = -10 …(i)
3x + 5y – 8 = 0
∴ 3x + 5y = 8 …(ii)
Equations (i) and (ii) are in ax + by = c form. Comparing the given equations with a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 6, b₁ = -3, c₁ = 10 and
a₂ = 3, b₂ = 5, c₂ = 8

ii. The given simultaneous equations are
4m – 2n = -4 …(i)
4m + 3n = 16 …(ii)
Equations (i) and (ii) are in am + bn = c form.
Comparing the given equations with a₁m + b₁n = c₁ and a₂m + b₂n = c₂, we get
a₁ = 4, b₁ = -2, c₁ = -4 and
a₂ = 4, b₂ = 3, c₂ = 16


∴ (m, n) = (1, 4) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are

iv. The given simultaneous equations are
7x + 3y = 15 …(i)
12y – 5x = 39
i.e. -5x + 12y = 39 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 7, b₁ = 3, c₁ = 15 and
a₂ = -5, b₂ = 12, c₂ = 39

v. The given simultaneous equations are

∴ 4(x + y – 8) = 2(3x – y)
∴ 4x + 4y – 32 = 6x – 2y
∴ 6x – 4x – 2y – 4y = -32
∴ 2x – 6y = -32
∴ x – 3y = -16 …(ii)[Dividing both sides by 2]
Equations (i) and (ii) are in ax + by = c form. Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 1, b₁ = -1, c₁ = -4 and
a₂ = 1, b₂ = -3, c₂ = -16

∴ (x, y) = (2, 6) is the solution of the given simultaneous equations.

Question 6.
Solve the following simultaneous equations:

Answer:
i. The given simultaneous equations are

Subtracting equation (iv) from (iii), we get

∴ (x, y) = (6, – 4) is the solution of the given simultaneous equations.

ii. The given simultaneous equations are

Adding equations (v) and (vi), we get

iii. The given simultaneous equations are


∴ (x, y) = (1, 2) is the solution of the given simultaneous equations.

iv. The given simultaneous equations are

∴ Equations (i) and (ii) become 7q – 2p = 5 …(iii)
8q + 7p = 15 …(iv)
Multiplying equation (iii) by 7, we get
49q – 14p = 35 …(v)
Multiplying equation (iv) by 2, we get
16q + 14p = 30 …(vi)
Adding equations (v) and (vi), we get

Substituting q = 1 in equation (iv), we get
8(1) + 7p = 15
∴ 8 + 7p = 15
∴ 7p = 15 – 8
∴ 7p = 7
∴ p = \(\frac { 7 }{ 7 } \) = 1
∴ (P, q) = (1,1)
Resubstituting the values of p and q, we get
1 = \(\frac { 1 }{ x } \) and 1 = \(\frac { 1 }{ y } \)
∴ x = 1 and y = 1
∴ (x, y) = (1, 1) is the solution of the given simultaneous equations.

v. The given simultaneous equations are

Resubstituting the values of p and q, we get

∴ 3x + 4y = 10 …(v)
and 2x – 3y = 1 …(vi)
Multiplying equation (v) by 3, we get
9x + 12y = 30 …(vii)
Multiplying equation (vi) by 4, we get
8x – 12y = 4 …(viii)
Adding equations (vii) and (viii), we get

Substituting x = 2 in equation (v), we get
3(2) + 4y = 10
⇒ 6 + 4y = 10
⇒ 4y = 10 – 6
⇒ y = 4/4 = 1
∴ y = 1
∴ (x, y) = (2, 1) is the solution of the given simultaneous equations.

Question 7.
Solve the following word problems, i. A two digit number and the number with digits interchanged add up to 143. In the given number the digit in unit’s place is 3 more than the digit in the ten’s place. Find the original number.
Solution:
Let the digit in unit’s place be x
and that in the ten’s place be y.

ii. Kantabai bought 1 \(\frac { 1 }{ 2 } \) kg tea and 5 kg sugar from a shop. She paid ₹ 50 as return fare for rickshaw. Total expense was ₹ 700. Then she realised that by ordering online the goods can be bought with free home delivery at the same price. So, next month she placed the order online for 2 kg tea and 7 kg sugar. She paid ₹ 880 for that. Find the rate of sugar and tea per kg.
Solution:
Let the rate of tea be ₹ x per kg and that of sugar be ₹ y per kg.
According to the first condition,
cost of 1 \(\frac { 1 }{ 2 } \) kg tea + cost of 5 kg sugar + fare for rickshaw = total expense

According to the second condition,
cost of 2 kg tea + cost of 7 kg sugar = total expense
2x + 7y = 880 …(ii)
Multiplying equation (i) by 2, we get
6x + 20y = 2600 …(iii)
Multiplying equation (ii) by 3, we get
6x + 21y = 2640 …(iv)
Subtracting equation (iii) from (iv), we get

∴ The rate of tea is ₹ 300 per kg and that of sugar is ₹ 40 per kg.

iii. To find number of notes that Anushka had, complete the following activity.

Solution:
Anushka had x notes of ₹ 100 and y notes of ₹ 50.
According to the first condition,
100x + 50y = 2500
∴ 2x + y = 50 …(i) [Dividing both sides by 50]
According to the second condition,
100y + 50x = 2000
∴ 2y + x = 40 … [Dividing both sides by 50]
i.e. x + 2y = 40
∴ 2x + 4y = 80 …(ii) [Multiplying both sides by 2]
Subtracting equation (i) from (ii), we get

∴ Anushka had 20 notes of ₹ 100 and 10 notes of ₹ 50.

iv. Sum of the present ages of Manish and Savita is 31, Manish’s age 3 years ago was 4 times the age of Savita. Find their present ages.
Solution:
Let the present ages of Manish and Savita be x years and y years respectively.
According to the first condition,
x + y = 31 …(i)
3 years ago,
Manish’s age = (x – 3) years
Savita’s age = (y – 3) years
According to the second condition,
(x – 3) = 4 (y – 3)
∴ x – 3 = 4y – 12
∴ x – 4y = -12 + 3
∴ x – 4y = -9 …(ii)
Subtracting equation (ii) from (i), we get

∴ x = 31 – 8
∴ x = 23
The present ages of Manish and Savita are 23 years and 8 years respectively.

v. In a factory the ratio of salary of skilled and unskilled workers is 5 : 3. Total salary of one day of both of them is ₹ 720. Find daily wages of skilled and unskilled workers.
Solution:
Let the daily wages of skilled workers be ₹ x
that of unskilled workers be ₹ y.
According to the first condition,

∴ The daily wages of skilled workers is ₹ 450 and that of unskilled workers is ₹ 270.

vi. Places A and B are 30 km apart and they are on a straight road. Hamid travels from A to B on bike. At the same time Joseph starts from B on bike, travels towards A. They meet each other after 20 minutes. If Joseph would have started from B at the same time but in the opposite direction (instead of towards A), Hamid would have caught him after 3 hours. Find the speed of Hamid and Joseph.
Solution:
Let the speeds of Hamid and Joseph be x km/hr andy km/hr respectively.
Distance travelled by Hamid in 20 minutes

According to the first condition,

∴ The speeds of Hamid and Joseph 50 km/hr and 40 km/hr respectively.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.4 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Practice Set 1.4 Algebra 10th Std Maths Part 1 Answers Chapter 1 Linear Equations in Two Variables

Question 1.
Solve the following simultaneous equations.

Solution:
i. The given simultaneous equations are

∴ Equations (i) and (ii) become
2p – 3q = 15 …(iii)
8p + 5q = 77 …(iv)
Multiplying equation (iii) by 4, we get
8p – 12q = 60 …(v)
Subtracting equation (v) from (iv), we get

ii. The given simultaneous equations are



Substituting x = 3 in equation (vi), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are

∴ Equations (i) and (ii) become
27p + 31q = 85 …(iii)
31p + 27q = 89 …(iv)
Adding equations (iii) and (iv), we get

iv. The given simultaneous equations are


Substituting x = 1 in equation (vi), we get
3(1) + y = 4
∴ 3 + y = 4
∴ y = 4 – 3 = 1
∴ (x, y) = (1, 1) is the solution of the given simultaneous equations.

Question 1.
Complete the following table. (Textbook pg. no. 16)
Solution:

Question 2.
In the above table the equations are not linear. Can you convert the equations into linear equations? (Textbook pg. no. 17)
Answer:
Yes, the above given simultaneous equations can be converted to a pair of linear equations by making suitable substitutions.

Steps for solving equations reducible to a pair of linear equations.

• Step 1: Select suitable variables other than those which are in the equations.
• Step 2: Replace the given variables with new variables such that the given equations become linear equations in two variables.
• Step 3: Solve the new simultaneous equations and find the values of the new variables.
• Step 4: By resubstituting the value(s) of the new variables, find the replaced variables which are to be determined.

Question 3.
To solve given equations fill the below boxes suitably. (Text book pg.no. 19)
Answer:

Question 4.
The examples on textbook pg. no. 17 and 18 obtained by transformation are solved by elimination method. If you solve these equations by graphical method and by Cramer’s rule will you get the same answers? Solve and check it. (Textbook pg. no. 18)

Solution:

The two lines intersect at point (1,-1).
∴ p = 1 and q = -1 is the solution of the simultaneous equations 4p + q = 3 and 2p – 3q = 5.
Re substituting the values of p and q, we get

The two lines intersect at point (0, -1).
∴ x = 0 and y = -1 is the solution of the simultaneous equations x – y = 1 and x + y = -1.
∴ (x, y) = (0, -1) is the solution of the given simultaneous equations.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Practice Set 1.3 Algebra 10th Std Maths Part 1 Answers Chapter 1 Linear Equations in Two Variables

Question 1.
Fill in the blanks with correct number.
Solution:

Question 2.
Find the values of following determinants.

Solution:

Question 3.
Solve the following simultaneous equations using Cramer’s rule.
i. 3x – 4y = 10 ; 4x + 3y = 5
ii. 4x + 3y – 4 = 0 ; 6x = 8 – 5y
iii. x + 2y = -1 ; 2x – 3y = 12
iv. 6x – 4y = -12 ; 8x – 3y = -2
v. 4m + 6n = 54 ; 3m + 2n = 28
vi. 2x + 3y = 2 ; x – \(\frac { y }{ 2 } \) = \(\frac { 1 }{ 2 } \)
Solution:
i. The given simultaneous equations are 3x – 4y = 10 …(i)
4x + 3y = 5 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 3, b₁ = -4, c₁ = 10 and
a₂ = 4, b₂ = 3, c₂ = 5

∴ (x, y) = (2, -1) is the solution of the given simultaneous equations.

ii. The given simultaneous equations are
4x + 3y – 4 = 0
∴ 4x + 3y = 4 …(i)
6x = 8 – 5y
∴ 6x + 5y = 8 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 4, b₁ = 3, c₁ = 4 and
a₂ = 6, b₂ = 5, c₂ = 8

∴ (x, y) = (-2, 4) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are
x + 2y = -1 …(i)
2x – 3y = 12 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = C₁ and a₂x + b₂y = c₂, we get
a₁ = 1, b₁ = 2, c₁ = -1 and
a₂ = 2, b₂ = -3, c₂ = 12

∴ (x, y) = (3, -2) is the solution of the given simultaneous equations.

iv. The given simultaneous equations are
6x – 4y = -12
∴ 3x – 2y = -6 …(i) [Dividing both sides by 2]
8x – 3y = -2 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 3, b₁ = -2, c₁ = -6 and
a₂ = 8, b₂ = -3, c₂ = -2

∴ (x, y) = (2, 6) is the solution of the given simultaneous equations.

v. The given simultaneous equations are
4m + 6n = 54
2m + 3n = 27 …(i) [Dividing both sides by 2]
3m + 2n = 28 …(ii)
Equations (i) and (ii) are in am + bn = c form.
Comparing the given equations with
a₁m + b₁n = c₁ and a₂m + b₂n = c₂, we get
a₁ = 2, b₁ = 3, c₁ = 27 and
a₂ = 3, b₂ = 2, c₂ = 28


∴ (m, n) = (6, 5) is the solution of the given simultaneous equations.

vi. The given simultaneous equations are
2x + 3y = 2 …(i)
x = \(\frac { y }{ 2 } \) = \(\frac { 1 }{ 2 } \)
∴ 2x – y = 1 …(ii) [Multiplying both sides by 2]
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 2, b₁ = 3, c₁ = 2 and
a₂ = 2, b₂ = -1, c₂ = 1

Question 1.
To solve the simultaneous equations by determinant method, fill in the blanks,
y + 2x – 19 = 0; 2x – 3y + 3 = 0 (Textbookpg.no. 14)
Solution:
Write the given equations in the form
ax + by = c.
2x + y = 19
2x – 3y = -3

Question 2.
Complete the following activity. (Textbook pg. no. 15)
Solution:

Question 3.
What is the nature of solution if D = 0? (Textbook pg. no. 16)
Solution:
If D = 0, i.e. a₁b₂ – b₁a₂ = 0, then the two simultaneous equations do not have a unique solution.
Examples:
i. 2x – 4y = 8 and x – 2y = 4
Here, a₁b₂ – b₁a₂ = (2)(-2) – (-4) (1)
= -4 + 4 = 0
Graphically, we can check that these two lines coincide and hence will have infinite solutions.

ii. 2x – y = -1 and 2x – y = -4
Here, a₁ b₂ – b₁ a₂ = (2)(-1) – (-1) (2)
= -2 + 2 = 0
Graphically, we can check that these two lines are parallel and hence they do not have a solution.

Question 4.
What can you say about lines if common solution is not possible? (Textbook pg. no. 16)
Answer:
If the common solution is not possible, then the lines will either coincide or will be parallel to each other.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Practice Set 1.2 Algebra 10th Std Maths Part 1 Answers Chapter 1 Linear Equations in Two Variables

10th Maths 2 Practice Set 1.2 Question 1.
Complete the following table to draw graph of the equations.
i. x + y = 3
ii. x – y = 4
Answer:
i. x + y = 3

ii. x – y = 4

Linear Equations In Two Variables Practice Set 1.2  Question 2.
Solve the following simultaneous equations graphically.
i. x + y = 6 ; x – y = 4
ii. x + y = 5 ; x – y = 3
iii. x + y = 0 ; 2x – y = 9
iv. 3x – y = 2 ; 2x – y = 3
v. 3x – 4y = -7 ; 5x – 2y = 0
vi. 2x – 3y = 4 ; 3y – x = 4
Solution:
i. The given simultaneous equations are
x + y = 6                                                                                                        x – y = 4
∴ y = 6 – x                                                                                                     ∴ y = x – 4
The two lines intersect at point (5, 1).
∴ x = 5 and y = 1 is the solution of the simultaneous equations x + y = 6 and x – y = 4.

ii. The given simultaneous equations are


The two lines intersect at point (4, 1).
∴ x = 4 and y = 1 is the solution of the simultaneous equations x+y = 5 and x – y = 3.

iii. The given simultaneous equations are


The two lines intersect at point (3, -3).
∴ x = 3 and y = -3 is the solution of the simultaneous equations x + y = 0 and 2x – y = 9.

iv. The given simultaneous equations are


The two lines intersect at point (-1, -5).
∴ x = -1 and y = -5 is the solution of the simultaneous equations 3x- y = 2 and 2x- y = 3.

v. The given simultaneous equations are


The two lines intersect at point (1, 2.5).
∴ x = 1 and y = 2.5 is the solution of the simultaneous equations 3x – 4y = -7 and 5x – 2y = 0.

vi. The given simultaneous equations are


The two lines intersect at point (8, 4).
∴ x = 8 and y = 4 is the solution of the simultaneous equations 2x – 3y = 4 and 3y – x = 4.

10th Math Part 2 Practice Set 1.2  Question 1.
Solve the following simultaneous equations by graphical method. Complete the following tables to get ordered pairs.

i. Plot the above ordered pairs on the same co-ordinate plane.
ii. Draw graphs of the equations.
iii. Note the co-ordinates of the point of intersection of the two graphs. Write solution of these equations. (Textbook pg. no. 8)
Solution:

The two lines intersect at point (-1, -2).
∴ (x , y) = (-1, -2) is the solution of the given simultaneous equations.

Mathematics Part 1 Standard 9 Practice Set 1.2 Answer  Question 1.
Solve the above equations by method of elimination. Check your solution with the solution obtained by graphical method. (Textbook pg. no. 8)
Solution:
The given simultaneous equations are
x – y = 1 …(i)
5x – 3y = 1 …(ii)
Multiplying equation (i) by 3, we get
3x – 3y = 3 …(iii)
Subtracting equation (iii) from (ii), we get

Substituting x = -1 in equation (i), we get
-1 -y= 1
∴ -y = 1 + 1
∴ -y = 2
∴ y = -2
∴ (x,y) = (-1, -2) is the solution of the given simultaneous equations.
∴ The solution obtained by elimination method and by graphical method is the same.

1.2 Maths Class 10 Question 2.
The following table contains the values of x and y co-ordinates for ordered pairs to draw the graph of 5x – 3y = 1.

i. Is it easy to plot these points?
ii. Which precaution is to be taken to find ordered pairs so that plotting of points becomes easy? (Textbook pg. no. 8)
Solution:
i. No

The above numbers are non-terminating and recurring decimals.
∴ It is not easy to plot the given points.

ii. While finding ordered pairs, numbers should be selected in such a way that the co-ordinates obtained will be integers.

Linear Equations ¡n Two Variables Class 10 Maths Question 3.
To solve simultaneous equations x + 2y = 4; 3x + 6y = 12 graphically, following are the ordered pairs.

Plotting the above ordered pairs, graph is drawn. Observe it and find answers of the following questions.

i. Are the graphs of both the equations different or same?
ii. What are the solutions of the two equations x + 2y = 4 and 3x + 6y = 12? How many solutions are possible?
iii. What are the relations between coefficients of x, coefficients of y and constant terms in both the equations?
iv. What conclusion can you draw when two equations are given but the graph is only one line? (Textbook pg. no. 9)
Solution:
i. The graphs of both the equations are same.
ii. The solutions of the given equations are (-2, 3), (0, 2), (1, 1.5), etc.
∴ Infinite solutions are possible.
iii. Ratio of coefficients of x = \(\frac { 1 }{ 3 } \)
Ratio of coefficients of y = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratios of coefficients of x = ratio of coefficients of y = ratio of the constant terms
iv. When two equations are given but the graph is only one line, the equations will have infinite solutions.

Class 10 Maths Part 1 Practice Set 1.2 Question 4.
Draw graphs of x- 2y = 4, 2x – 4y = 12 on the same co-ordinate plane. Observe it. Think of the relation between the coefficients of x, coefficients ofy and the constant terms and draw the inference. (Textbook pg. no. 10)
Solution:

ii. Ratio of coefficients of x =\(\frac { 1 }{ 2 } \)
Ratio of coefficients of y = \(\frac { -2 }{ -4 } \) = \(\frac { 1 }{ 2 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratio of coefficients of x = ratio of coefficients of y ratio of constant terms
iii. If ratio of coefficients of x = ratio of coefficients of y ≠ ratio of constant terms, then the graphs of the two equations will be parallel to each other.

Condition of consistency in Equations:

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.4 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.4 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
The number √2 is shown on a number line. Steps are given to show √3 on the number line using √2. Fill in the boxes properly and complete the activity.

The point Q on the number line shows the number ……….
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3
Solution:
The point Q on the number line shows the number √2
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

.. .[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.

Question 2.
Show the number √5 on the number line.
Solution:
Draw a number line and take a point Q at 2
such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴l(OR) = √5 units
…[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the number line and arc as C. The point C shows the number √5.

Question 3.
Show the number √7 on the number line.
Solution:
Draw a number line and take a point Q at 2 such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴ l(OR) = √5 units
… [Taking square root of both sides]
Draw an arc with centre O and radius OR.
Mark the point of intersection of the number line and arc as C. The point C shows the number √5.
Similarly, draw a line CD perpendicular to the number line through the point C such that l(CD) = 1 unit.
By Pythagoras theorem,
l(OD) = √6 units
The point E shows the number √6 .
Similarly, draw a line EP perpendicular to the number line through the point E such that l(EP) = 1 unit.
By Pythagoras theorem,
l(OP) = √7 units
The point F shows the number √7.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Practice Set 7.3 Geometry 10th Std Maths Part 2 Answers Chapter 7 Mensuration

Practice Set 7.3 Geometry Class 10 Question 1.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given : Radius (r) = 10 cm,
Measure of the arc (θ) = 54°
To find : Area of the sector.
Solution:
Area of sector = \(\frac{\theta}{360} \times \pi r^{2}\)
= \(\frac { 54 }{ 360 } \) × 3.14 × (10)²
= \(\frac { 3 }{ 20 } \) × 3.14 × 100
= 3 × 3.14 × 5
= 15 × 3.14
= 47.1 cm²
∴ The area of the sector is 47.1 cm².

Mensuration Practice Set 7.3 Question 2.
Measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
Given: Radius (r) = 18 cm,
Measure of the arc (θ) = 80°
To find: Length of the arc.
Solution:
Length of arc = \(\frac{\theta}{360} \times 2 \pi r\) × 2πr
= \(\frac { 8 }{ 360 } \) × 2 × 3.14 × 18
= \(\frac { 2 }{ 9 } \) × 2 × 3.14 × 18
= 2 × 2 × 3.14 × 2 = 25.12 cm
∴ The length of the arc is 25.12 cm.

Practice Set 7.3 Geometry Question 3.
Radius of a sector of a circle is 3.5 cm and length of its arc is 2.2 cm. Find the area of the sector.
Solution:
Given: Radius (r) = 3.5 cm,
length of arc (l) = 2.2 cm
To find: Area of the sector.
Solution:
Area of sector = \(\frac{l \times \mathrm{r}}{2}\)
= \(\frac{2.2 \times 3.5}{2}\)
= 1.1 × 3.5 = 3.85 cm²
∴ The area of the sector is 3.85 cm².

Question 4.
Radius of a circle is 10 cm. Area of a sector of the circle is 100 cm². Find the area of its corresponding major sector, (π = 3.14)
Given: Radius (r) = 10 cm,
area of minor sector =100 cm²
To find: Area of maj or sector.
Solution:
Area of circle = πr²
= 3.14 × (10)²
= 3.14 × 100 = 314 cm²
Now, area of major sector
= area of circle – area of minor sector
= 314 – 100
= 214 cm²
∴ The area of the corresponding major sector is 214 cm².

Question 5.
Area of a sector of a circle of radius 15 cm is 30 cm². Find the length of the arc of the sector.
Given: Radius (r) =15 cm,
area of sector = 30 cm²
To find: Length of the arc (l).
Solution:

∴ The length of the arc is 4 cm.

Practice Set 7.3 Question 6.
In the adjoining figure, radius of the circle is 7 cm and m (arc MBN) = 60°, find
i. Area of the circle.
ii. A(O-MBN).
iii. A(O-MCN).

Given: radius (r) = 7 cm,
m(arc MBN) = θ = 60°
Solution:
i. Area of circle = πr²
= \(\frac { 22 }{ 7 } \) × (7)²
= 22 × 7
= 154 cm²
∴ The area of the circle is 154 cm²

ii. Central angle (θ) = ∠MON = 60°
Area of sector = \(\frac{\theta}{360} \times \pi r^{2}\)
∴ A(O – MBN) = \(\frac { 60 }{ 360 } \) × \(\frac { 22 }{ 7 } \) × (7)²
\(\frac { 1 }{ 6 } \) × 22 × 7
= 25.67 cm²
= 25.7 cm²
∴ A(O-MBN) = 25.7 cm²

iii. Area of major sector = area of circle – area of minor sector
∴ A(O-MCN) = Area of circle – A(O-MBN)
= 154 – 25.7
∴ A(O-MCN) = 128.3 cm²

Question 7.
In the adjoining figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm. Find A(P-ABC).
Given: Radius (r) = 3.4 cm,
perimeter of sector 12.8 cm
To find: A(P-ABC)

Solution:
Perimeter of sector
= Iength of arc ABC + AP + CP

∴ 12.8 = l + 3.4 + 3.4
∴ 12.8 = l + 6.8
∴ l = 12.8 – 6.8 = 6cm

∴ A(P-ABC) = 10.2 cm²

7.3 Class 10 Question 8.
In the adjoining figure, O is the centre of the sector. ∠ROQ = ∠MON = 60°. OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and (π = \(\frac { 22 }{ 7 } \))

Given: ∠ROQ = ∠MON = 60°,
radius (r) = OR = 7 cm, radius (R) = OM = 21 cm
To find: Lengths of arc RXQ and arc MYN.
Solution:
i. Length of arc RXQ = \(\frac{\theta}{360} \times 2 \pi r\)
= \(\frac { 60 }{ 2 } \) × 2 × \(\frac { 22 }{ 7 } \) × 7
= \(\frac { 1 }{ 6 } \) × 2 × 22
= 7.33 cm
ii. Length of arc MYN = \(\frac{\theta}{360} \times 2 \pi R\)
= \(\frac { 60 }{ 2 } \) × 2 × \(\frac { 22 }{ 7 } \) × 21
= \(\frac { 1 }{ 6 } \) × 2 × 22 × 3
= 22 cm
∴ The lengths of arc RXQ and arc MYN are 7.33 cm and 22 cm respectively.

Question 9.
In the adjoining figure, if A(P-ABC) = 154 cm², radius of the circle is 14 cm, find
i. ∠APC,
ii. l(arc ABC).

Given: A(P – ABC) = 154 cm²,
radius (r) = 14 cm
Solution:
i. Let ∠APC = θ

Std 10 Geometry Mensuration Question 10.
Radius of a sector of a circle is 7 cm. If measure of arc of the sector is
i. 30°
ii. 210°
iii. three right angles, find the area of the sector in each case.
Given: Radius (r) = 7 cm
To find: Area of the sector.
Solution:
i. Measure of the arc (θ) = 30°

∴ Area of the sector is 12.83 cm².
ii. Measure of the arc (θ) = 210°

∴ Area of the sector is 89.83 cm².
iii. Measure of the arc (θ) = 3 right angle
= 3 × 90° = 270°

∴ Area of the sector is 115.50 cm².

Mensuration Practice Question 11.
The area of a minor sector of a circle is 3.85 cm² and the measure of its central angle is 36°. Find the radius of the circle.
Given: Area of minor sector = 3.85 cm²,
central angle (θ) = 36°
To find: Radius of the circle (r).
Solution:
Area of minor sector = \(\frac{\theta}{360} \times \pi r^{2}\)

∴ The radius of the circle ¡s 3.5 cm.

10th Geometry Practice Set 7.3 Question 12.
In the given figure, ꠸PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y and z.

Given: In rectangle PQRS,
PQ = 14 cm, QR = 21 cm
To find: Areas of the parts x, y and z.
Solution:

∠Q = ∠R = θ = 90° …[Angles of a rectangle]

For the sector (Q – PA),
PQ = QA …[Radii of the same circle]
∴ QA = 14 cm
Now, QR = QA + AR … [Q – A – R]
∴ 21 = 14 + AR
∴ AR = 7 cm

Area of rectangle = length × breadth
area of ꠸PQRS = PQ × QR
= 14 × 21
= 294 cm²
Area of part z = area of ꠸PQRS
– area of part x – area of part y
= 294 – 154 – 38.5
= 101.5 cm²
∴ The area of part x is 154 cm², the area of part y is 38,5 cm² and the area of part z is 101.5 cm².

Question 13.
∆ALMN is an equilat triangle. LM = 14 cm. As shown in figure, three sectors are drawn with vertices as centres and radius 7 cm. Find,

i. A (∆ LMN).
ii. Area of any one of the sectors.
iii. Total area of all the three sectors.
iv. Area of the shaded region. (\(\sqrt { 3 }\) = 1.732 )
Given: In equilateral triangle LMN, LM =14 cm,
radius of sectors (r) = 7 cm
Solution:
i. ∆LMN is an equilateral triangle.

ii. Central angle (θ) = 60° …[Angle of an equilateral triangle]

∴ Area of one sector = 25.67 cm²
iii. Total area of all three sectors
= 3 × Area of one sector
= 3 × 25.67
= 77.01 cm²
∴ Total area of all three sectors = 77.01 cm²
iv. Area of shaded region
= A(∆LMN) – total area of all three sectors
= 84.87 – 77.01
= 7.86 cm²
∴ Area of shaded region = 7.86 cm

Maharashtra Board Class 10 Maths Chapter 7 Mensuration Intext Questions and Activities

Mensuration Practice Set 7.3 Question 1.
Complete the following table with the help of given figure. (Textbook pg. no. 149)


Solution:

Question 2.
Observe the figures below. Radii of all circles are equal. Observe the areas of the shaded regions and complete the following table. (Textbook pg. no. 150)

Solution:

Thus, if measure of an arc of a circle is θ, then
Area of sector (A) = \(\frac{\theta}{360}\) × Area of circle
∴ Area of sector (A) = \(\frac{\theta}{360}\) × πr²

Mensuration In Maths Question 3.
In the following figures, radii of all circles are equal. Observe the length of arc in each figure and complete the table. (Textbook pg. no. 151)

Solution:

Thus, if the measure of an arc of a circle is 0, then
Length of arc (l) = \(\frac{\theta}{360}\) × circumference of circle
∴ Length of arc (l) = \(\frac{\theta}{360}\) × 2πr

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Practice Set 7.2 Geometry 10th Std Maths Part 2 Answers Chapter 7 Mensuration

Question 1.
The radii of two circular ends of frustum shaped bucket are 14 cm and 7 cm. Height of the bucket is 30 cm. How many litres of water it can hold? (1 litre = 1000 cm³)
Given: Radii (r₁) = 14 cm, and (r₂) = 7 cm,
height (h) = 30 cm
To find: Amount of water the bucket can hold.
Solution:
Volume of frustum = \(\frac { 1 }{ 3 } \) πh (r₁² + r₂² + r₁ × r₂)

∴ The bucket can hold 10.78 litres of water.

Question 2.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its
i. curved surface area,
ii. total surface area,
iii. volume, (π = 3.14)
Given: Radii (r₁) = 14 cm, and (r₂) = 6 cm,
height (h) = 6 cm
Solution:

i. Curved surface area of frustum
= πl (r₁ + r₂)
= 3.14 × 10(14 + 6)
= 3.14 × 10 × 20 = 628 cm²
∴ The curved surface area of the frustum is 628 cm².

ii. Total surface area of frustum
= πl (r₁+ r₂) + πr₁² + πr₂²
= 628 + 3.14 × (14)² + 3.14 × (6)²
= 628 + 3.14 × 196 + 3.14 × 36
= 628 + 3.14(196 + 36)
= 628 + 3.14 × 232
= 628 + 728.48
= 1356.48 cm²
∴ The total surface area of the frustum is 1356.48 cm².

iii. Volume of frustum
= \(\frac { 1 }{ 3 } \) πth(r₁² +r₂² + r₁ × r₂)
= \(\frac { 1 }{ 3 } \) × 3.14 × 6(14² + 6² + 14 × 6)
= 3.14 × 2(196 + 36 + 84)
= 3.14 × 2 × 316
= 1984.48 cm³
∴ The volume of the frustum is 1984.48 cm³.

Question 3.
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of frustum, complete the following activity. (π = \(\frac { 22 }{ 7 } \))
Solution:
Circumference1 = 27πr₁ = 132 cm

Curved surface area of frustum = π (r₁ + r₂) l
= π (21 + 14) × 25
=π × 35 × 35
= \(\frac { 22 }{ 7 } \) × 35 × 25
= 2750 cm²