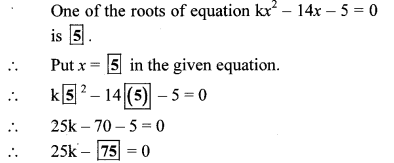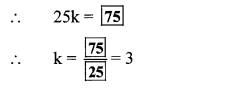Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.
Practice Set 2.1 Algebra 10th Std Maths Part 1 Answers Chapter 2 Quadratic Equations
Question 1.
Write any two quadratic equations.
Solution:
i. y2 – 7y + 12 = 0
ii. x2 – 8 = 0
Question 2.
Decide which of the following are quadratic
i. x2 – 7y + 2 = 0
ii. y2 = 5y – 10
iii. y2 + \(\frac { 1 }{ y } \) = 2
iv. x + \(\frac { 1 }{ x } \) = -2
v. (m + 2) (m – 5) = 03
vi. m3 + 3m2 – 2 = 3m3
Solution:
i. The given equation is x2 + 5x – 2 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 5, c = -2 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
ii. The given equation is
y2 = 5y – 10
∴ y2 – 5y + 10 = 0
Here, y is the only variable and maximum index of the variable is 2.
a = 1, b = -5, c = 10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
iii. The given equation is
y2 + \(\frac { 1 }{ y } \) = 2
∴ y3 + 1 = 2y …[Multiplying both sides by y]
∴ y3 – 2y + 1 = 0
Here, y is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.
iv. The given equation is
x + \(\frac { 1 }{ x } \) = -2
∴ x2 + 1 = -2x …[Multiplying both sides by x]
∴ x2 + 2x+ 1 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 2, c = 1 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
v. The given equation is
(m + 2) (m – 5) = 0
∴ m(m – 5) + 2(m – 5) = 0
∴ m2 – 5m + 2m – 10 = 0
∴ m2 – 3m – 10 = 0
Here, m is the only variable and maximum index of the variable is 2.
a = 1, b = -3, c = -10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
vi. The given equation is
m3 + 3m2 – 2 = 3m3
∴ 3m3 – m3 – 3m2 + 2 = 0
∴ 2m3 – 3m2 + 2 = 0
Here, m is the only variable and maximum
index of the variable is not 2.
∴ The given equation is not a quadratic equation.
Question 3.
Write the following equations in the form ax2 + bx + c = 0, then write the values of a, b, c for each equation.
i. 2y = 10 – y2
ii. (x – 1)2 = 2x + 3
iii. x2 + 5x = – (3 – x)
iv. 3m2 = 2m2 – 9
v. P (3 + 6p) = – 5
vi. x2 – 9 = 13
Solution:
i. 2y – 10 – y2
∴ y2 + 2y – 10 = 0
Comparing the above equation with
ay2 + by + c = 0, we get
a = 1, b = 2, c = -10
ii. (x – 1)2 = 2x + 3
∴ x2 – 2x + 12x + 3
x2 – 2x + 1 – 2x – 30
∴ x2 – 4x – 2 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = -4, c = -2
iii. x2 + 5x = – (3 – x)
∴ x2 + 5x = -3 + x
∴ x2 + 5x – x + 3 = 0
∴ x2 + 4x + 3 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = 4, c = 3
iv. 3m2 = 2m2 – 9
∴ 3m2 – 2m2 + 9 = 0
∴ m2 + 9 = 0
∴ m2 + 0m + 9 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 1, b = 0, c = 9
v. p (3 + 6p) = – 5
∴ 3p + 6p2 = -5
∴ 6p2 + 3p + 5 = 0
Comparing the above equation with
ap2 + bp + c = 0, we get
a = 6, b = 3, c = 5
vi. x2 – 9 = 13
∴ x2 – 9 – 13 = 0
∴ x2 – 22 = 0
∴ x2 + 0x – 22 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = 0, c = -22
Question 4.
Determine whether the values given against each of the quadratic equation are the roots of the equation.
i. x2 + 4x – 5 = 0; x = 1,-1
ii. 2m2 – 5m = 0; m = 2, \(\frac { 5 }{ 2 } \)
Solution:
i. The given equation is
x2 + 4x – 5 = 0 …(i)
Putting x = 1 in L.H.S. of equation (i), we get
L.H.S. = (1)2 + 4(1) – 5 = 1 + 4 – 5 = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation.
Putting x = -1 in L.H.S. of equation (i), we get
L.H.S. = (-1)2 + 4(-1) – 5 = 1 – 4 – 5 = -8
∴ LH.S. ≠ R.H.S.
∴ x = -1 ¡s not the root of the given quadratic equation.
ii. The given equation is
2m2 – 5m = 0 …(i)
Putting m = 2 in L.H.S. of equation (i), we get
L.H.S. = 2(2)2 – 5(2) = 2(4) -10 = 8 – 10 = -2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
Putting m = \(\frac { 5 }{ 2 } \) in L.H.S. of equation (i), we get
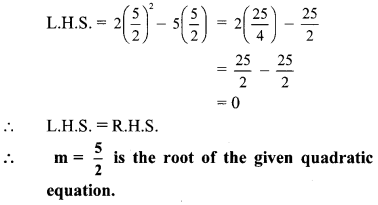
Question 5.
Find k if x = 3 is a root of equation kx2 – 10x + 3 = 0.
Solution:
x = 3 is the root of the equation kx2 – 10x + 3 = 0.
Putting x = 3 in the given equation, we get
k(3)2 – 10(3) + 3 = 0
∴ 9k – 30 +3 = 0
∴ 9k – 27 = 0
∴ 9k = 27
∴ k = \(\frac { 27 }{ 9 } \)
∴ k = 3
Question 6.
One of the roots of equation 5m2 + 2m + k = 0 is \(\frac { -7 }{ 5 } \) Complete the following activity to find the value of ‘k’.
Solution:

Question 1.
x2 + 3x – 5, 3x2 – 5x, 5x2; Write the polynomials In the index form. Observe the coefficients and fill in the boxes. (Textbook p. no. 31)
Answer:
Index form of the given polynomials:
x2 + 3x – 5, 3x2 – 5x + 0, 5x2 + 0x + 0
i. Coefficients of x2 are [1], [3] and [5] respectively, and these coefficients are non zero.
ii. Coefficients of x are 3, [-5] and [0] respectively.
iii. Constant terms are [-5], [0] and [0] respectively.
Here, constant terms of second and third polynomial is zero.
Question 2.
Complete the following table (Textbook p. no. 31)

Answer:

Question 3.
Decide which of the following are quadratic equations? (Textbook pg. no. 31)
i. 9y2 + 5 = 0
ii. m3 – 5m2 + 4 = 0
iii. (l + 2)(l – 5) = 0
Solution:
i. In the equation 9y2 + 5 = 0, [y] is the only variable and maximum index of the variable is [2].
∴ It [is] a quadratic equation.
ii. In the equation m3 – 5m2 + 4 = 0, [m] is the only variable and maximum index of the variable is not 2.
∴ It [is not] a quadratic equation.
iii. (l + 2)(l – 5) = 0
∴ l(l – 5) + 2(l – 5) = 0
∴ l2 – 5l + 2l – 10 = 0
∴ l2 – 3l – 10 = 0.
In this equation [l] is the only variable and maximum index of the variable is [2]
∴ it [is] a quadratic equation.
Question 4.
If x = 5 is a root of equation kx2 – 14x – 5 = 0, then find the value of k by completing the following activity. (Textbook pg, no. 33)
Solution: