Prasanna

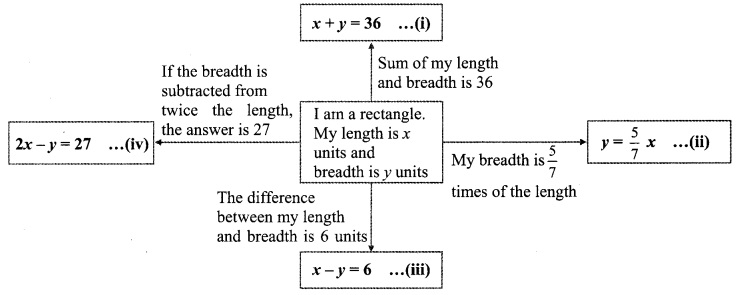
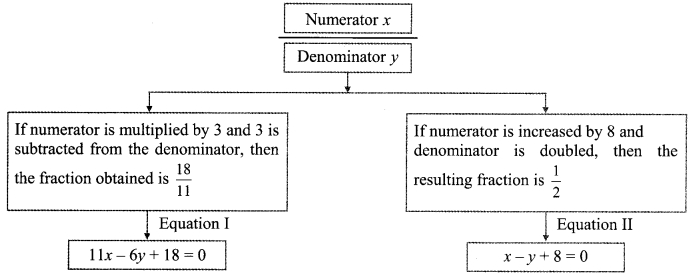
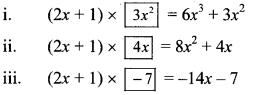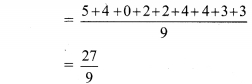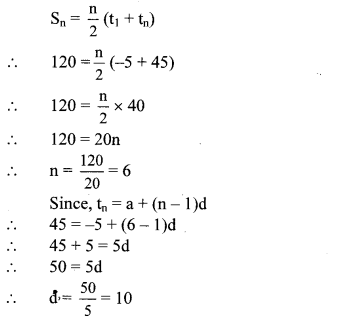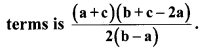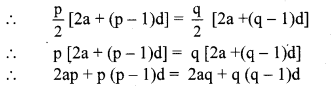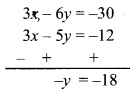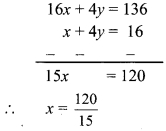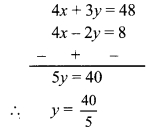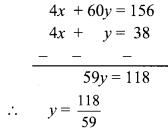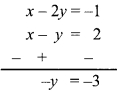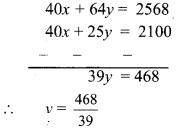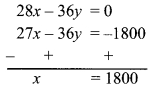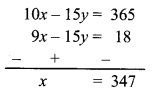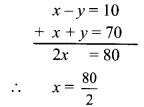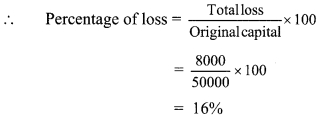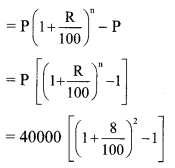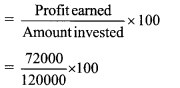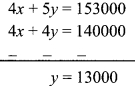Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Miscellaneous Exercise 2 8th Std Maths Answers Solutions.

Miscellaneous Exercise 2 8th Std Maths Answers

Question 1.
Questions and their alternative answers are given. Choose the correct alternative answer.
i. Find the circumference of a circle whose area is 1386 cm²? [Chapter 15]
(A) 132 cm²
(B) 132 cm
(C) 42 cm
(D) 21 cm²
Solution:
(B) 132 cm

Hint:
i. Area of the circle = πr²
1386 = \(\frac { 22 }{ 7 }\) x r²
r² = 1386 x \(\frac { 7 }{ 22 }\)
= 63 x 7
= 441
r = √441 … [Taking square root of both sides]
= 21 cm
Circumference of the circle = 2πr
= 2 x \(\frac { 22 }{ 7 }\) x 21
= 132 cm

ii. The side of a cube is 4 m. If it is doubled, how many times will be the volume of the new cube, as compared with the original cube? [Chapter 16]
(A) Two times
(B) Three times
(C) Four times
(D) Eight times
Solution:
(D) Eight times

Hint:
ii. Original volume = (4)³ = 64 cu.m
New side = 8 m
∴ New volume = (8)² = 512 cu.m
Now, \(\frac{\text { new volume }}{\text { original volume }}=\frac{512}{64}\) = 8
original volume 64
∴ volume of new cube will increase 8 times as compared to the volume of original cube.

Question 2.
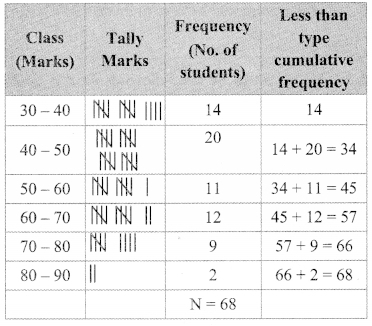
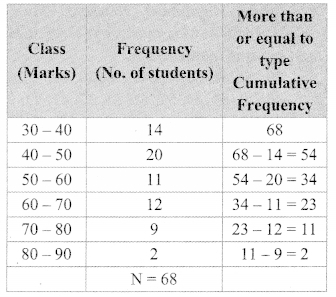
Pranalee was practicing for a 100 m running race. She ran 100 m distance 20 times. The time required, in seconds, for each attempt was as follows. [Chapter 11]
18, 17, 17, 16,15, 16, 15, 14,16, 15, 15, 17, 15, 16,15, 17, 16, 15, 14,15
Find the mean of the time taken for running.
Solution:

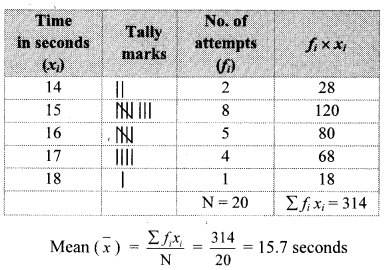
∴ The mean of the time taken for running 100 m race is 15.7 seconds.

Question 3.
∆DEF and ∆LMN are congruent in the correspondence EDF ↔ LMN. Write the pairs of congruent sides and congruent angles in the correspondence. [Chapter 13]
Solution:

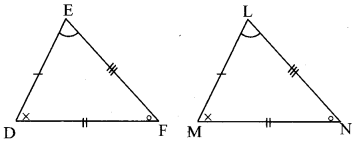
∆EDF ≅ ∆LMN
∴side ED ≅ side LM
side DF ≅ side MN
side EF ≅ side LN
∠E ≅∠L
∠D ≅∠M
∠F ≅∠N

Question 4.
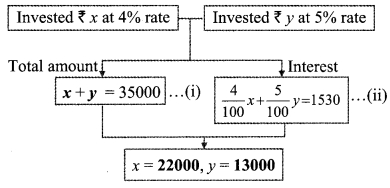
The cost of a machine is Rs 2,50,000. It depreciates at the rate of 4% per annum. Find the cost of the machine after three years. [Chapter 14]
Solution:
Here, P = Cost of the machine = Rs 2,50,000
R = Rate of depreciation = 4%
N = 3 Years
A = Depreciated price of the machine

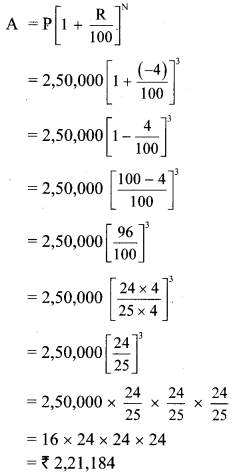
∴The cost of the machine after three years will be Rs 2,21,184.

Question 5.
In ☐ABCD, side AB || side DC, seg AE ⊥ seg DC. If l(AB) = 9 cm, l(AE) = 10 cm, A(☐ABCD) = 115 cm² , find l(DC). [Chapter 15]
Solution:
Given, side AB || side DC.
∴ ☐ABCD is a trapezium.

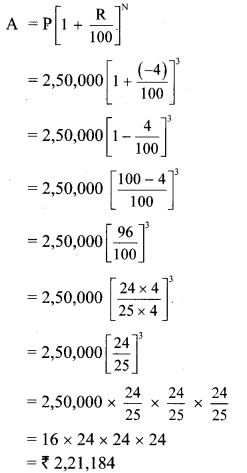
Given, l(AB) = 9 cm, l(AE) = 10 cm,
A(☐ABCD) = 115 cm²
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC) x l(AE)]
∴ 115 = \(\frac { 1 }{ 2 }\) x [9 + l(DC)] x 10
∴ \(\frac { 115 \times 2 }{ 10 }\) = 9 + l(DC)
∴ 23 = 9 + l(DC)
∴ l(DC) = 23 – 9
∴ l(DC) = 14cm

Question 6.
The diameter and height of a cylindrical tank is 1.75 m and 3.2 m respectively. How much is the capacity of tank in litre?
[π = \(\frac { 22 }{ 7 }\)] [Chapter 16]
Solution:
Given: For cylindrical tank:
diameter (d) = 1.75 m, height (h) = 3.2 m
To Find: Capacity of tank in litre
diameter (d) = 1.75 m
= 1.75 x 100
….[∵ 1 m = 100cm]
= 175 cm
∴ radius (r) = \(=\frac{\mathrm{d}}{2}=\frac{175}{2}\) cm
h = 3.2 cm
= 3.2 x 100
= 320 cm
Capacity of tank = Volume of the cylindrical tank
= πr²h

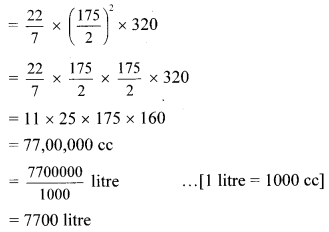
∴ The capacity of the tank is 7700 litre.

Question 7.
The length of a chord of a circle is 16.8 cm, radius is 9.1 cm. Find its distance from the centre. [Chapter 17]
Solution:

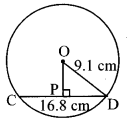
Let CD be the chord of the Circle with centre O.
Draw seg OP ⊥ chord CD
∴l(PD) = \(\frac { 1 }{ 2 }\) l(CD)
…[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(PD) = \(\frac { 1 }{ 2 }\) x 16.8 …[l(CD) = 16.8cm]
∴l(PD) = 8.4 cm …(i)
∴In ∆OPD, m∠OPD = 90°
∴[l(OD)]² = [l(OP)]² + [l(PD)]² …..[Pythagoras theorem]
∴(9.1)² = [l(OP)]² + (8.4)² … [From (i) and l(OD) = 9.1 cm]
∴(9.1)² – (8.4)² = [l(OP)]²
∴(9.1 + 8.4) (9.1 – 8.4) = [l(OP)]²
…[∵ a² – b² = (a + b) (a – b)]
∴17.5 x (0.7) = [l(OP)]²
∴12.25 = [l(OP)]²
i.e., [l(OP)]² = 12.25
∴l(OP) = √12.25
…[Taking square root of both sides]
∴l(OP) = 3.5 cm
∴The distance of the chord from the centre is 3.5 cm.

Question 8.
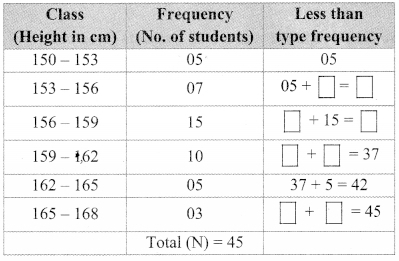
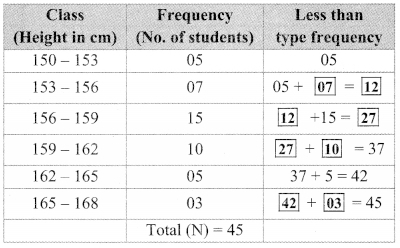
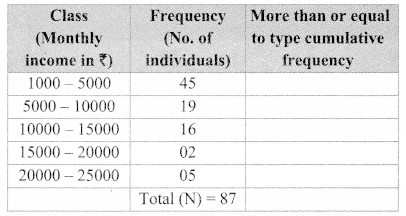
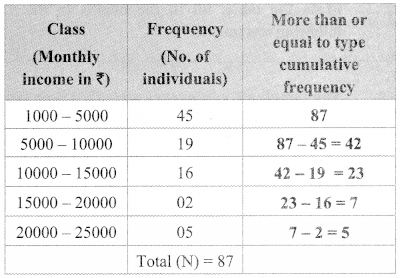
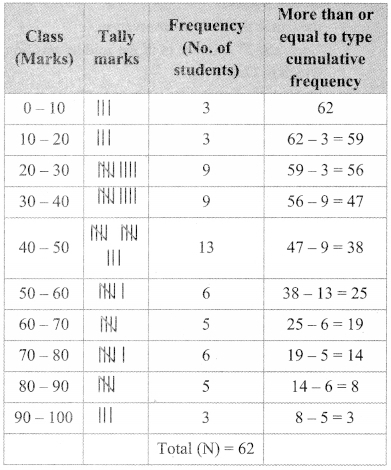
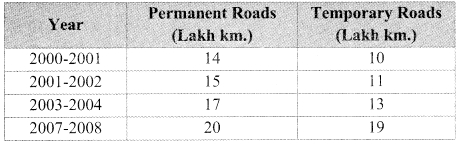
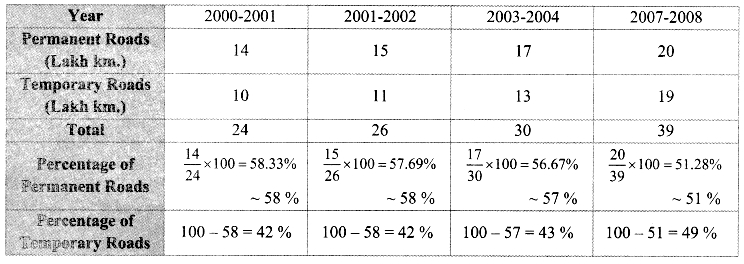
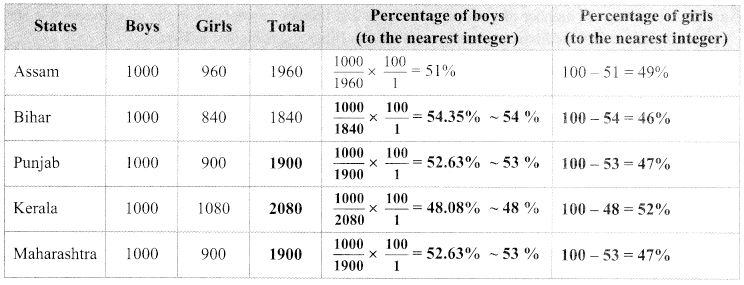
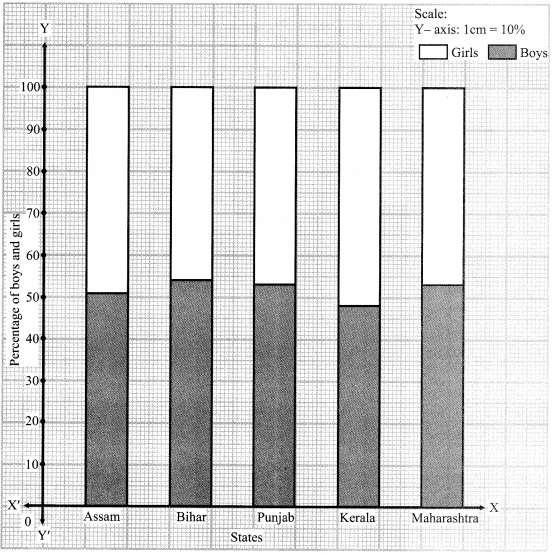
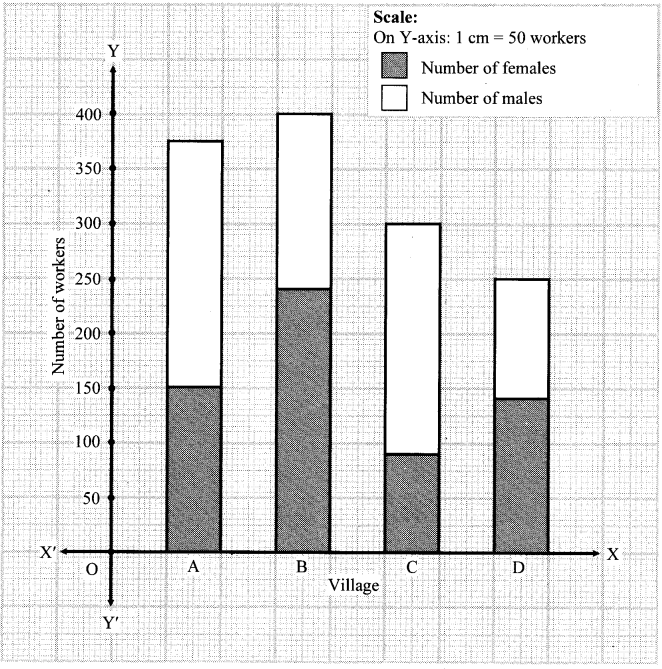
The following tables shows the number of male and female workers, under employment guarantee scheme, in villages A, B, C and D.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110

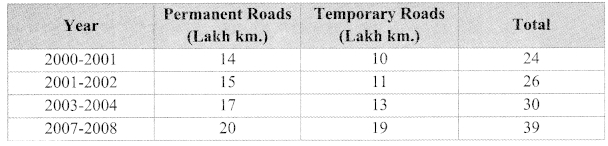
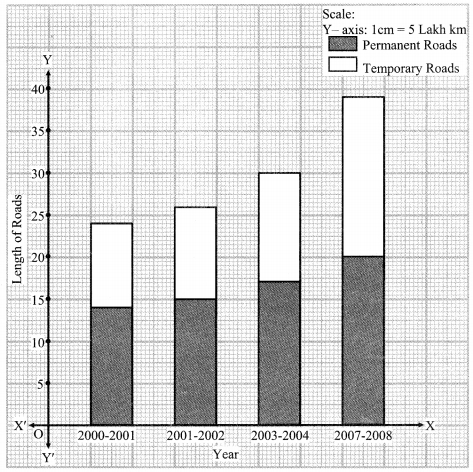
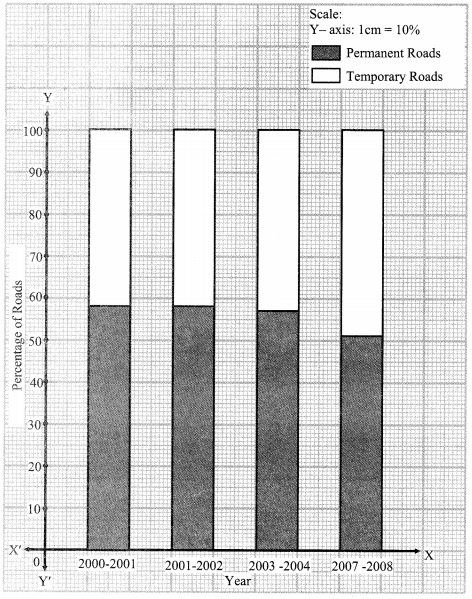
i. Show the information by a sub-divided bar-diagram.
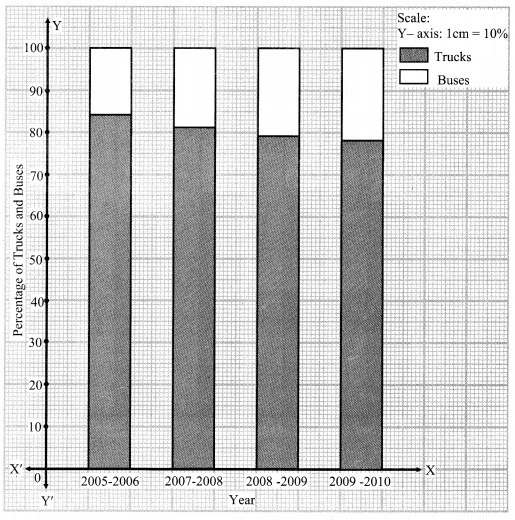
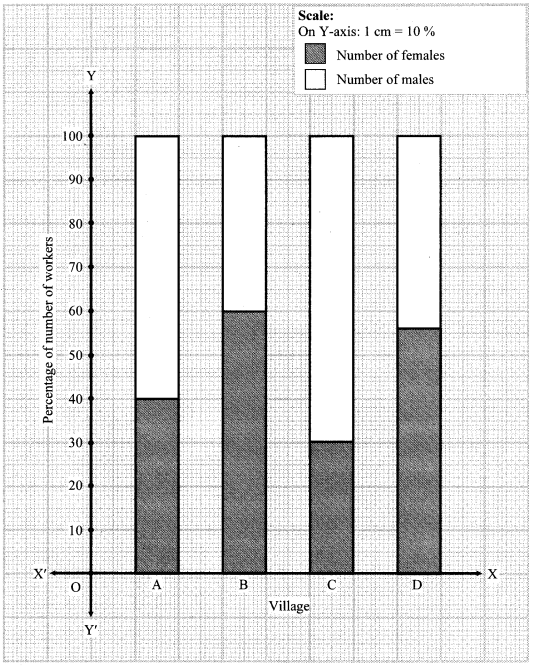
ii. Show the information by a percentage bar diagram. [Chapter 11]
Solution:
i.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250

ii.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250
Percentage of females	40%	60%	30%	56%
Percentage of males	60%	40%	70%	44%

Question 9.
Solve the following equations.
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
iii. 5(1 – 2x) = 9(1 -x)
[Chapter 12]
Solution:
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
∴ 17x + 68 + 8x + 48 = 11x + 55 + 15x + 45
∴ 17x + 8x + 68 + 48 = 11x + 15x + 55 + 45
∴ 25x + 116 = 26x + 100
∴ 25x + 116 – 116 = 26x + 100 – 116
… [Subtracting 116 from both the sides]
∴ 25x = 26x – 16
∴ 25x – 26x = 26x – 16 – 26x
… [Subtracting 26x from both the sides]
∴ -x = -16
∴ \(\frac{-x}{-1}=\frac{-16}{-1}\)
∴ x = 16

ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{3 y \times 2}{2 \times 2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4} \times 4+\frac{y+4}{4} \times 4=5 \times 4-\frac{y-2}{4} \times 4\)
……[Multiplying both the sides by 4]
∴ 6y + y + 4 = 20 – (y – 2)
∴ 7y + 4 = 20 – y + 2
∴ 7y + 4 = 22 – y
∴ 7y + 4 – 4 = 22 – y – 4
…..[Subtracting 4 from both the sides]
∴ 7y = 18 – y
∴ 7y + y = 18 – y + y
…[Adding y on both the sides]
∴ 8y = 18
∴ \(\frac{8 y}{8}=\frac{18}{8}\) … [Dividing both the sides by 8]
∴ \(y=\frac { 9 }{ 4 }\)

iii. 5(1 – 2x) = 9(1 – x)
∴ 5 – 10x = 9 – 9x
∴ 5 – 10x – 5 = 9 – 9x – 5
….[Subtracting 5 from both the sides]
∴ -10x = 4 – 9x
∴ -10x + 9x = 4 – 9x + 9x
… [Adding 9x on both the sides]
∴ -x = 4
∴ -x x (- 1) = 4 x (- 1)
… [Multiplying both the sides by – 1]
∴ x = – 4

Question 10.
Complete the activity according to the given steps.
i. Draw rhombus ABCD. Draw diagonal AC.
ii. Show the congruent parts in the figure by identical marks.
iii. State by which, test and in which correspondence ∆ADC and ∆ABC are congruent.
iv. Give reason to show ∠DCA ≅ ∠BCA, and ∠DAC ≅ ∠BAC
v. State which property of a rhombus is revealed from the above steps. [Chapter 13]
Solution:
a.

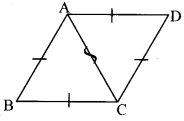
b. In ∆ADC and ∆ABC,
side AD ≅ side AB …..[Sides of a rhombus]
side DC ≅ side BC …..[Sides of a rhombus]
side AC ≅ side AC … [Common side]
∆ADC ≅ ∆ABC … [By SSS test]
∠DCA ≅ ∠BCA …[Corresponding angles of congruent triangles]
∠DAC ≅ ∠BAC …[Corresponding angles of congruent triangles]
From the above steps, property of rhombus revealed is ‘diagonal of a rhombus bisect the opposite angles’.

Question 11.
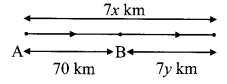
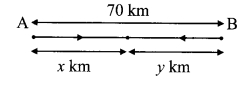
The shape of a farm is a quadrilateral. Measurements taken of the farm, by naming its corners as P, Q, R, S in order are as follows. l(PQ) = 170 m,
l(QR) = 250 m, l(RS) = 100 m, l(PS) = 240 m, l(PR) = 260 m.
Find the area of the field in hectare (1 hectare = 10,000 sq.m). [Chapter 15]
Solution:

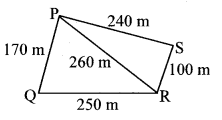
Area of the field = A(∆PQR) + A(∆PSR)
In ∆PQR, a = 170 m, b = 250 m, c = 260 m
Semiperimeter of ∆PQR = s

Area of the field = A(∆PQR) + A(∆PSR)
= 20400 + 12000
= 32400 sq.m
= \(\frac { 32400 }{ 10000 }\)
…[1 hectare = 10,000 sq.m]
= 3.24 hectares
∴ The area of the field is 3.24 hectares.

Question 12.
In a library, 50% of total number of books is of Marathi. The books of English are \(\frac { 1 }{ 3 }\) of Marathi books. The books on Mathematics are 25% of the English books. The remaining 560 books are of other subjects. What is the total number of books in the library? [Chapter 12]
Solution:
Let the total number of books in the library be x
50% of total number of books is of Marathi.
Number of Marathi books = 50% of x
= \(\frac { 50 }{ 100 }x\)
= \(\frac { x }{ 2 }\)
The books of English are \(\frac { 1 }{ 3 }\) of Marathi books.
Number of books of English = \(\frac{1}{3} \times \frac{x}{2}\)
= \(\frac { x }{ 6 }\)
The books on Mathematics are 25% of the English books.
Number of books of Mathematics
= 25% of \(\frac { x }{ 6 }\)
= \(\frac{25}{100} \times \frac{x}{6}\)
= \(\frac { x }{ 24 }\)
Since, there are 560 books of other subjects, the total number of books in the library are


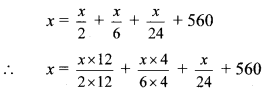
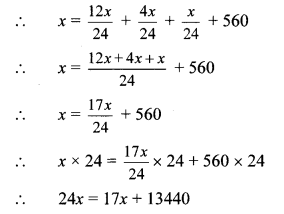
∴ 24x – 17x = 17x + 13440 – 17x
∴ 7x = 13440
∴ \(\frac{7 x}{7}=\frac{13440}{7}\)
∴ x = 1920
∴ The total number of books in the library are 1920.

Question 13.
Divide the polynomial (6x³ + 11x² – 10x – 7) by the binomial (2x + 1). Write the quotient and the remainder. [Chapter 10]
Solution:

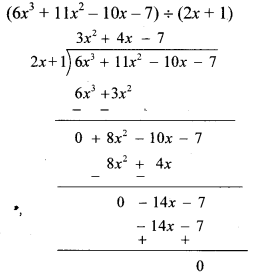
∴ Quotient = 3x² + 4x – 7,
remainder = 0
Explanation:

Maharashtra Board Class 8 Maths Solutions

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 7 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Problem Set 7 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Write the correct alternative answer for each of the following questions.

i. Which of the following data is not primary ?
(A) By visiting a certain class, gathering information about attendance of students.
(B) By actual visit to homes, to find number of family members.
(C) To get information regarding plantation of soyabean done by each farmer from the village Talathi.
(D) Review the cleanliness status of canals by actually visiting them.
Answer:
(C) To get information regarding plantation of soyabean done by each farmer from the village Talathi.

ii. What is the upper class limit for the class 25 – 35?
(A) 25
(B) 35
(C) 60
(D) 30
Answer:
(B) 35

iii. What is the class-mark of class 25 – 35?
(A) 25
(B) 35
(C) 60
(D) 30
Answer:
(D) 30

iv. If the classes are 0 – 10, 10 – 20, 20 – 30, …, then in which class should the observation 10 be included?
(A) 0 – 10
(B) 10 – 20
(C) 0 – 10 and 10-20 in these 2 classes
(D) 20 – 30
Answer:
(B) 10 – 20

v. If \(\overline { x }\) is the mean of x₁, x₂, ……. , x_n and \(\overline { y }\) is the mean of y₁, y₂, ….. y_n and \(\overline { z }\) is the mean of x₁,x₂, …… , x_n , y₁, y₂, …. y_n , then z = ?

Answer:
x₁, x₂, x₃, ……. , x_n
∴ \(\overline{x}=\frac{\sum x}{\mathrm{n}}\)
∴ n\(\overline{x}\) = ∑x
Similarly, n\(\overline{y}\) = ∑y
Now,

\(\text { (A) } \frac{\overline{x}+\overline{y}}{2}\)

vi. The mean of five numbers is 50, out of which mean of 4 numbers is 46, find the 5th number.
(A) 4
(B) 20
(C) 434
(D) 66
Answer:
5^th number = Sum of five numbers – Sum of four numbers
= (5 x 50) – (4 x 46)
= 250 – 184
= 66
(D) 66

vii. Mean of 100 observations is 40. The 9th observation is 30. If this is replaced by 70 keeping all other observations same, find the new mean.
(A) 40.6
(B) 40.4
(C) 40.3
(D) 40.7
Answer:
New mean = \(\frac { 4000-30+70 }{ 100 }\)
= 40.4
(B) 40.4

viii. What is the mode of 19, 19, 15, 20, 25, 15, 20, 15?
(A) 15
(B) 20
(C) 19
(D) 25
Answer:
(A) 15

ix. What is the median of 7, 10, 7, 5, 9, 10 ?
(A) 7
(B) 9
(C) 8
(D) 10
Answer:
(C) 8

x. From following table, what is the cumulative frequency of less than type for the class 30 – 40?

(A) 13
(B) 15
(C) 35
(D) 22
Answer:
Cumulative frequency of less than type for the class 30 – 40 = 7 + 3 + 12 + 13 = 35
(C) 35

Question 2.
The mean salary of 20 workers is ₹10,250. If the salary of office superintendent is added, the mean will increase by ₹ 750. Find the salary of the office superintendent.
Solution:
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations
The mean salary of 20 workers is ₹ 10,250.
∴ Sum of the salaries of 20 workers
= 20 x 10,250
= ₹ 2,05,000 …(i)
If the superintendent’s salary is added, then mean increases by 750
new mean = 10, 250 + 750 = 11,000
Total number of people after adding superintendent = 20 + 1 = 21
∴ Sum of the salaries including the superintendent’s salary = 21 x 11,000 = ₹ 2,31,000 …(ii)
∴ Superintendent salary = sum of the salaries including superintendent’s salary – sum of salaries of 20 workers
= 2, 31,00 – 2,05,000 …[From (i) and (ii)]
= 26,000
∴ The salary of the office superintendent is ₹ 26,000.

Question 3.
The mean of nine numbers is 77. If one more number is added to it, then the mean increases by 5. Find the number added in the data.
Solution:
∴ \( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations mean of nine numbers is 77
∴ sum of 9 numbers = 11 x 9 = 693 …(i)
If one more number is added, then mean increases by 5
mean of 10 numbers = 77 + 5 = 82
∴ sum of the 10 numbers = 82 x 10 = 820 …(ii)
∴ Number added = sum of the 10 numbers – sum of the 9 numbers = 820 – 693 … [From (i) and (ii)]
= 127
∴ The number added in the data is 127.

Question 4.
The monthly maximum temperature of a city is given in degree Celsius in the following data. By taking suitable classes, prepare the grouped frequency distribution table
29.2, 29.0, 28.1, 28.5, 32.9, 29.2, 34.2, 36.8, 32.0, 31.0, 30.5, 30.0, 33, 32.5, 35.5, 34.0, 32.9, 31.5, 30.3, 31.4, 30.3, 34.7, 35.0, 32.5, 33.5.29.0. 29.5.29.9.33.2.30.2
From the table, answer the following questions.
i. For how many days the maximum temperature was less than 34°C?
ii. For how many days the maximum temperature was 34°C or more than 34°C?
Solution:

i. Number of days for which the maximum temperature was less than 34°C
= 8 + 8 + 8 = 24
ii. Number of days for which the maximum temperature was 34°C or more than 34°C
= 5 + 1 = 6

Question 5.
If the mean of the following data is 20.2, then find the value of p.

Solution:

∴ 20.2 (30 + p) = 610 + 20p
∴ 606 + 20.2p = 610 + 20p
∴ 20.2p – 20p = 610 – 606
∴ 0.2p = 4
∴ p = \(\frac { 4 }{ 0.2 }\) = \(\frac { 40 }{ 2 }\) = 20
∴ p = 20

Question 6.
There are 68 students of 9th standard from Model Highschool, Nandpur. They have scored following marks out of 80, in written exam of mathematics.
70, 50, 60, 66, 45, 46, 38, 30, 40, 47, 56, 68,
80, 79, 39, 43, 57, 61, 51, 32, 42, 43, 75, 43,
36, 37, 61, 71, 32, 40, 45, 32, 36, 42, 43, 55,
56, 62, 66, 72, 73, 78, 36, 46, 47, 52, 68, 78,
80, 49, 59, 69, 65, 35, 46, 56, 57, 60, 36, 37,
45, 42, 70, 37,45, 66, 56, 47
By taking classes 30 – 40, 40 – 50, …. prepare the less than type cumulative frequency table. Using the table, answer the following questions:

i. How many students have scored marks less than 80?
ii. How many students have scored marks less than 40?
iii. How many students have scored marks less than 60?
Solution:
Class

i. 66 students have scored marks less than 80.
ii. 14 students have scored marks less than 40.
iii. 45 students have scored marks less than 60.

Question 7.
By using data in example (6), and taking classes 30 – 40, 40 – 50,… prepare equal to or more than type cumulative frequency table and answer the following questions based on it.
i. How many students have scored marks 70 or more than 70?
ii. How many students have scored marks 30 or more than 30?
Solution:

i. 11 students have scored marks 70 or more than 70.
ii. 68 students have scored marks 30 or more than 30.

Question 8.
There are 10 observations arranged in ascending order as given below.
45, 47, 50, 52, JC, JC + 2, 60, 62, 63, 74. The median of these observations is 53.
Find the value of JC. Also find the mean and the mode of the data.
Solution:
i. Given data in ascending order:
45,47, 50, 52, x, JC+2, 60, 62, 63, 74.
∴ Number of observations (n) = 10 (i.e., even)
∴ Median is the average of middle two observations
Here, the 5th and 6th numbers are in the middle position.
∴
∴ 106 = 2x + 2
∴ 106 – 2 = 2x
∴ 104 = 2x
∴ x = 52
∴ The given data becomes:
45, 47, 50, 52, 52, 54, 60, 62, 63, 74.

∴ The mean of the given data is 55.9.

iii. Given data in ascending order:
45, 47, 50, 52, 52, 54, 60, 62, 63, 74.
∴ The observation repeated maximum number of times = 52
∴ The mode of the given data is 52.

Maharashtra Board Class 9 Maths Chapter 7 Statistics Problem Set 7 Intext Questions and Activities

Question 1.
To show following information diagrammatically, which type of bar- diagram is suitable?
i. Literacy percentage of four villages.
ii. The expenses of a family on various items.
iii. The numbers of girls and boys in each of five divisions.
iv. The number of people visiting a science exhibition on each of three days.
v. The maximum and minimum temperature of your town during the months from January to June.
vi. While driving a two-wheeler, number of people wearing helmets and not wearing helmet in 100 families.
(Textbook pg. no. 112)
Solution:
i. Percentage bar diagram
ii. Sub-divided bar diagram
iii. Sub-divided bar diagram
iv. Sub-divided bar diagram
v. Sub-divided bar diagram
vi. Sub-divided bar diagram

Question 2.
You gather information for several reasons. Take a few examples and discuss whether the data is primary or secondary.
(Textbook pg. no, 113)
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.5 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Yield of soyabean per acre in quintal in Mukund’s field for 7 years was 10, 7, 5,3, 9, 6, 9. Find the mean of yield per acre.
Solution:

Mean = 7
The mean of yield per acre is 7 quintals.

Question 2.
Find the median of the observations, 59, 75, 68, 70, 74, 75, 80.
Solution:
Given data in ascending order:
59, 68, 70, 74, 75, 75, 80
∴ Number of observations(n) = 7 (i.e., odd)
∴ Median is the middle most observation
Here, 4th number is at the middle position, which is = 74
∴ The median of the given data is 74.

Question 3.
The marks (out of 100) obtained by 7 students in Mathematics examination are given below. Find the mode for these marks.
99, 100, 95, 100, 100, 60, 90
Solution:
Given data in ascending order:
60, 90, 95, 99, 100, 100, 100
Here, the observation repeated maximum number of times = 100
∴ The mode of the given data is 100.

Question 4.
The monthly salaries in rupees of 30 workers in a factory are given below.
5000, 7000, 3000, 4000, 4000, 3000, 3000,
3000, 8000, 4000, 4000, 9000, 3000, 5000,
5000, 4000, 4000, 3000, 5000, 5000, 6000,
8000, 3000, 3000, 6000, 7000, 7000, 6000,
6000, 4000
From the above data find the mean of monthly salary.
Solution:

∴ The mean of monthly salary is ₹ 4900.

Question 5.
In a basket there are 10 tomatoes. The weight of each of these tomatoes in grams is as follows:
60, 70, 90, 95, 50, 65, 70, 80, 85, 95.
Find the median of the weights of tomatoes.
Solution:
Given data in ascending order:
50, 60, 65, 70, 70, 80 85, 90, 95, 95
∴ Number of observations (n) = 10 (i.e., even)
∴ Median is the average of middle two observations
Here, 5th and 6th numbers are in the middle position
∴ Median = \(\frac { 70+80 }{ 2 }\)
∴ Median = \(\frac { 150 }{ 2 }\)
∴ The median of the weights of tomatoes is 75 grams.

Question 6.
A hockey player has scored following number of goals in 9 matches: 5, 4, 0, 2, 2, 4, 4, 3,3.
Find the mean, median and mode of the data.
Solution:
i. Given data: 5, 4, 0, 2, 2, 4, 4, 3, 3.
Total number of observations = 9


∴ The mean of the given data is 3.

ii. Given data in ascending order:
0,2, 2, 3, 3, 4, 4, 4,5
∴ Number of observations(n) = 9 (i.e., odd)
∴ Median is the middle most observation
Here, the 5^th number is at the middle position, which is 3.
∴ The median of the given data is 3.

iii. Given data in ascending order:
0,2, 2, 3, 3, 4, 4, 4,5
Here, the observation repeated maximum number of times = 4
∴ The mode of the given data is 4.

Question 7.
The calculated mean of 50 observations was 80. It was later discovered that observation 19 was recorded by mistake as 91. What Was the correct mean?
Solution:
Here, mean = 80, number of observations = 50
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations
∴ The sum of 50 observations = 80 x 50
= 4000
One of the observation was 19. However, by mistake it was recorded as 91.
Sum of observations after correction = sum of 50 observation + correct observation – incorrect observation
= 4000 + 19 – 91
= 3928
∴ Corrected mean

= 78.56
∴ The corrected mean is 78.56.

Question 8.
Following 10 observations are arranged in ascending order as follows. 2, 3 , 5 , 9, x + 1, x + 3, 14, 16, 19, 20. If the median of the data is 11, find the value of x.
Solution:
Given data in ascending order :
2, 3, 5, 9, x + 1, x + 3, 14, 16, 19, 20.
∴ Number if observations (n) = 10 (i.e., even)
∴ Median is the average of middle two observations
Here, the 5th and 6th numbers are in the middle position.
∴ \( \text { Median }=\frac{(x+1)+(x+3)}{2}\)
∴ 11 = \(\frac { 2x+4 }{ 2 }\)
∴ 22 = 2x + 4
∴ 22 – 4 = 2x
∴ 18 = 2x
∴ x = 9

Question 9.
The mean of 35 observations is 20, out of which mean of first 18 observations is 15 and mean of last 18 observations is 25. Find the 18th observation.
Solution:
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations
= Mean x Total number of observations
The mean of 35 observations is 20
∴ Sum of 35 observations = 20 x 35 = 700 ,..(i)
The mean of first 18 observations is 15
Sum of first 18 observations =15 x 18
= 270 …(ii)
The mean of last 18 observations is 25 Sum of last 18 observations = 25 x 18
= 450 …(iii)
∴ 18^th observation = (Sum of first 18 observations + Sum of last 18 observations) – (Sum of 35 observations)
= (270 + 450) – (700) … [From (i), (ii) and (iii)]
= 720 – 700 = 20
The 18^th observation is 20.

Question 10.
The mean of 5 observations is 50. One of the observations was removed from the data, hence the mean became 45. Find the observation which was removed.
Solution:
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations
The mean of 5 observations is 50
Sum of 5 observations = 50 x 5 = 250 …(i)
One observation was removed and mean of remaining data is 45.
Total number of observations after removing one observation = 5 – 1 = 4
Now, mean of 4 observations is 45.
∴ Sum of 4 observations = 45 x 4 = 180 …(ii)
∴ Observation which was removed
= Sum of 5 observations – Sum of 4 observations = 250 – 180 … [From (i) and (ii)]
= 70
∴ The observation which was removed is 70.

Question 11.
There are 40 students in a class, out of them 15 are boys. The mean of marks obtained by boys is 33 and that for girls is 35. Find out the mean of all students in the class.
Solution:
Total number of students = 40
Number of boys =15
∴ Number of girls = 40 – 15 = 25
The mean of marks obtained by 15 boys is 33
Here, sum of the marks obtained by boys
= 33 x 15
= 495 …(i)
The mean of marks obtained by 25 girls is 35 Sum of the marks obtained by girls = 35 x 25
= 875 …(ii)
Sum of the marks obtained by boys and girls = 495 + 875 … [From (i) and (ii)]
= 1370
∴ Mean of all the students

= 34.25
∴ The mean of all the students in the class is 34.25.

Question 12.
The weights of 10 students (in kg) are given below:
40, 35, 42, 43, 37, 35, 37, 37, 42, 37. Find the mode of the data.
Solution:
Given data in ascending order:
35, 35, 37, 37, 37, 37, 40, 42, 42, 43
∴ The observation repeated maximum number of times = 37
∴ Mode of the given data is 37 kg

Question 13.
In the following table, the information is given about the number of families and the siblings in the families less than 14 years of age. Find the mode of the data.

Solution:
Here, the maximum frequency is 25.
Since, Mode = observations having maximum frequency
∴ The mode of the given data is 2.

Question 14.
Find the mode of the following data.

Solution:
Here, the maximum frequency is 9.
Since, Mode = observations having maximum frequency
But, this is the frequency of two observations.
∴ Mode = 35 and 37

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.5 Intext Questions and Activities

Question 1.
The first unit test of 40 marks was conducted for a class of 35 students. The marks obtained by the students were as follows. Find the mean of the marks.
40, 35, 30, 25, 23, 20, 14, 15, 16, 20, 17, 37, 37, 20, 36, 16, 30, 25, 25, 36, 37, 39, 39, 40, 15, 16, 17, 30, 16, 39, 40, 35, 37, 23, 16.
(Textbook pg, no. 123)
Solution:
Here, we can add all observations, but it will be a tedious job. It is easy to make frequency distribution table to calculate mean.

= 27.31 marks (approximately)
∴ The mean of the mark is 27.31.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.

Problem Set 3 Algebra 10th Std Maths Part 1 Answers Chapter 3 Arithmetic Progression

Question 1.
Choose the correct alternative answer for each of the following sub questions.

i. The sequence – 10,- 6,- 2, 2, …
(A) is an A.P. Reason d = – 16
(B) is an A.P. Reason d = 4
(C) is an A.P. Reason d = – 4
(D) is not an A.P.
Answer:
(B)

ii. First four terms of an A.P. are …, whose first term is -2 and common difference is -2.
(A) -2, 0, 2, 4
(B) -2, 4,- 8, 16
(C) -2, -4, -6, -8
(D) -2,-4, -8, -16
Answer:
(C)

iii. What is the sum of the first 30 natural numbers?
(A) 464
(B) 465
(C) 462
(D) 461
Answer:
(B)

iv. For an given A.P. t₇ = 4, d = – 4, then a = ………
(A) 6
(B) 7
(C) 20
(D) 28
Answer:
(D)

v. For an given A.P. a = 3.5, d = 0, n = 101, then t_n = ….
(A) 0
(B) 3.5
(c) 103.5
(D) 104.5
Answer:
(B)

vi. In an A.P. first two terms are – 3, 4, then 21st term is ….
(A) -143
(B) 143
(C) 137
(D) 17
Answer:
(C)

vii. If for any A.P. d = 5, then t₁₈ – t₁₃ = ….
(A) 5
(B) 20
(C) 25
(D) 30
Answer:
(C)

viii. Sum of first five multiples of 3 is …
(A) 45
(B) 55
(C) 15
(D) 75
Answer:
(A)

ix. 15, 10, 5, … In this A.P. sum of first 10 terms is…
(A) -75
(B) -125
(C) 75
(D) 125
Answer:
(A)

x. In an A.P. 1^st term is 1 and the last term is 20. The sum of all terms is 399, then n = ….
(A) 42
(B) 38
(C) 21
(D) 19
Answer:
(B)

Hints:

Question 2.
Find the fourth term from the end in an
A.P.: -11, -8, -5, …, 49.
Solution:
The given A.P. is
-11,-8,-5, ……. 49
Reversing the A.P., we get 49, …, -5, -8, -11
Here, a = 49, d = -11 -(-8) = -11 + 8 = -3
Since, t_n = a + (n – 1)d
∴ t₄ = 49 + (4 – 1)(-3)
= 49 + (3) (-3)
= 49 – 9
= 40
∴ Fourth term from the end in the given A.P. is 40.
[Note: If an AY. is reversed, then the resulting sequence is also an A.P.]

Question 3.
In an A.P. the 10^th term is 46, sum of the 5^th and 7^th term is 52. Find the A.P.
Solution:
For an A.P., let a be the first term and d be the common difference.
t₁₀ = 46, t₅ + t₇ = 52 …[Given]
Since, t_n = a + (n – 1)d
∴ t₁₀ = a + (10 – 1)d
∴ 46 = a + 9d
i. e. a + 9d = 46 …(i)
Also, t₅ + t₇ = 52
∴ a + (5 – 1)d + a + (7 – 1)d = 52
∴ a + 4d + a + 6d = 52
∴ 2a + 10d = 52
∴ 2 (a + 5d) = 52
∴ a + 5d = \(\frac { 52 }{ 2 } \)
∴ a + 5d = 26 …(ii)
Subtracting equation (ii) from (i), we get

Substituting d = 5 in equation (ii), we get
a + 5(5) = 26
∴ a + 25 = 26
∴ a = 26 – 25 = 1
t₁ = a = 1
t₂ = t₁ + d = 1 + 5 = 6
t₃ = t₂ + d = 6 + 5 = 11
t₄ = t₃ + d = 11 + 5 = 16
The required A.P. is 1,6,11,16,….

Question 4.
The A.P. in which 4^th term is -15 and 9^th term is -30. Find the sum of the first 10 numbers.
Solution:
t₄ = -15, t9 = – 30 …[Given]
Since, t_n = a + (n – 1)d
∴ t₄ = a + (4 – 1)d
∴ – 15 = a + 3d
i. e. a + 3d = -15 …(i)
Also, t₉ = a + (9 – 1)d
∴ -30 = a + 8d
i.e. a + 8d = -30 …(ii)

∴ The sum of the first 10 numbers is -195.

Question 5.
Two given A.P.’s are 9, 7, 5, … and 24, 21, 18, … If nth term of both the .progressions are equal then find the value of n and n,h term.
Solution:
The first A.P. is 9, 7, 5,…
Here, a = 9, d = 7- 9 = -2
∴n^th term = a + (n – 1)d
= 9 + (n – 1) (-2)
= 9 – 2n + 2
= 11 – 2n
The second A.P. is 24, 21, 18, …
Here, a = 24, d = 21 – 24 = – 3
∴ n^th term = a + (n – 1)d
= 24 + (n – 1) (-3)
= 24 – 3n + 3
= 27 – 3n
Since, the nth terms of the two A.P.’s are equal.
∴ 11 – 2n = 27 – 3n
∴ 3n – 2n = 27 – 11
∴ n = 16
∴ t₁₆ = 9 + (16 – 1) (-2)
= 9 + 15 × (-2)
= 9 – 30
∴ t₁₆ = -21
∴ The values of n and n^th term are 16 and -21 respectively.

Question 6.
If sum of 3^rd and 8^th terms of an A.P. is 7 and sum of 7th and 14th terms is -3, then find the 10th term.
Solution:
for an A.P., let a be the first term and d be the common difference.
According to the first condition,
t₃ + tg = 7
∴ a + (3 – 1) d + a + (8 – 1)d = 7 …[∵ t_n = a + (n – 1)d]
∴ a + 2d + a + 7d = 7
∴ 2a + 9d = 7 …(i)
According to the second condition,
t₇ + t₁₄ = -3
∴ a + (7 – 1)d + a + (14 – 1 )d = -3
∴ a + 6d + a + 13d = -3
∴ 2a + 19 d = – 3 …(ii)
Subtracting equation (i) from (ii), we get

Question 7.
In an A.P. the first term is -5 and last term is 45. If sum of all numbers in the A.P. is 120, then how many terms are there? What is the common difference?
Solution:
Let the number of terms in the A.P. be n and the common difference be d.
Then, a = -5, t_n = 45, S_n = 120
Since, t_n = a + (n – 1)d
∴ 45 = -5 + (n – 1)d
∴ 45 + 5 = (n – 1)d
∴ (n – 1)d = 50 …(i)

Substituting n = 6 in equation (i), we get
(6 – 1)d = 50
∴ 5d = 50
∴ d = \(\frac { 50 }{ 5 } \) = 10
∴ There are 6 terms in the A.P. and the common difference is 10.

Alternate Method:
Let the number of terms in the A.P. be n.
Then, t₁ = a = -5, t_n = 45, S_n = 120

∴ There are 6 terms in the A.P. and the common difference is 10.

Question 8.
Sum of 1 to n natural numbers is 36, then find the value of n.
Solution:
The natural numbers from 1 to n are
1,2, 3, ……, n.
The above sequence is an A.P.
∴ a = 1, d = 2 – 1 = 1
S_n = 36 …[Given]
Now, S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
∴ 36 = \(\frac { n }{ 2 } \) [2(1) + (n – 1)(1)]
∴ 36 = \(\frac { n }{ 2 } \) (2 + n – 1)
∴ 36 × 2 = n (n + 1)
∴ 72 = n (n + 1)
∴ 72 = n² + n
∴ n² + n – 72 = 0
∴ n² + 9_n – 8n – 72 = 0
∴ n(n + 9) – 8 (n + 9) = 0
∴ (n + 9) (n – 8) = 0
∴ n + 9 = 0 or n – 8 = 0
∴ n = -9 or n = 8
But, n cannot be negative.
∴ n = 8
∴ The value of n is 8.

Question 9.
Divide 207 in three parts, such that all parts are in A.P. and product of two smaller parts will be 4623.
Solution:
Let the three parts of 207 that are in A.P. be
a – d, a, a + d
According to the first condition,
(a – d) + a + (a + d) = 207
∴ 3a = 207
∴ a = \(\frac { 207 }{ 3 } \)
∴ a = 69 …(i)
According to the second condition,
(a – d) × a = 4623
∴ (69 – d) × 69 = 4623 …[From (i)]
∴ 69 – d = \(\frac { 4623 }{ 69 } \)
∴ d = 69 – 67
∴ d = 2
∴ a – d = 69 – 2 = 67
a = 69
a + d = 69 + 2 = 71
∴ The three parts of 207 that are in A.P. are 67, 69 and 71.

Question 10.
There are 37 terms in an A.P., the sum of three terms placed exactly at the middle is 225 and the sum of last three terms is 429. Write the A.P.
Solution:
Since, there are 37 terms in the A.P.

Substituting d = 4 in equation (i), we get
3a + 54(4) = 225
∴ 3a + 216 = 225
∴ 3a = 225 – 216
∴ 3a = 9
∴ a = \(\frac { 9 }{ 3 } \) = 3
∴The required A. P. is
a, a + d, a + 2d, a + 3d, …., a + (n – 1)d
i.e. 3, 3 + 4,3 + 2 × 4, 3 + 3 × 4,…, 3 + (37 – 1)4
i.e. 3, 7,11,15, …,147

Question 11.
If first term of an A.P. is a, second term is b and last term is c, then show that sum of all

Solution:

Question 12.
If the sum of first p terms of an A.P. is equal to the sum of first q terms then show that the sum of its first (p + q) terms is zero, (p ≠ q)
Solution:
For an A.P., let a be the first term and d be the common difference.
The sum of first n terms of an A.P. is given by
Sn = [2a + (n – 1)d]
According to the given condition,
Sp = Sq


∴ The sum of the first (p + q) terms is zero

Question 13.
If m times the m^th term of an A.P. is equal to n times n^th term, then show that the (m + n)^th term of the A.P. is zero.
Solution:
According to the given condition,
mt_m = nt_n
∴ m[a + (m – 1)d] = n[a + (n – 1)d]
∴ ma + md(m – 1) = na + nd(n- 1)
∴ ma + m²d – md = na + n²d – nd
∴ ma + m²d – md – na – n²d + nd = 0
∴ (ma – na) + (m²d – n²d) – (md – nd) = 0
∴ a(m – n) + d(m² – n²) – d(m – n) = 0
∴ a(m – n) + d(m + n) (m – n) – d(m – n) = 0
∴ (m – n)[a + (m + n – 1) d] = 0
∴ [a+ (m + n – 1)d] = 0 …[Dividing both sides by (m – n)]
∴ t_(m+n) = 0
∴ The (m + n)^th term of the A.P. is zero.

Question 14.
₹ 1000 is invested at 10 percent simple interest. Check at the end of every year if the total interest amount is in A.P. If this is an A.P. then find interest amount after 20 years. For this complete the following activity.
Solution:

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.4 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Complete the following cumulative frequency table:

Solution:

Question 2.
Complete the following Cumulative Frequency Table:

Solution:

Question 3.
The data is given for 62 students in a certain class regarding their mathematics marks out of 100. Take the classes 0 – 10, 10 – 20,… and prepare frequency distribution
table and cumulative frequency table more than or equal to type.
55. 60, 81, 90, 45, 65, 45, 52, 30, 85, 20, 10,
75, 95, 09, 20, 25, 39, 45, 50, 78, 70, 46, 64,
42. 58. 31, 82, 27, 11, 78, 97, 07, 22, 27, 36,
35, 40, 75, 80, 47, 69, 48, 59, 32, 83, 23, 17,
77, 45, 05, 23, 37, 38, 35, 25, 46, 57, 68, 45.
47,49
From the prcparcd table, answer the following questions :
i. How many students obtained marks 40 or above 40?
ii. How many students obtained marks 90 or above 90?
iii. How many students obtained marks 60 or above 60?
iv. What is the cumulative frequency of equal to or more than type of the class 0 – 10?
Solution:

i. 38 students obtained marks 40 or above 40.
ii. 3 students obtained marks 90 or above 90.
iii. 19 students obtained marks 60 or above 60.
iv. Cumulative frequency of equal to or more than type of the class 0 – 10 is 62.

Question 4.
Using the data In example (3) above, prepare less than type cumulative frequency table and answer the following questions.
i. How many students obtained less than 40 marks?
ii. How many students obtained less than 10 marks?
iii. How many students obtained less than 60 marks?
iv. Find the cumulative frequency of the class 50 – 60.
Solution:

i. 24 students obtained less than 40 marks.
ii. 3 students obtained less than 10 marks.
iii. 43 students obtained less than 60 marks.
iv. Cumulative frequency of the class 50 – 60 is 43.

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.4 Intext Questions and Activities

Question 1.
The following information is regarding marks in mathematics, obtained out of 40, scored by 50 students of 9th std. ¡n the first unit test. (Textbook pg. no. 120)

From the table, fill in the blanks in the following statements.
i. For class interval 10 – 20 the lower class limit is _____ and upper class limit is _____
ii. How many students obtained marks less than 10? 2
iii. How many students obtained marks less than 20? 2 + ____ = 14
iv. How many students obtained marks less than 30? ______ + _____ = 34
v. How many students obtained marks less than 40? ______ + ______ =50
Solution:
i. 10, 20
iii. 12
iv. 14 + 20
v. 34 + 16

Question 2.
A sports club has organised a table-tennis tournaments. The following table gives the distribution of players ages. Find the cumulative frequencies equal to or more than the lower class limit and complete the table (Textbook pg. no. 121)
Solution:
Equal to lower limit or more than lower limit type of cumulative table.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.3 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
For class interval 20 – 25 write the lower class limit and the upper class limit.
Answer:
Lower class limit = 20
Upper class limit = 25

Question 2.
Find the class-mark of the class 35-40.
Solution:
Class-mark

∴ Class-mark of the class 35 – 40 is 37.5

Question 3.
If class-mark is 10 and class width is 6, then find the class.
Solution:
Let the upper class limit be x and the lower class limit be y.
Class mark = 10 …[Given]
Class-mark

∴ x + y = 20 …(i)
Class width = 6 … [Given]
Class width = Upper class limit – Lower class limit
∴ x – y = 6 …(ii)
Adding equations (i) and (ii),
x + y = 20
x – y = 6
2x = 26
∴ x = 13
Substituting x = 13 in equation (i),
13 + y = 20
∴ y = 20 – 13
∴ y = 7
∴ The required class is 7 – 13.

Question 4.
Complete the following table.

Solution:
Let frequency of the class 14 – 15 be x then, from table,
5 + 14 + x + 4 = 35
∴ 23 + x = 35
∴ x = 35 – 23
∴ x = 12

Question 5.
In a ‘tree plantation’ project of a certain school there are 45 students of ‘Harit Sena.’ The record of trees planted by each student is given below:
3, 5, 7, 6, 4, 3, 5, 4, 3, 5, 4, 7, 5, 3, 6, 6, 5, 3, 4, 5, 7, 3, 5, 6, 4, 4, 3, 5, 6, 6, 4, 3, 5 ,7, 3, 4, 5, 7, 6, 4, 3, 5, 4, 4, 7.
Prepare a frequency distribution table of the data.
Solution:

Question 6.
The value of n upto 50 decimal places is given below:
3.14159265358979323846264338327950288419716939937510
From this information prepare an ungrouped frequency distribution table of digits appearing after the decimal point.
Solution:

Question 7.
In the tables given below, class-mark and frequencies is given. Construct the frequency tables taking inclusive and exclusive classes.
i.

ii.

Solution:
i. Let the Lower class limit and upper class limit of the class mark 5 be x and y respectively.

∴x + y = 10
Here, class width = 15 – 5 = 10
But, Class width = Upper class limit – Lower class limit
∴ y – x = 10
∴ -x + y = 10 …(ii)
Adding equations (i) and (ii),
x+ y = 10
-x + y = 10
∴ 2y = 20
∴ y = 10
Substituting y = 10 in equation (i),
∴ x + 10 = 10
∴ x = 0
∴ class with class-mark 5 is 0 – 10
Similarly, we can find the remaining classes.
∴ frequency table taking inclusive and exclusive classes.

ii. Let the lower class limit and upper class limit of the class mark 22 be x andy respectively.

∴ x + y = 44 …(i)
Here, class width = 24 – 22 = 2
But, Class width = Upper class limit – Lower class limit
∴ y – x = 2
∴ -x + y = 2 …. (ii)
Adding equations (i) and (ii),
x + y = 44
– x + y= 2
2y = 46
∴ y = 23
Substituting y = 23 in equation (i),
∴ x + 23 = 44
∴ x = 21
∴ class with class-mark 22 is 21 – 23
Similarly, we can find the remaining classes
∴ frequency table taking inclusive and exclusive classes.

Question 8.
In a school, 46 students of 9th standard, were told to measure the lengths of the pencils in their compass-boxes in Centimetres. The data collected was as follows:
16, 15, 7, 4.5, 8.5, 5.5, 5, 6.5, 6, 10, 12, 13,
4.5, 4.9, 16, 11, 9.2, 7.3, 11.4, 12.7, 13.9, 16,
5.5, 9.9, 8.4, 11.4, 13.1, 15, 4.8, 10, 7.5, 8.5,
6.5, 7.2, 4.5, 5.7, 16, 5.7, 6.9, 8.9, 9.2, 10.2, 12.3, 13.7, 14.5, 10
By taking exclusive classes 0-5, 5-10, 10-15,…. prepare a grouped frequency distribution table.
Solution:

Question 9.
In a village, the milk was collected from 50 milkmen at a collection center in litres as given below:
27, 75, 5, 99, 70, 12, 15, 20, 30, 35, 45, 80, 77,
90, 92, 72, 4, 33, 22, 15, 20, 28, 29, 14, 16, 20,
72, 81, 85, 10, 16, 9, 25, 23, 26, 46, 55, 56, 66,
67, 51, 57, 44, 43, 6, 65, 42, 36, 7, 35
By taking suitable classes, prepare grouped frequency distribution table.
Solution:

Question 10.
38 people donated to an organisation working for differently abled persons. The amount in rupees were as follows:
101, 500, 401, 201, 301, 160, 210, 125, 175,
190, 450, 151, 101, 351, 251, 451, 151, 260,
360, 410, 150, 125, 161, 195, 351, 170, 225,
260, 290, 310, 360, 425, 420, 100, 105, 170, 250, 100
i. By taking classes 100 – 149, 150 – 199, 200 – 249… prepare grouped frequency distribution table.
ii. From the table, find the number of people who donated ₹350 or more.
Solution:
i.

ii. Number of people who donated ₹ 350 or more = 4 + 4 + 2 + 1 = 11

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.3 Intext Questions and Activities

Question 1.
The record of marks out of 20 in Mathematics in the first unit test is as follows:
20,6, 14, 10, 13, 15, 12, 14, 17. 17, 18, 1119,
9, 16. 18, 14, 7, 17, 20, 8, 15, 16, 10, 15, 12.
18, 17, 12, 11, 11, 10, 16, 14, 16, 18, 10, 7, 17,
14, 20, 17, 13, 15, 18, 20, 12, 12, 15, 10
Answer the following questions, from the above information.
a. How many students scored 15 marks?
b. How many students scored more than 15 marks?
c. How many students scored less than 15 marks?
d. What is the lowest score of the group?
e. What is the highest score of the group? (Textbook pg. no. 114)
Solution:
a. 5 students scored 15 marks.
b. 20 students scored more than 15 marks.
c. 25 students scored less than 15 marks.
d. 6 is the lowest score of the group.
e. 20 is the highest score of the group.

Question 2.
For the above Question prepare Frequency Distribution Table. (Textbook pg. no. 115)
Solution:

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.2 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Classify following information as primary or secondary data.
i. Information of attendance of every student collected by visiting every class in a school
ii. The information of heights of students was gathered from school records and sent to the head office, as it was to be sent urgently.
iii. In the village Nandpur, the information collected from every house regarding students not attending school.
iv. For science project, information of trees gathered by visiting a forest.
Answer:
i. Primary data
ii. Secondary data
iii. Primary data
iv. Primary data

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.1 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
The following table shows the number of Buses and Trucks in nearest lakh units. Draw percentage bar diagram. (Approximate the percentages to the nearest integer)

Solution:


Question 2.
In the table given below, the information is given about roads. Using this draw sub-divided and percentage bar diagram (Approximate the percentages to the nearest integer)

Solution:
i. Sub-divided bar diagram:

ii. Percentage bar diagram:

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.1 Intext Questions and Activities

Question 1.
A farmer has produced Wheat and Jowar in his field. The following joint bar diagram shows the production of Wheat and Jowar. From the gken diagram answer the following questions: (Textbook pg. no. 108)
i. Which crop production has increased consistently in 3 years?
ii. By how many quintals the production ofjowar has reduced in 2012 as compared to 2011?
iii. What is the difference between the production of wheat in 2010 and 2012 ?
iv. Complete the following table using this diagram.


Solution:
i. The crop production of wheat has increased consistently in 3 years.
ii. The production of jowar has reduced by 3 quintals in 2012 as compared to 2011.
iii. The difference between the production of wheat in 2010 and 2012 = 48 – 30 = 18 quintals
iv.

Question 2.
In the following table, the information of number of girls per 1000 boys is given for different states. Fill In the blanks and complete the table. (Textbook pg. no. 111)

Solution:
Draw percentage bar diagram from this information and discuss the findings from the diagram.

Question 3.
For the above given activity, the information of number of girls per 1000 boys is given for five states. The literacy percentage of these five states is given below. Assam (73%), Bihar (64%), Punjab (77%), Kerala (94%), Maharashtra (83%). Think of the number of girls and the literacy percentages in the respective states. Can you draw any conclusions from it? (Textbook pg. no. 112)
Solution:
By observing the number of girls per 1000 boys and literacy percentages in the given respective states, we can conclude that the literacy rate of girls is least in Bihar and is highest in Kerala.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

Problem Set 5 Algebra 9th Std Maths Part 1 Answers Chapter 5 Linear Equations in Two Variables

Question 1.
Choose the correct alternative answers for the following questions.

i. If 3x + 5y = 9 and 5x + 3y = 7, then what is the value of x + y ?
(A) 2
(B) 16
(C) 9
(D) 7
Answer:
(A) 2

ii. ‘When 5 is subtracted from length and breadth of the rectangle, the perimeter becomes 26’. What is the mathematical form of the statement ?
(A) x – y = 8
(B) x + y = 8
(C) x + y = 23
(D) 2x + y = 21
Answer:
(C) x + y = 23

iii. Ajay is younger than Vijay by 5 years. Sum of their ages is 25 years. What is Ajay’s age?
(A) 20 years
(B) 15 years
(C) 10 years
(D) 5 years
Answer:
(C) 10 years

Hints:
i. Adding the given equations,
3x+ 5y = 9
5x + 3y = 7
8x + 8y = 16
∴ x + y = 2 .. [Dividing both sides by 8]

ii. Let the length of the rectangle be ‘x’ and that of breadth be ‘y’.
Perimeter of rectangle = 2[(x – 5) + (y – 5)]
∴ 26 = 2(x + y – 10)
∴ x + y – 10 = 13
∴ x + y = 23

iii. Let the age of Ajay bex years.
∴ x + (x + 5) = 25
∴ 2x = 20
∴ x = 10 years

Question 2.
Solve the following simultaneous equations.
i. 2x + y = 5 ; 3x – y = 5
ii. x – 2y = -1 ; 2x – y = 7
iii. x + y = 11 ; 2x – 3y = 7
iv. 2x + y = -2 ; 3x – y = 7
V. 2x – y = 5 ; 3x + 2y = 11
vi. x – 2y – 2 ; x + 2y = 10
Solution:
ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = 10/5
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.

ii. x – 2y = -1
∴x = 2y – 1 … .(i)
∴ 2x – y = 7 ….(ii)
Substituting x = 2y – 1 in equation (ii),
2(2y – 1) – y = 7
∴ 4y – 2 – y = 7
∴ 3y = 7 + 2
∴ 3y = 9
∴ y = 9/3
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y – 1
∴ x = 2(3) – 1
∴ x = 6 – 1 = 5
∴ (5, 3) is the solution of the given equations.

iii. x + y = 11
∴ x = 11 – y …(i)
2x – 3y = 7 …….(ii)
Substituting x = 11 -y in equation (ii),
2(11 – y) – 3y = 7
∴ 22 – 2y – 3y = 1
∴ 22 – 5y = 7
∴ 22 – 7 = 5y
∴ 15 = 5y
∴ y = \(\frac { 15 }{ 5 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 11 – y
∴ x = 11 – 3 = 8
∴ (8, 3) is the solution of the given equations.

iv. 2x + y = -2 …(i)
3x – y = 7 …(ii)
Adding equations (i) and (ii),
2x + y = -2
+ 3x – y = l
5x = 5
∴ x = \(\frac { 5 }{ 5 }\)
∴ x = 1
Substituting x = 1 in equation (i),
2x + y = -2
∴ 2(1) +y = -2
2 + y = -2
∴ y = – 2 – 2
∴ y = -4
∴ (1, -4) is the solution of the given equations.

v. 2x – y = 5
∴ -y = 5 – 2x
∴ y = 2x – 5 …(i)
3x + 2y = 11 ……(ii)
Substituting y = 2x – 5 in equation (ii),
3x + 2(2x – 5) = 11
∴ 3x + 4x- 10= 11
∴ 7x = 11 + 10
∴ 7x = 21
∴ x = \(\frac { 21 }{ 7 }\)
∴ x = 3
Substituting x = 3 in equation (i),
y = 2x – 5
∴ y = 2(3) – 5
∴ y = 6 – 5 = 1
∴(3,1) is the solution of the given equations.

vi. x – 2y = -2
∴ x = 2y – 2 …(i)
x + 2y = 10 …..(ii)
Substituting x = 2y – 2 in equation (ii),
2y – 2 + 2y = 10
∴ 4y = 10 + 2
∴ 4y= 12
∴ y = \(\frac { 12 }{ 7 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y – 2
∴ x = 2(3) – 2
∴ x = 6 – 2 = 4
∴ (4, 3) is the solution of the given equations.

Question 3.
By equating coefficients of variables, solve the following equations. [3 Marks each]
i. 3x – 4y = 7 ; 5x + 2y = 3
ii. 5x + ly= 17 ; 3x – 2y = 4
iii. x – 2y = -10 ; 3x – 3y = -12
iv. 4x+y = 34 ; x + 4y = 16
Solution:
i. 3x – 4y = 7 …(i)
5x + 2y = 3 ….(ii)
Multiplying equation (ii) by 2,
10x + 4y = 6 …(iii)
Adding equations (i) and (iii),

∴ x = 1
Substituting x = 1 in equation (i),
3x – 4y = 7
∴ 3(1) – 4y = 7
∴ 3 – 4y = 7
∴ 3 – 7 = 4y
∴ -4 = 4y
∴ y = \(\frac { -4 }{ 4 }\)
∴ y = -1
∴ (1, -1) is the solution of the given equations.

ii. 5x + 7y = 17 …(i)
3x – 2y = 4 ….(ii)
Multiplying equation (i) by 2,
10x + 14y = 34 …(iii)
Multiplying equation (ii) by 7,
21x – 14y = 28 …..(iv)
Adding equations (iii) and (iv),

∴ x = 2
Substituting x = 2 in equation (ii),
3x – 2y = 4
∴ 3(2) – 2y = 4
∴ 6 – 2y = 4
∴ 6 – 4 = 2y
∴ 2 = 2y
∴ y = \(\frac { 2 }{ 2 }\)
∴ y = 1
∴ (2,1) is the solution of the given equations.

iii. x – 2y = -10 ….(i)
3x – 5y = -12 …….(ii)
Multiplying equation (i) by 3,
3x – 6y = -30 …(iii)
Subtracting equation (ii) from (iii),

∴ y = 18
Substituting y = 18 in equation (i),
x – 2y = -10
∴ x – 2(18) = -10
∴ x – 36 = -10
∴ x = -10 + 36 = 26
∴ (26, 18) is the solution of the given equations.

iv. 4x + y = 34 …(i)
x + 4y = 16 …… (ii)
Multiplying equation (i) by 4,
16x + 4y = 136 …(iii)
Subtracting equation (ii) from (iii),

x = 8
Substituting x = 8 in equation (i),
4x + y = 34
∴ 4(8) + y = 34
∴ 32 + y = 34
∴ y = 34 – 32 = 2
∴ (8, 2) is the solution of the given equations.

Question 4.
Solve the following simultaneous equations.

Solution:
i. \(\frac{x}{3}+\frac{y}{4}=4\)
Multiplying both sides by 12,
4x + 3y = 48 …(i)
\(\frac{x}{2}-\frac{y}{4}=1\)
Multiplying both sides by 8,
4x – 2y = 8 …..(ii)
Subtracting equation (ii) from (i),

∴ y = 8
Substituting y = 8 in equation (ii),
4x – 2y = 8
∴ 4x – 2(8) = 8
∴ 4x – 16 = 8
∴ 4x = 8+ 16
∴ 4x = 24
∴ x = \(\frac { 24 }{ 4 }\)
∴ x = 6
∴ (6, 8) is the solution of the given equations.

ii. \(\frac { x }{ 3 }\) + 5y = 13
Multiplying both sides by 3,
x + 15y = 39 …(i)
2x + \(\frac { y }{ 2 }\) =19
Multiplying both sides by 2,
4x + y = 38 …….(ii)
Multiplying equation (i) by 4,
4x + 60y = 156 …(iii)
Subtracting equation (ii) from (iii),
4x + 60y =156 4x + y= 38

∴ y = 2
Substituting y = 2 in equation (i),
x + 15y = 39
∴ x+ 15(2) = 39
∴ x + 30 = 39
∴ x = 39 – 30 = 9
∴ (9,2) is the solution of the given equations.

iii. \(\frac { 2 }{ x }\) + \(\frac { 3 }{ y }\) = 13
Multiplying both sides by 5,

Question 5.
A two digit number is 3 more than 4 times the sum of its digits. If 18 is added to this number, the sum is equal to the number obtained by interchanging the digits. Find the number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the first condition,
a two digit number is 3 more than 4 times the sum of its digits.
10y + x = 4(x + y) + 3
∴ 10y + x = 4x + 4y + 3
∴ x – 4x + 10y – 4y = 3
∴ – 3x + 6y = 3
Dividing both sides by -3,
x – 2y = -1 …(i)
According to the second condition,
if 18 is added to the number, the sum is equal to the number obtained by interchanging the digits.
10y + x + 18= 10x + y
∴ x – 10x + 10y – y = -18
∴ – 9x + 9y = -18
Dividing both sides by – 9,
x – y = 2 ……(ii)
Subtracting equation (ii) from (i),

∴ y = 3
Substituting y = 3 in equation (ii),
x – y = 2
∴ x – 3 = 2
∴ x = 2 + 3 = 5
∴ Original number = 10y + x
= 10(3) + 5
= 30 + 5
= 35
The required number is 35.

Question 6.
The total cost of 8 books and 5 pens is ₹ 420 and the total cost of 5 books and 8 pens is ₹321. Find the cost of 1 book and 2 pens.
Solution:
Let the cost of one book be ₹ x and the cost of one pen be ₹ y.
According to the first condition,
the total cost of 8 books and 5 pens is ₹ 420.
∴ 8x + 5y = 420 …(i)
According to the second condition, the total cost of 5 books and 8 pens is ₹ 321.
5x + 8y = 321 ….(ii)
Multiplying equation (i) by 5,
40x + 25y = 2100 …(iii)
Multiplying equation (ii) by 8,
40x + 64y = 2568 … (iv)
Subtracting equation (iii) from (iv),

∴ y = 12
Substituting y = 12 in equation (i),
8x + 5y = 420
∴ 8x + 5(12) = 420
∴ 8x + 60 = 420
∴ 8x = 420 – 60
∴ 8x = 360
∴ x = \(\frac { 360 }{ 8 }\)
∴ x = 45
Cost of 1 book and 2 pens = x + 2y
= 45 + 2(12)
= 45 + 24
= ₹69
∴ The cost of 1 book and 2 pens is ₹69.

Question 7.
The ratio of incomes of two persons is 9 : 7. The ratio of their expenses is 4 : 3. Every person saves ₹ 200, find the income of each.
Solution:
Let the income of first person be ₹ x and that of second person be ₹ y.
According to the first condition,
the ratio of their incomes is 9 : 7.
∴ \(\frac { x }{ y }\) = \(\frac { 9 }{ 7 }\)
∴ 7x = 9y
∴ 7x – 9y = 0 …….(i)
Each person saves ₹ 200.
Expenses of first person = Income – Saving = x – 200
Expenses of second person = y – 200
According to the second condition,
the ratio of their expenses is 4 : 3
∴ \(\frac { x – 200 }{ y – 200 }\) = \(\frac { 4 }{ 3 }\)
∴ 3(x – 200) = 4(y – 200)
∴ 3x – 600 = 4y – 800
∴ 3x – 4y = – 800 + 600
∴ 3x – 4y = -200 …(ii)
Multiplying equation (i) by 4,
28x-36y =0 …(iii)
Multiplying equation (ii) by 9,
27x-36y = -1800 …(iv)
Subtracting equation (iv) from (iii),

Substituting x = 1800 in equation (i),
7x – 9y = 0
∴ 7(1800) – 9y = 0
∴ 9y = 7 x 1800
∴ y = \(\frac { 7 \times 1800 }{ 9 }\)
y = 7 x 200
∴ y = 1400
∴ The income of first person is ₹ 1800 and that of second person is ₹ 1400.

Question 8.
If the length of a rectangle is reduced by 5 units and its breadth is increased by 3 units, then the area of the rectangle is reduced by 9 square units. If length is reduced by 3 units and breadth is increased by 2 units, then the area of rectangle will increase by 67 square units. Then find the length and breadth of the rectangle.
Solution:
Let the length of the rectangle be ‘x’ units and the breadth of the rectangle be ‘y’ units.
Area of the rectangle = xy sq. units
length of the rectangle is reduced by 5 units
∴ length = x – 5
breadth of the rectangle is increased by 3 units
∴ breadth = y + 3
area of the rectangle is reduced by 9 square units
∴ area of the rectangle = xy – 9
According to the first condition,
(x – 5)(y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y = -9 + 15
∴ 3x – 5y = 6 …(i)
length of the rectangle is reduced by 3 units
∴ length = x – 3
breadth of the rectangle is increased by 2 units
∴ breadth = y + 2
area of the rectangle is increased by 67 square units
∴ area of the rectangle = xy + 61
According to the second condition,
(x – 3)(y + 2) = xy + 67
∴ xy + 2x – 3y – 6 = xy + 67
∴ 2x – 3y = 67 + 6
∴ 2x – 3y = 73 …(ii)
Multiplying equation (i) by 3,
9x – 15y = 18 . ..(iii)
Multiplying equation (ii) by 5,
10x – 15y = 365 …(iv)
Subtracting equation (iii) from (iv), 10x- 15y= 365 9x-15y= 18

Substituting x = 347 in equation (ii),
2x – 3y = 73
∴ 2(347) – 3y = 73
∴ 694 – 73 = 3y
∴ 621 = 3y
∴ y = \(\frac { 621 }{ 3 }\)
∴ y = 207
∴ The length and breadth of rectangle are 347 units and 207 units respectively.

Question 9.
The distance between two places A and B on a road is 70 kilometres. A car starts from A and the other from B. If they travel in the same direction, they will meet in 7 hours. If they travel towards each other they will meet in 1 hour, then find their speeds.
Solution:
Let the speed of the car starting from A (first car) be ‘x’ km/hr and that starting from B (second car) be ‘y’ km/hr. (x > y)
According to the first condition,
Distance covered by the first car in 7 hours = 7x km
Distance covered by the second car in 7 hours = 7y km

If the cars are travelling in the same direction, 7x – 7y = 70
Dividing both sides by 7,
x – y = 10 …(i)
According to the second condition,
Distance covered by the first car in
1 hour = x km
Distance covered by the second car in 1 hour = y km

If the cars are travelling in the opposite direction
x + y = 70 …(ii)
Adding equations (i) and (ii),

∴ x = 40
Substituting x = 40 in equation (ii), x + y = 70
∴ 40 +y = 70
∴ y = 70 – 40 = 30
∴ The speed of the cars starting from places A and B are 40 km/hr and 30 km/hr respectively.

Question 10.
The sum of a two digit number and the number obtained by interchanging its digits is 99. Find the number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the given condition,
the sum of a two digit number and the number
obtained by interchanging its digits is 99.
∴ 10y + x + 10x +y = 99
∴ 11x + 11y = 99
Dividing both sides by 11,
x + y = 9
If y = 1, then x = 8
If y = 2, then x = 7
If y = 3, then x = 6 and so on.
∴ The number can be 18, 27, 36, … etc.

Maharashtra Board Class 9 Maths Chapter 5 Linear Equations in Two Variables Practice Set 5 Intext Questions and Activities

Question 1.
On the glasses of following spectacles, write numbers such that (Textbook pg. no. 82)
i. Their sum is 42 and difference is 16.

ii. Their sum is 37 and difference is 11.

iii. Their sum is 54 and difference is 20.

iv. Their sum is … and difference is … .

Answer:
ii. x + y = 37 and x – y = 11
∴ x = 24, y = 13
iii. x +y = 54 and x – y = 20
∴ x = 37, y =17

Question 2.
There are instructions written near the arrows in the following diagram. From this information form suitable equations and write in the boxes indicated by arrows. Select any two equations from these boxes and find their solutions. Also verify the solutions. By taking one pair of equations at a time, how many pairs can be formed ? Discuss the solutions for these pairs. (Textbook pg. no. 92)

Answer:
Here, if we take a pair of any two equations, we get following 6 pairs.

1. equation (i) and (ii)
2. equation (i) and (iii)
3. equation (i) and (iv)
4. equation (ii) and (iii)
5. equation (ii) and (iv)
6. equation (iii) and (iv)

Solution of each pair given above is (21, 15).
Here, all four equations are of same rectangle. By solving any two equations simultaneously, we get length and breadth of the rectangle.

Question 3.
Find the function.

∴ Given function = \(\frac { 6 }{ 14 }\)
Verify the answer obtained. (Textbook pg. no. 92)
Answer:
For the fraction\(\frac { 6 }{ 14 }\), if the numerator is multiplied by 3 and 3 is subtracted from the denominator, we get fraction \(\frac { 18 }{ 11 }\).
Similarly, for the fraction \(\frac { 6 }{ 14 }\), if the numerator is increased by 8 and the denominator is doubled, we get fraction \(\frac { 1 }{ 2 }\).

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.

Practice Set 6.1 Algebra 9th Std Maths Part 1 Answers Chapter 6 Financial Planning

Question 1.
Alka spends 90% of the money that she receives every month, and saves ₹ 120. How much money does she get monthly?
Solution:
Let Alka’s monthly income be ₹ x.
Alka spends 90% of the money that she receives every month.
∴ Amount spent by Alka = 90% of x
= \(\frac { 90 }{ 100 }\) × x = 0.9x 100
Now, Savings = Income – Expenditure
∴ 120 = x – 0.9x
∴120 = 0.1 x
∴ \(x=\frac{120}{0.1}=\frac{120 \times 10}{0.1 \times 10}\)
∴ x = 1200
Alka gets ₹ 1200 monthly.

Question 2.
Sumit borrowed a capital of ₹ 50,000 to start his food products business. In the first year he suffered a loss of 20%. He invested the remaining capital in a new sweets business and made a profit of 5%. How much was his profit or loss computed on his original capital ?
Solution:
Original capital borrowed by Sumit = ₹ 50000
Sumit suffered a loss of 20% in his food products business.
∴ Loss suffered in the first year = 20% of 50000
= \(\frac { 20 }{ 100 }\) × 50000
= ₹10000
Remaining capital = Original capital – loss suffered = 50000- 10000
= ₹ 40000
Sumit invested the remaining capital i.e. ₹ 40,000 in a new sweets business. He made a profit of 5%.
Profit in sweets business = 5% of 40000
= \(\frac { 5 }{ 100 }\) x 40000 100
= ₹ 2000
New capital with Sumit after the profit in new sweets business = 40000 + 2000 = ₹42000
Since, the new capital is less than the original capital, we can conclude that Sumit suffered a loss.
Total loss on original capital = Original capital – New capital
= 50000 – 42000 = ₹ 8000

∴ Sumit suffered a loss of 16% on the original capital.

Question 3.
Nikhil spent 5% of his monthly income on his children’s education, invested 14% in shares, deposited 3% in a bank and used 40% for his daily expenses. He was left with a balance of ₹ 19,000. What was his income that month?
Solution:
Let the monthly income of Nikhil be ₹ x.
Nikhil invested 14% in shares and deposited 3% in a bank.
∴ Total investment = (14% + 3%) of x
= 17% of x
= \(\frac { 17 }{ 100 }\) × x
= 0.1 7 x
Nikhil spent 5% on his children’s education and used 40% for his daily expenses.

∴ Total expenditure = (5% + 40%) of x
= 45% of x
= \(\frac { 45 }{ 100 }\) × x
= 0.45x
Amount left with Nikhil = 19,000
Amount left with Nikhil = Income – (Total investment + Total expenditure)
∴ 19000 = x – (0.17x + 0.45x)
∴ 19000 = x – 0.62x ,
∴ 19000 = 0.38x
∴ \(x=\frac{19000}{0.38}=\frac{19000 \times 100}{0.38 \times 100}=\frac{1900000}{38}\)
= 50000
∴ The monthly income of Nikhil is ₹ 50000.

Question 4.
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years. Mr. Fernandes invested ₹ 1,20,000 in a mutual fund for 2 years. After 2 years, Mr. Fernandes got ₹ 1,92,000. Whose investment turned out to be more profitable?
Solution:
Mr. Sayyad:
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years P = ₹ 40000, R = 8%, n = 2 years
∴ Compound interest (I)
= Amount (A) – Principal (P)

= 40000 [(1 +0.08)² – 1]
= 40000 [(1.08)² – 1]
= 40000(1.1664 – 1)
= 40000 (0.1664)
= ₹ 6656
∴ Mr. Sayyad’s percentage of profit Interest

Mr. Fernandes:
Amount invested by Mr. Fernandes in mutual fund = ₹ 120000
Amount received by Mr. Fernandes after 2 years = ₹ 192000
∴ Profit earned by Mr. Fernandes
= Amount received – Amount invested
= 192000- 120000
= ₹72000
∴ Mr. Fernandes percentage of profit Profit earned

= 60%
From (i) and (ii),
Investment of Mr. Fernandes turned out to be more profitable.

Question 5.
Sameera spent 90% of her income and donated 3% for socially useful causes. If she was left with ₹ 1750 at the end of the month, what was her actual income ?
Solution:
Let the actual income of Sameera be ₹ x.
Sameera spent 90% of her income and donated 3%.
∴ Sameera’s total expenditure
= (3% + 90%) of x
= 93% of x
= \(\frac { 93 }{ 100 }\) × x
= 0.93x
Now, Savings = Income – Expenditure
∴ 1750 = x-0.93x
∴ 1750 = 0.07x
\(x=\frac{1750}{0.07}=\frac{1750 \times 100}{0.07 \times 100}=\frac{175000}{7}=25000\)
∴ The actual income of Sameera is ₹ 25000.

Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Practice Set 6.1 Intext Questions and Activities

Question 1.
Amita invested some part of ₹ 35000 at 4% and the rest at 5% interest for one year. Altogether her gain was ₹ 1530. Find out the amounts she had invested at the two different rates. Write your answer in words. (Textbook pg. no. 97)
Solution:
Let the amount invested at the rate of 4% and 5% be ₹ x and ₹ y respectively.
According to the first condition, total amount invested = ₹ 35000
∴ x + y = 35000 …(i)
According to the second condition,
total interest received at 4% and 5% is ₹ 1530.
∴ 4 % of x + 5 % of y = 1530
∴ \(\frac { 4 }{ 100 }\) x x + \(\frac { 5 }{ 100 }\) x y = 1530
∴ 4x + 5y = 153000 …(ii)
Multiplying equation (i) by 4, we get
4x + 4y = 140000 …(iii)
Subtracting equation (iii) from (ii),

Substituting y = 13000 in equation (i),
x + 13000 = 35000
∴ x = 35000 – 13000 = 22000

∴ Amita invested ₹ 22000 at the rate of 4% and ₹ 13000 at the rate of 5%.