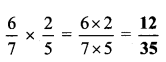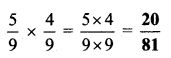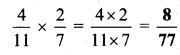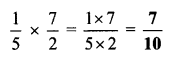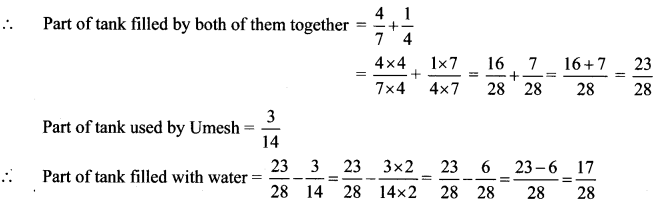Prasanna

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 34 Answers Solutions.

6th Standard Maths Practice Set 34 Answers Chapter 13 Profit-Loss

Question 1.
Cost price Rs 1600, selling price Rs 2800.
Solution:
Sanju bought goods worth Rs 1600 and sold them for Rs 2800. What was his profit in percentage?
Cost price = Rs 1600, Selling price = Rs 2800
Profit = Selling price – Cost price
= 2800 – 1600
= Rs 1200
Let Sanju make profit of x%.

∴ x = 75%
∴ Sanju made a profit of 75%.

Question 2.
Cost price Rs 2000, selling price Rs 1900.
Solution:
Rakhi bought books worth Rs 2000 and sold them for Rs 1900. What was her loss in percentage?
Cost price = Rs 2000, Selling price = Rs 1900
Loss = Cost price – Selling price .
= 2000 – 1900
= Rs 100
Let Rakhi incur a loss of x%.

∴ x = 5%
∴ Rakhi suffered a loss of 5%.

Question 3.
Cost price of 8 articles is Rs 1200 each, selling price Rs 1400 each.
Solution:
Pallavi bought 8 tables for Rs 1200 each and sold them for Rs 1400 each. What was the percentage of her profit or loss?
Cost price of 1 table = Rs 1200
∴ Cost price of 8 tables = 1200 x 8 = Rs 9600
Selling price of 1 table = Rs 1400
∴ Selling price of 8 tables = 1400 x8 = Rs 11200
Selling price is greater than the cost price.
∴ Pallavi made a profit.
∴ Profit = Selling price – Cost price
= 11200 – 9600
= Rs 1600
Let Pallavi make a profit of x%.

∴ Pallavi made a profit of \(16\frac { 2 }{ 3 }\) %.

Question 4.
Cost price of 50 kg grain Rs 2000, Selling price Rs 43 per kg.
Solution:
Ramesh bought 50 kg grains for Rs 2000 and sold it at the rate of Rs 43 per kg. Find the percentage of profit or loss.
Cost price of 50 kg grains = Rs 2000
Selling price of 1 kg grains = Rs 43
∴ Selling price of 50 kg grains= 43 x 50
= Rs 2150
Selling price is greater than the cost price.
∴ Ramesh made a profit.
∴ Profit = Selling price – Cost price
= 2150 – 2000
= Rs 150
Let Ramesh make profit of x%.

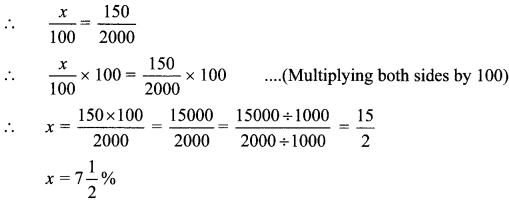
∴ Ramesh made a profit of \(7\frac { 1 }{ 2 }\) %.

Question 5.
Cost price Rs 8600, Transport charges Rs 250, Portage Rs 150, Selling price Rs 10000.
Solution:
Faruk bought a fridge for Rs 8600. He spent Rs 250 on transport and Rs 150 on portage.
If he sold the fridge for Rs 10,000, what was his percent profit or loss?
Total cost price of a fridge = Cost of fridge + Transportation cost + Portage
= 8600 + 250 + 150
= Rs 9000
∴ Selling price = Rs 10,000
Selling price is greater than the total cost price.
∴ Faruk made a profit.
Profit = Selling price – Total cost price
= 10000 – 9000
= Rs 1000
Let Faruk make a profit of x% on cost price.

∴ Faruk made a profit of \(11\frac { 1 }{ 9 }\) %.

Question 6.
Seeds worth Rs 20500, Labour Rs 9700, Chemicals and fertilizers Rs 5600, selling price Rs 28640.
Solution:
Ramchandra bought sunflower seeds worth Rs 20500. He spent Rs 9700 on labour and Rs 5600 on chemicals and fertilizers. He sold it for Rs 28640. What is the percentage of profit or loss?
Total cost price = Cost of seeds + Labour cost + Cost of chemicals and Fertilizers
= 20500 + 9700 + 5600
= Rs 35800
Selling price = Rs 28,640
The total cost price is greater than selling price.
∴ Ramchandra suffered a loss.
Loss = Total cost price – Selling price
= 35800- 28640
= Rs 7160
Let Ramchandra incur a loss of x%.

∴ x = 20%
∴ Ramchandra incurred a loss of 20%.

Maharashtra Board Class 6 Maths Chapter 13 Profit-Loss Practice Set 34 Intext Questions and Activities

Question 1.
Maths is fun! (Textbook pg. no. 72)

Arpita used 4 matchsticks to make a square. Then she took 3 more sticks and arranged them to make 2 squares. Another 3 sticks helped her to make 3 squares. How many sticks are needed to make 7 such squares in the same way? How many sticks are needed to make 50 squares?
Solution:
Matchsticks needed to make 7 squares = 4 + (6 × 3)
= 22
Matchsticks needed to make 50 squares= 4 + (49 × 3)
= 151

Question 2.
Project (Textbook pg. no. 72)
i. Relate instances of profit and loss that you have experienced. Express them as problems and solve the problems.
ii. Organize a fair. Gain the experience of selling things/trading. What was the expenditure on preparing or obtaining the good to be sold? How much were the sales worth? Write a composition about it or enact this entire transaction.
Solution:
(Students should attempt the activities on their own.)

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 12 Answers Solutions.

6th Standard Maths Practice Set 12 Answers Chapter 4 Operations on Fractions

Question 1.
Multiply:
i. \(\frac{7}{5} \times \frac{1}{4}\)
ii. \(\frac{6}{7} \times \frac{2}{5}\)
iii. \(\frac{5}{9} \times \frac{4}{9}\)
iv. \(\frac{4}{11} \times \frac{2}{7}\)
v. \(\frac{1}{5} \times \frac{7}{2}\)
vi. \(\frac{9}{7} \times \frac{7}{8}\)
vii. \(\frac{5}{6} \times \frac{6}{5}\)
viii. \(\frac{6}{17} \times \frac{3}{2}\)
Solution:
i. \(\frac{7}{5} \times \frac{1}{4}\)

ii. \(\frac{6}{7} \times \frac{2}{5}\)

iii. \(\frac{5}{9} \times \frac{4}{9}\)

iv. \(\frac{4}{11} \times \frac{2}{7}\)

v. \(\frac{1}{5} \times \frac{7}{2}\)

vi. \(\frac{9}{7} \times \frac{7}{8}\)

vii. \(\frac{5}{6} \times \frac{6}{5}\)

viii. \(\frac{6}{17} \times \frac{3}{2}\)

Question 2.
Ashokrao planted bananas on \(\frac { 2 }{ 7 }\) of his field of 21 acres. What is the area of the banana plantation?
Solution:
Area of banana plantation is \(\frac { 2 }{ 7 }\) of 21
∴ Area of banana plantation

∴ Area of banana plantation is 6 acres

Question 3.
Of the total number of soldiers in our army, \(\frac { 4 }{ 9 }\) are posted on the northern border and one-third of them on the north-eastern border. If the number of soldiers in the north is 5,40,000, how many are posted in the north-east?
Solution:
Number of soldiers posted on northern border = 5,40,000
Since, number of soldiers in north-east = one third of the soldiers on northern border
∴ Number of soldiers in the north-east

∴ The number of soldiers in the north-east is 1,80,000.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 25 Answers Solutions.

6th Standard Maths Practice Set 25 Answers Chapter 9 HCF-LCM

Question 1.
Find out the LCM of the following numbers.
i. 9,15
ii. 2,3,5
iii. 12,28
iv. 15,20
v. 8,11
Solution:
i. Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Multiples of 15 = 15, 30, 45
∴ LCM of 9 and 15 = 45

ii. Multiples of 2 = 2, 4,6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30
Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 5 = 5, 10, 15, 20, 25, 30
∴ LCM of 2,3 and 5 = 30

iii. Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
Multiples of 28 = 28, 56, 84
∴ LCM of 12 and 28 = 84

iv. Multiples of 15 = 15, 30, 45, 60, 75, 90, 105, 120
Multiples of 20 = 20, 40, 60
∴ LCM of 15 and 20 = 60

v. Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96
Multiples of 11 = 11, 22, 33, 44, 55, 66, 77, 88
∴ LCM of 8 and 11 = 88

Question 2.
Solve the following problems:
i. On the playground, if the children are made to stand for drill either 20 to a row or 25 to a row, all rows are complete and no child is left out. What is the lowest possible number of children in that school?

ii. Veena has some beads. She wants to make necklaces with an equal number of beads in each. If She makes necklaces of 16 or 24 or 40 beads, there is no bead left over. What is the least number of beads with her?

iii. An equal number of laddoos have been placed in 3 different boxes. The laddoos in the first box were distributed among 20 children equally, the laddoos in the second box among 24 children and those in the third box among 12 children. Not a single laddoo was left over. What was the minimum number of laddoos in the three boxes altogether?

iv. We observed the traffic lights at three different squares on the same big road. They turn green every 60 seconds, 120 seconds and 24 seconds. When the signals are switched on at 8 o’clock in the morning, all the lights were green. How long after that will all three signals turn green simultaneously again?

v. Given the fractions \(\frac { 13 }{ 45 }\) and \(\frac { 22 }{ 75 }\). Write their equivalent fractions with same denominators and add the fractions.
Solution:
i. The lowest possible number of children is equal to the lowest common multiple of 20 and 25.
Multiples of 20 = 20, 40, 60, 80, 100, 120, 140, 160, 180, 200
Multiples of 25 = 25, 50, 75, 100
∴ LCM of 20 and 25 = 100
∴ The least number of students in the school is 100.

ii. The least number of beads with Veena is equal to the lowest common multiple of 16,24 and 40.
Multiples of 16 = 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288
Multiples of 24 = 24, 48, 72, 96, 120, 144, 168, 192, 216, 240
Multiples of 40 = 40, 80, 120, 160, 200, 240
∴ LCM of 16, 24 and 40 = 240
∴ The least number of beads with Veena are 240.

iii. The lowest common multiple of 20,24 and 12 gives the minimum number of laddoos in one box.
Multiples of 20 = 20, 40, 60, 80, 100,120, 140, 160, 180, 200
Multiples of 24 = 24, 48, 72, 96, 120
Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
∴ LCM of 20, 24 and 12 = 120
∴ Minimum number of ladoos in 1 boxes =120
∴ Minimum number of ladoos in 3 boxes = 3 x 120 = 360
∴ The minimum number of ladoos in 3 boxes are 360.

iv. All three signals will turn green for lowest common multiple of 60 seconds, 120 seconds and 24 seconds.
Multiples of 60 = 60, 120, 180, 240, 300, 360, 420, 480
Multiples of 120 = 120, 240, 360
Multiples of 24 = 24, 48, 72, 96, 120
LCM of 60, 120 and 24 = 120
Since, 60 seconds = 1 minute
∴ 120 seconds = 2 minutes
∴ The signals will turn green simultaneously again after 120 seconds i.e. 2 minutes.

v. The lowest common multiple of 45 and 75 gives the same denominator.
Multiples of 45 = 45, 90, 135, 180, 225, 270, 315, 360, 405, 450
Multiples of 75 = 75, 150, 336
∴ LCM of 45 and 75 = 225

Maharashtra Board Class 6 Maths Chapter 9 HCF-LCM Practice Set 25 Intext Questions and Activities

Question 1.
Pravin, Bageshri and Yash are cousins who live in the same house. Pravin is an Army Officer. Bageshri is studying in a Medical College in another city. Yash lives in a nearby town in a hostel. Pravin can come home every 120 days.
Bageshri comes home every 45 days and Yash, every 30 days. All three of them left home at the same time on the 15th of June 2016. Their parents said, “We shall celebrate like a festival the day you all come home together.” Mother asked Yash, “What day will that be?”
Yash said, “The number of days after which we come back together must be divisible by 30, 120. That means we shall be back together on the 10th of June next year. That will certainly be a for us!”
How did Yash find the answer? (Textbook pg. no. 49)

Solution:
The day when Pravin, Bageshri and Yash come back together is lowest common multiple of 30, 45 and 120.
Multiples of 30: 30, 60, 90, 120, 150, 180,210, 240, 270, 300, 330, 360
Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360
Multiples of 120: 120, 240, 360
∴ They will come together after 360 days
Day when they left home = 15th June
∴ Day when they come back together = 15th June + 360 days
= 10th June next year
∴ Pravin, Bageshri and Yash will come back together on 10th June next year.

Question 2.
A Maths Riddle! (Textbook pg. no. 50)
We have four papers. On each of them there is a number on one side and some information on the other. The numbers on the papers are 7, 2, 15, 5. The information on the papers is given below in random order.
i. A number divisible by 7
ii. A prime number
iii. An odd number
iv. A number greater than 100
If the number on every paper is mismatched with the information on its other side, what is the number on the paper which says ‘A number greater than 100?
Solution:

Analysis	Reason	Outcome
The paper having information (iii) ‘an odd number’ can be mismatched with the number ‘2’ from the other available options.	Only the number ‘2’ is an even number, while the rest are odd numbers.	The number ‘2’ and (iii) ‘an odd number’ will appear on the opposite sides of the same paper.
Now, we are left with the numbers 7, 15 and 5. The paper having information (i) ‘a number divisible by 7′ can be mismatched with the number ‘5’.	The number ‘5’ is not divisible by 7.	The number ‘5’ and (i) ‘a number divisible by 7’ will appear on the opposite sides of the same paper.
Now, we are left with the numbers 7 and 15. The paper having information (ii) ‘a prime number’ can be mismatched with the number ‘15’.	The number ‘15’ is not a prime number.	Hence, the number ‘15’ and (ii) ‘a prime number’ will appear on the opposite sides of the same paper.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 11 Answers Solutions.

6th Standard Maths Practice Set 11 Answers Chapter 4 Operations on Fractions

Question 11.
What fractions do the points A and B show on the number lines below?

Solution:
(1) Each unit is divided in 6 parts
A is 5th division from 0
∴ \(A=\frac { 5 }{ 6 }\)

B is 10th division from 0
∴ \(B=\frac { 10 }{ 6 }\)

(2) Each unit is divided in 5 parts
A is 3rd division from 0
∴ \(A=\frac { 3 }{ 5 }\)

B is 7th division from 0
∴ \(B=\frac { 7 }{ 5 }\)

(3) Each unit is divided in 7 parts
A is 10th division from 0
∴ \(A=\frac { 10 }{ 7 }\)

B is 3rd division from 0
∴ \(B=\frac { 3 }{ 7 }\)

Question 2.
Show the following fractions on the number line:
i. \(\frac{3}{5}, \frac{6}{5}, 2 \frac{3}{5}\)
ii. \(\frac{3}{4}, \frac{5}{4}, 2 \frac{1}{4}\)
Solution:
i. \(\frac{3}{5}, \frac{6}{5}, 2 \frac{3}{5}\)

ii. \(\frac{3}{4}, \frac{5}{4}, 2 \frac{1}{4}\)

Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 11 Intext Questions and Activities

Question 1.
If we want to show the fractions \(\frac{3}{10}, \frac{9}{20}, \frac{19}{40}\) on the number line, how big should the unit be? (Textbook pg. no. 24)
Solution:
The denominators of the given fractions are not equal.
The numbers in the denominators 10, 20 and 40 have common multiple 40.
∴ Making the denominators equal, we get

∴ To represent these fractions on the numbers line, each main unit should be divided into 40 equal sub-units.

Therefore,
\(\frac{3}{10}=\frac{12}{40}\) is represented on 12th mark from 0.
\(\frac{9}{20}=\frac{18}{40}\) is represented on 18th mark from 0 and
\(\frac { 19 }{ 40 }\) is represented on 19 mark from 0.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 33 Answers Solutions.

6th Standard Maths Practice Set 33 Answers Chapter 13 Profit-Loss

Question 1.
Maganlal bought trousers for Rs 400 and a shirt for Rs 200 and sold them for Rs 448 and Rs 250 respectively. Which of these transactions was more profitable?
Solution:
Cost price of trousers = Rs 400
Selling price of trousers = Rs 448
Profit = Selling price – Cost price
= 448 – 400 = Rs 48
Let Maganlal make x % profit on selling trousers

∴ x = 12%
Cost price of shirt = Rs 200
Selling price of shirt = Rs 250
∴ Profit = Selling price – Cost price
= 250 – 200
= Rs 50
Let Maganlal make y% profit on selling shirt.

∴ y = 25%
∴ Transaction involving selling of shirt was more profitable.

Question 2.
Ramrao bought a cupboard for Rs 4500 and sold it for Rs 4950. Shamrao bought a sewing machine for Rs 3500 and sold it for Rs 3920. Whose transaction was more profitable?
Solution:
Cost price of cupboard = Rs 4500
Selling price of cupboard = Rs 4950
∴ Profit = Selling price – Cost price
= 4950 – 4500
= Rs 450
Let Ramrao make x% profit on selling cupboard

∴ x = 10%
Cost price of sewing machine = Rs 3500
Selling price of sewing machine = Rs 3920
∴Profit = Selling price – Cost price
= 3920 – 3500
= Rs 420
Shamrao make y% profit on selling sewing machine.

∴y = 12%
∴Shamrao’s transaction was more profitable.

Question 3.
Hanif bought one box of 50 apples for Rs 400. He sold all the apples at the rate of Rs 10 each. Was there a profit or loss? What was its percentage?
Solution:
Cost price of 50 apples = Rs 400
Selling price of one apple = Rs 10
∴ Selling price of 50 apples = 10 x 50 = Rs 500
Selling price is greater than the total cost price.
∴ Hanif made a profit.
∴ Profit = Selling price – Cost price
= 500 – 400
= Rs 100
Let Hanif make of x% profit on selling apples.

∴ x = 25%
∴ Hanif made a profit of 25%.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 24 Answers Solutions.

6th Standard Maths Practice Set 24 Answers Chapter 9 HCF-LCM

Question 1.
Find the HCF of the following numbers.
i. 45, 30
ii. 16, 48
iii. 39, 25
iv. 49, 56
v. 120, 144
vi. 81, 99
vii. 24, 36
viii. 25, 75
ix. 48, 54
x. 150, 225
Solution:
i. Factors of 45 = 1, 3, 5, 9,15, 45
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ HCF of 45 and 30 = 15

ii. Factors of 16 = 1, 2, 4, 8, 16
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
∴ HCF of 16 and 48 = 16

iii. Factors of 39 = 1, 3, 13, 39
Factors of 25 = 1, 5, 25
∴ HCF of 39 and 25 = 1

iv. Factors of 49 = 1, 7, 49
Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
∴ HCF of 49 and 56 = 7

v. Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 144 = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
∴ HCF of 120 and 144 = 24

vi. Factors of 81 = 1, 3, 9, 27, 81
Factors of 99 = 1, 3, 9, 11, 33, 99
∴ HCF of 81 and 99 = 9

vii. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
∴ HCF of 24 and 36 = 12

viii. Factors of 25 = 1, 5, 25
Factors of 75 = 1, 3, 5, 15, 25, 75
∴ HCF of 25 and 75 = 25

ix. Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 54 = 1, 2, 3, 6, 9, 18, 27, 54
∴ HCF of 48 and 54 = 6

x. Factors of 150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Factors of 225 = 1, 3, 5, 9, 15, 25, 45, 75, 225
∴ HCF of 150 and 225 = 75

Question 2.
If large square beds of equal size are to be made for planting vegetables on a plot of land 18 metres long and 15 metres wide, what is the maximum possible length of each bed?
Solution:
Length of the land = 18 m
Width of the land = 15 m
The maximum length of each bed will be the greatest common factor of 18 and 15.
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 15 = 1, 3, 5, 15
∴ HCF of 18 and 15 = 3
∴ The maximum possible length of each bed is 3 metres.

Question 3.
Two ropes, one 8 metres long and the other 12 metres long are to be cut into pieces of the same length. What will the maximum possible length of each piece be?
Solution:
Length of first rope = 8 m
Length of second rope = 12 m
The maximum length of each piece will be the greatest common factor of 8 and 12.
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
∴ HCF of 8 and 12 = 4
∴ The maximum possible length of each piece is 4 metres.

Question 4.
The number of students of Std 6th and Std 7th who went to visit the Tadoba Tiger Project at Chandrapur was 140 and 196 respectively. The students of each class are to be divided into groups of the same number of students. Each group can have a paid guide. What is the maximum number of students that can be there in each group? Why do you think each group should have the maximum possible number of students?
Solution:
Number of students of Std 6th = 140
Number of students of Std 7th = 196
The maximum number of students in each group will be the greatest common factor of 140 and 196.
Factors of 140 = 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Factors of 196 = 1, 2, 4, 7, 14, 28, 49, 98, 196
∴ HCF of 140 and 196 = 28
∴ Maximum students in each group are 28.
Each group should have maximum number students so that there will be minimum number of groups and hence minimum number of paid guides.

Question 5.
At the Rice Research Centre at Tumsar there are 2610 kg of seeds of the basmati variety and 1980 kg of the indrayani variety. If the maximum possible weight of seeds has to be filled to make bags of equal weight what would be the weight of each bag? How many bags of each variety will there be?
Solution:
Weight of basmati rice = 2610 kg
Weight of indrayani rice = 1980 kg
The weight of each bag will be the greatest common factor of 2610 and 1980.
Factors of 2610 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 29, 30, 45, 58, 87, 90, 145, 174, 261, 290, 435, 522, 870, 1305, 2610
Factors of 1980 = 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 18, 20, 22, 30, 33, 36, 44, 45, 55, 60, 66, 90, 99, 110, 132, 165, 180, 198, 220, 330, 396, 495, 660, 990, 1980
∴ HCF of 2610 and 1980 = 90
Maximum weight of each bag = 90 kg
Number of bags of basmati rice = 2610 ÷ 90 = 29
Number of bags of indrayani rice = 1980 ÷ 90 = 22
Maximum weight of each bag is 90 kg.
The number of bags of basmati rice is 29, and the number of bags of indrayani rice is 22.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 1 Answers Solutions Chapter 1 Geometrical Constructions.

Geometrical Constructions Class 7 Practice Set 1 Answers Solutions Chapter 1

Question 1.
Draw line segments of the lengths given below and draw their perpendicular bisectors:
i. 5.3 cm
ii. 6.7 cm
iii. 3.8 cm
Solution:
i.

Line AB is the perpendicular bisector of seg PQ.

ii.

Line UV is the perpendicular bisector of seg ST.

iii.

Line ST is the perpendicular bisector of seg LM.

Question 2.
Draw angles of the measures given below and draw their bisectors:
i. 105°
ii. 55°
iii. 90°
Solution:
i. 105°

ii. 55°

iii. 90°

Question 3.
Draw, an obtuse-angled triangle and a right-angled triangle. Find the points of concurrence of the angle bisectors of each triangle. Where do the points of concurrence lie?
Solution:

The points of concurrence of the angle bisectors of both the triangles lie in the interior of the triangles.

Question 4.
Draw a right-angled triangle. Draw the perpendicular bisectors of its sides. Where does the point of concurrence lie?
Solution:

The point of concurrence of the perpendicular bisectors of the sides of the right angled triangle lies on the hypotenuse.

Question 5.
Maithili, Shaila and Ajay live in three different places in the city. A toy shop is equidistant from the three houses. Which geometrical construction should be used to represent this? Explain your answer.
Solution:
Since, Maithili, Shaila and Ajay live in three different places, lines joining their houses will form a triangle.
The position of the toy shop which is equidistant from three houses can be found out by drawing the perpendicular bisector of the sides of the triangle joining the three houses.
The shop will be at the point of concurrence of the perpendicular bisectors.

Maharashtra Board Class 7 Maths Chapter 1 Geometrical Constructions Practice Set 1 Intext Questions and Activities

Question 1.
Draw a line segment PS of length 4cm and draw its perpendicular bisector. (Textbook pg. no. 1)

1. How will your verify that CD is the perpendicular bisector? m∠CMS = __°
2. Is l(PM) = l(SM)?

Solution:

1. Here, m∠CMS = 90°
2. Also, l(PM) = l(SM) = 2cm
   ∴ line CD is the perpendicular bisector of seg PS.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 23 Answers Solutions.

6th Standard Maths Practice Set 23 Answers Chapter 9 HCF-LCM

Question 1.
Write all the factors of the given numbers and list their common factors:
i. 12, 16
ii. 21, 24
iii. 25, 30
iv. 24, 25
v. 56, 72
Solution:
i. Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 16 = 1, 2, 4, 8, 16
∴ Common factors of 12 and 16 = 1, 2, 4

ii. Factors of 21 = 1, 3, 7, 21
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
∴ Common factors of 21 and 24 = 1, 3

iii. Factors of 25 = 1, 5, 25
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ Common factors of 25 and 30 = 1, 5

iv. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 25 = 1,5, 25
∴ Common factor of 24 and 25 = 1

v. Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
∴ Common factors of 56 and 72 = 1, 2, 4, 8

Maharashtra Board Class 6 Maths Chapter 9 HCF-LCM Practice Set 23 Intext Questions and Activities

Question 1.
In the empty boxes, write the proper words: dividend, divisor, quotient, remainder. (Textbook pg. no. 46)

Solution:

When we divide 36 by 4, the remainder is zero. Therefore, 4 is a factor of 36 and 36 is a multiple of 4. But, when we divide 65 by 9, the remainder is not zero. Therefore, 9 is not a factor of 65. Also, 65 is not a multiple of 9.

Question 2.
Write all the factors of the numbers 36 and 48. Also, list their common factors. (Textbook pg. no. 46)
Solution:
36 = 1 × 36
= 2 × 18
= 3 × 12
= 4 × 9
= 6 × 6

48 = 1 × 48
= 2 × 24
= 3 × 16
= 4 × 12
= 6 × 8

∴ Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Common factors of 36 and 48: [1] ,[2], [3], [4], [6], [12]

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 32 Answers Solutions.

6th Standard Maths Practice Set 32 Answers Chapter 13 Profit-Loss

Question 1.
From a wholesaler, Santosh bought 400 eggs for Rs 1500 and spent Rs 300 on transport. 50 eggs fell down and broke. He sold the rest at Rs 5 each. Did he make a profit or a loss? How much?
Solution:
Cost price of 400 eggs = Rs 1500
Transportation cost = Rs 300
∴ Total cost price of 400 eggs = Cost price of 400 eggs + Transportation cost
= 1500 + 300 = Rs 1800
50 eggs fell and broke
∴ Remaining eggs = 400 – 50 = 350
Selling price of 1 egg = Rs 5
∴ Selling price of 350 eggs = 5 x 350 = Rs 1750
Total cost price is greater than the selling price.
∴ Santosh suffered a loss.
Loss = Total cost price – Selling price
= 1800 – 1750
= Rs 50
∴ Santosh incurred a loss of Rs 50.

Question 2.
Abraham bought goods worth Rs 50000 and spent Rs 7000 on transport and octroi. If he sold the goods for Rs 65000, did he make a profit or a loss? How much?
Solution:
Cost price of goods = Rs 50000
Transportation cost and octroi = Rs 7000
∴ Total cost price for buying goods = Cost price of goods + Transportation cost and octroi
= 50000 + 7000 = Rs 57000
Selling price of goods = Rs 65000
Selling price is greater than the total cost price
∴ Abraham made a profit.
Profit = Selling price – Total cost price
= 65000 – 57000
= Rs 8000
∴ Abraham made a profit of Rs 8000.

Question 3.
Ajit Kaur bought a 50 kg sack of sugar for Rs 1750, but as sugar prices fell, she had to sell it at Rs 32 per kg. How much loss did she incur?
Solution:
Cost price of 50 kg sugar = Rs 1750
Selling price of 1 kg sugar = Rs 32
∴ Selling price of 50 kg sugar = 50 x 32 = Rs 1600
Loss = Total cost price – Selling price
= 1750 – 1600 = Rs 150
∴ Ajit Kaur incurred a loss of Rs 150.

Question 4.
Kusumtai bought 80 cookers at Rs 700 each. Transport cost her Rs 1280. If she wants a profit of Rs 18000, what should be the selling price per cooker?
Solution:
Cost price of one cooker = Rs 700
∴ Cost price of 80 cookers = 700 x 80 = Rs 56000
Transportation cost = Rs 1280
∴ Total cost price = Cost price of 80 cookers + Transportation cost
= 56000 + 1280
= Rs 57280
Profit = Rs 18000
Profit = Selling Price – Total Cost Price
∴ Required selling price = Total cost price + profit
= 57280 + 18000
= Rs 75280
∴ Selling price of 80 cookers = Rs 75280
∴ Selling price of 1 cooker = \(\frac { 75280 }{ 80 }\) = Rs 941
∴ The selling price per cooker should be Rs 941.

Question 5.
Indrajit bought 10 refrigerators at Rs 12000 each and spent Rs 5000 on transport. For how much should he sell each refrigerator in order to make a profit of Rs 20000?
Solution:
Cost price of 1 refrigerator = Rs 12000
Cost price of 10 refrigerator = 10 x 12000 = Rs 120000
Transportation cost = Rs 5000
∴ Total cost price of 10 refrigerators = Cost price of 10 refrigerators + Transportation cost
= 120000 + 5000 = Rs 125000
Profit = Rs 20000
Profit = Selling Price – Total Cost Price
∴ Required selling price = Total cost price + Profit
= 125000 + 20000 = Rs 145000
∴ Selling price of 10 refrigerators = Rs 145000
∴ Selling price of 1 refrigerator = \(\frac { 145000 }{ 10 }\) = Rs 14500
∴ Indrajit must sell each refrigerator at Rs 14500 to make a profit of Rs 20000.

Question 6.
Lalitabai sowed seeds worth Rs 13700 in her field. She had to spend Rs 5300 on fertilizers and spraying pesticides and Rs 7160 on labor. If, on selling her produce, she earned Rs 35400 what was her profit or her loss?
Solution:
Cost price of seeds = Rs 13700
Cost of fertilizers and pesticides = Rs 5300
Labor cost = Rs 7160
∴ Total cost price = Cost price of seeds + Cost of fertilizers and pesticides + Labor cost
= 13700 + 5300 + 7160
= Rs 26160
Selling price = Rs 35400
Selling price is greater than the total cost price.
∴ Lalitabai made a profit.
Profit = Selling price – Cost price
= 35400 – 26160
= Rs 9240
∴ Lalitabai made a profit of Rs 9240.

Maharashtra Board Class 6 Maths Chapter 13 Profit-Loss Practice Set 32 Intext Questions and Activities

Question 1.
At Diwali, in a certain school, the students undertook a Design a Diya project. They bought 1000 diyas for Rs 1000 and some paint for Rs 200. To bring the diyas to the school, they spent Rs 100 on transport. They sold the painted lamps at Rs 2 each. Did they make a profit or incur a loss? (Textbook pg. no. 67 and 68)

i. Is Anju right?
ii. What about the money spent on paints and transport?
iii. How much money was actually spent before the diyas could be sold?
iv. How much actual profit was made in this project of colouring the diyas and selling them?

Ans:
i. No, Anju is wrong.
Cost price of diyas also includes the painting and transportation cost.
∴ Total cost price of diyas = Cost of diyas + Cost of paint + Transportation cost
= 1000 + 200+ 100
= Rs 1300
ii. The cost of paint was Rs 200 and that for transportation was Rs 100. These costs are also to be added to the cost price of diyas.
iii. Rs 1300 was actually spent before the diyas could be sold.
iv. Total Cost Price of 1000 Diyas = Rs 1300
Selling Price of 1 Diya = Rs 2
∴ Selling Price of 1000 Diyas = 2 x 1000 = Rs 2000
∴ Profit = Selling Price – Total Cost Price
= 2000 – 1300
= Rs 700
∴ The profit made by coloring the diyas and selling them was Rs 700.

Question 2.
A farmer sells what he grows in his fields. How is the total cost price calculated? What does a farmer spend on his produce before he can sell it? What are the other expenses besides seeds, fertilizers and transport? (Textbook pg. no. 68)
Solution:
The farmer, in order to calculate the total cost price of his produce, needs to consider all the expenses associated with the growing and selling of his produce.

Following are the things on which farmer spends money before he can sell it.

1. Time and energy
2. Ploughing and tilling
3. Irrigation and electricity cost
4. Harvesting and cleaning
5. Packing

As given above, there are a multiple of costs to be included besides seeds, fertilizers and transport for the farmer to price its produce appropriately.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 10 Answers Solutions.

6th Standard Maths Practice Set 10 Answers Chapter 4 Operations on Fractions

Question 1.
Add:
i. \(6 \frac{1}{3}+2 \frac{1}{3}\)
ii. \(1 \frac{1}{4}+3 \frac{1}{2}\)
iii. \(5 \frac{1}{5}+2 \frac{1}{7}\)
iv. \(3 \frac{1}{5}+2 \frac{1}{3}\)
Solution:
i. \(6 \frac{1}{3}+2 \frac{1}{3}\)

ii. \(1 \frac{1}{4}+3 \frac{1}{2}\)

iii. \(5 \frac{1}{5}+2 \frac{1}{7}\)

iv. \(3 \frac{1}{5}+2 \frac{1}{3}\)

Question 2.
Subtract:
i. \(3 \frac{1}{3}-1 \frac{1}{4}\)
ii. \(5 \frac{1}{2}-3 \frac{1}{3}\)
iii. \(7 \frac{1}{8}-6 \frac{1}{10}\)
iv. \(7 \frac{1}{2}-3 \frac{1}{5}\)
Solution:
i. \(3 \frac{1}{3}-1 \frac{1}{4}\)

ii. \(5 \frac{1}{2}-3 \frac{1}{3}\)

iii. \(7 \frac{1}{8}-6 \frac{1}{10}\)

iv. \(7 \frac{1}{2}-3 \frac{1}{5}\)

Question 3.
Solve:
i. Suyash bought \(2\frac { 1 }{ 2 }\) kg of sugar and Ashish bought \(3\frac { 1 }{ 2 }\) kg. How much sugar did they buy altogether? If sugar costs Rs 32 per kg, how much did they spend on the sugar they bought?

ii. Aradhana grows potatoes in \(\frac { 2 }{ 5 }\) part of her garden, greens in \(\frac { 1 }{ 3 }\) part and brinjals in the remaining part. On how much of her plot did she plant brinjals?

iii. Sandeep filled water in \(\frac { 4 }{ 7 }\) of an empty tank. After that, Ramakant filled \(\frac { 1 }{ 4 }\) part more of the same tank. Then Umesh used \(\frac { 3 }{ 14 }\) part of the tank to water the garden. If the tank has a maximum capacity of 560 litres, how many litres of water will be left in the tank?
Solution:
i. Sugar bought by Suyash = \(2\frac { 1 }{ 2 }\) kg
Sugar bought by Ashish = \(3\frac { 1 }{ 2 }\) kg
∴ Total sugar bought by both

Cost of 1 kg of sugar = Rs 32
∴ Cost of 6 kg of sugar = 32 x 6
= Rs 192
∴ They bought 6 kg sugar altogether and the total money spent on sugar is Rs 192.

ii. Part of garden occupied by potatoes = \(\frac { 2 }{ 5 }\)
Part of garden occupied by greens = \(\frac { 1 }{ 3 }\)
Since brinjals are planted in the remaining part,
∴ (Part occupied by potatoes) + (part occupied by greens) + (part occupied by brinjals) = 1 entire garden.
∴ Part of garden occupied by brinjals = 1 – (part of garden occupied by potatoes + part of garden occupied by greens)

∴ Aradhana planted brinjals on \(\frac { 4 }{ 15 }\) part of her plot.

iii. Part of tank filled by Sandeep = \(\frac { 4 }{ 7 }\)
Part of tank filled by Ramakant = \(\frac { 1 }{ 4 }\)

Since maximum capacity of tank is 560 litres
∴ Quantity of water left in tank = \(\frac { 17 }{ 28 }\times560\) = 340 litres
∴ The quantity of water left in the tank is 340 litres.

Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 10 Intext Questions and Activities

Question 1.
How to do this subtraction: \(4 \frac{1}{4}-2 \frac{1}{2}\) ? Is it same as \(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\) ? (Textbook pg. no. 23)
Solution:
\(4 \frac{1}{4}-2 \frac{1}{2}\)

\(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\)

The subtraction \(4 \frac{1}{4}-2 \frac{1}{2}\) is the same as \(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\).