Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 25 Answers Solutions.
6th Standard Maths Practice Set 25 Answers Chapter 9 HCF-LCM
Question 1.
Find out the LCM of the following numbers.
i. 9,15
ii. 2,3,5
iii. 12,28
iv. 15,20
v. 8,11
Solution:
i. Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Multiples of 15 = 15, 30, 45
∴ LCM of 9 and 15 = 45
ii. Multiples of 2 = 2, 4,6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30
Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 5 = 5, 10, 15, 20, 25, 30
∴ LCM of 2,3 and 5 = 30
iii. Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
Multiples of 28 = 28, 56, 84
∴ LCM of 12 and 28 = 84
iv. Multiples of 15 = 15, 30, 45, 60, 75, 90, 105, 120
Multiples of 20 = 20, 40, 60
∴ LCM of 15 and 20 = 60
v. Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96
Multiples of 11 = 11, 22, 33, 44, 55, 66, 77, 88
∴ LCM of 8 and 11 = 88
Question 2.
Solve the following problems:
i. On the playground, if the children are made to stand for drill either 20 to a row or 25 to a row, all rows are complete and no child is left out. What is the lowest possible number of children in that school?
ii. Veena has some beads. She wants to make necklaces with an equal number of beads in each. If She makes necklaces of 16 or 24 or 40 beads, there is no bead left over. What is the least number of beads with her?
iii. An equal number of laddoos have been placed in 3 different boxes. The laddoos in the first box were distributed among 20 children equally, the laddoos in the second box among 24 children and those in the third box among 12 children. Not a single laddoo was left over. What was the minimum number of laddoos in the three boxes altogether?
iv. We observed the traffic lights at three different squares on the same big road. They turn green every 60 seconds, 120 seconds and 24 seconds. When the signals are switched on at 8 o’clock in the morning, all the lights were green. How long after that will all three signals turn green simultaneously again?
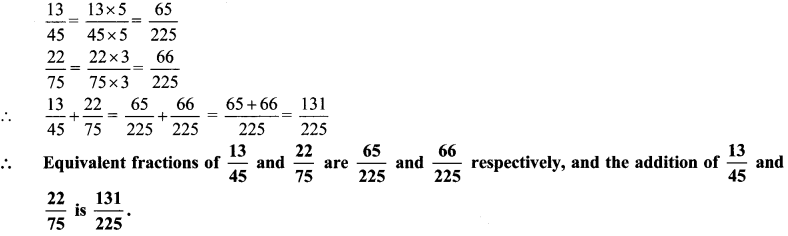
v. Given the fractions \(\frac { 13 }{ 45 }\) and \(\frac { 22 }{ 75 }\). Write their equivalent fractions with same denominators and add the fractions.
Solution:
i. The lowest possible number of children is equal to the lowest common multiple of 20 and 25.
Multiples of 20 = 20, 40, 60, 80, 100, 120, 140, 160, 180, 200
Multiples of 25 = 25, 50, 75, 100
∴ LCM of 20 and 25 = 100
∴ The least number of students in the school is 100.
ii. The least number of beads with Veena is equal to the lowest common multiple of 16,24 and 40.
Multiples of 16 = 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288
Multiples of 24 = 24, 48, 72, 96, 120, 144, 168, 192, 216, 240
Multiples of 40 = 40, 80, 120, 160, 200, 240
∴ LCM of 16, 24 and 40 = 240
∴ The least number of beads with Veena are 240.
iii. The lowest common multiple of 20,24 and 12 gives the minimum number of laddoos in one box.
Multiples of 20 = 20, 40, 60, 80, 100,120, 140, 160, 180, 200
Multiples of 24 = 24, 48, 72, 96, 120
Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
∴ LCM of 20, 24 and 12 = 120
∴ Minimum number of ladoos in 1 boxes =120
∴ Minimum number of ladoos in 3 boxes = 3 x 120 = 360
∴ The minimum number of ladoos in 3 boxes are 360.
iv. All three signals will turn green for lowest common multiple of 60 seconds, 120 seconds and 24 seconds.
Multiples of 60 = 60, 120, 180, 240, 300, 360, 420, 480
Multiples of 120 = 120, 240, 360
Multiples of 24 = 24, 48, 72, 96, 120
LCM of 60, 120 and 24 = 120
Since, 60 seconds = 1 minute
∴ 120 seconds = 2 minutes
∴ The signals will turn green simultaneously again after 120 seconds i.e. 2 minutes.
v. The lowest common multiple of 45 and 75 gives the same denominator.
Multiples of 45 = 45, 90, 135, 180, 225, 270, 315, 360, 405, 450
Multiples of 75 = 75, 150, 336
∴ LCM of 45 and 75 = 225
Maharashtra Board Class 6 Maths Chapter 9 HCF-LCM Practice Set 25 Intext Questions and Activities
Question 1.
Pravin, Bageshri and Yash are cousins who live in the same house. Pravin is an Army Officer. Bageshri is studying in a Medical College in another city. Yash lives in a nearby town in a hostel. Pravin can come home every 120 days.
Bageshri comes home every 45 days and Yash, every 30 days. All three of them left home at the same time on the 15th of June 2016. Their parents said, “We shall celebrate like a festival the day you all come home together.” Mother asked Yash, “What day will that be?”
Yash said, “The number of days after which we come back together must be divisible by 30, 120. That means we shall be back together on the 10th of June next year. That will certainly be a for us!”
How did Yash find the answer? (Textbook pg. no. 49)

Solution:
The day when Pravin, Bageshri and Yash come back together is lowest common multiple of 30, 45 and 120.
Multiples of 30: 30, 60, 90, 120, 150, 180,210, 240, 270, 300, 330, 360
Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360
Multiples of 120: 120, 240, 360
∴ They will come together after 360 days
Day when they left home = 15th June
∴ Day when they come back together = 15th June + 360 days
= 10th June next year
∴ Pravin, Bageshri and Yash will come back together on 10th June next year.
Question 2.
A Maths Riddle! (Textbook pg. no. 50)
We have four papers. On each of them there is a number on one side and some information on the other. The numbers on the papers are 7, 2, 15, 5. The information on the papers is given below in random order.
i. A number divisible by 7
ii. A prime number
iii. An odd number
iv. A number greater than 100
If the number on every paper is mismatched with the information on its other side, what is the number on the paper which says ‘A number greater than 100?
Solution:
| Analysis | Reason | Outcome |
| The paper having information (iii) ‘an odd number’ can be mismatched with the number ‘2’ from the other available options. | Only the number ‘2’ is an even number, while the rest are odd numbers. | The number ‘2’ and (iii) ‘an odd number’ will appear on the opposite sides of the same paper. |
| Now, we are left with the numbers 7, 15 and 5. The paper having information (i) ‘a number divisible by 7′ can be mismatched with the number ‘5’. | The number ‘5’ is not divisible by 7. | The number ‘5’ and (i) ‘a number divisible by 7’ will appear on the opposite sides of the same paper. |
| Now, we are left with the numbers 7 and 15. The paper having information (ii) ‘a prime number’ can be mismatched with the number ‘15’. | The number ‘15’ is not a prime number. | Hence, the number ‘15’ and (ii) ‘a prime number’ will appear on the opposite sides of the same paper. |