Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 35 Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 35
Determine whether the pairs of numbers given below are co-prime numbers.
(1) 22, 24
Answer:
Common factors of 22 and 24 are 1 and 2. (Not only 1 common factor) So, 22, 24 are not co-prime numbers.
(2) 14, 21
Answer:
Common factors of 14 and 21 are 1 and 7. So, this pair is not co-prime numbers.
(3) 10, 33
Answer:
Common factors of 10 and 33 is only 1. So, 10 and 33 are co-prime numbers.
(4) 11, 30
Answer:
Common factors of 11 and 30 is only 1. So, 11 and 30 are co-prime numbers.
(5) 5, 7
Answer:
Common factor of 5 and 7 is only 1. So, 5 and 7 are co-prime numbers.
(6) 15, 16
Answer:
Common factors of 15 and 16 is only 1. So, 15 and 16 are co-prime numbers.
(7) 50, 52
Answer:
Common factors of 50 and 52 are 1 and 2. So, 50 and 52 are not co-prime numbers.
(8) 17, 18
Answer:
Common factors of 17 and 18 is only 1. So, 17 and 18 are co-prime numbers.
Activity 1 :
- Write numbers from 1 to 60.
- Draw a blue circle around multiples of 2.
- Draw a red circle around multiples of 4.
- Do all numbers with a blue circle also have a red circle around them?
- Do all the numbers with a red circle have a blue circle around them?
- Are all multiples of 2 also multiples of 4?
- Are all multiples of 4 also multiples of 2?
Activity 2 :
- Write numbers from 1 to 60.
- Draw a triangle around multiples of 2.
- Draw a circle around multiples of 3.
- Now find numbers divisible by 6. Can you find a property that they share?
Eratosthenes’ method of finding prime numbers
Eratosthenes was a mathematician who lived in Greece about 250 BC. He discovered a method to find prime numbers. It is called Eratosthenes’ Sieve. Let us see how to find prime numbers between 1 and 100 with this method.

- 1 is neither a prime nor a composite number. Put a square [ ] around it
- 2 is a prime number, so put a circle around it.
- Next, strike out all the multiples of 2. This tells us that of these 100 numbers more than half of numbers are not prime numbers.
- The first number after 2 not yet struck off is 3. So, 3 is a prime number.
- Draw a circle around 3. Strike out all the multiples of 3.
- The next number after 3 not struck off yet is 5. So, 5 is a prime number.
- Draw a circle around 5. Put a line through all the multiples of 5.
- The next number after 5 without a line through it is 7. So, 7 is a prime number.
- Draw a circle around 7. Put a line through all the multiples of 7.
In this way, every number between 1 and 100 will have either a circle or a line through it. The circled numbers are prime numbers. The numbers with a line through them are composite numbers.
One more method to find prime numbers
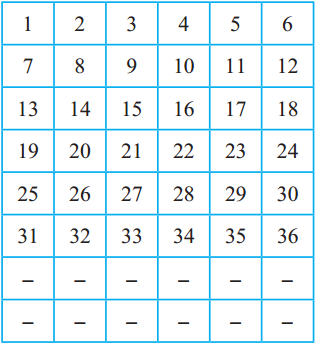
See how numbers from 1 to 36 have been arranged in six columns in the table alongside.
Continue in the same way and write numbers up to 102 in these six columns.
You will see that, in the columns for 2, 3, 4, and 6, all the numbers are composite numbers except for the prime numbers 2 and 3. This means that all the remaining prime numbers will be in the columns for 1 and 5. Now isn’t it easier to find them? So, go ahead, find the prime numbers!
Something more
- Prime numbers with a difference of two are called twin prime numbers. Some twin prime number pairs are 3 and 5, 5 and 7, 29 and 31 and 71 and 73. 5347421 and 5347423 are also a pair of twin prime numbers.
- There are eight pairs of twin prime numbers between 1 and 100. Find them.
- Euclid the mathematician lived in Greece about 300 BC. He proved that if prime numbers, 2, 3, 5, 7, ……., are written in serial order, the list will never end, meaning that the number of prime numbers is infinite.
Multiples and Factors Problem Set 35 Additional Important Questions and Answers
Determine whether the pairs of numbers given below are co-prime numbers.
(1) (12,18)
Answer:
Common factors of 12 and 18 are 1, 2, 3, 6. Hence 12 and 18 are not co-prime numbers.
(2) (26, 39)
Answer:
Common factors of 26 and 39 are 1 and 13. Hence, 26 and 39 are not co-prime numbers.
(3) (23, 29)
Answer:
Common factor of 23 and 29 is only 1. Hence, 23 and 29 are co-prime numbers.
(4) (28, 32)
Answer:
Common factors of 28 and 32 are 1, 2, 4 (not only 1). Hence, 28, 32 are not co-prime numbers.