Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 18 Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 18
Convert the given fractions into like fractions.
![]()
Solution :
8 is the multiple of 4 So, make 8, the common denominator \(\frac{3}{4}=\frac{3 \times 2}{4 \times 2}=\frac{6}{8}\).Thus 6/8 and 5/8are the required like fractions.
![]()
![]()
Solution :
The number 35 is a multiple of both 5 and 7 So, making 35 as the common denominater \(\frac{3}{5}=\frac{3 \times 7}{5 \times 7}=\frac{21}{35}, \frac{3}{7}=\frac{3 \times 5}{7 \times 5}=\frac{15}{35}\) Therefore, 21/35 and 15/35 are required like fractions.
![]()
Solution :
Here 10 is the multiples of 5. So make 10 as the common denominator \(\frac{4}{5}=\frac{4 \times 2}{5 \times 2}=\frac{8}{10}\). Thus 8/10 and 3/10 are required like fractions.
![]()
Solution :
Least common multiple of 9 and 6 is 18. So, make, 18 as the common denominator. \(\frac{2}{9}=\frac{2 \times 2}{9 \times 2}=\frac{4}{18}, \frac{1}{6}=\frac{1 \times 3}{6 \times 3}=\frac{3}{18}\). Thus, 4/18 and 3/18 are the required like fractions.
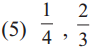
Solution :
Least common multiple of 4 and 3 is 12 So, make 12 as common denominator \(\frac{1}{4}=\frac{1 \times 3}{4 \times 3}=\frac{3}{12}, \frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12}\). so, \(\frac{3}{12}, \frac{8}{12}\) are required like fractions.
![]()
![]()
Solution :
Least common multiple of 6 and 5 is 30 So, make 30 as common denominator \(\frac{5}{6}=\frac{5 \times 5}{6 \times 5}=\frac{25}{30}, \frac{4}{5}=\frac{4 \times 6}{5 \times 6}=\frac{24}{30}\) So, \(\frac{25}{30}, \frac{24}{30}\) are required like fractions.
![]()
Solution :
Least common multiple of 8 and 6 is 24 So, make 24 as common denominator \(\frac{3}{8}=\frac{3 \times 3}{8 \times 3}=\frac{9}{24}, \frac{1}{6}=\frac{1 \times 4}{6 \times 4}=\frac{4}{24}\) So, \(\frac{9}{24}, \frac{4}{24}\) are required like fractions.
![]()
Solution :
Least common multiple of 6 and 9 is 18 So, make 18 as common denominator \(\frac{1}{6}=\frac{1 \times 3}{6 \times 3}=\frac{3}{18}, \frac{4}{9}=\frac{4 \times 2}{9 \times 2}=\frac{8}{18}\) So, 3/18 and 8/18 are the required like fractions.
![]()
Comparing like fractions
Example (1) A strip was divided into 5 equal parts. It means that each part is 1/5 . The coloured part is \(\frac{3}{5}=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\).
![]()
The white part is \(\frac{2}{5}=\frac{1}{5}+\frac{1}{5}\). The coloured part is bigger than the white part. This tells us that 3/5 is greater than 2/5. This is written as 3/5 > 2/5.
Example (2) This strip is divided into 8 equal parts. 3 of the parts have one colour and 4 have another colour. Here, 3/8 < 8/4.
![]()
In like fractions, the fraction with the greater numerator is the greater fraction.
Comparing fractions with equal numerators
You have learnt that the value of fractions with numerator 1 decreases as the denominator increases.
Even if the numerator is not 1, the same rule applies so long as all the fractions have a common numerator. For example, look at the figures below. All the strips in the figure are alike.
2 of the 3 equal parts of the strip ![]()
2 of the 4 equal parts of the strip 
2 of the 5 equal parts of the strip 
The figure shows that 2/3 > 2/4 > 5/2.
![]()
Of two fractions with equal numerators, the fraction with the greater denominator is the smaller fraction.
Comparing unlike fractions
Teacher : Suppose we have to compare the unlike fractions 3/5 and 4/7. Let us take an example to see how this is done. These two boys are standing on two blocks. How do we decide who is taller?
Sonu : But the height of the blocks is not the same. If both blocks are of the same height, it is easy to tell who is taller.
Nandu : Now that they are on blocks of equal height, we see that the boy on the right is taller.
Teacher : The height of the boys can be compared when they stand at the same height. Similarly, if fractions have the same denominators, their numerators decide which fraction is bigger.
Nandu : Got it! Let’s obtain the same denominators for both fractions.
Sonu : 5 × 7 can be divided by both 5 and 7. So, 35 can be the common denominator.
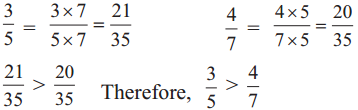
To compare unlike fractions, we convert them into their equivalent fractions so that their denominators are the same.
![]()
Fractions Problem Set 18 Additional Important Questions and Answers
Question 1.
\(\frac{5}{9}, \frac{17}{36}\)
Solution :
36 is the multiple of 9 So, make 36 the common denominator \(\frac{5}{9}=\frac{5 \times 4}{9 \times 4}=\frac{20}{36}\), Thus 20/36 and 17/36 are the required like fractions.
Question 2.
\(\frac{5}{6}, \frac{7}{9}\)
Solution:
Least common multiple of 6 and 9 is 18 So, make 18 as the common denominator \(\frac{5}{6}=\frac{5 \times 3}{6 \times 3}=\frac{15}{18}, \quad \frac{7}{9}=\frac{7 \times 2}{9 \times 2}=\frac{14}{18}\) So, 15/18 and 14/18 are the required like fractions.
![]()
Question 3.
\(\frac{7}{11}, \frac{3}{5}\)
Solution:
Least common multiple of 11 and 5 is 55 So, make 55 as the common denominator. \(\frac{7}{11}=\frac{7 \times 5}{11 \times 5}=\frac{35}{55}, \frac{3}{5}=\frac{3 \times 11}{5 \times 11}=\frac{33}{55}\). Thus 35/55 and 33/55 are required like fractions.