Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 8 Sound Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Physics Solutions Chapter 8 Sound
1. Choose the correct alternatives
Question 1.
A sound carried by the air from a sitar to a listener is a wave of the following type.
(A) Longitudinal stationary
(B)Transverse progressive
(C) Transverse stationery
(D) Longitudinal progressive
Answer:
(D) Longitudinal progressive
Question 2.
When sound waves travel from air to water, which of these remains constant?
(A) Velocity
(B) Frequency
(C) Wavelength
(D) All of above
Answer:
(B) Frequency
![]()
Question 3.
The Laplace’s correction in the expression for velocity of sound given by Newton is needed because sound waves
(A) are longitudinal
(B) propagate isothermally
(C) propagate adiabatically
(D) are of long wavelength
Answer:
(C) propagate adiabatically
Question 4.
Speed of sound is maximum in
(A) air
(B) water
(C) vacuum
(D) solid
Answer:
(D) solid
Question 5.
The walls of the hall built for music concerns should
(A) amplify sound
(B) Reflect sound
(C) transmit sound
(D) Absorb sound
Answer:
(D) Absorb sound
2. Answer briefly.
Question 1.
Wave motion is doubly periodic. Explain.
Answer:
i. A wave particle repeats its motion after a definite interval of time at every location, making it periodic in time.
ii. Similarly, at any given instant, the form of a wave repeats itself at equal distances making it periodic in space.
iii. Thus, wave motion is a doubly periodic phenomenon, i.e., periodic in time as well as periodic in space.
Question 2.
What is Doppler effect?
Answer:
The apparent change in the frequency of sound heard by a listener, due to relative motion between the source of sound and the listener is called Doppler effect in sound.
Question 3.
Describe a transverse wave.
Answer:
Transverse wave:
A wave in which particles of the medium vibrate in a direction perpendicular to the direction of propagation of the wave is called transverse wave.
Example: Ripples on the surface of water, light waves.
Characteristics of transverse waves:
- All the particles of medium in the path of wave vibrate in a direction perpendicular to the direction of propagation of wave with same period and amplitude.
- When transverse wave passes through the medium, the medium is divided into alternate crests i.e., regions of positive displacements and troughs i.e., regions of negative displacement, that are periodic in time.
- A crest and an adjacent trough form one cycle of a transverse wave. The distance between any two successive crests or troughs is called wavelength ‘λ’ of the wave.
- Crests and troughs advance in the medium and are responsible for transfer of energy.
- Transverse waves can travel only through solids and not through liquids and gases. Electromagnetic waves are transverse waves, but they do not require material medium for propagation.
- When transverse waves advance through a medium, there is no change of pressure and density at any point of the medium, but the shape changes periodically.
- Transverse wave can be polarised.
- Medium conveying a transverse wave must possess elasticity of shape, i.e., modulus of rigidity.
Question 4.
Define a longitudinal wave.
Answer:
A wave in which particles of medium vibrate in a direction parallel to the direction of propagation of the wave is called longitudinal wave. Example: Sound waves.
![]()
Question 5.
State Newton’s formula for velocity of sound.
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.
ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.
Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.
2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.
Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.
2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}\) ….(2)
3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³
4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P
Question 6.
What is the effect of pressure on velocity of sound?
Answer:
Effect of pressure:
i. Let v be the velocity of sound in air when the pressure is P and density is ρ.
ii. Using Laplace’s formula, we can write,
v = \(\sqrt{\frac {γP}{ρ}}\) ….(1)
iii. If V be the volume of a gas having mass M then, ρ = \(\frac {M}{V}\)
iv. Substituting ρ in equation (1), we get,
v = \(\sqrt{\frac {γPV}{M}}\) ….(2)
v. But according to Boyle’s law,
PV = constant (at constant temperature)
Also, M and γ are constant.
∴ v = constant
vi. Hence, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.
vii. For a gaseous medium, PV= nRT.
Substituting in equation (2), we get,
v = \(\sqrt{\frac {γnRT}{M}}\)
viii. Thus, even for a gaseous medium obeying ideal gas equation, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.
Question 7.
What is the effect of humidity of air on velocity of sound?
Answer:
Effect of humidity:
i. Let vm and vd be the velocities of sound in moist air and dry air respectively.
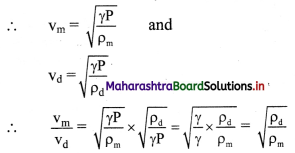
ii. Humid air contains a large proportion of water vapour. Density of water vapour at 0 °C is 0.81 kg/m³ while that of dry air at 0°C is 1.29 kg/m³. So, the density ρm of moist air is less than the density ρd of dry air i.e., ρm < ρd.
iii. Thus \(\frac {v_m}{v_d}\) > 1
∴ vm > vd
iv. Hence, sound travels faster in moist air than in dry air. It means that velocity of sound increases with increase in moistness (humidity) of air.
![]()
Question 8.
What do you mean by an echo?
Answer:
An echo is the repetition of the original sound because of reflection from some rigid surface at a distance from the source of sound.
Question 9.
State any two applications of acoustics.
Answer:
Application of acoustics in nature:
i. Bats apply the principle of acoustics to locate objects. They emit short ultrasonic pulses of frequency 30 kHz to 150 kHz. The resulting echoes give them information about location of the obstacle. This helps the bats to fly in even in total darkness of caves.
ii. Dolphins navigate underwater with the help of an analogous system. They emit subsonic frequencies which can be about 100 Hz. They can sense an object about 1.4 m or larger.
Medical applications of acoustics:
i. High pressure and high amplitude shock waves are used to split kidney stones into smaller pieces without invasive surgery. A reflector or acoustic lens is used to focus a produced shock wave so that as much of its energy as possible converges on the stone. The resulting stresses in the stone causes the stone to break into small pieces which can then be removed easily.
ii. Ultrasonic imaging uses reflection of ultrasonic waves from regions in the interior of body. It is used for prenatal (before the birth) examination, detection of anomalous conditions like tumour etc. and the study of heart valve action.
iii. Ultrasound at a very high-power level, destroys selective pathological tissues which is helpful in treatment of arthritis and certain type of cancer.
Underwater applications of acoustics:
i. SONAR (Sound Navigational Ranging) is a technique for locating objects underwater by transmitting a pulse of ultrasonic sound and detecting the reflected pulse.
ii. The time delay between transmission of a pulse and the reception of reflected pulse indicates the depth of the object.
iii. Motion and position of submerged objects like submarine can be measured with the help of this system.
Applications of acoustics in environmental and geological studies:
i. Acoustic principle has important application to environmental problems like noise control. The quiet mass transit vehicle is designed by studying the generation and propagation of sound in the motor’s wheels and supporting structures.
Reflected and refracted elastic waves passing through the Earth’s interior can be measured by applying the principles of acoustics. This is useful in studying the properties of the Earth.
Principles of acoustics are applied to detect local anomalies like oil deposits etc. making it useful for geological studies.
Question 10.
Define amplitude and wavelength of a wave.
Answer:
i. Amplitude (A): The largest displacement of a particle of a medium through which the wave is propagating, from its rest position, is called amplitude of that wave.
SI unit: (m)
ii. Wavelength (λ): The distance between two successive particles which are in the same state of vibration is called wavelength of the wave.
SI unit: (m)
Question 11.
Draw a wave and indicate points which are (i) in phase (ii) out of phase (iii) have a phase difference of π/2.
Answer:
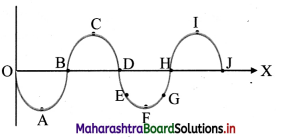
i. In phase point: A and F; B and H; C and I; D and J
ii. Out of phase points: A and B, B and D, FI and J, E and F,
iii. Point having phase difference of π/2: A and B; B and C; D; D and F; F and H; H and I; J and I
Question 12.
Define the relation between velocity, wavelength and frequency of wave.
Answer:
i. A wave covers a distance equal to the wavelength (λ) during one period (T).
Therefore, the magnitude of the velocity (v) is given by,
Magnitude of velocity = \(\frac {Distance covered}{Corresponding time}\)
ii. v = \(\frac {22}{7}\) i.e., v = λ × (\(\frac {1}{T}\)) …………….. (1)
iii. But reciprocal of the period is equal to the frequency (n) of the waves.
∴ \(\frac {1}{T}\) = n …………… (2)
iv. From equations (1) and (2), we get
v = nλ
i.e., wave velocity = frequency × wavelength.
Question 13.
State and explain principle of superposition of waves.
Answer:
Principle:
As waves don’t repulse each other, they overlap in the same region of the space without affecting each other. When two waves overlap, their displacements add vectorially.
Explanation:
i. Consider two waves travelling through a medium arriving at a point simultaneously.
ii. Let each wave produce its own displacement at that point independent of the others. This displacement can be given as,
y1 = displacement due to first wave.
y2 = displacement due to second wave.
iii. Then according to superposition of waves, the resultant displacement at that point is equal to the vector sum of the displacements due to all the waves.
∴\(\vec{y}\) = \(\vec{y_1}\) + \(\vec{y_2}\)
![]()
Question 14.
State the expression for apparent frequency when source of sound and listener are
i) moving towards each other
ii) moving away from each other
Answer:
i. Let,
n = actual frequency of the source.
n0 = apparent frequency of the source,
v = velocity of sound in air.
vs = velocity of the source.
vl = velocity of the listener.
ii. Apparent frequency heard by the listener is given by,
n = n0(\(\frac {v±v_L}{v±v_s}\))
Where upper signs (+ ve in numerator and -ve in denominator) indicate that source and observer move towards each other. Lower signs (-ve in numerator and +ve in denominator) indicate that source and listener move away from each other.
iii. If source and listener are moving towards each other, then apparent frequency is given by,
n = n0(\(\frac {v+v_L}{v-v_s}\)) i.e., apparent frequency increases.
iv. If source and listener are moving away from each other, then apparent frequency is given by,
n = n0(\(\frac {v-v_L}{v+v_s}\)) i.e., apparent frequency decreases.
Question 15.
State the expression for apparent frequency when source is stationary and listener is
1) moving towards the source
2) moving away from the source
Answer:
Let,
n = actual frequency of the source.
n0 = apparent frequency of the source,
v = velocity of sound in air.
vs = velocity of the source.
vl = velocity of the listener.
i. If listener is moving towards source then apparent frequency is given by,
n = n0(\(\frac {v+v_L}{v}\)) i.e., apparent frequency increases.
ii. If listener is receding away from source then apparent frequency is given by,
n = n0(\(\frac {v-v_L}{v}\)) i.e., apparent frequency decreases.
Question 16.
State the expression for apparent frequency when listener is stationary and source is.
(i) moving towards the listener
(ii) moving away from the listener
Answer:
Let,
n = actual frequency of the source.
n0 = apparent frequency of the source,
v = velocity of sound in air.
vs = velocity of the source.
vl = velocity of the listener.
i. If source is moving towards observer then apparent frequency is given by,
n = n0(\(\frac {v}{v-v_s}\)) i.e., apparent frequency increases.
ii. If source is receding away from observer then apparent frequency is given by,
n = n0(\(\frac {v}{v+v_s}\)) i.e., apparent frequency decreases.
Question 17.
Explain what is meant by phase of a wave.
Answer:
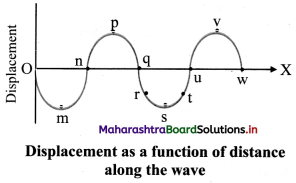
i. The state of oscillation of a particle is called the phase of the particle.
ii. The displacement, direction of velocity and oscillation number of the particle describe the phase of the particle at a place.
iii. Particles r and t (q and u or v and s) have same displacements but the directions of their velocities are opposite.
iv. Particles having same magnitude of displacements and same direction of velocity are said to be in phase during their respective oscillations. Example: particles v and p.
v. Separation between two particles which are in phase is wavelength (λ).
vi. The two successive particles differ by ‘1’ in their oscillation number i.e., if particle v is at its nth oscillation, particle p will be at its (n + 1)th oscillation as the wave is travelling along + X direction.
vii. In the given graph, if the disturbance (energy) has just reached the particle w, the phase angle corresponding to particle is 0°. At this instant, particle v has completed quarter oscillation and reached its positive maximum (sin θ = +1). The phase angle θ of this particle v is \(\frac {π^c}{2}\) = 90° at this instant.
viii. Phase angles of particles u and q are πc (180°) and 2rcc (360°) respectively.
ix. Particle p has completed one oscillation and is at its positive maximum during its second oscillation.
∴ phase angle = 2πc + \(\frac {π^c}{2}\)
= \(\frac {5π^c}{2}\)
x. v and p are the successive particles in the same state (same displacement and same direction of velocity) during their respective oscillations. Phase angle between these two differs by 2πc.
Question 18.
Define progressive wave. State any four properties.
Answer:
i. Waves in which a disturbance created at one place travels to distant points and keeps travelling unless stopped by an external force are known as travelling or progressive waves.
Properties of progressive waves are:
Amplitude, wavelength, period, double periodicity, frequency and velocity.
Question 19.
Distinguish between traverse waves and longitudinal waves.
Answer:
| Longitudinal wave | Transverse wave |
| 1. The particles of the medium vibrate along the direction of propagation of the wave. | 1. The particles of the medium vibrate perpendicular to the direction of propagation of the wave. |
| 2. Alternate compressions and rarefactions are formed. | 2. Alternate crests and troughs are formed. |
| 3. Periodic compressions and rarefactions, in space and time, produce periodic pressure and density variations in the medium. | There are no pressure and density, variations in the medium. |
| 4. For propagation of a longitudinal wave, the medium must be able to resist changes in volume. | For propagation of a transverse wave, the medium must be able to resist shear or change in shape. |
| 5. It can propagate through any material medium (solid, liquid or gas). | It can propagate only through solids. |
| 6. These waves cannot be polarised. | These waves can be polarised. |
| 7. eg.: Sound waves | eg.: Light waves |
Question 20.
Explain Newtons formula for velocity of sound. What is its limitation?
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.
ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.
Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.
2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.
Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.
2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}}\) ….(2)
3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³
4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P
Limitations:
1. Experimentally, it is found that the velocity of sound in air at N. T. P is 332 m/s. Thus, there is considerable difference between the value predicted by Newton’s formula and the experimental value.
2. Experimental value is 16% greater than the value given by the formula. Newton failed to provide a satisfactory explanation for the difference.
![]()
3. Solve the following problems.
Question 1.
A certain sound wave in air has a speed 340 m/s and wavelength 1.7 m for this wave, calculate
(i) the frequency
(ii) the period.
Answer:
Given: v = 340 m/s, λ = 1.7 m
To find: frequency (n), period (T)
Formulae:
i. n = \(\frac {v}{λ}\)
ii. T = \(\frac {1}{n}\)
Calculation: From formula, (i)
n = \(\frac {340}{1.7}\)
∴ n = 200 Hz
From formula, (ii)
T = \(\frac {1}{n}\) = \(\frac {1}{2×10^2}\)
= 5 × 10-3
…….. (using reciprocal Table)
∴ T = 0.005 s
Question 2.
A tuning fork of frequency 170 Hz produces sound waves of wavelength 2m. Calculate speed of sound.
Answer:
Given: n = 170 Hz, λ = 2 m
To find: velocity of sound (v)
Formula: v = nλ
Calculation: From formula,
v = 170 × 2
∴ v = 340 m/s
Question 3.
An echo-sounder in a fishing boat receives an echo from a shoal of fish 0.45s after it was sent. If the speed of sound in water is 1500 m/s, how deep is the shoal?
Answer:
Given: t = 0.45 s, v = 1500 m/s,
To Find: depth (d)
Formula: speed (v) = \(\frac {distance}{time}\)
Calculation:
For an echo distance travelled by the sound wave = 2 × (distance between echo sounder and shoal) (d)
v = \(\frac {2 × d}{t}\)
∴ d = \(\frac {1500 × 0.45}{2}\) = 337.5 m
Question 4.
A girl stands 170 m away from a high wall and claps her hands at a steady rateso that each clap coincides with the echo of the one before.
a) If she makes 60 claps in 1 minute, what value should be the speed of sound in air?
b) Now, she moves to another location and finds that she should now make 45 claps in 1 minute to coincide with successive echoes. Calculate her distance for the new position from the wall.
Answer:
i. When the girl makes 60 claps in 1 minute, the value of speed of is 340 m/s.
ii. The girl is at a distance of 226.67 m from the wall when she produces 45 claps per minute.
[Note: The answer given above is calculated in accordance with textual method considering the given data]
Question 5.
Sound wave A has period 0.015 s, sound wave B has period 0.025. Which sound has greater frequency?
Answer:
Given: TA = 0.015 s, TB = 0.025 s
To find: greater frequency (n)
Formula: n = \(\frac {1}{T}\)
Calculation: From formula,
nA = \(\frac {1}{T_A}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ nA = 66.67
…. (using reciprocal table)
nB = \(\frac {1}{T_B}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ nB = 40 Hz
…. (using reciprocal table)
∴ nA > nB
![]()
Question 6.
At what temperature will the speed of sound in air be 1.75 times its speed at N.T.P?
Answer:
Given:
vair = 1.75 VS.T.P = \(\frac {7}{4}\) vS.T.P
TS.T.P = 273 K
To find: temperature Tair
Formula: v ∝ √T
Calculation: From formula,

Question 7.
A man standing between 2 parallel eliffs fires a gun. He hearns two echos one after 3 seconds and other after 5 seconds. The separation between the two cliffs is 1360 m, what is the speed of sound?
Answer:
distance (s) = 1360 m,
time for first echo = 3 s,
time for second echo = 5 s
To Find : speed of sound (v)
Formula : speed = \(\frac {distence}{time}\)
Calculation:
Time for first echo = 3 s
∴ time taken by sound to travel given distance t1
= \(\frac {3}{2}\) = 1.5 s
Time for second echo = 5 s
∴ time taken by sound to travel given distance t2
= \(\frac {5}{2}\) = 2.5 s
∴Total time taken by sound to travel given distance, T = 1.5 + 2.5 = 4 s
From formula,
v = \(\frac {1360}{4}\)
∴v = 340 m/s
Question 8.
If the velocity of sound in air at a given place on two different days of a given week are in the ratio of 1 : 1.1. Assuming the temperatures on the two days to be same what quantitative conclusion can your draw about the condition on the two days?
Answer:
Let v1 and v2 be the velocity of sound on day 1 and day 2 respectively.
\(\frac {v_1}{v_2}\) = \(\frac {1}{1.1}\)
We know, v ∝ \(\frac {1}{√ρ}\)
Let ρ1 and ρ2 be the density of air on day 1 and day 2 respectively.
∴ \(\sqrt{\frac {ρ_2}{ρ_1}}\) = \(\frac {1}{1.1}\)
∴ \(\frac {ρ_2}{ρ_1}\) = (\(\frac {1}{1.1}\))²
∴ ρ1 = 1.1² ρ2 = 1.21 ρ²
From above equation, we can conclude,
ρ1 > ρ2
∴ v2 > v1 i.e., the velocity of sound is greater on the second day than on the first day.
We know, speed of sound in moist air (vm) is greater than speed of sound in dry air (vd).
∴ We can conclude, air is moist on second day and dry on the first day.
Question 9.
A police car travels towards a stationary observer at a speed of 15 m/s. The siren on the car emits a sound of frequency 250 Hz. Calculate the recorded frequency. The speed of sound is 340 m/s.
Answer:
Given: vs = 15 m/s, n0 = 250 Hz, v = 340 m/s
To find: Frequency (n)
Formula: n = n0(\(\frac {v}{v-v_s}\))
Calculation: As the source approaches listener, apparent frequency is given by,
n = 250 (\(\frac {340}{340-15}\)) = \(\frac {3400}{13}\)
∴ n = 261.54 Hz
![]()
Question 10.
The sound emitted from the siren of an ambulance has frequency of 1500 Hz. The speed of sound is 340 m/s. Calculate the difference in frequencies heard by a stationary observer if the ambulance initially travels towards and then away from the observer at a speed of 30 m/s.
Answer:
Given: vs = 30 m/s, n0 = 1500 Hz, v = 340 m/s
To find: Difference in apparent frequencies (nA – n’A)
Formulae:
i. When the ambulance moves towards he stationary observer then nA = n0(\(\frac {v}{v-v_s}\))
ii. When the ambulance moves away from the stationary observer then, n’A = n0(\(\frac {v}{v+v_s}\))
Calculation:
From formula (i), icon’ 340
nA = 1500(\(\frac {340}{340-30}\))
∴ nA = 1645 Hz
From (ii)
n’A = 1500(\(\frac {340}{340+30}\))
∴ nA = 1378 Hz
Difference between nA and n’A
= nA – n’A = 1645 – 1378 = 267 Hz
11th Physics Digest Chapter 8 Sound Intext Questions and Answers
Can you recall? (Textbook page no. 142)
i. What type of wave is a sound wave?
ii. Can sound travel in vacuum?
iii. What are reverberation and echo?
iv. What is meant by pitch of a sound?
Answer:
i. Sound wave is a longitudinal wave.
ii. Sound cannot travel in vacuum.
iii. a. Reverberation is the phenomenon in which sound waves are reflected multiple times causing a single sound to be heard more than once.
b. An echo is the repetition of the original sound because of reflection by some surface.
iv. The characteristic of sound which is determined by the value of frequency is called as the pitch of the sound.
Activity (Textbook page no. 144)
i. Using axes of displacement and distance, sketch two waves A and B such that A has twice the wavelength and half the amplitude of B.
ii. Determine the wavelength and amplitude of each of the two waves P and Q shown in figure below.
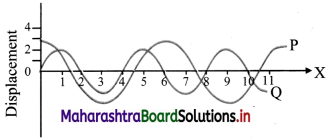
Answer:
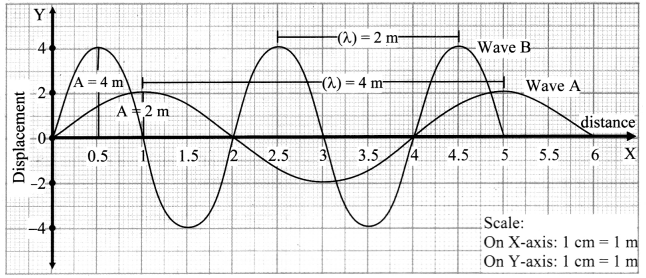
| Wave | Wavelength (λ) | Amplitude (A) |
| A | 4 m | 2 m |
| B | 2 m | 4 m |
| Wave | Wavelength (λ) | Amplitude (A) |
| P | 6 units | 3 units |
| Q | 4 units | 2 units |