Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 3 Motion in a Plane Important Questions and Answers.
Maharashtra State Board 11th Physics Important Questions Chapter 3 Motion in a Plane
Question 1.
Explain the term: Displacement.
Answer:
Displacement:
- Displacement of a particle for a time interval is the difference between the position vectors of the object in that time interval.
- Let \(\overrightarrow{\mathrm{x}_{1}}\) and \(\overrightarrow{\mathrm{x}_{2}}\) be the position vectors of a particle at time t1 and t2 respectively. Then the displacement \(\overrightarrow{\mathrm{S}}\) in time ∆t = (t2 – t\overrightarrow{\mathrm{s}}=\Delta \overrightarrow{\mathrm{x}}=\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathrm{x}}_{1}) is given by \(\overrightarrow{\mathrm{s}}=\Delta \overrightarrow{\mathrm{x}}=\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathrm{x}}_{1}\)
- Dimensions of displacement are equal to that of length i.e.. [L1M0T0].
- Displacement is a vector quantity.
- Example:
- For an object that has travelled through 1 m from time t1 to t2 along the positive X-direction, the magnitude of its displacement is I m and its direction is along the positive X-axis.
- On the other hand, for an object that has travelled through I m from time t1 to t1 along the positive Y-direction, the magnitude of its displacement remains the same i.e., I m but the direction of the displacement is along the positive Y-axis.
Question 2.
Explain the term: Path length.
Answer:
- Path length is the actual distance travelled by the particle during its motion.
- It is a scalar quantity.
- Dimensions of path length are equal to that of length i.e.. [L1M0T0]
- Example:
- If an object travels along the X-axis from x = 3 m to x = 6 m then the distance travelled is 3 m. In this case the displacement is also 3 m and its direction is along the positive X-axis.
- However, if the object now comes back to x 5, then the distance through which the object has moved increases to 3 + I = 4 m. Its initial position was x 3 m and the final position is now x = 5 m and thus, its displacement is ∆x = 5 – 3 = 2 m, i.e., the magnitude of the displacement is 2 m and its direction is along the positive X-axis.
- If the object now moves to x =1, then the distance travelled, i.e., the path length increases to 4 + 4 = 8 m while the magnitude of displacement becomes 3 – 1 = 2 m and its direction is along the negative X-axis.
![]()
Question 3.
Explain the terms:
i. Average velocity
ii. Instantaneous velocity
iii. Average speed
iv. Instantaneous speed
Answer:
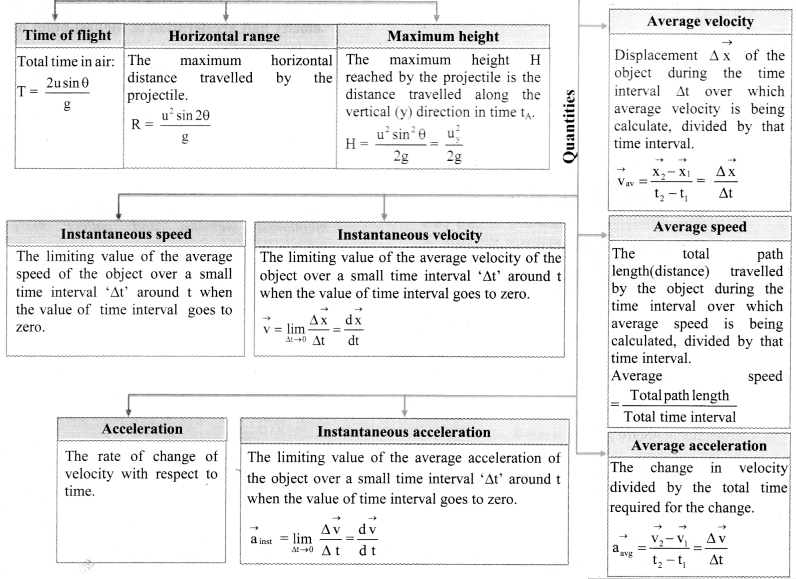
i) Average velocity:
- Average velocity (\(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\)) of an object is the displacement (\(\Delta \overrightarrow{\mathrm{x}}\)) of the object during the time interval (∆t) over which average velocity is being calculated, divided by that time interval.
- Average velocity = (\(\frac{\text { Displacement }}{\text { Time interval }}\))
\(\overrightarrow{\mathrm{V}_{\mathrm{av}}}=\frac{\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathrm{x}}_{1}}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}\) - Average velocity is a vector quantity.
- Its SI unit is m/s and dimensions are [M0L1T-1]
- For example, if the positions of an object are x +4 m and x = +6 m at times t = O and t = 1 minute respectively, the magnitude of its average velocity during that time is Vav = (6 – 4)1(1 – 0) = 2 m per minute and its direction will be along the positive X-axis.
∴ \(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\) = 2 i m/min
Where, i = unit vector along X-axis.
ii) Instantaneous velocity:
- The instantaneous velocity (\(\overrightarrow{\mathrm{V}}\)) is the limiting value of ¡he average velocity of the object over a small time interval (∆t) around t when the value of lime interval goes to zero.
- It is the velocity of an object at a given instant of time.
- \(\overrightarrow{\mathrm{v}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\)
where \(\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) derivative of \(\overrightarrow{\mathrm{x}}\) with respect to t.
iii) Average speed:
- Average speed of an object is the total path length (distance) travelled by the object during the time interval over which average speed is being calculated, divided by that time interval.
- Average speed = \(\frac{\text { Total path length }}{\text { Total time interval }}\)
- Average speed is a scalar quantity.
- Its S.I. unit is m/s and dimensions are [M0V1T-1].
- In rectilinear motion;
- If the motion of the object is only in one direction, then the magnitude of displacement will be equal to the path length and hence the magnitude of average velocity will be equal to the average speed.
- If the motion of the object reverses its direction, then the magnitude of displacement will be less then the path length and hence the magnitude of average velocity will be less than the average speed.
iv) Instantaneous speed:
The instantaneous speed is the limiting value of the average speed of the object over a small time interval ‘∆t’ around t when the value of time interval goes to zero.
Question 4.
Distinguish between uniform rectilinear motion and non-uniform rectilinear motion.
Answer:
| No. | Uniformly rectilinear motion | Non-uniform rectilinear motion |
| i. | The object is moving with constant velocity. | The object is moving with variable velocity. |
| ii. | The average and instantaneous velocities are same. | The average and instantaneous velocities are different. |
| iii. | The average and instantaneous speeds are the same. | The average and instantaneous speeds are different. |
| iv. | The average and instantaneous speeds are equal to the magnitude of the velocity. | The average speed will be different from the magnitude of average velocity. |
Question 5.
Explain the terms:
- Acceleration
- Average acceleration
- Instantaneous acceleration
Answer:
- Acceleration:
- Acceleration is the rate of change of velocity with respect to time.
- It is a vector quantity.
- Dimension: [M0L1T-2]
- If a particle moves with constant velocity, its acceleration is zero.
- Average acceleration:
- Average acceleration is the change in velocity divided by the total time required for the change.
- If \(\overrightarrow{\mathrm{v}_{\mathrm{1}}}\) and \(\overrightarrow{\mathrm{v}_{\mathrm{2}}}\) are the velocities of the T particle at time t1 and t2 respectively, then the change in velocity is \(\) and time required for this change is ∆t = t2 – t1
∴ \(\vec{a}_{a v}=\frac{\vec{v}_{2}-\vec{v}_{1}}{t_{2}-t_{1}}=\frac{\Delta \vec{v}}{\Delta t}\)
- Instantaneous acceleration:
- The instantaneous acceleration a is the limiting value of the average acceleration of the object over a small time interval ‘∆t’ around t when the value of time interval goes to zero.
\(\overrightarrow{\mathrm{a}}_{\text {inst }}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{v}}}{\mathrm{d} \mathrm{t}}\) - Instantaneous acceleration is the slope of the tangent to the velocity-time graph at a position corresponding to given instant of time.
[Note: Generally, when the term acceleration is used, it is an instantaneous acceleration.]
- The instantaneous acceleration a is the limiting value of the average acceleration of the object over a small time interval ‘∆t’ around t when the value of time interval goes to zero.
![]()
Question 6.
Draw and explain the position-time graph of:
- An object at rest.
- An object moving with uniform velocity along positive x-axis.
- An object moving with uniform velocity along negative x-axis.
- An object moving with non-uniform velocity.
- An object performing oscillatory motion with constant speed.
Answer:
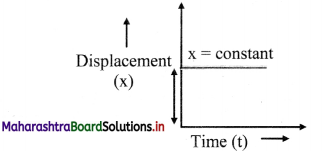
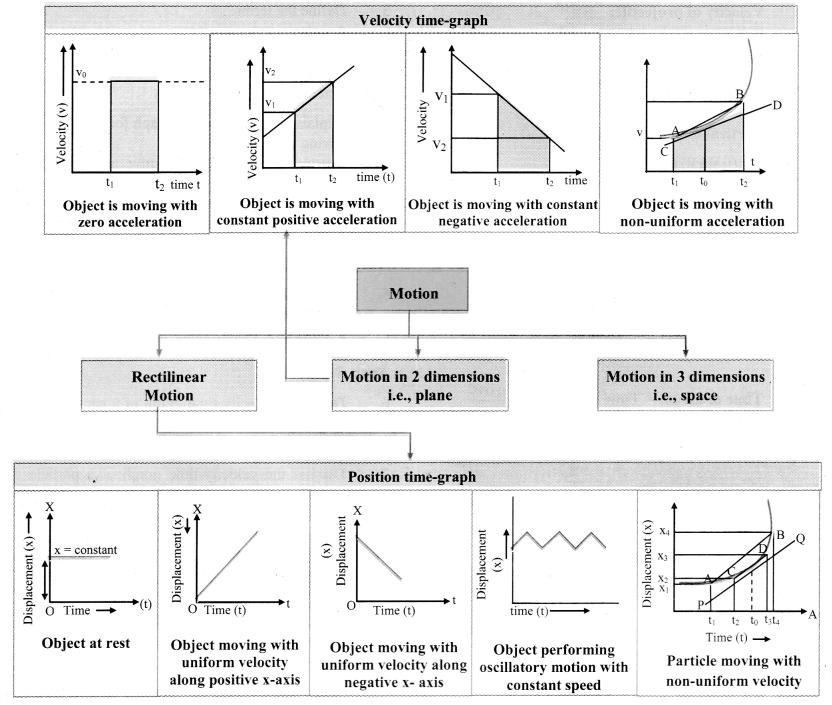
- The position-time graph of an object at rest:
- For an object at rest, the position-time graph is a horizontal straight line parallel to time axis.
- The displacement of the object is zero as there is no change in the object’s position.
- Slope of the graph is zero, which indicates that velocity of the particle is zero.
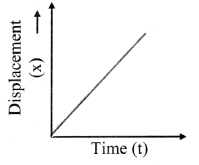
- The position-time graph of an object moving with uniform velocity along positive x-axis:
- When an object moves, the position of the particle changes with respect to time.
- Since velocity is constant, displacement is proportional to elapsed time.
- The graph is a straight line with positive slope, showing that the velocity is along the positive x-axis.
- In this case, as the motion is uniform, the average velocity and instantaneous velocity are equal at all times.
- Speed is equal to the magnitude of the velocity.
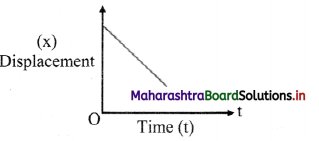
- Position-time graph of an object moving with uniform velocity along negative x- axis:
- The graph is a straight line with negative slope, showing that the velocity is along the negative x-axis.
- Displacement decreases with increase in time.
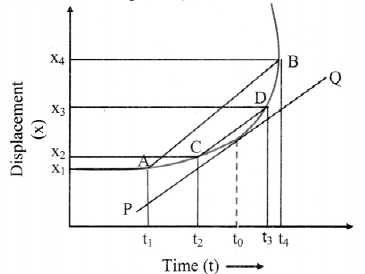
- Position-time graph of a particle moving with non-uniform velocity;
- When the velocity of an object changes with time, slope of the graph is different at different points. Therefore, the average and instantaneous velocities are different.
- Average velocity over time interval from t1 to t4 around time t0 = slope of line AB.
- Average velocity over time interval from t2 to t3 = slope of line CD
- On further reducing the time interval around t0, it can be deduced that, instantaneous interval at t0 = the slope of the tangent PQ at t0.
- Position-time graph of an object performing oscillatory motion with constant speed:
For an object performing oscillatory motion with constant speed, the direction of velocity changes from positive to negative and vice versa over fixed intervals of time.
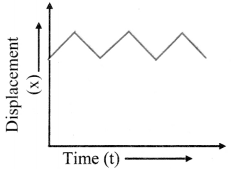
Question 7.
Explain the velocity-tune graphs of an object:
i) Moving with zero acceleration.
ii) Moving with constant positive acceleration.
iii) Moving with constant negative acceleration.
iv) Moving with non-uniform acceleration.
Answer:
i) Object is moving with zero acceleration:
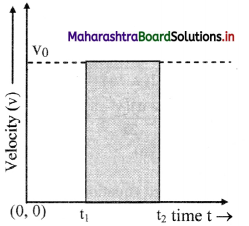
- As the acceleration is zero, the graph will be a straight line parallel to time axis.
- Velocity of the particle is constant as the acceleration is zero.
- Magnitude of displacement of object from t1 to t2 = v0 × (t2 – t1) shaded area under velocity-time graph.
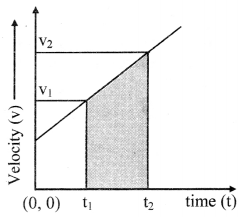
ii) Object is moving with constant positive acceleration:
- The velocity-time graph is linear.
- Velocity increases with increase in time. as acceleration is positive (along the direction of velocity).
- The area under the velocity-time graph between two instants of time t1 and t2 gives the displacement of the object during that time interval.
- Slope of the graph is \(\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}\) = positive acceleration
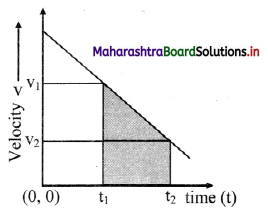
iii) Object is moving with constant negative acceleration:
- The velocity-time graph is linear.
- Velocity decreases with increase in time as acceleration is negative (opposite to the direction of velocities).
- The area tinder the velocity-time graph between two instants of time t1 and t2 gives the displacement 0f the object during that time interval.
- Slope of the graph is \(\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}\) negative acceleration
iv. Object is moving with non-uniform acceleration:
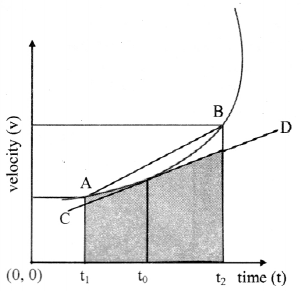
- Velocity-time graph is non-linear.
- The area under the velocity-time graph between two instants of time t1 and t2 gives the displacement of the object during that time interval area under the velocity-time curve =
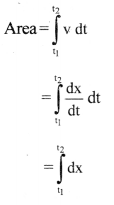
= x(t2) – x(t1)
= displacement of the object from t1 to t2.
Question 8.
A ball thrown vertically upwards from a point P on earth reaches a point Q and returns back to earth striking at a point R. Draw speed-time graph to depict the motion of the ball (Neglect air resistance).
Answer:
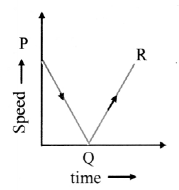
- A ball which is thrown up with a certain initial speed goes up with decreasing speed to a certain height where its speed becomes zero.
- Now, during its downward motion, the speed goes on increasing from zero and reaches its initial value when it strikes the ground.
- The speed-time graph for the motion of a ball is as shown in the figure.
![]()
Question 9.
Figure shows velocity-time graph for various situations. What does each graph indicate?
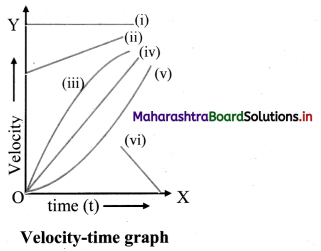
Answer:
- Initial velocity, u > 0. Also, velocity is constant with time. Hence, acceleration is zero.
- As finite initial velocity is increasing with time, acceleration, a > 0 and is constant.
- Initial velocity, u = 0. Velocity is increasing with time so, acceleration a is positive. But it is decreasing in magnitude with time.
- Initial velocity, u = 0. Velocity is linearly increasing with time. Hence, starting from rest acceleration is constant.
- Initial velocity, u = 0. Acceleration and velocity is increasing with time.
- Initial velocity u > 0. Velocity decreases and ultimately comes to rest. Hence, acceleration a < 0.
Question 10.
‘The distances travelled by an object starting from rest and having a positive uniform acceleration in successive seconds are in the ratio 1:3:5:7….’ Prove it.
Answer:
- Consider an object under free fall, Initial velocity u = 0, acceleration a = g
- The distance travelled by the object in equal time intervals t0 can be given by the second law of motion as,
s = ut0 + \(\frac{1}{2}\) gt02 - Distance travelled in the first time interval to,
s1 = 0 + \(\frac{1}{2}\)gt02 = \(\frac{1}{2}\) gt02
Substituting \(\frac{\mathrm{g}}{2}\) = A, we have s1 = At02 - Distance travelled in the time interval 2t0 = A (2t0)2
∴ The distance travelled in the second t0 interval, s2 = A(4t02 – t02) = 3At0\frac{\mathrm{g}}{2} = 3s1 - Distance travelled in the time interval 3t0 = A(3t0)2
∴ The distance travelled in the third to interval,
s3 = A (9t02 – 4t02) = 5 At02 = 5s1 - On continuing, it can be seen that the distances travelled, (s1 : s2 : s3 ….) are in the ratio (1 : 3 : 5 :….)
Question 11.
Explain the concept of relative velocity along a straight line with the help of an example.
Answer:
- Consider two trains A and B moving on two parallel tracks in the same direction.
- Case 1: Train B overtakes train A.
For a passenger in train A, train B appears to be moving slower than train A. This happens because the passenger in train A perceives the velocity of train B with respect to him/her i.e., the difference in the velocities of the two trains which is much smaller than the velocity of train A. - Case 2: Train A overtakes train B.
For a passenger in train A, train B appears to be moving faster than train A. This happens because the passenger in train A perceives the velocity of the train B w.r.t. to him/her i.e., the difference in the velocities of the two trains which is larger than the velocity of train A. - If \(\vec{v}_{\mathrm{A}}\) and \(\vec{v}_{\mathrm{B}}\) be the velocities of two bodies then relative velocity of A with respect to B is given by \(\vec{v}_{A B}=\vec{v}_{A}-\vec{v}_{B}\).
- Similarly the velocity of B with respect to A is given by, \(\vec{v}_{A B}=\vec{v}_{B}-\vec{v}_{A}\).
Thus, relative velocity of an object w.r.t. another object is the difference in their velocities - If two objects start form the same point at t = 0, with different velocities, distance between them increases with time in direct proportion to the relative velocity between them.
Solved Problems
Question 12.
A person walks from point P to point Q along a straight road ¡n 10 minutes, then turns back and returns to point R which ¡s midway between P and Q after further 4 minutes. If PQ is 1 km, find the average speed and velocity of the person in going from P to R.
Solution:
Given: time taken (t) = 10 + 4 = 14 minutes,
distance (s) = PQ + QR = 1 + 0.5 = 1.5 km,
displacement = PQ – QR = 1 – 0.5 = 0.5km
To find: Average speed, average velocity (v)

The average speed and average velocity of the person is 6.42 km/hr and 2.142 km/hr respectively.
![]()
Question 13.
A car moves at a constant speed of 60 km/hr for 1 km and 40 km/hr for next 1 km. What ¡s the average speed of the car?
Solution:
Given. v1 = 60 km/hr, x1 = 1 km,
v2 = 40 km/hr, x2 = 1 km
To find: Average speed of car (Vav)
Formula: vav = \(\frac{\text { total path length }}{\text { total time interval }}\)
Calculation: From given data,

∴ Average speed of car = 48 km/hr
The average speed of the car is 48 km/hr
Question 14.
A stone is thrown vertically upwards from the ground with a velocity 15 m/s. At the same instant a ball is dropped from a point directly above the stone from a height of 30 m. At what height from the ground will the stone and the ball meet and after how much time? (Use g = 10 m/s2 for ease of calculation).
Solution:
Let the stone and the ball meet after time t0. From second equation of motion, the distances travelled by the stone and the ball in that time is given as,
Sstone = 15 t0 – \(\frac{1}{2}\) gt02
Sball = \(\frac{1}{2}\) gt02
When they meet. Sstone + Sball = 30
∴ 15t0 – \(\frac{1}{2}\) gt02 + \(\frac{1}{2}\) gt02 = 30
t0 = \(\frac{30}{15}\) = 2 s
∴ Sstone = 15 (2) – \(\frac{1}{2}\) (10) (2)2 = 30 – 20 = 10 m
The stone and the ball meet at a height of 10 m after time 2s.
Question 15.
A ball is dropped from the top of a building 122.5 m high. How long will it take to reach the ground? What wilt be its velocity when it strikes the ground?
Solution:
Given: s = h = 122.5 m, u = 0,
a = g = 9.8 ms2
To find: i) Time taken to reach the ground (t)
ii) Velocity of ball when it strikes ground (v)
Formulae: i) s = ut + \(\frac{1}{2}\) at2
ii) v = u + gt
Calculation: From formula (i),
122.5 = 0 + \(\frac{1}{2}\) × 9.8 t2
t2 = \(\frac{122.5}{4.9}\) = 25
t = \(\sqrt {25}\) = 5 second
From formula (ii),
v = u + gt
v = 0 + 9.8 × 5 = 49 m/s
i) Time taken to reach the ground is 5 s.
ii) Velocity of the ball when it strikes the ground is 49 m/s.
![]()
Question 16.
The position vectors of three particles are given by
\(\overrightarrow{\mathrm{x}}_{1}=(5 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}) \mathrm{m}\), \(\overrightarrow{\mathrm{x}}_{2}=(5 \mathrm{t} \hat{\mathrm{i}}+5 \mathrm{t} \hat{\mathrm{j}}) \mathrm{m}\) and \(\overrightarrow{\mathrm{x}}_{3}=\left(5 \mathrm{t} \hat{\mathrm{i}}+10 \mathrm{t}^{2} \hat{\mathrm{j}}\right) \mathrm{m}\) as a function of time t.
Determine the velocity and acceleration for each, in SI units.
Solution:

v2 = \(\sqrt{5^{2}+5^{2}}\) = 5\(\sqrt{2}\) m/s
tan θ = \(\frac{5}{5}\) = 1
∴ θ = 45°
Direction of v2 makes an angle of 45° to the horizontal.

Thus, third particle is getting accelerated along the y-axis at 20 m/s2.
Question 17.
The initial velocity of an object is \(\overrightarrow{\mathrm{u}}=5 \hat{\mathrm{i}}+10 \hat{\mathrm{j}} \mathrm{m} / \mathrm{s}\). Its constant acceleration is \(\vec{a}=2 \hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}^{2}\). Determine the velocity and the displacement after 5 s.
Solution:

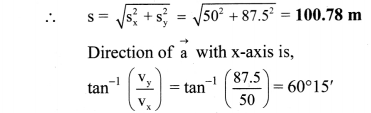
Question 18.
An aeroplane A, is travelling in a straight line with a velocity of 300 km/hr with respect to Earth. Another aeroplane B, is travelling in the opposite direction with a velocity of 350 km/hr with respect to Earth. What is the relative velocity of A with respect to B? What should be the velocity of a third aeroplane C moving parallel to A, relative to the Earth if it has a relative velocity of 100 km/hr with respect to A?
Solution:
Given: vA = 300 km/hr, vB = 350 km/hr,
vCA = 100 km/hr
To find: i) Velocity of plane A relative to B (vA – vB)
ii) Velocity of aeroplane C (vC)
Formula: i) vAB = vA – vB
ii) vCA = vC – vA
Calculations: From formula (i),
vAB = vA – vB = 300 – (-350)
∴ vAB = 650 km/hr
From formula (ii),
vC = vCA + vA = 100 + 300 = 400 km/hr
i) The relative velocity of A with respect to B is 650 km/hr.
ii) The velocity of plane C relative to Earth is 400 km/hr.
![]()
Question 19.
A car moving at a speed 10 m/s on a straight road is ahead of car B moving in the same direction at 6 m/s. Find the velocity of A relative to B and vice-versa.
Solution:
Given: vA = 10 m/s, vB = 6 m/s,
To find: i) Velocity of A relative to B (vA – vB)
ii) Velocity of B relative to A (vB – vA)
Formulae: i) vAB = vA – vB
ii) vBA = vB – vA
Calculation: From formula (i),
vAB = 10 – 6 = 4 m/s
From formula (ii),
vBA = 6 – 10 = -4 m/s
-ve sign indicates that driver of car A sees the car B lagging behind at the rate of 4 m/s.
∴ vAB = 4 m/s, vBA = -4 m/s
i) Velocity of A relative to B is 4 m/s.
ii) Velocity of B relative to A is -4 m/s.
Question 20.
Two trains 120 m and 80 m in length are running in opposite directions with velocities 42 km/h and 30 km/h respectively. In what time will they completely cross each other?
Solution:
Given: l1 = 120 m, l2 = 80 m,
vA = 42 km/h = 42 × \(\frac{5}{18}\) = \(\frac{35}{3}\) m/s,
vB = -30km/h= -30 × \(\frac{5}{18}\) = \(\frac{-25}{3}\) m/s
To find: Time taken by trains to cross each other (t)
Formula: Time = \(\frac{\text { Distance }}{\text { speed }}\)
Calculation :
Total distance to be travelled
= sum of lengths of two trains
= 120 + 80 = 200m
Relative velocity of A with respect to B is vAB,
vAB = vA – vB
= \(\frac{35}{3}\) – (\(\frac{-25}{3}\))
= \(\frac{60}{3}\)
∴ vAB = 20m/S
From formula,
∴ Time taken to cross each other (t) = \(\frac{\text { Distance }}{\text { speed }}\)
= \(\frac{200}{20}\)
= 10 s
Time taken by the two trains to cross each other is 10 s.
Question 21.
A jet aeroplane travelling at the speed of 500 km/hr ejects its products of combustion at speed of 1500 km/hr relative to jet plane. What is the relative velocity of the latter with respect to an observer on the ground?
Solution:
Let us consider the positive direction of motion towards the observer on the ground.
Suppose \(\vec{v}_{\mathrm{a}}\) and \(\vec{v}_{\mathrm{cj}}\) be the velocities of the aeroplane and relative velocity of combustion products w.r.t. aeroplane respectively.
∴ \(\vec{v}_{\mathrm{cj}}\) = 1,500 km/hr (towards the observer on the ground) and \(\vec{v}_{\mathrm{a}}\) = 500 km/hr (away from the observer on the ground)
∴ – \(\vec{v}_{\mathrm{a}}\) = -500 km/ hr (towards the observer on the ground)
Let \(\vec{v}_{\mathrm{c}}\) be the velocity of the combustion products towards the observer on ground then,
\(\vec{v}_{\mathrm{c} j}=\vec{v}_{\mathrm{c}}-\vec{v}_{\mathrm{a}}\)
∴ \(\vec{v}_{\mathrm{c} }=\vec{v}_{\mathrm{cj}}-\vec{v}_{\mathrm{a}}\)
= 1500 + (-500)
= 1000 km/hr
∴ \(\vec{v}_{\mathrm{c}}\) = 1000 km/hr
The relative velocity of the combustion products w.r.t. the observer is 1000 km/hr.
![]()
Question 22.
Derive the expression for average velocity and instantaneous velocity for the motion of an object in x-y plane.
Answer:
i) Consider an object to be at point A at time t1 in an x—y plane.
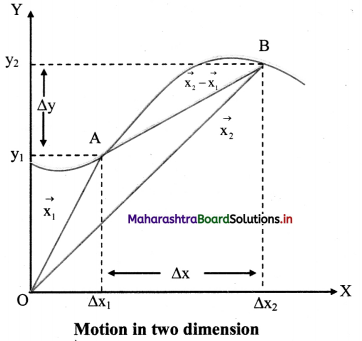
ii) At time t1, the position vector of the object is given as,

vii) The instantaneous velocity of the object at point A along the trajectory is along the tangent to the curve at A. This is shown by the vector AB.

Equation (3) is the slope of the tangent to the curve at the point at which we are calculating the instantaneous velocity.
Question 23.
Derive the expression for average acceleration and instantaneous acceleration for the motion of an object in x-y plane.
Answer:
i) Consider an object moving in an x-y plane.
Let the velocity of the particle be \(\vec{v}_{1}\) and \(\vec{v}_{2}\) at time t1 and t2 respectively.
ii) The average acceleration (\(\overrightarrow{\mathrm{a}}_{\mathrm{av}}\)) of the particle between t1 and t2 is given as,


Equation (1) is the slope of the tangent to the curve at the point at which we are calculating the instantaneous acceleration.
Question 24.
Explain relative velocity between two objects moving in a plane.
Answer:
- If \(\vec{v}_{A}\) and \(\vec{v}_{B}\) be the velocities of two bodies then relative velocity of A with respect to B is given by, \(\vec{v}_{A B}=\vec{v}_{A}-\vec{v}_{B}\)
- Similarly, the velocity of B with respect to A is given by, \(\vec{v}_{\text {BA }}=\vec{v}_{\text {B }}-\overrightarrow{v_{A}}\)
- Thus, the magnitudes of the two relative velocities are equal and their directions are opposite.
- For a number of objects A, B, C, D—Y, Z, moving with respect to the other. The velocity of A relative to Z can be given as, \(\overrightarrow{\mathrm{v}}_{\mathrm{AZ}}=\overrightarrow{\mathrm{v}}_{\mathrm{AB}}+\overrightarrow{\mathrm{v}}_{\mathrm{BC}}+\overrightarrow{\mathrm{v}}_{\mathrm{CD}}+\ldots+\overrightarrow{\mathrm{v}}_{\mathrm{XY}}+\overrightarrow{\mathrm{v}}_{\mathrm{YZ}}\)
The order of subscripts is: A → B → C → D → Z
![]()
Question 25.
Write a note on projectile motion.
Answer:
- An object in flight after being thrown with some velocity is called a projectile and its motion is called projectile motion.
- Example: A bullet fired from a gun, football kicked in air, a stone thrown obliquely in air etc.
- In projectile motion, the object is moving freely under the influence of Earth’s gravitational field.
- The projectile has two components of velocity, one in the horizontal i.e., along the x- direction and the other in the vertical i.e., along the y-direction.
- As acceleration due to gravity acts only along the vertically downward direction, the vertical component changes in accordance with the laws of motion with ax = 0 and ay = -g.
- As no force is acting in the horizontal direction, the horizontal component of velocity remains unchanged.
[Note: Retarding forces like air resistance etc. are neglected in projectile motion unless otherwise stated.]
Question 26.
Obtain an expression for the time of flight of a projectile.
Answer:
Expression for time of flight:
- Consider a body projected with velocity \(\vec{u}\), at an angle θ of projection from point O in the co-ordinate system of the X-Y plane, as shown in figure.
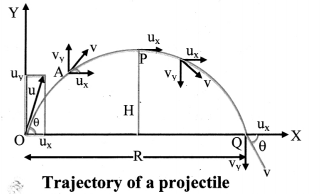
- The initial velocity \(\vec{u}\) can be resolved into two rectangular components:
ux = u cos θ (Horizontal component)
uy = u sin θ (Vertical component) - Thus, the horizontal component remains constant throughout the motion due to the absence of any force acting in that direction, while the vertical component changes according to, vy = uy + ay t with ay = – g and uy = u sin θ
- The components of velocity of the projectile at time t are given by, vx = ux = u cos θ
vy = uy – gt = u sin θ – gt ………….. (1) - At maximum height.
vy = 0, t = tA = time of ascent = time taken to reach maximum height.
∴ 0 = u sin θ – gtA ……..[From(l)]
u sin θ = gtA
tA = \(\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\) ………….. (2)
This is time of ascent of projectile. - The total time in air i.e., time of flight T is given as,
T = 2tA ………… [From(2)]
= \(\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) ………… (3)
Equation (3) represents time of flight of projectile.
Question 27.
Define Horizontal range of projectile:
Answer:
The maximum horizontal distance travelled by the projectile is called the horizontal range (R) of the projectile.
Solved Examples
Question 28.
An aeroplane Is travelling northward with a velocity of 300 km/hr with respect to the Earth. Wind is blowing from east to west at a speed of 100 km/hr. What is the velocity of the aeroplane with respect to the wind?
Solution:
Given:
velocity of aeroplane w.r.t Earth,
\(\vec{v}_{A E}=300 \hat{j}\)
velocity of wind w.r.t Earth,
\(\vec{v}_{w E}=-100 \hat{i}\)

![]()
Question 29.
A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontally with an initial speed of 15 ms-1. Neglecting air resistance, find the time taken by the stone to reach the ground, and the speed with which it hits the ground. Take = 9.8 m/s2.
Solution:
Given: h = 490m, ux = 15 ms-1, ay = 9.8 ms-1,
ax = 0
To find: i) Time taken (t)
ii) Velocity (v)
Formulae: i) t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\)
ii) v = \(\sqrt{v_{x}^{2}+v_{y}^{2}}\)
Calculation: t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\sqrt{\frac{2 \times 490}{9.8}}\) = 10 s
vx = ux + axt= 15 + 0 × 10 = 15 m/s
uy = uy + ayt = 0 + 9.8 × 10 = 98 m/s
∴ v = \(\sqrt{\mathrm{v}_{\mathrm{x}}^{2}+\mathrm{v}_{\mathrm{y}}^{2}}=\sqrt{15^{2}+98^{2}}\)
= 99.1 m/s
The stone taken 10 s to reach the ground and hits the ground with 99.1 m/s.
Question 30.
A body is projected with a velocity of 40 ms-1. After 2 s it crosses a vertical pole of height 20.4 m. Find the angle of projection and horizontal range of projectile, (g = 9.8 ms-2).
Solution:
Given: u = 40 ms-1, t = 2 s, y = 20.4 m,
ay = -9.8 m/s2
To find: i) Angle of projection (θ)
ii) Horizontal range of projectile (R)
Formulae: i) y = uy t + \(\frac{1}{2}\) ay t2
ii) R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)
Calculation: Taking vertical upward motion of the projectile from point of projection up to the top of vertical pole we have
uy = 40 sinθ,
From formula (i),
∴ 20.4 = 40 sinθ × 2 + \(\frac{1}{2}\) (-9.8) × 22
∴ 20.4 = 80 sinθ – 19.6
or sinθ = \(\frac{(20.4+19.6)}{80}=\frac{1}{2}\)
or θ = 30°.
From formula (ii),
Horizontal range = \(\frac{40^{2}}{9.8}\) sin 2 × 30°
= 141.4 m
The angle of projection is 30°. The horizontal range of projection is 141.4m
Question 31.
A stone is thrown with an initial velocity components of 20 m/s along the vertical, and 15 m/s along the horizontal direction. Determine the position and velocity of the stone after 3 s. Determine the maximum height that it will reach and the total distance travelled along the horizontal on reaching the ground. (Assume g = 10 m/s2)
Solution:
The initial velocity of the stone in x-direction = u cos θ = 15 m/s and in y-direction = u sin θ = 20 m/s
After 3 s, vx = u cos θ = 15 m/s
vy = u sin θ – gt
= 20 – 10(3)
= -10 m/s
10 m/s downwards.
∴ v = \(\sqrt{\mathrm{v}_{x}^{2}+\mathrm{v}_{\mathrm{y}}^{2}}=\sqrt{15^{2}+10^{2}}=\sqrt{225+100}=\sqrt{325}\)
∴ v = 18.03m/s
tan α = vy/vx = 10/15 = 2/3
∴ α = tan-1 (2/3) = 33° 41’ with the horizontal.
Sx = (u cos θ)t = 15 × 3 = 45m,
Sy = (u sin θ)t – \(\frac{1}{2}\)gt2 = 2o × 3 – 5(3)2
∴ Sy = 15m
The maximum vertical distance travelled is given by,
H = \(\frac{(\mathrm{u} \sin \theta)^{2}}{(2 \mathrm{~g})}=\frac{20^{2}}{(2 \times 10)}\)
∴ H = 20m
Maximum horizontal distance travelled
R = \(\frac{2 \cdot u_{x} \cdot u_{y}}{g}=\frac{2(15)(20)}{10}\) = 60 m
![]()
Question 32.
A body is projected with a velocity of 30 ms-1 at an angle of 300 with the vertical.
Find
i) the maximum height
ii) time of flight and
iii) the horizontal range
Solution:
Given:
30 ms-1, θ = 90° – 30° = 60°
To find: i) The maximum height reached (H)
ii) Time of flight (T)
iii) The horizontal range (R)

i) The maximum height reached by the body is 34.44 m.
ii) The time of flight of the body is 5.3 s.
iii) The horizontal range of the body is 79.53 m.
Question 33.
A projectile has a range of 50 m and reaches a maximum height of 10 m. What is the e1eation of the projectile?
Solution:
Given: R = 50m, H = 10 m
To find: Elevation of the projectile (θ)

∴ θ = tan-1 (0.8)
∴ θ = 38.66°
The elevation of the projectile is 38.66°
Question 34.
A bullet fired at an angle of 300 with the horizontal hits the ground 3 km away. By adjusting the angle of projection, can one hope to hit a target 5 km away? Assume the muzzle speed to be fixed and neglect air resistance.
Solution:
R = 3km = 3000m, θ = 30°,
Distance of target R’ = 5km
Horizontal range, R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)
∴ 3000 = \(\frac{\mathrm{u}^{2} \sin 60^{\circ}}{\mathrm{g}}\)
∴ \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}=\frac{3000}{\sin 60^{\circ}}=\frac{3000 \times 2}{\sqrt{3}}\) = 2000\(\sqrt {3}\)
Maximum horizontal range,
Rmax = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\) = 2000 \(\sqrt {3}\) m
= 2000 × 1.732 = 3464m = 3.46km
Since R’ > Rmax, Target cannot be hit.
Question 35.
Q.54. A ball is thrown at an angle θ and another ball ¡s thrown at an angle (90° – θ) with the horizontal direction from the same point with velocity 39.2 ms-1. The second ball reaches 50 m higher than the first balL find their individual heights. [Take g = 9.8 ms-2]
Solution:
For the first ball: Angle of projection = θ,
u = 39.2 ms-1
H = \(\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}\)
H = \(\frac{(39.2)^{2} \sin ^{2} \theta}{2 \times 9.8}\) …………… (i)
For the second ball: Angle of projection
= 90° – θ,
u = 39.2 ms-1,
maximum height reached = (H + 50) m
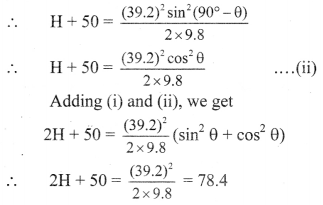
or 2H = 78.4 – 50 = 28.4
∴ H = 14.2 m
∴ Height of first ball = H = 14.2 m
Height of second ball = H + 50 = 14.2 + 50 = 64.2 m
i) Height reached by the first ball is 14.2 m.
ii) Height reached by the second ball is 64.2m.
![]()
Question 36.
A body is thrown with a velocity of 49 m/s at an angle of 30° with the horizontal. Find
i) the maximum height attained by it
ii) the time of flight and
iii) the horizontal range.
Solution:
Given: u = 49 m/s. θ = 30°
To find: i) The maximum height attained (H)
ii) The time of flight (T)
iii) The horizontal range (R)

i) The maximum height attained by the body is 30.625 m
ii) The time of flight of the body is 5 s.
iii) The horizontal range of the body is 212.2 m.
Question 37.
A fighter plane flying horizontally at a altitude of 1.5 km with a speed of 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with a muzzle velocity of 600 m/s to hit the plane? At what minimum altitude should the pilot fly to avoid being hit? [Take g = 10 m /s2]
Solution:
Given: h = 1.5 km = 1500 m,
u = 600 m/s,
y = 720 km/h = 720 × \(\frac{5}{18}\) = 200 m/s
To find: i) Angle of firing (θ)
ii) Minimum altitude (H)
Formula: H = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
Calculation:
Let the shell hit the plane t seconds after firing,
∴ 600 cos(90 – θ) × t = 200 t
∴ cos(90 – θ) = \(\frac{1}{6}\)
∴ 90° – θ = cos-1(\(\frac{1}{3}\))
cos -1(\(\frac{1}{3}\)) = 90° – θ
∴ 70°28’ = 90° – θ
∴ θ = 90° – cos-1 (\(\frac{1}{3}\))
∴ θ = 19°47’ with vertical
To avoid being hit, the plane must be at a minimum height, i.e., maximum height reached by the shell.
From formula,
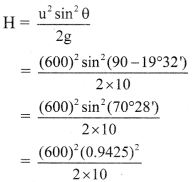
∴ H = 15.9 km
i) Angle made by gun with the vertical is 19°47′.
ii) Minimum altitude at which the pilot should fly is 15.9 km.
Question 38.
A both is thrown with a velocity of 40 m/s in a direction making an angle of 30° with the horizontal. Calculate
i) Horizontal range
ii) Maximum height and
iii) Time taken to reach the maximum height.
Solution:
Given: u = 40 m/s, θ = 30°
To find: i) Horizontal range (R)
ii) Maximum height (Hmax)
iii) Time to reach max. height (tA)

i) Horizontal range of the body is 141.4 m.
ii) Maximum height reached by the body is 20.41 m.
iii) Time taken by the body to reach the maximum height is 2.041 s.
![]()
Question 39.
If a child launches paper plane with a velocity of 6 m/s2 at an angle θ with vertical.
i) What will be the maximum range of the projectile?
ii) What will be the maximum height of the projectile?
iii) Will the plane hit a lady standing at a distance of 6m?
Solution:
i) Range of projectile to given by.
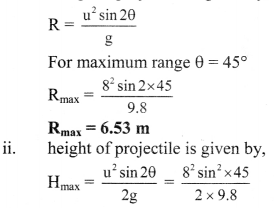
Hmax = 1.63 m
iii) As maximum range of projectile is 6.53 m and lady is standing 6m away, plane will hit the lady.
Question 40.
Explain the term uniform circular motion.
Answer:
- The motion of a body along the circumference of a circle with constant speed is called uniform circular motion.
- The magnitude of velocity remains constant and its direction is tangential to its circular path.
- The acceleration is of constant magnitude and it is perpendicular to the tangential velocity. It is always directed towards the centre of the circular path. This acceleration is called centripetal acceleration.
- The centripetal force provides the necessary centripetal acceleration.
- Examples of U.C.M:
- Motion of the earth around the sun.
- Motion of the moon around the earth.
- Revolution of electron around the nucleus of atom.
Question 41.
What is meant by period of revolution of U.C.M. Obtain an expression for the period of revolution of a particle performing uniform circular motion.
Answer:
The time taken by a particle performing uniform circular motion to complete one revolution is called as period of revolution. It is denoted by T.
Expression for time period:
During period T, particle covers a distance equal to circumference 2πr of circle with uniform speed v.

Question 42.
For a particle performing uniform circular motion, derive an expression for angular speed and state its unit.
Answer:
- Consider an object of mass m, moving with a uniform speed v, along a circle of radius r. Let T be the time period of revolution of the object, i.e., the time taken by the object to complete one revolution or to travel a distance of 2πr.
Thus, T = 2πr/v
∴ Speed, v = \(\frac{\text { Distance }}{\text { Time }}=\frac{2 \pi \mathrm{r}}{\mathrm{T}}\) …………….. (1) - During circular motion of a point object, the position vector of the object from centre of the circle is the radius vector r. Its magnitude is radius r and it is directed away from the centre to the particle, i.e., away from the centre of the circle.
- As the particle performs UCM, this radius vector describes equal angles in equal intervals of time.
- The angular speed gives the angle described by the radius vector.
- During one complete revolution, the angle described is 2π and the time taken is period T. Hence, the angular speed ω is given as, ….[From (1)]
ω = \(\frac{\text { Angle }}{\text { time }}=\frac{2 \pi}{\mathrm{T}}=\frac{\left(\frac{2 \pi \mathrm{r}}{\mathrm{T}}\right)}{\mathrm{r}}\) …………….. [From (1)]
= \(\frac{\mathrm{v}}{\mathrm{r}}\) - The unit of angular speed is radian/second.
![]()
Question 43.
Derive an expression for centripetal acceleration of a particle performing uniform circular motion.
Answer:
Expression for centripetal acceleration by calculus method:
i) Suppose a particle is performing U.C.M in anticlockwise direction.
The co-ordinate axes are chosen as shown in the figure.
Let,
A = initial position of the particle which lies on positive X-axis
P = instantaneous position after time t
θ = angle made by radius vector
ω = constant angular speed
\(\overrightarrow{\mathrm{r}}\) = instantaneous position vector at time t
ii) From the figure,
\(\vec{r}=\hat{i} x+\hat{j} y\)
where, \(\hat{i}\) and \(\hat{j}\) are unit vectors along X-axis and Y-axis respectively.
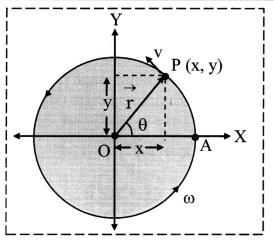
iii) Also, x = r cos θ and y = r sin θ
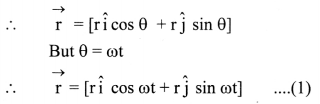
iv) Velocity of the particle is given as rate of change of position vector.

vi) From equation (1) and (2),
\(\overrightarrow{\mathrm{a}}=-\omega^{2} \overrightarrow{\mathrm{r}}\) ……….. (3)
Negative sign shows that direction of acceleration is opposite to the direction of position vector. Equation (3) is the centripetal acceleration.
vii) Magnitude of centripetal acceleration is given by,
a = ω2r
viii) The force providing this acceleration should also be along the same direction, hence centripetal.
∴ \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}=-\mathrm{m} \omega^{2} \overrightarrow{\mathrm{r}}\)
This is the expression for the centripetal force on a particle undergoing uniform circular motion.
ix) Magnitude of F = mω2r = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = mωv
Question 44.
Discuss the factors on which time period of conical pendulum depends.
Answer:
Time period of conical pendulum is given by,
T = 2π \(\sqrt{\frac{\cos \theta}{\mathrm{g}}}\) …………. (i)
where, l = length of the string
g = acceleration due to gravity
θ = angle of inclination
From equation (i), it is observed that period of conical pendulum depends on following factors.
i) Length of pendulum (l): Time period of conical pendulum increases with increase in length of pendulum, i.e., T ∝ \(\sqrt {l}\)
ii) Acceleration due to gravity (g): Time period of conical pendulum decreases with increase in g. i.e., T ∝ \(\frac{1}{\sqrt{g}}\)
iii) Angle of inclination (θ): As θ increases, cos θ decreases, hence, time period of conical pendulum decreases with increase in θ. (For 0 < θ < π) i.e., T ∝ \(\sqrt{\cos \theta}\)
Question 45.
Is there any limitation on semi vertical angle in conical pendulum? Give reason.
Answer:
Yes.
- For a conical pendulum, Period T ∝ \(\sqrt{\cos \theta}\)
∴ Tension F ∝ \(\frac{1}{\cos \theta}\)
Speed v ∝ \(\sqrt{\tan \theta}\)
With increase in angle θ, cos θ decreases and tan θ increases. For θ = 90°, T = 0, F = ∞ and v = ∞ which cannot be possible. - Also, θ depends upon breaking tension of string, and a body tied to a string cannot be resolved in a horizontal circle such that the string is horizontal. Hence, there is limitation of semi vertical angle in conical pendulum.
Solved Examples
Question 46.
An object of mass 50 g moves uniformly along a circular orbit with an angular speed of 5 rad/s. If the linear speed of the particle is 25 m/s, ¡s the radius of the circle? Calculate the centripetal force acting on the particle.
Solution:
Given: ω = 5 rad/s, v = 25 m/s,
m = 50 g = 0.05 kg
To find: radius (r), centipetal force (F)
Formula: i) v = ωr
ii) F = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\)
Calculation: From formula (i),
r = v/ω = 25/5 m = 5 m.
From formula (ii),
F = \(\frac{0.05 \times 25^{2}}{5}\) = 6.25 N.
i) Radius of the circle is 5 m.
ii) Centripetal force acting on the particle is 6.25 N.
![]()
Question 47.
An object is travelling in a horizontal circle with uniform speed. At t = 0, the velocity is given by \(\overrightarrow{\mathbf{u}}=20 \hat{\mathbf{i}}+35 \hat{\mathbf{j}}\) km/s. After one minute the velocity becomes \(\overrightarrow{\mathbf{v}}=-20 \hat{\mathbf{i}}-35 \hat{\mathbf{j}}\). What is the magnitude of the acceleration?
Solution:
Magnitude of initial and final velocities,
u= \(\sqrt{(20)^{2}+(35)^{2}}\) m/s
∴ u = \(\sqrt{1625}\) m/s
∴ u = 40.3 m/s
As the velocity reverses in 1 minute, the time period of revolution is 2 minutes.
T = \(\frac{2 \pi \mathrm{r}}{\mathrm{u}}\), giving r = \(\frac{\text { uT }}{2 \pi}\)
Now,
a = \(\frac{\mathrm{u}^{2}}{\mathrm{r}}=\frac{\mathrm{u}^{2} 2 \pi}{\mathrm{uT}}=\frac{2 \pi \mathrm{u}}{\mathrm{T}}=\frac{2 \times 3.142 \times 40.3}{2 \times 60}\)
= {antilog[log(3.142) + log(40.3) – log(60)]}
= {antilog(0.4972 + 1.6053 – 1.7782)}
= {antilog(0.3243)}
= 2.110.
∴ a = 2.11 m/s2
The magnitude of acceleration is 2.11 m/s2.
Question 48.
A racing car completes 5 rounds of a circular track in 2 minutes. Find the radius of the track if the car has uniform centripetal acceleration of π2/s2.
Solution:
Given: 5 rounds = 2πr(5),
t = 2minutes = 120s
To find: Radius (r)
Formula: acp = ω2r
Calculation: From formula,
acp = ω2r
∴ π2 = \(\frac{\mathrm{v}^{2}}{\mathrm{r}}\)
But v = \(\frac{2 \pi r(5)}{t}=\frac{10 \pi r}{t}\)
∴ π2 = \(\frac{100 \pi^{2} \mathrm{r}^{2}}{\mathrm{rt}^{2}}\)
∴ r = \(\frac{120 \times 120}{100}\) =144m
The radius of the track is 144 m.
Question 49.
A car of mass 1500 kg rounds a curve of radius 250m at 90 km/hour. Calculate the centripetal force acting on it.
Solution:
Given: m= 1500 kg, r = 250m,
v = 90 km/h = 90 × \(\frac{5}{18}\) = 25m/s
To find: Centripetal force (FCP)
Formula: FCP = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\)
Calculation: From formula,
FCP = \(\frac{1500 \times(25)^{2}}{250}\)
∴ FCP = 3750 N
The centripetal force acting on the car is 3750 N.
![]()
Question 50.
A one kg mass tied at the end of the string 0.5 m long is whirled ¡n a horizontal circle, the other end of the string being fixed. The breaking tension in the string is 50 N. Find the greatest speed that can be given to the mass.
Solution:
Given: Breaking tension, F = 50 N,
m = 1 kg, r = 0.5m
To find: Maximum speed (vmax)
Formula: B.T (F) = max. C.F \(\frac{m v_{\max }^{2}}{r}\)
Calculation: From formula,
v2max = \(\frac{F \times r}{m}\)
∴ v2max = \(\frac{50 \times 0.5}{1}\)
∴ vmax = \(\sqrt{50 \times 0.5}\) = 5 m/s
The greatest speed that can be given to the mass is 5 m/s.
Question 51.
A mass of 5 kg is tied at the end of a string 1.2 m long revolving in a horizontal circle. If the breaking tension in the string is 300 N, find the maximum number of revolutions per minute the mass can make.
Solution:
Given: Length of the string, r = 1.2 m,
Mass attached. m = 5 kg,
Breaking tension, T = 300 N
To find: Maximum number of revolutions per minute (nmax)
Formula: Tmax = Fmax = mrω2max
Calculation: From formula,
∴ 5 × 1.2 × (2πn)2 = 300
∴ 5 × 1.2 × 4π2n2 = 300
∴ n2max = \(\frac{300}{4 \times(3.142)^{2} \times 6.0}\) = 1.26618
∴nmax = \(\sqrt{1.26618}\) = 1.125 rev/s
∴ nmax = 1.125 × 60
∴ nmax = 67.5 rev/min
The maximum number of revolutions per minute made by the mass is 67.5 rev /min.
Question 52.
A coin placed on a revolving disc, with its centre at a distance of 6 cm from the axis of rotation just slips off when the speed of the revolving disc exceeds 45 r.p.m. What should be the maximum angular speed of the disc, so that when the coin is at a distance of 12 cm from the axis of rotation, it does not slip?
Solution:
Given. r1 = 6cm, r2 = 12cm, n1 = 45 r.p.m
To Find: Maximum angular speed (n2)
Formula: Max. C.F = mrω2
Calculation: Since, mr1ω12 mr2ω22 [As mass is constant]
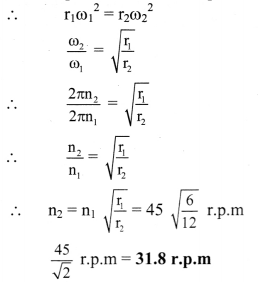
The maximum angular speed of the disc should be 31.8 r.p.m.
Question 53.
A stone of mass 0.25 kg tied to the end of a string is whirled in a circle of radius 1.5 m with a speed of 40 revolutions/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
Solution:
Given: m = 0.25 kg, r.= 1.5 m, Tmax = 200 N,
n = 40 rev. min-1 = \(\frac{40}{60}\) rev s-1
To find: i) Tension (T)
ii) Maximum speed (vmax)

i) The tension in the string is 6.55 N.
ii) The maximum speed with which the stone can be whirled around is 34.64 m s-1.
![]()
Question 54.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a vertical axis, calculate tension in the string. (g = 9.8 m/s2)
Solution:
Given: l = 120 cm = 1.2rn, r = 0.2m,
m = 150 g = 0.15 kg
To find: Tension in the string (T)

∴ Substituting in formula,
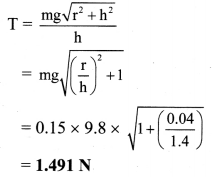
Tension in the string is 1.491 N.
Question 55.
A conical pendulum has length 50 cm. Its bob of mass 100 g performs uniform circular motion in horizontal plane, so as to have radius of path 30 cm. Find
i) The angle made by the string with vertical
ii) The tension in the supporting thread and
iii) The speed of bob.
Solution:
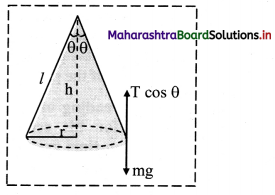
Given: l = 150 cm = 0.5 m, r = 30 cm = 0.3 m,
m = 100 g = 100 × 10-3 kg = 0.1 kg
To find: i) Angle made by the string with vertical (θ)
ii) Tension in the supporting thread (T)
iii) Speed of bob (y)
Formulae: i) tan θ = –\(\frac{r}{\mathrm{~h}}\)
ii) tan θ = \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\)
Calculation: By Pythagoras theorem, l2 = r2 + h2
h2 = l2 – r2
h2 = 0.25 – 0.09 = 0.16
h = 0.4m
i) From formula (1),
tan θ = \(\frac{0.3}{0.4}\) = 0.75
∴ θ = tan-1 (0.75)
θ = 36°52’
ii) The weight of bob is balanced by vertical component of tension T
∴ T cos θ = mg
cos θ = \(\frac{\mathrm{h}}{l}=\frac{0.4}{0.5}\) = 0.8
∴ T = \(\frac{\mathrm{mg}}{\cos \theta}=\frac{0.1 \times 9.8}{0.8}\)
∴ T = 1.225 N
iii) From formula (2),
v2 = rg tan θ
∴ v2 = 0.3 × 9.8 × 0.75 = 2.205
∴ v = 1.485 m/s
i) Angle made by the string with vertical is 36°52′. ‘
ii) Tension in the supporting thread is 1.225 N.
iii) Speed of the bob is 1.485 m/s
Apply Your Knowledge
Question 56.
Explain the variation of acceleration, velocity and distance with time for an object under free fall.
Answer:
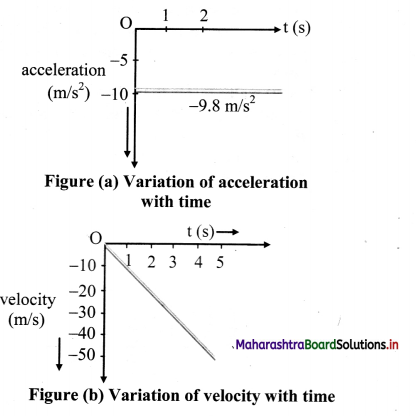
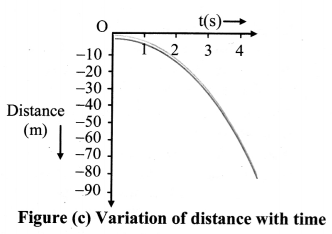
- For a free falling object, considering the downward direction as negative, the object is released from rest.
∴ initial velocity u = 0 and a = -g = -9.8 m/s2
∴ The kinematical equations become,
v = u + at = 0 – gt = -gt = -9.8t
s = ut + \(\frac{1}{2}\)at2 = o + \(\frac{1}{2}\)(-g)t2 = –\(\frac{1}{2}\) 9.8t2
= -4.9t2
v2 = u2 + 2as = 0 + 2(-g)s
= -2gs = -2 × 9.8s
= -19.6s - These equations give the velocity and the distance travelled as a function of time and also the variation of velocity with distance.
- The variation of acceleration, velocity and distance with the time is as shown in figure a, b and c respectively.
Question 57.
The position-time (x – t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in figure. Choose the correct entries in the brackets below.
i) (A/B) lives closer to the school than (B/A)
ii) (A/B) starts from the school earlier than (B/A)
iii) (A/B) walks faster than (B/A)
iv) A and B reach home at the (same/different) time
v) (A/B) overtakes (B/A) on the road (once/twice)
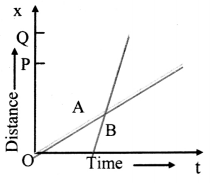
Answer:
- A lives closer to the school than B. This is because, OQ > OP, hence B has to cover larger distance than A.
- A starts from the school earlier than B. This is because, A starts at t = 0 whereas B starts at some finite time greater than zero.
- As slope of B is greater than that of A, hence B walks faster than A. iv. A and B reach home at different times.
- This is because the value of ‘t’ corresponding to P and Q for A and B respectively is different.
- B overtakes A on the road once. This is because A and B meet each other only once on their way back home. As B starts from school later than A and walks faster than A, hence B overtakes A once on his way home.
![]()
Question 58.
A bowler throws the ball up to correct distance by controlling his velocity and angle of throw, as shown in the figure given below
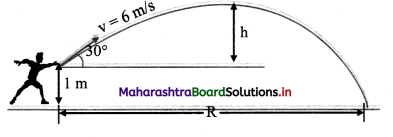
i) What will be the range of the projectile?
ii) What will be the height of the projectile from ground?
Answer:
- Range of projectile is given by,
R = \(\frac{u^{2} \sin 2 \theta}{g}=\frac{6^{2} \times \sin (2 \times 30)}{9.8}\)
R = 3.18 m - Height of projectile is given by,
H = \(\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=\frac{6^{2} \times \sin ^{2} 30}{2 \times 9.8}\) = 0.46m
Height achieved by ball from ground is
H = 0.46 + 1 = 1.46m
i) The range of the projectile is 3.18 m.
ii) The height of the projectile is 1.46 m.
Question 59.
A child takes reading of two cars running on highway, for his school project. He draws a position-time graph of the two cars as shown in the figure
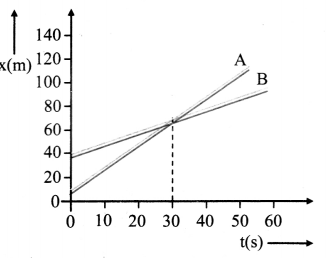
i) What is the velocity of two cars when they meet together?
ii) What is the difference in velocities of the two cars when they cover their maximum distance?
iii) What will be acceleration of the two cars in first 20 s?
Solution:
i) According to graph, the velocity of two cars when they meet each other are,
x = 70m
t = 308
v = \(\frac{x}{t}=\frac{70}{30}\) = 2.33 m/s
ii) According to graph, for maximum distance.
For 1st car,
x1 = 120m
t1 = 50 s
v1 = \(\frac{x_{1}}{t_{1}}=\frac{120}{50}\)
v1 = 2.4 m/s
For 2nd car,
x2 = 90 m
t2 = 60 s
v2 = \(\frac{x_{2}}{t_{2}}=\frac{90}{60}\)
v2 = 1.5 m/s
Difference in velocities is given by,
v1 – v2 = 2.4 – 1.5 = 0.9 m/s
iii) According to graph,
Acceleration of 1st car in first 20 s
v1 = \(\frac{\mathrm{x}_{1}}{\mathrm{t}}\)
v1 = \(\frac{60}{20}\)
v1 = 3 m/s
a1 = \(\frac{\mathrm{v}_{1}}{\mathrm{t}}=\frac{3}{20}\)
a1 = 0.15 m/s2
Acceleration of 2nd car in first 20 s
v2 = \(\frac{\mathrm{x}_{2}}{\mathrm{t}}\)
v2 = \(\frac{40}{20}\)
v2 = 2 m/s
a2 = \(\frac{\mathrm{v}_{2}}{\mathrm{t}}=\frac{2}{20}\)
a2 = 0.1 m/s2
Now,
a1 – a2 = 0.15 – 0.1
= 0.05 m/s2
i) The velocity of two cars when they meet together is 2.33 m/s.
ii) The difference in velocities of two cars when they cover maximum distance is 0.9 m/s.
iii) The accelerator of two cars in 20 s is 0.05 m/s2.
![]()
Question 60.
The speed of a projectile u reduces by 50% on reaching maximum height. What is the range on the horizontal plane?
Solution:
If θ is the angle of projection, then velocity of projectile at height point = u cos θ
u cos θ = \(\frac{50}{100}\) u = \(\frac{1}{2}\) u
or cos θ = \(\frac{1}{2}\) cos 60°
or θ = 60°
Horizontal range,
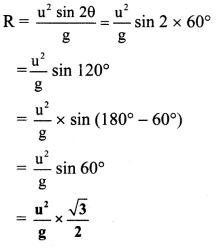
Question 61.
In projectile motion, vertical motion and horizontal motion are dependent of each other. Yes or No? Justify your answer.
Answer:
No. In projectile motion, the horizontal and vertical motion are independent of each other because both motions don’t affect each other.
Question 62.
In angular projection of a projectile, at highest point, what will be the components of horizontal and vertical velocities?
Answer:
At highest point of angular projection of a projectile, the horizontal component of its velocity is non zero and the vertical component of its velocity is momentarily zero.
Question 63.
What angle will be described between velocity and acceleration at highest point of projectile path?
Answer:
At highest point of projectile path, the angle between velocity and acceleration is 90°.
Quick Review

Multiple Choice Questions
Question 1.
The velocity-time relation of a particle starting from rest is given by v = kt where k = 2 m/s2. The distance travelled in 3 sec is
(A) 9 m
(B) 16 m
(C) 27 m
(D) 36 m
Answer:
(A) 9 m
Question 2.
If the particle is at rest, then the x – t graph can be only
(A) parallel to position – axis
(B) parallel to time – axis
(C) inclined with acute angle
(D) inclined with obtuse angle
Answer:
(B) parallel to time – axis
![]()
Question 3.
A body is thrown vertically upwards, maximum height is reached, then it will have
(A) zero velocity and zero acceleration.
(B) zero velocity and finite acceleration.
(C) finite velocity and zero acceleration.
(D) finite velocity and finite acceleration.
Answer:
(B) zero velocity and finite acceleration.
Question 4.
Which of the following is NOT a projectile?
(A) A bullet fired from gun.
(B) A shell fired from cannon.
(C) A hammer thrown by athlete.
(D) An aeroplane in flight.
Answer:
(D) An aeroplane in flight.
Question 5.
The range of projectile is 1 .5 km when it is projected at an angle of 15° with horizontal. What will be its range when it is projected at an angle of 45° with the horizontal?
(A) 0.75 km
(B) 1.5 km
(C) 3 km
(D) 6 km
Answer:
(C) 3 km
Question 6.
Which of the following remains constant for a projectile fired from the earth?
(A) Momentum
(B) Kinetic energy
(C) Vertical component of velocity
(D) Horizontal component of velocity
Answer:
(D) Horizontal component of velocity
Question 7.
In case of a projectile, what is the angle between the instantaneous velocity and acceleration at the highest point?
(A) 45°
(B) 1800
(C) 90°
(D) 0°
Answer:
(C) 90°
Question 8.
A player kicks up a ball at an angle θ with the horizontal. The horizontal range is maximum when θ is equal to
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer:
(B) 45°
![]()
Question 9.
The greatest height to which a man can throw a stone is h. The greatest distance to which he can throw it will be
(A) h/2
(B) 2h
(C) h
(D) 3h
Answer:
(B) 2h
Question 10.
Two balls are projected at an angle θ and (90° – θ) to the horizontal with the same speed. The ratio of their maximum vertical
heights is
(A) 1 : 1
(B) tan θ : 1
(C) 1 : tan θ
(D) tan2 θ : 1
Answer:
(D) tan2 θ : 1
Question 11.
When air resistance is taken into account while dealing with the motion of the projectile, to achieve maximum horizontal range, the angle of projection should be,
(A) equal to 45°
(B) less than 45°
(C) greater than 90°
(D) greater than 45°
Answer:
(D) greater than 45°
Question 12.
The maximum height attained by projectile is found to be equal to 0.433 of the horizontal range. The angle of projection of this projectile is
(A) 30°
(B) 45°
(C) 60°
(D) 75°
Answer:
(C) 60°
Question 13.
A projectile is thrown with an initial velocity of 50 m/s. The maximum horizontal distance which this projectile can travel is
(A) 64m
(B) 128m
(C) 5m
(D) 255m
Answer:
(D) 255m
Question 14.
A jet airplane travelling at the speed of 500 kmh-1 ejects the burnt gases at the speed of 1400 kmh-1 relative to the jet airplane. The speed of burnt gases relative to stationary observer on the earth is
(A) 2.8 kmh-1
(B) 190 kmh-1
(C) 700 kmh-1
(D) 900 kmh-1
Answer:
(D) 900 kmh-1
Question 15.
A projectile projected with certain angle reaches ground with
(A) double angle
(B) same angle
(C) greater than 90°
(D) angle between 90° and 180°
Answer:
(B) same angle
![]()
Question 16.
The time period of conical pendulum is _________.
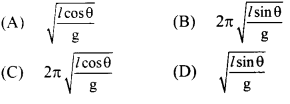
Answer:
(C) \(2 \pi \sqrt{\frac{l \cos \theta}{\mathrm{g}}}\)
Question 17.
A projectile projected with certain velocity reaches ground with (magnitude)
(A) zero velocity
(B) smaller velocity
(C) same velocity
(D) greater velocity
Answer:
(C) same velocity
Question 18.
The period of a conical pendulum in terms of its length (l), semivertical angle (θ) and acceleration due to gravity (g) is:
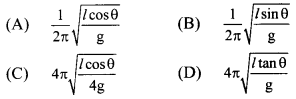
Answer:
(C) \(4 \pi \sqrt{\frac{l \cos \theta}{4 \mathrm{~g}}}\)
Question 19.
Consider a simple pendulum of length 1 m. Its bob performs a circular motion in horizontal plane with its string making an angle 600 with the vertical. The period of rotation of the bob is(Take g = 10 m/s2)
(A) 2s
(B) 1.4s
(C) 1.98 s
(D) none of these
Answer:
(B) 1.4s
Question 20.
The period of a conical pendulum is
(A) equal to that of a simple pendulum of same length l.
(B) more than that of a simple pendulum of same length l.
(C) less than that of a simple pendulum of same length l.
(D) independent of length of pendulum.
Answer:
(C) less than that of a simple pendulum of same length l.
Competitive Corner
Question 1.
Two particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed vA and vB respectively. Their time period of rotation is the same. The ratio of angular speed of A to that of B will be:
(A) rB : rA
(B) 1 : 1
(C) rA : rB
(D) vA : vB
Answer:
(B) 1 : 1
Hint:
Time period of rotation (A and B) is same

Question 2.
When an object is shot from the bottom of a long smooth inclined plane kept at an angle 60° with horizontal, it can travel a distance x1 along the plane. But when the inclination is decreased to 30° and the same object is shot with the same velocity, it can travel x2 distance. Then x1 : x2 will be:
(A) 1 : \(\sqrt {3}\)
(B) 1 : 2\(\sqrt {3}\)
(C) 1 : \(\sqrt {2}\)
(D) \(\sqrt {3}\) : 1
Answer:
(A) 1 : \(\sqrt {3}\)
Hint:
v2 = u2 + 2as
∴ v2 = u2 + 2 g sin θ x
sin θ. x = constant
∴ x ∝ \(\frac{1}{\sin \theta}\)
∴ \(\frac{x_{1}}{x_{2}}=\frac{\sin \theta_{2}}{\sin \theta_{1}}=\frac{1 / 2}{\sqrt{3} / 2}\) = 1 : \(\sqrt {3}\)
Question 3.
A person travelling in a straight line moves with a constant velocity v1 for certain distance x’ and with a constant velocity v2 for next equal distance. The average velocity y is given by the relation
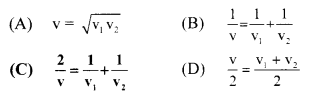
Answer:
(C) \(\frac{2}{v}=\frac{1}{v_{1}}+\frac{1}{v_{2}}\)
Hint:
Let, t’ be the time taken to travel distance ‘x’ with constant velocity ‘v1’
∴ t1 = \(\frac{\mathrm{x}}{\mathrm{v}_{2}}\)
Let ‘t2’ be the time taken to travel equal distance ‘x’ with constant velocity ‘v2‘
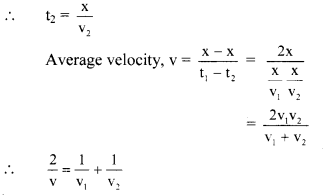
![]()
Question 4.
Two bullets are fired horizontally and simultaneously towards each other from roof tops of two buildings 100 m apart and of same height of 200 m, with the same velocity of 25 m/s. When and where will the two bullets collide? (g = 10 m/s2)
(A) They will not collide
(B) After 2 s at a height of 180 m
(C) After 2 s at a height of 20 m
(D) After 4 s at a height of 120 m
Answer:
(B) After 2 s at a height of 180 m
Hint:
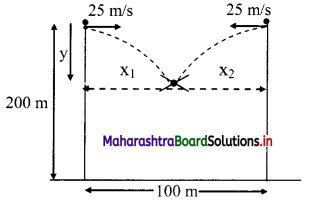
Let the bullets collide at time t
The horizontal displacement x1 and x2 is given by the equation
x1 = ut and x2 = ut
∴ x1 + x2 = 100
∴ 25t + 25t = 100
∴ t = 2s
Vertical displacement ‘y’ is given by
y = \(\frac{1}{2}\) gt2 = \(\frac{1}{2}\) × 10 × 22 = 20m
∴ h = 200 – 20= 180m
Question 5.
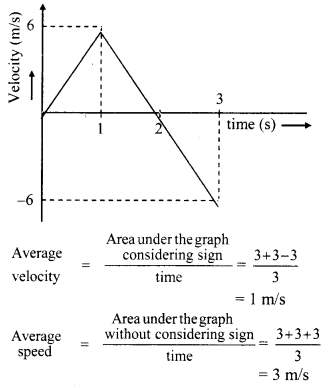
A toy car with charge q moves on a frictionless horizontal plane surface under the influence of a uniform electric field \(\vec{E}\). Due to the force q\(\vec{E}\), its velocity increases from 0 to 6 m/s in one second duration. At that instant the direction of the field is reversed. The car continues to move for two more seconds under the influence of this field. The average velocity and the average speed of the toy car between 0 to 3 seconds are respectively
(A) 2 m/s, 4 m/s
(B) 1 m/s, 3 m/s
(C) 1 m/s, 3.5 m/s
(D) 1.5 m/s, 3 m/s
Answer:
(B) 1 m/s, 3 m/s
Hint:
Car at rest attains velocity of 6 m/s in t1 = 1 s.
Now as direction of field is reversed, velocity of car will reduce to 0 m/s in next 1 s. i.e., at t2 = 2 s. But, it continues to move for next one second. This will give velocity of -6 m/s to car at t3 = 3 s.
Using this data, plot of velocity versus time will be
Question 6.
All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
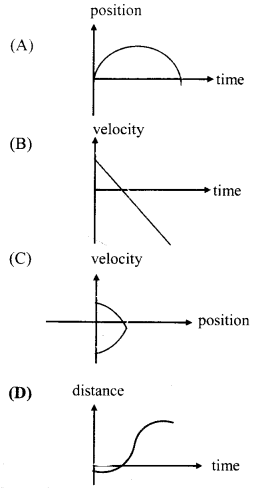
Answer:
(D)
Hint:
The graphs (A), (B) and (C) represent the uniformly retarded motion, i.e., velocity decreases uniformly. However, the slope of the curve in graph (D), indicates increasing velocity. Hence, graph (D) is incorrect.
![]()
Question 7.
A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then:
(A) T ∝ R(n+1)/2
(B) T ∝ Rn/2
(C) T ∝ R3/2 for any n
(D) T ∝ R\(\frac{n}{2}\)+1
Answer:
(A) T ∝ R(n+1)/2
Hint:
The centripetal force acting on the particle is provided by the central force,

Question 8.
Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be:
(A) \(\frac{\mathrm{t}_{1}+\mathrm{t}_{2}}{2}\)
(B) \(\frac{t_{1} t_{2}}{t_{2}-t_{1}}\)
(C) \(\frac{\mathbf{t}_{1} t_{2}}{\mathbf{t}_{2}+t_{1}}\)
(D) t1 – t2
Answer:
(C) \(\frac{\mathbf{t}_{1} t_{2}}{\mathbf{t}_{2}+t_{1}}\)
Hint:
Let velocity of Preeti be v1, velocity of escalator be v2 and distance travelled be L.

![]()
Question 9.
A body is thrown vertically upwards. Which one of the following graphs correctly represent the velocity vs time?
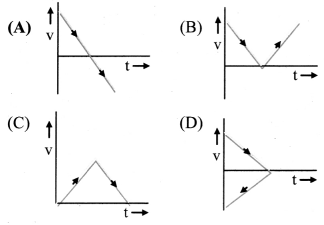
Answer:
(A)
Hint:
If a body is projected in vertically upward direction, then its acceleration is constant and negative. If direction of motion is positive i.e.. vertically up) and initial position of body is taken as origin, then the velocity decreases uniformly. At highest point its velocity is equal to zero and then it accelerates uniformly downwards returning to its reference position.