Maharashtra Board Class 11 Physics Important Questions Chapter 2 Mathematical Methods

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 2 Mathematical Methods Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 2 Mathematical Methods

Question 1.
Explain the representation of a vector graphically and symbolically.
Answer:

1. Graphical representation:
   A vector is graphically represented by a directed line segment or an arrow.
   eg.: displacement of a body from P to Q is represented as P → Q.
2. Symbolic representation:
   Symbolically a vector is represented by a single letter with an arrow above it, such as \(\overrightarrow{\mathrm{A}}\). The magnitude of the vector \(\overrightarrow{\mathrm{A}}\) is denoted as |A| or | \(\overrightarrow{\mathrm{A}}\) | or A.

Question 2.
A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector?
Answer:

1. For a physical quantity, only having magnitude and direction is not a sufficient condition to be a vector.
2. A physical quantity also has to obey vectors law of addition to be termed as vector.
3. Hence, anything that has magnitude and direction is not necessarily a vector.
   Example: Though current has definite magnitude and direction, it is not a vector.

Question 3.
Define and explain the following terms:
i. Zero vector (Null vector)
ii. Resultant vector
iii. Negative vectors
iv. Equal vectors
v. Position vector
Answer:
i. Zero vector (Null vector):
A vector having zero magnitude and arbitrary direction is called zero vector. It is denoted as \(\overrightarrow{0}\).
Example: Velocity vector of stationary particle, acceleration vector of a body moving with uniform velocity.

ii. Resultant vector:
The resultant of two or more vectors is defined as that single vector, which produces the same effect as produced by all the vectors together.

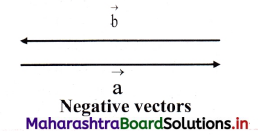
iii. Negative vectors:
A negative vector of a given vector is a vector of the same magnitude but opposite in direction to that of the given vector.
Negative vectors are antiparallel vectors.
In figure, \(\vec{b}\) = – \(\vec{a}\)

iv. Equal vectors:
Two vectors A and B representing same physical quantity are said to be equal if and only if they have the same magnitude and direction.

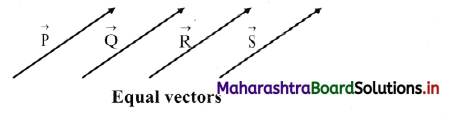
In the given figure |\(\overrightarrow{\mathrm{P}}\)| = |\(\overrightarrow{\mathrm{Q}}\)| = |\(\overrightarrow{\mathrm{R}}\)| = |\(\overrightarrow{\mathrm{S}}\)|

v. Position vector:
A vector which gives the position of a particle at a point with respect to the origin of chosen co-ordinate system is called position vector.

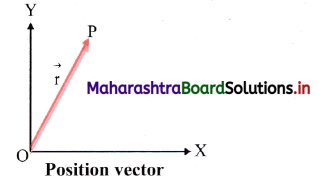
In the given figure \(\overrightarrow{\mathrm{OP}}\) represents position vector of \(\vec{P}\) with respect to O.

Question 4.
Whether the resultant of two vectors of unequal magnitude be zero?
Answer:
The resultant of two vectors of different magnitude cannot give zero resultant.

Question 5.
Define unit vector and give its physical significance.
Answer:
Unit vector: A vector having unit magnitude in a given direction is called a unit vector in that direction.
If \(\vec{p}\) is a non zero vector (P ≠ 0) then the unit vector \(\hat{\mathrm{u}}_{\mathrm{p}}\) in the direction of \(\overrightarrow{\mathrm{P}}\) is given by,
\(\hat{\mathrm{u}}_{\mathrm{p}}\) = \(\frac{\overrightarrow{\mathrm{P}}}{\mathrm{P}}\)
∴ \(\overrightarrow{\mathrm{P}}\) = \(\hat{u}_{p} P\)

Significance of unit vector:

i. The unit vector gives the direction of a given vector.

ii. Unit vector along X, Y and Z direction of a rectangular (three dimensional) coordinate is represented by \(\hat{\mathrm{i}}\), \(\hat{\mathrm{j}}\) and \(\hat{\mathrm{k}}\) respectively Such that \(\hat{\mathbf{u}}_{x}\) = \(\hat{\mathrm{i}}\), \(\hat{\mathbf{u}}_{y}\) = \(\hat{\mathrm{j}}\) and \(\hat{\mathbf{u}}_{z}\) = \(\hat{\mathrm{k}}\)
This gives \(\hat{\mathrm{i}}\) = \(\frac{\overrightarrow{\mathrm{X}}}{\mathrm{X}}\), \(\hat{\mathrm{j}}\) = \(\frac{\overrightarrow{\mathrm{Y}}}{\mathrm{X}}\) and \(\hat{\mathrm{k}}\) = \(\frac{\overrightarrow{\mathrm{Z}}}{\mathrm{Z}}\)

Question 6.
Explain multiplication of a vector by a scalar.
Answer:

1. When a vector \(\overrightarrow{\mathrm{A}}\) is multiplied by a scalar ‘s’, it becomes ‘s\overrightarrow{\mathrm{A}}’ whose magnitude is s times the magnitude of \(\overrightarrow{\mathrm{A}}\).
2. The unit of \(\overrightarrow{\mathrm{A}}\) is different from the unit of ‘s \(\overrightarrow{\mathrm{A}}\)’.
   For example,
   If \(\overrightarrow{\mathrm{A}}\) = 10 newton and s = 5 second, then s\(\overrightarrow{\mathrm{A}}\) = 10 newton × 5 second = 50 Ns.

Question 7.
Explain addition of vectors.
Answer:

1. The addition of two or more vectors of same type gives rise to a single vector such that the effect of this single vector is the same as the net effect of the original vectors.
2. It is important to note that only the vectors of the same type (physical quantity) can be added.
3. For example, if two vectors, \(\overrightarrow{\mathrm{P}}\) = 3 unit and \(\overrightarrow{\mathrm{Q}}\) = 4 unit are acting along the same line, then they can be added as, |\(\overrightarrow{\mathrm{R}}\)| = |\(\overrightarrow{\mathrm{P}}\)| + |\(\overrightarrow{\mathrm{Q}}\)|
   |\(\overrightarrow{\mathrm{R}}\)| = 3 + 4 = 7
   
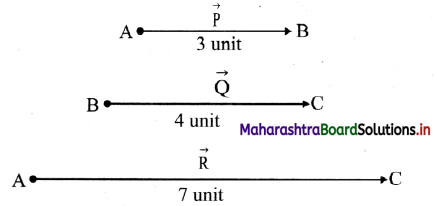
   [Note: When vectors are not in the same direction, then they can be added using triangle law of vector addition.]

Question 8.
State true or false. If false correct the statement and rewrite.
It is possible to add two vectors representing physical quantities having different dimensions.
Answer:
False.
It is not possible to add two vectors representing physical quantities having different dimensions.

Question 9.
Explain subtraction of vectors.
Answer:

1. When two vectors are anti-parallel (in the opposite direction) to each other, the magnitude
2. It is important to note that only vectors of the same type (physical quantity) can be subtracted.
3. For example, if two vectors \(\overrightarrow{\mathrm{P}}\) = 3 unit and \(\overrightarrow{\mathrm{Q}}\) = 4 unit are acting in opposite direction, they are subtracted as, |\(\overrightarrow{\mathrm{R}}\)| = ||\(\overrightarrow{\mathrm{P}}\)| – |\(\overrightarrow{\mathrm{Q}}\)||
   = |3 – 4| = 1 unit, directed along \(\overrightarrow{\mathrm{Q}}\)
   

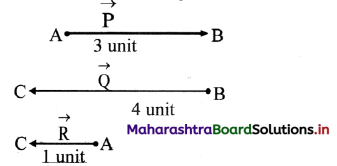
Question 10.
How can resultant of two vectors of a type inclined with each other be determined?
Answer:
When two vectors of a type are inclined with each other, their resultant can be determined by using triangle law of vector addition.

Question 11.
What is triangle law of vector addition?
Answer:
Triangle law of vector addition:
If two vectors describing the same physical quantity are represented in magnitude and direction, by the two sides of a triangle taken in order, then their resultant is represented in magnitude and direction by the third side of the triangle drawn in the opposite sense, i.e., from the starting point (tail) of the first vector to the end point (head) of the second vector.

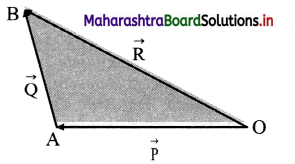
Let \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) be the two vectors of same type taken in same order as shown in figure.
∴ Resultant vector will be given by third side taken in opposite order, i.e., \(\overline{\mathrm{OA}}\) + \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{OB}}\)
∴ \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = \(\overrightarrow{\mathrm{R}}\)

Question 12.
Using triangle law of vector addition, explain the process of adding two vectors which are not lying in a straight line.
Answer:
i. Two vectors in magnitude and direction are drawn in a plane as shown in figure (a)
Let these vectors be \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\)

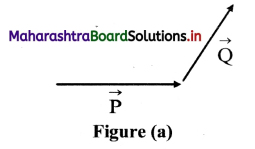
ii. Join the tail of \(\overrightarrow{\mathrm{Q}}\) to head of \(\overrightarrow{\mathrm{P}}\) in the given direction. The resultant vector will be the line which is obtained by joining tail of \(\overrightarrow{\mathrm{P}}\) to head of \(\overrightarrow{\mathrm{Q}}\) as shown in figure (b).

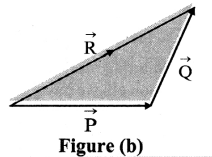
iii. If \(\overrightarrow{\mathrm{R}}\) is the resultant vector of \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) then using triangle law of vector addition, we have, \(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\)

Question 13.
Is it possible to add two velocities using triangle law?
Answer:
Yes, it is possible to add two velocities using triangle law.

Question 14.
Explain, how two vectors are subtracted. Find their resultant by using triangle law of vector addition.
Answer:

1. Let \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) be the two vectors in a plane as shown in figure (a).
   
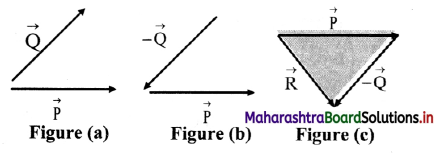
2. To subtract \(\overrightarrow{\mathrm{Q}}\) from \(\overrightarrow{\mathrm{P}}\), vector \(\overrightarrow{\mathrm{Q}}\) is reversed so that we get the vector –\(\overrightarrow{\mathrm{Q}}\) as shown in figure (b).
3. The resultant vector is obtained by –\(\overrightarrow{\mathrm{R}}\) joining tail of \(\overrightarrow{\mathrm{P}}\) to head of – \(\overrightarrow{\mathrm{Q}}\) as shown in figure (c).
4. From triangle law of vector addition, \(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{P}}\) + (-\(\overrightarrow{\mathrm{Q}}\)) = \(\overrightarrow{\mathrm{P}}\) – \(\overrightarrow{\mathrm{Q}}\)

Question 15.
Prove that: Vector addition is commutative.
Answer:
Commutative property of vector addition:
According to commutative property, for two
vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\), \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = \(\overrightarrow{\mathrm{Q}}\) + \(\overrightarrow{\mathrm{p}}\)

Proof:

i. Let two vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) be represented in magnitude and direction by two sides \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{AB}}\) respectively.

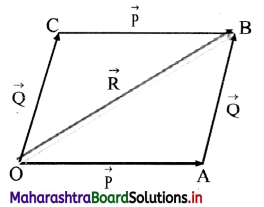
ii. Complete a parallelogramOABC such that
\(\overrightarrow{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{CB}}\) = \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{Q}}\) then join OB.

iii. In △OAB, \(\overrightarrow{\mathrm{OA}}\) + \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\)
(By triangle law of vector addition)
∴ \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = \(\overrightarrow{\mathrm{R}}\) … (1)
In △OCB, \(\overrightarrow{\mathrm{OC}}\) + \(\overrightarrow{\mathrm{CB}}\) = \(\overrightarrow{\mathrm{OB}}\)
(By triangle law of vector addition)
∴ \(\overrightarrow{\mathrm{Q}}\) + \(\overrightarrow{\mathrm{P}}\) = \(\overrightarrow{\mathrm{R}}\) … (2)

iv. From equation (1) and (2),
\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = \(\overrightarrow{\mathrm{Q}}\) + \(\overrightarrow{\mathrm{P}}\)
Hence, addition of two vectors obeys commutative law.

Question 16.
Prove that: Vector addition is associative.
Answer:
Associative property of vector addition:
According to associative property, for three vectors \(\overrightarrow{\mathrm{P}}\), \(\overrightarrow{\mathrm{Q}}\) and \(\overrightarrow{\mathrm{R}}\),
(\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\)) + \(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{P}}\) + (\(\overrightarrow{\mathrm{Q}}\) + \(\overrightarrow{\mathrm{R}}\))

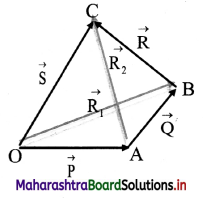
Proof:


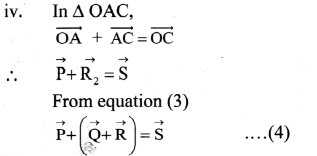
On comparing, equation (2) and (4), we get,
(\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\)) + \(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{P}}\) + (\(\overrightarrow{\mathrm{Q}}\) + \(\overrightarrow{\mathrm{R}}\))
Hence, associative law is proved.

Question 17.
State true or false. If false correct the statement and rewrite.
The subtraction of given vectors is neither commutative nor associative.
Answer:
True.

Question 18.
State and prove parallelogram law of vector addition and determine magnitude and direction of resultant vector.
Answer:

i. Parallelogram law of vector add addition;
If two vectors of same type starting from the same point (tails cit the same point), are represented in magnitude and direction by the two adjacent sides of a parallelogram then, their resultant vector is given in magnitude and direction, by the diagonal of the parallelogram starting from the same point.

ii. Proof:

a. Consider two vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) of the same type, with their tails at the point O’ and θ’ is the angle between \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) as shown in the figure below.

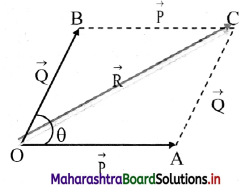
b. Join BC and AC to complete the parallelogram OACB, with \(\overline{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{P}}\) and \(\overline{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{Q}}\) as the adjacent sides. We have to prove that diagonal \(\overline{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{R}}\), the resultant of sum of the two given vectors.

c. By the triangle law of vector addition, we have,
\(\overrightarrow{\mathrm{OA}}\) + \(\overrightarrow{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{OC}}\) … (1)
As \(\overrightarrow{\mathrm{AC}}\) is parallel to \(\overrightarrow{\mathrm{OB}}\),
\(\overrightarrow{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{OB}}\) = \(\overrightarrow{\mathrm{Q}}\)
Substituting \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OC}}\) in equation (1) we have,
\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = \(\overrightarrow{\mathrm{R}}\)
Hence proved.

iii. Magnitude of resultant vector:

a. To find the magnitude of resultant vector \(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{OC}}\), draw a perpendicular from C to meet OA extended at S.

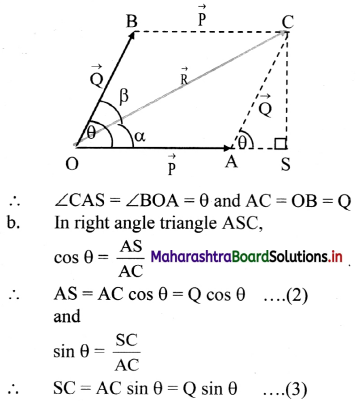
c. Using Pythagoras theorem in right angled triangle, OSC
(OC)² = (OS)² + (SC)²
= (OA + AS)² + (SC)²
∴ (OC)² = (OA)² + 2(OA).(AS) + (AS²) + (SC)² . . . .(4)

d. From right angle trianle ASC,
(AS)² + (SC)² = (AC)² …. (5)

e. From equation (4) and (5), we get
(OC)² = (OA)² + 2(OA) (AS) + (AC)²
… .(6)

f. Using (2) and (6), we get
(OC)² = (OA)² + (AC)² + 2(OA)(AC) cos θ
∴ R² = P² + Q² + 2 PQ cos θ
∴ R = \(\sqrt{\mathrm{P}^{2}+\mathrm{Q}^{2}+2 \mathrm{PQ} \cos \theta}\) ….(7)
Equation (7) gives the magnitude of resultant vector \(\overrightarrow{\mathrm{R}}\).

iv. Direction of resultant vector:
To find the direction of resultant vector \(\overrightarrow{\mathrm{R}}\), let \(\overrightarrow{\mathrm{R}}\) make an angle α with \(\overrightarrow{\mathrm{P}}\).

Equation (9) represents direction of resultant vector.
[Note: If β is the angle between \(\overrightarrow{\mathrm{R}}\) and \(\overrightarrow{\mathrm{Q}}\), it can be similarly derived that

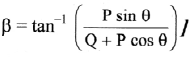
Question 19.
Complete the table for two vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) inclined at angle θ.

Answer:

Question 20.
The diagonal of the parallelogram made by two vectors as adjacent sides is not passing through common point of two vectors. What does it represent?
Answer:
The diagonal of the parallelogram made by two vectors as adjacent sides not passing through common point of two vectors represents triangle law of vector addition.

Question 21.
If | \(\overrightarrow{\mathbf{A}}\) + \(\overrightarrow{\mathbf{B}}\) | = | \(\overrightarrow{\mathbf{A}}\) – \(\overrightarrow{\mathbf{B}}\) | then what can be the
angle between \(\overrightarrow{\mathbf{A}}\) and \(\overrightarrow{\mathbf{B}}\) ?
Answer:
Let θ be the angle between \(\overrightarrow{\mathbf{A}}\) and \(\overrightarrow{\mathbf{B}}\), then

Thus, if |\(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)| = |\(\overrightarrow{\mathrm{A}}\) – \(\overrightarrow{\mathrm{B}}\) |, then vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) must be at right angles to each other.

Question 22.
Express vector \(\overrightarrow{\mathbf{A C}}\) in terms of vectors \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C B}}\) shown in the following figure.

Solution:
Using the triangle law of addition of vectors,
\(\overrightarrow{\mathbf{A C}}\) + \(\overrightarrow{\mathbf{C B}}\) = \(\overrightarrow{\mathbf{A B}}\)
∴\(\overrightarrow{\mathbf{A C}}\) = \(\overrightarrow{\mathbf{A B}}\) – \(\overrightarrow{\mathbf{C B}}\)

Question 23.
From the following figure, determine the resultant of four forces \(\overrightarrow{\mathbf{A}}_{1}\), \(\overrightarrow{\mathbf{A}}_{2}\), \(\overrightarrow{\mathbf{A}}_{3}\), \(\overrightarrow{\mathbf{A}}_{4}\).

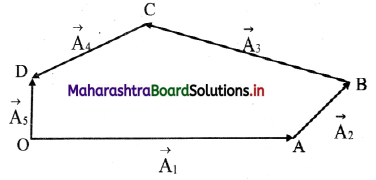
Solution:
Join \(\overrightarrow{\mathrm{OB}}\) to complete ∆OAB as shown in figure below

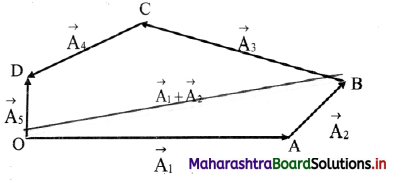
Now, using triangle law of vector addition,
\(\overrightarrow{\mathrm{OB}}\) = \(\overrightarrow{\mathrm{OA}}\) + \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{A}}_{1}\) + \(\overrightarrow{\mathrm{A}}_{2}\)
Join \(\overrightarrow{\mathrm{OC}}\) to complete triangle OBC as shown figure below
Similarly, \(\overrightarrow{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{OB}}\) + \(\overrightarrow{\mathrm{BC}}\) = \(\overrightarrow{\mathrm{A}}_{1}\) + \(\overrightarrow{\mathrm{A}}_{2}\) + \(\overrightarrow{\mathrm{A}}_{3}\)

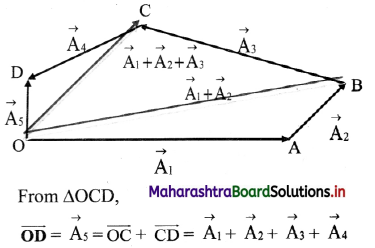
Answer:
\(\overrightarrow{O D}\) is the resultant of the four vectors.

Question 24.
Find the vector that should be added to the sum of (2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 3\(\hat{\mathbf{k}}\)) and (4\(\hat{\mathbf{i}}\) + 7\(\hat{\mathbf{j}}\) – 4\(\hat{\mathbf{k}}\)) to give a unit vector along the X-axis.
Solution:
Let vector \(\overrightarrow{\mathrm{p}}\) be added to get unit vector (\(\hat{\mathbf{i}}\)) along X-axis.
Sum of given vectors is given as,
(2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 3\(\hat{\mathbf{k}}\) ) + (4\(\hat{\mathbf{i}}\) + 7\(\hat{\mathbf{j}}\) – 4\(\hat{\mathbf{k}}\)) = 6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\)
According to given condition, (6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\)) + \(\hat{\mathbf{P}}\) = \(\hat{\mathbf{i}}\)
∴ \(\overrightarrow{\mathrm{P}}\) = \(\hat{\mathbf{i}}\) – (6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\)) = \(\hat{\mathbf{i}}\) – 6\(\hat{\mathbf{i}}\) – 2\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\) = -5\(\hat{\mathbf{i}}\) – 2\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\)
Answer:
The required vector is -5\(\hat{\mathbf{i}}\) – 2\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\).

Question 25.
If \(\overrightarrow{\mathbf{P}}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{Q}}\) = 2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\).Find
i. \(\overrightarrow{\mathbf{P}}\) + \(\overrightarrow{\mathbf{Q}}\)
ii. 3\(\overrightarrow{\mathbf{P}}\) – 2\(\overrightarrow{\mathbf{Q}}\)
Solution:
Given \(\overrightarrow{\mathbf{P}}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\), \(\overrightarrow{\mathbf{Q}}\) = 2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\)
To find:

i. \(\overrightarrow{\mathbf{P}}\) + \(\overrightarrow{\mathbf{Q}}\)
ii. 3\(\overrightarrow{\mathbf{P}}\) – 2\(\overrightarrow{\mathbf{Q}}\)

Calculation:

i. \(\overrightarrow{\mathbf{P}}\) + \(\overrightarrow{\mathbf{Q}}\) = (2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) – k) + (2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 2k)
= (2 + 2)\(\hat{\mathbf{i}}\) + (3 – 5)\(\hat{\mathbf{j}}\) + (-1 + 2)\(\hat{\mathbf{k}}\)
= 4\(\hat{\mathbf{i}}\) – 2\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\)

ii. 3\(\overrightarrow{\mathbf{P}}\) = 3(2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\)) = 6\(\hat{\mathbf{i}}\) + 9\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\)
2\(\overrightarrow{\mathbf{Q}}\) = 2(2\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\)) = 4\(\hat{\mathbf{i}}\) – 10\(\hat{\mathbf{j}}\) + 4\(\hat{\mathbf{k}}\)

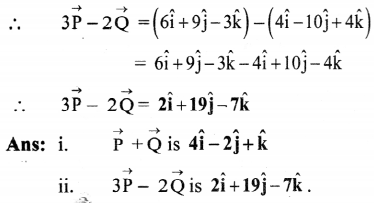
Question 26.
Find unit vector parallel to the resultant of the vectors \(\overrightarrow{\mathbf{A}}\) = \(\hat{\mathbf{i}}\) + 4\(\hat{\mathbf{j}}\) – 2\(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}\) = 3\(\hat{\mathbf{i}}\) – 5\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\).
Solution:
The resultant of \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) is,

Answer:
The required unit vector is \(\frac{1}{3 \sqrt{2}}\)(4\(\hat{\mathbf{i}}\) – \(\hat{\mathbf{j}}\) – \(\hat{\mathbf{k}}\))

Question 27.
Two forces, F₁ and F₂, each of magnitude 5 N are inclined to each other at 60°. Find the magnitude and direction of their resultant force.
Solution:
Given: F₁ = 5 N, F₂ = 5 N, θ = 60°
To find: Magnitude of resultant force (R),
Direction of resultant force (α)

Answer:
i. The magnitude of resultant force is 8.662 N.

ii. The direction of resultant force is 30° w.r.t. \(\overrightarrow{\mathrm{F}_{1}}\).

Question 28.
Water is flowing in a stream with velocity 5 km/hr in an easterly direction relative to the shore. Speed of a boat relative to still water is 20 km/hr. If the boat enters the stream heading north, with what velocity will the boat actually travel?
Answer:
The resultant velocity \(\overrightarrow{\mathrm{R}}\) of the boat can be obtained by adding the two velocities using ∆ OAB shown in the figure.

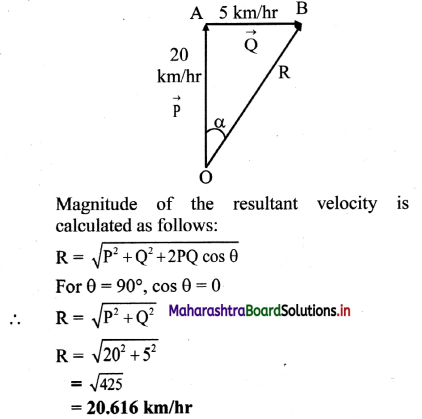
The direction ot the resultant velocity is

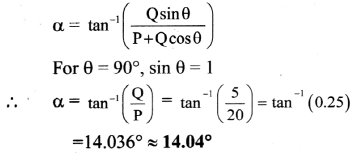
Answer: The velocity of the boat is 20.616 km/hr in a direction 14.04° east of north. .
[Note: tan^-1 (0.25) ≈ 14.04° which equals 14°2]

Question 29.
Rain is falling vertically with a speed of 35 m/s. Wind starts blowing at a speed of 12 m/s in east to west direction. In which direction should a boy waiting at a bus stop hold his umbrella? (NCERT)
Solution:
Let the velocity of rain and wind be \(\overrightarrow{\mathbf{V}_{\mathrm{R}}}\) and \(\overrightarrow{\mathbf{V}_{\mathrm{W}}}\), then resultant velocity \(\overrightarrow{\mathrm{v}}\) has magnitude of

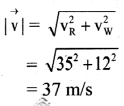
If \(\overrightarrow{\mathrm{v}}\) makes an angle θ with vertical then, from the figure

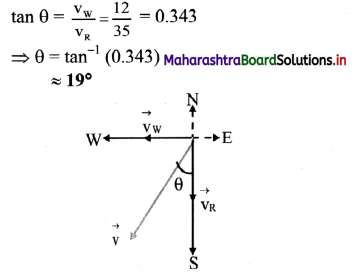
Answer: The boy should hold his umbrella in vertical plane at an angle of about 19° with vertical towards the east.

Question 30.
What are components of a vector?
Answer:

1. The given vector can be written as sum of two or more vectors along certain fixed directions. The vectors into which the given single vector is splitted are called components of the vector.
2. Let \(\overrightarrow{\mathrm{A}}\) = \(\mathrm{A}_{1} \hat{\alpha}\) + \(\mathrm{A}_{2} \hat{\beta}\) + \(\mathrm{A}_{3} \hat{\gamma}\) where, \(\hat{\alpha}\), \(\hat{\beta}\) and \(\hat{\gamma}\) are unit vectors along chosen directions. Then, A₁, A₂ and A₃ are known as components of \(\overrightarrow{\mathrm{A}}\) along three directions \(\hat{\alpha}\), \(\hat{\beta}\) and \(\hat{\gamma}\).
3. It two vectors are equal then, their corresponding components are also equal and vice-versa.
   

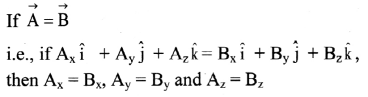
[Note: The magnitude of a vector is a scalar while each component of a vector is always a vector.]

Question 31.
What is meant by resolution of vector?
Answer:

1. The process of splitting a given vector into its components is called resolution of the vector.
2. Resolution of vector is equal to replacing the original vector with the sum of the component vectors.

Question 32.
That are rectangular components of vectors? Explain their uses.
Answer:
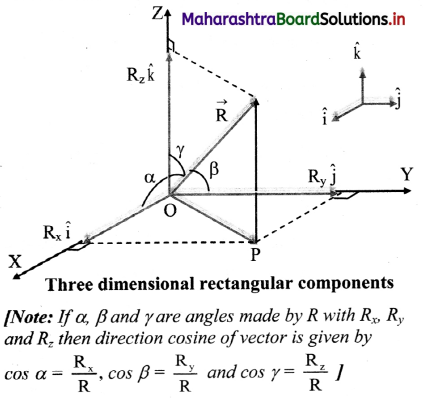
i. Rectangular components of a vector:
If components of a given vector are mutually perpendicular to each other then they are called rectangular components of that vector.

ii. Consider a vector \(
\overrightarrow{\mathrm{R}}
\) = \(
\overrightarrow{\mathrm{OC}}
\) originating from the origin O’ of a rectangular co-ordinate system as shown in figure.

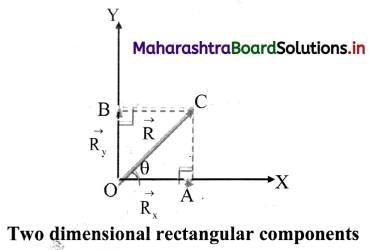
iii. Draw CA ⊥ OX and CB ⊥ OY.
Let component of \(
\overrightarrow{\mathrm{R}}
\) along X-axis \(
\overrightarrow{\mathrm{R}}_{\mathrm{x}}
\) and component of \(
\overrightarrow{\mathrm{R}}
\) along Y-axis = \(
\overrightarrow{\mathrm{R}}_{\mathrm{y}}
\)
By parallelogram law of vectors,

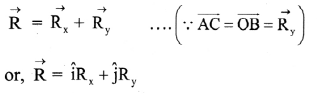
where, \(
\hat{i}
\) and \(
\hat{j}
\) are unit vectors along positive direction of X and Y axes respectively.

iv. If θ is angle made by \(
\overrightarrow{\mathrm{R}}
\) with X-axis, then

v. Squaring and adding equation (1) and (2) we get,

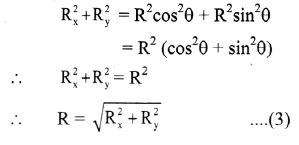
Equation (3) gives the magnitude of \(
\overrightarrow{\mathrm{R}}
\).

vi. Direction of \(
\overrightarrow{\mathrm{R}}
\) can be found out by dividing equation (2) by (1),

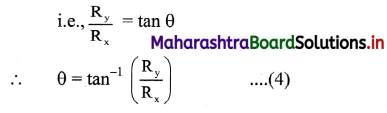
Equation (4) gives direction of \(
\overrightarrow{\mathrm{R}}
\)

vii. When vectors are noncoplanar, it becomes necessary to use the third dimension. If \(
\overrightarrow{\mathrm{R}}_{\mathrm{x}}
\), \(
\overrightarrow{\mathrm{R}}_{\mathrm{y}}
\) and \(
\overrightarrow{\mathrm{R}}_{\mathrm{z}}
\) are three rectangular components of \(
\overrightarrow{\mathrm{R}}
\) along X, Y and Z axes of a three dimensional rectangular cartesian co-ordinate system then.

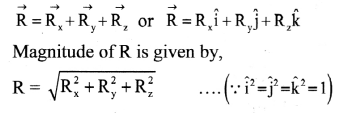
Question 33.
Find a unit vector in the direction of the vector 3\(
\hat{i}
\) + 4\(
\hat{j}
\).
Solution:

Question 34.
Given \(
\overrightarrow{\mathbf{a}}
\) = \(
\hat{\mathbf{i}}
\) + 2\(
\hat{\mathbf{j}}
\) and \(
\overrightarrow{\mathbf{b}}
\) = 2\(
\hat{\mathbf{i}}
\) + \(
\hat{\mathbf{j}}
\), what are the magnitudes of the two vectors? Are these two vectors equal?
Solution:

The magnitudes of \(
\vec{a}
\) and \(
\vec{b}
\) are equal. However, their corresponding components are not equal, i.e., a_x ≠ b_x and a_y ≠ b_y. Hence, the two vectors are not equal.
Answer:
Magnitudes of two vectors are equal, but vectors are unequal.

Question 35.
Find the vector drawn from the point (-4, 10, 7) to the point (3, -2, 1). Also find its magnitude.
Solution:
If \(
\overrightarrow{\mathrm{A}}
\) is a vector drawn from the point (x₁, y₁, z₁) to the point (x₂, y₂, z₂), then

Question 36.
In a cartesian co-ordinate system, the co-ordinates of two points P and Q are (2, 4, 4) and (-2, -3, 7) respectively, find \(
\overrightarrow{\mathbf{P Q}}
\) and its magnitude.
Solution:
Given: Position vector of P = (2,4,4)

∴ |\(
\overrightarrow{\mathrm{PQ}}
\)| = 8.6 units
Answer: Vector \(
\overrightarrow{\mathrm{PQ}}
\) is -4\(
\hat{\mathbf{i}}
\) – 7\(
\hat{\mathbf{j}}
\) + 3\(
\hat{\mathbf{k}}
\) and its magnitude is 8.6 units.

Question 37.
If \(
\overrightarrow{\mathbf{A}}
\) = 3\(
\hat{i}
\) + 4[/latex] = 3\(
\hat{j}
\) and \(
\overrightarrow{\mathbf{B}}
\) = 7\(
\hat{i}
\) + 24\(
\hat{j}
\), find a vector having the same magnitude as \(
\overrightarrow{\mathbf{B}}
\) and parallel to \(
\overrightarrow{\mathbf{A}}
\).
Solution:
The magnitude of vector \(
\overrightarrow{\mathrm{A}}
\) is | \(
\overrightarrow{\mathrm{A}}
\) |

Answer: The required vector is 15\(
\hat{\mathbf{i}}
\) + 20\(
\hat{\mathbf{j}}
\).

Question 38.
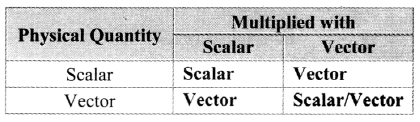
Complete the table.

Answer:

Question 39.
State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful.
i. Adding any two scalars,
ii. Adding a scalar to a vector of the same dimensions,
iii. Multiplying any vector by any scalar,
iv. Multiplying any two scalars,
v. Adding any two vectors. (NCERT)
Answer:

1. Not any two scalars can be added. To add two scalars it is essential that they represent same physical quantity.
2. This operation is meaningless. Only a vector can be added to another vector.
3. This operation is possible. When a vector is multiplied with a dimensional scalar, the resultant vector will have different dimensions.
   eg.: acceleration vector is multiplied with mass (a dimensional scalar), the resultant vector has the dimensions of force.
   When a vector is multiplied with non – dimensional scalar, it will be a vector having dimensions as that of the given vector.
   eg.: \(
   \overrightarrow{\mathrm{A}}
   \) × 3 = 3\(
   \overrightarrow{\mathrm{A}}
   \)
4. This operation is possible. Multiplication of non-dimensional scalars is simply algebraic multiplication. Multiplication of non dimensional scalars will result into scalar with different dimensions.
   eg.: Volume × density = mass.
5. Not any two vectors can be added. To add two vectors it is essential that they represent same physical quantity.

Question 40.
Explain scalar product of two vectors with the help of suitable examples.
Answer:
Scalar product of two vectors:

1. The scalar product of two non-zero vectors is defined as the product of the magnitude of the two vectors and cosine of the angle θ between the two vectors.
2. The dot sign is used between the two vectors to be multiplied therefore scalar product is also called dot product.
3. The scalar product of two vectors \(
   \overrightarrow{\mathrm{P}}
   \) and \(
   \overrightarrow{\mathrm{Q}}
   \) is given by, \(
   \overrightarrow{\mathrm{P}}
   \) . \(
   \overrightarrow{\mathrm{Q}}
   \) = PQ cos θ
   where, p = magnitude of \(
   \overrightarrow{\mathrm{P}}
   \), Q = magnitude of \(
   \overrightarrow{\mathrm{Q}}
   \)
   θ = angle between \(
   \overrightarrow{\mathrm{P}}
   \) and \(
   \overrightarrow{\mathrm{Q}}
   \)
4. Examples of scalar product:
   1. Power (P) is a scalar product of force (\(
      \overrightarrow{\mathrm{F}}
      \)) and velocity (\(
      \overrightarrow{\mathrm{v}}
      \))
      ∴ P = \(
      \overrightarrow{\mathrm{F}}
      \) . \(
      \overrightarrow{\mathrm{v}}
      \)
   2. Work is a scalar product of force (\(
      \overrightarrow{\mathrm{F}}
      \)) and displacement (\(
      \overrightarrow{\mathrm{s}}
      \)).
      ∴ W = \(
      \overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{s}}
      \)

Question 41.
Discuss characteristics of scalar product of two vectors.
Answer:
Characteristics of the scalar product of two vectors:
i. The scalar product of two vectors is equivalent to the product of magnitude of one vector with component of the other in the direction of the first.



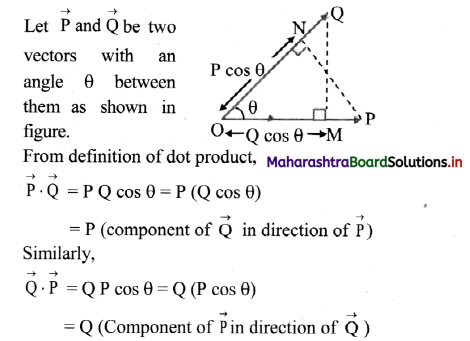
vi. Scalar product of two vectors is expressed in terms of rectangular components as
\(
\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}
\) = A_x + B_x + A_yB_y + A_zB_z

vii. For \(
\vec{a} \neq 0, \vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}
\) does not necessarily mean \(
\vec{b}
\) = \(
\vec{c}
\)

Question 42.
Complete the table vector given below:

Answer:

Question 43.
Define and explain vector product of two vectors with suitable examples.
Answer:
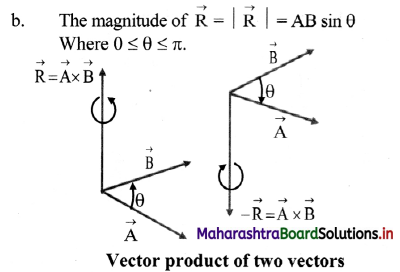
i. The vector product of two vectors is a third vector whose magnitude is equal to the product of magnitude of the two vectors and sine of the smaller angle θ between the two vectors.

ii. Vector product is also called cross product of vectors because cross sign is used to represent vector product.

iii. Explanation:

a. The vector product of two vectors \(
\overrightarrow{\mathrm{A}}
\) and \(
\overrightarrow{\mathrm{B}}
\), is a third vector \(
\overrightarrow{\mathrm{R}}
\) and is written as, \(
\overrightarrow{\mathrm{R}}
\) = \(
\overrightarrow{\mathrm{A}}
\) × \(
\overrightarrow{\mathrm{B}}
\) = AB sin θ \(
\hat{\mathrm{u}}_{\mathrm{r}}
\) where, \(
\hat{\mathrm{u}}_{\mathrm{r}}
\) is unit vector in direction of \(
\overrightarrow{\mathrm{R}}
\), i.e., perpendicular to plane containing two vectors. It is given by right handed screw rule.

c. Examples of vector product:

1. Force experienced by a charge q moving with velocity \(\overrightarrow{\mathrm{V}}\) in uniform magnetic field of induction (strength) \(\overrightarrow{\mathrm{B}}\) is given as \(\overrightarrow{\mathrm{F}}\) = q\(\overrightarrow{\mathrm{V}}\) × \(\overrightarrow{\mathrm{B}}\)

2. Moment of a force or torque (\(\begin{aligned}
&\rightarrow\\
&\tau
\end{aligned}\)) is the vector product of the position vector (\(\vec{r}\)) and the force (\(\overrightarrow{\mathrm{F}}\)).
i.e., \(\begin{aligned}
&\rightarrow\\
&\tau
\end{aligned}\) = \(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{F}}\)

3. The instantaneous velocity (\(\overrightarrow{\mathrm{v}}\)) of a rotating particle is equal to the cross product of its angular velocity (\(\vec{\omega}\)) and its position (\(\overrightarrow{\mathrm{r}}\)) from axis of rotation.
\(\overrightarrow{\mathrm{v}}\) = \(\overrightarrow{\mathrm{r}}\) × \(\vec{\omega}\)

Question 44.
State right handed screw rule.
Answer:
Statement of Right handed screw rule: Hold a right handed screw with its axis perpendicular to the plane containing vectors and the screw rotated from first vector to second vector through a small angle, the direction in which the screw tip would advance is the direction of the vector product of two vectors.

Question 45.
State the characteristics of the vector product (cross product) of two vectors.
Answer:
Characteristics of the vector product (cross product):
i. The vector product of two vectors does not obey the commutative law of multiplication.


vi. The magnitude of cross product of two vectors is numerically equal to the area of a parallelogram whose adjacent sides represent the two vectors.

Question 46.
Derive an expression for cross product of two vectors and express it in determinant form.
Answer:
Expression for cross product of two vectors:
i. Let two vectors \(\overrightarrow{\mathrm{R}}\) and \(\overrightarrow{\mathrm{Q}}\) be represented in magnitude and direction by,

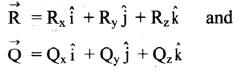
ii.

iii. Determinant form of cross product of two vectors \(\overrightarrow{\mathrm{R}}\) and \(\overrightarrow{\mathrm{Q}}\) is given by,

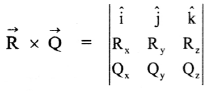
Question 47.
Show that magnitude of vector product of two vectors is numerically equal to the area of a parallelogram formed by the two
vectors.
Answer:
Suppose OACB is a parallelogram of adjacent sides, \(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{Q}}\).

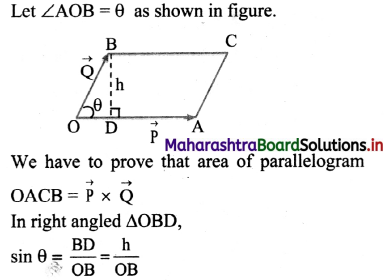
Question 48.
Distinguish between scalar product (dot product) and vector product (cross product).
Answer:

Question 49.
Given \(\overrightarrow{\mathbf{P}}\) = 4\(\hat{\mathbf{i}}\) – \(\hat{\mathbf{j}}\) + 8\(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{Q}}\) = 2\(\hat{\mathbf{i}}\) – m\(\hat{\mathbf{j}}\) + 4\(\hat{\mathbf{k}}\) find m if \(\overrightarrow{\mathbf{P}}\) and \(\overrightarrow{\mathbf{Q}}\) have the same direction. Solution:
Since \(\overrightarrow{\mathbf{P}}\) and \(\overrightarrow{\mathbf{Q}}\) have the same direction, their corresponding components must be in the same proportion, i.e.,

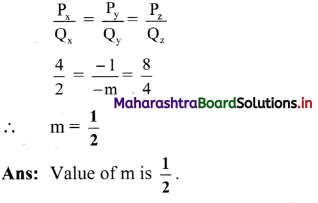
Question 50.
Find the scalar product of the two vectors \(\overrightarrow{\mathbf{v}}_{1}\) = \(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\mathbf{3} \hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{v}}_{2}\) = \(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}-\mathbf{5} \hat{\mathbf{k}}\)
Solution:

Answer: Scalar product of two given vectors is – 4.

Question 51.
A force \(\overrightarrow{\mathbf{F}}\) = \(4 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\) acting on a particle produces a displacement of \(\overrightarrow{\mathbf{S}}\) = \(\overrightarrow{\mathrm{s}}=2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+\mathbf{5} \hat{\mathbf{k}}\) where F is expressed in newton and s in metre. Find the work done by the force.
Solution:

Answer: The work done by the force is 41 J.

Question 52.
Find ‘a’ if \(\overrightarrow{\mathbf{A}}\) = \(3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+4 \hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}\) = \(\mathbf{a} \hat{\mathbf{i}}+2 \hat{\mathbf{j}}-\hat{\mathbf{k}}\) are perpendicular to one another.
Solution:

Question 53.
If \(\overrightarrow{\mathbf{A}}\) = \(5 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}+4 \hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}\) = \(2 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\) determine the angle between \(\) and \(\). Solution:
Solution:

Question 54.
Find the angle between the vectors
\(\overrightarrow{\mathbf{A}}\) = \(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}-\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}\) = \(-\hat{\mathbf{i}}+\hat{\mathbf{j}}-\mathbf{2} \hat{\mathbf{k}}\).
Solution:
Let angle between the vectors be θ

Answer: The angle between the vectors is 60°.

Question 55.
If \(\overrightarrow{\mathbf{A}}\) = \(2 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\) and \(\vec{B}\) = \(3 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\mathbf{5} \hat{\mathbf{k}}\), find the component of \(\overrightarrow{\mathbf{A}}\) along \(\overrightarrow{\mathbf{B}}\).
Solution:

Question 56.
\(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) are unit vectors along X-axis and Y-axis respectively. What is the magnitude and direction of the vector \(\hat{\mathbf{i}}+\hat{\mathbf{j}}\) and \(\hat{\mathbf{i}}-\hat{\mathbf{j}}\)? What are the components of a vector
\(\overrightarrow{\mathbf{A}}=2 \hat{\mathbf{i}}+\mathbf{3} \hat{\mathbf{j}}\) along the directions of \((\hat{\mathbf{i}}+\hat{\mathbf{j}})\) and \((\hat{\mathbf{i}}-\hat{\mathbf{j}})\)? (NCERT)
Answer:

Question 57.
The angular momentum \(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\), where \(\overrightarrow{\mathbf{r}}\) is a position vector and \(\overrightarrow{\mathrm{p}}\) is linear momentum of a body.

Solution:

Question 58.
If \(\overrightarrow{\mathbf{A}}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}-\hat{\mathbf{k}}\) are two vectors, find \(|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|\)
Answer:

Question 59.
Find unit vectors perpendicular to the plane of the vectors, \(\overrightarrow{\mathbf{A}}\) = \(\) and
\(\overrightarrow{\mathbf{B}}\) = \(2 \hat{\mathbf{i}}-\hat{\mathbf{k}}\)
Solution:
Let required unit vector be \(\hat{\mathrm{u}}\).

Question 60.
\(\overrightarrow{\mathbf{P}}\) = \(\hat{\mathbf{i}}+\mathbf{2} \hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{Q}}\) = \(2 \hat{\mathbf{i}}+\hat{\mathbf{j}}-2 \hat{\mathbf{k}}\) are two vectors, find the unit vector parallel to \(\overrightarrow{\mathbf{P}} \times \overrightarrow{\mathbf{Q}}\). Also find the vector perpendicular to P and Q of magnitude 6 units.
Solution:

Question 61.
Find the area of a triangle formed by \(\overrightarrow{\mathbf{A}}\) = \(\hat{3} \hat{\mathbf{i}}-4 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{B}}\) = \(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\boldsymbol{2} \hat{\mathbf{k}}\) as adjacent sides measure in metre. Solution:
Given: Two adjacent sides of triangle,
\(\overrightarrow{\mathrm{A}}\) = \(3 \hat{\mathrm{i}}-4 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}\), \(\overrightarrow{\mathrm{B}}\) = \(\hat{i}+\hat{j}-2 \hat{k}\)
To find: Area of triangle
Formula: Area of triangle =

Answer:
Area of the triangle is 6.1 m².

Question 62.
Find the derivatives of the functions,
i. f(x) = x⁸
ii. f(x) = x³ + sin x
Solution:
i. Using \(\frac{\mathrm{dx}^{\mathrm{n}}}{\mathrm{dx}}\) = nx^n-1,
\(\frac{d\left(x^{8}\right)}{d x}\) = 8x⁷

ii.

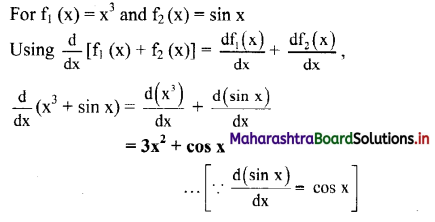
Question 63.
Find derivatives of e^2x – tan x
Solution:

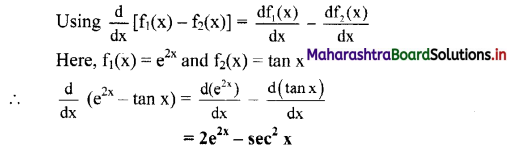
Question 64.
Find the derivatives of the functions.
f(x) = x³ sin x
Solution:
Using,

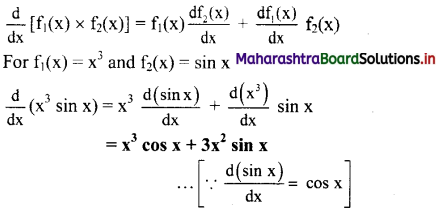
Question 65.
Find derivatives of \(\frac{d}{d x}(x \times \ln x)\)
Solution:
Using,

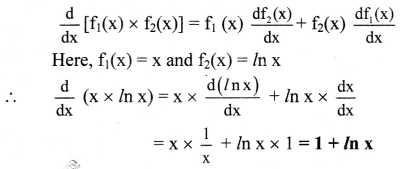
Question 66.
Evaluate the following integrals.

i. \(\int x^{8} d x\)
Solution:
Using formula \(\int x^{n} d x\) = \(\frac{x^{n+1}}{n+1}\),
\(\int x^{8} d x\) = \(\frac{x^{9}}{9}\)

ii. \(\int_{2}^{5} x^{2} d x\)
Answer:

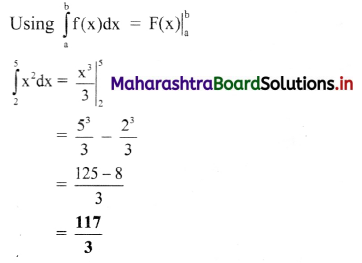
iii) \(\int(x+\sin x) d x\)
Solution:

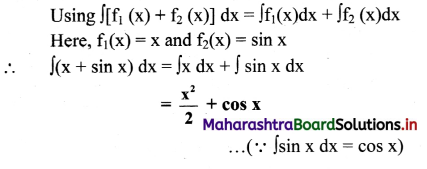
iv) \(\int\left(\frac{10}{x}+e^{x}\right) d x\)
Answer:

v) \(\int_{1}^{4}\left(x^{3}-x\right) d x\)
Answer:
Using,
f₁(x) – f₂(x) = \(\int f_{1}(x)-\int f_{2}(x)\)
Here,

Question 67.
A man applies a force of 10 N on a garbage crate. If another man applies a force of 8 N on the same crate at an angle of 60° with respect to previous, then what will be the resultant force and direction of the crate, if crate is stationary.
Answer:

Answer:
A resultant force of 15.62 N is applied on a crate at an angle of 26.56°.

Question 68.
A lady dropped her wallet in the parking lot of a super market. A boy picked the wallet up and ran towards the lady. He set off at 60° to the verge, heading towards the lady with a speed of 10 m s^-1, as shown in the diagram.
Find the component of velocity of boy directly across the parking strip.

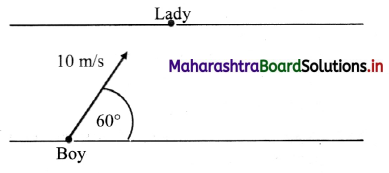
Answer:
The angle between velocity vector and the direction of path is 60°.
∴ Component of velocity across the parking strip
= v × cos 60°
= 10^-1 × cos 60°
= 5 m s^-1

Question 69.
On an open ground, a biker follows a track that turns to his left by an angle of 60° after every 600 m. Starting from a given turn, specify the displacement of the biker at the third and sixth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
Answer:
The path followed by the biker will be a closed hexagonal path. Suppose the motorist starts his journey from the point O.

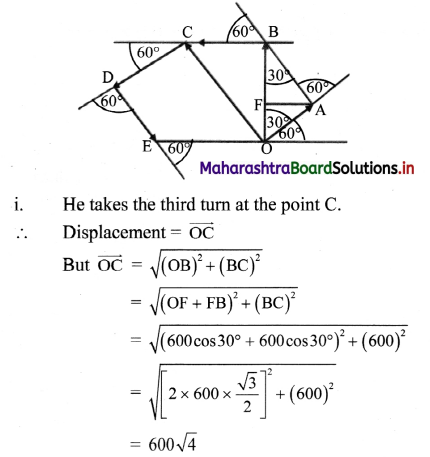
= 1200 m
= 1.2 km
∴ Total path length = \(|\overrightarrow{\mathrm{OA}}|+|\overrightarrow{\mathrm{AB}}|+|\overrightarrow{\mathrm{BC}}|\)
= 600 + 600 + 600
= 1800 m
= 1.8 km
The ratio of the magnitude of displacement to the total path-length = \(\frac{1.2}{1.8}\) = \(\frac{2}{3}\) = 0.67

ii. The motorist will take the sixth turn at O.
Displacement is zero.
path-length is = 3600 m or 3.6 km.
Ration of magnitude of displacement and path-length is zero.

Question 70.
What is the resultant of vectors shown in the figure below?

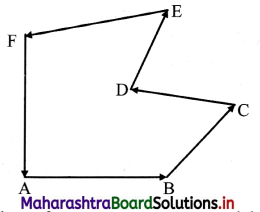
Answer:
If number of vectors are represented by the various sides of a closed polygon taken in one order then, their resultant is always zero.

Question 71.
If \(\overrightarrow{\mathbf{P}}\) is moving away from a point and \(\overrightarrow{\mathbf{Q}}\) is moving towards a point then, can their resultant be found using parallelogram law of vector addition?
Answer:
No. Resultant cannot be found by parallelogram law of vector addition because to apply law of parallelogram of vectors the two vectors and should either act towards a point or away from a point.

Question 72.
Which of the throwing is a vector?
(A) speed
(B) displacement
(C) mass
(D) time
Answer:
(B) displacement

Question 73.
The equation \(\vec{a}+\vec{a}=\vec{a}\) is
(A) meaningless
(B) always truc
(C) may he possible for limited values of a’
(D) true only when \(\overrightarrow{\mathrm{a}}=0\)
Answer:
(D) true only when \(\overrightarrow{\mathrm{a}}=0\)

Question 74.
The minimum number of numerically equal vectors whose vector sum can be zero is
(A) 4
(B) 3
(C) 2
(D) 1
Answer:
(C) 2

Question 75.
If \(\vec{A}+\vec{B}=\vec{A}-\vec{B}\) then vector \(\overrightarrow{\mathrm{B}}\) must be
(A) zero vector
(B) unit vector
(C) Non zero vector
(D) equal to \(\overrightarrow{\mathrm{A}}\)
Answer:
(A) zero vector

Question 76.
If \(\hat{\mathrm{n}}\) is the unit vector in the direction of \(\overrightarrow{\mathrm{A}}\), then,
(A) \(\hat{n}=\frac{\vec{A}}{|\vec{A}|}\)
(B) \(\hat{\mathrm{n}}=\overrightarrow{\mathrm{A}}|\overrightarrow{\mathrm{A}}|\)
(C) \(\hat{\mathrm{n}}=\frac{|\overrightarrow{\mathrm{A}}|}{\overrightarrow{\mathrm{A}}}\)
(D) \(\hat{\mathrm{n}}=\hat{\mathrm{n}} \times \overrightarrow{\mathrm{A}}\)
Answer:
(A) \(\hat{n}=\frac{\vec{A}}{|\vec{A}|}\)

Question 77.
Two quantities of 5 and 12 unit when added gives a quantity 13 unit. This quantity is
(A) time
(B) mass
(C) linear momentum
(D) speed
Answer:
(C) linear momentum

Question 78.
A force of 60 N acting perpendicular to a force of 80 N, magnitude of resultant force is
(A) 20N
(B) 70N
(C) 100 N
(D) 140 N
Answer:
(C) 100 N

Question 79.
A river is flowing at the rate of 6 km h^-1. A man swims across it with a velocity of 9 km h^-1. The resultant velocity of the man will be
(A) \(\sqrt{15} \mathrm{~km} \mathrm{~h}^{-1}\)
(B) \(\sqrt{45} \mathrm{~km} \mathrm{~h}^{-1}\)
(C) \(\sqrt{117} \mathrm{~km} \mathrm{~h}^{-1}\)
(D) \(\sqrt{225} \mathrm{~km} \mathrm{~h}^{-1}\)
Answer:
(C) \(\sqrt{117} \mathrm{~km} \mathrm{~h}^{-1}\)

Question 80.
If \(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}\) and magnitudes of \(\overrightarrow{\mathrm{A}}\), \(\overrightarrow{\mathrm{B}}\) and \(\overrightarrow{\mathrm{C}}\) are 5, 4 and 3 unit respectively, then angle between \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) is
(A) sin^-1 (3/4)
(B) cos^-1 (4/5)
(C) tan^-1 (5/3)
(D) cos^-1 (3/5)
Answer:
(B) cos^-1 (4/5)

Question 81.
If \(\vec{A}=\hat{i}+2 \hat{j}+3 \hat{k}\) and \(\overrightarrow{\mathrm{B}}=3 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}}\), then the area of parallelogram formed from these vectors as the adjacent sides will be
(A) 2\(\sqrt{3}\) square units
(B) 4\(\sqrt{3}\) square units
(C) 6\(\sqrt{3}\) square units
(D) 8\(\sqrt{3}\) square units
Answer:
(D) 8\(\sqrt{3}\) square units

Question 82.
A person moves from a point S and walks along the path which is a square of each side 50 m. He runs east, south, then west and finally north. Then the total displacement covered is
(A) 200m
(B) 100 m
(C) 50\(\sqrt{2}\) m
(D) zero
Answer:
(D) zero

Question 83.
The maximum value of magnitude of \((\vec{A}-\vec{B})\) is
(A) A – B
(B) A
(C) A + B
(D) \(\sqrt{\left(A^{2}+B^{2}\right)}\)
Answer:
(C) A + B

Question 84.
The magnitude of the X and Y components of \(\overrightarrow{\mathrm{A}}\) are 7 and 6. Also the magnitudes of the X and Y components of \(\vec{A}+\vec{B}\) are 11 and 9 respectively. What is the magnitude of
(A) 5
(B) 6
(C) 8
(D)
Answer:
(A) 5

Question 85.
What is the maximum n Limber of components into which a force can be resolved?
(A) Two
(B) Three
(C) Four
(D) Any number
Answer:
(D) Any number

Question 86.
The resultant of two vectors of magnitude \(|\overrightarrow{\mathrm{P}}|\) is also \(|\overrightarrow{\mathrm{P}}|\). They act at an angle
(A) 60°
(B) 90°
(C) 120°
(D) 180°
Answer:
(C) 120°

Question 87.
The vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are such that \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{C}}\) and A² + B² = C². Angle θ between positive directions of \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) is
(A) \(\frac{\pi}{2}\)
(B) 0
(C) π
(D) \(\frac{2 \pi}{3}\)
Answer:
(A) \(\frac{\pi}{2}\)

Question 88.
The expression \(\frac{1}{\sqrt{2}}(\hat{\mathrm{i}}+\hat{\mathrm{j}})\) is a
(A) unit vector
(B) null vector
(C) vector of magnitude \(\sqrt{2}\)
(D) scalar
Answer:
(A) unit vector

Question 89.
What is the angle between \(\hat{i}+\hat{j}+\hat{k}\) and \(\hat{\mathrm{i}}\)?
(A) 0°
(B) \(\frac{\pi}{6}\)
(C) \(\frac{\pi}{3}\)
(D) None of the above
Answer:
(D) None of the above

Question 90.
\((\overrightarrow{\mathrm{P}}+\overrightarrow{\mathrm{Q}})\) is a unit vector along X-axis. If \(\overrightarrow{\mathrm{P}}=\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}\) then \(\overrightarrow{\mathrm{Q}}\) is
(A) \(\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}\)
(B) \(\hat{\mathrm{j}}-\hat{\mathrm{k}}\)
(C) \(\hat{i}+\hat{j}+\hat{k}\)
(D) \(\hat{\mathrm{j}}+\hat{\mathrm{k}}\)
Answer:
(B) \(\hat{\mathrm{j}}-\hat{\mathrm{k}}\)

Question 91.
The magnitude of scalar product of the vectors \(\overrightarrow{\mathrm{A}}=2 \hat{\mathrm{i}}+5 \hat{\mathrm{k}}\) and \(\overrightarrow{\mathrm{B}}=3 \hat{\mathrm{i}}+4 \hat{\mathrm{k}}\) is
(A) 20
(B) 22
(C) 26
(D) 29
Answer:
(C) 26

Question 92.
Three vectors \(\overrightarrow{\mathrm{A}}\), \(\overrightarrow{\mathrm{B}}\) and \(\overrightarrow{\mathrm{C}}\) satisfy the relation \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) = 0 and \(\overrightarrow{\mathrm{A}}\). \(\overrightarrow{\mathrm{C}}\) = 0, then \(\overrightarrow{\mathrm{A}}\) is parallel to
(A) \(\overrightarrow{\mathrm{B}}\)
(B) \(\overrightarrow{\mathrm{C}}\)
(C) \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)
(D) \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{C}}\)
Answer:
(C) \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)

Question 93.
What vector must be added to the sum of two vectors \(2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+3 \hat{\mathrm{k}}\) and \(3 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}-2 \hat{\mathrm{k}}\) so that the resultant is a unit vector along Z axis?
(A) \(5 \hat{\hat{i}}+\hat{\mathrm{k}}\)
(B) \(-5 \hat{i}+3 \hat{j}\)
(C) \(3 \hat{j}+5 \hat{k}\)
(D) \(-3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}\)
Answer:
(B) \(-5 \hat{i}+3 \hat{j}\)

Question 94.
\(\overrightarrow{\mathrm{A}}=5 \overrightarrow{\mathrm{i}}-2 \overrightarrow{\mathrm{j}}+3 \overrightarrow{\mathrm{k}}\) and \(\overrightarrow{\mathrm{B}}=2 \overrightarrow{\mathrm{i}}+\overrightarrow{\mathrm{j}}+2 \overrightarrow{\mathrm{k}}\), then component of \(\overrightarrow{\mathrm{B}}\) along \(\overrightarrow{\mathrm{A}}\) is
(A) \(\frac{\sqrt{28}}{38}\)
(B) \(\frac{28}{\sqrt{38}}\)
(C) \(\frac{\sqrt{28}}{48}\)
(D) \(\frac{14}{\sqrt{38}}\)
Answer:
(D) \(\frac{14}{\sqrt{38}}\)

Question 95.
Choose the WRONG statement
(A) The division of vector by scalar is valid.
(B) The multiplication of vector by scalar is valid.
(C) The multiplication of vector by another vector is valid by using vector algebra.
(D) The division of a vector by another vector is valid by using vector algebra.
Answer:
(D) The division of a vector by another vector is valid by using vector algebra.

Question 96.
The resultant of two forces of 3 N and 4 N is 5 N, the angle between the forces is
(A) 30°
(B) 60°
(C) 90°
(D) 120°
Answer:
(C) 90°

Question 97.
The unit vector along \(\hat{\mathrm{i}}+\hat{\mathrm{j}}\) is
(A) \(\hat{\mathrm{k}}\)
(B) \(\hat{\mathrm{i}}+\hat{\mathrm{j}}\)
(C) \(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}}{\sqrt{2}}\)
(D) \(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}}{2}\)
Answer:
(C) \(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}}{\sqrt{2}}\)