Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 2 Introduction to Analytical Chemistry Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Chemistry Solutions Chapter 2 Introduction to Analytical Chemistry
1. Choose the correct option
Question A.
The branch of chemistry which deals with the study of separation, identification, and quantitative determination of the composition of different substances is called………………..
a. Physical chemistry
b. Inorganic chemistry
c. Organic chemistry
d. Analytical chemistry
Answer:
d. Analytical chemistry
Question B.
Which one of the following property of matter is Not quantitative in nature ?
a. Mass
b. Length
c. Colour
d. Volume
Answer:
c. Colour
Question C.
SI unit of mass is ……..
a. kg
b. mol
c. pound
d. m3
Answer:
a. kg
Question D.
The number of significant figures in 1.50 × 104 g is ………..
a. 2
b. 3
c. 4
d. 6
Answer:
b. 3
![]()
Question E.
In Avogadro’s constant 6.022 × 1023 mol-1, the number of significant figures is ……….
a. 3
b. 4
c. 5
d. 6
Answer:
b. 4
Question F.
By decomposition of 25 g of CaCO3, the amount of CaO produced will be ……………….
a. 2.8 g
b. 8.4 g
c. 14.0 g
d. 28.0 g
Answer:
c. 14.0 g
Question G.
How many grams of water will be produced by complete combustion of 12g of methane gas
a. 16
b. 27
c. 36
d. 56
Answer:
b. 27
Question H.
Two elements A (At. mass 75) and B (At. mass 16) combine to give a compound having 75.8 % of A. The formula of the compound is
a. AB
b. A2B
c. AB2
d. A2B3
Answer:
d. A2B3
Question I.
The hydrocarbon contains 79.87 % carbon and 20.13 % of hydrogen. What is its empirical formula ?
a. CH
b. CH2
c. CH3
d. C2H5
Answer:
c. CH3
![]()
Question J.
How many grams of oxygen will be required to react completely with 27 g of Al? (Atomic mass : Al = 27, O = 16)
a. 8
b. 16
c. 24
d. 32
Answer:
c. 24
Question K.
In CuSO4.5H2O the percentage of water is ……
(Cu = 63.5, S = 32, O = 16, H = 1)
a. 10 %
b. 36 %
c. 60 %
d. 72 %
Answer:
b. 36 %
Question L.
When two properties of a system are mathematically related to each other, the relation can be deduced by
a. Working out mean deviation
b. Plotting a graph
c. Calculating relative error
d. all the above three
Answer:
b. Plotting a graph
2. Answer the following questions
Question A.
Define : Least count
Answer:
The smallest quantity that can be measured by the measuring equipment is called least count.
Question B.
What do you mean by significant figures? State the rules for deciding significant figures.
Answer:
i. The significant figures in a measurement or result are the number of digits known with certainty plus one uncertain digit.
ii. Rules for deciding significant figures:
a. All non-zero digits are significant.
e.g. 127.34 g contains five significant figures which are 1, 2, 7, 3 and 4.
b. All zeros between two non-zero digits are significant, e.g. 120.007 m contains six significant figures.
c. Zeros on the left of the first non-zero digit are not significant. Such a zero indicates the position of the decimal point.
e.g. 0.025 has two significant figures, 0.005 has one significant figure.
d. Zeros at the end of a number are significant if they are on the right side of the decimal point,
e. g. 0.400 g has three significant figures and 400 g has one significant figure.
e. In numbers written is scientific notation, all digits are significant.
e.g. 2.035 × 102 has four significant figures and 3.25 × 10-5 has three significant figures.
![]()
Question C.
Distinguish between accuracy and precision.
Answer:
Accuracy:
- Accuracy refers to nearness of the measured value to the true value.
- Accuracy represents the correctness of the measurement.
- Accuracy is expressed in terms of absolute error and relative error.
- Accuracy takes into account the true or accepted value.
- Accuracy can be determined by a single measurement.
- High accuracy implies smaller error.
Precision:
- Precision refers to closeness of multiple readings of the same quantity.
- Precision represents the agreement between two or more measured values.
- Precision is expressed in terms of absolute deviation and relative deviation.
- Precision does not take into account the true or accepted value.
- Several measurements are required to determine precision.
- High precision implies reproducibility of the readings.
Question D.
Explain the terms percentage composition, empirical formula and molecular formula.
Answer:
Percentage Composition:
- The percentage composition of a compound is the percentage by weight of each element present in the compound.
- Quantitative determination of the constituent elements by suitable methods provides the percent elemental composition of a compound.
- If the percent total is not 100, the difference is considered as percent oxygen.
- From the percentage composition, the ratio of the atoms of the constituent elements in the molecule is calculated.
Empirical Formula:
The simplest ratio of atoms of the constituent elements in a molecule is called the empirical formula of that compound.
e.g. The empirical formula of benzene is CH.
Molecular Formula:
1. Molecular formula of a compound is the formula which indicates the actual number of atoms of the constituent elements in a molecule.
e.g. The molecular formula of benzene is C6H6.
2. It can be obtained from the experimentally determined values of percent elemental composition and molar mass of that compound.
3. Molecular formula can be obtained from the empirical formula if the molar mass is known.
Molecular formula = r × Empirical formula
Question E.
What is a limiting reagent ? Explain.
Answer:
Limiting reagent:
- The reactant which gets consumed and limits the amount of product formed is called the limiting reagent.
- When a chemist carries out a reaction, the reactants are not usually present in exact stoichiometric amounts, that is, in the proportions indicated by the balanced equation.
- This is because the goal of a reaction is to produce the maximum quantity of a useful compound from the starting materials. Frequently, a large excess of one reactant is supplied to ensure that the more expensive reactant is completely converted into the desired product.
- The reactant which is present in lesser amount gets consumed after some time and subsequently, no further reaction takes place, whatever be the amount left of the other reactant present.
Hence, limiting reagent is the reactant that gets consumed entirely and limits the reaction.
Question F.
What do you mean by SI units ? What is the SI unit of mass ?
Answer:
i. In 1960, the general conference of weights and measures proposed revised metric system, called International system of Units i.e. SI units, abbreviated from its French name.
ii. The SI unit of mass is kilogram (kg).
Question G.
Explain the following terms
(a) Mole fraction
(b) Molarity
(c) Molality
Answer:
(a) Mole fraction: Mole fraction is the ratio of number of moles of a particular component of a solution to the total number of moles of the solution.
If a substance ‘A’ dissolves in substance ‘B’ and their number of moles are nA and nB, respectively, then the mole fraction of A and B are given as:

(b) Molarity: Molarity is defined as the number of moles of the solute present in 1 litre of the solution. It is the most widely used unit and is denoted by M.
Molarity is expressed as follows:
Molarity (M) = \(\frac{\text { Number of moles of solute }}{\text { Volume of solution in litres }}\)
Molality: Molality is the number of moles of solute present in 1 kg of solvent. It is denoted by m. Molality is expressed as follows:
Molality (m) = \(\frac{\text { Number of moles of solute }}{\text { Mass of solvent in kilograms }}\)
![]()
Question H.
Define : Stoichiometry
Answer:
The study of quantitative relations between the amount of reactants and/or products is called stoichiometry.
Question I.
Why there is a need of rounding off figures during calculation ?
Answer:
- When performing calculations with measured quantities, the rule is that the accuracy of the final result is limited to the accuracy of the least accurate measurement.
- In other words, the final result cannot be more accurate than the least accurate number involved in the calculation.
- Sometimes, the final result of a calculation often contains figures that are not significant.
- When this occurs, the final result is rounded off.
Question J.
Why does molarity of a solution depend upon temperature ?
Answer:
- Molarity is the number of moles of the solute present in 1 litre of the solution. Therefore, molarity depends on the volume of the solution.
- Volume of the solution varies with the change in temperature.
Hence, molarity of a solution depends upon temperature.
Question M.
Define Analytical chemistry. Why is accurate measurement crucial in science?
Answer:
The branch of chemistry which deals with the study of separation, identification, qualitative and quantitative determination of the compositions of different substances, is called analytical chemistry.
1. The accuracy of measurement is of great concern in analytical chemistry. This is because faulty equipment, poor data processing, or human error can lead to inaccurate measurements. Also, there can be intrinsic errors in analytical measurement.
2. When measurements are not accurate, this provides incorrect data that can lead to wrong conclusions. For example, if a laboratory experiment requires a specific amount of a chemical, then measuring the wrong amount may result in an unsafe or unexpected outcome.
3. Hence, the numerical data obtained experimentally are treated mathematically to reach some quantitative conclusion.
4. Also, an analytical chemist has to know how to report the quantitative analytical data, indicating the extent of the accuracy of measurement, perform the mathematical operation, and properly express the quantitative error in the result.
![]()
3. Solve the following questions
Question A.
How many significant figures are in each of the following quantities ?
a. 45.26 ft
b. 0.109 in
c. 0.00025 kg
d. 2.3659 × 10-8 cm
e. 52.0 cm3
f. 0.00020 kg
g. 8.50 × 104 mm
h. 300.0 cg
Answer:
a. 4
b. 3
c. 2
d. 5
e. 3
f. 2
g. 3
h. 4
Question B.
Round off each of the following quantities to two significant figures :
a. 25.55 mL
b. 0.00254 m
c. 1.491 × 105 mg
d. 199 g
Answer:
a. 26 mL
b. 0.0025 m
c. 1.5 × 105 mg
d. 2.0 × 102 g
Question C.
Round off each of the following quantities to three significant figures :
a. 1.43 cm3
b. 458 × 102 cm
c. 643 cm2
d. 0.039 m
e. 6.398 × 10-3 km
f. 0.0179 g
g. 79,000 m
h. 42,150
i. 649.85
j. 23,642,000 mm
k. 0.0041962 kg
Answer:
a. 43 cm3
b. 4.58 × 104 cm
c. 643 cm2 (or 6.43 × 102 cm2)
d. 0.0390 m (or 3.90 × 10-2 m)
e. 6.40 × 10-3 km
f. 0.0179 g (or 1.79 × 10-2 m)
g. 7.90 × 104 m
h. 4.22 × 104 (or 42,200)
i. 6.50 × 102
j. 2.36 × 107 mm
k. 0.00420 kg (or 4.20 × 10-3 kg)
Question D.
Express the following sum to appropriate number of significant figures :
a. 2.3 × 103 mL + 4.22 × 104 mL + 9.04 × 103 mL + 8.71 × 105 mL;
b. 319.5 g – 20460 g – 0.0639 g – 45.642 g – 4.173 g
Answer:
To perform addition/subtraction operation, first the numbers are written in such a way that they have the same exponent. The coefficients are then added/subtracted.
a. (0.23 × 104 mL) + (4.22 × 104 mL) +(0.904 × 104 mL) + (87.1 × 104 mL)
= (0.23 + 4.22 + 0.904 + 87.1) × 104 mL
= 92.454 × 104 mL
= 9.2454 × 105
= 9.2 × 105 mL
b. 319.5 g – 20460 g – 0.0639 g – 45.642 g – 4.173 g
= – 20190.3789 g
= – 20190 g
Ans: Sum to appropriate number of significant figures = 9.2 × 105 mL
ii. Sum to appropriate number of significant figures = – 20190 g
[Note: In addition and subtraction, the final answer is rounded to the minimum number of decimal point of the number taking part in calculation. If there is no decimal point, then the final answer will have no decimal point.]
![]()
4. Solve the following problems
Question A.
Express the following quantities in exponential terms.
a. 0.0003498
b. 235.4678
c. 70000.0
d. 1569.00
Answer:
a. 0.0003498 = 3.498 × 10-4
b. 235.4678 = 2.354678 × 102
c. 70000.0 = 7.00000 × 104
d. 1569.00 = 1.56900 × 103
Question B.
Give the number of significant figures in each of the following
a. 1.230 × 104
b. 0.002030
c. 1.23 × 104
d. 1.89 × 10-4
Answer:
a. 4
b. 4
c. 3
d. 3
Question C.
Express the quantities in above (B) with or without exponents as the case may be.
Answer:
a. 12300
b. 2.030 × 10-3
c. 12300
d. 0.000189
Question D.
Find out the molar masses of the following compounds :
a. Copper sulphate crystal (CuSO4.5H2O)
b. Sodium carbonate, decahydrate (Na2CO3.10H2O)
c. Mohr’s salt [FeSO4(NH4)2SO4.6H2O]
(At. mass : Cu = 63.5; S = 32; O = 16; H = 1; Na = 23; C = 12; Fe = 56; N = 14)
Answer:
a. Molar mass of CuSO4.5H2O
= (1 × At. mass Cu) + (1 × At. mass S) + (9 × At. mass O) + (10 × At. mass H)
= (1 × 63.5) + (1 × 32) + (9 × 16) + (10 × 1)
= 63.5 + 32 + 144 + 10
= 249.5 g mol-1
Molar mass of CuSO4.5H2O = 249.5 g mol-1
b. Molar mass of Na2CO3.10H2O
= (2 × At. mass Na) + (1 × At. mass C) + (13 × At. mass O) + (20 × At. mass H)
= (2 × 23) + (1 × 12) + (13 × 16) + (20 × 1)
= 46 + 12 + 208 + 20
= 286 g mol-1
Molar mass of Na2CO3.10H2O = 286 g mol-1
c. Molar mass of [FeSO4(NH4)2SO4.6H2O]
= (1 × At. mass Fe) + (2 × At. mass S) + (2 × At. mass N) + (14 × At. mass O) + (20 × At. mass H)
= (1 × 56) + (2 × 32) + (2 × 14) + (14 × 16) + (20 × 1)
= 56 + 64 + 28 + 224 + 20
= 392 g mol-1
Molar mass of [FeSO4(NH4)2SO4.6H2O] = 392 g mol-1
![]()
Question E.
Work out the percentage composition of constituents elements in the following compounds :
a. Lead phosphate [Pb3(PO4)2],
b. Potassium dichromate (K2Cr2O7),
c. Macrocosmic salt – Sodium ammonium hydrogen phosphate, tetrahydrate (NaNH4HPO4.4H2O)
(At. mass : Pb = 207; P = 31; O = 16; K = 39; Cr = 52; Na = 23; N = 14)
Answer:
Given: Atomic mass: Pb = 207; P = 31; O = 16; K = 39; Cr = 52; Na = 23; N = 14
To find: The percentage composition of constituent elements
Formula:
![]()
Calculation:
i. Lead phosphate [Pb3(PO4)2]
Molar mass of Pb3(PO4)2 = 3 × (207) + 2 × (31) + 8 × (16) = 621 + 62 + 128 = 811 g mol-1
Percentage of Pb = \(\frac {621}{811}\) × 100 = 76.57%
Percentage of P = \(\frac {621}{811}\) × 100 = 7.64%
Percentage of O = \(\frac {128}{811}\) × 100 = 15.78%
ii. Potassium dichromate (K2Cr2O7)
Molar mass of K2Cr2O7 = 2 × (39) + 2 × (52) + 7 × (16) = 78 + 104 + 112 = 294 g mol-1
Percentage of K = \(\frac {78}{294}\) × 100 = 26.53%
Percentage of Cr = \(\frac {104}{294}\) × 100 = 35.37%
Percentage of O = \(\frac {112}{294}\) × 100 = 38.10%
iii. Microcosmic salt – Sodium ammonium hydrogen phosphate, tetrahydrate (NaNH4HPO4.4H2O)
Molar mass of NaNH4HPO4.4H2O = 1 × (23) + 1 × (14) + 1 × (31) + 13 × (1) + 8 × (16)
= 23 + 14 + 31 + 13 + 128 = 209 g mol-1
Percentage of Na = \(\frac {23}{209}\) × 100 = 11.00%
Percentage of N = \(\frac {14}{209}\) × 100 = 6.70%
Percentage of P = \(\frac {31}{209}\) × 100 = 14.83%
Percentage of H = \(\frac {13}{209}\) × 100 = 6.22%
Percentage of O = \(\frac {128}{209}\) × 100 = 61.24%
Ans: i. Mass percentage of Pb, P and O in lead phosphate [Pb3(PO4)2] are 76.57%, 7.64% and 15.78% respectively.
ii. Mass percentage of K, Cr and O in potassium dichromate (K2Cr2O7) are 26.53%, 35.37% and 38.10% respectively.
iii. Mass percentage of Na, N, P, H and O in NaNH4HPO4.4H2O are 11.00%, 6.70%, 14.83%, 6.22% and 61.24% respectively.
Question F.
Find the percentage composition of constituent green vitriol crystals (FeSO4.7H2O). Also find out the mass of iron and the water of crystallisation in 4.54 kg of the crystals. (At. mass : Fe = 56; S = 32; O = 16)
Answer:
Given: i. Atomic mass: Fe = 56; S = 32; O = 16
ii. Mass of crystal = 4.54 kg
To find: i. Mass percentage of Fe, S, H and O
ii. Mass of iron and water of crystallisation in 4.54 kg of crystal
Formula:
![]()
i. Molar mass of FeSO4.7H2O = 1 × (56) + 1 × (32) + 14 × (1) + 11 × (16)
= 56 + 32 + 14+ 176
= 278 g mol-1
Percentage of Fe = \(\frac {56}{278}\) × 100 = 20.14%
Percentage of S = \(\frac {32}{278}\) × 100 = 11.51%
Percentage of H = \(\frac {14}{278}\) × 100 = 5.04%
Percentage of O = \(\frac {176}{278}\) × 100 = 63.31%
ii. 278 kg green vitriol = 56 kg iron
∴ 4.54 kg green vitriol = x
∴ x = \(\frac{56 \times 4.54}{278}\)
Mass of 7H2O in 278 kg green vitriol = 7 × 18 = 126 kg
∴ 4.54 kg green vitriol = y
∴ y = \(\frac{126 \times 4.54}{278}\)
Ans: i. Mass percentage of Fe, S, H and O in FeSO4.7H2O are 20.14%, 11.51%, 5.04% and 63.31% respectively.
ii. Mass of iron in 4.54 kg green vitriol = 0.915 kg
Mass of water of crystallisation in 4.54 kg green vitriol = 2.058 kg
Question G.
The red colour of blood is due to a compound called “haemoglobin”. It contains 0.335 % of iron. Four atoms of iron are present in one molecule of haemoglobin. What is its molecular weight ? (At. mass : Fe = 55.84)
Answer:
Given: Iron percentage in haemoglobin = 0.335%
To find: Molecular weight of haemoglobin
Calculation: There are four atoms of iron in a molecule of haemoglobin. Four atoms of iron contribute 0.335% mass to a molecule of haemoglobin.
Mass of one Fe atom = 55.84 u
∴ Mass of 4 Fe atoms = 55.84 × 4 = 223.36 u = 0.335%
Let molecular weight of haemoglobin be x.
Hence,
\(\frac{223.36}{x}\) × 100 = 0.335%
∴ x = \(\frac{223.36}{0.335}\) × 100 = 66674.6 g mol-1
Ans: Molecular weight of haemoglobin = 66674.6 g mol-1
![]()
Question H.
A substance, on analysis, gave the following percent composition:
Na = 43.4 %, C = 11.3 % and O = 45.3 %. Calculate the empirical formula. (At. mass Na = 23 u, C = 12 u, O = 16 u).
Answer:
Given: Atomic mass of Na = 23 u, C = 12 u, and O = 16 u
Percentage of Na, C and O = 43.4%, 11.3% and 45.3% respectively.
To find: The empirical formula of the compound
Calculation:

Hence, empirical formula is Na2CO3.
Ans: Empirical formula of the compound = Na2CO3
Question I.
Assuming the atomic weight of a metal M to be 56, find the empirical formula of its oxide containing 70.0% of M.
Answer:
Given: Atomic mass of M = 56
Percentage of M = 70.0%
To find: The empirical formula of the compound
Calculation: % M = 70.0%
Hence, % O = 30.0%, Atomic mass of O = 16 u

Convert the ratio into whole number by multiplying by the suitable coefficient, i.e., 2.
Therefore, the ratio of number of moles of M : O is 2 : 3.
Hence, the empirical formula is M2O3.
Ans: Empirical formula of the compound = M2O3
Question J.
1.00 g of a hydrated salt contains 0.2014 g of iron, 0.1153 g of sulfur, 0.2301 g of oxygen and 0.4532 g of water of crystallisation. Find the empirical formula. (At. wt. : Fe = 56; S = 32; O = 16)
Answer:
Given: Atomic mass of Fe = 56, S = 32, and O = 16
Mass of iron, sulphur, oxygen and water = 0.2014 g, 0.1153 g, 0.2301 g and 0.4532 respectively.
To find: The empirical formula of the compound
Calculation: Since the mass of crystal is 1 g, the % iron, sulphur, oxygen and water = 20.14%, 11.53%, 23.01% and 4.32 % respectively.

Hence, empirical formula is FeSO4.7H2O.
Ans: Empirical formula of the compound = FeSO4.7H2O.
Question K.
An organic compound containing oxygen, carbon, hydrogen and nitrogen contains 20 % carbon, 6.7 % hydrogen and 46.67 % nitrogen. Its molecular mass was found to be 60. Find the molecular formula of the compound.
Answer:
Given: Percentage of carbon, hydrogen, nitrogen = 20%, 6.7%, 46.67% respectively.
Molar mass of the compound = 60 g mol-1
To find: The molecular formula of the compound
Calculation: % carbon + % hydrogen + % nitrogen = 20 + 6.7 + 46.67 = 73.37%
This is less than 100%. Hence, compound contains adequate oxygen so that the total percentage of elements is 100%.
Hence, % of oxygen = 100 – 73.37 = 26.63%

Hence, empirical formula is CH4N2O.
Empirical formula mass = 12 + 4 + 28 + 16 = 60 g mol-1
Hence,
Molar mass = Empirical formula mass
∴ Molecular formula = Empirical formula = CH4N2O
Ans: Molecular formula of the compound = CH4N2O
![]()
Question L.
A compound on analysis gave the following percentage composition by mass : H = 9.09; O = 36.36; C = 54.55. Mol mass of compound is 88. Find its molecular formula.
Answer:
Given: Percentage of H, O, C = 9.09%, 36.36%, 54.55% respectively.
Molar mass of the compound = 88 g mol-1
To find: The molecular formula of the compound
Calculation:

Hence, empirical formula is C2H4O.
Empirical formula mass = 24 + 4 + 16 = 44 g mol-1
Hence,
![]()
Molecular formula = r × empirical formula
Molecular formula = 2 × C2H2O = C4H8O2
Ans: Molecular formula of the compound = C4H8O2
Question M.
Carbohydrates are compounds containing only carbon, hydrogen and oxygen. When heated in the absence of air, these compounds decompose to form carbon and water. If 310 g of a carbohydrate leave a residue of 124 g of carbon on heating in absence of air, what is the empirical formula of the carbohydrate ?
Answer:
Given: Mass of carbon residue = 124 g, mass of carbohydrate = 310 g
To find: Empirical formula of the carbohydrate
Calculation: Since the 310 g of compound decomposes to carbon and water and the mass of carbon produced is 124 g, the remaining mass would be of water.
∴ Molar mass of water = 310 – 124 = 186 g
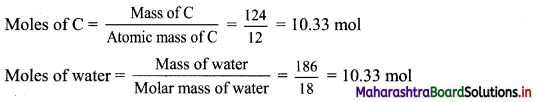
The ratio of number of moles of C : water = C : H2O = 1 : 1
Hence, empirical formula = CH2O
Ans: Empirical formula of the carbohydrate = CH2O
Question N.
Write each of the following in exponential notation :
a. 3,672,199
b. 0.000098
c. 0.00461
d. 198.75
Answer:
a. 3,672,199 = 3.672199 × 106
b. 0.000098 = 9.8 × 10-5
c. 0.00461 = 4.61 × 10-3
d. 198.75 = 1.9875 × 102
Question O.
Write each of the following numbers in ordinary decimal form :
a. 3.49 × 10-11
b. 3.75 × 10-1
c. 5.16 × 104
d. 43.71 × 10-4
e. 0.011 × 10-3
f. 14.3 × 10-2
g. 0.00477 × 105
h. 5.00858585
Answer:
a. 3.49 × 10-11 = 0.0000000000349
b. 3.75 × 10-1 = 0.375
c. 5.16 × 104 = 51,600
d. 43.71 × 10-4 = 0.004371
e. 0.011 × 10-3 = 0.000011
f. 14.3 × 10-2 = 0.143
g. 0.00477 × 105 = 477
h. 5.00858585 = 5.00858585
![]()
Question P.
Perform each of the following calculations. Round off your answers to two digits.

Answer:
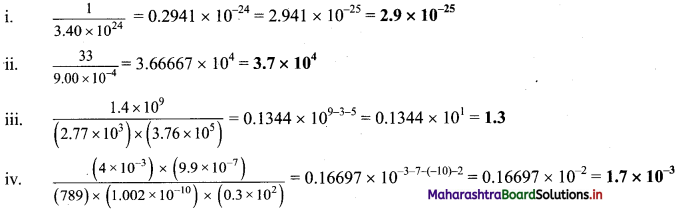
Question Q.
Perform each of the following calculations. Round off your answers to three digits.
a. (3.26 × 104) (1.54 × 106)
b. (8.39 × 107) (4.53 × 109)
c. \(\frac{8.94 \times 10^{6}}{4.35 \times 10^{4}}\)
d. \(\frac{\left(9.28 \times 10^{9}\right) \times\left(9.9 \times 10^{-7}\right)}{(511) \times\left(2.98 \times 10^{-6}\right)}\)
Answer:
i. (3.26 × 104) (1.54 × 106) = 5.0204 × 104+6 = 5.02 × 1010
ii. (8.39 × 107) (4.53 × 109) = 38.0067 × 107+9 = 38.0067 × 1016 = 3.80 x 1017
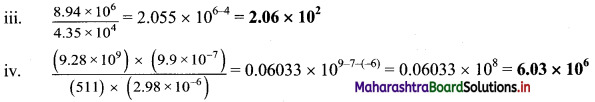
Question R.
Perform the following operations :
a. 3.971 × 107 + 1.98 × 104;
b. 1.05 × 10-4 – 9.7 × 10-5;
c. 4.11 × 10-3 + 8.1 × 10-4;
d. 2.12 × 106 – 3.5 × 105.
Answer:
Solution:
To perform addition/subtraction operation, first the numbers are written in such a way that they have the same exponent. The coefficients are then added/subtracted.
a. 3.971 × 107 + 1.98 × 104 = 3.971 × 107 + 0.00198 × 107 = (3.971 + 0.00198) × 107
= 3.97298 × 107
b. 1.05 × 10-4 – 9.7 × 10-5 = 10.5 × 10-5 – 9.7 × 10-5 = (10.5 – 9.7) × 10-5 = 0.80 × 10-5
= 8.0× 10-6
c. 4.11 × 10-3 + 8.1 × 10-4 = 41.1 × 10-4 + 8.1 × 10-4 = (41.1 + 8.1) × 10-4 = 49.2 × 10-4
= 4.92 × 10-3
d. 2.12 × 106 – 3.5 × 105 = 21.2 × 105 – 3.5 × 105 = (21.2 – 3.5) × 105 = 17.7 × 105
= 1.77 × 106
![]()
Question S.
A 1.000 mL sample of acetone, a common solvent used as a paint remover, was placed in a small bottle whose mass was known to be 38.0015 g. The following values were obtained when the acetone – filled bottle was weighed : 38.7798 g, 38.7795 g and 38.7801 g. How would you characterise the precision and accuracy of these measurements if the actual mass of the acetone was 0.7791 g ?
Answer:
Precision:
| Measurement | Mass of acetone observed (g) |
| 1 | 38.7798 – 38.0015 = 0.7783 |
| 2 | 38.7795 – 38.0015 = 0.7780 |
| 3 | 38.7801 – 38.0015 = 0.7786 |
Mean = \(\frac{0.7783+0.7780+0.7786}{3}\) = 0.7783 g
| Measurement | Mass of acetone observed (g) |
Absolute deviation (g) = |
| 1 | 0.7783 | 0 |
| 2 | 0.7780 | 0.0003 |
| 3 | 0.7786 | 0.0003 |
Mean absolute deviation = \(\frac{0+0.0003+0.0003}{3}\) = 0.0002
∴ Mean absolute deviation = ±0.0002 g
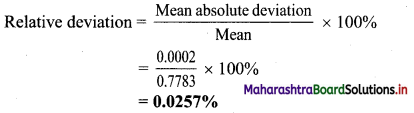
ii. Accuracy:
Actual mass of acetone = 0.7791 g
Observed value (average) = 0.7783 g
a. Absolute error = Observed value – True value
= 0.7783 – 0.7791
= – 0.0008 g

Ans: These observed values are close to each other and are also close to the actual mass. Therefore, the results are precise and as well accurate.
i. Relative deviation = 0.0257%
ii. Relative error = 0.1027%
[Note: i. As per the method given in textbook, the calculated value of relative deviation is 0.0257%.
ii. The negative sign in -0.1027% indicates that the experimental result is lower than the true value.]
Question T.
Your laboratory partner was given the task of measuring the length of a box (approx 5 in) as accurately as possible, using a metre stick graduated in milimeters. He supplied you with the following measurements: 12.65 cm, 12.6 cm, 12.65 cm, 12.655 cm, 126.55 mm, 12 cm.
a. State which of the measurements you would accept, giving the reason.
b. Give your reason for rejecting each of the others.
Answer:
a. The metre stick is graduated in millimetres i.e. 1 mm to 1000 mm, and 1 mm = 0.1 cm. Therefore, if the length is measured in centimetres, the least count of metre stick is 0.1 cm. The results 12.6 cm has the least count of 0.1 cm and is an acceptable result.
b. Since, the least count of metre stick is 0.1 cm or 1mm, the results such as 12.65 cm, 12.655 cm, 126.55 mm cannot be measured using this stick, and hence, these results are rejected. The result, 12 cm doesn’t include the least count and is rejected.
Question U.
What weight of calcium oxide will be formed on heating 19.3 g of calcium carbonate?
(At. wt. : Ca = 40; C = 12; O = 16)
Answer:
Given: Mass of CaCO3 consumed in reaction = 19.3 g
To find: Mass of CaO formed
Calculation: Calcium carbonate decomposes according to the balanced equation,
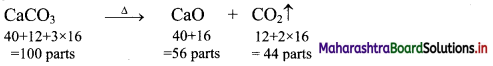
So, 100 g of CaCO3 produce 56 g of CaO.

Ans: Mass of CaO formed = 10.81 g
[Calculation using log table:
56 × 0.193
= Antilog10 [log10 (56) + log10 (0.193)]
= Antilog10 [1.7482 + \(\overline{1} .2856\)]
= Antilog10 [1.0338] = 10.81]
![]()
Question V.
The hourly energy requirements of an astronaut can be satisfied by the energy released when 34 grams of sucrose are “burnt” in his body. How many grams of oxygen would be needed to be carried in a space capsule to meet his requirement for one day?
Answer:
34 g of sucrose provides energy for an hour.
Hence, for a day, the mass of sucrose needed = 34 × 24 = 816g
The balanced equation is,
![]()
Thus, 342 g of sucrose requires 384 g of oxygen.
∴ 816 g of sucrose will require = \(\frac{816}{342}\) × 384 = 916 g of O2
Ans: Astronaut needs to carry 916 g of O2.