Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 8 Binomial Distribution Miscellaneous Exercise 8 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 8 Binomial Distribution Miscellaneous Exercise 8
(I) Choose the correct option from the given alternatives:
Question 1.
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 successes is
(a) √50
(b) 5
(c) 25
(d) 10
Answer:
(b) 5
![]()
Question 2.
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probablity of 2 successes is
(a) \(\frac{128}{256}\)
(b) \(\frac{219}{256}\)
(c) \(\frac{37}{256}\)
(d) \(\frac{28}{256}\)
Answer:
(d) \(\frac{28}{256}\)
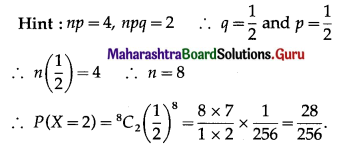
Question 3.
For a binomial distribution, n = 5. If P(X = 4) = P(X = 3) then p = ___________
(a) \(\frac{1}{3}\)
(b) \(\frac{3}{4}\)
(c) 1
(d) \(\frac{2}{3}\)
Answer:
(d) \(\frac{2}{3}\)
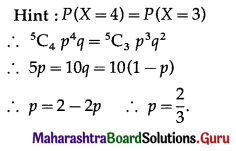
Question 4.
In a binomial distribution, n = 4. If 2 P(X = 3) = 3 P(X = 2) then p = ___________
(a) \(\frac{4}{13}\)
(b) \(\frac{5}{13}\)
(c) \(\frac{9}{13}\)
(d) \(\frac{6}{13}\)
Answer:
(c) \(\frac{9}{13}\)
![]()
Question 5.
If X ~ B (4, p) and P (X = 0) = \(\frac{16}{81}\), then P (X = 4) = ___________
(a) \(\frac{1}{16}\)
(b) \(\frac{1}{81}\)
(c) \(\frac{1}{27}\)
(d) \(\frac{1}{8}\)
Answer:
(b) \(\frac{1}{81}\)

Question 6.
The probability of a shooter hitting a target is \(\frac{3}{4}\). How many minimum numbers of times must he fie so that the probability of hitting the target at least once is more than 0·99?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) 4
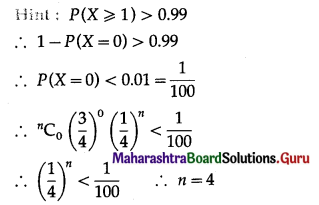
Question 7.
If the mean and variance of a binomial distribution are 18 and 12 respectively, then n = ___________
(a) 36
(b) 54
(c) 18
(d) 27
Answer:
(b) 54

(II) Solve the following:
Question 1.
Let X ~ B(10, 0.2). Find
(i) P(X = 1)
(ii) P(X ≥ 1)
(iii) P(X ≤ 8).
Solution:
X ~ B(10, 0.2)
∴ n = 10, p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
The p,m.f. of X is given by
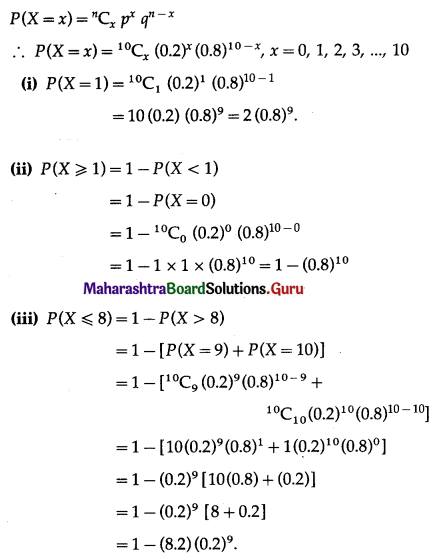
![]()
Question 2.
Let X ~ B(n, p).
(i) If n = 10, E(X) = 5, find p and Var(X).
(ii) If E(X) = 5 and Var(X) = 2.5, find n and p.
Solution:
X ~ B(n, p)
(i) Given: n = 10 and E(X) = 5
But E(X) = np
∴ np = 5.
∴ 10p = 5
∴ p = \(\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Var(X) = npq = 10(\(\frac{1}{2}\))(\(\frac{1}{2}\)) = 2.5.
Hence, p = \(\frac{1}{2}\) and Var(X) = 2.5
(ii) Given: E(X) = 5 and Var(X) = 2.5
∴ np = 5 and npq = 2.5
∴ \(\frac{n p q}{n p}=\frac{2.5}{5}\)
∴ q = 0.5 = \(\frac{5}{10}=\frac{1}{2}\)
∴ p = 1 – q = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Substituting p = \(\frac{1}{2}\) in np = 5, we get
n(\(\frac{1}{2}\)) = 5
∴ n = 10
Hence, n = 10 and p = \(\frac{1}{2}\)
Question 3.
If a fair coin is tossed 10 times and the probability that it shows heads (i) 5 times (ii) in the first four tosses and tail in the last six tosses.
Solution:
Let X = number of heads.
p = probability that coin tossed shows a head
∴ p = \(\frac{1}{2}\)
q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Given: n = 10
∴ X ~ B(10, \(\frac{1}{2}\))
The p.m.f. of X is given by
P(X = x) = \({ }^{n} C_{x} P^{x} q^{n-x}\)
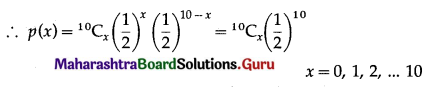
(i) P(coin shows heads 5 times) = P[X = 5]
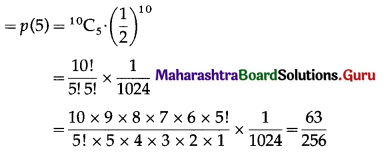
Hence, the probability that can shows heads exactly 5 times = \(\frac{63}{256}\)
(ii) P(getting heads in first four tosses and tails in last six tosses) = P(X = 4)

Hence, the probability that getting heads in first four tosses and tails in last six tosses = \(\frac{105}{512}\).
![]()
Question 4.
The probability that a bomb will hit a target is 0.8. Find the probability that out of 10 bombs dropped, exactly 2 will miss the target.
Solution:
Let X = the number of bombs hitting the target.
p = probability that bomb will hit the target
∴ p = 0.8 = \(\frac{8}{10}=\frac{4}{5}\)
∴ q = 1 – p = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Given: n = 10
∴ X ~ B(10, \(\frac{4}{5}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e.p(x) = \({ }^{10} \mathrm{C}_{x}\left(\frac{4}{5}\right)^{x}\left(\frac{1}{5}\right)^{10-x}\)
P(exactly 2 bombs will miss the target) = P(exactly 8 bombs will hit the target)
= P[X = 8]
= p(8)
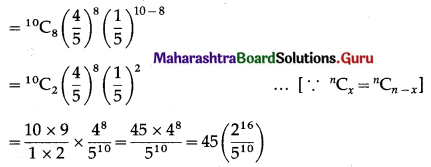
Hence, the probability that exactly 2 bombs will miss the target = 45\(\left(\frac{2^{16}}{5^{10}}\right)\)
Question 5.
The probability that a mountain bike travelling along a certain track will have a tire burst is 0.05. Find the probability that among 17 riders:
(i) exactly one has a burst tyre
(ii) at most three have a burst tyre
(iii) two or more have burst tyres.
Solution:
Let X = number of burst tyres.
p = probability that a mountain bike travelling along a certain track will have a tyre burst.
∴ p = 0.05
∴ q = 1 – p = 1 – 0.05 = 0.95
Given: n = 17
∴ X ~ B(17, 0.05)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} P^{x} q^{n-x}\)
i.e.(x) = \({ }^{17} \mathrm{C}_{x}(0.05)^{x}(0.95)^{17-x}\), x = 0, 1, 2, ……, 17
(i) P(exactly one has a burst tyre)
P(X = 1) = p(1) = \({ }^{17} \mathrm{C}_{1}\) (0.05)1 (0.95)17-1
= 17(0.05) (0.95)16
= 0.85(0.95)16
Hence, the probability that riders has exactly one burst tyre = (0.85)(0.95)16
![]()
(ii) P(at most three have a burst tyre) = P(X ≤ 3)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= p(0) + p(1) + p(2) + p(3)


Hence, the probability that at most three riders have burst tyre = (2.0325)(0.95)14.
(iii) P(two or more have tyre burst) = P(X ≥ 2)
= 1 – P(X < 2)
= 1 – [P(X = 0) + P(X = 1)]
= 1 – [p(0) + p(1)]
= 1 – [\({ }^{17} \mathrm{C}_{0}\) (0.05)0 (0.95)17 + \({ }^{17} \mathrm{C}_{1}\) (0.05)(0.95)16]
= 1 – [1(1)(0.95)17 + 17(0.05)(0.95)16]
= 1 – (0.95)16[0.95 + 0.85]
= 1 – (1.80)(0.95)16
= 1 – (1.8)(0.95)16
Hence, the probability that two or more riders have tyre burst = 1 – (1.8)(0.95)16.
Question 6.
The probability that a lamp in a classroom will be burnt out is 0.3. Six such lamps are fitted in the classroom. If it is known that the classroom is unusable if the number of lamps burning in it is less than four, find the probability that the classroom cannot be used on a random occasion.
Solution:
Let X = number of lamps burnt out in the classroom.
p = probability of a lamp in a classroom will be burnt
∴ p = 0.3 = \(\frac{3}{10}\)
∴ q = 1 – p = 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)
Given: n = 6
∴ X ~ B(6, \(\frac{3}{10}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e., p(x) = \({ }^{6} \mathrm{C}_{x}\left(\frac{3}{10}\right)^{x}\left(\frac{7}{10}\right)^{6-x}\)
Since the classroom is unusable if the number of lamps burning in it is less than four, therefore
P(classroom cannot be used) = P[X < 4]
= P[X = 0] + P[X = 1] + P[X = 2] + P[X = 3]
= p(0) + p(1) + p(2) + p(3)

Hence, the probability that the classroom cannot be used on a random occasion is 0.92953.
![]()
Question 7.
A lot of 100 items contain 10 defective items. Five items are selected at random from the lot and sent to the retail store. What is the probability that the store will receive at most one defective item?
Solution:
Let X = number of defective items.
p = probability that item is defective
∴ p = \(\frac{10}{100}=\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
Given: n = 5
∴ X ~ B(5, \(\frac{1}{10}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e., p(x) = \({ }^{5} C_{x}\left(\frac{1}{10}\right)^{x}\left(\frac{9}{10}\right)^{5-x}\)
P (store will receive at most one defective item) = P[X ≤ 1]
=P[X = 0] + P[X = 1]
= p(0) + p(1)
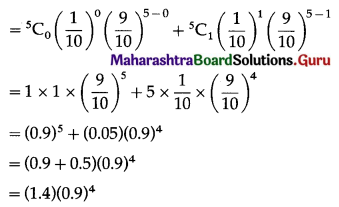
Hence, the probability that the store will receive at most one defective item is (1.4)(0.9)4.
Question 8.
A large chain retailer purchases a certain kind of electronic device from a manufacturer. The manufacturer indicates that the defective rate of the device is 3%. The inspector of the retailer picks 20 items from a shipment. What is the probability that the store will receive at most one defective item?
Solution:
Let X = number of defective electronic devices.
p = probability that device is defective
∴ p = 3% = \(\frac{3}{100}\)
∴ q = 1 – p = 1 – \(\frac{3}{100}\) = \(\frac{97}{100}\)
Given: n = 20
∴ X ~ B(20, \(\frac{3}{100}\))
The p.m.f. of X is given as:

Hence, the probability that the store will receive at most one defective item = (1.57)(0.97)19.
![]()
Question 9.
The probability that a certain kind of component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 tested components tested survive.
Solution:
Let X = number of tested components survive.
p = probability that the component survives the check test

Hence, the probability that exactly 2 of the 4 tested components survive is 0.3456.
Question 10.
An examination consists of 10 multiple choice questions, in each of which a candidate has to deduce which one of five suggested answers is correct. A completely unprepared student guesses each answer completely randomly. What is the probability that this student gets 8 or more questions correct? Draw the appropriate moral.
Solution:
Let X = number of correct answers.
p = probability that student gets correct answer
∴ p = \(\frac{1}{5}\)
∴ q = 1 – p = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Given: n = 10 (number of total questions)
∴ X ~ B(10, \(\frac{1}{5}\))
The p.m.f. of X is given by

Hence, the probability that student gets 8 or more questions correct = \(\frac{30.44}{5^{8}}\)
![]()
Question 11.
The probability that a machine will produce all bolts in a production run within specification is 0.998. A sample of 8 machines is taken at random. Calculate the probability that (i) all 8 machines (ii) 7 or 8 machines (iii) at most 6 machines will produce all bolts within specification.
Solution:
Let X = number of machines which produce the bolts within specification.
p = probability that a machine produce bolts within specification
p = 0.998 and q = 1 – p = 1 – 0.998 = 0.002
Given: n = 8
∴ X ~ B(8, 0.998)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e. p(x) = \({ }^{8} \mathrm{C}_{x}(0.998)^{x}(0.002)^{8-x}\), x = 0, 1, 2, …, 8
(i) P(all 8 machines will produce all bolts within specification) = P[X = 8]
= p(8)
= \({ }^{8} \mathrm{C}_{8}\) (0.998)8 (0.002)8-8
= 1(0.998)8 . (1)
= (0.998)8
Hence, the probability that all 8 machines produce all bolts with specification = (0.998)8.
(ii) P(7 or 8 machines will produce all bolts within i specification) = P (X = 7) + P (X = 8)

Hence, the probability that 7 or 8 machines produce all bolts within specification = (1.014)(0.998)7.
(iii) P(at most 6 machines will produce all bolts with specification) = P[X ≤ 6]
= 1 – P[x > 6]
= 1 – [P(X = 7) + P(X = 8)]
= 1 – [P(7) + P(8)]
= 1 – (1.014)(0.998)7
Hence, the probability that at most 6 machines will produce all bolts with specification = 1 – (1.014)(0.998)7.
Question 12.
The probability that a machine develops a fault within the first 3 years of use is 0.003. If 40 machines are selected at random, calculate the probability that 38 or more will develop any faults within the first 3 years of use.
Solution:
Let X = the number of machines who develop a fault.
p = probability that a machine develops a fait within the first 3 years of use
∴ p = 0.003 and q = 1 – p = 1 – 0.003 = 0.997
Given: n = 40
∴ X ~ B(40, 0.003)
The p.m.f. of X is given by

Hence, the probability that 38 or more machines will develop the fault within 3 years of use = (775.44)(0.003)38.
![]()
Question 13.
A computer installation has 10 terminals. Independently, the probability that anyone terminal will require attention during a week is 0.1. Find the probabilities that (i) 0 (ii) 1 (iii) 2 (iv) 3 or more, terminals will require attention during the next week.
Solution:
Let X = number of terminals which required attention during a week.
p = probability that any terminal will require attention during a week
∴ p = 0.1 and q = 1 – p = 1 – 0.1 = 0.9
Given: n = 10
∴ X ~ B(10, 0.1)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e. p(x) = \({ }^{10} C_{x}(0.1)^{x}(0.9)^{10-x}\), x = 0, 1, 2, …, 10
(i) P(no terminal will require attention) = P(X = 0)
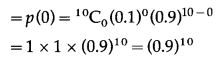
Hence, the probability that no terminal requires attention = (0.9)10
(ii) P(1 terminal will require attention)

Hence, the probability that 1 terminal requires attention = (0.9)9.
(iii) P(2 terminals will require attention)

Hence, the probability that 2 terminals require attention = (0.45)(0.9)8.
(iv) P(3 or more terminals will require attention)

Hence, the probability that 3 or more terminals require attention = 1 – (2.16) × (0.9)8.
Question 14.
In a large school, 80% of the pupil like Mathematics. A visitor to the school asks each of 4 pupils, chosen at random, whether they like Mathematics.
(i) Calculate the probabilities of obtaining an answer yes from 0, 1, 2, 3, 4 of the pupils.
(ii) Find the probability that the visitor obtains answer yes from at least 2 pupils:
(a) when the number of pupils questioned remains at 4.
(b) when the number of pupils questioned is increased to 8.
Solution:
Let X = number of pupils like Mathematics.
p = probability that pupils like Mathematics

(i) The probabilities of obtaining an answer yes from 0, 1, 2, 3, 4 of pupils are P(X = 0), P(X = 1), P(X = 2), P(X = 3) and P(X = 4) respectively

(ii) (a) P(visitor obtains the answer yes from at least 2 pupils when the number of pupils questioned remains at 4) = P(X ≥ 2)
= P(X = 2) + P(X = 3) + P(X = 4)

(b) P(the visitor obtains the answer yes from at least 2 pupils when number of pupils questioned is increased to 8)

![]()
Question 15.
It is observed that it rains 12 days out of 30 days. Find the probability that
(i) it rains exactly 3 days of the week.
(ii) it will rain at least 2 days of a given week.
Solution:
Let X = the number of days it rains in a week.
p = probability that it rains
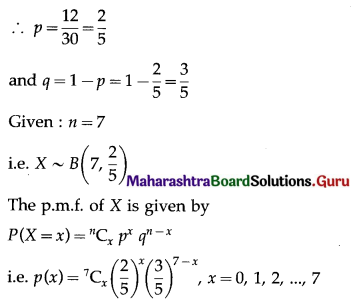
(i) P(it rains exactly 3 days of week) = P(X = 3)

Hence, the probability that it rains exactly 3 days of week = 0.2903.
(ii) P(it will rain at least 2 days of the given week)

Hence, the probability that it rains at least 2 days of a given week = 0.8414
Question 16.
If the probability of success in a single trial is 0.01. How many trials are required in order to have a probability greater than 0.5 of getting at least one success?
Solution:
Let X = number of successes.
p = probability of success in a single trial
∴ p = 0.01
and q = 1 – p = 1 – 0.01 = 0.99
∴ X ~ B(n, 0.01)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)

Hence, the number of trials required in order to have a probability greater than 0.5 of getting at least one success is \(\frac{\log 0.5}{\log 0.99}\) or 68.
![]()
Question 17.
In binomial distribution with five Bernoulli’s trials, the probability of one and two success are 0.4096 and 0.2048 respectively. Find the probability of success.
Solution:
Given: X ~ B(n = 5, p)
The probability of X success is


Hence, the probability of success is \(\frac{1}{5}\).