Maharashtra Board 12th Maths Solutions Chapter 7 Probability Distributions Ex 7.2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Probability Distributions Ex 7.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Probability Distributions Ex 7.2

Question 1.
Verify which of the following is p.d.f. of r.v. X:
(i) f(x) = sin x, for 0 ≤ x ≤ \(\frac{\pi}{2}\)
(ii) f(x) = x, for 0 ≤ x ≤ 1 and -2 – x for 1 < x < 2
(iii) fix) = 2, for 0 ≤ x ≤ 1.
Solution:
f(x) is the p.d.f. of r.v. X if
(a) f(x) ≥ 0 for all x ∈ R and

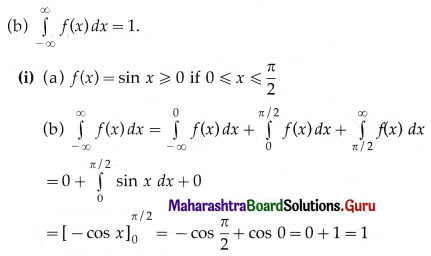
Hence, f(x) is the p.d.f. of X.

(ii) f(x) = x ≥ 0 if 0 ≤ x ≤ 1
For 1 < x < 2, -2 < -x < -1
-2 – 2 < -2 – x < -2 – 1
i.e. -4 < f(x) < -3 if 1 < x < 2
Hence, f(x) is not p.d.f. of X.

(iii) (a) f(x) = 2 ≥ 0 for 0 ≤ x ≤ 1

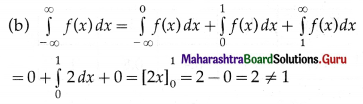
Hence, f(x) is not p.d.f. of X.

Question 2.
The following is the p.d.f. of r.v. X:
f(x) = \(\frac{x}{8}\), for 0 < x < 4 and = 0 otherwise.
Find
(a) P(x < 1.5)
(b) P(1 < x < 2) (c) P(x > 2).
Solution:

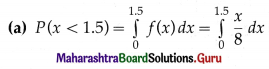
Question 3.
It is known that error in measurement of reaction temperature (in 0°C) in a certain experiment is continuous r.v. given by
f(x) = \(\frac{x^{2}}{3}\) for -1 < x < 2
= 0. otherwise.
(i) Verify whether f(x) is p.d.f. of r.v. X
(ii) Find P(0 < x ≤ 1)
(iii) Find the probability that X is negative.
Solution:

Question 4.
Find k if the following function represents p.d.f. of r.v. X
(i) f(x) = kx. for 0 < x < 2 and = 0 otherwise.
Also find P(\(\frac{1}{4}\) < x < \(\frac{3}{2}\)).
(ii) f(x) = kx(1 – x), for 0 < x < 1 and = 0 otherwise.
Also find P(\(\frac{1}{4}\) < x < \(\frac{1}{2}\)), P(x < \(\frac{1}{2}\)).
Solution:
(i) Since, the function f is p.d.f. of X

(ii) Since, the function f is the p.d.f. of X,

Question 5.
Let X be the amount of time for which a book is taken out of the library by a randomly selected students and suppose X has p.d.f.
f(x) = 0.5x, for 0 ≤ x ≤ 2 and = 0 otherwise.
Calculate:
(i) P(x ≤ 1)
(ii) P(0.5 ≤ x ≤ 1.5)
(iii) P(x ≥ 1.5).
Solution:
(i) P(x ≤ 1)

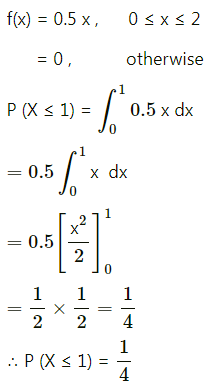
(ii) P(0.5 ≤ x ≤ 1.5)

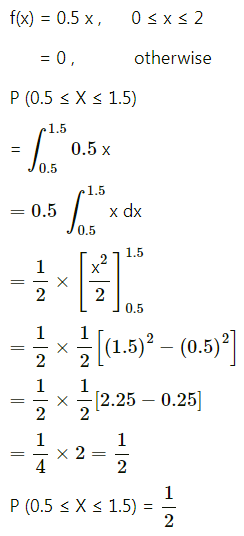
(iii) P(x ≥ 1.5)

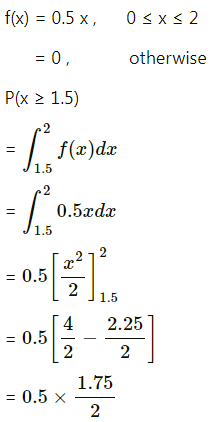
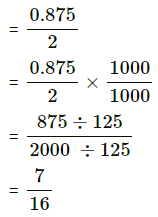
Question 6.
Suppose that X is waiting time in minutes for a bus and its p.d.f. is given by f(x) = \(\frac{1}{5}\), for 0 ≤ x ≤ 5 and = 0 otherwise. Find the probability that
(i) waiting time is between 1 and 3
(ii) waiting time is more than 4 minutes.
Solution:
(i) Required probability = P(1 < X < 3)

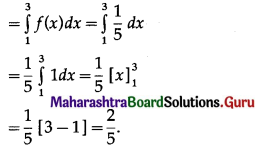
(ii) Required probability = P(X > 4)

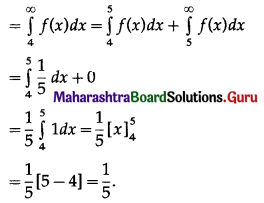
Question 7.
Suppose the error involved in making a certain measurement is a continuous r.v. X with p.d.f.
f(x) = k(4 – x²), -2 ≤ x ≤ 2 and 0 otherwise.
Compute:
(i) P(X > 0)
(ii) P(-1 < X < 1)
(iii) P(-0.5 < X or X > 0.5).
Solution:
Since, f is the p.d.f. of X,

Question 8.
The following is the p.d.f. of continuous r.v. X
f(x) = \(\frac{x}{8}\), for 0 < x < 4 and = 0 otherwise.
(i) Find expression for c.d.f. of X.
(ii) Find F(x) at x = 0.5, 1.7 and 5.
Solution:
(i) Let F(x) be the c.d.f. of X

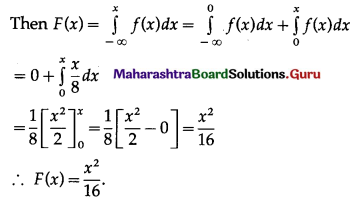
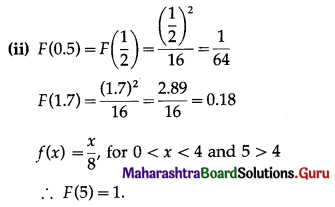
Question 9.
Given the p.d.f. of a continuous random r.v. X, f(x) = \(\frac{x^{2}}{3}\), for -1 < x < 2 and = 0 otherwise. Determine c.d.f. of X and hence find P(X < 1); P(X < -2), P(X > 0), P(1 < X < 2).
Solution:

Question 10.
If a r.v. X has p.d.f.
f(x) = \(\frac{c}{x}\) for 1 < x < 3, c > 0. Find c, E(X), Var (X).
Solution:
Since f(x) is p.d.f of r.v. X