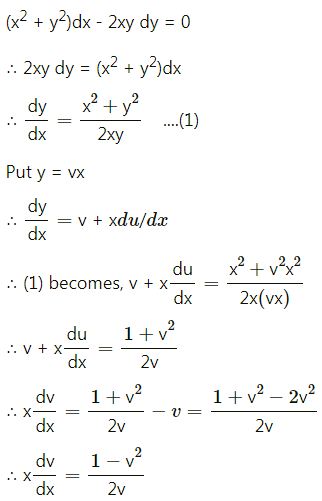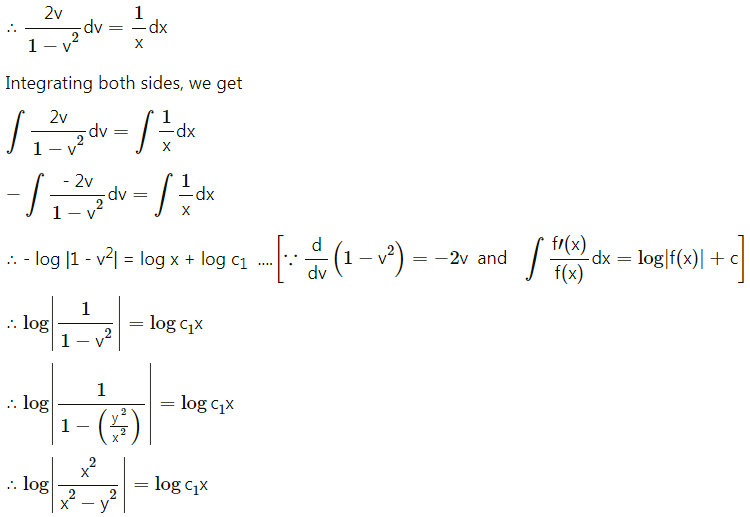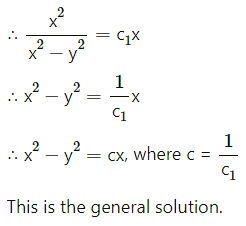Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.4 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.4
I. Solve the following differential equations:
Question 1.
\(x \sin \left(\frac{y}{x}\right) d y=\left[y \sin \left(\frac{y}{x}\right)-x\right] d x\)
Solution:

Question 2.
(x2 + y2) dx – 2xy . dy = 0
Solution:
(x2 + y2) dx – 2xy dy = 0
∴ 2xy dy = (x2 + y2) dx
∴ \(\frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y}\) ………(1)
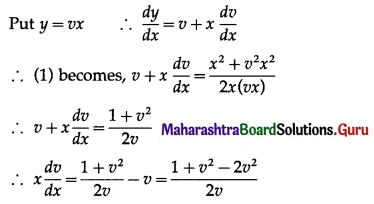
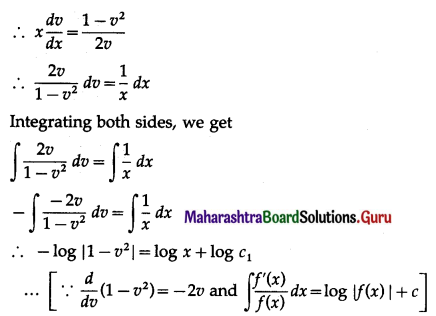
![]()
Question 3.
\(\left(1+2 e^{\frac{x}{y}}\right)+2 e^{\frac{x}{y}}\left(1-\frac{x}{y}\right) \frac{d y}{d x}=0\)
Solution:


Question 4.
y2 dx + (xy + x2) dy = 0
Solution:
y2 dx + (xy + x2) dy = 0
∴ (xy + x2) dy = -y2 dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ……..(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get


![]()
Question 5.
(x2 – y2) dx + 2xy dy = 0
Solution:
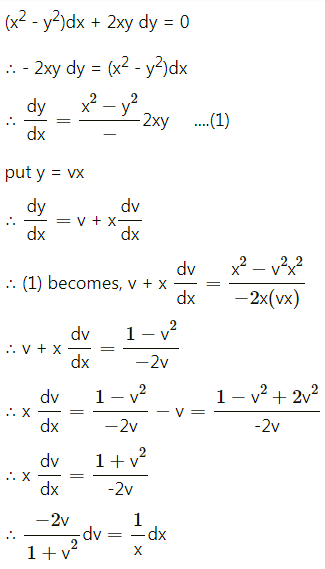
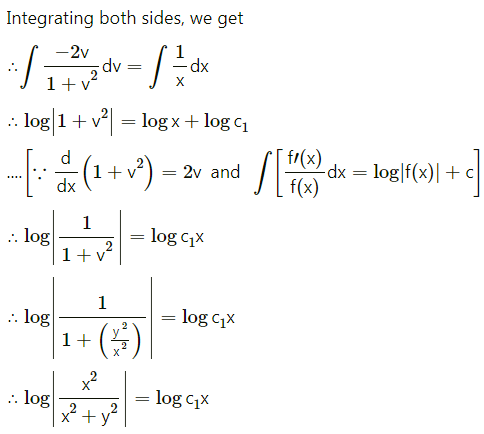
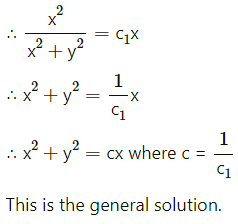
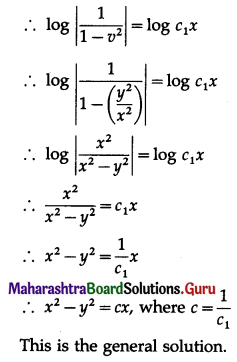
Question 6.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:



![]()
Question 7.
\(x \frac{d y}{d x}-y+x \sin \left(\frac{y}{x}\right)=0\)
Solution:


Question 8.
\(\left(1+e^{\frac{x}{y}}\right) d x+e^{\frac{x}{y}}\left(1-\frac{X}{y}\right) d y=0\)
Solution:


![]()
Question 9.
\(y^{2}-x^{2} \frac{d y}{d x}=x y \frac{d y}{d x}\)
Solution:


Question 10.
xy \(\frac{d y}{d x}\) = x2 + 2y2, y(1) = 0
Solution:


![]()
Question 11.
x dy + 2y · dx = 0, when x = 2, y = 1
Solution:
∴ x dy + 2y · dx = 0
∴ x dy = -2y dx
∴ \(\frac{1}{y} d y=\frac{-2}{x} d x\)
Integrating, we get

This is the general solution.
When x = 2, y = 1, we get
4(1) = c
∴ c = 4
∴ the particular solution is x2y = 4.
Question 12.
x2 \(\frac{d y}{d x}\) = x2 + xy + y2
Solution:
x2 \(\frac{d y}{d x}\) = x2 + xy + y2
∴ \(\frac{d y}{d x}=\frac{x^{2}+x y+y^{2}}{x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)

![]()
Question 13.
(9x + 5y) dy + (15x + 11y) dx = 0
Solution:
(9x + 5y) dy + (15x + 11y) dx = 0
∴ (9x + 5y) dy = -(15x + 11y) dx
∴ \(\frac{d y}{d x}=\frac{-(15 x+11 y)}{9 x+5 y}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)



Question 14.
(x2 + 3xy + y2) dx – x2 dy = 0
Solution:
(x2 + 3xy + y2) dx – x2 dy = 0
∴ x2 dy = (x2 + 3xy + y2) dx
∴ \(\frac{d y}{d x}=\frac{x^{2}+3 x y+y^{2}}{x^{2}}\) ………(1)


![]()
Question 15.
(x2 + y2) dx – 2xy dy = 0.
Solution: