Maharashtra Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Ex 4.2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Ex 4.2

Question 1.
Show that lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.
Solution:
Comparing the equation 3x² – 4 xy – 3y² = 0 with ax² + 2hxy + by² = 0, we get, a = 3, 2h = -4, b = -3 Since a + b = 3 + (-3) = 0, the lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.

Question 2.
Show that lines represented by x² + 6xy + gy²= 0 are coincident.
Question is modified.
Show that lines represented by x² + 6xy + 9y²= 0 are coincident.
Solution:
Comparing the equation x² + 6xy + 9y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 6, i.e. h = 3 and b = 9
Since h² – ab = (3)² – 1(9)
= 9 – 9 = 0, .
the lines represented by x² + 6xy + 9y² = 0 are coincident.

Question 3.
Find the value of k if lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other.
Solution:
Comparing the equation kx² + 4xy – 4y² = 0 with ax² + 2hxy + by² = 0, we get,
a = k, 2h = 4, b = -4
Since lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other,
a + b = 0
∴ k – 4 = 0 ∴ k = 4.

Question 4.
Find the measure of the acute angle between the lines represented by:
(i) 3x² – 4\(\sqrt {3}\)xy + 3y² = 0
Solution:
Comparing the equation 3x² – 4\(\sqrt {3}\)xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 3, 2h = -4\(\sqrt {3}\), i.e. h = -24\(\sqrt {3}\) and b = 3
Let θ be the acute angle between the lines.

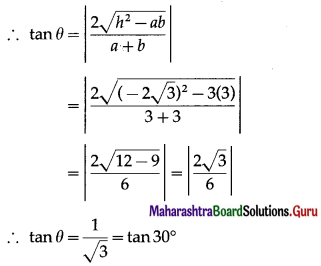
∴ θ = 30°.

(ii) 4x² + 5xy + y² = 0
Solution:
Comparing the equation 4x² + 5xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 5, i.e. h = \(\frac{5}{2}\) and b = 1.
Let θ be the acute angle between the lines.

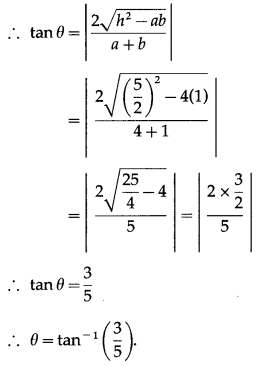
(iii) 2x² + 7xy + 3y² = 0
Solution:
Comparing the equation
2x² + 7xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 2, 2h = 7 i.e. h = \(\frac{7}{2}\) and b = 3
Let θ be the acute angle between the lines.


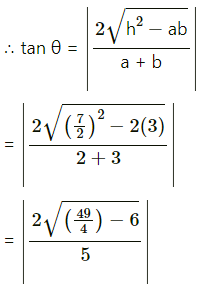
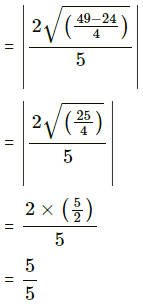
tanθ = 1
∴ θ = tan 1 = 45°
∴ θ = 45°

(iv) (a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0
Solution:
Comparing the equation
(a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0, with
Ax² + 2Hxy + By² = 0, we have,
A = a² – 3b², H = 4ab, B = b² – 3a².
∴ H² – AB = 16a²b² – (a² – 3b²)(b² – 3a²)
= 16a²b² + (a² – 3b²)(3a² – b²)
= 16a²b² + 3a⁴ – 10a²b² + 3b⁴
= 3a⁴ + 6a²b² + 3b⁴
= 3(a⁴ + 2a²b² + b⁴)
= 3 (a² + b²)²
∴ \(\sqrt{H^{2}-A B}\) = \(\sqrt {3}\) (a² + b²)
Also, A + B = (a² – 3b²) + (b² – 3a²)
= -2 (a² + b²)
If θ is the acute angle between the lines, then
tan θ = \(\left|\frac{2 \sqrt{H^{2}-A B}}{A+B}\right|=\left|\frac{2 \sqrt{3}\left(a^{2}+b^{2}\right)}{-2\left(a^{2}+b^{2}\right)}\right|\)
= \(\sqrt {3}\) = tan 60°
∴ θ = 60°

Question 5.
Find the combined equation of lines passing through the origin each of which making an angle of 30° with the line 3x + 2y – 11 = 0
Solution:
The slope of the line 3x + 2y – 11 = 0 is m₁ = \(-\frac{3}{2}\) .
Let m be the slope of one of the lines making an angle of 30° with the line 3x + 2y – 11 = 0.
The angle between the lines having slopes m and m1 is 30°.

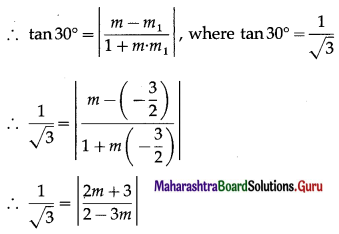
On squaring both sides, we get,
\(\frac{1}{3}=\frac{(2 m+3)^{2}}{(2-3 m)^{2}}\)
∴ (2 – 3m)² = 3 (2m + 3)²
∴ 4 – 12m + 9m² = 3(4m² + 12m + 9)
∴ 4 – 12m + 9m² = 12m² + 36m + 27
3m² + 48m + 23 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
3\(\left(\frac{y}{x}\right)^{2}\) + 48\(\left(\frac{y}{x}\right)\) + 23 = 0
∴ \(\frac{3 y^{2}}{x^{2}}+\frac{48 y}{x}\) + 23 = 0
∴ 3y² + 48xy + 23x² = 0
∴ 23x² + 48xy + 3y² = 0.

Question 6.
If the angle between lines represented by ax² + 2hxy + by² = 0 is equal to the angle between lines represented by 2x² – 5xy + 3y² = 0 then show that 100(h² – ab) = (a + b)².
Solution:
The acute angle θ between the lines ax² + 2hxy + by² = 0 is given by
tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\) ..(1)
Comparing the equation 2x² – 5xy + 3y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 2, 2h= -5, i.e. h = \(-\frac{5}{2}\) and b = 3
Let ∝ be the acute angle between the lines 2x² – 5xy + 3y² = 0.

This is the required condition.

Question 7.
Find the combined equation of lines passing through the origin and each of which making angle 60° with the Y- axis.
Solution:

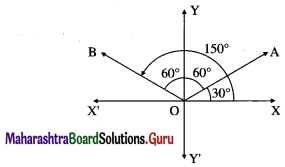
Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.