Maharashtra Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.1

Question 1.
Find the equations of tangents and normals to the curve at the point on it.
(i) y = x² + 2e^x + 2 at (0, 4)
Solution:

(ii) x³ + y³ – 9xy = 0 at (2, 4)
Solution:
x³ + y³ – 9xy = 0
Differentiating both sides w.r.t. x, we get


Hence, the equations of tangent and normal are 4x – 5y + 12 = 0 and 5x + 4y – 26 = 0 respectively.

(iii) x² – √3xy + 2y² = 5 at (√3, 2)
Solution:
x² – √3xy + 2y² = 5
Differentiating both sides w.r.t. x, we get

the slope of normal at (√3, 2) does not exist.
normal is parallel to Y-axis.
equation of the normal is of the form x = k
Since, it passes through the point (√3, 2), k = √3
equation of the normal is x = √3.
Hence, the equations of tangent and normal are y = 2 and x = √3 respectively.

(iv) 2xy + π sin y = 2π at (1, \(\frac{\pi}{2}\))
Solution:
2xy + π sin y = 2π
Differentiating both sides w.r.t. x, we get


Hence, the equations of tangent and normal are πx + 2y – 2π = 0 and 4x – 2πy + π² – 4 = 0 respectively.

(v) x sin 2y = y cos 2x at (\(\frac{\pi}{4}\), \(\frac{\pi}{2}\))
Solution:
x sin 2y = y cos 2x
Differentiating both sides w.r.t. x, we get



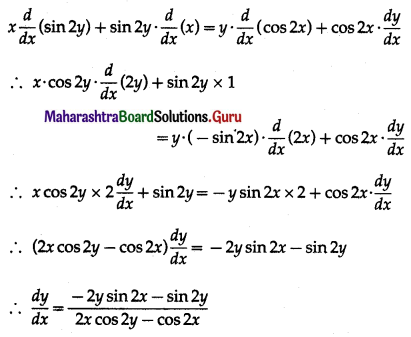
Hence, the equations of the tangent and normal are 2x – y = 0 and 4x + 8y – 5π = 0 respectively.

(vi) x = sin θ and y = cos 2θ at θ = \(\frac{\pi}{6}\)
Solution:
When θ = \(\frac{\pi}{6}\), x = sin\(\frac{\pi}{6}\) and y = cos\(\frac{\pi}{3}\)
∴ x = \(\frac{1}{2}\) and y = \(\frac{1}{2}\)
Hence, the point at which we want to find the equations of tangent and normal is (\(\frac{1}{2}\), \(\frac{1}{2}\))
Now, x = sin θ, y = cos 2θ
Differentiating x and y w.r.t. θ, we get


2y – 1 = x – \(\frac{1}{2}\)
4y – 2 = 2x – 1
2x – 4y + 1 = 0
Hence, equations of the tangent and normal are 4x + 2y – 3 = 0 and 2x – 4y + 1 = 0 respectively.

(vii) x = √t, y = t – \(\frac{1}{\sqrt{t}}\), at t = 4.
Solution:
When t = 4, x = √4 and y = 4 – \(\frac{1}{\sqrt{4}}\)
∴ x = 2 and y = 4 – \(\frac{1}{2}\) = \(\frac{7}{2}\)
Hence, the point at which we want to find the equations of tangent and normal is (2, \(\frac{7}{2}\)).
Now, x = √t, y = t – \(\frac{1}{\sqrt{t}}\)
Differentiating x and y w.r.t. t, we get



Hence, the equations of tangent and normal are 17x – 4y – 20 = 0 and 8x + 34y – 135 = 0 respectively.

Question 2.
Find the point of the curve y = \(\sqrt{x-3}\) where the tangent is perpendicular to the line 6x + 3y – 5 = 0.
Solution:
Let the required point on the curve y = \(\sqrt{x-3}\) be P(x₁, y₁).
Differentiating y = \(\sqrt{x-3}\) w.r.t. x, we get

Hence, the required points are (4, 1) and (4, -1).

Question 3.
Find the points on the curve y = x³ – 2x² – x where the tangents are parallel to 3x – y + 1 = 0.
Solution:
Let the required point on the curve y = x³ – 2x² – x be P(x₁, y₁).

Question 4.
Find the equations of the tangents to the curve x² + y² – 2x – 4y + 1 = 0 which are parallel to the X-axis.
Solution:
Let P (x₁, y₁) be the point on the curve x² + y² – 2x – 4y + 1 = 0 where the tangent is parallel to X-axis.
Differentiating x² + y² – 2x – 4y + 1 = 0 w.r.t. x, we get


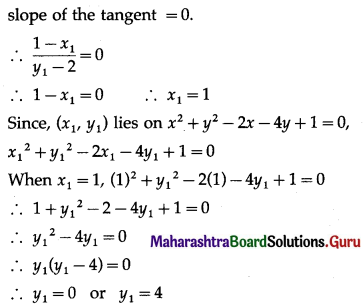
the coordinates of the points are (1, 0) or (1, 4)
Since the tangents are parallel to X-axis, their equations are of the form y = k
If it passes through the point (1, 0), k = 0, and if it passes through the point (1, 4), k = 4
Hence, the equations of the tangents are y = 0 and y = 4.

Question 5.
Find the equations of the normals to the curve 3x² – y² = 8, which are parallel to the line x + 3y = 4.
Solution:
Let P(x₁, y₁) be the foot of the required normal to the curve 3x² – y² = 8.
Differentiating 3x² – y² = 8 w.r.t. x, we get


Hence, the equations of the normals are x + 3y – 8 = 0 and x + 3y + 8 = 0.

Question 6.
If the line y = 4x – 5 touches the curve y² = ax³ + b at the point (2, 3), find a and b.
Solution:
y² = ax³ + b
Differentiating both sides w.r.t. x, we get

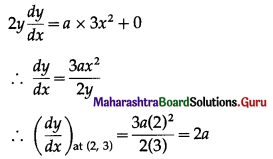
= slope of the tangent at (2, 3)
Since, the line y = 4x – 5 touches the curve at the point (2, 3), slope of the tangent at (2, 3) is 4.
2a = 4 ⇒ a = 2
Since (2, 3) lies on the curve y² = ax³ + b
(3)² = a(2)³ + b
9 = 8a + b
9 = 8(2) + b …… [∵ a = 2]
b = -7
Hence, a = 2 and b = -7.

Question 7.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which y-coordinate is changing 8 times as fast as the x-coordinate.
Solution:
Let P(x₁, y₁) be the point on the curve 6y = x³ + 2 whose y-coordinate is changing 8 times as fast as the x-coordinate.

Question 8.
A spherical soap bubble is expanding so that its radius is increasing at the rate of 0.02 cm/sec. At what rate is the surface area increasing, when its radius is 5 cm?
Solution:
Let r be the radius and S be the surface area of the soap bubble at any time t.
Then S = 4πr²
Differentiating w.r.t. t, we get

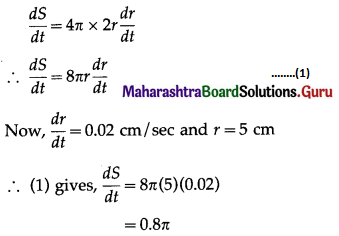
Hence, the surface area of the soap bubble is increasing at the rate of 0.87c cm² / sec.

Question 9.
The surface area of a spherical balloon is increasing at the rate of 2 cm²/sec. At what rate is the volume of the balloon is increasing, when the radius of the balloon is 6 cm?
Solution:
Let r be the radius, S be the surface area and V be the volume of the spherical balloon at any time t.
Then S = 4πr² and V = \(\frac{4}{3} \pi r^{3}\)
Differentiating w.r.t. t, we get

Hence, the volume of the spherical balloon is increasing at the rate of 6 cm³ / sec.

Question 10.
If each side of an equilateral triangle increases at the rate of √2 cm/sec, find the rate of increase of its area when its side of length is 3 cm.
Solution:
If x cm is the side of the equilateral triangle and A is its area, then \(A=\frac{\sqrt{3}}{4} x^{2}\)
Differentiating w.r.t. f, we get

Hence, rate of increase of the area of equilateral triangle = \(\frac{3 \sqrt{6}}{2}\) cm² / sec.

Question 11.
The volume of a sphere increases at the rate of 20 cm³/sec. Find the rate of change of its surface area, when its radius is 5 cm.
Solution:
Let r be the radius, S be the surface area and V be the volume of the sphere at any time t.
Then S = 4πr² and V = \(\frac{4}{3} \pi r^{3}\)
Differentiating w.r.t. t, we get

Hence, the surface area of the sphere is changing at the rate of 8 cm²/sec.

Question 12.
The edge of a cube is decreasing at the rate of 0.6 cm/sec. Find the rate at which its volume is decreasing, when the edge of the cube is 2 cm.
Solution:
Let x be the edge of the cube and V be its volume at any time t.
Then V = x³
Differentiating both sides w.r.t. t, we get

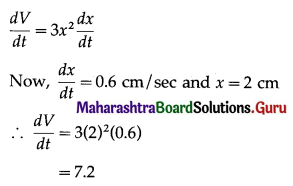
Hence, the volume of the cube is decreasing at the rate of 7.2 cm³/sec.

Question 13.
A man of height 2 meters walks at a uniform speed of 6 km/hr away from a lamp post of 6 meters high. Find the rate at which the length of the shadow is increasing.
Solution:
Let OA be the lamp post, MN the man, MB = x, his shadow, and OM = y, the distance of the man from the lamp post at time t.

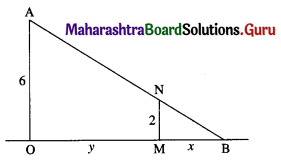
Then \(\frac{d y}{d t}\) = 6 km/hr is the rate at which the man is moving at away from the lamp post.
\(\frac{d x}{d t}\) is the rate at which his shadow is increasing.
From the figure,
\(\frac{x}{2}=\frac{x+y}{6}\)
6x = 2x + 2y
4x = 2y
x = \(\frac{1}{2}\) y
\(\frac{d x}{d t}=\frac{1}{2} \frac{d y}{d t}=\frac{1}{2} \times 6=3 \mathrm{~km} / \mathrm{hr}\)
Hence, the length of the shadow is increasing at the rate of 3 km/hr.

Question 14.
A man of height 1.5 meters walks towards a lamp post of height 4.5 meters, at the rate of (\(\frac{3}{4}\)) meter/sec.
Find the rate at which
(i) his shadow is shortening
(ii) the tip of the shadow is moving.
Solution:

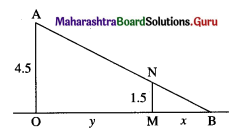
Let OA be the lamp post, MN the man, MB = x his shadow and OM = y the distance of the man from lamp post at time t.
Then \(\frac{d y}{d t}=\frac{3}{4}\) is the rate at which the man is moving towards the lamp post.
\(\frac{d x}{d t}\) is the rate at which his shadow is shortening.
B is the tip of the shadow and it is at a distance of x + y from the post.
\(\frac{d}{d t}(x+y)=\frac{d x}{d t}+\frac{d y}{d t}\) is the rate at which the tip of the shadow is moving.
From the figure,
\(\frac{x}{1.5}=\frac{x+y}{4.5}\)
45x = 15x + 15y
30x = 15y
x = \(\frac{1}{2}\)y
\(\frac{d x}{d t}=\frac{1}{2} \cdot \frac{d y}{d t}=\frac{1}{2}\left(\frac{3}{4}\right)=\left(\frac{3}{8}\right) \text { metre/sec }\)
and \(\frac{d x}{d t}+\frac{d y}{d t}=\frac{3}{8}+\frac{3}{4}=\left(\frac{9}{8}\right) \text { metres } / \mathrm{sec}\)
Hence (i) the shadow is shortening at the rate of (\(\frac{3}{8}\)) metre/sec, and
(ii) the tip of shadow is moving at the rate of (\(\frac{9}{8}\)) metres/sec.

Question 15.
A ladder 10 metres long is leaning against a vertical wall. If the bottom of the ladder is pulled horizontally away from the wall at the rate of 1.2 metres per second, find how fast the top of the ladder is sliding down the wall, when the bottom is 6 metres away from the wall.
Solution:

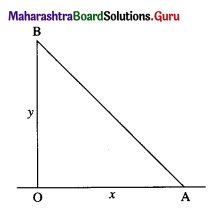
Let AB be the ladder, where AB = 10 metres.
Let at time t seconds, the end A of the ladder be x metres from the wall and the end B be y metres from the ground.
Since, OAB is a right angled triangle, by Pythagoras’ theorem
x² + y² = 10² i.e. y² = 100 – x²
Differentiating w.r.t. t, we get
2y \(\frac{d y}{d t}\) = 0 – 2x \(\frac{d x}{d t}\)
∴ \(\frac{d y}{d t}=-\frac{x}{y} \cdot \frac{d x}{d t}\) ……..(1)
Now, \(\frac{d x}{d t}\) = 1.2 metres/sec is the rate at which the bottom at of the ladder is pulled horizontally and \(\frac{d y}{d t}\) is the rate at which the top of ladder B is sliding.
When x = 6, y² = 100 – 36 = 64
y = 8
(1) gives \(\frac{d y}{d t}=-\frac{6}{8}(1.2)=-\frac{6}{8} \times \frac{12}{10}\)
\(=-\frac{9}{10}=-0.9\)
Hence, the top of the ladder is sliding down the wall, at the rate of 0.9 metre/sec.

Question 16.
If water is poured into an inverted hollow cone whose semi-vertical angle is 30° so that its depth (measured along the axis) increases at the rate of 1 cm/sec. Find the rate at which the volume of water increases when the depth is 2 cm.
Solution:

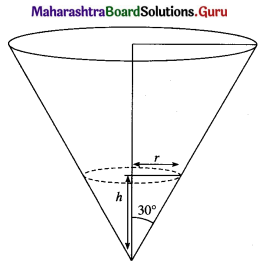
Let r be the radius, h be the height, θ be the semi-vertical angle and V be the volume of the water at any time t.

Hence, the volume of water is increasing at the rate of \(\left(\frac{4 \pi}{3}\right)\) cm3/sec.