Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.1
I. Evaluate the following limits:
Question 1.
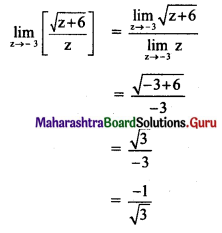
\(\lim _{z \rightarrow-3}\left[\frac{\sqrt{Z+6}}{Z}\right]\)
Solution:
Question 2.
\(\lim _{y \rightarrow-3}\left[\frac{y^{5}+243}{y^{3}+27}\right]\)
Solution:

![]()
Question 3.
\(\lim _{z \rightarrow-5}\left[\frac{\left(\frac{1}{z}+\frac{1}{5}\right)}{z+5}\right]\)
Solution:

II. Evaluate the following limits:
Question 1.
\(\lim _{x \rightarrow 3}\left[\frac{\sqrt{2 x+6}}{x}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 2}\left[\frac{x^{-3}-2^{-3}}{x-2}\right]\)
Solution:
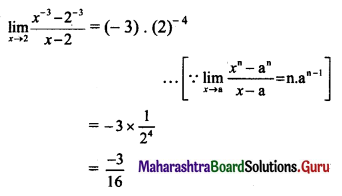
Question 3.
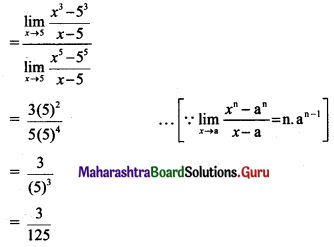
\(\lim _{x \rightarrow 5}\left[\frac{x^{3}-125}{x^{5}-3125}\right]\)
Solution:

![]()
Question 4.
If \(\lim _{x \rightarrow 1}\left[\frac{x^{4}-1}{x-1}\right]=\lim _{x \rightarrow a}\left[\frac{x^{3}-a^{3}}{x-a}\right]\), find all possible values of a.
Solution:

III. Evaluate the following limits:
Question 1.
\(\lim _{x \rightarrow 1}\left[\frac{x+x^{2}+x^{3}+\ldots \ldots \ldots+x^{n}-n}{x-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 7}\left[\frac{(\sqrt[3]{x}-\sqrt[3]{7})(\sqrt[3]{x}+\sqrt[3]{7})}{x-7}\right]\)
Solution:

Question 3.
If \(\lim _{x \rightarrow 5}\left[\frac{x^{k}-5^{k}}{x-5}\right]\) = 500, find all possible values of k.
Solution:

Question 4.
\(\lim _{x \rightarrow 0}\left[\frac{(1-x)^{8}-1}{(1-x)^{2}-1}\right]\)
Solution:


![]()
Question 5.
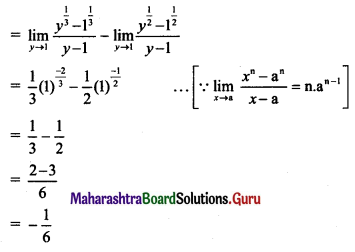
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt[3]{1+x}-\sqrt{1+x}}{x}\right]\)
Solution:

Question 6.
\(\lim _{y \rightarrow 1}\left[\frac{2 y-2}{\sqrt[3]{7+y}-2}\right]\)
Solution:
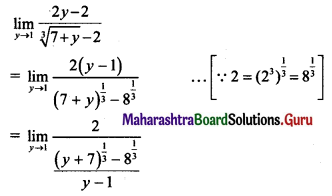

Question 7.
\(\lim _{z \rightarrow a}\left[\frac{(z+2)^{\frac{3}{2}}-(a+2)^{\frac{3}{2}}}{z-a}\right]\)
Solution:

Question 8.
\(\lim _{x \rightarrow 7}\left[\frac{x^{3}-343}{\sqrt{x}-\sqrt{7}}\right]\)
Solution:

![]()
Question 9.
\(\lim _{x \rightarrow 1}\left(\frac{x+x^{3}+x^{5}+\ldots+x^{2 n-1}-n}{x-1}\right)\)
Solution:


IV. In the following examples, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
Question 1.
\(\lim _{x \rightarrow 2}(2 x+3)=7\)
Solution:
We have to find some δ so that
\(\lim _{x \rightarrow 2}(2 x+3)=7\)
Here a = 2, l = 1 and f(x) = 2x + 3
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |(2x + 3) – 7| < ∈
∴ |2x + 4| < ∈
∴ 2(x – 2)|< ∈
∴ |x – 2| < \(\frac{\epsilon}{2}\)
∴ δ ≤ \(\frac{\epsilon}{2}\) such that
|2x + 4| < δ ⇒ |f(x) – 7| < ∈
Question 2.
\(\lim _{x \rightarrow-3}(3 x+2)=-7\)
Solution:
We have to find some δ so that
\(\lim _{x \rightarrow-3}(3 x+2)=-7\)
Here a = -3, l = -7 and f(x) = 3x + 2
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |3x + 2 – (-7)| < ∈
∴ |3x + 9| < ∈
∴ |3(x + 3)| < ∈
∴ |x + 3| < \(\frac{\epsilon}{3}\)
∴ δ < \(\frac{\epsilon}{3}\) such that
|x + 3| ≤ δ ⇒ |f(x) + 7| < ∈
![]()
Question 3.
\(\lim _{x \rightarrow 2}\left(x^{2}-1\right)=3\)
Solution:
We have to find some δ > 0 such that
\(\lim _{x \rightarrow 2}\left(x^{2}-1\right)=3\)
Here, a = 2, l = 3 and f(x) = x2 – 1
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |(x2 – 1) – 3| < ∈
∴ |x2 – 4| < ∈
∴ |(x + 2)(x – 2)| < ∈ …..(i)
We have to get rid of the factor |x + 2|
As |x – 2| < δ
-δ < x – 2 < δ
∴ 2 – δ < x < 2 + δ
Since δ can be assumed as very small, let us choose δ < 1
∴ 1 < x < 3
∴ 3 < x + 2 < 5 …..(Adding 2 throughout)
∴ |x + 2| < 5
∴ |(x + 2)(x – 2)| < 5|x – 2| ……(ii)
From (i) and (ii), we get
5|x – 2|< ∈
∴ x – 2 < \(\frac{\epsilon}{5}\)
If δ = \(\frac{\epsilon}{5}\), |x – 2| < δ ⇒ |x2 – 4| < ∈
∴ We choose δ = min{\(\frac{\epsilon}{5}\), 1} then
|x – 2| < δ ⇒ |f(x) – 3| < ∈
![]()
Question 4.
\(\lim _{x \rightarrow 1}\left(x^{2}+x+1\right)=3\)
Solution:
We have to find some δ > 0 such that
\(\lim _{x \rightarrow 1}\left(x^{2}+x+1\right)=3\)
Here a = 1, l = 3 and f(x) = x2 + x + 1
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |x2 + x + 1 – 3| < ∈
∴ |x2 + x – 2| < ∈
∴ |(x + 2)(x – 1)| < ∈ …..(i)
We have to get rid of the factor |x + 2|
As |x – 1| < δ
-δ < x – 1 < δ
∴ 1 – δ < x < 1 + δ
Since δ can be assumed as very small, let us choose δ < 1
∴ 0 < x < 2
∴ 2 < x + 2 < 4
∴ |x + 2| < 4
∴ |(x + 2)(x – 1)|< 4 |x – 1| …..(ii)
From (i) and (ii), we get
4|x – 1| < ∈
∴ |x – 1| < \(\frac{\epsilon}{4}\)
If δ = \(\frac{\epsilon}{4}\),
|x – 1| < δ ⇒ x2 + x – 2 < ∈
∴ We choose δ = min{\(\frac{\epsilon}{4}\), 1} then
|x – 1| < δ ⇒ |f(x) – 3| < ∈