Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(A) Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(A)
I. Select the correct option from the given alternatives.
Question 1.
The determinant D = \(\left|\begin{array}{ccc}
a & b & a+b \\
b & c & b+c \\
a+b & b+c & 0
\end{array}\right|\) = 0, if
(a) a, b, c are in A.P.
(b) a, b, c are in G.P.
(c) a, b, c are in H.P.
(d) α is a root of ax2 + 2bx + c = 0
Answer:
(b) a, b, c are in G.P.
Hint:
Applying R3 → R3 – (R1 + R2), we get
\(\left|\begin{array}{llc}
a & b & a+b \\
b & c & b+c \\
0 & 0 & -(a+2 b+c)
\end{array}\right|=0\)
∴ a[-c(a + 2b + c) – 0] – b[-b(a + 2b + c) – 0] + (a + b) (0 – 0) = 0
∴ (-ac + b2) (a + 2b + c) = 0
∴ -ac + b2 = 0 or a + 2b + c = 0
∴ b2 = ac
∴ a, b, c are in G.P.
![]()
Question 2.
If \(\left|\begin{array}{lll}
x^{k} & x^{k+2} & x^{k+3} \\
y^{k} & y^{k+2} & y^{k+3} \\
z^{k} & z^{k+2} & z^{k+3}
\end{array}\right|\) = (x – y) (y – z) (z – x) \(\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\) then
(a) k = -3
(b) k = -1
(c) k = 1
(d) k = 3
Answer:
(b) k = -1
Hint:
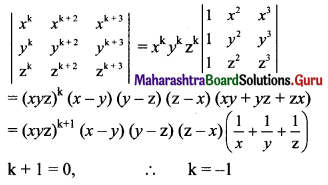
Question 3.
Let D = \(\left|\begin{array}{ccc}
\sin \theta \cdot \cos \phi & \sin \theta \cdot \sin \phi & \cos \theta \\
\cos \theta \cdot \cos \phi & \cos \theta \cdot \sin \phi & -\sin \theta \\
-\sin \theta \cdot \sin \phi & \sin \theta \cdot \cos \phi & 0
\end{array}\right|\) then
(a) D is independent of θ
(b) D is independent of φ
(c) D is a constant
(d) \(\frac{d D}{d}\) at θ = \(\frac{\pi}{2}\) is equal to 0
Answer:
(b) D is independent of φ
Question 4.
The value of a for which the system of equations a3x + (a + 1)y + (a + 2)3 z = 0, ax + (a + 1)y + (a + 2)z = 0 and x + y + z = 0 has a non zero solution is
(a) 0
(b) -1
(c) 1
(d) 2
Answer:
(b) -1
Hint:
The given system of equations will have a non-zero solution, if

Question 5.
\(\left|\begin{array}{lll}
b+c & c+a & a+b \\
q+r & r+p & p+q \\
y+z & z+x & x+y
\end{array}\right|=\)
(a) 2 \(\left|\begin{array}{lll}
c & b & a \\
r & q & p \\
z & y & x
\end{array}\right|\)
(b) 2 \(\left|\begin{array}{lll}
b & a & c \\
q & p & r \\
y & x & z
\end{array}\right|\)
(c) 2 \(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
(d) 2 \(\left|\begin{array}{lll}
a & c & b \\
p & r & q \\
x & z & y
\end{array}\right|\)
Answer:
(c) 2 \(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
Hint:

![]()
Question 6.
The system 3x – y + 4z = 3, x + 2y – 3z = -2 and 6x + 5y + λz = -3 has atleast one solution when
(a) λ = -5
(b) λ = 5
(c) λ = 3
(d) λ = -13
Answer:
(a) λ = -5
Hint:
The given system of equations will have more than one solution if

Question 7.
If x = -9 is a root of \(\left|\begin{array}{lll}
x & 3 & 7 \\
2 & x & 2 \\
7 & 6 & x
\end{array}\right|=0\), has other two roots are
(a) 2, -7
(b) -2, 7
(c) 2, 7
(d) -2, -7
Answer:
(c) 2, 7
Hint:

Question 8.
If \(\left|\begin{array}{ccc}
6 i & -3 i & 1 \\
4 & 3 i & -1 \\
20 & 3 & i
\end{array}\right|\) = x + iy, then
(a) x = 3, y = 1
(b) x = 1, y = 3
(c) x = 0, y = 3
(d) x = 0, y = 0
Answer:
(d) x = 0, y = 0
Question 9.
If A(0, 0), B(1, 3) and C(k, 0) are vertices of triangle ABC whose area is 3 sq.units, then the value of k is
(a) 2
(b) -3
(c) 3 or -3
(d) -2 or 2
Answer:
(d) -2 or 2
![]()
Question 10.
Which of the following is correct?
(a) Determinant is a square matrix
(b) Determinant is number associated to matrix
(c) Determinant is a number associated with a square matrix
(d) None of these
Answer:
(c) Determinant is a number associated with a square matrix
II. Answer the following questions.
Question 1.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
Solution:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
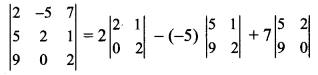
= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113
(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
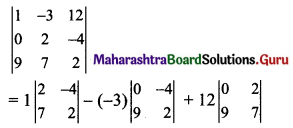
= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76
![]()
Question 2.
Evaluate determinant along second column \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 2 & -2 \\
0 & 1 & -2
\end{array}\right|\)
Solution:

Question 3.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & 3 & 5 \\
400 & 600 & 1000 \\
48 & 47 & 18
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
101 & 102 & 103 \\
106 & 107 & 108 \\
1 & 2 & 3
\end{array}\right|\)
by using properties.
Solution:


Question 4.
Find the minors and cofactors of elements of the determinants.
(i) \(\left|\begin{array}{ccc}
-1 & 0 & 4 \\
-2 & 1 & 3 \\
0 & -4 & 2
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right|\)
Solution:



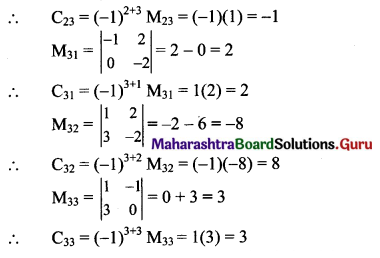
Question 5.
Find the values of x, if
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
⇒ 1(-10x2 + 10x) – 4(5x2 + 5) + 20(2x + 2) = 0
⇒ -10x2 + 10x – 20x2 – 20 + 40x + 40 = 0
⇒ -30x2 + 50x + 20 = 0
⇒ 3x2 – 5x – 2 = 0 …..[Dividing throughout by (-10)]
⇒ 3x2 – 6x + x – 2 = 0
⇒ 3x(x – 2) + 1(x – 2) = 0
⇒ (x – 2) (3x + 1) = 0
⇒ x – 2 = 0 or 3x + 1 = 0
⇒ x = 2 or x = \(-\frac{1}{3}\)
(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
⇒ 1(4 – 16) – 2x(1 – 16) + 4x(1 – 4) = 0
⇒ 1(-12) – 2x(-15) + 4x(-3) = 0
⇒ -12 + 30x – 12x = 0
⇒ 18x = 12
⇒ x = \(\frac{12}{18}=\frac{2}{3}\)
![]()
Question 6.
By using properties of determinant, prove that \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:

Question 7.
Without expanding the determinants, show that

Solution:
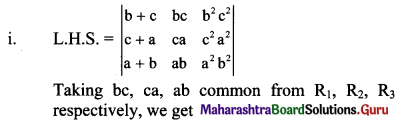


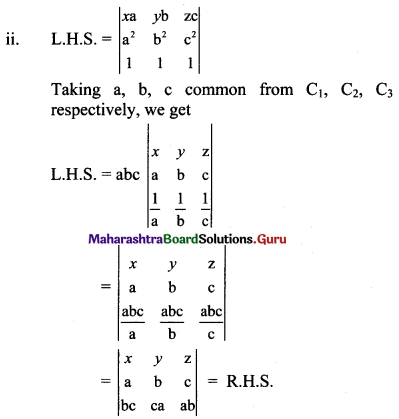


Question 8.
If \(\left|\begin{array}{lll}
a & 1 & 1 \\
1 & b & 1 \\
1 & 1 & c
\end{array}\right|=0\) then show that \(\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}=1\)
Solution:
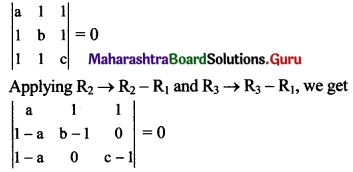

Question 9.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
(ii) \(\frac{1}{x}+\frac{1}{y}=\frac{3}{2}, \quad \frac{1}{y}+\frac{1}{z}=\frac{5}{6}, \quad \frac{1}{z}+\frac{1}{x}=\frac{4}{3}\)
(iii) 2x + 3y + 3z = 5, x – 2y + z = -4, 3x – y – 2z = 3
(iv) x + y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
(i) Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1
D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0
Dx = \(\left|\begin{array}{ccc}
1 & -1 & 1 \\
8 & 2 & 3 \\
1 & 1 & -4
\end{array}\right|\)
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40
Dy = \(\left|\begin{array}{ccc}
2 & 1 & 1 \\
1 & 8 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-32 – 3) -1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80
Dz = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 8 \\
3 & 1 & 1
\end{array}\right|\)
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,
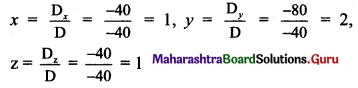
∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.
![]()
(ii) Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
∴ The given equations become
p + q = \(\frac{3}{2}\)
i.e., 2p + 2q = 3
i.e., 2p + 2q + 0 = 3
q + r = \(\frac{5}{6}\)
i.e., 6q + 6r = 5,
i.e., 0p + 6q + 6r = 5
r + p = \(\frac{4}{3}\)
i.e., 3r + 3p = 4,
i.e., 3p + 0q + 3r = 4
D = \(\left|\begin{array}{lll}
2 & 2 & 0 \\
0 & 6 & 6 \\
3 & 0 & 3
\end{array}\right|\)
= 2(18 – 0) -2(0 – 18) + 0
= 2(18) – 2(-18)
= 36 + 36
= 72 ≠ 0
Dp = \(\left|\begin{array}{lll}
3 & 2 & 0 \\
5 & 6 & 6 \\
4 & 0 & 3
\end{array}\right|\)
= 3(18 – 0) – 2(15 – 24) + 0
= 3(18) – 2(-9)
= 54 + 18
= 72
Dq = \(\left|\begin{array}{lll}
2 & 3 & 0 \\
0 & 5 & 6 \\
3 & 4 & 3
\end{array}\right|\)
= 2(15 – 24) – 3(0 – 18) + 0
= 2(-9) – 3(-18)
= -18 + 54
= 36
Dr = \(\left|\begin{array}{lll}
2 & 2 & 3 \\
0 & 6 & 5 \\
3 & 0 & 4
\end{array}\right|\)
= 2(24 – 0) – 2(0 – 15) + 3(0 – 18)
= 2(24) – 2(-15) + 3(-18)
= 48 + 30 – 54
= 24
By Cramer’s Rule,

∴ x = 1, y = 2 and z = 3 are the solutions of the given equations.
(iii) Given equations are
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3
D = \(\left|\begin{array}{ccc}
2 & 3 & 3 \\
1 & -2 & 1 \\
3 & -1 & -2
\end{array}\right|\)
= 2(4 + 1) – 3(-2 – 3) + 3(-1 + 6)
= 2(5) – 3(-5) + 3(5)
= 10 + 15 + 15
= 40 ≠ 0
Dx = \(\left|\begin{array}{ccc}
5 & 3 & 3 \\
-4 & -2 & 1 \\
3 & -1 & -2
\end{array}\right|\)
= 5(4 + 1) – 3(8 – 3) + 3(4 + 6)
= 5(5) – 3(5) + 3(10)
= 25 – 15 + 30
= 40
Dy = \(\left|\begin{array}{ccc}
2 & 5 & 3 \\
1 & -4 & 1 \\
3 & 3 & -2
\end{array}\right|\)
= 2(8 – 3) – 5(-2 – 3) + 3(3 + 12)
= 2(5) – 5(-5) + 3(15)
= 10 + 25 + 45
= 80
Dz = \(\left|\begin{array}{ccc}
2 & 3 & 5 \\
1 & -2 & -4 \\
3 & -1 & 3
\end{array}\right|\)
= 2(-6 – 4) – 3(3 + 12) + 5(-1 + 6)
= 2(-10) – 3(15) + 5(5)
= -20 -45 + 25
= -40
By Cramer’s Rule,
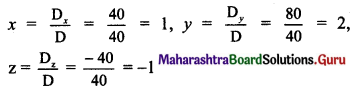
∴ x = 1, y = 2 and z = -1 are the solutions of the given equations.
(iv) Given equations are
x – y + 2z = 7
3x + 4y – 5z = 5
2x – y + 3z = 12
D = \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right|\)
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0
Dx = \(\left|\begin{array}{ccc}
7 & -1 & 2 \\
5 & 4 & -5 \\
12 & -1 & 3
\end{array}\right|\)
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7) + 1(75) + 2(-53)
= 49 + 75 – 106
= 18
Dy = \(\left|\begin{array}{ccc}
1 & 7 & 2 \\
3 & 5 & -5 \\
2 & 12 & 3
\end{array}\right|\)
= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6
Dz = \(\left|\begin{array}{ccc}
1 & -1 & 7 \\
3 & 4 & 5 \\
2 & -1 & 12
\end{array}\right|\)
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53) + 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,
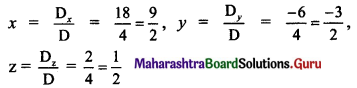
∴ x = \(\frac{9}{2}\), y = \(\frac{-3}{2}\) and z = \(\frac{1}{2}\) are the solutions of the given equations.
![]()
Question 10.
Find the value of k, if the following equations are consistent.
(i) (k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
(ii) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
(iii) (k – 2)x + (k – 1)y = 17, (k – 1)x +(k – 2)y = 18 and x + y = 5
Solution:
(i) Given equations are
(k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
Since these equations are consistent,

⇒ 2(2k + 2 + 2k – 2) – 0 + (k – 1) (4 – 0) = 0
⇒ 2(4k) + (k – 1)4 = 0
⇒ 8k + 4k – 4 = 0
⇒ 12k – 4 = 0
⇒ k = \(\frac{4}{12}=\frac{1}{3}\)
(ii) Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3, i.e., 2x – y – 3 = 0.
Since these equations are consistent,
\(\left|\begin{array}{rrr}
3 & 1 & -2 \\
k & 2 & -3 \\
2 & -1 & -3
\end{array}\right|=0\)
⇒ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ 3(-9) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ -27 + 3k – 6 + 2k + 8 = 0
⇒ 5k – 25 = 0
⇒ k = 5
(iii) Given equations are
(k – 2)x + (k – 1)y = 17
⇒ (k – 2)x + (k – 1)y – 17 = 0
(k – 1)x + (k – 2)y = 18
⇒ (k – 1)x + (k – 2)y – 18 = 0
x + y = 5
⇒ x + y – 5 = 0
Since these equations are consistent,
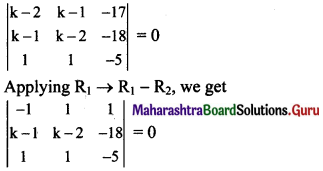
⇒ -1(-5k + 10 + 18) – 1(-5k + 5 + 18) + 1(k – 1 – k + 2) = 0
⇒ -1(-5k + 28) – 1(-5k + 23) + 1(1) = 0
⇒ 5k – 28 + 5k – 23 + 1 = 0
⇒ 10k – 50 = 0
⇒ k = 5
Question 11.
Find the area of triangle whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
(ii) P(3, 6), Q(-1, 3), R(2, -1)
(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
(i) Here, A(x1, y1) = A(-1, 2)
B(x2, y2) = B(2, 4)
C(x3, y3) = C(0, 0)
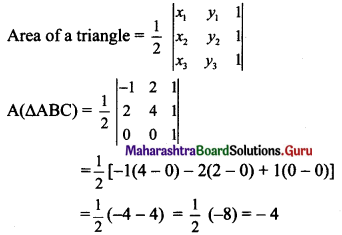
Since area cannot be negative,
A(ΔABC) = 4 sq.units
(ii) Here, P(x1, y1) = P(3, 6)
Q(x2, y2) = Q(-1, 3)
R(x3, y3) = R(2, -1)

A(ΔPQR) = \(\frac{25}{2}\) sq.units
(iii) Here, L(x1, y1) = L(1, 1)
M(x2, y2) = M(-2, 2)
N(x3, y3) = N(5, 4)

Since area cannot be negative,
A(ΔLMN) = \(\frac{13}{2}\) sq.units
![]()
Question 12.
Find the value of k,
(i) if the area of a triangle is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
(ii) if area of triangle is \(\frac{33}{2}\) square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution:
(i) Here, P(x1, y1) = P(k, 0)
Q(x2, y2) = Q(4, 0)
R(x3, y3) = R(0, 2)
A(ΔPQR) = 4 sq.units

(ii) Here, L(x1, y1) = L(3, -5), M(x2, y2) = M(-2, k), N(x3, y3) = N(1, 4)
A(ΔLMN) = \(\frac{33}{2}\) sq. units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
\(\pm \frac{33}{2}=\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
-2 & k & 1 \\
1 & 4 & 1
\end{array}\right|\)
⇒ \(\pm \frac{33}{2}=\frac{1}{2}\) [3(k – 4) – (-5) (-2 – 1) + 1 (-8 – k)]
⇒ ±33 = 3k – 12 – 15 – 8 – k
⇒ ±33 = 2k – 35
⇒ 2k – 35 = 33 or 2k – 35 = -33
⇒ 2k = 68 or 2k = 2
⇒ k = 34 or k = 1
Question 13.
Find the area of quadrilateral whose vertices are A(0, -4), B(4, 0), C(-4,0), D (0, 4).
Solution:
A(0, -4), B(4, 0), C(-4, 0), D(0, 4)
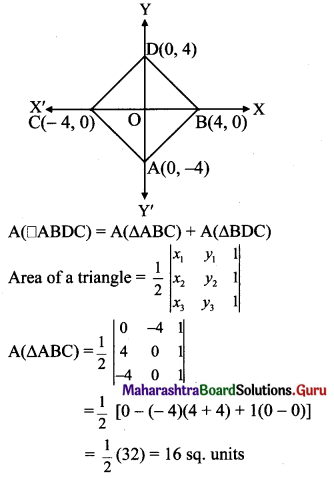

∴ A(ABDC) = A(ΔABC) + A(ΔBDC)
= 16 + 16
= 32 sq.units
Question 14.
An amount of ₹ 5000 is put into three investments at the rate of interest of 6%, 7%, and 8% per annum respectively. The total annual income is ₹ 350. If the combined income from the first two investments is ₹ 70 more than the income from the third, find the amount of each investment.
Solution:
Let the amount of each investment be ₹ x, ₹ y and ₹ z.
According to the given conditions,
x + y + z = 5000,
6% x + 7% y + 8% z = 350




∴ The amounts of investments are ₹ 1750, ₹ 1500, and ₹ 1750.
![]()
Question 15.
Show that the lines x – y = 6, 4x – 3y = 20 and 6x + 5y + 8 = 0 are concurrent. Also, find the point of concurrence.
Solution:
Given equations of the lines are
x – y = 6, i.e., x – y – 6 = 0 ……(i)
4x – 3y = 20, i.e., 4x – 3y – 20 = 0 …..(ii)
6x + 5y + 8 = 0 ……(iii)
The given lines will be concurrent, if

= 1(-24 + 100) – (-1) (32 + 120) – 6(20 + 18)
= 1(76) + 1(152) – 6(38)
= 76 + 152 – 228
= 0
∴ The given lines are concurrent.
To find the point of concurrence, solve any two equations.
Multiplying (i) by 5, we get
5x – 5y – 30 = 0 …….(iv)
Adding (iii) and (iv), we get
11x – 22 = 0
∴ x = 2
Substituting x = 2 in (i), we get
2 – y – 6 = 0
∴ y = -4
∴ The point of concurrence is (2, -4).
Question 16.
Show that the following points are collinear using determinants:
(i) L(2, 5), M(5, 7), N(8, 9)
(ii) P(5,1), Q(1, -1), R(11, 4)
Solution:
(i) Here, L(x1, y1) = L(2, 5)
M(x2, y2) = M(5, 7)
N(X3 y3) = N(8, 9)
If A(ΔLMN) = 0, then the points L, M, N are collinear.

∴ The points L, M, N are collinear.
![]()
(ii) Here, P(x1, y1) = P(5, 1)
Q(x2, y2) = Q(1, -1)
R(x3, y3) = R(11, 4)
If A(ΔPQR) = 0, then the points P, Q, R are collinear.

∴ The points P, Q, R are collinear.