Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Linear Inequations Miscellaneous Exercise 8 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 8 Linear Inequations Miscellaneous Exercise 8
Solve the following system of inequalities graphically.
Question 1.
x ≥ 3, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:

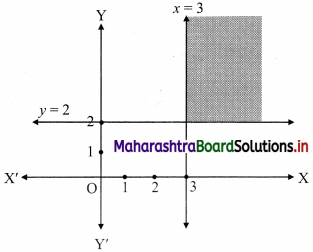
The shaded portion represents the graphical solution.
Question 2.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:
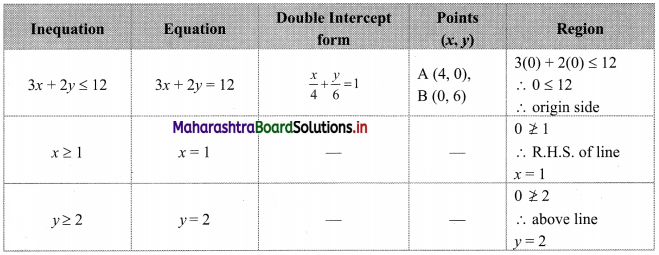
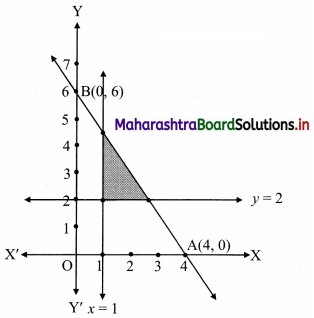
The shaded portion represents the graphical solution.
![]()
Question 3.
2x + y ≥ 6, 3x + 4y < 12
Solution:
To find a graphical solution, construct the table as follows:
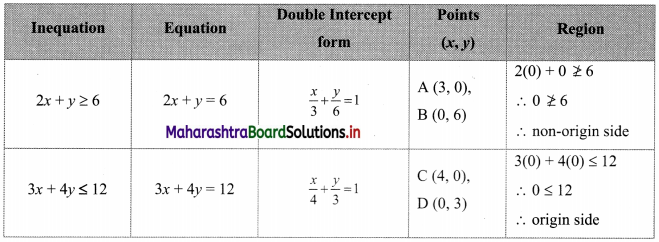
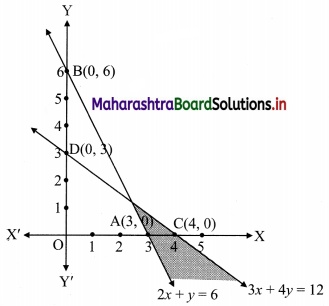
The shaded portion represents the graphical solution.
Question 4.
x + y ≥ 4, 2x – y ≤ 0
Solution:
To find a graphical solution, construct the table as follows:
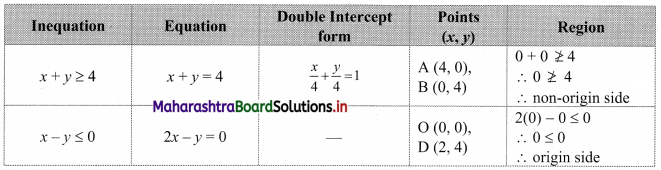
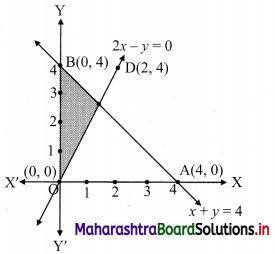
The shaded portion represents the graphical solution.
Question 5.
2x – y ≥1, x – 2y ≤ -1
Solution:
To find a graphical solution, construct the table as follows:

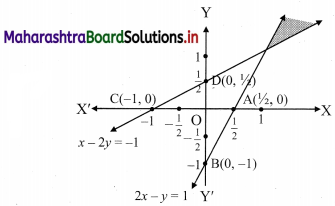
The shaded portion represents the graphical solution.
![]()
Question 6.
x + y ≤ 6, x + y ≥ 4
Solution:
To find a graphical solution, construct the table as follows:
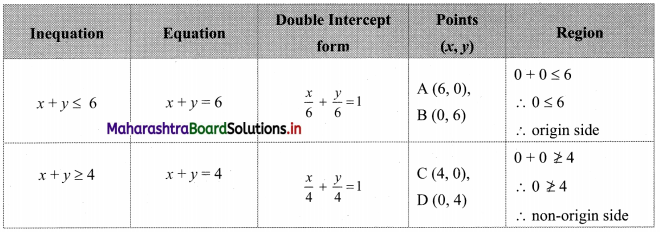
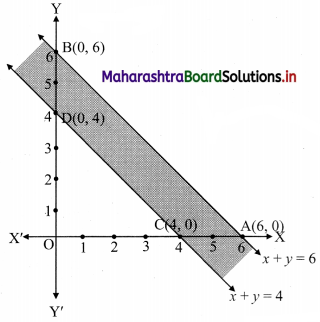
The shaded portion represents the graphical solution.
Question 7.
2x + y ≥ 8, x + 2y ≥ 10
Solution:
To find a graphical solution, construct the table as follows:
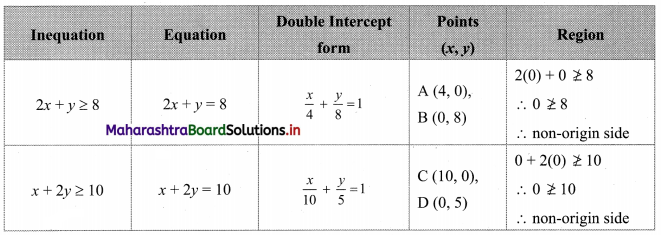
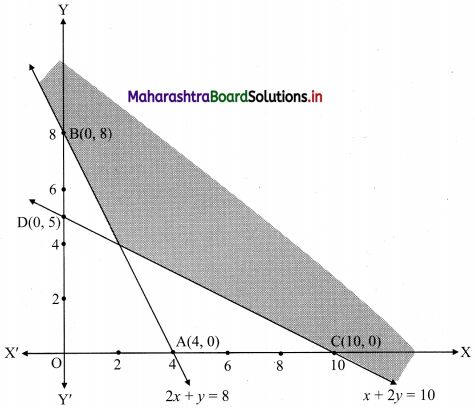
The shaded portion represents the graphical solution.
Question 8.
x + y ≤ 9, y > x, x ≥ 0
Solution:
To find a graphical solution, construct the table as follows:

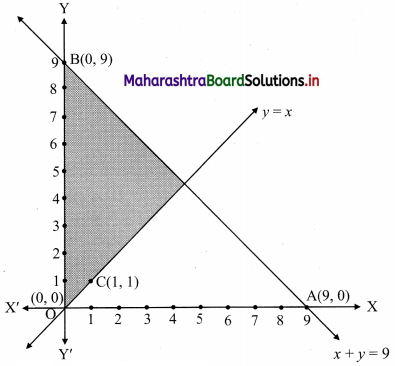
The shaded portion represents the graphical solution.
![]()
Question 9.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:
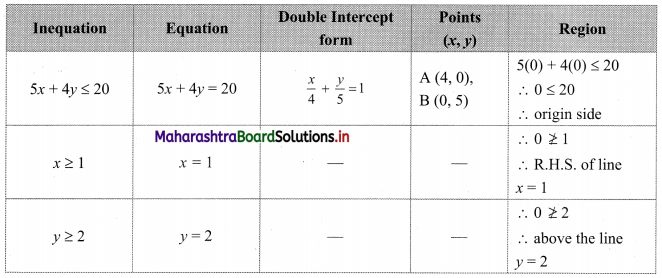
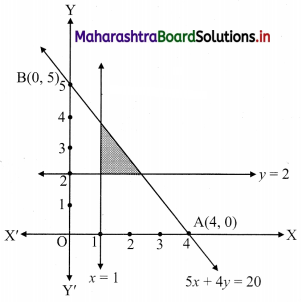
The shaded portion represents the graphical solution.
Question 10.
3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:
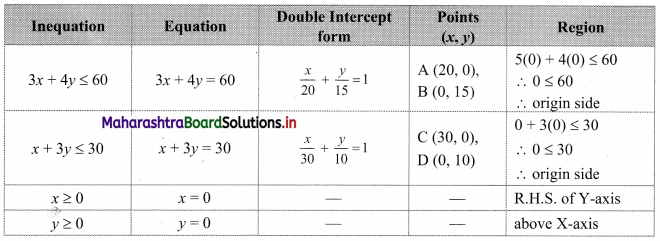
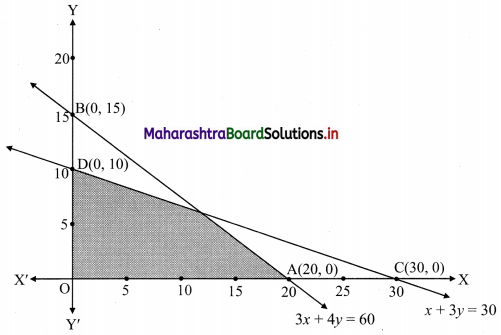
The shaded portion represents the graphical solution.
Question 11.
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solution:
To find a graphical solution, construct the table as follows:
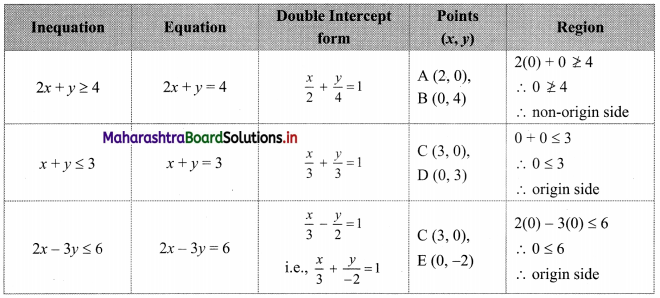
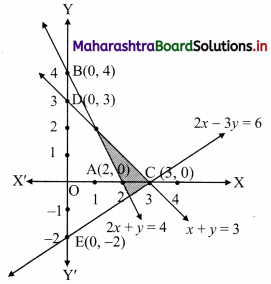
The shaded portion represents the graphical solution.
![]()
Question 12.
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solution:
To find a graphical solution, construct the table as follows:
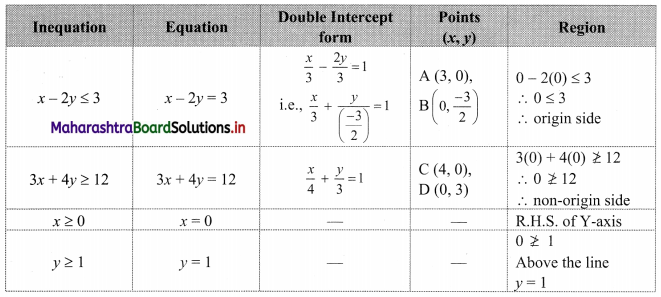
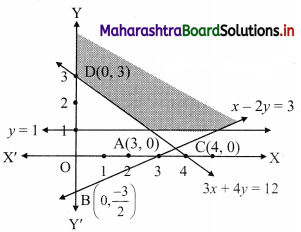
The shaded portion represents the graphical solution.
Question 13.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:
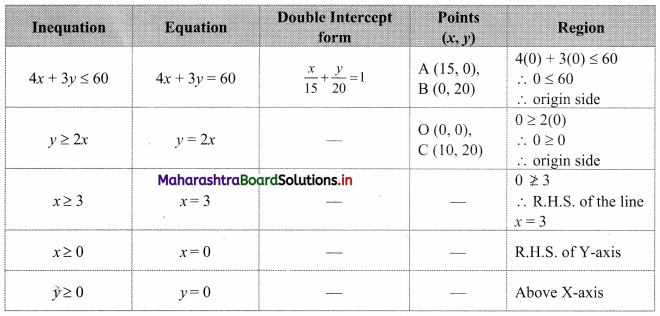
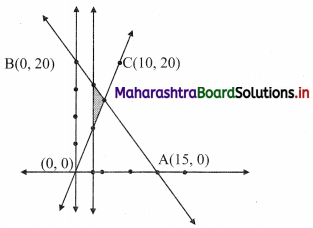
The shaded portion represents the graphical solution.
Question 14.
3x + 2y ≤ 150, x + 4y ≥ 80, x ≤ 15, y ≥ 0, x ≥ 0
Solution:
To find a graphical solution, construct the table as follows:
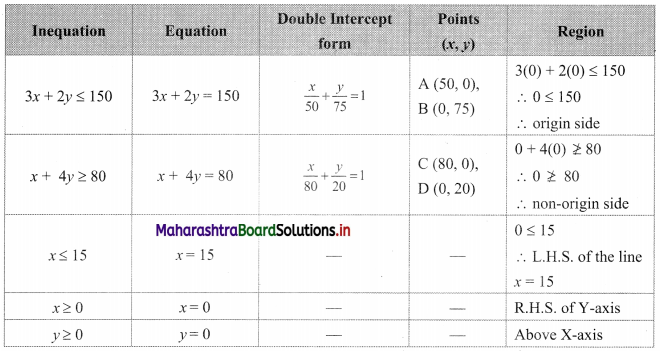
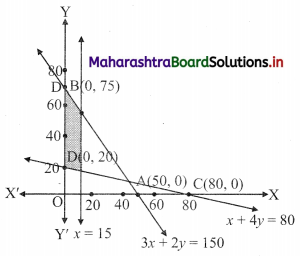
The shaded portion represents the graphical solution.
![]()
Question 15.
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:
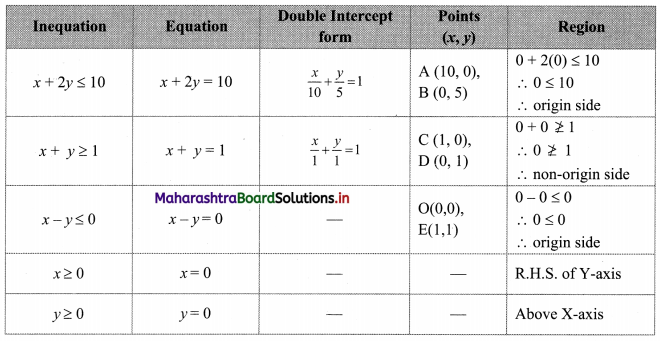
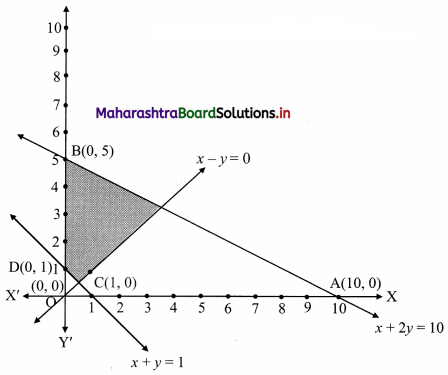
The shaded portion represents the graphical solution.