Maharashtra Board 11th Commerce Maths Solutions Chapter 8 Linear Inequations Ex 8.2

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Linear Inequations Ex 8.2 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 8 Linear Inequations Ex 8.2

Question 1.
Solve the following inequations graphically in a two-dimensional plane
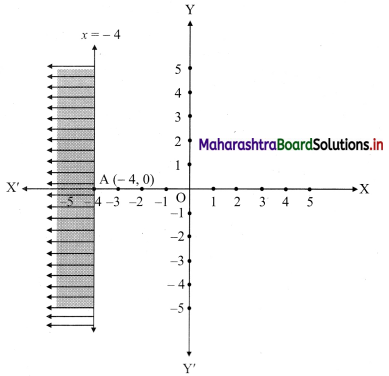
(i) x ≤ -4
Solution:
Given, inequation is x ≤ -4
∴ corresponding equation is x = -4
It is a line parallel to Y-axis passing through the point A(-4, 0)
Origin test:
Substituting x = 0 in inequation, we get
0 ≤ -4 which is false.
∴ Points on the origin side of the line do not satisfy the inequation.
So the points on the non-origin side of the line and points on the line satisfy the inequation
∴ all the points on the line and left of it satisfy the given inequation.
The shaded portion represents the solution set.

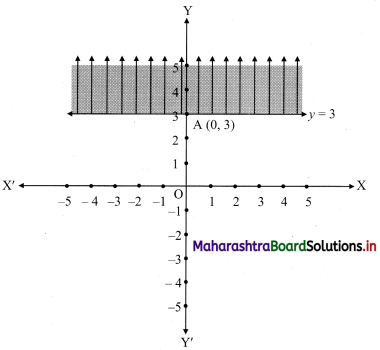
(ii) y ≥ 3
Solution:
Given, inequation is y ≥ 3
∴ corresponding equation is y = 3
It is a line parallel to X-axis passing through point A(0, 3)
Origin test:
Substituting y = 0 in inequation, we get
0 ≥ 3 which is false.
∴ Points on the origin side of the line do not satisfy the inequation
∴ Points on the non-origin side of the line satisfy the inequation.
∴ all the points on the line and above it satisfy the given inequation.
The shaded portion represents the solution set.

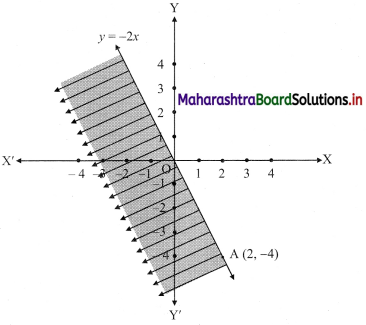
(iii) y ≤ -2x
Solution:
Given, inequation is y ≤ -2x
∴ corresponding equation is y = -2x
It is a line passing through origin O(0, 0).
To draw the line, we need one more point.
To find another point on the line, we can take any value of x,
say, x = 2.
∴ substituting x = 2 in y = -2x, we get
y = -2(2)
∴ y = -4
∴ another point on the line is A(2, -4)
Now, the origin test is not possible as the origin lies on the line y = -2x
So, choose a point which does not lie on the line say, (2, 1)
∴ substituting x = 2, y = 1 in inequation, we get
1 ≤ -2(2)
∴ 1 ≤ -4 which is false.
∴ the points on the side of the line y = -2x, where (2, 1) lies do not satisfy the inequation.
∴ all the points on the line y = -2x and on the opposite side of the line where (2, 1) lies, satisfy the inequation
The shaded portion represents the solution set.

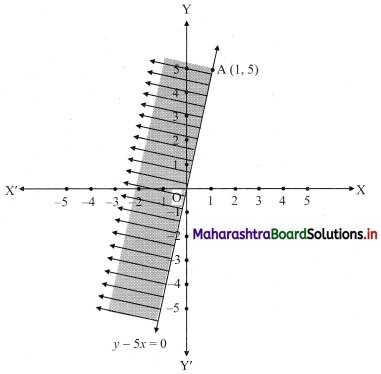
(iv) y – 5x ≥ 0
Solution:
Given, inequation is y – 5x ≥ 0
∴ corresponding equation is y – 5x = 0
It is a line passing through the point O(0, 0)
To draw the line, we need one more point.
To find another point on the line,
we can take any value of x, say, x = 1.
Substituting x = 1 in y – 5x = 0, we get
y – 5(1) = 0
∴ y = 5
∴ Another point on the line is A(1, 5)
Now origin test is not possible as the origin lies on the line y = 5x
∴ choose a point that does not lie on the line, say (3, 2).
∴ substituting x = 3, y = 2 in inequation, we get
2 – 5(3) ≥ 0
∴ 2 – 10 ≥ 0
∴ -8 ≥ 0 which is false.
∴ the points on the side of line y = 5x where (3, 1) lies do not satisfy the inequation.
∴ the points on the line y = 5x and on the opposite of the line where (3, 2) lies, satisfy the inequation.
The shaded portion represents the solution set.

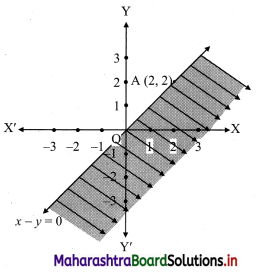
(v) x – y ≥ 0
Solution:
Given, inequation is x – y ≥ 0
∴ Corresponding equation is x – y = 0
It is a line passing through origin O(0, 0)
To draw the line we need one more point.
To find another point on the line, we can take any value of x,
Say, x = 2.
∴ substituting x = 2 in x – y = 0, we get
2 – y = 0
∴ y = 2
∴ another point on the line is A(2, 2)
Now origin test is not possible as the origin lies on the line y = x
∴ choose a point which not lie on the line say (3, 1)
∴ substituting x = 3, y = 1 in inequation, we get
3 – 1 ≥ 0
∴ 2 ≥ 0 which is true.
∴ all the points on line x – y = 0 and the points on the side where (3, 1) lies satisfy the inequation
The shaded portion represents the solution set.

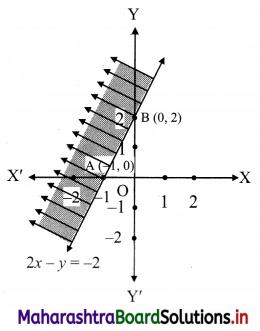
(vi) 2x – y ≤ -2
Solution:
Given, inequation is 2x – y ≤ -2
∴ corresponding equation is 2x – y = -2
∴ \(\frac{2 x}{-2}-\frac{y}{-2}=\frac{-2}{-2}\)
∴ \(\frac{x}{-1}+\frac{y}{2}=1\)
∴ intersection of line with X-axis is A(-1, 0),
intersection of line with Y-axis is B(0, 2)
Origin test:
Substituting x = 0, y = 0 in the given inequation, we get
2(0) – (0) ≤ -2
∴ 0 ≤ -2
which is false.
∴ Points on the origin side of the line do not satisfy the inequation.
∴ Points on the non-origin side of the line satisfy the inequation
∴ all the points on the line and above it satisfy the given inequation.
The shaded portion represents the solution set.

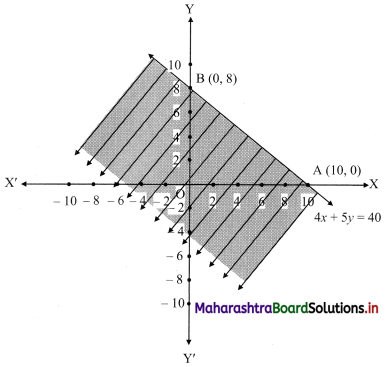
(vii) 4x + 5y ≤ 40
Solution:
Given, inequation is 4x + 5y ≤ 40
∴ Corresponding equation is 4x + 5y = 40
∴ \(\frac{4 x}{40}+\frac{5 y}{40}=\frac{40}{40}\)
∴ \(\frac{x}{10}+\frac{y}{8}=1\)
∴ Intersection of line with X-axis is A(10, 0)
Intersection of line with Y-axis is B(0, 8)
Origin test:
Substituting x = 0, y = 0 in the inequation, we get
4(0) + 5(0) ≤ 40
∴ 0 ≤ 40 which is true.
∴ all the points on the origin side of the line and points on the line satisfy the given inequation.
The shaded portion represents the solution set.

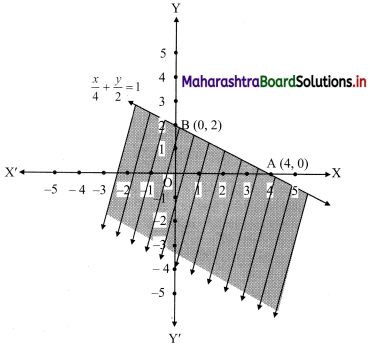
(viii) \(\left(\frac{1}{4}\right) x+\left(\frac{1}{2}\right) y\) ≤ 1
Solution:
Given, inequation is \(\left(\frac{1}{4}\right) x+\left(\frac{1}{2}\right) y\) ≤ 1
∴ corresponding equation is \(\frac{x}{4}+\frac{y}{2}\) = 1
∴ intersection of line with X-axis is A(4, 0),
intersection of line with Y-axis is B(0, 2)
Origin test:
Substituting x = 0, y = 0 in the given inequation, we get
\(\frac{1}{4}(0)+\frac{1}{2}(0)\) ≤ 1
∴ 0 ≤ 1 which is true.
∴ all the points on the origin side of the line and points on the line satisfy the given inequation.
The shaded portion represents the solution set.

Question 2.
Mr. Rajesh has ₹ 1,800 to spend on fruits for the meeting. Grapes cost ₹ 150 per kg. and peaches cost ₹ 200 per kg. Formulate and solve it graphically.
Solution:
Let x and y be the number of kgs. of grapes and peaches bought.
The cost of grapes is ₹ 150/- per kg, cost of peaches is ₹ 200/- per kg.
∴ cost of v kg of grapes is ₹ 150x
and the cost of y kg of peaches is ₹ 200y.
Mr. Rajesh has ₹ 1800 to spend on fruits.
∴ the total cost of grapes and peaches must be less than or equal to ₹ 1800.
∴ required inequation is 150x + 200y ≤ 1800
i.e., 3x + 4y ≤ 36 ……(i)
Since the number of kg of grapes and peaches can not be negative
∴ x ≥ 0, y ≥ 0
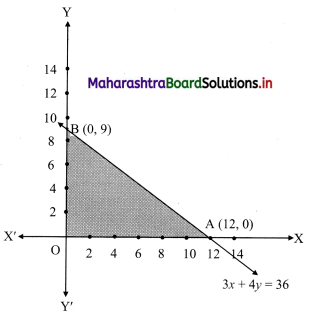
Now, corresponding equation is 3x + 4y = 36
∴ \(\frac{3 x}{36}+\frac{4 y}{36}=\frac{36}{36}\)
∴ \(\frac{x}{12}+\frac{y}{9}=1\)
∴ the intersection of the line with the X-axis is A(12, 0)
the intersection of the line with the Y-axis is B(0, 9)
Origin test:
Substituting x = 0, y = 0 in inequation, we get
3(0) + 4(0) ≤ 36
∴ 0 ≤ 36 which is true.
∴ all the points on the origin side of the line and points on the line satisfy the inequation.
Also, x ≥ 0, y ≥ 0
∴ the solution set is the points on the sides of the triangle OAB and in the interior of ∆OAB.
∴ the shaded portion represents the solution set.

Question 3.
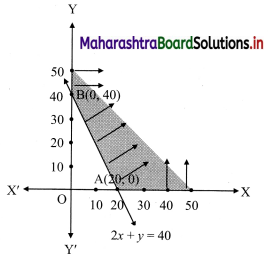
The Diet of the sick person must contain at least 4000 units of vitamin. Each unit of food F₁ contains 200 units of vitamin, whereas each unit of food F₂ contains 100 units of vitamins. Write an inequation to fulfill a sick person’s requirements and represent the solution set graphically.
Solution:
Let the diet of the sick person contain, x units of food F₁ and y units of food F₂.
Since each unit of food F₁ contains 200 units of vitamins.
∴ x units of food F₁ contain 200x units of vitamins.
Also, each unit of food F₂ contains 100 units of vitamins.
y units of food F₂ contain 100y units of vitamins.
Now, Diet for a sick person must contain at least 4000 units of vitamins.
∴ he must take food F₁ and F₂ in such away that total vitamins must be greater than or equal to 4000.
∴ required inequation is 200x + 100y ≥ 4000
i.e., 2x + y ≥ 40
Also x and y cannot be negative.
∴ x ≥ 0, y ≥ 0
Corresponding equation is 2x + y = 40
∴ \(\frac{2 x}{40}+\frac{y}{40}=\frac{40}{40}\)
∴ \(\frac{x}{20}+\frac{y}{40}=1\)
∴ intersection of line with X-axis is A(20, 0)
intersection of line with Y-axis is B(0, 40)
Origin test:
Substituting x = 0, y = 0 in inequation, we get
2(0) + (0) ≥ 40
∴ 0 ≥ 40 which is false
∴ all the points on the non origin side of the line and points on the line satisfy the inequation.
Also, x ≥ 0, y ≥ 0
∴ the solution set is as shown in the figure.